- 1Economic and Technology Research Institute of State Grid Shandong Electric Power Company, Jinan, China
- 2School of Electrical and Electronic Engineering, North China Electric Power University, Beijing, China
The large-scale access of distributed sources to the grid has brought great challenges to the safe and stable operation of the grid. At the same time, energy storage equipment is of great importance to effectively enhance the consumption of renewable energy and ensure the safe and stable operation of the grid. This paper proposes a method for optimal allocation of grid-side energy storage considering static security, which is based on stochastic power flow analysis under semi-invariant method. Firstly,according to the load, wind power and photovoltaic probability model, a system stochastic power flow model is constructed. Furthermore, the fault probability and fault severity indicators are established from two dimensions of branch power flow and node voltage. And combine the fault probability and severity indicators to establish a static security assessment indicators system. Then, a grid-side energy storage planning model is constructed from the perspective of energy storage operators. Finally, an improved genetic algorithm is used to solve the two-stage planning and operation problem proposed in this paper, and simulation analysis is conducted based on the IEEE-30 node system. The results show that the energy storage configuration considering static security constraints can effectively reduce the fault probability and the severity of fault overlimit. The simulation and case study verify that the proposed energy storage allocation method can effectively improve the static security of the system.
1. Introduction
With the goal of “Double-Carbon” by 2020, the country is fully developing renewable energy generation technology. The renewable energy output has the characteristics of weak controllability and strong randomness, and its large-scale access will definitely bring great challenges to the safe operation of the power grid (Bagheri et al., 2019). Energy storage technology has the advantages of balancing the load, maintaining the frequency and voltage stability of the grid, providing energy buffer for the grid, etc. The large-scale access of energy storage system is an inevitable trend for the future development of the grid (Dowling et al., 2020). Therefore, it is important to study the configuration of energy storage capacity considering static security to effectively enhance the consumption of renewable energy, ensure the safe and stable operation and reduce the investment cost of the grid (Albertus et al., 2020).
At present, domestic, and international research has focused on three aspects of energy storage equipment to improve the flexibility (Zhou et al., 2021; Zhang et al., 2022), operational stability (Mahmoud et al., 2022b), and security of power systems. Among them, the role of energy storage for power system security enhancement is discussed in three dimensions: topological vulnerability (Martinez-Rico et al., 2021), grid security power supply capacity (Li et al., 2022; Mahmoud et al., 2022a), and transient security (Wang et al., 2021), respectively. An integrated planning and operation method is proposed in (Martinez-Rico et al., 2021), which is for optimal allocation of energy storage based on the active network loss and voltage offset indicators. This effectively improves the structural strength of the grid topology and ensures grid voltage stability. In literature (Mahmoud et al., 2022a), based on Robust and optimized DVR controller, Harris Hawks optimization algorithm is used to enhance the voltage quality of low-voltage smart distribution. The literature (Li et al., 2022) proposes a new grid-connected wind power generation system based on an improved topology and controller, which considers both state-of-charge and energy storage configurations. And can effectively improve the overall efficiency of the power generation system and extend the lifespan of the energy storage batteries, improving the safe operation and power supply reliability of the grid system. In the context of distributed energy storage, a preventive control strategy is proposed in Wang et al. (2021). The strategy is for grid current overload and transient instability based on the barrier function and energy function. And achieve a guarantee of transient security using a unified power flow controller. Although the numerous utilities played by energy storage in power systems are considered in current research on energy storage configurations, the mechanism of interaction between system energy storage configurations and static security is rarely clarified, which ignoring the potential of energy storage configurations to enhance system static security.
The basic idea of traditional security assessment methods is to establish a set of expected accidents to check system security (Kundur et al., 1994), which is difficult to adapt to the security analysis of power grids after a high proportion of renewable energy is connected, so static security analysis considering uncertainty has received extensive attention from scholars in practical research and application. The static security assessment methods considering uncertainty can be divided into Monte Carlo simulation method (Song et al., 2003; Hajian et al., 2013; Zhang et al., 2015; Dashtdar et al., 2022) and analytical method (Su, 2010; Bu et al., 2012; Amraee and Ranjbar, 2013; Zhang et al., 2020). The Monte Carlo simulation method is used to obtain statistical characteristics of parameters by observing the model or process through sampling, and its computational effort is not affected by the size of the power system, which in turn is used in some complex power systems (Hajian et al., 2013). In Dashtdar et al. (2022), a combination of genetic algorithm and artificial bee colony algorithm is adopted to solve the optimization problem of power grid under demand-side management. The literature (Zhang et al., 2015) used a Monte Carlo method to extract the fault states of the system and establish static security assessment metrics to analyze the static security of the power system. However, the final value obtained by the Monte Carlo method is only an estimated value, and there is a certain contradiction between its calculation accuracy and calculation speed, while the analytical method based on probability theory can obtain the distribution of parameters through a smaller number of calculations, thus becoming a research hotspot in static security analysis research (Song et al., 2003). Among them, the analytical method includes network method, fault tree method, event tree method, and state space method. In the literature (Su, 2010), the security assessment is carried out by building an event tree to determine the optimal maintenance plan to mitigate the system security risk from an economic point of view. Besides, in the literature (Bu et al., 2012), the dynamic Bayesian network method is applied to assess the reliability of intelligent substation monitoring system. Since the uncertainty method considers the probability of occurrence of each operating state, the analytical method is difficult to be practically applied for large-scale power grids due to the complexity of the steps, so there are few methods to efficiently achieve the security assessment of power grids under uncertainty in the current research.
In view of the above shortcomings, the following two problems of system static security remain unsolved: (1) the potential of energy storage configuration in improving system static security is not fully considered; (2) Currently solving algorithms based on Monte Carlo simulation method and analytical method are difficult to realize efficient evaluation and solution of power grid security under uncertainty. In this paper, an optimal allocation method of grid-side energy storage is proposed, which examines the static security assessment of power system. Under the expected accident set, the static security analysis of the system is carried out based on the semi-invariant stochastic power flow method. This method applies energy storage configuration to improve the static security of power system reasonably, and has the characteristics of general probability distribution and time series. At the same time, considering the influence of uncertainty on the static security of the system, it can effectively improve the solution speed and reduce the system investment cost. The main contributions of this paper including the following:
1) A grid-side energy storage configuration method considering the static security of power system is developed, which is implemented through a planning and operation two-stage optimization framework constructed in this paper.
2) Combining the stochastic power flow with static safety assessment, the uncertainty of renewable energy and load are considered in the probability assessment process. In addition, the fault probability and fault severity indexes are built from the perspective of branch power flow and nodal voltage.
3) To decoupled the two-stage interactive problem, a heuristic genetic algorithm is applied, where an adaptive crossover and mutation probability is proposed to adjust the probability of crossover and mutation with chromosome fitness. Besides, the stochastic power flow is solved through the semi-invariant stochastic power flow method, which inserted into the heuristic genetic algorithm.
The remainder of this paper is structured as follows: The modeling of stochastic power flow and static safety assessment indexes are established in Section II. The configuration of energy storage model is presented in Section III. The heuristic genetic algorithm combined with the semi-invariant method is introduced in Section IV. The case studies and the conclusions are provided in Sections V and VI, respectively.
2. Static security assessment method based on stochastic currents
2.1. Stochastic power flow model
2.1.1. Load probability model
Load uncertainty is assumed to obey a normal distribution in most stochastic power flow studies, and the nodes are considered to be either mutually independent or linearly correlated in terms of injected power. In this paper, a stochastic model of the active and reactive power of the system load that conforms to a normal distribution is developed as follows (Yang et al., 2022):
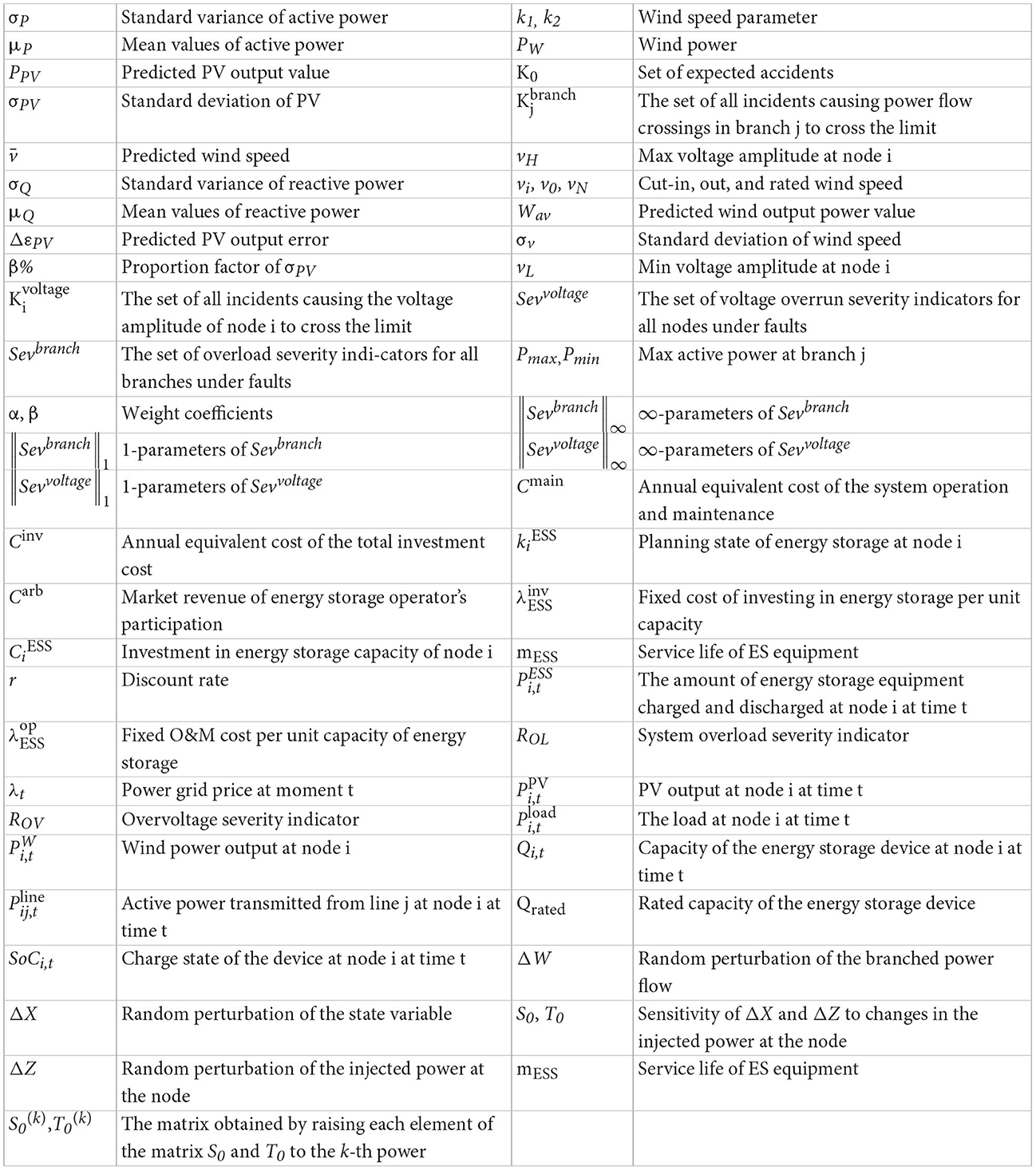
where σP, σQ are the standard variance of the active and reactive power of the random load, respectively; μP, μQ are the mean values of the active and reactive power of the random load, respectively.
2.1.2. Photovoltaic probability model
When considering the uncertainty of PV output, it can be described by superimposing the predicted PV output value PPV on the prediction error ΔεPV, i.e., PV output can be expressed as:
The standard deviation of the PV prediction error ΔεPV can be considered to follow a normal distribution with 0 as the mean and σPV as the standard deviation, and its probability density function can be expressed as Ren et al. (2014):
where σPV is proportional to the predicted output, i.e., σPV = PPV × β%, β% is the standard deviation σPV as a proportional factor of the predicted PV output. The analysis of the actual data shows that the probability distribution of the PV output error follows a normal distribution when the weather is quite sunny.
2.1.3. Wind power probability model
The wind speed prediction error can be considered as a normally distributed random variable with a mean of 0 and a standard deviation of σv. If the wind speed prediction is denoted by , the probability density function for the actual wind speed v = + Δv can be expressed as:
where the variance of the wind speed prediction deviation is generally taken as τ% of the predicted value, i.e., σv2 = × τ%.
The wind power output depends on the wind speed and the wind power output expression can be expressed as Yang et al. (2022):
where /(); k2 = PN/(); PN is the rated wind power; vi, v0, vN are the cut-in, cut-out and rated wind speed, respectively; PW is the wind power; l(v) indicates that the wind power is a function of the wind speed. The available wind power in a wind farm is a mixed random variable and is assumed to be Wav = nwPW, the predicted value of wind farm output power.
2.2. Static security assessment metrics under N−1 contemplated failure sets
2.2.1. Static security probability indicators
The set of expected accidents K0 can be represented as the full set of all fault sets, and the probability that power flow Pj of a branch j cross the limit in the event of an accident Kn event can be expressed as:
where Pmax is the maximum value of active power allowed to be transmitted by branch j, obtained from the thermal stability limit current, Pmin is the minimum value of active power allowed to be transmitted by branch j; Fpq(·) is the cumulative distribution function of active and reactive power of the branch power flow under fault Kn.
In the case of an accidental Kn event, the probability that the voltage viat node i cross the limit can be expressed as:
where vH is the maximum voltage amplitude allowed at node i, if exceeding the maximum voltage amplitude constraint will cause voltage collapse; vL is the minimum voltage amplitude allowed at node i, if less than the minimum voltage amplitude constraint will cause system low voltage instability; Fvθ(·) is the cumulative distribution function of node voltage amplitude and phase angle.
2.2.2. Power flow overload severity indicator
The branch power flow overload severity represents the power flow on each line as a percentage of the transmission capacity limit. And the severity indicator is defined as the degree of branch j power flow overload for all fault conditions. The power flow overload of branch j can be expressed as:
where is the set of all incidents causing power flow crossings in branch j.
Let the vector Sevbranch represent the set of overload severity indicators for all branches in the system under various faults, and define the system power flow current overload severity indicator ROL based on Sevbranch as:
where α and β are weight coefficients satisfying a sum of 1; and are the 1-parameters and ∞-parameters of the vector Sevbranch, respectively.
2.2.3. Voltage overrun severity indicator
The node voltage overvoltage severity represents the percentage of node voltage amplitude that deviates from the normal amplitude limit, defined as the degree of node i voltage overvoltage for all faults that may occur. The overlimit of node i can be expressed as:
where is the set of all incidents that cause the voltage amplitude of node i to cross the limit.
Let the vector Sevvoltage represent the set of node voltage overlimit severity indicators for all nodes in the system under various faults, and define the system node voltage overlimit severity indicator ROV based on Sevvoltage as:
where and are the 1-parameters and ∞-parameters of the vector Sevvoltage, respectively.
3. Grid-side energy storage configurations
3.1. Objective function
The energy storage operator plans the storage configuration capacity at each node on the grid side with the objective function of minimizing the total cost, where the total cost consists of three parts: total investment cost, operation and maintenance (O&M) cost, and the operator's arbitrage revenue. So, the objective function over the planning horizon is expressed as
where Cinv is the annual equivalent cost of the total investment cost; Cmain is the annual equivalent cost of the system operation and maintenance cost; Carb is the energy storage operator's participation in market arbitrage revenue.
In the formula, the annual equivalent investment cost can be expressed as:
where is the planning state of energy storage at node i, = 1 is represented to be put into construction, otherwise 0; is the investment energy storage capacity of node i; is the fixed cost of investing in energy storage per unit capacity; r is the discount rate; mESS is the service life of energy storage equipment; CN is the set of nodes to be selected for investment in the planning area.
Operation and maintenance cost refers to the annual cost of energy storage equipment in the O&M process, which includes equipment maintenance costs and corresponding labor costs. In this paper, various operation and maintenance costs are considered together as unit operation and maintenance cost , and the annual equivalent operation and maintenance cost can be expressed as:
where is the fixed operation and maintenance cost per unit capacity of energy storage.
Because when the operator charges the grid at low tariffs and discharges the grid at high tariffs to generate revenue, the arbitrage revenue of the energy storage operator can be expressed as follows:
where λt is the power grid price at moment t, and is the amount of energy storage equipment charged and discharged at node i at time t, where discharging is positive and charging is negative.
3.2. Constraints
3.2.1. Planning constraints
Limitations on the scale of investment in energy storage equipment, taking into account the limitations of construction space and investment costs:
where CESS_max, CESS_min are the upper and lower limits of the installed capacity of the node energy storage.
3.2.2. Operational constraints
3.2.2.1. System static security constraints
Based on the system static security assessment method proposed in 2.2, the grid company constrains the static security indicators during system operation to ensure that the system does not experience power flow and voltage's overlimit under the N-1 expected accident set.
where , , prmax are the maximum limits of the system power flow overload severity indicator, the system node voltage crossing severity indicator, and the probability of the system not meeting the static security constraints.
3.2.2.2. Nodal power balance constraints
where is the active power transmitted from line j at node i at time t; is the PV output at node i at time t; is the wind power output at node i at time t; is the load at node i at time t.
3.2.2.3. SOC of energy storage equipment constraints
where PESS_max is the charging and discharging capacity upper limit of the energy storage device, considering the safe operation of the energy storage device, its charging and discharging capacity cannot exceed PESS_max. Qi, t is the capacity of the energy storage device at node i at time t, and Qrated is the rated capacity of the energy storage device. SoCi, t is the charge state of the device at node i at time t. SoCmax, SoCmin are the upper and lower limits of the charge state of the energy storage device. η0 is the charging and discharging efficiency of the energy storage device.
4. Genetic algorithm solution for energy storage configuration under semi-invariant method
4.1. Stochastic power flow model based on semi-invariant method
Traditional stochastic power flow calculations are linearized at the base run of the power flow. And the probability density function of the state variables and the branch power flow is obtained by a convolution operation as usual. The semi-invariant method transforms the convolution operation of the random variables into an algebraic operation of semi-invariance, which greatly simplifies the calculation.
Assuming that the random perturbations of the injected power at each node are independent of each other, linearizing the AC power flow current equation at the base run yields (Bin et al., 2022):
where ΔX is the random perturbation of the state variable, ΔW is the random perturbation of the branched power flow, ΔZ is the random perturbation of the injected power at the node; S0, T0 are the sensitivity of the state variable and the branched power flow to changes in the injected power at the node, respectively.
According to the additivity of semi-invariance, the k-th order semi-invariance of the random perturbation ΔW of the nodal injected power is equal to the sum of the random perturbation ΔWPV of the PV output and the random perturbation ΔWW of the wind power output. The order semi-invariance of the random perturbation ΔWl of the load is as follows:
On the basis of the k-th order semi-invariance of order ΔW, the semi-invariance of order ΔX and ΔZ can be calculated as follows.
Where and represents the matrix obtained by raising each element of the matrix S0 and T0 to the k-th power.
The coefficient Cv of the Gram-Charlier series can be derived from the central distance by finding the corresponding central distance through the semi-invariance of ΔX and ΔZ. The distribution function of the random variable is expressed as an expansion of the Gram-Charlier series of the following form:
where F(x) is the cumulative distribution function of the random variable: f(x) is the probability density function of the random variable; Φ(x) and φ(x) are the cumulative and probability density functions of the standard normal distribution, respectively, which can be derived from Hermite polynomials.
4.2. Genetic algorithm solving process for energy storage configuration
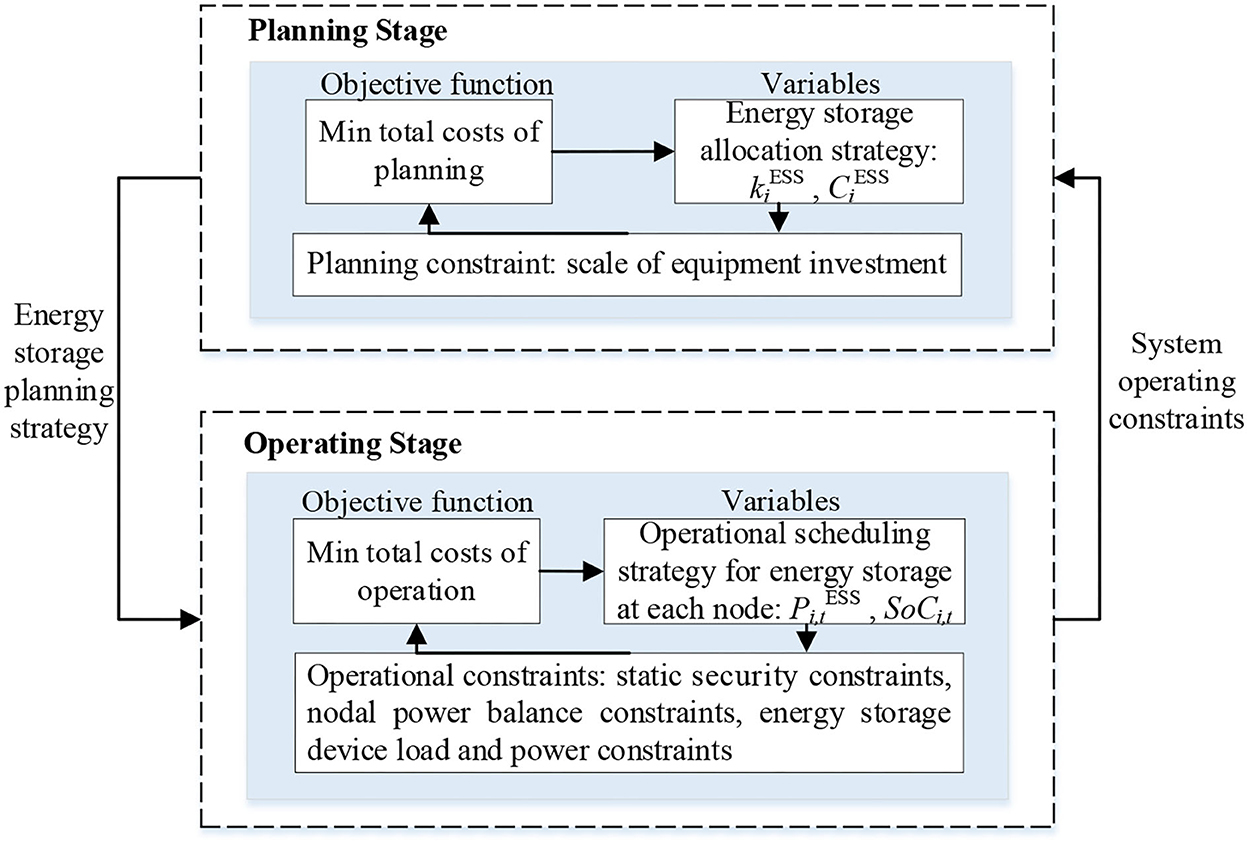
In this paper, a two-stage energy storage allocation optimization model for planning and operation is constructed, in which the planning-side energy storage capacity allocation strategy and the operation-side energy storage operation scheduling strategy interact with each other, and if the system in the operation stage does not satisfy the static security constraints under the expected accident set, the energy storage allocation strategy needs to be readjusted in the planning stage. Among them, the overall framework diagram of this paper is shown in Figure 1.
Genetic algorithms are commonly used to solve two-level mixed-integer programming problems. In view of the scalability of the solution, the traditional enumeration method is not suitable for solving large-scale problems, and the process is slow and difficult. Meanwhile, analytical algorithms such as Benders' algorithm are often used to deal with complex mixed-integer linear programming problems, which are difficult to apply to the non-linear programming problems in this paper. In contrast, a heuristic genetic algorithm is used to decouple the two phases of the planning operation, but given that traditional genetic algorithms tend to fall into local optima and converge slowly, this paper optimizes the strategies by means of improving crossover and variational operations, and ultimately selects the optimal solution.
The heuristic genetic algorithm consists of three basic elements: encoding, chromosome, and fitness function. In the planning problem constructed in this paper (Liu et al., 2010; Chen et al., 2022), the encoding process is the mapping of the set of energy storage allocation strategies into the genetic space in binary form, and in the genetic space, the chromosome is a description of the set of all planning solutions. And the fitness function is the objective function of the operator to optimize the energy storage allocation (Rudnick et al., 2001). Based on the basic elements, the genetic algorithm consists of three computational processes: selection, crossover and variation. In addition, chromosomes with high fitness in the selection process have a higher probability of appearing in the subsequent crossover mutation process, and new chromosomes are obtained by adaptive crossover and mutation operations introduced as follows.
Adaptive crossover and mutation approach can adjust the probability of crossover and mutation with chromosome fitness, with smaller crossover and mutation probabilities obtained when individual chromosome fitness is higher than population fitness, and larger probabilities obtained when individual chromosome fitness is lower than population fitness. The smaller mutation probability allows good individuals to be retained, while the larger mutation probability accelerates mutation to obtain new chromosomes. This improved scheme can effectively prevent the population from forming local convergence and falling into a local optimum during initial evolution, improving the performance of the genetic algorithm for optimal solution.
According to the Algorithm 1 mentioned above, the basic steps for solving this paper are as follows.
(1) Setting the initial strategy of the grid-side planning strategy and forming the initial parent chromosome.
(2) Solving the optimal operation strategy of the system based on the energy storage configuration strategy, using the semi-invariant random power flow method to obtain the random distribution of node voltages and branch currents, obtaining the system static security index values, checking whether the system static security constraint is satisfied. If not, proceeding directly to the next step, and if the constraint is satisfied, proceeding to Step 4.
(3) Obtaining the offspring chromosome through a two-point crossover and mutation operation, and get a new parent chromosome by comparing the value of fitness function between offspring chromosome and the parent chromosome, and furthermore returning to Step 2.
(4) Select parent chromosome. And if the current chromosome has a higher fitness than the optimal chromosome, the current chromosome becomes the optimal, if it is not the optimal chromosome, it is eliminated until the number of iterations reaches the upper limit, the optimal strategy set is output in the end.
5. Case study
5.1. Case setup
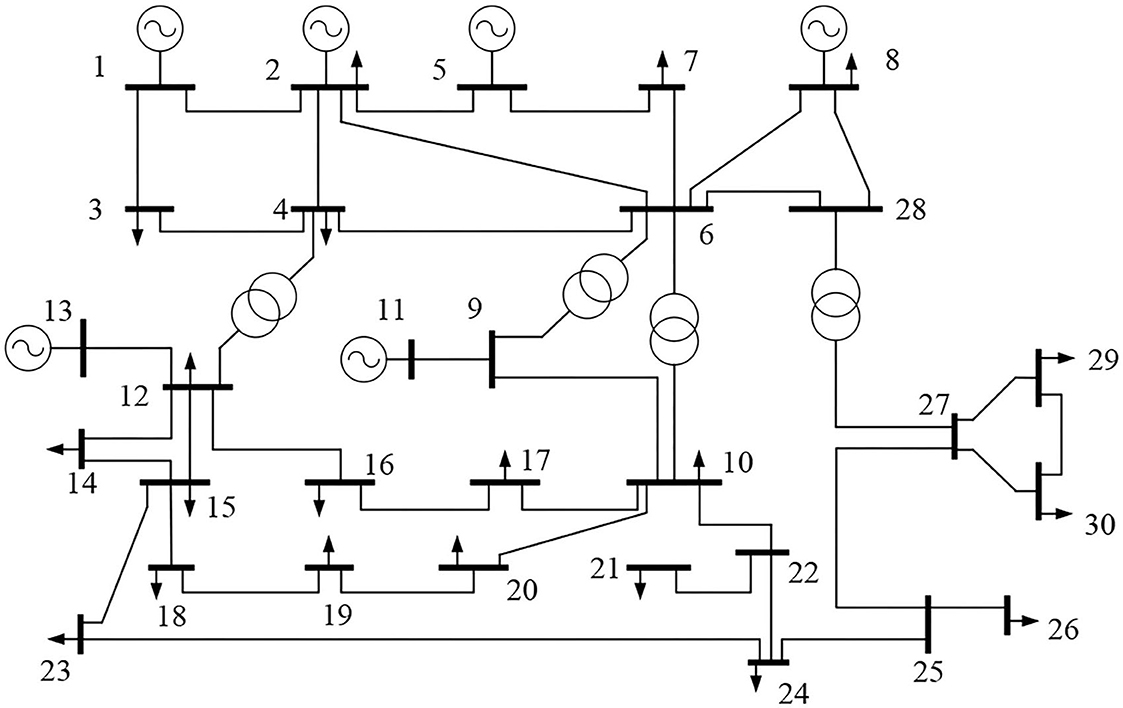
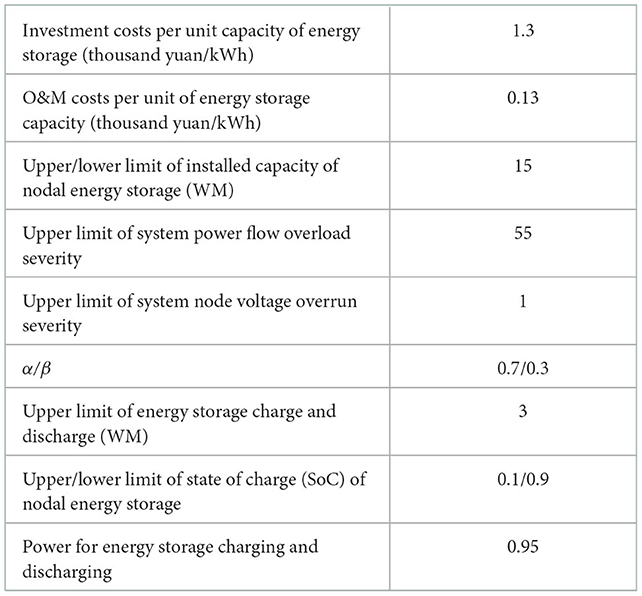
In this paper, simulation tests are conducted based on the IEEE-30 node system, as shown in Figure 2. There are six thermal power units in the system, and the maximum active output is distributed between 3 and 8MW. Renewable energy units with a capacity of 3MW are connected at nodes 22 and 27, and priority is given to the consumption of renewable energy units when dispatching. In this paper, it is assumed that the system load, PV output and wind speed meet normal distribution, where the standard deviation of load and wind speed is 20% of the mean value, and the standard deviation of PV output is 20% of its rated power. The expected fault set includes 6 units shutdown faults and 41 line three-phase short-circuit faults, a total of 47 fault types, which are tested for N-1 faults. The time-sharing tariff settings are shown in Figure A1 in Supplementary material, and the relevant parameters are set as shown in Table 1. See Table A1 in the Supplementary material for limits of each branch power flow constraint, and the upper and lower limits of each node voltage are 0.96 ~ 1.04 p.u.
In order to verify the rationality of this paper, two comparative cases are set up for analysis as follows.
Case 1: The static security constraint of system operation is considered in the process of energy storage configuration.
Case 2: The static security constraint of system operation is not considered in the process of energy storage configuration.
5.2. Optimized results
5.2.1. Energy storage configuration strategy
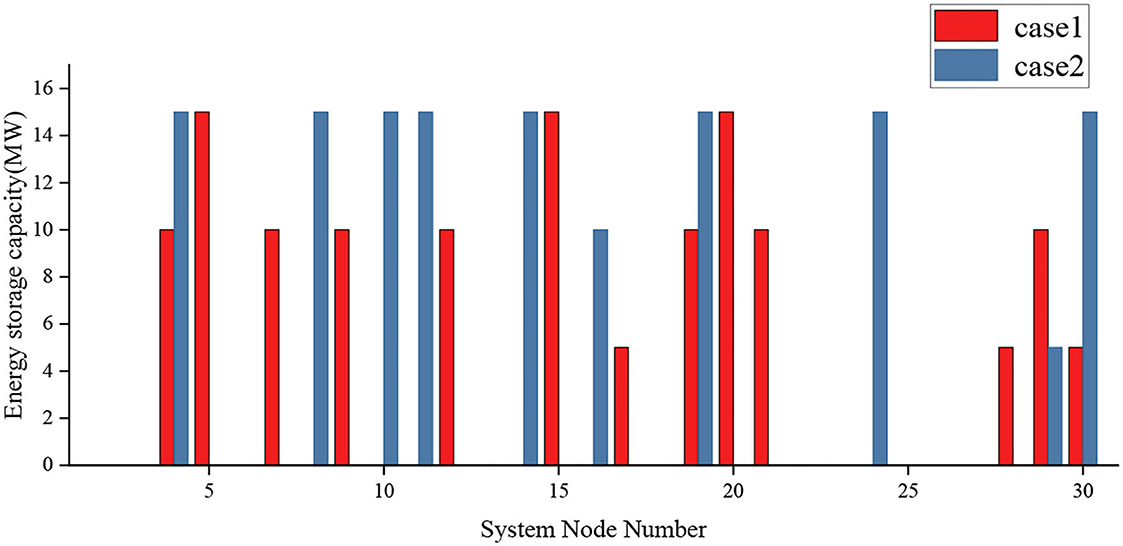
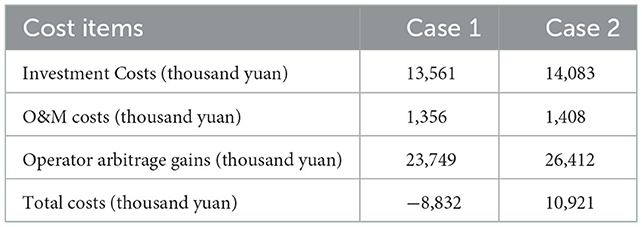
The results are shown in Figure 3, where a total of 130 MW of energy storage capacity is allocated in Case 1 and 135 MW in Case 2, compared to a total of 5 MW in Case 1. The cost comparison between Case 1 and 2 for the operator is shown in Table 2, where the investment cost of Case 1 is 3.71% lower than that of Case 2, but the revenue of the operator is also 2.663 million yuan lower. This results in an overall reduction of 19.2% in the operator's total revenue under Case 2 compared to Case 1, taking into account the investment operation and maintenance costs and revenue.
5.2.2. System static security indicators
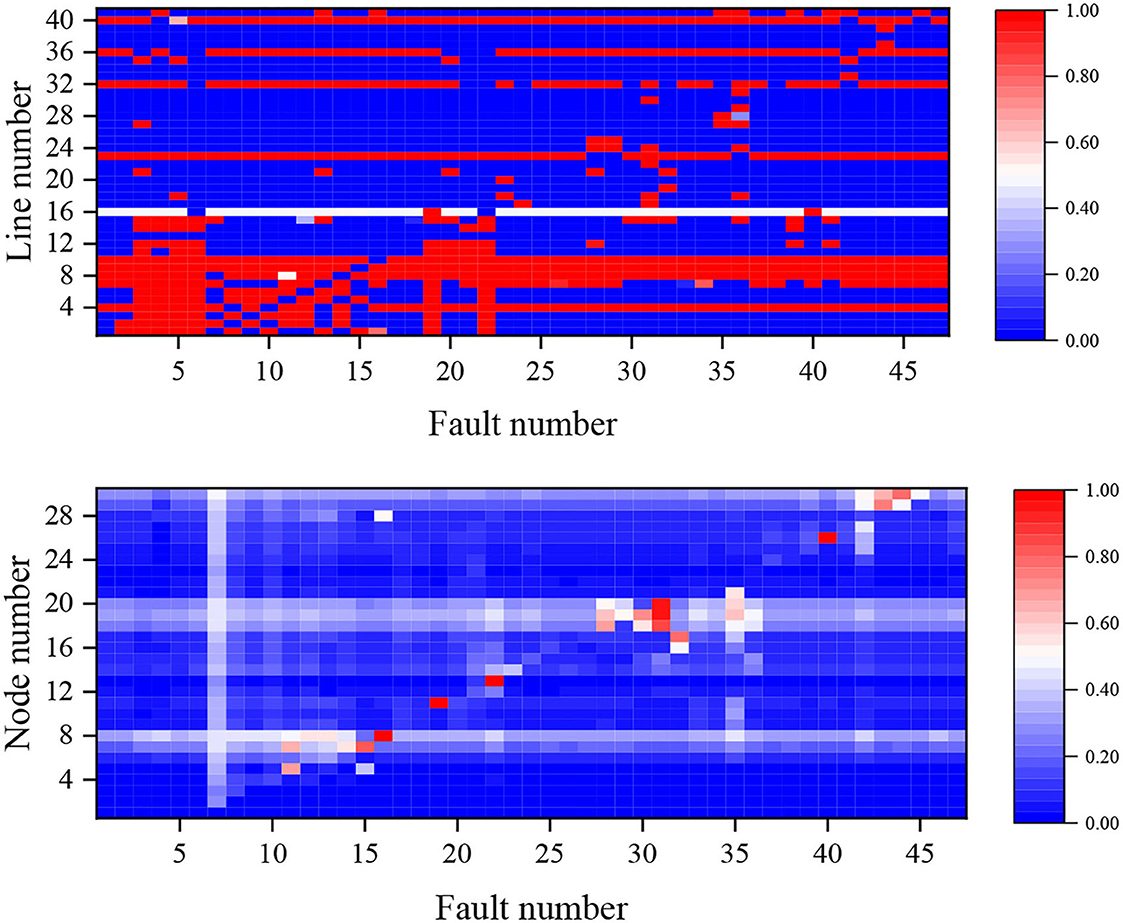
The power flow current overload probability of each branch and the voltage overvoltage probability of each node under an N−1 fault for Case 1 are shown in Figure 4. The branches with the highest probability of power flow overlimit under all faults are branches 9 and 10, both of which have a 97.87% probability of power flow overlimit. At the same time node 19 has the highest probability of 38.66% of voltage overlimit under all faults due to the high load on its connected branches, while node 3 has the lowest probability of 1.12%.
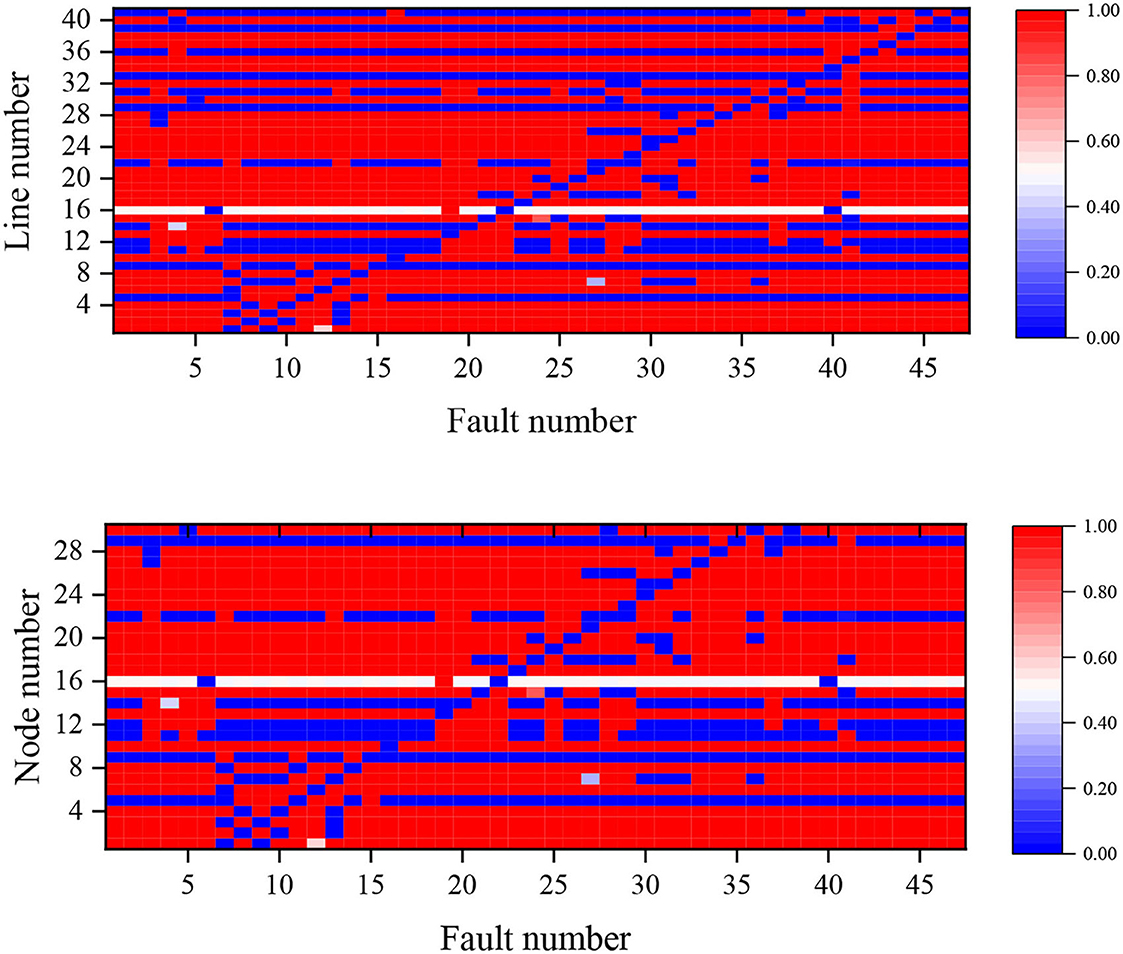
The power flow current crossing probability of each branch and the voltage crossing probability of each node under an N−1 fault for Case 2 are shown in Figure 5. For all fault conditions, branches 10, 12, 15, and 34 have the highest power flow overrun probability of 97.87%. Node 26 also has a maximum probability of 48.49% for all fault conditions due to the large load connected to it, in contrast to Node 5 which has a minimum probability of 1.29%.
Further considering the overall probability of failure for Case 1 and 2, analysis of the data shows that the average value of the probability of power flow overload before and after the addition of the static security constraint is reduced by 9.75%, and the average value of the probability of node voltage overvoltage is reduced by 1.61%. It can be concluded that the system overlimit probability is reduced after considering the static security constraint, and the expected static security enhancement effect is achieved.
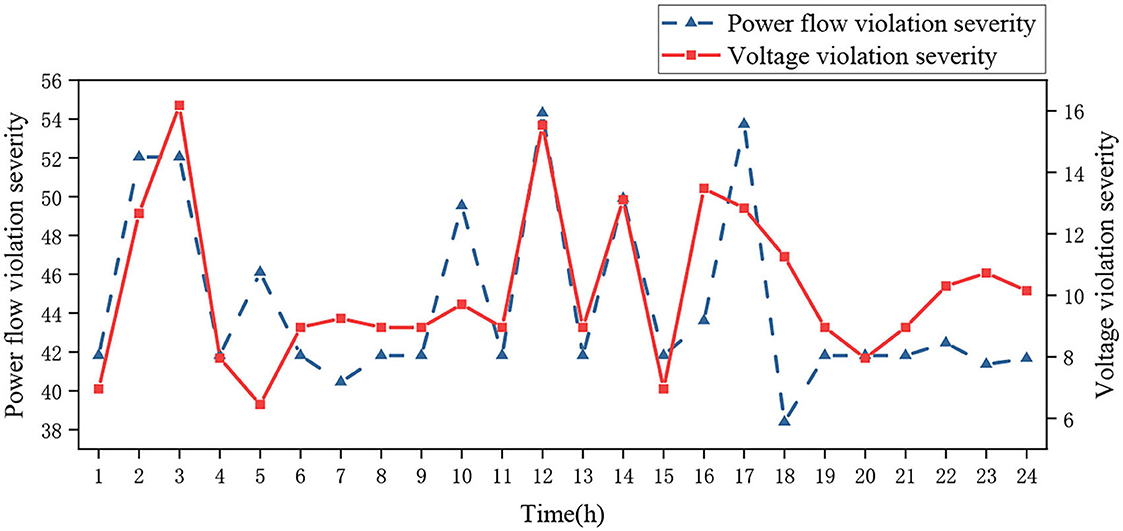
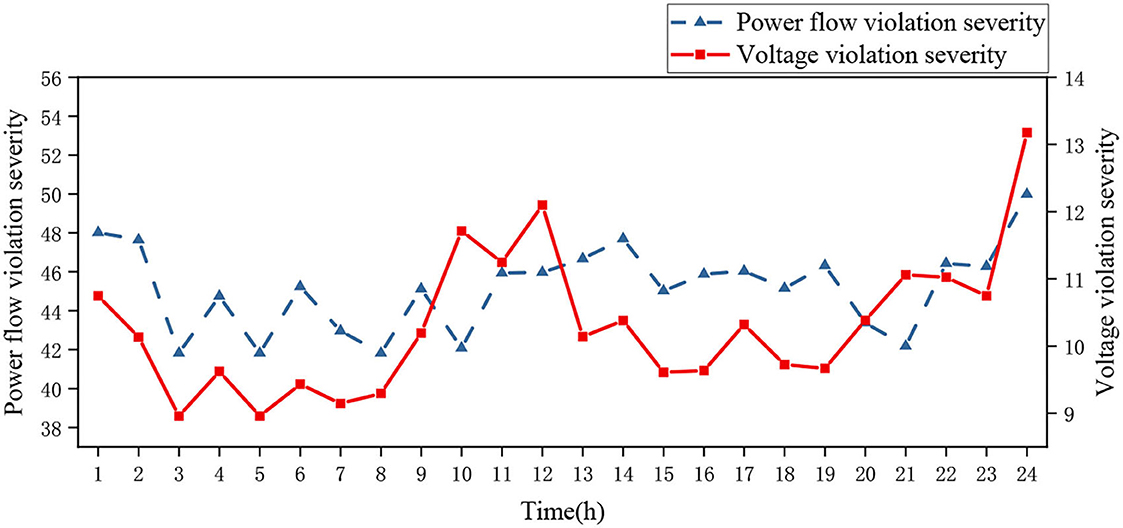
Figures 6, 7 show the severity of branch currents and node voltage overlimit under N−1 faults for Case 1 and 2 energy storage configuration strategies. The average value of the branch power flow current overload severity for Case 1 is 44.70 and the average value of the node voltage overlimit severity is 10.17 in 24 h. At 12 h, the power flow and voltage overlimit severity indicators both reach the maximum value of 54.30 and 15.53 due to excessive load access. At 18 h, the power flow overload severity reaches the minimum of 38.39, and at 5 h, the voltage overlimit severity reaches the minimum of 6.45.
In Case 2, the average value of branch power flow current overload severity is 45.17 and the average value of nodal voltage overlimit severity is 10.31 in 24 h. The maximum values of system power flow current and voltage overrun severity are 49.99 and 13.17 at 24 h due to each branch load access, while the minimum values of power flow current and voltage overlimit severity are 41.82 and 8.96 at 3 and 5 h.
In comparison with Figures 6, 7, the system severity indicators of Case 1 and 2 show that the average values of the branch power flow current severity and node voltage severity of Case 1 are reduced by 18.67 and 3.26, respectively, compared with those of Case 2. So, in the future, it is necessary to strengthen the management of the power flow currents of branch 8, 9, and 10, and the voltages of node 8, 19, 20, and 30. In conclusion, by comparing the probability of failure and current and voltage overrun indicators of Case 1 and 2, it's obvious that Case 1 with static security constraints has better performance. It can effectively reduce the probability of failure and severity of power flow current and voltage violation.
5.2.3. Sensitivity analysis
To further verify the effectiveness of the planning method proposed in this paper when the proportion of renewable energy sources connected to the grid increases. The static security indicators of the energy storage allocation strategies in Case 1 and 2 are analyzed on the basis of Case 1 and 2 with 4 and 6 renewable energy units connected.
Under the four renewable energy units, the average values of power flow current and voltage overlimit failure probability under the static security configuration are 32.02 and 15.04%. Compared with 56.71 and 27.99% without considering static safety constraints, the fault probability decreased by 43.54 and 46.27%. Although the improvement in the severity of overruns is not significant, the reduction in the probability of overruns of branch currents and nodes by nearly 50% is still an effective improvement in static security.
Similarly, with 6 renewable energy units connected, the probability of branch power flow current and node voltage overlimit probability are reduced by 51.55 and 45.17% respectively. And the overlimit severity indicators of power flow current and voltage are reduced by 0.3828 and 0.24849, respectively. There is no doubt that with more renewable energy units connected in the grid, storage configuration considering static security can effectively reduce failure probability and maintain the system at a good level than Case 2.
6. Conclusion
In this paper, we propose an optimal grid-side energy storage allocation method that takes into account the static security assessment of the power system, and verify that the proposed energy storage allocation method can effectively improve the static security of the system in a power system with a high percentage of renewable energy penetration by analyzing the IEEE-30 node system. The average value of power flow overlimit probability before and after adding static security constraints is reduced by 9.75%, and the average value of node voltage overlimit probability is reduced by 1.61% at the same time, the system power flow overload severity is reduced by 1.05% and node voltage overlimit severity is reduced by 1.38%. When the proportion of renewable energy is further increased, that is, the number of renewable energy units is increased to 4 or even 6. By comparing the mean fault probability, when 4 units are connected in the energy storage configuration with constraints considered, the failure probability of the system power flow and voltage overlimit the violation is reduced by 24.69 and 12.95% compared with the case without considering constraints. The failure probability of 6 units is also reduced by 29.23 and 13.49%. In addition, the overlimit severity indicator also decreases to a certain extent, which indicates that the energy storage configuration considering the static security constraints of the system proposed in this paper is useful. It can effectively guarantee the safe and stable operation of the power system through the coordinated energy use of the energy storage station, relieve the pressure of the higher branch power flow and node voltage at the same time.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was sponsored by the Technology Project (Research on key technologies of power system safety assessment and margin improvement based on renewable energy) of State Grid Shandong Electric Power Company Economic and Technological Research Institute with Grant No. 520625210007.
Conflict of interest
XT, LZ, XM, and QB were employed by Economic and Technology Research Institute of State Grid Shandong Electric Power Company.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsgr.2022.1110871/full#supplementary-material
References
Albertus, P., Manser, J. S., Litzelman, S. (2020). Long-duration electricity storage applications, economics, and technologies. Joule 4, 21–32. doi: 10.1016/j.joule.2019.11.009
Amraee, T., Ranjbar, S. (2013). Transient instability prediction using decision tree technique. IEEE Trans. Power Syst. 28, 3028–3037. doi: 10.1109/TPWRS.2013.2238684
Bagheri, A., Zhao, C., Qiu, F., Wang, J. (2019). Resilient transmission hardening planning in a high renewable penetration era. IEEE Trans. Power Syst. 34, 873–882. doi: 10.1109/TPWRS.2018.2872893
Bin, J., Liao, K., Li, B. (2022). High dimensional model and risk assessment of interlocking faults with source load randomness,” in Proceedings of the CSU-ESPA, 1–12. doi: 10.19635/j.cnki.csu-epsa.001118
Bu, S. Q., Du, W., Wang, H. F., Chen, Z., Xiao, L. Y., Li, H. F. (2012). Probabilistic analysis of small-signal stability of large-scale power systems as affected by penetration of wind generation. IEEE Trans. Power Syst. 27, 762–770. doi: 10.1109/TPWRS.2011.2170183
Chen, L., Li, Y., Chen, Y., Liu, N., Li, C., Zhang, H. (2022). Emergency resources scheduling in distribution system: from cyber-physical-social system perspective. Electr. Power Syst. Res. 210, 108114. doi: 10.1016/j.epsr.2022.108114
Dashtdar, M., Flah, A., Hosseinimoghadam, S. M. S., Kotb, H., Jasi'nska, E., Gono, R., et al. (2022). Optimal operation of microgrids with demand-side management based on a combination of genetic algorithm and artificial bee colony. Sustainability 14, 6759. doi: 10.3390/su14116759
Dowling, J. A., Rinaldi, K. Z., Ruggles, T. H., Davis, S. J., Yuan, M., Tong, F., et al. (2020). Role of long-duration energy storage in variable renewable electricity systems. Joule 4, 1907–1928. doi: 10.1016/j.joule.2020.07.007
Hajian, M., Rosehart, W. D., Zareipour, H. (2013). Probabilistic power flow by Monte Carlo simulation with latin supercube sampling. IEEE Trans. Power Syst. 28, 1550–1559. doi: 10.1109/TPWRS.2012.2214447
Kundur, P., Balu, N. J., Lauby, M. G. (1994). Power System Stability and Control, Vol. 7. New York, NY: McGraw-Hill.
Li, C., Xi, Y., Lu, Y., Liu, N., Chen, L., Ju, L., et al. (2022). Resilient outage recovery of a distribution system: co-optimizing mobile power sources with network structure. Protect. Control Mod. Power Syst. 7, 459–471. doi: 10.1186/s41601-022-00256-9
Liu, C., Shahidehpour, M., Wu, L. (2010). Extended benders decomposition for two-stage SCUC. IEEE Trans. Power Syst. 25, 1192–1194. doi: 10.1109/TPWRS.2009.2038019
Mahmoud, M. M., Esmail, Y. M., Atia, B. S., Kamel, O. M., AboRas, K. M., Bajaj, M., et al. (2022a). Voltage quality enhancement of low-voltage smart distribution system using robust and optimized dvr controllers: application of the harris hawks algorithm. Int. Trans. Elec. Energy Syst. 2022, 4242996. doi: 10.1155/2022/4242996
Mahmoud, M. M., Ratib, M. K., Aly, M. M., Abdel–Rahim, A. M. M. (2022b). Application of whale optimization technique for evaluating the performance of wind-driven PMSG under harsh operating events. Proc. Integr. Optim. Sustain. 6, 447–470. doi: 10.1007/s41660-022-00224-8
Martinez-Rico, J., Zulueta, E., de Argandoña, I. R., Fernandez-Gamiz, U., Armendia, M. (2021). Multi-objective optimization of production scheduling using particle swarm optimization algorithm for hybrid renewable power plants with battery energy storage system. J. Mod. Power Syst. Clean Energy 9, 285–294. doi: 10.35833/MPCE.2019.000021
Ren, Z., Yan, W., Zhao, X., Li, W., Yu, J. (2014). Chronological probability model of photovoltaic generation. IEEE Trans. Power Syst. 29, 1077–1088. doi: 10.1109/TPWRS.2013.2293173
Rudnick, H., Palma, R., da Silva, E. L., Gil, H. A., Areiza, J. M. (2001). Transmission network expansion planning under an improved genetic algorithm [discussion and closure]. IEEE Trans. Power Syst. 16, 930–931. doi: 10.1109/59.962451
Song, Y., Guo, Y., Lu, Z. (2003). An improved probabilistic stability assessment method and its application. Power Syst. Technol. 3, 23–27. doi: 10.1007/978-1-4471-3735-1
Su, C. L. (2010). Stochastic evaluation of voltages in distribution networks with distributed generation using detailed distribution operation models. IEEE Trans. Power Syst. 25, 786–795. doi: 10.1109/TPWRS.2009.2034968
Wang, P., Song, J., Liang, F., Shi, F., Kong, X., Xie, G., et al. (2021). Equivalent model of multi-type distributed generators under faults with fast-iterative calculation method based on improved PSO algorithm. Protect. Control Mod. Power Syst. 6, 371–382. doi: 10.1186/s41601-021-00207-w
Yang, R., Liu, J., Zeng, P., Yang, G., Sun, Q., Li, Y. (2022). “Regional integrated energy system planning considering the dependence of multiple heterogeneous sources and charges,” in Automation of Electric Power Systems, 31–39.
Zhang, D., Hu, Y., Gao, Y. (2022). Flexibility improvement of CHP unit for wind power accommodation. J. Mod. Power Syst. Clean Energy. 10, 731–742. doi: 10.35833/MPCE.2020.000630
Zhang, Z., Li, Y., He, L., Yao, F. (2015). “Application of Monte Carlo methods in static security risk assessment of power systems,” in Electrical Measurement and Instrumentation, 106–111.
Zhang, Z., Yao, R., Huang, S., Chen, Y., Mei, S., Sun, K. (2020). An online search method for representative risky fault chains based on reinforcement learning and knowledge transfer. IEEE Trans. Power Syst. 35, 1856–1867. doi: 10.1109/TPWRS.2019.2951171
Zhou, B., Fang, J., Ai, X., Yao, W., Wen, J. (2021). Flexibility-enhanced continuous-time scheduling of power system under wind uncertainties. IEEE Trans. Sustain. Energy 12, 2306–2320. doi: 10.1109/TSTE.2021.3089696
Nomenclature
Keywords: grid-side energy storage configuration, static security of power system, stochastic, semi-invariant stochastic power flow method, Benders' algorithm
Citation: Tian X, Zhao L, Tong C, Meng X, Bo Q, Chen Y and Liu N (2023) Optimal configuration of grid-side energy storage considering static security of power system. Front. Smart Grids 1:1110871. doi: 10.3389/frsgr.2022.1110871
Received: 29 November 2022; Accepted: 28 December 2022;
Published: 12 January 2023.
Edited by:
Mohit Bajaj, Graphic Era University, IndiaReviewed by:
Hossam Kotb, Alexandria University, EgyptSrikanth Goud B, Anurag Group of Institutions, India
Mohamed Metwally Mahmoud, Aswan University, Egypt
Copyright © 2023 Tian, Zhao, Tong, Meng, Bo, Chen and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xin Tian,  YWF0aWFueGluQDE2My5jb20=
YWF0aWFueGluQDE2My5jb20=
 Xin Tian1*
Xin Tian1* Chenjie Tong
Chenjie Tong Yubing Chen
Yubing Chen