Raffaele Mezzenga- 1Department of Health Sciences and Technology, ETH Zurich, Zurich, Switzerland
- 2Department of Materials, ETH Zurich, Zurich, Switzerland
Nanoconfined water differs significantly from bulk water and challenges our common understanding of liquid water in both its most fundamental features, as well as in many applied aspects which stem out from its peculiar behavior. This brief perspective pinpoints both challenges associated with the study of water under soft nanoconfinement as well as some opportunities which arise from it, and which would not be at reach with standard bulk water. A special focus is given to the strong nanoconfinement (∼1–10 nm) offered by inverse lipidic mesophases, viewed as a natural soft nanoconfinement environment for water.
Introduction
From the cellular environment, to pharmaceutical applications, physics, chemistry and nanotechnology, interest in water under soft nanoconfinement has been constantly growing, mostly due to the fact that many real biological examples feature water in conditions which are far from bulk-like, and thus, do not meet our common stereotypes of water. However, there are precise reasons why nanoconfined water may offer a platform to study water under environmental conditions not possible or applicable to bulk water itself. The most notorious one is the capability of nanoconfined water to enter the so called no man land region of the phase diagram without the formation of ice, i.e., the range of temperature between TH = −41°C, at which homogeneous nucleation of ice occurs and roughly TX ≈ −113°C, the so-called crystallization-onset temperature (Smart, 2017). This is a remarkable result in a temperature range within which even homogeneous nucleation of ice from bulk water cannot be avoided, neither upon cooling (ice formation from liquid water below TH) nor upon heating (ice formation from supercooled glassy water above TX). The only other known way to avoid ice formation in the no-man land region is to escape thermodynamics via cooling rates of the order of 105–106 K/s, so fast that only a handful of methods exist to realize this experimentally (Debenedetti and Stanley, 2003; Cerveny et al., 2016). But nanoconfined water challenges our understanding of water in many other aspects, touching on relaxation dynamics, hydrogen bonding coordination, structure, solubility, reactivity, and many more. This short perspective aims, within the allowed limits of space, at briefly highlighting the challenges and opportunities arising from water under soft nanoconfinement, making a parallel among these two extremes and taking bulk water as benchmark reference. Given the limited allowed length, this perspective is by no means meant to comprehensively discuss the peculiarities of nanoconfined water, for which extensive literature already exists (Ortiz-Young et al., 2013; Huber, 2015; Knight et al., 2019). Instead, the main objective is to point at opportunities which are yet to be fully appreciated within the wide body of literature, showcasing some less-known aspects of nanoconfined water.
Types of soft nanoconfinement
Possibly the most frequent soft nanoconfinement system studied is that formed by reverse micelles (RM) in which water is confined within a dispersed continuous hydrophobic phase, typically an oil, by the help of a surfactant. In this form of nanoconfinement water is most often organized within spherical micelles of a size typically ranging between 1 and 15 nm (Moilanen et al., 2009; Das et al., 2013; Yuan et al., 2017), although worm like micelles are also possible using typically ionic surfactants (Martiel et al., 2014). At larger hydration levels, where bulk water dominates, the range of nanoconfined water increases to 5–100 nm, and the RM are more frequently referred as microemulsions (Moulik and Paul, 1998). A second form of soft nanoconfinement is the one offered by inverse lipidic mesophases in which water is confined within 0D, 1D, 2D, and 3D symmetries depending on the lipid used, the amount of water and the temperature considered. A graphic summary of the main symmetries involved in lipidic mesophases is given in Figure 1A. Typical confinement in these systems forces water within domains ranging between 1 nm and 50 nm, but most typically within the 3–5 nm range (Mezzenga et al., 2019; Aleandri and Mezzenga, 2020). A third way to achieve soft nanoconfinement for water is via high concentration of solutes of molecular (e.g., glycerol) or macromolecular (polysaccharides, proteins, DNA, etc.) nature. This strategy may change the properties of water to the point that freezing can be completely suppressed or water nearly entirely immobilized at the solute/water interface. This specific form of soft nanoconfinement will not be considered in this short perspective mostly for reasons of space, but also because it differs substantially form the first two in such that a straightforward length-scale for the nanoconfinement cannot be easily defined. Interested readers are referred to more extensive literature dealing with this topic (Hatakeyama et al., 2010; Yan et al., 2018; Das Mahanta et al., 2023).
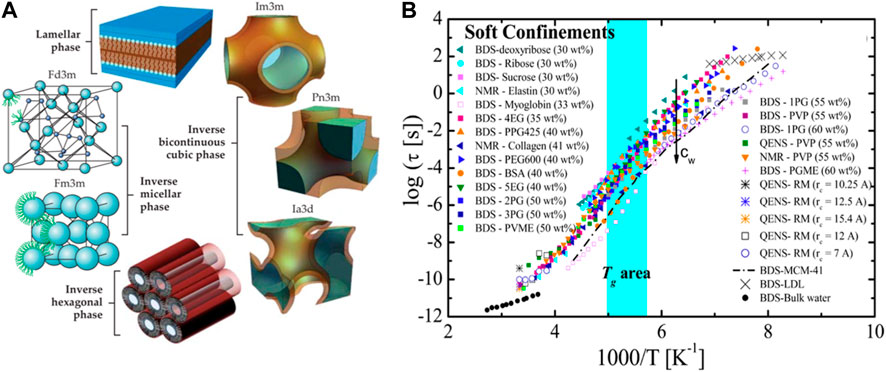
FIGURE 1. (A) A summary of main symmetries involved in lipid mesophases soft nanoconfinement. Reproduced with permission from Aleandri and Mezzenga (2020), AIP copyrights. (B) Relaxation time of water vs. inverse of temperature for most known soft nanoconfinement systems known. Reproduced with permission from Cerveny et al. (2016), ACS copyrights.
Challenges
Depression of water freezing point
Certainly the most well understood feature of nanoconfined water is the depression of the freezing point, which is rationalized via the well-established Gibbs–Thompson equation, according to which the temperature depression (Tm,B- Tm,N), where Tm,B and Tm,N are the freezing temperature of bulk and nanoconfined water, respectively, scales with the diameter d of the confining pore as (Tm,B- Tm,N) ∼ 1/d. The Gibbs–Thompson equation explains well the depression of the freezing point of water under medium and strong nanoconfinement, typically down to 4 nm (Corti et al., 2021), but as the equation diverges only for d→0, the complete suppression of freezing observed in several soft nanoconfined systems is not correctly explained. This has led to an empirical modification of the equation into Tm,B- Tm,N ∼ 1/(d-t) where t is the thickness of the un-freezable liquid bound to the pore wall. This allows for the possibility of full suppression of crystallization at a critical, yet finite size of t (Corti et al., 2021). For comparison water in (hard) confined silica hexagonal mesopores (MCM-41) of less than 4 nm, does not freeze at any temperature (Yoshida et al., 2008). The reason for such a behavior is that ice needs to overcome a critical nucleus size in order to growth, as in any systems undergoing nucleation and growth. Many systems have been shown to depress or suppress crystallization of ice due to soft nanoconfinement, although the level of temperature depression depends on the various system.
Glass transition
While the effects of nanoconfinement are relatively well understood in first order thermodynamic transitions of water (freezing/melting), the situation with second (or higher order) transitions is far from being univocally established. Glass transition (Tg) of water under nanoconfinement is a clear example. The exact location of the glass transition temperature of bulk water is already debated and depending on how it is measured, different values have been obtained. It is generally agreed, however, that it locates between 136 K and 165 K (Johari et al., 1987; Velikov et al., 2001; Debenedetti and Stanley, 2003), although some recent reports even suggest a Tg of bulk water as high as (or even higher than) 190 K (Cerveny et al., 2016). The location of glass transition of water under confinement is obviously more uncertain. Basic considerations would suggest the Tg of confined water to be depressed over the corresponding Tg of the bulk water: for example, it is well established that nanoconfinement disrupt the h-bonding network and therefore speeds up relaxation of water: based on this argument alone one would expect that at the same cryogenic temperature nanoconfinement causes increased mobility and thus lower Tg of water (Cerveny et al., 2016). Similar conclusions can be reached by invoking the concept of water cluster, as originally introduced by Frank and Wen (1957), which is perturbed by neighboring molecules (Némethy and Scheeaga, 1962), or as in the present case, whose size is limited by the nanoconfinement, promoting liquid-like behavior over more viscous/glassy behavior, i.e., a depression on glass transition. A slightly more elaborated concept supporting the same idea of Tg depression with confinement is the idea proposed by Adam and Gibbs (1965), predicting cooperative re-arranging regions (CRR), within which the molecules move cooperatively and beyond which motion of molecules becomes independent. A decrease in temperature would generally lead to an increase in the size of CRR, which a consequent shift towards more viscous/glassy behavior; as confinement sets a limit to the maximum CRR size, however, at a given temperature, glassy behaviour can no longer be enhanced by cooling. In other words, confinement set a lower boundary to the possible Tg, promoting liquid like over glassy behavior (Spehr et al., 2011).
From an experimental point of view, however, resolving unambiguously the glass transition of water under nanoconfinement is not trivial. The main complications reside in resolving alpha relaxation from other possible relaxation and critical phenomena. A recent review provides three different scenarios to interpret the physical origins of low temperature relaxation of water under nanoconfinement (Cerveny et al., 2016). Yet, some universality traits can be captured when the relaxation time extracted by various methods, among which broadband dielectric spectroscopy (BDS), nuclear magnetic resonance (NMR) and quasi-elastic neutron scattering (QENS), is plotted against 1/T (See Figure 1B). Although different soft confining systems affect water relaxation in different ways, a crossover temperature is observed from an Arrhenius dependence at low temperature to a super-Arrhenius behavior at high temperature, often modelled via a Vogel−Fulcher−Tamman (VFT) relation (Gallo et al., 2010). Furthermore, increasing the water content leads in all cases to faster relaxation times, in some cases by four orders of magnitude. The tentative glass region in Figure 1B extends from 172 to 200 K; yet comparison with bulk Tg of water is problematic both from an experimental and theoretical point of view (Cerveny et al., 2016). This transition of relaxation times (and hence viscosity) from an Arrhenius dependence at low temperature to a super-Arrhenius behavior upon heating is also called a strong-to-fragile transition, where strong is a synonym of Arrhenius-like behavior.
Dynamic of water
The peculiarities of water under soft nanoconfinement are apparent also when studying the dynamic and diffusion behavior. In general, different techniques probe different characteristic times. A large body of literature has been devoted to this topic and excellent reviews are available. Here we briefly summarize the salient features of the dynamic of nanoconfined water. To start, different techniques probe different timescales: molecular vibrations (10–100 fs) are typically probed by linear spectroscopies, as FT-IR and Raman, and non-linear ones as sum frequency generation spectroscopy (SFG); molecular rotation (1–100 ps) are accessible via IR pump-probe experiments and two-dimensional rotational spectroscopy, while timescales of 1 ns or more are typically probed by molecular fluorescence techniques (Perakis et al., 2016). A recent review by Levinger and Swafford provides a nice overview on some of the most widely used techniques such as Steady-State and Time-Resolved Infrared Spectroscopy, IR time-resolved anisotropy, vibrational echoes, and two-dimensional IR spectroscopy (Levinger and Swafford, 2009). The majority of experimental results available to date has been generated using ultrafast laser spectroscopy in reverse micelles using pump-probe techniques, that is a fluorescent probe which is excited first and whose fluorescence time behavior is studied during its solvation by the surrounding water molecules. Almost all studies converge towards a general picture in which, nanoconfined water exhibits a bimodal distribution of the relaxation times, with one relaxation time typical of bulk water (∼ps) and a much slower time of the order of hundreds of ps (Bhattacharyya and Bagchi, 2000). By studying the fluorescence dynamics at various water content, the two components and their relative weight can be resolved, with the conclusion that the fast-relaxing water-like behavior component is reminiscent of bulk-like water, whereas the slow relaxation is the signature of the confined or interfacial water. This has led to a widely adopted core-shell model in which bulk-like properties of water vanish at a confinement of the order of w0 = 2, i.e., when 2 water molecules for surfactant are present, pretty much independently from the molecular traits of the surfactant. The main challenge here is that, since the greatest majority of fluorescent probes are poorly water soluble, it becomes difficult to separate the effect of nanoconfinement from the effect of interfaces (Levinger and Swafford, 2009). Yet, similar conclusions are also reached by techniques not relying on fluorescence, such as in the case of quasi-elastic neutron scattering (QENS) (Spehr et al., 2011), further supporting the core-shell model.
Translational and rotational diffusion of nanoconfined water present features which may be seen as even more puzzling. In general, rotational diffusion of water in reverse micelles is found to exhibit a slow mode in near proximity of interfaces and a bulk-like behavior far (beyond ∼0.8 nm) from the interfaces, provided the water hydration is such to reach bulk-like properties, i.e., w0 = 7.5 (Pieniazek et al., 2009). The translational diffusion coefficient is found to follow similar trends; yet, a distinction must be made among free self-diffusion of water in nanoconfined geometries and neat macroscopic flow (forced flow) under a pressure drop: in forced flow: the general view is that water flow in nanopores deviates significantly from the ideal no-slip conditions of the Hagen–Poiseuille model, with a positive effective slip length at the interface for hydrophobic interfaces and a negative effective slip length at hydrophilic interfaces. Here, hydrophilic and hydrophobic refer to contact angles lower/larger than 90° and to water-interface h-bonding stronger/weaker than water-water pairs, respectively (Lynch et al., 2020). Compared to the ideal Hagen–Poiseuille model this leads to a “super-diffusion” in hydrophobic nanopores, such as carbon nanotubes, and an under-diffusion in hydrophilic nanopores. Yet, recent contributions have highlighted the oversimplification of such a scheme and stressed the necessity to modify the effective slip length, as a linear sum of true slip, (a direct function of the contact angle), and an apparent slip, depending on the spatial features of nanoconfined water (Wu et al., 2017). In general, however, whether self-diffusion or effective diffusion are considered, deviations from the bulk-like behavior and the Hagen–Poiseuille ideal case become more pronounced with the level of nanoconfinement.
Opportunities
Water reactivity
The effect of nanoconfinement on water reactivity has been recently reviewed by Corti et al. (2021), who have discussed the correlation between confinement and increased reaction rates in several model reactions from microdroplets to nanodroplets. Although enhanced reactivity of organic reactions in reverse micelles has been known for decades, a quantitative breakthrough came with the work of Fallah-Araghi et al. (2014), who proposed a quantitative model based on the effect of interfaces, capable to preferentially adsorb the reactant over the product, and speeding up the reaction via a non-catalytic reaction-adsorption scheme. Notably, the model proposed by these authors was able to correctly describe the ∼1/d dependence of the effective reaction rate of bimolecular synthetic reactions over the confining geometry feature size, d. This was further supported by Wilson et al. (2020), who confirmed numerically the ∼1/d dependence of the equilibrium constant reactants/products by comparing stochastic simulations and experiments on imine synthesis. These studies address the effect of confinement in simple, model organic reactions, but set an important ground on which understanding more complex biochemical reactions, such as those involving enzymes and macromolecules.
Enzymatic reactions
Enzymatic reactions may highly benefit from confined geometries across different length scales. The general effect of surface and volume confinement on enzymatic reactions have been recently reviewed by Küchler et al. (2016), who have discussed conditions of mild confinement. Here, given the brevity of this perspective, we focus on enzymatic reactions under strong soft nanoconfinement provided by lipidic mesophases, since in these systems the confinement, generally strong (<3 nm), can also be released by the help of co-surfactants.
A first distinction must be made on the type of enzyme considered: for example, Sun et al. (2016) demonstrated that while membrane-bound enzymes such as D-fructose dehydrogenase (FDH) preserve full activity within lipidic mesophases and follow the classic Michaelis−Menten kinetics, as a result of the “natural” reconstitution within lipid bilayers (although organized according to bicontinuous cubic phase symmetries), bulk enzymes such as horse radish peroxidase (HRP) do follow a different kinetics, which can better be rationalized by the Hill model, typical of bound enzymes. This immediately demonstrates that the very same nanoconfinement environment imparts different behavior to different types of enzymes (membrane-bound vs. soluble). Additionally, and more generally, soluble enzymes do no follow only different kinetics, but also lead to different fate of the converted substrate. Vallooran et al. (2016) were the first to show that various enzymes confined within lipidic cubic mesophases may lead to the crystallization of converted substrates due to the decreased solubility of the substrates after enzymatic reaction in nanoconfined water compared to bulk water. The crystals of enzymatically converted substrates were easily detectable via simple cross-polarized microscopy or even optical observation due to the transparent and isotropic background of the host bicontinuos mesophases. By connecting HRP to antibodies, Vallooran et al. (2016) extended this concept to detection of biomarkers (e.g., glucose, cholesterol), bacteria (E. Coli), viruses (HIV, Ebola) and even parasites (malaria), establishing a general platform for bio-detection via enzymatic reactions run under the strong soft nanoconfinement of lipidic mesophases. As Vallooran et al. (2019) further demonstrated, the molecular mechanism for this crystallization (and hence detection) is really based on the peculiar status of nanoconfined water, within which solubility of organic substances changes significantly: by releasing the nanoconfinement from a diameter of 2.6 nm–7.6 nm using co-surfactants capable to swell the lipidic mesophase channels, the same authors showed that the crystals change from microcrystals, to needle-like, to then fully dissolve upon further relaxation of nanoconfinement. Additionally, on top of this effect, different symmetries of the same mesophases do also affect the activity of the enzyme: Sun et al. (2015) showed that the connectivity of the topology may influence the activity of the enzyme at the same confinement level (water channel): four-fold connected bicontinuous cubic phases of Pn3m symmetry were found to impart higher activity to HRP than three-folded Ia3d bicontinuous cubic phases and 1-fold (columnar) hexagonal phases, respectively.
The strong lipidic nanoconfinement offered by lipidic mesophases opens new opportunities and enable expanding the scope of enzymatic reactions in general. Salvati Manni et al. (2019) realized that a modification of common lipid (monolinolein) tails preventing lipid from crystallizing at low temperature, gives access to undercooled water down to 6 K. Yao et al. (2021) expanded this concept to more common lipids (phytantriol) without needs of chemical modification and went on showing the possibility to run enzymatic reactions at cryogenic conditions at temperatures well below those of freezing bulk water (See Figure 2 for details). In a first work they used both simple enzymatic reactions of HRP as well as cascading reactions of glucose oxidase and HRP to demonstrate not only the possibility to run these reactions below 0°C, but even to do so with increased turnover. The reason was found on stabilization of molecular intermediates of enzymatic reactions which are short-living at ordinary temperatures but that can be preserved at lower temperatures. In a second work, they expanded cryogenic enzymatic reactions in lipidic mesophases to Benzaldehyde lyase (Zhou et al., 2021). Interestingly, the unique soft nanoconfinement offered by lipidic mesophases has also been used to host enzymatic reactions with optimized stereochemistry synthesis. Zhou et al. (2018) showed that asymmetric synthesis of carbohydrates can be performed with increased turn-over by using aldolase nanoconfined in lipidic mesophases. In that specific case, the increased efficiency was understood to be a result of eased access of the substrate to the catalytic reaction center, located at the glycerol rich lipid−water interface, highlighting again the combined effects nanoconfined water with increased surface-volume ratios typical of strong nanoconfinement. Very recently Züblin et al. (2023) demonstrated that enzymatic polymerization of polysaccharides is highly enhanced in molecular weight and yield when performed under lipidic mesophase nanoconfinement compared to bulk, and even that it is possible to run the same enzymatic polymerization at cryogenic temperatures, further expanding the reach of enzymatic reactions in-meso.
- Cryogenic Properties
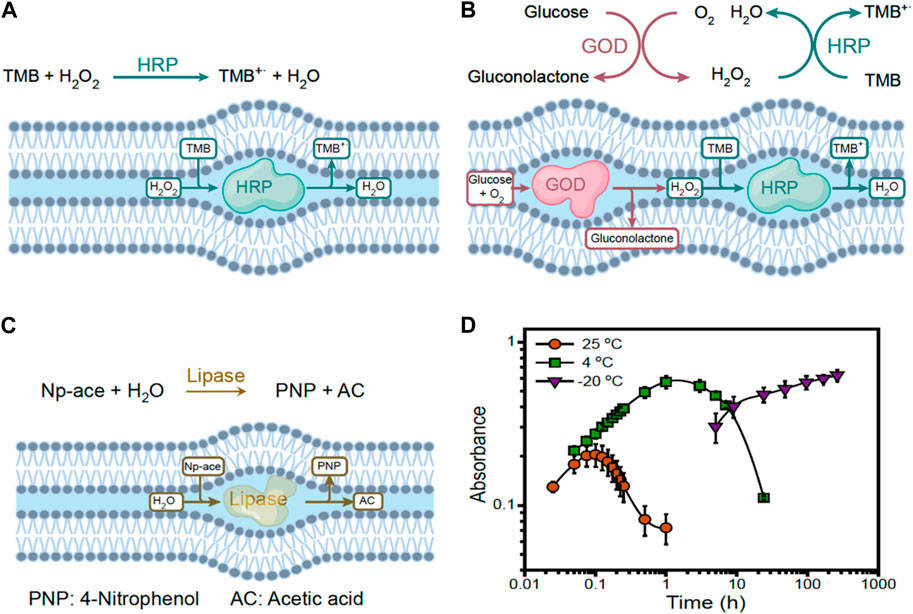
FIGURE 2. Typical enzymatic reactions explored at cryogenic conditions under lipidic mesophase soft nanoconfinement. (A) TMB oxidation by HRP; (B) TMB oxidization by GOD-HRP cascade reaction; (C) Hydrolysis of 4-Nitrophenyl acetate (Np-ace) by lipase; (D) Kinetic curves of GOD-HRP cascade reaction at 25, 4, and −20°C, as sketched in panel (B). Reproduced with permission from Yao et al. (2021).
Before closing this brief perspective, we touch on two additional possible applications arising from the unique cryogenic properties of water within lipidic mesophases: low-temperature reconstitution of biological macromolecules and possible liquid storage of water for lunar manned applications.
The first application is motivated by the fact that lipid mesophases are ideal matrices to reconstitute and even crystallize membrane proteins via the so-called in-meso method (Landau et al., 1996). As a lamellar intermediate is presumed to be the structure assisting the reconstitution step prior to in-meso crystallization, it appears reasonable to expect reconstitution of membrane proteins and other biomacromolecules within the lamellar phase of those lipidic mesophases capable of escaping water and lipid crystallization (Yao et al., 2021).
The second application is motivated by a recent conceptual proposal suggesting phytantriol-water mesophases as a cyclic storage system for maintaining liquid water on the surface of the moon in anticipation of man-based lunar missions expected by the Global Exploration Roadmap before the end of this decade (Banica et al., 2023). The most fascinating aspect is that these two very diverse applications appear to be enabled by using the very same soft nanoconfinement system (water and phytantriol) and the very same mesophase symmetry (lamellar).
Outlook and conclusion
In this short perspective I have highlighted only a few of the many opportunities arising from the peculiar status of water under soft nanoconfinement, some rudiments of the physical background needed to understand at least the basic features and how these could be serving in disparate fields ranging from chemical and enzymatic reactions in “soft nanoreactors,” to cryogenic reconstitution and preservation of biological macromolecules, to the most exotic application of liquid water storage on the surface of the moon. The overarching theme of this article is centered on the contrasting behavior between the ubiquity of liquid water and the diverse applications stemming out from its unique behavior under soft nanoconfinement. This contribution is meant to stimulate further our investigation of the many physical and chemical properties of nanoconfined water, which are still poorly understood, and to shed light on the plethora of applications possible for water under soft nanoconfinement.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
RM: Conceptualization, Formal Analysis, Funding acquisition, Project administration, Resources, Validation, Visualization, Writing–original draft, Writing–review and editing.
Funding
The author declares financial support was received for the research, authorship, and/or publication of this article. Open access funding by ETH Zurich.
Acknowledgments
I am most thankful to Dr. Yang Yao and Dr. Serena Alfarano for literature suggestions and insightful discussions.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adam, G., and Gibbs, J. H. (1965). On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J. Chem. Phys. 43 (1), 139–146. doi:10.1063/1.1696442
Aleandri, S., and Mezzenga, R. (2020). The physics of lipidic mesophase delivery systems. Phys. Today 73 (7), 38–44. doi:10.1063/PT.3.4522
Banica, M. C., Altorfer, T., Inauen, J., Wichser, D., Dudli, D., Sutter, M. W., et al. (2023). Conceptual assessment of a lipid-based liquid water storage system for lunar life support and exploration. J. Aerosp. Eng. 36 (6), 04023084. doi:10.1061/JAEEEZ.ASENG-5187
Bhattacharyya, K., and Bagchi, B. (2000). Slow dynamics of constrained water in complex geometries. J. Phys. Chem. A 104 (46), 10603–10613. doi:10.1021/JP001878F
Cerveny, S., Mallamace, F., Swenson, J., Vogel, M., and Xu, L. (2016). Confined water as model of supercooled water. Chem. Rev. 116 (13), 7608–7625. doi:10.1021/ACS.CHEMREV.5B00609
Corti, H. R., Appignanesi, G. A., Barbosa, M. C., Bordin, J. R., Calero, C., Camisasca, G., et al. (2021). Structure and dynamics of nanoconfined water and aqueous solutions. Eur. Phys. J. E 44 (11), 136–150. doi:10.1140/EPJE/S10189-021-00136-4
Das, A., Patra, A., and Mitra, R. K. (2013). Do the physical properties of water in mixed reverse micelles follow a synergistic effect: a spectroscopic investigation. J. Phys. Chem. B 117 (13), 3593–3602. doi:10.1021/JP3102833
Das Mahanta, D., Dennis, A., Brown, R., Pezzotti, S., Han, S., Schwaab, G., et al. (2023). Local solvation structures govern the mixing thermodynamics of glycerol–water solutions. Chem. Sci. 14 (26), 7381–7392. doi:10.1039/D3SC00517H
Debenedetti, P. G., and Stanley, H. E. (2003). Supercooled and glassy water. Phys. Today 56 (6), 40–46. doi:10.1063/1.1595053
Fallah-Araghi, A., Meguellati, K., Baret, J. C., El Harrak, A., Mangeat, T., Karplus, M., et al. (2014). Enhanced chemical synthesis at soft interfaces: a universal reaction-adsorption mechanism in microcompartments. Phys. Rev. Lett. 112 (2), 028301. doi:10.1103/PHYSREVLETT.112.028301
Frank, H. S., and Wen, W. Y. (1957). Ion-solvent interaction. Structural aspects of ion-solvent interaction in aqueous solutions: a suggested picture of water structure. Discuss. Faraday Soc. 24 (0), 133–140. doi:10.1039/DF9572400133
Gallo, P., Rovere, M., and Chen, S. H. (2010). Dynamic crossover in supercooled confined water: understanding bulk properties through confinement. J. Phys. Chem. Lett. 1 (4), 729–733. doi:10.1021/JZ9003125
Hatakeyama, T., Tanaka, M., and Hatakeyama, H. (2010). Thermal properties of freezing bound water restrained by polysaccharides. J. Biomaterials Sci. Polym. Ed. 21 (14), 1865–1875. doi:10.1163/092050610X486946
Huber, P. (2015). Soft matter in hard confinement: phase transition thermodynamics, structure, texture, diffusion and flow in nanoporous media. J. Phys. Condens. Matter 27 (10), 103102. doi:10.1088/0953-8984/27/10/103102
Johari, G. P., Hallbrucker, A., and Mayer, E. (1987). The glass–liquid transition of hyperquenched water. Nature 330 (6148), 552–553. doi:10.1038/330552a0
Knight, A. W., Kalugin, N. G., Coker, E., and Ilgen, A. G. (2019). Water properties under nano-scale confinement. Sci. Rep. 9 (1), 8246. doi:10.1038/s41598-019-44651-z
Küchler, A., Yoshimoto, M., Luginbühl, S., Mavelli, F., and Walde, P. (2016). Enzymatic reactions in confined environments. Nat. Nanotechnol. 11 (5), 409–420. doi:10.1038/nnano.2016.54
Landau, E. M., Ju¨rg, J., Rosenbusch, P., and Kaback, H. R. (1996). Lipidic cubic phases: a novel concept for the crystallization of membrane proteins. Proc. Natl. Acad. Sci. 93 (25), 14532–14535. doi:10.1073/PNAS.93.25.14532
Levinger, N. E., and Swafford, L. A. (2009). Ultrafast dynamics in reverse micelles. Annu. Rev. Phys. Chem. 60, 385–406. doi:10.1146/ANNUREV.PHYSCHEM.040808.090438
Lynch, C. I., Rao, S., and Sansom, M. S. P. (2020). Water in nanopores and biological channels: a molecular simulation perspective. Chem. Rev. 120 (18), 10298–10335. doi:10.1021/ACS.CHEMREV.9B00830
Martiel, I., Sagalowicz, L., and Mezzenga, R. (2014). Viscoelasticity and interface bending properties of lecithin reverse wormlike micelles studied by diffusive wave spectroscopy in hydrophobic environment. Langmuir 30 (35), 10751–10759. doi:10.1021/LA502748E
Mezzenga, R., Seddon, J. M., Drummond, C. J., Boyd, B. J., Schröder-Turk, G. E., and Sagalowicz, L. (2019). Nature-inspired design and application of lipidic lyotropic liquid crystals. Adv. Mater. 31 (35), 1900818. doi:10.1002/ADMA.201900818
Moilanen, D. E., Fenn, E. E., Wong, D., and Fayer, M. D. (2009). Geometry and nanolength scales versus interface interactions: water dynamics in AOT lamellar structures and reverse micelles. J. Am. Chem. Soc. 131 (23), 8318–8328. doi:10.1021/JA901950B
Moilanen, D. E., Fenn, E. E., Wong, D., and Fayer, M. D. (2009). Water dynamics at the interface in AOT reverse micelles. J. Phys. Chem. B 113 (25), 8560–8568. doi:10.1021/JP902004R
Moulik, S. P., and Paul, B. K. (1998). Structure, dynamics and transport properties of microemulsions. Adv. Colloid Interface Sci. 78 (2), 99–195. doi:10.1016/S0001-8686(98)00063-3
Némethy, G., and Scheeaga, H. A. (1962). Structure of water and hydrophobic bonding in proteins. I. A model for the thermodynamic properties of liquid water. J. Chem. Phys. 36 (12), 3382–3400. doi:10.1063/1.1732472
Ortiz-Young, D., Chiu, H. C., Kim, S., Voïtchovsky, K., and Riedo, E. (2013). The interplay between apparent viscosity and wettability in nanoconfined water. Nat. Commun. 4 (1), 2482–2486. doi:10.1038/ncomms3482
Perakis, F., Marco, L.De, Shalit, A., Tang, F., Kann, Z. R., Kühne, T. D., et al. (2016). Vibrational spectroscopy and dynamics of water. Chem. Rev. 116 (13), 7590–7607. doi:10.1021/ACS.CHEMREV.5B00640
Pieniazek, P. A., Lin, Y. S., Chowdhary, J., Ladanyi, B. M., and Skinner, J. L. (2009). Vibrational spectroscopy and dynamics of water confined inside reverse micelles. J. Phys. Chem. B 113 (45), 15017–15028. doi:10.1021/JP906784T
Salvati Manni, L., Assenza, S., Duss, M., Vallooran, J. J., Juranyi, F., Jurt, S., et al. (2019). Soft biomimetic nanoconfinement promotes amorphous water over ice. Nat. Nanotechnol. 14 (6), 609–615. doi:10.1038/s41565-019-0415-0
Smart, A. G. (2017). Supercooled water survives in no-man’s-land. Phys. Today 70 (2), 18–21. doi:10.1063/PT.3.3452
Spehr, T. L., Frick, B., Zamponi, M., and Stühn, B. (2011). Dynamics of water confined to reverse AOT micelles. Soft Matter 7 (12), 5745–5755. doi:10.1039/C1SM05204G
Sun, W., Vallooran, J. J., Fong, W. K., and Mezzenga, R. (2016). Lyotropic liquid crystalline cubic phases as versatile host matrices for membrane-bound enzymes. J. Phys. Chem. Lett. 7 (8), 1507–1512. doi:10.1021/ACS.JPCLETT.6B00416
Sun, W., Vallooran, J. J., and Mezzenga, R. (2015). Enzyme kinetics in liquid crystalline mesophases: size matters, but also topology. Langmuir 31 (15), 4558–4565. doi:10.1021/ACS.LANGMUIR.5B00579
Vallooran, J. J., Assenza, S., and Mezzenga, R. (2019). Spatiotemporal control of enzyme-induced crystallization under lyotropic liquid crystal nanoconfinement. Angew. Chem. 131 (22), 7367–7371. doi:10.1002/ANGE.201901078
Vallooran, J. J., Handschin, S., Pillai, S. M., Vetter, B. N., Rusch, S., Beck, H. P., et al. (2016). Lipidic cubic phases as a versatile platform for the rapid detection of biomarkers, viruses, bacteria, and parasites. Adv. Funct. Mater. 26 (2), 181–190. doi:10.1002/ADFM.201503428
Velikov, V., Borick, S., and Angell, C. A. (2001). The glass transition of water, based on hyperquenching experiments. Science 294 (5550), 2335–2338. doi:10.1126/SCIENCE.1061757
Wilson, K. R., Prophet, A. M., Rovelli, G., Willis, M. D., Rapf, R. J., and Jacobs, M. I. (2020). A kinetic description of how interfaces accelerate reactions in micro-compartments. Chem. Sci. 11 (32), 8533–8545. doi:10.1039/D0SC03189E
Wu, K., Chen, Z., Li, J., Li, X., Xu, J., and Dong, X. (2017). Wettability effect on nanoconfined water flow. Proc. Natl. Acad. Sci. U. S. A. 114 (13), 3358–3363. doi:10.1073/PNAS.1612608114
Yan, C., Kramer, P. L., Yuan, R., and Fayer, M. D. (2018). Water dynamics in polyacrylamide hydrogels. J. Am. Chem. Soc. 140 (30), 9466–9477. doi:10.1021/JACS.8B03547
Yao, Y., Zhou, T., Färber, R., Grossner, U., Floudas, G., and Mezzenga, R. (2021). Designing cryo-enzymatic reactions in subzero liquid water by lipidic mesophase nanoconfinement. Nat. Nanotechnol. 16 (7), 802–810. doi:10.1038/s41565-021-00893-5
Yoshida, K., Yamaguchi, T., Kittaka, S., Bellissent-Funel, M. C., and Fouquet, P. (2008). Thermodynamic, structural, and dynamic properties of supercooled water confined in mesoporous MCM-41 studied with calorimetric, neutron diffraction, and neutron spin echo measurements. J. Chem. Phys. 129 (5), 054702. doi:10.1063/1.2961029
Yuan, R., Yan, C., Nishida, J., and Fayer, M. D. (2017). Dynamics in a water interfacial boundary layer investigated with IR polarization-selective pump-probe experiments. J. Phys. Chem. B 121 (17), 4530–4537. doi:10.1021/ACS.JPCB.7B01028
Zhou, T., Vallooran, J. J., Assenza, S., Szekrenyi, A., Clapés, P., and Mezzenga, R. (2018). Efficient asymmetric synthesis of carbohydrates by aldolase nano-confined in lipidic cubic mesophases. ACS Catal. 8 (7), 5810–5815. doi:10.1021/ACSCATAL.8B01716
Zhou, T., Yao, Y., Zhang, Q., and Mezzenga, R. (2021). Cryogenic activity and stability of benzaldehyde lyase enzyme in lipidic mesophases-nanoconfined water. Chem. Commun. 57 (46), 5650–5653. doi:10.1039/D1CC01315G
Keywords: nanoconfinement, supercooling, glass transition, glasses, lipid mesophases, lyotropic liquid crystals, cryo-enzymatic reactions
Citation: Mezzenga R (2023) Challenges and opportunities from water under soft nanoconfinement. Front. Soft Matter 3:1324589. doi: 10.3389/frsfm.2023.1324589
Received: 19 October 2023; Accepted: 07 November 2023;
Published: 23 November 2023.
Edited by:
Yuka Tabe, Waseda University, JapanReviewed by:
Yuri Gerelli, National Research Council (CNR), ItalyCopyright © 2023 Mezzenga. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Raffaele Mezzenga, cmFmZmFlbGUubWV6emVuZ2FAaGVzdC5ldGh6LmNo