
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Soft Matter, 17 April 2023
Sec. Polymers
Volume 3 - 2023 | https://doi.org/10.3389/frsfm.2023.1161141
This article is part of the Research TopicEditors’ Showcase 2023: PolymersView all 8 articles
The dynamics of lithium ions and polymer chains were investigated at the molecular scale in the model polymer electrolyte Poly (ethylene oxide) (PEO)/Lithium bis(trifluoromethanesulfonyl)imide as a function of temperature. This system is known to present an intermediate range order from the arrangement of neighboring chain segments as well as an extended range order of cylindrically arranged chains. The collective dynamics of the systems at lengthscales matching these structural features was measured using Neutron Spin Echo spectroscopy, gaining insights into their lifetime. Moreover, using isotope substitution techniques the dynamics of the lithium ions with respect to the other atoms was probed. The obtained results are compared with the conductivity and the lithium self-diffusion coefficient measured by NMR to gain experimental insight on the molecular processes triggering lithium transport.
The need to improve the sustainability, performance, and safety of lithium batteries urges the scientific community in the search for alternatives to currently employed electrolytes based on organic solvents. One of the possible families of alternative candidates are solid polymer electrolytes, which, being non-flammable and not dispersive, would significantly reduce safety concerns. However, this class of materials in general do not currently offer the conductivities required for practical applications. The system most intensely studied is Poly (ethylene oxide) which is able to dissolve large amounts of lithium ions and, in the melt phase, afford conductivities of the order of 10−3 S/cm. (Meyer, 1998). In PEO, lithium ions are coordinated with the ether oxygens of the polymer chains and the conduction mechanism proceeds through jumps of the ion among different ether oxygen cages. In particular, one of the most common salts employed is lithium bis(trifluoromethanesulfonyl)imide (LiTFSI), because, in PEO, it is mostly dissociated even at elevated lithium content; (Borodin and Smith, 2006); this has been attributed to relatively large size of the anion and the consequent delocalization of its charge.
The detailed structure of the lithium ions environment in PEO/LiTFSI was determined using Neutron Diffraction with Isotopic Substitution (NDIS), taking advantage of the fact that the coherent scattering length of 6Li and 7Li is different; (Mao et al., 2000a). Measurements were carried out on homologues samples of P(EO)7.57LiTFSI and P(EO)7.56LiTFSI, their difference providing the correlations between lithium ions and the other atoms in the system. The proposed structural picture from this study is that each Li+ ion is coordinated to five ether oxygens, with an interatomic distance of ≈2 Å corresponding to a peak in the structure factor at Q ≈ 2π/2 Å−1 ≈ 3 Å−1 (Q being the exchanged wavevector in the neutron scattering experiment). The main structure factor peak is located at ≈1.5 Å−1 and is referred to as the Intermediate Range Order (IRO) peak; the main origin of this feature, which is common to the electrolyte and the pure polymer, is the intersegmental correlation of the PEO. Furthermore, together with the peaks described above at ≈1.5 Å−1 and ≈3 Å−1, which are present both in the pure polymer and the electrolyte, the addition of the salt induces the presence of a peak in the static structure factor at ≈0.6 Å−1, which is absent in pure PEO, indicating a longer range structuring, referred to as the Extended Range Ordering (ERO). This feature is reminiscent of what is observed in crystalline c-P (EO)6LiAsF6, although in this case it is retained in the liquid phase. The ERO is attributed to the presence of pairs of PEO coils, bonding lithium ions, which interlock to form cylinders arranged in a 2D dense random packing, with the TFSI− anions occupying the spaces between them. (Mao et al., 2000a). It was speculated that these cylindrical arrangement of the PEO coils might provide pathways for the lithium transport. Similarly, the possibility that long range ordering could provide directed pathways for lithium transport was also proposed on the basis of QuasiElastic Neutron Scattering (QENS) results on PEO/LiClO4. (Fullerton-Shirey and Maranas, 2009).
The conduction mechanism of the Li+ ions requires, therefore, the breaking of the Li-O association and is accompanied by fast relaxation of the local polymer chain structure. Stretching of the polymer main chain as well as the flip of the local ether oxygen away from the cation, could cause the decay of the Li-O cage and the release of the cation. In fact, the temperature dependence of the conductivity correlates to the α-relaxation as measured using Dielectric Spectroscopy (DS). (Do et al., 2013). Moreover, it has been shown how the cation concentration dependence of conductivity is proportional to the behavior of the Rouse rate of the entropy driven dynamics of the chains as measured using QENS. (Mongcopa et al., 2018). These findings are in agreement with classical theories which assume proportionality between conductivity and the polymer segmental dynamics; although this assumption has been criticized, it appear to hold valid for electrolytes where lithium is dissolved in PEO. (Wang et al., 2012). The macroscopic self-diffusion coefficient of both cations and anions in PEO can be measured using pulsed field gradient Nuclear Magnetic Resonance (NMR). In the limit of ideal solution behavior, the conductivity can be calculated from the measured diffusion coefficient of the ions, and good agreement has been found at least for salt concentrations of [Li]/[EO] = rs = 0.08 (here [Li] and [EO] indicate the lithium salt and ethylene oxide monomer molar content, respectively) and lower. (Timachova et al., 2015). However, uncovering the details of lithium transport requires insights at the molecular level on both the polymer and ion dynamics. Such insights are offered by Molecular Dynamics simulations (Borodin and Smith, 2006; Maitra and Heuer, 2007; Diddens et al., 2010; Do et al., 2013) but are challenging to obtain experimentally. High resolution neutron spectroscopy methods (Gardner et al., 2020) provide nanoscopic length- (from the Angstrom to tens of Angstroms) and time- (from the picosecond to tens of nanoseconds) scale insights; moreover, neutron scattering experiments can take advantage of isotopic substitution techniques and are sensitive to light atoms such as hydrogen. For these reasons, neutron scattering methods are well suited to investigate the polymer dynamics (Richter et al., 2005; Sakai and Arbe, 2009) in polymer electrolytes. In fact, QENS techniques have been used to investigate the single particle dynamics of the hydrogen atoms of the polymer chain in several PEO electrolytes. (Mao et al., 2000b; Triolo et al., 2002; Fullerton-Shirey and Maranas, 2009). Moreover, using Neutron Spin Echo (NSE) spectrometers, the collective structural relaxation of the PEO chains was investigated in several PEO based lithium electrolytes employing deuterated chains, thus obtaining information on the segmental dynamics of the polymer chains. (Mao et al., 2002; Saboungi et al., 2002).
As detailed above, dynamic neutron scattering was used to investigate both the Rouse dynamics of the PEO chains (Mongcopa et al., 2018) and the segmental dynamics of the IRO in PEO/LiTFSI electrolytes. However, the collective dynamics over larger length scales, in the region often referred to as the mesoscale, (Novikov et al., 2013), was not probed before. In fact, in electrolytes showing longer range order, the dynamics of the larger scale structures has been shown to be relevant for the conduction mechanism (Yamaguchi et al., 2015) and other transport properties. (Bertrand et al., 2017; Yamaguchi et al., 2017; Yamaguchi and Faraone, 2017; Yamaguchi et al., 2018; Yamaguchi et al., 2019; Zhai et al., 2021). In this work, using NSE we investigated the dynamics of model polymer electrolyte P(EO)7.5LiTFSI at Q values matching the ERO and IRO peaks, as a function of temperature to relate the mesoscale dynamics to ion transport. Moreover, for the first time, we employed 6Li and 7Li isotopic substitution methods to experimentally measure on the same sample the mutual dynamics of lithium with respect to the PEO chains, as well as the collective PEO dynamics at the nanoscale. In this paper, first, a more detailed introduction to dynamic neutron scattering methods and neutron spin echo will be provided. Details on the sample preparation and experimental setup will be reported in Section 3. The results obtained in this work and their discussion will be found in Section 4. The final section will summarize the insights obtained.
The objective of a dynamic neutron scattering experiment is the measurement of the double differential scattering cross-section,
Where Ntot is the total number of atoms in the sample, kf and ki represent the moduli of the scattered and incoming neutron wavevector, respectively, and Q = |Q| = |kf-ki| is the modulus of the exchanged wavevector. The dynamic structure factor is defined as the Fourier transform of the Intermediate Scattering Function (ISF), I(Q,t):
The ISF is a property of the sample defined as:
Here, ⟨⟩ indicates the ensemble average and ri (rj) is the position of the i (j)-th atom in the sample, whose scattering length (which describes the scattering probability of a neutron by a nuclei) is bi (bj). Eq. 3 details how the magnitude of the exchanged wavevector, Q, defines the length scale at which the dynamics is probed. As described below, a neutron spin echo spectrometer measures the Fourier transform of S(Q,E), the ISF directly. The scattering length of an atom depends on its isotopic nature as well as on its nuclear spin state. Since these two quantities are uncorrelated to their position, Eq. 3, can be rewritten as:
where Ntot is the total number of atoms in the system.
The i (j)-th atom can be defined as the n (m)-th atom of the specie α (β), allowing us to write:
It follows:
Where Nα and Nβ are the number of atoms of the specie α and β, respectively.
Eq. 6 defines the neutron scattered beam as the sum of a coherent and incoherent component. The coherent and incoherent components yield information on the collective, i.e., mutual, and self, i.e., single particle, dynamics of the atoms in the sample, respectively. The coherent ISF is the sum of the partial ISFs, Iαβ(Q,t), of all the possible atomic specie couples; their contributions being weighted by the product of the coherent scattering lengths,
In a static neutron scattering experiment the energy of the scattering beam is not analyzed, which is equivalent, within certain approximations, to integrate Eq. 2 over E from -∞ to ∞. This corresponds to taking the value of the ISF at t = 0, which defines the static structure factor, S(Q):
The coherent scattering contribution to S(Q) is modulated in Q by the atomic spatial arrangements whereas the incoherent scattering contribution is constant.
NSE is the neutron scattering method which allows to probe dynamics at the largest length scales and longest time scales among all neutron spectroscopic techniques. (Gardner et al., 2020). The method employs a polarized neutron beam; the neutron’s spin precesses in a magnetic field before and after scattering by the samples. An opportune π flipper reverses the spin direction such, that the magnetic field experienced by the neutron after scattering effectively unwinds the precession accumulated in the first arm. For a purely elastic scatterer, apart from instrumental effects, the initial polarization is recovered. Sample dynamics alters the neutrons’ velocity, i.e., energy, resulting in a loss of polarization. The measured polarization relates directly to the ISF, the Fourier transform of the S (Q,E), the probability distribution of exchanged energy. In a NSE spectrometer the energy resolution is decoupled from the monochromaticity of the incoming beam, which affords to investigate dynamics process up to tens of nanoseconds, which corresponds to an energy resolution of the order of tens of neV. In NSE the signal is encoded through the beam polarization. While the coherent scattering contribution does not alter the polarization of the neutron beam, the incoherent scattering contribution flips the polarization of the neutron beam for a fraction of 2/3 of the scattered beam. Hence, the ISF measured by NSE, INSE(Q,t), is not the sum of the coherent and incoherent contributions but is given by:
Moreover, in general NSE measurements yield the normalized ISF:
Deuterated PEO with a molecular mass of 24 kDa [dP24k(EO)] and a dispersity (Đ) of 1.06 was synthesized by high vacuum anionic polymerization techniques using potassium ethoxide-d5 as the initiator and tetrahydrofuran (THF) as the solvent. This polymer was characterized Malvern OMNISEC system equipped a light scattering detector and a refractive index detector, two PLgel mixed-C columns and one PLgel guard column. THF was the eluent with a flow rate of 1 mL/min at 30°C. This sample was employed for the measurements performed at the NIST Center for Neutron Research (NCNR). Deuterated PEO with a molecular mass of 14 kDa [dP14k(EO)] and Đ = 1.09 was further purchased from PolymerSource. LiTFSI was purchased from Sigma-Aldrich. 6LiTFSI (isotopic purity 95%) was purchased from Iolitec. All materials were employed without further purification. As for the NDIS study by Mao et al. (2000a), the salt content was rs = 1/7.5 = 0.13, close to the maximum conductivity and within the crystallinity gap for low to medium molecular weight polymers.
PEO/LiTFSI samples were obtained by dissolving opportune amounts by weight of PEO and LiTFSI in acetonitrile. The solvent was removed in a vacuum oven at 90°C for 2 days. Samples were evenly spread on aluminum foil and wrapped in a cylindrical shape within a cylindrical aluminum can. The can was sealed in a helium glove box. Sample thickness was less than 1 mm and multiple scattering was deemed not to be of a concern because of the high transmission of the samples, which was greater than 0.90, and the fact that the measurements were performed in correspondence of strong correlation peaks1. Moreover, 6Li has a large absorption cross-section of 940 barn, much larger than natural lithium. The high transmission of the samples indicates that neutron absorption was not a significant factor.
All the measurements were performed in the melt state at 348 K or above. (Zheng et al., 2018).
NSE measurements were carried out at the National Institute of Standards and Technology (NIST) Center for Neutron Research (NCNR) (Rosov et al., 2000) using the instrument located on NG-A. Data were collected on dP24k(EO)7.5LiTFSI (hereafter referred as sample 1a) at Q values of 0.55 Å−1 and 1.45 Å−1, in correspondence with the ERO and IRO peaks, as a function of temperature using incoming wavelength, λ, of 6 Å with a Δλ/λ ≈ 17%. The resulting probed time range was from 4 ps to 18 ns.
The recently commissioned Wide Angle neutron Spin echo Spectrometer (WASP) at the Institut Laue-Langevin (ILL) offers capabilities to measure the Intermediate Scattering Function (ISF) in the time range from few picoseconds to several nanoseconds covering a wide exchanged wavevector Q range with unprecedented accuracy and efficiency. This spectrometer was employed to collect data on homologues PEO/LiTFSI samples differing only for their isotopic composition as follows: i) dP14k(EO)7.5LiTFSI (sample 1b); and ii) dP14k(EO)7.56LiTFSI (sample 2). Here Li indicates natural lithium which contains 7.5% of 6Li and 92.5% of 7Li. Two incoming neutron λs were employed, namely, 4 Å and 7 Å, with a Δλ\λ ≈ 18%; 4 Å provided a Q range from 0.41 Å−1 to 2.2 Å−1 and times from 1 ps to 1 ns; and 7 Å gave a Q range from 0.2 Å−1 and 1.3 Å−1 and times from 7 ps to 7 ns, respectively.
Figure 1A) reports the static structure factor of sample 1a, as measured using the NSE at NCNR. Employing polarized neutrons allows us to separate the coherent and incoherent contributions. (Chen et al., 2019). The results are in good agreement with previous reports (Mao et al., 2000a) identifying both ERO and IRO peaks. The inset Figure 1C) is a sketch depicting the PEO chains (red lines) cylindrical arrangement around the lithium ions (blue dots) to form a 2D dense random packing. The double arrowed lines indicate the distance corresponding to the ERO (dotted) and IRO (continuous). At both the structure factor peaks, at Q = 0.55Å−1 and Q = 1.45 Å−1, the coherent neutron scattering signal dominates over the incoherent one. It is therefore possible by a measurement in correspondence of the peaks to extract information on the collective dynamics in the system, the relative motion of the atoms with respect to each other; this also in view of the fact, that in a NSE measurement of the ISF the incoherent scattering contribution is suppressed by a factor of three (see Eq. 11). Therefore, since the ISFs reported in this work using NSE are the same as the ones which could be obtained employing another type of neutron spectrometer the superscript NSE will be omitted from the ISF notation, e.g., INSE(Q,t) = I(Q,t).
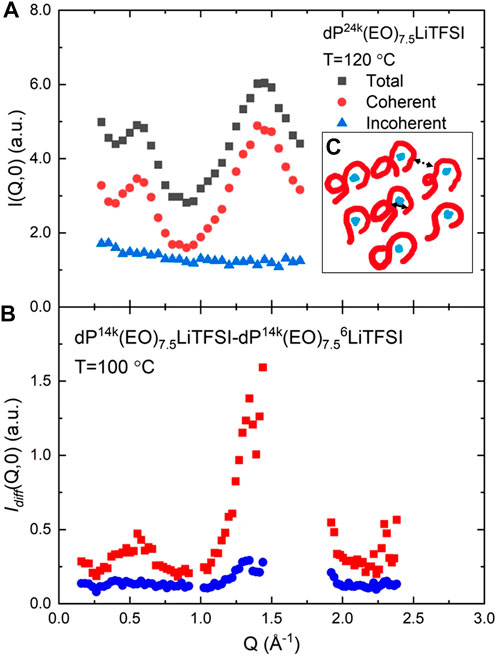
FIGURE 1. Structure factors and their coherent and incoherent fraction as determined using polarized diffraction. (A) sample 1a, measured at NCNR; (B) Idiff (Q,0), obtained from sample 1b and sample 2 on WASP. The vertical scale is in arbitrary units and the intensity in the two plots should not be directly compared; as a reference for the reader, the incoherent intensity of Idiff (Q,0) is about 10 times smaller than that of sample 1b. Within (A), the inset (C) is a sketch depicting the PEO chains (red lines) cylindrical arrangement around the lithium ions (blue dots) to form a 2D dense random packing. The double arrowed lines indicate the distance corresponding to the ERO (dotted) and IRO (continuous).
The use of isotopic labeled lithium allows us to gather specific information on the radial correlations of the lithium ions with respect to the other atoms in the systems. The scattering strength of atoms in the two samples are identical except for the Lithium atoms. The pair correlation terms not containing Li atoms will be identical, and when we subtract the signal from the two samples they will cancel. With reference to Eq. 7, we write:
Idiff(Q,t) yields an ISF where only the partials ISFs of lithium to the other atoms are present (ILiβ(Q,t)), whereas all the other partials cancel out. These results for the static structure factor are reproduced in Figure 1B. Idiff(Q) present the same ERO and IRO peaks as the sample measured at NCNR. Furthermore, since the salt is mostly dissociated and the lithium ion average distance can be estimated to be ≈ 6 Å, for the IRO Eq. 13 can be further simplified:
Eq. 14 makes explicit that at the IRO, Idiff (Q,t) contains information on the relative motion of the lithium cations with respect to the PEO segments, only. In fact, a comparison with the radial correlation function reported in (3) suggests that the peak at Q ≈ 1.45 Å−1 arises from the correlations between lithium and the hydrogens atoms of PEO.
The presence of the ERO peak in Idiff(Q), although much less pronounced than in the fully deuterated sample, indicates that the long range correlations among the PEO cylindrical structures are retained in the lithium ion correlations, consistently with the picture of the ions occupying the center of the cylinders. However, at the ERO, the summation in Eq. 13 has to run over all atomic species, lithium and TFSI included, because over distances of ≈2π/0.55 Å = 11 Å, correlations between different lithium ions as well as between lithium and TFSI, cannot be ruled out.
Figures 2, 3A report the ISFs measured in correspondence of the ERO and IRO peaks on sample1 and sample1a, respectively. At these salt content and polymer chain lengths, transport properties of relevance of the polymer have reached a plateau, (Timachova et al., 2015), so that the difference in polymer molecular mass for sample 1a and sample 1b is irrelevant. The data have been analyzed using the phenomenological stretched exponential function, as previously done on similar samples: (Mao et al., 2002; Saboungi et al., 2002):
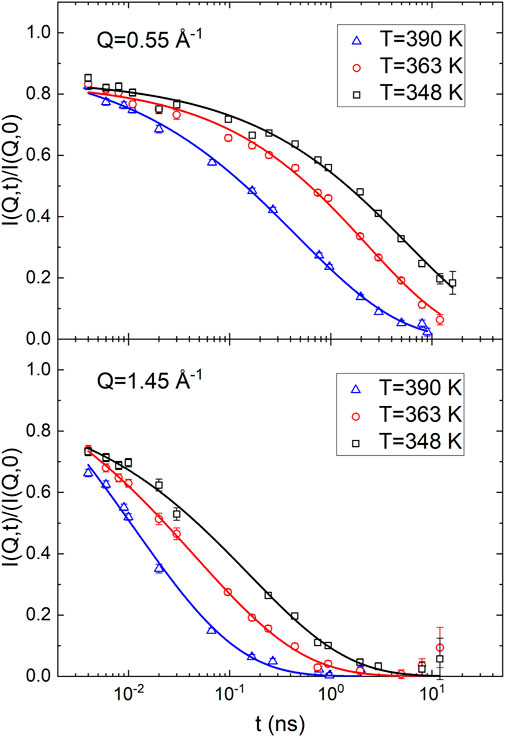
FIGURE 2. The normalized ISF of sample 1a, dP (EO)7.5LiTFSI, measured at NCNR. The continuous lines are fit using Eq. 15. Error bars represent standard deviation.
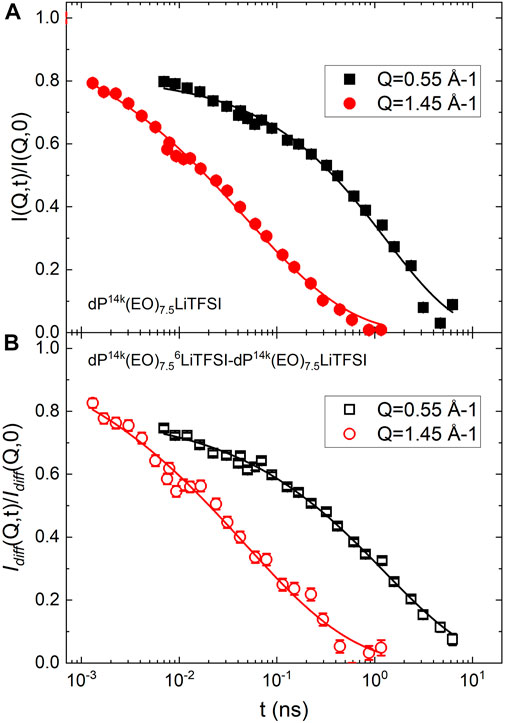
FIGURE 3. (A) The normalized ISF of sample 1b measured on WASP at the ERO and IRO peaks at a temperature of 373 K. (B) The normalized ISF Idiff (Q,0)/Idiff (Q,0) measured on WASP using the data from sample 1b and sample 2 at the ERO and IRO peaks at a temperature of 373 K. In both (A,B) the continuous lines are fit using Eq. 15. Error bars represent standard deviation.
The stretched exponential function reduces to a simple exponential relaxation if the stretching exponent β = 1; however, β < 1 is often observed in polymer systems and the stretching of the function is commonly associated with the presence of a distribution of relaxation times. For example, in most polymers, the dynamics at the interchain peak displays β values hardly dependent on T and in the range between 0.4 and 0.5; (Arbe et al., 2002); in Poly (1,3-butadiene), Poly (isobutylene) (PIB), and Poly (vinyl chloride) (PVC) the stretching exponent of the ISF at the first structure factor peak was found to be 0.45, (Richter et al., 1988), 0.55, (Richter et al., 1998), and 0.50, (Arbe et al., 2002), respectively. The amplitude factor could be less than 1 if relaxation processes too fast to be in the experimental window are present.
Figure 3B shows Idiff(Q,t), in correspondence of the same ERO and IRO peaks. The data are also analyzed in terms of a stretched exponential function.
Tables 1, 2 report the obtained fit parameters for the analysis of the ISF data collected at NCNR and on WASP, respectively. In correspondence of the ERO, the amplitude parameter is less than one indicating that the relaxation process consists of a fast local dynamics, followed by a longer decay process which completely erases the correlations over the length scales probed. However, at the IRO peak the parameter A is equal 1, within experimental uncertainties, indicating the absence of fast relaxational processes. A two steps relaxation, as observed at Q = 0.55 Å−1, is not uncommon when probing collective dynamics of extended structures; thermal fluctuations induce small scale rearrangements that are not able to totally erase the molecular structural correlations. Only after several ‘attempts’ the long-range structuring, the ERO in this case, is destroyed. We will discuss this concept again later in connection to lithium diffusion.
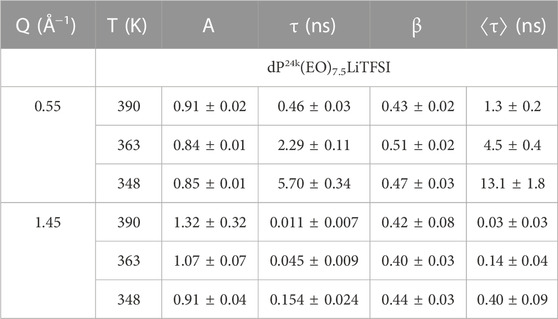
TABLE 1. Fitting results for the ISF data on dP24k(EO)7.5LiTFSI collected at NCNR. Uncertainties represent standard errors.
At both Q values probed, the stretching exponent takes values well below 1, in the range between 0.4 and 0.6. Values of the stretching exponent within this range are typical of polymer systems. Borrowing concepts developed for the single particle dynamics of hydrogen atoms in polymers, such finding is explained in terms of either a homogeneous scenario, where the dynamics of each scatterer is intrinsically stretched, or a heterogeneous scenario, where a distribution of relaxation times originated by the existence of heterogeneity causes the stretching. (Arbe et al., 1998). In the former case, as, for example, the Rouse dynamics which predicts a stretching exponent of 0.5 for the single particle dynamics of the atoms in the polymer chains, the dynamics maintains its Gaussian nature for its lengthscale dependence and the relaxation times scale with Q−2/β. In the heterogeneous scenario, the relaxation time would scale as Q−2. The presence of lithium ions associated to the ether oxygens of a fraction of the PEO segments, effectively introducing an additional friction, produces local inhomogeneities at the nanoscopic scale. Therefore it is not surprising that whereas QENS data on dPEO at the IRO peak could be analyzed using β = 0.5, (Brodeck et al., 2009), the addition of salt leads to a slight reduction of the stretching exponent. An analysis of the Q dependence of τ could not be carried out here; however, the reasoning above and the comparison of β values obtained for pure PEO and the electrolyte suggest that both the homogeneous and heterogeneous scenario are at play in the stretching of the ISFs measured.
In order to take into account the effect of β, Figure 4 reports the temperature dependence of the average relaxation time,
where Γ(x) is the gamma function.
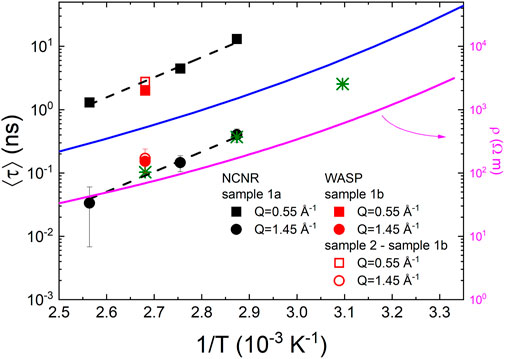
FIGURE 4. Arrhenius plot of the average relaxation times. The green asterisks are the data reported in (16) for Q = 1.5 Å−1. The blue line reports the temperature dependence of the relaxation time obtained with dielectric spectroscopy on P(EO)10LiTFSI (Do et al., 2013). The magenta line, referring to the right axis, is the conductivity, estimated using the parametrization outlined in ref. (Zheng et al., 2018). The dashed lines are the results of a global fit to an Arrhenius law (equation). Error bars represent standard error.
In correspondence of the IRO, when compared with the results reported for pure PEO, (Brodeck et al., 2009), the obtained
l = 5.8 Å being the PEO segment length. (Niedzwiedz et al., 2008) The corresponding timescale can be estimated as:
Where ξ0 is the friction coefficient. A parametric equation for ξ0 as a function of the salt content rs in PEO/LiTFSI at 363 K has been provided in (6) resulting in
In (16), the temperature dependence of the ISF was analyzed using a Mode Coupling Theory (MCT) (Gotze and Sjogren, 1992) approach with a power law dependence for a critical temperature assumed to be 18% higher than the measured glass transition temperature, Tg ≈ 207 K. In the present work, given the relatively narrow range of temperatures probed a simpler Arrhenius law was used to analyze the data:
where EA is the activation energy, R the gas constant, and τ0 is the elementary time scale.
The data at Q = 0.55 Å−1 and Q = 1.45 Å−1 were fitted separately to (5) giving the same EA, within experimental uncertainty. Therefore, the data at the IRO peak and ERO peak were fitted globally assuming the same activation energy, EA, but allowing τ0 to be different for the intermediate and extended range order dynamics. We obtain EA = 61 kJ/mol ± 4 kJ/mol. This value is estimated to be 3 times larger than the one obtainable from previous QENS results on dPEO. (Brodeck et al., 2009). The presence of lithium leads to an increased energy barrier for the PEO chain movements and slower dynamics in general.
It is instructive to compare the obtained relaxation times with those from dielectric spectroscopy. In general, the timescale probed at the main structure factor peak in molecular liquids and glass formers is associated with the structural relaxation, the timescale of motion outside the nearest neighbor cage. (Luo et al., 2020; Luo et al., 2021). This timescale is often found to match the slowest, referred to as α, relaxation process in the dielectric spectra. However, notable exceptions are found, especially when multiple length scales or dynamic processes are present. (Sillrén et al., 2014; Arbe et al., 2016). The blue line in Figure 4 represents the temperature dependence of the α-relaxation time obtained using dielectric spectroscopy on P(EO)10LiTFSI. (Do et al., 2013). The relaxation times are parametrized using an empirical Vogel Fulcher Tammann (VFT) relation:
where
Although a direct comparison cannot be carried out because the lithium content was different, it is interesting that the results from DS, a spectroscopic technique which generally cannot associate a specific lengthscale to the dynamic process probed, lays in between the dynamics of IRO and ERO peaks. This is not unusual because both the chain and cylinders dynamics might contribute to the dielectric signal and are a visible in a non-separable but broader distribution of relaxation times well beyond a Debye relaxation in the dielectric spectra. They just separate at specific temperatures caused by the different activation energies. In molecular liquids which present a long-range ordering signaled by a pre-peak, a feature in the structure factor at values smaller than the main peak, similar to the ERO peak, the dielectric signal has been reported in some cases to lay in between the dynamics measured at the pre-peak and at the main peak using NSE; (Sillrén et al., 2014); in other cases, the dynamics at the main peak and the pre-peak give rise to distinguishably different dielectric processes. (Bertrand et al., 2017).
The α-relaxation measured by DS in (5) is also relevant because it has the same temperature dependence as the conductivity. A more direct comparison with the conductivity for rs = 0.13 can be carried out using the parametrization employed in (27). A slightly different expression for a VFT temperature dependence of the conductivity, σ, was used:
where T0 was taken to be 50°C below the concentration dependent Tg. Figure 4 reports, together with the ⟨τ⟩ values obtained with NSE, the resistivity, ρ = 1/σ, obtained using (21) and the values of Aσ,
The discrepancy between the temperature dependence of the NSE results and of the resistivity and α-relaxation challenges some common assumptions. As mentioned above, the correlation between the segmental dynamics of the polymer and the conductivity (Nitzan and Ratner, 1994) is a generally [although not always (Wang et al., 2012)] accepted principle and was reported to be valid especially for PEO. (Wang et al., 2012). Our results put in evidence that spectroscopic techniques such as DS might be sensitive to the polymer dynamics over multiple length scales. On the other hand, the connection between the Rouse dynamics of the chains and the conductivity as a function of rs has been recently established; (Mongcopa et al., 2018); however, the Rouse dynamics, although reflected in the motion of each segment, describes the behavior of the whole chain and as such mostly reflects in the dynamics over length scales larger than the inter segmental distance. Therefore, the hierarchical nature of polymer dynamics should be taken into account.
We turn now our attention on the insight obtained through the use of isotopic substitution on WASP. As mentioned above the ISFs measured on sample 1b reflect mostly the dynamics of the PEO chains, whereas Idiff is sensitive to the mobility of the lithium ions with respect to the polymer chains and the other atoms. A remarkable coincidence in the time scale measured for sample 1b and Idiff is observed. This implies a strong correlation between the chain and lithium dynamics. As mentioned above, it is well established that lithium transport is strongly correlated to the segmental dynamic in PEO/LiTFSI electrolytes. However, the timescale of lithium and polymer motions could not be probed experimentally at the molecular scale, before. However, MD simulations suggest that a rearrangement of polymer chains is required for the long distance transport of lithium. (Diddens et al., 2010). Interestingly, it was also indicated that lithium ions can separate from an originally PEO oxygen but tend to reassociate with it unless a contemporary chain restructuring takes place, which then triggers the segmental hopping of the lithium cation. (Diddens et al., 2010). This picture is consistent with the finding of a fast process in the ERO dynamics. The fact that ⟨τ⟩ for sample 1b and Idiff are the same within experimental uncertainty supports a scenario in which polymer chain movements trigger the lithium transport.
To gain further insight and allow a direct comparison with lithium self-diffusion coefficients, an effective mutual average diffusion coefficient can be obtained from the fitting of Idiff as:
The obtained values are reported in Table 3. As implied above, the diffusion coefficient at the IRO is larger than the one estimated at the ERO. This can be explained considering that at shorter length scales faster local motions are probed. In the case of systems which shows structuring over multiple length scales, as, for example, ionic liquids, different dynamic regimes are probed over different length scales. (Berrod et al., 2017; Ferdeghini et al., 2017). Usually, the values obtained at smaller Q are more relevant for the macroscopic transport properties, however, strong structuring might influence the effective diffusion coefficient values. Therefore, a comparison of our ⟨D⟩ with macroscopic self-diffusion coefficient of lithium would be instructive. Using PG-NMR, Gorecky, et al. (Gorecki et al., 1995) investigated the temperature dependence of the cation and anion diffusion in PEO/LiTFSI at various rs;. From their data at rs = 0.125, we estimate the lithium self-diffusion coefficient to be ≈ 0.4 10−7 cm2/s at 373 K. This value can be directly compared with ⟨D⟩. The slight difference in rs is not concerning because in this region of rs the transport properties of the cation are not strongly dependent on rs; in fact, the lithium diffusion coefficients reported by Gorecky, et al. for rs = 0.125 and 0.167 are almost coincident. As far as the Mw of the polymer is concerned, Gorecky, et al. employed PEO with a much longer chain length (Mw = 900 kDa), however, as mentioned above our study has already reached the plateau region in the lithium diffusion as function of the product rs×NPEO, and therefore this difference should not produce significant inconsistencies. (Timachova et al., 2015). Finally, we note that the activation energy for the lithium self-diffusion coefficient is 38.6 kJ/mol, about 2/3 of the one measured for ⟨τ⟩; however, here the comparison is made at 373 K, about the middle of the temperature range of relevance between the PEO melting temperature and the temperature at which possible degradation effects might ensue. The lithium self-diffusion coefficient is about a factor of three slower than ⟨D⟩ at the ERO and almost an order of magnitude slower than ⟨D⟩ at the IRO. This comparison indicates that both IRO and ERO needs to relax for the lithium transport to take place. Rather than providing channels for ease of transport the ERO might play the role of cages which need to be broken to allow long distance transport of the cation. However, additional dynamic processes, likely over even larger length scales, are required for the mobility of the lithium ions to be triggered. The concept of tortuosity, invoked to describe transport in nanostructuring ionic liquids, (Ferdeghini et al., 2017), might be helpful to rationalize the observed differences between the microscopic and macroscopic diffusion coefficients.
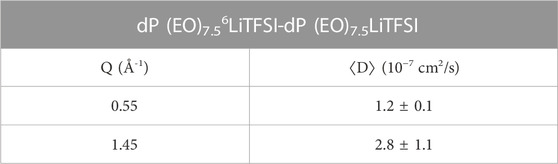
TABLE 3. Effective average mutual diffusion coefficient of lithium ions at T = 373 K. Uncertainties represent standard errors.
In conclusion, the relaxation dynamics of the IRO and ERO in model polymer electrolyte PEO/LiTFSI was investigated using neutron spin echo. The data obtained at the Q value corresponding to the IRO are in good agreement with previous reports, whereas the data at the ERO are reported here for the first time. The timescale of the ERO relaxation is almost an order of magnitude slower than that of the IRO which indicates both that the cylindrical structures originating the ERO have a finite lifetime and also that they are rather stable. In fact, comparison with the time scale of the Rouse dynamics of the chains suggests that the entropic motion of the chain might be the origin of the ERO decay. However, IRO and ERO dynamics have the same temperature dependence suggesting that the same underlying motion triggers both. The α-relaxation timescale as probed by DS lies in between the timescale of the IRO and ERO dynamics, it has a different temperature dependence which on the other hand matches that of lithium resistivity.
Moreover, isotopic substitution allowed to probe the dynamics of lithium with respect to the other atoms and to estimate a mutual diffusion coefficient. A remarkable similarity between the timescale of the lithium mutual dynamics and the polymer dynamics indicates a strong correlation between lithium and segmental motions.
These results both highlight the strong correlation between the lithium and polymer chain dynamics and at the same time show that processes over larger length scales are required to allow long distance lithium transport. Further investigation of the connection between mesoscale structures and dynamics, such as the ERO and the chain Rouse motion, are required to better understand the mobility of lithium in polymer electrolyte and facilitate the rational design of new materials with improved performance.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
AF, SF, and MO initiated the research. KH synthesized the deuterated PEO sample with Mw = 24 kDa and characterized it. AF prepared the samples. PF performed the experiment on WASP. AF performed the experiment at NCNR. AF and PF analyzed the data. AF wrote the manuscript. All authors contributed to the writing and editing of the paper as well as engaged in useful discussions throughout the experiments.
Access to the NSE spectrometer at the NCNR was provided by the Center for High Resolution Neutron Scattering, a partnership between the National Institute of Standards and Technology and the National Science Foundation under Agreement No. DMR-2010792.
One of the deuterated PEO was synthesized at the Center for Nanophase Materials Sciences (CNMS), which is a US Department of Energy, Office of Science User Facility at Oak Ridge National Laboratory.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1Generally, multiple scattering is spread out in Q and, therefore, not as intense as a strong scattering peak. However, a strong peak may sometime originate a significant multiple scattering contribution, but usually at a different Q value; a possible exception would be when measuring at very small scattering angles.
2Because the incoming neutron wavelength distribution was above 10 %, the small difference in Q for the two sets of data is not significant.
Arbe, A., Colmenero, J., Monkenbusch, M., and Richter, D. (1998). Dynamics of glass-forming polymers: "Homogeneous" versus "heterogeneous" scenario. Phys. Rev. Lett. 81 (3), 590–593. doi:10.1103/physrevlett.81.590
Arbe, A., Malo de Molina, P., Alvarez, F., Frick, B., and Colmenero, J. (2016). Dielectric susceptibility of liquid water: Microscopic insights from coherent and incoherent neutron scattering. Phys. Rev. Lett. 117 (18), 185501. doi:10.1103/physrevlett.117.185501
Arbe, A., Moral, A., Alegria, A., Colmenero, J., Pyckhout-Hintzen, W., Richter, D., et al. (2002). Heterogeneous structure of poly(vinyl chloride) as the origin of anomalous dynamical behavior. J. Chem. Phys. 117 (3), 1336–1350. doi:10.1063/1.1485283
Berrod, Q., Ferdeghini, F., Zanotti, J. M., Judeinstein, P., Lairez, D., Sakai, V. G., et al. (2017). Ionic liquids: Evidence of the viscosity scale-dependence. Sci. Rep. 7, 2241. doi:10.1038/s41598-017-02396-7
Bertrand, C. E., Self, J. L., Copley, J. R. D., and Faraone, A. (2017). Nanoscopic length scale dependence of hydrogen bonded molecular associates' dynamics in methanol. J. Chem. Phys. 146 (19), 194501. doi:10.1063/1.4983179
Borodin, O., and Smith, G. D. (2006). Mechanism of ion transport in amorphous poly(ethylene oxide)/LiTFSI from molecular dynamics simulations. Macromolecules 39 (4), 1620–1629. doi:10.1021/ma052277v
Brodeck, M., Alvarez, F., Arbe, A., Juranyi, F., Unruh, T., Holderer, O., et al. (2009). Study of the dynamics of poly(ethylene oxide) by combining molecular dynamic simulations and neutron scattering experiments. J. Chem. Phys. 130 (9), 094908. doi:10.1063/1.3077858
Chen, W. C., Watson, S., Qiu, Y. M., Rodriguez-Rivera, J. A., and Faraone, A. (2019). Wide-angle polarization analysis on the multi-axis crystal spectrometer for the study of collective and single particle dynamics of methanol at its prepeak. Phys. B-Condensed Matter 564, 166–171. doi:10.1016/j.physb.2018.11.060
Diddens, D., Heuer, A., and Borodin, O. (2010). Understanding the lithium transport within a rouse-based model for a PEO/LiTFSI polymer electrolyte. Macromolecules 43 (4), 2028–2036. doi:10.1021/ma901893h
Do, C., Lunkenheimer, P., Diddens, D., Gotz, M., Weiss, M., Loidl, A., et al. (2013). Li+ transport in poly(ethylene oxide) based electrolytes: Neutron scattering, dielectric spectroscopy, and molecular dynamics simulations. Phys. Rev. Lett. 111 (1), 018301. doi:10.1103/physrevlett.111.018301
Ferdeghini, F., Berrod, Q., Zanotti, J-M., Judeinstein, P., Sakai, V. G., Czakkel, O., et al. (2017). Nanostructuration of ionic liquids: Impact on the cation mobility. A multi-scale study. Nanoscale 9 (5), 1901–1908. doi:10.1039/c6nr07604a
Fullerton-Shirey, S. K., and Maranas, J. K. (2009). Effect of LiClO4 on the structure and mobility of PEO-based solid polymer electrolytes. Macromolecules 42 (6), 2142–2156. doi:10.1021/ma802502u
Gardner, J. S., Ehlers, G., Faraone, A., and Sakai, V. G. (2020). High-resolution neutron spectroscopy using backscattering and neutron spin-echo spectrometers in soft and hard condensed matter. Nat. Rev. Phys. 2 (2), 103–116. doi:10.1038/s42254-019-0128-1
Gorecki, W., Jeannin, M., Belorizky, E., Roux, C., and Armand, M. (1995). Physical-properties of solid polymer electrolyte peo(litfsi) complexes. J. Physics-Condensed Matter 7 (34), 6823–6832. doi:10.1088/0953-8984/7/34/007
Gotze, W., and Sjogren, L. (1992). Relaxation processes in supercooled liquids. Rep. Prog. Phys. 55 (3), 241–376. doi:10.1088/0034-4885/55/3/001
Luo, P., Zhai, Y. Q., Leao, J. B., Kofu, M., Nakajima, K., Faraone, A., et al. (2021). Neutron spin-echo studies of the structural relaxation of network liquid ZnCl2 at the structure factor primary peak and prepeak. J. Phys. Chem. Lett. 12 (1), 392–398. doi:10.1021/acs.jpclett.0c03146
Luo, P., Zhai, Y. Q., Senses, E., Mamontov, E., Xu, G. Y., Faraone, A., et al. (2020). Influence of kosmotrope and chaotrope salts on water structural relaxation. J. Phys. Chem. Lett. 11 (21), 8970–8975. doi:10.1021/acs.jpclett.0c02619
Maitra, A., and Heuer, A. (2007). Cation transport in polymer electrolytes: A microscopic approach. Phys. Rev. Lett. 98 (22), 227802. doi:10.1103/physrevlett.98.227802
Mao, G., Saboungi, M-L., Price, D. L., Armand, M., Mezei, F., and Pouget, S. (2002). α-Relaxation in PEO−LiTFSI polymer electrolytes. Macromolecules 35 (2), 415–419. doi:10.1021/ma010108e
Mao, G., Saboungi, M-L., Price, D. L., Armand, M. B., and Howells, W. S. (2000). Structure of liquid PEO-LiTFSI electrolyte. Phys. Rev. Lett. 84 (24), 5536–5539. doi:10.1103/physrevlett.84.5536
Mao, G. M., Perea, R. F., Howells, W. S., Price, D. L., and Saboungi, M. L. (2000). Relaxation in polymer electrolytes on the nanosecond timescale. Nature 405 (6783), 163–165. doi:10.1038/35012032
Meyer, W. H. (1998). Polymer electrolytes for lithium-ion batteries. Adv. Mater 10 (6), 439–448. doi:10.1002/(sici)1521-4095(199804)10:6<439:aid-adma439>3.0.co;2-i
Mongcopa, K. I. S., Tyagi, M., Mailoa, J. P., Samsonidze, G., Kozinsky, B., Mullin, S. A., et al. (2018). Relationship between segmental dynamics measured by quasi-elastic neutron scattering and conductivity in polymer electrolytes. Acs Macro Lett. 7 (4), 504–508. doi:10.1021/acsmacrolett.8b00159
Niedzwiedz, K., Wischnewski, A., Monkenbusch, M., Richter, D., Genix, A. C., Arbe, A., et al. (2007). Polymer chain dynamics in a random environment: Heterogeneous mobilities. Phys. Rev. Lett. 98 (16), 168301. doi:10.1103/physrevlett.98.168301
Niedzwiedz, K., Wischnewski, A., Pyckhout-Hintzen, W., Allgaier, J., Richter, D., and Faraone, A. (2008). Chain dynamics and viscoelastic properties of poly(ethylene oxide). Macromolecules 41 (13), 4866–4872. doi:10.1021/ma800446n
Nitzan, A., and Ratner, M. A. (1994). Conduction in polymers - dynamic disorder transport. J. Phys. Chem. 98 (7), 1765–1775. doi:10.1021/j100058a009
Novikov, V. N., Schweizer, K. S., and Sokolov, A. P. (2013). Coherent neutron scattering and collective dynamics on mesoscale. J. Chem. Phys. 138 (16), 164508. doi:10.1063/1.4802771
Richter, D., Arbe, A., Colmenero, J., Monkenbusch, M., Farago, B., and Faust, R. (1998). Molecular motions in polyisobutylene: A neutron spin-echo and dielectric investigation. Macromolecules 31 (4), 1133–1143. doi:10.1021/ma971340g
Richter, D., Frick, B., and Farago, B. (1988). Neutron-spin-echo investigation on the dynamics of polybutadiene near the glass-transition. Phys. Rev. Lett. 61 (21), 2465–2468. doi:10.1103/physrevlett.61.2465
Richter, D., Monkenbusch, M., Arbe, A., and Colmenero, J. (2005). Neutron spin echo in polymer systems. Adv. Polym. Sci. 1742005, 1–221.
Rosov, N., Rathgeber, S., and Monkenbusch, M. (2000). “Neutron spin echo spectroscopy at the NIST center for neutron research,” in Scattering from polymers: Characterization by X-rays, neutrons, and light. Editors P. Cebe, B. S. Hsiao, and D. J. Lohse (ACS Symposium Series), 103–116.
Saboungi, M. L., Price, D. L., Mao, G. M., Fernandez-Perea, R., Borodin, O., Smith, G. D., et al. (2002). Coherent neutron scattering from PEO and a PEO-based polymer electrolyte. Solid State Ionics 147 (3-4), 225–236. doi:10.1016/s0167-2738(02)00026-7
Sakai, V. G., and Arbe, A. (2009). Quasielastic neutron scattering in soft matter. Curr. Opin. Colloid & Interface Sci. 14 (6), 381–390. doi:10.1016/j.cocis.2009.04.002
Sillrén, P., Matic, A., Karlsson, M., Koza, M., Maccarini, M., Fouquet, P., et al. (2014). Liquid 1-propanol studied by neutron scattering, near-infrared, and dielectric spectroscopy. J. Chem. Phys. 140 (12), 124501. doi:10.1063/1.4868556
Timachova, K., Watanabe, H., and Balsara, N. P. (2015). Effect of molecular weight and salt concentration on ion transport and the transference number in polymer electrolytes. Macromolecules 48 (21), 7882–7888. doi:10.1021/acs.macromol.5b01724
Triolo, A., Lo Celso, F., Passerini, S., Arrighi, V., Lechner, R. E., Frick, B., et al. (2002). Segmental dynamics in polymer electrolytes. Appl. Phys. a-Materials Sci. Process. 74, S493–s495. doi:10.1007/s003390201882
Wang, Y. Y., Agapov, A. L., Fan, F., Hong, K. L., Yu, X., Mays, J., et al. (2012). Decoupling of ionic transport from segmental relaxation in polymer electrolytes. Phys. Rev. Lett. 108 (8), 088303. doi:10.1103/physrevlett.108.088303
Yamaguchi, T., and Faraone, A. (2017). Analysis of shear viscosity and viscoelastic relaxation of liquid methanol based on molecular dynamics simulation and mode-coupling theory. J. Chem. Phys. 146 (24), 244506. doi:10.1063/1.4990408
Yamaguchi, T., Faraone, A., and Nagao, M. (2019). Collective mesoscale dynamics of liquid 1-dodecanol studied by neutron spin-echo spectroscopy with isotopic substitution and molecular dynamics simulation. J. Phys. Chem. B 123 (1), 239–246. doi:10.1021/acs.jpcb.8b10299
Yamaguchi, T., Saito, M., Yoshida, K., Yamaguchi, T., Yoda, Y., and Seto, M. (2018). Structural relaxation and viscoelasticity of a higher alcohol with mesoscopic structure. J. Phys. Chem. Lett. 9 (2), 298–301. doi:10.1021/acs.jpclett.7b02907
Yamaguchi, T., Yonezawa, T., Yoshida, K., Yamaguchi, T., Nagao, M., Faraone, A., et al. (2015). Relationship between structural relaxation, shear viscosity, and ionic conduction of LiPF6/propylene carbonate solutions. J. Phys. Chem. B 119 (51), 15675–15682. doi:10.1021/acs.jpcb.5b08701
Yamaguchi, T., Yoshida, K., Yamaguchi, T., Nagao, M., Faraone, A., and Seki, S. (2017). Decoupling between the temperature-dependent structural relaxation and shear viscosity of concentrated lithium electrolyte. J. Phys. Chem. B 121 (37), 8767–8773. doi:10.1021/acs.jpcb.7b04633
Zhai, Y. Q., Luo, P., Nagao, M., Nakajima, K., Kikuchi, T., Kawakita, Y., et al. (2021). Relevance of hydrogen bonded associates to the transport properties and nanoscale dynamics of liquid and supercooled 2-propanol. Phys. Chem. Chem. Phys. 23 (12), 7220–7232. doi:10.1039/d0cp05481j
Keywords: solid polymer electrolytes (SPE), lithium ion batteries, neutron spin echo, intermediate range order (IRO), extended range order (ERO), polymer dynamics, lithium diffusion
Citation: Falus P, Faraone A, Förster S, Hong K and Ohl M (2023) Dynamics of the extended and intermediate range order in model polymer electrolyte poly(ethylene oxide) and lithium bis(trifluoromethanesulfonyl)imide. Front. Soft. Matter 3:1161141. doi: 10.3389/frsfm.2023.1161141
Received: 07 February 2023; Accepted: 31 March 2023;
Published: 17 April 2023.
Edited by:
Michael Vogel, Darmstadt University of Technology, GermanyReviewed by:
Daisuke Kawaguchi, Kyushu University, JapanCopyright © 2023 Falus, Faraone, Förster, Hong and Ohl. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Antonio Faraone, YWZhcmFvbmVAbmlzdC5nb3Y=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.