Novel findings deduced from the microscopic kinetics model contest the classical nucleation theory

In this study, we revisit the microscopic kinetics model considering crystal nucleation as reversible attachment and detachment of units from growing clusters. Based on the variation of the rate constants of attaching and detaching with cluster size, we derive some findings that contest the classical nucleation theory. First, the equivalent thermodynamic parameters are deduced from the rate constants, which reveal that the interfacial free energy per area varies with cluster size and finally levels off. Second, if the crystal is not perfect, at the melting point, the nucleation barrier will be definite rather than infinitely large. Third, it is predicted that the critical nuclei size does not vary with supersaturation. Fourth, when the neighboring units from the same polymer chain are used for crystal nucleation, the attaching rate constant should decrease with cluster size, which is distinctly different from the same attaching rate constant in the nucleation of small molecular crystals. These interesting findings show that teaching the old dog (the microscopic kinetics model) new tricks could lead to new findings and deepen our understanding of crystal nucleation.

1 Introduction

Crystallization is a type of self-organization of a variety of motifs, such as atoms, small molecules, polymers, and motifs with a larger size, such as colloid particles, via crystallization; matter obtains compact and ordered structure with strong interaction among the unit motifs, which enables the material to be strong, heat or electric conductive, optically active, etc. The properties of crystalline materials vary considerably with the crystalline structures, which depend on both the chemical structures and the crystallization process. In the past decades, the knowledge of crystallization has greatly benefited the design and manufacture of crystalline materials.

Two types of theories, the thermodynamic and kinetic theories, have been applied to crystallization. The thermodynamic crystallization theories consider crystallization as a first-order phase transition between two phases with different orders and thermodynamic properties. According to the thermodynamic description of heterogeneous systems, as developed by Gibbs (1928), the free energy of a crystal embryo consists of two components: the bulk free energy and the interfacial energy. It is assumed that the interfacial energy per area and the gain of free energy per volume are independent of crystal size, which is termed as capillary approximation. According to the frame, crystallization proceeds via nucleation; that is, it passes a free-energy barrier. In the classical nucleation theory (CNT), melt directly transforms into crystal during crystallization, and crystal directly transforms into melt during melting. In contrast, Strobl (2000), Strobl (2006), and Lee et al. (2016) propose that during crystallization, melt transforms into mesophase, which is further stabilized to form crystals. However, in all the aforementioned theories, the order parameters change abruptly; namely, crystallization is the transformation between several distinct states with different orders. This basic assumption leads to difficulties when these crystallization theories are applied to treat nucleation at an early stage, where the crystal nuclei may have thermodynamic properties different from those of the bulk crystals.

On the other hand, kinetic theories assume that crystallization involves a series of attaching onto and detaching from the various clusters with different sizes. The scheme was originally proposed by Volmer and Weber (1926) and Becker and Döring (1935). Later, Turnbull and Fisher used such a microscopic scheme to obtain the rate of primary nucleation (Turnbull and Fisher, 1949). These efforts have contributed to the classical nucleation theory (CNT). In the field of polymer crystallization, Hoffman and Lauritzen proposed the surface nucleation theory and applied the microscopic kinetics model to obtain the rate of secondary nucleation on existing crystal surfaces, considering the stem with fixed length as a motif of attaching and detaching (Lauritzen and Hoffman, 1960; Hoffman et al., 1976; Hoffman and Miller, 1997). The free energy for the formation of the first chain stem on the flat growth plane is the energy barrier for the surface nucleation. Lamellae with a thickness less than the minimum value have higher free energy than the melt, so they are unstable. When the lamellar thickness exceeds the minimum value, it will demonstrate decreased growth rate with increasing thickness due to the arising energy barrier. Price applied the Markoff chain model to treat the crystallization of stems with different lengths on the smooth surface of polymer single crystals, where the basic attaching and detaching motif was a segment (Price, 1961). Later, the pinning effect due to folds and crystallization on rough crystal surface was considered by Sadler and Gilmer, who attributed the energy barrier of polymer crystallization to the entropy barrier, and the simulation results agreed with the observations (Sadler and Gilmer, 1984; Sadler and Gilmer, 1986). Doye and Frenkel (1999) suggested that the stem thickness allowing for steady growth of the lamellae rather than that for the fastest growth was chosen. Muthukumar took into account the entropy of the connecting loops and proposed that folded polymer lamellae rather than extended chain crystals of high molecular weight polymers are thermodynamically stable (Muthukumar, 2004).

Though these kinetic theories of polymer crystallization agree with the experimental results in some aspects, there are still some unsolved problems: first, the rate constants of attaching and detaching were coupled by thermodynamics, considering both the interfacial free energy and bulk free energy according to the capillary approximation; it is still in the frame work of Gibbs. Second, CNT was directly applied to obtain the crystal nucleation rate of flexible polymer chains, but the covalent linking of segments on a polymer chain has not been fully addressed. As we know, CNT is derived from the crystallization of small molecules, in which each motif is not correlated in kinetics and thus can be treated with the Markov process. However, for polymer chains, the attaching and detaching of covalently linked segments in a polymer chain should be a non-Markov process. As a result, small molecules can crystallize to form crystals with infinite size in all the three dimensions, while flexible polymer chains form lamellar crystals with thicknesses around several to tens of nanometers due to the back and forth folding of the chains.

Though intensive work has contributed to the field of crystallization and a lot of theories have been proposed, which can interpret some aspects of experimental observations, there are still some open questions that remain (Armistead and Goldbeck-Wood, 1992; Zhang et al., 2017; Xu et al., 2021). Some of them are listed as follows:

What does the interfacial free energy mean, and does it vary with crystal size?

Do undercooling and supersaturation have the same effect on crystal nucleation?

What is the difference between crystal nucleation of polymer chains and small molecules?

To further understand the remaining questions, considering crystal nucleation from the root of the theories, namely, revisiting the microscopic kinetics model, would be a natural option. In the past century, the microscopic kinetics model has been proposed and applied to interpret the nucleation and growth of crystals. However, the merits of the model have been shadowed by complicated mathematics equations. In this work, we revisit the microscopic kinetics model and derive the equivalent thermodynamic parameter, such as bulk free-energy change per unit and interfacial free energy per area. In the following section, we show that the microscopic kinetics model can reveal the nature of interfacial free energy and the different kinetics of small molecules and flexible polymer chains, which will help answer the aforementioned questions and shed new light on the understanding of crystallization.

2 Microscopic kinetics model for crystallization nucleation of small molecules

The microscopic process of crystallization from melt can be well described by the cluster-growth scheme, which was proposed by Volmer and Weber (1926), Becker and Döring (1935). The scheme shows a series of cascaded elementary processes describing the attaching and detaching of a motif from the clusters, as presented in Figure 1. The smallest unit (motif) can be atoms, molecules, polymer chain stems and colloidal particles, other clusters, etc. This scheme works for crystallization from quiescent melt or solution, in which the collision of clusters can be omitted due to much slower rates. Otherwise, when there are external forces, collision of clusters should be considered.

FIGURE 1

FIGURE 1. Microscopic kinetic process of crystal nucleation. $k_i^{+}$ and $k_i^{-}$ indicate the rate constant of a motif attaching to and detaching from the cluster with i motifs, respectively.

Theoretically, the scheme in Figure 1 can describe both nucleation and spinodal-like crystallization. Nucleation occurs if the attaching rate constants $k_i^{+}$ are smaller than the detaching rate constants $k_i^{-}$ for clusters smaller than critical nuclei, and the attaching rate constants become larger than the detaching rate constants for clusters larger than the critical nuclei. Otherwise, if the attaching rate constant is larger than the detaching rate constant for all the clusters, crystallization would proceed without an energy barrier, resulting in spinodal-like crystallization behavior.

2.1 Correlation of the microscopic kinetics model to thermodynamic theories

From the rate constants of attaching and detaching, the equivalent thermodynamics can be derived (Xu et al., 2021). The free-energy difference between a molar motif in clusters with size i + 1 and a molar motif in clusters with size i can be calculated from the microscopic kinetics:

$\Delta g_{i,i-1}=g_i-g_{i-1}=RTln\frac{k_i^{-}}{k_i^{+}},(1)$

where $g_i$ is the chemical potential of the cluster with size i. The free-energy change for formation of crystal clusters with size i is

${\displaystyle \sum }_{j=2}^i\left(g_j-g_{j-1}\right)={\displaystyle \sum }_{j=2}^{i}RT\mathit{ln}\frac{k_j^{-}}{k_j^{+}}.(2)$

For simplicity, we consider the one-dimensional crystallization of small molecules shown in Figure 2A. Thus, the free-energy change for the formation of crystal clusters equals the area of the blue region subtracted by the green region (Figure 2B), which is the same as the area of the red region subtracted by the area of the gray region (Figures 2C, D).

FIGURE 2

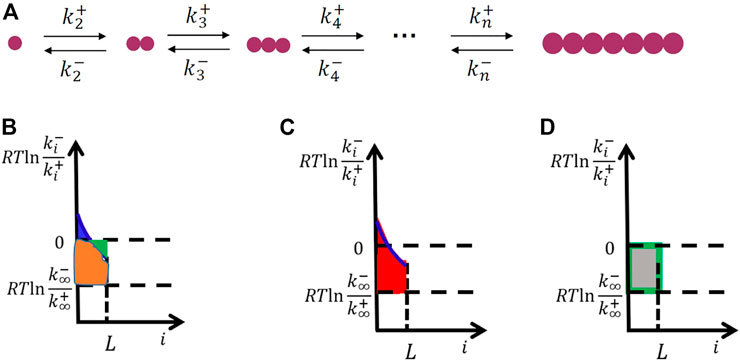
FIGURE 2. Microscopic kinetics model for crystal nucleation in one dimension (the simplest case) (A) and the derivation of interfacial free energy from the microscopic kinetics model (B–D). The free-energy change for the formation of crystal clusters equals the area of the blue region subtracted by the green region (B), which is the same as the area of the red region (the interfacial free energy) (C) subtracted by the area of the gray region (the change of bulk free energy during crystallization) (D).

In classical nucleation theory, the free-energy change for the formation of crystal clusters with size i is

$∆G=2\sigma +i∆g,(3)$

where $\sigma$ and $∆g$ indicate the end surface free energy per unit cross-section and the bulk free-energy change of one unit after crystallization.

For bulk crystals,

$∆g=RTln\frac{k_{\infty }^{-}}{k_{\infty }^{+}}.(4)$

Since the area of the gray region gives $-i∆g$, the area of the red region should equal $2\sigma$.

The microscopic kinetics model shows that even the bulk free-energy change of attaching a unit is considered independent of cluster size; the interfacial free energy should vary with cluster size. It first increases with size and finally levels off only when the cluster size is larger than the correlation length $L^{*}$, as demonstrated in Figure 3. Consequently, the clusters with size less than $L^{*}$ can be treated as the intermediate states (or mesophase) during crystallization. The capillary approximation in classical nucleation theory that both interfacial free energy per area and bulk free-energy change per unit is independent of crystal size stands only after the crystal size is larger than the correlation length $L^{*}$. At present, we do not know the size of the correlation length, $L^{*}$. However, it should be larger than the conventional critical nuclei size, as indicated by Figure 4.

FIGURE 3

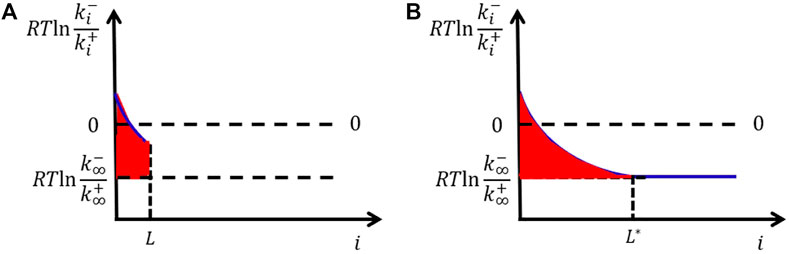
FIGURE 3. Variation of interfacial free energy per area with cluster size (A). The area of the red region gives the interfacial free energy per area, which increases with cluster size and finally levels off (B).

FIGURE 4

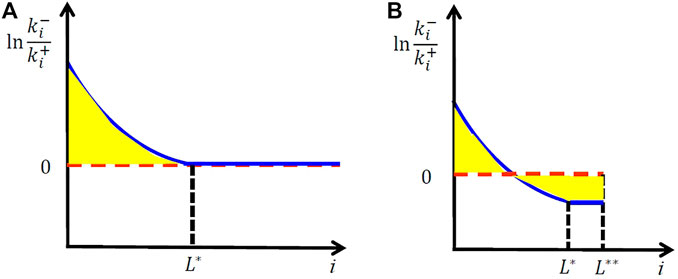
FIGURE 4. Microscopic kinetics at the melting point of a perfect crystal with infinite size (A) and those for a crystal with finite correlation size.

If there was an infinitely large perfect crystal, it should melt only at the temperature where

$∆g=RTln\frac{k_{\infty }^{-}}{k_{\infty }^{+}}=0.(5)$

At the lower temperature, the negative $∆g$ will lead to a negative total free-energy change of an infinitely large perfect crystal, so it will not melt. As shown in Figure 5A, at the melting point of the infinitely large perfect crystal, the energy barrier for crystal melting will be zero; thus, the crystal could not exist with large superheating, which contradicts the experimental observation. According to CNT, the critical size should be infinitely large when the supercooling diminishes. Otherwise, if there is a maximum correlation size, $L^{**}$, for a perfect crystal, at the melting point, the energy barrier for crystal nucleation and melting should be the same, both of which are of finite value. We expect the latter case will be the truth, which needs further investigation.

FIGURE 5

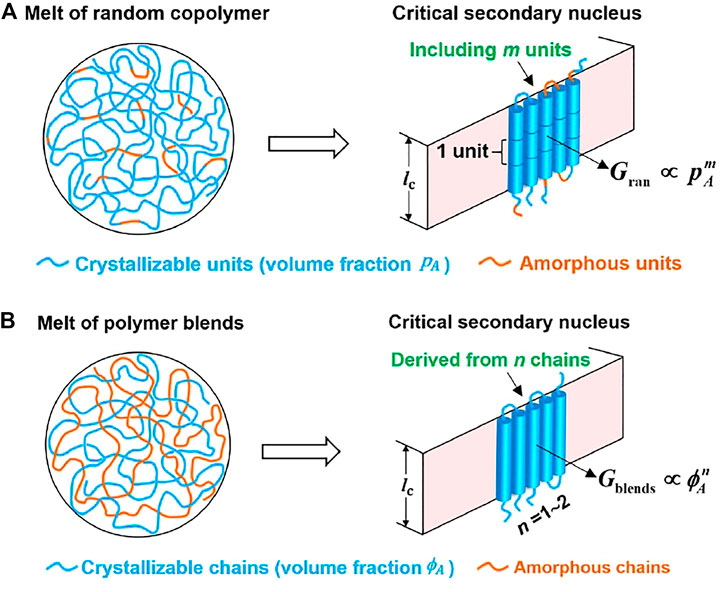
FIGURE 5. Method to determine the number of units (m) and that of chains (n) in a critical nucleus via variation of the secondary nucleation rate with the volume percentage of crystallizable units in the random copolymers and the volume percentage of crystallizable chains in polymer blends, respectively.

3 How to determine the critical size of crystal nuclei?

At medium to low supercooling, nucleation is the rate-limiting step of crystallization. The energy barrier related to the formation of the critical nuclei predominantly affects the nucleation rate. Determination of the size of the critical nucleus is a key for understanding the mechanism of nucleation and allows testing theories. However, it has been a great challenge for both experimentalists and theorists to quantify the critical size of crystal nuclei, especially for polymer chains. Though real-time observations of crystal nucleation have been achieved (Ono and Kumaki, 2018; Jeon et al., 2021), the size of critical nuclei is not easy to quantify. On the other hand, theoretical calculation of the size needs the thermodynamic parameters of the nuclei, which may be different from those of the mature crystals (Okada and Hikosaka, 2013; Anzai et al., 2015).

3.1 Determining critical nuclei size via nucleation theorem

Kashchiev (1982) proposed the first nucleation theorem, which stated that the derivative of the nucleation work with respect to the bulk Gibbs free-energy difference between the molten state and the crystalline state equaled the critical nucleus size with a trivial bias. Ford (1997) and Ford (2004) gave the proofs of the nucleation theorems based on statistical thermodynamics, and Schmelzer further commented on the theorem (Schmelzer, 2001).

According to the first nucleation theorem proposed by Kashchiev (1982), the following equation is applied to determine the critical nucleus size:

$\frac{dW*}{d\Delta g}=-n*+{\left.\frac{\partial F_s}{\partial \Delta g}\right|}_{n=n*},(6)$

where W* is the nucleation work of the critical nucleus, which is equal to the nucleation barrier. n is the number of crystallization units in the cluster, and n* is the number of crystallization units in the critical nucleus. Δg is the absolute value of bulk Gibbs free-energy difference of one crystallization unit when crystallizing from the amorphous state. For a one-component system, Δg is also the difference of the chemical potential between the old and new phase during crystallization and is often named as Δμ, as in the original paper of Kashchiev 13, 17, 23. Fs is the total surface free-energy of the cluster. Generally, Fs is weakly dependent on Δg, so the latter term in Eq. 2 can be omitted.

We consider that diluting the crystallizable units with non-crystallizable units in the melt causes no thermal effect but only the change of entropy during melting, Δs, since Δs is equal to $k_B$ lnx, with x indicating the volume fraction of crystallizable units. The following equation can be obtained:

$\Delta g=\Delta g_0+k_B{T}_c\mathit{ln}x.(7)$

The classical nucleation theory gives the relationship between crystal growth rate G and the nucleation work W* as follows (Eqs 7–9):

$G=A\mathit{exp}\left(-W*/k_B{T}_c\right),(8)$

where A is a pre-exponential factor containing the diffusion term. Combining Eqs 2–4, we obtain

$\frac{\partial \mathit{ln}G}{\partial \mathit{ln}x}=n*+C,(9)$

where C is determined by the derivative of lnA with respect to lnx and is usually very small (between 0 and 1). Equation 5 reveals that the slope of the fitting straight line of lnG with respect to lnx can be regarded as the critical secondary nucleus size n* (Šarić et al., 2016). Using Eq. 5, we determined the number of urea molecules in a critical secondary nucleus of urea/poly (ethylene oxide) inclusion compound crystals (Gao et al., 2019).

3.2 Determining critical nuclei size via microscopic kinetics of stochastic nucleation

We have also proposed a method for computing the critical size of lamellar crystals of folded polymer chains via a combination of the theoretical probability of stochastically choosing crystallizable units and the measured nucleation kinetics (Zhang et al., 2019; Zhang et al., 2020). We assume that nucleation is a stochastic process to choose the right conformation for homopolymers and both the crystallizable units and the right conformation for the diluted system (random copolymers or miscible homopolymer/amorphous polymer blend). When the homopolymer and diluted system have the same viscosity and dilution has not caused change of enthalpy, we can easily obtain the relationship between the nucleation rate of the diluted system and that of homopolymer.

For homopolymer chains, the rate to form critical nuclei consisting of m repeating units is termed as $i_{\mathit{hom}}$. The probability for each repeating unit to adopt an ordered conformation appropriate for nucleation is p. Thus, the probability to have m repeating units packed together in order is $p^m$. For each nucleation event during time τ, $M$ trials in total have been tried to find the ordered conformations for nucleation. So, the rate of nucleation is as follows:

$i_{\mathit{hom}}=\frac{M{p}^m}{\tau }.(10)$

For random copolymer chains with the volume fraction of crystallizable repeating units (A) as $p_A$, there are also $M$ trials during the time τ, provided that the copolymer and homopolymer have the same viscosity. However, among the M trials in random copolymers, only those choosing m crystallizable units simultaneously, $p_A^m$, are possible candidates for nucleation. Among these $M{\mathit{p}}_{\mathit{A}}^{\mathit{m}}$ trials, the number of successful trials where all the m A units possess the right ordered conformation for nucleation is $M{p}_A^m{p}^m$. Consequently, the nucleation rate of random copolymer chains is deduced:

$i_{\mathit{ran}}=M{p}_A^m{p}^m/\tau =p_A^m{i}_{\mathit{hom}},(11)$

where $i_{\mathit{ran}}$ and $i_{\mathit{hom}}$ represent the nucleation rate in random copolymers and homopolymers, respectively. $p_A$ is the volume fraction of crystallizable repeating units in the random copolymer chains, and m is the number of crystallized units in a critical nucleus.

We deduced that the exponent in a power-law relation between nucleation rate and the probability to choose a crystallizable unit from random copolymer chains consisting of crystallizable and non-crystallizable units gives the number of crystallizing units within a critical nucleus. The method was originally proposed by Andrews et al., though there was a mistake in the equation (Andrews et al., 1971). The slope of the double logarithmic plot of nucleation rate of random copolymers versus the content of crystallizable units rather than the slope minus one gives the number of units in a critical nucleus. For miscible blends of crystallizable and amorphous polymer chains, the nucleation rate as a function of the probability to find a crystallizable polymer chain in the melt also follows a power-law relation with the exponent related to the number of polymer chains in each critical nucleus. Based essentially on the probability to select a crystallizing unit or a chain during crystal nucleation, the number of units or chains in a critical nucleus could be determined. This approach does not require prior knowledge on the detailed nucleation pathway. A critical secondary nucleus of poly (butylene succinate) was determined to consist of 15–27 butylene succinate units, corresponding to 5 to 8 stems when the polymers were isothermally crystallized from quiescent melt at temperatures ranging from 70°C to 95°C. These stems in a critical secondary nucleus are derived from one or two polymer chains and the number of chains decreased with rising crystallization temperature. Our results contest the classical Lauritzen–Hoffman theory, which expected that the critical secondary nucleus was formed by a single stem.

Our approach can be generally applied to the lamellar crystals of other crystallizable flexible polymers, such as poly (L-lactide) and poly (L-lactide)/poly (D-lactide) stereocomplex crystals. In addition, our approach is not limited to secondary nucleation and can be adopted for primary nucleation as well.

3.3 Will dilution change the critical nuclei size?

We have determined the critical size of secondary nuclei in PEO/urea inclusion compounds (Gao et al., 2019) and the size of primary nuclei in P3HT crystallized from supersaturated solution via the first nucleation theorem (Wu et al., 2022). In addition, the number of crystallizable units in folded lamellar crystals of poly (butylene succinate) and poly (L-lactide) were obtained from the slope of lnG-lnpA (Zhang et al., 2019; Zhang et al., 2020). All the experimental results show that the number of crystallizable units in a critical secondary nucleus does not vary with the dilution ratio, which contradicts the deduction that the critical nuclei size should vary with the supersaturation.

Before dilution, the bulk free-energy change of the critical nuclei is

$\Delta g\left(n^{*}\right)=g_{n^{*}}-n^{*}{g}_1,(12)$

where $g_{n^{*}}$ is the free energy of 1 M critical nuclei (each with $n^{*}$ units), and $g_1$ is the free energy of 1 M amorphous units. We now consider the simplest case that the crystallizable unit A is replaced by some non-crystallizable units B while mixing of the two types of units leads to only the change of entropy and the enthalpy does not change.

${\Delta g}^{\prime }\left(n^{*}\right)=g_{n^{*}}^{\prime }-n^{*}{g}_1^{\prime },(13)$

where $g_{n^{*}}^{\prime }$ and $g_1^{\prime }$ are the free energy of 1 M critical nuclei (each with $n^{*}$ units) and that of 1 M amorphous crystallizable units after dilution, respectively.

$g_{n^{*}}^{\prime }-g_{n^{*}}=-RTln\frac{C_{n^{*}}^{\prime }}{C_{n^{*}}},(14)$

$g_1-g_1^{\prime }=-RTln\frac{C_1^{\prime }}{C_1},(15)$

where $C_{n^{*}}^{\prime }$ and $C_1^{\prime }$ are the equilibrium concentration of critical nuclei (each with $n^{*}$ units) and that of amorphous crystallizable units after dilution, respectively. $C_{n^{*}}$ and $C_1$ are the equilibrium concentration of critical nuclei (each with $n^{*}$ units) and that of amorphous units before dilution, respectively.

At equilibrium, we have:

$\frac{C_{n^{*}}}{C_1^{n^{*}}}={\displaystyle \prod _2^{n^{*}}}\frac{k_j^{+}}{k_j^{-}},(16)$

$\frac{C_{n^{*}}^{\prime }}{{\left.{\left(C\right.}_1^{\prime }\right)}^{n^{*}}}={\displaystyle \prod _2^{n^{*}}}\frac{k_j^{+}}{k_j^{-}}.(17)$

Combining the abovestated equations, we obtain

${\Delta g}^{\prime }\left(n^{*}\right)-\Delta g\left(n^{*}\right)=g_{n^{*}}^{\prime }-g_{n^{*}}-n^{*}\left(g_1-g_1^{\prime }\right)=0.(18)$

Since the critical nuclei and the amorphous units are both diluted, $\Delta g$ does not change with dilution. Consequently, the critical nuclei size will not vary with dilution, though the nucleation rate considerably slows down after dilution.

Therefore, both experimental results and theoretical deductions confirm that dilution will not change the size of critical nuclei, which contests the classical nucleation theory.

4 Crystallization of flexible polymer chains is a non-Markov process

Crystallization of small molecules is a Markov process, in which all the attaching rate constant per surface area is a constant for different clusters. As a result, the size of small molecular crystals will increase linearly with time when crystallized from bulk melt. However, crystallization of flexible polymer chains is a non-Markov process. If we want to use the Markov process shown in Figure 6 and Figure 7 to describe polymer crystallization, the attaching rate constant for the covalently linked segments should vary with the number of attached segments according to the following equation:

$k_i=A\mathit{exp}\left(-bi\right).(19)$

FIGURE 6

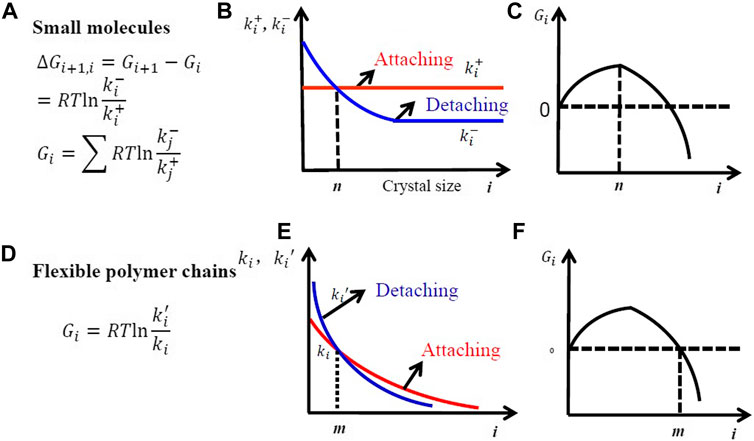
FIGURE 6. Free-energy change (A), the rate constants of attaching and detaching (B), and the variation of the free energy of crystal nuclei with size (C) during crystal nucleation in small molecules. Free-energy change (D), the rate constants of attaching and detaching (E), and the variation of the free energy of crystal nuclei with size (F) during crystal nucleation in flexible polymer chains. The symbol s and q indicate the number of small molecules and that of segments in a folded chain in a critical nucleus.

FIGURE 7

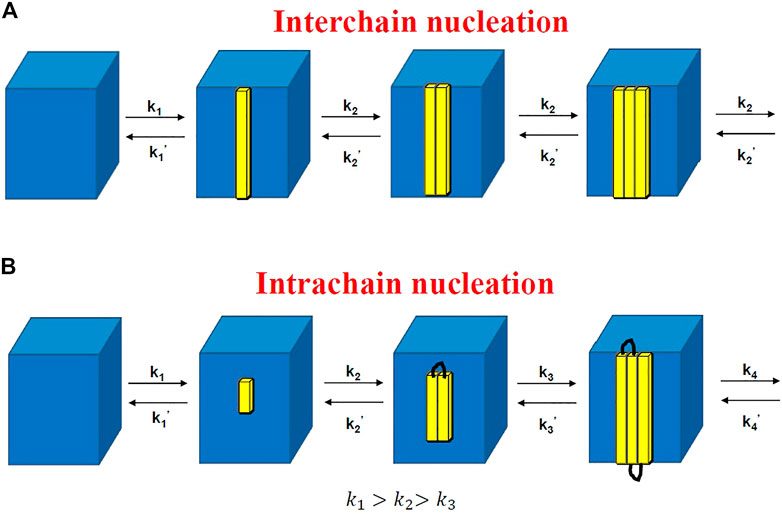
FIGURE 7. Rate constants of attaching and detaching for interchain nucleation (A) and those for intrachain nucleation (B). The former is similar to the crystal nucleation of small molecules (Markov process), while the latter is a non-Markov process.

The decreasing attaching rate constant is due to the increasing entropic barrier for intrachain nucleation because the probability to attach a new segment from the same chain should decrease with the number of attached segments from one chain. This leads to the increase of lamellar thickness with logarithm of time.

The non-Markov nature indicates that the segments in one chain could not attach or detach independently. In fact, the kinetics of attaching the $i$^th segments should be approximately equal to that of attaching all the $i$ segments in one step, which holds true for detaching as well.

To derive the rate of secondary nucleation, Hoffman and Lauritzen assumed that the attaching rate of the third stem was the same as that of the second stem, which only stands for interchain nucleation; that is, the stems should be chosen from different chains, or they are completely far away from each other even though they are located in the same chain. In our theory, for the adjacent chain folding (intrachain nucleation), the entropic barrier of secondary nucleation should be proportional to the total length of all the adjacent folded stems rather than one stem length. Another difference between the Hoffman–Lauritzen theory and the theory proposed here is that a critical secondary nucleus of polymer crystallization consists of different numbers of stems. The former predicted one stem, while ours expected multiple stems in each secondary nucleus.

The effect of chain length can be briefly discussed using the kinetics model. There is competition between intrachain and interchain nucleation. Intrachain nucleation is thermodynamically favored but kinetically unfavored compared with interchain nucleation (Zhang et al., 2019). As a result, only a portion of the chain adopts adjacent folding in a nucleus, and further growth of the nucleus will use stems from other chains. This is the reason why it is only a portion of the chain rather than the whole chain that takes part in adjacent chain folding. As a result, the chain length will have a limited effect on the number of adjacent chain folds and the rate of attaching and detaching. However, with increasing molecular weight, the rate of chain diffusion should decrease. These two factors, namely, attaching/detaching and chain diffusion, work together to slow down polymer crystallization with rising molecular weight.

5 Conclusion

The microscopic kinetics model considering attaching and detaching is at the root of the classical nucleation theory, which has been modified and extended to polymer crystallization. In this perspective, we revisit the microscopic kinetics model and deduce some interesting findings from variations of the rate constants of attaching and detaching with cluster size. First, even though we assume that the bulk free-energy change per unit is a constant, the interfacial free energy should increase with cluster size and finally level off after reaching a critical cluster size. Second, there may not exist a perfect infinitely large crystal, which has no energy barrier of melting at the melting point. Third, dilution with inert non-solvent (no change of enthalpy during mixing) will not change the critical nuclei size. Four, intrachain nucleation of flexible polymer chains is a non-Markov process, in which the rate constant of attaching should decrease with more neighboring units from the same chain attached. These four deductions contest the classical nucleation theory and prove the power of the microscopic kinetics model. Teaching the old model new tricks is expected to deepen our understanding of crystal nucleation.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

The author confirms being the sole contributor of this work and approved it for publication.

Funding

This study was supported by the National Key Research and Development Program of China (No. 2021YFD1700700) and the National Natural Science Foundation of China (Grant Nos. 21873054 and 21861132018).

Acknowledgments

The author thanks Alexander von Humboldt Foundation for the research fellowship and for experienced researchers during his research stay in University of Freiburg, Germany, in 2011. Application for the research fellowship in 2010 was the starting point of the idea in this work. The author is deeply grateful to Prof. Gert Strobl, Prof. Günter Reiter, Prof. Wenbing Hu, and Prof. Yanbin Huang for the inspiring discussions.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Andrews, E. H., Owen, P. J., and Singh, A. (1971). Microkinetics of lamellar crystallization in a long chain polymer. Proc. R. Soc. Lond. A 324, 79–97.

Google Scholar

Anzai, T., Kawauchi, M., Kawauchi, T., and Kumaki, J. (2015). Crystallization behavior of single isotactic poly(methyl methacrylate) chains visualized by atomic force microscopy. J. Phys. Chem. B 119, 338–347. doi:10.1021/jp5090923

PubMed Abstract | CrossRef Full Text | Google Scholar

Armistead, K., and Goldbeck-Wood, G. (1992). Polymer crystallization theories. Adv. Polym. Sci. 19, 219–311.

Google Scholar

Becker, R., and Döring, W. (1935). Kinetische behandlung der keimbildung in übersättigten dämpfen. Ann. Phys. 416, 719–752. doi:10.1002/andp.19354160806

CrossRef Full Text | Google Scholar

Doye1, J. P. K., and Frenkel, D. (1999). The mechanism of thickness selection in the Sadler-Gilmer model of polymer crystallization. J. Chem. Phys. 110, 7073–7086. doi:10.1063/1.478613

CrossRef Full Text | Google Scholar

Ford, I. J. (1997). Nucleation theorems, the statistical mechanics of molecular clusters, and a revision of classical nucleation theory. Phys. Rev. E 56, 5615–5629. doi:10.1103/physreve.56.5615

CrossRef Full Text | Google Scholar

Ford, I. J. (2004). Statistical mechanics of nucleation: A review. P. I. Mech. Eng. C-J. Mech. 218, 883–899. doi:10.1243/0954406041474183

CrossRef Full Text | Google Scholar

Gao, Y., Zhang, S., Shi, J., Guo, B., and Xu, J. (2019). Study of the crystal growth mechanism and critical secondary nucleus size of poly(ethylene oxide)/urea inclusion compound. Cryst. Growth Des. 19, 3834–3842. doi:10.1021/acs.cgd.9b00289

CrossRef Full Text | Google Scholar

Gibbs, J. W. (1928). The collected works, Thermodynamics. New York: Longmans Green and Co.

Google Scholar

Hoffman, J. D., Davis, G. T., and Lauritzen, J. I. (1976). The rate of crystallization of linear polymers with chain folding. In Treatise on Solid State Chemistry. Berlin, Germany: Springer, 497–614.

CrossRef Full Text | Google Scholar

Hoffman, J. D., and Miller, R. L. (1997). Kinetic of crystallization from the melt and chain folding in polyethylene fractions revisited: Theory and experiment. Polymer 38, 3151–3212. doi:10.1016/s0032-3861(97)00071-2

CrossRef Full Text | Google Scholar

Jeon, S., Heo, T., Hwang, S.-Y., Ciston, J., Bustillo, K. C., Reed, B. W., et al. (2021). Reversible disorder-order transitions in atomic crystal nucleation. Science 371, 498–503. doi:10.1126/science.aaz7555

PubMed Abstract | CrossRef Full Text | Google Scholar

Kashchiev, D. (1982). On the relation between nucleation work, nucleus size, and nucleation rate. J. Chem. Phys. 76, 5098–5102. doi:10.1063/1.442808

CrossRef Full Text | Google Scholar

Lauritzen, J., and Hoffman, J. D. (1960). Theory of formation of polymer crystals with folded chains in dilute solution. J. Res. Natl. Bur. Stand. A 64, 73–102. doi:10.6028/jres.064a.007

CrossRef Full Text | Google Scholar

Lee, J., Yang, J., Kwon, S. G., and Hyeon, T. (2016). Nonclassical nucleation and growth of inorganic nanoparticles. Nat. Rev. Mater. 1, 16034. doi:10.1038/natrevmats.2016.34

CrossRef Full Text | Google Scholar

Muthukumar, M. (2004). Nucleation in polymer crystallization. Adv. Chem. Phys. 128, 1–64.

CrossRef Full Text | Google Scholar

Okada, K. N., and Hikosaka, M. (2013) Polymer nucleation in handbook of polymer crystallization. Editors Ewa Piorkowska, and Gregory C. Rutledge (Netherlands: John Wiley and Sons).

Google Scholar

Ono, Y., and Kumaki, J. (2018). In situ real-time observation of polymer folded-chain crystallization by atomic force microscopy at the molecular level. Macromolecules 51, 7629–7636. doi:10.1021/acs.macromol.8b01428

CrossRef Full Text | Google Scholar

Price, F. P. (1961). Markoff chain model for growth of polymer single crystals. J. Chem. Phys. 35, 1884–1892. doi:10.1063/1.1732160

CrossRef Full Text | Google Scholar

Sadler, D., and Gilmer, G. (1984). A model for chain folding in polymer crystals: Rough growth faces are consistent with the observed growth rates. Polymer 25, 1446–1452. doi:10.1016/0032-3861(84)90108-3

CrossRef Full Text | Google Scholar

Sadler, D. M., and Gilmer, G. (1986). Rate-theory model of polymer crystallization. Phys. Rev. Lett. 56, 2708–2711. doi:10.1103/physrevlett.56.2708

PubMed Abstract | CrossRef Full Text | Google Scholar

Šarić, A., Michaels, T. C. T., Zaccone, A., Knowles, T. P. J., and Frenkel, D. (2016). Kinetics of spontaneous filament nucleation via oligomers: Insights from theory and simulation. J. Chem. Phys. 145, 211926. doi:10.1063/1.4965040

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmelzer, J. W. P. (2001). Comments on the nucleation theorem. J. Colloid Interface Sci. 242, 354–372. doi:10.1006/jcis.2001.7798

CrossRef Full Text | Google Scholar

Strobl, G. (2006). Crystallization and melting of bulk polymers: New observations, conclusions and a thermodynamic scheme. Prog. Polym. Sci. 31, 398–442. doi:10.1016/j.progpolymsci.2006.01.001

CrossRef Full Text | Google Scholar

Strobl, G. (2000). From the melt via mesomorphic and granular crystalline layers to lamellar crystallites: A major route followed in polymer crystallization? Eur. Phys. J. E 3, 165–183. doi:10.1007/s101890070030

CrossRef Full Text | Google Scholar

Turnbull, D., and Fisher, J. C. (1949). Rate of nucleation in condensed systems. J. Chem. Phys. 17, 71–73. doi:10.1063/1.1747055

CrossRef Full Text | Google Scholar

Volmer, M., and Weber, A. (1926). Keimbildung in übersättigten gebilden. Z. Phys. Chem. 119, 277–301. doi:10.1515/zpch-1926-11927

CrossRef Full Text | Google Scholar

Wu, T., Chandran, S., Zhang, Y., Zheng, T., Pfohl, T., Xu, J., et al. (2022). Primary nucleation in metastable solutions of poly (3-hexylthiophene). Macromolecules 55, 3325–3334. doi:10.1021/acs.macromol.1c02193

CrossRef Full Text | Google Scholar

Xu, J., Reiter, G., and Alamo, R. G. (2021). Concepts of nucleation in polymer crystallization. Crystals 11, 304. doi:10.3390/cryst11030304

CrossRef Full Text | Google Scholar

Zhang, M. C., Gao, Y., Guo, B. H., and Xu, J. (2017). A review on polymer crystallization theories. Crystals 7, 4. doi:10.3390/cryst7010004

CrossRef Full Text | Google Scholar

Zhang, S. J., Guo, B. H., Reiter, G., and Xu, J. (2020). Estimation of the size of critical secondary nuclei of melt-grown poly(l-lactide) lamellar crystals. Macromolecules 53, 3482–3492. doi:10.1021/acs.macromol.0c00113

CrossRef Full Text | Google Scholar

Zhang, S. J., Han, J. R., Gao, Y., Guo, B. H., Reiter, G., and Xu, J. (2019). Determination of the critical size of secondary nuclei on the lateral growth front of lamellar polymer crystals. Macromolecules 52, 7439–7447. doi:10.1021/acs.macromol.9b01270

CrossRef Full Text | Google Scholar