Pattern formation, structure and functionalities of wrinkled liquid crystal surfaces: A soft matter biomimicry platform

This review presents an integrated theoretical and computational characterization and analysis of surface pattern formation in chiral and achiral liquid crystal self-assembly and the mechanical/optical/tribological/tissue engineering surface functionalities that emerge from various wrinkling processes. Strategies to target surface patterns include linear, non-linear, multidirectional and multiscale wrinkling phenomena. The focus of the review is to show the unique surface structure-functionalities that emerge from anisotropic liquid crystal soft matter, eliminating or reducing the need of aggressive solvents, extreme pressure/temperature conditions, erosion and other surface morphing approaches. The surface pattern formation theoretical-modelling- computational results are then connected and validated with actual biological surfaces that are considered solid liquid crystal analogues, such as exocuticles of insects, fish scales, and flowers. A unique feature of the in silico surface pattern formation platform used throughout this review is the generalized liquid crystal shape equation that includes surface anchoring elasticity, membrane elasticity, and stress loads from liquid crystals orientation gradients. Clear characterization of surface shapes, curvatures, roughness, that are behind surface functionalities are introduced and applied to strengthen validation of predictions with actual nature’s surfaces. Wrinkling scaling laws, and the dependence of material properties on morphing mechanisms are elucidated. The predictions capture very well the two-scale wrinkling patterns in tulips, wrinkling gradients that display water sensor capabilities, egg carton shapes in rose petals and their potential for cell alignment, and the ability to create surface roughness with targeted kurtosis and skewness to control and optimize friction and tribological functionalities. The results are summarized in terms of surface geometry (open or closed) mechanisms and phenomena (anchoring, membrane elasticity), material properties (anchoring coefficients, membrane bending modulus, Frank elasticity), wrinkling scales and scaling laws (amplitude, wave-lengths, skewness, kurtosis) and functionalities (optical iridescence, friction, wettability, structural color, curvature-driven cell alignment and differentiation). Taken together, the range of surface geometries and surface functionalities captured by the liquid crystal biomimetic in silico platform provides a foundation for future experimental green manufacturing pathways based on anisotropic soft matter.

1 Introduction

Liquid crystallinity is a state of matter between solid and liquid when rod-like molecules align along a preferred macroscopic orientation (characterized by a unit vector or director n), exhibiting non-Newtonian viscous fluidity and anisotropy (Rey and Tsuji, 1998; Rey and Denn, 2002; Rey, 2009). Solid liquid crystal analogues are frozen liquid crystals due to external stimuli such as the presence of crosslinkers (Liang et al., 2021), and laser or plasma-triggered polymerization (Wang et al., 2018; Kameche et al., 2020). Solid liquid crystal analogues are ubiquitous in biological systems (Mazur et al., 1982). For example, chitin fibres with a helical structure form the exoskeleton of shimmering beetles (Sharma et al., 2009; Mitov, 2017), responsible for the structural colour. A similar structure is also found in mantis shrimps Weaver et al. (2012); Patek et al. (2004) and Homarus americanus (Raabe et al., 2007; Nikolov et al., 2015), which plays a significant role in their exceptional mechanical endurance. Biological plywood and human compact bones are other typical liquid crystal analogues, whose cellulose and collagen fibres align in a chiral liquid crystalline-like hierarchy, known as the Bouligand architecture (Cowin, 2004; Lagerwall et al., 2014; Gutierrez and Rey, 2017). Cellulose-based liquid crystals have various applications (Habibi et al., 2010; Li et al., 2021) such as serving as a steam engine driven by humidity (Geng et al., 2013), biofibres’ surface morphology sensor (Aguirre et al., 2016), piezoelectric sensor (Csoka et al., 2012; Rajala et al., 2016), water-based lubricant (Noroozi et al., 2014; Shariatzadeh and Grecov, 2019; Zakani et al., 2022), inducing long-range order in a semiconducting polymer (Risteen et al., 2017). The unique spatiotemporal and structural colours (Chagas et al., 2020; Saraiva et al., 2020; Silva et al., 2021) makes celluloses a promising optical material (Lagerwall et al., 2014; Ličen et al., 2016; Anyfantakis et al., 2020). Other examples such as DNA both in vivo (Bouligand, 1972) and in vitro (Chow et al., 2010), viruses Ilca et al. (2019), spider silk (Saravanan, 2006; Kluge et al., 2008), fibroblasts and osteoblasts (Kemkemer et al., 2000a; Kemkemer et al., 2000b) are also natural liquid crystal analogues in biological system. Theory, computation (Murugesan et al., 2011; Murugesan and Rey, 2010b; Murugesan and Rey, 2010c; Abou-Dakka et al., 2012; Khadem and Rey, 2019a; Khadem and Rey, 2019b; Khadem and Rey, 2021), and modelling (De Luca and Rey, 2003; Murugesan and Rey, 2010a; Gutierrez and Rey, 2014a; Gutierrez and Rey, 2014b; Murugesan et al., 2015; Aguilar Gutierrez and Rey, 2016; Gutierrez and Rey, 2016) of these systems are evolving and active fields seeking to link biological processes and liquid crystal self-assembly and liquid crystal self-organization (Park et al., 2021) to eventually contribute to biomimetic engineering of functional surfaces (Monaenkova et al., 2012; Lehnert et al., 2013; Tsai et al., 2014). The approach to link natures’ shapes and bionsipired functional surfaces is liquid crystal capillary science:

$\text{natures’\hspace{0.17em}shape}\underset{\text{extract\hspace{0.17em}principles}}{\stackrel{\text{LC\hspace{0.17em}contributions\hspace{0.17em}to\hspace{0.17em}biology}}{\to }}\text{liquid\hspace{0.17em}crystal\hspace{0.17em}capillary\hspace{0.17em}}\text{science}\stackrel{\text{biomimetics}}{\to }\text{bioinspired\hspace{0.17em}functional\hspace{0.17em}surfaces}$

Various classes of surface corrugations were observed in liquid crystal analogues (Tan et al., 2020) including creasing, folding, wrinkling (Yoo and Lee, 2005; Wu et al., 2007; Cutolo et al., 2020), and ridges (Jin, 2014; Wang and Zhao, 2015). Surface creasing is mostly studied in swelling-induced hydrogels (Trujillo et al., 2008; Zhou et al., 2017; Dortdivanlioglu et al., 2021), elastomers (Hong et al., 2009; Chen et al., 2012; Liu et al., 2019; Guan et al., 2022) and growth-driven soft tissues (Jin et al., 2011). Folding emerges in biological membrane system, such as in the Golgi apparatus (Norlén, 2001), mitochondrion membranes (Perkins and Frey, 2000; Joubert and Puff, 2021) and cortical folding (Mangin et al., 2004; Striedter et al., 2015; Garcia et al., 2018). The morphologies of biological membranes determine their functionalities. For example, the smooth endoplasmic reticulum sythesizes lipids and phospholipids (Cartwright and Higgins, 2001; Wilkinson et al., 2002), while folded rough endoplasmic reticulum is responsible for the secreted proteins (Lodish et al., 1983; Mandon et al., 2013). The surface corrugations usually perform a multiscale structure. Compared to creasing and folding, surface wrinkling has a smoother structure. Creasing, folding and wrinkling patterns can interconvert. For example, thermo-responsive wrinkling patterns can transform into foldings and can be applied to soft actuators (Tokudome et al., 2016). For load-driven surface corrugations, the creasing pattern appears at a lower critical compressive loading compared with the wrinkling pattern, which have both been validated experimentally (Gent and Cho, 1999; Cai et al., 2012) and theoretically (Karpitschka et al., 2017; Ciarletta, 2018; Ciarletta and Truskinovsky, 2019).

Surface pattern formation, characterization and functionality are formulated using differential geometry (Koenderink and Van Doorn, 1992; Kornev and Shugai, 1998; Kornev et al., 1999; Gutierrez and Rey, 2018; Zhang et al., 2018; Wang et al., 2020b; Alimov et al., 2021). A local surface patch has two principal surface curvatures κ₁ and κ₂ (κ₁ < κ₂), which can be used to describe surface geometry, as in the mean curvature H = (κ₁ + κ₂)/2 and the Gaussian curvature K = κ₁κ₂. The signs of (H, K) are used to classify surfaces such as cylinders, domes, and saddles. These geometric quantities (H, K) comingle shape and length scales since H and K have dimensions of the reciprocal length but another measure can be used that avoids this commingling of shape and length scale. Hence it is useful to use the dimensional Casorati curvedness C) and the normalized, dimensionless shape parameter S), developed in the previous literature (Koenderink and Van Doorn, 1992; Gutierrez and Rey, 2018; Wang et al., 2020b). The curvedness characterizes the amplitude of wrinkling, while the shape parameter is a dimensionless scalar that differentiates spherical, cylindrical and saddles patches. In this manuscript, we focus on 1D and 2D open surface corrugations. A 1D surface corrugation (for example, Figure 1C) shows a wrinkling profile along a single direction (x or y) and has a vanishing Gaussian curvature. A 2D surface corrugation (Figure 1F) depends on two orthogonal directions (x and y). Complex synthetic and biological surfaces have a spatial distribution of amplitudes and shapes and hence distribution functions are required. A global statistical method can be applied to study surface roughness (Tayebi and Polycarpou, 2004; Hansson and Hansson, 2011; Sedlaček et al., 2012). The local curvatures and global geometric statistics determine the surface functionalities. For example, a cytoskeleton organization can be topology-induced on a local concave (S = −1), convex (S = +1), and hyperboloid surface (S = 0) (Yang et al., 2022). Torn plastic sheets and leave’s photosynthesis are also geometry-driven wrinkling process (Nath et al., 2003; Sharon et al., 2004; Sharon et al., 2007). Other examples of curvature-dependent applications in tissue engineering (Rumpler et al., 2008; Blanquer et al., 2017) can be found in regulating stem cell migration and differentiation (Werner et al., 2017), the behaviours of cellular growth (Park et al., 2009) and early osteogenesis Ozdemir et al. (2013), bone tissue regeneration (Zadpoor, 2015) and scaffolds with various geometry (Bidan et al., 2013).

FIGURE 1

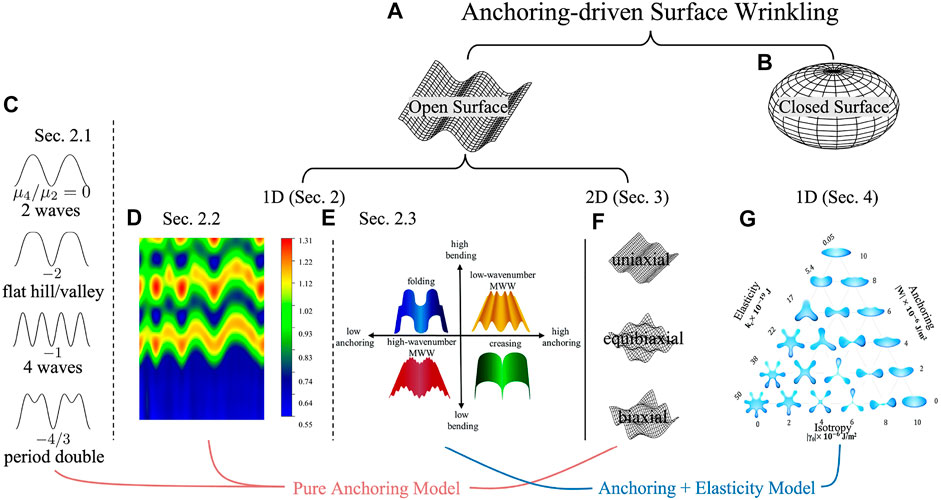
FIGURE 1. Structure, organization, and contents of this review on liquid crystal biomimetics of functional surfaces via surface pattern formation (wrinkling, folding, and creasing). The generic anchoring-driven surface wrinkling phenomenon is observed in both open surfaces (A) and closed surfaces (B). (C) 1D surface studied with a higher order quartic anchoring model. (D) 1D surface with spatially varying helix pitch. (E) 1D surface evaluated by a quadratic anchoring model, with consideration of membrane bending elasticity. (F) 2D surface studied with a quadratic anchoring model. (G) The morphology of 1D droplet is evaluated by an anchoring model modified with membrane bending elasticity. (D) Is reprinted from (Rofouie et al., 2015a), with the permission of AIP Publishing. (E) Is reproduced from (Rofouie et al., 2017a) with permission from the Royal Society of Chemistry. (G) Is reproduced from (Rofouie et al., 2017b) with permission from the Royal Society of Chemistry.

There are multiple ways to generate surface corrugation, such as the presence of plasma (Nania et al., 2015; Cheng et al., 2016; Cheng et al., 2017) or laser (Hu et al., 2017; Wang J. et al., 2019), electric (Lin et al., 2020) or magnetic field Wu and Destrade (2021); Tokarev et al. (2014), and stress field (Rodriguez-Hernandez, 2015). The change of humidity (Zhang et al., 2020), pH González-Henríquez et al. (2018), temperature (Park et al., 2015), polymerization (Bergmann et al., 2020; Junisu et al., 2022) and drying process Izawa (2017) also disturb surface wrinkling. Surface corrugations are widely used in bioinspired multifunctional materials, such as the flexoelectric materials (Castles et al., 2011; Herrera-Valencia and Rey, 2014; Rey et al., 2014b; Herrera Valencia and Rey, 2018; Zhang et al., 2021) and curvature-induced magnetochiral materials (Hertel, 2013; Sloika et al., 2014). A liquid crystal surface coated with surfactants shows elasticity, whose classical theory is first proposed by Helfrich (Helfrich, 1973), and further completed by Ou-Yang (Zhong-Can and Helfrich, 1987). The membrane elastic model successfully predicted the biconcave discs observed in human red blood cells and was validated in the literature (Seifert et al., 1991; Kuzman et al., 2004; Mu et al., 2020; Martínez-Balbuena et al., 2021). Theoretical research of surface wrinkling patterns by Helfrich elastic theory is studied in (Baumgart et al., 2005; Bian et al., 2020). However, the elastic model of a system with open free edges is problematic. Tu (Tu, 2010; Zhan-Chun, 2013) proved that if line tension is finite, an open membrane cannot have constant non-zero mean curvature (Tu and Ou-Yang, 2014). More numerical solutions to surfaces’ shapes by using a pure elastic model are studied in (Umeda et al., 2005; Li et al., 2013). However, all the models discussed above require an external force field, such as an electric (Lin et al., 2020) or magnetic field Wu and Destrade (2021), or the presence of mechanical stress (Rodriguez-Hernandez, 2015). The anchoring model (Rey, 2010; Rey and Herrera-Valencia, 2012; Rey et al., 2014a) on the other hand, enables the discussion of self-assembled structure, which is a unique architecture observed in liquid crystal. The anchoring model (Rey, 2007; Rey and Murugesan, 2011; Rey et al., 2013) is a prevailing method when multiscale wrinkling patterns are formed. The anchoring model is based on the anisotropic nature of the interfacial tension of liquid crystals (Rey, 1999a; Rey, 2000a; Rey, 2000c; Cheong et al., 2001; Rey, 2001b; Cheong and Rey, 2002a; Cheong and Rey, 2002b; Cheong and Rey, 2002c; Zhou et al., 2002; Rey, 2007; Kim et al., 2016). The total interfacial (surface) tension involving a liquid crystal of orientation n (n = −n, n² = 1) at a surface with outward unit normal k is: γ = γ₀ + μ₂ (n ⋅k)² + μ₄ (n ⋅k)⁴ + …. The presence of liquid crystalline orientation n) and anisotropic surface tension μ₂ (n ⋅k)² + μ₄ (n ⋅k)⁴ + … creates a new pathway to surface pattern formation models and predictions based on liquid crystalline self-assembly and self-organization. For example, capillary pressures can include dilation, tilting and orientation contributions, enriching the number and types of forces and torques that can be used to create wrinkling and folding patterns, close to those observed in nature, likewise tangential forces due to anchoring and orientation gradients generate new types of Marangoni flow beside the usual thermo- and chemo-capillarity (Rey, 1999c). Generalizations to liquid crystal-membrane models, that combine anchoring and membrane elasticity yield shape diagrams that naturally incorporate the three shaping modes of bending, creasing, and folding (Yoo and Lee, 2005; Wu et al., 2007; Jin, 2014; Wang and Zhao, 2015; Cutolo et al., 2020) and point to a rich unexplored area of surface pattern formation in soft matter.

In this review we summarize key principles and most significant applications of liquid crystal capillarity applied to synthetic and biological surface pattern formation, building on our previous contributions (Rey, 1999a; Rey, 2000a; Rey, 2000c; Cheong et al., 2001; Rey, 2001b; Cheong and Rey, 2002a; Cheong and Rey, 2002b; Cheong and Rey, 2002c; Rey, 2007) and shedding light on the origin of scaling laws, material properties, and optical/sensor/actuator/wetting/tribological functionalities. Some of the issues of key phenomena, processes, mechanisms, and functionalities presented in this review are.

1. What are the new capillary pressure contributions to shape generation arising from liquid crystal anisotropic interfacial tension?

2. What are the scaling laws relating orientation n) length scales and anchoring coefficients W), and wrinkling amplitudes and wrinkling wavelengths?

3. What are the new phenomena arising from higher order (quartic as opposed to just quadratic) formulations of the anchoring energy, including multiple wrinkling scales and amplitudes?

4. What is the role and impact of surface orientation gradients (∇_surfacen) on shape generation? Is there a connection between basic orientation deformation modes (known as splay, bend) and mean surface curvature H)?

5. What is needed to generate biaxial wrinkling, such as those found in egg cartons and their variants?

6. What are typical surface geometry statistics (important in tribology, friction, and wetting), including kurtosis and skewness, emerge from different wrinkling patterns?

7. What are distinct surface functionalities, such as optical, tribology, wetting, that are captured by the liquid crystal anchoring-driven wrinkling?

8. What are the new surface pattern formation modes that emerge by combining liquid crystal anchoring and membrane bending elasticity?

Answering these questions provides the framework to develop bioinspired functional surfaces via the liquid crystal biomimetic platform.

Figure 1 presents a flowchart of the organization and flow of information in this review. The anchoring-driven surface wrinkling patterns appear in both open surfaces (such as tulip petals) and closed surfaces (such as drops or tactoids). In Section 1 we introduce the background and motivation for studying the surface of liquid crystal analogues found in nature. In Section 2.1 we review the 1D open surface corrugation governed by the pure anchoring model and the application to friction. In Section 2.2, we review the influence of the helix pitch of cholesteric liquid crystal analogues on the geometry and the application in diffraction gratings. The membrane elastic model is introduced in Section 2.3 for obtaining a more complex wrinkling pattern, with application in surface wettability. In Section 3, we focus on the 2D open surface corrugations. In Section 4, we review the wrinkling profile of the liquid crystal droplet with an enclosing elastic membrane. The closed droplet morphology reviewed in Section 4 shows a completely different wrinkling mechanism compared to the open surface discussed in Section 2 and Section 3. The bulk-surface interaction plays a significant role in the wrinkling formation of a closed droplet, which can be neglected for an open surface. In this review, wrinkling is emphasized but creasing and folding are also discussed.

2 1 D open surface wrinkling: Cylindrical patterns

2.1 Pure anchoring model with application to friction

The multiscale surface wrinkling is a unique structure observed in many plants (Lin et al., 2017; Schauer et al., 2017), for example, the Queen of the Night tulip (Oh et al., 2019), Yunnan rhododendron, daisy Ursinia calendulifolia (Antoniou Kourounioti et al., 2013) and Hibiscus trionum (Vignolini et al., 2015; Chen et al., 2021). The tulip Queen of the Night exhibits glossy and iridescent colour due to the scattering and diffraction effect (Figure 2B). The special optical effect for those petals plays an important role to attract bees Whitney et al. (2009), further benefiting the pollination van der Kooi et al. (2015). The important point here is that the surface is composed of larger and smaller features that can be approximated by two-scale wrinkling. Figure 2 presents the biological example and numerical simulation for 1D open surface wrinkling. Figure 2A shows the AFM image of the cylindrical surface corrugations observed on Tulip Queen of the Night. Figure 2B is the schematic of how the wrinkling geometry affects the glossy and iridescent colour of tulip petals by light scattering and diffraction.

FIGURE 2

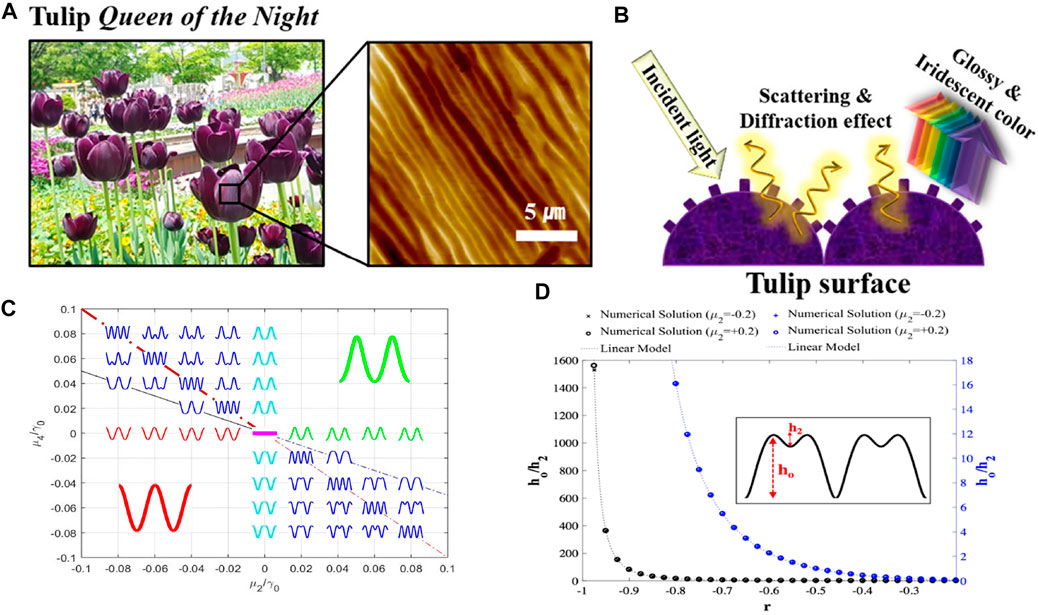
FIGURE 2. Biological cylindrical (corrugation with a single wave-vector) wrinkling patterns and the simulation results. (A) AFM image of Queen of the Night tulip petals. (B) The optical effects on the surface of tulip petals. (C) Dimensionless parametric anchoring μ_4*− μ_2* space and characteristic wrinkling profiles, where the pink line in the centre represents a flat surface. (D) Representative two scale wrinkling and definition of large (h₀) and small (h₂) wrinkling scales. In (C) we observe: (I) up-down symmetry between second and fourth quadrants and between first and third quadrants and (ii) the maximal two scale wrinkling appears below and above the diagonal line (red dash-dot line) crossing the 2–4th quadrants. (A) and (B) are reprinted with permission from (Oh et al., 2019). Copyright ⓒ 2019, American Chemical Society. (C) and (D) are reproduced from (Rofouie et al., 2018) with permission from the Royal Society of Chemistry.

The anchoring model is developed to describe the multiscale cylindrical surface wrinkling profile and the pattern formation mechanism (Rofouie et al., 2014; Rofouie et al., 2015a; Rofouie et al., 2015b; Rofouie et al., 2018; Wang Z. et al., 2019; Wang et al., 2020a). A cylindrical surface means 1D wrinkling as in a simple corrugation, with one-directional wave-vector. As mentioned above, the anisotropic surface energy density γ is described by the Rapini-Papoular equation, which regards γ as a function of the director n of liquid crystal, and the surface unit normal k Stewart (2019); Sonin (1995); Rey (2000a); Rey (2000c); Cheong et al. (2001); Cheong and Rey (2002a); Cheong and Rey (2002b); Cheong and Rey (2002c); Rey, (2007):

$\frac{\gamma }{{\gamma }_0}=1+{\mu }_2^{*}{\left(\mathbf{n}\cdot \mathbf{k}\right)}^2+{\mu }_4^{*}{\left(\mathbf{n}\cdot \mathbf{k}\right)}^4+\text{higher\hspace{0.17em}order\hspace{0.17em}terms}(1)$

where γ₀ is the isotropic surface tension, ${\mu }_2^{*}$ is the dimensionless quadratic anchoring coefficient, and ${\mu }_4^{*}$ is the dimensionless quartic anchoring coefficient. Eq. 1 implies that by reversing n → −n or k → −k, the surface energy density is unaffected. The contribution from higher order terms can be neglected due to −1 ≤ n ⋅k = cos θ ≤ 1, where θ is the angle between surface normal k and director n, as shown in Figure 3. Planar anchoring (Figure 3A) and homeotropic anchoring (Figure 3B) correspond to θ = π/2 and θ = 0, respectively. Figure 3D shows the normalized surface tension reduction as a function of θ by assigning different μ₄/μ₂ values. The maximum surface tension reduction occurs at a different position, implying a complex wrinkling phenomenon dependent on μ₄/μ₂. The stable surface wrinkling profile is controlled by the momentum balance equation along k-direction (Rey, 1997a; Rey, 1997b; Rey, 1999a; Rey, 1999c; Rey, 2001a; Rey, 2001b; Wang Z. et al., 2019):

$\text{bulk\hspace{0.17em}stress\hspace{0.17em}jump}\left(f_b,p_c\right)={\nabla }_s\cdot \mathit{\xi }(2)$

where p_c is the pressure difference between the liquid crystal phase and the isotropic phase, f_b is the bulk elastic energy density, ξ is the Cahn-Hoffman capillary vector (Hoffman and Cahn, 1972; Cahn and Hoffman, 1998). The capillary vector ξ is a useful tool to model surface pattern formation and can be seen as the sum of a Lagrange multiplier or constraint (normal component) and the Lagrangian derivative (tangential component):

$\mathit{\xi }=\underset{{\mathit{\xi }}_{\perp }:\text{constraint}}{\underbrace{\gamma \mathbf{k}}}+\underset{{\mathit{\xi }}_{\perp }:\text{Lagrangian\hspace{0.17em}derivative}}{\underbrace{{\mathbf{I}}_s\cdot \frac{\delta F_s}{\delta \mathbf{k}}}},{\mathbf{I}}_s=\mathbf{I}-\mathbf{k}\mathbf{k}(3)$

where F_s is the total surface free energy obtained from the area integral of the interfacial tension. An open surface has a vanishing stress jump (Wang et al., 2020a), which results in the governing equation (Wang et al., 2022)

$0=\underset{\text{Dilation\hspace{0.17em}Pressure}}{\underbrace{-\frac{\partial {\mathit{\xi }}_{\perp }}{\partial \mathbf{k}}:{\left({\nabla }_{\left(\sigma \right)}\mathbf{k}\right)}^T}}\underset{\text{Director\hspace{0.17em}Pressure}}{\underbrace{-\frac{\partial {\mathit{\xi }}_{\Vert }}{\partial \mathbf{n}}:{\left({\nabla }_{\left(\sigma \right)}\mathbf{n}\right)}^T}}\underset{\text{Rotation\hspace{0.17em}Pressure}}{\underbrace{-\frac{\partial {\mathit{\xi }}_{\Vert }}{\partial \mathbf{k}}:{\left({\nabla }_{\left(\sigma \right)}\mathbf{k}\right)}^T}}(4)$

Eq. 4 captures the wrinkling patterns on the tulip petals (Rofouie et al., 2014; 2015b; a, 2018), which are the cancellation effects between the dilation pressure, director pressure and rotation pressure. The director pressure depends on the director field n, which is the driving force of the wrinkling profile. To eliminate the director pressure, a surface patch induces a local rotation (rotation pressure) and local dilation (dilation pressure), which changes the geometry by affecting k, and is performed as self-assembly.

FIGURE 3

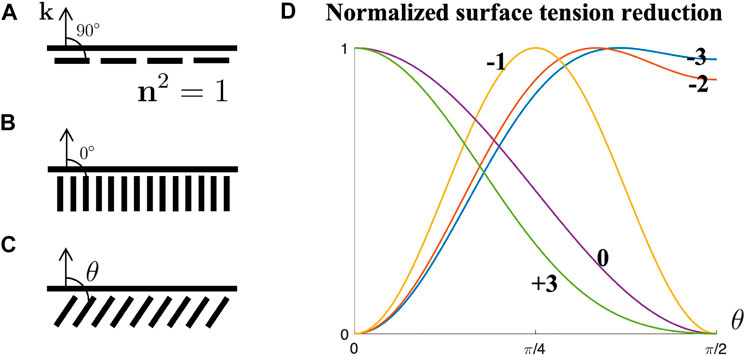
FIGURE 3. (A) Planar anchoring. (B) Homeotropic anchoring. (C) Oblique anchoring. (D) Normalized surface tension reduction Norm [(γ − γ₀)/μ₂] as a function of oblique angle θ with varying μ₄/μ₂ value.

Figure 2C is the anchoring parameter space μ₄ − μ₂, superposed with the computed surface wrinkling profiles h(x). The wrinkling parametric space is characterized by a resonant line (thick red line) and a damping line (thin black line). Maximal two-scale wrinkling occurs above and below the resonant line. Two-scale wrinkling only arises in quartic anchoring models when the anchoring coefficients have opposite signs (−+) or (+−). Figure Figure2d) shows representative two-scale wrinkling profiles and defines the large (h₀)and small (h₂) scales of the amplitudes. The solution of the shape equation and analysis (Rofouie et al., 2018) reveals the presence of novel quadratic scaling laws for two-scale h₀, h₂ wrinkling:

$\frac{h_0}{h_2}=\frac{{\left({\mu }_2/2{\mu }_4\right)}^2}{{\left(1+{\mu }_2/2{\mu }_4\right)}^2}(5)$

whose critical value h₀/h₂ = 2 is easily accessible by the anchoring coefficients. Four fundamental wrinkling modes: two waves, flat hill/valley, four waves and periodic double are summarized in Figure 1C.

In partial summary these results clearly show that multiscale wrinkling emerging from higher order anchoring energies is a simple manifestation of the coupling between liquid crystal orientation n) and local surface geometry k) and the scaling law and up-down symmetry is hence fertile in surface functionalities.

Having described and analyzed 1D two-scale wrinkling due to higher order anchoring, next we discuss functionalities arising from rough, non-planar surfaces that we are able to produce in silico using the shape Equation 4. The surface wrinkling is often studied along with the roughness characterization due to its effects on surface friction, restitution, and adhesion Persson et al. (2004); Emmens (1988); Li et al. (2020a). Two significant roughness parameters are the skewness (Ssk) and kurtosis (Sku), corresponding to the third-order and fourth-order moment information of wrinkling profile distribution function (Tayebi and Polycarpou, 2004). Skewness and kurtosis are dimensionless parameters that are scaled by the third and fourth order of standard deviation. A normal distribution results in a vanishing skewness and Sku = 3. The higher the absolute value of skewness, the larger the deviation from the normal distribution. Positive skewness implies a surface with tall peaks, and negative skewness implies a surface with low valleys (see Figure 4B). The kurtosis portrays how much sharp peaks or valleys contribute to the surface profile (see Figure 4C). The skewness-kurtosis plot (Figure 4D) can be used to study the roughness of biological surface topography (Wainwright et al., 2017), thermal-hydraulic performance Liao et al. (2020, 2021), normal contact stiffness (Belhadjamor et al., 2020) and other processes (Wang Y. et al., 2021; Ba et al., 2021).

FIGURE 4

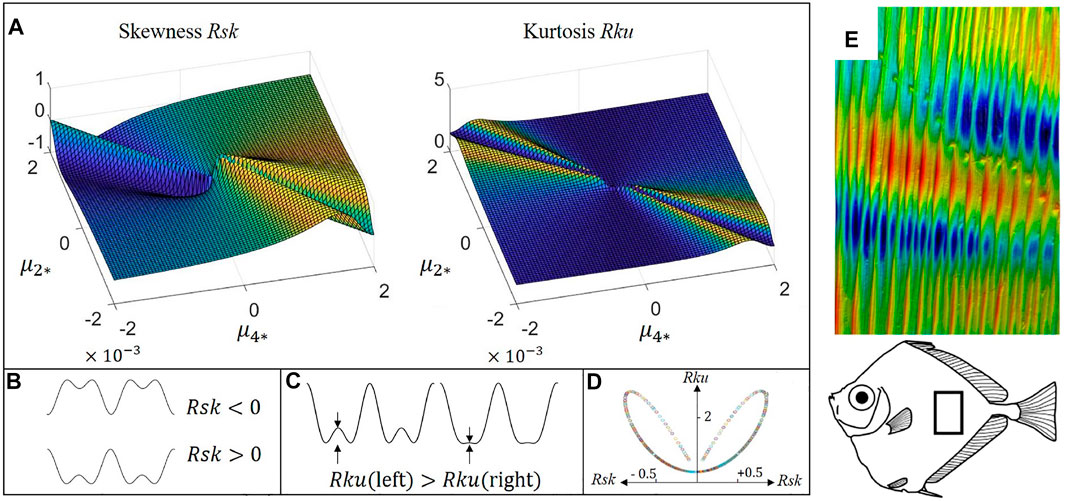
FIGURE 4. Computed surface roughness parameter skewness and kurtosis (Tayebi and Polycarpou, 2004) as a function of dimensionless anchoring parameters, with applications found on the fish surfaces: (A) The skewness and kurtosis computed from the pure anchoring model. (B) and (C) are the schematics of the physical meaning of skewness and kurtosis, respectively. (D) Is the skewness-kurtosis plot obtained from (A). (E) The cylindrical surface wrinkling of spotted tinselfish (Xenolepidichthys dalgleishi): 9.22 mm × 13.6 mm, amplitude z:388 μm. (A–D) are reprinted with permission from (Wang et al., 2020a). Copyright (2020) by the American Physical Society. (E) Is reprinted with permission from (Wainwright et al., 2017). Copyright (2017) by the John Wiley & Sons.

Figure 4a) shows representative results of skewness and kurtosis using Eq. 4. The wrinkling pattern shows rich skewness and kurtosis information when the two anchoring coefficients have opposite sign. A bioinspired application is found on fish scalps; Figure 4E shows the cylindrical wrinkling profile of spotted tinselfish, whose skewness and kurtosis data are evaluated in (Wainwright et al., 2017). Most of the surfaces are approximated close to a normal distribution, showing an almost vanishing skewness, and such surface can be easily obtained by setting μ₂ = μ₄ in pure anchoring model (see Figure 4A). Figure 4D shows that the anchoring model produces a wide range of skewness and kurtosis, with maximum values max (Rku) ≈ 3 and max (Rsk) ≈ 1. Positive skewness implies a surface with sharp peaks, which is mostly obtained by setting μ₄ > 0 and μ₂ < 0. Such surface is observed in triggerfish (Rsk = 0.42), armored catfish (Rsk = 0.13), and trout with mucus (Rsk = 0.15). On the contrary, negative skewness (μ₄ < 0 and μ₂ > 0) is observed in squirrelfish (Rsk = −0.11) and hammerhead shark (Rsk = −0.14). Most biological surfaces also show a kurtosis smaller but close to 3, implying a surface lacking of extreme peaks or valleys, for example, bonefish (Rku = 2.9), squirrelfish (Rku = 3), armored catfish (Rku = 2.8). Some extreme values of kurtosis can also be found in longnose butterflies (Rku = 4.1) and red maple leaves (Rku = 4.3) (Wainwright et al., 2017).

In partial summary, moving in the anchoring parameter space generates (Figure 2C) a kurtosis-skewness bilobal loop (Figure 4d)) that captures a wide range of functional biological surfaces, including butterflies, maple leaves, and tinsel fish. The experiment validation can be found in (Maeda, 1999; Kirkwood and Fuller, 2009; Fernandes et al., 2013).

2.2 Surface with varying amplitude and optical applications

The most abundant examples of solid liquid crystal analogues in nature display the Bouligand architecture, or cholesteric liquid crystal (Patek et al., 2004; Sharma et al., 2009; Weaver et al., 2012; Sharma V. et al., 2014; Mitov, 2017). The helix pitch of cholesteric liquid crystal P₀ is the distance under which the chiral director field n undergoes a full rotation: n(x) = n (x + P₀). In Section 2.1, P₀ was considered as a constant, which in nature, could be sometimes unrealistic. The humidity of the environment changes the helix pitch, which further affects the surface profile and its optical properties. For example, beetles Dynastes hercules, Coptocycla, Tmesisternus isabellae (Hinton and Jarman, 1972; Hadley, 1979; Liu et al., 2009) and vascular plant Selaginella willdenowii (Lee and Lowry, 1975) can adjust their structural colour to the humidity of environment.

The Frank energy density is dependent to the Frank constant K (Priest, 1973; Straley, 1973), the helix pitch P₀ and the director field n: f_b = f_b (K, P₀x), n) (Rofouie et al., 2015a). Including f_b and solving Eq. 2 yields the numerical solutions to the wrinkling profile with varying helix pitch P₀x).

Figure 5 shows representative numerical simulations of surface wrinkling profiles with varying amplitude. Figure 5a) demonstrates how the following four significant factors appearing in our shape equation manipulate the wrinkling profile (Rofouie et al., 2015a): 1) the dimensionless quadratic anchoring coefficient W/γ₀ (equivalent to 2μ* in Equation 1, 2) the elasto-capillary length scale K/γ₀, 3) the micron scale pitch in dry state P_dry, and 4) the hydration-driven pitch gradient (P_wet − P_dry)/L, respectively. Figure 5A to Figure 5D verifies that by increasing all the four factors, the amplitude is enhanced. The surface amplitude doubles if the anchoring coefficient is also doubled. However, multiplying K/γ₀ by 100 does not change wrinkling amplitude significantly, showing a highly non-linear effect. Figure 5C shows that higher P_dry results in a larger periodicity. And Figure 5D shows the both the amplitude and periodicity increase. They are dependent on the x-axis due to the gradient effect.

FIGURE 5

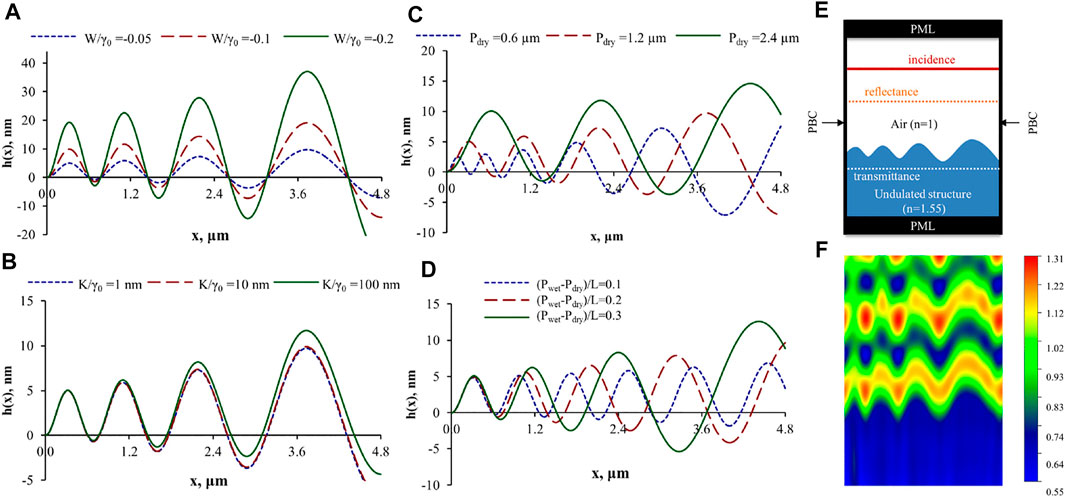
FIGURE 5. (A–D) Surface profiles h(x) with increasing wrinkling amplitudes and wave-lengths, driven by changes in the orientation spatial scales due to changes in spatial hydration levels; increasing the pitch P₀ by water absorption increase the wrinkling scales. Basic parameters are defined by K/γ₀=1 nm, P_dry =1.2 μm (P_wet − P_dry)/L =0.2 and W/γ₀=−0.05 (W =2μ₂). (A) Basic parameters are used except for W/γ₀. (B) Basic parameters are used except for K/γ₀. (C) Basic parameters are used except for P_dry. (D)Basic parameters are used except for (P_wet − P_dry)/L. (E) 2D schematic of air-CCLC (cellulosic cholesteric liquid crystal) interface with varying pitch. (F) Scattered electric field of 480 nm normal incident light for (E) with periodic boundary condition on the left and right wall. Reprinted from (Rofouie et al., 2015a), with permission of AIP publishing.

The periodicity shown in Figure 5A to d is around 1,000 nm, which is the same order as the wavelength of visible light. If the visible light is the incident light, the iridescence and colours appear due to diffraction grating (Vignolini et al., 2013) (a schematic is previously shown in Figure 2B). Figure 5F presents the scattering patterns for a surface with varying pitch (Figure 5E) with blue incident light (wavelength: 480 nm). The scattering and diffraction effect of surface wrinkling on beetles’ exoskeletons cause iridescent colours (Sharma et al., 2009). The sensitivity of structural colour to humidity of beetles (Kim et al., 2010; Sun et al., 2021) is directly generated by varying pitch. The simulation result is validated by (Terris et al., 1992), as shown in (Rofouie et al., 2015a).

In partial summary, the general liquid crystal shape Equation 4 contains the mechanisms to generate variable spatial wrinkling due to spatial gradients in water content. The wrinkling can be used as water sensors when coupled to optical responses. This is another example of liquid crystal surface functionality that bio-mimics structural colour in nature.

2.3 Elastic anchoring model with application in hydrophobicity

The Rapini-Papoular anchoring model in Eq. 1 captures the anisotropic nature of liquid crystal films through the surface unit normal k. In biological membranes, the compressive strain and tensile lead to a contribution that is dependent to the gradient of k. Such mechanical effects are found in cell membrane (Lamparter and Galic, 2020; Jia et al., 2022), human neurons (Bianchi et al., 2019), mitochondria (Bostwick et al., 2016) and others (Azzari et al., 2021; Bagnani et al., 2021; Harbola et al., 2021). The Helfrich elastic model was applied to study the shape of red blood cell (Martínez-Balbuena et al., 2021) and lipid bilayer structure (Campelo et al., 2014). The elastic contribution to the anisotropic surface tension (Rofouie et al., 2017a) yields a membrane-liquid crystal tension (Rey, 1999b; 2003; Shams et al., 2015)

$\gamma ={\gamma }_0+\frac{k_c}{2}{\kappa }^2+\frac{W}{2}{\left(\mathbf{n}\cdot \mathbf{k}\right)}^2(6)$

where κ is the surface curvature and k_c the bending rigidity (Helfrich, 1973). By introducing the compression $T_0={\gamma }_0-(k_c/2){\kappa }_0^2$, Eq. 2 reduces to a second order ordinary differential equation.

Figure 6A and b present the daisy Bellis perennis and the SEM micrograph. Smaller corrugations are observed on top of a larger wrinkling peak, unlike Figure 2A. This delicate wrinkling pattern implies that another wrinkling mechanism should also play a role besides pure anchoring model. Figure 6C to f show the numerical simulations by introducing the elastic contribution into our shape Equation 4. Rofouie revealed that the chiral liquid crystal-membrane model is similar to a driven pendulum (Rofouie et al., 2017a), and four critical parameters were introduced to analyze the multiscale wrinkling patterns shown in Figure 6A and b:

$l_{\text{chiral}}=P_0,l_{\text{membrane}}=\sqrt{\frac{k_c}{|T_0|}},\omega =\frac{l_{\text{chiral}}}{l_{\text{membrane}}}=\frac{P_0}{\sqrt{k_c/|T_0|}},\bar{W}=\frac{W}{T_0}(7)$

l_chiral and l_membrane are the two length scales. ω is the dimensionless winding number, and the dimensionless $\bar{W}$ is the ratio of anchoring effect to mechanical compression. The pair $(\omega ,\bar{W})$ can be used to categorize different models: pure anchoring model (CLC) implies that ω → ∞ and $\bar{W}=W/{\gamma }_0$; pure elastic model M) implies that $\omega =\bar{W}=0$; and anchoring-elastic model (CLC-M) has finite values for both ω and $\bar{W}$. The limit cycles and phase plots (as used in a pendulum model) for the three models are demonstrated in Figure 6E and f. Clearly, the elastic-liquid crystal model creates a complex wrinkling profile due to the constructive interaction of stress load and anchoring.

FIGURE 6

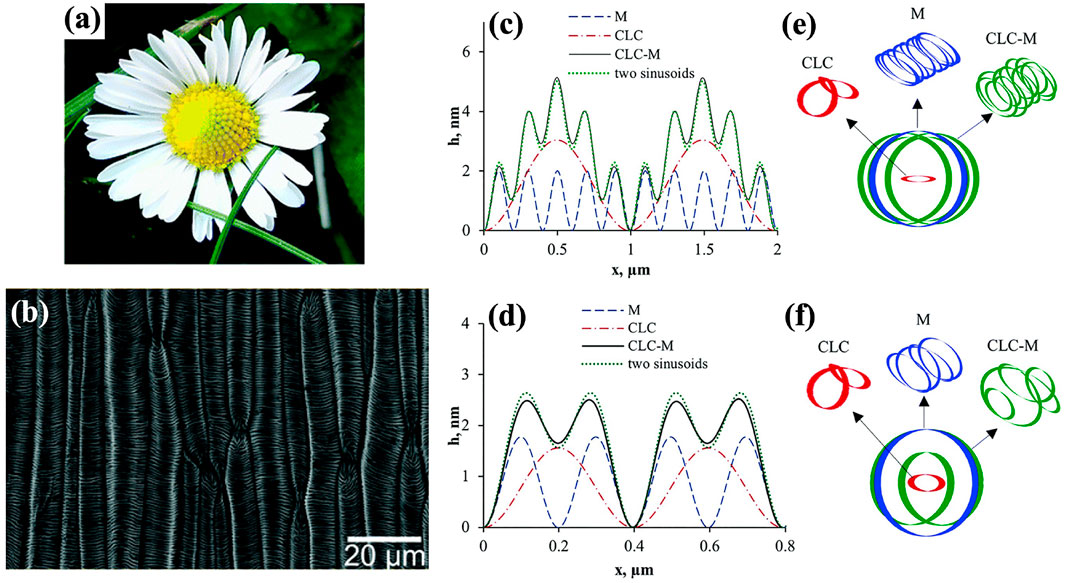
FIGURE 6. (A) and (B) Daisy Bellis perennis and the SEM micrograph. (C) To (F), numerical results of surface profile and the corresponding limit cycles and phase plots of elastic model (M), anchoring model (CLC), and anchoring-elastic model (CLC-M) computed at W =−1 × 10⁻⁴ J/m², k_c = 5 × 10⁻¹⁸ J, T₀=−5 × 10⁻³ J/m² (C) and (E), P₀=1.98 μm, ω =10. (D) and (F), P₀=0.79 μm, ω =4. (A) and (B) are used with permission of Royal Society of Chemistry (2017), from (Schauer et al., 2017); permission conveyed through Copyright Clearance Center, Inc. (C–F) are reproduced from (Rofouie et al., 2017a) with permission from the Royal Society of Chemistry.

The wettability of multiscale wrinkling patterns on an elastic membrane is commonly studied (Jun et al., 2017; Li et al., 2019; Liu et al., 2022) due to its influence on surface chemical and physical properties (Vatansever et al., 2012; Deng et al., 2019; Zhou et al., 2020). Figure 7B and c demonstrate how the contact angle of the water droplet varies with different surfaces. The contact angle increases by 20.6° from an unwrinkled surface to a wrinkled surface, which validates that the contact angle is a tunable parameter that is dependent on the wrinkling profile. A significant control parameter is the dimensionless ratio of the height over spacing in the buckles (H_b/S_b) (Byeon et al., 2020). reveals a linear relationship between the contact angle and H_b/S_b. The contact angle increases up to ∼60° with varying H_b/S_b. In partial summary, desired surface wettability can be achieved by adjusting the surface materials. To study the complex 1D open surface wrinkling, biomimetic approaches such as beetles-derived polarizers, and fish-skin inspired swimming suits can be widely applied in environmental-friendly industries.

FIGURE 7

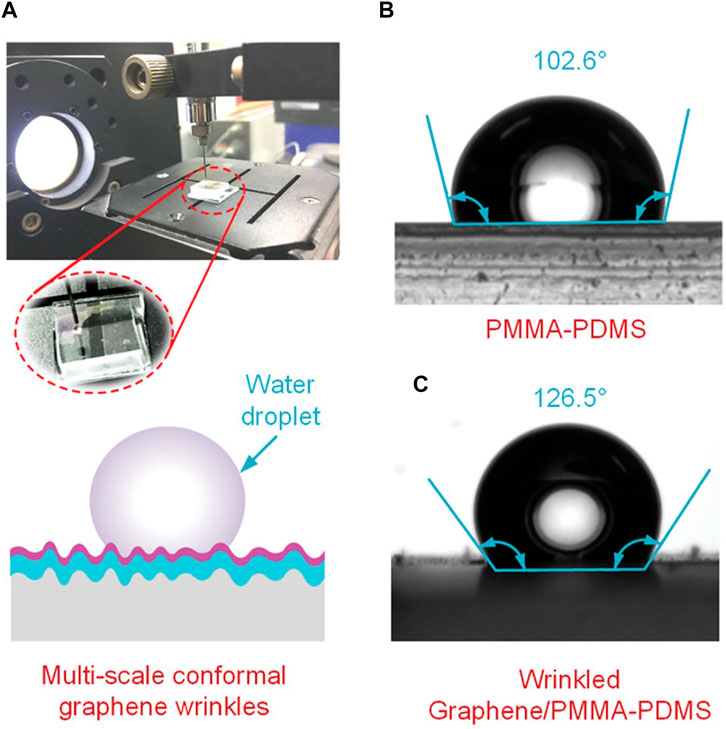
FIGURE 7. (A) Testing platform and schematic. (B) and (C) The material and the wrinkling profile of supporting surface affect the contact angle. Reprinted with permission from (Hu et al., 2020). Copyright (2020) by the John Wiley & Sons.

3 2D open surface wrinkling: Egg carton corrugations

The egg carton surface is a ubiquitous nature’s and engineering pattern that appear in various materials and processes, such as the electropolished zirconum (nm-scale), the papillae of rose petals (Figure 8A) and dactyl club (µm-scale), erosion-driven rocks (cm-scale) and others (Abukhdeir and Vlachos, 2011; Seeber et al., 2011).

FIGURE 8

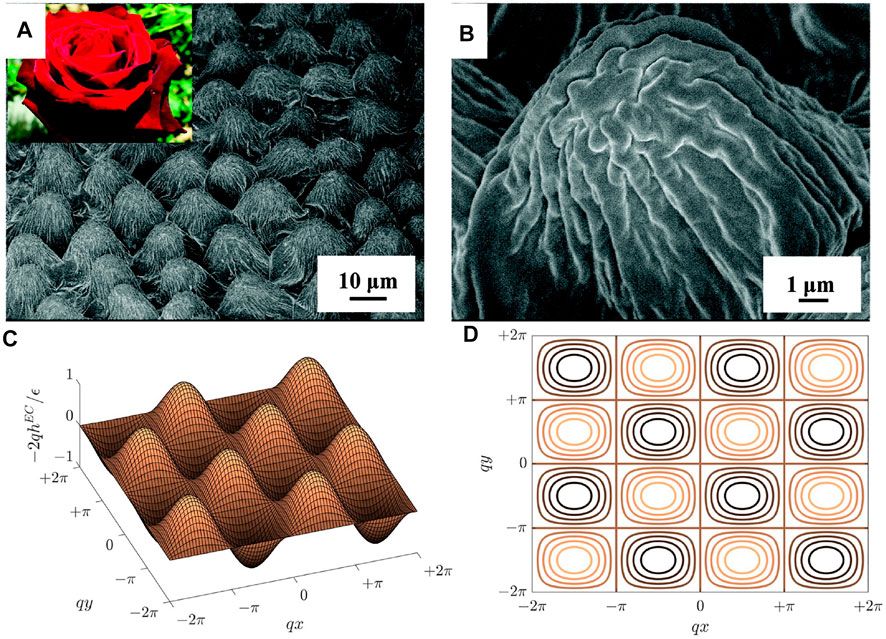
FIGURE 8. (A) and (B) SEM images of the surface of rose petal surface. (C) The egg carton wrinkling profile from pure anchoring model solved in 2D. (D) The top view of (C). (A) and (B) are reprinted with permission from (Feng et al., 2008). Copyright ⓒ 2008 American Chemical Society. (C) and (D) are reprinted from (Wang Z. et al., 2021), Copyright (2021), with permission from Elsevier.

Eq. 4 is the governing equation to the anchoring-driven wrinkling phenomenon in a 2D open surface. By applying a periodic boundary condition, Eq. (4) leads to a highly non-linear second-order partial differential equation. Using a perturbation method by expanding the surface energy and unit normal as follows (Wang Z. et al., 2021)

$\gamma ={\gamma }_0+ϵ{\gamma }^{\left(1\right)}+\dots ,\mathbf{k}=\widehat{{\mathit{\delta }}_z}+ϵ{\mathbf{k}}^{\left(1\right)}+\dots (8)$

where ϵ is a small parameter, $\widehat{{\mathit{\delta }}_z}$ is a unit vector perpendicular to the (x, y)-plane and upper index 1) represents the first-order correction which leads to a linear shape equation. The solution to the shape equation reduces to a novel and revealing linear equation that connect geometry to orientation:

$H=2ϵf\left(\mathbf{n},{\nabla }_s\mathbf{n}\right)+{\mathcal{O}}^{\left(1\right)}\left(\dots \right)(9)$

where H is the mean curvature. Eq. 9 contains significant information: anchoring-driven wrinkling profiles along different directions can be superposed to create a complex wrinkling pattern. In Section 2, uniaxial wrinkling along direction z is simply sin qz. An egg carton surface naturally arises if two wrinkling profiles along orthogonal direction (x + y) and (x − y) superpose, as shown in Figure 8C and d, which verifies the egg carton structure observed on papillae of rose petal in Figure 8A and b. A 2D surface egg carton wrinkling is the result of balancing the dilation pressure, rotation pressure and director pressure as shown in Eq. 4, which shares the same wrinkling mechanism as a 1D surface discussed in Section 2.1.

The second order derivatives of wrinkling profiles contains information of principal curvatures κ₁ < κ₂. The mean curvature H = (κ₁ + κ₂)/2, deviatoric curvature D = (κ₂ − κ₁)/2 > 0, Gaussian curvature K = κ₁κ₂, Casorati curvature $C=\sqrt{({\kappa }_1^2+{\kappa }_2^2)/2}$ and the normalized, dimensionless shape parameter S = (2/π) arctan (H/D) are the primary parameters to categorize basic shape information (Koenderink and Van Doorn, 1992; Wang et al., 2020b). By integrating information from these five measures, a complete characterization is made beyond the classical one based only on (H, K).

Figure 9A shows the curvature lines for three primary shapes: sphere (magenta), cylinder (cyan) and saddle (yellow). An egg carton surface contains rich curvature features that can smoothly vary between those three primary shapes. Figure 9B is solved from Eq. 4 without linear approximation. The solution surface is composed by 5/31 egg carton, 10/31 cylinder, and 16/31 asymmetric biaxial wrinkling contribution. The non-linearity provides a more complex curvature distribution, shown in Figure 9B.

FIGURE 9

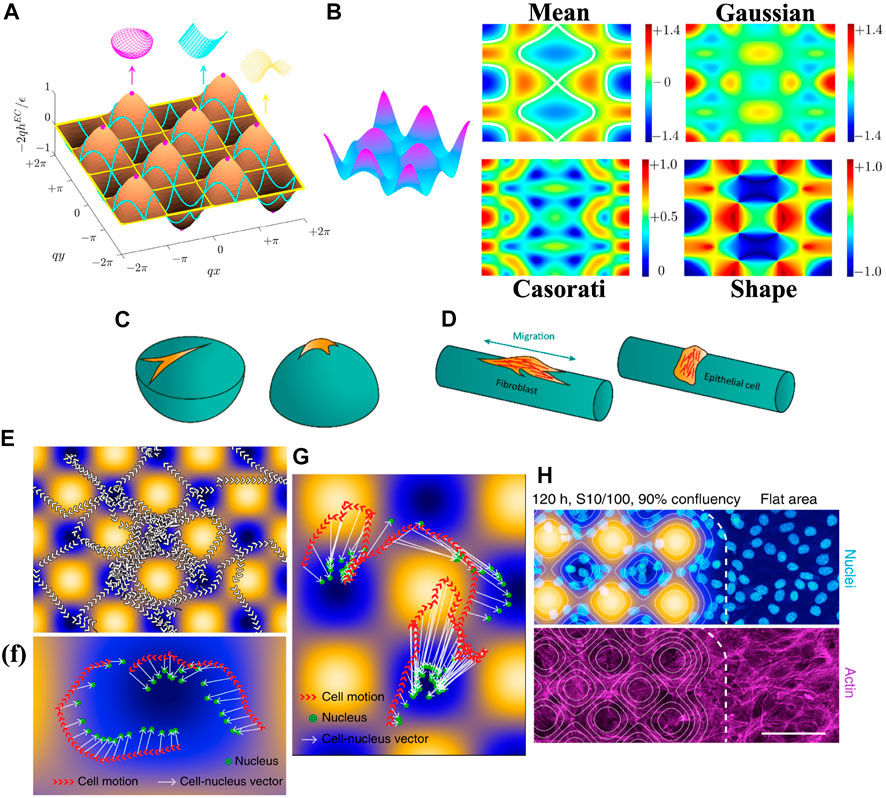
FIGURE 9. (A–D) present curvature-induced cell alignment. (A) The curvature lines on an egg carton surface. Megenta points represent local spheres. Cyan and purples curves represent the local cylinders and local saddles, respectively. (B) A surface with 5/31 egg carton wrinkling, 10/31 cylindrical wrinkling, and 16/31 asymmetric biaxial wrinkling pattern. The dimensionless mean, Gaussian, Casorati curvatures and shape parameter distribution on the surface. (C) Concave and convex spheres do not support the cells in the same way. (D) Fibroblastic-like cells tend to align along the long axis of cylinder, while epithelial cells prefer to wrap the cylinder. (E–H) present curvature-induced cell migration. (E) Tracking of nuclei. Arrows represent moving direction. Arrowheads indicate movement direction. (F) and (G) Tracking of cells and nuclei barycenters of cells on egg carton surface. (H) Cells stained for DNA and actin. Scale bars: 100 µm. (A) Is reprinted from (Wang Z. et al., 2021), Copyright (2021), with permission from Elsevier. (B) Is reprinted from (Wang et al., 2022). Copyright (2020) by the American Physical Society. (C) and (D) are reproduced under CC-BY-4.0 (Callens et al., 2020). (E–H) are reproduced under CC-BY-4.0 (Pieuchot et al., 2018).

The control of local shapes has a prevailing application in cell biology (Malheiro et al., 2016; Werner et al., 2017; Bade et al., 2018; Pieuchot et al., 2018; Werner et al., 2018; Callens et al., 2020). Figure 9C and d are the schematics and experimental results of how geometry affects cell and tissue organization.

For a concave surface, the cell tends to be stretched, showing an upward stretched cell morphology. However, a convex surface allows cells to fully spread all over the surface, as shown in Figure 9C. A local cylinder has one vanishing principal curvature, providing two orthogonal directions for cell organization. Fibroblasts and mesenchymal stromal cells tend to avoid curvature and orient along the long axis (Hwang et al., 2009; Soiné et al., 2016; Bade et al., 2017; Werner et al., 2019), while epithelial cells prefer to wrap around the cylinder (Rovensky and Samoilov, 1994; Svitkina et al., 1995; Yevick et al., 2015; Werner et al., 2018), shown in Figure 9D (Bade et al., 2018). discussed the cell organization on a saddle surface, creating more complex scenarios where no clear conclusions have been made (Bade et al., 2018; Werner et al., 2019; Callens et al., 2020).

Cell migration, rather than static alignment, has also been observed to be highly dependent on the curvature of the substrate. For a convex cylinder (H > 0), hBMSCs migrate increasingly for the increasing curvature, while those on a concave cylinder (H < 0) show non-aligned mode and no angular preference Werner et al. (2018; 2019). For a spherical surface, fibroblasts and mesenchymal stromal cells (MSCs) migrate faster if H < 0 (Park et al., 2009; Werner et al., 2017). Figure 9E presents the result of curvature-induced cell migration on an egg carton surface. The arrows show the tendency of cells to move with peripheral protrusions while maintaining a close distance of their nuclei to surface minima, see Figure 9F (Pieuchot et al., 2018). Figure 9G shows that the cell’s nuclei are closer to the nearest surface minimum than the cell center, and the direction of the cell-nucleus vector always leads to the surface minima. The nuclei of cells tend to avoid the convex region and concentrate more on the concave region, exhibiting three times higher densities than flat region (see Figure 9H). The nucleus is a viscoelastic solid stiffer than the cytoskeleton (Guilak et al., 2000; Dahl and Kalinowski, 2011; Lammerding, 2011; Simon and Wilson, 2011). Experiments show force transmission between nucleus and cytoskeleton (Crisp et al., 2006; Dahl et al., 2008). For example, the deformation of the nucleus affects chromatin and further alters gene expression (Thomas et al., 2002; Cho et al., 2017; Szczesny and Mauck, 2017). Higher osteocalcin levels in MSCs were observed on a spherical surface, while on a planar surface, higher cytoskeletal forces were generated for osteogenic commitment (McBeath et al., 2004; Lammerding et al., 2006; Callens et al., 2020). The alignment and migration of cells are sensitive to the local curvature distribution (from Figure 9), therefore, cell nuclei are ideal curvature sensors (Wang et al., 2009; Anselme et al., 2018), and the control of curvature allows the engineering design for cell migration (Lauffenburger and Horwitz, 1996; Danuser et al., 2013; Yevick et al., 2015; He and Jiang, 2017; Xi et al., 2017) and differentiation (McNamara et al., 2010; Eyckmans and Chen, 2014; Marino et al., 2014; Kim et al., 2015; Dobbenga et al., 2016; Lo et al., 2016).

In partial summary, two orthogonal wave vector solutions to the liquid crystal shape equation generates uniaxial, equibiaxial and biaxial egg cartons with a rich spatial distribution of (H, K, C) curvatures and shapes S) that can be tuned and leveraged for biological applications such as tissue engineering due to the potential of the outstanding control of cell growth, differentiation and motion.

4 1D closed surface wrinkling: Droplets and tactoids

In this section, we present a review on the geometry of liquid crystal droplet enclosed by an elastic membrane. This structure is commonly discovered in bilayer lipid vesicles (Lawaczeck et al., 1976; Mueller et al., 1983; Liu et al., 2020), monolayer vesicles (Kunitake et al., 1981; Bauduin et al., 2011; Nam et al., 2019), chiral rafts (Sharma P. et al., 2014) and lyotropic liquid crystals (Iwashita and Tanaka, 2006; Tortora and Lavrentovich, 2011).

(Guevara et al., 2019) studied four types of lipid-base droplets. Lipid-based droplets are essential carriers for mRNA encapsulation, which plays an important role in mRNA delivery. Lipoplexes are formed by cationic liposeomes and the phosphate backbone of mRNA (Elouahabi and Ruysschaert, 2005; Wasungu and Hoekstra, 2006; Guevara et al., 2020). Lipoplexes sometimes perform high instability and low transfection efficiency, and lipid nanoparticles are promising alternatives (Guevara et al., 2020; 2019). The lipid nanoparticle consists of pH-responsive or cationic lipids enclosing polyanionic mRNA (Guevara et al., 2020). Lipid-polymer hybrid nanoparticles can be both bilayer and monolayer, showing different functionalities (Islam et al., 2018). The hybrid mRNA delivery organization has a higher nuclei acid condensation efficiency and tunable surface with multifunctionalities (Guevara et al., 2019).

Figure 10A shows a phospholipid-coated liquid crystal droplet. Compared with lipid-based droplets (Guevara et al., 2019; 2020), the surfactant-coated liquid crystal droplets have a larger scale (around 20 µm). The structure in Figure 10A can be used for biosensors, such as detecting antigens, pathogens, proteins, and antimicrobial peptides (Lowe et al., 2010; Bao et al., 2019). The bulk-surfactant interaction affects the surface orientation of the director (Brake et al., 2003a; b). Especially, it has been shown that for such droplet, a critical length R ∼ K/W determines the dominating factor between elasticity and surface anchoring, where surface anchoring energy ∼ WR² and elastic energy ∼ KR He et al. (2014); Gupta et al. (2009); Miller and Abbott (2013). Besides the bulk-interface interaction, the surface of surfactant-coated liquid crystal droplet also responds to the environment such as pH, which further controls the director orientation inside the bulk (see Figure 10B.

FIGURE 10

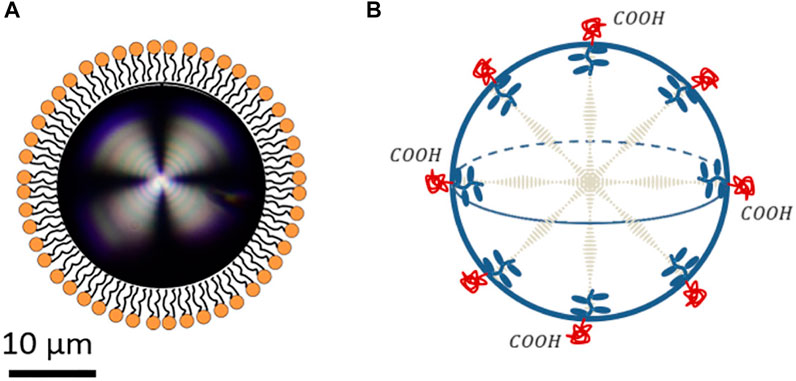
FIGURE 10. Some examples of elastic anisotropic droplets. (A) Phospholipid-coated liquid crystal droplet. (B) pH-sensitive cholesteric liquid crystal droplet. (A) is reproduced under CC-BY-4.0 (Paterson et al., 2020). (B) Is reprinted with permission from (Lee et al., 2016). Copyright 2016, American Chemical Society.

Rofouie et al. follow the theory from (Rey, 2000b; 2006b; a, 2004b; a, Rey, 2005; Gurevich et al., 2014). Introducing Eq. 6 into Eq. 2 and assuming a non-vanishing pressure difference p_c between the bulk and outer surface, the numerical solution solved with a periodic boundary condition results various morphologies of 1D droplet with an elastic membrane. The numerical solutions are given by Figure 11. Two dimensionless parameters are used in the simulation: the scaled anchoring coefficient 0 < |W/γ₀| < 2 and the bending elasticity number $0.05<\alpha =p_c{R}_0^3/k_c<50$ (Meister et al., 1996; Ghochani et al., 2010; Boal, 2012), where R₀ is the spontaneous radius and is a constant R₀ = 0.5 μm in the simulation (Rofouie et al., 2017b). The pressure bending number $\beta ={\gamma }_0{R}_0^2/k_c$ measures the ratio of the surface tension to the bending elasticity, while anchoring bending number $\omega =W{R}_0^2/k_c$ measures the ratio of the anchoring to the bending elasticity.

FIGURE 11

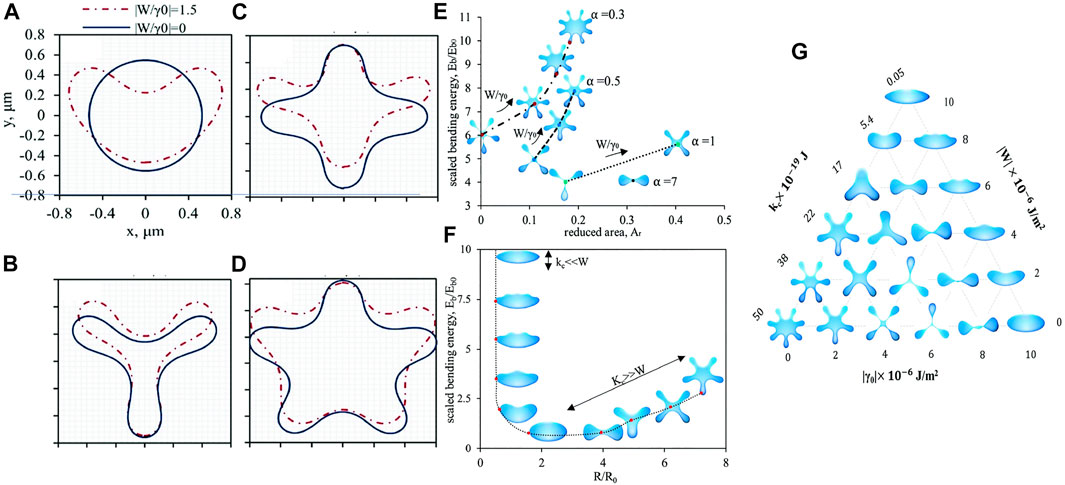
FIGURE 11. Numerical simulation of 1D droplet with an elastic membrane. (A) α =2.5, β =1.25, 2-fold symmetry. (B) α =0.15, β =0.075, 3-fold symmetry. (C) α =0.08, β =0.04, 4-fold symmetry. (D) α =0.05, β =0.025, 5-fold symmetry. (E) The relationship between scaled bending energy and reduced area for α =0.3, 0.5, 0.7 and 1. (F) The relationship between scaled bending energy and the ratio of radius to the spontaneous radius R/R₀ for various k_c. (G) The ternary phase diagram for different combinations of bending rigidity k_c, surface tension γ₀ and anchoring coefficient W. Reproduced from (Rofouie et al., 2017b) with permission from the Royal Society of Chemistry.

Figure 11 presents the membrane shape with (W ≠ 0) or without (W = 0) anisotropy. 2-fold (a)), 3-fold (b)), 4-fold (c)) and 5-fold (d)) symmetry are observed by varying the bending elasticity number α and the pressure bending number β. The morphology symmetry breaks when the anisotropic anchoring (W ≠ 0) is introduced. The curvature on the top of the membrane increases when the anchoring is enhanced. Comparing a) to d), the anchoring effect becomes less important in the symmetry breaking if the morphology shows more folds. Figure 11A is the stomatocyte shape observed in red blood cells (Tachev et al., 2004; Hajjawi, 2013; Muñoz et al., 2014; Geekiyanage et al., 2019).

Figure 11E presents the relationship between the scaled bending energy and the reduced area for α = 0.3, 0.5, 0.7 and 1. A larger anchoring effect (higher W/γ₀) results in more folds, which enhances the scaled bending energy due to higher curvature. Figure 11f) demonstrates the effect of bending elasticity. A decreasing bending elasticity results in decreasing folds, where the morphology undergoes transition from 5-fold starfish to discocyte, ellipsoid, stomatocyte, umbonate (Chen et al., 2005; May et al., 2007), umbilicate (Sakamoto et al., 2017) and undulate (Suhandono et al., 2016), which are commonly used to describe red blood cells and bacterial colonies. A vanishing k_c yields a spindle-like shape. The transition follows the curve in Figure 11F. In the end, by combining the three surface effects: bending elasticity k_c, surface tension γ₀ and anchoring coefficient W, the morphologies are summarized in Figure 11G. Increasing k_c and reducing γ₀ raises the number of folds while increasing W intensifies the asymmetry breaking on the top and bottom of a droplet.

In partial summary, simple extensions of the liquid crystal shape equation that include membrane elasticity generate morphology phase diagrams that include most of the observed cell shapes beyond the usual liquid crystal tactoids (Bagnani et al., 2018; Nyström et al., 2018; Gârlea et al., 2019; Li et al., 2020b; Almohammadi et al., 2022). Some dynamics simulation of self-assembly can be found in (Khayyatzadeh et al., 2015; Han et al., 2017; Fu and Abukhdeir, 2018).

5 Conclusion and outlook

We presented a systematic review of recent experimental and theoretical literature of surface wrinkling patterns and morphology, and bioinspired applications of liquid crystal analogues. Table 1 summarizes the key aspects of different physical models (second row), wrinkling mechanisms and material parameters (third and fourth rows) and functionality (fifth row) of various biological systems that were discussed. The table shows the diversity of surface patterns and observed functionalities that can be captured by anisotropic soft matter capillarity.

TABLE 1

TABLE 1. Summary of surface wrinkling morphology observed in experiment and theoretical simulation.

Tulip Queen of the Night and spotted tinselfish show uniaxial surface corrugation, governed by the anchoring effect due to the preferred orientation of the cellulose and chitin fibres. The roughness of tulip petals and spotted tinselfish determines their optical and friction behaviour. The iridescence and glossy colour attract insects and further benefit pollination. In addition, an optimized surface roughness favours better swimming dynamics. The humidity of the environment changes the helix pitch of beetles’ exoskeleton and vascular plants. The varying helix pitch disturbs the structural colour and diffraction grating, which makes beetles natural humidity detectors. Due to the significant role played by the elastic interface, the daisy flower petals show more complex multiscale corrugations. Both the anchoring and elasticity of petals govern the wrinkling patterns of daisy and kalanchoe blossfeldiana. Experiments validate that such a complex wrinkling profile enlarges contact angle, and it shed light on bioinspired hydrophobic materials. In partial summary, elastic biomimetic membranes governed by surface anchoring show complex wrinkling patterns, where the anchoring strength, elastic modulus and helix pitch are the dominant factors that control self-assembly and surface geometry.

Rose petals and dactyl club exhibit egg carton surfaces, where the non-vanishing Gaussian curvature contains rich geometric information. The egg carton surface of the biocompatible scaffold has been widely studied due to its promising application in controlling cell migration and cell differentiation. In the end, we also present a discussion on the morphology of lipid vesicles and surfactant-coated liquid crystals. A droplet displays complex anisotropy and morphology due to topological constraints. The curvature information of the elastic interface supports various biological applications such as mRNA encapsulation and virus/protein sensors. In partial summary, a tactoid with an elastic membrane is subjected to the topological constraint and performs an asymmetric profile that is highly dependent on the bulk-surface correlations.

In conclusion, liquid crystal capillary science, self-assembly and self-organization, and surface pattern formation were integrated to replicate, characterize, and shed light on many biological surfaces and functionalities. The outlook of this emerging field is rich in opportunities, which include surfactants, flow and mass transfer shaping, and reaction-polymerization-aggregation surface morphing, bioinspired diffraction gratings and structural colours, tunable and biodegradable scaffold for cell differentiation and tissue growth.

Author contributions

ZW, PS, and AR contributed to conception of the study. ZW wrote the first draft, prepared the figures and bibliography. ZW, PS and AR revised the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work is supported by the Natural Science and Engineering Research Council of Canada (NSERC) (Grant number: 223086). AR is thankful to McGill University for financial support through the James McGill Professor appointment. ZW is thankful to the Faculty of Engineering for MEDA scholarship program to assist his PhD study.

Acknowledgments

AR and PS are thankful for financial support from the Natural Science and Engineering Research Council of Canada (NSERC), and to Compute Canada and CLUMEQ for access and assistance to high performance computing. AR wishes to acknowledge the fundamental contributions of Gino de Luca, Ahmad Sayyed Khadem, Oscar Aguilar Gutierrez, Yogesh Murugesan, Oscar Matus Rivas, E.E. Herrera Valencia, Ziheng Wang, Pardis Rofouie, Yun Yan, Gaurav Gupta, Dana Grecov, Won Hee Han, Philip K. Chan, Ezequiel Soule, Nasser Mohieddin Abukhdeir, Susanta K Da, Samir Mushrif, Paul M. Phillips, Mojdeh Golmohammadi, Luiz R. P de Andrade Lima, Alireza Shams, Dae Kun Hwang, Benjamin Wincure, Ae-Gyeong Cheong, Hang Hu, Mohan Srinivasarao, Linda Reven, and Raffaele Mezzenga.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abou-Dakka, M., Herrera-Valencia, E., and Rey, A. D. (2012). Linear oscillatory dynamics of flexoelectric membranes embedded in viscoelastic media with applications to outer hair cells. J. Newt. Fluid Mech. 185, 1–17. doi:10.1016/j.jnnfm.2012.07.007

CrossRef Full Text | Google Scholar

Abukhdeir, N. M., and Vlachos, D. G. (2011). Nanoscale surface pattern evolution in heteroepitaxial bimetallic films. ACS Nano 5, 7168–7175. doi:10.1021/nn201979q

PubMed Abstract | CrossRef Full Text | Google Scholar

Aguilar Gutierrez, O. F., and Rey, A. D. (2016). Characterization methodology for biological plywoods based on characteristic cross-section patterns. J. Renew. Mater. 4, 241–250. doi:10.7569/jrm.2016.634119

CrossRef Full Text | Google Scholar

Aguirre, L. E., de Oliveira, A., Seč, D., Čopar, S., Almeida, P. L., Ravnik, M., et al. (2016). Sensing surface morphology of biofibers by decorating spider silk and cellulosic filaments with nematic microdroplets. Proc. Natl. Acad. Sci. 113, 1174–1179. doi:10.1073/pnas.1518739113

PubMed Abstract | CrossRef Full Text | Google Scholar

Alimov, M. M., Bazilevsky, A. V., and Kornev, K. G. (2021). Soap film on two noncircular frames. Phys. Fluids 33, 052104. doi:10.1063/5.0047461

CrossRef Full Text | Google Scholar

Almohammadi, H., Khadem, S. A., Bagnani, M., Rey, A. D., and Mezzenga, R. (2022). Shape and structural relaxation of colloidal tactoids. Nat. Commun. 13, 2778–2810. doi:10.1038/s41467-022-30123-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Anselme, K., Wakhloo, N. T., Rougerie, P., and Pieuchot, L. (2018). Role of the nucleus as a sensor of cell environment topography. Adv. Healthc. Mater. 7, 1701154. doi:10.1002/adhm.201701154

CrossRef Full Text | Google Scholar

Antoniou Kourounioti, R. L., Band, L. R., Fozard, J. A., Hampstead, A., Lovrics, A., Moyroud, E., et al. (2013). Buckling as an origin of ordered cuticular patterns in flower petals. J. R. Soc. Interface 10, 20120847. doi:10.1098/rsif.2012.0847

PubMed Abstract | CrossRef Full Text | Google Scholar

Anyfantakis, M., Jampani, V. S., Kizhakidathazhath, R., Binks, B. P., and Lagerwall, J. P. (2020). Responsive photonic liquid marbles. Angew. Chem. 132, 19422–19429. doi:10.1002/ange.202008210

CrossRef Full Text | Google Scholar

Azzari, P., Bagnani, M., and Mezzenga, R. (2021). Liquid–liquid crystalline phase separation in biological filamentous colloids: Nucleation, growth and order–order transitions of cholesteric tactoids. Soft Matter 17, 6627–6636. doi:10.1039/d1sm00466b

PubMed Abstract | CrossRef Full Text | Google Scholar

Ba, E. C. T., Dumont, M. R., Martins, P. S., Drumond, R. M., Martins da Cruz, M. P., and Vieira, V. F. (2021). Investigation of the effects of skewness rsk and kurtosis rku on tribological behavior in a pin-on-disc test of surfaces machined by conventional milling and turning processes. Mater. Res. 24. doi:10.1590/1980-5373-mr-2020-0435

CrossRef Full Text | Google Scholar

Bade, N. D., Kamien, R. D., Assoian, R. K., and Stebe, K. J. (2017). Curvature and rho activation differentially control the alignment of cells and stress fibers. Sci. Adv. 3, e1700150. doi:10.1126/sciadv.1700150

PubMed Abstract | CrossRef Full Text | Google Scholar

Bade, N. D., Xu, T., Kamien, R. D., Assoian, R. K., and Stebe, K. J. (2018). Gaussian curvature directs stress fiber orientation and cell migration. Biophysical J. 114, 1467–1476. doi:10.1016/j.bpj.2018.01.039

CrossRef Full Text | Google Scholar

Bagnani, M., Nystrom, G., De Michele, C., and Mezzenga, R. (2018). Amyloid fibrils length controls shape and structure of nematic and cholesteric tactoids. Acs Nano 13, 591–600. doi:10.1021/acsnano.8b07557

PubMed Abstract | CrossRef Full Text | Google Scholar

Bagnani, M., Azzari, P., De Michele, C., Arcari, M., and Mezzenga, R. (2021). Elastic constants of biological filamentous colloids: estimation and implications on nematic and cholesteric tactoid morphologies. Soft Matter 17, 2158–2169. doi:10.1039/d0sm01886d

PubMed Abstract | CrossRef Full Text | Google Scholar

Bao, P., Paterson, D. A., Harrison, P. L., Miller, K., Peyman, S., Jones, J. C., et al. (2019). Lipid coated liquid crystal droplets for the on-chip detection of antimicrobial peptides. Lab a Chip 19, 1082–1089. doi:10.1039/c8lc01291a

CrossRef Full Text | Google Scholar

Bauduin, P., Prevost, S., Farràs, P., Teixidor, F., Diat, O., and Zemb, T. (2011). A theta-shaped amphiphilic cobaltabisdicarbollide anion: transition from monolayer vesicles to micelles. Angew. Chem. 123, 5410–5412. doi:10.1002/ange.201100410

CrossRef Full Text | Google Scholar

Baumgart, T., Das, S., Webb, W. W., and Jenkins, J. T. (2005). Membrane elasticity in giant vesicles with fluid phase coexistence. Biophysical J. 89, 1067–1080. doi:10.1529/biophysj.104.049692

CrossRef Full Text | Google Scholar

Belhadjamor, M., Belghith, S., Mezlini, S., and El Mansori, M. (2020). Numerical study of normal contact stiffness: Non-gaussian roughness and elastic–plastic behavior. Proc. Institution Mech. Eng. Part J J. Eng. Tribol. 234, 1368–1380. doi:10.1177/1350650119893520

CrossRef Full Text | Google Scholar

Bergmann, J. B., Moatsou, D., Surapaneni, V. A., Thielen, M., Speck, T., Wilts, B. D., et al. (2020). Polymerization-induced wrinkled surfaces with controlled topography as slippery surfaces for colorado potato beetles. Adv. Mater. Interfaces 7, 2000129. doi:10.1002/admi.202000129

CrossRef Full Text | Google Scholar

Bian, X., Litvinov, S., and Koumoutsakos, P. (2020). Bending models of lipid bilayer membranes: Spontaneous curvature and area-difference elasticity. Comput. Methods Appl. Mech. Eng. 359, 112758. doi:10.1016/j.cma.2019.112758

CrossRef Full Text | Google Scholar

Bianchi, F., Pereno, V., George, J. H., Thompson, M. S., and Ye, H. (2019). Membrane mechanical properties regulate the effect of strain on spontaneous electrophysiology in human ipsc-derived neurons. Neuroscience 404, 165–174. doi:10.1016/j.neuroscience.2019.02.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Bidan, C. M., Kommareddy, K. P., Rumpler, M., Kollmannsberger, P., Fratzl, P., and Dunlop, J. W. (2013). Geometry as a factor for tissue growth: towards shape optimization of tissue engineering scaffolds. Adv. Healthc. Mater. 2, 186–194. doi:10.1002/adhm.201200159

PubMed Abstract | CrossRef Full Text | Google Scholar

Blanquer, S. B., Werner, M., Hannula, M., Sharifi, S., Lajoinie, G. P., Eglin, D., et al. (2017). Surface curvature in triply-periodic minimal surface architectures as a distinct design parameter in preparing advanced tissue engineering scaffolds. Biofabrication 9, 025001. doi:10.1088/1758-5090/aa6553

PubMed Abstract | CrossRef Full Text | Google Scholar

Boal, D. H. (2012). Mechanics of the cell. Cambridge, United Kingdom: Cambridge University Press.

Google Scholar

Bostwick, J., Miksis, M., and Davis, S. (2016). Elastic membranes in confinement. J. R. Soc. Interface 13, 20160408. doi:10.1098/rsif.2016.0408

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouligand, Y. (1972). Twisted fibrous arrangements in biological materials and cholesteric mesophases. Tissue Cell 4, 189–217. doi:10.1016/s0040-8166(72)80042-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Brake, J. M., Mezera, A. D., and Abbott, N. L. (2003a). Active control of the anchoring of 4 ‘-pentyl-4-cyanobiphenyl (5cb) at an aqueous-liquid crystal interface by using a redox-active ferrocenyl surfactant. Langmuir 19, 8629–8637. doi:10.1021/la034469u

CrossRef Full Text | Google Scholar

Brake, J. M., Mezera, A. D., and Abbott, N. L. (2003b). Effect of surfactant structure on the orientation of liquid crystals at aqueous-liquid crystal interfaces. Langmuir 19, 6436–6442. doi:10.1021/la034132s

CrossRef Full Text | Google Scholar

Byeon, M., Cho, S. K., Um, M. S., Lee, J. H., Kim, E. S., and Choi, W. J. (2020). Enhancing hydrophobicity of polymer thin film-coated surface by wrinkling method. Macromol. Res. 28, 1104–1110. doi:10.1007/s13233-020-8158-1

CrossRef Full Text | Google Scholar

Cahn, J., and Hoffman, D. (1998). “A vector thermodynamics for anisotropic surfaces—ii. curved and faceted surfaces,” in The selected works of John W. Cahn, 315–324.

Google Scholar

Cai, S., Chen, D., Suo, Z., and Hayward, R. C. (2012). Creasing instability of elastomer films. Soft Matter 8, 1301–1304. doi:10.1039/c2sm06844c

CrossRef Full Text | Google Scholar

Callens, S. J., Uyttendaele, R. J., Fratila-Apachitei, L. E., and Zadpoor, A. A. (2020). Substrate curvature as a cue to guide spatiotemporal cell and tissue organization. Biomaterials 232, 119739. doi:10.1016/j.biomaterials.2019.119739

PubMed Abstract | CrossRef Full Text | Google Scholar

Campelo, F., Arnarez, C., Marrink, S. J., and Kozlov, M. M. (2014). Helfrich model of membrane bending: from gibbs theory of liquid interfaces to membranes as thick anisotropic elastic layers. Adv. colloid interface Sci. 208, 25–33. doi:10.1016/j.cis.2014.01.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Cartwright, I. J., and Higgins, J. A. (2001). Direct evidence for a two-step assembly of apob48-containing lipoproteins in the lumen of the smooth endoplasmic reticulum of rabbit enterocytes. J. Biol. Chem. 276, 48048–48057. doi:10.1074/jbc.m104229200

PubMed Abstract | CrossRef Full Text | Google Scholar

Castles, F., Morris, S., and Coles, H. (2011). The limits of flexoelectricity in liquid crystals. AIP Adv. 1, 032120. doi:10.1063/1.3624725

CrossRef Full Text | Google Scholar

Chagas, R., Silva, P. E., Fernandes, S. N., Žumer, S., and Godinho, M. H. (2020). Playing the blues, the greens and the reds with cellulose-based structural colours. Faraday Discuss. 223, 247–260. doi:10.1039/d0fd00020e

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J., Groves, R., Zheng, Y., Civerolo, E., Viveros, M., and Freeman, M. (2005). Two Xylella fastidiosa genotypes associated with almond leaf scorch disease on the same location in California. Phytopathology 95, 708–714. doi:10.1094/phyto-95-0708

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, D., Cai, S., Suo, Z., and Hayward, R. C. (2012). Surface energy as a barrier to creasing of elastomer films: An elastic analogy to classical nucleation. Phys. Rev. Lett. 109, 038001. doi:10.1103/physrevlett.109.038001

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, C., Airoldi, C. A., Lugo, C. A., Bay, R. K., Glover, B. J., and Crosby, A. J. (2021). Flower inspiration: Broad-angle structural color through tunable hierarchical wrinkles in thin film multilayers. Adv. Funct. Mater. 31, 2006256. doi:10.1002/adfm.202006256

CrossRef Full Text | Google Scholar

Cheng, X., Meng, B., Chen, X., Han, M., Chen, H., Su, Z., et al. (2016). Single-step fluorocarbon plasma treatment-induced wrinkle structure for high-performance triboelectric nanogenerator. Small 12, 229–236. doi:10.1002/smll.201502720

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng, X., Miao, L., Su, Z., Chen, H., Song, Y., Chen, X., et al. (2017). Controlled fabrication of nanoscale wrinkle structure by fluorocarbon plasma for highly transparent triboelectric nanogenerator. Microsystems Nanoeng. 3, 16074–16079. doi:10.1038/micronano.2016.74

CrossRef Full Text | Google Scholar

Cheong, A.-G., and Rey, A. D. (2002a). Cahn–hoffman capillarity vector thermodynamics for curved liquid crystal interfaces with applications to fiber instabilities. J. Chem. Phys. 117, 5062–5071. doi:10.1063/1.1498821

CrossRef Full Text | Google Scholar

Cheong, A.-G., and Rey, A. D. (2002b). Cahn-hoffman capillarity vector thermodynamics for liquid crystal interfaces. Phys. Rev. E 66, 021704. doi:10.1103/physreve.66.021704

CrossRef Full Text | Google Scholar

Cheong, A.-G., and Rey, A. D. (2002c). Capillary instabilities in a thin nematic liquid crystalline fiber embedded in a viscous matrix. Continuum Mech. Thermodyn. 14, 263–279. doi:10.1007/s001610200093

CrossRef Full Text | Google Scholar

Cheong, A.-G., Rey, A. D., and Mather, P. T. (2001). Capillary instabilities in thin nematic liquid crystalline fibers. Phys. Rev. E 64, 041701. doi:10.1103/physreve.64.041701

CrossRef Full Text | Google Scholar

Cho, S., Irianto, J., and Discher, D. E. (2017). Mechanosensing by the nucleus: From pathways to scaling relationships. J. Cell Biol. 216, 305–315. doi:10.1083/jcb.201610042

PubMed Abstract | CrossRef Full Text | Google Scholar

Chow, M. H., Yan, K. T., Bennett, M. J., and Wong, J. T. (2010). Birefringence and dna condensation of liquid crystalline chromosomes. Eukaryot. Cell 9, 1577–1587. doi:10.1128/ec.00026-10

PubMed Abstract | CrossRef Full Text | Google Scholar

Ciarletta, P., and Truskinovsky, L. (2019). Soft nucleation of an elastic crease. Phys. Rev. Lett. 122, 248001. doi:10.1103/physrevlett.122.248001

PubMed Abstract | CrossRef Full Text | Google Scholar

Ciarletta, P. (2018). Matched asymptotic solution for crease nucleation in soft solids. Nat. Commun. 9, 496–497. doi:10.1038/s41467-018-02979-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Cowin, S. C. (2004). Do liquid crystal-like flow processes occur in the supramolecular assembly of biological tissues? J. Newt. fluid Mech. 119, 155–162. doi:10.1016/j.jnnfm.2004.01.012

CrossRef Full Text | Google Scholar

Crisp, M., Liu, Q., Roux, K., Rattner, J., Shanahan, C., Burke, B., et al. (2006). Coupling of the nucleus and cytoplasm: role of the linc complex. J. Cell Biol. 172, 41–53. doi:10.1083/jcb.200509124

PubMed Abstract | CrossRef Full Text | Google Scholar

Csoka, L., Hoeger, I. C., Rojas, O. J., Peszlen, I., Pawlak, J. J., and Peralta, P. N. (2012). Piezoelectric effect of cellulose nanocrystals thin films. ACS Macro Lett. 1, 867–870. doi:10.1021/mz300234a

PubMed Abstract | CrossRef Full Text | Google Scholar

Cutolo, A., Pagliarulo, V., Merola, F., Coppola, S., Ferraro, P., and Fraldi, M. (2020). Wrinkling prediction, formation and evolution in thin films adhering on polymeric substrata. Mater. Des. 187, 108314. doi:10.1016/j.matdes.2019.108314

CrossRef Full Text | Google Scholar

Dahl, K. N., and Kalinowski, A. (2011). Nucleoskeleton mechanics at a glance. J. Cell Sci. 124, 675–678. doi:10.1242/jcs.069096

PubMed Abstract | CrossRef Full Text | Google Scholar

Dahl, K. N., Ribeiro, A. J., and Lammerding, J. (2008). Nuclear shape, mechanics, and mechanotransduction. Circulation Res. 102, 1307–1318. doi:10.1161/circresaha.108.173989

PubMed Abstract | CrossRef Full Text | Google Scholar

Danuser, G., Allard, J., and Mogilner, A. (2013). Mathematical modeling of eukaryotic cell migration: insights beyond experiments. Annu. Rev. Cell Dev. Biol. 29, 501–528. doi:10.1146/annurev-cellbio-101512-122308

PubMed Abstract | CrossRef Full Text | Google Scholar

De Luca, G., and Rey, A. (2003). Monodomain and polydomain helicoids in chiral liquid-crystalline phases and their biological analogues. Eur. Phys. J. E 12, 291–302. doi:10.1140/epje/i2002-10164-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Deng, S., Rhee, D., Lee, W.-K., Che, S., Keisham, B., Berry, V., et al. (2019). Graphene wrinkles enable spatially defined chemistry. Nano Lett. 19, 5640–5646. doi:10.1021/acs.nanolett.9b02178

PubMed Abstract | CrossRef Full Text | Google Scholar

Dobbenga, S., Fratila-Apachitei, L. E., and Zadpoor, A. A. (2016). Nanopattern-induced osteogenic differentiation of stem cells–a systematic review. Acta biomater. 46, 3–14. doi:10.1016/j.actbio.2016.09.031

PubMed Abstract | CrossRef Full Text | Google Scholar

Dortdivanlioglu, B., Yilmaz, N. E. D., Goh, K., Zheng, X., and Linder, C. (2021). Swelling-induced interface crease instabilities at hydrogel bilayers. J. Elast. 145, 31–47. doi:10.1007/s10659-020-09810-8

CrossRef Full Text | Google Scholar

Elouahabi, A., and Ruysschaert, J.-M. (2005). Formation and intracellular trafficking of lipoplexes and polyplexes. Mol. Ther. 11, 336–347. doi:10.1016/j.ymthe.2004.12.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Emmens, W. (1988). “The influence of surface roughness on friction,” in Proceeding 15th Congress of International Deep Drawing Research Group (IDDRG), 63–70.

Google Scholar

Eyckmans, J., and Chen, C. S. (2014). Sticky mechanical memory. Nat. Mater. 13, 542–543. doi:10.1038/nmat3989

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng, L., Zhang, Y., Xi, J., Zhu, Y., Wang, N., Xia, F., et al. (2008). Petal effect: a superhydrophobic state with high adhesive force. Langmuir 24, 4114–4119. doi:10.1021/la703821h

PubMed Abstract | CrossRef Full Text | Google Scholar

Fernandes, S. N., Geng, Y., Vignolini, S., Glover, B. J., Trindade, A. C., Canejo, J. P., et al. (2013). Structural color and iridescence in transparent sheared cellulosic films. Macromol. Chem. Phys. 214, 25–32. doi:10.1002/macp.201200351

CrossRef Full Text | Google Scholar

Fu, F., and Abukhdeir, N. M. (2018). Chiral symmetry-breaking dynamics in the phase transformation of nematic droplets. Liq. Cryst. 45, 1078–1083. doi:10.1080/02678292.2017.1410241

CrossRef Full Text | Google Scholar

Garcia, K., Kroenke, C., and Bayly, P. (2018). Mechanics of cortical folding: stress, growth and stability. Philosophical Trans. R. Soc. B Biol. Sci. 373, 20170321. doi:10.1098/rstb.2017.0321

CrossRef Full Text | Google Scholar

Gârlea, I. C., Dammone, O., Alvarado, J., Notenboom, V., Jia, Y., Koenderink, G. H., et al. (2019). Colloidal liquid crystals confined to synthetic tactoids. Sci. Rep. 9, 20391–20411. doi:10.1038/s41598-019-56729-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Geekiyanage, N. M., Balanant, M. A., Sauret, E., Saha, S., Flower, R., Lim, C. T., et al. (2019). A coarse-grained red blood cell membrane model to study stomatocyte-discocyte-echinocyte morphologies. PLoS One 14, e0215447. doi:10.1371/journal.pone.0215447

PubMed Abstract | CrossRef Full Text | Google Scholar

Geng, Y., Almeida, P. L., Fernandes, S. N., Cheng, C., Palffy-Muhoray, P., and Godinho, M. H. (2013). A cellulose liquid crystal motor: a steam engine of the second kind. Sci. Rep. 3, 1028–1035. doi:10.1038/srep01028

PubMed Abstract | CrossRef Full Text | Google Scholar

Gent, A., and Cho, I. (1999). Surface instabilities in compressed or bent rubber blocks. Rubber Chem. Technol. 72, 253–262. doi:10.5254/1.3538798

CrossRef Full Text | Google Scholar

Ghochani, M., Nulton, J., Salamon, P., Frey, T., Rabinovitch, A., and Baljon, A. (2010). Tensile forces and shape entropy explain observed crista structure in mitochondria. Biophysical J. 99, 3244–3254. doi:10.1016/j.bpj.2010.09.038

CrossRef Full Text | Google Scholar

González-Henríquez, C. M., Alfaro-Cerda, P. A., Veliz-Silva, D. F., Sarabia-Vallejos, M. A., Terraza, C. A., and Rodriguez-Hernandez, J. (2018). Micro-wrinkled hydrogel patterned surfaces using ph-sensitive monomers. Appl. Surf. Sci. 457, 902–913. doi:10.1016/j.apsusc.2018.07.022

CrossRef Full Text | Google Scholar

Guan, X., Reddipalli, L., Butler, D. T., Liu, Q., and Velankar, S. S. (2022). Rate-dependent creasing of a viscoelastic liquid. Extreme Mech. Lett. 55, 101784. doi:10.1016/j.eml.2022.101784

CrossRef Full Text | Google Scholar

Guevara, M. L., Persano, S., and Persano, F. (2019). Lipid-based vectors for therapeutic mrna-based anti-cancer vaccines. Curr. Pharm. Des. 25, 1443–1454. doi:10.2174/1381612825666190619150221

PubMed Abstract | CrossRef Full Text | Google Scholar

Guevara, M. L., Persano, F., and Persano, S. (2020). Advances in lipid nanoparticles for mrna-based cancer immunotherapy. Front. Chem. 8, 589959. doi:10.3389/fchem.2020.589959

PubMed Abstract | CrossRef Full Text | Google Scholar

Guilak, F., Tedrow, J. R., and Burgkart, R. (2000). Viscoelastic properties of the cell nucleus. Biochem. Biophys. Res. Commun. 269, 781–786. doi:10.1006/bbrc.2000.2360

PubMed Abstract | CrossRef Full Text | Google Scholar

Gupta, J. K., Sivakumar, S., Caruso, F., and Abbott, N. L. (2009). Size-dependent ordering of liquid crystals observed in polymeric capsules with micrometer and smaller diameters. Angew. Chem. Int. Ed. 48, 1680–1683. doi:10.1002/ange.200804500

CrossRef Full Text | Google Scholar

Gurevich, S., Soule, E., Rey, A., Reven, L., and Provatas, N. (2014). Self-assembly via branching morphologies in nematic liquid-crystal nanocomposites. Phys. Rev. E 90, 020501. doi:10.1103/physreve.90.020501

CrossRef Full Text | Google Scholar

Gutierrez, O. F. A., and Rey, A. D. (2014a). Chiral graded structures in biological plywoods and in the beetle cuticle. Colloid Interface Sci. Commun. 3, 18–22. doi:10.1016/j.colcom.2015.04.001

CrossRef Full Text | Google Scholar

Gutierrez, O. F. A., and Rey, A. D. (2014b). Structure characterisation method for ideal and non-ideal twisted plywoods. Soft Matter 10, 9446–9453. doi:10.1039/c4sm01803f

PubMed Abstract | CrossRef Full Text | Google Scholar

Gutierrez, O. F. A., and Rey, A. D. (2016). Geometric reconstruction of biological orthogonal plywoods. Soft matter 12, 1184–1191. doi:10.1039/c5sm02214b

PubMed Abstract | CrossRef Full Text | Google Scholar

Gutierrez, O. F. A., and Rey, A. D. (2017). Biological plywood film formation from para-nematic liquid crystalline organization. Soft matter 13, 8076–8088. doi:10.1039/c7sm01865g

PubMed Abstract | CrossRef Full Text | Google Scholar

Gutierrez, O. F. A., and Rey, A. D. (2018). Extracting shape from curvature evolution in moving surfaces. Soft Matter 14, 1465–1473. doi:10.1039/c7sm02409f

PubMed Abstract | CrossRef Full Text | Google Scholar

Habibi, Y., Lucia, L. A., and Rojas, O. J. (2010). Cellulose nanocrystals: chemistry, self-assembly, and applications. Chem. Rev. 110, 3479–3500. doi:10.1021/cr900339w

PubMed Abstract | CrossRef Full Text | Google Scholar

Hadley, N. F. (1979). Wax secretion and color phases of the desert tenebrionid beetle cryptoglossa verrucosa (leconte). Science 203, 367–369. doi:10.1126/science.203.4378.367

PubMed Abstract | CrossRef Full Text | Google Scholar

Hajjawi, O. S. (2013). Ionic and osmotic equilibria of human red blood cells. Am. J. Sci. Res., 177–187.

Google Scholar

Han, Y., Bizmark, N., Abukhdeir, N. M., and Ioannidis, M. A. (2017). Dynamics of ethyl cellulose nanoparticle self-assembly at the interface of a nematic liquid crystal droplet. Phys. Chem. Chem. Phys. 19, 24955–24960. doi:10.1039/c7cp04421f

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansson, K. N., and Hansson, S. (2011). Skewness and kurtosis: important parameters in the characterization of dental implant surface roughness—a computer simulation. Int. Sch. Res. Notices.

Google Scholar

Harbola, V., Crossley, S., Hong, S. S., Lu, D., Birkholzer, Y. A., Hikita, Y., et al. (2021). Strain gradient elasticity in srtio3 membranes: bending versus stretching. Nano Lett. 21, 2470–2475. doi:10.1021/acs.nanolett.0c04787

PubMed Abstract | CrossRef Full Text | Google Scholar

He, X., and Jiang, Y. (2017). Substrate curvature regulates cell migration. Phys. Biol. 14, 035006. doi:10.1088/1478-3975/aa6f8e

PubMed Abstract | CrossRef Full Text | Google Scholar

He, S., Liang, W., Cheng, K.-L., Fang, J., and Wu, S.-T. (2014). Bile acid–surfactant interactions at the liquid crystal/aqueous interface. Soft Matter 10, 4609–4614. doi:10.1039/c4sm00486h

PubMed Abstract | CrossRef Full Text | Google Scholar

Helfrich, W. (1973). Elastic properties of lipid bilayers: theory and possible experiments. Z. für Naturforsch. C 28, 693–703. doi:10.1515/znc-1973-11-1209

CrossRef Full Text | Google Scholar

Herrera Valencia, E. E., and Rey, A. D. (2018). Electrorheological model based on liquid crystals membranes with applications to outer hair cells. Fluids 3, 35. doi:10.3390/fluids3020035

CrossRef Full Text | Google Scholar

Herrera-Valencia, E., and Rey, A. D. (2014). Actuation of flexoelectric membranes in viscoelastic fluids with applications to outer hair cells. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 372, 20130369. doi:10.1098/rsta.2013.0369

CrossRef Full Text | Google Scholar

Hertel, R. (2013). “Curvature-induced magnetochirality,” in Spin (World Scientific), 3, 1340009. doi:10.1142/s2010324713400092

CrossRef Full Text | Google Scholar

Hinton, H., and Jarman, G. (1972). Physiological colour change in the hercules beetle. Nature 238, 160–161. doi:10.1038/238160a0

CrossRef Full Text | Google Scholar

Hoffman, D. W., and Cahn, J. W. (1972). A vector thermodynamics for anisotropic surfaces: I. fundamentals and application to plane surface junctions. Surf. Sci. 31, 368–388. doi:10.1016/0039-6028(72)90268-3

CrossRef Full Text | Google Scholar

Hong, W., Zhao, X., and Suo, Z. (2009). Formation of creases on the surfaces of elastomers and gels. Appl. Phys. Lett. 95, 111901. doi:10.1063/1.3211917

CrossRef Full Text | Google Scholar

Hu, H.-W., Haider, G., Liao, Y.-M., Roy, P. K., Ravindranath, R., Chang, H.-T., et al. (2017). Wrinkled 2d materials: A versatile platform for low-threshold stretchable random lasers. Adv. Mater. 29, 1703549. doi:10.1002/adma.201703549

CrossRef Full Text | Google Scholar

Hu, K.-M., Liu, Y.-Q., Zhou, L.-W., Xue, Z.-Y., Peng, B., Yan, H., et al. (2020). Delamination-free functional graphene surface by multiscale, conformal wrinkling. Adv. Funct. Mater. 30, 2003273. doi:10.1002/adfm.202003273

CrossRef Full Text | Google Scholar

Hwang, C. M., Park, Y., Park, J., Lee, K., Sun, K., Khademhosseini, A., et al. (2009). Controlled cellular orientation on plga microfibers with defined diameters. Biomed. microdevices 11, 739–746. doi:10.1007/s10544-009-9287-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Ilca, S. L., Sun, X., El Omari, K., Kotecha, A., de Haas, F., DiMaio, F., et al. (2019). Multiple liquid crystalline geometries of highly compacted nucleic acid in a dsrna virus. Nature 570, 252–256. doi:10.1038/s41586-019-1229-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Islam, M. A., Xu, Y., Tao, W., Ubellacker, J. M., Lim, M., Aum, D., et al. (2018). Restoration of tumour-growth suppression in vivo via systemic nanoparticle-mediated delivery of pten mrna. Nat. Biomed. Eng. 2, 850–864. doi:10.1038/s41551-018-0284-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Iwashita, Y., and Tanaka, H. (2006). Self-organization in phase separation of a lyotropic liquid crystal into cellular, network and droplet morphologies. Nat. Mater. 5, 147–152. doi:10.1038/nmat1580

PubMed Abstract | CrossRef Full Text | Google Scholar

Izawa, H. (2017). Preparation of biobased wrinkled surfaces via lignification-mimetic reactions and drying: a new approach for developing surface wrinkling. Polym. J. 49, 759–765. doi:10.1038/pj.2017.52

CrossRef Full Text | Google Scholar

Jia, J., Chong, S., Yu, L., and Yao, Y. (2022). Cell membrane tensile strain under cyclic compression: A viscoelastic myoblast finite element model. Med. Nov. Technol. Devices 16, 100155. doi:10.1016/j.medntd.2022.100155

CrossRef Full Text | Google Scholar

Jin, L., Cai, S., and Suo, Z. (2011). Creases in soft tissues generated by growth. EPL Europhys. Lett. 95, 64002. doi:10.1209/0295-5075/95/64002

CrossRef Full Text | Google Scholar

Jin, L. (2014). Mechanical instabilities of soft materials: creases, wrinkles, folds, and ridges. Ph.D. thesis. Cambridge, MA, United States: Harvard University.

Google Scholar

Joubert, F., and Puff, N. (2021). Mitochondrial cristae architecture and functions: Lessons from minimal model systems. Membranes 11, 465. doi:10.3390/membranes11070465

PubMed Abstract | CrossRef Full Text | Google Scholar

Jun, K., Kim, D., Ryu, S., and Oh, I.-K. (2017). Surface modification of anisotropic dielectric elastomer actuators with uni-and bi-axially wrinkled carbon electrodes for wettability control. Sci. Rep. 7, 6091–6099. doi:10.1038/s41598-017-06274-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Junisu, B. A., Chang, I. C.-Y., Lin, C.-C., and Sun, Y.-S. (2022). Surface wrinkling on polymer films. Langmuir 38, 3907–3916. doi:10.1021/acs.langmuir.2c00156

PubMed Abstract | CrossRef Full Text | Google Scholar

Kameche, F., Heni, W., Telitel, S., Ge, D., Vidal, L., Dumur, F., et al. (2020). Plasmon-triggered living photopolymerization for elaboration of hybrid polymer/metal nanoparticles. Mater. Today 40, 38–47. doi:10.1016/j.mattod.2020.03.023

CrossRef Full Text | Google Scholar

Karpitschka, S., Eggers, J., Pandey, A., and Snoeijer, J. (2017). Cusp-shaped elastic creases and furrows. Phys. Rev. Lett. 119, 198001. doi:10.1103/physrevlett.119.198001

PubMed Abstract | CrossRef Full Text | Google Scholar

Kemkemer, R., Kling, D., Kaufmann, D., and Gruler, H. (2000a). Elastic properties of nematoid arrangements formed by amoeboid cells. Eur. Phys. J. E 1, 215–225. doi:10.1007/s101890050024

CrossRef Full Text | Google Scholar

Kemkemer, R., Teichgräber, V., Schrank-Kaufmann, S., Kaufmann, D., and Gruler, H. (2000b). Nematic order-disorder state transition in a liquid crystal analogue formed by oriented and migrating amoeboid cells. Eur. Phys. J. E 3, 101–110. doi:10.1007/s101890070023

CrossRef Full Text | Google Scholar

Khadem, S. A., and Rey, A. D. (2019a). Theoretical platform for liquid-crystalline self-assembly of collagen-based biomaterials. Front. Phys. 7, 88. doi:10.3389/fphy.2019.00088

CrossRef Full Text | Google Scholar

Khadem, S. A., and Rey, A. D. (2019b). Thermodynamic modelling of acidic collagenous solutions: from free energy contributions to phase diagrams. Soft matter 15, 1833–1846. doi:10.1039/c8sm02140f

PubMed Abstract | CrossRef Full Text | Google Scholar

Khadem, S. A., and Rey, A. D. (2021). Nucleation and growth of cholesteric collagen tactoids: A time-series statistical analysis based on integration of direct numerical simulation (dns) and long short-term memory recurrent neural network (lstm-rnn). J. Colloid Interface Sci. 582, 859–873. doi:10.1016/j.jcis.2020.08.052

PubMed Abstract | CrossRef Full Text | Google Scholar

Khayyatzadeh, P., Fu, F., and Abukhdeir, N. M. (2015). Field-driven dynamics of nematic microcapillaries. Phys. Rev. E 92, 062509. doi:10.1103/physreve.92.062509

CrossRef Full Text | Google Scholar

Kim, J. H., Lee, S.-Y., Park, J., and Moon, J. (2010). “Humidity sensors mimicking cuticle of hercules beetles,” in SENSORS, 2010 IEEE (IEEE), 805–808.

Google Scholar

Kim, H. Y., Pang, M.-F., Varner, V. D., Kojima, L., Miller, E., Radisky, D. C., et al. (2015). Localized smooth muscle differentiation is essential for epithelial bifurcation during branching morphogenesis of the mammalian lung. Dev. Cell 34, 719–726. doi:10.1016/j.devcel.2015.08.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, J. Y., Nayani, K., Jeong, H. S., Jeon, H.-J., Yoo, H.-W., Lee, E. H., et al. (2016). Macroscopic alignment of chromonic liquid crystals using patterned substrates. Phys. Chem. Chem. Phys. 18, 10362–10366. doi:10.1039/c5cp07570j

PubMed Abstract | CrossRef Full Text | Google Scholar

Kirkwood, J. E., and Fuller, G. G. (2009). Liquid crystalline collagen: a self-assembled morphology for the orientation of mammalian cells. Langmuir 25, 3200–3206. doi:10.1021/la803736x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kluge, J. A., Rabotyagova, O., Leisk, G. G., and Kaplan, D. L. (2008). Spider silks and their applications. Trends Biotechnol. 26, 244–251. doi:10.1016/j.tibtech.2008.02.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Koenderink, J. J., and Van Doorn, A. J. (1992). Surface shape and curvature scales. Image Vis. Comput. 10, 557–564. doi:10.1016/0262-8856(92)90076-f

CrossRef Full Text | Google Scholar

Kornev, K., and Shugai, G. (1998). Thermodynamic and hydrodynamic peculiarities of a foam lamella confined in a cylindrical pore. Phys. Rev. E 58, 7606–7619. doi:10.1103/physreve.58.7606

CrossRef Full Text | Google Scholar

Kornev, K. G., Neimark, A. V., and Rozhkov, A. N. (1999). Foam in porous media: thermodynamic and hydrodynamic peculiarities. Adv. colloid interface Sci. 82, 127–187. doi:10.1016/s0001-8686(99)00013-5

CrossRef Full Text | Google Scholar

Kunitake, T., Nakashima, N., Takarabe, K., Nagai, M., Tsuge, A., and Yanagi, H. (1981). Vesicles of polymeric bilayer and monolayer membranes. J. Am. Chem. Soc. 103, 5945–5947. doi:10.1021/ja00409a071

CrossRef Full Text | Google Scholar

Kuzman, D., Svetina, S., Waugh, R., and Žekš, B. (2004). Elastic properties of the red blood cell membrane that determine echinocyte deformability. Eur. Biophysics J. 33, 1–15. doi:10.1007/s00249-003-0337-4

CrossRef Full Text | Google Scholar

Lagerwall, J. P., Schütz, C., Salajkova, M., Noh, J., Hyun Park, J., Scalia, G., et al. (2014). Cellulose nanocrystal-based materials: from liquid crystal self-assembly and glass formation to multifunctional thin films. NPG Asia Mater. 6, e80. doi:10.1038/am.2013.69

CrossRef Full Text | Google Scholar

Lammerding, J., Fong, L. G., Ji, J. Y., Reue, K., Stewart, C. L., Young, S. G., et al. (2006). Lamins a and c but not lamin b1 regulate nuclear mechanics. J. Biol. Chem. 281, 25768–25780. doi:10.1074/jbc.m513511200

PubMed Abstract | CrossRef Full Text | Google Scholar

Lammerding, J. (2011). Mechanics of the nucleus. Compr. Physiol. 1, 783–807. doi:10.1002/cphy.c100038

PubMed Abstract | CrossRef Full Text | Google Scholar

Lamparter, L., and Galic, M. (2020). Cellular membranes, a versatile adaptive composite material. Front. Cell Dev. Biol. 8, 684. doi:10.3389/fcell.2020.00684

PubMed Abstract | CrossRef Full Text | Google Scholar

Lauffenburger, D. A., and Horwitz, A. F. (1996). Cell migration: a physically integrated molecular process. Cell 84, 359–369. doi:10.1016/s0092-8674(00)81280-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Lawaczeck, R., Kainosho, M., and Chan, S. I. (1976). The formation and annealing of structural defects in lipid bilayer vesicles. Biochim. Biophys. Acta (BBA)-Nucleic Acids Protein Synthesis 443, 313–330. doi:10.1016/0005-2736(76)90032-8

CrossRef Full Text | Google Scholar

Lee, D. W., and Lowry, J. B. (1975). Physical basis and ecological significance of iridescence in blue plants. Nature 254, 50–51. doi:10.1038/254050a0

CrossRef Full Text | Google Scholar

Lee, H.-G., Munir, S., and Park, S.-Y. (2016). Cholesteric liquid crystal droplets for biosensors. ACS Appl. Mater. interfaces 8, 26407–26417. doi:10.1021/acsami.6b09624

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehnert, M. S., Monaenkova, D., Andrukh, T., Beard, C. E., Adler, P. H., and Kornev, K. G. (2013). Hydrophobic–hydrophilic dichotomy of the butterfly proboscis. J. R. Soc. Interface 10, 20130336. doi:10.1098/rsif.2013.0336

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Zhang, H., Qiu, F., and Shi, A.-C. (2013). Emergence and stability of intermediate open vesicles in disk-to-vesicle transitions. Phys. Rev. E 88, 012719. doi:10.1103/physreve.88.012719

CrossRef Full Text | Google Scholar

Li, S., Wu, K., Yuan, H., Zhang, J., Liu, G., and Sun, J. (2019). Formation of wrinkled patterns in metal films deposited on elastic substrates: Tunability and wettability. Surf. Coatings Technol. 362, 35–43. doi:10.1016/j.surfcoat.2019.01.088

CrossRef Full Text | Google Scholar

Li, X., Dong, M., Jiang, D., Li, S., and Shang, Y. (2020a). The effect of surface roughness on normal restitution coefficient, adhesion force and friction coefficient of the particle-wall collision. Powder Technol. 362, 17–25. doi:10.1016/j.powtec.2019.11.120

CrossRef Full Text | Google Scholar

Li, X., Sánchez-Ferrer, A., Bagnani, M., Adamcik, J., Azzari, P., Hao, J., et al. (2020b). Metal ions confinement defines the architecture of g-quartet, g-quadruplex fibrils and their assembly into nematic tactoids. Proc. Natl. Acad. Sci. 117, 9832–9839. doi:10.1073/pnas.1919777117

CrossRef Full Text | Google Scholar

Li, T., Chen, C., Brozena, A. H., Zhu, J., Xu, L., Driemeier, C., et al. (2021). Developing fibrillated cellulose as a sustainable technological material. Nature 590, 47–56. doi:10.1038/s41586-020-03167-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, Z., Zhao, Y., Gao, H., Wang, D., Miao, Z., Cao, H., et al. (2021). The relationship between crosslinker, liquid crystal, and magnetic nanomaterial doping on electro-optical properties of pdlc. Liq. Cryst. 48, 2016–2026. doi:10.1080/02678292.2021.1919767

CrossRef Full Text | Google Scholar

Liao, W., Liu, X., Li, G., and Chen, T. (2020). Evaluation of thermal-hydraulic performance of dimpled tube from the perspective of skewness and kurtosis. Int. J. Therm. Sci. 156, 106469. doi:10.1016/j.ijthermalsci.2020.106469

CrossRef Full Text | Google Scholar

Liao, W., Luo, Y., and Chen, T. (2021). Thermal-hydraulic performance analysis of outward convex corrugated tubes based on skewness and kurtosis. Int. J. Therm. Sci. 165, 106970. doi:10.1016/j.ijthermalsci.2021.106970

CrossRef Full Text | Google Scholar

Ličen, M., Majaron, B., Noh, J., Schütz, C., Bergström, L., Lagerwall, J., et al. (2016). Correlation between structural properties and iridescent colors of cellulose nanocrystalline films. Cellulose 23, 3601–3609. doi:10.1007/s10570-016-1066-z

CrossRef Full Text | Google Scholar

Lin, G., Chandrasekaran, P., Lv, C., Zhang, Q., Tang, Y., Han, L., et al. (2017). Self-similar hierarchical wrinkles as a potential multifunctional smart window with simultaneously tunable transparency, structural color, and droplet transport. ACS Appl. Mater. Interfaces 9, 26510–26517. doi:10.1021/acsami.7b05056

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, I.-T., Choi, Y. S., Wojcik, C., Wang, T., Kar-Narayan, S., and Smoukov, S. K. (2020). Electro-responsive surfaces with controllable wrinkling patterns for switchable light reflection–diffusion–grating devices. Mater. Today 41, 51–61. doi:10.1016/j.mattod.2020.09.028

CrossRef Full Text | Google Scholar

Liu, F., Dong, B., Liu, X., Zheng, Y., and Zi, J. (2009). Structural color change in longhorn beetles tmesisternus isabellae. Opt. express 17, 16183–16191. doi:10.1364/oe.17.016183

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Q., Ouchi, T., Jin, L., Hayward, R., and Suo, Z. (2019). Elastocapillary crease. Phys. Rev. Lett. 122, 098003. doi:10.1103/physrevlett.122.098003

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, H., Wang, L., Hu, Y., Huang, Z., Sun, Y., Dong, S., et al. (2020). Dna thermotropic liquid crystals controlled by positively charged catanionic bilayer vesicles. Chem. Commun. 56, 3484–3487. doi:10.1039/d0cc00980f

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, A., Yao, Y., Yao, J., and Liu, T. (2022). Droplet spreading induced wrinkling and its use for measuring the elastic modulus of polymeric thin films. Macromolecules 55, 3877–3885. doi:10.1021/acs.macromol.2c00345

CrossRef Full Text | Google Scholar

Lo, Y.-P., Liu, Y.-S., Rimando, M. G., Ho, J. H.-C., Lin, K.-h., and Lee, O. K. (2016). Three-dimensional spherical spatial boundary conditions differentially regulate osteogenic differentiation of mesenchymal stromal cells. Sci. Rep. 6, 21253. doi:10.1038/srep21253

PubMed Abstract | CrossRef Full Text | Google Scholar

Lodish, H. F., Kong, N., Snider, M., and Strous, G. J. (1983). Hepatoma secretory proteins migrate from rough endoplasmic reticulum to golgi at characteristic rates. Nature 304, 80–83. doi:10.1038/304080a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Lowe, A. M., Ozer, B. H., Bai, Y., Bertics, P. J., and Abbott, N. L. (2010). Design of surfaces for liquid crystal-based bioanalytical assays. ACS Appl. Mater. interfaces 2, 722–731. doi:10.1021/am900753v

PubMed Abstract | CrossRef Full Text | Google Scholar

Maeda, H. (1999). An atomic force microscopy study of ordered molecular assemblies and concentric ring patterns from evaporating droplets of collagen solutions. Langmuir 15, 8505–8513. doi:10.1021/la981738l

CrossRef Full Text | Google Scholar

Malheiro, V., Lehner, F., Dinca, V., Hoffmann, P., and Maniura-Weber, K. (2016). Convex and concave micro-structured silicone controls the shape, but not the polarization state of human macrophages. Biomater. Sci. 4, 1562–1573. doi:10.1039/c6bm00425c

PubMed Abstract | CrossRef Full Text | Google Scholar

Mandon, E. C., Trueman, S. F., and Gilmore, R. (2013). Protein translocation across the rough endoplasmic reticulum. Cold Spring Harb. Perspect. Biol. 5, a013342. doi:10.1101/cshperspect.a013342

PubMed Abstract | CrossRef Full Text | Google Scholar

Mangin, J.-F., Riviere, D., Cachia, A., Duchesnay, E., Cointepas, Y., Papadopoulos-Orfanos, D., et al. (2004). A framework to study the cortical folding patterns. Neuroimage 23, S129–S138. doi:10.1016/j.neuroimage.2004.07.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Marino, A., Filippeschi, C., Genchi, G. G., Mattoli, V., Mazzolai, B., and Ciofani, G. (2014). The osteoprint: a bioinspired two-photon polymerized 3-d structure for the enhancement of bone-like cell differentiation. Acta biomater. 10, 4304–4313. doi:10.1016/j.actbio.2014.05.032

PubMed Abstract | CrossRef Full Text | Google Scholar

Martínez-Balbuena, L., Arteaga-Jiménez, A., Hernández-Zapata, E., and Urrutia-Buñuelos, E. (2021). Application of the helfrich elasticity theory to the morphology of red blood cells. Am. J. Phys. 89, 465–476. doi:10.1119/10.0003452

CrossRef Full Text | Google Scholar

May, M., Ortiz, G. J., Wendland, L. D., Rotstein, D. S., Relich, R. F., Balish, M. F., et al. (2007). Mycoplasma insons sp. nov., a twisted mycoplasma from green iguanas (iguana iguana). FEMS Microbiol. Lett. 274, 298–303. doi:10.1111/j.1574-6968.2007.00847.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Mazur, G. D., Regier, J. C., and Kafatos, F. C. (1982). “Order and defects in the silkmoth chorion, a biological analogue of a cholesteric liquid crystal,” in Insect ultrastructure (Springer), 150–185.

CrossRef Full Text | Google Scholar

McBeath, R., Pirone, D. M., Nelson, C. M., Bhadriraju, K., and Chen, C. S. (2004). Cell shape, cytoskeletal tension, and rhoa regulate stem cell lineage commitment. Dev. Cell 6, 483–495. doi:10.1016/s1534-5807(04)00075-9

PubMed Abstract | CrossRef Full Text | Google Scholar

McNamara, L. E., McMurray, R. J., Biggs, M. J., Kantawong, F., Oreffo, R. O., and Dalby, M. J. (2010). Nanotopographical control of stem cell differentiation. J. Tissue Eng. 1, 120623. doi:10.4061/2010/120623

PubMed Abstract | CrossRef Full Text | Google Scholar

Meister, R., Dumoulin, H., Hallé, M.-A., and Pieranski, P. (1996). The anchoring of a cholesteric liquid crystal at the free surface. J. de Physique II 6, 827–844. doi:10.1051/jp2:1996214

CrossRef Full Text | Google Scholar

Miller, D. S., and Abbott, N. L. (2013). Influence of droplet size, ph and ionic strength on endotoxin-triggered ordering transitions in liquid crystalline droplets. Soft Matter 9, 374–382. doi:10.1039/c2sm26811f

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitov, M. (2017). Cholesteric liquid crystals in living matter. Soft Matter 13, 4176–4209. doi:10.1039/c7sm00384f

PubMed Abstract | CrossRef Full Text | Google Scholar

Monaenkova, D., Lehnert, M. S., Andrukh, T., Beard, C. E., Rubin, B., Tokarev, A., et al. (2012). Butterfly proboscis: combining a drinking straw with a nanosponge facilitated diversification of feeding habits. J. R. Soc. Interface 9, 720–726. doi:10.1098/rsif.2011.0392

PubMed Abstract | CrossRef Full Text | Google Scholar

Mu, W., Ou-Yang, Z., and Cao, J. (2020). The stability of spherocyte membranes: Theoretical study. EPL Europhys. Lett. 128, 38001. doi:10.1209/0295-5075/128/38001

CrossRef Full Text | Google Scholar

Mueller, P., Chien, T., and Rudy, B. (1983). Formation and properties of cell-size lipid bilayer vesicles. Biophysical J. 44, 375–381. doi:10.1016/s0006-3495(83)84311-2

CrossRef Full Text | Google Scholar

Muñoz, S., Sebastián, J., Sancho, M., and Álvarez, G. (2014). Elastic energy of the discocyte–stomatocyte transformation. Biochim. Biophys. Acta (BBA)-Biomembranes 1838, 950–956. doi:10.1016/j.bbamem.2013.10.020

CrossRef Full Text | Google Scholar

Murugesan, Y. K., and Rey, A. D. (2010a). Modeling textural processes during self-assembly of plant-based chiral-nematic liquid crystals. Polymers 2, 766–785. doi:10.3390/polym2040766

CrossRef Full Text | Google Scholar

Murugesan, Y. K., and Rey, A. D. (2010b). Structure and rheology of fiber-laden membranes via integration of nematodynamics and membranodynamics. J. Newt. fluid Mech. 165, 32–44. doi:10.1016/j.jnnfm.2009.08.009

CrossRef Full Text | Google Scholar

Murugesan, Y. K., and Rey, A. D. (2010c). Thermodynamic model of structure and shape in rigid polymer-laden membranes. Macromol. theory simulations 19, 113–126. doi:10.1002/mats.200900044

CrossRef Full Text | Google Scholar

Murugesan, Y. K., Pasini, D., and Rey, A. D. (2011). Microfibril organization modes in plant cell walls of variable curvature: a model system for two dimensional anisotropic soft matter. Soft Matter 7, 7078–7093. doi:10.1039/c1sm05363a

CrossRef Full Text | Google Scholar

Murugesan, Y. K., Pasini, D., and Rey, A. D. (2015). Self-assembly mechanisms in plant cell wall components. J. Renew. Mater. 3, 56–72. doi:10.7569/jrm.2014.634124

CrossRef Full Text | Google Scholar

Nam, J., Kim, Y., Kim, J. G., and Seo, M. (2019). Self-assembly of monolayer vesicles via backbone-shiftable synthesis of janus core–shell bottlebrush polymer. Macromolecules 52, 9484–9494. doi:10.1021/acs.macromol.9b01429

CrossRef Full Text | Google Scholar

Nania, M., Matar, O. K., and Cabral, J. T. (2015). Frontal vitrification of pdms using air plasma and consequences for surface wrinkling. Soft Matter 11, 3067–3075. doi:10.1039/c4sm02840f

PubMed Abstract | CrossRef Full Text | Google Scholar

Nath, U., Crawford, B. C., Carpenter, R., and Coen, E. (2003). Genetic control of surface curvature. Science 299, 1404–1407. doi:10.1126/science.1079354

PubMed Abstract | CrossRef Full Text | Google Scholar

Nikolov, S., Fabritius, H., Friák, M., and Raabe, D. (2015). Integrated multiscale modeling approach for hierarchical biological nanocomposites applied to lobster cuticle. Bulg. Chem. Commun. 47, 423–432.

Google Scholar

Norlén, L. (2001). Skin barrier formation: the membrane folding model. J. Invest. Dermatol. 117, 823–829. doi:10.1046/j.0022-202x.2001.01445.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Noroozi, N., Grecov, D., and Shafiei-Sabet, S. (2014). Estimation of viscosity coefficients and rheological functions of nanocrystalline cellulose aqueous suspensions. Liq. Cryst. 41, 56–66. doi:10.1080/02678292.2013.834081

CrossRef Full Text | Google Scholar

Nyström, G., Arcari, M., and Mezzenga, R. (2018). Confinement-induced liquid crystalline transitions in amyloid fibril cholesteric tactoids. Nat. Nanotechnol. 13, 330–336. doi:10.1038/s41565-018-0071-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Oh, J. H., Woo, J. Y., Jo, S., and Han, C.-S. (2019). Iridescent and glossy effect on polymer surface using micro-/nanohierarchical structure: Artificial queen of the night tulip petals. ACS Appl. Mater. interfaces 11, 26442–26447. doi:10.1021/acsami.9b06376

PubMed Abstract | CrossRef Full Text | Google Scholar

Ozdemir, T., Xu, L.-C., Siedlecki, C., and Brown, J. L. (2013). Substrate curvature sensing through myosin iia upregulates early osteogenesis. Integr. Biol. 5, 1407–1416. doi:10.1039/c3ib40068a

CrossRef Full Text | Google Scholar

Park, J. Y., Lee, D. H., Lee, E. J., and Lee, S.-H. (2009). Study of cellular behaviors on concave and convex microstructures fabricated from elastic pdms membranes. Lab a Chip 9, 2043–2049. doi:10.1039/b820955c

CrossRef Full Text | Google Scholar

Park, H.-G., Jeong, H.-C., Jung, Y. H., and Seo, D.-S. (2015). Control of the wrinkle structure on surface-reformed poly (dimethylsiloxane) via ion-beam bombardment. Sci. Rep. 5, 12356–12358. doi:10.1038/srep12356

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, S. M., Bagnani, M., Yun, H. S., Han, M. J., Mezzenga, R., and Yoon, D. K. (2021). Hierarchically fabricated amyloid fibers via evaporation-induced self-assembly. ACS Nano 15, 20261–20266. doi:10.1021/acsnano.1c08374

PubMed Abstract | CrossRef Full Text | Google Scholar

Patek, S. N., Korff, W., and Caldwell, R. L. (2004). Deadly strike mechanism of a mantis shrimp. Nature 428, 819–820. doi:10.1038/428819a

PubMed Abstract | CrossRef Full Text | Google Scholar

Paterson, D. A., Bao, P., Abou-Saleh, R. H., Peyman, S. A., Jones, J. C., Sandoe, J. A., et al. (2020). Control of director fields in phospholipid-coated liquid crystal droplets. Langmuir 36, 6436–6446. doi:10.1021/acs.langmuir.0c00651

PubMed Abstract | CrossRef Full Text | Google Scholar

Perkins, G., and Frey, T. (2000). Recent structural insight into mitochondria gained by microscopy. Micron 31, 97–111. doi:10.1016/s0968-4328(99)00065-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Persson, B. N., Albohr, O., Tartaglino, U., Volokitin, A., and Tosatti, E. (2004). On the nature of surface roughness with application to contact mechanics, sealing, rubber friction and adhesion. J. Phys. Condens. matter 17, R1–R62. doi:10.1088/0953-8984/17/1/r01

PubMed Abstract | CrossRef Full Text | Google Scholar

Pieuchot, L., Marteau, J., Guignandon, A., Dos Santos, T., Brigaud, I., Chauvy, P.-F., et al. (2018). Curvotaxis directs cell migration through cell-scale curvature landscapes. Nat. Commun. 9, 3995–4013. doi:10.1038/s41467-018-06494-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Priest, R. G. (1973). Theory of the frank elastic constants of nematic liquid crystals. Phys. Rev. A 7, 720–729. doi:10.1103/physreva.7.720

CrossRef Full Text | Google Scholar

Raabe, D., Al-Sawalmih, A., Yi, S., and Fabritius, H. (2007). Preferred crystallographic texture of α-chitin as a microscopic and macroscopic design principle of the exoskeleton of the lobster homarus americanus. Acta Biomater. 3, 882–895. doi:10.1016/j.actbio.2007.04.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Rajala, S., Siponkoski, T., Sarlin, E., Mettanen, M., Vuoriluoto, M., Pammo, A., et al. (2016). Cellulose nanofibril film as a piezoelectric sensor material. ACS Appl. Mater. interfaces 8, 15607–15614. doi:10.1021/acsami.6b03597

PubMed Abstract | CrossRef Full Text | Google Scholar

Rey, A. D., and Denn, M. M. (2002). Dynamical phenomena in liquid-crystalline materials. Annu. Rev. Fluid Mech. 34, 233–266. doi:10.1146/annurev.fluid.34.082401.191847

CrossRef Full Text | Google Scholar

Rey, A. D., and Herrera-Valencia, E. E. (2012). Liquid crystal models of biological materials and silk spinning. Biopolymers 97, 374–396. doi:10.1002/bip.21723

PubMed Abstract | CrossRef Full Text | Google Scholar

Rey, A. D., and Murugesan, Y. K. (2011). Mechanical model for fiber-laden membranes. Continuum Mech. Thermodyn. 23, 45–61. doi:10.1007/s00161-010-0160-y

CrossRef Full Text | Google Scholar

Rey, A. D., and Tsuji, T. (1998). Recent advances in theoretical liquid crystal rheology. Macromol. Theory Simul. 7, 623–639. doi:10.1002/(sici)1521-3919(19981101)7:6<623:aid-mats623>3.0.co;2-e

CrossRef Full Text | Google Scholar

Rey, A. D., Servio, P., and Herrera-Valencia, E. (2013). Bioinspired model of mechanical energy harvesting based on flexoelectric membranes. Phys. Rev. E 87, 022505. doi:10.1103/physreve.87.022505

CrossRef Full Text | Google Scholar

Rey, A. D., Herrera-Valencia, E., and Murugesan, Y. K. (2014a). Structure and dynamics of biological liquid crystals. Liq. Cryst. 41, 430–451. doi:10.1080/02678292.2013.845698

CrossRef Full Text | Google Scholar

Rey, A. D., Servio, P., and Herrera Valencia, E. E. (2014b). Stress-sensor device based on flexoelectric liquid crystalline membranes. ChemPhysChem 15, 1405–1412. doi:10.1002/cphc.201300600

PubMed Abstract | CrossRef Full Text | Google Scholar

Rey, A. D. (1997a). Linear stability theory of break-up dynamics of nematic liquid crystalline fibers. J. de Physique II 7, 1001–1011. doi:10.1051/jp2:1997166

CrossRef Full Text | Google Scholar

Rey, A. D. (1997b). Thermodynamic stability analysis of liquid-crystalline polymer fibers. Indust. Eng. Chem. Res. 36, 1114–1121. doi:10.1021/ie9604637

CrossRef Full Text | Google Scholar

Rey, A. D. (1999a). Marangoni flow in liquid crystal interfaces. J. Chem. Phys. 110, 9769–9770. doi:10.1063/1.478943

CrossRef Full Text | Google Scholar

Rey, A. D. (1999b). Nemato-capillarity theory and the orientation-induced marangoni flow. Liq. Cryst. 26, 913–917. doi:10.1080/026782999204606

CrossRef Full Text | Google Scholar

Rey, A. D. (1999c). Tension gradients and marangoni flows in nematic interfaces. Phys. Rev. E 60, 1077–1080. doi:10.1103/physreve.60.1077

CrossRef Full Text | Google Scholar

Rey, A. D. (2000a). Modeling the wilhelmy surface tension method for nematic liquid crystals. Langmuir 16, 845–849. doi:10.1021/la9902542

CrossRef Full Text | Google Scholar

Rey, A. D. (2000b). Viscoelastic theory for nematic interfaces. Phys. Rev. E 61, 1540–1549. doi:10.1103/physreve.61.1540

CrossRef Full Text | Google Scholar

Rey, A. D. (2000c). Young–laplace equation for liquid crystal interfaces. J. Chem. Phys. 113, 10820–10822. doi:10.1063/1.1324993

CrossRef Full Text | Google Scholar

Rey, A. D. (2001a). Generalized young-laplace equation for nematic liquid crystal interfaces and its application to free-surface defects. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A. Mol. Cryst. Liq. Cryst. 369, 63–74. doi:10.1080/10587250108030009

CrossRef Full Text | Google Scholar

Rey, A. D. (2001b). Irreversible thermodynamics of liquid crystal interfaces. J. Newt. fluid Mech. 96, 45–62. doi:10.1016/s0377-0257(00)00143-9

CrossRef Full Text | Google Scholar

Rey, A. D. (2003). A model of capillary rise of nematic liquid crystals. Langmuir 19, 3677–3685. doi:10.1021/la020750h

CrossRef Full Text | Google Scholar

Rey, A. D. (2004a). Thermodynamic model of surfactant adsorption on soft liquid crystal interfaces. Langmuir 20, 11473–11479. doi:10.1021/la048642d

PubMed Abstract | CrossRef Full Text | Google Scholar

Rey, A. D. (2004b). Thermodynamics of soft anisotropic interfaces. J. Chem. Phys. 120, 2010–2019. doi:10.1063/1.1635357

PubMed Abstract | CrossRef Full Text | Google Scholar

Rey, A. D. (2005). Mechanics of soft-solid–liquid-crystal interfaces. Phys. Rev. E 72, 011706. doi:10.1103/physreve.72.011706

CrossRef Full Text | Google Scholar

Rey, A. D. (2006a). Anisotropic fluctuation model for surfactant-laden liquid-liquid crystal interfaces. Langmuir 22, 3491–3493. doi:10.1021/la060092r

PubMed Abstract | CrossRef Full Text | Google Scholar

Rey, A. D. (2006b). Mechanical model for anisotropic curved interfaces with applications to surfactant-laden liquid-liquid crystal interfaces. Langmuir 22, 219–228. doi:10.1021/la051974d

PubMed Abstract | CrossRef Full Text | Google Scholar

Rey, A. D. (2007). Capillary models for liquid crystal fibers, membranes, films, and drops. Soft Matter 3, 1349–1368. doi:10.1039/b704248p

PubMed Abstract | CrossRef Full Text | Google Scholar

Rey, A. D. (2009). Flow and texture modeling of liquid crystaline materials. Rheol. Rev. 6, 71–135.

Google Scholar

Rey, A. D. (2010). Liquid crystal models of biological materials and processes. Soft Matter 6, 3402–3429. doi:10.1039/b921576j

CrossRef Full Text | Google Scholar

Risteen, B. E., Blake, A., McBride, M. A., Rosu, C., Park, J. O., Srinivasarao, M., et al. (2017). Enhanced alignment of water-soluble polythiophene using cellulose nanocrystals as a liquid crystal template. Biomacromolecules 18, 1556–1562. doi:10.1021/acs.biomac.7b00121

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodriguez-Hernandez, J. (2015). Wrinkled interfaces: Taking advantage of surface instabilities to pattern polymer surfaces. Prog. Polym. Sci. 42, 1–41. doi:10.1016/j.progpolymsci.2014.07.008

CrossRef Full Text | Google Scholar

Rofouie, P., Pasini, D., and Rey, A. D. (2014). Nanostructured free surfaces in plant-based plywoods driven by chiral capillarity. Colloids Interface Sci. Commun. 1, 23–26. doi:10.1016/j.colcom.2014.06.003

CrossRef Full Text | Google Scholar

Rofouie, P., Pasini, D., and Rey, A. (2015a). Tunable nano-wrinkling of chiral surfaces: Structure and diffraction optics. J. Chem. Phys. 143, 114701. doi:10.1063/1.4929337

PubMed Abstract | CrossRef Full Text | Google Scholar

Rofouie, P., Pasini, D., and Rey, A. D. (2015b). Nano-scale surface wrinkling in chiral liquid crystals and plant-based plywoods. Soft Matter 11, 1127–1139. doi:10.1039/c4sm02371d

PubMed Abstract | CrossRef Full Text | Google Scholar

Rofouie, P., Pasini, D., and Rey, A. (2017a). Multiple-wavelength surface patterns in models of biological chiral liquid crystal membranes. Soft Matter 13, 541–545. doi:10.1039/c6sm02619b

PubMed Abstract | CrossRef Full Text | Google Scholar

Rofouie, P., Pasini, D., and Rey, A. D. (2017b). Morphology of elastic nematic liquid crystal membranes. Soft Matter 13, 5366–5380. doi:10.1039/c7sm00977a

PubMed Abstract | CrossRef Full Text | Google Scholar

Rofouie, P., Wang, Z., and Rey, A. (2018). Two-wavelength wrinkling patterns in helicoidal plywood surfaces: imprinting energy landscapes onto geometric landscapes. Soft Matter 14, 5180–5185. doi:10.1039/c8sm01022f

PubMed Abstract | CrossRef Full Text | Google Scholar

Rovensky, Y., and Samoilov, V. (1994). Morphogenetic response of cultured normal and transformed fibroblasts, and epitheliocytes, to a cylindrical substratum surface. possible role for the actin filament bundle pattern. J. Cell Sci. 107, 1255–1263. doi:10.1242/jcs.107.5.1255

PubMed Abstract | CrossRef Full Text | Google Scholar

Rumpler, M., Woesz, A., Dunlop, J. W., Van Dongen, J. T., and Fratzl, P. (2008). The effect of geometry on three-dimensional tissue growth. J. R. Soc. Interface 5, 1173–1180. doi:10.1098/rsif.2008.0064

PubMed Abstract | CrossRef Full Text | Google Scholar

Sakamoto, M., Iino, T., and Ohkuma, M. (2017). Faecalimonas umbilicata gen. nov., sp. nov., isolated from human faeces, and reclassification of eubacterium contortum, eubacterium fissicatena and clostridium oroticum as faecalicatena contorta gen. nov., comb. nov., faecalicatena fissicatena comb. nov. and faecalicatena orotica comb. nov. Int. J. Syst. Evol. Microbiol. 67, 1219–1227. doi:10.1099/ijsem.0.001790

PubMed Abstract | CrossRef Full Text | Google Scholar

Saraiva, D. V., Chagas, R., Abreu, B. M. d., Gouveia, C. N., Silva, P. E., Godinho, M. H., et al. (2020). Flexible and structural coloured composite films from cellulose nanocrystals/hydroxypropyl cellulose lyotropic suspensions. Crystals 10, 122. doi:10.3390/cryst10020122

CrossRef Full Text | Google Scholar

Saravanan, D. (2006). Spider silk-structure, properties and spinning. J. Text. Appar. Technol. Manag. 5, 1–20.

Google Scholar

Schauer, S., Worgull, M., and Hölscher, H. (2017). Bio-inspired hierarchical micro-and nano-wrinkles obtained via mechanically directed self-assembly on shape-memory polymers. Soft Matter 13, 4328–4334. doi:10.1039/c7sm00154a

PubMed Abstract | CrossRef Full Text | Google Scholar

Sedlaček, M., Podgornik, B., and Vižintin, J. (2012). Correlation between standard roughness parameters skewness and kurtosis and tribological behaviour of contact surfaces. Tribol. Int. 48, 102–112. doi:10.1016/j.triboint.2011.11.008

CrossRef Full Text | Google Scholar

Seeber, M., Zdyrko, B., Burtovvy, R., Andrukh, T., Tsai, C.-C., Owens, J. R., et al. (2011). Surface grafting of thermoresponsive microgel nanoparticles. Soft Matter 7, 9962–9971. doi:10.1039/c1sm05924f

CrossRef Full Text | Google Scholar

Seifert, U., Berndl, K., and Lipowsky, R. (1991). Shape transformations of vesicles: Phase diagram for spontaneous-curvature and bilayer-coupling models. Phys. Rev. A 44, 1182–1202. doi:10.1103/physreva.44.1182

PubMed Abstract | CrossRef Full Text | Google Scholar

Shams, A., Yao, X., Park, J. O., Srinivasarao, M., and Rey, A. D. (2015). Disclination elastica model of loop collision and growth in confined nematic liquid crystals. Soft Matter 11, 5455–5464. doi:10.1039/c5sm00708a

PubMed Abstract | CrossRef Full Text | Google Scholar

Shariatzadeh, M., and Grecov, D. (2019). Aqueous suspensions of cellulose nanocrystals as water-based lubricants. Cellulose 26, 4665–4677. doi:10.1007/s10570-019-02398-w

CrossRef Full Text | Google Scholar

Sharma, V., Crne, M., Park, J. O., and Srinivasarao, M. (2009). Structural origin of circularly polarized iridescence in jeweled beetles. science 325, 449–451. doi:10.1126/science.1172051

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharma, P., Ward, A., Gibaud, T., Hagan, M. F., and Dogic, Z. (2014). Hierarchical organization of chiral rafts in colloidal membranes. Nature 513, 77–80. doi:10.1038/nature13694

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharma, V., Crne, M., Park, J. O., and Srinivasarao, M. (2014). Bouligand structures underlie circularly polarized iridescence of scarab beetles: A closer view. Mater. Today Proc. 1, 161–171. doi:10.1016/j.matpr.2014.09.019

CrossRef Full Text | Google Scholar

Sharon, E., Marder, M., and Swinney, H. L. (2004). Leaves, flowers and garbage bags: Making waves. Am. Sci. 92, 254–261. doi:10.1511/2004.47.932

CrossRef Full Text | Google Scholar

Sharon, E., Roman, B., and Swinney, H. L. (2007). Geometrically driven wrinkling observed in free plastic sheets and leaves. Phys. Rev. E 75, 046211. doi:10.1103/physreve.75.046211

CrossRef Full Text | Google Scholar

Silva, P. E., Chagas, R., Fernandes, S. N., Pieranski, P., Selinger, R. L., and Godinho, M. H. (2021). Travelling colourful patterns in self-organized cellulose-based liquid crystalline structures. Commun. Mater. 2, 79–10. doi:10.1038/s43246-021-00182-7

CrossRef Full Text | Google Scholar

Simon, D. N., and Wilson, K. L. (2011). The nucleoskeleton as a genome-associated dynamic’network of networks. Nat. Rev. Mol. Cell Biol. 12, 695–708. doi:10.1038/nrm3207

PubMed Abstract | CrossRef Full Text | Google Scholar

Sloika, M. I., Kravchuk, V. P., Sheka, D. D., and Gaididei, Y. (2014). Curvature induced chirality symmetry breaking in vortex core switching phenomena. Appl. Phys. Lett. 104, 252403. doi:10.1063/1.4884957

CrossRef Full Text | Google Scholar

Soiné, J. R., Hersch, N., Dreissen, G., Hampe, N., Hoffmann, B., Merkel, R., et al. (2016). Measuring cellular traction forces on non-planar substrates. Interface focus 6, 20160024. doi:10.1098/rsfs.2016.0024

PubMed Abstract | CrossRef Full Text | Google Scholar

Sonin, A. A. (1995). The surface physics of liquid crystals. Philadelphia, PA, United States: Gordon & Breach Science.

Google Scholar

Stewart, I. W. (2019). The static and dynamic continuum theory of liquid crystals: A mathematical introduction. Boca Raton, FL, United States: CRC Press.

Google Scholar

Straley, J. (1973). Frank elastic constants of the hard-rod liquid crystal. Phys. Rev. A 8, 2181–2183. doi:10.1103/physreva.8.2181

CrossRef Full Text | Google Scholar

Striedter, G. F., Srinivasan, S., and Monuki, E. S. (2015). Cortical folding: when, where, how, and why? Annu. Rev. Neurosci. 38, 291–307. doi:10.1146/annurev-neuro-071714-034128

PubMed Abstract | CrossRef Full Text | Google Scholar

Suhandono, S., Kusumawardhani, M. K., and Aditiawati, P. (2016). Isolation and molecular identification of endophytic bacteria from rambutan fruits (nephelium lappaceum l.) cultivar binjai. HAYATI J. Biosci. 23, 39–44. doi:10.1016/j.hjb.2016.01.005

CrossRef Full Text | Google Scholar

Sun, J., Wu, W., Tian, L., Li, W., Zhang, F., and Wang, Y. (2021). Investigation of the selective color-changing mechanism of dynastes tityus beetle (coleoptera: Scarabaeidae). Sci. Rep. 11, 808–810. doi:10.1038/s41598-020-80699-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Svitkina, T. M., Rovensky, Y. A., Bershadsky, A. D., and Vasiliev, J. M. (1995). Transverse pattern of microfilament bundles induced in epitheliocytes by cylindrical substrata. J. Cell Sci. 108, 735–745. doi:10.1242/jcs.108.2.735

PubMed Abstract | CrossRef Full Text | Google Scholar

Szczesny, S. E., and Mauck, R. L. (2017). The nuclear option: evidence implicating the cell nucleus in mechanotransduction. J. Biomech. Eng. 139, 0210061–02100616. doi:10.1115/1.4035350

PubMed Abstract | CrossRef Full Text | Google Scholar

Tachev, K. D., Danov, K. D., and Kralchevsky, P. A. (2004). On the mechanism of stomatocyte–echinocyte transformations of red blood cells: experiment and theoretical model. Colloids Surfaces B Biointerfaces 34, 123–140. doi:10.1016/j.colsurfb.2003.12.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, Y., Hu, B., Song, J., Chu, Z., and Wu, W. (2020). Bioinspired multiscale wrinkling patterns on curved substrates: An overview. Nano-Micro Lett. 12, 101–142. doi:10.1007/s40820-020-00436-y

CrossRef Full Text | Google Scholar

Tayebi, N., and Polycarpou, A. A. (2004). Modeling the effect of skewness and kurtosis on the static friction coefficient of rough surfaces. Tribol. Int. 37, 491–505. doi:10.1016/j.triboint.2003.11.010

CrossRef Full Text | Google Scholar

Terris, B., Twieg, R., Nguyen, C., Sigaud, G., and Nguyen, H. (1992). Force microscopy of chiral liquid-crystal surfaces. EPL Europhys. Lett. 19, 85–90. doi:10.1209/0295-5075/19/2/005

CrossRef Full Text | Google Scholar

Thomas, C. H., Collier, J. H., Sfeir, C. S., and Healy, K. E. (2002). Engineering gene expression and protein synthesis by modulation of nuclear shape. Proc. Natl. Acad. Sci. 99, 1972–1977. doi:10.1073/pnas.032668799

PubMed Abstract | CrossRef Full Text | Google Scholar

Tokarev, A., Lee, W.-K., Sevonkaev, I., Goia, D., and Kornev, K. G. (2014). Sharpening the surface of magnetic paranematic droplets. Soft Matter 10, 1917–1923. doi:10.1039/c3sm52655k

PubMed Abstract | CrossRef Full Text | Google Scholar

Tokudome, Y., Kuniwaki, H., Suzuki, K., Carboni, D., Poologasundarampillai, G., and Takahashi, M. (2016). Thermoresponsive wrinkles on hydrogels for soft actuators. Adv. Mater. Interfaces 3, 1500802. doi:10.1002/admi.201500802

CrossRef Full Text | Google Scholar

Tortora, L., and Lavrentovich, O. D. (2011). Chiral symmetry breaking by spatial confinement in tactoidal droplets of lyotropic chromonic liquid crystals. Proc. Natl. Acad. Sci. 108, 5163–5168. doi:10.1073/pnas.1100087108

PubMed Abstract | CrossRef Full Text | Google Scholar

Trujillo, V., Kim, J., and Hayward, R. C. (2008). Creasing instability of surface-attached hydrogels. Soft Matter 4, 564–569. doi:10.1039/b713263h

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsai, C.-C., Monaenkova, D., Beard, C. E., Adler, P. H., and Kornev, K. G. (2014). Paradox of the drinking-straw model of the butterfly proboscis. J. Exp. Biol. 217, 2430–2138. doi:10.1242/jeb.109447

CrossRef Full Text | Google Scholar

Tu, Z., and Ou-Yang, Z. (2014). Recent theoretical advances in elasticity of membranes following helfrich’s spontaneous curvature model. Adv. colloid interface Sci. 208, 66–75. doi:10.1016/j.cis.2014.01.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Tu, Z. (2010). Compatibility between shape equation and boundary conditions of lipid membranes with free edges. J. Chem. Phys. 132, 084111. doi:10.1063/1.3335894

PubMed Abstract | CrossRef Full Text | Google Scholar

Umeda, T., Suezaki, Y., Takiguchi, K., and Hotani, H. (2005). Theoretical analysis of opening-up vesicles with single and two holes. Phys. Rev. E 71, 011913. doi:10.1103/physreve.71.011913

CrossRef Full Text | Google Scholar

van der Kooi, C. J., Dyer, A. G., and Stavenga, D. G. (2015). Is floral iridescence a biologically relevant cue in plant–pollinator signaling? New Phytol. 205, 18–20. doi:10.1111/nph.13066

PubMed Abstract | CrossRef Full Text | Google Scholar

Vatansever, F., Burtovyy, R., Zdyrko, B., Ramaratnam, K., Andrukh, T., Minko, S., et al. (2012). Toward fabric-based flexible microfluidic devices: Pointed surface modification for ph sensitive liquid transport. ACS Appl. Mater. interfaces 4, 4541–4548. doi:10.1021/am3008664

PubMed Abstract | CrossRef Full Text | Google Scholar

Vignolini, S., Moyroud, E., Glover, B. J., and Steiner, U. (2013). Analysing photonic structures in plants. J. R. Soc. Interface 10, 20130394. doi:10.1098/rsif.2013.0394

PubMed Abstract | CrossRef Full Text | Google Scholar

Vignolini, S., Moyroud, E., Hingant, T., Banks, H., Rudall, P. J., Steiner, U., et al. (2015). The flower of h ibiscus trionum is both visibly and measurably iridescent. New Phytol. 205, 97–101. doi:10.1111/nph.12958

PubMed Abstract | CrossRef Full Text | Google Scholar

Wainwright, D. K., Lauder, G. V., and Weaver, J. C. (2017). Imaging biological surface topography in situ and in vivo. Methods Ecol. Evol. 8, 1626–1638. doi:10.1111/2041-210x.12778

CrossRef Full Text | Google Scholar

Wang, Q., and Zhao, X. (2015). A three-dimensional phase diagram of growth-induced surface instabilities. Sci. Rep. 5, 8887–8910. doi:10.1038/srep08887

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, N., Tytell, J. D., and Ingber, D. E. (2009). Mechanotransduction at a distance: mechanically coupling the extracellular matrix with the nucleus. Nat. Rev. Mol. Cell Biol. 10, 75–82. doi:10.1038/nrm2594

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Wang, S., Zhang, S., Scherman, O. A., Baumberg, J. J., Ding, T., et al. (2018). Plasmon-directed polymerization: Regulating polymer growth with light. Nano Res. 11, 6384–6390. doi:10.1007/s12274-018-2163-0

CrossRef Full Text | Google Scholar

Wang, J., Zheng, Y., Li, L., Liu, E., Zong, C., Zhao, J., et al. (2019). All-optical reversible azo-based wrinkling patterns with high aspect ratio and polarization-independent orientation for light-responsive soft photonics. ACS Appl. Mater. Interfaces 11, 25595–25604. doi:10.1021/acsami.9b07349

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Rofouie, P., and Rey, A. D. (2019). Surface anchoring effects on the formation of two-wavelength surface patterns in chiral liquid crystals. Crystals 9, 190. doi:10.3390/cryst9040190

CrossRef Full Text | Google Scholar

Wang, Z., Servio, P., and Rey, A. D. (2020a). Mechanogeometry of nanowrinkling in cholesteric liquid crystal surfaces. Phys. Rev. E 101, 062705. doi:10.1103/physreve.101.062705

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Servio, P., and Rey, A. D. (2020b). Rate of entropy production in evolving interfaces and membranes under astigmatic kinematics: Shape evolution in geometric-dissipation landscapes. Entropy 22, 909. doi:10.3390/e22090909

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Dorgham, A., Liu, Y., Wang, C., Ghanbarzadeh, A., Wilson, M. C., et al. (2021). Towards optimum additive performance: A numerical study to understand the influence of roughness parameters on the zinc dialkyldithiophosphates tribofilm growth. Lubr. Sci. 33, 1–14. doi:10.1002/ls.1522

CrossRef Full Text | Google Scholar

Wang, Z., Servio, P., and Rey, A. (2021). Biaxial nanowrinkling in cholesteric surfaces: Egg carton surfaces through chiral anchoring. Colloid Interface Sci. Commun. 41, 100372. doi:10.1016/j.colcom.2021.100372

CrossRef Full Text | Google Scholar

Wang, Z., Servio, P., and Rey, A. (2022). Wrinkling pattern formation with periodic nematic orientation: From egg cartons to corrugated surfaces. Phys. Rev. E 105, 034702. doi:10.1103/physreve.105.034702

PubMed Abstract | CrossRef Full Text | Google Scholar

Wasungu, L., and Hoekstra, D. (2006). Cationic lipids, lipoplexes and intracellular delivery of genes. J. Control. Release 116, 255–264. doi:10.1016/j.jconrel.2006.06.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Weaver, J. C., Milliron, G. W., Miserez, A., Evans-Lutterodt, K., Herrera, S., Gallana, I., et al. (2012). The stomatopod dactyl club: a formidable damage-tolerant biological hammer. Science 336, 1275–1280. doi:10.1126/science.1218764

PubMed Abstract | CrossRef Full Text | Google Scholar

Werner, M., Blanquer, S. B., Haimi, S. P., Korus, G., Dunlop, J. W., Duda, G. N., et al. (2017). Surface curvature differentially regulates stem cell migration and differentiation via altered attachment morphology and nuclear deformation. Adv. Sci. 4, 1600347. doi:10.1002/advs.201600347

CrossRef Full Text | Google Scholar

Werner, M., Kurniawan, N. A., Korus, G., Bouten, C. V., and Petersen, A. (2018). Mesoscale substrate curvature overrules nanoscale contact guidance to direct bone marrow stromal cell migration. J. R. Soc. Interface 15, 20180162. doi:10.1098/rsif.2018.0162

PubMed Abstract | CrossRef Full Text | Google Scholar

Werner, M., Petersen, A., Kurniawan, N. A., and Bouten, C. V. (2019). Cell-perceived substrate curvature dynamically coordinates the direction, speed, and persistence of stromal cell migration. Adv. Biosyst. 3, 1900080. doi:10.1002/adbi.201900080

CrossRef Full Text | Google Scholar

Whitney, H. M., Kolle, M., Andrew, P., Chittka, L., Steiner, U., and Glover, B. J. (2009). Floral iridescence, produced by diffractive optics, acts as a cue for animal pollinators. Science 323, 130–133. doi:10.1126/science.1166256

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilkinson, S. R., Taylor, M. C., Touitha, S., Mauricio, I. L., Meyer, D. J., and Kelly, J. M. (2002). Tcgpxii, a glutathione-dependent trypanosoma cruzi peroxidase with substrate specificity restricted to fatty acid and phospholipid hydroperoxides, is localized to the endoplasmic reticulum. Biochem. J. 364, 787–794. doi:10.1042/bj20020038

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, B., and Destrade, M. (2021). Wrinkling of soft magneto-active plates. Int. J. Solids Struct. 208, 13–30. doi:10.1016/j.ijsolstr.2020.10.020

CrossRef Full Text | Google Scholar

Wu, X.-F., Dzenis, Y. A., and Strabala, K. W. (2007). Wrinkling of a charged elastic film on a viscous layer. Meccanica 42, 273–282. doi:10.1007/s11012-007-9054-x

CrossRef Full Text | Google Scholar

Xi, W., Sonam, S., Beng Saw, T., Ladoux, B., and Teck Lim, C. (2017). Emergent patterns of collective cell migration under tubular confinement. Nat. Commun. 8, 1517–1615. doi:10.1038/s41467-017-01390-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Y., Xu, T., Bei, H.-P., Zhang, L., Tang, C.-Y., Zhang, M., et al. (2022). Gaussian curvature–driven direction of cell fate toward osteogenesis with triply periodic minimal surface scaffolds. Proc. Natl. Acad. Sci. 119, e2206684119. doi:10.1073/pnas.2206684119

PubMed Abstract | CrossRef Full Text | Google Scholar

Yevick, H. G., Duclos, G., Bonnet, I., and Silberzan, P. (2015). Architecture and migration of an epithelium on a cylindrical wire. Proc. Natl. Acad. Sci. 112, 5944–5949. doi:10.1073/pnas.1418857112

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoo, P. J., and Lee, H. H. (2005). Morphological diagram for metal/polymer bilayer wrinkling: Influence of thermomechanical properties of polymer layer. Macromolecules 38, 2820–2831. doi:10.1021/ma048452+

CrossRef Full Text | Google Scholar

Zadpoor, A. A. (2015). Bone tissue regeneration: the role of scaffold geometry. Biomaterials Sci. 3, 231–245. doi:10.1039/c4bm00291a

PubMed Abstract | CrossRef Full Text | Google Scholar

Zakani, B., Entezami, S., Grecov, D., Salem, H., and Sedaghat, A. (2022). Effect of ultrasonication on lubrication performance of cellulose nano-crystalline (cnc) suspensions as green lubricants. Carbohydr. Polym. 282, 119084. doi:10.1016/j.carbpol.2021.119084

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhan-Chun, T. (2013). Challenges in the theoretical investigations of lipid membrane configurations. Chin. Phys. B 22, 028701. doi:10.1088/1674-1056/22/2/028701

CrossRef Full Text | Google Scholar

Zhang, C., Beard, C. E., Adler, P. H., and Kornev, K. G. (2018). Effect of curvature on wetting and dewetting of proboscises of butterflies and moths. R. Soc. open Sci. 5, 171241. doi:10.1098/rsos.171241

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, D., Davoodi, P., Li, X., Liu, Y., Wang, W., and Huang, Y. Y. S. (2020). An empirical model to evaluate the effects of environmental humidity on the formation of wrinkled, creased and porous fibre morphology from electrospinning. Sci. Rep. 10, 18783–18789. doi:10.1038/s41598-020-74542-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, M., Yan, D., Wang, J., and Shao, L.-H. (2021). Ultrahigh flexoelectric effect of 3d interconnected porous polymers: modelling and verification. J. Mech. Phys. Solids 151, 104396. doi:10.1016/j.jmps.2021.104396

CrossRef Full Text | Google Scholar

Zhong-Can, O.-Y., and Helfrich, W. (1987). Instability and deformation of a spherical vesicle by pressure. Phys. Rev. Lett. 59, 2486–2488. doi:10.1103/physrevlett.59.2486

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, J., Collard, D. M., Park, J. O., and Srinivasarao, M. (2002). Control of the anchoring behavior of polymer-dispersed liquid crystals: Effect of branching in the side chains of polyacrylates. J. Am. Chem. Soc. 124, 9980–9981. doi:10.1021/ja027162a

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, Z., Li, Y., Wong, W., Guo, T., Tang, S., and Luo, J. (2017). Transition of surface–interface creasing in bilayer hydrogels. Soft Matter 13, 6011–6020. doi:10.1039/c7sm01013c

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, L., Hu, K., Zhang, W., Meng, G., Yin, J., and Jiang, X. (2020). Regulating surface wrinkles using light. Natl. Sci. Rev. 7, 1247–1257. doi:10.1093/nsr/nwaa052

PubMed Abstract | CrossRef Full Text | Google Scholar