Electro-optic response of bipolar nematic liquid crystal confined in oblate spheroid

Electro-optic response of liquid crystals (LCs) relies on the molecular reorientation of LCs under external electric field and is important for a wide spectrum of applications. Here, we uncover an interesting electro-optic response of 5CB nematic LC confined in an oblate spheroid and subjected to external electric field. Under the planar anchoring, the nematic LC spheroid adopts a bipolar structure with the bipolar axis laid in the horizontal film plane. When a threshold electric field E_F, is applied, the bipolar structure reorients from the horizontal configuration (LC molecules align along long axis direction) to the vertical configuration (LC molecules align along short axis direction), involving the competition of elastic energy, surface anchoring energy and electric field energy. In contrast to bipolar nematic LC droplets, the vertical configuration does not relax to the low-energy horizontal configuration after removing E; we argue that is due to the oblate shape of the nematic LC spheroid, which traps the bipolar structure in a local energy minimum. We use continuum simulation to demonstrate the detailed response and the reorientation dynamics of bipolar nematic spheroids under E field, showing consistent results with the experiments and confirming the proposed switching mechanism. Nevertheless, the vertical configuration of the bipolar structure could relax to the low-energy horizontal configuration by thermal cycling. Our studies provide clear experimental results that show the characteristics of the electro-optic response of oblate LC spheroids, which have both fundamental and practical implications.

1 Introduction

Liquid crystals (LCs) exhibit both features of ordered crystalline solids and disordered flowing liquids (De Gennes and Prost, 1993; Barón, 2001; Shao et al., 2020; Wang et al., 2020; Goodby et al., 2014). Technological applications of LCs strongly rely on the control of LC molecular orientation; such controls are generally achieved through surface anchoring (Han and Yoon, 2021), geometrical confinement (Yang et al., 2022a), and external electric field (Goodby et al., 2014; Shabanov et al., 1998; Chen et al., 2013; Di Profio et al., 2002). The reorientation of LC molecules then modulates the transmitted light, which is commonly used in applications. The director configuration and the electro-optic response of LC under various surface anchorings and geometrical confinements have been studied, such as LCs sandwiched between two parallel plates (Xie and Higgins, 2004), confined in droplet (Yang et al., 2021), (De Luca and Rey, 2007), nested in cylindrical capillary (Noh et al., 2016) or filled in another nontrivial geometries (Nicoletta et al., 2001; Fernández-Nieves et al., 2007; Nakata et al., 2012), giving rise to many interesting phenomena (Yang et al., 2022b; Feng et al., 2021; Poulin et al., 1997).

The behavior of LC dispersed in polymer remains one of the most interesting topics, as polymer-dispersed liquid crystal (PDLC) being one of most great applications of LC. Either homeotropic or planar surface anchoring could be achieved by engineering the boundary condition of LC droplets (Poulin and Weitz, 1998; Yu et al., 2011; Moreno-Razo et al., 2012). When sodium dodecyl sulfate (SDS) presents at the interface, SDS enforces a homeotropic anchoring on the LC molecules, which then adopt a radial director configuration. Under a planar anchoring imposed by polyvinyl alcohol (PVA), LC molecules tend to be parallel to the interface and the director field engenders two-point disclinations positioned at opposite poles of the droplet, forming a bipolar structure (Higgins, 2000). Since LC droplets adopt different director configurations under different surface anchoring conditions, their electro-optic response critically depends on the boundary conditions (Huang et al., 2021). Nevertheless, planar anchoring is usually achieved through appropriate material engineering or processing technique and PDLC devices generally rely on the reorientation of bipolar nematic LC droplets under external electric field.

PDLC-based smart windows, for example, work by switching between strongly scattering and transparent states. Under the planar anchoring, birefringent nematic LC droplets dispersed in the polymer matrix are a collection of randomly oriented bipolar droplets, with the nematic director, n, aligned on average along the bipolar axis. Due to the mismatch of the refractive indices between the LC droplets and the polymer, light normally incident on PDLC films is strongly scattered by the nematic LC droplets, showing an opaque OFF state. A transparent ON state is achieved when a sufficiently large electric field, E_F, is applied. Under E_F, Fréedericksz transition of the director field occurs and the optical axis of the nematic LC droplets reorients along the E field, matching the refractive indices between the LC droplets and the polymer index and thus reducing the scattering of incident light. When the E field is removed, PDLC films generally relax to the scattering state to minimize elastic distortions. The biggest challenge of PDLC films is the high energy cost, which requires a continuously applied voltage to keep the ON state. Therefore, innovations of new materials or switching modes are critical for solving the problem and developing new devices.

Here, we uncover a unique electro-optic response of 5CB nematic LC confined in oblate spheroids, suggesting that the ON state could be free of applied voltage, and demonstrate that the ON state without applied voltage phenomena depend critically on the aspect ratio of spheroids and the switching dynamics. The oblate LC spheroids are prepared by the shrinkage force of a drying PVA film and nematic LC in the spheroids adopts a bipolar structure with its bipolar axis lying in the horizontal film plane. A threshold electric field E_F, is required to overcome the free energy difference between the horizontal and vertical configurations and induce the reorientation of the bipolar axis. Different from spherical LC droplets, which restore to their original low-energy state after removing E, oblate LC spheroids are trapped in the vertical configuration. Instead, oblate LC spheroids could relax to the low-energy horizontal configuration by a thermal cycling. The switching behavior is qualitatively different from all previous experimental observations. The detail of the switching is adequately captured by polarized optical microscope (POM) observations and further confirmed by continuum simulations, both of which show consistent results.

2 Materials and methods

2.1 Materials

5CB, 4-cyano-4′-pentylbiphenyl (98%; purchased from Yantai Xianhua, China), has a LC phase sequence of I (35.5°C) N. 10 mg 5CB is dissolved in 400 mg chloroform (purchased from Hushi, China). The mixture of 5CB in chloroform is emulsified in an aqueous solution of 10 wt% polyvinyl alcohol (PVA, MW: 13,000–23,000 g/mol, 87–89% hydrolyzed; Sigma-Aldrich, United States) by a XH-D vortex mixer. After emulsification, 5CB droplets are kept at room temperature in stationary for 1 week, during which chloroform evaporates slowly. After the evaporation of chloroform, some 5CB droplets in the PVA solution are placed on top of an ITO glass slide. During the drying process, PVA starts to form a layer of polymer film, squeezing spherical 5CB droplets into oblate spheroids with a = c > b, where a and b are the semi-major and semi-minor axes, respectively. 5CB droplets are trapped in the polymer film of PVA thus couldn’t mobilize freely. The shape of oblate spheroids is measured by fluorescent confocal microscope. For a sphere with an original radius of r = 4.8 μm, the obtained oblate spheroid has a = c = 6.5 μm and b = 2.6 μm with an aspect ratio of L = a/b∼2.5. Oblate spheroids of different size have a similar aspect ratio. The dried sample is then covered by another ITO glass slide using 20 μm-thick spacers. The temperature of the sample is controlled by a hot stage (INSTEC, United States) with an accuracy of 0.01°C and the sample is heated or cooled at a constant rate of 2°C/min.

2.2 Methods

A DC voltage is applied perpendicular to the horizontal film plane. The voltage is generated by a function generator (Rigol, China) and amplified by a DC amplifier (Aigtek, China). The electric field strength is varied from 0.4 V/μm to 1.2 V/μm. The threshold electric field, E_F, is measured by gradually increasing the voltage until the bipolar structure changes from the horizontal configuration to the vertical configuration. To switch the bipolar oblate spheroids using magnetic field, the sample is placed in a magnetic field with a strength of ∼70 mT for 3 hours, which is generated by two cylindrical NdFeB magnets placed face-to-face at a certain distance between each other.

Optical images of oblate LC spheroids are obtained using a polarized optical microscope (CX40P, Sunny Optical Technology, China) mounted with a digital CCD camera (Oplenic, China). The size of oblate spheroids is measured by ImageJ software.

The continuum simulations are based on a Landau-de Gennes free energy function in terms of a Q-tensor description. The total free energy of the nematic consists of a short-range free energy, a long-range elastic energy, an electric energy, and a surface energy:

$F={\int }_{\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{k}}dV\left\{\frac{A}{2}\left(1-\frac{U}{3}\right)Q_{ij}{Q}_{ij}-\frac{AU}{3}{Q}_{ij}{Q}_{jk}{Q}_{ki}+\frac{AU}{3}{\left(Q_{ij}{Q}_{ij}\right)}^2\right\}+{\int }_{\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{k}}dV\left\{\frac{1}{2}L\frac{\partial Q_{ij}}{\partial x_k}\frac{\partial Q_{ij}}{\partial x_k}\right\}+{\int }_{\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{k}}dV\left\{\frac{1}{2}{\epsilon }_a{E}_i{Q_{ij}E}_j\right\}+{\int }_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}}dS\left\{W{\left({\stackrel{\sim }{Q}}_{ij}-{\stackrel{\sim }{Q}}_{ij}^{\perp }\right)}^2\right\}$

where A and U are material parameters describing the thermodynamics of the nematic, L is the elastic constant under one-constant approximation, ${\epsilon }_a$ is the dielectric anisotropy of the nematic, and W is the surface anchoring strength for degenerate planar anchoring condition. For uniaxial nematic, Q-tensor can be written as $Q_{ij}=S\left(n_i{n}_j-{\delta }_{ij}/3\right)$ with S and n being the scalar order parameter and the director field, respectively. For degenerate planar anchoring, we further define ${\stackrel{\sim }{Q}}_{ij}=Q_{ij}+S_0{\delta }_{ij}/3$ and ${\stackrel{\sim }{Q}}_{ij}^{\perp }=P_{ik}{\stackrel{\sim }{Q}}_{kl}{P}_{ki}$ with projection operator $P_{ij}={\delta }_{ij}-{\nu }_i{\nu }_j$ and ν, a unit vector representing surface normal. A commonly used Ginsburg-Landau algorithm is adopted here to find free energy minimums, which correspond to experimentally accessible states. A finite difference scheme is used to carry out the calculation. The following values are used for the simulations: $A=1.17\times {10}^5$ J·m³, $U=3.5$, $L=6$ pN, ${\epsilon }_a=5.8{\epsilon }_0$ (Meier & Saupe, 1966). ${\epsilon }_0$ is the vacuum permittivity. $W={10}^{-5}\sim {10}^{-1}$ N/m has been used to explore anchoring effects.

3 Results and discussions

5CB is first dissolved in chloroform and emulsified in an aqueous PVA solution, which prevents 5CB droplets from coalescing and imposes a planar anchoring on the LC director, as shown in Figures 1A,B. As chloroform evaporates, spherical 5CB nematic droplets adopt a bipolar director configuration and there is no preferred direction of the bipolar axis due to the spherical symmetry, as modelled in Figure 1C and shown in Supplementary Figure S1. Spherical LC droplets are then squeezed into oblate spheroids by the shrinkage force of a drying PVA film with the spheroid’s minor axis perpendicular to the horizontal film plane, as confirmed by the fluorescent confocal microscope image in Supplementary Figure S1. Oblate spheroids have an average aspect ratio of l = a/b∼2.5, where a and b are the lengths of the semi-major and semi-minor axes, respectively. In the oblate spheroids, the bipolar axis tends to lie in the horizontal film plane to minimize the total elastic energy, as shown in Figure 1D. When an electric or magnetic (E/B) field surpassing a certain threshold is applied perpendicular to the film plane, LC molecules reorient to align their director along the E/B field, leading to a vertical configuration, as suggested in Figure 1E. Unexpected behavior is observed upon removal of the E/B field: the bipolar structure is trapped in the high-energy vertical configuration for at least 1 year. The switching behavior is very different from that of spherical bipolar LC droplets, which restore to their original state after removing E. Instead, the vertical configuration could relax to the low-energy horizontal state by a thermal cycling of N-I-N phase transitions.

FIGURE 1

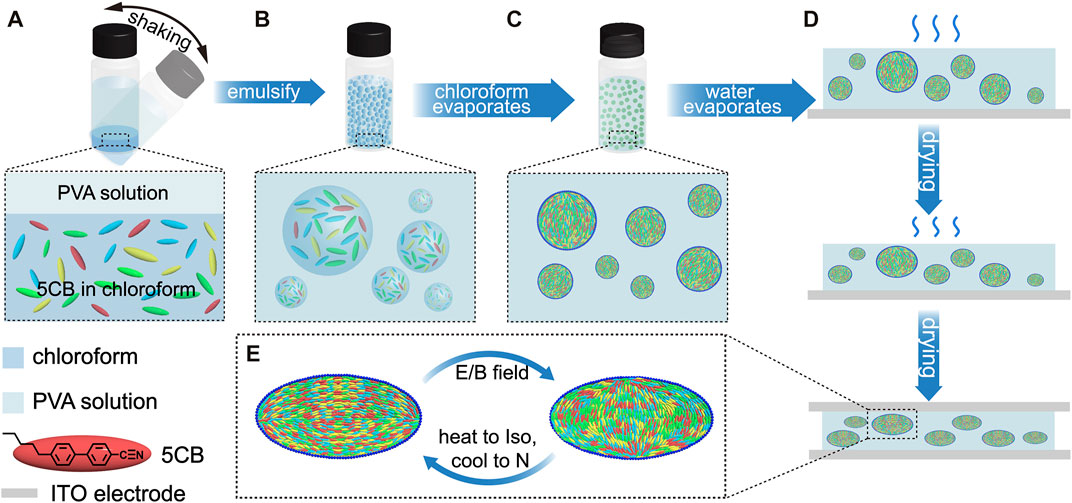
FIGURE 1. Electro-optic response of 5CB bipolar nematic confined in oblate spheroids under planar anchoring. (A) and (B) 5CB is first dissolved in chloroform and emulsified in the PVA solution. (C) As chloroform evaporates, 5CB nematic spheres adopt a bipolar director configuration under the planar alignment imposed by PVA. (D) When the spherical droplets are squeezed into oblate spheroids under the shrinkage force of the drying PVA film, the bipolar axis is confined in the horizontal plane to reduce elastic distortion. (E) Under a threshold E or B field, the bipolar structure reorients to the vertical configuration and is trapped there when the external field is removed. The vertical configuration could relax to the low-energy horizontal configuration through a temperature cycle of N-Iso-N phase transitions.

A photomicrograph of a typical oblate nematic LC spheroid is shown in Figure 2A. The bipolar axis connecting the two disclinations at the opposite poles of the spheroid lies in the horizontal film plane, making an angle of 10^o with respect to the analyser. The bipolar axis rotates within the horizontal plane when the sample stage is rotated and the dark brushes could be modelled by the director field shown in the top view in Figure 2A. Application of an electric field will place a torque on the nematic LC molecules, trying to align them along the E direction. However, only above E_F, the director of 5CB nematic starts to reorient along the E field with the bipolar axis moved to the vertical position, showing four dark brushes. The circular symmetry of the vertical configuration is confirmed by the invariance of the optical texture when the sample stage is rotated, as shown in Figure 2B. Interestingly, the bipolar director field remains in the high-energy vertical configuration even when the E field is removed. Once the sample is heated to isotropic and then cooled down to nematic, the bipolar director field relaxes to the low-energy horizontal configuration again, as shown in Figure 2C. A similar switching behavior is also observed under a threshold magnetic field, as shown in Supplementary Figure S3.

FIGURE 2

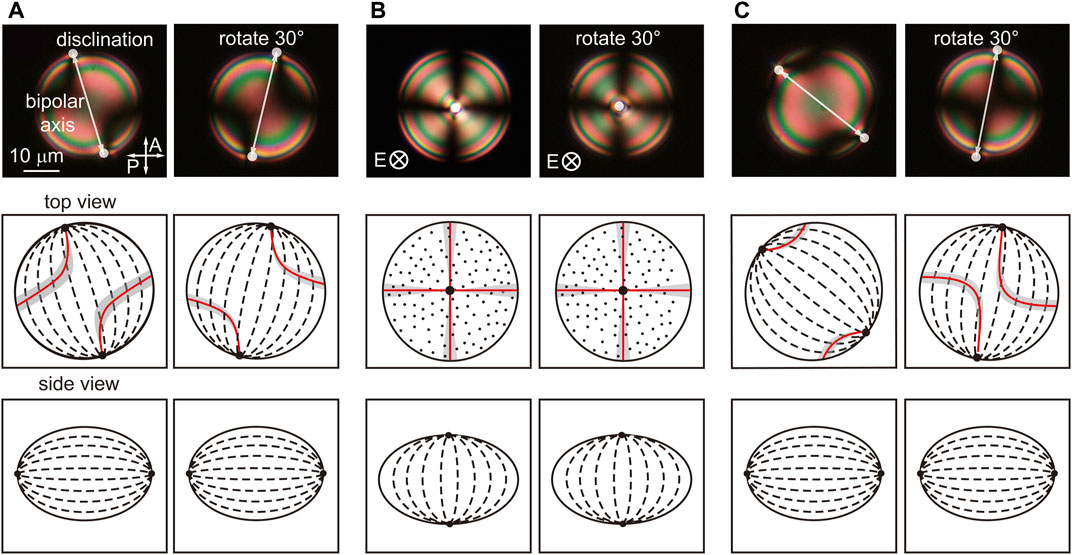
FIGURE 2. Electro-optic response of oblate nematic LC spheroids. (A) Optical texture of an oblate 5CB nematic spheroid under planar anchoring, showing a typical bipolar director field with the bipolar axis lying in the horizontal plane. The top view shows the director field at the middle plane and the side view shows the director field at the side plane. (B) Under a threshold electric field, LC molecules reorient along the E field and the bipolar axis switches to the vertical position, showing four dark brushes. Because of the circular symmetry, the optical texture remains unchanged when the sample is rotated. The bipolar structure is trapped in the vertical configuration after removing the E field. (C) Relaxation of the bipolar structure to the low-energy horizontal configuration is achieved when the sample is heated up to isotropic and then cooled down to nematic.

To elucidate the underlying mechanism of the electro-optic response, we systematically investigate the parameters that influence the switching behavior. The threshold electric field required to switch the bipolar structure from the horizontal configuration to the vertical configuration strongly depends on the strength of the planar surface anchoring, as shown in Figure 3A. If the planar surface anchoring strength is zero, there is no preferred direction for the director at the surface and the ground state is a uniform director field without any distortion. In this case, all orientations are degenerate and it only requires a very small electric field to reorient the director. When the planar surface anchoring strength is not zero, the free energy is a balance between elastic energy and surface energy and is expressed as F=F_elastic + F_surface = 1/2[k₁(▽• $\overrightarrow{n}$)² + k₂($\overrightarrow{n}$•▽× $\overrightarrow{n}$)² + k₃($\overrightarrow{n}$ ×▽× $\overrightarrow{n}$)²] +1/2Wsin²(θ), where k₁, k₂ and k₃ are the elastic constants, n is the molecular director, W is the surface anchoring strength and θ is the polar angle. When the planar surface anchoring strength is finite, the vertical configuration of the bipolar structure has a larger elastic distortion, thus costing a higher free energy, and the ground state of the bipolar structure is the horizontal configuration with the bipolar axis parallel to the horizontal plane. Therefore, it requires an external electric field to overcome the free energy difference and reorient the bipolar structure from the horizontal configuration to the vertical configuration.

FIGURE 3

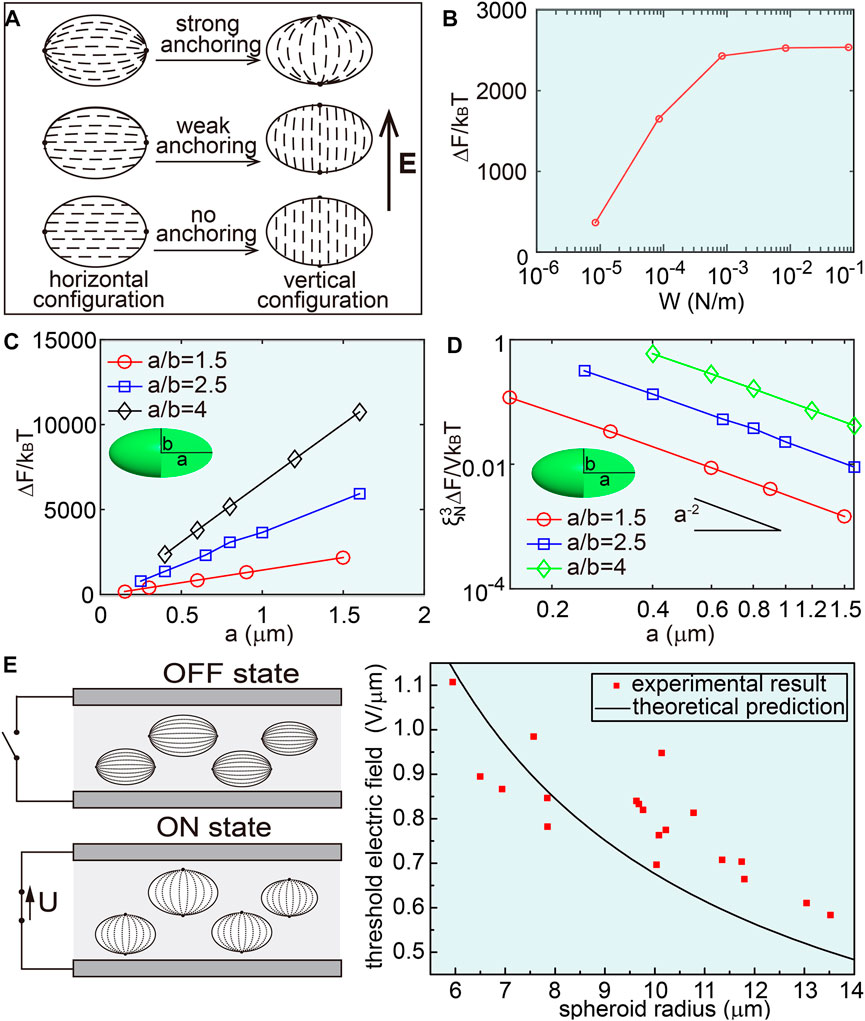
FIGURE 3. Energy landscape of the bipolar structure and electric switching between the horizontal and vertical configurations. (A) Model of director reorientation of oblate nematic LC spheroid under different planar anchoring strength when a threshold electric field is applied. (B) The free energy difference between the horizontal and vertical configurations increases as the planar surface anchoring strength increases. When the surface anchoring strength is large enough, the free energy difference reaches a plateau. (C) Under a strong planar surface anchoring strength (W = 0.1 N/m), the free energy difference increases when the aspect ratio of the spheroid increases or the size of the spheroid increases. (D) The free energy density difference decreases when the size of spheroid increases. (E) Dependence of the threshold electric field required to reorient the nematic spheroid on the size of the spheroid. The red square dots are experimental results, while the black curve is the theoretical prediction.

To calculate the free energy landscape of the bipolar structure, we carry out continuum simulations to determine the free energy difference between the horizontal and vertical configurations and the threshold E field required to reorient the bipolar structure between the two configurations. The free energy difference, ∆F, as a function of planar surface anchoring strength is shown in Figure 3B. As expected, the free energy difference increases as the surface anchoring strength increases and a larger electric field is thus required to overcome the free energy difference. When the surface anchoring strength is large enough, the free energy difference reaches a plateau. If we assume a large surface anchoring strength of W = 0.1 N/m, the free energy difference ∆F is linearly proportional to the size of the oblate spheroid, i.e., $∆F\propto a$, where a is the major radius, as shown in Figure 3C; however, the free energy density difference $∆F/V$ decreases on the order of $∆F/V\propto a^{-2}$, as shown in Figure 3D. Therefore, a smaller electric field is required to reorient LC molecules in a larger oblate spheroid, which is directly confirmed by the experimental results, as shown in Figure 3E. In a simple model of isolated dielectric oblate spheroid embedded in a uniform medium under strong planar anchoring, the threshold electric field E_F is given by the equation (Amundson, 1996)

$E=\frac{V}{d}\approx \frac{{2{\epsilon }_M+\epsilon }_{LC}}{3{\epsilon }_M}\frac{\sqrt{l^2-1}}{a}{\left(\frac{4\pi k}{∆\epsilon }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$

where ε_M∼8 is the effective dielectric constant of the PVA film, ε_LC∼13.3 is the dielectric constant of 5CB, a = 6.5 μm is the major radius, L = a/b = 2.5 is the aspect ratio, k = 6.2 pN is the elastic constant of 5CB under one-constant-approximation, and ∆ε = ε_∥-ε_⊥ = 11.5 is the dielectric anisotropy of 5CB. The theoretical calculation also suggests that the threshold electric field is inversely proportional to the size of oblate spheroid, which is consistent with the experimental results, as shown in Figure 3E.

A series of snapshots unveiling the dynamics of director reorientation under electric field is shown in Figure 4. When there is no electric field or the electric field is small, the bipolar director field stays in the low-energy horizontal configuration, as shown in Figures 4A–C. When the applied electric field reaches a threshold value, Fréedericksz transition occurs to reduce the electric field energy and LC molecules in the oblate spheroid reorient along the E field with the texture being essentially dark under POM as shown in Figure 4D. Subsequently, the two disclinations of the bipolar structure move in opposite directions until the bipolar axis points along the vertical direction, showing four dark brushes, as shown in Figures 4E–H. The switching process under E_F is also captured by the continuum simulations, which show consistent results with the experimental observations, as shown in Figures 4I–P.

FIGURE 4

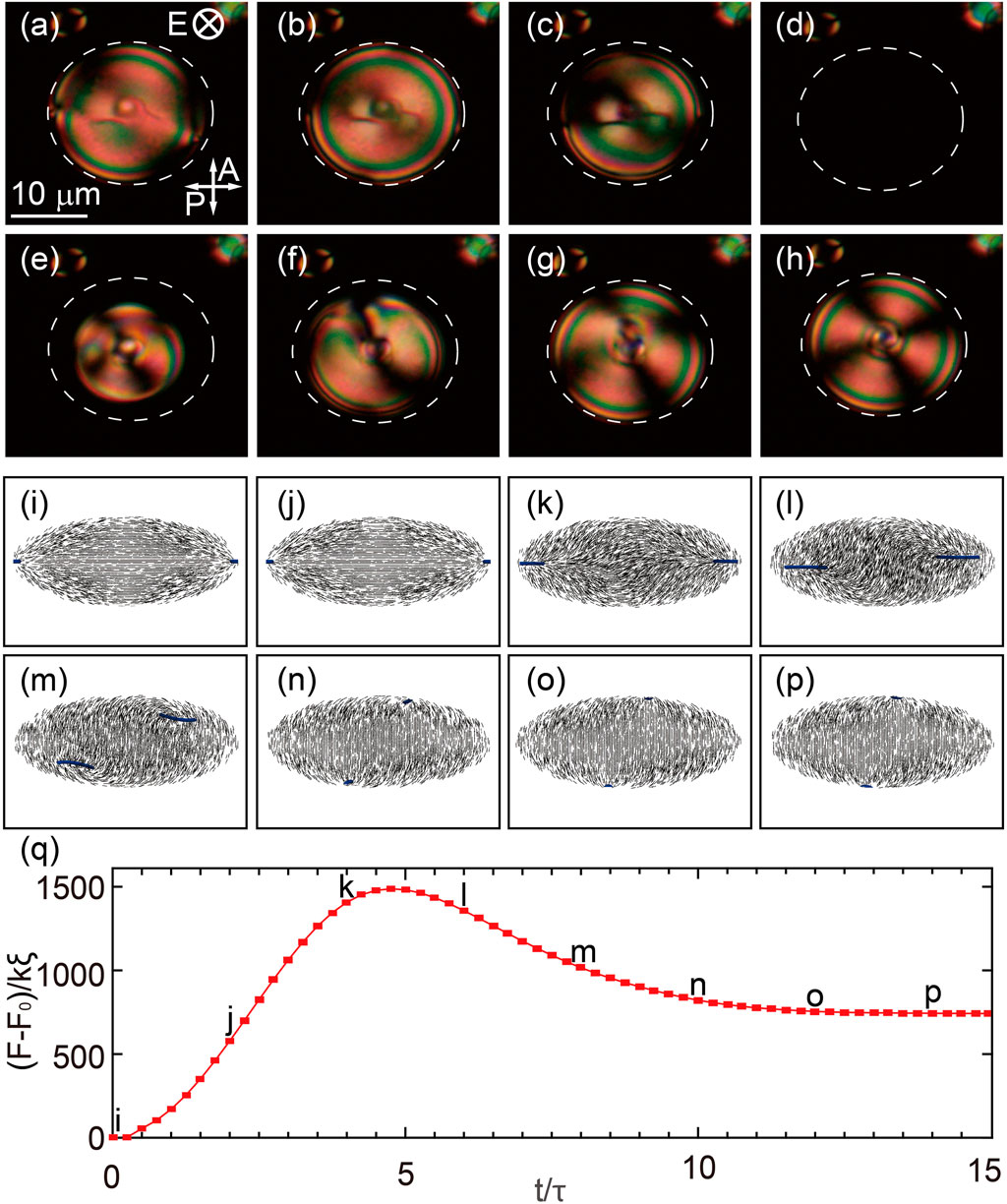
FIGURE 4. Reorientation dynamics of oblate nematic spheroid under a threshold E field. (A–H) A sequence of POM snapshots showing the reorientation of an oblate bipolar spheroid from the horizontal configuration to the vertical configuration under E_F. Under E_F, Fréedericksz transition occurs with most LC molecules aligned along E and the optical texture being essentially dark. Then, the bipolar axis reorients along the vertical direction, showing four dark brushes. The time interval of the snapshots is 4s (I–P) The switching process is also captured by the continuum simulations. Fréedericksz transition occurs with most LC molecules aligned along E, when E reaches E_F. The two disclinations then move to the top and bottom of the oblate spheroid, respectively. (Q) The free energy difference during the switching process, suggesting that the bipolar structure is trapped in a local minimum of the vertical configuration after removing E_F.

The switching behavior of oblate LC spheroids is qualitatively different from previous experimental observations and we propose that the behavior is attributed to the unique shape of oblate spheroid. Generally, a threshold E field is required to reorient the bipolar axis of spherical LC droplets in PDLCs along the E field, as the polymer matrix that penetrates the LC/polymer interface presumably pins the director of LC molecules below E_F. When E_F is removed, the orientation of the bipolar axis will return to its original direction. However, in oblate spheroids with a large aspect ratio, e.g., L = a/b = 2.5, the energy landscape of the bipolar structure shows a local minimum in the vertical configuration and thus the bipolar structure could be trapped in the high-energy vertical configuration after removing E_F, as shown in Figure 4Q. The unique electro-optic response of oblate nematic spheroids also benefits from the movement of the two disclinations and the reorientation of the bipolar axis after the Fréedericksz transition. Otherwise, the director field would relax to its original ground state, since director reorientation via Fréedericksz transition is reversible.

4 Conclusion

Combinations of experiments, theoretical analyses and continuum simulations are used to investigate the electro-optic response of nematic LCs confined in oblate spheroids. Upon an application of a threshold E field, the reorientation dynamics of bipolar oblate spheroids are unveiled: LC molecules reorient first via Fréedericksz transition, which are followed by the movement of the two disclinations and the reorientation of the bipolar axis. Different from spherical droplets, bipolar oblate spheroids show a unique switching behavior that the bipolar axis does not relax to its original low-energy horizontal configuration after removing E_F. The underlying mechanism of the electro-optic response must recognize the importance of the geometry confinement, which induces the reorientation of the bipolar axis after Fréedericksz transition and traps the bipolar structure in a local minimum. The discovery and the full understanding of the switching behavior are critical for the developments of new optical devices, such as low-energy-cost smart PDLCs.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

CY and DC conceived of and designed this study. LF and RC contributed to part of the study design. RZ contributed to part of simulation. CY and DC wrote the manuscript with input from all authors. RZ and DC supervised the study.

Funding

This work is supported by Zhejiang Provincial Natural Science Foundation of China (Grant No. LY20B060027), National Natural Science Foundation of China (Grant No. 21878258).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor UT declared a past co-authorship with the author RZ.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsfm.2022.1022077/full#supplementary-material

References

Amundson, K. (1996). Electro-optic properties of a polymer-dispersed liquid-crystal film: Temperature dependence and phase behavior. Phys. Rev. E 53, 2412–2422. doi:10.1103/physreve.53.2412

PubMed Abstract | CrossRef Full Text | Google Scholar

Barón, M. (2001). Definitions of basic terms relating to low-molar-mass and polymer liquid crystals (IUPAC Recommendations 2001). Pure Appl. Chem. 73, 845. doi:10.1351/pac200173050845

CrossRef Full Text | Google Scholar

Chen, D., Porada, J. H., Hooper, J. B., Klittnick, A., Shen, Y., Tuchband, M. R., et al. (2013). Chiral heliconical ground state of nanoscale pitch in a nematic liquid crystal of achiral molecular dimers. Proc. Natl. Acad. Sci. U. S. A. 110, 15931–15936. doi:10.1073/pnas.1314654110

PubMed Abstract | CrossRef Full Text | Google Scholar

De Gennes, P.-G., and Prost, J. (1993). The physics of liquid crystals. Germany: Oxford University Press.

Google Scholar

De Luca, G., and Rey, A. D. (2007). Point and ring defects in nematics under capillary confinement. J. Chem. Phys. 127, 104902. doi:10.1063/1.2775451

PubMed Abstract | CrossRef Full Text | Google Scholar

Di Profio, G., Nicoletta, F. P., De Filpo, G., and Chidichimo, G. (2002). Reverse-mode operation switchable nematic emulsions. Langmuir 18, 3034–3038. doi:10.1021/la011217p

CrossRef Full Text | Google Scholar

Feng, W., Liu, D., and Broer, D. J. (2021). Functional liquid crystal polymer surfaces with switchable topographies. Small Struct. 2, 2000107. doi:10.1002/sstr.202000107

CrossRef Full Text | Google Scholar

Fernández-Nieves, A., Vitelli, V., Utada, A. S., Link, D. R., Márquez, M., Nelson, D. R., et al. (2007). Novel defect structures in nematic liquid crystal shells. Phys. Rev. Lett. 99, 157801. doi:10.1103/physrevlett.99.157801

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodby, J. W., Collings, P. J., Kato, T., Tschierske, C., Gleeson, H., Raynes, P., et al. (2014). Handbook of liquid crystals, 8 volume set. Germany: John Wiley & Sons.

Google Scholar

Han, M. J., and Yoon, D. K. (2021). Advances in Soft materials for sustainable electronics. Engineering 7, 564–580. doi:10.1016/j.eng.2021.02.010

CrossRef Full Text | Google Scholar

Higgins, D. A. (2000). Probing the mesoscopic chemical and physical properties of polymer-dispersed liquid crystals. Adv. Mat. 12, 251–264. doi:10.1002/(sici)1521-4095(200002)12:4<251:aid-adma251>3.0.co;2-4

CrossRef Full Text | Google Scholar

Huang, S., Huang, Y., and Li, Q. (2021). Photodeformable liquid crystalline polymers containing functional additives: Toward photomanipulatable intelligent Soft systems. Small Struct. 2, 2170024. doi:10.1002/sstr.202170024

CrossRef Full Text | Google Scholar

Meier, G., and Saupe, A. (1966). Dielectric relaxation in nematic liquid crystals. Mol. Cryst. 1, 515–525. doi:10.1080/15421406608083290

CrossRef Full Text | Google Scholar

Moreno-Razo, J. A., Sambriski, E. J., Abbott, N. L., Hernández-Ortiz, J. P., and de Pablo, J. J. (2012). Liquid-crystal-mediated self-assembly at nanodroplet interfaces. Nature 485, 86–89. doi:10.1038/nature11084

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakata, M., Chen, D., Shao, R., Korblova, E., Maclennan, J. E., Walba, D. M., et al. (2012) Electro-optic response of the anticlinic, antiferroelectric liquid-crystal phase of a biaxial bent-core molecule with tilt angle near 45∘°. Phys. Rev. E 85, 031704, doi:10.1103/physreve.85.031704

PubMed Abstract | CrossRef Full Text | Google Scholar

Nicoletta, F. P., Lanzo, J., De Filpo, G., and Chidichimo, G. (2001). Effect of surfactant molecules on the electrooptical properties of nematic emulsions. Langmuir 17, 534–536. doi:10.1021/la001149r

CrossRef Full Text | Google Scholar

Noh, J., Reguengo De Sousa, K., and Lagerwall, J. P. F. (2016). Influence of interface stabilisers and surrounding aqueous phases on nematic liquid crystal shells. Soft Matter 12, 367–372. doi:10.1039/c5sm01944c

PubMed Abstract | CrossRef Full Text | Google Scholar

Poulin, P., Stark, H., Lubensky, T. C., and Weitz, D. A. (1997). Novel colloidal interactions in anisotropic fluids. Science 275, 1770–1773. doi:10.1126/science.275.5307.1770

PubMed Abstract | CrossRef Full Text | Google Scholar

Poulin, P., and Weitz, D. A. (1998). Inverted and multiple nematic emulsions. Phys. Rev. E 57, 626–637. doi:10.1103/physreve.57.626

CrossRef Full Text | Google Scholar

Shabanov, A., Presnyakov, V., Zyryanov, V., and Vetrov, S. (1998). Bipolar nematic droplets with rigidly fixed poles in the electric field. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A. Mol. Cryst. Liq. Cryst. 321, 245–258. doi:10.1080/10587259808025091

CrossRef Full Text | Google Scholar

Shao, B., Wan, S., Yang, C., Shen, J., Li, Y., You, H., et al. (2020). Engineered anisotropic fluids of rare-earth nanomaterials. Angew. Chem. Int. Ed. Engl. 59, 18370–18374. doi:10.1002/ange.202007676

CrossRef Full Text | Google Scholar

Wang, X., Yang, C., Cai, L., and Chen, D. (2020). The rheology property of organogels based on 3D helical nanofilament bnetworks self-assembled by bent-core liquid crystals. Acta Phys. Sin. 69, 086102–86111. doi:10.7498/aps.69.20200332

CrossRef Full Text | Google Scholar

Xie, A., and Higgins, D. A. (2004). Electric-field-induced dynamics in radial liquid crystal droplets studied by multiphoton-excited fluorescence microscopy. Appl. Phys. Lett. 84, 4014–4016. doi:10.1063/1.1748846

CrossRef Full Text | Google Scholar

Yang, C., Chen, L., Zhang, R., Chen, D., Arriaga, L. R., and Weitz, D. A. (2022b). Local high-density distributions of phospholipids induced by the nucleation and growth of smectic liquid crystals at the interface. Chin. Chem. Lett. 33, 3973–3976. doi:10.1016/j.cclet.2021.11.016

CrossRef Full Text | Google Scholar

Yang, C., Wu, B., Ruan, J., Zhao, P., Chen, L., Chen, D., et al. (2021). 3D-Printed biomimetic systems with synergetic color and shape responses based on oblate cholesteric liquid crystal droplets. Adv. Mat. 33, 2006361. doi:10.1002/adma.202006361

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, C., Wu, B., Ruan, J., Zhao, P., Shan, J., Zhang, R., et al. (2022a). Mechanochromic responses of cholesteric liquid crystal droplets with nanoscale periodic helical structures showing reversible and tunable structural color. ACS Appl. Polym. Mat. 4, 463–468. doi:10.1021/acsapm.1c01362

CrossRef Full Text | Google Scholar

Yu, H., Dong, C., Zhou, W., Kobayashi, T., and Yang, H. (2011). Wrinkled liquid-crystalline microparticle-enhanced photoresponse of PDLC-like films by coupling with mechanical stretching. Small 7, 3039–3045. doi:10.1002/smll.201101098

PubMed Abstract | CrossRef Full Text | Google Scholar