Scaled RTLS BRDF model extended to high zenith angles

The Ross-Thick Li-Sparse (RTLS) model provides a good description of the surface bidirectional reflectance distribution function (BRDF) for zenith angles (ZA) up to ∼60°–70°. At higher zenith angles, the behaviour of the RTLS model is not well constrained. This becomes a limiting factor for the processing of geostationary satellite data covering the full range of solar and view zenith angles. Here, we propose a scaled sRTLS model extending the zenith angle range to ∼80°–84° and demonstrate an improved performance based on examples from the processing of GOES-16 ABI data using MAIAC algorithm.

1 Introduction

Surface Bidirectional Reflectance Distribution Function (BRDF) is a key property of the land surface describing its reflectance as a function of the sun-view geometry. The BRDF model was originally introduced by the MODIS and MISR science teams as standard products (Martonchik et al., 1998; Schaaf et al., 2002). The BRDF model has many uses: it defines surface albedo as a function of solar zenith angle (SZA) and aerosol optical depth (e.g., Lyapustin, 1999; Lucht et al., 2000) and provides albedo parameterization for use in climate models (e.g., Liang et al., 2005). It is used in Earth System Simulation Experiments (OSSE) to support mission formulation and sensor requirements and test processing algorithms. BRDF is widely used for normalization to a standard view geometry supporting detection of land surface change and fire-burnt scars (e.g., Roy et al., 2005; Giglio et al., 2018; Schläpfer et al., 2015), separating vegetation seasonality from variations in view geometry over tropics (e.g., Bi et al., 2015) etc. In the Multi-Angle Implementation of Atmospheric correction (MAIAC) algorithm, the 1 km spectral BRDF is used for accurate cloud and cloud shadow detection as well as for fast and un-ambiguous retrieval of snow fraction and snow grain size for detected snow (Lyapustin et al., 2018). BRDF-normalization became a standard component of on-orbit sensor calibration helping characterize long-term calibration trends and cross-calibrate different sensors over quasi-stable desert calibration sites (Lyapustin et al., 2014; Lyapustin et al., 2023).

The NASA MODIS and VIIRS data processing over land uses the reciprocal Ross-Thick Li-Sparse (RTLS) BRDF model introduced at the turn of the century (Lucht et al., 2000). This is a linear model using volumetric scattering and geometric-optics kernels which are functions of the sun-view geometry only. Linearity of this model allowed Lyapustin and Knyazikhin (2001) to develop an accurate semi-analytical expression for the top of atmosphere radiance as a function of three model parameters, and an accurate BRDF-coupled algorithm for atmospheric correction (Lyapustin et al., 2012; Lyapustin et al., 2018).

Over two decades of NASA MODIS observations have demonstrated a reliable performance of the RTLS model globally over snow-free land. Except near the principal plane, the RTLS model has a rather good accuracy over a snow as well although it falls behind the specialized two-parameter radiative transfer-based snow model with surface roughness (Lyapustin et al., 2010). Despite its general success, the RTLS model is not properly constrained at high zenith angles above 60°–70° (e.g., Gao et al., 2000). RTLS model works well for MODIS with its maximal scan angle of 55° which translates to the maximal view zenith angle (VZA) ∼62° when accounting for the Earth curvature. However, the VIIRS sensor, a follow-on to MODIS, has the maximal VZA∼72° at the edge of scan. The modern geostationary satellites (e.g., ABI on GOES 16–18; AHI on HIMAWARI 8–9) observe both the full range of solar zenith angle (SZA) variation, and high VZA near the disk edge. This stipulates the need to revisit the RTLS model and extend the range of valid zenith angles to ∼84° [μ = cos (VZA) ∼ 0.1].

2 Standard and scaled RTLS models

RTLS is a semi-empirical linear model, represented as a sum of isotropic, geometric, and volume scattering components as originally introduced by Roujean et al. (1992):

$\rho \left({\mu }_0,\mu ,\varphi \right)=k_i+k_v{F}_v\left({\mu }_0,\mu ,\varphi \right)+k_g{F}_g\left({\mu }_0,\mu ,\varphi \right).(1)$

It uses predefined geometric functions (kernels), F_v, F_g, to describe different angular shapes. The kernels are independent of the land surface conditions. The bidirectional reflectance of a pixel is characterized by a combination of three kernel weights, $\overrightarrow{K}={\left\{k_i,k_v,k_g\right\}}^T$.

The volumetric scattering (Ross-thick) kernel is expressed as:

$F_v={\left(\overline{\mu }+{\overline{\mu }}_0\right)}^{-1}\left[\left(\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.-\xi \right)\mathit{cos}\xi +\mathit{sin}\xi \right]\left[1+{\left(1+\raisebox{1ex}{$\xi $}\!\left/ \!\raisebox{-1ex}{${\xi }_0$}\right.\right)}^{-1}\right]-\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$4$}\right..(2)$

Here, $\overline{\mu }=\mu$ and ${{\overline{\mu }}_0=\mu }_0$ are positively defined cosines of view and solar zenith angles and ξ is angle of scattering, $\mathit{cos}\xi ={\mu }_0\mu +\sqrt{\left(1-{\mu }_0^2\right)}\sqrt{\left(1-{\mu }^2\right)}\mathit{cos}\phi$. The relative azimuth $\phi$ is defined such that the backscattering direction (hotspot) is at $\phi =0°$. Similar to Vermote et al. (2008), the V-kernel (Equation 2) is shown with the multiplicative hotspot factor with width of ${\xi }_0=1.5°$ following Maignan et al. (2004), though we keep the original normalization of Lucht et al. (2000). We should mention that the standard RTLS kernel F_v does not include this hotspot term.

The geometric (Li-Sparse) kernel F_g is given by:

$F_g=∆\left({\mu }_0,\mu ,\varphi \right)+\left(1+\mathit{cos}\xi \right)/\left(2\overline{\mu }{\overline{\mu }}_0\right),(3)$

$∆\left({\mu }_0,\mu ,\varphi \right)=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\pi $}\right.\left(t-\mathit{sin}t\mathit{cos}t-\pi \right)m$, where $m=1/\overline{\mu }+1/{\overline{\mu }}_0$ is an airmass factor, and

$\mathit{cos}t=2/m\sqrt{t{g}^2{\theta }_0+t{g}^2\theta -2tg{\theta }_{0}tg\theta \mathit{cos}\phi +{\left(tg{\theta }_{0}tg\theta \mathit{sin}\phi \right)}^2}.$

The geometric term represents reflectance reduction by shadows from the elevated ellipsoidal protrusions (e.g., trees), and thus the general hot spot effect (Li and Strahler, 1992). The volumetric kernel represents light scattering in vegetation media with randomly oriented leaves. It is a linearized version developed by Roujean et al. (1992) based on the single scattering model in vegetation Ross (1981).

The RTLS kernel shapes are illustrated by black lines in Figure 1 in the principal plane (0°–180°), cross plane, and diagonal plane (45°–135°) which is close to a typical view geometry of MODIS.

Figure 1

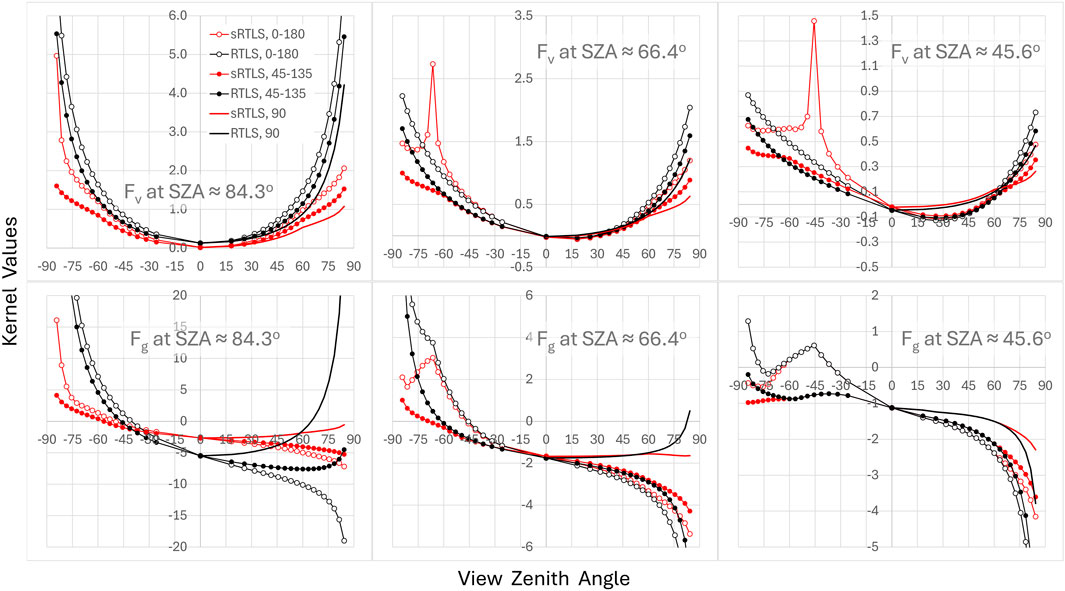
Figure 1. Dependence of F_v (top) and F_g (bottom) on view zenith angle at different solar angles and relative azimuths (RA). The positive and negative VZA values represent the forward scattering (RA = 0°–90°) and the backscattering (RA = 90°–180°) view geometries, respectively. The legend for different RAs is shown in the first plot. Kernels of the standard RTLS model and of scaled (sRTLS) model are presented in black and red, respectively.

Both F_v at SZA = 84.3° and F_g at all shown solar angles rapidly increase in amplitude past 60°–70° and are truncated in the plots before reaching maximal VZA = 84.3°. This instability of kernels is generated by $\overline{\mu }$, ${\overline{\mu }}_0$ or their sum in denominator and by the air mass factor m, specifically ${\left(\overline{\mu }+{\overline{\mu }}_0\right)}^{-1}$ in F_v and in terms m and 1 $/\left(2\overline{\mu }{\overline{\mu }}_0\right)$ in F_g. Limitations of the RTLS model at high zenith angles were discussed in the relevant publications (e.g., Li and Strahler, 1986; Wanner et al., 1995): they include the lack of multiple shadowing, assumption of a black solar and view (obscuration) shadows, the equivalency of the solar and obscuration shadows, the neglect of the diffuse light, of effect of the tree/canopy height variations and others. Our goal is not to develop a much more complex BRDF model by incorporating these effects, but rather suggest a simple normalization or scaling solution which improves model performance at high zenith angles. For practical purposes, we consider the range of angles up to ∼84° (μ ∼ 0.1). The idea is to slow down a rapid increase of ${\mu }^{-1}$ at VZA > 60°. For instance, replacing μ with its square root at μ = 0.1 gives $1/\sqrt{\mu }$ ∼3.16 instead of $1/\mu =10$. Thus, the barred symbols are defined as linearly scaled between $\mu$ and $\sqrt{\mu }$ below $\mu =0.5$:

$\overline{\mu }=\mu ,\mu \ge 0.5,$

$\overline{\mu }=w\mu +\left(1-w\right)\sqrt{\mu },w=\mu /0.5,\mu <0.5.(4)$

In summary, the scaled sRTLS model, given by Equations 1–4, differs from the standard RTLS by adding the hotspot factor in F_v and using scaled values $\overline{\mu }$, ${\overline{\mu }}_0$ at zenith angles above 60°. Scaled kernels, illustrated in red in Figure 1, show constrained behaviour at high zenith angles. The difference increases with SZA and is highest at SZA = 84.3°.

3 Analysis based on GOES 16 ABI data

MAIAC algorithm has long been adapted to processing of HIMAWARI-8,9 AHI and GOES 16–18 ABI observations (e.g., Li et al., 2019; She et al., 2019) with some further research developments (Wang et al., 2022). MAIAC sits at the core of the GeoNEX (Geostationary NASA Earth eXchange) project, a collaborative effort led by scientists from NASA, NOAA, and many other research institutes around the world (Nemani et al., 2020). The goal of GeoNEX is to create a suite of globally unified and consistent science products from the constellation of latest operational geostationary satellite sensors (Chen et al., 2021; Wang et al., 2020; Hashimoto et al., 2021; Wang et al., 2022; Zhang et al., 2022; Li et al., 2023; Shen et al., 2023; Gao et al., 2024). An atmospheric correction algorithm that rigorously accounts for varying sun-sensor geometries and surface BRDF is thus essential to the success of all the downstream products and the overarching goal of GeoNEX.

The original MAIAC-Geo includes standard MAIAC algorithm components (Lyapustin et al., 2018), namely, cloud, cloud shadow and snow detection, aerosol retrieval and atmospheric correction producing spectral bidirectional reflectance factors (BRF), commonly called surface reflectance, spectral albedo and daily BRDF model parameters. Similarly to MAIAC MODIS, we also provide snow fraction and snow grain size for detected snow, and smoke plume injection height for detected wildfires (Lyapustin et al., 2020).

For each pixel, the MAIAC-Geo atmospheric correction uses the BRDF-coupled radiative transfer model (Lyapustin et al., 2012; Lyapustin et al., 2018) and the BRDF model from the previous day to derive a BRF for each ABI observation acquired every 10 min. At the end of the day, it combines all daily BRFs and derives an updated BRDF model that provides the best fit to the multi-angle BRF dataset. At the onset, when BRDF is not initialized, MAIAC uses a Lambertian surface reflectance model and computes Lambert Equivalent Reflectance (LER). Once an initial approximation of the BRDF model is derived from LERs, the full BRF/BRDF processing rapidly converges to its full accuracy in 1–2 days. The full BRDF inversion, producing parameters $\left\{k_i,k_v,k_g\right.$} is performed on days with low-to-moderate cloud coverage, when observations cover the full range of SZA and scattering angles. On partly cloudy days, with at least 10 cloud-free observations and representative angular coverage of low, medium and high SZA ranges, we adjust the BRDF magnitude by scaling it to the retrieved BRFs assuming stable BRDF shape from previous retrievals. This approach is similar to the MODIS BRDF\albedo backup algorithm, flagged as lower quality magnitude inversion (Schaaf et al., 2002), and is also used in the MAIAC MODIS/VIIRS algorithms (Lyapustin et al., 2018). In both inversion and scaling cases we calculate the standard deviation (σ) representing daily goodness of fit.

This work uses GOES-16 ABI data over the East Coast United States in 2020 and 2023 to illustrate performance of both the standard RTLS and proposed sRTLS models. The annual variation of the view geometry (scattering angle) is illustrated in Figure 2. For most pixels, excluding those near the edge of disk at extreme view angles, the scattering angle approaches the hotspot (exact backscattering) twice a year according to seasonal change in the local solar elevation (Li et al., 2021). The total range of daily variation of scattering angle changes little between second decades of March and October but decreases towards the turn of the year. We should mention that MAIAC follows the convention used in the radiative transfer theory where the backscattering corresponds to the relative azimuth and scattering angle of 180° contrary to the definition used in the RTLS model.

Figure 2

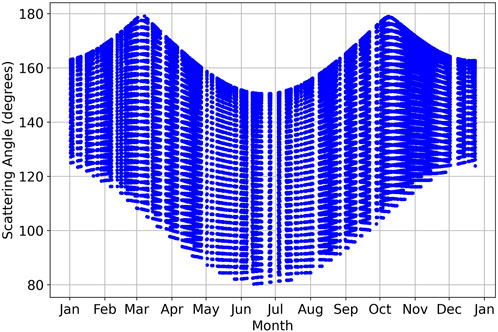
Figure 2. Annual change of scattering angle for GOES-16 ABI observation of Washington, DC, United States.

Figures 3, 4 show the results of processing for two pixels representing an urban area of Washington, DC (Pix1), and a forested area about 100 km north-east (Pix2), viewed approximately at VZA ∼ 45°. In both cases, we show the results typical for the hotspot view geometry (a) and for the regular geometry (b). The dots show the BRF retrieved using RTLS (black) and sRTLS (red) BRDF models, and the LER (blue). The empty circles connected by solid line show the best fit BRDF models. The first Figure 3A shows 5 consecutive days 64–68 of 2023 of mostly cloud-free observations. During this time period, SZA_max ≈ VZA which captures the hotspot with maximal daily scattering angles between 177.5° and 179.1°. The retrievals are shown for four channels, Blue (0.47 μm), Red (0.64 μm), NIR (0.86 μm) and shortwave IR (SWIR, 2.24 μm). Both sRTLS and RTLS models provide a very similar match to the retrieved BRFs. The main differences appear near the hotspot and at high SZAs. Due to the Maignan hotspot factor, the sRTLS model fits the hotspot direction well: the BRF-BRDF difference near the hot spot does not exceed 0.01 in all four channels. The RTLS model significantly underestimates the hotspot reflectance by 0.025 (Blue), 0.04 (Red), 0.055 (NIR), 0.052 (SWIR). At high SZAs, the sRTLS model gives higher values of BRF and by design, higher BRDF. In the legend, the BRF obtained with sRTLS model is called sBRF. The difference sBRF-BRF as well as sBRF-LER is negligible in the SWIR but it increases towards the Blue with increase of the diffuse/direct radiation ratio due to higher atmospheric optical depth and Rayleigh-aerosol scattering of light. For instance, at SZA ∼ 80° the difference reaches sBRF-BRF ∼ 0.02 in the blue channel. Such difference may persist throughout the year (e.g., Figure 3B).

Figure 3

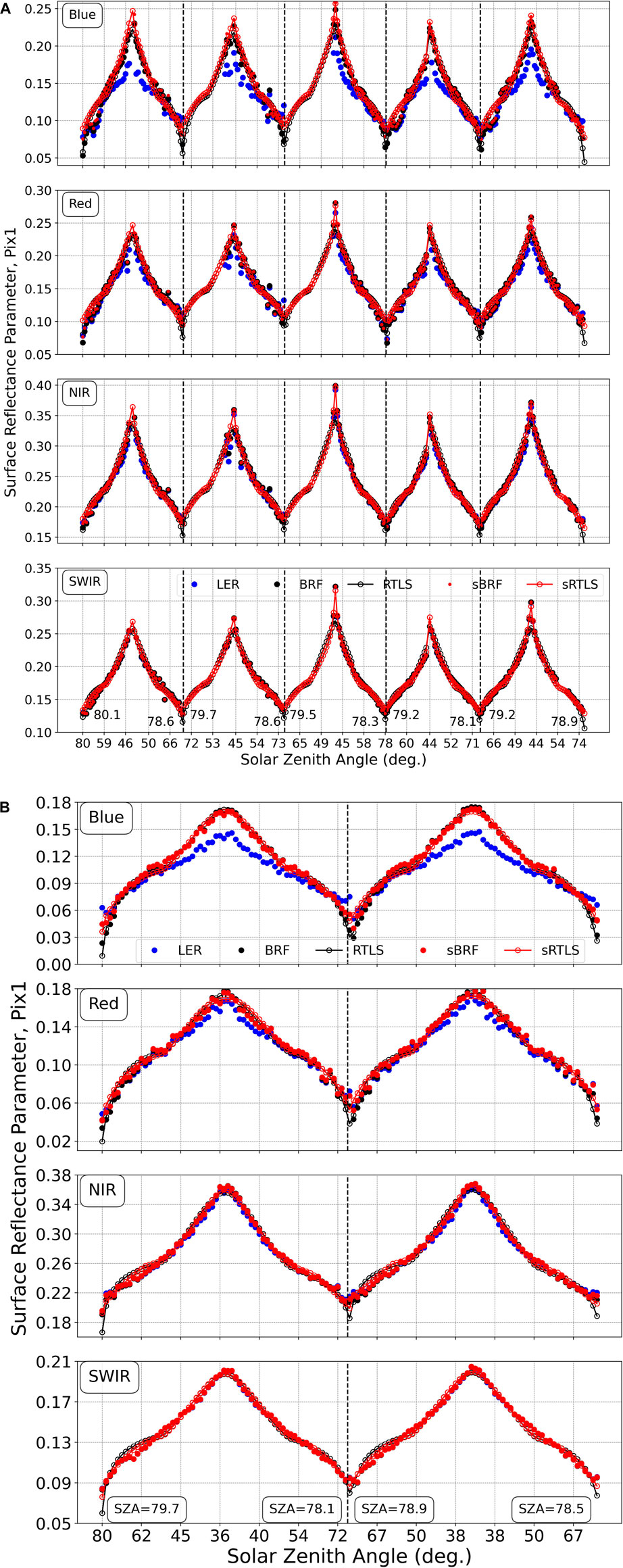
Figure 3. Surface reflectance and approximating BRDF models for the urban (downtown Washington, DC) area. The results are shown for the near hotspot view geometry [(A) March 5–9, 2023], and for the regular geometry [(B), Sept. 15–16, 2023]. The retrieved surface reflectance is shown by the solid dots (blue–LER; red–sRTLS, black–RTLS). The open symbols connected with lines give the respective best fit BRDF using RTLS (black) and sRTLS (red) models.

Figure 4

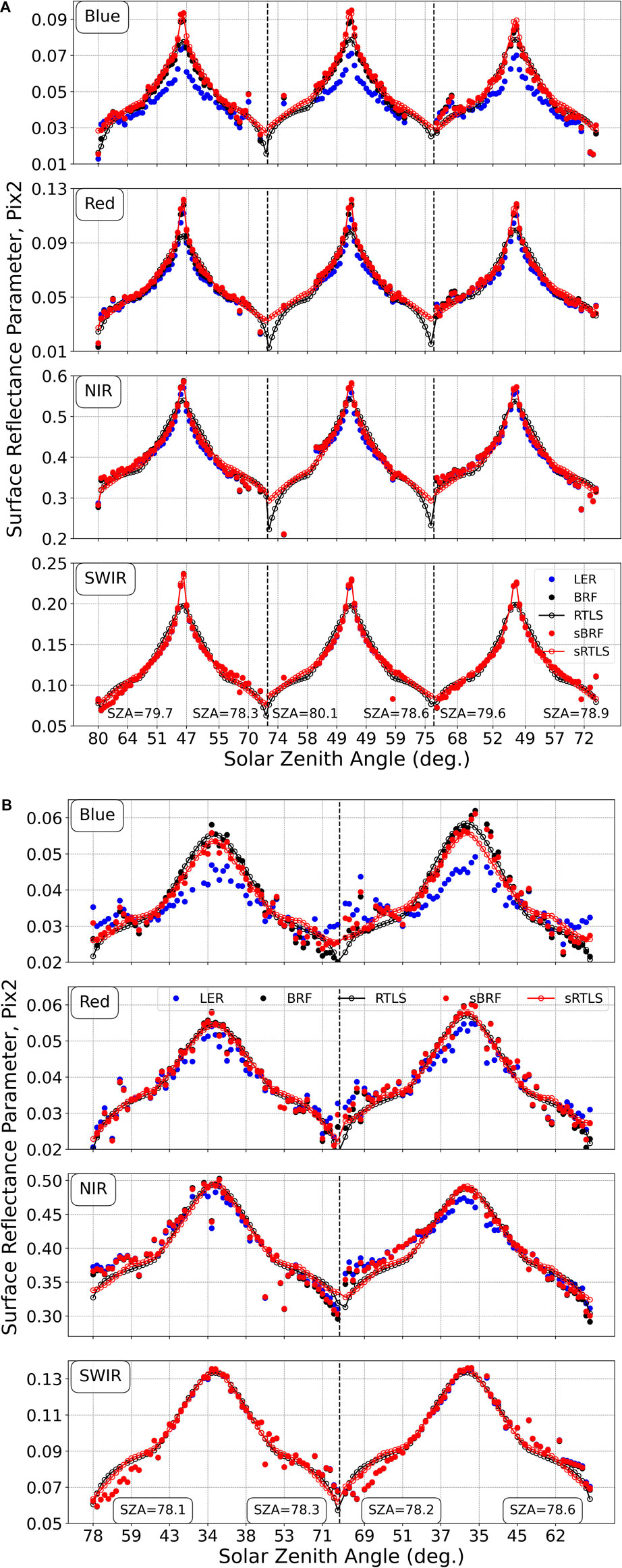
Figure 4. The same as in Figure 3 but for the forested area. The results are shown for the near hotspot view geometry [(A) October 11–13, 2023], and for the regular geometry [(B), September 5–6, 2020].

The difference in BRDF shape between the two models at high SZA is strongly manifested for the forested pixel (Pix2). Figure 4A shows the reflectance values for days 284–286 coinciding with the fall hotspot period (max γ = 178.7°). Similarly to the urban pixel (A), the RTLS model underestimates the reflectance from 0.012 (Blue) to ∼0.05 (NIR), while the sRTLS model provides the good match to the BRF. The RTLS BRDF displays a characteristic “shelf” at SZA ∼ 58°–65° with rapid decrease at higher angles. The difference in data fit is best visible in the SWIR channel. In this case, sBRF and BRF are nearly identical, and the sRTLS model provides a significantly better match.

Figures 3, 4 also shows the LER by blue dots. The Lambertian surface model is widely used for atmospheric correction, e.g., by the MODIS and VIIRS standard AC algorithm (Vermote and Kotchenova, 2008). This approximate model simplifies the radiative transfer problem and allows for faster atmospheric correction using significantly smaller look-up tables. The LER has a good accuracy at longer NIR-SWIR wavelengths, when Rayleigh and aerosol optical depths are low, but it has a systematic bias at shorter wavelengths (e.g., Wang et al., 2010; Lyapustin et al., 2021) which is also apparent in Figures 3, 4. The maximal LER bias ∼22% is near the hotspot signature.

Figure 5 shows histograms of daily standard deviations (σ) from all pixels over an area of 250 × 250 km² centred at the NASA Goddard Space Flight Center, during the full year of 2020. The results are shown for four channels, with Blue (0.47 μm) and Red (0.64 μm) represented by the respective colors, and NIR (0.86 μm) and SWIR (2.24 μm) shown in brown and black, respectively. Solid and dashed lines represent the sRTLS and the standard RTLS models, respectively. One can see that sRTLS model gives a better fit in all bands shifting histograms of standard deviation towards smaller values. The use of sRTLS model slightly improves the mean standard deviation, computed as the normalized first moment of the distribution, by (2-4) 10^–4, in the Blue-SWIR bands except Red (10^–5). While the mean reduction of σ is low, being distributed over up to 60–100 observations per day, the main impact on both BRFs and BRDF fit is at high zenith angles and near the hotspot and can be significant as we demonstrated earlier.

Figure 5

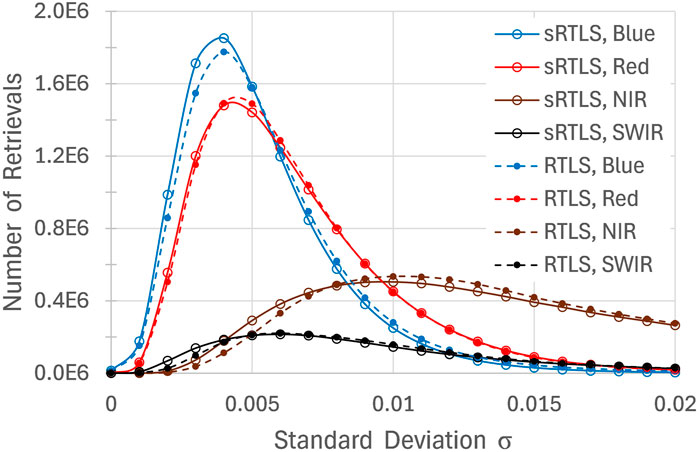
Figure 5. Histogram of standard deviation of BRF-BRDF daily fit at 1 km resolution in Blue, Red, NIR and SWIR ABI channels from MAIAC-Geo processing over an area of 250 × 250 km² centred at NASA GSFC during 2020. Solid and dashed lines represent sRTLS and standard RTLS models, respectively.

4 Conclusion

Developed in late 1990s, RTLS has been a highly successful model describing BRDF of the land surface for climate models and many applications listed in the Introduction. The model works well for zenith angles up to ∼60°–70° but its accuracy deteriorates at higher zenith angles and near the hotspot. This limits its use in processing of geostationary observations and in applications using high zenith angles. In this work, we described a simple practical solution that allows to extend the range of the sRTLS model to higher zenith angles. sRTLS improves the accuracy both near the hotspot directions and at zenith angles above ∼70° which is achieved by adding the multiplicative hotspot factor of Maignan et al. (2004) and by scaling the cosines of zenith angles in the RTLS model at ZA > 60°, respectively. We tested the model using GOES-16 ABI data processing for zenith angles up to ∼80° which is currently set as a limit in MAIAC-Geo look-up tables. Further extension to higher zenith angles would require consideration of the Earth sphericity (e.g., Korkin et al., 2022) in MAIAC look-up tables which is currently under development. It should be mentioned that the introduced modification of the BRDF model is expected to have a very minor effect on the surface albedo except at high SZAs where the difference may become noticeable. The analysis related to surface albedo will be published elsewhere.

In MAIAC, knowledge of surface BRDF is used for detection of clouds and cloud shadows. At high solar zenith angles, both problems increase in complexity as the contrast from clouds diminishes and the length of shadows grows. Thus, the improvement in the BRDF model performance at high zenith angles becomes critical for the total processing accuracy of geostationary data, including both aerosol retrieval and atmospheric correction. In this regard, the particular benefits of the sRTLS model are expected at high latitudes which experience the most rapid climate change effects. Through the improved aerosol data quality in the morning and pre-dawn hours, this development is also expected to benefit the air quality monitoring from geostationary satellites, in particular the analysis of diurnal cycle of air pollution related to traffic commute patterns, industrial activities and other sources.

The sRTLS model has been implemented in MAIAC MODIS Collection 6.1 algorithm, in version 2 MAIAC VIIRS algorithm, and in MAIAC-Geo algorithm for AHI HIMAWARI and GOES-16–18 ABI data. The spectral BRF, sRTLS model parameters and albedo from ABI and AHI are reported in the NASA GeoNEX Level 2 land products, which are publicly accessible from the project data portal (https://data.nas.nasa.gov/geonex/data.php). In addition, a set of open-source software tools (in R and Python) has been developed to subset, analyse, and visualize these products at specified locations and time ranges, which are also freely accessible online (https://github.com/nasa/GeoNEXTools).

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AL: Conceptualization, Funding acquisition, Investigation, Methodology, Software, Supervision, Writing–original draft. YW: Data curation, Investigation, Software, Writing–review and editing. SK: Software, Visualization, Writing–review and editing. CS: Writing–review and editing. WW: Writing–review and editing. ZW: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The research of AL, YW, SK was supported by NASA MODIS Maintenance Program and NASA NNH19ZDA001N-ESROGSS, Earth Science Research from Operational Geostationary Satellite Systems.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bi, J., Knyazikhin, S., Choi, T., Park, J., Barichivich, P., Ciais, R., et al. (2015). Sunlight mediated seasonality in canopy structure and photosynthetic activity of Amazonian rainforests. Environ. Res. Lett. 10 (6), 064014. doi:10.1088/1748-9326/10/6/064014

CrossRef Full Text | Google Scholar

Chen, Y., Sun, K., Li, W., Chen, C., Li, P., Bai, T., et al. (2021). Prototyping of LAI and FPAR retrievals from GOES-16 advanced baseline imager data using global optimizing algorithm. IEEE J. Sel. Top. Appl. Earth Observations Remote Sens. 14, 6937–6950. doi:10.1109/jstars.2021.3094647

CrossRef Full Text | Google Scholar

Gao, F., Li, X., Strahler, A., and Schaaf, C. (2000). Evaluation of the Li transit kernel for BRDF modeling. Remote Sens. Rev. 19 (1-4), 205–224. doi:10.1080/02757250009532419

CrossRef Full Text | Google Scholar

Gao, S., Zhang, X., Zhang, H. K., Shen, Y., Roy, D. P., Wang, W., et al. (2024). A new constant scattering angle solar geometry definition for normalization of GOES-R ABI reflectance times series to support land surface phenology studies. Remote Sens. Environ. 315, 114407. doi:10.1016/j.rse.2024.114407

CrossRef Full Text | Google Scholar

Giglio, L., Boschetti, L., Roy, D. P., Humber, M. L., and Justice, C. O. (2018). The Collection 6 MODIS burned area mapping algorithm and product. Rem. Sens. Environ. 217, 72–85. doi:10.1016/j.rse.2018.08.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Hashimoto, H., Wang, W., Dungan, J. L., Li, S., Michaelis, A. R., Takenaka, H., et al. (2021). New generation geostationary satellite observations support seasonality in greenness of the Amazon evergreen forests. Nat. Commun. 12 (1), 684. doi:10.1038/s41467-021-20994-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Korkin, S., Yang, E.-S., Spurr, R., Emde, C., Zhai, P., Krotkov, N., et al. (2022). Numerical results for polarized light scattering in a spherical atmosphere. JQSRT 287, 108194. doi:10.1016/j.jqsrt.2022.108194

CrossRef Full Text | Google Scholar

Li, R., Wang, D., Wang, W., and Nemani, R. (2023). A GeoNEX-based high-spatiotemporal-resolution product of land surface downward shortwave radiation and photosynthetically active radiation. Earth Syst. Sci. Data 15 (3), 1419–1436. doi:10.5194/essd-15-1419-2023

CrossRef Full Text | Google Scholar

Li, S., Wang, W., Hashimoto, H., Xiong, J., Vandal, T., Yao, J., et al. (2019). First provisional land surface reflectance product from geostationary satellite Himawari-8 AHI. Remote Sens. 11 (24), 2990. doi:10.3390/rs11242990

CrossRef Full Text | Google Scholar

Li, X., and Strahler, A. H. (1986). Geometric – optical bidirectional reflectance modeling of a conifer forest canopy. IEEE Trans. Geosci. Remote Sens. GE-24 (6), 906–919. doi:10.1109/tgrs.1986.289706

CrossRef Full Text | Google Scholar

Li, X., and Strahler, A. H. (1992). Geometric – optical bidirectional reflectance modeling of the discrete crown vegetation canopy: effect of crown shape and mutual shadowing. IEEE Trans. Geosci. Remote Sens. 30, 276–292. doi:10.1109/36.134078

CrossRef Full Text | Google Scholar

Li, Z., Roy, D. P., and Zhang, H. K. (2021). The incidence and magnitude of the hot-spot bidirectional reflectance distribution function (BRDF) signature in GOES-16 Advanced Baseline Imager (ABI) 10 and 15 minute reflectance over north America. Remote Sens. Environ. 265, 112638. doi:10.1016/j.rse.2021.112638

CrossRef Full Text | Google Scholar

Liang, X.-Z., Xu, M., Gao, W., Kunkel, K., Slusser, J., Dai, Y., et al. (2005). Development of land surface albedo parameterization based on Moderate Resolution Imaging Spectroradiometer (MODIS) data. J. Geophys. Res. 110, D11107. doi:10.1029/2004JD005579

CrossRef Full Text | Google Scholar

Lucht, W., Schaaf, C. B., and Strahler, A. H. (2000). An algorithm for the retrieval of albedo from space using semiempirical BRDF models. IEEE Trans. Geosci. Remote Sens. 38, 977–998. doi:10.1109/36.841980

CrossRef Full Text | Google Scholar

Lyapustin, A., Gatebe, C., Kahn, R., Brandt, R., Redemann, J., Russell, P., et al. (2010). Analysis of snow bidirectional reflectance from ARCTAS Spring-2008 Campaign. Atmos. Chem. Phys. 10 (9), 4359–4375. doi:10.5194/acp-10-4359-2010

CrossRef Full Text | Google Scholar

Lyapustin, A., and Knyazikhin, Yu. (2001). Green’s function method in the radiative transfer problem. I: homogeneous non-Lambertian surface. Appl. Opt. 40, 3495–3501. doi:10.1364/AO.40.003495

PubMed Abstract | CrossRef Full Text | Google Scholar

Lyapustin, A., Wang, Y., Korkin, S., and Huang, D. (2018). MODIS collection 6 MAIAC algorithm. Atmos. Meas. Tech. 11, 5741–5765. doi:10.5194/amt-11-5741-2018

CrossRef Full Text | Google Scholar

Lyapustin, A., Zhao, F., and Wang, Y. (2021). A comparison of multi-angle implementation of atmospheric correction and MOD09 daily surface reflectance products from MODIS. Front. Remote Sens. 2, 712093. doi:10.3389/frsen.2021.712093

CrossRef Full Text | Google Scholar

Lyapustin, A. I. (1999). Atmospheric and geometrical effects on land surface albedo. J. Geophys. Res. 104, 4127–4143. doi:10.1029/1998jd200064

CrossRef Full Text | Google Scholar

Lyapustin, A. I., Wang, Y., Korkin, S., Kahn, R., and Winker, D. (2020). MAIAC thermal technique for smoke injection height from MODIS. IEEE Geosci. Remote Sens. Lett. 17 (5), 730–734. doi:10.1109/LGRS.2019.2936332

CrossRef Full Text | Google Scholar

Lyapustin, A. I., Wang, Y., Laszlo, I., Hilker, T., Hall, F., Sellers, P., et al. (2012). Multi-angle implementation of atmospheric correction for MODIS (MAIAC): 3. Atmospheric correction. Rem. Sens. Env. 127, 385–393. doi:10.1016/j.rse.2012.09.002

CrossRef Full Text | Google Scholar

Lyapustin, A. I., Wang, Y., Xiong, X., Meister, G., Platnick, S., Levy, R., et al. (2014). Scientific impact of MODIS C5 calibration degradation and C6+ improvements. Atmos. Meas. Tech. 7, 4353–4365. doi:10.5194/amt-7-4353-2014

CrossRef Full Text | Google Scholar

Lyapustin, A. I., Wang, Y., Choi, M., Xiong, X., Angal, A., Wu, A., et al. (2023). Calibration of the SNPP and NOAA 20 VIIRS sensors for continuity of the MODIS Climate Data Records. Rem. Sens. Environ. 295, 113717. doi:10.1016/j.rse.2023.113717

CrossRef Full Text | Google Scholar

Maignan, F., Bréon, F. M., and Lacaze, R. (2004). Bidirectional reflectance of Earth targets: evaluation of analytical models using a large set of spaceborne measurements with emphasis on the hot spot. Remote Sens. Environ. 90 (2), 210–220. doi:10.1016/j.rse.2003.12.006

CrossRef Full Text | Google Scholar

Martonchik, J. V., Diner, D. J., Pinty, B., Verstraete, M. M., Myneni, R. B., Knyazikhin, Y., et al. (1998). Determination of land and ocean reflective, radiative, and biophysical properties using multiangle imaging. IEEE Trans. Geosci. Remote Sens. v36 (4), 1266–1281. doi:10.1109/36.701077

CrossRef Full Text | Google Scholar

Nemani, R., Wang, W., Hashimoto, H., Michaelis, A., Vandal, T., Lyapustin, A., et al. (2020). “GeoNEX: a geostationary earth observatory at NASA Earth exchange: earth monitoring from operational geostationary satellite systems,” in IGARSS 2020-2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September 2020 - 02 October 2020 (IEEE), 128–131.

CrossRef Full Text | Google Scholar

Ross, J. K. (1981). in The radiation regime and architecture of plant stands. Editor W. Junk (Norwell, MA: Artech House), 392.

Google Scholar

Roujean, J.-L., Leroy, M., and Deschamps, P. Y. (1992). A bidirectional reflectance model of the Earth’s surface for the correction of the remote sensing data. J. Geophys. Res. 97 (20), 455–520. doi:10.1029/92JD01411

CrossRef Full Text | Google Scholar

Roy, D. P., Jin, Y., Lewis, P. E., and Justice, C. O. (2005). Prototyping a global algorithm for systematic fire-affected area mapping using MODIS time series data. Rem. Sens. Environ. 97 (2), 137–162. doi:10.1016/j.rse.2005.04.007

CrossRef Full Text | Google Scholar

Schaaf, C. B., Gao, F., Strahler, A. H., Lucht, W., Li, X., Tsang, T., et al. (2002). First operational BRDF, albedo, nadir reflectance products from MODIS. Rem. Sens. Environ. 83, 135–148. doi:10.1016/S0034-4257(02)00091-3

CrossRef Full Text | Google Scholar

Schläpfer, D., Richter, R., and Feingersh, T. (2015). Operational BRDF effects correction for wide-field-of-view optical scanners (BREFCOR). IEEE Trans. Geoscience Remote Sens. 53 (4), 1855–1864. doi:10.1109/TGRS.2014.2349946

CrossRef Full Text | Google Scholar

She, L., Zhang, H., Wang, W., Wang, Y., and Shi, Y. (2019). Evaluation of the multi-angle implementation of atmospheric correction (MAIAC) aerosol algorithm for Himawari-8 data. Remote Sens. 11 (23), 2771. doi:10.3390/rs11232771

CrossRef Full Text | Google Scholar

Shen, Y., Zhang, X., Yang, Z., Ye, Y., Wang, J., Gao, S., et al. (2023). Developing an operational algorithm for near-real-time monitoring of crop progress at field scales by fusing harmonized Landsat and Sentinel-2 time series with geostationary satellite observations. Remote Sens. Environ. 296, 113729. doi:10.1016/j.rse.2023.113729

CrossRef Full Text | Google Scholar

Vermote, E., Justice, C. O., and Breon, F. (2008). Towards a generalized approach for correction of the BRDF effect in MODIS directional reflectances. IEEE Trans. Geosci. Remote Sens. 47, 898–908. doi:10.1109/tgrs.2008.2005977

CrossRef Full Text | Google Scholar

Vermote, E. F., and Kotchenova, S. (2008). Atmospheric correction for the monitoring of land surfaces. J. Geophys. Res. 113, D23S901–12. doi:10.1029/2007JD009662

CrossRef Full Text | Google Scholar

Wang, W., Li, S., Hashimoto, H., Takenaka, H., Higuchi, A., Kalluri, S., et al. (2020). An introduction to the geostationary-NASA earth exchange (GeoNEX) products: 1. Top-of-atmosphere reflectance and brightness temperature. Remote Sens. 12 (8), 1267. doi:10.3390/rs12081267

CrossRef Full Text | Google Scholar

Wang, W., Wang, Y., Lyapustin, A., Hashimoto, H., Park, T., Michaelis, A., et al. (2022). A novel atmospheric correction algorithm to exploit the diurnal variability in hypertemporal geostationary observations. Remote Sens. 14, 964. doi:10.3390/rs14040964

CrossRef Full Text | Google Scholar

Wang, Y., Lyapustin, A., Privette, J., Cook, R., SanthanaVannan, S. K., Vermote, E., et al. (2010). Assessment of biases in MODIS surface reflectance due to lambertian approximation. Rem. Sens. Environ. 114, 2791–2801. doi:10.1016/j.rse.2010.06.013

CrossRef Full Text | Google Scholar

Wanner, W., Li, X., and Strahler, A. H. (1995). On the derivation of kernels for kernel-driven models of bidirectional reflectance. J. Geophys. Res. 100 (D10), 21077–21089. doi:10.1029/95jd02371

CrossRef Full Text | Google Scholar

Zhang, X., Shen, Y., Gao, S., Wang, W., and Schaaf, C. (2022). Diverse responses of multiple satellite-derived vegetation greenup onsets to dry periods in the amazon. Geophys. Res. Lett. 49 (20), e2022GL098662. doi:10.1029/2022gl098662

CrossRef Full Text | Google Scholar