- 1Science Systems and Applications, Inc., Lanham, MD, United States
- 2NASA Goddard Spaceflight Center, Greenbelt, MD, United States
- 3Swiss Federal Institute of Aquatic Science and Technology, Department of Surface Waters-Research and Management, Dübendorf, Switzerland
- 4GESTAR II, University of Maryland Baltimore-County, Baltimore, MD, United States
- 5Geo-Sensing and Imaging Consultancy, Trivandrum, Kerala, India
- 6Department of Geography, University of Zurich, Zürich, Switzerland
Given the use of machine learning-based tools for monitoring the Water Quality Indicators (WQIs) over lakes and coastal waters, understanding the properties of such models, including the uncertainties inherent in their predictions is essential. This has led to the development of two probabilistic NN-algorithms: Mixture Density Network (MDN) and Bayesian Neural Network via Monte Carlo Dropout (BNN-MCD). These NNs are complex, featuring thousands of trainable parameters and modifiable hyper-parameters, and have been independently trained and tested. The model uncertainty metric captures the uncertainty present in each prediction based on the properties of the model—namely, the model architecture and the training data distribution. We conduct an analysis of MDN and BNN-MCD under near-identical conditions of model architecture, training, and test sets, etc., to retrieve the concentration of chlorophyll-a pigments (Chl a), total suspended solids (TSS), and the absorption by colored dissolved organic matter at 440 nm (acdom (440)). The spectral resolutions considered correspond to the Hyperspectral Imager for the Coastal Ocean (HICO), PRecursore IperSpettrale della Missione Applicativa (PRISMA), Ocean Colour and Land Imager (OLCI), and MultiSpectral Instrument (MSI). The model performances are tested in terms of both predictive residuals and predictive uncertainty metric quality. We also compared the simultaneous WQI retrievals against a single-parameter retrieval framework (for Chla). Ultimately, the models’ real-world applicability was investigated using a MSI satellite-matchup dataset
1 Introduction
Satellite remote sensing has proven to be a valuable tool for monitoring the biogeochemical properties and health status of global water bodies, particularly in the face of ongoing climate change and anthropogenic pressures (Michalak, 2016; Greb et al., 2018). Remote sensing enables large-scale mapping of near-surface Water Quality Indicators (WQIs), such as chlorophyll-a concentration (Chl
Over the last few decades, dozens of approaches have been developed to retrieve WQIs from remote sensing, spanning empirical band ratios (Mittenzwey et al., 1992; O’Reilly et al., 1998), physics-based semi-analytical algorithms (Gons et al., 2002; Maritorena et al., 2002; Gilerson et al., 2010; Siegel et al., 2013), and machine learning (ML) algorithms like random forests or support vector machines (Kwiatkowska and Fargion, 2003; Cao et al., 2020). Many of these algorithms are regionally tuned and demonstrate high accuracy when optimized with local datasets corresponding to specific aquatic environments such as coastal waters. However, these algorithms often fail to generalize across environments with varying optical complexities due to the need for adaptive selection of algorithm coefficients or parameters when applied beyond their initial calibration region. One approach to deal with regional variability is the development of optical water types (OWT) based switching or blending schemes to combine various regional models (Moore et al. 2014; Jackson et al. 2017; Spyrakos et al. 2018). Another avenue to overcome local limitations is to develop neural networks with large, representative datasets. NNs demonstrate promising capacities in handling samples from diverse water conditions (Schiller and Doerffer, 1999; Gross et al., 2000; Ioannou et al., 2011; Vilas et al., 2011; Jamet et al., 2012; Kajiyama et al., 2018; Pahlevan et al., 2020; Smith et al., 2021; Werther et al., 2022).
The primary hurdle in our ability to leverage the information and predictions from such models/algorithms in human monitoring activities are the various sources of uncertainties present in these estimations. The first source of uncertainties in such predictions are the uncertainties inherently present in the data, including imperfect atmospheric correction (AC) (Moses et al., 2017; Pahlevan et al., 2021a; IOCCG report, 2010), complex variability in the composition and structure of water-column constituents (IOCCG report, 2000), and the presence of signal from neighboring natural/manmade targets (Sanders et al., 2001; Odermatt et al., 2008; Castagna and Vanhellemont, 2022). The second source of uncertainty for data-based product estimation techniques stems from the data distribution used to design and validate the methods. The performance of these techniques is guaranteed only under the assumption that the training and test distributions are similar, which cannot be strictly guaranteed in satellite remote sensing datasets. These uncertainties can adversely impact the reliability of the retrieved remote sensing products (e.g., Chl
Most retrieval approaches are typically deterministic in nature and do not inherently provide uncertainties associated with their estimates. To overcome this limitation, these methods are coupled with independent frameworks, such as optical water types (Neil et al., 2019; Liu et al., 2021), to provide indirect estimates of uncertainty. However, this integrated approach can introduce additional complexities and can hamper the effectiveness/interpretation of the uncertainty due to the disparate nature of the combined methodologies. This scenario accentuates the need for methods that can directly and effectively address uncertainty in their fundamental structure. Despite their potential, neural network models have largely remained unexplored in their capacity to provide uncertainty information about a WQI estimate. To bridge this gap, recent advancements leverage neural networks built on the principles of probability theory, culminating in the development of probabilistic neural networks. These networks model the output as a probability distribution, and specifically predict the parameters of a specific distribution as the output. These approaches model the prediction uncertainties as degrees of belief or confidence in each outcome, marking a critical shift from point-based to probability-density-based modeling. These methodological advancements have seen the application of two probabilistic neural networks to aquatic remote sensing: the Mixture Density Network (MDN) (Pahlevan et al., 2020; Smith et al., 2021) and the Bayesian Neural Network based on Monte Carlo Dropout (BNN-MCD) (Werther et al., 2022). Both these methods outperform classical WQI estimation techniques for optical remote sensing data. Despite their excellent performance on held-out test sets, these model behaviors and operations are not easily understood/interpreted. Given the complexity of these models, specific tools are required which can help end-users interpret the quality and reliability of these predictions. One such tool is the prediction uncertainty; both the MDN (Saranathan et al., 2023) and the BNN-MCD (Werther et al., 2022) have a well-defined procedure to capture the ML-specific uncertainty in the predictions/estimations in a single metric. Despite the availability of such a metric, much work needs to be done to understand the specific properties of each model’s uncertainty metric, especially in comparison to each other.
Recognizing these shortcomings, this study seeks to investigate the recently developed MDN and BNN-MCD models comprehensively. To ensure a consistent evaluation of their performances in both multi- and hyperspectral domains, the two models are analyzed under identical conditions - utilizing the same parameter settings, training, and test datasets, etc. This analysis permits a direct comparison of their performance and capabilities, which in turn illuminates their optimal application. Notably, while some prior approaches to WQI have focused on both single-parameter and multi-parameter inversion schemes, the literature lacks a clear comparison of the two schemes. Given that machine learning algorithms are naturally designed to handle multi-parameter estimations, it would be valuable to clearly identify the effect of simultaneous inversion vis-à-vis an individual inversion framework, our work aims to shed light on this important yet unexplored area. We therefore evaluate the individual performances of these models in retrieving a single WQI (specifically Chla) and their ability to retrieve the same parameter in combinations of WQIs, i.e., simultaneously. To scrutinize the robustness of these models, we analyze them using a community dataset referred to as GLObal Reflectance for Imaging and optical sensing of Aquatic environments (GLORIA), containing in situ measurements over inland and coastal water sites (Lehmann et al., 2023). To span a wide range of spectral capabilities available through current and future missions, we test these models at the spectral resolutions of the MultiSpectral Instrument (MSI) (Drusch et al., 2012), the Ocean and Land Colour Instrument (OLCI) (Nieke et al., 2015), the PRecursore IperSpettrale della Missione Applicativa (PRISMA) (Candela et al., 2016) and Hyperspectral Imager for Coastal Ocean (HICO) (Lucke et al., 2011) in our experiments.
The main purpose of this in-depth analysis of the MDN and BNN-MCD models is to increase our understanding of the underlying probabilistic model assumptions, compare performances on common datasets, and investigate the uncertainty provision. In doing so, our study contributes to a more comprehensive understanding of probability-density estimating machine learning algorithms in satellite remote sensing, paving the way for more reliable decision-making in water quality monitoring, aquatic ecosystem assessment, and coastal zone management.
2 Datasets
In this study, three different types of datasets are used for analysis. The first dataset is made up of collocated in situ measurements of remote sensing reflectance (Rrs) and WQIs and was used for model creation and validation. Second, a matchup dataset composed of satellite reflectance data is also considered. The WQI measurements corresponding to each satellite Rrs were performed in situ at (almost) the same time as the satellite acquisitions. Finally, satellite images cubes are analyzed qualitatively using both algorithms to get a sense of how these models perform on these datasets.
2.1 GLORIA in situ dataset
The in situ dataset used in this study is GLORIA (Lehmann et al., 2023). GLORIA contains paired measurements of spectral remote sensing reflectance (Rrs) (Mobley, 1999), and various WQIs such as Chl
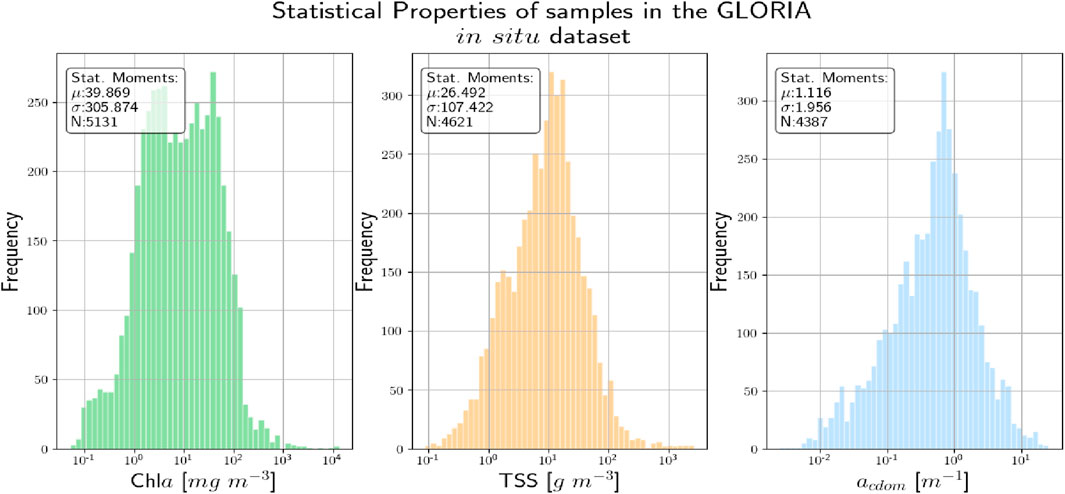
Figure 2. The statistical distribution of the various biogeochemical variables in the GLORIA in situ database.
The spectral coverage was further restricted to spectral bands <724 nm as the 400–724 nm range contains most information content, and both in situ and MSI-derived matchup Rrs data (see Section 2.2) beyond this range (i.e., in the near-infrared; NIR) carry large uncertainties (Pahlevan et al., 2021a), adding noise to subsequent analyses. To further ensure data quality, any spectra in the GLORIA dataset that has been flagged as having issues like (random) noise, sun-glint correction issues (baseline shift), or instrument miscalibrations have eliminated from consideration. The distribution of the values of the different WQIs in the GLORIA dataset, showing the range of conditions covered, is shown in Figure 2. It is important to mention that although GLORIA contains approximately
The samples in the GLORIA dataset are measured in the best-case scenario, in terms of the techniques used and the measurement environment chosen, etc., and are expected to have a very high SNR (significantly higher than what is seen in satellite datasets). Due to its comparatively high SNR, predictive efforts focused on these datasets are expected to be more successful than when applied to noisier satellite datasets [N.B.: While the samples in the GLORIA dataset are expected to have a higher SNR, it should be noted that these measurements are not error/noise-free. Possible sources of error include random/systematic noise in field instrument measurements, operation errors, non-ideal environmental conditions, and inaccuracies in laboratory based Chla measurements.]. Satellite data which are the primary data source for the application of such models are expected to be significantly noisier but given the paucity of satellite Rrs with collocated measures of the WQI, in situ datasets like GLORIA are being primarily used for model training and evaluation.
2.2 Satellite matchup dataset
As was briefly mentioned in the previous section, while given their widespread availability in situ datasets are primarily used for machine learning model training and validation, these statistics might not be directly transferable to satellite datasets. To track/present the effect of satellite data acquisition on model performance, we also test the model performance on an MSI matchup dataset. The matchup dataset consists of Rrs spectra which are extracted from atmospherically corrected MSI imagery for which near concurrent in situ Chl
2.3 Multispectral and hyperspectral satellite data
Additionally, some well-studied satellite image cubes at both multi- and hyperspectral resolutions were used to provide some qualitative analysis of the model performance for satellite data. We focus on images from the multispectral sensors of the Chesapeake Bay, a large tidal estuary in the U.S. The images were processed using the ACOLITE
3 Methods
3.1 Algorithms and settings
This subsection will briefly describe the MDN and BNN-MCD models, we briefly describe their underlying theory, architecture, and parameters. We will also describe here the core hyperparameter settings for the two algorithms used in this manuscript.
3.1.1 Mixture Density Networks
The task of inferring target WQIs from Rrs is inherently an inverse problem (Mobley, 1994). This presents a challenge as the relationship between algorithm input (Rrs) and output (WQIs) is not direct and may have multiple feasible solutions (Sydor et al., 2004). Traditional methods struggle to handle this complexity and may result in oversimplified solutions that overlook significant relationships. Mixture Density Networks (MDNs) have emerged as an effective strategy for handling these inverse problems (Pahlevan et al., 2020; Smith et al., 2021). MDNs are capable of outputting probability distributions - specifically a Gaussian Mixture Model (GMM) (Bishop, 1994). Unlike single output estimates from conventional approaches, GMMs describe an entire range of possible outcomes as a probability distribution, which is particularly advantageous for scenarios with multi-modal output distributions. Provided with enough components, GMMs have the capacity to model distributions of arbitrary complexity (Sydor et al., 2004; Defoin-Platel and Chami, 2007).
Mathematically, a MDN estimates the target variable as an explicit distribution conditioned on the input. As described, a MDN models the output distribution as a GMM, as described in Eq. 1:
where
The associated MDN uncertainty is shown to be well approximated by the standard deviation of the distribution predicted by the MDN for a specific sample and parameter (Choi et al., 2018). Since the output of the MDN is a GMM, the standard deviation is given by Eq. 2:
Finally, the estimated uncertainty is converted into a percentage value relative to the predicted value (or the final point estimate from the model) according to Eq. 3:
Recent work on MDN applications for the Chl a estimation has shown that the estimated uncertainty metric successfully captures the distortion effects in the data such as noisy data, novel test data, and presence of atmospheric distortions in the data (Saranathan et al., 2023).
3.1.2 Bayesian Neural Network based on monte-carlo dropout (BNN-MCD)
Bayesian Neural Networks (BNNs) build upon the architecture of traditional neural networks by integrating probabilistic modeling into each network component such as weights and biases. Since BNN incorporate probabilistic modeling into each step of the network architecture such models can leverage the probabilistic nature of the model output. Since full Bayesian modeling is computationally intractable, one approach for Bayesian approximation of neural networks is the Monte Carlo Dropout (MCD) strategy, as demonstrated by Werther et al. (2022). MCD combines two components: Monte Carlo sampling and the application of dropout to the network weights. The dropout procedure operates by substituting each fixed weight (
where
3.1.3 Architecture details and training of the two neural network models
To enable a robust comparison between the two probabilistic NN algorithms described above, efforts were made to ensure all the architectural hyperparameters associated with the model implementation corresponding to each algorithm are kept in common. In keeping with this effort, the base neural network, i.e., the input and hidden layers for both the algorithm models are made the same. The full details of this base neural network are given in Table. 1. The only differences between the two models are in the shape/structure of the output layer and the use of dropout even in the output stage for the BNN-MCD. In terms of data preprocessing, to stay consistent with prior work (Pahlevan et al., 2020; O’Shea et al., 2021; Smith et al., 2021; Saranathan et al., 2023), both the input data (i.e., Rrs) and the output data (WQIs) are scaled to improve model performance. The same pre-processing steps are used in both prediction pipelines. The Rrs data were scaled using a simple inter-quartile range (IQR) scaling to minimize the effect of the outliers. The output parameters (specifically Chl a and TSS) contain values over a very large range (0–1000 mg/m3). To minimize the effects of the larger magnitudes on model performance, we first apply a simple log-scaling. The parameter distributions post-log-scaling are shown in Figure 2 (the x-axis is in the log-scale). Finally, the output variables are also scaled to fit in the range

Table 1. The architecture and training hyper-parameters of the Base Neural Network used by both the MDN and BNN-MCD algorithms in this manuscript.
The full prediction pipelines for the two algorithms are shown schematically in Figure 3. As described above both pipelines use the same preprocessing and base neural networks. The main intrinsic model differences are the number of components in the output in each network and the mode in which the output is estimated from the distribution. An additional difference is that for the MDN, ten models are trained, and the output is the median point estimate of the ensemble. The BNN-MCD output is with the MC-Dropout active as mentioned in Section 3.2. In our experiments
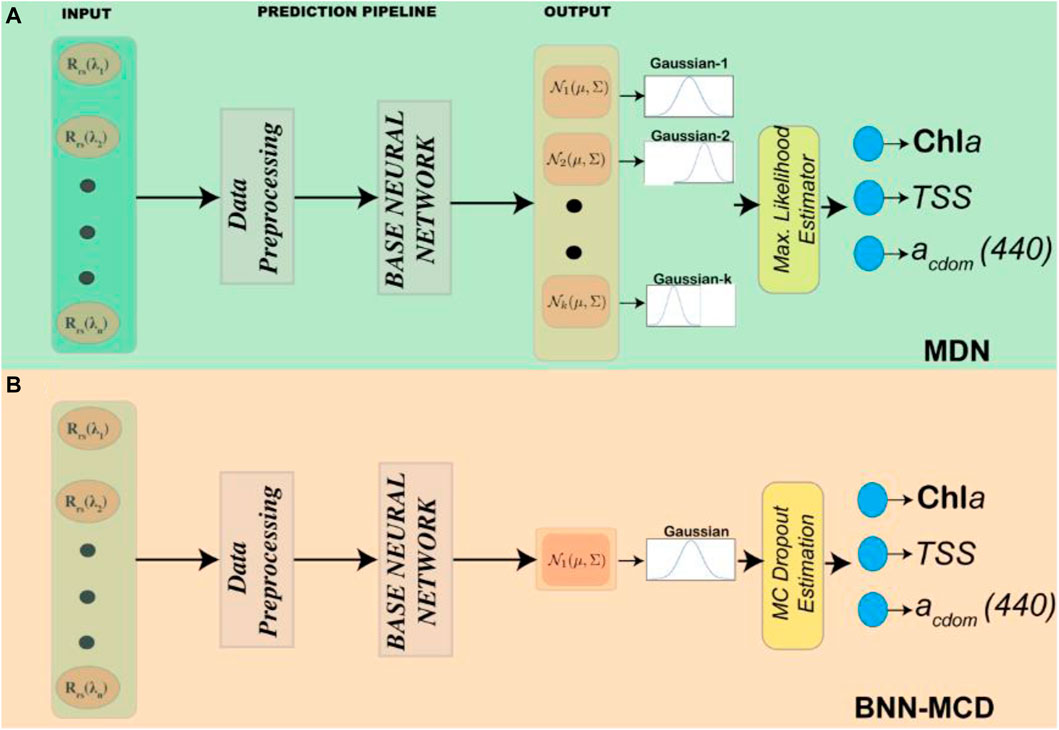
Figure 3. A schematic representation of the full prediction pipeline for the (A) MDN and (B) BNN-MCD, both pipelines leverage the same base neural network defined in Table. 1.
3.2 Evaluation strategies
This subsection outlines the various experiments conducted to analyze the models corresponding to the two probabilistic neural networks. First, we establish the metrics used to evaluate the performance of these models in terms of both predictive residuals and estimated uncertainty (Section. 3.2.1). We then proceed to evaluate the model performances using the GLORIA in situ dataset (Section. 3.2.2). We further gauge the generalization performance of the two models using a leave-one-out approach (Section. 3.2.3), followed by comparing the performance of single-parameter models to that of multi-parameter models (Section. 3.2.4). The final subsection is dedicated to the satellite matchup assessment (Section. 3.2.5).
3.2.1 Evaluation metrics: Predictive performance and uncertainty
The choice of metrics plays a key role in comparing the performance of different models. For the WQI estimation we use a variety of metrics to measure the difference between the true and predicted values referred to as residuals. We thus consider a suite of well-established metrics for measuring predictive (regression) residuals. These metrics are similar to the ones used in previous publications (Seegers et al., 2018; Pahlevan et al., 2020; O’Shea et al., 2021; Smith et al., 2021; Werther et al., 2022), like the Root Mean Squared Log Error (
Additionally, the estimated uncertainties are compared using the following metrics.
1. Sharpness (
where
2. The Coverage Factor (
The best-performing models will have simultaneously a low value for sharpness along with a high value for the coverage factor.
3.2.2 Model training and held-out (test) set assessment
The first experiment compares and contrasts the performance of the two algorithms on the labeled GLORIA in situ dataset (see Section 2.1 for details). The performance of the MDN and BNN-MCD are tested for parameter retrievals and uncertainty estimation for the three parameters of interest at the spectral resolution of all four sensors (MSI, OLCI, HICO, and PRISMA). Further, the dataset is divided into two groups using a
3.2.3 Leave-one-out assessment
The results of the previous
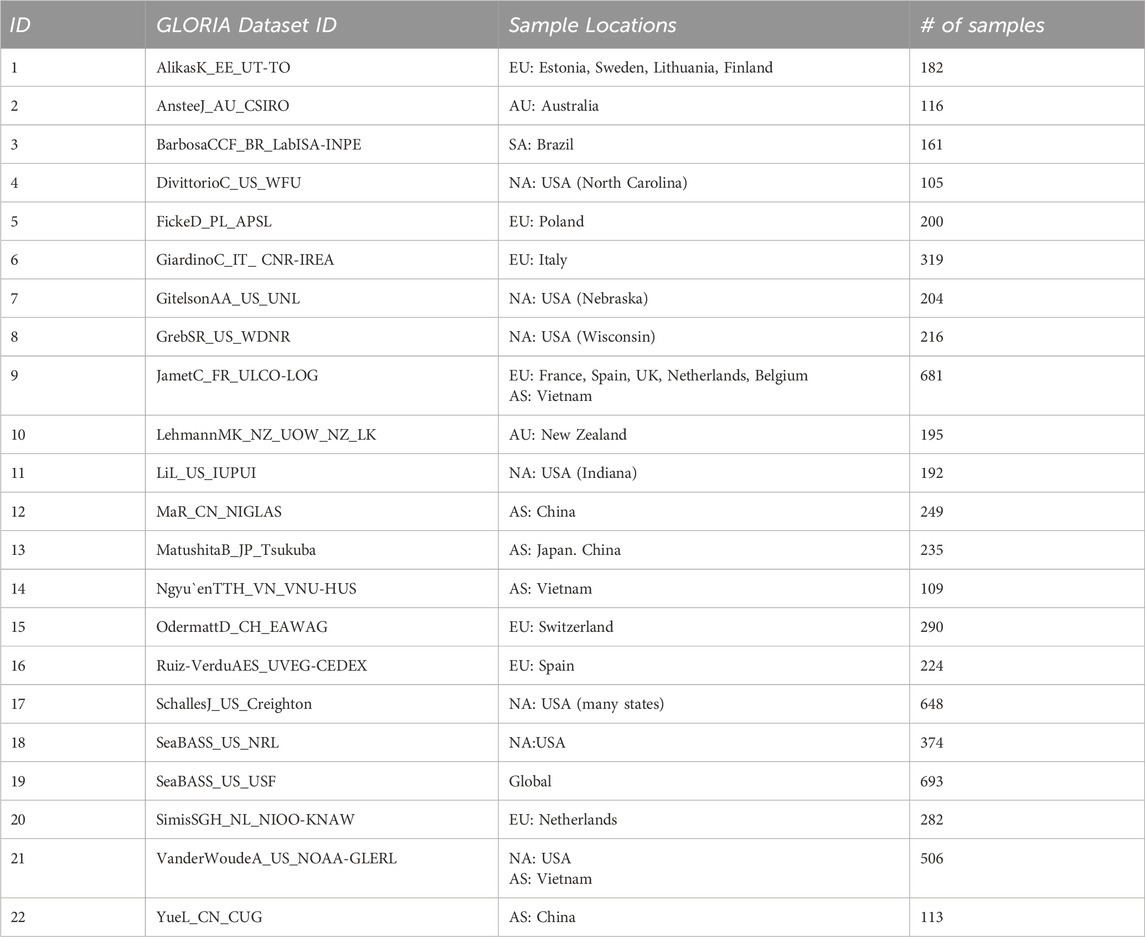
Table 2. The different component subsets of the GLORIA dataset used for Leave-One-Out Validation [N.B.: Column-2 provides the GLORIA dataset IDs for each left out dataset in the analysis.].
It is important to note that some of these data sources contain in situ data from various regions and timeframes (e.g., SeaWiFS Bio-optical Archive and Storage System; SeaBASS). Additionally, not all regions have in situ measurements for all the WQIs considered in this manuscript, which limits our ability to evaluate the algorithm performances for specific indicators within selected datasets. While the LOO approach provides valuable insights into the model’s capacity to handle novel data, it is inherently constrained by the extent of variability captured within the GLORIA dataset. Consequently, when applied globally, this method may encounter locations where the model’s generalization capabilities significantly deviate from those suggested by the GLORIA data. This underscores the potential for encountering performance outliers not adequately represented in the current dataset. Despite these limitations, this LOO analysis is valuable to more accurately assess the individual model’s ability to generalize to unseen data from different geographic locations and water conditions.
3.2.4 Individual retrieval vs. simultaneous retrieval
The comparison of individual (single parameter) versus simultaneous (multi-parameter) retrievals of target variables offers a unique opportunity to better understand the performances and uncertainties associated with the two probabilistic neural network models. Single parameter estimation algorithms (Lee and Carder, 2002; Gitelson et al., 2007), offer precise understanding and interpretability of individual variables while minimizing the complexity introduced by multi-dimensional inter-dependencies. On the other hand, machine learning algorithms are naturally equipped to handle simultaneous retrieval, capitalizing on the inherent correlations and inter-dependencies among multiple variables. This capability offers a nuanced view of aquatic ecosystems by considering the correlations between WQIs. For instance, elevated phytoplankton biomass generally corresponds with increased TSS levels. Conversely, variations in CDOM absorption might not exhibit the same dependencies. Here we investigate the trade-off between the simplicity and interpretability offered by a single-target retrieval and the comprehensive representation of aquatic ecosystems provided by simultaneous estimation. For this purpose, we compare the Chla estimation from a dedicated model, such as those presented previously (Pahlevan et al., 2020; Werther et al., 2022) to the Chl
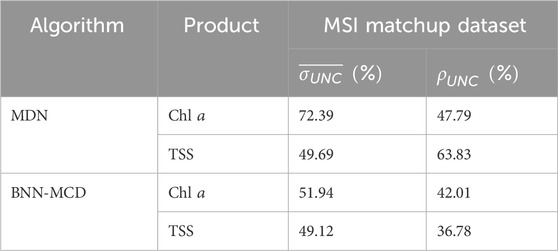
3.2.5 Performance on MSI matchup dataset
The match-up experiment tests and compares the performance of the different algorithms on the satellite matchup data from MSI images described in Section. 2.2. The performance of the models on this dataset would provide the user with some idea of the performance gap that exists when applying these models trained on high quality/low noise in situ datasets to satellite data. Given the additional complexities of the atmospheric correction and residual calibration biases (IOCCG report 2010; Warren et al., 2019), enhanced sensor noise, and distortions present in satellite derived Rrs products, it is expected that the performance of these models on the satellite data will be significantly poorer. The available matchup dataset has corresponding in situ measurements for only Chla and TSS. In this scenario, using the full multiparameter model defined in Sec 3.2.2 is not appropriate as some of the performance gap for this model might be due to the allocation of model capacity to acdom (440) estimation. To avoid this issue, we retrain the model using the in situ GLORIA data but using only Chla and TSS as outputs (the rest of the model settings are the same as in Sec. 3.2.2). Post-training, we apply this newly trained dual output model to the matchup data and estimate prediction performance and uncertainty.
4 Results
This section compares and contrasts the results of the two algorithms across the different experiments described in Section. 3.2.
4.1 Held-out assessment
The performance profiles of the two algorithms - MDN and BNN-MCD–in terms of predictive residuals are summarized in Table 3, where the best-performing model for each sensor and metric is highlighted in bold. While the results present a nuanced landscape, some trends do emerge. For instance, the MDN generally outpaces the BNN-MCD in terms of the MdSA metric by approximately 2%–5% across all three WQIs studied. It also exhibits slope values closer to the ideal of 1, albeit by a narrow margin of 1%–2%. Conversely, the BNN-MCD surpasses the MDN in RMSLE by margins of 0.02–0.04 and also shows superior performance in MAE - leading by 5–20 mg m-3 for Chla and 1–3 g m-3 for TSS, although it falls behind slightly in estimating acdom (440) by about 0.06 m-1. SSPB performance is more sensor-specific, but it is noteworthy that both models demonstrate a low bias (≤10%) across all WQIs.
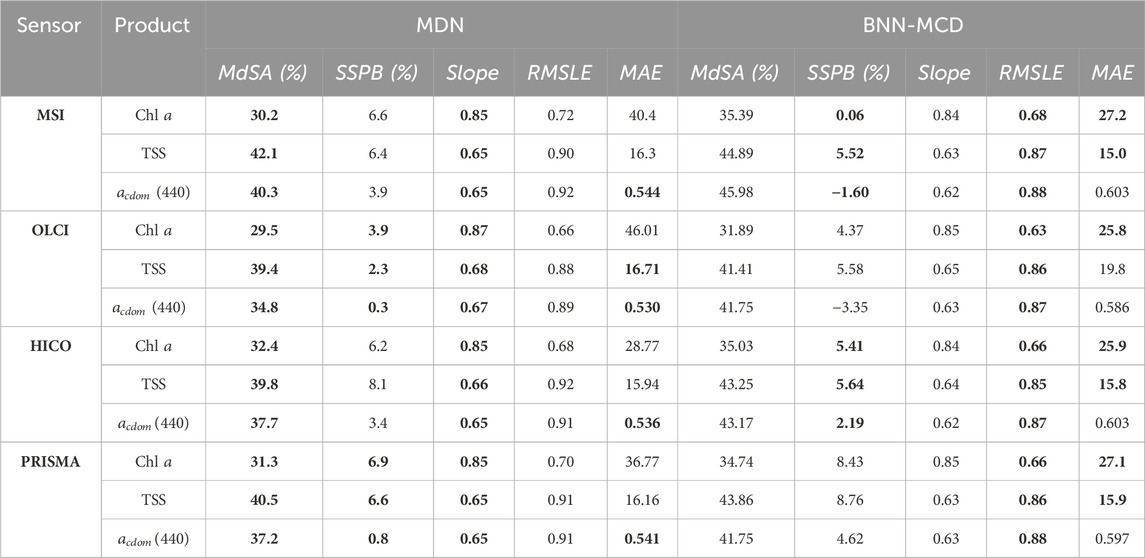
Table 3. Comparison of the performance of the MDN and BNN-MCD across different WQIs for the in situ data at various sensor resolutions. MAE is reported in terms of the physical units of each parameter, i.e., mg m-3, g m-3, m-1 for Chl
The uncertainty metrics across different WQIs and sensors are summarized in Table. 4. Intriguingly, the MDN generally exhibits lower confidence with sharpness values
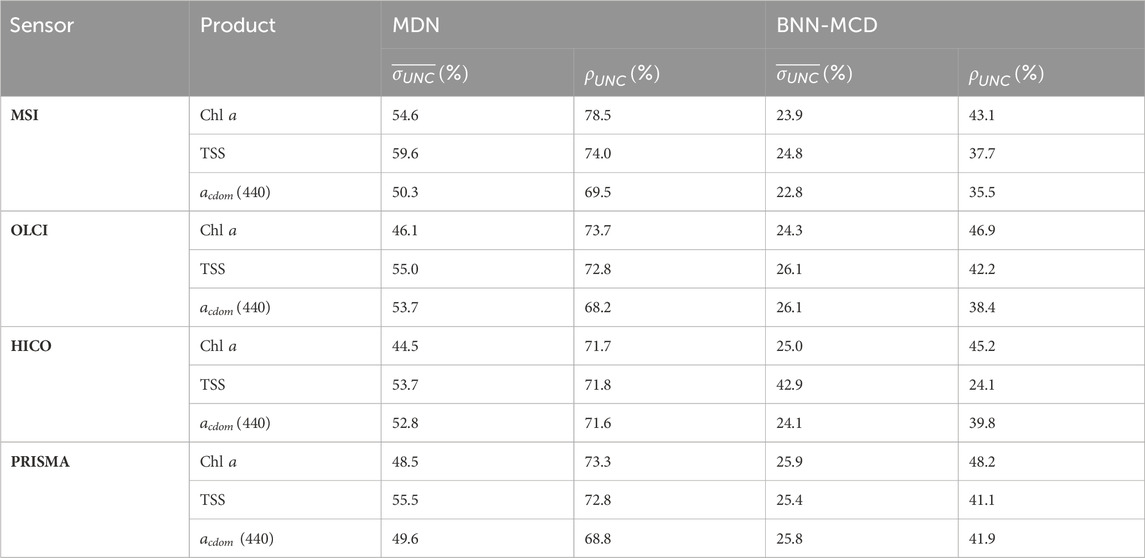
Table 4. Comparison of the different uncertainty metrics for the MDN and BNN-MCD for the different parameters at the resolution of different spectral sensors.
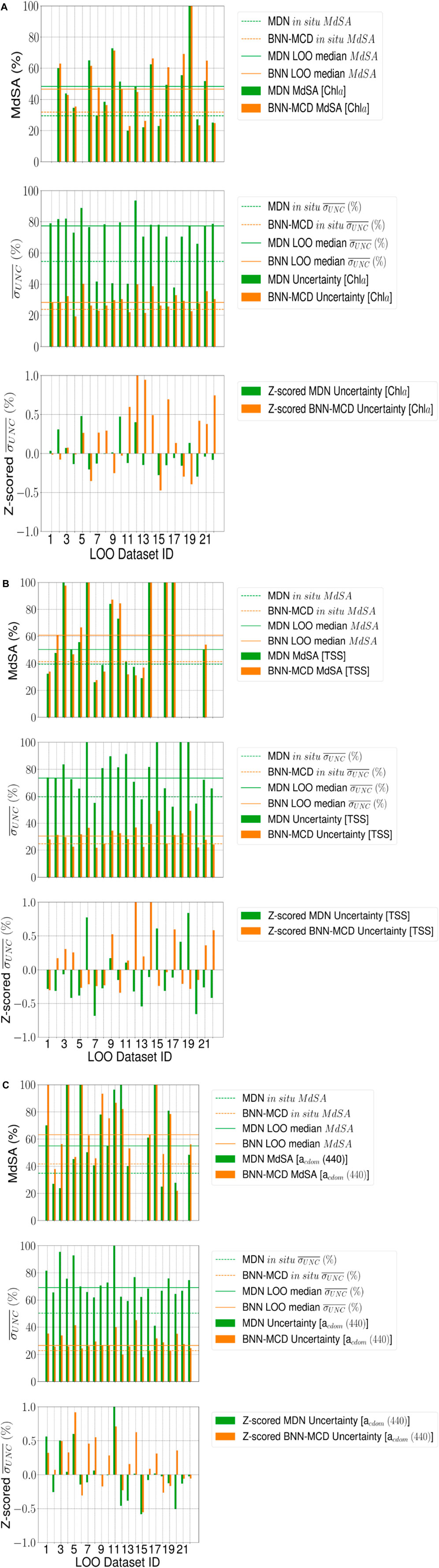
4.2 Leave-one-out assessment
For a large majority of the left-out test sets (∼17-19 out of 22 left out datasets, with the exact number based on the specific WQI) the prediction error (measured using
The lack of clarity in uncertainty trends could arise from multiple factors that influence the basic uncertainty metric (
Generally, both models report very similar trends for most datasets across the different WQIs for both MdSA and z-scored
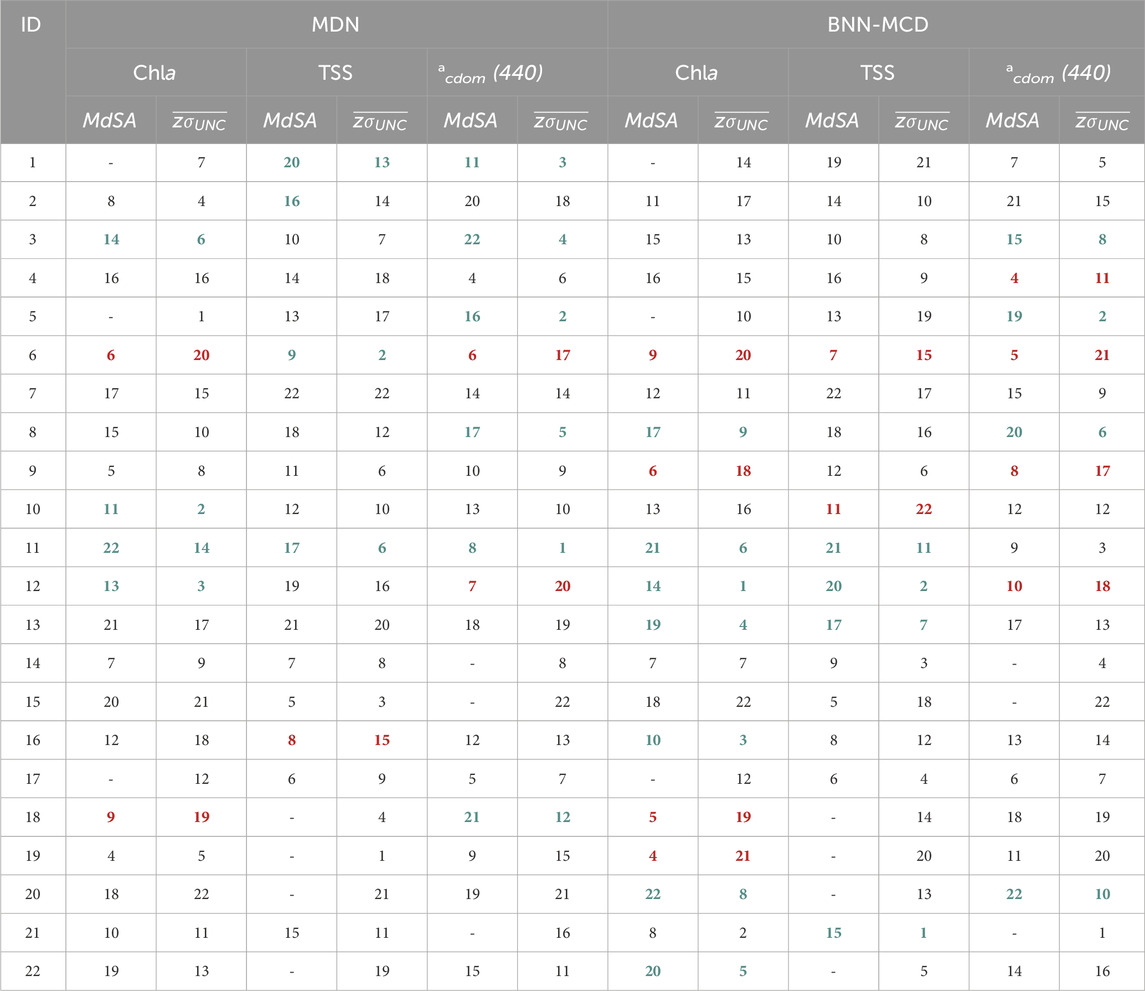
Table 5. Comparing rankings of predictive error (MdSA) and z-scored uncertainty (
4.3 Individual retrievals vs. simultaneous retrievals
Overall, the performance of the simultaneous models is slightly better compared to the single-parameter models. Table. 6 shows the effect of the individual (referred to by the label as ‘Base’) versus simultaneous estimation (referred to by the label as ‘Sim’) of Chl
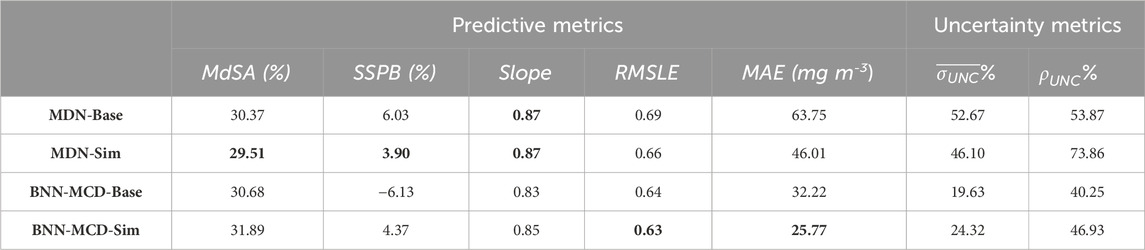
Table 6. Comparison of MDN individual (‘Base’) and simultaneous (‘Sim’) estimators for Chlorophyll-a estimation, both parameter and uncertainty estimations on the held-out test set. MAE is reported in terms of the physical units of the parameter, i.e., mg m−3, g m−3, m−1 for Chla, TSS, and acdom (440), respectively. The other metrics are either (%) or unitless. The bolded cells indicate the best performance of a specific metric.
4.4 MSI matchup assessment
The results of the parameter estimation for the two models on the MSI matchup dataset are shown in Figure 5. Similar to the MDN performance in Pahlevan et al., 2022, there is a rather significant drop-off in performance across the two algorithms relative to the performance we observed on the in situ matchup dataset. For example,
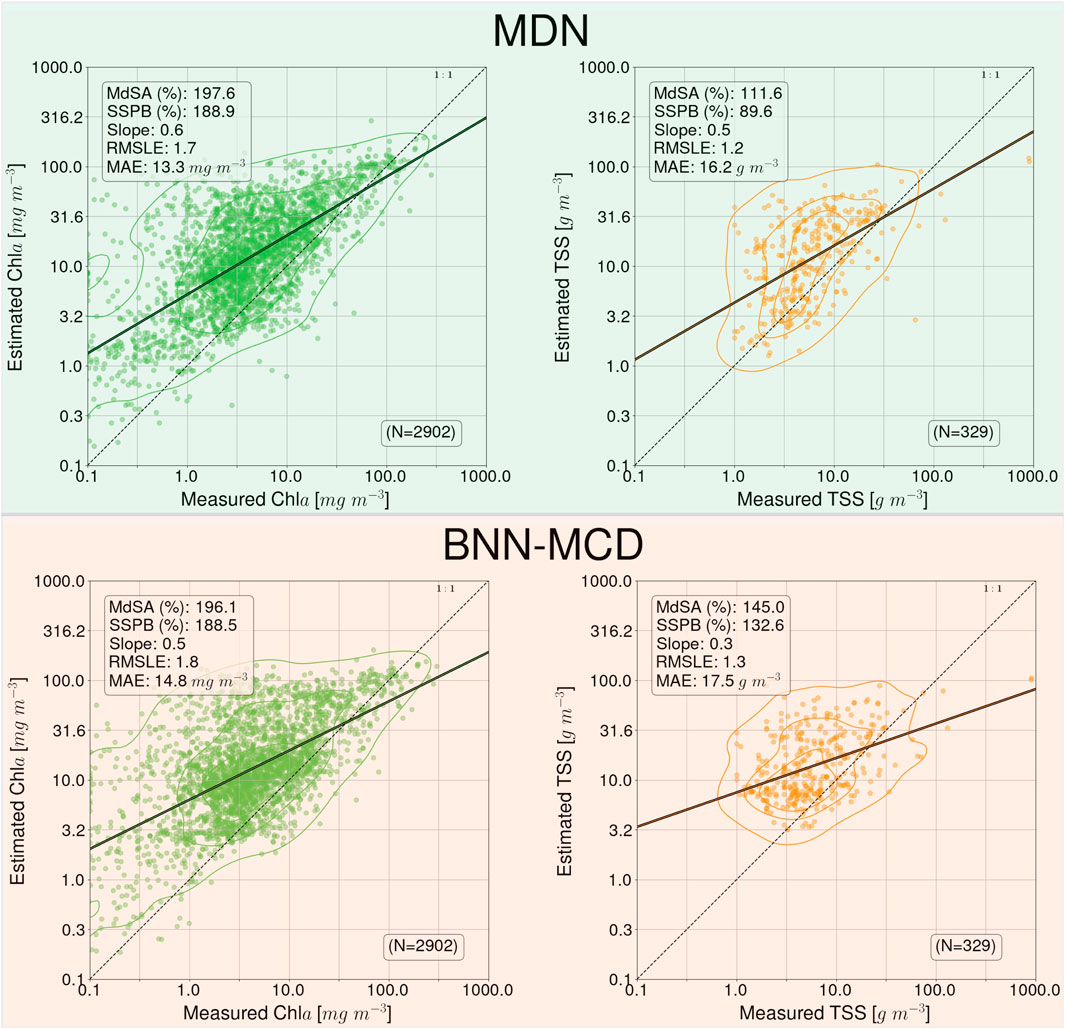
Figure 5. Performance of the MDN and BNN-MCD models for WQI estimation on the ACOLITE corrected MSI matchup dataset.
4.5 Prediction performance on satellite data
This section displays some maps generated by the two models for different satellite datacubes across different missions, at varying spectral resolutions. In particular, WQI and associated uncertainty maps for different multispectral and hyperspectral sensors over the Chesapeake Bay are shown in Figures 6–8. There is general agreement between the spatial trends of WQIs predicted by the two models. Figure 6 shows that the MSI-derived maps from the two models are quite similar for all three parameters, although localized differences in the spatial distributions and magnitudes are occasionally observed. The MDN uncertainty maps seem more uniform, with the BNN-MCD uncertainty exhibiting more spatial variation (note that, in general, the BNN-MCD uncertainty maps capture a broader dynamic range relative to the MDN). In Figure 7, we note some differences, while the spatial trends (i.e., regions with high and low values) are quite similar for the parameters predicted by the two algorithms, there are some differences, with the MDN predictions being slightly lower for Chla and slightly higher for TSS and acdom (440) relative to the BNN-MCD predictions. The uncertainty maps for the OLCI cube in Figure 7 also display clearly different trends, indicating that the models are not in concert, as was seen for the MSI images (shown in Figure 6). For the HICO maps of the Chesapeake Bay (shown in Figure 8), there is a clear agreement between the models in the main stem of the bay, however, in the coastal shelves (at the bottom of the image) there are clear disagreements on the predicted values, with BNN-MCD returning high TSS and acdom (440) in comparison to those from MDN. These pixels also suffer from high uncertainty (especially for the MDN), indicating rather low confidence in these predictions. The highly elevated uncertainties likely indicate high uncertainties in Rrs products. The HICO acquisition of Lake Erie (see Figure 9) again shows general agreements in terms of predicted parameter values with localized differences in uncertainties. That said, MDN estimates of Chla are generally higher than those of BNN-MCD while its acdom (440) predictions are lower. The PRISMA maps of Lake Trasimeno (see Figure 10) for both algorithms continue to show the same general trends, without significant discrepancies in their spatial variability.
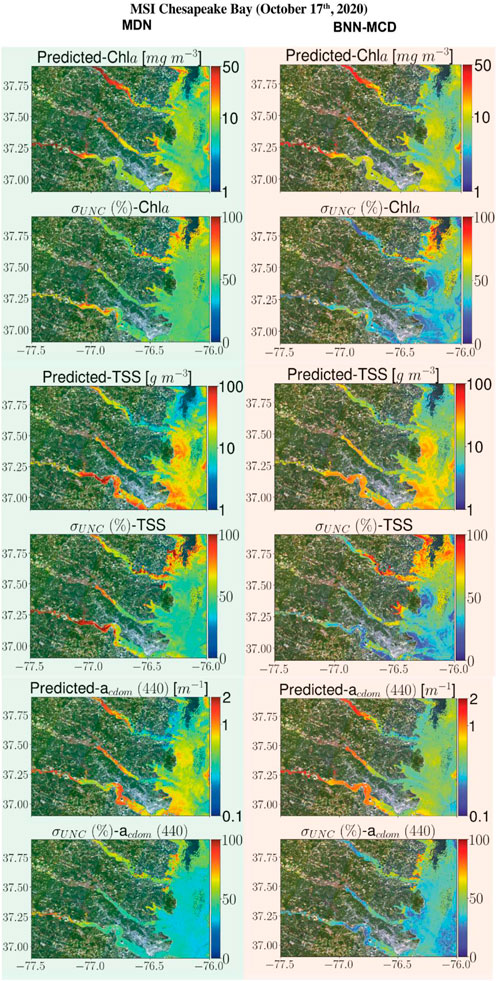
Figure 6. Comparing the MDN (on the left) and BNN-MCD (on the right) estimated parameters and uncertainty for the MSI acquisition of Chesapeake Bay.
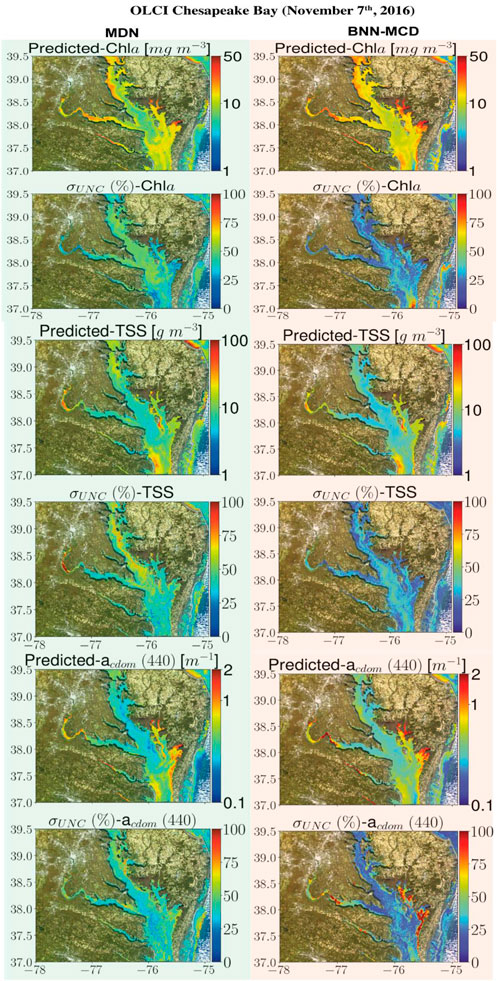
Figure 7. Comparing the MDN (on the left) and BNN-MCD (on right) estimated parameters and uncertainty for the OLCI acquisition of Chesapeake Bay.

Figure 8. Comparing the MDN (on the left) and BNN-MCD (on right) estimated parameters and uncertainty for the HICO acquisition of Chesapeake Bay.
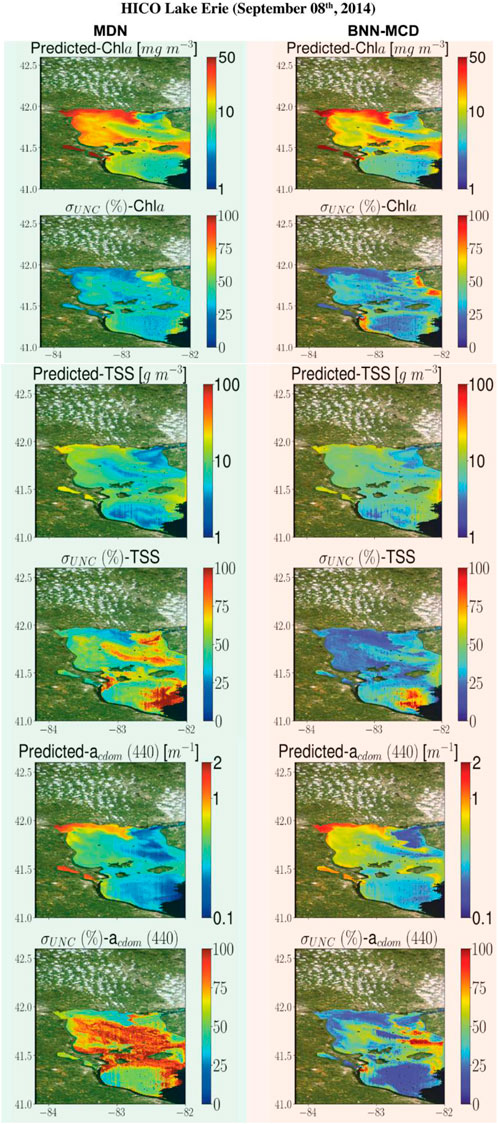
Figure 9. Comparing the MDN (on the left) and BNN-MCD (on right) estimated parameters and uncertainty for the HICO acquisition of Lake Erie.
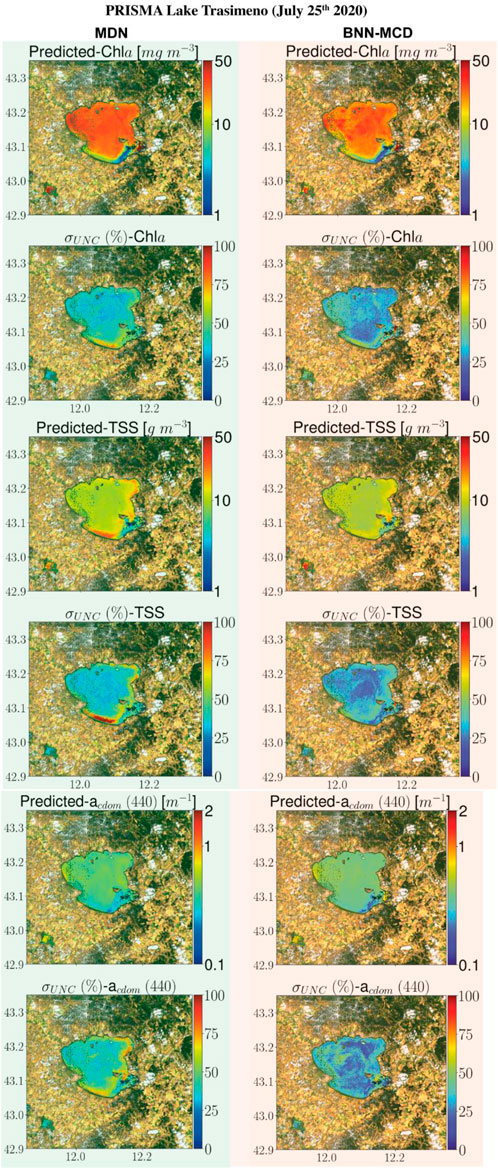
Figure 10. Comparing MDN (on the left) and BNN-MCD (on right) estimated parameters and uncertainty for the PRISMA acquisition of Lake Trasimeno.
5 Discussion
5.1 WQI estimation from spectral samples
Across the different experiments performed in this manuscript it appears that the two probabilistic neural network models have very similar performances in terms of the WQI estimation. On the held-out test dataset the residuals of the two algorithms are very similar across the different sensors and WQIs (see Section 5.1; Table 3 for full results). On the held-out test set the MDN performs better for outlier insensitive
While the performance of these models is quite impressive when applied to in situ data (even the left-out samples), the performance does not hold up when these models are applied to the satellite matchup datasets. Possible causes for such deterioration could be the imperfect atmospheric correction manifest in satellite-derived Rrs in the form of overcorrection or under-correction of aerosol and water-surface contributions by the atmospheric correction processor. It is also possible the satellite sensors have lower SNR relative to the dedicated sensors used for acquiring the in situ
5.2 Model specific uncertainty estimate
In terms of uncertainty estimation, the main takeaway is that there are fundamental differences in the average uncertainty score per prediction, the MDN is has high uncertainties in the range of around 50% of the predicted value per sample on the held-out test set, while the BNN-MCD appears more confident and shows uncertainties in the range of ∼22% of the predicted value per sample on the held-out test set. While the sharpness estimates (as shown by the BNN-MCD) is preferable, it should be noted that MDN uncertainty is an upper bound on the prediction residual for a much larger fraction of the held-out test set samples (
Similar results are also seen for the raw uncertainty numbers of the LOO experiments, i.e., the BNN-MCD results have a higher sharpness relative to the MDN across all the left-out test sets. The inability of these probabilistic models to generalize to these left-out datasets in terms of predictive performance is also echoed by increases in uncertainty relative to the values seen in the held-out datasets for both probabilistic models. This is encouraging as it indicates that the uncertainty metric can flag the conditions where higher residuals are present. Another observation is that the overall uncertainty (in the form of
One such dataset, is the dataset containing samples over Italian waters (Dataset ID: six in Table 2), wherein models face significant issues, and despite poor estimation performance, both models estimate rather low uncertainty for samples in this dataset. Perhaps, some of these issues could be traced back to possible differences in the data acquisition for the samples in this dataset. There are also other examples wherein the models suffer from high errors with disproportionately low uncertainty, but these apply to specific parameters, such as Dataset ID: 18 for Chla estimation, and Dataset ID: 12 for
The regularization enabled by simultaneous estimation also has a pronounced impact on the uncertainties. For both models, the concurrent models show significant improvements in the coverage factor
The general trend of the MDN poorer average sharpness
5.3 WQI and uncertainty maps on satellite image datasets
The WQI maps (Figures 6–10) offered a qualitative perspective on the sensitivity of the models to uncertainties in input Rrs maps and enabled underscoring similarities and discrepancies for different satellite sensors with varying spectral capabilities. Although similarities exist among the map product estimates, disagreements can be found across the maps. For instance, MDN-derived acdom (440) in MSI maps exhibit larger values than those of BNN-MCD on the west stem of the Chesapeake Bay and its tributaries, although the corresponding TSS and Chla maps are generally on par. The largest differences are observed in HICO-derived maps (Figure 8), where BNN-MCD returns higher constituent concentrations and organic content along the main stem of and outside the Chesapeake Bay. Without in situ data sets, it is difficult to offer any insights into the relative accuracy of these products; nonetheless, these product estimates provide evidence of major discrepancies in models’ performance in practical applications, as shown in Figure 5. These observations support the need for comprehensive assessments of future models in real-world applications.
The relative performance of models in uncertainty estimation is generally aligned well with our held-out or LOO analyses (Section. 4.1, 4.2). Of note is that similar to the matchup analyses in Figure 5, pixel uncertainties are >50% (MDN) and >25% (BNN-MCD) for most maps, which is consistent with our observations on the level of uncertainty in the MSI matchup data (Table 7). There are, however, exceptions to this statement where BNN-MCD outputs larger uncertainties at local scales (see MSI and HICO uncertainty maps of Chla in Figures 6, 9). Overall, for reliable use of uncertainty estimates, the most critical aspect of uncertainty estimates is consistency in time and space, an exercise that can be examined in the future.
6 Conclusion
This manuscript provides the first comprehensive comparison of the two state-of-the-art ML algorithms, the MDN and the BNN-MCD, similarly trained, tested, and deployed for data from multiple satellite missions. Model performance was analyzed in terms of both WQI estimates and estimates of associated model-specific uncertainties. The algorithms were tested under similar conditions, such as training data distributions, model architecture, comparison metrics, using various methods, including testing on held-out test sets, tests under a LOO scheme. Overall, we observe that the performance of the two probabilistic neural networks is quite similar across many experiments, such as prediction residuals on the 50:50 held-out test set (∼30–35% for Chla, 45%–50% for TSS, and 40%–45% for acdom (440)), and the leave-one-out type experiments (∼40–45% for Chla, 55%–60% for TSS, and 40%–50% for acdom (440)). The MDN predictions appear to fit the bulk of the samples well with some outliers, whereas the BNN-MCD predictions have fewer outliers and fit global distribution better. In terms of model-specific uncertainty, the MDN generates higher uncertainties, in general, ∼50% of the predicted values for in situ samples, while the BNN-MCD uncertainties are closer to ∼20–25% of the predicted values. That said, the MDN uncertainty provides better coverage of the error with coverage factors of ∼65–75%, while the corresponding coverage of the BNN-MCD is ∼50%. The LOO experiments also show that for left-out datasets, the ranks of prediction errors and uncertainties are quite comparable (generally between 5-6 ranks of each other). Overall, it appears that these model-specific uncertainty metrics, while capable of flagging/identifying test samples with higher relative residuals, the exact uncertainty values are heavily dependent on model properties, and significant work still needs to be done to calibrate/scale these metrics into easily interpretable quantities of for (e.g., expected prediction residuals) human interpretation.
Another, important contribution of this manuscript is the validation of effect of simultaneous estimation on the performance of these machine learning models. For this purpose, the BNN-MCD was also extended into the simultaneous estimation paradigm, and both models were tested in this scheme against a dedicated single-parameter (Chla) estimator. It is noted that the simultaneous WQI retrieval outperforms individual retrieval and displays improvements across most of the regression residuals considered in this project. Additionally, while the uncertainty metrics do not appear to show massive changes in the average sharpness there are clear improvements in the coverage of the estimated uncertainty values. Both models were also tested on the satellite matchup datasets to provide some insight into the performance when these models were applied to satellite-derived
Future research should aim to broaden the comparison between MDNs and BNN-MCDs by introducing other probabilistic modeling techniques. This expansion will provide more nuanced insights into the interplay between training data and model type. Additionally, recalibration techniques like Platt scaling (Platt, 1999) or Isotonic regression (Barlow and Brunk, 1972) can be employed to refine the model-specific uncertainty estimates, potentially mitigating some of the limitations identified in this study concerning predictive uncertainty. A further promising avenue is to employ labeled samples to devise a mapping between estimated uncertainties and actual predictive errors. Another important avenue of research in the uncertainty estimation would be the combination of the different data and physical sources along with ML-model based uncertainty to get a comprehensive metric for the expected residual in the final prediction/estimate. For this purpose, we are considering the use Monte Carlo (MC) sampling-based techniques (Kroese et al., 2013) that can be used to propagate uncertainties from different operations like atmospheric correction, elimination of adjacency effects, down to downstream products like WQI estimates (Zhang, 2021).
Data availability statement
Publicly available datasets were analyzed in this study. The GLORIA dataset can be found here: https://doi.pangaea.de/10.1594/PANGAEA.948492.
Author contributions
AS: Data Curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft, Writing–review and editing, MW: Formal Analysis, Methodology, Investigation, Writing–original draft, Writing–review and editing. SB: Data Curation, Methodology, Writing–review and editing. DO: Supervision, Funding Acquisition, Resources, Writing–review and editing. NP: Conceptualization, Supervision, Funding Acquisition, Resources, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the National Aeronautics and Space Administration (NASA) Research Opportunities in Space and Earth Sensing (ROSES) under grants 80NSSC20M0235 and 80NSSC21K0499 associated with the Phytoplankton, Aerosol, Cloud, Ocean Ecosystem (PACE) Science and Applications Team and the Ocean Biology and Biogeochemistry (OBB) program, respectively. This work was also supported by the Swiss National Science Foundation scientific exchange grant number IZSEZ0_217542 and grant Lake3P number 204783. PRISMA 953 Products© of the Italian Space Agency (ASI) used in the experiments was delivered under an ASI License to use.
Acknowledgments
We also acknowledge the public in situ databases as part of NOAA’s Great Lakes monitoring program, the Chesapeake Bay Program, and their 946 partners.
Conflict of interest
Authors AS and NP were employed by Science Systems and Applications, Inc.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsen.2024.1383147/full#supplementary-material
Footnotes
1https://www.canada.ca/en/environment-climate-change/services/freshwater-quality-monitoring/online-data.htm
2https://www.waterqualitydata.us
3https://nwis.waterdata.usgs.gov/nwis
References
Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Craig, C., et al. (2016). Tensorflow: large-scale machine learning on heterogeneous distributed systems. arXiv Preprint arXiv:1603.04467.
Balasubramanian, S. V., Pahlevan, N., Smith, B., Binding, C., Schalles, J., Loisel, H., et al. (2020). Robust algorithm for estimating total suspended solids (TSS) in inland and nearshore coastal waters. Remote Sens. Environ. 246, 111768. doi:10.1016/j.rse.2020.111768
Barlow, R. E., and Brunk, H. D. (1972). The isotonic regression problem and its dual. J. Am. Stat. Assoc. 67 (337), p140–p147. doi:10.2307/2284712
Bresciani, M., Giardino, C., Fabbretto, A., Pellegrino, A., Mangano, S., Free, G., et al. (2022). Application of new hyperspectral sensors in the remote sensing of aquatic ecosystem health: exploiting PRISMA and DESIS for four Italian lakes. Resources 11 (2), 8. doi:10.3390/resources11020008
Busetto, L., and Ranghetti, L. (2021). Prismaread: a tool for facilitating access and analysis of PRISMA L1/L2 hyperspectral imagery V1. 0.0. 2020. Available Online: Lbusett. Github. Io/Prismaread/.
Candela, L., Formaro, R., Guarini, R., Loizzo, R., Longo, F., and Varacalli, G. (2016). “The PRISMA mission,” in 2016 IEEE international geoscience and remote sensing symposium (IGARSS) (IEEE), 253–256.
Cao, Z., Ma, R., Duan, H., Pahlevan, N., Melack, J., Shen, M., et al. (2020). A machine learning approach to estimate chlorophyll-a from landsat-8 measurements in inland lakes. Remote Sens. Environ. 248, 111974. doi:10.1016/j.rse.2020.111974
Castagna, A., and Vanhellemont, Q. (2022). Sensor-agnostic adjacency correction in the frequency domain: application to retrieve water-leaving radiance from small lakes. doi:10.13140/RG.2.2.35743.02723
Choi, S., Lee, K., Lim, S., and Oh, S. (2018). “Uncertainty-aware learning from demonstration using mixture density networks with sampling-free variance modeling,” in 2018 IEEE international conference on robotics and automation (ICRA) (IEEE), 6915–6922.
Defoin-Platel, M., and Chami, M. (2007). How ambiguous is the inverse problem of ocean color in coastal waters? J. Geophys. Res. Oceans 112 (C3). doi:10.1029/2006jc003847
Drusch, M., Bello, U. D., Carlier, S., Colin, O., Fernandez, V., Gascon, F., et al. (2012). Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 120, 25–36. doi:10.1016/j.rse.2011.11.026
Gilerson, A., Herrera-Estrella, E., Foster, R., Agagliate, J., Hu, C., Ibrahim, A., et al. (2022). Determining the primary sources of uncertainty in retrieval of marine remote sensing reflectance from satellite ocean color sensors. Front. Remote Sens. 3, 857530. doi:10.3389/frsen.2022.857530
Gilerson, A. A., Gitelson, A. A., Zhou, J., Gurlin, D., Moses, W., Ioannou, I., et al. (2010). Algorithms for remote estimation of chlorophyll-a in coastal and inland waters using red and near infrared bands. Opt. Express 18 (23), 24109–24125. doi:10.1364/oe.18.024109
Gitelson, A. A., Schalles, J. F., and Hladik, C. M. (2007). Remote chlorophyll-a retrieval in turbid, productive estuaries: Chesapeake Bay case study. Remote Sens. Environ. 109 (4), p464–p472. doi:10.1016/j.rse.2007.01.016
Gons, H. J., Rijkeboer, M., and Ruddick, K. G. (2002). A chlorophyll-retrieval algorithm for satellite imagery (medium resolution imaging spectrometer) of inland and coastal waters. J. Plankton Res. 24 (9), 947–951. doi:10.1093/plankt/24.9.947
IOCCG (2018). Earth observations in support of global water quality monitoring. Editors S. Greb, A. Dekker, and C. Binding (Dartmouth, NS, Canada: International Ocean-Colour Coordinating Group (IOCCG)), –125pp. (Reports of the International Ocean-Colour Coordinating Group, No. 17). doi:10.25607/OBP-113
Gross, L., Thiria, S., Frouin, R., and Mitchell, B. G. (2000). Artificial neural networks for modeling the transfer function between marine reflectance and phytoplankton pigment concentration. J. Geophys. Res. Oceans 105 (C2), 3483–3495. doi:10.1029/1999jc900278
Ibrahim, A., Franz, B., Ahmad, Z., Healy, R., Knobelspiesse, K., Gao, B.-C., et al. (2018). Atmospheric correction for hyperspectral ocean color retrieval with application to the hyperspectral imager for the Coastal Ocean (HICO). Remote Sens. Environ. 204, 60–75. doi:10.1016/j.rse.2017.10.041
Ioannou, I., Gilerson, A., Gross, B., Moshary, F., and Ahmed, S. (2011). Neural network approach to retrieve the inherent optical properties of the Ocean from observations of MODIS. Appl. Opt. 50 (19), 3168–3186. doi:10.1364/ao.50.003168
IOCCG (2000). “Remote sensing of Ocean Colour in coastal, and other optically-complex, waters,” in International Ocean Colour coordinating group: dartmouth, Canada.
IOCCG (2010). “Atmospheric correction for remotely-sensed ocean-colour products,” in IOCCG reports series, international Ocean Colour coordinating group: dartmouth, Canada.
IOCCG (2019). “Uncertainties in Ocean Colour remote sensing,” in International Ocean Colour coordinating group. Editor F. Mélin (Canada: Dartmouth).
Jackson, T., Sathyendranath, S., and Mélin, F. (2017). An improved optical classification scheme for the Ocean Colour Essential Climate Variable and its applications. Remote Sens. Environ. 203, 152–161. doi:10.1016/j.rse.2017.03.036
Jamet, C., Loisel, H., and Dessailly, D. (2012). Retrieval of the spectral diffuse attenuation coefficientK<i>d</i>(λ) in open and coastal ocean waters using a neural network inversion. J. Geophys. Res. Oceans 117 (C10). doi:10.1029/2012jc008076
Kajiyama, T., D’Alimonte, D., and Zibordi, G. (2018). Algorithms merging for the determination of Chlorophyll-${a}$ concentration in the black sea. IEEE Geoscience Remote Sens. Lett. 16 (5), 677–681. doi:10.1109/lgrs.2018.2883539
Kroese, D. P., Taimre, T., and Botev, Z. I. (2013). Handbook of Monte Carlo methods. John Wiley and Sons.
Kwiatkowska, E. J., and Fargion, G. S. (2003). Application of machine-learning techniques toward the creation of a consistent and calibrated global chlorophyll concentration baseline dataset using remotely sensed ocean color data. IEEE Trans. Geoscience Remote Sens. 41 (12), 2844–2860. doi:10.1109/tgrs.2003.818016
Lee, Z., and Carder, K. L. (2002). Effect of spectral band numbers on the retrieval of water column and bottom properties from ocean color data. Appl. Opt. 41 (12), 2191–2201. doi:10.1364/ao.41.002191
Lehmann, M. K., Gurlin, D., Pahlevan, N., Alikas, K., Anstee, J., Balasubramanian, S. V., et al. (2023). Gloria - a globally representative hyperspectral in situ dataset for optical sensing of water quality. Scientific Data in press.
Liu, X., Steele, C., Simis, S., Warren, M., Tyler, A., Spyrakos, E., et al. (2021). Retrieval of Chlorophyll-a concentration and associated product uncertainty in optically diverse lakes and reservoirs. Remote Sens. Environ. 267, 112710. doi:10.1016/j.rse.2021.112710
Lucke, R. L., Corson, M., McGlothlin, N. R., Butcher, S. D., Wood, D. L., Korwan, D. R., et al. (2011). Hyperspectral imager for the Coastal Ocean: instrument description and first images. Appl. Opt. 50 (11), 1501–1516. doi:10.1364/ao.50.001501
Ludovisi, A., and Gaino, E. (2010). Meteorological and water quality changes in Lake Trasimeno (umbria, Italy) during the last fifty years. J. Limnol. 69 (1), 174. doi:10.4081/jlimnol.2010.174
Maritorena, S., Siegel, D. A., and Peterson, A. R. (2002). Optimization of a semianalytical ocean color model for global-scale applications. Appl. Opt. 41 (15), 2705–2714. doi:10.1364/ao.41.002705
Michalak, A. M. (2016). Study role of climate change in extreme threats to water quality. Nature 535 (7612), 349–350. doi:10.1038/535349a
Mittenzwey, K.-H., Ullrich, S., Gitelson, A. A., and Kondratiev, K. Y. (1992). Determination of chlorophyll a of inland waters on the basis of spectral reflectance. Limnol. Oceanogr. 37 (1), 147–149. doi:10.4319/lo.1992.37.1.0147
Mobley, C. D. (1999). Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 38 (36), 7442–7455. doi:10.1364/ao.38.007442
Moore, T. S., Dowell, M. D., Bradt, S., and Ruiz Verdu, A. (2014). An optical water type framework for selecting and blending retrievals from bio-optical algorithms in lakes and coastal waters. Remote Sens. Environ. 143, 97–111. doi:10.1016/j.rse.2013.11.021
Moses, W. J., Sterckx, S., Montes, M. J., De Keukelaere, L., and Knaeps, E. (2017). Atmospheric correction for inland waters, in bio-optical modeling and remote sensing of inland waters. Elsevier, 69–100.
Neil, C., Spyrakos, E., Hunter, P. D., and Tyler, A. N. (2019). A global approach for chlorophyll-a retrieval across optically complex inland waters based on optical water types. Remote Sens. Environ. 229, 159–178. doi:10.1016/j.rse.2019.04.027
Nieke, J., Mavrocordatos, C., Craig, D., Berruti, B., Garnier, T., Riti, J.-B., et al. (2015). “Ocean and Land color imager on sentinel-3,” in Optical payloads for space missions (Chichester, UK: John Wiley and Sons, Ltd), 223–245.
Odermatt, D., Kiselev, S., Heege, T., Kneubühler, M., and Itten, K. (2008). “Adjacency effect considerations and air/water constituent retrieval for Lake Constance,” in 2nd MERIS/AATSR workshop. Frascati, Italy. University of Zurich, 1–8. 22 September 2008 - 26 September 2008.
O’Reilly, J. E., Maritorena, S., Mitchell, B. G., Siegel, D. A., Carder, K. L., Garver, S. A., et al. (1998). Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. Oceans 103 (C11), 24937–24953. doi:10.1029/98jc02160
Pahlevan, N., Mangin, A., Balasubramanian, S. V., Smith, B., Alikas, K., Arai, K., et al. (2021a). ACIX-aqua: a global assessment of atmospheric correction methods for landsat-8 and sentinel-2 over lakes, rivers, and coastal waters. Remote Sens. Environ. 258, 112366. doi:10.1016/j.rse.2021.112366
Pahlevan, N., Smith, B., Alikas, K., Anstee, J., Barbosa, C., Binding, C., et al. (2022). Simultaneous retrieval of selected optical water quality indicators from landsat-8, sentinel-2, and sentinel-3. Remote Sens. Environ. 270, 112860. doi:10.1016/j.rse.2021.112860
Pahlevan, N., Smith, B., Binding, C., Gurlin, D., Lin, Li, Bresciani, M., et al. (2021b). Hyperspectral retrievals of phytoplankton absorption and chlorophyll-a in inland and nearshore coastal waters. Remote Sens. Environ. 253, 112200. doi:10.1016/j.rse.2020.112200
Pahlevan, N., Smith, B., Schalles, J., Binding, C., Cao, Z., Ma, R., et al. (2020). Seamless retrievals of chlorophyll-a from sentinel-2 (MSI) and sentinel-3 (OLCI) in inland and coastal waters: a machine-learning approach. Remote Sens. Environ. 240, 111604. doi:10.1016/j.rse.2019.111604
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830.
Platt, J. (1999). Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Adv. large margin Classif. 10 (3), 61–74.
Reynolds, N., Blake, A. S., Guertault, L., and Nelson, N. G. (2023). Satellite and in situ cyanobacteria monitoring: understanding the impact of monitoring frequency on management decisions. J. Hydrology 619, 129278. doi:10.1016/j.jhydrol.2023.129278
Richter, R., and Schläpfer, D. (2002). Geo-atmospheric processing of airborne imaging spectrometry data. Part 2: atmospheric/topographic correction. Int. J. Remote Sens. 23 (13), 2631–2649. doi:10.1080/01431160110115834
Sanders, L. C., Schott, J. R., and Raqueño, R. (2001). A VNIR/SWIR atmospheric correction algorithm for hyperspectral imagery with adjacency effect. Remote Sens. Environ. 78 (3), 252–263. doi:10.1016/s0034-4257(01)00219-x
Saranathan, A. M., Smith, B., and Pahlevan, N. (2023). Per-pixel uncertainty quantification and reporting for satellite-derived chlorophyll-a estimates via mixture density networks. IEEE Trans. Geoscience Remote Sens. 61, 1–18. doi:10.1109/tgrs.2023.3234465
Schiller, H., and Doerffer, R. (1999). Neural network for emulation of an inverse model operational derivation of case II water properties from MERIS data. Int. J. Remote Sens. 20 (9), 1735–1746. doi:10.1080/014311699212443
Seegers, B. N., Stumpf, R. P., Schaeffer, B. A., Loftin, K. A., and Werdell, P. J. (2018). Performance metrics for the assessment of satellite data products: an ocean color case study. Opt. Express 26 (6), 7404–7422. doi:10.1364/oe.26.007404
Shea, O., Ryan, E., Pahlevan, N., Smith, B., Boss, E., Gurlin, D., et al. (2023). A hyperspectral inversion framework for estimating absorbing inherent optical properties and biogeochemical parameters in inland and coastal waters. Remote Sens. Environ. 295, 113706. doi:10.1016/j.rse.2023.113706
Shea, O., Ryan, E., Pahlevan, N., Smith, B., Bresciani, M., Todd, E., et al. (2021). Advancing cyanobacteria biomass estimation from hyperspectral observations: demonstrations with HICO and PRISMA imagery. Remote Sens. Environ. 266, 112693. doi:10.1016/j.rse.2021.112693
Siegel, D. A., Behrenfeld, M. J., Maritorena, S., McClain, C. R., Antoine, D., Bailey, S. W., et al. (2013). Regional to global assessments of phytoplankton dynamics from the SeaWiFS mission. Remote Sens. Environ. 135, 77–91. doi:10.1016/j.rse.2013.03.025
Smith, B., Pahlevan, N., Schalles, J., Ruberg, S., Errera, R., Ma, R., et al. (2021). A chlorophyll-a algorithm for landsat-8 based on mixture density networks. Front. Remote Sens. 1, 623678. doi:10.3389/frsen.2020.623678
Spyrakos, E., O'donnell, R., Hunter, P. D., Miller, C., Scott, M., Simis, S. G. H., et al. (2018). Optical types of inland and coastal waters. Limnol. Oceanogr. 63 (2), 846–870. doi:10.1002/lno.10674
Sydor, M., Gould, R. W., Arnone, R. A., Haltrin, V. I., and Goode, W. (2004). Uniqueness in remote sensing of the inherent optical properties of ocean water. Appl. Opt. 43 (10), 2156–2162. doi:10.1364/ao.43.002156
Troyanskaya, O., Cantor, M., Sherlock, G., Brown, P., Hastie, T., Tibshirani, R., et al. (2001). Missing value estimation methods for DNA microarrays. Bioinformatics 17 (6), 520–525. doi:10.1093/bioinformatics/17.6.520
Vanhellemont, Q., and Ruddick, K. (2021). Atmospheric correction of sentinel-3/OLCI data for mapping of suspended particulate matter and chlorophyll-a concentration in Belgian turbid coastal waters. Remote Sens. Environ. 256, 112284. doi:10.1016/j.rse.2021.112284
Vilas, L. G., Spyrakos, E., and Palenzuela, J. M. T. (2011). Neural network estimation of chlorophyll a from MERIS full resolution data for the coastal waters of Galician rias (NW Spain). Remote Sens. Environ. 115 (2), 524–535. doi:10.1016/j.rse.2010.09.021
Wang, M., and Gordon, H. R. (1994). Radiance reflected from the Ocean–atmosphere System: synthesis from individual components of the aerosol size distribution. Appl. Opt. 33 (30), 7088–7095. doi:10.1364/ao.33.007088
Warren, M. A., Simis, S. G. H., Martinez-Vicente, V., Poser, K., Bresciani, M., Alikas, K., et al. (2019). Assessment of atmospheric correction algorithms for the sentinel-2A MultiSpectral imager over coastal and inland waters. Remote Sens. Environ. 225, 267–289. doi:10.1016/j.rse.2019.03.018
Werdell, J. P., and Bailey, S. (2005). An improved in-situ bio-optical data set for ocean color algorithm development and satellite data product validation. Remote Sens. Environ. 98 (1), 122–140. doi:10.1016/j.rse.2005.07.001
Werther, M., and Burggraaff, O. (2023). Dive into the unknown: embracing uncertainty to advance aquatic remote sensing. J. Remote Sens. 3. doi:10.34133/remotesensing.0070
Werther, M., Odermatt, D., Simis, S. G. H., Gurlin, D., Lehmann, M. K., Kutser, T., et al. (2022). A bayesian approach for remote sensing of chlorophyll-a and associated retrieval uncertainty in oligotrophic and mesotrophic lakes. Remote Sens. Environ. 283, 113295. doi:10.1016/j.rse.2022.113295
Keywords: water quality indicators (WQIs), optical remote sensing, advanced neural networks, uncertainty estimation, multispectral and hyperspectral sensors
Citation: Saranathan AM, Werther M, Balasubramanian SV, Odermatt D and Pahlevan N (2024) Assessment of advanced neural networks for the dual estimation of water quality indicators and their uncertainties. Front. Remote Sens. 5:1383147. doi: 10.3389/frsen.2024.1383147
Received: 06 February 2024; Accepted: 10 June 2024;
Published: 18 July 2024.
Edited by:
Evangelos Spyrakos, University of Stirling, United KingdomReviewed by:
Md Mamun, Southern Methodist University, United StatesElizabeth C. Atwood, Plymouth Marine Laboratory, United Kingdom
Copyright © 2024 Saranathan, Werther, Balasubramanian, Odermatt and Pahlevan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Arun M. Saranathan, YXJ1bi5zYXJhbmF0aGFuQHNzYWlocS5jb20=
 Arun M. Saranathan
Arun M. Saranathan Mortimer Werther
Mortimer Werther Sundarabalan V. Balasubramanian4,5
Sundarabalan V. Balasubramanian4,5 Nima Pahlevan
Nima Pahlevan