- Earth Observation Unit, Magellium Artal Group, Toulouse, France
Above-water radiometry (AWR) methods have been developed to provide “ground-truth” (or fiducial) measurements for calibration and validation of the water color satellite missions. AWR is also an important tool for environmental survey from dedicated field missions. Under clear sky, the critical step of AWR is to retrieve the water-leaving radiance from radiometric measurements of the upward radiance that also includes the reflection of the direct sunlight and diffuse skylight reflected by the wind ruffled water surface toward the sensor. In order to correct for the surface reflection, sky radiance measurements are performed and converted into surface radiance through a factor often called “sea surface reflectance factor” or “effective Fresnel reflectance coefficient”. Based on theoretical and practical considerations, this factor was renamed surface-to-sky radiance ratio,
1 Introduction
Optical remote sensing has become a critical tool to monitor oceanic, coastal or inland aquatic environments and their inherent ecosystems thanks to multispectral or hyperspectral measurements of the water-leaving radiance
For this purpose, field measurements are efficient tools provided that their own data quality is sufficiently high and that their attached uncertainties are metrologically quantified. Two different systems were installed for quality evaluation of the historical “ocean color” satellite sensors (e.g., MERIS, MODIS, SeaWiFS): in-water and above-water radiometric systems (Hooker et al., 2002; Zibordi et al., 2002). Both systems possess their own advantages and weaknesses regarding either the implementation in the field or data processing for retrieval of Lw at the exact water surface level (denoted as 0+). For instance, retrieval of water-leaving radiance from in-water radiometric methods is very sensitive to extrapolation at 0+ from the measured underwater profile of the upward radiance (Antoine et al., 2008; Hooker et al., 2013). It is worth noting that for turbid or highly absorbing waters, potentially encountered in coastal or lake environments, in-water methods are impracticable due to rapid loss of light (signal) with depth (e.g., within the first tens of centimeter). As for above-water system, the main issue is to remove the sun and sky light reflected on the water surface. Those inherent difficulties were in part alleviated by the development of dedicated protocols (Mueller and Austin, 1995; Zibordi et al., 2019).
For operational calibration and validation activities of the in-orbit satellite missions, dense time-series are needed to maximize the number of match-up points between reference field measurements and satellite acquisitions. This necessitates the installation of “unattended” radiometric systems with quasi-continuous acquisitions over time. To this end, the AERONET-OC network has been developed since 2002 to provide Lw time-series for open and coastal waters, as well as inland waters, based on an above-water multispectral system (Zibordi et al., 2009). Recently, this network has been complemented by an hyperspectral setup based on the same above-water radiometry procedures (Goyens et al., 2022). In addition to the fixed platforms equipped by those networks, above-water radiometry methods are also deployed on small to big ships including research vessels (Ondrusek et al., 2022), ferries (Nasiha et al., 2022) or even dugout canoes (Marinho et al., 2021) to enable gathering of large amounts of data to document the optical diversity of aquatic environments and consequently help to improve satellite remote sensing capabilities (Pahlevan et al., 2021).
For satellite validation purposes, fiducial measurements are acquired under clear sky conditions, i.e., in absence of clouds in the vicinity. In this case, the water surface is illuminated by the direct sunlight and the diffuse skylight originating from scattering by molecules and aerosols of the overlying atmosphere. Part of this light enters the water body where the radiation is altered through absorption and scattering caused by the water molecules as well as the presence of dissolved and particulate matter. Thus, as already mentioned, the water-leaving radiance carries useful information to estimate parameters related to the OAWC, such as phytoplankton or sediment concentration proxies, and the in-water light regime (e.g., water transparency). The other part is reflected by the wind ruffled air-water interface contributing to the surface component of the upward radiance. The main principle of above-water radiometry (AWR) relies on a couple of measurements: 1) the total radiance coming from the water body and surface measured with an oblique angle (typically 40°), and 2) downward radiance of the direction that would be specularly reflected by a conceptual flat surface toward the sensor used for 1). The second term is converted into the surface radiance to be removed using a factor that should account for the reflection of the air-water interface considering its roughness properties (Mobley, 1999). This factor is usually defined as “a coefficient that represents the fraction of incident skylight that is reflected back towards the water-viewing sensor at the air-water interface and is the Fresnel reflectance coefficient for a flat water surface”, see (Ruddick et al., 2019) where the authors argue to name this term “effective Fresnel reflectance coefficient”. Note that other terms are also found in the literature with, for instance, sea surface reflectance factor (Mobley, 1999) or radiance reflectance factor (Mobley, 2015).
In general, the water surface is “crinkled” by gusts of wind modifying its roughness and in turn its reflection properties (Preisendorfer and Mobley, 1986). The main consequence is that the surface-reflected skylight toward the water-viewing sensor originates from many parts of the celestial hemisphere. This can be understood as a superposition of Fresnel reflections integrated over all the hemispherical directions implying that the “effective Fresnel reflectance coefficient” is sensitive to 1) the wave distribution, including gravitary and capillary waves (Mobley, 2015), 2) the radiance distribution within the celestial dome (Mobley, 1999), 3) the polarization state of light (Harmel, Gilerson, Tonizzo, et al., 2012). These three points should be accounted for in the computation of the “effective Fresnel reflectance coefficient”. The first tabulated values were calculated based on Monte-Carlo method to the radiative transfer equation under a simplified atmosphere and without accounting for polarization (Mobley, 1999). Further computations included polarization effects but for a pure Rayleigh atmosphere (i.e., no aerosol), (Mobley, 2015). Nevertheless, the two kinds of values were evaluated based on an in situ data set showing no significant impact on the Lw retrievals from an AERONET-OC site (Zibordi, 2016). Other studies provided values considering polarization and impact of a few aerosol types (Zhang et al., 2017; Gilerson et al., 2018). The consideration of both polarization and aerosol optical properties enabled the reproduction of the spectral variation of the sky to surface radiance conversion factor observed from the field (Lee et al., 2010; Lin et al., 2023).
It is proposed in this study to expand those computations for all potential viewing geometries for a comprehensive set of air-water interface roughness properties and aerosol types encompassing realistic models for open ocean, coastal, and inland areas (including polluted areas and desert dust). The effects of water surface and aerosol types are taken into account through full vector radiative transfer computations to provide pre-computed tabulated values. The main terms and equations to achieve such computations are detailed in the next section. A specific attention is paid to the nomenclature of the different terms to exemplify possible accordance between theoretical and applicative notations in used in the field of aquatic remote sensing. The uncertainty attached to unknown or partially known input parameters to the modeled values are computed based on Gaussian error propagation. Finally, recommendations to reduce uncertainty in AWR procedures are given based on separate treatment of the diffuse and direct light components, supplementary atmospheric measurements and adaptable viewing geometries.
2 Material and method
2.1 Theoretical background
2.1.1 Radiance components
Above-water radiometry (AWR) methodology mainly relies on (i) radiance measurements performed with a sensor pointed downward to the water, Lt, (ii) measurements of the sky radiance,
where θs and θv are the sun and viewing zenith angles,
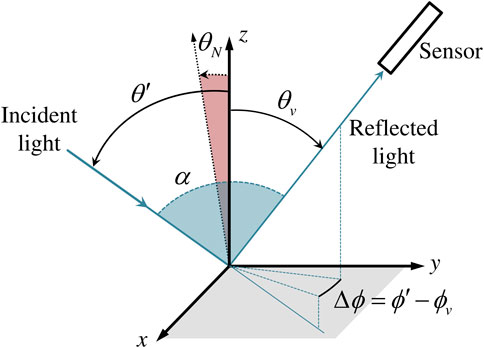
FIGURE 1. Viewing geometry convention:
The first AWR protocols were based on the computation of the Fresnel reflection factor to practically compute the surface radiance Lsurf from the sky radiance
The surface component
The diffuse part is related to radiation that has undergone at least one scattering event. Conversely, the direct component is defined as the part of the sunlight radiation that has undergone reflection onto the water surface but no scattering interaction within the atmosphere. This latter component was first called Kumatage (Spooner, 1822). Thereafter, denominations such as sheen, glint or sparkle were used (Hulburt, 1934) before Cox and Munk popularized the term glitter (Cox and Munk, 1954). In the 1960s, with the first satellite pictures of Applications Technology Satellites 1 and 3 (McClain and Strong, 1969) the term sunglint has been used until today. All those terms were inspired by the very dynamic nature of the sunglint “flashes” that are controlled by the rapidly propagating waves at the water surface. Based on this erratic modulation of the sunglint intensity, protocols were designed to remove the direct component of light from Lt by taking the minimum values over a sequential series of acquisitions (Hooker et al., 2002; Zibordi et al., 2019). Moreover, recent studies investigated and proposed correction schemes for the sunglint component of the measured signal Lt (Groetsch et al., 2017; Goyens and Ruddick, 2023).
Based on those considerations, it is advocated in this study to separate the diffuse and the direct contributions to further the performances of the AWR correction schemes as already advocated in previous studies (Harmel, Gilerson, Hlaing, et al., 2012; Zhang et al., 2017). On the other hand, several names might be found in the literature for
2.1.2 Polarized nature of light
The electromagnetic radiation of light may be fully defined using the Stokes formalism. According to this formalism, four independent terms are grouped within the so-called Stokes vector that can be written using successively the indicial, Stokes (Stokes, 1852), Perrin (Perrin, 1942), and Chandrasekhar (Chandrasekhar, 1947; Chandrasekhar, 1960) nomenclatures:
Here, the indicial notation is preferred to get more compact equations. Using radiance unit, the term
with
with E0 the extraterrestrial solar irradiance. Note that in this formalism, the minus sign before µ indicates downward direction. In Eq. 7, the
Based on those equation, the surface-to-sky radiance ratio,
In Mobley’s calculations (Mobley, 1999; Mobley, 2015), there is no distinction between diffuse and direct light within the Monte-Carlo resolution of the radiative transfer equation done for a pure Rayleigh atmosphere (i.e., no aerosols included). It is easy to show, in this case, that the direct sunglint component contributes to the spectral dependency of
2.1.3 Air-water interface
As seen in Eq. 7, the Stokes vector of the air-water interface stems from the coupling between the sky geometrical distribution of
with
The BRD matrix can be written as:
where
For practical comparison with other studies, the variance of the slope distribution is also given in wind speed unit through the Cox-Munk parameterization, hereafter denoted as equivalent Cox-Munk wind speed:
2.2 Aerosol models
The aerosols in the atmosphere strongly impact the sky radiance distribution and polarization. To encompass the great variety of aerosol contents of the atmosphere, the radiative transfer simulations (i.e., resolution of Eq. 6) were performed based on the Optical Properties of Aerosols and Clouds (OPAC) models (Hess et al., 1998). The OPAC aerosol models were generated based on a mixture of pure components. Those components are representative of the main aerosol properties retrieved at the global scale. One advantage of those models is to consider non-spherical particles and the spectral variation of the complex refractive index (
where
with RH the relative humidity of the atmosphere. Following the same rule of hygroscopic growth, the complex refractive index of the wet aerosols is given by:
where
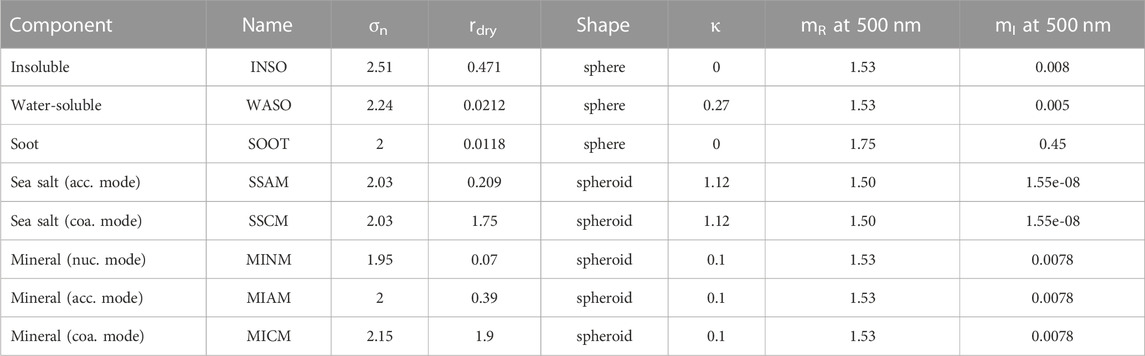
TABLE 2. Description of the microphysical parameters of the OPAC components for aerosol modeling. The refractive index values are given for the dry part. The abbreviations acc., coa. and nuc. stand for accumulation, coarse and nucleation, respectively.
The aerosol components listed above are representative of a single “species” whereas in natural conditions aerosols consist of a mixture of those components. The OPAC model provides typical mixtures of those components that are given in Table 3 for the models used in this study. The following codes were used to generate the scattering matrix with Mie theory for homogeneous sphere (Mishchenko et al., 2000), T-matrix for ellipsoidal/spheroidal particles (Mishchenko et al., 2004), those computations were extended for large particle sizes with the “Improved Geometric Optics Method” (Yang et al., 2007). The computations were performed through the MOPSMAP package (Modeled optical properties of ensembles of aerosol particles) coded in FORTRAN and based on pre-computed look-up tables (Gasteiger and Wiegner, 2018).
2.3 Radiative transfer computation
The diffuse component of the Stokes vectors of the air-water interface,
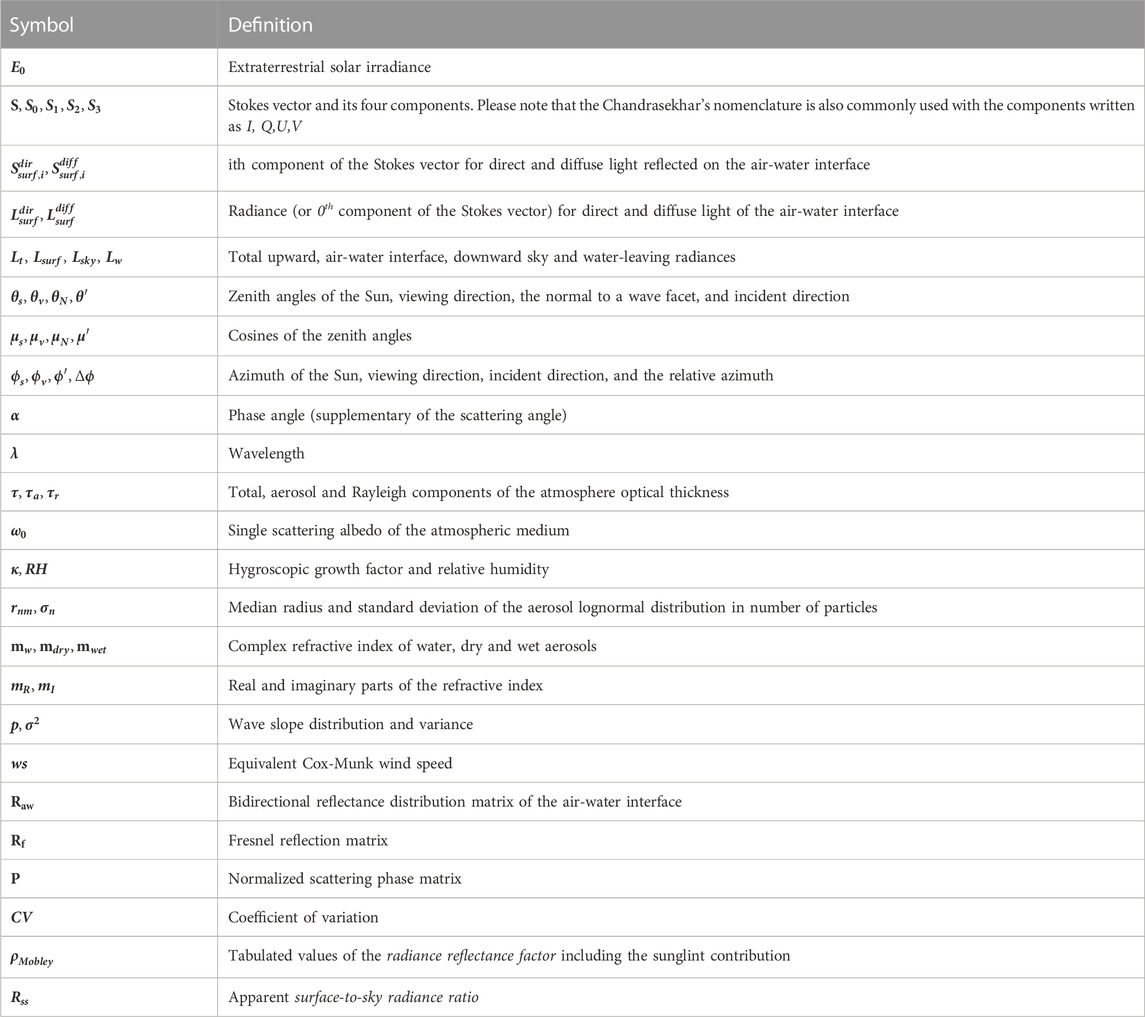
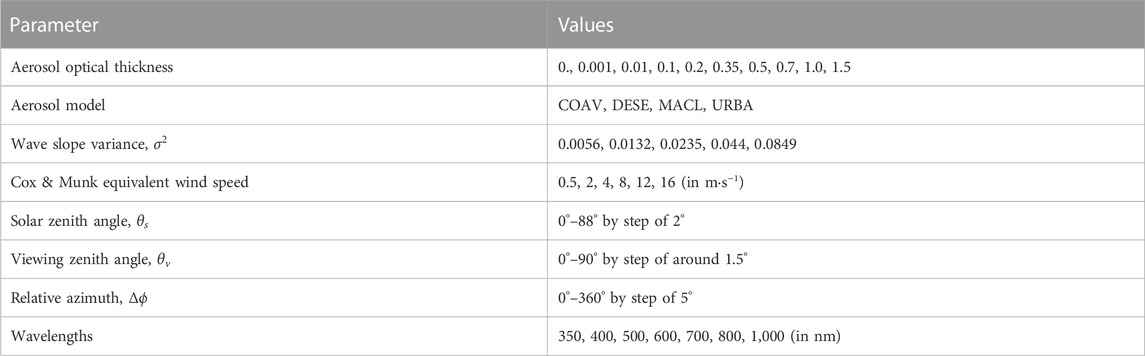
The computations were repeated for a comprehensive series of input parameters which are listed in Table 4. The atmosphere is modeled as a mixture of non-absorbing molecules (i.e., Rayleigh scattering) and aerosols. The Rayleigh optical thickness,
2.4 Uncertainty calculus
The surface-to-sky radiance ratios,
where Nx is the number of input parameters and
Following uncertainty estimation based on large scale comparisons (Harmel and Chami, 2012; Levy et al., 2013), the errors were modeled as linear function as follows:
3 Results
3.1 Rayleigh atmosphere
The surface-to-sky radiance ratio is first shown for a pure Rayleigh atmosphere (i.e., no aerosol). To illustrate the computation the downward (celestial) and upward (surface) radiance distribution are plotted in Figure 2 given in normalized radiance unit (i.e., actual radiance multiplied by
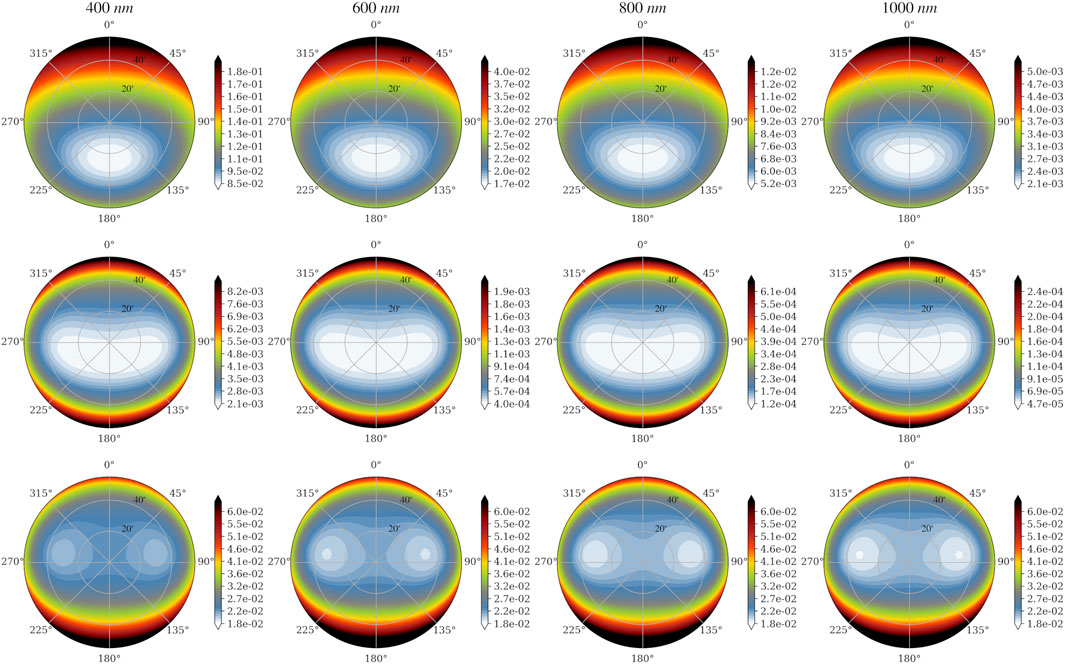
FIGURE 2. Polar view of the downward sky radiance
Beside this spectral dependence,
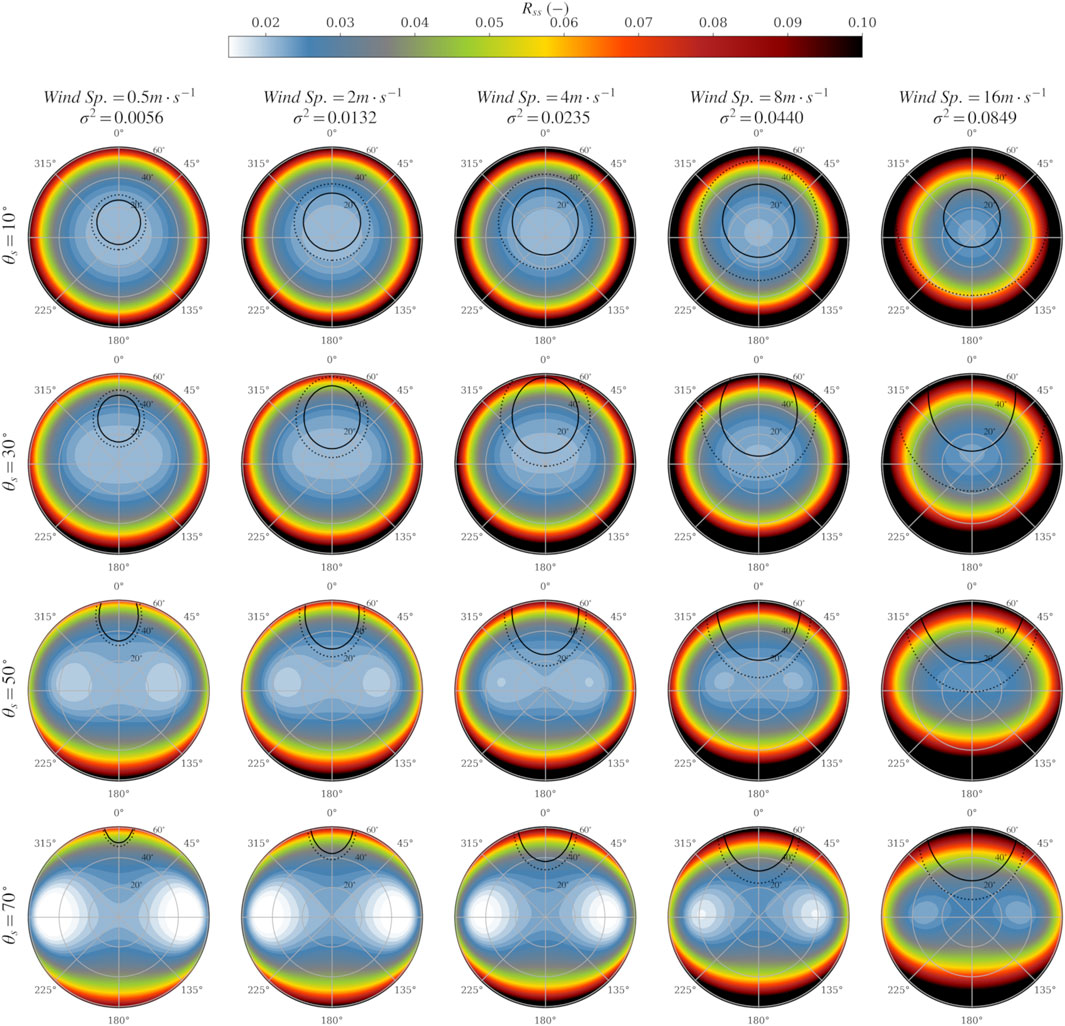
FIGURE 3. Polar diagrams of the surface-to-sky radiance ratios,
Another view of the
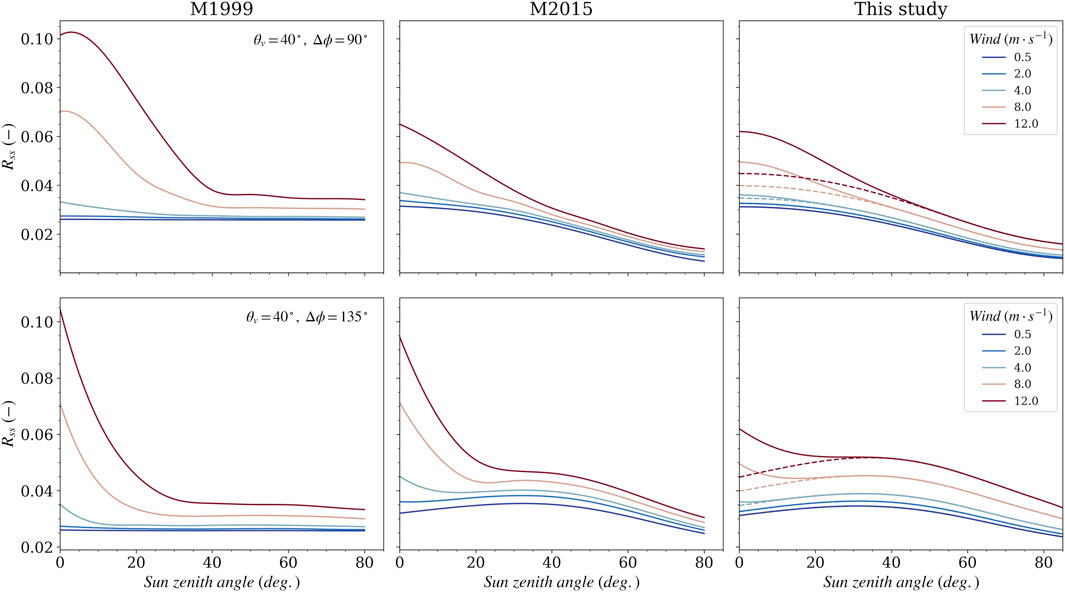
FIGURE 4. Tabulated values of the surface-to-sky ratio computed (first column) without consideration of polarization (Mobley, 1999), (second column) accounting for polarization within a Rayleigh atmosphere (Mobley, 2015) and (third column) this study for pure diffuse light (dashed curves) and with addition of the sunglint component (solid curves). Geometry and equivalent Cox-Munk wind speed are indicated in the insets.
The spectral values of
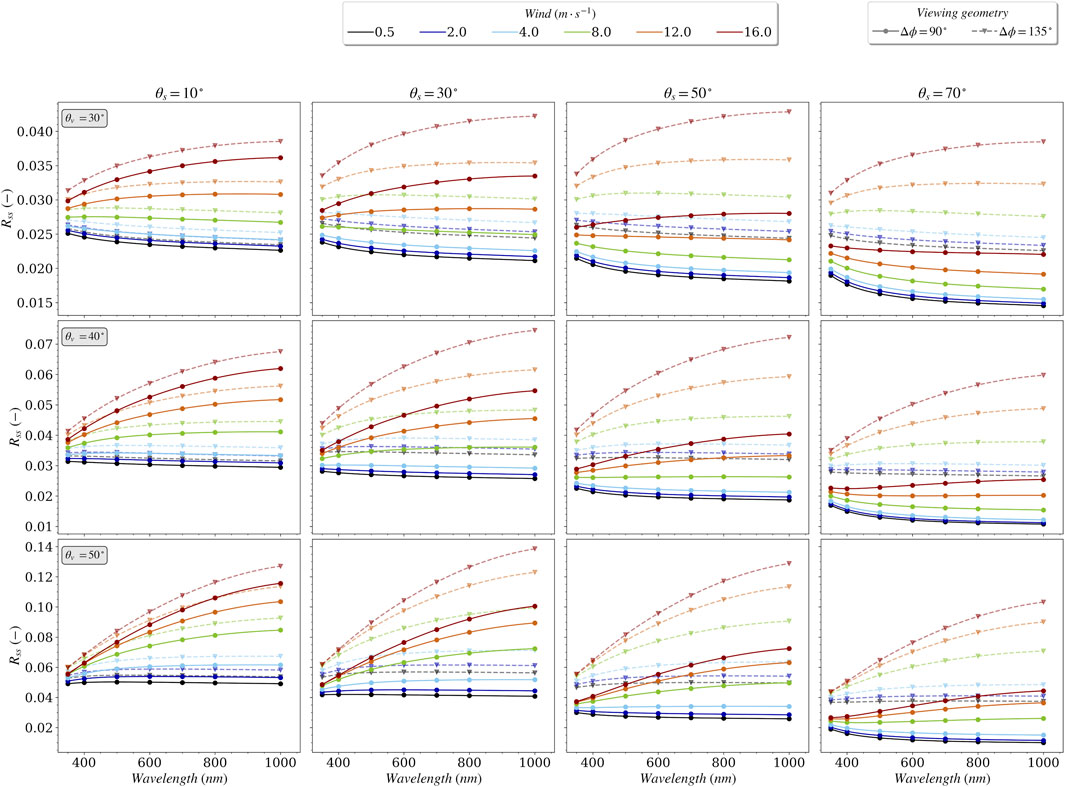
FIGURE 5. Spectral values of the surface-to-sky radiance factor,
3.2 Impact of aerosols
3.2.1 Spectral considerations
The presence of aerosols in the atmosphere modifies the downward radiance distribution but also the state of polarization of the celestial hemisphere. The impact of aerosols on the spectral values of
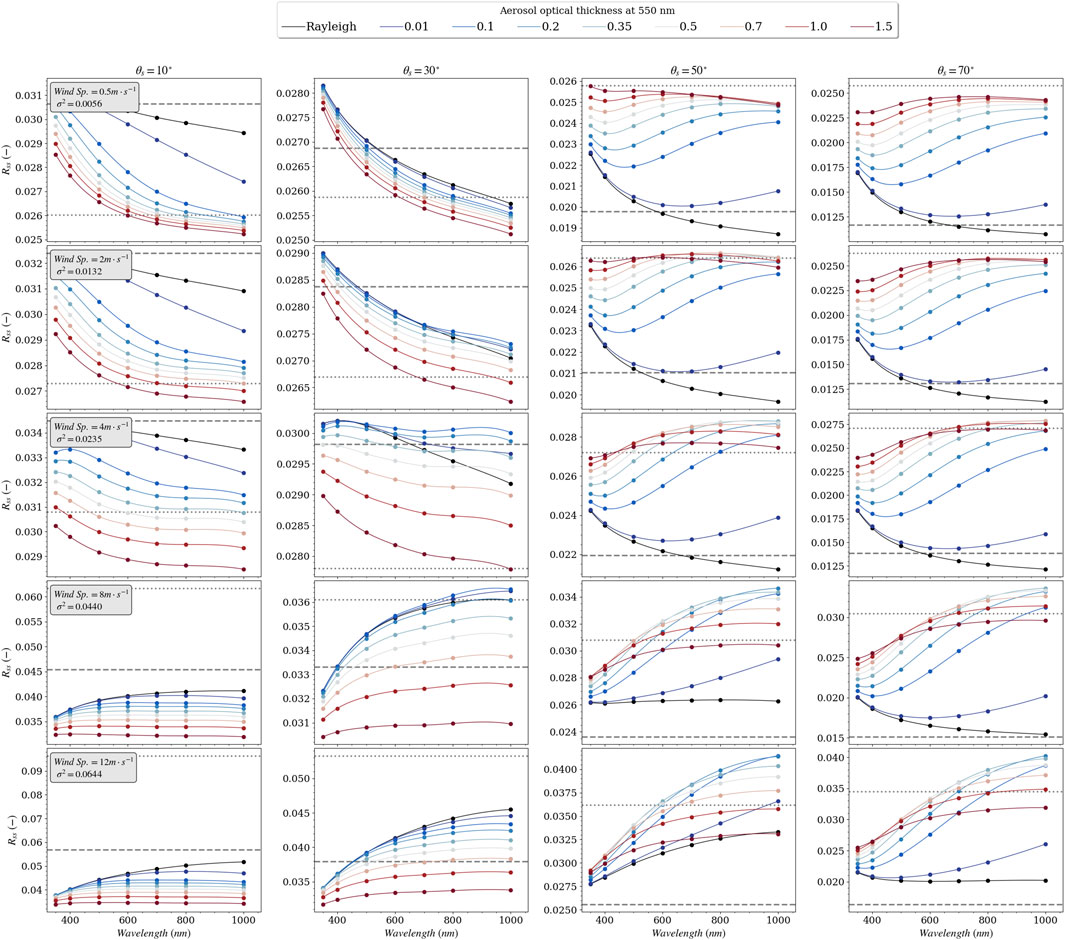
FIGURE 6. Spectral values the surface-to-sky radiance factor,
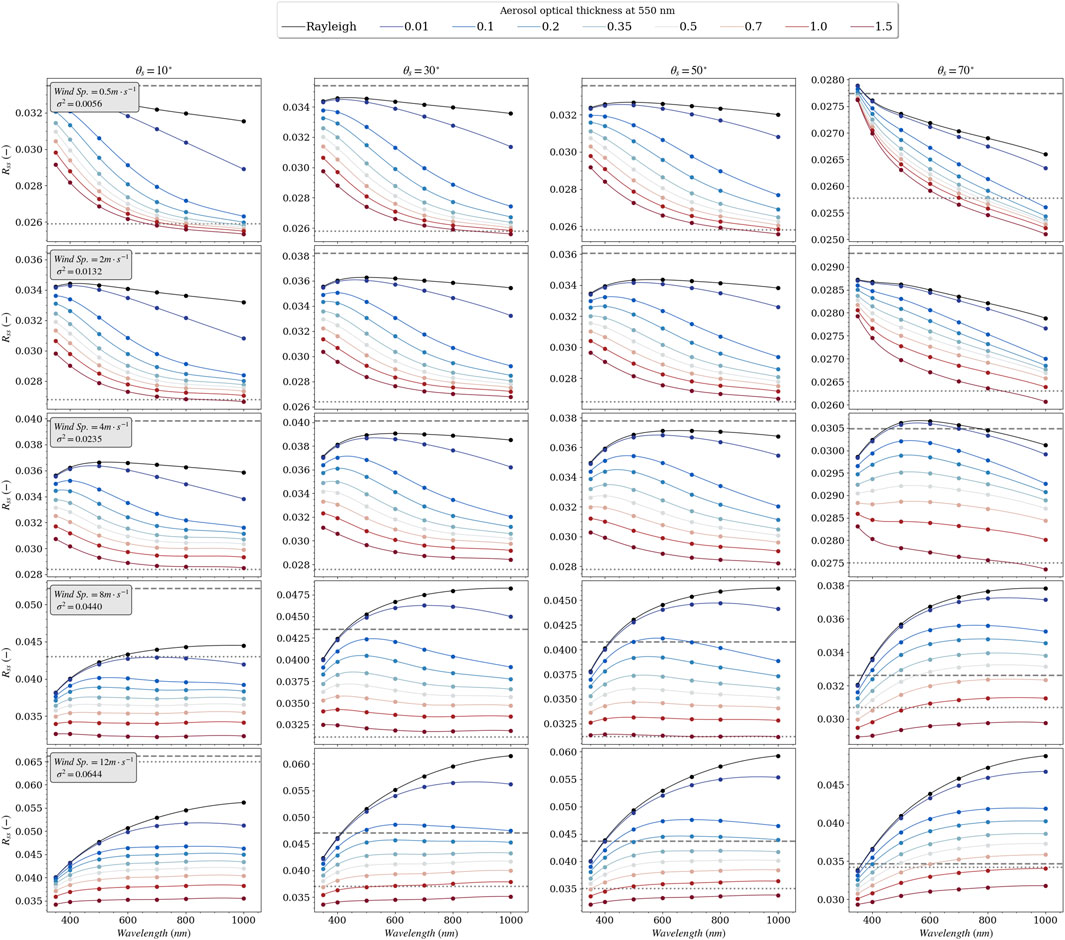
FIGURE 7. Similar to Figure 6 for relative azimuth 135°.
3.2.2 Directional considerations
In order to examine the sensitivity of
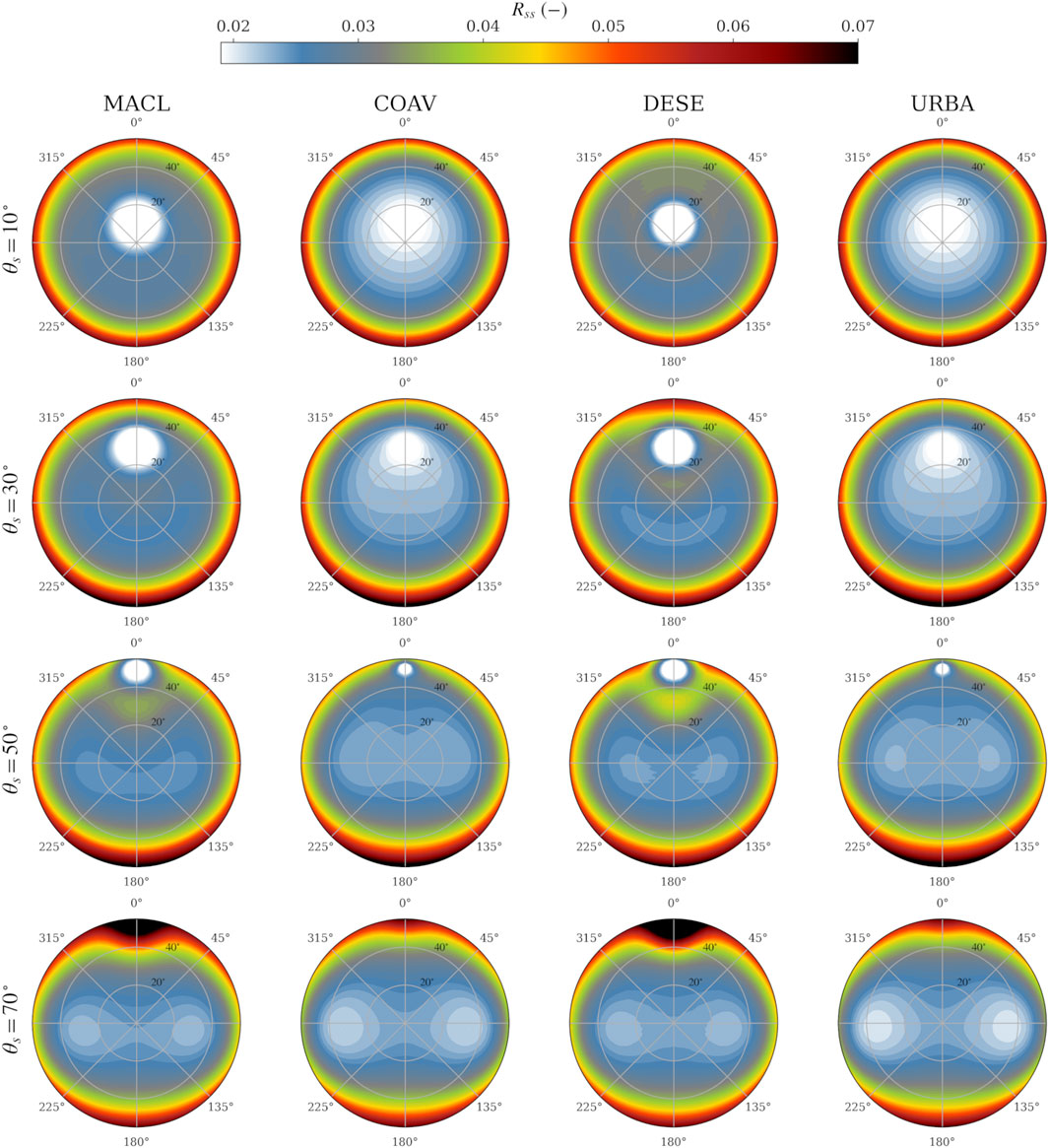
FIGURE 8. Polar diagrams of
Most of the protocols advise to use a viewing zenith angle of 40°. On the other hand, for fixed platforms the sensor can either be rotated to get a constant relative azimuth with respect to the Sun or just left immobile making the relative azimuth change over the course of a day (Harmel et al., 2011). In order to examine the impacts of varying solar and azimuth angles, it is practical to replot the polar diagrams for all the solar zenith angles by fixing the viewing angle. Figure 9 shows this kind of polar diagram for the MACL conditions and several water surface states. Similar figures are provided in the Supplementary Material for the other aerosol models. From this figure, it can be noted that the lowest
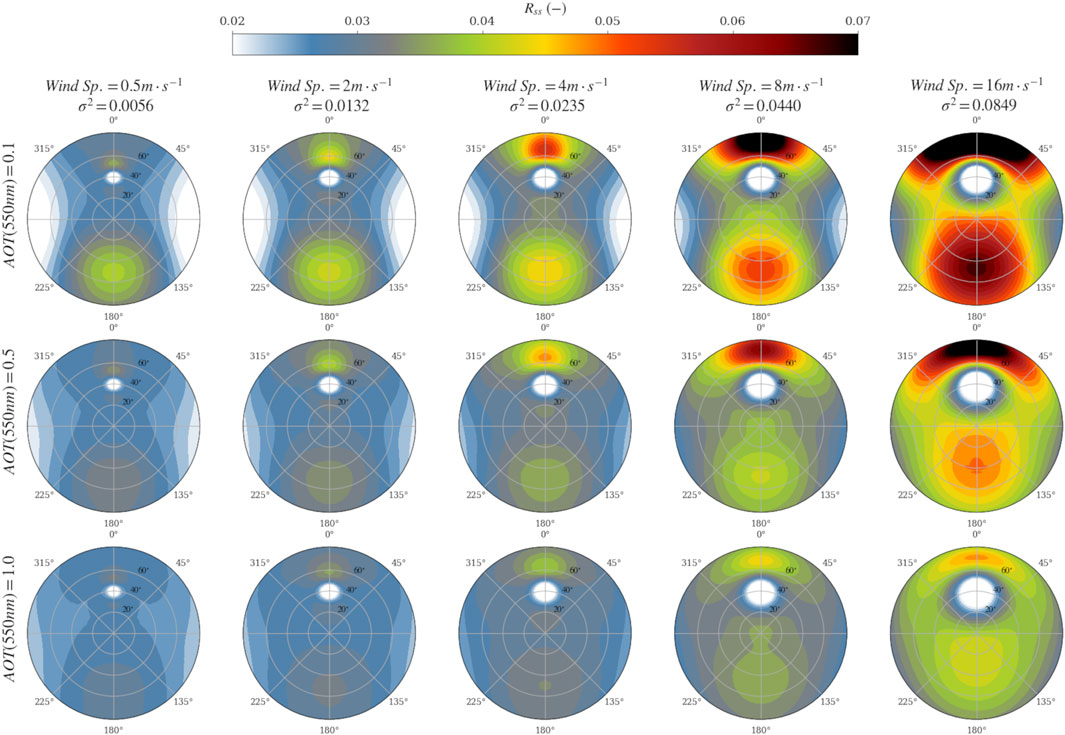
FIGURE 9. (polar diagram: contour circles indicate solar zenith angles) Directional values of
3.3 Uncertainties
3.3.1 Aerosol models
As shown in the previous figures, the aerosol optical thickness and the aerosol model produce significant modifications of the skylight reflected by the air-water interface toward the AWR sensor. In practice, it is far from being obvious to exactly know the exact optical properties of the aerosol load in presence. The directional variability of
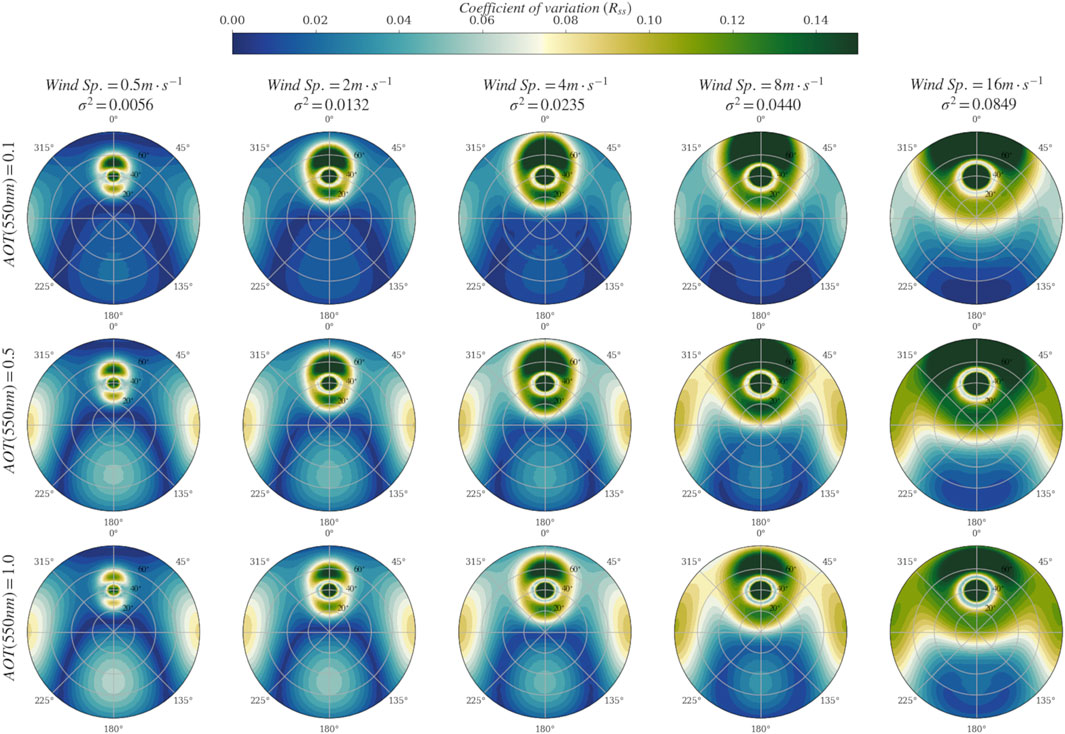
FIGURE 10. (polar diagram: contour circles indicate solar zenith angles) Coefficient of variation due to unknown aerosol model computed from the following OPAC models: Maritime clean, Continental average, Desert dust, Urban for a relative humidity of 70%. Values computed at 600 nm for a viewing angle of 40° for diverse (columns) wind speeds (or wave slope variances, σ2) and (rows) aerosol optical thicknesses.
3.3.2 Propagation of errors from aerosol optical thickness and wind speed
The uncertainties of the surface-to-sky radiance ratio were computed based on Eqs 21 and 22 to account for the propagation of the errors attached to the input parameters. The two numerical parameters
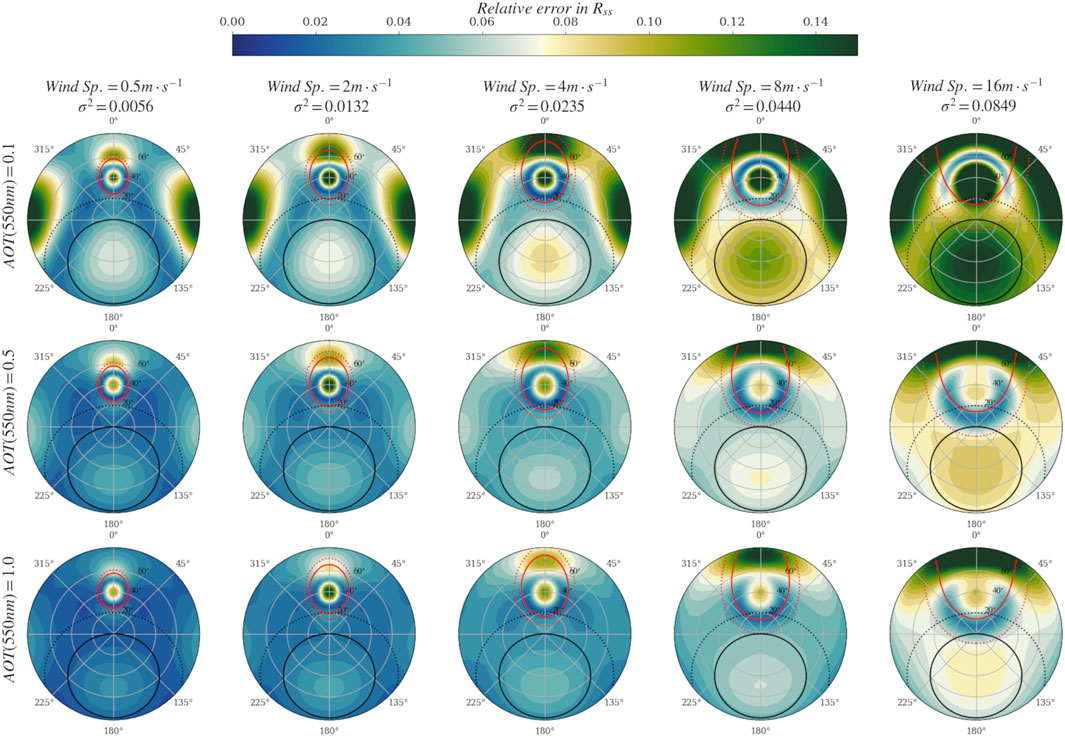
FIGURE 11. (polar diagram: contour circles indicate solar zenith angles) Relative uncertainty in
Another interesting aspect is the angular distribution of the uncertainty. Finding the viewing geometry to minimize the uncertainty might help improve the performances of the overall AWR process. For clear atmosphere conditions (i.e.,
4 Discussion
4.1 Diffuse and direct light
In this study, it has been proposed to separate the contribution of the diffuse skylight from the direct component of the sunglint radiance to correct AWR measurements for surface reflection. This is the main difference with previously proposed values of the sky to surface radiance conversion factor provided by Mobley (1999) assuming unpolarized light and Mobley (2015) which account for polarization where the sunglint is embedded. Those values were computed for a fixed wavelength (e.g., 550 nm) assuming the factor is spectrally neutral (Mobley, 2015). It has been shown that the inclusion of the sunglint should also take into account the spectral variation of the direct atmospheric transmittance through the dependency of the total optical thickness including the aerosol effect on it. Other studies provided spectral values of this factor from unpolarized (Lin et al., 2023) or full vector (Gilerson et al., 2018) radiative transfer computations. But, both studies included the sunglint contribution to the final computation. Note that another study explicitly separated the diffuse and direct contributions recommending a two-step procedure for respective corrections of sky and sun lights (Zhang et al., 2017). It has been shown in Figure 4 that inclusion of sunglint induces significant discrepancies especially for low solar zenith angle (i.e., Sun close to zenith). On the other hand, it was already noted that the application of standard procedure that takes the quantile 20% of the measured Lt (Hooker et al., 2002) with factor including the sunglint contribution generally leads to overcorrecting the water signal in the current AERONET-OC processing with increased uncertainty for high Sun elevation (Harmel et al., 2011; Harmel et al., 2012). Moreover, the usual wave statistics fail to reproduce the sunglint signal based on surface wind speed measurements over short time scale and/or small spatial extent (Kay et al., 2009). This study provides spectral values for diffuse light correction for a comprehensive set of environmental conditions that can help to further constrain the dedicated sunglint correction step as recently proposed (Goyens and Ruddick, 2023). It can also be foreseen that preliminary diffuse light correction could help to extract the sunglint signal from spectral measurement where the water-leaving radiance is negligible (e.g., shortwave-infrared) as done for atmospheric correction of optical satellite (Harmel et al., 2018).
4.2 Surface roughness
The presented results are based on the isotropic Cox-Munk wave slopes statistics (Cox and Munk, 1954). This model was used due to its simplicity to be included in radiative transfer calculation. The surface-to-sky radiance ratio has been tabulated using the equivalent Cox-Munk wind speed but also with the variance of the wave slope distribution. This enables the use of the appropriate value based on water surface state information instead of wind speed that may be uncorrelated to actual surface roughness as already mentioned (Kay et al., 2009). Nevertheless, perspectives of this work should include advanced numerical simulations of the wave spectra (from gravities to capillaries) and their slope distributions provided by several theoretical studies based on the Monte-Carlo approach (Mobley, 2015; D’Alimonte and Kajiyama, 2016; Foster and Gilerson, 2016; Hieronymi, 2016). Another approach could be based on direct measurements of the wave distribution from polarimetric measurements (Zappa et al., 2008)) or from multi-angular upwelling radiance measurements as recently suggested (Goyens and Ruddick, 2023).
4.3 Aerosol approach
As it has been shown, the presence of aerosols significantly modifies the surface-to-sky radiance ratio through their optical thickness but also the inherent optical properties defining the aerosol model to be used. These modifications arise even for low values of the aerosol optical thickness. Even if the viewing geometry can be adapted to minimize uncertainty due to partially known aerosol properties, as shown in Figures 10, 11, it is necessary to document the presence of aerosol load during data acquisitions. This can easily be done from the measurements provided by the AERONET-OC network (Zibordi et al., 2009) for which measurements are routinely operated to provide spectral aerosol optical thickness (Zibordi et al., 2021) or further optical properties (Dubovik et al., 2000; O’Neill et al., 2003). For another important network called HYPERNETS, the installed system, the HYperspectral Pointable System for Terrestrial and Aquatic Radiometry (HYPSTAR), could also be used to concurrently monitor the aerosol optical properties but it is not currently the case for routine operation (Goyens et al., 2022). A recent study showed the benefits of incorporating a pyranometer in the AWR system enabling distinctive measurements of the direct and diffuse part of the downwelling irradiance (Jordan et al., 2022). For this kind of system, the pyranometer measurements could also be used to retrieve the aerosol parameters (Alexandrov et al., 2002).
Above-water radiometry methods are also deployed on small to big ships including research vessels (Ondrusek et al., 2022), ferries (Nasiha et al., 2022) or even dugout canoes (Marinho et al., 2021). In such conditions, the aerosol properties are not always acquired concurrently. A first approach could be to use the aerosol data provided by the operational reanalysis models such as Copernicus’ CAMS or NASA’s MERRA which provide aerosol optical properties worldwide with acceptable uncertainties (Gueymard and Yang, 2020). Another practical approach would be to systematically perform aerosol data acquisition within AWR protocols. For this purpose, hand-held sun photometers could be advantageously exploited to provide spectral aerosol optical thickness (Porter et al., 2001; Knobelspiesse et al., 2004).
4.4 Impacts of geometrical configuration
The above-water radiometry procedure is based on a well-calibrated radiometer positioned in predetermined viewing configuration by setting both the viewing zenith angle and the relative azimuth. Even if the choice of viewing geometries for real-world installation may suffer limitations due to the constraints imposed by the vessel/platform superstructure or associated shadowing, it is worth documenting the most optimal geometries that help minimize uncertainties. This study showed that the absolute value of surface-to-sky radiance ratio is very variable with these two parameters but also the uncertainty attached to
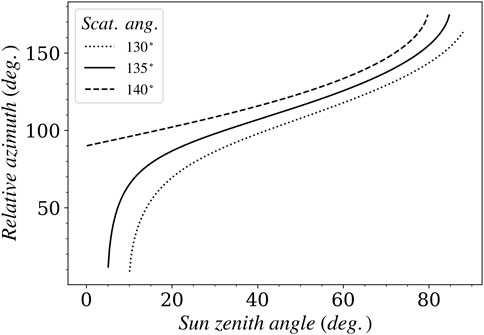
FIGURE 12. Optimal viewing geometry of above-water radiometer for a viewing zenith angle of 40° according to lowest uncertainty attached to the Rss factor which is centered on scattering angle 135°, see Figure 11.
5 Conclusion
The impact of aerosols, polarization and water surface roughness on above-water radiometry (AWR) measurements was analyzed based on full vector radiative transfer computations. Based on theoretical and practical considerations, the parameter to convert the downward sky radiance measurements into the surface-reflected radiance was renamed surface-to-sky radiance ratio,
It has been shown that knowledge on aerosol load and type is critical to correct for reflected skylight even for very low amounts in the atmosphere. Uncertainties attached to
The computations presented in this study still need to be further applied on actual in situ data sets. To this end, tabulated values are provided as a multidimensional data set based on the network Common Data Form (netCDF file). It is worth highlighting that the tabulated values must be used under clear sky conditions only since heterogeneous atmospheres with clouds or fully overcast conditions were not considered. Nevertheless, those values could be used to develop optimal methods to proceed with non-ideal conditions as in (Groetsch et al., 2017; Pitarch et al., 2020; Borges et al., 2022). The correction of the sunglint component is not taken into account in the tabulated values but methods based on separation of diffuse and direct light developed for atmospheric correction could be further investigated (Harmel et al., 2018). Even if the results have been discussed for monodirectional radiometer, the tabulated values are also suitable for correction of AWR multi-view radiometric camera if the viewing geometry of each pixel is known (Carrizo et al., 2019; Gilerson et al., 2020). Finally, the theoretical scheme presented here could be easily adapted to provide spectral values to correct polarimetric measurements of the water system.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
TH: Conceptualization, Data curation, Funding acquisition, Investigation, Methodology, Software, Visualization, Writing–original draft.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. French National Program for Remote Sensing (PNTS-2019-13).
Acknowledgments
The author is thankful to Alexandre Castagna and the GEO AquaWatch Nomenclature Group for insightful discussions. The editor and the two reviewers are also gratefully acknowledged for their subtle and enriching comments.
Conflict of interest
TH was employed by Magellium Artal Group.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsen.2023.1307976/full#supplementary-material
References
Adams, J. T., and Kattawar, G. W. (1997). Neutral points in an atmosphere-ocean system. 1: upwelling light field’, Applied Optics. Opt. Soc. Am. 36 (9), 1976–1986. doi:10.1364/ao.36.001976
Alexandrov, M. D., Lacis, A. A., Carlson, B. E., and Cairns, B. (2002). Remote sensing of atmospheric aerosols and trace gases by means of multifilter rotating shadowband radiometer. Part II: climatological applications. J. Atmos. Sci. 59 (3), 544–566. doi:10.1175/1520-0469(2002)059<0544:rsoaaa>2.0.co;2
Antoine, D., d'Ortenzio, F., Hooker, S. B., Bécu, G., Gentili, B., Tailliez, D., et al. (2008). Assessment of uncertainty in the ocean reflectance determined by three satellite ocean color sensors (MERIS, SeaWiFS and MODIS-A) at an offshore site in the Mediterranean Sea (BOUSSOLE project). J. Geophys. Res. Am. Geophys. Union 113 (C7), C07013. doi:10.1029/2007JC004472
Bodhaine, B. A., Wood, B. N., Dutton, G., and Slusser, R. J. (1999). On Rayleigh optical depth calculations. J. Atmos. Ocean. Technol. 16 (11), 1854–1861. doi:10.1175/1520-0426(1999)016<1854:ORODC>2.0.CO;2
Borges, H. D., Martinez, J. M., Harmel, T., Cicerelli, R. E., Olivetti, D., and Roig, H. L. (2022). Continuous monitoring of suspended particulate matter in tropical inland waters by high-frequency, above-water radiometry. Sensors 22 (22), 8731. doi:10.3390/S22228731
Carrizo, C., Gilerson, A., Foster, R., Golovin, A., and El-Habashi, A. (2019). Characterization of radiance from the ocean surface by hyperspectral imaging’, Optics Express. Opt. Publ. Group 27 (2), 1750. doi:10.1364/oe.27.001750
Chami, M., Lafrance, B., Fougnie, B., Chowdhary, J., Harmel, T., and Waquet, F. (2015). OSOAA: a vector radiative transfer model of coupled atmosphere-ocean system for a rough sea surface application to the estimates of the directional variations of the water leaving reflectance to better process multi-angular satellite data over the ocean’, Optics Express. OSA 23 (21), 27829–27852. doi:10.1364/OE.23.027829
Chami, M., Santer, R., and Dilligeard, E. (2001). Radiative transfer model for the computation of radiance and polarization in an ocean-atmosphere system: polarization properties of suspended matter for remote sensing. Appl. Opt. 40 (15), 2398–2416. doi:10.1364/ao.40.002398
Chandrasekhar, S. (1947). The transfer of radiation in stellar atmospheres. Bull. Amer. Math. Soc. 53, 641–711. doi:10.1090/s0002-9904-1947-08825-x
Cox, C., and Munk, W. (1956). in Slopes of the sea surface deduced from photographs of sun glitter, Scripps Institution of Oceanography. Editors C. Cox, and W. Munk La Jolla, CA, United States: (Scripps Institution of Oceanography).
Cox, C., and Munk, W. H. (1954). Statistics of the sea surface derived from sun glitter. J. Mar. Res. 13 (2), 198–227.
D’Alimonte, D., and Kajiyama, T. (2016). Effects of light polarization and waves slope statistics on the reflectance factor of the sea surface’, Optics Express. Opt. Soc. Am. 24 (8), 7922. doi:10.1364/OE.24.007922
Deuze, J. L., Herman, M., and Santer, R. (1989). Fourier-series expansion of the transfer equation in the atmosphere ocean system. J. of Quantitative Spectrosc. Radiat. Transf. 41 (6), 483–494. doi:10.1016/0022-4073(89)90118-0
Dubovik, O., Smirnov, A., Holben, B. N., King, M. D., Kaufman, Y. J., Eck, T. F., et al. (2000). Accuracy assessments of aerosol optical properties retrieved from Aerosol Robotic Network (AERONET) Sun and sky radiance measurements. J. Geophys. Res. 105 (D8), 9791–9806. doi:10.1029/2000jd900040
Foster, R., and Gilerson, A. (2016). Polarized transfer functions of the ocean surface for above-surface determination of the vector submarine light field. Appl. Opt. 55 (33), 9476–9494. doi:10.1364/AO.55.009476
Franz, B. A., Bailey, S. W., Werdell, P. J., and McClain, C. R. (2007). Sensor-independent approach to the vicarious calibration of satellite ocean color radiometry. Appl. Opt. 46 (22), 5068–5082. doi:10.1364/ao.46.005068
Fraser, R. S. (1968). Atmospheric neutral points over water. JOSA 58 (8), 1029–1031. doi:10.1364/JOSA.58.001029
Gasteiger, J., and Wiegner, M. (2018). MOPSMAP v1.0: a versatile tool for the modeling of aerosol optical properties. Copernic. GmbH 11 (7), 2739–2762. Geoscientific Model Development. doi:10.5194/GMD-11-2739-2018
Giardino, C., Brando, V. E., Gege, P., Pinnel, N., Hochberg, E., Knaeps, E., et al. (2019). Imaging spectrometry of inland and coastal waters: state of the art, achievements and perspectives. Surv. Geophys. 40 (3), 401–429. doi:10.1007/s10712-018-9476-0
Gilerson, A., Carrizo, C., Foster, R., and Harmel, T. (2018). Variability of the reflectance coefficient of skylight from the ocean surface and its implications to ocean color. Opt. Express 26 (8), 9615–9633. doi:10.1364/OE.26.009615
Gilerson, A., Carrizo, C., Ibrahim, A., Foster, R., Harmel, T., El-Habashi, A., et al. (2020). Hyperspectral polarimetric imaging of the water surface and retrieval of water optical parameters from multi-angular polarimetric data. Appl. Opt. Opt. Soc. 59 (10), C8. doi:10.1364/ao.59.0000c8
Gilerson, A., Herrera-Estrella, E., Agagliate, J., Foster, R., Gossn, J. I., Dessailly, D., et al. (2023). Determining the primary sources of uncertainty in the retrieval of marine remote sensing reflectance from satellite ocean color sensors II. Sentinel 3 OLCI sensors. Front. Remote Sens. Front. 4, 1146110. doi:10.3389/FRSEN.2023.1146110
Goyens, C., Beyer, J. E., Xiao, X., and Hambright, K. D. (2022). Using hyperspectral remote sensing to monitor water quality in drinking water reservoirs. Remote Sens. 14 (21), 5607. doi:10.3390/RS14215607
Goyens, C., and Ruddick, K. (2023). Improving the standard protocol for above-water reflectance measurements: 1. Estimating effective wind speed from angular variation of sunglint. Appl. Opt. 62 (10), 2442. doi:10.1364/ao.481787
Groetsch, P. M. M., Gege, P., Simis, S. G. H., Eleveld, M. A., and Peters, S. W. M. (2017). Validation of a spectral correction procedure for sun and sky reflections in above-water reflectance measurements’, Optics Express. Opt. Soc. Am. 25 (16), A742. doi:10.1364/OE.25.00A742
Gueymard, C. A., and Yang, D. (2020). Worldwide validation of CAMS and MERRA-2 reanalysis aerosol optical depth products using 15 years of AERONET observations, Atmospheric Environment 117216. doi:10.1016/j.atmosenv.2019.117216
Harmel, T., and Chami, M. (2012). Determination of sea surface wind speed using the polarimetric and multidirectional properties of satellite measurements in visible bands’, Geophysical Research Letters. AGU 39 (19), L19611. doi:10.1029/2012GL053508
Harmel, T., Chami, M., Tormos, T., Reynaud, N., and Danis, P.-A. (2018). Sunglint correction of the Multi-Spectral Instrument (MSI)-SENTINEL-2 imagery over inland and sea waters from SWIR bands. Remote Sens. Environ. 204, 308–321. doi:10.1016/j.rse.2017.10.022
Harmel, T., Gilerson, A., Hlaing, S., Tonizzo, A., Legbandt, T., Weidemann, A., et al. (2011). Long island sound coastal observatory: assessment of above-water radiometric measurement uncertainties using collocated multi and hyperspectral systems. Appl. Opt. 50 (30), 5842–5860. doi:10.1364/AO.50.005842
Harmel, T., Gilerson, A., Hlaing, S., Weidemann, A., Arnone, R., and Ahmed, S. (2012). Long Island Sound Coastal Observatory: assessment of above-water radiometric measurement uncertainties using collocated multi and hyper-spectral systems: reply to comment. Appl. Opt. OSA 51 (17), 3893–3899. doi:10.1364/AO.51.003893
Harmel, T., Gilerson, A., Tonizzo, A., Chowdhary, J., Weidemann, A., Arnone, R., et al. (2012). Polarization impacts on the water-leaving radiance retrieval from above-water radiometric measurements. Appl. Opt. 51 (35), 8324–8340. doi:10.1364/AO.51.008324
Hess, M., Koepke, P., and Schult, I. (1998). Optical properties of aerosols and clouds: the software package OPAC. Bull. Am. Meteorological Soc. 79 (5), 831–844. doi:10.1175/1520-0477(1998)079<0831:OPOAAC>2.0.CO;2
Hieronymi, M. (2016). Polarized reflectance and transmittance distribution functions of the ocean surface’, Optics Express. Opt. Soc. Am. 24 (14), A1045–A1068. doi:10.1364/OE.24.0A1045
Hooker, S. B., Lazin, G., Zibordi, G., and McLean, S. (2002). An evaluation of above- and in-water methods for determining water-leaving radiances. J. Atmos. Ocean. Technol. 19 (4), 486–515. doi:10.1175/1520-0426(2002)019<0486:aeoaai>2.0.co;2
Hooker, S. B., Morrow, J. H., and Matsuoka, A. (2013). Apparent optical properties of the Canadian Beaufort Sea - Part 2: the 1% and 1 cm perspective in deriving and validating AOP data products. Biogeosciences 10 (7), 4511–4527. doi:10.5194/BG-10-4511-2013
Hu, C., Carder, K. L., and Muller-Karger, F. E. (2001). How precise are SeaWiFS ocean color estimates? Implications of digitization-noise errors. Remote Sens. Environ. 76 (2), 239–249. doi:10.1016/s0034-4257(00)00206-6
Hulburt, E. O. (1934). The polarization of light at sea. J. of Opt. Soc. of Am. 24 (2), 35–42. doi:10.1364/josa.24.000035
Jordan, T. M., Simis, S. G. H., Grötsch, P. M. M., and Wood, J. (2022). Incorporating a hyperspectral direct-diffuse pyranometer in an above-water reflectance algorithm. Remote Sens. 14 (10), 2491. doi:10.3390/RS14102491
Kay, S., Hedley, J. D., and Lavender, S. (2009). Sun glint correction of high and low spatial resolution images of aquatic scenes: a review of methods for visible and near-infrared wavelengths’, Remote Sensing. Mol. Divers. Preserv. Int. 1 (4), 697–730. doi:10.3390/rs1040697
Kedenburg, S., Vieweg, M., Gissibl, T., and Giessen, H. (2012). Linear refractive index and absorption measurements of nonlinear optical liquids in the visible and near-infrared spectral region’, Optical Materials Express. Opt. Soc. Am. 2 (11), 1588–1611. doi:10.1364/OME.2.001588
Knobelspiesse, K. D., Pietras, C., Fargion, G. S., Wang, M., Frouin, R., Miller, M. A., et al. (2004). Maritime aerosol optical thickness measured by handheld sun photometers. Remote Sens. Environ. 93 (1–2), 87–106. doi:10.1016/j.rse.2004.06.018
Lee, Z. P., Ahn, Y. H., Mobley, C., and Arnone, R. (2010). Removal of surface-reflected light for the measurement of remote-sensing reflectance from an above-surface platform’, Optics Express. Opt. Soc. Am. 18 (25), 26313–26324. doi:10.1364/oe.18.026313
Lenoble, J., Herman, M., Deuzé, J., Lafrance, B., Santer, R., and Tanré, D. (2007). A successive order of scattering code for solving the vector equation of transfer in the earth’s atmosphere with aerosols. J. Quantitative Spectrosc. Radiat. Transf. 107 (3), 479–507. doi:10.1016/j.jqsrt.2007.03.010
Levy, R. C., Mattoo, S., Munchak, L. A., Remer, L. A., Sayer, A. M., Patadia, F., et al. (2013). The Collection 6 MODIS aerosol products over land and ocean. Atmos. Meas. Tech. 6 (11), 2989–3034. doi:10.5194/amt-6-2989-2013
Lin, J., Lee, Z., Tilstone, G. H., Liu, X., Wei, J., Ondrusek, M., et al. (2023). Revised spectral optimization approach to remove surface-reflected radiance for the estimation of remote-sensing reflectance from the above-water method. Opt. Express 31 (14), 22964–22981. doi:10.1364/OE.486981
Marinho, R. R., Harmel, T., Martinez, J. M., and Filizola Junior, N. P. (2021). Spatiotemporal dynamics of suspended sediments in the negro river, amazon basin, from in situ and sentinel-2 remote sensing data. ISPRS Int. J. Geo-Information 10 (2), 86. doi:10.3390/ijgi10020086
Max, J.-J. J., and Chapados, C. (2009). Isotope effects in liquid water by infrared spectroscopy. III. H2O and D2O spectra from 6000 to 0 cm(-1). J. Chem. Phys. 131 (18), 184505. doi:10.1063/1.3258646
McClain, E. P., and Strong, A. E. (1969). On anomalous dark patches in satellite-viewed sunglint areas. Mon. Weather Rev. 97 (12), 875–884. doi:10.1175/1520-0493(1969)097<0875:OADPIS>2.3.CO;2
Mishchenko, M. I., Videen, G., Babenko, V. A., Khlebtsov, N. G., Wriedt, T., et al. (2004). T-matrix theory of electromagnetic scattering by particles and its applications: a comprehensive reference database. J. Quant. Spectrosc. Radiat. Transf. 88, 357–406. doi:10.1016/j.jqsrt.2004.05.002
Mishchenko, M. I., Hovenier, J. W., and Travis, L. D. (2000). in Light scattering by nonspherical particles: theory, measurements, and applications. Editors M. I. Mishchenko, J. W. Hovenier, and L. D. Travis (San Diego: Academic Press).
Mobley, C. D. (1999). Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 38 (36), 7442–7455. doi:10.1364/AO.38.007442
Mobley, C. D. (2015). Polarized reflectance and transmittance properties of windblown sea surfaces’, Applied Optics. Opt. Soc. Am. 54 (15), 4828. doi:10.1364/AO.54.004828
Mobley, C. D., Chai, F., Xiu, P., and Sundman, L. K. (2015). Impact of improved light calculations on predicted phytoplankton growth and heating in an idealized upwelling-downwelling channel geometry. J. Geophys. Res. Oceans 120 (2), 875–892. doi:10.1002/2014JC010588
Mueller, J. L., and Austin, R. W. (1995). in Ocean Optics Protocols for SeaWiFS validation, revision 1, SeaWiFS technical report series. Greenbelt, Maryland: NASA technical memorandum 104566. Editors S. B. Hooker, E. R. Firestone, and J. G. Acker
Munk, W. (2009). An inconvenient sea truth: spread, steepness, and skewness of surface slopes’, annual Review of marine science. Annu. Rev. 1 (1), 377–415. doi:10.1146/annurev.marine.010908.163940
Nasiha, H. J., Wang, Z., Giannini, F., and Costa, M. (2022). Spatial variability of in situ above-water reflectance in coastal dynamic waters: implications for satellite match-up analysis’, Frontiers in remote sensing. Frontiers 3, 876748. doi:10.3389/FRSEN.2022.876748
Ondrusek, M., Wei, J., Menghua, W., Eric, S., Charles, K., Alex, G., et al. (2022) Report for dedicated JPSS VIIRS ocean color calibration/validation cruise: gulf of Mexico in april 2021. doi:10.25923/X2Q6-9418
O’Neill, N. T., Eck, T. F., Smirnov, A., Holben, B. N., and Thulasiraman, S. (2003). Spectral discrimination of coarse and fine mode optical depth. J. Geophys. Res. Am. Geophys. Union 108 (D17), 4559. doi:10.1029/2002JD002975
Pahlevan, N., Mangin, A., Balasubramanian, S. V., Smith, B., Alikas, K., Arai, K., et al. (2021). ACIX-Aqua: a global assessment of atmospheric correction methods for Landsat-8 and Sentinel-2 over lakes, rivers, and coastal waters. Remote Sens. Environ. 258, 112366. doi:10.1016/j.rse.2021.112366
Perrin, F. (1942). Polarization of light scattered by isotropic opalescent media. J. Chem. Phys. 10, 415–427. doi:10.1063/1.1723743
Pitarch, J., Talone, M., Zibordi, G., and Groetsch, P. (2020). Determination of the remote-sensing reflectance from above-water measurements with the “3C model”: a further assessment’, Optics Express. Opt. Soc. 28 (11), 15885. doi:10.1364/oe.388683
Porter, J. N., Miller, M., Pietras, C., and Motell, C. (2001). Ship-based sun photometer measurements using microtops sun photometers. J. Atmos. Ocean. Technol. 18 (5), 765–774. doi:10.1175/1520-0426(2001)018<0765:SBSPMU>2.0.CO;2
Preisendorfer, R. W., and Mobley, C. D. (1986). Albedos and glitter patterns of a wind-roughened sea surface. J. Phys. Oceanogr. 16, 1293–1316. doi:10.1175/1520-0485(1986)016<1293:AAGPOA>2.0.CO;2
Quan, X., and Fry, E. S. (1995). Empirical equation for the index of refraction of seawater.’, Applied optics. Opt. Soc. Am. 34 (18), 3477–3480. doi:10.1364/AO.34.003477
Ruddick, K. G., Voss, K., Boss, E., Castagna, A., Frouin, R., Gilerson, A., et al. (2019). A review of protocols for fiducial reference measurements of water-leaving radiance for validation of satellite remote-sensing data over water. Remote Sens. 11 (19), 2198. doi:10.3390/RS11192198
Segelstein, D. J. (1981). The complex refractive index of water. Kansas City, USA: University of Missouri--Kansas City.
Stokes, G. G. (1852). On the composition and resolution of streams of polarized light from different sources. Trans. Camb. Philos. Soc. 3 (9), 233–259.
Werdell, P. J., McKinna, L. I., Boss, E., Ackleson, S. G., Craig, S. E., Gregg, W. W., et al. (2018). An overview of approaches and challenges for retrieving marine inherent optical properties from ocean color remote sensing. Prog. Oceanogr. 160, 186–212. doi:10.1016/j.pocean.2018.01.001
Yang, P., Feng, Q., Hong, G., Kattawar, G. W., Wiscombe, W. J., Mishchenko, M. I., et al. (2007). Modeling of the scattering and radiative properties of nonspherical dust-like aerosols. J. Aerosol Sci. 38 (10), 995–1014. doi:10.1016/J.JAEROSCI.2007.07.001
Zappa, C. J., Banner, M. L., Schultz, H., Corrada-Emmanuel, A., Wolff, L. B., and Yalcin, J. (2008). Retrieval of short ocean wave slope using polarimetric imaging’, Measurement Science and Technology. IOP Publ. 19 (5), 055503. doi:10.1088/0957-0233/19/5/055503
Zhai, P. W., Hu, Y., Chowdhary, J., Trepte, C. R., Lucker, P. L., and Josset, D. B. (2010). A vector radiative transfer model for coupled atmosphere and ocean systems with a rough interface. J. Quantitative Spectrosc. Radiat. Transf. 111 (7–8), 1025–1040. doi:10.1016/j.jqsrt.2009.12.005
Zhang, X., He, S., Shabani, A., Zhai, P. W., and Du, K. (2017). Spectral sea surface reflectance of skylight. Opt. Express 25 (4), A1–A13. doi:10.1364/OE.25.0000A1
Zibordi, G. (2016). Experimental evaluation of theoretical sea surface reflectance factors relevant to above-water radiometry’, Optics Express. OSA 24 (6), A446. doi:10.1364/oe.24.00a446
Zibordi, G., et al. (2019). “Protocols for satellite ocean colour data validation,” in Situ optical radiometry. Editors K. J. Voss, B. C. Johnson, and J. L. Mueller (Dartmouth, NS, Canada: IOCCG Protocol Series IOCCG Ocea). IOCCG 3. doi:10.25607/OBP-691
Zibordi, G., Holben, B. N., Talone, M., D’Alimonte, D., Slutsker, I., Giles, D. M., et al. (2021). Advances in the ocean color component of the aerosol robotic network (AERONET-OC)’, Journal of Atmospheric and oceanic Technology. Am. Meteorological Soc. 38 (4), 725–746. doi:10.1175/JTECH-D-20-0085.1
Zibordi, G., Hooker, S. B., Berthon, J. F., and D'Alimonte, D. (2002). Autonomous above-water radiance measurements from an offshore platform: a field assessment experiment. J. Atmos. Ocean. Technol. 19 (5), 808–819. doi:10.1175/1520-0426(2002)019<0808:aawrmf>2.0.co;2
Zibordi, G., Mélin, F., Berthon, J. F., Holben, B., Slutsker, I., Giles, D., et al. (2009). AERONET-OC: a network for the validation of ocean color primary products. J. Atmos. Ocean. Technol. 26, 1634–1651. doi:10.1175/2009jtecho654.1
Keywords: above-water radiometry, aerosol, water-leaving radiance, polarization, cal/val activities
Citation: Harmel T (2023) Apparent surface-to-sky radiance ratio of natural waters including polarization and aerosol effects: implications for above-water radiometry. Front. Remote Sens. 4:1307976. doi: 10.3389/frsen.2023.1307976
Received: 05 October 2023; Accepted: 28 November 2023;
Published: 21 December 2023.
Edited by:
Clemence Goyens, Royal Belgian Institute of Natural Sciences, BelgiumReviewed by:
Hui Ying Pak, Nanyang Technological University, SingaporeThomas Jordan, Plymouth Marine Laboratory, United Kingdom
Copyright © 2023 Harmel. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tristan Harmel, dHJpc3Rhbi5oYXJtZWxAbWFnZWxsaXVtLmZy
 Tristan Harmel
Tristan Harmel