Computation of Optical Properties of Core-Shell Super-Spheroids Using a GPU Implementation of the Invariant Imbedding T-Matrix Method

Particles with internal inclusions or cores are ubiquitous in the atmosphere. One example is dust particles coated with water-soluble aerosols such as sulfate or nitrate. For these particles, the dust non-sphericity and the core-shell structure of the particle both fundamentally impact the optical properties. However, it is challenging to obtain an accurate and comprehensive parameterization of the optical properties of coated atmospheric particles. Recent studies have found that super-spheroids could provide a robust model for representing the non-sphericity of irregular particles, such as dust, sea salt, and ice particles. This important finding warrants further investigations on coated super-spheroids for the development of mixed-aerosol models. In this study, we developed a GPU version of the invariant imbedding T-matrix program (GPU-IITM) to improve the computational efficiency. This version allows for efficient computation of the optical properties of coated super-spheroids with extensive shape parameters and refractive indices. The GPU-IITM is 8–25 times more efficient than the conventional CPU-IITM, depending on the size parameter of the coated super-spheroids. The single-scattering properties of coated super-spheroids computed from the GPU-IITM allows for close examination of the optical differences between homogeneous and inhomogeneous particles. As an example, we present the linear depolarization ratios (LDRs) of coated super-spheroids, which have implications in active lidar remote-sensing research. We found that the LDR decreases obviously as the real part of the shell’s refractive index increases from 1.3 to 1.6. Greater LDRs occur for particles with a thin coating, while a rounder shape of the particle decreases the LDRs. However, special attention should be given to nearly spherical particles, for which the LDRs could be enhanced. In comparison to homogeneous particles, the degree of enhancement decreases or increases depending on whether the shell’s refractive index is smaller or larger than the core refractive index.

Introduction

Studies on atmospheric radiative transfer and remote sensing fundamentally require accurate knowledge of the optical properties of various aerosol particles (Dubovik et al., 2006; Dubovik et al., 2019; Xu, et al., 2021). However, due to the complexity of particle shapes and mixing states, it has been extremely challenging to develop a universal approach to modelling atmospheric particles. Substantial progress has been achieved in understanding the impact of particle non-sphericity and inhomogeneity on the optical properties by using a number of idealized geometries or “realistic” replicas of microscopic images of particles. Kahnert et al. (2014) and Yang et al. (2018) reviewed research efforts in developing non-spherical aerosol and ice models, respectively.

Regarding the mixing state of multiple aerosol components, the particle mixtures in the atmosphere can be appropriately classified as external, semi-external, and internal mixtures (Mishchenko et al., 2004). Based on a two-component model, the optical properties of semi-external and external mixtures have been found to be similar with relatively small differences. However, the optical properties of internal mixtures (one or multiple aerosol components imbedded in a large host particle) could be significantly different from those of external mixtures. An internally mixed aerosol optics scheme is important in remote sensing studies and is fundamentally required in general circulation models, and the weather research and forecasting models for quantifying the impact of aerosols on the planetary boundary layer (e.g., Bauer et al., 2007; Wang et al., 2015; Chen et al., 2021; Wang et al., 2022).

Internal mixing scenarios are ubiquitous in the atmosphere and are primarily associated with the coagulation and coalescence of particles, or the condensation of gas precursors on aerosol surfaces with possible heterogeneous reactions (Tomasi et al., 2017). One important example is dust particles mixed with other types of aerosols. When dust aerosols are transported in the atmosphere, it is quite common to see dust particles mixed with air pollutants such as black carbon, organic carbon, sulfate and nitrate. Dust particles and water-soluble aerosols normally form a core-shell structure. Li and Shao (2009) collected aerosol samples during episodes of brown haze and dust in Beijing, China. The transmission electron microcopy (TEM) coupled with energy-dispersive X-ray microanalysis was used to analyze 332 mineral dust particles, and it was found that ∼90% of dust particles were covered with nitrate coatings. Based on an analysis of 8,441 particles sampled in Northern Europe and Western Africa, Unga et al. (2018) found that 60% of urban and 20% of desert dust particles presented residuals of coatings. Recently, Wang et al. (2021) reported that internally mixed particles are more common during haze days than non-haze days. For these internally mixed particles, both the particle non-sphericity and the core-shell structure should be carefully examined to quantify their impact on the optical properties (Bauer et al., 2007; Zhang et al., 2020; Zhang et al., 2022).

There have been various advancements in relevant computational techniques, such as the T-matrix method (Mishchenko et al., 2002; Mackowski and Mishchenko, 1996; Bi and Yang, 2014), the discrete dipole approximation method (Purcell and Pennypacker, 1973; Draine, 1988; Yurkin and Hoekstra, 2007), and the finite-difference/pseudo-spectral time domain method (Yang and Liou, 1996; Liu et al., 2012). These techniques make it easier to perform case studies with a few shape parameters and refractive indices in constrained ranges of the shape and size parameters. However, it is still challenging to perform extensive simulations of optical properties even for a well-defined simple model, particularly when the size parameter is large.

To facilitate applications related to atmospheric radiative transfer and remote sensing studies, continual research efforts are required to comprehensively examine the optical properties of particles in terms of the variation of shape and size parameters and the refractive indices. For example, in a previous study, we systematically examined the optical properties of non-spherical particles in a super-spheroidal shape space (Bi et al., 2018a). Later, a super-spheroidal model was applied to model the optical properties of dust aerosols, sea salts, and ice crystals (Bi et al., 2018b; Lin et al., 2018; Sun et al., 2021; Li et al., 2022). We believe that the advantages of the super-spheroidal model in remote sensing and climate research warrant further investigations of coated super-spheroids for the study of the optical properties of internally mixed aerosol models.

In this study, we implemented a coated super-spheroid model in the invariant imbedding T-matrix program (IITM) to compute the optical properties. The IITM is appliable to arbitrarily shaped and inhomogeneous particles. The original IITM code developed by Bi et al. (2013a, 2013b), Bi and Yang (2014), and Bi et al. (2018a, 2018b) was built upon the OpenMP architecture with central-processing-unit (CPU) threading. To improve the computational efficiency of the IITM, we developed an implementation of it on a graphics processing unit (GPU) called GPU-IITM. GPUs have advantages in parallel processing due to their massive computation cores. GPU acceleration has been applied in light-scattering research to improve the computational efficiency (e.g., Huntemann et al., 2011; Iadarola et al., 2012; Egel et al., 2017).

The remainder of this paper is organized as follows. In Section 2, we describe the coated super-spheroidal model and computational parameters for the optical property calculation. The IITM algorithm and the GPU implementation are briefly introduced, and a test of the performance of GPU-IITM is presented with numerical examples. Computational results of coated super-spheroids are given in Section 3. We focused on the backscattering linear depolarization ratio (LDR), which is an important quantity that is relevant to light detection and ranging (lidar) observations of aerosol mixtures. We examined the LDRs of coated super-spheroids with respect to the refractive index of the coating layer and comprehensively investigated how the aspect ratio and the roundness parameters of the particles impact the LDRs. In particular, we compared the optical properties of coated super-spheroids and homogeneous super-spheroids and discussed relevant implications in lidar remote sensing.

Methods

Coated Super-Spheroidal Model

The super-spheroid equation in a Cartesian coordinate system is (Barr, 1981):

$\begin{array}{c}{\left(\frac{\text{x}}{\text{a}}\right)}^{\frac{2}{n}}+{\left(\frac{\text{y}}{\text{a}}\right)}^{\frac{2}{n}}+{\left(\frac{\text{z}}{\text{c}}\right)}^{\frac{2}{n}}=1,\end{array}(1)$

where a and c are the horizontal and vertical semi-axes, respectively, and $n$ is called the roundness parameter (Bi et al., 2018a). The overall shape is determined by the aspect ratio (a/c) and the roundness parameter ($n$). We used two super-spheroidal equations to define a coated super-spheroid. The aspect ratio and the roundness parameter of the shell and internal core can vary independently.

Figure 1 shows a few examples illustrating the geometry of coated super-spheroids. The roundness parameter of the internal core ($n_{core}$) is fixed at 2.6, at which the overall shape of the internal core is concave. The optical similarity between the concave super-spheroid model particle and realistic dust was examined by comparing theoretical simulations (Lin et al., 2018) and scattering matrices measured in a laboratory (Muñoz et al., 2012). Super-spheroids with a roundness parameter in the range of 2.4–3.0 were found to be optimal for representing dust particles in optical property calculation. This finding was confirmed by comparing the observations from the Polarization and Anisotropy of Reflectances for Atmospheric Sciences coupled with Observations from a Lidar and radiative transfer simulations under dusty sky conditions (Lin et al., 2021). Additional comparison of observations using high spectral resolution lidar (HSRL) and the backscattering calculations (Kong et al., 2022) also supported this conclusion. Therefore, the choice of $n=2.6$ is believed to be representative for developing coated dust aerosol models.

FIGURE 1

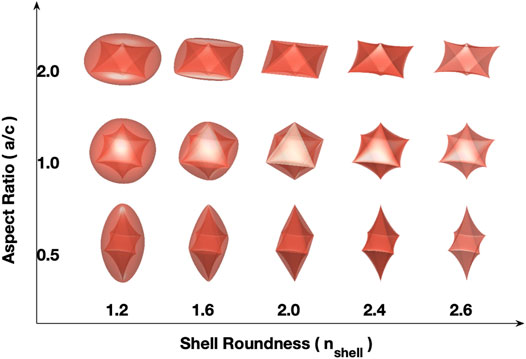
FIGURE 1. Examples of coated super-spheroids. The roundness of core is fixed at 2.6 and 11 aspect ratios ranging from 0.5 to 2.0 and nine shell roundness parameters ranging from 1.0 to 2.6 are considered in the GPU-IITM simulations.

In defining the coated super-spheroid, we assume that the semi-major axes of the shell and the core are identical. For close examination of the optical property variation with respect to particle shapes, we considered 11 aspect ratios ranging from 0.5 to 2.0, as well as nine shell roundness parameters ranging from 1.0 to 2.6. The reason is that coated dust particles have no particular shape and could be diverse.

When the shell roundness parameter is identical to the core roundness parameter (2.6), the particles are basically an internal core without a coating—that is, homogeneous super-spheroids. When the shell roundness parameter is 1.0, the particle is an inhomogeneous sphere ($a/c=1$) or an inhomogeneous spheroid ($a/c\ne 1$), which is a well-formed rounded particle. In this study, the maximum size parameter of coated super-spheroids was assumed to be 50, although the size parameter of coarse-mode dust can be larger than 50 at visible wavelengths. The size parameter is defined in terms of the semi-major axes, namely, $2\pi /\lambda ·\max \left(a,c\right)$, where $\lambda$ is the wavelength of the incident light in the medium. In the computation, the resolution of size parameter is 0.1, one and two when the size parameter is in the range of [0.1,10] [10,20], and [20,50], respectively.

The real part of the complex refractive index of dust particles ranges from 1.4 to 1.6, whereas the imaginary part is on the order 10⁻³ at short wavelengths (e.g., Di Biagio et al., 2019; Zong et al., 2021). Therefore, we considered three real parts (1.4, 1.5, and 1.6) and four imaginary parts (5 × 10⁻⁴, 0.001, 0.005, and 0.01) to resolve potential uncertainties. For the shell part, we considered four real parts (1.3, 1.4, 1.5, and 1.6) and seven imaginary parts (10⁻⁷, 10⁻⁵, 10⁻⁴, 0.001, 0.005, 0.01, 0.05), which allow us to study different shell compositions, including water-soluble aerosols such as sulfate, nitrate, and sea salt aerosols.

The refractive index of water-soluble aerosols depends on the ambient relative humidity, so it usually varies between 1.33 and 1.55. According to Mishchenko et al. (2016), sulfate’s refractive indices at a relative humidity of 50% are 1.3813, 1.3684, and 1.3595 at 355, 532, and 1,064 nm, respectively. These values are little bit smaller than those reported by Bauer et al. (2007). The real part of the complex refractive index in a wavelength range of 300–2000 nm is between 1.3685 and 1.4247 for sulfate and between 1.3745 and 1.4205 for nitrate at 75% relative humidity. In this study, all numerical simulations were carried out at anchor points instead of refractive indices at specific wavelengths and relative humidity. The complex refractive indices involved in the GPU-IITM simulations are given in Table 1. In the following, the shell and core refractive indices are denoted as $m_{shell}=m_R^s+i{m}_I^s$ and $m_{core}=m_R^c+i{m}_I^c$, respectively.

TABLE 1

TABLE 1. The refractive indices used in the GPU-IITM simulations. The shell and core refractive indices are denoted as $m_{shell}=m_R^s+i{m}_I^s$ and $m_{core}=m_R^c+i{m}_I^c$, respectively. The values of $m_R^s$ in the parentheses indicates that simulations were carried out for a portion of nearly spherical shapes.

The IITM and Graphics Processing Unit Implementation

Consider the electromagnetic wave scattering by a macroscopic particle in a non-absorbing medium. The incident and scattered electric fields in terms of suitable vector spherical wave functions can be expanded as follows (Mishchenko, et al., 2002):

$E^{inc}\left(r\right)={\displaystyle \sum _{l=1}^{\infty }{a}_{l}Rg{M}_l\left(kr\right)}+b_{l}Rg{N}_l\left(kr\right)(2)$

$E^{sca}\left(r\right)={\displaystyle \sum _{l=1}^{\infty }{p}_l{M}_l\left(kr\right)}+q_l{N}_l\left(kr\right)(3)$

Thus, the T-matrix $\overline{\overline{T}}$ is defined by relating the expansion coefficients $\left(p_l,q_l\right)$ and $\left(a_l,b_l\right)$:

$\left[\begin{array}{c}{p}_l\\ q_l\end{array}\right]={\displaystyle \sum _{j=1}^{\infty }\left[\begin{array}{cc}{\overline{\overline{T}}}_{lj}^{11}& {\overline{\overline{T}}}_{lj}^{12}\\ {\overline{\overline{T}}}_{lj}^{21}& {\overline{\overline{T}}}_{lj}^{22}\end{array}\right]\left[\begin{array}{c}{a}_j\\ b_j\end{array}\right]},l=1,\infty .(4)$

In Eqs 2, 3, $k$ is the wave vector in the medium, Rg $M_l$ and $Rg{N}_l$ are the regular vector spherical functions, and $M_l$ and $N_l$ are the irregular vector spherical functions. The subscript $l=n\left(n+1\right)+m$, which is defined with respect to the total angular momentum number $n$ and the projected angular momentum $m$, which ranges from $-n$ to $n$. The T-matrix contains all the information involved in the light scattering process.

In the IITM method, coated super-spheroids are discretized into multiple spherical layers. The invariant imbedding equation to compute the T-matrix is (Bi and Yang, 2014):

$\overline{\overline{T}}\left(r_p\right)={\overline{\overline{Q}}}_{11}\left(r_p\right)+\left[\overline{\overline{I}}+{\overline{\overline{Q}}}_{12}\left(r_p\right)\right]{\left[\overline{\overline{I}}-\overline{\overline{T}}\left(r_{p-1}\right){\overline{\overline{Q}}}_{12}\left(r_p\right)\right]}^{-1}\overline{\overline{T}}\left(r_{p-1}\right)\left[\overline{\overline{I}}+{\overline{\overline{Q}}}_{21}\left(r_p\right)\right],(5)$

where $r_p$ is the radius of p-th layer, $\overline{\overline{T}}$ is the T-matrix of a particle composed of $p$ layers, $\overline{\overline{I}}$ is a unit matrix, and ${\overline{\overline{Q}}}_{ij}$ is a super-matrix. A 2D diagram is given in Figure 2. For convenience, the initial T-matrix $\overline{\overline{T}}\left(r_0\right)$ was computed from Lorenz-Mie theory at the position of the inscribed sphere $\left(r_0\right)$.

FIGURE 2

FIGURE 2. A geometric illustration of the invariant imbedding principle.

All ${\overline{\overline{Q}}}_{ij}$ matrices are computed from a common U-matrix $\overline{\overline{U}}$, which contains all the information on the particle shape and refractive index. Specifically, $\overline{\overline{U}}\left(r_p\right)$ is defined as an integral of special angular functions over the spherical surface indicated by $r_p$ . The refractive indices of either the core or the shell are chosen for computing the matrix $\overline{\overline{U}}\left(r_p\right)$, which depends on whether the location of the spherical surface is within the core or the shell. If the partial surface is located in the surrounding medium, the relevant integral in $\overline{\overline{U}}\left(r_p\right)$ is zero. The super-spheroid model has 4-fold symmetry such that $\overline{\overline{T}}$ is block diagonalized. For convenience, Eq. 5 can be separated into four independent equations for numerical implementation, which is similar to the procedure for ice crystals, which have 6-fold rotational symmetry (Bi and Yang, 2014). A complete formulation of the IITM for arbitrarily shaped non-spherical particles is available from Bi et al. (2013a) and Bi and Yang (2014).

To implement the IITM algorithm based on a GPU, we used the OpenACC and Compute Unified Device Architecture (CUDA) libraries. The OpenACC directives were added to the IITM code in a similar way to the use of OpenMP. Matrix multiplication and division were accelerated by the CUDA libraries. Large matrix multiplication was implemented using the cuBLAS library, and matrix division was implemented using the cuSOLVER library. The procedure of the GPU acceleration is illustrated in Figure 3. Four sub-matrices of the T-matrix are calculated separately in parallel. With each process by the MPI, one GPU is linked with the process to calculate one sub-T-matrix. For each new layer, the algorithm starts the calculation of the U-matrix, which is the only part that is dependent on the shape and refractive index.

FIGURE 3

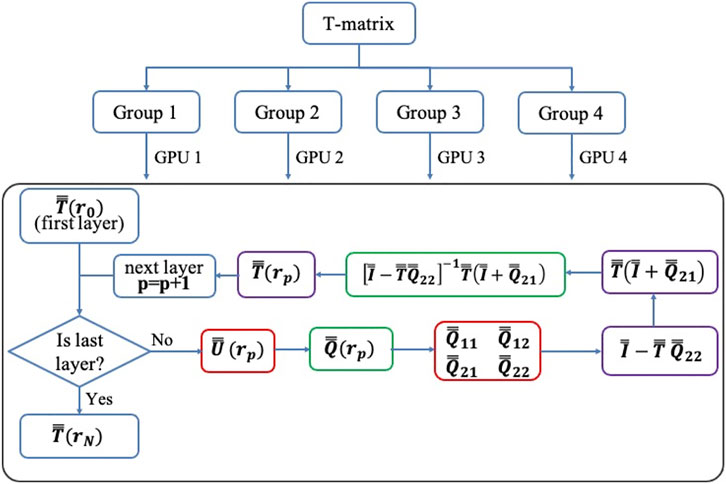
FIGURE 3. A flowchart of the GPU-IITM in calculating the T-matrix. The colored boxes means that GPU acceleration was used. The red boxes use OpenACC, and the green boxes use cuSOLVER for matrix division, and the purple boxes use cuBLAS for matrix multiplication.

The performance of the GPU-IITM was compared with that of the CPU version. For the numerical test, 24 Intel Xeon E5 CPUs were used, while two NVIDIA Tesla K80 accelerators were used for the GPU code. One Tesla K80 card contains two GPUs. The computational parameters of coated super-spheroids are $n_{core}=2.6$ (core roundness), $n_{shell}=1.5$ (shell roundness), $a/c=1.0$ (for both the shell and core), $m_{core}=1.5+\text{i}0.001$ (the core’s refractive index), and $m_{shell}=1.3+10$⁻⁷i (the shell’s refractive index). Figure 4 shows the wall-clock time when using 24 CPUs and four GPUs as function of the size parameter. The GPU-IITM implementation is about 8.4–25.9 times more efficient than the CPU implementation, and the GPU acceleration becomes more obvious as the size parameter increases. A drop in the computational time was identified when the size parameter was around 20 because the radius step ($r_p-r_{p-1}$) was changed from 0.1 to 0.2 in the IITM algorithm. Although the computations in this study were carried out at size parameters smaller than 50, the GPU-IITM can be applied to larger size parameters. The maximum size parameter that the current GPU-IITM code can handle depends on the video random access memory. Using a GPU of 12-Gb memory, the maximum size parameter is found to be ∼70. Note that the current GPU-IITM code exploits the symmetry of T-matrix so that different GPUs have no data communication. For arbitrarily shaped particles lacking any rotational symmetry, the GPU implementation requires additional technical effort and the acceleration ratio of GPU found in this study may decrease.

FIGURE 4

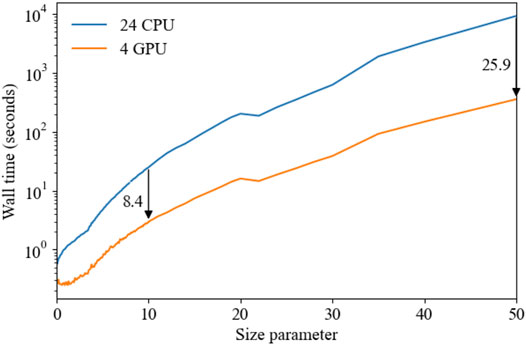
FIGURE 4. A comparison of the computational wall-clock time used for computing the optical properties of coated super-spheroid by using GPUs and CPUs. The wall-clock time ratios (the CPU time divided by the GPU time) are 8.4 and 25.9 at two chosen size parameters of 10 and 50 (indicated with arrows), respectively.

All the optical properties are computed from the T-matrix. However, in this study, we focus on analyzing the LDRs of coated super-spheroids. LDRs with direct backscattering are computed from the elements $P_{11}$ and $P_{22}$ of the scattering matrix:

$LDR\left(\theta ={180}^o\right)=\frac{1-P_{22}\left({180}^o\right)/P_{11}\left({180}^o\right)}{1+P_{22}\left({180}^o\right)/P_{11}\left({180}^o\right)}.(6)$

For randomly oriented particles, $P_{22}\left({180}^o\right)/P_{11}\left({180}^o\right)$ can be proven to be larger than zero and smaller than unity, which is fundamentally related to the reciprocal symmetry in electromagnetic wave scattering (Mishchenko and Hovenier, 1995). As such, LDR is smaller than unity. However, the magnitudes of LDR have no simple relation with the particle shape and refractive index. It seems that the only known fact is that the LDR is zero for a homogeneous or layered sphere and has low values when the size parameter is small. This makes it valuable to perform systematical assessments of LDRs based on a rigorous computational method.

Results and Discussion

We first look at the impact of the refractive index on the LDRs. For simplicity, let the core refractive index be $m_{shell}=$ 1.5 + i0.005, which is a representative value of atmospheric dust. To examine the impact of absorption of the shell on the LDRs, Figure 5 shows the results of coated super-spheroids with six refractive indices of the shell, which have a fixed real part (1.3) and an imaginary part ranging from 10⁻⁵ to 0.05. The size parameter ranges from 0.1 to 50. The comparison indicates that the LDRs are relatively small when the size parameter is small (<10), regardless of the shape, the inhomogeneity and refractive indices. As expected, this feature should be consistent with the homogeneous cases. Furthermore, low LDR values were identified when the roundness parameter ($n_{shell}$) was unity, at which the particle is an inhomogeneous sphere. However, the LDRs are not exactly zeros because the internal core is a non-spherical particle.

FIGURE 5

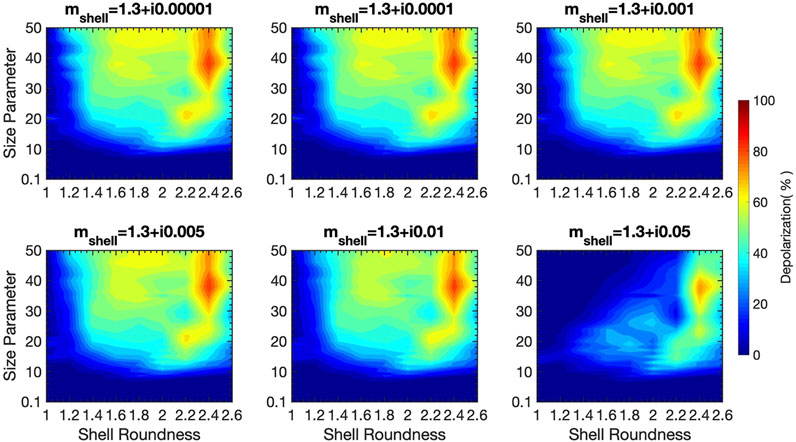
FIGURE 5. Linear depolarization ratios as function of size parameter and shell roundness. The core roundness is fixed to 2.6, and the aspect ratio is 1.0. The core refractive index is 1.5 + i0.005.

Five imaginary parts of the shell’s refractive index (10⁻⁵, 10⁻⁴, 10⁻³,0.005, and 0.01) were found to have similar impacts on the LDRs, although differences are expected to be large when the size parameter is sufficiently large (beyond 50 in the present study). Of particular interest is that coated super-spheroids at all refractive indices have higher LDRs when the shell roundness is ∼2.4, with which the particle has a thin coating (the particles are homogeneous super-spheroids at $n=2.6$). When the roundness parameter is larger than 2.2, the LDRs for the shell’s refractive index, $m_{shell}=1.3+i0.05$ are not so different from the other shell refractive indices. This phenomenon occurs because the absorption in the shell is not significant when the coating layer is thin, even with a large imaginary part of 0.05. However, as the shell roundness parameter decreases (<2.2), the absorption in the shell (with larger volume) should become strong enough to efficiently absorb an incident wave, causing lower LDRs upon backscattering.

Next, the imaginary part of the shell’s refractive index, $m_I^s$, was fixed at 0.00001 because the variation of $m_I^s$ between 0.00001 and 0.01 has little impact on the LDRs. $m_I^s=0.05$ was no longer considered because coating aerosols in the atmosphere are weakly absorptive at visible wavelengths except for black carbon or brown carbon. In the latter case, however, an aggregate black carbon model for the coating layer or a semi-external mixture model is more appropriate than a complete coating, and readers are referred to a previous study (Tang et al., 2019).

Next, we examined the impact of the particles’ aspect ratio on the LDRs. Figure 6 shows the results of coated super-spheroids with 11 aspect ratios. The refractive indices of the core and shell are 1.5 + i0.005 and 1.3 + i0.00001, respectively. For each aspect ratio, we examined the dependence of LDRs on the shell roundness parameter and the size parameter. Of most interest is that LDRs are higher around the shell roundness ($n_{shell}$) of 2.4 for all aspect ratios. As the aspect ratio varies, overall, the LDRs are relatively small when the ratio becomes extreme (e.g., for cases when the aspect ratio is smaller than 0.7 or larger than 1.8). As the shell roundness parameter decreases, the overall shape becomes an octahedron at $n=2.0$ and a spheroid at $n=1.0$. Optically, for $a/c<=0.7$ and $a/c>=1.6$, the LDRs have low values when ∼ $1.4<n<\sim 2.0$, but have relatively large values when the particle shape is close to a spheroid.

FIGURE 6

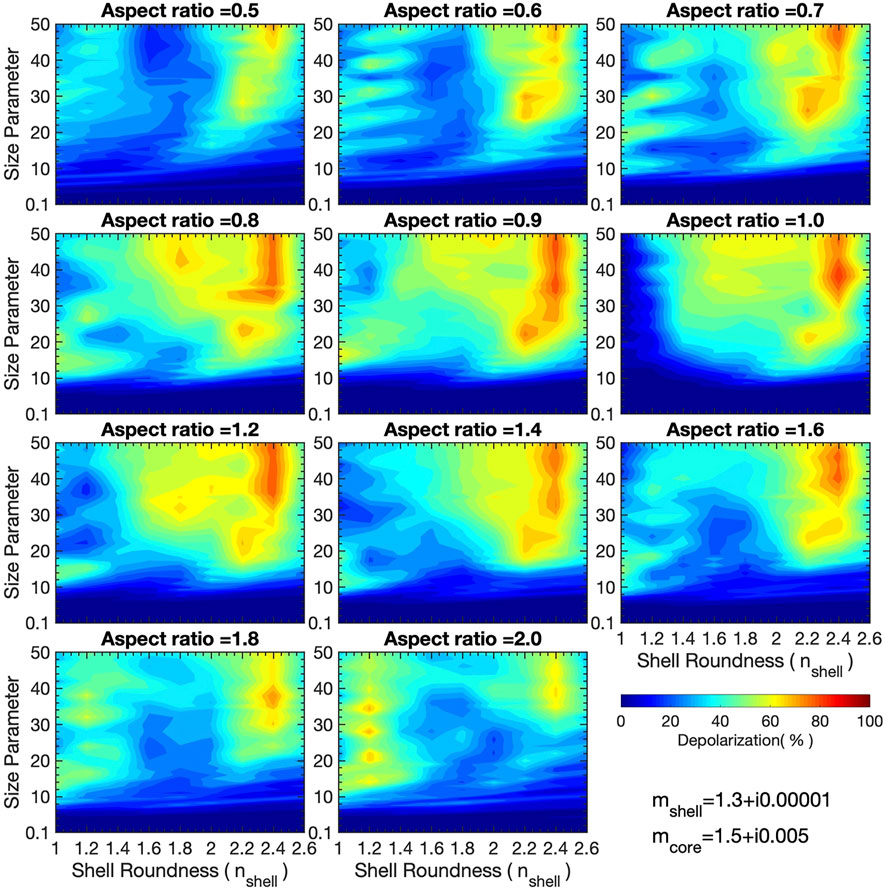
FIGURE 6. Linear depolarization ratios of coated super-spheroids with 11 aspect ratios (0.5–2.0) and nine shell roundness parameters (from 1.0 to 2.6). The core roundness is fixed at 2.6. The size parameter ranges from 0.1 to 50. The refractive indices of the core and shell are 1.5 + i0.005 and 1.3 + i0.00001, respectively.

Figures 7–9 are similar to Figure 6 except that the real parts of the shells’ refractive indices are different. When the shell’s refractive index is 1.4 + i0.00001, the results are similar to those at 1.3 + i0.00001 but with the decreased LDR values. LDRs further decrease when $m_R^s$ increases to 1.5 (Figure 8) and 1.6 (Figure 9). The fundamental reason is similar to the findings of a previous study for homogeneous super-spheroids (Bi et al., 2018a). As the real part increases, the external reflection (with no depolarization) becomes stronger, and the higher-order wave transmitted to backscattering (with high depolarization) is weaker, which results in smaller LDRs in the total backscattering. This mechanism is different from that of an aggregate particle, where multiple external reflections can also cause the depolarization of incident light, which is expected to increase as the real part of refractive index increases (e.g., Liu et al., 2022). Figure 8 can be reasonably viewed as a case of homogeneous spheroids because the refractive indices of the core and shell are close. Thus, visual comparison of Figures 6–9 reveals the impact of particle inhomogeneity.

FIGURE 7

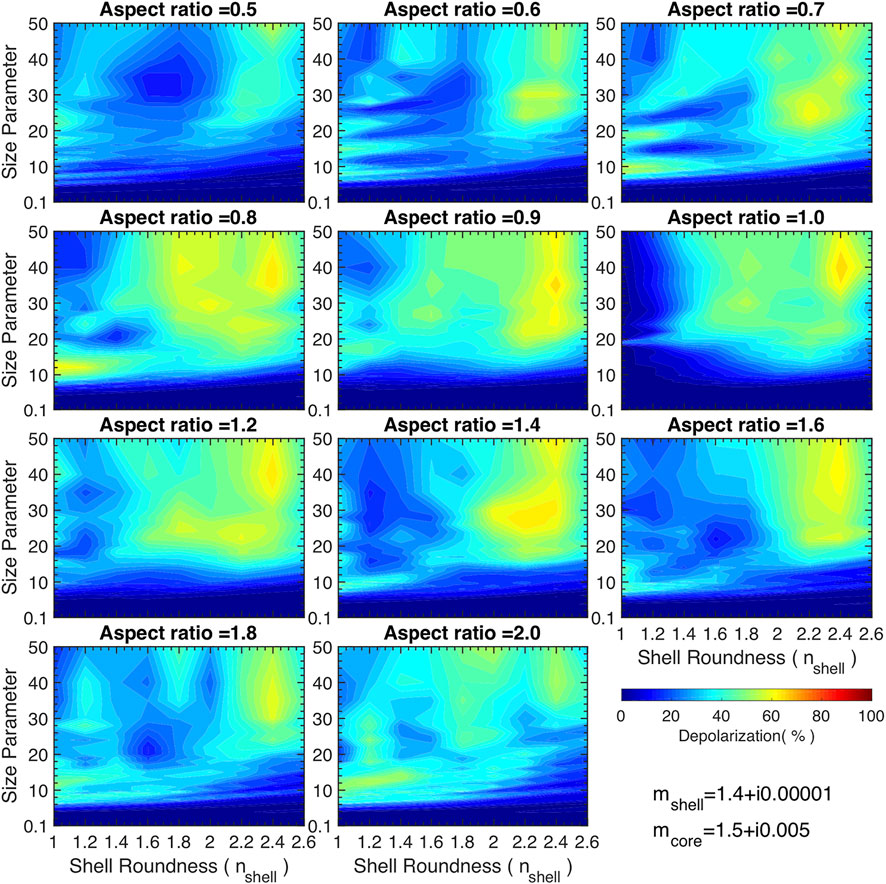
FIGURE 7. Linear depolarization ratios of coated super-spheroids with 11 aspect ratios (0.5–2.0) and nine shell roundness parameters (from 1.0 to 2.6). The core roundness is fixed at 2.6. The size parameter ranges from 0.1 to 50. The refractive indices of the core and shell are 1.5 + i0.005 and 1.4 + i0.00001, respectively.

FIGURE 8

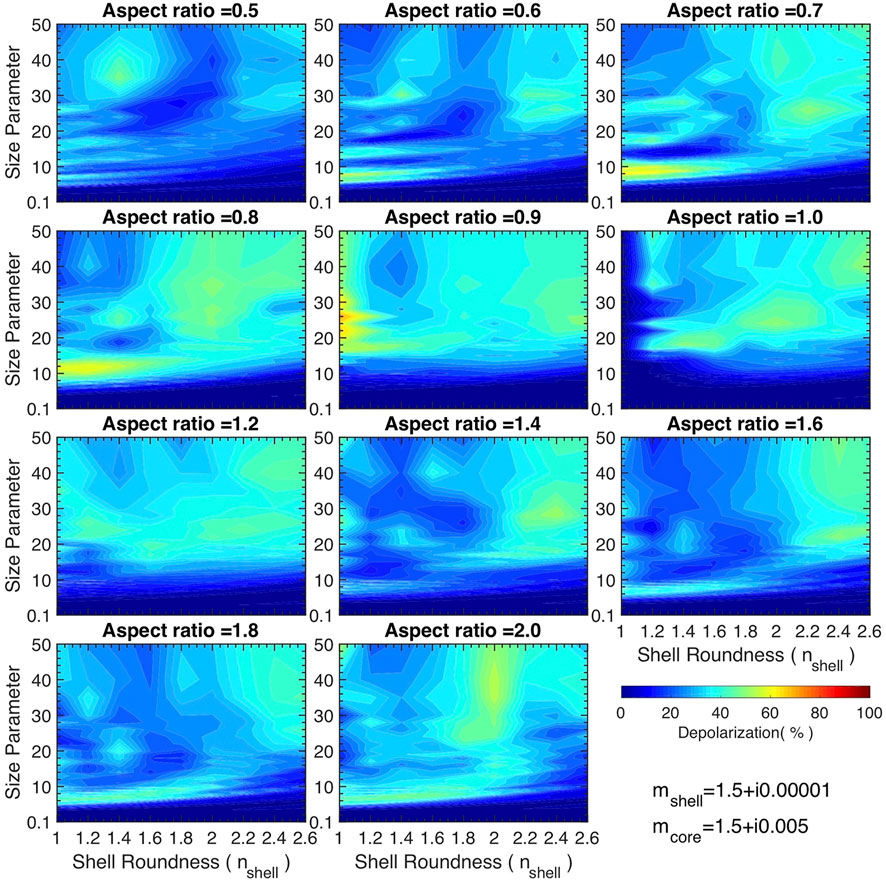
FIGURE 8. Linear depolarization ratios of coated super-spheroids with 11 aspect ratios (0.5–2.0) and nine shell roundness parameters (from 1.0 to 2.6). The core roundness is fixed at 2.6. The size parameter ranges from 0.1 to 50. The refractive indices of the core and shell are 1.5 + i0.005 and 1.5 + i0.00001, respectively.

FIGURE 9

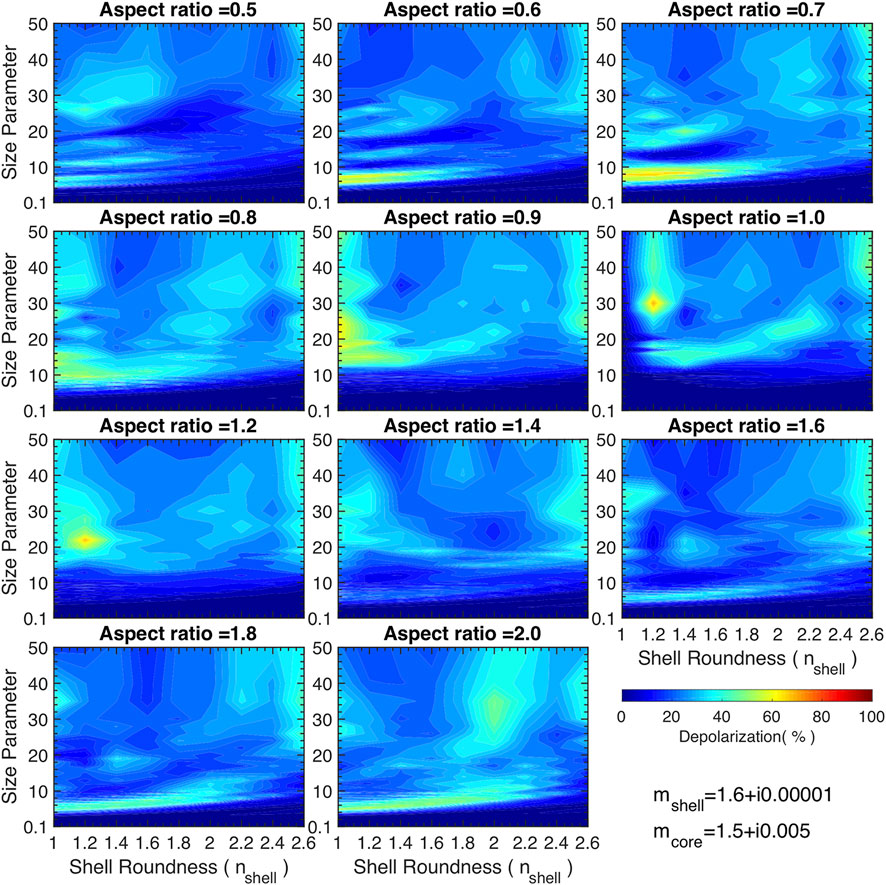
FIGURE 9. Linear depolarization ratios of coated super-spheroids with 11 aspect ratios (0.5–2.0) and nine shell roundness parameters (from 1.0 to 2.6). The core roundness is fixed at 2.6. The size parameter ranges from 0.1 to 50. The refractive indices of the core and shell are 1.5 + i0.005 and 1.6 + i0.00001, respectively.

Nearly spherical particles are nonspherical particles of which both the aspect ratios and roundness parameters are close to unity. For these particles, the LDRs could be enhanced, which can be clearly seen in the cases (aspect ratio = 0.9 and the roundness parameters close to unity) shown in Figures 6–9. Mishchenko and Hovenier (1995) first discovered the remarkable phenomenon of LDRs peaking at aspect ratios of spheroids very close to unity at a refractive index close to 1.5. For homogeneous spheroids and super-spheroids, higher LDRs for nearly spherical particles were closely examined by resolving the refractive index variation in previous studies by using a Debye series technique (Bi et al., 2018a; 2018b). It was found that higher LDRs (>∼60%) are common for optically soft particles (the real part of the complex refractive index is smaller than ∼1.2). However, for larger real parts of the complex refractive indices (>1.3), higher LDRs (>∼60%) are almost only observed for nearly spherical particles. This unique phenomenon disappears as the refractive index exceeds 1.7. We note that Gialitaki et al. (2020) recently explored the use of near-spherical-shaped particles to reproduce the triple-wavelength HSRL observations.

To further examine the LDRs of nearly spherical coated super-spheroids, Figure 10 shows the LDRs for inhomogeneous spheroidal particles with aspect ratios of 0.8–1.2 and a fine resolution of 0.01. For the purpose of comparison, the LDRs for homogeneous spheroids are shown in Figure 11. The refractive index of homogeneous spheroids is the same as that of the shell’s refractive index shown in Figure 10. It is evident that the LDRs for inhomogeneous spheroids are smaller than those of homogeneous spheroids when the real part of the shell’s refractive index (1.3, 1.35, and 1.45) is smaller than the core refractive index (1.5). However, enhanced LDRs are still obvious when the real part of the shell’s refractive index (e.g., $m_R^s=1.45$) is close to the core refractive index ($m_R^c=\mathrm{1..5}$). The conclusion holds the same when $m_R^s=1.48$ (results not shown). When the shell’s refractive index is 1.5 + i0.00001, the particle is almost homogeneous except that the imaginary parts of the shell and core refractive index have some difference. As such, the LDRs for homogeneous and inhomogeneous spheroids are close. Interestingly, when the real part of the shell’s refractive index (1.6) is larger than that of the core (1.5), the LDRs of inhomogeneous spheroids are larger than those of homogeneous spheroids.

FIGURE 10

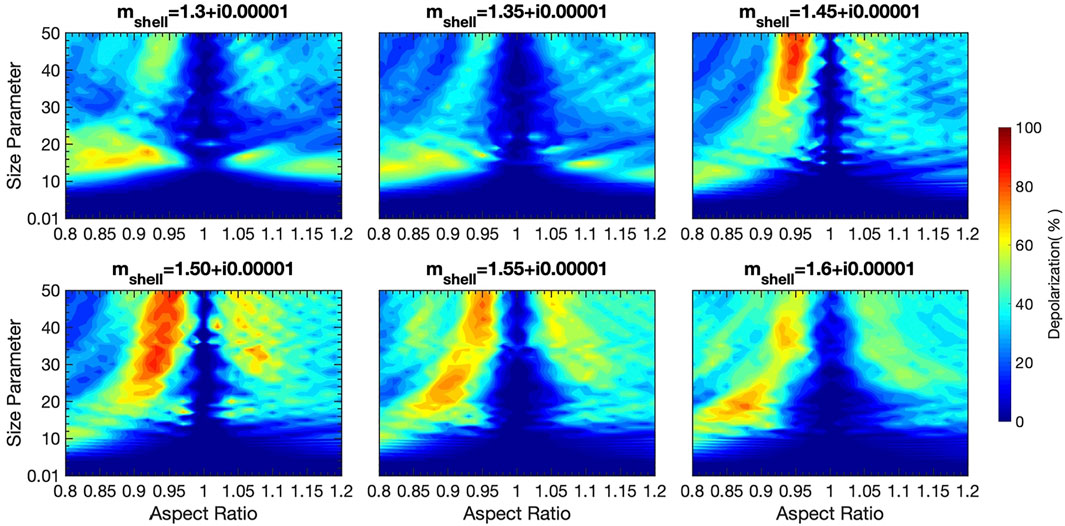
FIGURE 10. Linear depolarization ratios for nearly spherical particles (inhomogeneous spheroids). The core refractive index is 1.5 + i0.005. When the aspect ratio is unity, LDRs are small but not exactly zeros because the core is a non-spherical particle.

FIGURE 11

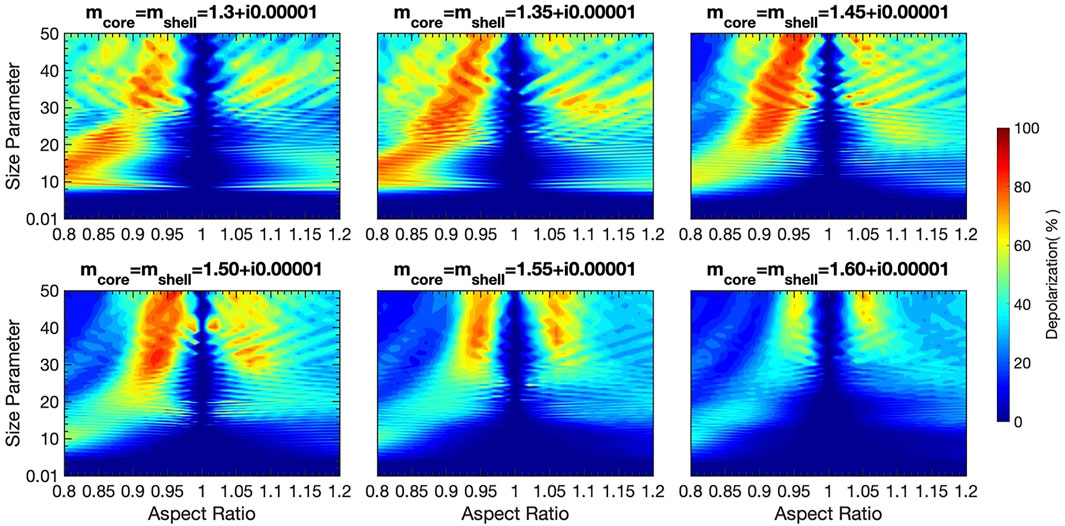
FIGURE 11. Linear depolarization ratios for nearly spherical particles (homogeneous spheroids). Both the shell and core refractive indices are identical.

From the previous results, it is clear that the LDRs of coated super-spheroids are significantly different from those of homogeneous super-spheroids. The most interesting phenomenon could be the higher LDRs for super-spheroids with thin coating. The conditions of a thin coating might be relevant to dust particles in an ambient atmospheric environment when the relative humidity is not high. Previous findings of higher LDRs for nearly spherical homogeneous particles might still be interesting for coated dust particles because nearly spherical coated dust could be common for high relative humilities according to TEM images. The refractive indices of the coating (sulfate, nitrate, and water aerosols) are smaller than the refractive index of dust, which causes lower LDRs in comparison with homogeneous particles with respect to the shell’s refractive index. However, higher LDRs are still observable, particularly when the refractive index of water-soluble aerosols is close to the refractive index of dust.

For particles with a high degree of non-sphericity, the refractive index of the coating shell is critical to the LDRs. The LDRs are generally larger for smaller real parts of the shell’s refractive indices. This feature is quite interesting because the required condition for the refractive index (<∼1.4) is close to real situations. Therefore, we believe that these findings from a purely theoretical simulation might be useful for relevant optical interpretation in lidar observations. Future work could involve a systematic comparison between simulations and lidar observations of dust particles in a polluted region, which could provide interesting and important results.

Conclusion

We have developed a GPU implementation of IITM for computing the optical properties of coated super-spheroids, which was much more efficient than the conventional CPU implementation. The acceleration ratio was from approximately 8–25 depending on the size parameter. Based on the GPU-IITM implementation, the optical properties of coated super-spheroids with extensive shapes, sizes, and refractive indices were obtained, and comparisons of the results of coated super-spheroids with those of homogeneous super-spheroids were carried out. Substantial differences could occur, particularly in the lidar backscattering optical properties.

Higher LDRs were found when dust particles had thin coatings. However, the LDRs decreased as the coating particles became rounder. In addition, the LDRs decreased obviously as the real part of the shell’s refractive index increased from 1.3 to 1.6. Special attention should be given to nearly spherical particles, for which the LDRs could be higher, particularly when the real part of shell’s refractive index is close to or larger than the core refractive index. The higher LDRs found for homogeneous nearly spherical particles in the refractive range of 1.3–1.5 were lower when the particle inhomogeneity was incorporated. These findings are expected to have implications in lidar remote sensing, particularly on hazy days when dust particles are mixed with air pollutants.

In this study, we only focused on analyzing the difference of LDRs caused by the particle shell-structure. The differences in the extinction efficiency, single-scattering albedo, and phase matrix are relevant for improving the radiative transfer simulations in remote sensing and climate modeling. However, the analysis of these factors in applications of atmospheric models is beyond the scope of this study. Readers are referred to a recent publication on the evaluation of an internally mixed scheme in the weather-research and forecasting model (Wang et al., 2022).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

LB: Conceptualization, Methodology, Investigation, Software, Writing; ZW: Methodology, Software, Editorial; WH: Discussion, Editorial, Funding; WL: Discussion, Editorial; XZ: Discussion, Editorial, Funding.

Funding

This research was supported by the NSFC Major Project (42090030) and the National Natural Science Foundation of China (42022038).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge Ms. Rui Liu at the Training Center of Atmospheric Sciences of Zhejiang University for her help with managing computing resources. A portion of the computations were performed on the National Supercomputer Center in Guangzhou (NSCC-GZ), Tianjin (NSCC-TJ), and Wuxi (NSCC-WX) and the cluster at State Key Lab of CAD&CG at Zhejiang University. We acknowledge the use of cuSOLVER (https://docs.nvidia.com/cuda/cusolver/index.html) and cuBLAS (https://docs.nvidia.com/cuda/cublas/index.html) libraries.

References

Barr, A. H. (1981). Superquadrics and Angle-Preserving Transformations. IEEE Comp. Graphics Appl. 1 (01), 11–23. doi:10.1109/mcg.1981.1673799

CrossRef Full Text | Google Scholar

Bauer, S. E., Mishchenko, M. I., Lacis, A. A., Zhang, S., Perlwitz, J., and Metzger, S. M. (2007). Do sulfate and Nitrate Coatings on mineral Dust Have Important Effects on Radiative Properties and Climate Modeling? J. Geophys. Res. 112, D06307. doi:10.1029/2005jd006977

CrossRef Full Text | Google Scholar

Bi, L., Lin, W., Liu, D., and Zhang, K. (2018a). Assessing the Depolarization Capabilities of Nonspherical Particles in a Super-ellipsoidal Shape Space. Opt. Express 26 (2), 1726–1741. doi:10.1364/oe.26.001726

PubMed Abstract | CrossRef Full Text | Google Scholar

Bi, L., Lin, W., Wang, Z., Tang, X., Zhang, X., and Yi, B. (2018b). Optical Modeling of Sea Salt Aerosols: The Effects of Nonsphericity and Inhomogeneity. J. Geophys. Res. Atmos. 123, 543–558. doi:10.1002/2017jd027869

CrossRef Full Text | Google Scholar

Bi, L., and Yang, P. (2014). Accurate Simulation of the Optical Properties of Atmospheric Ice Crystals with the Invariant Imbedding T-Matrix Method. J. Quantitative Spectrosc. Radiative Transfer 138, 17–35. doi:10.1016/j.jqsrt.2014.01.013

CrossRef Full Text | Google Scholar

Bi, L., Yang, P., Kattawar, G. W., and Mishchenko, M. I. (2013b). A Numerical Combination of Extended Boundary Condition Method and Invariant Imbedding Method Applied to Light Scattering by Large Spheroids and Cylinders. J. Quantitative Spectrosc. Radiative Transfer 123, 17–22. doi:10.1016/j.jqsrt.2012.11.033

CrossRef Full Text | Google Scholar

Bi, L., Yang, P., Kattawar, G. W., and Mishchenko, M. I. (2013a). Efficient Implementation of the Invariant Imbedding T-Matrix Method and the Separation of Variables Method Applied to Large Nonspherical Inhomogeneous Particles. J. Quantitative Spectrosc. Radiative Transfer 116, 169–183. doi:10.1016/j.jqsrt.2012.11.014

CrossRef Full Text | Google Scholar

Chen, S.-L., Chang, S.-W., Chen, Y.-J., and Chen, H.-L. (2021). Possible Warming Effect of fine Particulate Matter in the Atmosphere. Commun. Earth Environ. 2, 208. doi:10.1038/s43247-021-00278-5

CrossRef Full Text | Google Scholar

Di Biagio, C., Formenti, P., Balkanski, Y., Caponi, L., Cazaunau, M., Pangui, E., et al. (2019). Complex Refractive Indices and Single-Scattering Albedo of Global Dust Aerosols in the Shortwave Spectrum and Relationship to Size and Iron Content. Atmos. Chem. Phys. 19, 15503–15531. doi:10.5194/acp-19-15503-2019

CrossRef Full Text | Google Scholar

Draine, B. T. (1988). The Discrete-Dipole Approximation and its Application to Interstellar Graphite Grains. ApJ 333, 848–872. doi:10.1086/166795

CrossRef Full Text | Google Scholar

Dubovik, O., Li, Z., Mishchenko, M. I., Tanré, D., Karol, Y., Bojkov, B., et al. (2019). Polarimetric Remote Sensing of Atmospheric Aerosols: Instruments, Methodologies, Results, and Perspectives. J. Quantitative Spectrosc. Radiative Transfer 224, 474–511. doi:10.1016/j.jqsrt.2018.11.024

CrossRef Full Text | Google Scholar

Dubovik, O., Sinyuk, A., Lapyonok, T., Holben, B. N., Mishchenko, M., Yang, P., et al. (2006). Application of Spheroid Models to Account for Aerosol Particle Nonsphericity in Remote Sensing of Desert Dust. J. Geophys. Res. 111, D11208. doi:10.1029/2005jd006619

CrossRef Full Text | Google Scholar

Egel, A., Pattelli, L., Mazzamuto, G., Wiersma, D. S., and Lemmer, U. (2017). CELES: CUDA-Accelerated Simulation of Electromagnetic Scattering by Large Ensembles of Spheres. J. Quantitative Spectrosc. Radiative Transfer 199, 103–110. doi:10.1016/j.jqsrt.2017.05.010

CrossRef Full Text | Google Scholar

Gialitaki, A., Tsekeri, A., Amiridis, V., Ceolato, R., Paulien, L., Kampouri, A., et al. (2020). Is the Near-Spherical Shape the "new Black" for Smoke? Atmos. Chem. Phys. 20, 14005–14021. doi:10.5194/acp-20-14005-2020

CrossRef Full Text | Google Scholar

Huntemann, M., Heygster, G., and Hong, G. (2011). Discrete Dipole Approximation Simulations on GPUs Using OpenCL-Application on Cloud Ice Particles. J. Comput. Sci. 2 (3), 262–271. doi:10.1016/j.jocs.2011.05.011

CrossRef Full Text | Google Scholar

Iadarola, G., Forestiere, C., Dal Negro, L., Villone, F., and Miano, G. (2012). GPU-accelerated T-Matrix Algorithm for Light-Scattering Simulations. J. Comput. Phys. 231 (17), 5640–5652. doi:10.1016/j.jcp.2012.03.008

CrossRef Full Text | Google Scholar

Kahnert, M., Nousiainen, T., and Lindqvist, H. (2014). Review: Model Particles in Atmospheric Optics. J. Quantitative Spectrosc. Radiative Transfer 146, 41–58. doi:10.1016/j.jqsrt.2014.02.014

CrossRef Full Text | Google Scholar

Kong, S., Sato, K., and Bi, L. (2022). Lidar Ratio-Depolarization Ratio Relations of Atmospheric Dust Aerosols: The Super‐Spheroid Model and High Spectral Resolution Lidar Observations. JGR Atmospheres 127, e2021JD035629. doi:10.1029/2021JD035629

CrossRef Full Text | Google Scholar

Li, M., Bi, L., Lin, W., Weng, F., He, S., and Zhang, X. (2022). The Inhomogeneity Effect of Sea Salt Aerosols on the TOA Polarized Radiance at the Scattering Angles Ranging from 170° to 175°. IEEE Trans. Geosci. Remote Sensing 60 (1–12), 4102912. doi:10.1109/tgrs.2021.3099026

CrossRef Full Text | Google Scholar

Li, W. J., and Shao, L. Y. (2009). Observation of Nitrate Coatings on Atmospheric Mineral Dust Particles. Atmos. Chem. Phys. 9 (6), 1863–1871. doi:10.5194/acp-9-1863-2009

CrossRef Full Text | Google Scholar

Lin, W., Bi, L., and Dubovik, O. (2018). Assessing Superspheroids in Modeling the Scattering Matrices of Dust Aerosols. J. Geophys. Res. Atmospheres 123, 13917–13943. doi:10.1029/2018jd029464

CrossRef Full Text | Google Scholar

Lin, W., Bi, L., Weng, F., Li, Z., and Dubovik, O. (2021). Capability of Superspheroids for Modeling PARASOL Observations under Dusty‐Sky Conditions. J. Geophys. Res. Atmos. 126 (1), e2020JD033310. doi:10.1029/2020jd033310

CrossRef Full Text | Google Scholar

Liu, C., Lee Panetta, R., and Yang, P. (2012). Application of the Pseudo-spectral Time Domain Method to Compute Particle Single-Scattering Properties for Size Parameters up to 200. J. Quantitative Spectrosc. Radiative Transfer 113, 1728–1740. doi:10.1016/j.jqsrt.2012.04.021

CrossRef Full Text | Google Scholar

Liu, L., Schuster, G. L., Moosmüller, H., Stamnes, S., Cairns, B., and Chowdhary, J. (2022). Optical Properties of Morphologically Complex Black Carbon Aerosols: Effects of Coatings. J. Quantitative Spectrosc. Radiative Transfer 281, 108080. doi:10.1016/j.jqsrt.2022.108080

CrossRef Full Text | Google Scholar

Mackowski, D. W., and Mishchenko, M. I. (1996). Calculation of the T Matrix and the Scattering Matrix for Ensembles of Spheres. J. Opt. Soc. Am. A. 13, 2266–2278. doi:10.1364/josaa.13.002266

CrossRef Full Text | Google Scholar

Mishchenko, M. I., Travis, L. D., and Lacis, A. A. (2002). Scattering, Absorption and Emission of Light by Small Particles. Cambridge: Cambridge University Press.

Google Scholar

Mishchenko, M. I., Dlugach, J. M., and Liu, L. (2016). Linear Depolarization of Lidar Returns by Aged Smoke Particles. Appl. Opt. 55, 9968–9973. doi:10.1364/ao.55.009968

PubMed Abstract | CrossRef Full Text | Google Scholar

Mishchenko, M. I., and Hovenier, J. W. (1995). Depolarization of Light Backscattered by Randomly Oriented Nonspherical Particles. Opt. Lett. 20 (12), 1356–1358. doi:10.1364/OL.20.001356

PubMed Abstract | CrossRef Full Text | Google Scholar

Mishchenko, M. I., Liu, L., Travis, L. D., and Lacis, A. A. (2004). Scattering and Radiative Properties of Semi-external versus External Mixtures of Different Aerosol Types. J. Quantitative Spectrosc. Radiative Transfer 88, 139–147. doi:10.1016/j.jqsrt.2003.12.032

CrossRef Full Text | Google Scholar

Muñoz, O., Moreno, F., Guirado, D., Dabrowska, D. D., Bolten, H., and Hovenier, J. W. (2012). The Amsterdam-Granada Light Scattering Database. J. Quantitative Spectrosc. Radiative Transfer 113 (7), 565–574.

Google Scholar

Purcell, E. M., and Pennypacker, C. R. (1973). Scattering and Absorption of Light by Nonspherical Dielectric Grains. ApJ 186, 705–714. doi:10.1086/152538

CrossRef Full Text | Google Scholar

Sun, L.-H., Bi, L., and Yi, B. (2021). The Use of Superspheroids as Surrogates for Modeling Electromagnetic Wave Scattering by Ice Crystals. Remote Sensing 13 (9), 1733. doi:10.3390/rs13091733

CrossRef Full Text | Google Scholar

Tang, X., Bi, L., Lin, W., Liu, D., Zhang, K., and Li, W. (2019). Backscattering Ratios of Soot-Contaminated Dusts at Triple LiDAR Wavelengths: T-Matrix Results. Opt. Express 27 (4), A92–A116. doi:10.1364/OE.27.000A92

PubMed Abstract | CrossRef Full Text | Google Scholar

Tomasi, C., Fuzzi, S., and Kokhanovsky, A. (2017). Atmospheric Aerosols: Life Cycles and Effects on Air Quality and Climate. Weinheim, Germany: Wiley, 708.

Google Scholar

Unga, F., Choël, M., Derimian, Y., Deboudt, K., Dubovik, O., and Goloub, P. (2018). Microscopic Observations of Core-Shell Particle Structure and Implications for Atmospheric Aerosol Remote Sensing. J. Geophys. Res. Atmospheres 123, 13944–13962. doi:10.1029/2018jd028602

CrossRef Full Text | Google Scholar

Wang, H., Shi, G. Y., Zhang, X. Y., Gong, S. L., Tan, S. C., Chen, B., et al. (2015). Mesoscale Modelling Study of the Interactions between Aerosols and PBL Meteorology during a Haze Episode in China Jing-Jin-Ji and its Near Surrounding Region - Part 2: Aerosols' Radiative Feedback Effects. Atmos. Chem. Phys. 15, 3277–3287. doi:10.5194/acp-15-3277-2015

CrossRef Full Text | Google Scholar

Wang, W., Shao, L., Mazzoleni, C., Li, Y., Kotthaus, S., Grimmond, S., et al. (2021). Measurement Report: Comparison of Wintertime Individual Particles at Ground Level and above the Mixed Layer in Urban Beijing. Atmos. Chem. Phys. 21, 5301–5314. doi:10.5194/acp-21-5301-2021

CrossRef Full Text | Google Scholar

Wang, Z., Bi, L., Wang, H., Wang, Y., Han, W., and Zhang, X. (2022). Evaluation of a New Internally-Mixed Aerosol Optics Scheme in the Weather Research and Forecasting Model. J. Quantitative Spectrosc. Radiative Transfer 283, 108147. doi:10.1016/j.jqsrt.2022.108147

CrossRef Full Text | Google Scholar

Xu, F., Gao, L., Redemann, J., Flynn, C. J., Espinosa, W. R., da Silva, A. M., et al. (2021). A Combined Lidar-Polarimeter Inversion Approach for Aerosol Remote Sensing over Ocean. Front. Remote Sens. 2, 620871. doi:10.3389/frsen.2021.620871

CrossRef Full Text | Google Scholar

Yang, P., Hioki, S. S., Saito, M., Kuo, C.-P., Baum, B., and Liou, K.-N. (2018). A Review of Ice Cloud Optical Property Models for Passive Satellite Remote Sensing. Atmosphere 9, 499. doi:10.3390/atmos9120499

CrossRef Full Text | Google Scholar

Yang, P., and Liou, K. N. (1996). Finite-difference Time Domain Method for Light Scattering by Small Ice Crystals in Three-Dimensional Space. J. Opt. Soc. Am. A. 13, 2072–2085. doi:10.1364/josaa.13.002072

CrossRef Full Text | Google Scholar

Yurkin, M. A., and Hoekstra, A. G. (2007). The Discrete Dipole Approximation: an Overview and Recent Developments. J. Quantitative Spectrosc. Radiative Transfer 106, 558–589. doi:10.1016/j.jqsrt.2007.01.034

CrossRef Full Text | Google Scholar

Zhang, X., Duan, J., Dai, C., and Wei, H. (2020). Linear Depolarization Ratios of Nitrate-Coated mineral Dust Particles in Haze Episodes. Appl. Opt. 59, 2057–2064. doi:10.1364/ao.385225

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Wei, H., Zou, S., Duan, J., Li, W., and Dai, C. (2022). Effect of Nitrate Coatings on the Optical Properties of mineral Dust Particles during the Haze Aging Process. J. Quantitative Spectrosc. Radiative Transfer 277, 107966. doi:10.1016/j.jqsrt.2021.107966

CrossRef Full Text | Google Scholar

Zong, R., Weng, F., Bi, L., Lin, X., Rao, C., and Li, W. (2021). Impact of Hematite on Dust Absorption at Wavelengths Ranging from 02 to 10 μm: an Evaluation of Literature Data Using the T-Matrix Method. Opt. Express 29 (11), 17405–17427. doi:10.1364/oe.427611

PubMed Abstract | CrossRef Full Text | Google Scholar