- 1Optical Remote Sensing Laboratory, The City College of New York, New York, NY, United States
- 2Earth and Environmental Sciences, The Graduate Center, New York, NY, United States
- 3Remote Sensing Division, Naval Research Laboratory, Washington, DC, United States
- 4College of Marine Science, University of South Florida, St. Petersburg, FL, United States
- 5NASA Goddard Space Flight Center, Greenbelt, MD, United States
Uncertainties in the retrieval of the remote sensing reflectance, Rrs, from Ocean Color (OC) satellite sensors have a strong impact on the performance of algorithms for the estimation of chlorophyll-a, mineral concentrations, and inherent optical properties (IOPs). The uncertainties are highest in the blue bands. The total radiance measured at the top of the atmosphere captures the instantaneous state of the atmosphere-ocean system: the in-water conditions, sky and Sun glint reflected from the wind-roughened ocean surface, as well as light scattered from molecules and aerosols in the atmosphere. Each of these components has associated uncertainties, and when combined with the additional uncertainties from the instrument noise and the atmospheric correction process, they contribute to the total uncertainty budget for the retrieved Rrs. We analyzed the contribution of each component uncertainties to the total Rrs uncertainties in SNPP-VIIRS level 2 products, taking advantage of the spectral differences between the components. We examined multiple scenes in the open ocean and coastal waters at spatial resolutions ranging from 2250 to 5250 m by comparing the retrieved Rrs to in situ measurements made at several AERONET-OC sites and at the MOBY site. It was shown that uncertainties associated with the molecular (Rayleigh) scattering play the most significant role, while the contributions of other components are usually smaller. Uncertainties in Rayleigh scattering are primarily attributed to the variability of Rayleigh optical thickness (ROT) with a standard deviation of approximately 1.5% of ROT, which can largely explain the frequency of negative Rrs retrievals as observed using the current standard atmospheric correction process employed by NASA. Variability of the sky light reflected from the ocean surface in some conditions also contributed to uncertainties in the blue; water variability proportional to Rrs had a very pronounced peak in the green at coastal sites.
Introduction
Ocean Color (OC) is indicative of ocean health and biochemistry, and for that reason is listed as an essential climate variable (ECV) (IOCCG, 2008). The color of a water body is determined by scattering and absorption of pure water and its natural constituents, such as phytoplankton, non-algal particles, and colored dissolved organic matter (CDOM) (Mobley, 1994). Some phytoplankton species form harmful algal blooms (HABs), which can be toxic and affect human and marine life, and more generally the health of the ecosystem, fishing industry, and recreation activities (IOCCG, 2021). Typically, less than 10 percent of the top of the atmosphere (TOA) radiance is due to the water signal at sea level (Gordon and Morel, 1983), with the remainder originating from scattering processes in the atmosphere and reflections of the Sun and sky on the wave-roughened water surface. It is paramount to accurately estimate radiances at the surface level from the ones at the TOA, as uncertainties propagate into the retrieval of water parameters, characteristics of in-water particulates, concentrations of chlorophyll-a, and detection of algal blooms (IOCCG, 2010; IOCCG, 2019).
Atmospheric correction uncertainties stem at least partially from the estimation of aerosol models, and air–water interface effects due to sky and Sun light reflections at the wind-roughened air–water interface (Gordon and Wang, 1992; Gordon and Wang, 1994; Frouin et al., 1996; Wang and Bailey, 2001; Ahmad et al., 2010; Frouin et al., 2019). Atmospheric correction uncertainties often have a stronger impact on retrievals in coastal waters with low water reflectance values in the blue bands (Carrizo et al., 2019; Groetsch et al., 2020; Wei et al., 2020). Currently, high uncertainties in the blue reflectance observations are widely acknowledged (IOCCG, 2019; Wei et al., 2020; Li et al., 2019; Herrera-Estrella et al., 2020). However, little is known about the specific dependencies of uncertainties concerning their spectral and scaling behavior in various water areas, and their dependence on meteorological conditions.
The spectra of aerosol radiances in coastal areas are significantly affected by the presence of absorbing aerosols (Gordon et al., 1997; Ransibrahmanakul and Stumpf, 2006; Shi and Wang, 2007). Atmospheric correction processing schemes for the current satellite sensors do not account for this effect due to a lack of information about aerosol parameters, and it is assumed that this leads to negative values of Rrs in blue bands (Frouin et al., 2019). This makes the estimation of chlorophyll concentration and water parameters inaccurate in such waters. Several partial solutions to this problem are found in the existing literature and include more complex processing in the atmospheric correction (Gordon et al., 1997; Oo et al., 2008), removal of the uncertainty as a power law-like “artifact” with exponent -6 (Ransibrahmanakul and Stumpf, 2006), neural network approaches (Fan et al., 2021), utilization of atmospheric correction algorithms based on the fitting of Rayleigh spectra (Steinmetz et al., 2011; Zhang et al., 2019), and simply avoiding blue bands in algorithms for the retrieval of water parameters (El-Habashi et al., 2019; Gilerson et al., 2021). The upcoming NASA PACE mission (Werdell et al., 2019) will have the hyperspectral Ocean Color Instrument (OCI) and two polarimeters on board, which are expected to provide broader information on aerosol parameters. With these, atmospheric correction processing is expected to be significantly improved. However, for the current sensors, it is important to have a more accurate understanding of the impact of absorbing aerosols on Rrs retrievals.
There are differences in the terminology regarding “uncertainties.” In the Guide to Uncertainty in Measurement (Sayer et al., 2020), uncertainty is defined as an expression of the dispersion of the measurand (in our case, Rrs retrieved from satellite observations), and it is often represented as one standard deviation around the retrieved value. In our case, the standard deviation would represent Rrs uncertainties due to spatial variability (Herrera-Estrella et al., 2021), where the difference between the mean Rrs value and “true” Rrs value is up to 4–5 times greater than one standard deviation. In this work, uncertainties of Rrs will be described as the root mean square difference (RMSD) between the mean Rrs value determined from satellite data and in situ Rrs, which is considered as a “true” value, similar to the approach in IOCCG (2019).
The estimation of the uncertainties can be carried out by the comparison of the parameters determined from the satellite imagery with the “true” values. These comparisons can be made in clear waters, where all the water parameters can be connected to the concentration of chlorophyll-a, [Chl] (Hu et al., 2013). Another approach is to compare data from satellite sensors with field measurements from offshore platforms, autonomous systems such as the AERONET-OC network (Zibordi et al., 2009, 21), buoys like Marine Optical BuoY (MOBY) (Clark et al., 1997), and from ships (Moore et al., 2015). Specifically, the (Moore et al., 2015) uncertainties in Rrs were estimated for seven optical water types (OWT) using data from the SeaBASS optical database (Werdell et al., 2003) for the MOBY site, the BOUSSOLE mooring site in the Mediterranean Sea (Antoine et al., 2008), and AERONET-OC sites within 5 × 5 pixel boxes, plus/minus 3 h differences. It was found that Rrs uncertainties are generally the highest in the blue part of the spectrum in both clear and coastal waters.
In yet another approach, using Monte Carlo (MC) simulations for Sea-viewing Wide Field-of-view Sensor (SeaWiFS) observations (Franz et al., 2016), the retrieval process for Rrs was repeated 1000 times, and uncertainties in Rrs were then estimated as the “standard deviation of the 1000 perturbed Rrs retrievals in each band.” This derived uncertainty was interpreted “as the precision of the Rrs retrieval due to instrument noise.” It was about 4 times smaller than the observed Rrs uncertainties based on in situ validation (Moore et al., 2015).
Furthermore, in the study by Herrera-Estrella et al. (2021), a model was developed to evaluate the spectral composition of Rrs uncertainties, which was applied to characterize uncertainties due to the Rrs spatial distribution in images from the Visible Infrared Imaging Radiometer Suite (VIIRS) sensor on the SNPP platform and the Landsat-8 Operational Land Imager (OLI) at different spatial resolutions. Most of these uncertainties were attributed to the surface effects and water variability conditions.
In this work, a similar model is applied to estimate the spectral components of the uncertainties in Rrs retrieval by comparing SNPP VIIRS satellite data and in situ data from the MOBY site and eight AERONET-OC stations in US and European waters.
In Theoretical Considerations in the Estimation of Uncertainties, the model (Herrera-Estrella et al., 2021) is replicated with several modifications, in VIIRS Satellite and AERONET-OC, data satellite and in situ data are described, and the results are presented in Results. Discussion and conclusions are provided in Discussion and Conclusion.
Theoretical Considerations in the Estimation of Uncertainties
Main Relationships
The main radiometric quantity in the processing of satellite data is the remote sensing reflectance, Rrs, which is defined as the ratio of the water-leaving radiance to the downwelling irradiance at the sea surface,
where
where radiances
In addition,
where
Then, from Eqs 1, 2 for
Uncertainties from all the components included in Eqs 1–3 in the recording of the signal and in the retrieval process need to be taken into account. Normalizing by the downwelling irradiance,
Variances for the quantities at TOA
It was shown in the study by Herrera-Estrella et al. (2021) that estimated
All other standard deviation components in Eq. 4, except
where
In Eq. 6a,
The uncertainty due to the aerosol component was estimated in two ways, both based on aerosol radiance. The first way is analogous to that of the other radiance components, using normalized radiance with a proportionality coefficient (
with
Eq. 5 includes VIIRS vicarious calibration uncertainties, where sensor gains are determined by the comparison of the water-leaving radiance from VIIRS after atmospheric correction with in situ measurements at the MOBY site (Franz et al., 2007).
For each available matchup between the satellite and AERONET-OC measurements, all radiance spectra in Eqs 6a–d were calculated, then spectra were averaged over the total number of available measurements. Mean spectra were then used in the fitting procedure based on Eq. 5, together with
It should be emphasized that the spectral shapes of the main components in Eqs 6a–e are of primary interest: changes in values, which were assumed constant in the model, do not affect these shapes nor the contribution of the corresponding uncertainties from these components to the total,
with
Biases were also calculated as
Following Eqs 5, 6, coefficients of variation (CVs) can be further determined by normalizing the
where the total CV on the left side represents
Optimization Procedure
With all
where
These coefficients, once used to scale their corresponding radiance components, were interpreted as an indication of the major contributing components to the total observed Rrs variance
Visible Infrared Imaging Radiometer Suite Satellite and AERONET-OC Data
VIIRS Data
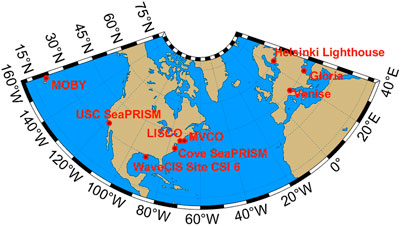
Satellite imagery was downloaded for the period from January 2012 to October 2021 for the area of the Marine Optical BuoY (MOBY) in Hawaii and eight Aerosol Robotic Network for Ocean Color (AERONET-OC) sites (Figure 1): the University of South California (USC), Venise, Gloria, the Martha’s Vineyard Coastal Observatory (MVCO), COVE, WaveCIS, the Long Island Sound Coastal Observatory (LISCO), and the Helsinki Lighthouse (HLT).
VIIRS’s Satellite Level 2 imagery, version 2018.0, was downloaded from the NASA Ocean Color website https://oceancolor.gsfc.nasa.gov (Gordon and Wang 1994; Siegel et al., 2000; Bailey et al., 2010). Standard NASA Level 2 data files for the VIIRS include geophysical products of the atmosphere and ocean, such as aerosol optical thickness, remote sensing reflectance, Rrs(λ), in the visible wavelengths 410, 443, 486, 551, and 671 nm, and the level 2 quality flags. However, Sun zenith angle, sensor viewing angle, sensor azimuth angle, scattering angle, total radiance, and aerosol radiance are obtained from SeaDAS version 7.5.3 after processing VIIRS’s Satellite Level 1A imagery for those files that passed the matchup selection.
Pixels flagged by at least one of the following conditions were excluded: land, cloud, failure in the atmospheric correction, stray light (except for LISCO), bad navigation quality, high or moderate glint, negative Rayleigh-corrected radiance, negative water-leaving radiance, viewing angle larger than 60°, and solar zenith angle larger than 70°.
The VIIRS’s pixel resolution for the reflectance bands at nadir is 750 m. A file is selected if at least half of the pixels in the set plus one was flag-free. Pixels used for matchup comparison were averaged over 3 spatial resolutions: 2250, 3750, and 5250 m (3 × 3, 5 × 5, and 7 × 7 pixel boxes), centered at the AERONET site (Hlaing et al., 2013). Average Rrs(λ) and the standard deviation among pixels, geometry, and radiance were recorded.
In addition, aerosol radiances were also downloaded from SeaDAS for the comparison with aerosol radiances simulated based on parameters from AERONET-OC sites.
AERONET-OC Data
The ocean color component of the Aerosol Robotic Network (AERONET-OC) was implemented to support long-term ocean color investigations by collecting normalized water-leaving radiance and aerosol optical depth data using the SeaPRISM autonomous radiometer systems deployed on offshore fixed platforms (Zibordi et al., 2009; Zibordi et al., 2020). The SeaPRISM system is a CIMEL Electronique CE-318/CE-318T sunphotometer, used to retrieve atmospheric optical thickness and other atmospheric parameters, and modified to perform radiance measurements with a full-angle field of view of 1.2° to determine the total radiance from the sea surface,
The aerosol optical depth, aerosol inversions, and ocean color data used in this analysis are version 3 level 1.5 data, which has been cloud-screened and quality-controlled to ensure the accuracy of the data. All matchups were observed within a ±2 h window between the satellite overpass and in situ observation (Zibordi et al., 2009; Zibordi et al., 2020). The spectrum was classified as coastal water if Rrs (412) ≤ 0.006, and as open ocean water if Rrs (412) > 0.006. More detailed information on AERONET-OC sites is listed in Table 1. At the Venise site, there were a large number of observations with both Rrs (412) ≤ 0.006 and Rrs (412) > 0.006, and they are presented separately. Due to the site location, Venise waters with Rrs (412) > 0.006 are far from clear sea waters, but the term remained to formally separate different types of the spectra. At a few other sites, there were a small number of spectra with Rrs (412) > 0.006; these were not considered because there were not enough data for reliable averaging and fitting procedures.
The quality of Rrs(λ) data depends on the wind speed (Zibordi et al., 2009; Zibordi et al., 2020). Due to the accepted algorithm to minimize the impact of Sun glint on the measurements of the total above water radiance, which takes into account the lowest two out of 11 measurements, with increasing wind speeds above 5 m/s, water-leaving radiance becomes slightly lower. As can be seen in the following text, for several stations, that increased
Marine Optical BuoY Data
Marine Optical BuoY (MOBY) radiometry data are used by the NASA-OBPG as part of ocean color validation and vicarious calibration activities (Clark et al., 1997). MOBY is an autonomous anchored buoy offshore of Lanai, Hawaii. On each day of deployment, it collects several measurements of upwelling radiance from sensors on its underwater arms (at approximately 1, 5, and 9 m depth) and downwelling irradiance from sensors on its underwater arms as well as at the surface (Voss et al., 2017).
From the MOBY “gold” directory, the MOBY data that matched the bands from the VIIRS were collected when the existing data were matched up with ±2 h of the satellite overpass.
The main atmospheric parameters at the studied sites determined from the AC processing and AERONET retrievals are provided in Table 2. Absorbing aerosols were noticeable at several sites with the average
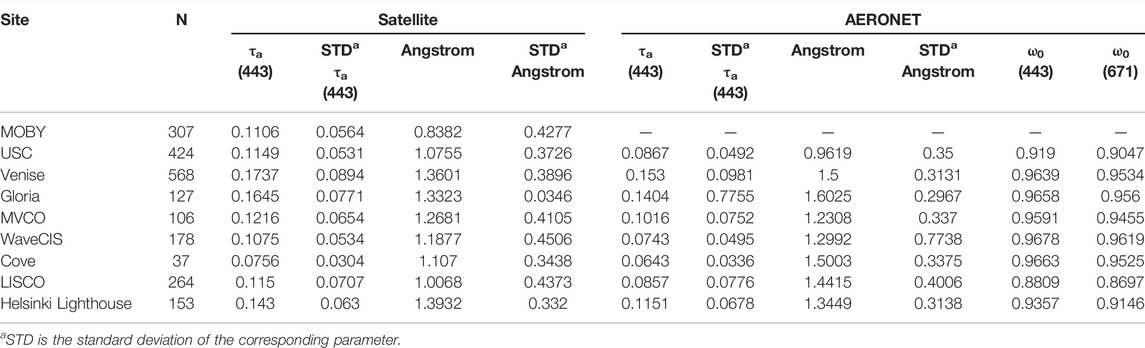
TABLE 2. Average atmospheric parameters at the sites of the study determined from satellite and AERONET retrievals.
Results
Mean Rrs(λ) spectra from the MOBY site and eight AERONET-OC stations are shown in Figure 2A. They represent water areas from very clear (MOBY and USC), moderate coastal (Venise, Gloria, MVCO, WaveCIS, and COVE), and very coastal (LISCO and HLT) waters with Rrs(λ) standard deviations shown in Figure 2B. Corresponding
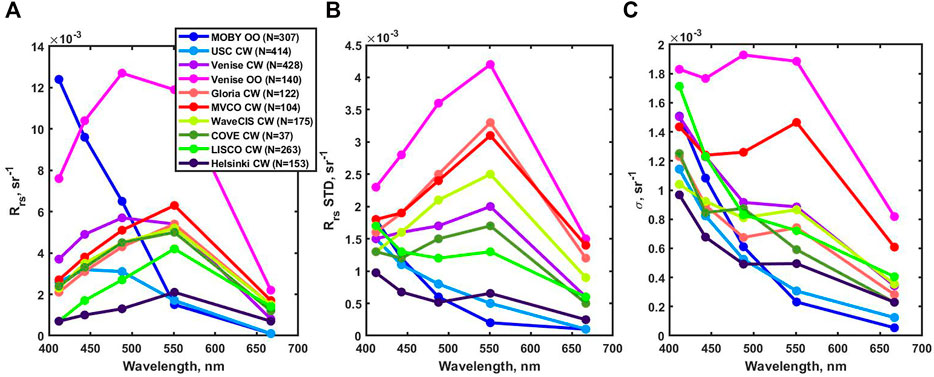
FIGURE 2. (A) Mean Rrs (λ) spectra from the AERONET-OC, (B) standard deviations of Rrs (λ), and (C) corresponding uncertainties spectra
First, the results of processing Eq. 5 without the
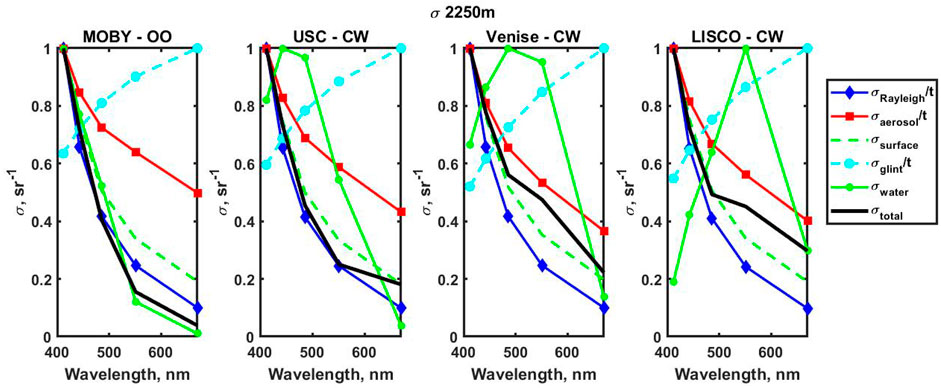
FIGURE 3. Normalized spectra for the MOBY, USC, Venise, and LISCO sites (3 × 3 pixels, 2250 m resolution).
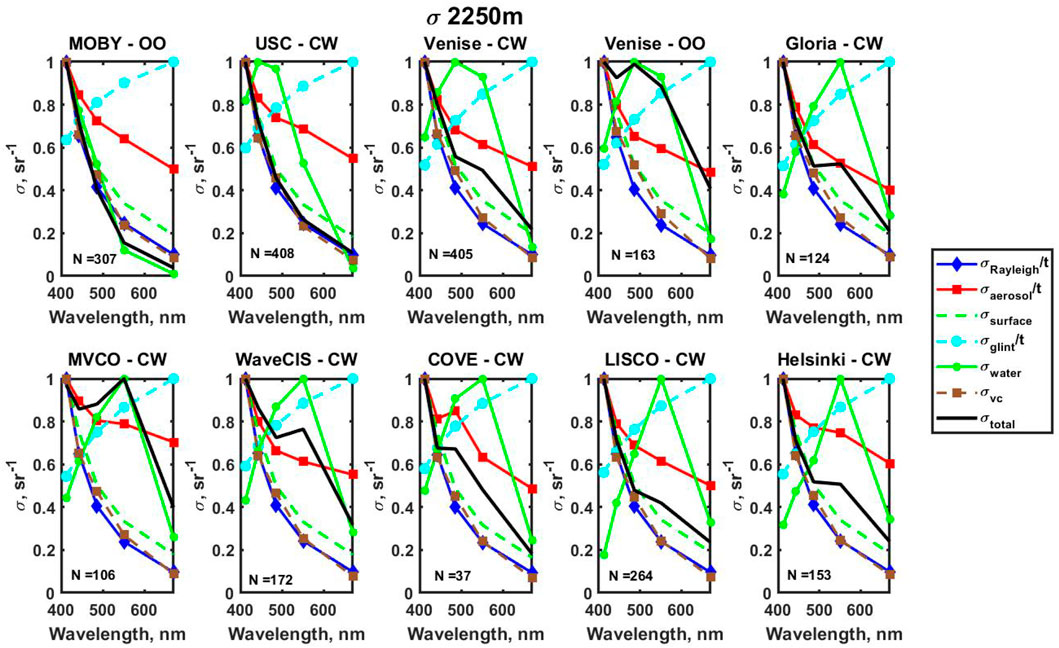
Results of the fitting are presented in Figure 4 for the case when
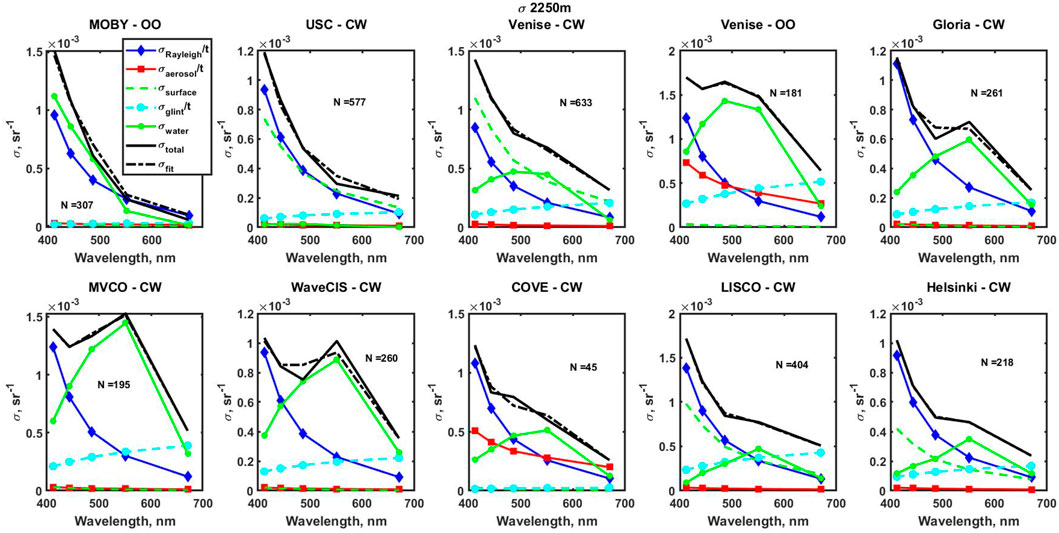
FIGURE 4. Results of fitting for all areas of the study.
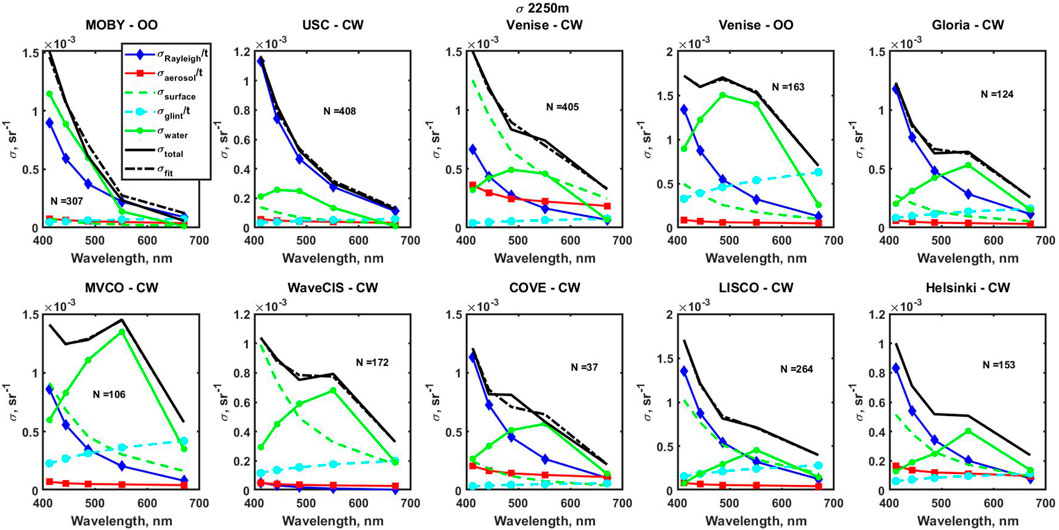
FIGURE 5. Results of fitting for all areas of the study.
While there are some differences in the spectral components for these two cases, the main results remain the same. The main uncertainty for all the areas of AERONET-OC stations from clear waters to very coastal comes from the Rayleigh component, which is typically assumed to be well defined in the atmospheric correction process (Mobley et al., 2016) and to be pre-calculated in a very accurate manner. The presence of the strong Rayleigh component in the total
The second major impact on the total
Another important thing to be noted is that the optimization algorithm cannot easily distinguish between the components with a similar spectral behavior, particularly in the case of Rayleigh scattering and surface effects, and, to a lesser degree, aerosol scattering (cf. Figure 3). By the very definition of optimization, the procedure maximizes the efficiency in reconstructing the total uncertainty, which may include the singular utilization of one component at the expense of all others. This too may explain the general small contribution of the aerosol component, as well as sudden switches between the Rayleigh scattering and surface contributions like in the case of the WaveCIS site when the formulation of
The spectral composition of
As was shown before (Herrera- Estrella et al., 2021), there is almost no spatial variability of water measured by Rrs(λ) in the MOBY area. However, the second main spectral component in
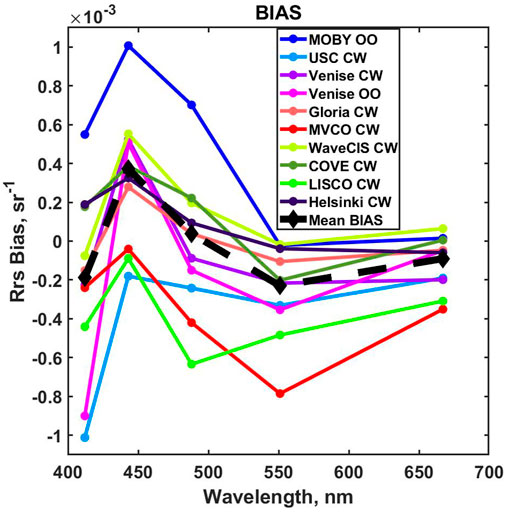
Spectral biases of Rrs(λ) at all the sites are shown in Figure 6, with the global mean bias shown as a dashed line. This was calculated from all spectra excluding the ones for the MOBY site and from the LISCO site since the stray light flag was suspended for LISCO. This bias spectrum resembles the bias at the MOBY site, which will be smaller in the blue bands if the mean bias is subtracted. Bias at MOBY was already reduced in the VIIRS reprocessing 2018 in comparison with 2014 reprocessing (Franz et al., 2018), which improved the quality of NASA products.
As was mentioned before, the results of the fitting were slightly different for different wind speed brackets. These differences are demonstrated in Figure 7 where fitting results are presented for Venise and LISCO sites for three wind speed intervals as well as averaged over all cases.
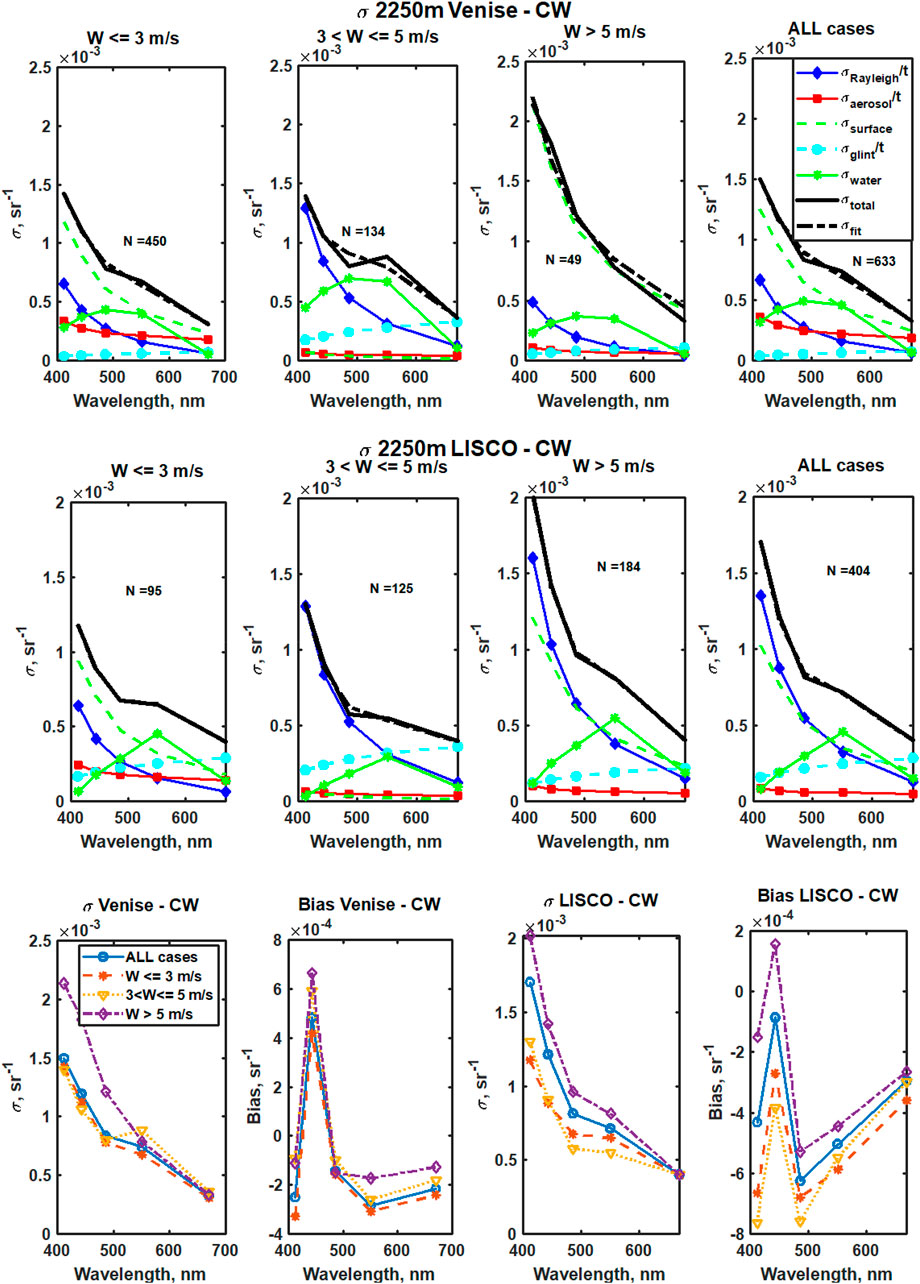
FIGURE 7. Separation of the fitting results by the wind speed, Venise, and LISCO sites: Venise (top row), LISCO (middle row),
Surface effects were small at 3 < W ≤5 m/s and more noticeable at W > 5 m/s. This pattern was typical for most of the AERONET-OC sites. Some presence of the surface effects at low wind speeds W < 3 m/s is probably associated with the specifics of processing of the SeaPRISM data and/or accuracy of Cox–Munk surface slopes model (Cox and Munk, 1954) for the coastal sites in the satellite data processing. The uncertainty of the Rayleigh component is the highest in most cases, especially in the blue part of the spectra followed by water variability components and sometimes surface effects.
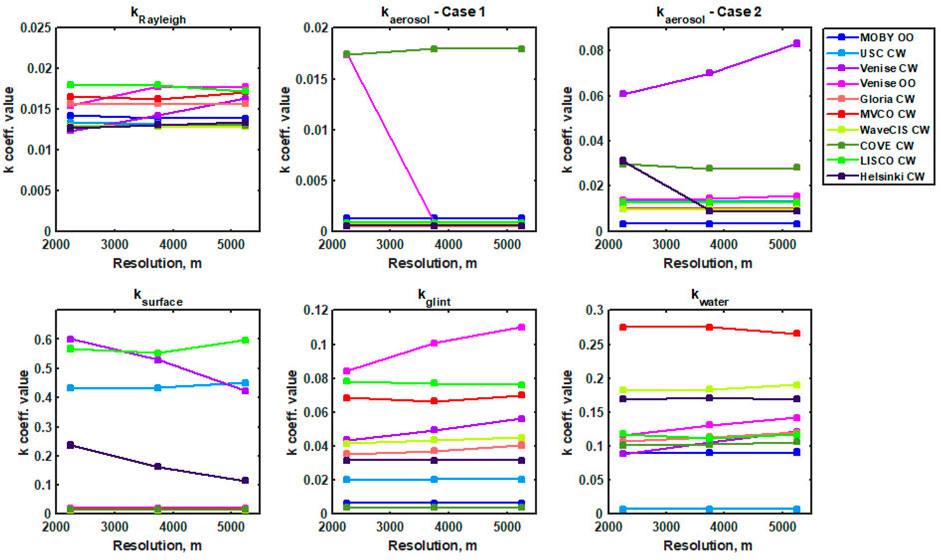
Fitting coefficients k from Eq. 5 for all stations are provided in Figure 8 as a function of the spatial resolution based on 3 × 3, 5 × 5, and 7 × 7 pixel processing by the model. There are no significant changes in the coefficients with an increase of the averaged area. The coefficients have different ranges of values for different parameters: they are smaller for
Total uncertainties
The results of data processing with
The results of fitting with the inclusion of
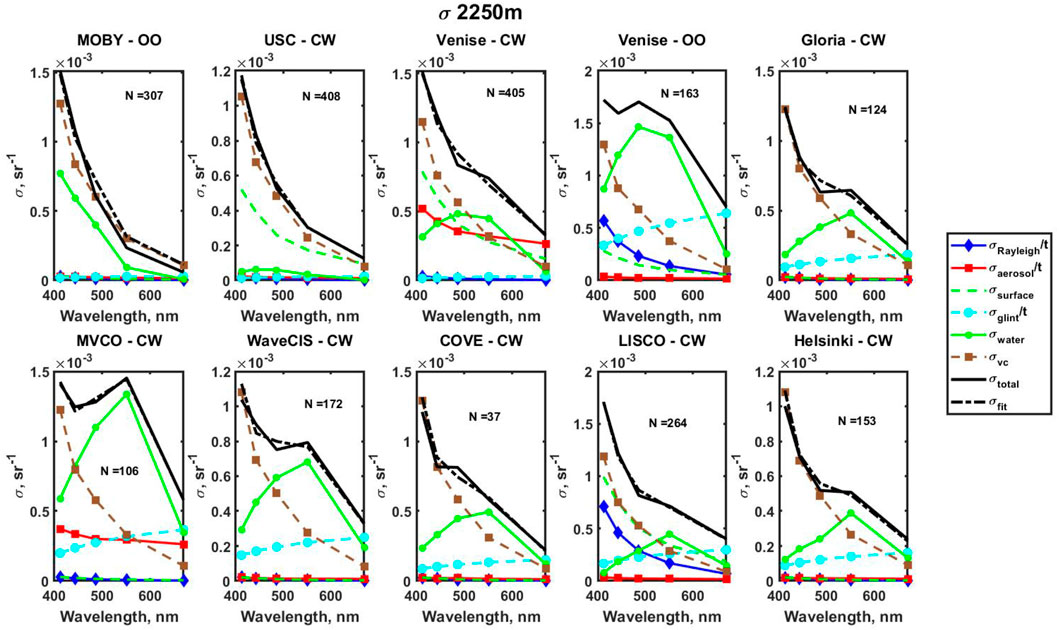
FIGURE 10. Results of fitting for all areas of the study with
Now the main uncertainty for all the AERONET-OC stations from clear water to very coastal water comes from the
CV spectra for all sites are shown in Figure 11 for both in situ and satellite data, with a typical increase of CV in the blue bands reaching about 2–2.5 at the very coastal sites where Rrs values are especially low. As expected, CVs are also high in the red part of the spectra for the clear water sites like USC because of the low Rrs values at those wavelengths.
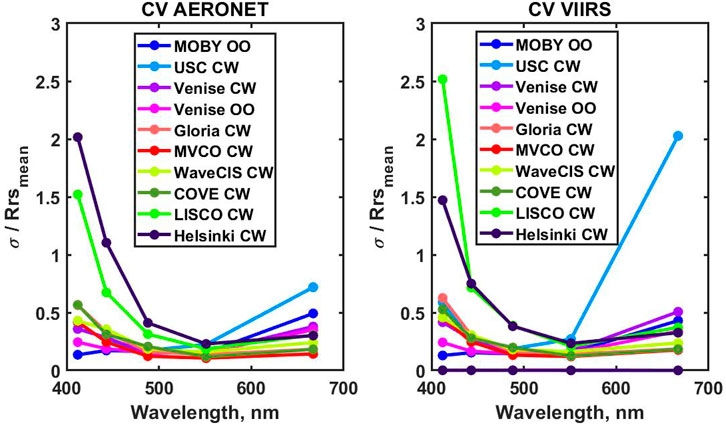
FIGURE 11. CV spectra for all sites of the study: the in situ data (left) and the VIIRS data (right).
SeaPRISM measurements together with data processing introduce their own uncertainties, which need to be considered in the uncertainties’ budget. According to Gergely and Zibordi (2014), the CV for the Venise site at 412 nm is about 5% and at the Helsinki site is about 27% with the differences mostly due to the different Rrs values. Considering the Rrs spectra shown in Figure 2A, this corresponds to
Distributions of the individual spectra
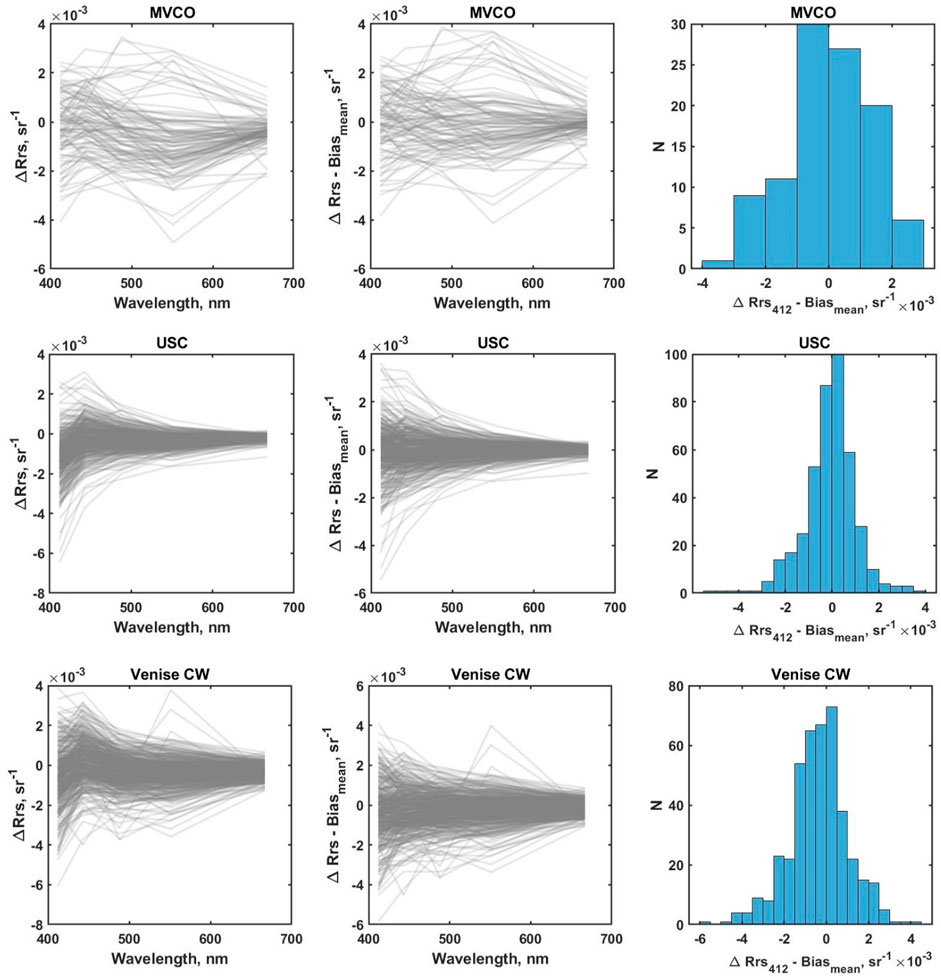
FIGURE 12. Analysis of the
Finally, the
Discussion and Conclusion
The model developed for the separation of remote sensing reflectance uncertainties into their spectral components is applied to the uncertainties’ spectra from the matchups of satellite and AERONET-OC data and MOBY measurements. It was shown that the main component in Rrs uncertainties at all the AERONET-OC sites is the Rayleigh-type component at the level of (0.8–1.4) ×10–3 sr−1 at 412 nm based on Figure 5, which with
A comparison of
The main parameter in
Variability of
Thus, negative values of the Rayleigh component uncertainty, possibly together with the effect of absorbing aerosols at low actual Rrs (412) values, create negative Rrs (412) in the atmospheric correction processing. Similar effects with both positive and negative uncertainties most likely exist at higher Rrs (412) as well, inducing variability in Rrs (λ), but they are not explicitly visible as errors. They can just slightly affect the estimation of chlorophyll concentrations and water inherent optical properties.
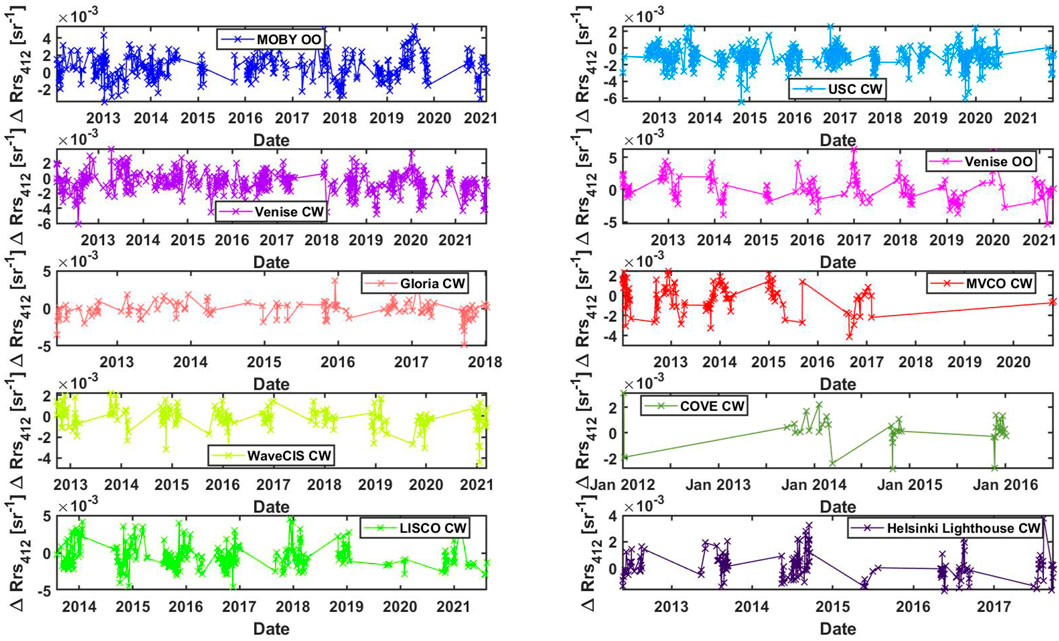
The time series of
It can be seen that
It is possible that the methodology applied in this work underestimates the contribution of aerosols to the total uncertainties because of the difficulty to determine actual spectra of aerosol uncertainties and their spectral variability in various conditions. This contribution should be further analyzed using different approaches. Part of the uncertainties can come from inaccuracies in the computations of the Rayleigh and other components by vector radiative transfer codes. While current VRT codes calculate the Rayleigh component with uncertainties of a fraction of a percent (typically below 0.1%) (Kokhanovsky et al., 2010), related uncertainties should be carefully monitored.
One source of additional uncertainties in
As mentioned earlier, uncertainties can also include other errors due to detectors, polarization effects, stray light, etc., and such errors were not included in the model. Based on the similarity of the spectra of standard deviations of the vicarious gains from several satellite sensors shown in Figure 13, the contributions of these effects appear to be small for these sensors, which does not exclude the possibility that these terms will be larger for other sensors with different designs or radiometric performance.
Without the uncertainty due to changes of
Based on the analysis of biases of Rrs in Figure 6, the bias at the MOBY site is the highest and is positive. At the AERONET-OC sites, biases are positive at a few stations and negative at a few others. The reasons for such variability should be further studied. Biases in the 412–489 nm range can be partially improved by the slight change of gain values at these wavelengths.
In addition to the MOBY site, the USC site can also be considered for the vicarious calibration. It has minimal water variability and provides full information on aerosol parameters. This information together with the measured water-leaving radiance can be used for the calibration through the simulation of the total radiances (Bailey et al., 2010; Hlaing et al., 2014) in addition to the current approaches of the vicarious calibration (Franz et al., 2007; Werdell et al., 2007).
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
AG, EH-E and RF formulated the original concept of the model. EH-E processed satellite and AERONET-OC data. All the authors participated in the uncertainty analysis from different components and provided critical feedback to the final manuscript.
Funding
The funding of this study was provided by the NOAA JPSS Cal/Val and JPSS PGRR programs, CESSRST Grant, NA16SEC4810008, and the NASA OBB Grant, 80NSSC21K0562.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank NASA OBPG for the satellite imagery, and NASA AERONET Group for processing of the satellite data and support of the operation at the LISCO site. We are grateful to Kenneth Voss and the MOBY team for the MOBY data, PIs of AERONET-OC sites: Giuseppe Zibordi (Venise, Gloria, HLT), Brent Holben (COVE), Heidi Sosik and Hui Feng (MVCO), Robert Arnone, Alan Wiedemann, Bill Gibson, and Sherwin Ladner (WaveCIS). We also thank the Graduate Center of the City University of New York, The City College of New York, NOAA Center for Earth System Sciences and Remote Sensing Technologies, and NOAA Office of Education, Educational Partnership Program for fellowship support for EH-E. The statements contained within the research article are not the opinions of the funding agency or the U.S. government but reflect the authors’ opinions. We are grateful to two reviewers whose recommendations led to the improvement of the manuscript.
References
Ahmad, Z., Franz, B. A., McClain, C. R., Kwiatkowska, E. J., Werdell, J., Shettle, E. P., et al. (2010). New Aerosol Models for the Retrieval of Aerosol Optical Thickness and Normalized Water-Leaving Radiances from the SeaWiFS and MODIS Sensors over Coastal Regions and Open Oceans. Appl. Opt. 49, 5545. doi:10.1364/AO.49.005545
Antoine, D., d'Ortenzio, F., Hooker, S. B., Bécu, G., Gentili, B., Tailliez, D., et al. (2008). Assessment of Uncertainty in the Ocean Reflectance Determined by Three Satellite Ocean Color Sensors (MERIS, SeaWiFS and MODIS-A) at an Offshore Site in the Mediterranean Sea (BOUSSOLE Project). J. Geophys. Res. 113, C07013. doi:10.1029/2007JC004472
Bailey, S. W., Franz, B. A., and Werdell, P. J. (2010). Estimation of Near-Infrared Water-Leaving Reflectance for Satellite Ocean Color Data Processing. Opt. Express 18, 7521–7527. doi:10.1364/OE.18.007521
Bisson, K. M., Boss, E., Werdell, P. J., Ibrahim, A., Frouin, R., and Behrenfeld, M. J. (2021). Seasonal Bias in Global Ocean Color Observations. Appl. Opt. 60 (23), 6978–6988. doi:10.1364/ao.426137
Bodhaine, B. A., Wood, N. B., Dutton, E. G., and Slusser, J. R. (1999). On Rayleigh Optical Depth Calculations. J. Atmos. Oceanic Technol. 16, 1854–1861. doi:10.1175/1520-0426(1999)016<1854:orodc>2.0.co;2
Carrizo, C., Gilerson, A., Foster, R., Golovin, A., and El-Habashi, A. (2019). Characterization of Radiance from the Ocean Surface by Hyperspectral Imaging. Opt. Express 27 (2), 1750–1768. doi:10.1364/oe.27.001750
Clark, D. K., Gordon, H. R., Voss, K. J., Ge, Y., Broenkow, W., and Trees, C. (1997). Validation of Atmospheric Correction over the Oceans. J. Geophys. Res. 102, 17209–17217. doi:10.1029/96JD03345
Coleman, T. F., and Li, Y. (1996). An Interior Trust Region Approach for Nonlinear Minimization Subject to Bounds. SIAM J. Optim. 6 (2), 418–445. doi:10.1137/0806023
Coleman, T. F., and Li, Y. (1994). On the Convergence of interior-reflective Newton Methods for Nonlinear Minimization Subject to Bounds. Math. Programming 67 (2), 189–224. doi:10.1007/BF01582221
Cox, C., and Munk, W. (1954). Measurement of the Roughness of the Sea Surface from Photographs of the Sun's Glitter. J. Opt. Soc. Am. 44 (11), 838–850. doi:10.1364/josa.44.000838
El-Habashi, A., Ahmed, S., Ondrusek, M., and Lovko, V. (2019). Analyses of Satellite Ocean Color Retrievals Show Advantage of Neural Network Approaches and Algorithms that Avoid Deep Blue Bands. J. Appl. Rem. Sens. 13 (2), 1. doi:10.1117/1.JRS.13.024509
Estrella, E. H., Gilerson, A., Foster, R., and Groetsch, P. (2021). Spectral Decomposition of Remote Sensing Reflectance Variance Due to the Spatial Variability from Ocean Color and High-Resolution Satellite Sensors. J. Appl. Rem. Sens. 15 (2), 024522. doi:10.1117/1.JRS.15.024522
Fan, Y., Li, W., Chen, N., Ahn, J.-H., Park, Y.-J., Schroeder, T., et al. (2021). OC-SMART: A Machine Learning Based Data Analysis Platform for Satellite Ocean Color Sensors. Remote Sensing Environ. 253, 112236. doi:10.1016/j.rse.2020.112236
IOCCG (2019). “Uncertainties in Ocean Colour Remote Sensing,” in Reports No. 18 of the International Ocean-Colour Coordinating Group. Editor F. Mélin (Dartmouth, NS: IOCCG). doi:10.25607/OBP-696)
Franz, B. A., Bailey, S. W., Eplee, R. E., Lee, S., Patt, F. S., Proctor, C., et al. (2018) NASA Multi-Mission Ocean Color Reprocessing 2018.0.”in Proc. Of Ocean Optics XXIV. Dubrovnik, Croatia.
Franz, B. A., Bailey, S. W., Werdell, P. J., and McClain, C. R. (2007). Sensor-independent Approach to the Vicarious Calibration of Satellite Ocean Color Radiometry. Appl. Opt. 46, 5068. doi:10.1364/AO.46.005068
Franz, B. A., and Karaköylü, E. M. (2016). “Estimating Uncertainty in the Retrieval of Water-Leaving Reflectance from Spaceborne Ocean Color Sensors: Effect of Instrument Noise.” in Proc. of Ocean Opties. Victoria, B.C.. Available at: https://www.researchgate.net/profile/Bryan-Franz-2/publication/309313055_Estimating_uncertainty_in_the_retrieval_of_water-leaving_reflectance_from_spaceborne_ocean_color_sensors_effect_of_instrument_noise/links/5809267408ae993dc0509fe1/Estimating-uncertainty-in-the-retrieval-of-water-leaving-reflectance-from-spaceborne-ocean-color-sensors-effect-of-instrument-noise.pdf
Frouin, R. J., Franz, B. A., Ibrahim, A., Knobelspiesse, K., Ahmad, Z., Cairns, B., et al. (2019). Atmospheric Correction of Satellite Ocean-Color Imagery during the PACE Era. Front. Earth Sci. 7, 145. doi:10.3389/feart.2019.00145
Frouin, R., Schwindling, M., and Deschamps, P.-Y. (1996). Spectral Reflectance of Sea Foam in the Visible and Near-Infrared: In Situ Measurements and Remote Sensing Implications. J. Geophys. Res. 101 (C6), 14361–14371. doi:10.1029/96jc00629
Gergely, M., and Zibordi, G. (2014). Assessment of AERONET-OC LWN Uncertainties. Metrologia 51, 40–47. doi:10.1088/0026-1394/51/1/40
Gilerson, A., Carrizo, C., Foster, R., and Harmel, T. (2018). Variability of the Reflectance Coefficient of Skylight from the Ocean Surface and its Implications to Ocean Color. Opt. Express 26 (8), 9615–9633. doi:10.1364/oe.26.009615
Gilerson, A., Malinowski, M., Herrera, E., Tomlinson, M. C., Stumpf, R. P., and Ondrusek, M. E. (2021). Estimation of Chlorophyll-A Concentration in Complex Coastal Waters from Satellite Imagery. Proc. SPIE 11752ocean Sensing Monit. XIII. doi:10.1117/12.2588004
Gordon, H. R., Du, T., and Zhang, T. (1997). Remote Sensing of Ocean Color and Aerosol Properties: Resolving the Issue of Aerosol Absorption. Appl. Opt. 36, 8670. doi:10.1364/AO.36.008670
Gordon, H. R., and Morel, A. Y. (1983). “In-water Algorithms,” in Remote Assessment of Ocean Color for Interpretation of Satellite Visible Imagery: A Review. (Berlin, Germany: Springer-Verlag). doi:10.1007/978-1-4684-6280-710.1007/978-1-4684-6280-7_3
Gordon, H. R., and Wang, M. (1994). Retrieval of Water-Leaving Radiance and Aerosol Optical Thickness over the Oceans with SeaWiFS: a Preliminary Algorithm. Appl. Opt. 33, 443–452. doi:10.1364/ao.33.000443
Gordon, H. R., and Wang, M. (1992). Surface-roughness Considerations for Atmospheric Correction of Ocean Color Sensors 1: The Rayleigh-Scattering Component. Appl. Opt. 31 (21), 4247–4260. doi:10.1364/ao.31.004247
Groetsch, P. M. M., Foster, R., and Gilerson, A. (2020). Exploring the Limits for Sky and Sun Glint Correction of Hyperspectral Above-Surface Reflectance Observations. Appl. Opt. 59 (9), 2942–2954. doi:10.1364/ao.385853
Herrera-Estrella, E., Grotsch, P., Gilerson, A., Malinowski, M., and Ahmed, S. (2020). Blue Band Reflectance Uncertainties in Coastal Waters and Their Impact on Retrieval Algorithms. Proc. SPIE 11420 Ocean Sensing Monit. XII, 1142006. doi:10.1117/12.2559895
Hlaing, S., Gilerson, A., Foster, R., Wang, M., Arnone, R., and Ahmed, S. (2014). Radiometric Calibration of Ocean Color Satellite Sensors Using AERONET-OC Data. Opt. Express 22, 23385–23401. doi:10.1364/OE.22.023385
Hlaing, S., Harmel, T., Gilerson, A., Foster, R., Weidemann, A., Arnone, R., et al. (2013). Evaluation of the VIIRS Ocean Color Monitoring Performance in Coastal Regions. Remote Sensing Environ. 139, 398–414. doi:10.1016/j.rse.2013.08.013
Hu, C., and Carder, K. L. (2002). Atmospheric Correction for Airborne Sensors: Comment on a Scheme Used for CASI. Remote Sens. Environ. 79 (1), 134–137. doi:10.1016/S0034-4257(01)00232-2
Hu, C., Feng, L., and Lee, Z. (2013). Uncertainties of SeaWiFS and MODIS Remote Sensing Reflectance: Implications from clear Water Measurements. Remote Sensing Environ. 133, 168–182. doi:10.1016/j.rse.2013.02.012
Kokhanovsky, A. A., Budak, V. P., Cornet, C., Duan, M., Emde, C., Katsev, I. L., et al. (2010). Benchmark Results in Vector Atmospheric Radiative Transfer. J. Quantitative Spectrosc. Radiative Transfer 111 (12-13), 1931–1946. doi:10.1016/j.jqsrt.2010.03.005
Lamquin, N., Bourg, L., Lerebourg, C., Martin-Lauzer, F. R., Kwiatkowska, E., and Dransfeld, S. (2017). System Vicarious Calibration of Sentinel-3 OLCI. Conference of Characterization and Radiometric Calibration for Remote Sensing. USA: CALCON. Utah.
Li, J., Jamet, C., Zhu, J., Han, B., Li, T., Yang, A., et al. (2019). Error Budget in the Validation of Radiometric Products Derived from OLCI Around the China Sea from Open Ocean to Coastal Waters Compared with MODIS and VIIRS. Remote Sensing 11 (20), 2400. doi:10.3390/rs11202400
Mobley, C. D. (1994). Light and Water: Radiative Transfer in Natural Waters. San Diego, CA: Academic Press.
Mobley, C. D., Werdell, J., Franz, B., Ahmad, Z., and Bailey, S. (2016). Atmospheric Correction for Satellite Ocean Color Radiometry - A Tutorial and Documentation of the Algorithms Used by the NASA Ocean Biology Processing Group. Greenbelt, MD, 73. NASA/TM-2016-217551. doi:10.13140/RG.2.2.23016.78081
Moore, T. S., Campbell, J. W., and Feng, H. (2015). Characterizing the Uncertainties in Spectral Remote Sensing Reflectance for SeaWiFS and MODIS-Aqua Based on Global In Situ Matchup Data Sets. Remote Sensing Environ. 159, 14–27. doi:10.1016/j.rse.2014.11.025
IOCCG (2010). “Atmospheric Correction for Remotely-Sensed Ocean-Colour Products,” in Reports No. 10 of the International Ocean-Colour Coordinating Group. Editor M. Wang (Dartmouth, NS: IOCCG).
Oo, M., Vargas, M., Gilerson, A., Gross, B., Moshary, F., and Ahmed, S. (2008). Improving Atmospheric Correction for Highly Productive Coastal Waters Using the Short Wave Infrared Retrieval Algorithm with Water-Leaving Reflectance Constraints at 412 Nm. Appl. Opt. 47 (21), 3846–3859. doi:10.1364/AO.47.003846
Qi, L., Lee, Z., Hu, C., and Wang, M. (2017). Requirement of Minimal Signal-To-Noise Ratios of Ocean Color Sensors and Uncertainties of Ocean Color Products. J. Geophys. Res. Oceans 122 (3), 2595–2611. doi:10.1002/2016jc012558
Ransibrahmanakul, V., and Stumpf, R. P. (2006). Correcting Ocean Colour Reflectance for Absorbing Aerosols. Int. J. Remote Sensing 27 (9), 1759–1774. doi:10.1080/01431160500380604
Sayer, A. M., Govaerts, Y., Kolmonen, P., Lipponen, A., Luffarelli, M., Mielonen, T., et al. (2020). A Review and Framework for the Evaluation of Pixel-Level Uncertainty Estimates in Satellite Aerosol Remote Sensing. Atmos. Meas. Tech. 13, 373–404. doi:10.5194/amt-13-373-2020
IOCCG (2021). “Observation of Harmful Algal Blooms with Ocean Colour Radiometry,” in Reports No. 20 of the International Ocean-Colour Coordinating Group. Editors S. Bernard, R. Kudela, L. Robertson Lain, and G. C. Pitcher (Dartmouth, NS: IOCCG). doi:10.25607/OBP-1042)
Shi, W., and Wang, M. (2007). Detection of Turbid Waters and Absorbing Aerosols for the MODIS Ocean Color Data Processing. Remote Sensing Environ. 110 (2), 149161–161. doi:10.1016/j.rse.2007.02.013
Siegel, D. A., Wang, M., Maritorena, S., and Robinson, W. (2000). Atmospheric Correction of Satellite Ocean Color Imagery: the Black Pixel assumption. Appl. Opt. 39 (21), 3582–3591. doi:10.1364/ao.39.003582
Smith, S. R., Legler, D. M., and Verzone, K. V. (2001). Quantifying Uncertainties in NCEP Reanalyses Using High-Quality Research Vessel Observations. J. Clim. 14 (20), 4062–4072. doi:10.1175/1520-0442(2001)014<4062:quinru>2.0.co;2
Steinmetz, F., Deschamps, P.-Y., and Ramon, D. (2011). Atmospheric Correction in Presence of Sun Glint: Application to MERIS. Opt. Express 19 (10), 9783–9800. doi:10.1364/OE.19.009783
Teillet, P. M. (1990). Rayleigh Optical Depth Comparisons from Various Sources. Appl. Opt. 29 (13), 1897–1900. doi:10.1364/AO.29.001897
IOCCG (2008). “Why Ocean Colour? the Societal Benefits of Ocean-Colour Technology,” in Report No. 7 of the International Ocean-Colour Coordinating Group. Editors T. Platt, N. Hoepffner, V. Stuart, and C. Brown (Dartmouth, NS: IOCCG). doi:10.25607/OBP-97)
Tynes, H. H., Kattawar, G. W., Zege, E. P., Katsev, I. L., Prikhach, A. S., and Chaikovskaya, L. I. (2001). Monte Carlo and Multicomponent Approximation Methods for Vector Radiative Transfer by Use of Effective Mueller Matrix Calculations. Appl. Opt. 40 (3), 400–412. doi:10.1364/ao.40.000400
Voss, K. J., Gordon, H. R., Flora, S., Johnson, B. C., Yarbrough, M., Feinholz, M., et al. (2017). A Method to Extrapolate the Diffuse Upwelling Radiance Attenuation Coefficient to the Surface as Applied to the Marine Optical Buoy (MOBY). J. Atmos. Ocean Technol. 34 (7), 1423–1432. doi:10.1175/JTECH-D-16-0235.1
Wang, M. (1999). Atmospheric Correction of Ocean Color Sensors: Computing Atmospheric Diffuse Transmittance. Appl. Opt. 38, 451–455. doi:10.1364/AO.38.000451
Wang, M., and Bailey, S. W. (2001). Correction of Sun Glint Contamination on the SeaWiFS Ocean and Atmosphere Products. Appl. Opt. 40 (27), 4790–4798. doi:10.1364/ao.40.004790
Wang, M., and Gordon, H. R. (2002). Calibration of Ocean Color Scanners: How Much Error Is Acceptable in the Near Infrared? Rem. Sens 82 (2-3), 497–504. doi:10.1016/s0034-4257(02)00072-x
Wei, J., Yu, X., Lee, Z., Wang, M., and Jiang, L. (2020). Improving Low-Quality Satellite Remote Sensing Reflectance at Blue Bands over Coastal and Inland Waters. Remote Sensing Environ. 250, 112029. doi:10.1016/j.rse.2020.112029
Werdell, P. J., Bailey, S., Fargion, G., Pietras, C., Knobelspiesse, K., Feldman, G., et al. (2003). Unique Data Repository Facilitates Ocean Color Satellite Validation. Eos Trans. AGU 84 (38), 377–387. doi:10.1029/2003EO380001
Werdell, P. J., Bailey, S. W., Franz, B. A., Morel, A., and McClain, C. R. (2007). On-orbit Vicarious Calibration of Ocean Color Sensors Using an Ocean Surface Reflectance Model. Appl. Opt. 46 (23), 5649–5666. doi:10.1364/AO.46.005649
Werdell, P. J., Behrenfeld, M. J., Bontempi, P. S., Boss, E., Cairns, B., Davis, G. T., et al. (2019). The Plankton, Aerosol, Cloud, Ocean Ecosystem Mission: Status, Science, Advances. Bull. Am. Meteorol. Soc. 100 (9), 1775–1794. doi:10.1175/BAMS-D-18-0056.1
Xiong, X., Angal, A., Chang, T., Chiang, K., Lei, N., Li, Y., et al. (2020). MODIS and VIIRS Calibration and Characterization in Support of Producing Long-Term High-Quality Data Products. Remote Sensing 12 (19), 3167. doi:10.3390/rs12193167
Zhang, M., Hu, C., and Barnes, B. B. (2019). Performance of POLYMER Atmospheric Correction of Ocean Color Imagery in the Presence of Absorbing Aerosols. IEEE Trans. Geosci. Remote Sensing 57 (9), 6666–6674. doi:10.1109/TGRS.2019.2907884
Zibordi, G., Holben, B. N., Talone, M., D’Alimonte, D., Slutsker, I., Giles, D. M., et al. (2021). Advances in the Ocean Color Component of the Aerosol Robotic Network (AERONET-OC). J. Atmos. Ocean Technol. 38 (4), 725–746. doi:10.1175/JTECH-D-20-0085.1
Keywords: remote sensing reflectance, uncertainties, AERONET-OC, Rayleigh scattering, Rayleigh optical thickness, atmospheric correction
Citation: Gilerson A, Herrera-Estrella E, Foster R, Agagliate J, Hu C, Ibrahim A and Franz B (2022) Determining the Primary Sources of Uncertainty in Retrieval of Marine Remote Sensing Reflectance From Satellite Ocean Color Sensors. Front. Remote Sens. 3:857530. doi: 10.3389/frsen.2022.857530
Received: 18 January 2022; Accepted: 11 March 2022;
Published: 27 April 2022.
Edited by:
Lino Augusto Sander De Carvalho, Federal University of Rio de Janeiro, BrazilReviewed by:
Alexei Lyapustin, National Aeronautics and Space Administration, United StatesFabio Marcelo Breunig, Federal University of Santa Maria, Brazil
Copyright © 2022 Gilerson, Herrera-Estrella, Foster, Agagliate, Hu, Ibrahim and Franz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alexander Gilerson, Z2lsZXJzb25AY2NueS5jdW55LmVkdQ==
 Alexander Gilerson
Alexander Gilerson Eder Herrera-Estrella
Eder Herrera-Estrella Robert Foster
Robert Foster Jacopo Agagliate
Jacopo Agagliate Chuanmin Hu
Chuanmin Hu Amir Ibrahim
Amir Ibrahim Bryan Franz
Bryan Franz