Unique NISTAR-Based Climate GCM Diagnostics of the Earth’s Planetary Albedo and Spectral Absorption Through Longitudinal Data Slicing

Deep Space Climate Observatory (DSCOVR) measurements of Earth’s reflected solar and emitted thermal radiation permit a unique model/data comparison perspective that is not readily available from other satellite data. The key factor is the unique Lissajous orbital viewing geometry from the Lagrangian L1 point, which enables a continuous view of Earth’s sunlit hemisphere. The National Institute of Standards and Technology Advanced Radiometer (NISTAR) is the DSCOVR Mission energy budget instrument, which views the reflected and emitted radiation of the Earth’s sunlit hemisphere by means of single pixel active cavity full-spectrum (Band-A, 0.2–100 μm) and filtered solar wavelength (Band-B, 0.2–4.0 μm; and Band-C, 0.7–4.0 μm) radiometer measurements. An additional solar wavelength photodiode channel (0.3–1.1 μm) provides a calibration reference. The objective of this study is the assessment of climate GCM performance via direct model/data comparisons. Such comparisons are difficult due to quasi-chaotic natural variability present in real-world observational data and in climate GCM simulations. This is where the unique DSCOVR viewing geometry makes possible the longitudinal data slicing methodology for more direct model/data comparison. The key point of the longitudinal slicing approach is that data integration over the entire sunlit hemisphere eliminates the quasi-chaotic meteorological weather-scale noise, while preserving intra-seasonal and planetary-scale variability. The rotation of the Earth that retrieves this climate-style, large-scale longitudinal and seasonal variability. The hemispheric averaging is accomplished automatically in NISTAR measurements with its single-pixel view of the Earth. For climate GCMs, this requires implementing the Sunlit Hemisphere Sampling (SHS) scheme to operate on the GCM run-time output data, utilizing the DSCOVR Satellite Ephemeris data to assure precise viewing geometry between NISTAR measurements and GCM output data, while averaging out the meteorological weather noise. However, GCM generated data are radiative fluxes, while NISTAR (and EPIC) measurements are near-backscattered radiances. Conversing NISTSR measurements into radiative fluxes cannot be accomplished using NISTAR data alone, even with detailed support from conventional satellite data. But the identical viewing geometry of Earth’s sunlit hemisphere, and synergistic analyses of EPIC data make it feasible for this conversion of NISTAR near-backscatter radiances into radiative fluxes.

Introduction

Figure 1 is a schematic representation of the NISTAR and EPIC measurements from the Lagrangian L1 point 1.4 to 1.6 × 10⁶ km from the Earth in the direction of the Sun, where the disk-image of the Earth is roughly the size of the Moon as viewed from Earth. To be specific, the DSCOVR Satellite is not precisely located at the Lagrangian L1 point. The DSCOVR Satellite is actually orbiting around the Lagrangian L1 point in a Lissajous orbit (Koon et al., 2000) as shown in Figure 2. The Lissajous orbit is forever evolving in shape with a roughly 6-month period. The solar illumination of the earth is determined by the Solar Ephemeris whereby (in the GCM simulations) the grid-box local solar zenith angle changes are updated on an hourly basis, as is the seasonal change in solar irradiance due to the Earth’s orbital motion around the Sun. But, for viewing Earth from the Lissajous orbit, the DSCOVR Satellite viewing geometry must conform to the specification given by the DSCOVR Satellite Ephemeris.

FIGURE 1

FIGURE 1. Schematic diagram of NISTAR view of the Earth’s sunlit hemisphere from the Lissajous orbit around the solar Lagrangian L1 point. NISTAR views the entire sunlit hemisphere as a single pixel in 4 broadband channels, while companion instrument EPIC records spatially resolved images.

FIGURE 2

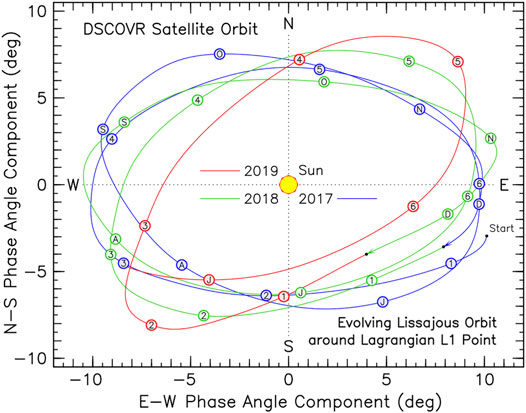
FIGURE 2. The phase angle (also Sun-Earth-Satellite angle, or 180°—scattering angle) defines the angular separation between the DSCOVR Satellite and the Sun, as viewed from the Earth. The color-coded sky-map traces its evolving Lissajous orbital path around the Lagrange L1 point starting from 1 January 2017 (blue) to 27 June 2019 (red). The directions N S, and W E, represent the Satellite displacement relative to the Sun. Circles depict the mid-month orbital positions with the numbers 1 to 6 representing months January to June of the first orbit of the year, and the letters J to D standing for July to December of the second orbit of the year.

The changes in DSCOVR viewing geometry directly affect the amount of reflected SW radiation that NISTAR and EPIC receive (Marshak et al., 2021), and require explicit use of the DSCOVR Satellite Ephemeris in the GCM SHS modeling to account for the changing GCM grid-box projected area, as seen from the DSCOVR Satellite perspective. With this explicit SHS modeling in place, the GCM SHS sampled output data are collected with the same Sun-Satellite viewing geometry of Earth as is the case for NISTAR and EPIC observational data. The principal unresolved difference that remains is that the GCM data are radiative fluxes, whereas the NISTAR and EPIC data are near-backscatter radiances.

The Lissajous orbit also has a radial component that affects the radial Earth-Satellite distance (Marshak et al., 2018), which instills an inverse square distance dependence in the Earth reflected and emitted radiances. Since NISTAR views the Earth as a single pixel, the NISTAR measurements need to be normalized to a fixed standard distance. For EPIC, the size of the Earth’s image on the detector automatically changes in response to the distance change.

NISTAR: Cavity Radiometer Data

NISTAR, the DSCOVR Mission’s global energy budget instrument, is a cavity radiometer with four broadband channels designed to measure the reflected and emitted radiation eminating from the Earth’s sunlit hemisphere. As described in Figure 3, Band-A is an open filter position, measuring the Total Outgoing radiation (TOR) over the solar and thermal spectral regions (0.2–100 μm). Given that NISTAR observations of the Earth are from the vicinity of the Lagrangian L1 point, and are near zero phase angle, the expected reflected solar SW flux from the sunlit hemisphere would be near 200 Wm^–2, and the outgoing longwave (OLR) near 240 Wm^–2. However, the NISTAR data are near-backscattered radiances that are sensitive to phase angle variability (Marshak et al., 2021). The NISTAR near-backscattered radiance-to-flux conversion is still an ongoing endeavor. Because of the complexity, it may be that a uniform scaling factor might not be adequate for the radiance to flux conversion. Accordingly, the NISTAR data are still being expressed in their relative radiance units, as indicated in the figure labels.

FIGURE 3

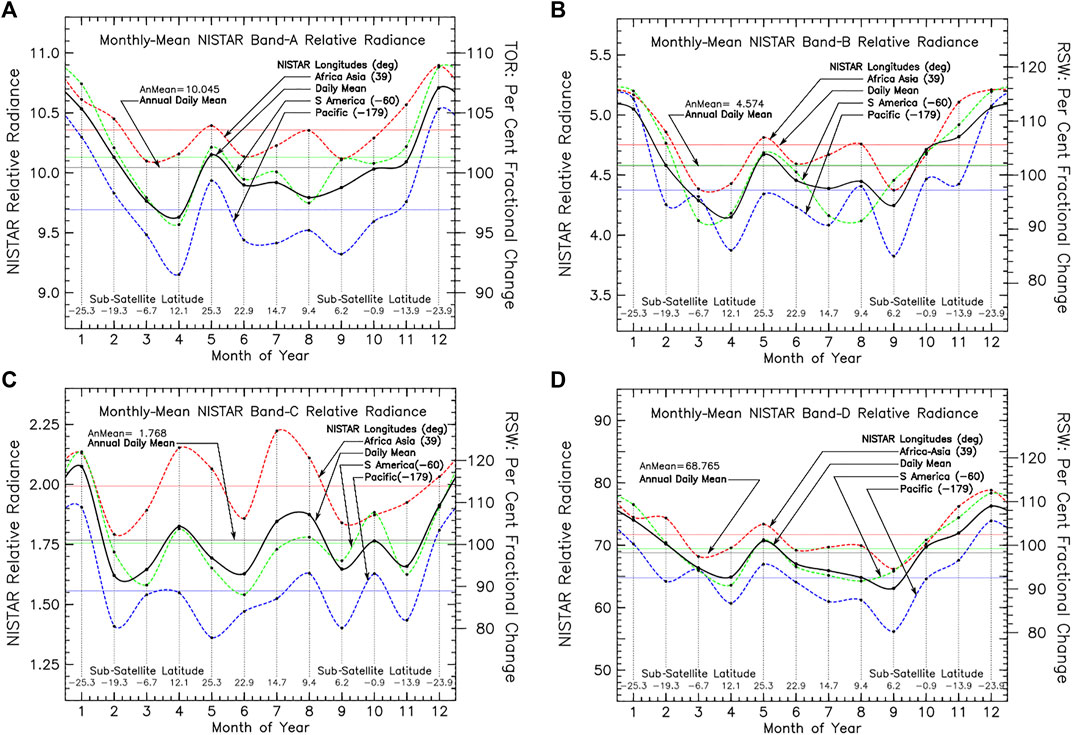
FIGURE 3. Four-hour averaged NISTAR measurements for year 2017 of the longitudinally sliced seasonal variability of the Band-A (0.2–100 μm) Total Outgoing Radiation TOR (A), Band-B (0.2–4 μm) Reflected Solar Radiation RSR (B), Band-C (0.7–4 μm) Near-Infrared Reflected Solar Radiation NIR (C), and Band-D Silicon Diode (0.3–1.1 μm) Visible Reflected Solar Radiation VIS (D). The heavy black lines depict (longitudinal) full day averages. The colored lines represent the longitudinal slicing as the Earth rotates, whereby the specified geographical area with the high-noon Sun is also identified by its central meridian. The seasonal change in the Lissajous orbital sub-satellite latitude is tabulated at figure bottom.

There is seasonal asymmetry clearly evident in the NISTAR data directly attributable to the (Figure 2) Lissajous orbital phase angle change that shifts the DSCOVR Satellite viewing geometry of the Earth. In January, the DSCOVR sub-satellite latitude is at its southern extreme (−25.3^o). With its Lissajous orbital motion oriented in the same direction as the change in solar declination, by mid-May NISTAR is viewing the Earth from its northern extreme (+25.3^o). It then takes until December to return to its southern extreme.

The seasonal variability of longitudinally sliced NISTAR data is shown in Figure 3. Monthly-mean averages are accumulated for different geographic regions, based on their sub-solar longitude as the Earth rotates. The respective color-coded lines correspond to the central meridian of a major landmass area (Africa-Asia, 39° E longitude), a mostly ocean view of the sunlit hemisphere (Pacific Ocean, 179° W longitude), and an intermediate land-ocean region (S America 60° W longitude). The NISTAR data are also tabulated in accord with the Greenwich Mean Time (GMT), where each hour of GMT corresponds to a 15^o shift in longitude. Notably, the continental Africa-Asia region has the highest reflectivity, while the Pacific region has the lowest reflectivity, with S America in between. NISTAR Band-A also includes a thermal component, for which the highest day-time surface temperature would occur over the Africa-Asia region, and the lowest over the Pacific.

NISTAR Band-C measures the NIR (0.7–4 μm) portion of the reflected solar radiation, compared to (0.2–4 μm) for Band-B. This selects the spectral region that is most sensitive to the elevated spectral reflectivity of vegetation, located longward of the 0.7 μm chlorophyl red edge. Compared to the Band-B RSR measurement, the NISTAR Band-C measurement shows strong enhancement over the Africa-Asia region, thus qualifying as the “vegetation” channel.

Band-D (0.3–1.1 μm) is a silicon diode measurement, intended more as a calibration reference. It is similar to the Band-B spectral response, but with a reduced NIR contribution. The heavy black line depicts measurements averaged over a full rotation of the Earth, and thus all longitudes. It serves as reference for the longitudinal variability that is displayed by the longitudinal data slicing.

Figure 4 further illustrates how the low signal-to-noise problem complicates the analysis of NISTAR active cavity measurements. In the NISTAR active cavity approach, the electrical current that acts to maintain a fixed cavity temperature needs to be averaged over a substantial time interval to diminish the background noise. In Figure 3, the NISTAR Level 1B data are near-hourly averages spanning roughly 15^o in longitude, thus averaging out a substantial amount of longitudinal variability. Meanwhile, in Figure 4, the selected meridional data samples are from shorter time-averaged NISTAR Level 1B data products, corresponding to longitudinal swaths of approximately 4° in width. Figure 4 seasonal plots show far greater noisiness than Figure 3, particularly for Band-C, for which the April-May and July-August peaks become truncated, clearly demonstrating the need for data averaging to reduce the data noise. However, given that direct averaging of Figure 4 data does not fully reproduce Figure 3 results, points to potential data artifacts, or to more complex calibration issues.

FIGURE 4

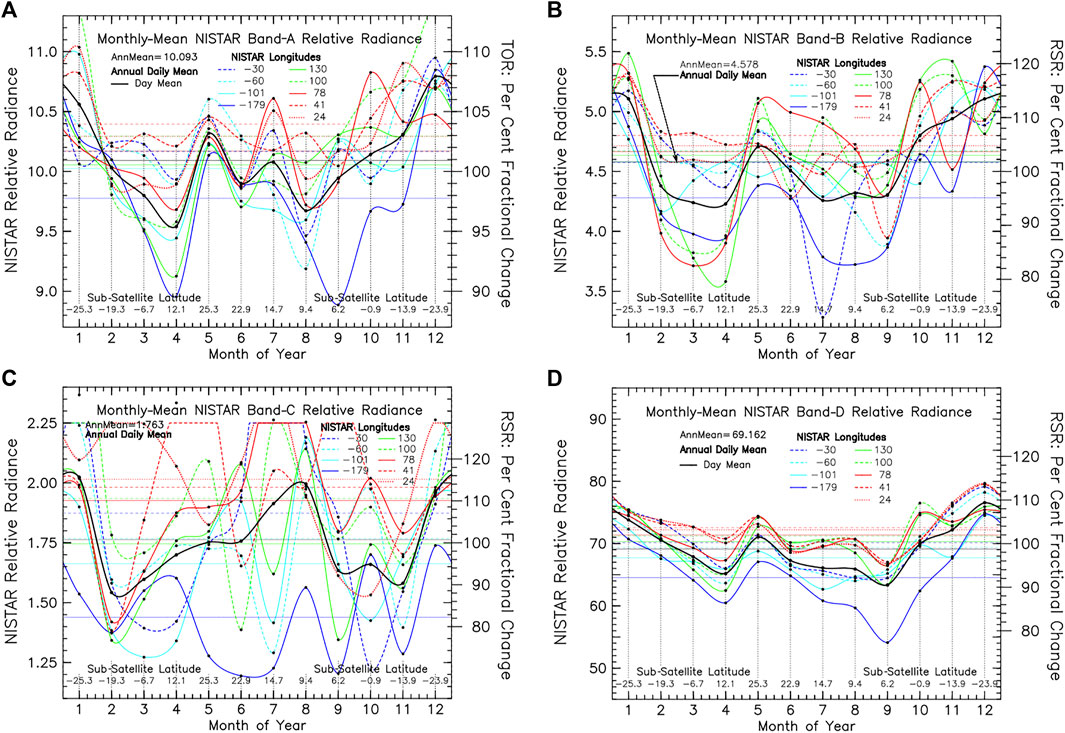
FIGURE 4. NISTAR measurements for year 2017 of the longitudinally sliced seasonal variability of the Band-A (0.2–100 μm) Total Outgoing Radiation TOR (A), Band-B (0.2–4 μm) Reflected Solar Radiation RSR (B), Band-C (0.7–4 μm) Near-Infrared Reflected Solar Radiation NIR (C), and Band-D Silicon Diode (0.3–1.1 μm) Visible Reflected Solar Radiation VIS (D). The underlying NISTAR measurements here are basically the same as in Figure 3 heavy black lines depict the daily (longitudinal) average. The NISTAR Relative Radiance units are the archived data units.

There are several different sources for the increased noisiness of the data. While a few of the plotted points might appear to be artifacts, there is a physical basis behind the enhanced variability. Part of the problem is in the sampling. For example, the monthly-means for March are interpolated points, since no data are archived for that month. Also, there are some months with only a few days of archived data, which would bias the seasonal context of the points from their monthly-mean position, due to the large shifts in orbital position that the DSCOVR spacecraft can undergo in just 1 month (see Figure 2). But the change in the sunlit fraction projected area of the image disk is small, varying only by ∼0.25%, from 0.995.

On the other hand, the radiative effects of the rapidly changing phase angle have a more significant effect. It is within the near-backscatter range of phase angles (especially for scattering angles greater than 175^o) that the reflected radiation particularly sensitive to small changes in the scattering angle. For spherical (liquid water) cloud droplets, the magnitude of backscattered radiation depends not only on cloud optical depth, but also on the cloud particle size, including the size distribution variance (e.g., Hansen and Travis, 1974). Also, depending on the precise viewing geometry, oriented ice crystals can exhibit substantial increased in brightness (Marshak et al., 2017). Thus, there is little doubt that much of the variability seen in the NISTAR data arises from a changing distribution in the cloud and land/ocean surface contributions, each with a different set of phase angle dependent backscattering properties. It is unlikely the climate GCM radiative fluxes will be expressible in terms of the near-backscattered radiances any time soon. Meanwhile, efforts are continuing to refine the sunlit hemisphere-mean radiance-to-flux conversion factors based on EPIC image analyses.

The design feature of the DSCOVR measurements is that taking the difference between Band-A and Band-B would isolate the LW component of the outgoing thermal radiation (OLR), which might also have a backscatter phase angle dependence, but to a much lesser degree than the SW measurements. The main calibration issue that affects the OLR determination is the need to determine the absolute transmission characteristics of the Band-B transmission filter. This needs to be determined indirectly because of no internal calibration source in the instrument. Then the remaining SW (beyond Band-B) needs to be characterized and subtracted to isolate the OLR signal.

Figure 5 depicts the unique spectral ratios that are available from NISTAR data. One obvious advantage of spectral ratios is that to first order, most of the NISTAR calibration, backscattered radiance, and viewing geometry issues cancel out. But more importantly, the NISTAR NIR/SW spectral ratio, that straddles the chlorophyl 0.7 μm red edge, is a key climate-specific measurement that is not readily available from the current satellite data. The choice of this spectral pivot point identifies vegetated regions on the basis of their higher NIR spectral albedo. Thus, as the Earth rotates, longitudinal slicing identifies and ranks the geographical regions by their NIR reflectivity. This is a novel diagnostic of GCM radiative modeling performance, and also serves as a biosphere identifier in exoplanet studies (Carlson et al., 2019).

FIGURE 5

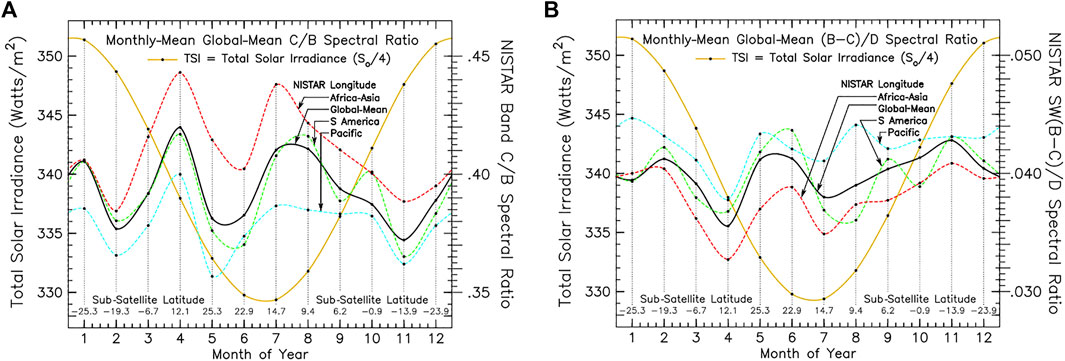
FIGURE 5. Seasonal variability of longitudinally sliced NISTAR Band-C (0.7–4 μm)/Band-B (0.2–4 μm) NIR/SW spectral ratio for year 2017 (A), and the inverse VIS/VIS + spectral ratio of Bands-(B-C) (0.2–0.7 μm)/Band-D (0.3–1.1 μm) (B). The colored curves represent longitudinally sliced hemispheric views of geographical regions identified by their noon-time meridians. The heavy black lines represent full-day averages. The heavy yellow curves depict the seasonal variation of the Total Solar Irradiance (TSI) as referenced by the Y-axis scale at left.

Figure 5 shows the maximum spectral ratio (red line) to be over Africa-Asia in April and July. As expected, the minimum spectral ratio is over the Pacific (blue), but the large April-to-May seasonal variability is not expected, and could indicate that NIR water vapor absorption or GCM cloud distribution inaccuracies could also be a factor. At Figure 5B, the inverse (B–C)/D ratio emphasizes visible cloudy areas. Also shown is the seasonal TSI, depicted by the heavy yellow curve (and Y-axis at left), showing no apparent correlation with the seasonal variability of the NISTAR data.

A somewhat better view of the seasonal variability is obtained in the pinwheel format shown in Figure 6, where the NISTAR data are plotted as a function of the DSCOVR sub-satellite latitude. This is possible since the DSCOVR satellite effectively makes two full orbits per year. This also illustrates more clearly the effect of the Lissajous orbit on the seasonal variability of the NISTAR data stream. As shown in Figure 6A, the DSCOVR sub-satellite latitude is at its southern extreme (−25.3^o) in January. Because the Lissajous orbital motion is oriented in the same direction as the solar declination change, by mid-May NISTAR is viewing the Earth from its northern extreme (+25.3^o). It then takes until December to return to its southern extreme. The solid red line illustrates the rapid January-to-May northward trek for the Africa-Asia meridian, while the much slower May-to-December southward return trek is denoted by the red dash line. Notable on the southward return trek is the pronounced June-to-September chlorophyl-fueled hump that can be associated with the northern hemisphere growing season (with its peak in July). At Figure 6B are the corresponding results from the GISS ModelE2 NIR/SW spectral ratio output data. On the positive side, the relative order of the longitudinal slicing agrees with the NISTAR data. But, the amplitude and seasonal variability of the GCM surface albedo climatology is far too small.

FIGURE 6

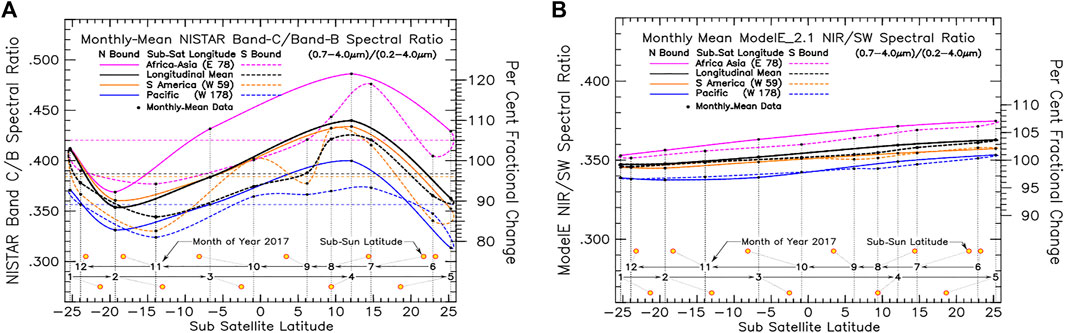
FIGURE 6. Seasonal variability of longitudinally sliced NISTAR Band-C (0.7–4 μm)/Band-B (0.2–4 μm) NIR/SW spectral ratio for year 2017 (A), expressed in pinwheel format, and plotted as a function of the DSCOVR sub-satellite latitude. Noted at figure bottom are the mid-month positions of the DSCOVR spacecraft in terms of its sub-satellite location (numbers identify the month of year 2017), and the corresponding sub-solar latitude (declination) denoted by the yellow circles. At (B) are the corresponding NIR/SW spectral ratio results from the GISS ModelE2 reflected SW diagnostics output data sampled in accord with the DSCOVR Satellite Ephemeris viewing geometry and aggregated over the sunlit hemisphere.

Figure 7A illustrates the basic features of the seasonal variability of the Earth’s global energy balance. The annual-mean global average Total Solar Irradiance (TSI) is 340.2 Wm^–2 (Kopp and Lean, 2011). The heavy yellow curve depicts the seasonal TSI radiative forcing change due to the Earth’s orbital motion, which in ModelE2 is defined by the Solar Ephemeris. The red dash curve is the ModelE2 Total Outgoing Radiation (TOR = RSR + OLR) run for thousands of years to global energy balance equilibrium under pre-industrial conditions. The red curve is the ModelE2 TOR for current climate conditions, which displays the current global-mean energy imbalance of 1.14 Wm^–2, showing also that there is seasonal variability present in the global energy imbalance. Compared to the TSI radiative forcing, the TOR amplitude is much reduced, but with a bimodality in phase. The observational data from CERES (Loeb et al., 2018) and ISCCP (Zhang et al., 2004) depicted by the green and blue dash curves, respectively, exhibit similar variability, but with a phase shift by about a month compared to the ModelE2 data. The differences may be small in the absolute sense, but they are significant. The climate system response to applied TSI forcing is not simply a radiative issue, but also involves land/ocean energy transports, sequestration and transport of absorbed solar energy, and its later release to the atmosphere.

FIGURE 7

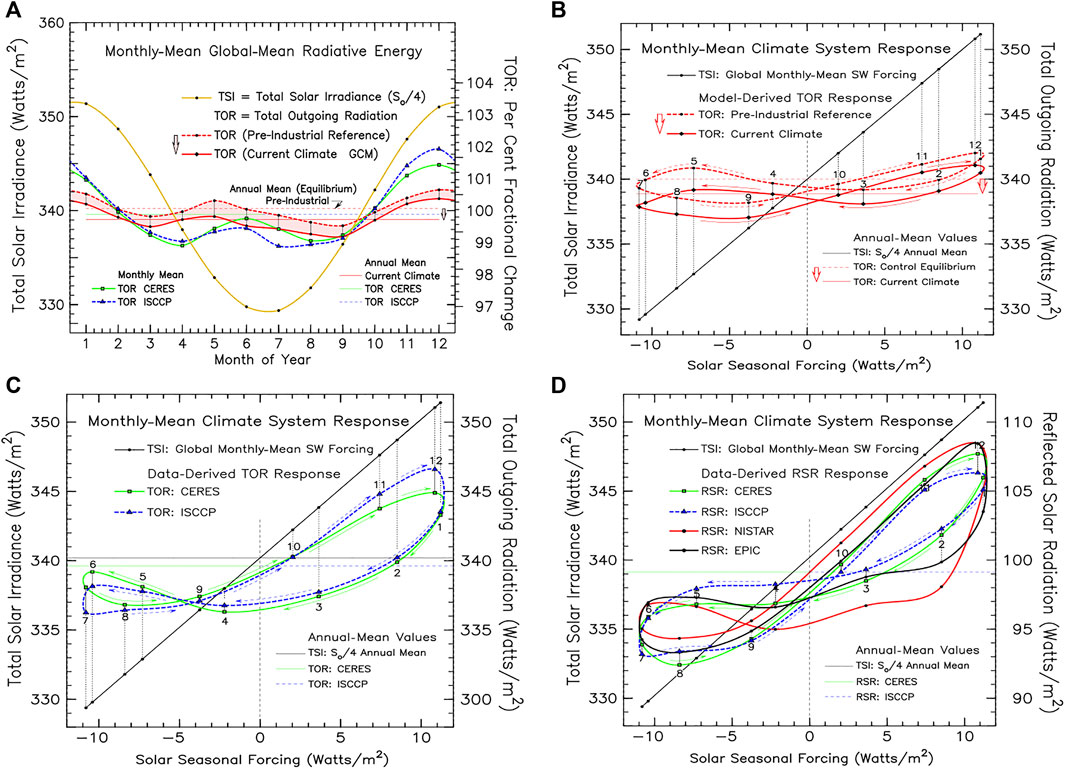
FIGURE 7. Seasonal energy balance of the Earth between the incoming Total Solar Irradiance (TSI) and the Total Outgoing Radiation (TOR) computed by the GISS ModelE2 for current climate (solid red line) and pre-industrial (red dash line) conditions with comparison to CERES and ISCCP data (A). The heavy yellow line depicts the seasonal change in TSI radiative forcing. The CERES and ISCCP TOR determinations are depicted by the green and blue dash lines, respectively. (B) displays the GCM seasonal TOR variability in pinwheel format (relative to the Solar Seasonal Forcing). (C) displays the CERES and ISCCP seasonal TOR variability, shown in (A), in the same pinwheel format. (D) compares the reflected solar radiation RSR in pinwheel format between CERES and ISCCP results and NISTAR Band-B (solid red) and EPIC (black) derived SW flux results. The numbered black dots connected by the vertical dotted lines refer to the monthly-mean mid-points of TSI and the corresponding reflected SW flux.

Upper right displays the ModelE2 results in the more compact pinwheel format that provides a more compact perspective on the seasonal variability of the global energy variables. Since the TSI changes are precisely known in time and magnitude, TSI radiative forcing can serve as the X-axis. All climate variables are in fact functions of solar radiative forcing, with the time of year defining the Y-axis of the variable. Thus, on the left side Y-scale, TSI traces out the black slanted line with the black dots marking the monthly mean TSI values of the year, with July at the negative extreme and January at the positive extreme. Likewise, on the right-side Y-axis, the ModelE2 TOR monthly means are plotted in accord with the time-of-year that is also implicit with the X-axis solar forcing. If the heat capacity of the climate variable was close to zero, the pinwheel path of that variable would be a slanted line like that of the TSI forcing that retraces itself. If, on the other hand, the heat capacity was infinitely large, the pinwheel path would then be a horizontal line equal to its global annual-mean value. As it is, the ModelE2 TOR traces out near-horizontal bow-tie shaped figures with basically equal lobes that are rotating clockwise in the northern hemisphere winter lobe and in the counter-clockwise direction in the summer lobes. The seasonal change in global energy imbalance appears to be more pronounced in the NH summer lobes.

Figure 7C shows the CERES and ISCCP TOR data in pinwheel format. Except for a few points in April, July, and November, December, there is close agreement between CERES and ISCCP. As in the case of ModelE2, the direction of pinwheel rotation is clockwise in the NH winter lobe and counter-clockwise in the summer lobe. However, the winter lobe is much larger than the summer lobe for CERES and ISCCP. While the CERES/ISCCP NH summer lobe is mostly horizontal, the winter lobe exhibits a strongly inclined slope. The pinwheel shape, slope, directionality, and hysteresis are the product of virtually all of the GCM physical processes. It may well be that the CERES and ISCCP TOR results are suggesting the ModelE2 coupled atmosphere-ocean treatment may be seasonally too rigid, and that there should be some seasonal shift in model dynamics that can simulate a somewhat smaller heat capacity during the NH winter months relative to the summer. To sort out the different possibilities, future GCM runs are needed to identify and quantify the factors that affect the shape and slope of the pinwheel response to the seasonal change in solar radiative forcing.

The Figure 7D shows the reflected SW in pinwheel format for the CERES and ISCCP results and NISTAR Band-B (solid red) and EPIC (black) derived SW flux results. There is qualitative agreement between the CERES/ISCCP pinwheels and the NISTAR/EPIC pinwheels as to overall shape, slope orientation, and direction of rotation. But the agreement is much tighter between CERES and ISCCP then with EPIC and NISTAR. The EPIC results are a first step in the conversion of backscattered spectral radiances into their radiative flux equivalents (Su et al., 2018; Su et al., 2020). For this, the EPIC spectral radiances were converted to broadband fluxes using MODIS/CERES-based regression relationships, and then, by means of the CERES angular distribution models, into the EPIC reflected SW fluxes, which were then integrated over the sunlit hemisphere to produce the monthly-mean data points for the EPIC pinwheel. The EPIC global-mean CERES-based cloud anisotropy factors were also used to convert NISTAR data into radiative flux units for the NISTAR pinwheel (Su et al., 2018).

Compared to TOR pinwheels in Lower left, the RSR pinwheels exhibit somewhat steeper orientation and more equality in lobe size. Otherwise, the direction rotation remains clockwise in NH winter lobes and counter-clockwise in the summer lobes. Higher frequency oscillation that are evident in the EPIC and NISTAR pinwheels, but not in the CERES/ISCCP pinwheels, are likely residuals originating from phase angle backscatter and Earth-Satellite distance changes due to the Lissajous orbital motion.

As illustrated in Figure 8 the pinwheel format representations enable a concise comparison of global energy budget components, and they underscore the need for precise radiance-to-flux conversion for a more productive model/data intercomparison. Top row of Figure 8 displays NISTAR Band-A, Band-B, and Bands-(A-B) monthly-mean, full-day average Level 1B radiance data in pinwheel format representing the TOR, RSR, and OLR global energy budget components (but with twice the solar SW included in TOR, and incomplete subtraction of the total SW in the OLR component). The heavy green pinwheels represent the Level 1B NISTAR data as archived without having the Earth-Satellite distance dependence due to the Lissajous orbital motion removed. Since NISTAR views the Earth as a single pixel, the changing Lissajous orbital distance imparts an inverse square variance on the NISTAR measurement. While the changing Earth-Satellite distance effect on the size of the sunlit fraction of the projected disk image is tiny (0.25%), and thus of little concern, the distance square effect on the NISTAR measurement can be as large as ± 13.8%, given that the Lissajous orbital distance of the DSCOVR Satellite from Earth ranges from a minimum near 1.4 × 10⁶ km to a maximum near 1.6 × 10⁶ km.

FIGURE 8

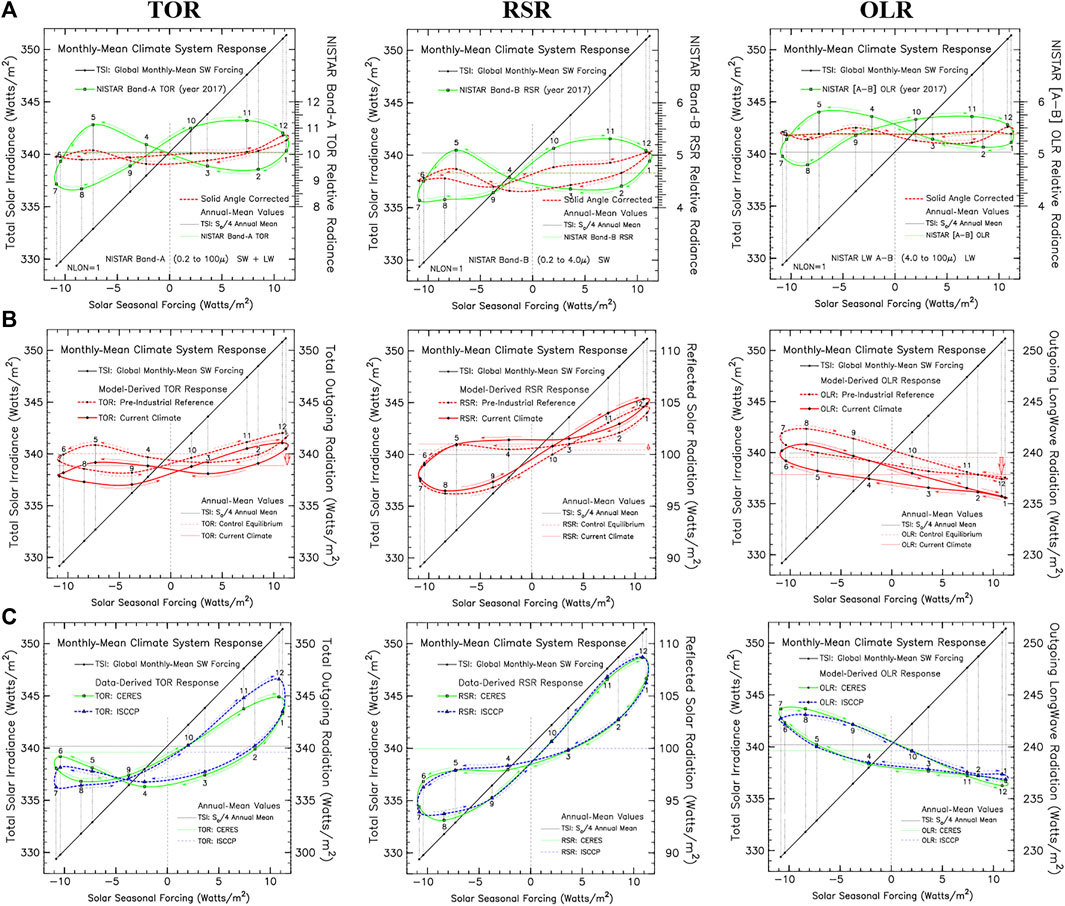
FIGURE 8. (A) Seasonal NISTAR data for Total Outgoing Radiation (TOR), Reflected Solar Radiation (RSR), and Outgoing Longwave Radiation (OLR) in pinwheel format. The heavy green pinwheels are full-day (longitudinal) average Level 1B monthly-mean data. The red-dash curves represent the green pinwheel data but include inverse square Earth-Satellite distance correction. (B) Seasonal variability of global monthly-mean ModelE2 TOR, RSR, OLR pinwheels for pre-industrial (red dash) and current climate (solid red) conditions. (C) Seasonal variability of global monthly-mean CERES (green) and ISCCP (blue dash) pinwheels for TOR, RSR, and OLR.

The changing Earth-Satellite distance effect on the NISTAR pinwheel shape is significant, as shown by the red dash distance normalization. Radiance-to-flux conversion is also a much-needed transformation for model/data comparison. Due to its complexity, simple scaling is not sufficient. Another significant factor involved in the pinwheel comparison is the fact that the NISTAR pinwheel is for a projected image of the sunlit hemisphere, where latitudinal viewing perspective from the Lissajous orbital position comes into play, while the CERES, ISCCP, and GCM pinwheels represent global-mean averages in satellite retrieval data product format. Based on these considerations, the NISTAR RSR pinwheel in Figure 8 is transformed into the Figure 7D RSR pinwheel that is more like the EPIC and CERES/ISCCP RSR pinwheels. Thus, except for the spectral ratio results (for which the distance change, backscatter radiance, and viewing geometry issues cancel out), the full analysis of NISTAR measurements is still a work in progress, despite its promising prospects.

The Figure 8B displays the ModelE2 TOR, RSR, and OLR pinwheels, showing in more detail the seasonal change in the global energy budget between the pre-industrial and current climate conditions. Overall, there has been a decrease by 1.14 Wm^–2 in global-mean energy balance, as indicated by the TOR pinwheel. Interestingly, this has been accompanied by a modest increase in RSR by 0.55 Wm^–2, and a dominating decrease in OLR by 1.69 Wm^–2. Moreover, the RSR increase has occurred during the months of September to April, with hardly any change taking place in the reflected SW during the summer months of May to August. For RSR, the pinwheel direction of rotation is the same as for TOR, clockwise in the NH winter lobe and counter-clockwise in the summer, with the summer lobe being substantially larger than the winter lobe. For the OLR pinwheel, there is little change in shape between pre-industrial and current climate, just an overall decrease in OLR by 1.69 Wm^–2 due to accumulating greenhouse gas radiative forcing. But, the OLR pinwheel shape, orientation, and rotation are quite different from the RSR pinwheel. Instead of two lobes, it is basically a single large summer lobe, with the winter lobe shrunken down to near-nothing. The slope of the OLR pinwheel orientation is negative, and the direction of rotation is clockwise, opposite that of the RSR pinwheel.

For comparison, Figure 8C displays the CERES (green) and ISCCP (blue dash) pinwheels for TOR, RSR, and OLR. The CERES and ISCCP pinwheels are in good agreement with each other. The RSR lobes are near-equal in size and are closely oriented in slope with the TSI slanted line. Their direction of rotation is the same as that of the TOR pinwheels, clockwise in the NH winter lobe and counter-clockwise in the summer lobe. The CERES and ISCCP OLR pinwheels are very similar to the ModelE2 OLR pinwheels, in shape, size, orientation, and direction of rotation. Perhaps that should not be surprising since climate GCMs are typically tuned to reproduce the historic trend in global surface temperature, with less attention focused on the accuracy of the reflected SW radiation. If the ModelE2 global surface temperatures are in agreement with observations, then it is likely that the OLR is also in agreement.

However, there is a small but persistent difference between the CERES and ISCCP OLR pinwheels in July and also in December. In July, the CERES OLR is about 1 Wm^–2 higher than ISCCP, and in December, the CERES OLR is about 1 Wm^–2 lower than ISCCP. This difference is most likely due to a difference in cloud altitude, and less likely to cloud fraction, since the CERES and ISCCP RSR pinwheels show no significant differences. Thus, CERES appears to detect clouds at a lower altitude than ISCCP in July, but at a higher altitude in December. Or, it is also possible that CERES detects more ice clouds (with lower emissivity) in the July time frame, and fewer ice clouds than ISCCP during December.

The RSR slope difference between CERES/ISCCP and ModelE2 is harder to explain. It can’t simply be due to clouds, since clouds also affect the OLR. It would need to be limited to seasonal cloud albedo or cloud optical depth differences, to which the OLR is less sensitive. Ultimately, it is the GCM energy transports and energy sequestration that must be involved in defining the pinwheel. The NISTAR and EPIC data are essential for resolving the pinwheel differences between the CERES/ISCCP and ModelE2 pinwheels. At this point in time, NISTAR data calibration and signal-to-noise issues limit their effectiveness. EPIC data analysis has made more rapid progress and serve as a bridge to NISTAR data improvement.

Discussion

NISTAR and EPIC measurements provide a unique perspective of the Earth’s sunlit hemisphere from their Lissajous orbit vantage point, which makes possible a new format model/data comparison. Because the climate system is highly variable both in space and in time with differences in viewing geometry, spatial resolution, and diurnal cycle sampling time between observations and climate model output, this can produce biases and distortion. In addition, both climate GCMs and the real world operate in quasi-chaotic fashion, which produces a “natural” uncorrelated variability that is an unavoidable source of uncertainty in model/data comparisons.

This “weather noise” problem is mitigated by integrating the input data over the entire sunlit hemisphere, which NISTAR does naturally with its single-pixel observations, and EPIC with its full-disk image analysis. This approach provides broad-brush climate-type information that summarizes the climate system’s response to the seasonally changing solar radiative forcing. These sunlit-disk data points are further averaged over time as monthly-means. With weather noise averaged out, the rotation of the Earth preserves the longitudinal variability of the land/ocean distribution, and retains planetary-scale fluctuations such as the MJO and ENSO/La Niña variability. Longitudinal slicing is then used to display the data.

On the climate GCM end, identical space-time sampling can be implemented to integrate the GCM run-time output data over the sunlit hemisphere to reproduce the viewing geometry identical to that of the DSCOVR Satellite NISTAR and EPIC measurements. That is accomplished with the Sunlit Hemisphere Sampling (SHS) simulator that has been installed in the GISS ModelE2 to generate climate-style output data with the same self-consistent space-time sampling as the NISTAR data. The key difference that still remains is that the GCM data are in radiative flux format, while NISTAR data are near-backscatter radiances.

The anisotropy problem is largely alleviated in the case of the NISTAR Band-C/Band-B spectral ratio analysis, which is a more robust measurement in that the viewing geometry, calibration, and backscattered radiance issues are, for the most part, cancel out. This spectral ratio measurement is of fundamental importance since there are no similar measurements available from conventional satellite data. The NISTAR spectral ratio measurements have demonstrated their value as a novel radiative modeling diagnostic tool to assess climate GCM performance, showing for example, that the GISS ModelE2 does not have sufficient seasonal or longitudinal spectral variability in reflected SW flux, although ModelE2 does reproduce the relative longitudinal ordering that is seen in the NISTAR data (Carlson et al., 2019).

However, because of spectral dependence of the backscatter radiance-to-flux anisotropy, there might be only partial anisotropy cancelation in the Band-C/Band-B spectral ratio. The anisotropy parameter is likely to be larger for Band-B than it is for Band-C (Marshak et al., 2021), in which case the NISTAR spectral ratio variability would be reduced, thus mitigating the spectral ratio disagreement between NISTAR and ModelE2 in Figure 6. Such reduction in the NISTAR spectral ratio amplitude would improve the comparison with the GCM results. The coming CERES/Libera mission should help to resolve all of these spectral ratio issues.

For added perspective, the NISTAR data comparison in Figure 6 uses the pinwheel format for the spectral ratio comparison. Here, the DSCOVR sub-satellite latitude serves as the X-axis, helping to highlight the relative importance of the Lissajous orbital motion on the seasonal asymmetry that is apparent in the time-series plots. The DSCOVR Satellite is at its southern-most extreme in January of 2017. Its orbital motion, when in phase with the change in solar declination, carries it to its northern-most extreme in only 4 months by May. The return trip which is out of phase with the solar declination change, takes about 8 months to get back to the southern-most extreme by January of the following year. This asymmetric change in the Lissajous orbital viewing perspective accounts for much of the seasonal asymmetry that is evident in the time-series plot in Figure 5.

The “bow-tie” shaped pinwheel perspective t in Figures 7, 8, uses the (–11 Wm^–2 to +11 Wm^–2) change in the solar seasonal radiative forcing as the reference X-axis, which is appropriate for the NISTAR global energy balance visualization. In this format, the left Y-axis and the slanted line refer to the incident solar irradiance, for which the maximum TSI is at the upper right corner in January, and minimum TSI at lower left in July. The right-hand Y-axis represents the reflected SW flux, with the implicit time dependence inferred from the seasonal solar radiative forcing, which defines the placement of the monthly-mean data points.

If the heat capacity of the climate system was negligible, and the reflected SW flux was directly proportional to TSI, the shape of the reflected SW pinwheel response would be a slanted line that tracks the change in TSI. For a very large heat capacity, the pinwheel shape would simply be a horizontal line. As it is, the Earth’s climate system has both a large heat capacity and the added complexity that a large amount of heat energy is being sequestered by the southern oceans during the NH winter months, transported northward, and then added to the outgoing LW radiation during the NH summer months, with corresponding changes in the global cloud cover. As shown by the CERES/ISCCP reflected solar radiation (RSR) pinwheels in Figure 8, maximum RSR occurs in December.

The decrease in RSR is more rapid than the decrease in the TSI, with increasing energy going into ocean for sequestration. This imparts a clockwise rotation to the NH winter lobe of the pinwheel. The enhanced decrease in RSR (and planetary albedo) continues through March, slowing down substantially from March to June, as TSI undergoes its most rapid decrease. As a result, this shifts the pinwheel into its NH summer lobe where the direction of rotation is counter-clockwise since the rate of change during this time period is more rapid for TSI than it is for RSR. There is an accelerated RSR decrease from June to August as TSI reaches its minimum in July, and begins increasing again. This completes the pinwheel NH summer lobe turn-around, setting it up for a more in-step return back to its December maximum. The CERES/ISCCP RSR seasonal change in the reflected SW radiation is in close agreement with the EPIC results while the results at individual meridians exhibit a high degree of seasonal variability.

Except for its much smaller NH winter lobe, the ModelE2 RSR pinwheel in Figure 8 is basically similar to the CERES/ISCCP RSR pinwheel. The NISTAR RSR pinwheel has little resemblance, implying significant seasonal variability for the RSR backscattered radiance to flux conversion. But, the overall slope of the NISTAR RSR pinwheel is actually in better agreement with the slope of the ModelE2 RSR pinwheel, than it is with the slopes of the CERES and ISCCP RSR pinwheels. The NISTAR OLR pinwheel shows little similarity to the ModelE2/CERES/ISCCP OLR pinwheels. It is probable that in this case that the problem may be the incomplete subtraction of solar radiation in the NISTAR Band-A minus the Band-B differencing. Interestingly, the orientation of the OLR pinwheel, which is practically orthogonal to the RSR pinwheel orientation, underscores the phase difference between the energy sequestration and that of the solar SW radiative forcing.

While NISTAR was designed to produce hemisphere-averaged energy budget data of the Earth without numerical aggregation, the problem is that the NISTAR data are near-backscattered radiances that are aggregated from a broad range of contributors which have different backscattering properties, with an ever-changing viewing geometry that makes quantitative comparison to climate GCM data problematic. It would appear that essentially real-time anisotropy correction is needed to convert the near-backscattered NISTAR radiances into radiative fluxes with sufficient accuracy for global energy balance analysis and comparisons (Su et al., 2015; 2021).

The importance of accounting for near-backscattered radiation of NISTAR and EPIC measurements is discussed in by Marshak et al. (2021). Their Figure 7 shows large differences and strong dependence on the scattering angle of reflected radiation by ice and water clouds in the near-backscatter direction with the region between 175^º to 180^º scattering angle being most prominent. Ice cloud and water cloud particles have scattering functions that are different in this near-backscatter angle range. Moreover, flat-plate ice cloud particles often appear in oriented configuration to cause glint (Marshak et al., 2017). Furthermore, there are finite sized scatterers in vegetation canopies that can cast shadows. In such vegetation canopies, shadowing is minimized under backscatter conditions, and thus produce enhanced brightening for decreasing phase angle (Marshak et al., 2021). Mishchenko et al. (2002) describe exact vector theory results for coherent backscattering for discrete random media, showing sharply-peaked backscattering brightness enhancement by over 50% for spherical particulates at 0° phase angle, compared to phase angles just larger than 10°.

The principal climate system constituents, ocean, land, snow, ice, vegetation, as well as aerosols, water and ice clouds, possess significantly different backscattering properties. As a result, the sunlit-hemisphere anisotropy parameter that would describe the hemisphere-mean anisotropy of NISTAR data will vary as the mix of climate constituents changes due to the rotation of the Earth, and also in response to the Lissajous orbital change in phase angle. Basically, there is no simple methodology to define the NISTAR sunlit-hemisphere anisotropy parameter to convert backscattered NISTAR radiances into radiative flux equivalents with sufficient accuracy for quantitative global energy balance comparisons to climate GCM simulations, which are invariably in the form of radiative fluxes.

To help address this situation, a study was initiated by Su et al. (2018; 2020) to convert EPIC spectral radiances into reflected SW fluxes to calibrate the NISTAR Band-B backscatter radiances. For this, the EPIC spectral radiances were converted to broadband SW radiances using MODIS/CERES-based regression relationships, and then transformed to radiative fluxes using the CERES angular distribution models. These transformations were performed at the pixel level. Integration over the entire sunlit hemisphere converted each EPIC image into a single climate-style data point of reflected SW flux. In way, 5388 EPIC images for year 2017 were processed to generate a table of 12 × 24 monthly-mean planetary albedo points.

These sunlit hemisphere averages were normalized relative to the CERES global annual-mean value for reflected SW radiative flux of 99.1 Wm^–2 (Loeb et al., 2018), and divided by the Total Solar Irradiance 340.2 Wm^–2 (Kopp and Lean, 2011), The tabulated EPIC planetary albedo points serve as the input data for the longitudinal slicing methodology to map and analyze the seasonal and longitudinal variability of the Earth’s global energy balance in terms of its planetary albedo, as described in our companion paper (Carlson et al., 2022). They are also the first order reference for NISTAR Band-B anisotropy calibration for converting the near-backscatter radiances to radiative fluxes. The process of NISTAR radiometry channel calibration is a complex iterative endeavor that involves characterization of the Band-B and Band-C cutoff filter transmission properties, which must be accomplished while simultaneously battling poor signal-to-noise as the radiometer channel calibration is being established. Also, as the Earth rotates, the anisotropy parameter derived from EPIC data keeps changing as the land/ocean/cloud distribution changes and as the EPIC viewing geometry changes.

In view of the above, it has become clear that the accuracy of the NISTAR Band-B radiative flux is totally dependent on the successful outcome of the EPIC data conversion to radiative flux. If the principal objective of NISTAR measurements was only to serve an observational reference for the seasonal variability of the Earth’s global energy balance geared to climate GCM comparisons, then the NISTAR measurements could well be viewed as largely superfluous. But, as already noted, it is the spectral discrimination such as the Band-C/Band-B spectral ratio, which to a large extent is not directly dependent on precise radiance-to-flux conversion, that makes the NISTAR measurements unique. With more precise calibration, there are other spectral interval combinations available such as Vis Band (Band-B—Band-C, 0.2–0.7 μm), the Near-IR Band (Band-D—Vis Band, 0.7–1.1 μm), and the Mid-IR Band (Band-B—Band-D, 1.1–4 μm). The Vis Band samples the least absorbing part of the solar spectrum, while the Near-IR and Mid-IR Bands sample spectral regions with different amounts of absorption by water vapor and reflection by surface vegetation. Nevertheless, the usefulness of these NISTAR spectral intervals for differentiating the radiative effects of clouds, water vapor, and surface vegetation are strongly dependent on the stability of the NISTAR radiometric calibration and the effectiveness of the data noise suppression for the present Level 1B version of the NISTAR data compilation that has been the topic of this study to assess and analyze.

Overall, it is the longitudinal slicing aspect of the NISTAR and EPIC data that makes DSCOVR Mission measurements so unique in their role as key climate modeling diagnostic tools. In our prior NISTAR line plot data comparisons, radiative flux comparability was the key objective. Thus, accurate radiance-to-flux conversion was required. Also available are Hovmöller format comparisons, specifically optimized for geographical pattern visualization that are a natural fit to longitudinal slicing, and are shown in Figure 9 for NISTAR Band-B (Left), and photodiode Band-D (Right).

FIGURE 9

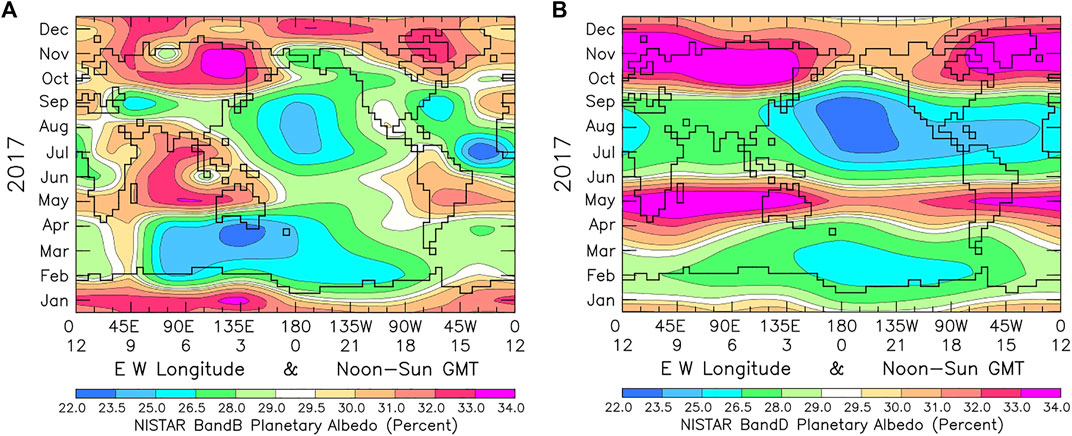
FIGURE 9. (A) NISTAR solar shortwave (SW) near-backscatter relative radiances for year 2017 from Figure 4B for Band-B (0.2–4 μm), and (B) for photodiode Band-D (0.3–1.1 μm) from Figure 4D, displayed as planetary albedo in Hovmöller format. In both cases, the NISTAR relative radiances are uniformly normalized to the CERES global annual-mean of 99.1 Wm–2 (Loeb et al. (2018), to yield a global annual-mean of 29.1 percent for the planetary albedo. In the Hovmöller format, the Y-scale has the time running upward starting from January at the bottom, through December at the top. The X-scale has the longitude running from 0° E longitude at the left and 0° W longitude at the right. The X-scale also references the GMT of the noon-time Sun, starting at GMT = 0 at the Date Line at the center, increasing westward toward the left, as the Earth rotates. A 5 ° × 4 ° GCM world map is included for geographic reference.

Since terrestrial weather patterns typically tend to evolve in the East-West direction, rather than North-South, Hovmöller (1949) found it more informative to average meteorological data over the North-South dimension, before plotting the latitude-averaged data as a function of longitude, with time increasing upward along the Y-axis. For convenience the X-scale is centered over the Central Pacific Ocean Date Line, and also includes the Greenwich Mean Time (GMT) of the high-noon Sun at that longitude. By nature of their single-pixel measurement, NISTAR data are automatically in Hovmöller format. Each point on the Hovmöller map represents a sunlit-hemisphere average (with both latitudinal and longitudinal meteorological activity averaged out). The rotation of the Earth retrieves the planetary-scale variability, hence longitudinal slicing by the Earth’s rotation. To facilitate geographic location of different longitudes, a coarse-grid GCM 5° × 4° world map is included.

Figure 9A shows NISTAR Band-B backscattered relative radiance data from Figure 4A arbitrarily normalized to a planetary albedo (with global annual-mean equal to the CERES value of 29.1%, Loeb et al., 2018), interpolated to cover the full range of longitude and GMT, and replotted in Hovmöller format. This arbitrary action implies the assumption of a globally uniform annual-mean anisotropy parameter for transforming the NISTAR backscattered radiances of uncertain calibration into radiative fluxes that match the CERES global annual-mean flux of 99.1 Wm^–2. The objective is to assess and demonstrate how the “vanilla” version of the NISTAR Band-B data compares relative to the more idealized version derived from the analysis of EPIC data described in our companion paper (Carlson et al., 2021), which is also a part of the DSCOVR EPIC/NISTAR: 5-years of Observing Earth from the first Lagrangian Point.

Figure 10A is the EPIC version of what the ideal NISTAR Band-B planetary albedo data for year 2017 should look like in their Hovmöller format (from Carlson et al., 2021, their Figure 3). What stands out in the Hovmöller format is the evolving pattern of variability, in particular, the 2017 February-March La Niña feature with the 30° peak-to-peak longitudinal waves, that is not readily apparent in the NISTAR/EPIC line plots. The world map places this La Niña feature as occurring in the mid-Pacific, with the longitudinal waves extending some 90° eastward.

FIGURE 10

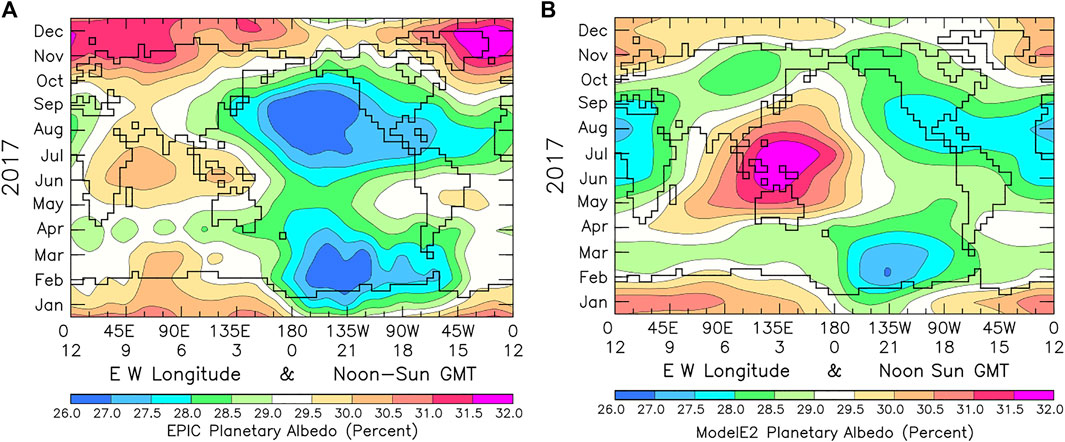
FIGURE 10. Hovmöller-style contour plot of the EPIC (A) and the GISS ModelE2 (B) planetary albedo for the year 2017. In both cases, the EPIC and GCM SW flux is normalized to the CERES global annual-mean of 99.1 Wm–2 (Loeb et al. (2018), to yield a global annual-mean of 29.1 percent for the planetary albedo. The Y-scale has time running upward starting with January at the bottom through December at the top. The X-scale is longitude running from 0° E longitude at the left to 0° W longitude at the right. GMT references the location of high-noon Sun. The world map is included for longitudinal reference. The data for the EPIC (A) and GISS ModelE2 (B) year 2017 planetary albedo are reproduced here from Carlson et al. (2021) modeling results.

In terms of the overall pattern of variability, NISTAR Band-B planetary albedo in Figure 9 shows strong resemblance to the EPIC results in Figure 10, re-affirming the thinking that the NISTAR data have the intrinsic stand-alone capability to detect changes in climate system variability, such as La Niña activity, even without resolving the anisotropy issue. Though the sparse longitudinal sampling of the NISTAR Band-B data (in Figures 4, 9) precludes conclusive confirmation, there is reason to expect that with higher longitudinal sampling, the Band-B data would have detected the longitudinal wave activity that is seen in Figure 10A EPIC data. The main reason why the February-March La Niña feature does not appear in the Figure 9 NISTAR Band-B data is because the NISTAR March data are missing in all of the NISTAR data channels. Hence, the plotted results for March are all spline interpolation values. Another take-away on this topic is that data averaging for noise suppression needs to be carefully managed in order to preserve the longitudinal information. It is anticipated that the now available Version 3 of the NISTAR Level 1B of archived data with improved calibration and noise reduction will permit improved model/data cmparisons.

Other conclusions that can be drawn from the comparison of Figures 9, 10, given that the range of variability for the NISTAR Band-B planetary albedo is substantially larger than for the EPIC planetary albedo, is that the radiance-to-flux conversion exhibits space-time variability. Also, the space-time variability of the relative brightness ratios is such that the anisotropy parameter does not maintain the same time dependence with longitude, or the same longitudinal dependence with time. This implies that a significant fraction of the anisotropy dependence must come from changong ice and water cloud distributions, which have different backscattering properties, and thus require real-time EPIC image analyses (e.g., Su et al., 2018; 2020) in order to convert NISTAR Band-B radiances into radiative fluxes.

The Figure 9 comparison of NISTAR Band-B (Left) with the photodiode Band-D results (Right) identifies the large decreases in reflected radiance that are evident in Band-B data in Figure 4, and appear as bull’s-eye features in Figure 9A during March-April, June, July, September and November, but are absent in the photodiode Band-D Hovmöller map in Figure 9B. Band-D has less absorption, but with better signal-to-noise than Band-B. But the Figure 9 Band-B/Band-D comparison also shows what may be a calibration inconsistency. As denoted in the NISTAR line-plot Figure 3 through 6, the DSCOVR sub-Satellite latitude is 25.3° S in January, 25.3° N in June, and 23.9° S in December. Why is the Band-D reflectance so much smaller in January when the DSCOVR Satellite is even more strongly over Antarctica in January than in December?

For Band-B, the relative reflectance level over the E longitude region is approximately the same for January, June and December, contrary to the Band-D results. By comparison the EPIC planetary albedos in Figure 10A, are by far the highest in November-December, but with peak reflectivity occurring over the 0° to 45° W longitude Atlantic Ocean region, while the NISTAR Band-B October-November peak is over the 135° E longitude East-Asia region. Most likely, this regional difference in reflectance must be due to the regional differences in near-backscatter ice and water cloud distributions, but Australia land-surface albedos may also be involved.

However, the more far-reaching take-away from the Figure 9 Band-B/Band-D comparison are the spectral differences between Band-B and Band-D that become most evident during the summer months June through September over the continental longitudes. Band-B includes the Mid-IR (1.1–4 μm) spectral region that is not being measured by the photodiode Band-D, which, over vegetated areas, would add significantly more to the reflected radiation, than over the ocean areas.

Clearly, the other spectral intervals that are possible with the NISTAR spectral bands, such as the Band-B—Band-C, Vis Band (0.2–0.7 μm), the Band-D—Band-B + Band-C, Near-IR Band (0.7–1.1 μm), and Band-B—Band-D, Mid-IR Band (1.1–4 μm). These synthesized NISTAR spectral bands are designed to provide improved spectral discrimination that would be more effective in differentiating between the different climate system constituents. The Vis Band, with minimum atmospheric absorption, would be the primary cloud assessment band. The Near-IR Band would have sensitivity to cloud, vegetation albedo, and moderate water vapor absorption, while the Mid-IR Band would be more sensitive to vegetated surface albedo and to strong water vapor absorption. However, because of calibration inconsistencies and the obvious artifacts in the NISTAR Figure 4 Band-B and Band-C data, Hovmöller plots for these spectral bands are not yet ready for prime time. In addition, it is also more than likely that the anisotropy parameters needed to transform the synthesized spectral radiances into radiative fluxes would also differ greatly between the different spectral bands.

Figure 10B displays the Hovmöller contour map for the planetary albedo for the GISS ModelE2 climate GCM for the year 2017. As discussed in Carlson et al. (2021), the EPIC vs. ModelE2 was used to deduce that the GISS ModelE2 overestimated clouds over ocean areas and underestimated clouds over the continental land areas, in addition to identifying the year 2017 La Niña feature in the EPIC planetary albedo data. In comparing the normalized NISTAR Band-B planetary albedo in Figure 9A with the GCM results in Figure 10, it is clear that NISTAR Band-B results, even with the arbitrary anisotropy normalization, are a far closer fit to the EPIC planetary albedo, than the ModelE2 results. Also, from this comparison, it is clear from Figure 9A that the maximum summer-month planetary albedo (hence, cloud reflectivity) occurs over the Asia continental longitudes, while the significantly higher GCM planetary albedo occurs over the East-Asia/West-Pacific Ocean region. These are conclusions that could have been reached independently just from direct comparison to NISTAR Band-B data, without requiring the benefit from EPIC data insight.

Furthermore, the claim was made that NISTAR measurements should also be capable of detecting La Niña activity by means of Hovmöller contour maps of longitudinally sliced monthly-mean NISTAR Band-B radiances. Because of overly sparse longitudinal sampling, this conjecture could not be fully demonstrated with the present data. Actually, it is the spectral discrimination of NISTAR data that is their strong point. This was demonstrated earlier in the study by Carlson et al. (2019) regarding the capabilities of the NISTAR Band-C/Band-B spectral ratio for constraining climate GCM treatment of the spectral absorption of solar radiation, and identifying a biosphere signature through the spectral partitioning at the 0.7 μm vegetation red edge. The additional Vis, Near-IR, and Mid-IR synthetic spectral bands (also still to be demonstrated) further expand on the unique NISTAR data capability of spectral discrimination between key constituents of the climate system, that remains unmatched by EPIC data, or by any other current satellite measurements.

On the other hand, the EPIC data are unique in providing the sunlit-hemisphere integrated longitudinally sliced radiative fluxes along with the corresponding cloud radiative properties that enable a more complete understanding of the seasonal and longitudinal variability of Earth’s planetary albedo including identification of the 2017 La Niña feature in the 2017/2018 EPIC planetary albedo data and providing of observational constraints for climate GCM cloud treatment constraints (Carlson et al., 2021). Moreover, there are additional unique enhancements of the EPIC data analyses that can be implemented to further enhance model/data comparisons of climate GCM modeling results. In particular, this involves data integration over the sunlit hemisphere, so as to retain latitudinal information, and to include other climate system variables in the EPIC Composite database that has enabled cloud properties to be added to the list of La Niña feature subject to longitudinal slicing. This is a capability that can be readily implemented in the climate GCM output data sampling, but cannot be reproduced within the NISTAR data processing.

In view of the foregoing, the DSCOVER Mission instruments EPIC and NISTAR, each in its own way, and as a complimentary synergistic matching pair, working together they provide a unique advance in quantitative model/data intercomparison. The key for this advancement is the longitudinal slicing capability made possible by the viewing geometry of the Earth’s sunlit hemisphere from the Lagrangian L1 point, and by the rotation of the Earth. The DSCOVR Satellite viewing geometry, which can be precisely reproduced in the climate GCM output data sampling, provides for identical space-time sampling of the observational, as well as of the GCM generated output data. Integrating the observational data over the sunlit hemisphere in the EPIC images, as well as in the single-pixel NISTAR measurement, averages out the weather noise, resulting in climate-style data points that retain planetary-scale information about the climate system. The same principles apply to the corresponding integration of the climate GCM output data over the sunlit hemisphere in accord with the Lissajous orbit viewing geometry from the Lagrangian L1 point. As an additional point, the near-hourly EPIC images of Earth’s sunlit hemisphere correspond closely to the GCM output data sampling for a 1-h radiation time step.

The nature of the longitudinally sliced variability is planetary scale and subtle, as evident from the year 2017 La Niña feature, which is accompanied by characteristic longitudinal oscillations exhibiting a 30° (∼3,000 km) peak-to-peak variability. Comparing individual EPIC images from February 2017 with similar images from February 2018, shows no discernable differences in cloud distribution or other cloud properties. Yet the feature persists.

Some Future Considerations

The principal objective of this study was to assess the capabilities of the first version of the NISTAR Level 1B data. Difficulties with the initial data quality led to some of the NISTAR objectives to be performed through EPIC data analysis. This dual approach has led to an improved understanding of the NISTAR data limitations and capabilities. Given that both NISTAR and EPIC measurements are near-backscatter radiances, radiance-to-flux conversion is key for model/data comparisons, since the climate GCM output data are all radiative flux based. For NISTAR, there is no real option for a data-based radiance-to-flux conversion. But for EPIC data, using MODIS-based regression relationships and CERES angle models, Su et al. (2018) developed the EPIC radiance-to-flux conversion procedure, which has made possible our NISTAR/EPIC/ModelE2 intercomparisons.

Now that the Version 3 NISTAR Level 1B data have become available, there is every expectation that the improved calibration and signal-to-noise management will make good in demonstrating that Band-B data with improved longitudinal resolution should be able to duplicate the EPIC La Niña activity detection without the need for radiance-to-flux conversion. Similarly, Hovmöller plots of the synthetic Vis, Near-IR, and Mid-IR NISTAR spectral bands even without radiance-to-flux conversion should enable improved discrimination between different climate system constituents. Thus, the (0.2–0.7 μm) Vis Band should respond more directly to cloud variability, and the (0.7–1.1 μm) Near-IR Band would have more sensitivity to cloud, vegetation albedo, and moderate water vapor absorption, while the (1.1–4 μm) Mid-IR Band would be more sensitive to vegetated surface albedo and strong water vapor absorption.

There is of course a need for having available the anisotropy parameters for the for the synthetic Vis, Near-IR, and Mid-IR NISTAR spectral bands, if for no other reason than to see if there is a significant difference in the Hovmöller plot patterns for the NISTAR near-backscatter radiances compared to radiative fluxes. The EPIC-based analysis is unlikely to provide this information since the EPIC-based radiative fluxes are derived for the full SW spectrum. What would be helpful here, would be to develop a climatology of anisotropy parameters for the synthesized spectral bands that would provide an approximate value for the spectral anisotropy parameters. Anything more would be an enormous computational burden.

For the NISTAR-derived (Band-A—Band-B) LW thermal flux determination, there is no other substitute for the EPIC-derived radiance-to-flux conversion factors. Here, the EPIC results for reflected solar SW flux are absolutely essential for accurate determination of the NISTAR LW radiative flux. This involves a potentially scene-dependent spectral calibration of Band-B filter transmission, and accurate knowledge of the near-backscattered anisotropy to enable the accurate subtraction of the NISTAR Band-B near-backscattered radiance from Band-A radiance to obtain the NISTAR LW back-scattered thermal emission, which then needs to be converted to a LW radiative flux.

Since the NISTAR no-filter (0.2–100 μm) Band-A makes full spectrum measurements, there is sometimes expressed expectation that global energy balance (or imbalance) determination might be possible. That lofty goal is well beyond the reach of any NISTAR, or EPIC measurement. That is because there is no definitive way to confirm the calibration of the spectral transmissivity of the Band-B filter, and even when the Band-B filter transmission has been accounted for, the LW emissivity in the viewing direction is dependent on the atmospheric temperature profile and the vertical cloud distribution.

It is also possible that an iterative inverse approach could be successfully utilized to resolve the NISTAR LW radiative flux determination. Figure 8 shows that the CERES, ISCCP, and GCM OLR pinwheel renditions of the LW radiative fluxes are in basic agreement. The approach would then be to see what it takes to convert the NISTAR Band-A—Band-B near-backscattered radiances into pinwheel format so as to reproduce the seasonal pinwheel variability.

Nevertheless, the seasonal variability of global reflected SW radiation and global emitted LW radiation provides compelling observational constraints and a diagnostic assessment of climate GCM performance. Thus, it is important to have an observational basis for all aspects of the SW and LW components of the global energy balance and their seasonal variability. To this end, satellite measurements have shown that, on an annual basis, reflected solar SW radiation is nearly identical from both hemispheres despite large differences in land-ocean distribution (Vonder Haar and Suomi, 1971). The large differences in surface albedo, imply significant compensation to achieve hemispheric symmetry in reflected solar SW radiation. This has been further analyzed and quantified (e.g., Voigt et al., 2013, 2014; Stephens et al., 2015). This is just one example where the modeling and understanding of the NISTAR global SW and LW measurements requires going beyond what is currently available. NISTAR measurements with their single-pixel capability are clearly limited to recording only a global-mean LW and SW response. However, the asymmetric hemispheric components that form the global NISTAR response could be fully resolved in the EPIC and GCM sunlit hemisphere integrated results.

Application to Exoplanet Observations

By their very nature, the NISTAR single-pixel measurements of the sunlit hemisphere from a shifting Lissajous orbital position do have more than a passing similarity to current ongoing exoplanet observations, except that for exoplanet observations, the typical viewing geometry covers a far more extreme range of phase angle than the small change in phase angle for NISTAR measurements. We commented on this aspect in our earlier (Carlson et al., 2019) paper. The basic NISTAR data stream is a continuous time-series acquisition of single-pixel measurements of the Earth, made for several different spectral intervals, as the Earth continues to rotate. That is the same basic format that applies to exoplanet observing. The biggest difference is that for the Earth, we know precisely the rotation period, length of year, tilt of rotation axis, the land/ocean geography, clouds, atmospheric structure and composition, etc. For exoplanets, all of these quantities are unknowns that need to be determined.

In earlier studies, Jiang et al. (2018) used spatially resolved EPIC images of Earth as proxies to simulate exoplanet observations by constructing a NISTAR-like time-series from the EPIC data. A similar analysis regarding the information content in EPIC data was also performed by Yang et al. (2018), and more recently by Boyd et al. (2022). In these examples, EPIC images of the Earth sunlit hemisphere are used as the starting point where all the input data are known, and where the changing viewing geometry is also known. From this, a single-pixel time-series is generated, that can then be inverted to retrieve the basic input information such as the Earth’s rotation period, as well as changing land/ocean and cloud distributions. In a similar study, Gu et al. (2021) constructed single point spectral light curves from a year of EPIC images to serve as exoplanet proxy data, and then applied a Principal Component analysis for their spectral image reconstruction.

In our experience with NISTAR and with the sunlit hemisphere averaged EPIC data, where the information content resides in the longitudinal ordering of the data time-series, we found that the optimum in display to be the Hovmöller format contour map. The success of this approach relies on the longitudinal precision in tabulating the time-series observational data relative to the Earth’s rotation period. Here, the precision of the data resides in the time of data acquisition and that relationship to the Earth’s period of rotation. The amplitude of each data point’s intensity is displayed less precisely via the more limited resolution of the Hovmöller color bar. The Hovmöller approach was able to extract and display the year 2017 La Niña feature and the associated planetary-scale longitudinal oscillations that were not otherwise discernable in the time-series line plots.

Also important in probing the Earth’s biosphere, and similarly for exoplanet studies, is selecting spectral intervals that will emphasize the space-time variability that is associated with some physical spectral characteristic. As an example, the choice of the 0.7 μm vegetation red edge pivot point for the NISTAR Band-C enable the NISTAR Band-C/Band-B spectral ratio to be sensitive in identifying vegetated surface albedos. Clearly, this is partial to the terrestrial climate system. But then, that is probably part of the objective to facilitate the identification of Earth-like exoplanets in preference to all others.

Conclusions

This paper describes a unique model/data comparison approach. Longitudinal slicing consists of averaging observational and model generated data over the entire sunlit hemisphere, and by using the rotation of the Earth to extract the longitude dependent information. This is made possible by the unique NISTAR viewing geometry from the DSCOVR Satellite location in its Lissajous orbit around the Lagrangian L1 point. From there, NISTAR makes single-pixel measurements of reflected solar and emitted thermal radiation from the entire sunlit hemisphere of the Earth.

The principal advantage of the longitudinal slicing methodology is that the sampling of climate GCM output data with the same viewing geometry as the DSCOVR Mission NISTAR and EPIC measurements establishes a precise and self-consistent space-time sampling between observational data and climate model generated output data. In the process, this averaging of data over the entire sunlit hemisphere averages out the quasi-chaotic meteorological weather noise, but preserves the large-scale seasonal and planetary-scale variability.

The unique aspect of the NISTAR measurements is in providing observational constraints and diagnostic support for climate GCM performance evaluation in the form of seasonal and longitudinal broadband spectral comparisons that are not available from other satellite data sources. The NISTAR Band-C/Band-B spectral ratio in particular, has established that the treatment of absorbed solar SW radiation in the GISS ModelE2 exhibits inadequate spectral contrast between SW radiation that is absorbed shortward of 0.7 μm, and the radiation that is absorbed longward of 0.7 μm. This deficiency in spectral absorption points to inadequate specification of the vegetated surface albedo and/or the radiative modeling of the absorption of SW radiation under cloudy sky conditions.

The NISTAR full-disk single-pixel measurements of the sunlit hemisphere of Earth are also a realistic example and test case for the analysis of exoplanet observations. The NISTAR data stream is a time-series of reflected solar radiation which can be inverted and analyzed to infer basic aspects of the terrestrial climate system such as planet’s rotation rate, seasonal change, polar icecaps, and climate system variability.

Data Availability Statement

Publicly available datasets were analyzed in this study. The NISTAR Level 1B data and the EPIC data used here are available from the Langley DAAC as well as OPeNDAP. DSCOVR data used for this study can be downloaded from: https://eosweb.larc.nasa.gov/project/dscovr/dscovr_nistar_1lb_2.

Author Contributions

BC and Al developed the concept for the longitudinal slicing of hemisphere-mean data and NISTAR spectral ratio as a biosphere signature. AL and GR developed the Sunlit Hemisphere Sampling (SHS) code. GR coded and ran the ModelE2 SHS simulations. WS converted the EPIC spectral radiances into radiative fluxes and produced the hemisphere-mean tables of EPIC SW fluxes and the composite cloud properties. AM assisted with NISTAR data and DSCOVR Ephemeris data, providing insight on topical emphasis and relevance to DSCOVR Mission objectives. Al, BC, GR, WS, and AM wrote and edited the text. AL made most of the figures.

Funding

Funding for this investigation has been provided by the NASA DSCOVR Project through WBS grant 437949.02.07.01.13.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank the NASA Earth Science Research Division managed by Jack Kaye, and the DSCOVR Program managed by Richard Eckman for support.

References

Boyd, P. T., Wilson, E. L., Smale, A. P., Supsinskas, P., Livengood, T. A., and Hewagama, T. (2022). EarthShine: Observing Our World as an Exoplanet from the Surface of the Moon. J. Astron. Telesc. Instrum. Syst. (Jatis) 8, 014003. doi:10.1117/1.JATIS.8.1.014003

CrossRef Full Text | Google Scholar

Carlson, B. E., Lacis, A. A., Russell, G., Marshak, A., and Su, W. (2021). Unique Observational Constraints on the Seasonal and Longitudinal Variability of the Earth’s Planetary Albedo and Cloud Distribution Inferred from EPIC Measurements. Frontiers in Remote Sensing.

Google Scholar

Carlson, B., Lacis, A., Colose, C., Marshak, A., Su, W., and Lorentz, S. (2019). Spectral Signature of the Biosphere: NISTAR Finds it in Our Solar System from the Lagrangian L-1 point. Geophys. Res. Lett. 46, 10679–10686. doi:10.1029/2019GL083736

CrossRef Full Text | Google Scholar

Gu, L., Fan, S., Li, J., Bartlett, S. J., Natraj, V., Jiang, J. H., et al. (2021). Earth as a Proxy Exoplanet: Deconstructing and Reconstructing Spectrophotometric Light Curves. Astronomical J. 161 (3), 122. doi:10.3847/1538-3881/abd54a

CrossRef Full Text | Google Scholar

Hansen, J., and Travis, L. (1974). Light Scattering in Planetary Atmospheres. Space Sci. Rev. 16, 527–610. doi:10.1007/BF00168069

CrossRef Full Text | Google Scholar

Hovmöller, E. (1949). The Trough-And-ridge Diagram. Tellus 1 (2), 62–66. doi:10.3402/tellusa.v1i2.8498

CrossRef Full Text | Google Scholar

Jiang, J. H., Zhai, A. J., Herman, J., Zhai, C., Hu, R., Su, H., et al. (2018). Using Deep Space Climate Observatory Measurements to Study the Earth as an Exoplanet. Astronomical J. 156 (1), 26. doi:10.3847/1538-3881/aac6e2

CrossRef Full Text | Google Scholar

Koon, W. S., Lo, M. W., Marsden, J. E., and Ross, S. D. (2000). “Dynamical Systems, the Three-Body Problem and Space Mission Design,” in Proceedings of the International Conference on Differential Equations Berlin 1999. Editors B. Fiedler, K. Groger, and J. Sprekels (IEEE). doi:10.1142/446910.1142/9789812792617_0222

CrossRef Full Text | Google Scholar

Kopp, G., and Lean, J. (2011). A New, Lower Value of Total Solar Irradiance: Evidence and Climate Significance. Geophys. Res. Lett. 38, L01706. doi:10.1029/2010gl045777

CrossRef Full Text | Google Scholar

Loeb, N. G., Doelling, D. R., Wang, H., Su, W., Nguyen, C., Corbett, J. G., et al. (2018). Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) Top-Of-Atmosphere (TOA Data Product. J. Clim. 31, 895–918. doi:10.1175/JCI-D-17-0208.110.1175/jcli-d-17-0208.1

CrossRef Full Text | Google Scholar

Marshak, A., Delgado-Bonal, A., and Knyazikhin, Y. (2021). Efect of Scattering Angle on Earth’s Reflectance. Front. Remote Sensing. 2, 719610. doi:10.3389/frsen.2021.719610

CrossRef Full Text | Google Scholar

Marshak, A., Herman, J., Szabo, A., Blank, K., Simon, C., Cede, A., et al. (2018). Earth Observations from DSCOVR EPIC Instrument. Bull. Am. Meteorol. Soc. 99, 1829–1850. doi:10.1175/BAMS-D-17-0223.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Marshak, A., Varnai, T., and Kostinski, A. (2017). Terrestrial Glint Seen from Deep Space: Oriented Ice Crystals Detected from the Lagrangian point. Geophys. Res. Lett. 44, 5197–5202. doi:10.1002/2017GL073248

CrossRef Full Text | Google Scholar

Mishchenko, M., Tishkovets, V., and Litvinov, P. (2002). “Exact Results of the Vector Theory of Coherent Backscattering from Discrete Random media: an Overview,” in Optics of Cosmic Dust. Editors G. Videen,1, and M. Kocifaj (Dordrecht: Kluwer Academic Publishers), 239–260. doi:10.1007/978-94-010-0628-6_15

CrossRef Full Text | Google Scholar

Stephens, G. L., O'Brien, D., Webster, P. J., Pilewski, P., Kato, S., and Li, J. (2015). The Albedo of Earth. Rev. Geophys. 53, 141–163. doi:10.1002/2014RG000449

CrossRef Full Text | Google Scholar

Su, W., Liang, L., Duda, D. P., Khlopenkov, K., and Thieman, M. M. (2021). Global Daytime Mean Shortwave Flux Consistency under Varying EPIC Viewing Geometries. Front. Remote Sens 2, 747859. doi:10.3389/frsen.2021.747859

CrossRef Full Text | Google Scholar

Su, W., Corbett, J., Eitzen, Z., and Liang, L. (2015). Next-Generation Angular Distribution Models for Top-Of-Atmosphere Radiative Flux Calculation from CERES Instruments: Methodology. Atmos. Meas. Tech. 8, 611–632. doi:10.5194/amt-8-611-2015

CrossRef Full Text | Google Scholar

Su, W., Liang, L., Doelling, D. R., Minnins, P., Duda, D. P., Khopenkov, K., et al. (2018). Determining the Shortwave Radiative Flux from Earth Polychromatic Imaging Camera. J. Geophys. Res. 123, 11479–11491. doi:10.1029/2018jd029390

CrossRef Full Text | Google Scholar

Su, W., Minnis, P., Liang, L., Duda, D. P., Khlopenkov, K., Thieman, M., et al. (2020). Determining the Daytime Earth Radiative Flux from National Institute of Standards and Technology Advanced Radiometer (NISTAR) Measurements. Atmos. Meas. Tech. 13, 429–443. doi:10.5194/amt-13-429-2020

CrossRef Full Text | Google Scholar

Voigt, A., Stevens, B., Bader, J., and Mauritsen, T. (2014). Compensation of Hemispheric Albedo Asymmetries by Shifts of the ITCZ and Tropical Clouds. J. Clim. 27, 1029–1045. doi:10.1175/JCLI-D-13-00205.1

CrossRef Full Text | Google Scholar

Voigt, A., Stevens, B., Bader, J., and Mauritsen, T. (2013). The Observed Hemispheric Symmetry in Reflected Shortwave Irradiances. J. Clim. 26, 468–477. doi:10.1175/jcli-d-12-00132.1

CrossRef Full Text | Google Scholar

Vonder Haar, T. H., and Suomi, V. E. (1971). Measurements of the Earth’s Radiation Budget from Satellite during a Five-Year Period. Part I: Extended Time and Space Means. J. Atmos. Sci. 28, 305–314. doi:10.1175/1520-0469(1971)028<0305:moterb>2.0.co;2

CrossRef Full Text | Google Scholar

Yang, W., Marshak, A., Varnai, T., and Kostincki, A. (2018). EPIC Spectral Observations of Variability in Earth’s Global Reflectance. Remote Sens. 10, 254. doi:10.3390/rs10020254

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y.-C., Rossow, W. B., Lacis, A. A., Oinas, V., and Mishchenko, M. I. (2004). Calculation of Radiative Fluxes from the Surface to Top of Atmosphere Based on ISCCP and Other Global Data Sets: Refinements of the Radiative Transfer Model and the Input Data. J. Geophys. Res. 109, D19105. doi:10.1029/2003JD004457

CrossRef Full Text | Google Scholar