An Operational Methodology for Validating Satellite-Based Snow Albedo Measurements Using a UAV

Snow albedo is highly variable over multiple temporal and spatial scales. This variability is more pronounced in areas that experience seasonal snowpack. Satellite retrievals, physically based models and parameterizations for snow albedo all require ground-based measurements for calibration, initialization, and validation. Ground measurements are generally made using upward and downward-facing pyranometers at opportunistically located weather stations that are sparsely distributed, particularly in mountainous regions. These station-based measurements cannot capture the spatial variability of albedo across the land surface. Uncrewed Aerial Vehicles (UAVs) equipped with upward and downward-facing pyranometers provide near-surface measurements of broadband albedo that are spatially distributed across landscapes, offering improvements over in-situ sensors. At the hillslope to watershed scale albedo measurements from UAVs taken over heterogeneous terrain are a function of the spatial variability in albedo and topography within the downward-facing sensor’s field-of-view (FOV). In this research we propose methods for topographic correction of UAV snow albedo measurements and comparison to gridded satellite albedo products. These methods account for the variability of surface topography and albedo within the sensor FOV, sensor tilt, and the angular response of pyranometers. We applied the proposed methodologies to UAV snow albedo measurements collected over an alpine meadow in southwest Montana, United States (45.23°, −111.28°). Sensitivity analyses were conducted to determine the effect of altering the processing FOV (PFOV) for both topographic corrections and comparison to coincident Landsat 8-derived albedo measurements. Validation from ground-based albedo measurements showed the topographic correction to reduce albedo measurement error considerably over mildly sloping terrain. Our sensitivity analyses demonstrated that outcomes from the topographic correction and satellite comparison are highly dependent on the specified PFOV. Based on field observations and analyses of UAV albedo measurements made at different altitudes, we provide guidelines for strategizing future UAV albedo surveys. This research presents considerable advances in the standardization of UAV-based albedo measurement. We establish the foundation for future research to utilize this platform to collect near-surface validation measurements over heterogeneous terrain with high accuracy and consistency.

1 Introduction

The albedo of snow exerts a significant control on Earth’s energy balance and water cycle. In mountainous areas that experience seasonal snowpack, snow albedo is highly variable throughout space and time (Seidel et al., 2016). While the surface albedo of glaciers, ice sheets, and snow-free areas also exert a controlling influence on Earth’s climate (Ingram et al., 1989; Dumont et al., 2012; Shaw et al., 2021), this paper specifically addresses the albedo of seasonal snow at the hillslope to watershed scales (10–1,000 s of m²). The spatiotemporal variability of snow albedo at the seasonal timescale directly influences the timing and magnitude of snowmelt and runoff as well as climatic fluctuations over longer timescales (Hall and Qu, 2006). The transition from high to low-albedo snow at the onset of ablation can transform the surface from a net reflector of shortwave radiation to a net absorber, resulting in rapid melting and drastic changes to the climate and landscape (Wiscombe and Warren, 1980; Hall, 1988).

Satellite retrievals, physically based models, and parameterizations for snow albedo all require ground-based measurements for calibration, initialization, and validation. Under a rapidly changing climate, empirical parameterizations will become increasingly unrepresentative of current conditions (Dozier, 2011). Improvement of physically based energy balance models and snow albedo parameterizations is dependent on high-quality distributed measurements that capture the spatial variability of the surface at a variety of spatial and temporal scales, to satisfy the needs of individual products (Bales et al., 2006; Molotch and Bales, 2006; Rhoades et al., 2018).

1.1 Spatial Scales of Snow Albedo

Ideally, snow and hydrological models explicitly represent processes at the true scale at which they operate (Blöschl and Sivapalan, 1995). In order to properly inform the scaling of these models, measurements must be made at spatial and temporal scales that correspond to the process scales that drive changes in hydroclimatology (Blöschl, 1999).

Although relatively little work has been done to quantify the scale of spatial variability of snow albedo, much focus has been placed on quantifying spatial scales of snow properties such as depth, density, and stratigraphy, and environmental properties such as elevation and radiative forcing (Schweizer et al., 2008). These processes that control spatial variability of snow accumulation and ablation directly control and respond to changes in albedo via changes in grain size, impurity concentration, and depth (Warren and Wiscombe, 1980; Wiscombe and Warren, 1980; Warren, 1984). Thus, we can deduce that snow albedo varies at spatial scale(s) similar to these snow and environmental properties. However, scales of spatial variability of these properties identified in previous studies is highly dependent on the individual process, study location, and sampling strategy. Integral scales range from 1 m at the point scale, 1–100 m at the hillslope scale, to 100–1,000 m at the watershed scale (Schweizer et al., 2008; Clark et al., 2011). Other controls on snow albedo such as impurity content and average solar zenith angle can vary at broader, hemispherical scales (Cui et al., 2021). Given the wide range in process scales, snow albedo measurements should have the ability to deploy over local to broad regions in order to capture the underlying variability of this governing property.

1.2 Temporal Scales of Snow Albedo

The importance of snow albedo in terms of its influence on the state of the snowpack is variable throughout an individual season. During the accumulation season, available solar energy is low and snow is metamorphosing slowly, so its albedo is of minimal importance. Maximum variability in albedo occurs when snow surface temperatures approach 0°C at the onset of melt (Aoki et al., 2003). This spatial variability in albedo is the primary control behind spatial differences in ablation and snow density (Grünewald et al., 2010; Wetlaufer et al., 2016). The importance of spatial variability in shortwave forcing on snowmelt and metamorphism diminishes throughout melt as spatial variability in ablation is increasingly controlled by advective heat transport from snow-free areas (Grünewald et al., 2010; Wetlaufer et al., 2016). Thus, it is critical to capture the spatial variability of snow albedo at the onset of melt. Additionally, snow albedo varies on a daily timescale as a function of solar zenith angle (Wiscombe and Warren, 1980). Diurnal fluctuations in zenith angle also influence the snow’s albedo through physical changes to the snowpack due to melting, sublimation, and refreezing (Pirazzini, 2004). Solar geometry controls the proportion of the snow surface that is shaded by tree cover and surrounding slopes, and therefore directly influences the land surface albedo (Webster and Jonas, 2018). Given that snow albedo varies at multiple temporal scales, measurement strategies should provide the flexibility to be deployed during critical times of the ablation season at multiple times within individual days.

1.3 Current Methods of Measuring Snow Albedo

Spaceborne sensors such as Landsat 7 Enhanced Thematic Mapper (ETM+), Landsat 8 (LS8) Operational Land Imager (OLI) and NASA’s Moderate Resolution Imaging Spectrometer (MODIS) are capable of informing spatially distributed mass balance models at a global extent through assimilation techniques (Xu and Shu, 2014; Bair et al., 2019; Kumar et al., 2020). Remotely-sensed observations provide advantages over empirical parameterizations for snow albedo, particularly in areas where shortwave radiative forcing dominates the energy balance (Molotch et al., 2004). Satellite products require complex processing to account for atmospheric and geometric sources of error. Additional uncertainty is introduced through narrow to broadband conversions, angular modeling and spatial variability in albedo at the sub-pixel scale. Satellite albedo products therefore require ground-based (in-situ) albedo measurements for calibration and validation (Schaaf et al., 2002; Qu et al., 2015). The importance of these calibration and validation data are highlighted in the National Academies of Science 2017 Decadal Strategy for Earth Observation from Space, which identifies snow albedo a primary targeted observable (National Academies of Sciences, Engineering, and Medicine, 2018). Improvement of spaceborne techniques for measuring fundamental snow properties is of critical importance for addressing the global implications of a rapidly changing climate.

Ground-based (in-situ) measurements of snow albedo are most commonly made by taking the ratio of surface-reflected (K↑) to incoming (K↓) radiation measured by a pair of downward and upward-facing pyranometers.

$\begin{array}{c}\alpha =\frac{\left(K\uparrow \right)}{\left(K\downarrow \right)}\end{array}(1)$

Broadband pyranometers measure shortwave irradiance (∼300–3,000 nm), which composes 99% of insolation, thus the energy driving the earth system. These sensors have a hemispherical field-of-view (FOV), and their measurement ratio represents the bi-hemispherical reflectance (BHR), of a surface (Schaepman-Strub et al., 2006). Since snow reflects light anisotropically (Bourgeois et al., 2006; Dumont et al., 2010), this measurable reflectance quantity is particularly useful because it captures for the bidirectional reflectance properties of a surface.

Dual pyranometers are often installed at opportunistically located weather stations that are sparsely distributed, especially in mountainous environments. Additionally, since these measurements are fixed over a single point, they inherently do not capture the spatial variability in snow properties that exists in complex alpine headwaters. The locational biases of these ground-based albedo monitoring sites inhibits their utility for informing and assessing spatially distributed products (Dozier, 2011).

While the resolutions of available satellite albedo products narrowly allow for explicit representation of variability in snow albedo at the hillslope scale (e.g., 30 m × 30 m cell from Landsat 7 or 8), station measurements are restricted to the point scale. Methods for capturing processes between these scales are constrained by cost-prohibitive airborne surveys (Molotch et al., 2004; Seidel et al., 2016) and recently, uncrewed aerial vehicles (UAVs) (Ryan et al., 2017; Webster and Jonas, 2018). An illustrative example of the scaling differences between satellite, in-situ, and UAV surveys is provided in Figure 1.

FIGURE 1

FIGURE 1. Illustrative example showing the difference in measurement scale between point-based weather stations, satellite grids, and UAV surveys.

UAVs provide the means to resolve the spatial variability of snow albedo at high resolutions from the individual hillslope to watershed scale, and have the flexibility to be deployed at critical times during the onset of ablation at different times within a single day. These spatially distributed sets of near-surface albedo measurements can be used to supplement calibration and validation data from AWS (Burkhart et al., 2017; Ryan et al., 2017; Levy et al., 2018; Canisius et al., 2019; Sproles et al., 2020). UAV-based snow albedo measurements provide the means to bridge the scaling gap between in-situ snow albedo measurements and satellite observations (Sproles et al., 2020). However, the utility of these validation measurements depends heavily on processing strategy.

Measurement uncertainty in broadband albedo measurements stem from interactions between the sensing platform, atmosphere, and ground surface that increase in complexity as more variability is present within the sensor’s FOV (Henderson-Sellers and Wilson, 1983). A major source of error in pyranometer albedo measurements over complex terrain is topography (Grenfell et al., 1994; Jonsell et al., 2003; Wu et al., 2018). Since the tilt of the sensing platform is rarely equal to the tilt of the terrain below, the flux density of the direct solar beam will be different for both surfaces. To account for this difference in measured irradiance, the upward-facing pyranometer measurements need to be corrected to represent the amount of energy received by the tilted ground surface, which requires knowledge of the slope and aspect of the ground surface as well as the tilt and tilt direction of the sensor (Bogren et al., 2015; Weiser et al., 2016). The magnitude of topographic error in albedo measurements also depends on the atmospheric state, adding further complexity to required corrections (Picard et al., 2020). Various topographic correction schemes have been proposed and implemented on albedo data at AWS (Grenfell et al., 1994; Weiser et al., 2016; Bair et al., 2019; Picard et al., 2020), but none have been applied to UAV-based measurements. Since UAV platforms acquire measurements over variable terrain, the topographic correction should account for this variability while considering directional response of the pyranometer.

1.4 Scaling Uncertainties

Uncertainties can arise when correcting for topography or comparing pyranometer measurements to satellite pixels, due to differences in measurement scale between platforms and surface variability (Lhermitte et al., 2014; Ryan et al., 2017b; Canisius et al., 2019). The large measurement footprint of pyranometers makes processing and interpretation of measurements difficult over variable terrain, as a single measurement is an integration of the variability within the sensing footprint. Moreover, this footprint is dependent on the altitude of the sensor and the FOV (Figure 2; Brock, 2001).

FIGURE 2

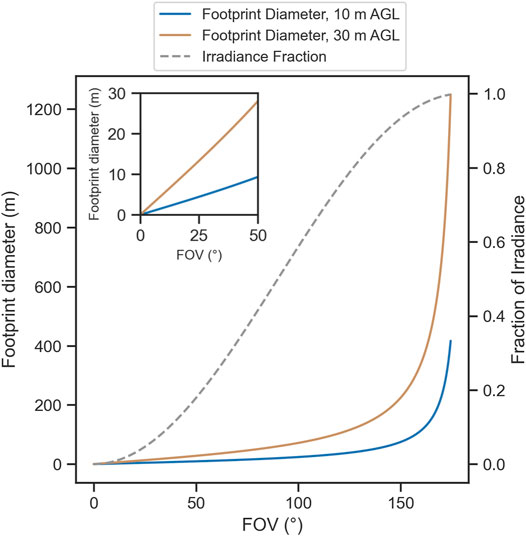
FIGURE 2. Pyranometer footprint diameter over a flat surface as a function of FOV, for measurement altitudes of 10 m and 30 m. The corresponding fraction of measured irradiance (secondary y-axis) at each FOV is plotted in grey.

The angular response of a pyranometer can be described by Lambert’s Cosine Law, stating that irradiance (W/m²) received by the sensing element varies as a function of the cosine of the viewing angle (Brock, 2001). Since pyranometers have a near-cosine response, measurements of spatially heterogenous terrain do not represent a geometric average of irradiance over an area, but rather a weighted average that is a function of the relative albedos of different surface components and their spatial organization relative to nadir. Therefore, the measured albedo depends on the sensor’s location in x, y, and z space as well as the spatial scale of variability in albedo at the surface. Since the downward-facing pyranometer has a hemispherical field of view, it casts a hypothetically infinite measurement footprint on the surface. This makes it difficult to attribute a scale to pyranometer albedo measurements, as the field of view needs to be constrained to be less than 180° for the purpose of applying processing and comparing to other products. To date, the UAV albedo research has differed in the way they compare UAV albedo to satellite-derived albedo. Some have taken the point-to-pixel approach, without explicitly considering the FOV of the pyranometers onboard the UAV (Sproles et al., 2020). Others have specified an arbitrary restricted processing-FOV (PFOV) for the pyranometer data ranging from 60° (Ryan et al., 2017) to 90° (Canisius et al., 2019) to 162° (Levy et al., 2018) in order to project the sensing footprint onto the ground. The studies that have defined restricted PFOVs have differed in the way they integrate the satellite pixels within the downward-facing pyranometer’s footprint. If UAV albedo measurements are to be used to validate and calibrate models and satellite albedo products, it is critical that processing strategies are consistent between studies.

The underlying goal of this research is to provide the insights and methodologies required to deploy UAV albedo platforms over spatially variable terrain at the slope to watershed scale, process the measurements, and compare them to external satellite-based products. We address the research objective in three parts. 1) We first demonstrate the behavior of UAV albedo measurements over surfaces with spatially variable albedo, and show how these measurements scale with measurement altitude. 2) We then present a topographic correction that accounts for both the tilt of the UAV platform and spatial variability of terrain. The topographic correction is validated with ground-based snow albedo measurements. The approach used in the topographic correction is leveraged in a methodology for comparing UAV albedo measurements to satellite data. Implications of altering the PFOV are determined for both the topographic correction and comparison to LS8 albedo measurements. 3) A sensitivity analysis is performed to determine topographic survey requirements for the proposed correction. This research provides steps towards a standardized framework for UAV albedo surveys and the accompanying processing workflows to ensure high measurement accuracy and allow interoperability of the measurement technique across different research and applications.

2 Materials and Methods

2.1 Uncrewed Aerial Vehicle and Sensors

We utilized a DJI Matrice 210 V2 quadcopter (Figure 3) to perform both snow albedo and Structure-from-Motion (SfM) photogrammetry surveys. When performing photogrammetric surveys, the UAV was equipped with a Zenmuse X5S digital camera (20.8 MP). During albedo flights, the UAV was equipped with upward and downward-facing Kipp and Zonen PR1 pyranometers and a Meteon 2.0 datalogger that recorded measurements at one second intervals. The pyranometers were factory-calibrated within 2 years of deployment. These particular sensors are well suited for deployment on a UAV, as the casing is 3D-printed with a lightweight resin material and response times are reasonably fast (<0.2 s). The albedo measurements are temperature-corrected, making these sensors ideal for use in cold environments. The sensors and datalogger were mounted to the UAV with 3D-printed mounts that were fabricated using polylactic acid (PLA) filament.

FIGURE 3

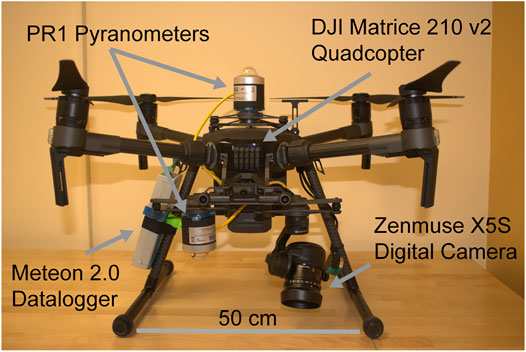
FIGURE 3. UAV setup consisting of upward and downward-facing pyranometers, a digital camera, and a datalogger.

Before each field outing, the datalogger was synced to a computer’s time to remove any drift in its real-time clock. The UAV compass was calibrated in the field prior to flights to minimize geolocational uncertainty. Maximum flight times for this UAV in winter conditions at the study area (elevation 2,650 m) ranged between 12 and 16 min, depending on temperature and wind speeds. Specifications for the UAV, camera, and sensors can be found in Supplementary Table S1.

2.2 Preliminary Tarpaulin Experiments

To develop a basic understanding of how albedometer measurements of a heterogeneous surface scale with altitude, and to inform survey design, an experiment over a controlled environment was conducted. The controlled environment consisted of a low-albedo asphalt surface overlain by different arrangements of circular tarpaulins with varying albedos. UAV albedo data from vertical flights over the different tarpaulin configurations informed UAV survey design and data processing methodologies. Results from these preliminary flights and their interpretations can be found in Supplementary Figure S1.

2.3 Study Area

During March–May of 2021, UAV data was collected at “Namaste Valley” (45.2316°N, 111.4768°W, elevation 2,650 m), an alpine meadow environment located at the head of the Muddy Creek drainage, which flows into the South Fork of the West Fork of the Gallatin River in southwest MT, United States (Figure 4A). The meadow is proximal to patches of dense conifer, but is largely composed of mildly undulating vegetation- and rock-free snow cover in the winter (Figure 4B).

FIGURE 4

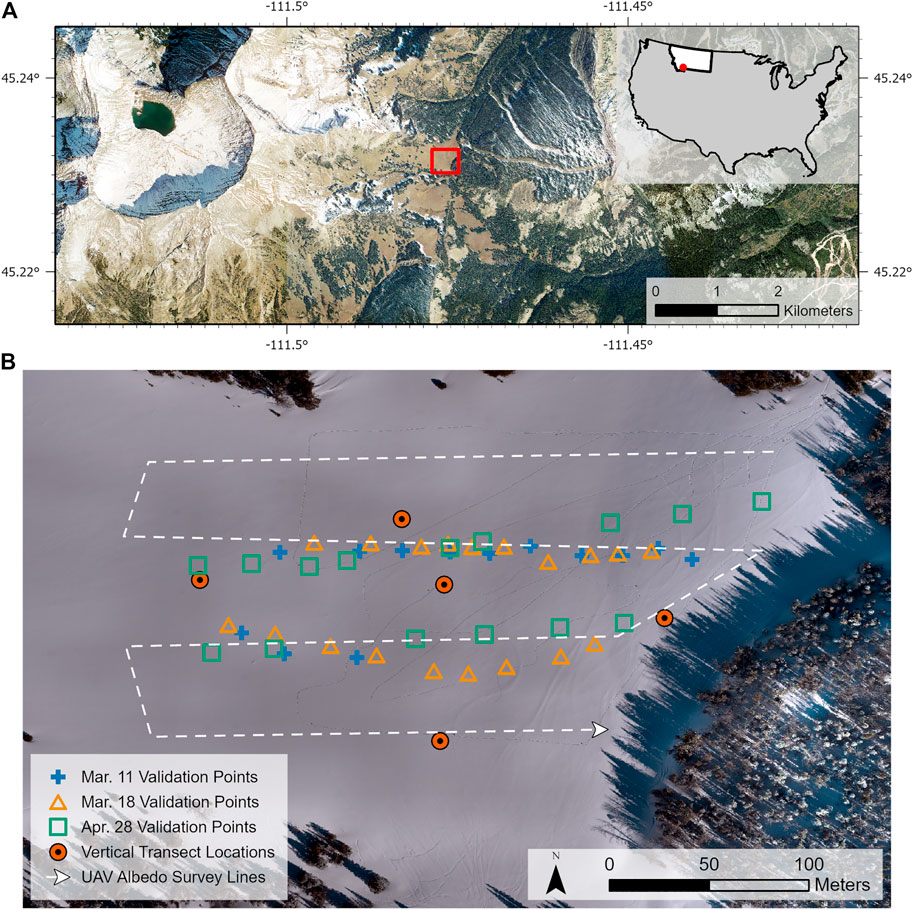
FIGURE 4. (A) Namaste Valley study area, southwest MT, USA is outlined in red. (B) Wintertime orthomosaic of the study area showing UAV albedo survey transect lines, ground validation measurement locations, and vertical UAV albedo flight locations.

Since there are a variety of solar aspects, Namaste Valley is an ideal location to investigate the effects of topography and albedo heterogeneity on albedo measurements. Slope angles in this study area range from 5° to 20°, and slope aspects exist at all cardinal directions besides north. Flights were completed on three days with clear skies (March 11, March 18, and April 28) during the 2021 season. These field days were timed to correspond with a coincident LS8 pass over. Ground observations prior to UAV flights made from a handheld weather meter recorded maximum wind speeds of 5 m/s. The UAV platform maintained stability in all wind conditions encountered during the field days.

2.4 Field Methods

Universal Ground Control Software (V4.4, 2021) was used to pre-program missions prior to field days. Separate flight plans were created for photogrammetry and albedo flights. Photogrammetry flights surveyed the area in a cross-hatched pattern at 100 m AGL, collecting ∼250 total images with 75% horizontal and vertical overlap with the camera gimbal fixed at a 90° tilt. The target resolution for photogrammetric reconstruction was 5 cm/pixel. Prior to each photogrammetry survey, the camera aperture, ISO, and shutter speed were adjusted to avoid oversaturating highly reflective snow-covered pixels, while maintaining contrast over darker, tree-covered areas. The camera was set with an aperture of f-stop f/10, ISO of 100, and shutter speed of 1/1,000 s. Nine ground control points (GCPs) were distributed evenly throughout the field area to provide accurate geographic control for the surveys. GCPs were surveyed in using an Emlid Reach RS2 Global Navigation Satellite System (GNSS) receiver. The RTK-corrected GNSS points had high accuracy, and geolocational uncertainty for the models had an average of 5 cm.

Albedo surveys consisted of both lawn-mower style horizontal transects and vertical ascending/descending transects over a single point. Horizontal transects were performed at altitudes of 10, 15, 20, and 30 m AGL, and were programmed to maintain consistent AGL altitude. These flight lines were oriented approximately E–W across the study area. This orientation was selected because it allowed for sampling of the most topographic variability and landcover heterogeneity. Vertical transects extended from 20 to 60 m AGL and were flown over five locations randomly distributed throughout the study area. For all albedo flights, the UAV flew at a velocity of 2 m/s, and measurements were logged every second. Considering the response time of the sensors and the geolocational uncertainty of the onboard GNSS receiver, UAV measurement positional uncertainty was 1.9 m.

Directly after flights, ground validation albedo measurements were taken using two Kipp and Zonen PR1 pyranometers mounted on a tri-axis adjustable tripod (Figure 5A.). The tripod was fitted with a Witmotion WT901C-TTL inertial measurement unit (IMU) that streamed the angular orientation of the pyranometers to a mobile device. This IMU had an accuracy of 0.05° for pitch and roll, and 1° for yaw. Prior to departure to the field, the tripod was leveled on a flat ground surface with its legs fully extended. The angle offsets required to obtain this plane-parallel leveling were recorded and replicated in the field to obtain slope-parallel albedo measurements. Horizontal albedo measurements were then obtained by adjusting the tripod angle until the IMU read <0.8° tilt on the X and Y axes. The boom extended 1.8 m from the tripod, and the pyranometers were 1.5 m above the surface when the tripod axis was parallel with the snow surface. The tripod legs were placed on disks to ensure they remained on the snow surface. This minimized uncertainty due to differential penetration of the legs into the snow for the slope-parallel measurements. Since the horizontal measurements were leveled with the IMU, they were not impacted by leg penetration. The pyranometers were positioned to be as far as possible from the tripod legs and observer, but they still obstructed the sensor FOV. These effects on albedo are assumed to be minimal based upon the assessment of how the UAV landing gear and data logger impact albedo measurements (Sproles et al., 2020; Supplementary Figure S2). Observer and observer shadow were assumed to produce a consistent, albeit negligible difference in the measured reflected radiation as well.

FIGURE 5

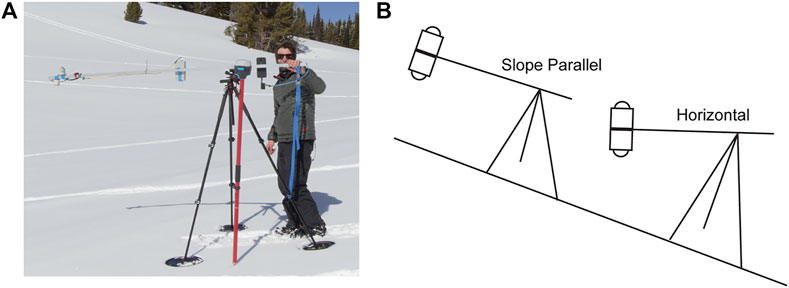
FIGURE 5. (A) Ground validation instrumentation consisting of upward and downward-facing pyranometers, an IMU, and datalogger mounted on a boom extending from a tri-axis adjustable tripod. (B) Slope parallel and horizontal pyranometer positionings for ground validation albedo measurements. Slope parallel measurements were interpreted as the true albedo of the surface. Horizontal measurements simulated measurement from a horizontal UAV platform, and were corrected for topography.

At each location, albedo measurements were recorded every second, yielding 20–100 measurements at both slope parallel and horizontal positions (Figure 5B).

An RTK-corrected GNSS position was recorded at each validation point. Measurements were taken every 5 m along two predefined transects (Figure 4B) and 15–20 validation positions were measured on each field day (47 total), as time allowed. Since it was often difficult to hold the tripod perfectly stable due to the imbalance of the tripod setup and wind, we used an arithmetic average of the measurements for each sensor orientation at each position for analysis.

2.5 Data Processing

2.5.1 Preprocessing

A schematic of the data processing pipeline is provided in Figure 6. All data processing was performed in Python (please refer to the Data Availability Statement). Data from the UAV and datalogger were merged before processing. DJI flight logs were converted into .csv format using the DatCon 3 software (V3.1.0, 2021). Fields from the UAV flight logs and pyranometer datalogger were merged based on the respective timestamp.

FIGURE 6

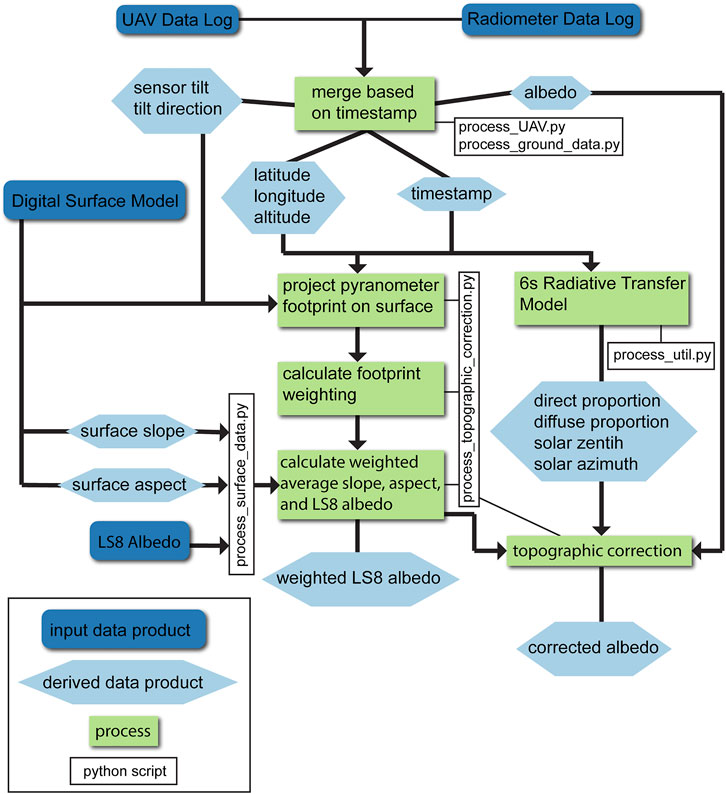
FIGURE 6. Workflow detailing the processing and topographic correction of the field data. The names of the Python scripts handling each component of the processing chain are provided. Python code for the workflow can be found at https://github.com/GEOSWRL/UAV-albedo.

Since the UAV legs are non-retractable and the datalogger was mounted to the landing gear, these obstructions inherently affected the downward-facing irradiance measurement. To account for this, a side-by-side calibration of irradiance was performed and it was determined that the legs and datalogger reduced measured radiation by less than 2%, and the downward-facing measurements were adjusted accordingly (Supplementary Figure S2). Sproles et al. (2020) filtered albedo measurements based on a maximum tilt threshold of 5° based on tilt error analyses (Bogren et al., 2015). In this study we did not filter based on tilt in order be able to qualitatively assess the tilt component of the tilt-topography correction.

2.5.2 Topographic Correction

Weiser et al. (2016) present a topographic correction for fixed locations that accounts for sensor and ground surface tilt where ${\alpha }_{true}$ is the true snow-surface albedo, ${\alpha }_{meas}$ is the measured albedo, $p_{diff}$ is the proportion of diffuse irradiance, $p_{dir}$ is the proportion of direct irradiance, ${\theta }_s$ is the inclination angle of the slope, ${\theta }_p$ is the inclination angle of the pyranometer, and ${\theta }_z$ is the solar zenith angle.

$\begin{array}{c}{\alpha }_{true}={\alpha }_{meas}\left(\frac{p_{diff}\ast cos{\theta }_z+ p_{dir}\ast cos{\theta }_p }{p_{diff}\ast cos{\theta }_z+ p_{dir}\ast cos{\theta }_s}\right)\end{array}(2)$

$cos{\theta }_p$ and $cos{\theta }_s$ were calculated using the sensor tilt (${\sigma }_p$), sensor tilt direction (${\gamma }_p$), surface slope (${\sigma }_s$), surface aspect (${\gamma }_s$), solar zenith, and solar azimuth (${\phi }_s)$.

$\begin{array}{c}cos{\theta }_p=sin{\theta }_{z}cos{\phi }_{s}sin{\sigma }_{p}cos{\gamma }_p+sin{\theta }_{z}sin{\phi }_{s}sin{\sigma }_{p}sin{\gamma }_p+cos{\theta }_{z}cos{\sigma }_p\end{array}(3)$

$\begin{array}{c}cos{\theta }_s=sin{\theta }_{z}cos{\phi }_{s}sin{\sigma }_{s}cos{\gamma }_s+sin{\theta }_{z}sin{\phi }_{s}sin{\sigma }_{s}sin{\gamma }_s+cos{\theta }_{z}cos{\sigma }_s\end{array}(4)$

For each timestamp, the Py6s radiative transfer model (Wilson, 2013) was used to compute the relative direct and diffuse proportions of irradiance, and solar geometries. A continental aerosol profile and atmospheric profile based on location and date were used as input parameters for the radiative transfer model. Direct and diffuse proportions of irradiance were modeled for clear skies as observed in the field. The direct proportion varied between 0.51 and 0.54 on March 11, 0.54 and 0.58 on March 18, and 0.66 and 0.67 on April 28. These proportions, which control the magnitude of the topographic correction, aligned well with expectations for the distribution of incoming radiation during winter at this field site.

The Weiser et al. (2016) correction equation assumes that the surface is planar, and does not consider terrain variability within the downward-sensor’s FOV that inherently affects the quantity of surface-reflected irradiance. Since UAV-based SfM photogrammetry allows for construction of high-resolution (<10 cm) snow surface models, topographic corrections can be developed to account for the impact of variability in slope and aspect within the sensing footprint. We leverage this capability and propose a variation of the Weiser et al. (2016) correction that differs from the original in its calculation of ${\sigma }_s$ and ${\gamma }_s$.

The most physically consistent approach for relating pyranometer measurements to surface properties is to compare each pyranometer measurement to a cosine-weighted average of the pixels within a defined PFOV (Jäkel et al., 2019; Malle et al., 2019; Malle et al., 2021). The proposed correction calculates a cosine-weighted mean of ${\sigma }_s$ and ${\gamma }_s$ for every pixel (n) that lies within the specified PFOV of the downward-facing pyranometer, which is also dependent on altitude (Figure 7). For a single albedo measurement, ${\gamma }_s$ used in its topographic correction is calculated as follows, where $w_i$ is the weighting factor of an individual pixel, ${\theta }_i$ is the incidence angle between an individual pixel and the sensing platform, and ${\gamma }_i$ is the aspect of an individual pixel.

$\begin{array}{c}{w}_i=\frac{\text{cos}\left({\theta }_i\right)}{{{\displaystyle \sum }}_i^n\text{cos}\left({\theta }_i\right)}\end{array}(5)$

$\begin{array}{c}{\gamma }_s={\displaystyle \sum }_i^n{w}_i\ast {\gamma }_i\end{array}(6)$

FIGURE 7

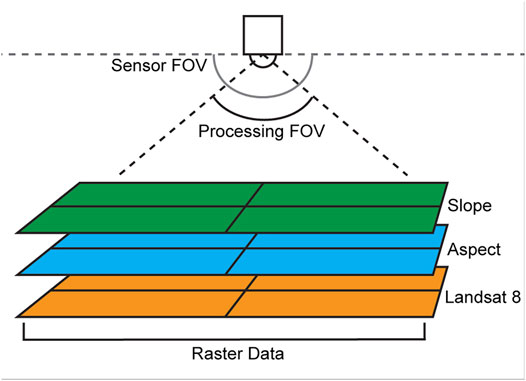
FIGURE 7. Depiction of difference between the true sensor FOV and the PFOV. The pyranometer measurement is always influenced from the area within its 180° FOV. The PFOV is required to project a measurement footprint onto the ground, and determines the extent and weighting of raster data used in the topographic correction and satellite comparison.

2.5.2.1 Surface Models

For each field day, as well as a day during the summer when no snow was present, the 3D surface models used in the topographic correction were generated using SfM photogrammetry in Agisoft Metashape Professional software (V1.7.4, 2021). Snow cover often produces challenges for photogrammetric reconstruction due to surface homogeneity. This leads to low confidence in tie point positions and a noisy surface. Additionally, the bare-ground model had a rough surface due to short and variable vegetation. The original SfM DEMs had resolutions of ∼10 cm and visibly contained an unrealistic amount of surface roughness. This roughness produced unrealistically high slopes and inaccurate aspect calculations, which combined propagated error into the topographic corrections. In order to produce smooth elevation models that could be used in a topographic correction, the DEMs were generated from meshes as opposed to dense clouds, and the models were exported at a resolution of 1 m. This relatively coarse resolution was chosen because it effectively smoothed out the anomalous small-scale surface roughness, and was not excessively detailed considering the geolocational uncertainty of the UAV. In addition to snow-surface and bare-ground DEMs, a 10 m 3DEP DEM (USGS, 2017) is used to compare results of the topographic correction with the resolution and source of the elevation dataset. A 10 m DEM was used for this purpose as this resolution of DEM is widely available in the United States, and elsewhere, providing greater transferability of our methods.

Since the high-resolution models only covered the extent of the UAV survey, the downward-facing pyranometer viewed terrain outside the SfM survey area, even at relatively low altitudes (Figure 2). To account for this, the high-resolution models were fused with the 10 m 3DEP DEM to cover these external portions of the study area. This mitigates any bias between field days, as the extents of the photogrammetric models varied slightly between days. The generated surface models were used to derive the topographic parameters for the tilt-topography correction.

2.6 Trees and Tree Shading

SfM has a difficult time reconstructing the geometry of trees, and overall there is high uncertainty regarding the anisotropic reflectance of trees and other significantly heterogeneous surfaces (Strahler et al., 1999). Therefore, topographic data from these areas should not be included in the topographic corrections of pyranometer measurements over snow, and the radiance signal from these portions of the scene should not be corrected. Moreover, since the albedo of tree-shaded areas is mainly a function of the magnitude of tree shading as opposed to snow physical properties (Malle et al., 2021), interpretations of the physical controls on measured albedo depend on the ability to partition measurements based on fractions composed of trees and shading. This partitioning was out of the scope of this research, and the implications are discussed in Limitations and Future Work.

2.7 Validation Measurements

The tilt-topography correction was first applied to the ground-based validation measurements. Ground measurements were corrected using the SfM snow surface models generated for each day as these models account for the greatest amount of terrain variability and were anticipated to produce the highest-accuracy corrections. The ground albedo measurements taken parallel to slope represent the closest approximation of the true albedo of the surface (Wu et al., 2018). The ground measurements taken at the horizontal plane position were corrected for topography and validated against the uncorrected slope-parallel measurements. These two sets of measurements are most comparable for validation purposes because each horizontal measurement had a corresponding slope-parallel measurement with a nearly identical projected footprint and sky view factor.

2.8 Satellite Comparison

The UAV measurements were topographically corrected and compared to synchronous LS8 OLI-derived albedo. LS8 Tier 1 top-of-atmosphere (TOA) reflectance was corrected for topography using a c-correction (Teillet et al., 2014), which has been demonstrated to have the highest accuracy over variable snow-covered landscapes (Meyer et al., 1993; Traversa et al., 2021). The satellite imagery was masked for cloud cover using the Google Earth Engine simple cloud score threshold of <0.2. Albedo was calculated based on TOA reflectance using the equation (Liang, 2001):

$\begin{array}{c}\alpha =0.356b_2+0.130b_4+0.737b_5+0.085b_6+0.072b_7-0.0018\end{array}(7)$

This equation was selected because it has been shown to have higher accuracy than other Landsat albedo algorithms (Naegeli et al., 2017; Traversa et al., 2021).

LS8 measurements were compared to UAV albedo measurements by taking the cosine-weighted average of LS8 pixels within the PFOV of the downward-facing sensor (Figure 7).

3 Results

3.1 Field of View

3.1.1 Validation of Topographic Correction With Ground Point Measurements

The ground-based albedo measurements taken at the horizontal position were corrected for topography and compared with the measurements taken parallel to slope. A sensitivity analysis was conducted to determine the impact of PFOV on the topographic correction from 47 ground positions (3,918 total measurements) at the Namaste Valley field area taken on three clear-sky days. Each measurement was corrected using PFOVs of 60°–178° at 5° intervals at a fixed altitude of 1.5 m. The PFOV specified in the topographic correction determines the contributing area for the calculation of the terrain parameters, although the real field of view of the sensor is always hemispherical. Since these measurements were taken very close to the surface (1.5 m), there is minimal terrain variability incorporated in the sensor’s footprint for a majority of the measurement locations. The mean absolute error for the uncorrected horizontal measurements as compared with the slope-parallel measurements was 0.05 (Figure 8A). This error plots on a horizontal line in Figure 8A because it is not processed and therefore not dependent on the specified PFOV. Overall the topographic correction reduced absolute error of albedo by 0.02–0.03 (Figure 8A). It is apparent that the PFOV negligibly affects the absolute error for these measurements, and there was a slight increase in absolute error for high PFOVs (155°–178°). Although the differences in absolute error with different PFOVs were very small, there was an observed tendency of decreasing mean absolute error with increasing PFOV from 60° to 150° that becomes visible when the y-axis is enhanced (Figure 8B). At PFOVs greater than 150°, absolute error increases abruptly and exhibits a high degree of variability.

FIGURE 8

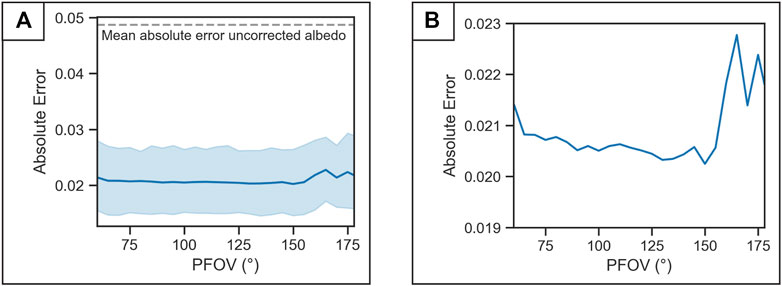
FIGURE 8. (A) Absolute error of the topographically corrected horizontally-positioned ground measurements at different PFOVs. The mean is shown with a solid blue line and the blue shaded area represents one standard deviation. Mean absolute error of uncorrected horizontal measurements is shown with a dashed grey line. (B) The same data from (A) with a reduced y-axis extent to highlight the decrease in absolute error from 60° to 150° PFOV, and abrupt increase in absolute error from 150° to 178° PFOV.

3.1.2 Uncrewed Aerial Vehicle Vertical Transects

An additional FOV sensitivity analysis was conducted on the UAV vertical transect data collected over snow at Namaste Valley on April 28, 2021. A total of 384 albedo measurements from five vertical transect locations were corrected for topography at varying PFOVs and compared with LS8 albedo. Due to lengthy processing times, these data were corrected using PFOVs from 60° to 178° at 10° intervals. For any given PFOV, these measurements incorporate more terrain and albedo variability than the ground validation measurements since they were taken at much higher altitudes (20–70 m). Increasing the PFOV in this analysis has two effects on the results. It both increases the amount of terrain incorperated into the topographic correction, and alters the number and spatial weighting of LS8 pixels that were averaged and compared to each pyranometer measurement. Raw error, calculated as the difference between LS8 albedo and topographically corrected UAV albedo, was positive (∼0.05) and consistent for PFOVs of 60°–130° (Figure 9). From 130° to 160° raw error decreased to mostly negative values and was relatively consistent and negative (−0.1) at PFOVs greater than 160° (Figure 9). Decreasing RMSE of the UAV measurements as compared to LS8 was observed with increasing PFOV until it reached a minimum at 140°, after which point the RMSE increased abruptly, peaking at 0.109 at a PFOV of 178° (Figure 9).

FIGURE 9

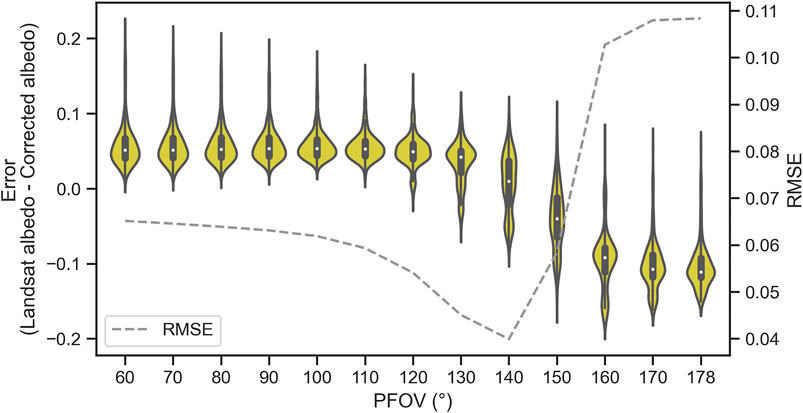
FIGURE 9. Violin plot displaying the raw error of UAV albedo data from vertical transects, as compared with Landsat 8 albedo (primary y-axis). Each violin (yellow) represents the distribution of this error for all vertical transect measurements processed at a specific PFOV (x-axis). The dashed grey line shows the RMSE (secondary y-axis) between the topographically corrected UAV data and LS8 data for all PFOVs.

The methodology for topographic correction and comparison to LS8 was designed to account for changes in measurement scale with altitude. Therefore, the comparison between UAV and LS8 albedo should show no dependence on altitude. To identify any potential altitude dependence, linear regressions were performed between altitude and raw error for the datasets processed at different PFOVs.

Figure 10A shows the relationships between raw error and altitude for a select number of PFOVs, and regression statistics for all PFOVs can be found in Supplementary Table S2. From PFOVs of 60°–130°, error was positive and increased with measurement altitude. For these smaller PFOVs, the projected footprints were focused over the high-albedo meadow area (Figure 10B). R² for the linear regression was 0.43 at 60° and decreased consistently along with the slope of the line to ∼0° and r² = 0 at a PFOV of 140°. At PFOVs greater than 140°, error was negative and increased with altitude. At these higher PFOVs, projected footprints covered broad areas with considerable tree cover (Figure 10B). R² and the slope of the fit line both increased consistently from 0 at 140° PFOV to a slope of 0.002 and r² = 0.44 at a PFOV of 178°. Although all correlation coefficients were relatively low, there appeared to be a tendency towards increasing correlation and dependence of error on altitude as the PFOV got further away from 140° in either direction.

FIGURE 10

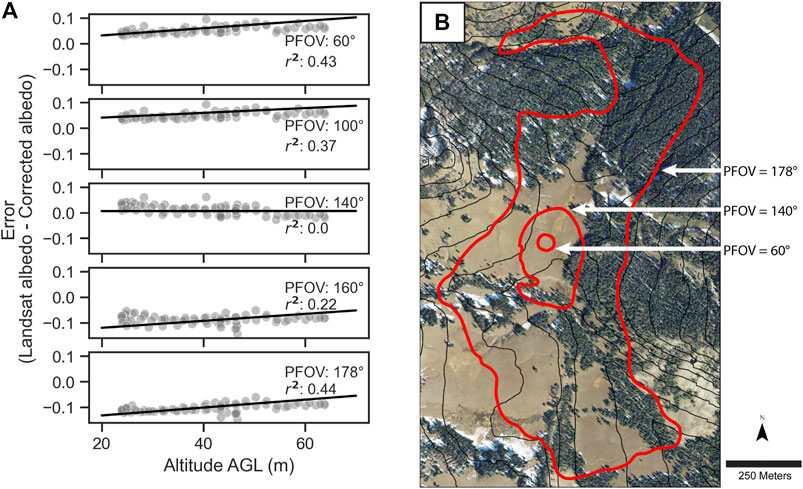
FIGURE 10. (A) UAV error, as compared with Landsat 8 albedo for the vertical transect data as a function of UAV altitude AGL. Subplots show the vertical transect UAV albedo data topographically corrected with varying PFOV. Solid black lines represent the linear regression on the data from each scatterplot, highlighting the altitude-dependence of the satellite comparison at different PFOVs. The correlation coefficients (r²) are displayed for each line. Regression statistics for this data at the full range of tested PFOVs can be found in Supplementary Table S2. (B) Map displaying the extent of the projected footprints (in red) at three different PFOVs for a single vertical transect measurement point (30 m AGL) located in the center of the study area. Elevation contours are displayed in black at a 20 m interval.

3.2 Topographic Data Source and Albedo Survey

Based on results from the field of view sensitivity analyses, 4,562 albedo measurements from the lawn-mower style albedo surveys were topographically corrected using a PFOV of 140°. These surveys demonstrate what an operational validation survey might look like. These survey data were also used to assess the performance of the tilt-topography correction relative to Landsat-8 albedo, and to compare how the hypothetical survey results vary when different topographic data sources are used.

On March 18, uncorrected albedo was highest (0.96) in the western half of the study area where the surface has the highest solar exposure, and was lowest (0.43) on the eastern portion of the study area that bordered trees and tree-shaded snow (Figure 11A). The topographic correction lowered albedo on the western, solar-aspect slopes, and slightly increased albedo over the eastern portion of the study area that was composed of low-sloping (<8°), south-west aspects (Figure 11B). For the 20 m AGL flight on all field days, overall, uncorrected albedo was unrealistically high. The topographic correction lowered the spread of values to align more closely with the range of LS8 albedo (Figure 11C). UAV albedo also measured a larger range of values than LS8 at this altitude.

FIGURE 11

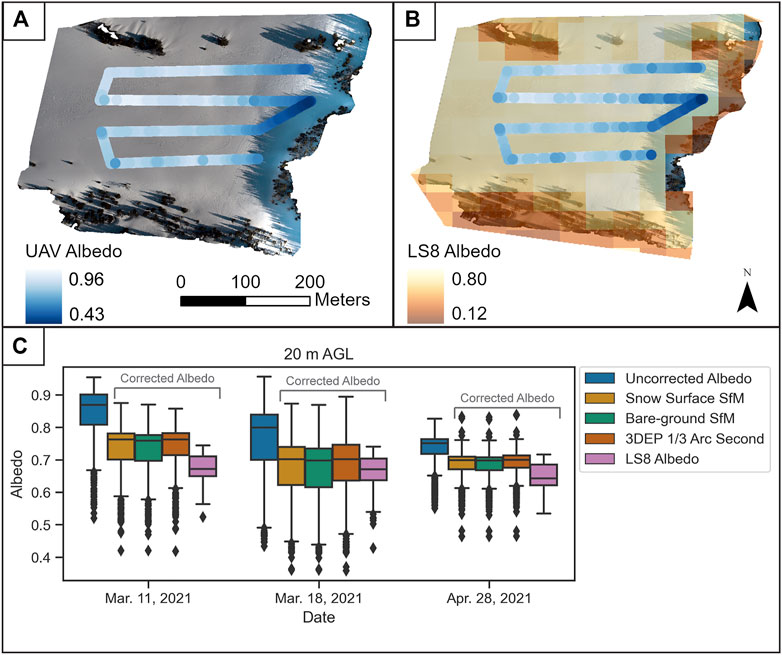
FIGURE 11. (A) Uncorrected UAV albedo survey at 20 m AGL on March 18, 2021. (B) UAV albedo data topographically corrected (PFOV = 140°) using the 1 m SfM snow surface model for March 18. LS8-observed albedo is shown in semi-transparent yellow-orange. (C) Box plot comparing uncorrected UAV albedo, UAV albedo topographically corrected (PFOV = 140°) using the three different surface models, and LS8 albedo. UAV measurements were collected at 20 m AGL on March 11 (time = 10:50 MT, ${\theta }_z$ = 63°), March 18 (time = 9:50 MT, ${\theta }_z$ = 58°), and April 28 (time = 10:40 MT, ${\theta }_z$ = 38°).

A Kruskal-Wallis test compared the UAV albedo data that were corrected using different topography sources (as compared with LS8 albedo). A p-value below 0.05 (Supplementary Table S3) indicates that the difference in the means between the two compared corrections is statistically significant. Results indicate that the SfM snow-surface and bare-ground models produced a negligible difference in corrected albedo for all altitudes on all field days (Figure 12). The UAV albedo corrections that utilized the 3DEP 10 m DEM had significantly higher RMSE compared to LS8 albedo than the corrections with SfM models at 10 m AGL for all three dates (Figure 12). At survey altitudes above 15 m AGL, the 3DEP 1/3 Arc Second corrections consistently produced albedos that were statistically indifferent to the measurements corrected with the snow surface SfM model (Figure 12). Agreement between the 3DEP corrections and the bare ground SfM corrections tended to be greater at higher survey altitudes as well.

FIGURE 12

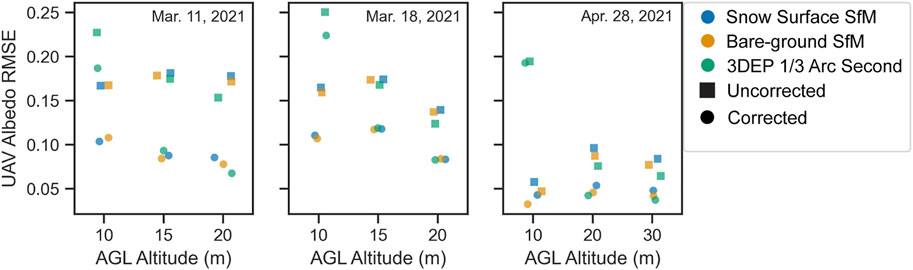
FIGURE 12. RMSE of corrected (circles) and uncorrected (squares) UAV albedo data as compared with LS8 albedo at different survey altitudes on each field day. Colors indicate the surface model used in the topographic correction.

4 Discussion

4.1 Ground-Based Validation Measurements

Ground-based measurements provided validation for the proposed topographic correction. The mean absolute error of albedo in uncorrected ground-based measurements was considerable (0.05), with respect to the acceptable error threshold for albedo inputs into general circulation climate models (Henderson-Sellers and Wilson, 1983). After correction, error was reduced to an average of 0.02, indicating that a considerable portion of this error was due to topography. We can conclude that topographic corrections for albedo measurements are necessary in mildly sloping terrain (<20°), and that the proposed correction performed well for the range of slope angles and aspects in the study area. The remaining error can potentially be explained by field-of-view interference by the platform and observer, or imperfect alignment of the slope-parallel measurements to the slope and aspect of the surface directly beneath the sensors. Performance of this topographic correction is uncertain in steeper terrain, as it was validated on slopes <20°. In steeply sloping terrain, radiation reflected from the surrounding environment would impact the relative diffuse and direct proportions of irradiance. Radiation reflected from surrounding slopes was not accounted for by the radiative transfer model and could introduce error into the correction over steeper terrain.

Without correction, the effect of topography can potentially mask the true spatial variability in snow albedo. It was observed that uncorrected albedo was unrealistically high over slopes with a lower average solar incidence angle. On these slopes the snow generally experiences faster metamorphism leading to increasing grain sizes and lower albedo. In this case the unrealistically high measured albedo would mask the effect of snow grain metamorphosis.

PFOV sensitivity analysis of the topographically-corrected ground measurements provided valuable insights into the dependence of the correction on this user-specified parameter. It was anticipated that the topographic correction would increasingly reduce error as the PFOV was expanded to incorporate more terrain visible to the pyranometer. It is important to note that given the low height of the sensors above the ground (1.5 m), the footprint never incorporated much topographic variability. As a result, increasing the PFOV minimally affected the calculated terrain parameters and topographic correction. The apparent decrease in absolute error from a PFOV of 60°–150° observed in the ground measurements was marginal, yet robust (3,918 measurements). The subtlety of this decrease was expected due to the nature of the terrain, but anticipated to be steeper for the UAV albedo data. Since the sensors onboard the UAV were deployed at much higher altitudes, their footprints incorporated a higher degree of terrain variability.

The abrupt increase in error observed for PFOVs above 150° was likely a function of extending the footprint to areas that were obstructed by trees and not actually contributing to the signal, which is something the viewshed algorithm did not account for. Additionally, shaded snow cover does not need to be corrected for topography since the irradiance in these areas is completely diffuse. Since the calculation of the terrain parameters within the projected footprint did not exclude shaded areas, their terrain would have been incorporated into the topographic correction. The energy entering the sensors from these peripheral areas is also impacted by the imperfect cosine response of the sensors.

4.2 Processing Field of View: Uncrewed Aerial Vehicle Vertical Transects

Results from the PFOV sensitivity analyses of the vertical transect data aligned with observations from the ground validation measurements. Both analyses reported minimal RMSE in UAV albedo at PFOVs around 140°. For the vertical transect data, the reduction in RMSE with increasing PFOV up to 140° was likely a function of two things: 1) more terrain within the pyranometer FOV was accounted for in the topographic correction and 2) more Landsat pixels were incorporated into the weighted average of LS8 albedo. The reduction in RMSE with increasing PFOV was greater for the vertical transect data than the reduction in RMSE observed in the ground validation data. This was likely because the vertical transect UAV albedo measurements (20–70 m AGL) incorporated more terrain and variability than the ground validation measurements (1.5 m above the snow surface). The RMSE of the vertical transect measurements were also dependent on the cosine-weighted LS8 albedo (also determined by the PFOV). Increasing the PFOV allowed for more variability in albedo to be accounted for in the LS8 weighting and averaging.

Abrupt increases in RMSE were observed past 140° PFOV. RMSE increases were observed to occur at lower PFOVs for measurements made closer to trees. This demonstrates the need to incorporate shading and trees into the viewshed algorithm and topographic correction. Theoretically, as the PFOV increases, RMSE should continue to decrease, and we anticipate that this would be observed if trees were accounted for.

There were some clear patterns in altitude dependence of the satellite comparison with different PFOVs. The raw error of UAV albedo with respect to LS8 albedo increased with UAV altitude at small PFOVs. Since the vertical transects were focused over the snow-covered meadow (high albedo), the UAV incorporated an increasing portion of lower albedo surfaces (trees and shaded snow) into its albedo measurements at higher altitudes. With a low PFOV (60°) the LS8 albedo weighting did not include these lower albedo areas surrounding the snow-covered meadow (Figure 10B), resulting in a weighted LS8 albedo values that were too high. At the PFOVs nearing 180°, the raw error of UAV albedo with respect to LS8 albedo tended to decrease with increasing UAV altitude. This phenomenon can be explained by tree shading, where trees would have blocked areas with lower albedos from the sensor’s view. Since the viewshed algorithm did not account for tree shading, the pixels used for the weighted Landsat average included these areas that the sensor could not see (Figure 10B). This issue would have been particularly pronounced for measurements made at the lowest flight altitudes, and decreased in significance as the UAV ascended above tree-level. The observed patterns between raw error and altitude at the lowest PFOVs were clearly driven by the spatial variability in the surface characteristics of this specific field area. At the highest PFOVs, the observed tendencies were a result of the inability of our method to account for trees.

Minimal dependence of RMSE between UAV and LS8 albedo was found at a PFOV of 140°. At this PFOV a balance was struck between incorporating too many as opposed to not enough pixels for both the topographic correction and weighting of LS8 pixels (Figure 10B). Therefore, this PFOV was used in the subsequent analysis of the topographic data source.

4.3 Topographic Data Source

Topographic correction reduced the RMSE between UAV albedo and LS8 albedo for the lawnmower UAV surveys at all altitudes regardless of the topographic correction data source at a PFOV of 140° (Figure 12). The only exception was for the flight at 10 m on April 28 that was processed with the 3DEP 1/3 arc second DEM, where the change in RMSE was negligible. It is important to note that the LS8 albedo product provides a good approximation of the true surface albedo, but is also susceptible to error. Therefore, discrepancies between the UAV and satellite data cannot be attributed solely to issues with the UAV data processing. However, given that the two data sources underwent two completely different processing workflows and agree well overall, both methodologies indicate that they are performing well.

The SfM snow surface models were assumed to produce the highest-accuracy correction of the UAV albedo data. However, it was observed that the differences between UAV albedo corrected using the snow surface SfM models and the bare-ground SfM models were not statistically significant. We conclude that a single bare-ground SfM surface model at a 1 m resolution is sufficient for correcting UAV data at all altitudes in this alpine meadow.

The UAV albedo data corrected with the 3DEP 1/3 arc second DEM showed highest disagreement with the bare-ground and snow surface SfM models at lower flight altitudes (10–15 m). At these altitudes, the UAV measurements were likely influenced by terrain variability that the coarser DEM was not able to resolve. At flight altitudes above 15 m, the 3DEP DEM surface produced topographic corrections that were statistically indifferent to those produced with the SfM elevation surfaces. At these higher altitudes, the small scale (1–10 m) terrain variability did not considerably impact the UAV albedo measurements. These results indicate that a 3DEP 1/3 arc second DEM can be used to correct UAV albedo data for topography when flying at sufficiently high altitudes (20–30 m) in this study area.

4.4 Field Area Disturbances

On each field outing, the fresh snow was disturbed by ski tracks when GCPs were placed. Additionally, prior to April 28, the field area was disturbed by snowmobile tracks. These tracks had a very low roughness height (<5 cm) and were not visible in the 1 m SfM surface models. Ground-based measurements were taken at locations far enough away from the tracks to mitigate any error induced by them. Moreover, given their low roughness height with respect to the footprint of even the ground-based measurements they were assumed to negligibly affect the measured albedo.

4.5 Limitations and Future Work

Topographically heterogeneous non-snow objects such as trees, rocks, and cliffs will be present in most mountainous field areas. Since shaded snow-covered areas beneath trees do not receive direct irradiance, their measured albedos do not require topographic correction. This partitioning of the correction was out of the scope of this research. The failure to account for tree-shading likely resulted in overcorrection of the UAV measurements taken proximal to the forested area, and introduced error in the topographic correction and comparison to LS8 albedo at PFOVs >140°. Future work could utilize a downward-facing fisheye camera in addition to a downward-facing pyranometer (Webster and Jonas, 2018; Jäkel et al., 2019) to effectively account for these areas during topographic correction and satellite comparison.

Clear-sky weather is quite rare in many mountainous regions during the winter. Moreover, cloud cover exerts a non-negligible control on shortwave forcing and the energy balance as a whole (Stapf et al., 2020). Cloud cover inherently affects the proportion of direct irradiance and thus the impact of topography on UAV measurements. Therefore, the radiative transfer model should account for rapidly-changing cloud cover and its impact on the proportions of irradiance components. This could be accomplished ideally with a pyrheliometer and a shaded upward facing pyranometer to continuously measure the individual irradiance components. A less expensive approach could utilize a fisheye camera to capture hemispherical sky view imagery, from which cloud cover could be automatically quantified (Roupioz et al., 2015) and related to pyranometer measurements to approximate the effects of clouds on incoming irradiance (Pfister et al., 2003).

Future work should build upon the findings of this research by addressing the aforementioned uncertainties, and applying the methodology over broader, more variable terrain. Our results are not necessarily restricted to snow covered areas. The same physical principles behind the topographic correction and satellite comparison apply to non-snow surfaces. Attempts should be made to deploy the platform over fractional snow cover and snow-free landcover.

The comparison of UAV data to LS8 served multiple purposes. Primarily, this comparison demonstrated a methodology of comparing UAV albedo measurements to an external spatially distributed albedo product. The PFOV sensitivity analyses demonstrated the disparity of possible outcomes of such a comparison that is entirely dependent on the specified PFOV. In order for UAV albedo measurements to be comparable across studies, and to provide dependable validation of spatially distributed albedo products, an optimal PFOV needs to be determined and agreed upon. We provide the necessary first steps to accomplishing this, and identified that tree cover was the primary inhibiting factor in doing so.

The RMSE calculations between UAV and Landsat albedo were intended to serve as a baseline estimate of the agreement between the two datasets, as opposed to a validation of one or the other. It was apparent that after topographic correction, LS8 and UAV albedo measurements agreed quite well, and best when the PFOV was 140°. Since the ultimate goal of this work is to provide robust validation for satellite albedo measurements, a comparison of UAV albedo measurements to a high-quality validation source is required. UAV or airborne hyperspectral imagery would provide the means to adequately validate these measurements.

4.6 Survey Recommendations

This research provided a demonstration of a potential configuration for a UAV albedo validation survey using a lawn-mower pattern. Although this pattern is standard for various UAV survey applications, it may not be optimal for capturing a comprehensive representation of spatial variability in snow albedo. Since the platform collected an albedo measurement every second (∼2 m), there was a much higher measurement density in the long direction of the transects. Directional bias could be removed by filtering points to provide equal spacing, but this would reduce the measurement density. If future surveys are conducted in a circular or spiraling pattern, the small measurement spacing can be preserved while sampling equally in all horizontal directions.

Measurement altitude is accounted for in the weightings of terrain parameters for topographic correction and satellite pixels for comparison. Therefore, UAV albedo survey altitude can be variable. The preliminary tarpaulin experiment demonstrated that the spatial scale of observed variability increases with flight altitude. In order to observe small scale (1–10 m) variability in albedo, the UAV should be flown at the lowest possible altitude. The minimum feasible flight altitude exists where obstacles can be successfully avoided and the snow surface is unaffected by the turbulence of the UAV rotors. From observations in the field this minimum flight altitude was determined to be ∼10 m when fresh snow was present at the surface. As flight altitude increases, the observed variability will be progressively smoothed out as the sensing footprint increases.

With regards to requirements for topographic data sources, we found that high resolution (1 m) SfM surface models produced the highest-accuracy topographic corrections overall. However, at our field site a coarser (10 m) DEM can also be used to correct for topography as long as the UAV is flying above 15 m AGL (Supplementary Table S3). Given that UAV surveys are limited by battery life, time spent collecting photogrammetry imagery over the sloping snow surface should instead be put towards collecting imagery over trees, to allow for their surfaces to be incorporated in the processing methodologies.

5 Conclusion

This research presents considerable advances in the operationalization of UAV-based snow albedo measurement. UAV platforms are capable of bridging the scaling gap between in-situ and satellite-based snow albedo measurements, and we provide the requisite methodologies to accomplish this. We demonstrated the capabilities of this specific UAV platform to collect albedo measurements in alpine headwaters. Insights gained in the field and during analyses can be used to guide future UAV albedo survey designs.

The presented methods for data processing consider the unique pyranometer response and the dependence of UAV albedo measurement scale on altitude. It can be concluded that in order for UAV-based snow albedo measurements to be directly comparable across different research, it is critical that processing strategies are consistent. Through sensitivity analysis we determined that the PFOV exerts a dominant control on the outcome of topographic correction and comparison to gridded satellite products. Improvements to the existing methodology to account for tree cover will allow for the identification of an optimal PFOV that can be standardized across research applications.

The capability of UAV-based remote sensing platforms is progressing rapidly. These systems provide the unique opportunity to observe earth system processes at high resolutions across broad areas for a fraction of the cost of airborne surveys. In order to harness the full potential of these novel systems the community needs to maximize interoperability of methods and data between different research and applications. This research provides the necessary first steps in standardizing UAV-based albedo measurement, so that future work can build upon the platform to answer critical science questions.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: data doi: 10.5281/zenodo.5338942 code: https://github.com/GEOSWRL/UAV-albedo.git.

Author Contributions

AM: Co-developed research objectives, led field campaign, analyzed data, and drafted and revised manuscript. ES: Conceptualized initial exploratory project, co-developed research objectives, assisted with fieldwork, provided scientific input, and provided revisions of the manuscript. JH: Assisted in ideation of primary research objectives, assisted with fieldwork, provided scientific input and revised manuscript. JS: Assisted in ideation of primary research objectives, contributed scientific input and revisions of the manuscript. CG: Contributed scientific input and revisions of the manuscript.

Funding

The initial concept exploration for this project was funded by an incubator grant from the Earth Science Information Partners (ESIP) and ESIP Labs. Additional seed funding was provided by MontanaView through a Remote Sensing Research Fellowship. The primary support for this research was provided by funding from the USGS National Innovation Center, USGS National Land Imaging Program, and a Montana NASA EPSCoR Research Initiation Award, under NASA cooperative agreement number 80NSSC19M0064.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank the Yellowstone Club and Yellowstone Club Ski Patrol, especially Doug McCabe and Griffin Dittmar, for providing access to the field site and assistance with fieldwork. We would also like to acknowledge Roxanne Holmes, Ross Palomaki, and Madeline Beck for assistance with collecting field data. Lastly, the authors would like to thank Henry MacEachern for providing graphic design consultation for a number of the figures included in this manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsen.2021.767593/full#supplementary-material

References

Aoki, T., Hachikubo, A., and Hori, M. (2003). Effects of Snow Physical Parameters on Shortwave Broadband Albedos. J. Geophys. Res. 108 (D19), 4616. doi:10.1029/2003JD003506

CrossRef Full Text | Google Scholar

Bair, E. H., Rittger, K., Skiles, S. M., and Dozier, J. (2019). An Examination of Snow Albedo Estimates from MODIS and Their Impact on Snow Water Equivalent Reconstruction. Water Resour. Res. 55, 7826–7842. doi:10.1029/2019WR024810

CrossRef Full Text | Google Scholar

Bales, R. C., Molotch, N. P., Painter, T. H., Dettinger, M. D., Rice, R., and Dozier, J. (2006). Mountain Hydrology of the Western United States. Water Resour. Res. 42, W08432. doi:10.1029/2005WR004387

CrossRef Full Text | Google Scholar

Blöschl, G., and Sivapalan, M. (1995). Scale Issues in Hydrological Modelling: A Review. Hydrol. Process. 9 (3-4), 251–290. doi:10.1002/hyp.3360090305

CrossRef Full Text | Google Scholar

Blöschl, G. (1999). Scaling Issues in Snow Hydrology. Hydrol. Process. 13 (14–15), 2149–2175. doi:10.1002/(sici)1099-1085(199910)13:14/15<2149:aid-hyp847>3.0.co;2-8

CrossRef Full Text | Google Scholar

Bogren, W. S., Burkhart, J. F., and Kylling, A. (2015). Tilt Error in Cryospheric Surface Radiation Measurements at High Latitudes: A Model Study. Cryosphere Discuss. 9, 4355–4376. doi:10.5194/tcd-9-4355-2015

CrossRef Full Text | Google Scholar

Bourgeois, C. S., Calanca, P., and Ohmura, A. (2006). A Field Study of the Hemispherical Directional Reflectance Factor and Spectral Albedo of Dry Snow. J. Geophys. Res. 111, D20108. doi:10.1029/2006JD007296

CrossRef Full Text | Google Scholar

Brock, F. V. (2001). Meteorological Measurement Systems. Oxford, England: Oxford University Press.

Google Scholar

Burkhart, J. F., Kylling, A., Schaaf, C. B., Wang, Z., Bogren, W., Storvold, R., et al. (2017). Unmanned Aerial System Nadir Reflectance and MODIS Nadir BRDF-Adjusted Surface Reflectances Intercompared over Greenland. The Cryosphere 11 (4), 1575–1589. doi:10.5194/tc-2016-264

CrossRef Full Text | Google Scholar

Canisius, F., Wang, S., Croft, H., Leblanc, S. G., Russell, H. A. J., Chen, J., et al. (2019). A UAV-Based Sensor System for Measuring Land Surface Albedo: Tested over a Boreal Peatland Ecosystem. Drones 3, 27. doi:10.3390/drones3010027

CrossRef Full Text | Google Scholar

Clark, M. P., Hendrikx, J., Slater, A. G., Kavetski, D., Anderson, B., Cullen, N. J., et al. (2011). Representing Spatial Variability of Snow Water Equivalent in Hydrologic and Land-Surface Models: A Review. Water Resour. Res. 47 (7), W07539. doi:10.1029/2011WR010745

CrossRef Full Text | Google Scholar

Cui, J., Shi, T., Zhou, Y., Wu, D., Wang, X., and Pu, W. (2021). Satellite-based Radiative Forcing by Light-Absorbing Particles in Snow across the Northern Hemisphere. Atmos. Chem. Phys. 21 (1), 269–288. doi:10.5194/acp-21-269-2021

CrossRef Full Text | Google Scholar

Dozier, J. (2011). Mountain Hydrology, Snow Color, and the Fourth Paradigm. Eos Trans. AGU 92, 373–374. doi:10.1029/2011EO430001

CrossRef Full Text | Google Scholar

Dumont, M., Brissaud, O., Picard, G., Schmitt, B., Gallet, J.-C., and Arnaud, Y. (2010). High-Accuracy Measurements of Snow Bidirectional Reflectance Distribution Function at Visible and NIR Wavelengths - Comparison with Modelling Results. Atmos. Chem. Phys. 10, 2507–2520. doi:10.5194/acp-10-2507-2010

CrossRef Full Text | Google Scholar

Dumont, M., Gardelle, J., Sirguey, P., Guillot, A., Six, D., Rabatel, A., et al. (2012). Linking Glacier Annual Mass Balance and Glacier Albedo Retrieved from MODIS Data. Cryosphere 6 (6), 1527–1539. doi:10.5194/tc-6-1527-2012

CrossRef Full Text | Google Scholar

Grenfell, T. C., Warren, S. G., and Mullen, P. C. (1994). Reflection of Solar Radiation by the Antarctic Snow Surface at Ultraviolet, Visible, and Near-Infrared Wavelengths. J. Geophys. Res. 99 (D9), 18669–18684. doi:10.1029/94JD01484

CrossRef Full Text | Google Scholar

Grünewald, T., Schirmer, M., Mott, R., and Lehning, M. (2010). Spatial and Temporal Variability of Snow Depth and Ablation Rates in a Small Mountain Catchment. Cryosphere 4 (2), 215–225. doi:10.5194/tc-4-215-2010

CrossRef Full Text | Google Scholar

Hall, A., and Qu, X. (2006). Using the Current Seasonal Cycle to Constrain Snow Albedo Feedback in Future Climate Change. Geophys. Res. Lett. 33 (3), L03502. doi:10.1029/2005GL025127

CrossRef Full Text | Google Scholar

Hall, D. K. (1988). Assessment of Polar Climate Change Using Satellite Technology. Rev. Geophys. 26 (1), 26–39. doi:10.1029/RG026i001p00026

CrossRef Full Text | Google Scholar

Henderson-Sellers, A., and Wilson, M. F. (1983). Surface Albedo Data for Climatic Modeling. Rev. Geophys. 21 (8), 1743–1778. doi:10.1029/RG021i008p01743

CrossRef Full Text | Google Scholar

Ingram, W. J., Wilson, C. A., and Mitchell, J. F. B. (1989). Modeling Climate Change: An Assessment of Sea Ice and Surface Albedo Feedbacks. J. Geophys. Res. 94 (D6), 8609–8622. doi:10.1029/JD094iD06p08609

CrossRef Full Text | Google Scholar

Jäkel, E., Stapf, J., Wendisch, M., Nicolaus, M., Dorn, W., and Rinke, A. (2019). Validation of the Sea Ice Surface Albedo Scheme of the Regional Climate Model HIRHAM-NAOSIM Using Aircraft Measurements during the ACLOUD/PASCAL Campaigns. Cryosphere 13, 1695–1708. doi:10.5194/tc-13-1695-2019

CrossRef Full Text | Google Scholar

Jonsell, U., Hock, R., and Holmgren, B. (2003). Spatial and Temporal Variations in Albedo on Storglaciären, Sweden. J. Glaciol. 49, 59–68. doi:10.3189/172756503781830980

CrossRef Full Text | Google Scholar

Kumar, S., Mocko, D., Vuyovich, C., and Peters-Lidard, C. (2020). Impact of Surface Albedo Assimilation on Snow Estimation. Remote Sens. 12 (4), 645. doi:10.3390/rs12040645

CrossRef Full Text | Google Scholar

Levy, C., Burakowski, E., and Richardson, A. (2018). Novel Measurements of Fine-Scale Albedo: Using a Commercial Quadcopter to Measure Radiation Fluxes. Remote Sens. 10, 1303. doi:10.3390/rs10081303

CrossRef Full Text | Google Scholar

Lhermitte, S., Abermann, J., and Kinnard, C. (2014). Albedo over Rough Snow and Ice Surfaces. Cryosphere 8, 1069–1086. doi:10.5194/tc-8-1069-2014

CrossRef Full Text | Google Scholar

Liang, S. (2001). Narrowband to Broadband Conversions of Land Surface Albedo I. Remote Sens. Environ. 76 (2), 213–238. doi:10.1016/S0034-4257(00)00205-4

CrossRef Full Text | Google Scholar

Malle, J., Rutter, N., Mazzotti, G., and Jonas, T. (2019). Shading by Trees and Fractional Snow Cover Control the Subcanopy Radiation Budget. J. Geophys. Res. Atmos. 124, 3195–3207. doi:10.1029/2018JD029908

CrossRef Full Text | Google Scholar

Malle, J., Rutter, N., Webster, C., Mazzotti, G., Wake, L., and Jonas, T. (2021). Effect of Forest Canopy Structure on Wintertime Land Surface Albedo: Evaluating CLM5 Simulations with In‐Situ Measurements. Geophys. Res. Atmos. 126, e34118. doi:10.1029/2020JD034118

CrossRef Full Text | Google Scholar

Meyer, P., Itten, K. I., Kellenberger, T., Sandmeier, S., and Sandmeier, R. (1993). Radiometric Corrections of Topographically Induced Effects on Landsat TM Data in an alpine Environment. ISPRS J. Photogramm. Remote Sens. 48 (4), 17–28. doi:10.1016/0924-2716(93)90028-L

CrossRef Full Text | Google Scholar

Molotch, N. P., and Bales, R. C. (2006). Comparison of Ground-Based and Airborne Snow Surface Albedo Parameterizations in an alpine Watershed: Impact on Snowpack Mass Balance. Water Resour. Res. 42 (5), W05410. doi:10.1029/2005WR004522

CrossRef Full Text | Google Scholar

Molotch, N. P., Painter, T. H., Bales, R. C., and Dozier, J. (2004). Incorporating Remotely-Sensed Snow Albedo into a Spatially-Distributed Snowmelt Model. Geophys. Res. Lett. 31 (3), L03501. doi:10.1029/2003GL019063

CrossRef Full Text | Google Scholar

Naegeli, K., Damm, A., Huss, M., Wulf, H., Schaepman, M., and Hoelzle, M. (2017). Cross-Comparison of Albedo Products for Glacier Surfaces Derived from Airborne and Satellite (Sentinel-2 and Landsat 8) Optical Data. Remote Sens. 9 (2), 110. doi:10.3390/rs9020110

CrossRef Full Text | Google Scholar

National Academies of Sciences, Engineering, and Medicine (2018). Thriving on Our Changing Planet: A Decadal Strategy for Earth Observation from Space. Washington, DC: The National Academies Press. (

Google Scholar

Pfister, G., McKenzie, R. L., Liley, J. B., Thomas, A., Forgan, B. W., and Long, C. N. (2003). Cloud Coverage Based on All-Sky Imaging and its Impact on Surface Solar Irradiance. J. Appl. Meteorol. 42 (10), 1421–1434. doi:10.1175/1520-0450(2003)042<1421:ccboai>2.0.co;2

CrossRef Full Text | Google Scholar

Picard, G., Dumont, M., Lamare, M., Tuzet, F., Larue, F., Pirazzini, R., et al. (2020). Spectral Albedo Measurements over Snow-Covered Slopes: Theory and Slope Effect Corrections. Cryosphere 14, 1497–1517. doi:10.5194/tc-14-1497-2020

CrossRef Full Text | Google Scholar

Pirazzini, R. (2004). Surface Albedo Measurements over Antarctic Sites in Summer. J. Geophys. Res. 109, D20118. doi:10.1029/2004JD004617

CrossRef Full Text | Google Scholar

Qu, Y., Liang, S., Liu, Q., He, T., Liu, S., and Li, X. (2015). Mapping Surface Broadband Albedo from Satellite Observations: A Review of Literatures on Algorithms and Products. Remote Sens. 7, 990–1020. doi:10.3390/rs70100990

CrossRef Full Text | Google Scholar

Rhoades, A. M., Jones, A. D., and Ullrich, P. A. (2018). Assessing Mountains as Natural Reservoirs with a Multimetric Framework. Earth's Future 6 (9), 1221–1241. doi:10.1002/2017EF000789

CrossRef Full Text | Google Scholar

Roupioz, L., Colin, J., Jia, L., Nerry, F., and Menenti, M. (2015). Quantifying the Impact of Cloud Cover on Ground Radiation Flux Measurements Using Hemispherical Images. Int. J. Remote Sens. 36 (19–20), 5087–5104. doi:10.1080/01431161.2015.1084440

CrossRef Full Text | Google Scholar

Ryan, J. C., Hubbard, A., Box, J. E., Brough, S., Cameron, K., Cook, J. M., et al. (2017). Derivation of High Spatial Resolution Albedo from UAV Digital Imagery: Application over the Greenland Ice Sheet. Front. Earth Sci. 5 (40), 6218–6225. doi:10.3389/feart.2017.00040

CrossRef Full Text | Google Scholar

Ryan, J. C., Hubbard, A., Irvine‐Fynn, T. D., Doyle, S. H., Cook, J. M., Stibal, M., et al. (2017b). How Robust Are In Situ Observations for Validating Satellite‐Derived Albedo over the Dark Zone of the Greenland Ice Sheet? Geophys. Res. Lett. 44, 6218–6225. doi:10.1002/2017GL073661

CrossRef Full Text | Google Scholar

Schaaf, C. B., Gao, F., Strahler, A. H., Lucht, W., Li, X., Tsang, T., et al. (2002). First Operational BRDF, Albedo Nadir Reflectance Products from MODIS. Remote Sens. Environ. 83, 135–148. doi:10.1016/S0034-4257(02)00091-3

CrossRef Full Text | Google Scholar

Schaepman-Strub, G., Schaepman, M. E., Painter, T. H., Dangel, S., and Martonchik, J. V. (2006). Reflectance Quantities in Optical Remote Sensing-Definitions and Case Studies. Remote Sens. Environ. 103, 27–42. doi:10.1016/j.rse.2006.03.002

CrossRef Full Text | Google Scholar

Schweizer, J., Kronholm, K., Jamieson, J. B., and Birkeland, K. W. (2008). Review of Spatial Variability of Snowpack Properties and its Importance for Avalanche Formation. Cold Regions Sci. Technol. 51 (2), 253–272. doi:10.1016/j.coldregions.2007.04.009

CrossRef Full Text | Google Scholar

Seidel, F. C., Rittger, K., Skiles, S. M., Molotch, N. P., and Painter, T. H. (2016). Case Study of Spatial and Temporal Variability of Snow Cover, Grain Size, Albedo and Radiative Forcing in the Sierra Nevada and Rocky Mountain Snowpack Derived from Imaging Spectroscopy. Cryosphere 10, 1229–1244. doi:10.5194/tc-10-1229-2016

CrossRef Full Text | Google Scholar

Shaw, T. E., Ulloa, G., Farías-Barahona, D., Fernandez, R., Lattus, J. M., and McPhee, J. (2021). Glacier Albedo Reduction and Drought Effects in the Extratropical Andes, 1986-2020. J. Glaciol. 67 (261), 158–169. doi:10.1017/jog.2020.102

CrossRef Full Text | Google Scholar

Sproles, E. A., Mullen, A., Hendrikx, J., Gatebe, C., and Taylor, S. (2020). Autonomous Aerial Vehicles (AAVs) as a Tool for Improving the Spatial Resolution of Snow Albedo Measurements in Mountainous Regions. Hydrology 7 (3), 41. doi:10.3390/hydrology7030041

CrossRef Full Text | Google Scholar

Stapf, J., Ehrlich, A., Jäkel, E., Lüpkes, C., and Wendisch, M. (2020). Reassessment of Shortwave Surface Cloud Radiative Forcing in the Arctic: Consideration of Surface-Albedo-Cloud Interactions. Atmos. Chem. Phys. 20 (16), 9895–9914. doi:10.5194/acp-20-9895-2020

CrossRef Full Text | Google Scholar

Strahler, A., Lucht, W., Schaaf, C., Tsang, T., Gao, F., and Muller, J. (1999). MODIS BRDF/Albedo Product: Algorithm Theoretical Basis Document Version 5.0.

Google Scholar

Teillet, P. M., Guindon, B., and Goodenough, D. G. (2014). On the Slope-Aspect Correction of Multispectral Scanner Data. Can. J. Remote Sens. 8, 84–106. doi:10.1080/07038992.1982.10855028

CrossRef Full Text | Google Scholar

Traversa, G., Fugazza, D., Senese, A., and Frezzotti, M. (2021). Landsat 8 OLI Broadband Albedo Validation in Antarctica and Greenland. Remote Sens. 13 (4), 799. doi:10.3390/rs13040799

CrossRef Full Text | Google Scholar

USGS (2017). 1/3rd Arc-Second Digital Elevation Models (DEMs) - USGS National Map 3DEP Downloadable Data Collection: U.S. Reston, VA: Geological Survey.

Google Scholar

V1.7.4 (2021). A.M. Agisoft Metashape Professional. [Online]. Agisoft LLC. Available at: https://www.agisoft.com/ (Accessed 2021).

Google Scholar

V3.1.0 (2021). D. DatCon Software [Online]. Available at: https://datfile.net/Doc/intro.html (Accessed 2021).

V4.4 (2021). U. Universal Ground Control Station. [Online]. SPH Engineering (Accessed 2021).

Google Scholar

Warren, S. G., and Wiscombe, W. J. (1980). A Model for the Spectral Albedo of Snow. II: Snow Containing Atmospheric Aerosols. J. Atmos. Sci. 37, 2734–2745. doi:10.1175/1520-0469(1980)037<2734:amftsa>2.0.co;2

CrossRef Full Text | Google Scholar

Warren, S. G. (1984). Impurities in Snow: Effects on Albedo and Snowmelt (Review). A. Glaciol. 5, 177–179. doi:10.1017/s0260305500003700

CrossRef Full Text | Google Scholar

Webster, C., and Jonas, T. (2018). Influence of Canopy Shading and Snow Coverage on Effective Albedo in a Snow-Dominated evergreen Needleleaf forest. Remote Sens. Environ. 214, 48–58. doi:10.1016/j.rse.2018.05.023

CrossRef Full Text | Google Scholar

Weiser, U., Olefs, M., Schöner, W., Weyss, G., and Hynek, B. (2016). Correction of Broadband Snow Albedo Measurements Affected by Unknown Slope and Sensor Tilts. Cryosphere 10, 775–790. doi:10.5194/tc-10-775-2016

CrossRef Full Text | Google Scholar

Wetlaufer, K., Hendrikx, J., and Marshall, L. (2016). Spatial Heterogeneity of Snow Density and its Influence on Snow Water Equivalence Estimates in a Large Mountainous Basin. Hydrology 3 (1), 3. doi:10.3390/hydrology3010003

CrossRef Full Text | Google Scholar

Wilson, R. T. (2013). Py6S: A Python Interface to the 6S Radiative Transfer Model. Comput. Geosci. 51, 166–171. doi:10.1016/j.cageo.2012.08.002

CrossRef Full Text | Google Scholar

Wiscombe, W. J., and Warren, S. G. (1980). A Model for the Spectral Albedo of Snow. I: Pure Snow. J. Atmos. Sci. 37, 2712–2733. doi:10.1175/1520-0469(1980)037<2712:amftsa>2.0.co;2

CrossRef Full Text | Google Scholar

Wu, S., Wen, J., You, D., Hao, D., Lin, X., Xiao, Q., et al. (2018). Characterization of Remote Sensing Albedo over Sloped Surfaces Based on DART Simulations and In Situ Observations. J. Geophys. Res. Atmos. 123 (16), 8599–8622. doi:10.1029/2018jd028283

CrossRef Full Text | Google Scholar

Xu, J., and Shu, H. (2014). Assimilating MODIS-Based Albedo and Snow Cover Fraction into the Common Land Model to Improve Snow Depth Simulation with Direct Insertion and Deterministic Ensemble Kalman Filter Methods. J. Geophys. Res. Atmos. 119, 684–710. doi:10.1002/2014JD022012

CrossRef Full Text | Google Scholar