Quantifying CO2 Emissions of Power Plants With CO2 and NO2 Imaging Satellites

One important goal of the Copernicus CO₂ monitoring (CO2M) mission is to quantify CO₂ emissions of large point sources. We analyzed the feasibility of such quantifications using synthetic CO₂ and NO₂ observations for a constellation of CO2M satellites. Observations were generated from kilometer-scale COSMO-GHG simulations over parts of the Czech Republic, Germany and Poland. CO₂ and NO_X emissions of the 15 largest power plants (3.7–40.3 Mt CO₂ yr⁻¹) were quantified using a data-driven method that combines a plume detection algorithm with a mass-balance approach. CO₂ and NO_X emissions could be estimated from single overpasses with 39–150% and 33–116% uncertainty (10–90th percentile), respectively. NO₂ observations were essential for estimating CO₂ emissions as they helped detecting and constraining the shape of the plumes. The uncertainties are dominated by uncertainties in the CO2M observations (2–72%) and limitations of the mass-balance approach to quantify emissions of complex plumes (25–95%). Annual CO₂ emissions could be estimated with 23–119% and 18–65% uncertainties with two and three satellites, respectively. The uncertainty in the temporal variability of emissions contributes about half to the total uncertainty. The estimated uncertainty was extrapolated to determine uncertainties for point sources globally, suggesting that two satellites would be able to quantify the emissions of up to 300 point sources with <30% uncertainty, while adding a third satellite would double the number to about 600 point sources. Annual NO_X emissions can be determined with better accuracy of 16–73% and 13–52% with two and three satellites, respectively. Estimating CO₂ emissions from NO_X emissions using a CO₂:NO_X emission ratio may thus seem appealing, but this approach is significantly limited by the high uncertainty in the emission ratios as determined from the same CO2M observations. The mass-balance approach studied here will be particularly useful for estimating emissions in countries where power plant emissions are not routinely monitored and reported. Further reducing the uncertainties will require the development of advanced atmospheric inversion systems for emission plumes and an improved constraint on the temporal variability of emissions using additional sources of information such as other satellite observations or energy demand statistics.

1 Introduction

The Paris Agreement on climate change aims to limit global warming to well below 2.0°C above pre-industrial temperatures (UNFCCC, 2015), which requires a rapid and drastic reduction in global carbon dioxide (CO₂) emissions in the coming decades (Rockström et al., 2017). The majority of anthropogenic CO₂ emissions is confined to emission hot spots such as large cities, power plants, and industrial facilities. To monitor the emissions of these hot spots and provide decision makers with independent atmospheric information, CO₂ observations from satellites with imaging capability have been identified as a critical component in a global CO₂ emission monitoring system, which aims at supporting the global stocktake agreed upon in the enhanced transparency framework (ETF) established as part of the Paris Agreement (Ciais et al., 2015; Pinty et al., 2018; Janssens-Maenhout et al., 2020).

Therefore, the European Commission and the European Space Agency (ESA), together with the European Organization for the Exploration of Meteorological Satellites (EUMETSAT) and the European Center for Medium-range Weather Forecasts (ECMWF), are preparing the Copernicus CO₂ Monitoring (CO2M) mission, which is envisioned as a constellation of satellites equipped with imaging spectrometers measuring CO₂, methane, and nitrogen dioxide (NO₂) along a 250 km wide swath with 4 km² spatial resolution (Sierk et al., 2019; ESA Earth and Mission Science Division, 2020). The satellites will carry additional supporting instruments for aerosols and clouds. The launch of the first satellite is planned for 2025 to contribute to the second global stocktake of 2028, which addresses the emissions of the year 2026.

Several observing system simulation experiments (OSSE) have been conducted to analyze the potential of CO₂ imaging spectrometers to quantify emissions of cities and large point sources (e.g., Bovensmann et al., 2010; Pillai et al., 2016; Broquet et al., 2018; Kuhlmann et al., 2019a; Hill and Nassar, 2019; Lespinas et al., 2020; Wang et al., 2020). Case studies have also shown the potential to estimate CO₂ emissions of point sources from the narrow swath of the Orbiting Carbon Observatory 2 (OCO-2, e.g., Nassar et al., 2017; Reuter et al., 2019; Wu et al., 2020; Zheng et al., 2020).

Point source emissions can be estimated directly from satellite observations in combination with wind information using different flavors of data-driven methods that, for example, fit a Gaussian plume or apply a mass-balance approach (e.g., Beirle et al., 2011; Fioletov et al., 2015; Varon et al., 2018; Lorente et al., 2019). The appeal of these methods is that they do not require performing expensive atmospheric transport simulations, which allows them to be applied globally to large amounts of satellite observations. However, a thorough understanding of the potential and limitations of these methods is still lacking, especially in connection with the CO2M NO₂ imaging spectrometer, which can be used either qualitatively to guide the detection of the CO₂ plumes (Reuter et al., 2019; Kuhlmann et al., 2019a; Kuhlmann et al., 2020a) or quantitatively by converting NO₂ emission estimates to CO₂ estimates applying an appropriate NO_x:CO₂ emission ratio (Reuter et al., 2014).

Mass-balance approaches have only been applied to a small number of emission plumes and are likely biased toward cases under favourable observation conditions, i.e., cloud-free scenes without complex turbulent flow and with low variability in the CO₂ background field due to other anthropogenic sources or biospheric fluxes. However, to quantify annual emissions, frequent estimates are crucial to reduce the uncertainties caused by hourly and daily fluctuations in emissions (Hill and Nassar, 2019). Consequently, all quantifiable plumes should be included for gaining a more representative annual estimate, even those derived under less optimal conditions, which may limit the individual accuracy of a mass balance approach (e.g., Kuhlmann et al., 2020a; Wolff et al., 2020).

In this study, we investigate how well point source emissions can be quantified with combined CO₂ and NO₂ images, whereas a large number of sources was considered under different observation conditions. The study is based on synthetic CO2M observations that were generated in the SMARTCARB project from high-resolution atmospheric transport simulations with the COSMO-GHG model. The observations were generated for a constellation of up to six CO2M satellites for a domain encompassing parts of Germany, Poland and the Czech Republic for the year 2015 (Brunner et al., 2019; Kuhlmann et al., 2019a; Kuhlmann et al., 2019b; Kuhlmann et al., 2020b). We estimate annual CO₂ emissions of 15 large power plants either directly from the CO₂ observations or indirectly from the NO₂ observations together with an estimate of the NO_x:CO₂ emission ratio. The individual emission plumes are detected using a plume detection algorithm and estimated using a mass-balance approach. The mass-balance approach was chosen, because it makes fewer assumptions about the shape of the plume than the Gaussian plume inversion. We furthermore investigate the potential impact of NO_x emission reductions expected in the future due to more stringent air quality regulations on the accuracy of CO₂ emission estimates.

The setup with synthetic observations and precisely known emissions presented here provides new insights into the main sources of uncertainty making it possible to analyze which factors are driving the uncertainty in these estimates, and how well annual mean emissions can be determined depending on the number of satellites in the CO2M constellation.

2 Data and Methods

2.1 Synthetic Satellite Observations

The study is based on synthetic satellite observations of the CO2M mission generated from atmospheric transport simulations. The simulations and synthetic observations are described in more detail in Brunner et al. (2019) and Kuhlmann et al. (2019a), and are publicly available: Kuhlmann et al. (2020b). Here, only the essential characteristics of the dataset are repeated briefly.

The imaging spectrometer on the CO2M satellites will sample along a 250-km wide swath with a pixel size of 4 km² (Sierk et al., 2019). It will retrieve column-averaged dry air mole fractions of CO₂ (XCO₂) from measurements in the near infrared (NIR) and shortwave infrared spectral range (SWIR) and NO₂ tropospheric column densities in the visible spectral range (Sierk et al., 2019; ESA Earth and Mission Science Division, 2020). The mission will also carry a Multi Angle Polarimeter (MAP) and Cloud Imager (CLIM) for measuring aerosols and clouds to better characterize the photon paths in order to minimize systematic errors in the trace gas retrievals (Rusli et al., 2021).

Atmospheric transport simulations of CO₂ and NO_x were performed with the COSMO-GHG model (Jähn et al., 2020) at about 1 km × 1 km resolution for a domain encompassing parts of Germany, Poland and the Czech Republic with hourly output for the whole year 2015 (Figure 1). Lateral boundary conditions, anthropogenic emissions and biospheric fluxes were accounted for in great detail, in order to generate a “nature run” of CO₂ and NO_x concentrations that should closely resemble true atmospheric conditions. For computational efficiency, NO_x was simulated as an idealized tracer with a constant exponential decay time of 4 h rather than explicitly accounting for its complex photochemistry.

FIGURE 1

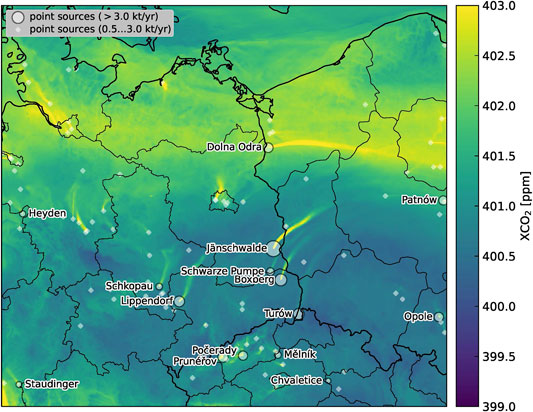
FIGURE 1. COSMO-GHG model domain with spatial distribution of the largest point sources (white dots). The image shows an example XCO₂ model field on November 2, 2015.

Synthetic observations were then generated from the high resolution simulations for a hypothetical constellation of six CO2M satellites using orbit simulations and applying different levels of noise according to different precision requirements as specified by ESA. The satellites were assumed to fly in a sun-synchronous orbit with an overpass time of 11:30 local time. In each constellation, satellites were spaced with equal angular distance in a common orbit. As an example, Figure 2 shows a constellation of six satellites. Constellations of two or three satellites could then be composed, for example, of the satellites “a” and “d” or “a”, “c” and “e”, respectively.

FIGURE 2

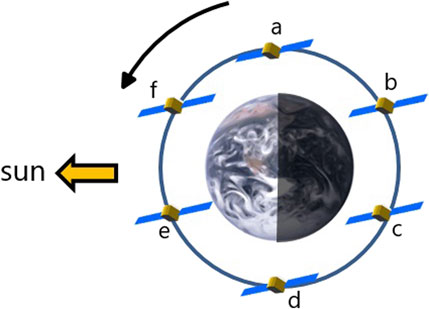
FIGURE 2. Sketch of a constellation of six CO2M satellites (a–f) equally spaced in a common sun-synchronous orbit.

To generate the synthetic observations of XCO₂ and tropospheric columns of NO₂, the simulated fields were sampled along the 250 km wide swath of the six orbits and mapped onto satellite pixels of the size of 2 km × 2 km. A low and high-noise instrument scenario was created for both the XCO₂ and ${\text{NO}}_2$ observations. For XCO₂, random noise was computed and added to the simulated XCO₂ pixel values using the error parametrization of Buchwitz et al. (2013) with a single sounding precision of 0.5 and 0.7 ppm, respectively, for a ground pixel with a spectral reflectance typical of vegetation and a solar zenith angle (SZA) of 50 (VEG50 scenario). XCO₂ random uncertainties were computed as a function of surface reflectance in NIR and SWIR channel and SZA. Systematic errors were not included. The NO₂ column densities were assumed to have a single sounding precision of 1.0 and 2.0 × 10¹⁵ molecules per cm⁻² for clear sky conditions and higher errors for cloudy scenes, approximately doubling at 30% cloud fraction. XCO₂ observations were rigorously filtered for clouds using a cloud threshold of 1%. A threshold of 30% was used for the NO₂ observations, which can tolerate larger cloud fractions. Cloud fractions were taken from the same COSMO-GHG simulation, which also produced the CO₂ and NO₂ fields.

2.2 CO₂ and NO_x Emissions of Point Sources

Plume detection and emission quantification was performed for the 15 largest point sources in the domain (all being power plants), which are labeled in Figure 1 by their names. Their annual mean CO₂ and NO_x emissions at satellite overpass time (10:30 UTC) as used in the simulations are listed in Table 1. The values are approximately 20% higher than true annual mean emissions due to the diurnal cycle of the emissions prescribed in the simulations and the CO2M overpass time. The three largest power plants have CO₂ emissions comparable or larger than those of the city of Berlin with 20 Mt yr⁻¹.

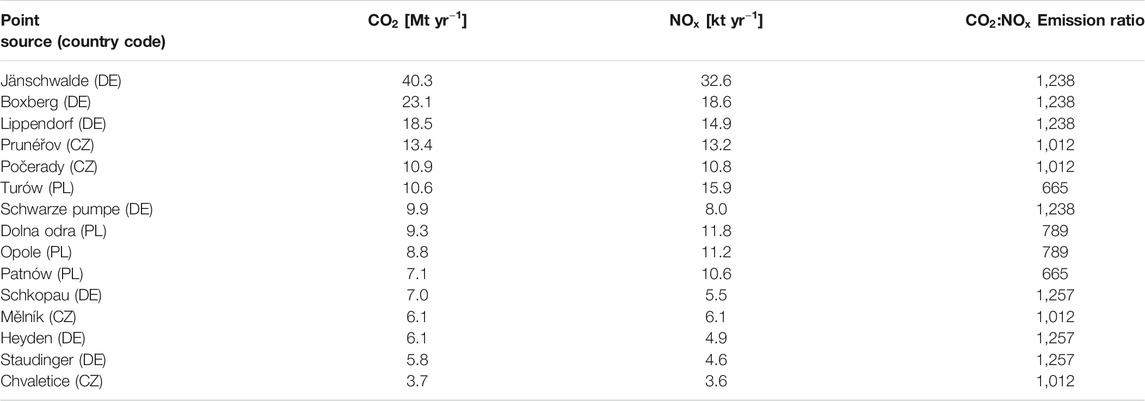
TABLE 1

TABLE 1. ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ source strengths at satellite overpass time (10:30 UTC) of the 15 largest point sources (>3.0 kt yr⁻¹ annual mean) in the study area according to the TNO/MACC-3 inventory. The values are total anthropogenic emissions in a COSMO grid cell (about 1 km × 1 km) and therefore can be somewhat higher than the emissions from the facilities alone if there were other sources present in the grid cell. These 15 point sources represent 28 and 17% of total ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ emissions in the model domain, respectively.

The CO₂ and NO_x emissions used in this study are based on the TNO/MACC-3 inventory for the year 2015. However, since 2017 a new EU regulation is in effect that requires a significant reduction of NO_x emissions for large combustion plants (European Commission, 2017, Table 3). For lignite-fuelled power plants, the regulation requires new plants built after ratification of the regulation to reduce NO_x concentrations in the flue gas to 50–85 mg m⁻³. Existing power plants need to reduce flue gas concentrations to <85–150 mg m⁻³ by 2021. NO_X concentrations of up to 200 mg m⁻³ were allowed prior to the new regulation.

Based on reported NO_x flue gas concentrations for German power plants (Tebert, 2017), we expect that for existing power plants NO_x emissions will be reduced by 20–50% compared to the emissions assumed in our simulations. Power plants built after 2017 would have even lower emissions up to a third of the assumed levels. To study the influence of a future reduction of NO_x emissions on our results, we scale anthropogenic NO_x fields in the simulations with factors of 0.3, 0.5, and 0.8.

Since CO₂ emissions are not affected by these regulations, CO₂:NO_X emission ratios will increase in the future. Table 1 shows that emission ratios (on a mass per mass basis) are considerably lower in the Czech Republic (CZ) and Poland (PL) than in Germany (DE), suggesting that stronger NO_X reductions will be required in these countries to fulfill the new regulation. Supplementary Table S1 shows emission ratios for 2015 and 2017 based on self-reported emissions published in the E-PRTR database in 2019. For many power plants higher emission ratios are reported for 2017 compared to 2015 and also compared to the ratios used in our study, likely because operators already started strengthening emission reduction procedures. Note that emissions of point sources in the TNO/MACC-3 inventory can deviate somewhat from the E-PRTR database, because emissions from point sources were scaled in TNO/MACC-3 to resolve discrepancies between national totals and the totals of all individual point sources within a country (H. Denier van der Gon, personal communication).

2.3 Plume Detection Algorithm

A first version of our plume detection algorithm was presented in Kuhlmann et al. (2019a). The algorithm identifies coherent structures of satellite pixels of CO₂ or NO₂ that are significantly enhanced above background, and assigns these structures to a source. Emission plumes can either be detected from CO₂ or from NO₂ observations. With the first version of our algorithm we could demonstrate that CO₂ emission plumes can be detected better from NO₂ observations due to their higher signal-to-noise ratio and lower sensitivity to clouds (Kuhlmann et al., 2019a).

An important limitation of the first version was that the background within the plume was derived from a simulated background tracer. It thus relied on information that would not be available from real satellite observations. Furthermore, the algorithm required a large degree of fine-tuning and visual control. In order to overcome these limitations, an improved version was developed here, which does not depend on model simulated background fields anymore. Furthermore, the algorithm can now detect a predefined list of sources instead of a single source, and automatically recognizes overlapping plumes originating from multiple sources.

The improved algorithm consists of four steps described in the following. In the first step, pixels significantly enhanced above background are detected based on a statistical test applied to the following signal-to-noise ratio (SNR):

$SNR=\frac{X_{\text{obs}}-X_{\text{bg}}}{\sqrt{{\sigma }_{\text{rand}}^2+{\sigma }_{\text{sys}}^2}}\ge z_q(1)$

where $X_{\text{obs}}$ is the satellite observation, $X_{\text{bg}}$ is the background field, ${\sigma }_{\text{rand}}$ and ${\sigma }_{\text{sys}}$ are the local random and systematic errors in the satellite image. The SNR can be used in a statistical z-test to compute the likelihood that the XCO₂ or NO₂ value of a pixel is enhanced above the background. $z_q$ is the threshold for which the SNR is significant with a probability q assuming that the test statistics can be approximated by a normal distribution (see Kuhlmann et al., 2019a, for details). In this study, the threshold $z_q$ was set to 2.33, which corresponds to a probability q of 0.99 that the XCO₂ or NO₂ value is significantly enhanced above the background.

Instead of taking $X_{\text{obs}}$ as the value of the satellite pixel alone, it is computed as a local mean averaged over surrounding pixels. In the first version of the algorithm, the local mean was computed using an uniform kernel with neighborhoods of different sizes. Here, a Gaussian kernel of width ${\sigma }_g$ is used instead, which has the advantage of providing a gentler and more adjustable smoothing making the algorithm more adaptable to different plume sizes.

In the first version of the algorithm, the background field was derived from a simulated background tracer. In the improved version, it is computed by applying a median filter to the satellite image. The filter computes the background as the local median in a 100 × 100 pixels window, assuming that the majority of pixels in the window consists of background pixels outside of the plume.

The random noise ${\sigma }_{\text{rand}}^2$ was taken from the single sounding precision of the XCO₂ or NO₂ observations. The systematic error ${\sigma }_{\text{sys}}^2$ can be interpreted as a threshold for variance in the background, e.g., caused by CO₂ variations due to biospheric fluxes, or also as a smallest possible error for a very large filter. In this study, ${\sigma }_{\text{sys}}$ was set to 0.2 ppm for XCO₂ and 0.5 × 10¹⁵ molecules per cm⁻² for NO₂ observations.

The threshold $z_q$ and the systematic error ${\sigma }_{\text{sys}}$ need to be carefully chosen to balance the requirements of detecting a sufficiently large number of pixels to be able to apply the mass-balance approach while avoiding the detection of many overlapping plumes and false detections. Avoiding false detection of pixels not belonging to the plume was particularly challenging in the presence of a spatial gradient in the background field. The values used here were found to be suitable for detecting power plant plumes (Kuhlmann et al., 2019a; Kuhlmann et al., 2019b).

In the second step, the detected pixels are grouped into regions (plumes). A standard labeling algorithm is used for this purpose. Enhanced pixels are considered connected if they are horizontal, vertical or diagonal neighbors.

In the third step, a region of enhanced pixels is assigned to a point source, if the pixels overlap with a circle of radius 5 km surrounding the source. The improved version of the algorithm is now able to detect and flag plumes, that actually represent overlapping plumes originating from multiple sources. For this purpose we created a list of all point sources in the model domain that have NO_x emissions larger than 3 kt yr⁻¹ based on the TNO/MACC-3 inventory. Figure 1 shows a map of the XNO₂ field simulated for November 3, 2015 and the location of the 15 largest sources.

In the fourth step, a centerline is fitted for each plume as a two-dimensional curve to the detected pixels. We include pixels outside of the plume within a distance of 5 km with low weight to make the fit more robust especially at the start and end of the plume. We also add the source location with high weight to force the centerline through that point. Finally, a polygon is drawn around the plume that follows the centerline and extends over the full width of the plume.

Figure 3 shows an example of the output of the algorithm. Longitude and latitude of the detected pixels are converted to a plume coordinate system consisting of arc length of the centerline from the source location and distance perpendicular to the centerline (see Kuhlmann et al., 2020a, for details). The width of the polygon corresponds to the maximum width of the detected plume rounded up to the next full 2 km. In along-plume direction, the polygon extends from the source to the end of the plume rounded up to the next full 5 km. The polygon is divided in 5 km wide sub-polygons in along-plume direction. In addition, a second polygon is drawn between 2 and 12 km upstream of the source that provides information about CO₂ values upstream of the source. The different polygons and sub-polygons are required for the mass-balance method as described below.

FIGURE 3

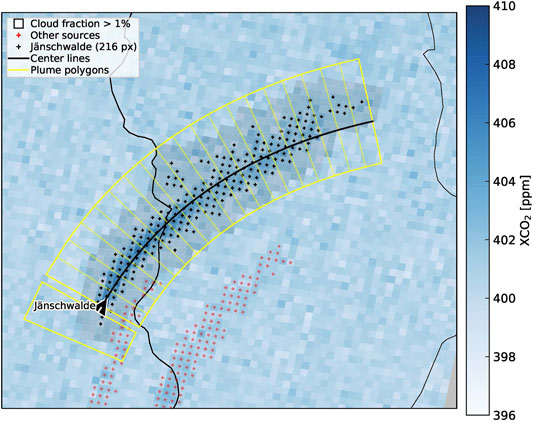
FIGURE 3. Sketch of detected CO₂ plume with detected pixels, center line, and the polygon up- and downstream of the source.

2.4 Mass-Balance Approach

Emissions of a source can be estimated as the difference between the mass flux into and out of a volume containing the source. Here, fluxes out of the volume were computed as the fluxes through the sub-polygons determined by the plume detection algorithm downstream of the source. Under the assumption of steady-state conditions, this is equivalent to the emission, since the inflow upstream of the source is zero if we only consider enhancements above background. The only additional information that cannot be deduced from the satellite observations is an estimate of the wind speed inside the plume.

The fluxes are the product of line densities and wind speed. Line densities (units of kg m⁻¹) are computed by integrating total column densities (units of kg m⁻²) perpendicular to the plume’s centerline. To obtain the column densities attributable to the source, the background field needs to be subtracted. The background was estimated from the pixels surrounding the plume assuming that it is a spatially smooth field. For this purpose, the detected pixels of the plume as well as other pixels marked as significantly enhanced above background by the plume detection algorithm were removed. The resulting gaps were then filled using normalized convolution with a Gaussian filter of width σ = 10 pixels. To have a consistent method for the estimation of CO₂ and NO_x emissions, we always compute the CO₂ and NO₂ background from the same detected pixels.

Note that the plume detection algorithm already required an estimation of the CO₂ or NO₂ background field. However, the background levels computed by that more simple algorithm were found to be generally overestimated (as compared to the true simulated background). Using that background would therefore result in an underestimation of the CO₂ emissions.

After subtracting the background, line densities were computed by integrating the column densities in across-plume direction. To maximize the usage of information contained in the image, this was done for all sub-polygons every 5 km along the plume (Figure 3) by fitting a Gaussian curve

$c_p\left(y\right)=\frac{q}{\sqrt{2\pi }\sigma }\text{exp}\left(-\frac{{\left(y-\mu \right)}^2}{2{\sigma }^2}\right)(2)$

with total column density enhancement in the plume $c_p$, line density q, shift μ and standard width σ. The ${\text{CO}}_2$ and ${\text{NO}}_2$ enhancements were fitted simultaneously to share the same position (shift) and standard width of the Gaussian curve. Since relative uncertainties are smaller for ${\text{NO}}_2$ than for ${\text{CO}}_2$, the ${\text{NO}}_2$ observations effectively constrain these parameters. Only ${\text{NO}}_2$ column densities were fitted when no ${\text{CO}}_2$ observations were available, for example, due to cloud cover. To avoid misfits the computed flux was used only if at least one observation was available every 5 km in across-plume direction over the full width of the detected plume.

To convert line densities into a flux, the effective transport wind speed u of the plume is required. This wind speed should correspond to the mean speed of horizontal transport of the tracer and therefore needs to account for different flow speeds at different altitudes. Since the vertical distribution of the mass of the emitted tracer cannot be deduced from the satellite observations and will usually not be known, simplified assumptions have to be made. Here, we assume that the distribution corresponds to the vertical emission profile for combustion in the energy sector (SNAP-1). This profile was used in the simulations for most power plants except for some of the largest ones (Boxberg, Jänschwalde, Lippendorf, Schwarze Pumpe, Turów, Patnów), for which plume rise was computed explicitly (Brunner et al., 2019). With this assumption, the wind speed was computed as the vertically averaged horizontal wind speed (from the COSMO-GHG model) at the source location and at the time of the overpass weighted by the SNAP-1 emission profile.

For ${\text{CO}}_2$, the fluxes computed for all individual sub-polygons were averaged to obtain an estimate of the mean source strength. To obtain ${\text{NO}}_{\text{x}}$ emissions from ${\text{NO}}_2$ observations, we have to account for the chemical depletion of ${\text{NO}}_{\text{x}}$ downwind of the source and for the fact that only a fraction of ${\text{NO}}_{\text{x}}$ is available as ${\text{NO}}_2$. The ${\text{NO}}_{\text{x}}$ flux therefore depends on plume distance as

$Q\left(x\right)=f\cdot Q_0\cdot \text{exp}\left(-\frac{x}{u\cdot \tau }\right)\text{if}x>0(3)$

with ${\text{NO}}_2$:${\text{NO}}_{\text{x}}$ conversion factor f, wind speed u, chemical lifetime τ, and source strength $Q_0$. The conversion factor f was set to a constant value of 1.32 following the suggestion of Beirle et al. (2011). The source strength $Q_0$ and the lifetime τ were obtained by fitting a curve to the individual fluxes $Q\left(x\right)$. True decay times in the atmosphere are expected to vary between about one and several hours. In our simulations, the decay time was set to a constant value of 4 h. If the number of polygons was insufficient for fitting a lifetime, we estimated the ${\text{NO}}_{\text{x}}$ emissions only from the two polygons closest to the source assuming that no decay occurred over this short distance.

Equations 2, 3 were solved using the trust region reflective algorithm (Branch et al., 1999) implemented in the Python Scipy library (Version 1.4.1, Virtanen et al., 2020). The algorithm allows defining bounds for the fitting parameters, which was used to avoid negative line densities and emissions (see Supplementary Table S2 in the supplement).

Several checks have been implemented to avoid erroneous detection and correspondingly wrong emission estimates. The criteria have been chosen to be easily applicable to real observations and to avoid visual inspection of the results as much as possible. The checks are the following:

• Plumes are not used when they overlap more than one source.

• Plumes are not used when the direction of the center curve and the wind direction disagree by more than ± 45°.

• Plumes are not used when the “upstream polygon” contains more than five detected plume pixels. This criterion removes cases where the plume overlaps with an upstream source that is outside the swath or covered by clouds.

• Line densities are not computed for polygons that do not have valid satellite observations inside the detected plume every 5 km in across plume direction. The criterion removes misfits when observations near the plume center are missing.

• Line densities are not computed when the sub-polygon is not fully inside the swath.

• Line densities or fitted emissions are not used when the curve fit failed, because the number of observations/fluxes was too small or their uncertainties were too large.

2.5 Uncertainties

Uncertainties of the mass-balance approach are caused by instrument noise, uncertainties in the effective transport wind speed, uncertainties in estimating the background, and a general “methodological uncertainty” such as the assumption of steady-state conditions.

Since the number of successful estimates is relatively small and varies strongly between the sources, we tested and compared several different ways of estimating the systematic and random uncertainties. The first approach is based on comparing the estimated emissions to the true emissions, which are known in our synthetic model framework but would not be known in reality. Differences between estimated and true emissions were used to compute a median bias (MB) and standard deviation (SD). Relative values were computed by dividing by the mean emissions at satellite overpass time (10:30 UTC). Since the differences are not necessarily normally distributed, we computed the 16–84th percentile range (PR) and divided this range by two to be comparable with the standard deviation.

In a second approach, which is also applicable to real observations without knowledge of the true emissions, the uncertainty is computed by error propagation from the uncertainties in line density ${\sigma }_{q_0}$ and wind speed ${\sigma }_u$

${\sigma }_Q=\sqrt{{\sigma }_{q_0}^2\cdot u^2+{\sigma }_u^2\cdot {\left(\frac{Q}{u}\right)}^2}(4)$

Here, ${\sigma }_{q_0}$ is the uncertainty of the line density at the source (x = 0), which is estimated as the standard error of the mean of the individual line densities estimated for the individual polygons. This largely captures the influence of instrument noise which affects the accuracy of the computed line densities. Larger plumes allow estimating the emissions from a larger number of polygons and each polygon may extend over more pixels in across plume direction, which reduces the uncertainty. For wind speed we assume a fixed uncertainty of ${\sigma }_u=0.5\mathrm{m}{\mathrm{s}}^{\mathrm{-1}}$, which is a typical uncertainty of the wind field in a global meteorological analysis product (Martin et al., 2021).

Additional uncertainties due methodological and background errors are difficult to quantify. In order to provide a realistic estimate of the overall uncertainty, we add to the emission uncertainty described in Eq. 4 a constant factor m proportional to the emission strength and add an offset b, so that the overall uncertainty is consistent with the PRs estimated by the first approach. PRs are used because SDs overestimate the variance of the estimates due to outliers. The uncertainty is then given by

$s_Q=\sqrt{{\sigma }_Q^2+{\left(Q\cdot m+b\right)}^2}(5)$

where Q is the ${\text{CO}}_2$ or ${\text{NO}}_{\text{x}}$ annual mean emissions at overpass time.

Estimating the uncertainty of the ${\text{CO}}_2$:${\text{NO}}_{\text{x}}$ emission ratios is more challenging. Standard error propagation relying on Gaussian errors does not work in this case, because the distribution of the ratios is heavy-tailed. We therefore estimate the uncertainty as the standard deviation of the individually estimated ratios.

2.6 Annual Emissions and Emission Ratios

The accuracy of an annual mean estimate derived from individual overpasses on a small number of days depends critically on how well the temporal variability of emissions is captured. In this study, the COSMO-GHG simulations used hourly emission fields as input, which were derived from annual emissions using fixed diurnal, weekly and seasonal time profiles (see Supplementary Figure S2) for the different source categories of the Selected Nomenclature for Air Pollution (SNAP) (Pouliot et al., 2012; Jähn et al., 2020). At satellite overpass, both ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ emissions from power plants are about 20% higher than the daily mean. The weekly cycle has a reduction by about 20% on weekends and the seasonal emissions are about 20% higher than the annual mean in winter and about 20% lower in summer. However, real hour-to-hour and day-to-day variability is expected to deviate significantly from these mean temporal profiles depending on actual energy demands (e.g., Nassar et al., 2013; Hill and Nassar, 2019; Super et al., 2020).

Annual emissions were obtained by fitting a low order C-spline to the individual estimates collected by all satellites present in a constellation of a given size. We used periodic boundary conditions to smoothly connect the end and the beginning of the year. The fitted curve is then integrated to obtain annual emissions. Their uncertainties are estimated by error propagation from the random uncertainties of the individual estimates. The low-order spline accounts for a seasonal cycle varying slowly with time but does not account for more rapid day-to-day variability.

Since CO2M is in a sun-synchronous orbit with fixed overpass time, individual estimates are only representative of emissions a few hours before the satellite overpass but not for the daily mean (Broquet et al., 2018). It is therefore necessary to apply a correction factor to obtain true annual mean emissions, which introduces an additional source of uncertainty. We assume here that a mean diurnal cycle can be obtained from electricity demand statistics or other observations (e.g., ground-based monitoring networks or geostationary satellites), while deviations from such a mean behavior need to be accounted for in the uncertainty budget.

Hill and Nassar (2019) analyzed the hour-to-hour and day-to-day variability of emissions for the 50 largest power plants in the United States. They found that after subtracting a mean seasonal and diurnal cycle, the remaining hour-to-hour $s_h$ and day-to-day $s_d$ variabilities were 28.7 and 31.0%, respectively. We use these values to estimate the uncertainty associated with the temporal variability. Since these variations were computed after subtracting a mean diurnal and seasonal cycle, we implicitly assume that a mean cycle can be obtained accurately. To compute the overall relative uncertainty ${\sigma }_Q$, we assume that the errors are independent and reduce with the number of successful estimates n:

${\sigma }_Q=\sqrt{s_Q^2+\frac{s_d^2}{n}+\frac{s_h^2}{n}}(6)$

where $s_Q$ is the estimated (relative) uncertainty obtained from integrating the seasonal cycle, $s_d$ the day-to-day and $s_h$ the hour-to-hour uncertainty (Hill and Nassar, 2019).

Note that we do not apply any sampling bias correction factor for the diurnal cycle but compare with the annual mean emissions at satellite overpass. Since our results (e.g., detection threshold and uncertainties) depend on the emission strength at overpass, this makes it easier to generalize our results in case diurnal cycles are different.

2.7 Quantitative Usage of NO₂ Observations

Since ${\text{NO}}_2$ observations will be available from the CO2M mission with much higher accuracy and better temporal coverage due to the lower sensitivity to clouds, it is appealing to use ${\text{NO}}_{\text{x}}$ emission estimates quantitatively to estimate ${\text{CO}}_2$ emissions. We tested this idea by deriving ${\text{CO}}_2$ emissions directly from satellite ${\text{NO}}_2$ measurements and applying a constant ${\text{CO}}_2$:${\text{NO}}_{\text{x}}$ emission ratio computed from those overpasses, where both ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ emissions could be estimated reliably. Since ratios are very sensitive to outliers, especially when ${\text{NO}}_{\text{x}}$ estimates are close to zero, we filter the time series of ratios for outliers more than 1.5× outside the interquartile range (25th–75th percentile).

The emission ratio is used to convert the estimated annual ${\text{NO}}_{\text{x}}$ emissions to ${\text{CO}}_2$ emissions. The uncertainty of the emission ratio is computed from the scatter of the individual estimates. Annual mean ratios were used because individual estimates are too uncertain. For comparison, we also compute ${\text{CO}}_2$ emissions from ${\text{NO}}_{\text{x}}$ estimates using the true emission ratio taken from the bottom-up inventory.

3 Results

3.1 Example of Individual CO₂ and NO_x Emission Estimates

Figure 4 shows examples of detected plumes from ${\text{CO}}_2$ observations with low noise (${\sigma }_{\text{VEG}50}$ = 0.5 ppm) and ${\text{NO}}_2$ observations with high noise (${\sigma }_{\text{ref}}$ = 2 × 10¹⁵ cm^–2) on November 2, 2015, which was mostly cloud-free, a situation that is actually quite rare. With the ${\text{NO}}_2$ observations, all nine plumes in the swath are detected, whereas only six plumes are detected with the ${\text{CO}}_2$ observations and the plumes are also smaller and shorter. True and false positive rates of the plume detection algorithm depend on the parameters used in the algorithm (Eq. 1), i.e., threshold $z_q$, systematic error ${\sigma }_{\text{sys}}$, width of Gaussian filter used for computing the local mean ${\sigma }_g$, and size of the neighborhood $n_{\text{bg}}$ used for computing the background field. The parameters used here worked well in general but were not optimized to maximize the number of detectable plumes. The number of detected pixels can be increased using a lower threshold $z_q$ or a lower systematic error ${\sigma }_{\text{sys}}$. However, this will increase the number of overlapping plumes (e.g., Boxberg, Jänschwalde and Schwarze Pumpe) and the number of false positives. In the worst case it can even cause a whole region to be marked as detected when background variability is very high (e.q., in the northwestern Czech Republic).

FIGURE 4

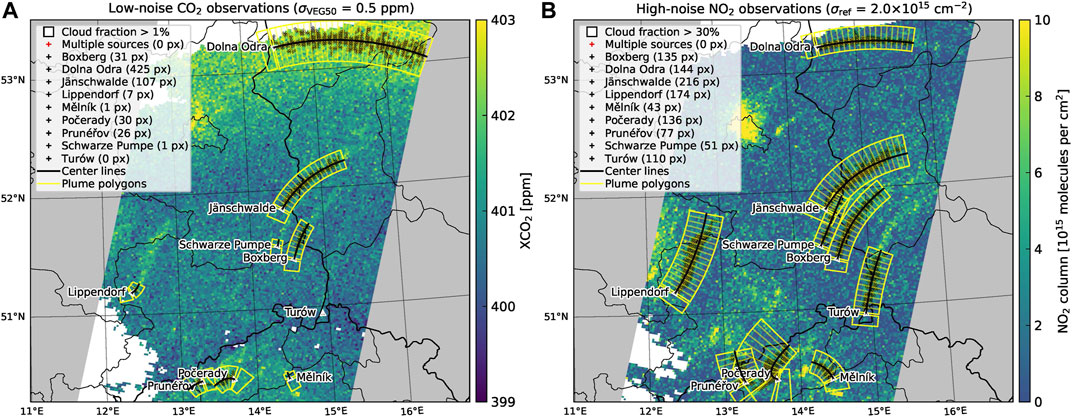
FIGURE 4. Comparing plume detection using (A) CO₂ observations with low noise (${\sigma }_{\text{VEG}50}$ = 0.5 ppm) and (B) NO₂ observations with high noise (${\sigma }_{\text{ref}}$ = 2 × 10¹⁵ cm⁻²). The triangular marker shows the location of the source and the wind direction in the model field. The bright yellow region in the central top left of panel B is the city of Berlin.

Figure 5 shows an example of the application of the mass-balance approach for the coal-fired power plant near Mělník (CZ). The true ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ emissions of the point source at satellite overpass are 7.4 Mt yr^–1 and 7.2 kt yr^–1, respectively, resulting in a ${\text{CO}}_2$:${\text{NO}}_{\text{x}}$ emission ratio of about 1,028. The example is based on high-noise ${\text{CO}}_2$ and ${\text{NO}}_2$ observations. While the plume appears quite isolated in the ${\text{CO}}_2$ observations (Figure 5A), the ${\text{NO}}_2$ image shows several smaller point sources in the vicinity (Figure 5B) which, however, do not overlap with the power plant plume.

FIGURE 5

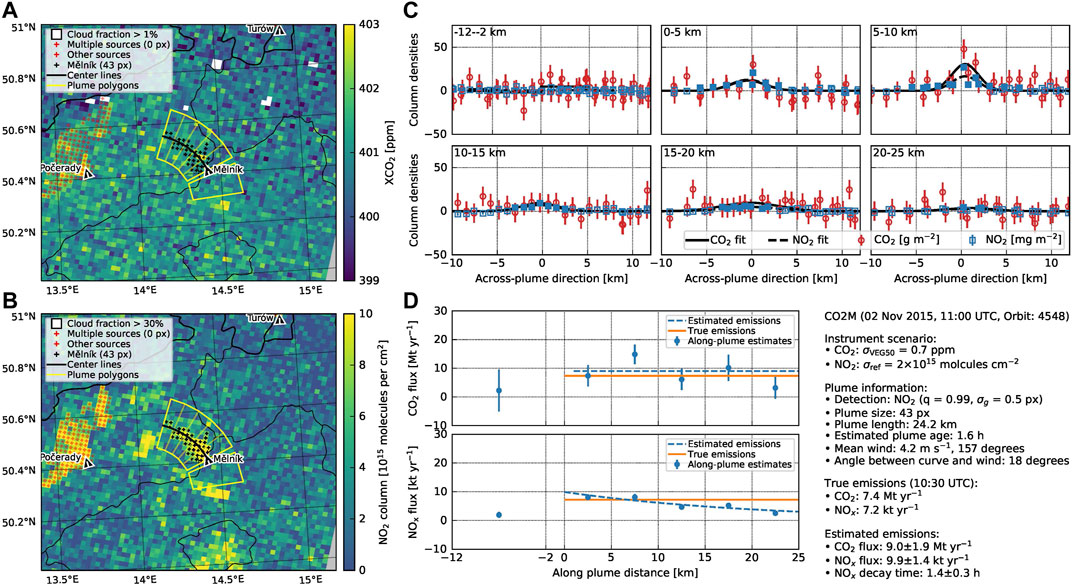
FIGURE 5. Exemplary application of the mass balance approach for the point source near Mělník (CZ). (A) CO₂ and (B) NO₂ satellite image with detected plumes and polygons for computing line densities. (C) Across plume CO₂ and NO₂ values for the six polygons and fitted Gaussian curves. (D) CO₂ and NO_x fluxes along the centerline and estimated CO₂ and NO_x emissions.

The centerline was fitted to the 43 satellite pixels of the detected ${\text{NO}}_2$ plume. The length of the plume is 24 km and the width is roughly 10 km. Since the wind speed in this case was about 4.2 m s^–1, the oldest ${\text{CO}}_2$ at the end of the plume was emitted about 1.6 h ago. The center curve and the wind direction are in good agreement with a discrepancy of only 18°.

The plume length of 24 km allows drawing five polygons for subsequent mass balance analysis. Figure 5C shows ${\text{CO}}_2$ and ${\text{NO}}_2$ observations in these five polygons and in the polygon upstream of the source. The computed ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ fluxes and their uncertainties are shown in Figure 5D. Note that only uncertainties in satellite observations and wind speed are included in the error bars. The ${\text{CO}}_2$ fluxes are close to zero upstream of the source as expected and increase to 9.0 ± 1.9 Mt yr^–1 downstream in good agreement with the true emissions of 7.4 Mt yr^–1. In contrast to ${\text{CO}}_2$, the ${\text{NO}}_{\text{x}}$ fluxes decay with distance from the source. The estimated emissions are about 40% larger than the true emissions in this example. The estimated decay time of 1.2 ± 0.3 h is lower than the true decay time of 4 h. The uncertainties of individual estimates are discussed in detail in Section 3.3.

3.2 Number of Successful CO₂ and NO_x Emission Estimates

The number of successful ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ emission estimates per year is an important factor determining how well annual mean emissions can be quantified (Hill and Nassar, 2019). Since the plumes are detected from the ${\text{NO}}_2$ observations, the number depends not only on the number of cloud-free overpasses but also on the ${\text{NO}}_{\text{x}}$ emission strength. Figure 6 shows the number of detected plumes per source from which ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ emissions could be estimated successfully plotted against the ${\text{NO}}_{\text{x}}$ emission of the source.

FIGURE 6

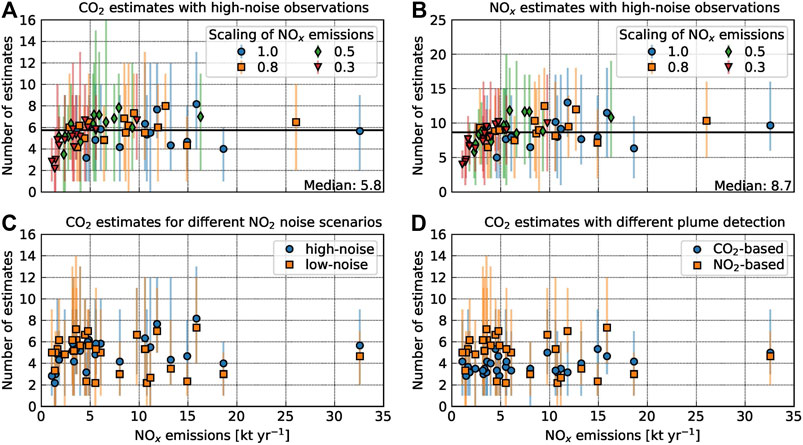
FIGURE 6. Number of successful (A)${\text{CO}}_2$ and (B)${\text{NO}}_{\text{x}}$ emission estimates per satellite and year for different ${\text{NO}}_{\text{x}}$ emission strengths using the high-noise scenarios for both species. The markers denote the median for a constellation of six satellites and the error bars the range for individual satellites. The horizontal line shows the median for all sources. The different markers and colors indicate the scaling applied to the ${\text{NO}}_{\text{x}}$ emissions. Panel (C) shows the number successful ${\text{CO}}_2$ estimates from plumes detected from low-and high-noise ${\text{NO}}_2$ observations and panel (D) shows the number of ${\text{CO}}_2$ estimates when either low-noise ${\text{CO}}_2$ or ${\text{NO}}_2$ observations are used for detecting the plumes.

Figure 6A shows the number of successful ${\text{CO}}_2$ emission estimates for high-noise ${\text{CO}}_2$ and ${\text{NO}}_2$ observations. The median number of successful estimates per source and satellite is about six. The scatter of this number is quite large because of the different temporal and spatial coverage of the different satellites. The number of successful estimates drops by about 50% for ${\text{NO}}_{\text{x}}$ emissions smaller than 3 kt yr^–1. For the strongest ${\text{NO}}_{\text{x}}$ reduction scenario (scaling factor: 0.3), nine out of the 15 power plants would still have emissions larger than 3 kt yr^–1.

For these weak ${\text{NO}}_{\text{x}}$ sources (<3 kt yr^–1), low-noise ${\text{NO}}_2$ observations would be better suited. Figure 6C shows that the number of estimates remains roughly the same even for the weakest sources when low-noise ${\text{NO}}_2$ observations are available. Surprisingly, the number gets smaller when using low-noise ${\text{NO}}_2$ observations for some sources. These sources are in close vicinity of other sources (e.g., Boxberg and Schwarze Pumpe), so that the larger plumes detected with the low-noise instrument are more likely to overlap with neighboring plumes and are therefore discarded by the algorithm. Note that this issue could be overcome by increasing the threshold $z_q$ for specific point sources or regions.

The number of successful ${\text{CO}}_2$ estimates is lower when the plumes are detected from the low-noise ${\text{CO}}_2$ observations instead of low-noise ${\text{NO}}_2$ observations (Figure 6D), because ${\text{CO}}_2$ observations are more affected by clouds and are less pronounced above the background levels.

The number of successful estimates of ${\text{NO}}_{\text{x}}$ emissions is about 50% larger than for ${\text{CO}}_2$ (Figure 6B), because emission quantification is also possible for partly cloudy scenes as ${\text{NO}}_2$ observations have a lower sensitivity to clouds. As for ${\text{CO}}_2$ detection, the number of estimates drops by about 50% for weak sources (<3 kt yr^–1). When plumes are detected from low-noise ${\text{NO}}_2$ observations instead, the numbers remain similar but they do not drop anymore for the weakest sources (not shown). For some non-isolated plumes, the number of successful estimates is again reduced because of more overlapping plumes.

3.3 Uncertainty of Individual Emission Estimates

The total estimated random uncertainties were computed with Eq. 5. The median uncertainties obtained from the mass-balance algorithm ${\sigma }_Q$ were scaled to match the PRs of the time series using a slope of m = 34% and an intercept of b = 0.33 Mt yr^–1 for ${\text{CO}}_2$ emissions and a slope of m = 28% and an intercept of b = 0.54 kt yr^–1 for ${\text{NO}}_{\text{x}}$ emissions (Supplementary Figure S1). The resulting median estimated random uncertainties are shown in Figures 7A,B. The uncertainties increase linearly with source strength, which is mostly a consequence of linear term quantifying methodological and background uncertainties in Eq. 5. For ${\text{CO}}_2$ emissions, the uncertainty is 31% of the source strength plus an offset of 2.0 Mt yr^–1. For ${\text{NO}}_{\text{x}}$ emissions, the uncertainty is similarly 29% with a smaller offset of 0.8 kt yr^–1. Uncertainties of individual ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ estimates have a wide range from 39 to 150% and 33–116% (10–90th percentile), respectively.

FIGURE 7

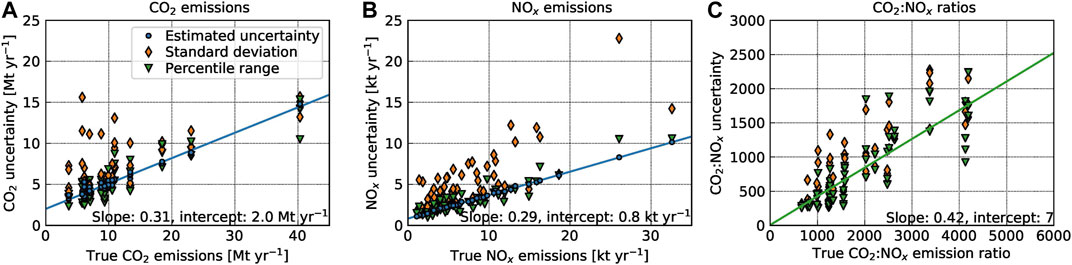
FIGURE 7. Random uncertainty of estimated (A)${\text{CO}}_2$ and (B)${\text{NO}}_{\text{x}}$ emissions as well as (C)${\text{CO}}_2$:${\text{NO}}_{\text{x}}$ emission ratios using different measures. Standard deviation and percentile range were computed from the differences between estimated and true emissions. Regression lines were fitted to estimated uncertainties (panel A and B) and percentile ranges (panel C) to obtain slope and intercept.

For weak sources (<10 Mt yr^–1), the total ${\text{CO}}_2$ uncertainty is dominated by the uncertainties in ${\text{XCO}}_2$ observations (35–72%), because emission plumes of weak sources are generally small with less than 100 pixels. The additional scaling of uncertainties accounts for 25–65% of the total uncertainty. For strong sources (>10 Mt yr^–1), uncertainties of ${\text{XCO}}_2$ observations only account for 2–44% due to the larger plumes, while the additional scaling accounts for 54–94%. Wind speed uncertainty contributes less than 5% to the total uncertainty. This component only includes uncertainties in the simulated wind speeds, but not possible deviations between wind direction and plume centerline or wind speed errors due to uncertainties in the plume injection height. These sources of uncertainty are included in the additional scaling factor, which also accounts for other methodological uncertainties. For example, some plumes were found to exhibit a highly turbulent behavior with puff-like structures and meandering paths that cannot be described well by our approach. Furthermore, our approach assumes that the ${\text{CO}}_2$ background is spatially smooth, while the true ${\text{CO}}_2$ background may deviate from this assumption due to other anthropogenic sources and biospheric fluxes. These deviations can be a significant source of uncertainty as shown for the city of Berlin (Kuhlmann et al., 2020a).

For ${\text{NO}}_{\text{x}}$ emission estimates, the uncertainties contributed by the ${\text{NO}}_2$ observations and the wind speed are only in the range 1–23% and 4–10%, respectively. A large fraction of the total uncertainty is due to other factors as indicated by the rather large contribution of the scaling factor with 72–93%. The contribution of the ${\text{NO}}_2$ uncertainty increases to 3–38% when ${\text{NO}}_{\text{x}}$ emissions are scaled by 0.3.

Figure 7C shows SDs and PRs of the individual ${\text{CO}}_2$:${\text{NO}}_{\text{x}}$ emission ratios for the fifteen power plant sources. The relative uncertainty is about 42% for a ratio of 1,000 with an intercept close to zero.

The ${\text{CO}}_2$ emissions can be over-or underestimated varying between −25 and +42% (median bias) with +9% on average. The ${\text{NO}}_{\text{x}}$ emissions are all overestimated by 26% on average (range: 8–47%). The most likely reason is that the assumed constant ${\text{NO}}_2$:${\text{NO}}_{\text{x}}$ conversion factor f of 1.32 taken from literature is a too strong simplification, which is also not consistent with the way ${\text{NO}}_{\text{x}}$ was treated in our simulations. In these, the ${\text{NO}}_2$ to $\text{NO}$ ratio was assumed to depend solely on the total ${\text{NO}}_{\text{x}}$ concentration following Düring et al. (2011). Since the relation is not linear, it cannot be applied to total columns. Emission ratios are underestimated because ${\text{NO}}_{\text{x}}$ emissions were overestimated by 14% (range: −53 to +7%).

3.4 Distribution of Emission Estimates Over the Year

How well annual mean emissions can be quantified depends on the number of individual estimates available during a year and on how well they capture temporal variability including the seasonal cycle of emissions. As an example, Figure 8 shows the time series of estimates of ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ emissions for the Jänschwalde and Mělník power plants for a constellation of three satellites. The black lines show the true emissions at satellite overpass time (10:30 UTC). The weekly and seasonal cycle is clearly visible in the true emissions. Since ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ emissions from power plants have the same time profiles, the ${\text{CO}}_2$:${\text{NO}}_{\text{x}}$ emission ratios do not depend on time in our simulations. However, since the true emissions were computed as the sum of all emissions in the 1 km × 1 km cell of the model grid, which may include emissions from other sectors with different ${\text{CO}}_2$:${\text{NO}}_{\text{x}}$ ratios, the ratios may show a weak temporal variability. This is true for the relatively weak point source at Mělník, whereas the strong point source at Jänschwalde has no time-dependent emission ratios.

FIGURE 8

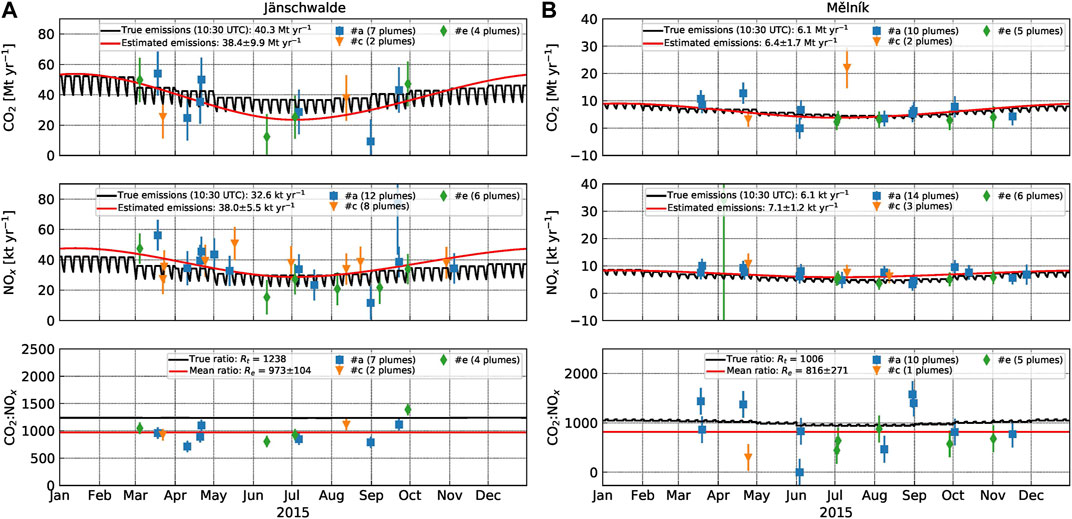
FIGURE 8. Time series of estimated ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ emissions and ${\text{CO}}_2$:${\text{NO}}_{\text{x}}$ emission ratios at (A) Jänschwalde and (B) Mělník for a constellation of three satellites for high-noise ${\text{CO}}_2$ and ${\text{NO}}_2$ observations. The different colored markers denote the satellite in the constellation.

At Jänschwalde, 13 successful ${\text{CO}}_2$ and 26 ${\text{NO}}_{\text{x}}$ estimates are available with a large spread from 2 to 7 ${\text{CO}}_2$ estimates for individual satellites. At Mělník, the numbers are 17 and 23 successful ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ estimates, respectively. For both point sources, temporal coverage is low in winter due to frequent cloud cover resulting in zero successful estimates for this constellation. The number of individual estimates of ${\text{CO}}_2$:${\text{NO}}_{\text{x}}$ emission ratios is driven by, and hence equal to, the number of ${\text{CO}}_2$ estimates. The number can be smaller in rare cases when the ${\text{NO}}_{\text{x}}$ decay time could not be estimated reliably. Since ratios are very sensitive to outliers, especially when ${\text{NO}}_{\text{x}}$ estimates are close to zero, we also filter the time series for outliers that are more than 1.5× outside the interquartile range (25th–75th percentile).

As mentioned above, the annual mean emissions were computed by integrating the C-spline fitted to the individual estimates. At Mělník, the shape of the seasonal cycle is fitted well. The annual ${\text{CO}}_2$ and NO_x emissions are estimated to 6.4 ± 1.7 Mt yr^–1 and 7.1 ± 1.2 kt yr^–1 agreeing with the true emissions within the estimated uncertainties. At Jänschwalde, the lack of estimates in winter results in an overestimation in winter, but again the annual mean emissions agree with the true emissions within the estimated uncertainties. The ratios were estimated as 816 ± 271 (33%) for Mělník and 973 ± 104 (11%) for Jäschwalde. Their uncertainties were computed from the goodness of the fit.

3.5 Annual Emissions

Figure 9 compares annual mean estimates obtained for all 15 power plants with true annual emissions at satellite overpass (10:30 UTC) for high-noise ${\text{CO}}_2$ and ${\text{NO}}_2$ observations. The small markers show the individual results for the 20 different constellations of three satellites that could be constructed from the six simulated satellites (a–f). The large marker shows the median of all 20 combinations and its estimated uncertainty. Regression lines were fitted for the median and for the individual constellations.

FIGURE 9

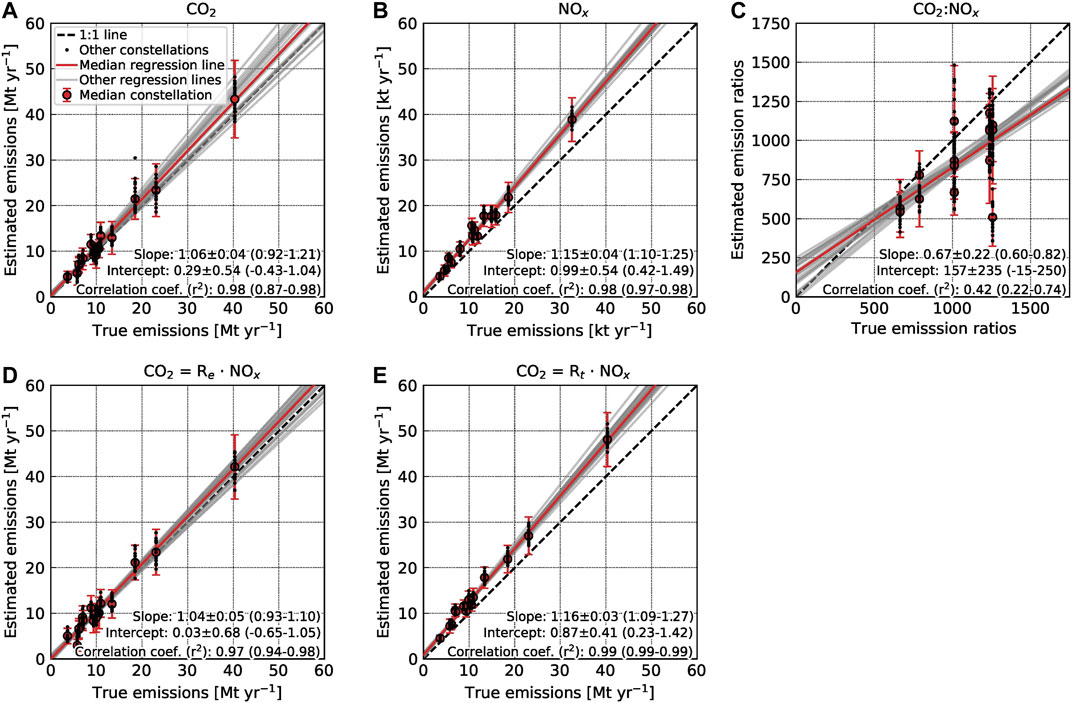
FIGURE 9. Annual estimates of (A)${\text{CO}}_2$ and (B)${\text{NO}}_{\text{x}}$ emissions and (C) emission ratios for a constellation of three satellites for the 15 largest point sources in the model domain with high-noise ${\text{CO}}_2$ and ${\text{NO}}_2$ observations. In addition, ${\text{CO}}_2$ emissions were obtained from (D) the annual ${\text{NO}}_{\text{x}}$ emissions using an estimated emissions ratio $R_e$ and (E) the true emission ratio $R_t$ used in the simulations. Large markers show the median constellation and small markers the 20 possible combinations of three satellites that could be constructed as permutations of the six simulated satellites. Regression lines were fitted to the median as well as to the individual constellations. Slope, intercept and Pearson correlation coefficient $r^2$ are displayed for the median and for the range of the 20 constellations. True emissions correspond to emissions at satellite overpass at 10:30 UTC.

The ${\text{CO}}_2$ emissions correlate very well with the true emissions with a Pearson correlation coefficient ($r^2$) ranging from 0.87 to 0.98, a slope ranging from 0.92 to 1.21, and an intercept slightly larger than zero (Figure 9A). ${\text{NO}}_{\text{x}}$ emissions correlate even better with $r^2$ ranging from 0.97 to 0.98, but emissions are slightly overestimated (Figure 9B). It should be noted that this comparison does not include uncertainties from hour-to-hour and day-to-day variability of emissions, because these factors were not included in our simulations.

Figure 9C compares the estimated annual mean ratios with the true emission ratios. The correlation between estimated and true emission ratios is quite low with $r^2$ ranging from 0.22 to 0.74. The ratios were underestimated due to overestimated ${\text{NO}}_{\text{x}}$ emissions.

Figures 9D,E compare ${\text{CO}}_2$ emissions estimated from ${\text{NO}}_{\text{x}}$ emissions using either the estimated emission ratio $R_e$ or the true ratio $R_t$. When the estimated ratios are used, correlation is high with $r^2$ ranging from 0.94 to 0.98 and a slope ranging from 0.93 to 1.10. Since ${\text{NO}}_{\text{x}}$ emissions were overestimated and ratios were underestimated, estimated ${\text{CO}}_2$ emissions have only a small bias. When using the true emission ratio, the positive bias of the ${\text{NO}}_{\text{x}}$ emissions carries over to the ${\text{CO}}_2$ emissions resulting in an overestimation of the ${\text{CO}}_2$ emissions. The correlation coefficient, on the other hand, is higher with $r^2$ of 0.99, because ${\text{NO}}_{\text{x}}$ emissions were estimated with higher accuracy than ${\text{CO}}_2$ emissions due to the lower uncertainty of individual estimates and the larger number of successful estimates.

Figure 10 shows the estimated uncertainty of annual ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ emissions for the 15 power plants for constellations of either two or three CO2M satellites. The markers denote the median uncertainties and the bars the range obtained for individual constellations. The uncertainties were computed by error propagation following Eq. 6. The overall uncertainty is thus driven by the precision of the individual estimates and the number of successful estimates and includes an estimate of the uncertainty due to hour-to-hour and day-to-day variability of emissions.

FIGURE 10

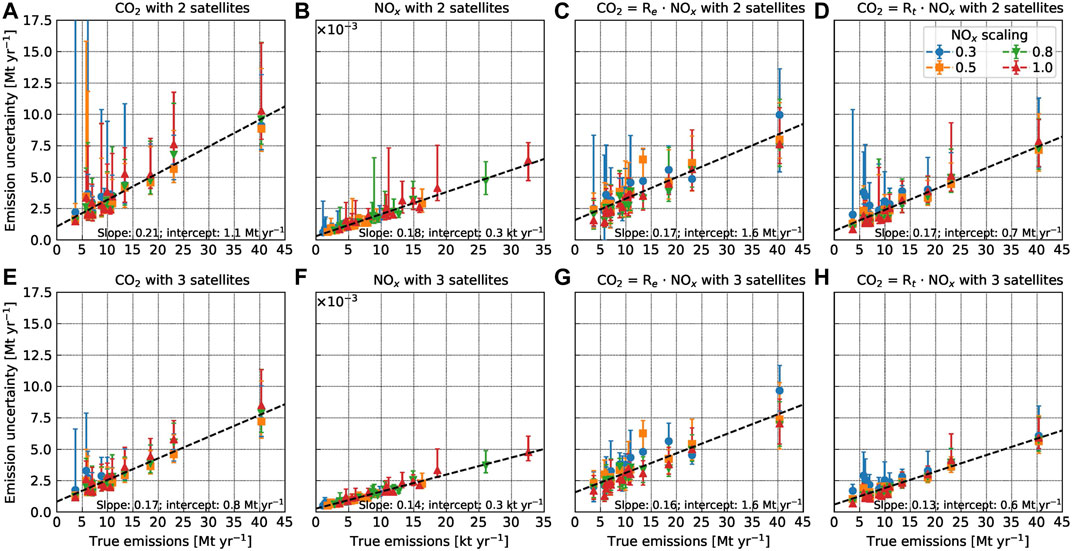
FIGURE 10. Estimated uncertainty of annual mean of emissions of (A)${\text{CO}}_2$ and (B)${\text{NO}}_{\text{x}}$ for constellations of two CO₂M satellites (median (symbols) and range (bars) over all constellations). Uncertainties are also shown for ${\text{CO}}_2$ estimates using ${\text{NO}}_{\mathit{x}}$ estimates and (C) estimated and (D) true ${\text{CO}}_2$:${\text{NO}}_{\mathit{x}}$ emission ratios. (E–H) shows the same but for constellations of three CO2M satellites.

Uncertainties range from 23–119% and 18–65% for CO₂ emission estimates for two and three satellites, respectively, considering the future reduction of NO_x emissions. For NO_x emissions, uncertainties range from 16–73% and 13–52% for two and three satellites, respectively. In general, the uncertainty is proportional to the source strength Q and can be described by a regression line with slope m and intercept b. For ${\text{CO}}_2$, the uncertainty has a slope of 21% and an intercept of 1.1 Mt yr^–1 for two satellites with no large differences for different ${\text{NO}}_{\text{x}}$ scaling factors (Figure 10A). This suggests that the plumes could be detected well from the ${\text{NO}}_2$ observations even if ${\text{NO}}_{\text{x}}$ emissions would be reduced significantly in the future with improved cleaning technology. The contribution of uncertainty in the temporal variability is roughly 50% of the total uncertainty. The uncertainty of ${\text{NO}}_{\text{x}}$ emissions has a similar dependency on true emissions (Figure 10B), but tends to be smaller than for ${\text{CO}}_2$ (m = 0.18 and b = 0.3 kt yr^–1).

When ${\text{CO}}_2$ emissions are quantified using ${\text{NO}}_{\text{x}}$ emissions and the estimated ${\text{CO}}_2$:${\text{NO}}_{\text{x}}$ emission ratio (Figures 10C,G), the uncertainty is similar or larger than the uncertainty computed for ${\text{CO}}_2$ emissions, because of the high uncertainties of the estimated emission ratios. The uncertainty increases for smaller scaling factors, because the uncertainty of weaker ${\text{NO}}_{\text{x}}$ is higher. If the true emission ratio would be known, ${\text{CO}}_2$ emission could be estimated from ${\text{NO}}_{\text{x}}$ emissions with lower uncertainty but only when ${\text{NO}}_{\text{x}}$ emissions are not reduced drastically.

The median uncertainties are only slightly smaller for three satellites than for two, but the range between individual constellations is much smaller. A constellation of three satellites is thus less likely to produce highly uncertain results due to insufficient coverage than a constellation of two.

Figure 11A shows the number of annual ${\text{CO}}_2$ emission estimates with a given uncertainty threshold for point sources with ${\text{CO}}_2$ emissions between 9 and 11 Mt yr^–1 (i.e., Pocerady, Turow, Schwarze Pumpe, and Dolna Odra; see table 1). The numbers were computed considering all possible constellations of two or three satellites. Separate lines are shown for the different ${\text{NO}}_{\text{x}}$ scaling factors, which affect the detectability of the plumes. A constellation of three satellites would be able to quantify annual ${\text{CO}}_2$ emissions in about 80–95% of cases with an uncertainty of 30% or better. A constellation of two satellites could only quantify less than 70% of point sources with similar accuracy. It is interesting to note that these numbers were relatively independent of the ${\text{NO}}_{\text{x}}$ scaling factor as long as it remained greater than or equal to 0.5.

FIGURE 11

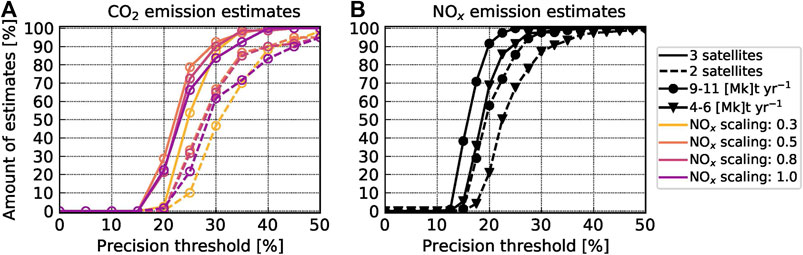
FIGURE 11. Number of successful (A)${\text{CO}}_2$ and (B)${\text{NO}}_{\text{x}}$ estimates for a given precision threshold considering constellations of two or three satellites and different ${\text{NO}}_{\text{x}}$ scaling factors. For ${\text{CO}}_2$, point sources with source strengths from 9 to 11 Mt yr⁻¹ were considered while for ${\text{NO}}_{\text{x}}$, sources with four to six and 9–11 kt yr⁻¹ were considered.

In terms of annual ${\text{NO}}_{\text{x}}$ emissions, two and three satellites could quantify nearly 100% of point sources with emissions of the order of 10 kt yr^–1 with an uncertainty of 30%. For a smaller source of the order of 5 kt yr^–1, the numbers would reduce to 70 and 95%, respectively.

3.6 Global Application of the Mass-Balance Approach

The mass-balance approach can be applied globally, because it does not require any additional expensive atmospheric transport simulations, but solely relies on wind information that is available from global analysis and reanalysis products. A database of points sources is available through the global map of emissions clumps (Wang et al., 2019), which lists about 900 point sources with ${\text{CO}}_2$ emissions larger than 3.5 Mt yr^–1 at CO2M overpass time (Figure 12A). We use a threshold of 3.5 Mt yr^–1 here, because it is close to the weakest source in our study (Table 1).

FIGURE 12

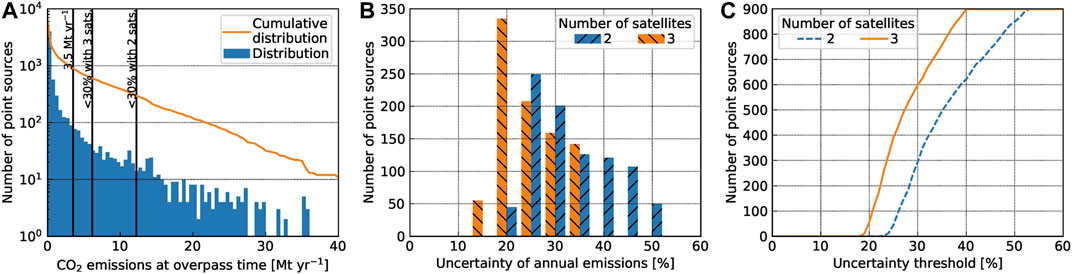
FIGURE 12. (A) Distribution of point sources based on ${\text{CO}}_2$ emissions at satellite overpass (11:30 local time) from Wang et al. (2019). (B) Estimated uncertainty of annual emissions for point sources >3.5 Mt yr⁻¹ for a constellation of two or three CO2M satellites. (C) Number of point sources that can be quantified with an uncertainty below given threshold with two or three CO2M satellites.

To upscale our results, we use the regression lines found for the uncertainties of annual emissions (Figures 10A,E) to calculate uncertainties of all point sources. We expect that our results are sufficiently representative for the sources in the database, because about 90% of them are located in the mid-latitudes (23.4°–66.5°) like our study area (50°N—55°N) and thus have a similar number of satellite overpasses ranging from 1.1 to 2.7 per 11 days repeat cycle compared to 1.7 in our study area.

Figure 12B shows the uncertainties of annual emissions computed for the 900 point sources for a constellation of two and three satellites showing that adding a third satellite reduces uncertainties from 35 to 28% on average. As a result, two satellites would be able to quantify annual emissions with an uncertainty <30% for only 300 point sources, while three satellites could quantify emissions for 600 point sources (Figure 12C). The 300 and 600 sources account for total emissions of 6,000 Mt yr^–1 and 8,700 Mt yr^–1, which are about 16 and 24% of global anthropogenic emissions.

Therefore, adding a third CO2M satellite has the potential to double the number of quantifiable point sources. Since our analysis used the regression lines in Figure 10, the numbers are likely overestimated, because some point sources are insufficiently covered by the satellites (Figure 11). However, this would especially affect a constellation of two satellites making it likely that we still underestimate the benefit of a third satellite here.

4 Discussion

In this study, we used synthetic CO2M satellite observations to investigate the potential of a constellation of ${\text{CO}}_2$ and ${\text{NO}}_2$ imaging satellites for quantifying the emissions of large point sources. The observations were generated for scenarios with low- and high-noise ${\text{CO}}_2$ and ${\text{NO}}_2$ instruments. ${\text{NO}}_2$ observations were additionally multiplied with different scaling factors (0.3, 0.5, 0.8, and 1.0) to study the expected future reduction of ${\text{NO}}_{\text{x}}$ emissions in Europe. Our study did not include systematic errors in ${\text{CO}}_2$ and ${\text{NO}}_2$ satellite observations. The effects of systematic errors due to aerosols have been investigated in the AEROCARB study and the CHE project that showed that these errors can be minimized when using additional information provided by the MAP instrument (Houweling et al., 2019; Reum and Houweling, 2020; Rusli et al., 2021).

We have developed an advanced data-driven method to quantify point source emissions in a semi-automated way. The method identifies the location of power plant plumes using a plume detection algorithm and quantifies both ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ emissions using a mass-balance method applied to the detected plume. The algorithm includes several checks to avoid outliers and correspondingly wrong emission estimates making it a suitable tool for an operational service that can be applied globally.

Individual ${\text{CO}}_2$ and ${\text{NO}}_{\text{x}}$ emissions were estimated with an accuracy <51% and <37% for a source strength >10 Mt yr^–1 and >10 kt yr^–1, respectively. ${\text{NO}}_2$ observations were essential for detecting the plume and constraining the shape of the Gaussian curves fitted to the individual plume cross-sections. They remained useful even for scenarios of reduced ${\text{NO}}_{\text{x}}$ emissions expected in the future due to more stringent air quality regulations. For weak ${\text{NO}}_{\text{x}}$ sources (<3 kt yr^–1), low-noise ${\text{NO}}_2$ observations were found to be beneficial for successfully detecting the plume and quantifying the emissions.

The uncertainties in our emission estimates are dominated by uncertainties in the ${\text{XCO}}_2$ and ${\text{NO}}_2$ observations, the background field and limitations of the mass-balance approach. The uncertainties estimated here are larger than those estimated by Nassar et al. (2017) (8–53%) for ${\text{CO}}_2$ emissions from power plants deduced from OCO-2 observations but are similar to estimates by Reuter et al. (2019) (23–72%). These studies are based on a small number of cases and are likely biased toward optimal observation conditions, while in our study the mass-balance approach was applied to every detectable plume. Model studies show that in case of highly turbulent plumes, uncertainties of the order of 10–20% are obtained when applying a mass-balance method even in the case where the 3D plume distribution and wind field is known perfectly (Kuhlmann et al., 2021; Wolff et al., 2020). Our results for power plants are also similar to those obtained for the city of Berlin, for which an uncertainty of about 50% was estimated for individual satellite overpasses (Kuhlmann et al., 2020a).

For a constellation of two satellites, annual CO₂ and NO_x emissions were estimated with an uncertainty of 23–119% and 16–73%, respectively. Adding a third CO2M satellite reduced uncertainties to 18–65% for CO₂ and 13–52% for NO_x emission estimates. The uncertainty includes an estimate of the uncertainty in the temporal variability of emissions that accounts for about 50% to the total uncertainty. Since annual ${\text{NO}}_{\text{x}}$ emissions can be determined with better accuracy due to the larger number of individual estimates, estimating ${\text{CO}}_2$ emissions directly from the ${\text{NO}}_{\text{x}}$ emissions by applying a representative ${\text{CO}}_2$:${\text{NO}}_{\text{x}}$ emission ratio seems appealing. However, this approach was found to suffer significantly from the high uncertainty in the ${\text{CO}}_2$:${\text{NO}}_{\text{x}}$ emission ratios determined from the same CO2M observations, especially when considering a future reduction of ${\text{NO}}_{\text{x}}$ emissions. The accuracy of our annual estimates is larger than previous OSSE studies that estimated uncertainties of about 5–10% (Lespinas et al., 2020; Wang et al., 2020). However, these studies ignored the transport model error and the impact of uncertainties in the ${\text{CO}}_2$ background due to other anthropogenic emissions and biospheric fluxes that are included in our study.

In our simulations, we assumed a constant ${\text{NO}}_2$ to ${\text{NO}}_{\text{x}}$ conversion factor and a constant ${\text{NO}}_{\text{x}}$ lifetime, which are strong simplifications. ${\text{NO}}_{\text{x}}$ is emitted from combustion sources primarily in the form of NO but is then partially converted to ${\text{NO}}_2$ by reaction with ozone. With increasing distance from the source, ${\text{NO}}_2$ typically becomes the dominant component of ${\text{NO}}_{\text{x}}$. The partitioning depends on the intensity of solar radiation, temperature, and ozone levels and thus changes not only with distance from the source but also with altitude above surface. In addition, the lifetime of ${\text{NO}}_{\text{x}}$ depends on the concentrations of OH radicals, which in turn depend on multiple factors including the concentrations of ${\text{NO}}_2$ themselves. Close to ${\text{NO}}_{\text{x}}$ sources, OH levels are low due to rapid reaction with ${\text{NO}}_2$ to ${\text{HNO}}_3$. With decreasing ${\text{NO}}_2$ levels downwind due to dilution and conversion to ${\text{HNO}}_3$, OH levels increase, thereby reducing ${\text{NO}}_{\text{x}}$ lifetime. As a consequence, ${\text{NO}}_2$:${\text{CO}}_2$ ratios change with distance from the source, and are different under different weather conditions. Such complicating factors need to be accounted for when trying to estimate ${\text{CO}}_2$ emissions from ${\text{NO}}_2$ observations, which remains appealing since ${\text{NO}}_2$ can be measured from satellites such as TROPOMI (and upcoming sun-synchronous and geostationary satellites) with good accuracy and with much better spatial and temporal coverage compared to the CO2M mission. However, full chemistry simulations are required to fully explore the potential and limitations of this approach rather than assuming a constant lifetime as in our simulations. Since conducting chemistry simulations at global scale with sufficient spatial resolution is computationally too expensive, a look-up table of ${\text{NO}}_2$-to-${\text{NO}}_{\text{x}}$ conversion factors and ${\text{NO}}_2$ lifetimes could alternatively be generated from a library of chemistry simulations and/or emulated ${\text{NO}}_{\text{x}}$ chemistry.

Our study shows that CO2M will likely be able to quantify ${\text{CO}}_2$ point sources with annual emissions larger than 3.5 Mt yr^–1 using a mass-balance approach. To determine the number of quantifiable plumes worldwide, we applied our estimated uncertainty to a global database of point sources (Wang et al., 2019), which showed that a constellation of two CO2M satellites would be able to quantify about 300 sources worldwide with an uncertainty <30%. Adding a third CO2M satellite would double the number of quantifiable point sources, because many more weaker sources can be quantified with an uncertainty <30%. A constellation of three satellites is also more likely to observe a point source under good conditions, e.g., not frequently too close to the edge of the swath, which increases the number of individual estimates and reduces the uncertainty of the annual emissions. A constellation of at least three CO2M satellites will likely be necessary to provide sufficient spatial and temporal coverage for quantifying annual emissions with sufficient accuracy especially for weak sources and at lower latitudes where the temporal coverage is smaller.

The mass-balance approach applied in this study has the advantage that it can be applied easily without expensive atmospheric transport simulations. However, the approach suffers from relatively high uncertainties of individual estimates for complex plumes and from uncertainties associated with the sparse temporal sampling of the varying emissions. Estimates could be significantly improved with additional information, for example, from atmospheric transport simulations, energy demand statistics and additional observations (e.g., ground-based networks and geostationary NO₂ satellites). Such information will become available, for example, through the future Copernicus ${\text{CO}}_2$ monitoring and verification support services, which has the potential to substantially reduce uncertainties of power plant emission estimates from CO2M observations.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author. The Python code used for detecting the plumes and quantifying the emissions is publicly available at: https://gitlab.com/empa503/remote-sensing/ddeq.

Author Contributions

GK developed, implemented, applied and evaluated the methods for estimating CO₂ emissions, and wrote the manuscript with input from all co-authors. DB supervised and led the SMARTCARB-2 project. SH was member of the SMARTCARB-2 project team and contributed critical input to the manuscript. YM accompanied the study as ESA project officer and provided critical inputs and reviews during all phases of the project.

Funding

This study was conducted in the context of the project SMARTCARB funded by the European Space Agency (ESA) under contract no. 4000119599/16/NL/FF/mg and supported by the EU Horizon-2020 project CHE under grant no. 776186. The views expressed here can in no way be taken to reflect the official opinion of ESA. COSMO-GHG calculations were carried out at the Swiss National Supercomputing Center (CSCS) under project ID s862.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsen.2021.689838/full#supplementary-material

References

Beirle, S., Boersma, K. F., Platt, U., Lawrence, M. G., and Wagner, T. (2011). Megacity Emissions and Lifetimes of Nitrogen Oxides Probed from Space. Science 333, 1737–1739. doi:10.1126/science.1207824

PubMed Abstract | CrossRef Full Text | Google Scholar

Bovensmann, H., Buchwitz, M., Burrows, J. P., Reuter, M., Krings, T., Gerilowski, K., et al. (2010). A Remote Sensing Technique for Global Monitoring of Power Plant CO₂ Emissions from Space and Related Applications. Atmos. Meas. Tech. 3, 781–811. doi:10.5194/amt-3-781-2010

CrossRef Full Text | Google Scholar

Branch, M. A., Coleman, T. F., and Li, Y. (1999). A Subspace, interior, and Conjugate Gradient Method for Large-Scale Bound-Constrained Minimization Problems. SIAM J. Sci. Comput. 21, 1–23. doi:10.1137/S1064827595289108

CrossRef Full Text | Google Scholar

Broquet, G., Bréon, F.-M., Renault, E., Buchwitz, M., Reuter, M., Bovensmann, H., et al. (2018). The Potential of Satellite Spectro-Imagery for Monitoring CO₂ Emissions from Large Cities. Atmos. Meas. Tech. 11, 681–708. doi:10.5194/amt-11-681-2018

CrossRef Full Text | Google Scholar

Brunner, D., Kuhlmann, G., Marshall, J., Clément, V., Fuhrer, O., Broquet, G., et al. (2019). Accounting for the Vertical Distribution of Emissions in Atmospheric CO₂ Simulations. Atmos. Chem. Phys. 19, 4541–4559. doi:10.5194/acp-19-4541-2019

CrossRef Full Text | Google Scholar

Buchwitz, M., Reuter, M., Bovensmann, H., Pillai, D., Heymann, J., Schneising, O., et al. (2013). Carbon Monitoring Satellite (CarbonSat): Assessment of Atmospheric CO₂ and CH₄ Retrieval Errors by Error Parameterization. Atmos. Meas. Tech. 6, 3477–3500. doi:10.5194/amt-6-3477-2013

CrossRef Full Text | Google Scholar

Ciais, P., Crisp, D., Gon, H. v. d., Engelen, R., Heimann, M., Janssens-Maenhout, G., et al. (2015). Towards a European Operational Observing System To Monitor Fossil CO₂ Emissions - Final Report From the Expert Group. European Commission, Copernicus Climate Change Service. Report

Google Scholar

Düring, I., Bächlin, W., Ketzel, M., Baum, A., Friedrich, U., and Wurzler, S. (2011). A New Simplified NO/NO₂ Conversion Model under Consideration of Direct NO₂-Emissions. metz 20, 67–73. doi:10.1127/0941-2948/2011/0491

CrossRef Full Text | Google Scholar

ESA Earth and Mission Science Division, (2020). Tech. rep. Version 3.0. Copernicus CO₂ Monitoring Mission Requirements Document (MRD), Available at: https://esamultimedia.esa.int/docs/EarthObservation/CO2M_MRD_v3.0_20201001_Issued.pdf. (access:1 October 2020)

Google Scholar

European Commission (2017). Commission Implementing Decision (EU) 2017/1442 of 31 July 2017 Establishing Best Available Techniques (BAT) Conclusions, under Directive 2010/75/eu of the European Parliament and of the Council, for Large Combustion Plants (Notified under Document C(2017) 5225) (Text with EEA relevance.). Available at: https://eur-lex.europa.eu/eli/dec_impl/2017/1442/oj (Accessed July 31, 2017).

Google Scholar

Fioletov, V. E., McLinden, C. A., Krotkov, N., and Li, C. (2015). Lifetimes and Emissions of SO₂ from point Sources Estimated from OMI. Geophys. Res. Lett. 42, 1969–1976. doi:10.1002/2015GL063148

CrossRef Full Text | Google Scholar

Hill, T., and Nassar, R. (2019). Pixel Size and Revisit Rate Requirements for Monitoring Power Plant CO₂ Emissions from Space. Remote Sensing 11, 1608. doi:10.3390/rs11131608

CrossRef Full Text | Google Scholar

Houweling, S., Landgraf, J., van Heck, H., Vlemmix, T., and Tao, W. (2019). AEROCARB – Study on Use of Aerosol Information for Estimating Fossil CO₂ Emissions - Final Report: Synthesis and Recommendation of ESA Study RFP/3-14860/17./NL/FF/gp. Version 2.0 Tech. rep

Jähn, M., Kuhlmann, G., Mu, Q., Haussaire, J.-M., Ochsner, D., Osterried, K., et al. (2020). An Online Emission Module for Atmospheric Chemistry Transport Models: Implementation in COSMO-GHG v5.6a and COSMO-ART v5.1-3.1. Geosci. Model. Dev. 13, 2379–2392. doi:10.5194/gmd-13-2379-2020

CrossRef Full Text | Google Scholar

Janssens-Maenhout, G., Pinty, B., Dowell, M., Zunker, H., Andersson, E., Balsamo, G., et al. (2020). Toward an Operational Anthropogenic CO2 Emissions Monitoring and Verification Support Capacity. Bull. Am. Meteorol. Soc. 101, E1439–E1451. doi:10.1175/BAMS-D-19-0017.1

CrossRef Full Text | Google Scholar

Kuhlmann, G., Broquet, G., Marshall, J., Clément, V., Löscher, A., Meijer, Y., et al. (2019a). Detectability of CO2 Emission Plumes of Cities and Power Plants with the Copernicus Anthropogenic CO₂ Monitoring (CO2M) mission. Atmos. Meas. Tech. 12, 6695–6719. doi:10.5194/amt-12-6695-2019

CrossRef Full Text | Google Scholar

Kuhlmann, G., Brunner, D., Broquet, G., and Meijer, Y. (2020a). Quantifying CO₂ Emissions of a City with the Copernicus Anthropogenic CO₂ Monitoring Satellite mission. Atmos. Meas. Tech. 13, 6733–6754. doi:10.5194/amt-13-6733-2020

CrossRef Full Text | Google Scholar

Kuhlmann, G., Clément, V., Marschall, J., Fuhrer, O., Broquet, G., Schnadt-Poberaj, C., et al. (2019b). SMARTCARB - Use of Satellite Measurements of Auxiliary Reactive Trace Gases for Fossil Fuel Carbon Dioxide Emission Estimation, Final Report of ESA Study Contract n°4000119599/16/NL/FF/mg. Tech. rep., Empa, Swiss Federal Laboratories for Materials Science and Technology. Switzerland: Dübendorf. doi:10.5281/zenodo.4034266

CrossRef Full Text | Google Scholar

Kuhlmann, G., Clément, V., Marshall, J., Fuhrer, O., Broquet, G., Schnadt-Poberaj, C., et al. (2020b). Synthetic XCO₂, CO and NO₂ Observations for the CO2M and Sentinel-5 Satellites. doi:10.5281/zenodo.4048228

CrossRef Full Text

Kuhlmann, G., Henne, S., Löscher, A., Meijer, Y., and Brunner, D. (2021). SMARTCARB 2 – Use Of Satellite Measurements of Auxiliary Reactive Trace Gases for Fossil Fuel Carbon Dioxide Emission Estimation (Phase 2), Final Report Of ESA Study Contract n4000119599/16/NL/FF/mg. Tech. rep., Empa, Swiss Federal Laboratories for Materials Science and Technology. Switzerland: Dübendorf. doi:10.5281/zenodo.4674167

CrossRef Full Text | Google Scholar

Lespinas, F., Wang, Y., Broquet, G., Bréon, F.-M., Buchwitz, M., Reuter, M., et al. (2020). The Potential of a Constellation of Low Earth Orbit Satellite Imagers to Monitor Worldwide Fossil Fuel CO₂ Emissions from Large Cities and point Sources. Carbon Balance Manage 15, 1–12. doi:10.1186/s13021-020-00153-4

CrossRef Full Text | Google Scholar

Lorente, A., Boersma, K. F., Eskes, H. J., Veefkind, J. P., Van Geffen, J. H. G. M., de Zeeuw, M. B., et al. (2019). Quantification of Nitrogen Oxides Emissions from Build-Up of Pollution over Paris with TROPOMI. Sci. Rep. 9, 1–10. doi:10.1038/s41598-019-56428-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, A., Weissmann, M., Reitebuch, O., Rennie, M., Geiß, A., and Cress, A. (2021). Validation of Aeolus Winds Using Radiosonde Observations and Numerical Weather Prediction Model Equivalents. Atmos. Meas. Tech. 14, 2167–2183. doi:10.5194/amt-14-2167-2021

CrossRef Full Text | Google Scholar

Nassar, R., Hill, T. G., McLinden, C. A., Wunch, D., Jones, D. B. A., and Crisp, D. (2017). Quantifying CO₂ Emissions from Individual Power Plants from Space. Geophys. Res. Lett. 44 (10), 917–933. doi:10.1002/2017GL074702

CrossRef Full Text | Google Scholar

Nassar, R., Napier-Linton, L., Gurney, K. R., Andres, R. J., Oda, T., Vogel, F. R., et al. (2013). Improving the Temporal and Spatial Distribution of CO₂ Emissions from Global Fossil Fuel Emission Data Sets. J. Geophys. Res. Atmos. 118, 917–933. doi:10.1029/2012JD018196

CrossRef Full Text | Google Scholar

Pillai, D., Buchwitz, M., Gerbig, C., Koch, T., Reuter, M., Bovensmann, H., et al. (2016). Tracking City CO2 Emissions from Space Using a High-Resolution Inverse Modelling Approach: a Case Study for Berlin, Germany. Atmos. Chem. Phys. 16, 9591–9610. doi:10.5194/acp-16-9591-2016

CrossRef Full Text | Google Scholar

Pinty, B., Janssens-Maenhout, G., Dowell, M., Zunker, H., Brunhe, T., Ciais, P., et al. (2018). An Operational Anthropogenic CO₂ Emissions Monitoring & Verification Support Capacity - Baseline Requirements, Model Components And Functional Architecture. Report. doi:10.2760/39384

CrossRef Full Text | Google Scholar

Pouliot, G., Pierce, T., Denier van der Gon, H., Schaap, M., Moran, M., and Nopmongcol, U. (2012). Comparing Emission Inventories and Model-Ready Emission Datasets between Europe and North America for the AQMEII Project. Atmos. Environ., 53, 4–14. doi:10.1016/j.atmosenv.2011.12.041

CrossRef Full Text | Google Scholar

Reum, F., and Houweling, S. (2020). Impact of Urban Aerosols on Satellite-Retrieved CO₂, CHE Project, Deliverable 2.7 Tech. Rep. Available at:https://www.che-project.eu/sites/default/files/2020-12/CHE-D2-7-V1-0.pdf (access: May 20, 2021).

Google Scholar

Reuter, M., Buchwitz, M., Hilboll, A., Richter, A., Schneising, O., Hilker, M., et al. (2014). Decreasing Emissions of NO_x Relative to CO₂ in East Asia Inferred from Satellite Observations. Nat. Geosci 7, 792–795. doi:10.1038/ngeo2257

CrossRef Full Text | Google Scholar

Reuter, M., Buchwitz, M., Schneising, O., Krautwurst, S., O'Dell, C. W., Richter, A., et al. (2019). Towards Monitoring Localized CO₂ Emissions from Space: Co-located Regional CO₂ and NO₂ Enhancements Observed by the OCO-2 and S5P Satellites. Atmos. Chem. Phys. 19, 9371–9383. doi:10.5194/acp-19-9371-2019

CrossRef Full Text | Google Scholar

Rockström, J., Gaffney, O., Rogelj, J., Meinshausen, M., Nakicenovic, N., and Schellnhuber, H. J. (2017). A Roadmap for Rapid Decarbonization. Science 355, 1269–1271. doi:10.1126/science.aah3443

PubMed Abstract | CrossRef Full Text | Google Scholar

Rusli, S. P., Hasekamp, O., aan de Brugh, J., Fu, G., Meijer, Y., and Landgraf, J. (2021). Anthropogenic CO₂ Monitoring Satellite mission: the Need for Multi-Angle Polarimetric Observations. Atmos. Meas. Tech. 14, 1167–1190. doi:10.5194/amt-14-1167-2021

CrossRef Full Text | Google Scholar

Sierk, B., Bézy, J.-L., Löscher, A., and Meijer, Y. (2019). The European CO₂ Monitoring Mission: Observing Anthropogenic Greenhouse Gas Emissions from Space 11180. Proceedings, International Conference on Space Optics — ICSO 2018. 12 July 2019. Chania, Greece. 111800M. doi:10.1117/12.2535941

CrossRef Full Text | Google Scholar

Super, I., Dellaert, S. N. C., Visschedijk, A. J. H., and Denier van der Gon, H. A. C. (2020). Uncertainty Analysis of a European High-Resolution Emission Inventory of CO₂ and CO to Support Inverse Modelling and Network Design. Atmos. Chem. Phys. 20, 1795–1816. doi:10.5194/acp-20-1795-2020

CrossRef Full Text | Google Scholar

Tebert, C. (2017). Stickstoffoxid-Emissionen aus Kohlekraftwerken: Minderungspotenzial auf Basis von Messdaten der Jahre 2016 und 2017,Tech. rep. Auftraggeber: Bund für Umwelt und Naturschutz Deutschland e.V. (BUND) und Klima-Allianz Deutschland. Available at: https://www.bund.net/fileadmin/user_upload_bund/publikationen/kohle/kohle_stickoxid_emissionen_gutachten.pdf (access:September 2, 2020).

Google Scholar

UNFCCC (2015). Paris Agreement, FCCC/CP/2015/L.9/Rev1. Available at: http://unfccc.int/resource/docs/2015/cop21/eng/l09r01.pdf.

Google Scholar

Varon, D. J., Jacob, D. J., McKeever, J., Jervis, D., Durak, B. O. A., Xia, Y., et al. (2018). Quantifying Methane point Sources from fine-scale Satellite Observations of Atmospheric Methane Plumes. Atmos. Meas. Tech. 11, 5673–5686. doi:10.5194/amt-11-5673-2018

CrossRef Full Text | Google Scholar

Virtanen, P., Gommers, R., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., et al. (2020). SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 17, 261–272. doi:10.1038/s41592-019-0686-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Broquet, G., Bréon, F.-M., Lespinas, F., Buchwitz, M., Reuter, M., et al. (2020). PMIF v1.0: Assessing the Potential of Satellite Observations to Constrain CO₂ Emissions from Large Cities and point Sources over the globe Using Synthetic Data. Geosci. Model. Dev. 13, 5813–5831. doi:10.5194/gmd-13-5813-2020

CrossRef Full Text | Google Scholar

Wang, Y., Ciais, P., Broquet, G., Bréon, F.-M., Oda, T., Lespinas, F., et al. (2019). A Global Map of Emission Clumps for Future Monitoring of Fossil Fuel CO₂ Emissions from Space. Earth Syst. Sci. Data 11, 687–703. doi:10.5194/essd-11-687-2019

CrossRef Full Text | Google Scholar

Wolff, S., Ehret, G., Kiemle, C., Amediek, A., Quatrevalet, M., Wirth, M., et al. (2020). Determination of the Emission Rates of CO₂ Point Sources with Airborne Lidar. Atmos. Meas. Tech. Discuss. 2020, 1–28. doi:10.5194/amt-2020-390

CrossRef Full Text | Google Scholar

Wu, D., Lin, J. C., Oda, T., and Kort, E. A. (2020). Space-based Quantification of Per Capita CO₂ Emissions from Cities. Environ. Res. Lett. 15, 035004. doi:10.1088/1748-9326/ab68eb

CrossRef Full Text | Google Scholar

Zheng, B., Chevallier, F., Ciais, P., Broquet, G., Wang, Y., Lian, J., et al. (2020). Observing Carbon Dioxide Emissions over China's Cities and Industrial Areas with the Orbiting Carbon Observatory-2. Atmos. Chem. Phys. 20, 8501–8510. doi:10.5194/acp-20-8501-2020

CrossRef Full Text | Google Scholar