Recency-based spatio-temporal similarity exploration for POI recommendation in location-based social networks

Point-of-interest (POI) recommendation is one of the primary tasks of location-based social networks (LBSNs). With user data in bulk, extracting useful information and addressing issues such as data sparsity and cold-start problems looming large in collaborative filtering become difficult. One of the plausible solutions is to incorporate contextual information into the recommendation process. In this article, we propose a Recency-based Spatio-Temporal Similarity Exploration (RSTSE) for POI recommendation that utilizes the recency-based trust estimation among the prospective neighbors of the target user. The trust level is categorized into two heads: direct trust, which can be extracted from the peer group information of the user, and indirect trust, which is measured based on venue popularity, temporal recency, radial proximity, and transitivity. The approach consists of two phases. In the incipient phase, POIs are extracted based on the preferences of potential neighbors, including the users who are recognized peers, the users with similar visiting histories in the spatial and temporal context, and the users with friend-of-friend relations. The telic phase involves Neural Collaborative Filtering (NCF) to capture the linear and non-linear user–POI interactions better. RSTSE has been evaluated on three real-world datasets, namely, Gowalla, Foursquare, and Weeplaces, and the results suggest efficacy over other state-of-the-art approaches.

1 Introduction

Location-based social networks (LBSNs), also called Location Mobile Social Network (LMSNs), have become quite popular with the emergence of precise location acquisition techniques and personal devices. They provide a platform for users to share their locations and word-of-mouth opinions about different venues. Thus, LBSN data contain public contents, such as location and personal contents such as reviews, tags, and tips, ascertained from people of different demographics, cultures, geography, and interests. LBSN is defined by the moniker, “3+1” framework, as it consists of three layers and one timeline shared by all the layers (Roick and Heuser, 2013). The three layers are: (1) the geographic layer, (2) the social layer, and (3) the content layer. The geographic layer consists of the user's location information, POI location, and the user's mobility information. The social layer, as the name suggests, bears the information about the explicit relationships between different users, i.e., the peer group of the user. The last layer is the content layer, which comprises user-generated contents such as review summary, tips, and tags, and the categorical classification of the venues. Figure 1 depicts the diagrammatic illustration of the “3+1” framework. The last component of this framework and perhaps the paramount one is the timeline. Every instance in the LBSN is attached to a particular timestamp, which might contain a discrete time, a time range or information about the period in the user–POI interaction pattern. Several location-based services, such as Foursquare, Yelp, and Twitter, have witnessed a spike in users since the advent of the faster communication paradigm. According to Yelp Press¹, 33.03 million unique devices used Yelp in 2022, and 40% of Yelp users in the United States are 55 years or above. LBSN data can be utilized for several tasks, one crucial being POI recommendations. Any real-world geographical information, such as malls, shops, garages, and restaurants, can be called POIs. Unlike traditional recommendations, recommending POI in line with the interest and inclination of the user is quite challenging (Liu, 2018). The most important issue is data sparsity, which arises due to the limited physical accessibility of the POIs to the users. Additionally, not all users are equally socially active and hence might not post their check-in information, thereby further aggravating the situation. The second important issue is the cold-start problem. It has three dimensions. First, the cold-start users are those with no past historical check-in records; thus, it becomes difficult to extract the user's preferences for such users. Second, cold-start POIs are the new venues and are, hence, not that popular. Thus, these POIs are neglected even though they might suit the user's interests. The third is users visiting unfamiliar places; thus, the recommendation requires extrapolating the user's preferences across domains to satisfy their predilections. The third major problem is the absence of negative feedback where the user's check-in at a place is recorded as positive feedback inherently. This ignores the possibility of disliking the venues. Another major issue is the dynamic context, in which the preferences are subject to space, time, mood, weather, cognition, etc. Thus, including auxiliary information can alleviate these drawbacks and make the recommendation process more efficacious. The results of the POI recommendation can be used in different fields, especially traffic management, city development, and the tourism industry (Duan et al., 2020; Chen et al., 2023a). Expanding their customer reach also provides multifold advantages to business owners and advertising agencies.

Figure 1

Figure 1. LBSN “3+1” framework.

POI recommendation is based on several factors such as location, time, familiarity with a place, social circle, and demographics. The most important factor is geographical information, which has two dimensions: the proximity of the location to the current location and the popularity of the location within the region. Several approaches proposed in the past used geographical information in its entirety as mentioned in Liu et al. (2013), Lian et al. (2014), and Liu et al. (2020), but they suffered from data sparsity. Most of the earlier approaches were collaborative filtering (CF)-oriented, where the similarity estimation was elementary to recommend POIs based on similar tastes. These approaches succumbed to data sparsity due to unrated POIs. The methods proffered in Griesner et al. (2015), Li et al. (2015), Cai et al. (2018), and Cheng et al. (2023), used spatial information in conjunction with temporal context and provided enhanced results. Contextual information was imbibed in the recommendation process to supplement the preference mining and address the impending issues as elaborated in Chen et al. (2015), Zhao et al. (2015), and Yu et al. (2020). Next to spatio-temporal factors, social context is of utmost importance. We can decipher the popular POIs within a peer group from a social perspective. An important aspect of considering social information is social link prediction. The direct social links are easily accessible, but not all users are socially active, so these data are not very reliant. Rios et al. (2018) suggested to mine social links prospectively from different records of LBSN data. Community detection algorithms have been widely used in different fields, such as food recommendation (Rostami et al., 2022), healthcare (Rostami et al., 2023), and privacy tasks (Javed et al., 2018). Their results have also been extrapolated in the field of social networks. Link prediction algorithms (Dong et al., 2013) have also been used to decipher similar users for different objectives in varied fields (Bordbar et al., 2022; Kumar et al., 2022). POI recommendation systems have utilized similarity measures like Jaccard coefficients (Pan et al., 2019) and cosine similarity index (Song et al., 2019) to extract similar users. On critical analysis of the earlier approaches, we inferred that the similarity indices utilize only historical data to find similar users. This recedes their reliability, especially in the case of POI recommendation, as users' preferences change with the time, seasons, location, etc. Thus, the information decay should be accounted for. The recency in the data is seldom considered, so the recommendations produced are stale. The time-variant information analysis of both spatial and temporal contents is crucial to similarity probing.

1.1 Research objectives

In this article, we propose a recency-aware similar user mining approach based on the spatial and temporal context in combination with a modified link prediction algorithm called Recency-based Spatio-Temporal Similarity Exploration (RSTSE) for POI recommendation to increase the expanse of social neighbors besides the acknowledged social peers. The major contributions of this approach are as follows:

1. We exploit the implicit and explicit social trust levels to count the impact of the social groups and latent neighbors on the user's POI preference. The implicit trust is calculated based on the direct social peer group information in the LBSN data, and the model is termed as RSTSE-Implicit.

2. For explicit trust computation, we consider the following cases:

(a) We propose Recency-based Spatio-Temporal Similarity Exploration on Spatial Visits (RSTSE-V), where we consider the spatial coincidence of a visit wherein we mine the users who have visited the same places as the target users at any point in time, and these users are considered spatial neighbors.

(b) The temporal co-occurrence of visits also encapsulates the prospective temporal neighbors whose visitation time for POIs coincides with that of the target. These co-occurrences of visits are used in Recency-based Spatio-Temporal Similarity Exploration on Temporal visits (RSTSE-T) to learn the sequential POI preferences of the users.

(c) In Recency-based Spatio-Temporal Similarity Exploration on Distance threshold (RSTSE-D), we propose a bounded radial network to include the users within the specified threshold to adjunct the popular POIs that might interest the users. Such users are referred to as Radial Nets of the given user.

(d) Recency-based Spatio-Temporal Similarity Exploration on Transitive Relation (RSTSE-Trans) utilizes a modified Adamic-Adar algorithm that prunes the mutual connections as social bridges to extrapolate the popular POIs.

3. The problems associated with cold-start users or socially inactive users are overcome by recommending POIs based on their popularity at the current time and within the bounded radial network of the user. The user ascertains the distance threshold for the radial network to precisely search for the potential neighbors within the user's proximity. Hence, RSTSE-D caters to new users as efficiently as the old ones.

4. The user's geographical location projects the physical accessibility of the POIs to the users as well as the region-of-interest (ROI). While immediate accessibility is desirable, the ROI consideration is useful in recommending the POIs within reach considering moveability. We propose to find similar users who have visited the same places as the target users but are not in the known friend circle of the user or the users within the ROI and perform preference mining with their check-in records. The Recency-based Spatio-Temporal Similarity Exploration-Combination model (RSTSE-C) model combines the faculties of RSTSE-Implicit, RSTSE-V, RSTSE-T, RSTSE-D, and RSTSE-Trans.

5. The ablation study of six approaches, namely, RSTSE-D, RSTSE-T, RSTSE-V, RSTSE-Trans, and RSTSE-C, over different user scenarios excerpted from the data also supports our claims.

1.2 Research hypothesis

The study aims to empirically test many important assertions on the performance, flexibility, and utility of RSTSE to boost POI recommendation accuracy and satisfaction among users within LBSNs. The claims are based on addressing the current limitations of conventional recommendation techniques. By leveraging conceptual frameworks and empirical evaluation, the purpose of this research is to shed light on the following hypotheses:

H1: In instances when user behavior data are limited or inconsistent, the RSTSE methodology will outperform traditional baseline methods in terms of suggestion accuracy.

H2: Recommendations that are more relevant to the preferences of specific users will be produced by integrating both explicit and implicit social trust levels.

H3: It states that RSTSE will utilize temporal and spatial contextual clues to efficiently address the cold start problem and provide good recommendations for new users as well as those with little social participation.

H4: The RSTSE technique will show resilience and efficacy in providing personalized and relevant POI recommendations across multiple LBSN contexts, demonstrating scalability and generalization across varied user scenarios and geographic locations.

The remaining article is organized as follows: Section 2 discusses eminent works proposed recently. Section 3 elaborates on the methodology used. Section 4 demonstrates the results obtained and discusses the outcomes. Section 5 concludes the research paper by discussing the future scope.

2 Related work

Several previous methods deployed different aspects of LBSN data. A highly exploited factor is the geographical location. Rahmani et al. (2020) proposed a local geographical based logistic matrix factorization (LGLMF) model to capture both the user's geographic visitation pattern within the region of interest (ROI) and the location-based popularity of the POI. Xu et al. (2021b) proposed a novel hybrid POI recommendation model (NHRM) that exploited spatio-temporal attributes and is a combination of three different models: the first model captured the user's perspective, the second harnessed the location-user dependencies, and the last model utilized categorical information to substantiate the POI recommendation. Acharya et al. (2023) proposed a spatial griding method where the ROIs closer to the user location were mined, and POIs based on spatial grids were recommended using long-and-short-term memory (LSTM). Qin et al. (2023) proposed a contrastive learning method, DisenPOI, based on a dual graph for POI recommendation that relied on disentangling sequential and geographical effects. The bi-directional spatio-temporal dependence and users dynamic preference (bi-STDDP) method proposed by Xi et al. (2019) addressed the issue of dynamic preferences by including the bi-directional spatio-temporal aspects. The spatial location was exploited globally, but temporal information was mined locally. Chen et al. (2022) proposed a keywords-enhanced deep reinforcement learning (KDRL) framework that integrates reinforcement learning and keyword information for travel recommendation. They adopted the Markov decision process for simultaneously modeling informative keywords of the clicked products.

In addition to spatial-temporal features, the social aspect is also featured in several methods in various forms to augment the POI recommendation. Gan and Tan (2023) proposed a combination of multiple graph convolutional networks and independent attention network, the MGCAN framework, that incorporates sequential patterns and different contextual factors and captures the user's preferences. Wang et al. (2021) proffered an attention mechanism and graph-based model, ASGNN, that utilized graph learning for check-in sequences and an attention mechanism to capture user-POI dependencies and long- and short-term preferences. Cai et al. (2022) proposed a graph convolution network (GCN)-based friends-aware graph collaborative filtering (FG-CF) method, wherein the GCN was used to form the neighbor, social, and ego embeddings, which were further utilized concomitantly with a non-linear combination of the neighbors' aggregated message to provide final POI recommendation. The DeepPOF method proposed by Safavi and Jalali (2022) harnessed the social impact using convolution neural network (CNN) in combination with deep learning methods and mean shift clustering for similarity estimation. Yue et al. (2020) posited a side information and self-attention network (SSANet) framework that deployed the Gaussian kernel technique for the geographical method, an attention mechanism to capture the interaction modules, and Node2vec for harnessing the social information. RecPOID method (Safavi and Jalali, 2021) employed fuzzy c-mean clustering to find similar friends and a 10-layer CNN model to extrapolate the important features from spatio-temporal information. Wei et al. (2023) proposed a multi-context-based next location recommendation (MCLR) model wherein the high-order location and location semantic graph were used to capture the location-location dependencies. The approach also utilized the preference modeling from a friend's perspective by including the selected peers only. Dai et al. (2022) proffered a spatial-temporal representation learning framework for the personalized and successive POI recommendation (PPR) method based on graphs. This approach combined the socio and spatial-temporal features obtained from the user's check-in data. The method modeled sequential patterns in four perspectives: POI-user, POI-time, user-user, and user-POI dependencies. Zhang et al. (2019) proposed a framework that fused multi-tag information with social and geographical data ascertained from the user check-in records into matrix factorization (MF). Haldar et al. (2022) propounded the socio-spatial co-engaged location selection (SSLS) method to recommend the POIs that tune to the interests of the users and their friends and to diversify the expanse of recommended POIs in social-spatial space. Different learning paradigms, such as meta-learning (Ning et al., 2022), adversarial learning (Zhao et al., 2022), and reinforcement learning (Huang et al., 2021), have been applied to increase the performance of recommendation systems.

The inclusion of semantic information has also provided enhanced results. The geotagged image-based POI recommendation algorithm, the context-aware POI recommendation algorithm (POIRA), as proposed in Sun (2021), utilized a two-layer stacked double-sparse autoencoder for efficiently mining textual, emotional, and geographical contents. Chen et al. (2023b) posited a multi-objective reinforcement learning for trip recommendation (MORL-Trip) framework to capture the user dynamic preferences and model temporal and spatial constraints. It deploys Markov decision process on the actor-critic framework and enhances the state representation with geographical information updates and auxiliary information from real-time locations. The model catered to accuracy, popularity, and diversity. Wang K. et al. (2023) used social linkages and semantic aspects to enhance the performance of LSTM. This approach used the combination of attention mechanism and LSTM (LSA). Acharya and Mohbey (2023) proposed the differential privacy-based social network detection-based POI recommendation model (DPSND-Rec) method that protected privacy using Laplacian noise and exploited the spatio-temporal neighbors for social linkage mining. A real-time event embedding was proposed in Hao et al. (2019) that used CNN to capture the textual information and a multimodal embedding for location, time, and text extraction. Wang et al. (2020) proposed the light location recommendation (LLRec) system to recommend the POIs on mobile devices. It utilized a variant of RNN, FastGRNN (Kusupati et al., 2018), and teacher-student learning framework to utilize the relevant localized data for cloud-based training effectively.

2.1 Research gap

The above-cited works have imbibed social and spatio-temporal factors to enhance accuracy, yet they have ignored the explicit and implicit trust factors. These involve the social ties veiled within the spatial visits and temporal trajectory. Furthermore, the social links are not exploited based on recency, and hence, the recommendation preferences are not in line with the user's present interests. Moreover, traditional recommendation approaches in LBSNs rely on rudimentary models that do not adequately reflect users' individual preferences and behavioral patterns. In terms of the recommender system, the primary focus is to recommend POIs precisely and accurately. With these factors being ignored, the recommendation accuracy achieved is also very low. The cold-start problem is magnified in these approaches tenfold, and the system fails to meet their needs. We propose a recency-aware neighborhood estimation strategy that utilizes spatio-temporal co-occurrences in visits based on the current time and mines the probable POIs. Furthermore, it serves the cold-start users well because we use user-defined time and location to deduce the potential similar neighbors. One of the major issues in POI recommendation is overcoming the popularity bias and fairness issue (Rahmani et al., 2022). It is critical to understand the inherent preference pattern in the personalized recommendation, in addition to the trade-off existing between accuracy and fairness. Massimo and Ricci (2021) analyzed two aspects of this problem. First, the impact of biasing toward popular items on precise recommendations. Second, what users prefer between precise and accurate recommendations or novel and diversified recommendations. Through RSTSE-C we aim to overcome this issue by capturing the impact of implicitly trusted friends to reduce the reliance on globally popular items and promote diversity. We also include the preferences of explicitly trusted friends and prioritize the trusted friends based on the similarity measures, thus, further reducing the impact of popular items. The combinations of both levels of trust are parameter-controlled and thus the final recommendations are the mix of both trustworthy and personalized POIs. With this, we incorporate diversity within the process and hence recommendations can focus on both niche and POIs of user's interest.

3 Methodology

There are two phases of the RSTSE-C method. The incipient phase has three steps. First, constructing the location interaction sequence of the user from the historical check-in data and ascertaining the location and the time for which recommendation is required. The second step involves implicit and explicit trusted neighbor estimation. We compute the potential POIs using the estimated neighbors in the third step. In the telic phase, the Neural Collaborative Filtering (NCF) unit captures the linear and non-linear interactions and facilitates the final recommendations. Table 1 summarizes various symbols used in RSTSE-C for better user understanding.

Table 1

Table 1. Summary of symbols used in RSTSE-C.

3.1 Problem definition

Definition 1: POI: POI is any real-world location, say, p, such that $\mathcal{L}$ ={ p₁, p₂, …p_n}, where $\mathcal{L}$ denotes the set of n available POIs. Each $p_iϵ\mathcal{L}$ is identified with a triplet (v_id, lat_i, lng_i), where v_idrefers to a unique ID provided to each POI, lat_i, and lng_i denote the latitude and longitude of the POI.

Definition 2: check-in: The user's visitation at a POI is termed check-in and is characterized by the user's unique user-id, POI's unique ID, its coordinates, the user's time of visitation, and the category of the POI.

Definition 3: location interaction pattern $({\mathcal{P}}^{\text{I}})$: For every user $uϵ\mathcal{U}$ where $\mathcal{U}$ is the set of m users, we extrapolate the frequency of visit to each POI and normalize it to construct a location interaction pattern, such that for j-th user, ${\mathcal{P}}_j^I=\left\{{lp}_1,l{p}_2,\dots .{lp}_k\right\}$ where lp_k denotes the normalized frequency at the k-th POI calculated as in Equation 1.

$\begin{array}{ll}l{p}_k=\{\begin{array}{c}\frac{{\mathcal{V}}_{(u,p_k)}}{\Sigma {\mathcal{V}}_{(u,p_k)}}ifuvisitsPOIp\\ 0otherwise\end{array}& (1)\end{array}$

where, ${\mathcal{V}}_{(u,p_k)}$ is the frequency of the visit of user u to the k-th POI.

Problem 1: POI recommendation from user's perspective: The user's decision to visit a POI is affected not only by the POI's location but also by popularity among their peers and similar users. The popularity pattern of the POI is time-sensitive. For example, a coffee shop is a hotspot in the morning, and a bar is a hotspot in the evening. Moreover, the POI recommendation system must serve the new users as efficiently as others. The dearth of data should not affect the performance. Hence, the use of spatial-temporal content alone cannot suffice the scenario. Neighborhood effects must be integrated effectively to alleviate the impending issues.

Problem2: neighborhood estimation: The friend circle of the user shapes their preferences. However, social links are not confined to known friends. Correlations can be ravaged even in the temporal context, spatial grids, and ROIs. These connections are dormant yet can be extremely useful to mine the popular POIs, especially for cold-start users. There are two major challenges to this approach. First, how much trust can be propagated to different social links in different aspects? Second, the social links are often overlapped; how can we bifurcate them efficiently to serve the purpose?

3.2 Implicitly trusted neighbors (RSTSE-IMPLICIT)

Let N be the set of all friends v, for the user u such that v ϵ N_u, and $u,vϵ\mathcal{U}$. We attempt to provide a relevance score S_u,v to each peer of the user. It has two aspects. First, a friend whose check-in coincides more with the target user, such friends are allotted a higher weightage. We utilize the inverse Kullback-Leibler (KL) divergence score (Feng et al., 2018). We create a ${\mathcal{P}}^{\text{I}}$ for each user and his friends. This provides us with the probability distribution of their preferences. Let ${\mathcal{P}}_{\text{u}}^{\text{I}}$ and ${\mathcal{P}}_{\text{v}}^{\text{I}}$ denote the probability distribution of preferences for the target user and the friends, respectively. Then, we calculate the KL divergence score between the target user's preferences and his friends. This annotates the difference in tastes. A lower KL divergence suggests more similarity. Based on the inverse KL divergence score, we assign the weights w_KL to each friend of the user. Equations 2, 3 describe the process mathematically. Second, an inactive friend or a friend whose check-in records are older to the time of reference cannot be relied to capture the relevant trend in POIs. Their check-ins cannot reflect popularity, temporal or seasonal propensity of different POIs. Furthermore, newer check-ins might include newer POIs that are more popular recently. This concept can also be utilized in allocating weights to different peers as more active a friend is recently, the more priority should be allotted to them so that their records bear greater influence in the recommendation process and consequent decision making. This is decided by using one-dimensional power law (Adamic and Huberman, 2000) and activity recency. To measure recency, we use the max timestamp of the users from the check-in information which is used by one-dimensional power law to compute the weights w_1D as denoted in Equations 4, 5. Finally, to calculate the implicit trust relevance, score S_u,v, we deploy a weighted sum approach as illustrated by Equation 6. The different friends of the user are sorted in the descending order of the score. For each user, using the friend's data, we extract the POIs L_u,l visited by the friends of the users, ranked by the score of friends who visited them.

$\begin{array}{ll}KL({\mathcal{P}}_u^I\left|\right|{\mathcal{P}}_V^I)={\displaystyle \sum _j}{\mathcal{P}}_u^I(j).\text{ log}\frac{{\mathcal{P}}_u^I(j)}{{\mathcal{P}}_v^I(j)}& (2)\end{array}$

$\begin{array}{ll}{w}_{KL}=\frac{1}{KL({\mathcal{P}}_u^I\left|\right|{\mathcal{P}}_v^I)+ϵ}& (3)\end{array}$

$\begin{array}{ll}{w}_{1D}={\displaystyle {\int }_0^{{t_s}_{u,v}}}{f}_{(p(t_s))(z)dz}=1-1{(+{t_s}_{u,v})}^{-{\beta }_0}& (4)\end{array}$

$\begin{array}{ll}{f}_{p(t_s)}=({\beta }_0-1){(1+t_s)}^{-{\beta }_0},t_s\ge 0,{\beta }_0>1& (5)\end{array}$

$\begin{array}{ll}{S}_{u,v}=\{\begin{array}{c}\lambda *w_{KL}+(1-\lambda )*w_{1D}if{w}_{KL}and{w}_{1D}arerelevant\\ 0otherwise\end{array}& (6)\end{array}$

where ${\mathcal{P}}_u^I(j)$, ${\mathcal{P}}_v^I(j)$ are the probability of j-th POI in the preference distribution, ϵ is the trivial positive quantity of value 1e − 10, and β₀, and λ are the controlling parameters whose values are set to 1.5 and 0.4, respectively.

3.3 Explicit trust estimation

3.3.1 Spatial neighbors (RSTSE-V)

In the real world, different users often have overlapping interests and hence have common visitation patterns. Figure 2 depicts the scenario. Using the spatial coincidence of visits, we aim to find the social links that are otherwise hidden within spatial grids. For this, we compute the preference distribution of each user using ${\mathcal{P}}^{\text{I}}$. Considering the impact of information decay, we utilize the time decay-based Jaccard similarity calculation method to identify the similarities between the neighbors, j_v. User's recent visits are important and can aid in identifying the popular POIs at the current time; hence, we use the exponential decay function. The recent co-occurrences are given higher weightage than the older ones. We calculate the time difference t_d between the reference timestamp defined by the target user and the time of co-occurrence of the visit. Then, the decay function is applied to t_d to compute the impact score of co-occurrences denoted by D_t. Concomitantly, we estimate the Jaccard similarity index of co-occurrences using these preference distributions. The mathematical process is denoted by Equations 7, 8. The obtained similarity score is multiplied by the respective time decay of the user–POI interaction for each of the common POI between the target user and the other users as in Equation 9. This provides us with the similar user order by the time-decayed similarity index $S_{u,v}^{st}$. The relevant POIs in RSTSE-V are obtained by considering both the personal preferences and the influence of peer groups. We extract the POIs from the user's preference distribution and combine it with the POIs from top 10 similar users sorted based on $S_{u,v}^{st}$ and form the relevant POI set $L_{u,v}^{st}$.

$\begin{array}{ll}{D}_t=e^{-\sigma .t_d}& (7)\end{array}$

$\begin{array}{ll}{j}_v=\frac{\left|{lp}_u\right|\cap \left|l{p}_v\right|}{\left|l{p}_u\right|\cup \left|l{p}_v\right|}& (8)\end{array}$

$\begin{array}{ll}{S}_{u,v}^{st}=j_v*D_t& (9)\end{array}$

where σ is the decay parameter set to 0.1.

Figure 2

Figure 2. Possibility of spatial co-occurrences.

3.3.2 Temporal neighbors (RSTSE-T)

Temporal content is quintessential for POI recommendation as it encapsulates two intriguing aspects. First, the preference for periodicity with time. The second is temporal asymmetry. POIs that are popular during the morning are not popular in the evening. Figure 3 depicts the analysis of the Gowalla dataset based on temporal aspects of a month. The check-in pattern is highly dynamic. RSTSE-T attempts to find the explicit trust relevance of the temporal neighbors who are not the user's direct friends, but their temporal trajectory has a similar pattern. To reduce the model's overfitting effect and complexity, we divide the 24-h time zone T in two windows; z₁, working hours from 8 A.M. to 8 P.M. and z₂, leisure hours from 8 P.M to 8 A.M. Next, we estimate the time difference t_θ between the reference time established by the target user and the timestamp of the user–POI interaction. The lesser this difference, the more recent the check-in activity and vice-versa. Penalize the older interaction by the penalization function τ^p as in Equation 10. If the t_θ is higher than the 6 h, i.e., halfway between the time slot, then the penalty is higher. Form a user–POI time matrix, p_u,t,p, where each entry record is a penalty amount as in Equation 11. Calculate the similarity between each pair of users u,v using this user-POI penalty matrix p_u,t,p and p_v,t,p as in Equation 12. Sort the temporal neighbors with the highest $S_{u,v}^t$, and compute the prospective POIs set $L_{u,v}^t$.

$\begin{array}{ll}{\tau }^p=\text{log}(1+\omega *t_{\theta }),\omega >0.6if{t}_{\theta }>6Hrs& (10)\end{array}$

$\begin{array}{ll}{p}_{u,t,p}=l{p}_k*{\tau }^p& (11)\end{array}$

$\begin{array}{ll}{S}_{u,v}^t=\frac{{\displaystyle {\sum }_{tϵT}}{\displaystyle {\sum }_{pϵL}}{p}_{u,t,p}.p_{v,t,p}}{\sqrt{{\displaystyle {\sum }_{tϵT}}{\displaystyle {\sum }_{pϵL}}{p}_{u,p,t}^2}\sqrt{{\displaystyle {\sum }_{tϵT}}{\displaystyle {\sum }_{pϵL}}{p}_{v,p,t}^2}}& (12)\end{array}$

where ω is the penalizing factor and set to 0.6 for t_θ < 6 Hrs and 0.8 for t_θ > 6 Hrs.

Figure 3

Figure 3. Temporal analysis of Gowalla dataset.

3.3.3 RadialNets within the bounded zone (RSTSE-D)

As per Tobler's first law of geography (Miller, 2004), near POIs are more closely related than distant POIs, so in RSTSE- D, we confide in the radial proximity of the POIs. The user defines the threshold distance d, which forms a bounded functional region Z_l. Then, using the location coordinates of the target user, we measure the Haversine distance between the target user's location and coordinates of all POIs $p_iϵ\mathcal{L}$. Then filter out POIs p_dl within the threshold d. For each of these POIs, we extract the users, sim_user as per Equation 13, who have visited them. Such users are called Radial Nets. Then, we estimate their activity ratio, a_r (Equation 14) which is the ratio visits of the user at the p_dl and the total number of visits of similar user. With a_r sort the users in the descending order. For each sim_user, calculate the preference distribution for each p_dl. This reflects the user's likelihood of visiting the POIs. Using this distribution, we compute the top POIs set $L_{u,p,d}^{poi}$ within Z_l. Figure 4 depicts the process of RSTSE-D.

$\begin{array}{ll}sim\text{\_}user={\mathcal{P}}_k^I|kϵp_{d_l}& (13)\end{array}$

$\begin{array}{ll}{a}_r(u|\mathcal{U})=\frac{{\mathcal{V}}_u(p_{d_l})}{{\displaystyle {\sum }_{p_{d_l}ϵ\mathcal{L}}}sim\text{\_}user(p_{d_l})}& (14)\end{array}$

Figure 4

Figure 4. RSTSE-D flowchart.

3.3.4 SocialBridges in mutual connections (RSTSE-Trans)

Friend-of-friend relations have substantial potential to impact the user's decision to visit a POI. We model them as transitive relations and consider them as SocialBridges. In RSTSE-Trans, we propose modifying the Adamic Adar algorithm (Adamic and Adar, 2003). Per the basic Algorithm, the rare items have more weight than the bulk ones. Figure 5 explains the same. A and B have a common neighbor, C. However, in case 1, C is more shared with other users than in case 2. Thus, there are more chances of connections between A and B in case 2. Mathematically, Adamic Adar is represented as in Equation 15.

$\begin{array}{ll}S\left(A,B\right)={\displaystyle \sum _{CϵN(A)\cap N(B)}\frac{1}{\text{log}\left|N\left(C\right)\right|}}& (15)\end{array}$

where N (A), N (B), and N (C) are the neighbor set of A, B, and C.

Figure 5

Figure 5. Illustration of Adamic Adar.

Modifying Adamic Adar: Social networks are dynamic. Their mutual connections cannot always be taken to have the same preferences. We aim to incorporate the preferences of only neighbors with similar tastes to the target user. Link prediction algorithm Adamic Adar predicts the possibility of the link based on the sharing of the common connection, as already explained. We propose a group anchor effect according to which if the location interaction pattern of the group (A, C) is not similar to the group (B, C), then the probability of a link between A and B is negligent. For this, we compute the interaction frequency based on the recent visits for (A, C) and (B, C). For the given time window τ, we compute the recency-based weight ω_t for the interaction between the group and the POI using the user-defined reference time t and the interaction time T. These weights are normalized to deduce the interaction pattern IP for the concerned group. The normalized weights are used to calculate the similarity score R_A,C,B between the two groups. These scores are then utilized in modified Adamic Adar to estimate the probable likelihood of the link $S_{u,v}^{trans}$. Equations 16–19 represent the process mathematically.

$\begin{array}{ll}{\omega }_t=\frac{1-(t-T)}{\tau }& (16)\end{array}$

$\begin{array}{ll}I{P}_{A,C}=\frac{\sum {\omega }_t}{\sum {\omega }_{\tau ,(A,C)}}& (17)\end{array}$

$\begin{array}{ll}{R}_{A,C,B}=si{m}_{(A,C)and(B,C)}=\frac{{\displaystyle {\sum }_{pϵL}}I{P}_{A,C}.I{P}_{B,C}}{\sqrt{{\displaystyle {\sum }_{pϵL}}I{P}_{A,C}^2}\sqrt{{\displaystyle {\sum }_{pϵL}}I{P}_{B,C}^2}}& (18)\end{array}$

$\begin{array}{ll}{S}_{u,v}^{trans}={\displaystyle \sum _{wϵN(u)\cap N(v)}}\frac{R_{A,C,B}}{\text{log}\left|N(w)\right|+1}& (19)\end{array}$

The POI set $L_{u,p}^{trans}$ for the user, u is calculated considering the neighbors and their preference for the POIs unvisited by the target user. Rank them to filter the higher-ranking potential POIs $L_u^{trans}$ that might interest users.

In RSTSE-C, the complete set of neighboring POIs is identified as in Equation 20.

$\begin{array}{r}{L_u=(1-\alpha -\beta -\gamma -\delta )L}_{u,v}\\ +\left(\alpha L_{u,v}^{st}+\beta L_{u,v}^t+\gamma L_{u,v}^{trans}+\delta L_{u,v,p,d}^{poi}\right)& (20)\end{array}$

where α, β, γ, δ are the assigned weights to balance the similarity count of neighbors such that α + β + γ + δ = 1.

3.4 Recommendation using neural collaborative filtering

RSTSE-C uses neural collaborative filtering (NCF) (He et al., 2017) for top-k POI recommendation. Figure 6 shows a schematic framework of our approach. We use user embeddings, POI embeddings (Equation 21), and social embeddings (Equation 20) to mine the appropriate POIs.

$\begin{array}{ll}{S}_u={\displaystyle \sum }(S_{u,v},S_u^{st},S_u^t,S_{u,p,d}^{poi},S_u^{trans})& (21)\end{array}$

Figure 6

Figure 6. A schematic diagram of RSTSE framework.

3.4.1 Interactions between users and popular POIs

GMF in NCF deploys element-wise products to capture the latent feature vector. We use one-hot encoding on user_id and POI_id and form the user's latent feature vector R_Uu, POI latent feature vector Q_Lp, trusted user latent feature vector TU_Sp, and neighbor feature vector N_Su using user vectors U_u, popular POIs vector L_u, and the neighbors N_u as in Equation 22.

$\begin{array}{ll}\{\begin{array}{c}{R}_{U_u}={\lambda }_1{U}_u\\ Q_{L_p}={\lambda }_{2\text{u}}\\ {TU}_{S_p}={\lambda }_3{L}_u\\ N_{S_u}={\lambda }_4{N}_u\end{array}& (22)\end{array}$

where λ₁, λ₂, λ₃, and λ₄ define the controlling parameters. We augment NCF using an attention mechanism and obtain the final user vector $R_{U_u}^{\prime }$ and POI vector ${LQ}_{L_p}^{\prime }$ respectively as in Equations 23, 24.

$\begin{array}{ll}{\varphi }^{GMF}=R_{U_u}^{\prime }\odot {LQ}_{L_p}^{\prime }& (23)\end{array}$

$\begin{array}{ll}\hat{y}=a{t}_{out}^{\prime }(h^t(R_u\odot {LQ}_l))& (24)\end{array}$

where $a{t}_{out}^{\prime }$ = sigmoid function $\sigma (x)=\frac{1}{1+e^{-x}}$ and h^t is edge weight for output.

3.4.2 Capturing non-linear interaction between users and popular POIs

MLP unit of NCF learns the non-linear user–POI interactions as shown in Equation 25. The final output function of MLP using the ReLU activation function is as per Equation 26.

$\begin{array}{ll}\{\begin{array}{c}{z}_1={\varphi }_0(R_u,{LQ}_l)=\left[\begin{array}{c}{R}_u\\ {LQ}_l\end{array}\right]\\ {\varphi }_1^{MLP}(z_1)=a{t}_1(W_2^t{z}_1+b_2)\\ ....\\ {\varphi }_O^{MLP}(z_{o-1})=a{t}_o(W_o^t{z}_{0-1}+b_o)\end{array}& (25)\end{array}$

where $W_i^t$, b_i, and at_i are the weight matrix, bias vector, and activation function for the i-th layer.

$\begin{array}{ll}{\widehat{y}}_{MLP}=\sigma (h^t\left({\varphi }_O^{MLP}\left(z_{0-1}\right)+c\right)& (26)\end{array}$

The final recommendations from the NCF are obtained using the recommendations of both the GMF and MLP units as per Equation 27.

$\begin{array}{ll}\{\begin{array}{c}{\varphi }^{GMF}={R^{\prime }}_{U_u}\odot LQ{\prime }_{L_p}\\ {\varphi }_O^{MLP}\left(z_{o-1}\right)=a{t}_o(W_o^t(a{t}_{o-1}\left(\dots .a_2\left(W_2^t\left[\begin{array}{c}{R}_u\\ L{Q}_l\end{array}\right]+b_2\right)\mathrm{..}\right))\\ {\widehat{y}}_u=\sigma (h^t\left[\begin{array}{c}{\varphi }^{GMF}\\ {\varphi }^{MLP}\end{array}\right])\end{array}& (27)\end{array}$

where σ is the activation function.

4 Experiment and results

In this section, we explain the experimental setup and the results obtained. We also compare our model with state-of-the-art approaches and results surface our claims.

4.1 Experimental setup

The experimentation was carried out on an Intel(R) Core (TM) i7-6700 CPU @ 3.40GHz 3.41 GHz processor with 64-bit Windows 10 operating system installed. The memory capacity is 16 gigabytes. The programming was performed in Python 3.7 using the Jupyter Notebook environment. We utilized different libraries like numpy for computing operations, pandas for data manipulation and visualization, and scikit-learn for model analysis and computing performance. We also deployed the deep learning framework TensorFlow 6 1.2.0.

4.2 Data source and description

The experiment was done using three publicly available real-world location-based social networking (LBSN) datasets: Foursquare,² Gowalla,³ and Weeplaces (see footnote³). The recordings of Gowalla span from February 2009 to October 2010. The Foursquare dataset included in this study spans from April 2012 to September 2013. The Weeplaces datasets encompass a period spanning from November 2003 to June 2011. The spatial distribution of the three datasets is described in Figure 7 for 150,000 records. Also, as Foursquare datsets are concentrated more over United States of America (USA), we have plotted its distribution focusing on USA only. Records are characterized by quantifying the number of individuals utilizing a specific service, the number of POIs available, and the number of instances in which users have checked in. Every individual entry in the dataset is referred to as a check-in, which includes the user's unique identifier (user_ID), the POI's identifier (poi_ID), the latitude and longitude coordinates of the POI, the timestamp indicating the time of the visit, category information of the POIs, and friendship information of the users. Table 2 represents the various field present in the datasets along with their description. Figure 8 provides snippets from the data files of Gowalla data. Figure 8A denotes the five records for user_ID 0. The first column depicts the user_ID, the second column depicts the poi_ID, the third column denotes the frequency of visit of the user_ID at the respective poi_ID, and the fourth column denotes the timestamp of the visit to the respective poi_ID. Similarly, Figure 8B depicts the coordinate information of the different POIs. The first column depicts the poi_ID, the second column represents the latitude, and third column represents the longitude of the respective POIs. Figure 8C represents the friend data of different users. The first column presents the user_ID, and the second column depicts the friend information. All the user_ID and poi_ID are numeric data.

Figure 7

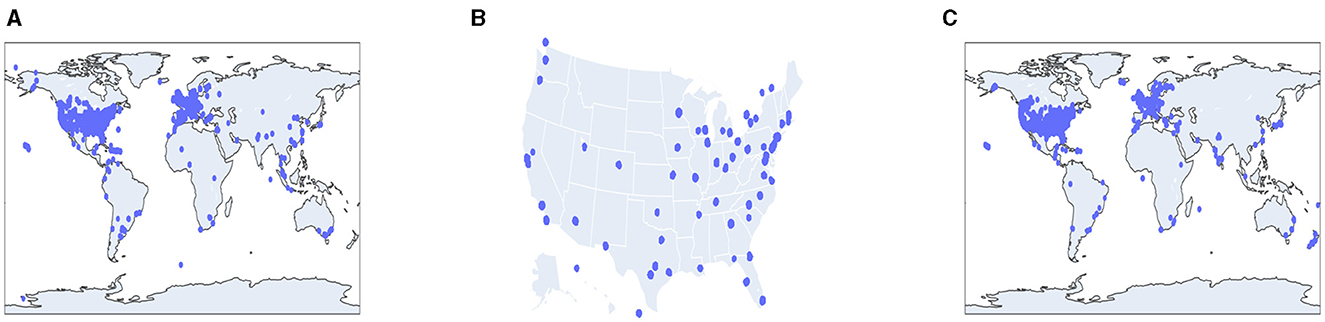
Figure 7. Spatial distribution of different datasets. (A) Weeplaces, (B) Foursquare, and (C) Gowalla.

Table 2

Table 2. Field description for datasets.

Figure 8

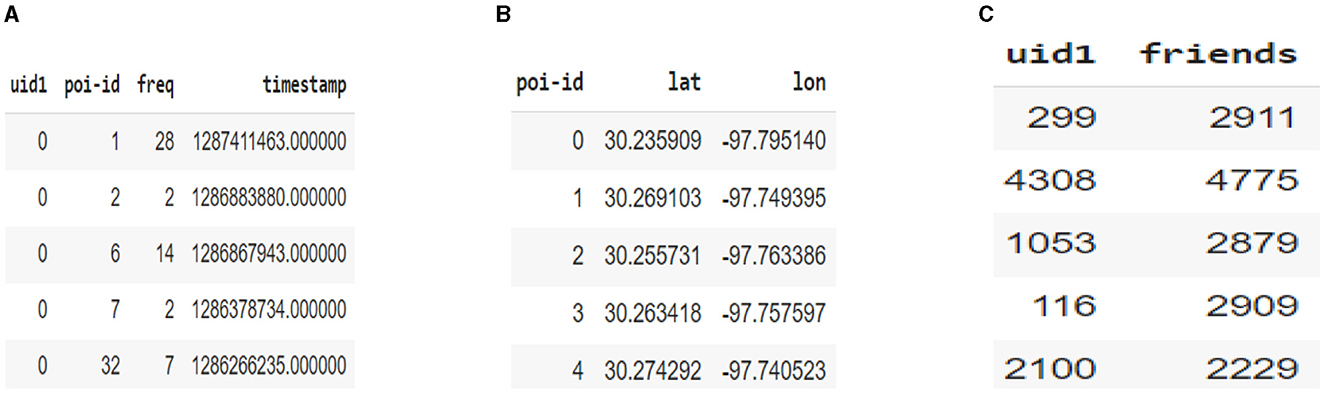
Figure 8. Illustration from data files of Gowalla. (A) check-ins data (B) POI coordinates' file (C) friends' data.

To avoid the impact of the geographical clustering phenomenon (Cho et al., 2011) and enhance the quality of our findings, we have excluded individuals with fewer than 15 check-in records and points of interest (POIs) with fewer than 10 check-ins in Gowalla dataset. Similarly, in Foursquare, we have filtered the users with <10 check-ins and the POIs with <10 users. Table 3 presents the statistical information of the dataset characteristics after filtering the data. Table 4 depicts the top-5 visited categories along with the number of check-ins in each recorded for the Gowalla and Weeplaces datasets. Further analysis showed that, from 6 A.M. to 6 P.M., the work/home category had maximum check-ins. Bars recorded maximum check-ins around 2 A.M. We have selected early 70% check-ins for training, most recent 20% check-ins as test data and the rest 10% as tuning data. Figure 9 presents the results of the social-correlation study conducted on the Gowalla dataset. This analysis examines the number of followers and the number of individuals the user is following, as well as the probability density function in degrees.

Table 3

Table 3. Datasets characteristics after pre-processing.

Table 4

Table 4. Datasets category-wise characteristics.

Figure 9

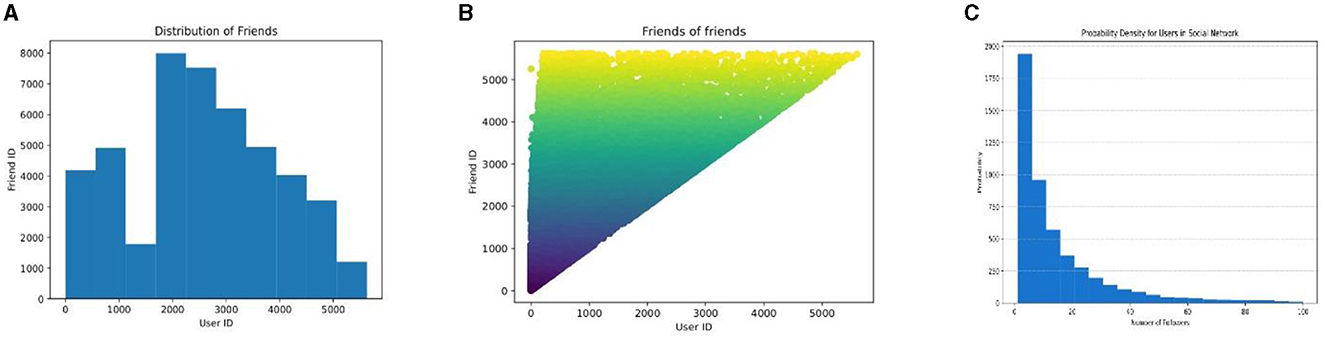
Figure 9. Social correlation analysis of Gowalla. (A) No. of followers of each user. (B) No. of people, each user is following. (C) PDF of in degrees.

4.3 Evaluation metrics

The performance was evaluated based on the following metrics :

1. Precision@k and Recall@k: Precision@k is defined as the ratio of POIs available for the recommendation to the k recommended POIs as per Equation 28. Recall@k is obtained by taking the ratio of available POIs to the N total POIs of the test set as in Equation 29.

$\begin{array}{ll}Precision@k=\frac{1}{n}{\displaystyle \sum _{u=1}^n}\frac{|I^{recom}\cap I^{test}|}{k}& (28)\end{array}$

$\begin{array}{ll}Recall@k=\frac{1}{n}{\displaystyle \sum _{u=1}^n}\frac{|I^{recom}\cap I^{test}|}{\left|I^{test}\right|}& (29)\end{array}$

where I^recom represents top-k POIs recommended, I^test is obtained from the POIs present in the test set, and k is varied to 5, 10, 15, and 20.

2. Acc@k: It is computed as the ratio of correct recommendations obtained to the total records present in the test set |D_test|. Equation 30 depicts the formula used. Here, k is varied to 5 and 10 only.

$\begin{array}{ll}Acc@k=\frac{\#hits@k}{\left|D_{test}\right|}& (30)\end{array}$

3. NDCG@k: It evaluates the recommendation system's performance by assigning higher ranks to top recommendations. The mathematical formulas used are expressed in Equations 31–34.

$\begin{array}{ll}re{l}_i=\{\begin{array}{c}1ifrecommendedPOIisingroundtruth\\ 0otherwise\end{array}& (31)\end{array}$

$\begin{array}{ll}IDCG@k={\displaystyle \sum _{i=1}^k}\frac{1}{{\text{log}}_2(i+1)}& (32)\end{array}$

$\begin{array}{ll}DCG@k={\displaystyle \sum _{i=1}^k}\frac{2^{re{l}_i}i-1}{{\text{log}}_2(i+1)}& (33)\end{array}$

$\begin{array}{ll}NDCG@k=\frac{DCG@k}{IDCG@K}& (34)\end{array}$

4. F-score: It is defined mathematically as in Equation 35. A higher F-score suggests a higher performance of the recommendation model. k is set to 5 and 10 only.

$\begin{array}{ll}F-score@k=\frac{2*Precision@k*Recall@k}{Precision@k+Recall@k}& (35)\end{array}$

4.4 Baseline methods

The model's performance has been evaluated against several state-of-the-art approaches as illustrated below. We have also imbibed ablation study in our work by using different aspects in entirety, i.e., RSTSE-C, RSTSE-V, RSTSE-T, RSTSE-D, and RSTSE-Trans.

1. FG-CF (Cai et al., 2022): A GCN-based approach that deploys users' social links and interaction modules.

2. PPR and GCN-LSTM (Dai et al., 2022): An LSTM-based model that uses social linkages via heterogeneous graphs and spatial information for recommending POIs.

3. DeepPoF (Safavi and Jalali, 2022): It uses deep CNN for computing social ties hidden in the location and spatial distribution of the user's activity region.

4. RecPOID (Safavi and Jalali, 2021): It uses a 10-layered CNN structure for mining the geographical and temporal similarity of the users.

5. NGPR (Yu et al., 2022): A POI recommendation method that integrates the time period and the users heterogeneous graph modeling with category information, geographic distance, and POI popularity.

6. CPAM (Yu et al., 2021): It combines the SG-PEM and the LMF models. While SG-PEM models vector representation for mining user similarity, LMF models users' personalized preferences.

7. SNPM (Yin et al., 2023): It is a Sequence-based Neighbour Search and Prediction Model (SNPM) for next POI recommendation that utilizes Sequence-based, Dynamic Neighbor Graph (SDNG) for seraching similarity in neighbourhood and posit a Multi-Step Dependency Prediction model (MSDP).

8. DAN-SNR (Huang et al., 2020): It uses a self-attention network combined with RNN to recommend POIs using sequential and social influence.

9. Flashback (Yang et al., 2020): It uses spatio-temporal contexts to search past hidden states with a high predictive power for location prediction.

10. STAN (Luo et al., 2021): An attention network-based model that harnesses spatio-temporal effect to model non-consecutiveness in check-ins and correlation.

11. GSBPL (Wang D. et al., 2023): A self-supervised behavior pattern that uses geographical and social context to encapsulate the implicit behavior patterns and short-term dynamic preferences.

12. LSTM (Hochreiter and Schmidhuber, 1997): The state-of-the-art approach of deep learning.

13. LLRec (Wang et al., 2020): An RNN-based model that adopts local device training.

14. PREFER (Guo et al., 2021): A federated learning model that utilizes user-independent parameters.

15. DCLR (Long et al., 2023): A decentralized collaborative filtering approach using geographical and semantically similar approaches.

16. PRBPL (Liu et al., 2021): A pairwise ranking approach to model geographical and categorical POI data.

17. Trust based (Xu et al., 2021a): A spatio-temporal trust mining approach.

18. Spatial binning (Acharya et al., 2023): Spatial binning for ROI mining using LSTM.

4.5 Experiments results

4.5.1 Precision@k and Recall@k

Table 5 illustrates the Precision@k results juxtaposed to different baselines. Precision@5 was the least for RecPOID for the Gowalla dataset, followed by a spike in FG-CF and PPR. DeepPOF performed better than others due to the incorporation of mean shift clustering to simulate the geographical latitude and longitude of the location. A similar trend was observed in Precision@10, @15, and @20. Among our models, RSTSE-Trans showed the lowest precision and was outperformed by RSTSE-T indicating temporal similarity in transient network for SocialBridges was not that effective. The performance model of RSTSE-Implicit and RSTSE-V was much comparative followed by RSTSE-C. In Gowalla, RSTSE-D showed a higher performance as opposed to the other two datasets. This anomaly might be due to inherent data distribution.

Table 5

Table 5. Precision results for Gowalla and foursquare.

For the Foursquare dataset, we have evaluated only four versions. CPAM performed quite poorly in precision statistics, observed from the Precision@10 and Precision@20 results. NGPR showed an increased performance, but the PPR model outperformed it. A similar trend was observed for recall statistics as well. Our approach outperformed every baseline method. The lowest precision was observed for RSTSE-D primarily as it encompasses a large ROI for POI recommendation. RSTSE-T performed better than RSTSE-D and RSTSE-V. RSTSE-C showed the highest performance as it imbibes all the versions. In recall for the Foursquare dataset, the lowest recall was observed for RSTSE-T, followed by RSTSE-D. RSTSE-V exhibited a high recall but was subdued by RSTSE-C.

Table 6 shows the Recall@k statistics (k = 5, 10, 15, and 20) for the Gowalla dataset. The lowest performance was shown by RecPOID, which FG-CF surpassed. The highest performance among the baselines was recorded for the PPR model for recall statistics. Among the models proposed for Gowalla dataset, the highest recall was noted for RSTSE-C, followed by the RSTSE-Implicit model. The next highest performance was shown by RSTSE-V, which shows the importance of geographical factors in the POI recommendation process. RSTSE-T and RSTE-trans recorded lower performances.

Table 6

Table 6. Recall results for Gowalla.

4.5.2 NDCG@k and accuracy

Figure 10 illustrates the values of NDCG@5 and NDCG@10 for the Gowalla and Weeplaces datasets. The discrepancy in data dissemination is visible in the larger decline of Gowalla compared with Weeplaces. The results compared with different state-of-the-art approaches illustrate the performance of our model. The different versions of the model RSTSE, namely, RSTSE-V, RSTSE-T, and RSTSE-C, perform better than any other method. Furthermore, RSTSE-T performs slightly lower than RSTSE-V and RSTSE-C for both datasets primarily due to the temporal content taken solely for the recommendation.

Figure 10

Figure 10. (A) NDCG@5 and @10 for Gowalla. (B) NDCG@5 and @10 for Weeplaces.

Applying the RSTSE algorithm on the Gowalla platform yielded an accuracy rate of 54.04%. Similarly, the Weeplaces platform achieved an accuracy rate of 35.73%, while the Foursquare platform reported an accuracy rate of 46.74%. The observed discrepancy can be attributed to the intrinsic variations in geographical distribution, as elucidated in Section 4.2, We have compared the baselines with the complete model RSTSE-C. Table 7 depicts the variations in accurcay@5 and acc@10 for the Gowalla datasets. Our model surpasses all other baseline models and presents a competitive technique for POI recommendation. The results presented in Table 7 were calculated at epochs 25 for better comparisons. The accuracy also varies with epochs. After 30, we observed a stabilization in accuracy. Also, at epoch 48, we observed a decline in the accuracy, and the optimal epoch selected was 25.

Table 7

Table 7. Accuracy comparisons of Gowalla @5 and @10.

4.5.3 Ablation study

To assess the efficacy of our suggested methodology, we examine five different versions of the RSTSE framework. Each employs a different component in its entirety. Table 8 presents accuracy variations for different versions of Gowalla and Weeplaces datasets. As the epochs increased, the accuracy increased with the stabilization after 30, as explained in Section 4.2. On Gowalla, the highest accuracy was obtained on the RSTE-V followed by RSTSE- Implicit. RSTSE-C showed an accuracy of 46.45%. According to the Gowalla dataset, after using the RSTSE-C method, it was shown that RSTSE-V scored higher than other versions. This indicates that geographical considerations significantly influence the choice of check-in at a POI. Users prefer visiting a POI close to a previously visited POI, suggesting a tendency for connectedness between nearby locations. In the context of the Weeplaces dataset, principally due to the geographical distribution patterns seen in the check-in records RSTSE-C shows the highest accuracy. The RSTSE-D model exhibits a decrease in accuracy due to its limited focus on relationships within a confined geographic region, which may result in overlooking the fine details of adjacent POIs and the temporal dependencies of distant POIs. In addition, another contributing element to the observed disparity in performance is the uniformity of the component's contributions across various datasets. The influence of geographical factors is more pronounced in the context of Gowalla, but temporal check-ins are regarded as more dependable within the framework for Weeplaces. RSTSE-C displayed limited accuracy. RSTSE-Trans and RSTSE-T showed very low accuracy for Weeplaces hence we have not reported them.

Table 8

Table 8. Variation of accuracy for Gowalla and Weeplaces for different versions of RSTSE.

4.5.4 Parameter tuning

Equation 20 has suggested that there exist four weight parameters denoted as α, β, γ, and δ. The ideal values for these four parameters are determined by evaluating several iterations of RSTSE. For the Gowalla dataset, the ideal value obtained was 0.3 for α, 0.22 for β, 0.28 for γ, and 0.2 for δ. For the Foursquare dataset, due to the dearth of friendship data, we modeled only RSTSE-C, RSTSE-T, RSTSE-D, and RSTSE-Implicit. The values of hyperparameters were set as α = 0.4, β = 0.4, and δ = 0.2. If the value of α was increased beyond this value, the results neared the accuracy of RSTSE-T. To demark the impact of RSTSE-V, we opted for this value. Similarly, using the hit-and-trial method on Weeplaces, the value of α is 0.25 and the value of δ is 0.25. The learning rate was set as 0.0001. We have used Adam optimized. At these optimal settings, the F-scores at 5, 10, and 20 values for the Weeplaces dataset are compared in Table 9. Table 10 displays the top 5 recommended POIs compared with the actual POI for a randomly selected user. The recommended POIs provided by RSTSE demonstrate that new and unexplored POIs were suggested to the user, ensuring no duplication with the existing POIs. This implies that our model is effective.

Table 9

Table 9. F-score comparison for Weeplaces.

Table 10

Table 10. Comparisons between recommended POIs and real check-ins.

4.5.5 Memory and time analysis

The record of memory and time consumed for the Gowalla dataset is depicted in Table 11. As the number of epochs increased, the consumed time also increased and so was the memory used. Furthermore, variation in time consumption is observed by decreasing the learning rate.

Table 11

Table 11. Memory and time consumption for RSTSE models on the Gowalla dataset.

4.6 Cold-start users

Cold-start users refer to individuals who have a restricted or non-existent amount of data. Providing recommendations for POIs to users with specific preferences and requirements poses a significant challenge. The proposed RSTSE approach has the potential to offer effective recommendations for users by leveraging user similarity and trust networks within a geographical and temporal framework. Users new to the system are provided recommendations based on RSTSE-Trans and RSTSE-D. Using the user-specified reference time and the distance threshold, the system can build a network of social neighbors for the target user within the ROI. This enables the provision of POI recommendations for consumers with limited historical data, only relying on their present location.

Further, in RSTSE-Trans, with temporal context, the recent check-ins of the other users can be ascertained. Since there are no previous social links between the target users and the other users, the system considers every user group as a similar user with the similarity index 1 and calculates the potential SocialBridges. The preference mining is done on these social links. The results are combined with the results of RSTSE-D to facilitate the final recommendations provided. The recommendations for the cold-start users often encapsulate the serendipity, i.e., new POIs are also recommended.

4.7 Complexity analysis

Different components of RSTSE contribute a significant amount to its complexity. Let |U| represents the cardinality of the set of users in the dataset. The computation of KL divergence takes O(k*N), where N is the unique POIs and k is the number of friends. The overall complexity of mining implicitly trusted neighbors is O(k*max(N, M)), where M is the integration method of one-dimensional power law. RSTSE-V has three elements, a decay rate with the complexity of O(n), where n is the number of co-occurrences, Jaccard coefficient for spatial co-occurrences with complexity of O(k), where k is the number of users with spatial co-occurrences and POIs probability calculation with complexity of O(k*N). The overall complexity here is thus O(max(n, k, k*N)). The RSTSE-T framework considers the time dimension when considering the user's social group. The computational complexity of this operation is determined by the variables representing the number of users in the temporal dimensions (k), the number of time slots (T), and the number of POIs. As a result, the complexity may be expressed as O(|k*U|*|T|*(|L| + |U|)), where |k*U| represents the product of the number of users and the temporal dimension, |T| represents the number of time slots, and (|L| + |U|) represents the sum of the number of points of interest and the number of users. We determine the time complexity of RSTSE-D based on set U, the POIs L, and the potential neighbors within the proximity. Specifically, it may be expressed as O(|U/|∧2|*|L|). In RSTSE-Trans, the recommendation is achieved using peer groups and a modified Adamic-Adar algorithm. The algorithm's temporal complexity is contingent upon the cardinality of the user set U and the magnitude of the user's direct social relationships, denoted as M. The time complexity of this procedure is determined to be O(|U|∧3 * M).

4.8 Discussion

RSTSE-C utilizes spatial co-occurrences, temporal coincidences, and radial activity zones for mining the dormant social linkages besides using the social link data provided already. The ablation study, with each aspect individually, presents some intriguing facts. First, the social circle of the user does not necessarily suggest similarity. The KL divergence scores were evidence. We cannot leverage equal importance to all our direct friends. Second, the time decay is quintessential in the POI recommendation; otherwise, the stale recommendations are bound to come. Third, the group anchor effect is dominant yet unexplored in recent research. The probability of linking with the friend of a friend is not only less but also decreases with the expanse of the group. Fourth, different types of friends have different importance in POI recommendation, as evidenced by the probability scores. The study of RSTSE-C and its variants exhibit promising results in terms of evaluation metrics. However, the model depends heavily on the user's data. The quality of data bears a great influence on the recommendation process. Hence, if the LBSN data are incomplete, noisy, or biased, the POI recommendations will be affected adversely.

The latent vector dimension D was set to 64 to accommodate a suitable trade-off between the training time and information modeling. Accuracy stabilized after D=64. The threshold distance d value needs to be carefully set, as the larger the value, the more POIs will exhibit the phenomenon of clustering and overlapping. It was thus set to 100 for Foursquare and 50 for Gowalla. This variation was to include enough number of results for each user. The values of k for top-k recommendations were also kept low to check the results, alleviating the impact of biases in the bulk of data present in the ground truth. Our focus in the model is recency and proximity; in the future, we aim to include popularity bias and seasonal preferences in the data mining. Utilizing different aspects of multimodal data, such as text, image, time series, and sensor data, we aim to enhance accuracy and explore the diversity aspect too.

5 Conclusion

This study proposes a RSTSE approach for jointly modeling social and spatio-temporal information. It has two phases. The incipient phase involves estimating potential neighbors and the probability estimation of the POI to be recommended from the target users' perspective. The telic phase is an NCF-based POI recommendation. The social ties in this research are exploited by the friends' relations and the spatial, temporal, and location precepts. We attempt to address the issue of cold-start users and data sparsity by jointly modeling the current location and reference time given by the user. This allows the information decay and recency in the check-in data. The results suggest that social relations are quintessential in POI recommendation as they encapsulate several hidden, overlooked dependencies. The critical analysis of the results suggested that the spatial factor dominates the recommendation process. The social factor needs to be used concomitantly with the other attributes to enhance the process. Solely leveraging the POI recommendation on either of the factors would not suffice. Furthermore, not all social ties have the same importance. We deciphered that spatial co-occurrence of the visit veiled important social neighbors more than any other factor. The group anchor effect proposed was also dominant, as suggested by the results. In this approach, we provided a way to distinguish between the friend's relationship and acquaintance relations and their probable impact on POI recommendation.

In the future, we aim to extend this approach to cross-domain recommendation, wherein auxiliary information concerning the domain characteristics is imperative in addition to the social, spatial, and temporal information. Incorporating a mechanism to learn the short-term and long-term dependencies from the user's check-ins and model the dynamic preference change would also be an intriguing task. Additionally, we aim to utilize different learning paradigms such as meta-learning and adversarial learning to incorporate sequential POI recommendations. The exploitation of explicit and implicit social trust levels also poses privacy concerns. The outcome of the approach can be used in business proliferation, healthcare, real-time event planning, etc.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MA: Conceptualization, Data curation, Methodology, Resources, Validation, Visualization, Writing – original draft. KM: Formal analysis, Investigation, Supervision, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

We extend our sincere gratitude to the editor and the reviewers for providing their valuable insight through comments and reviews that refined and improved our work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^https://www.yelp-press.com/news

2. ^https://sites.google.com/site/yangdingqi/home/foursquare-dataset

3. ^https://www.yongliu.org/datasets/

References

Acharya, M., and Mohbey, K. K. (2023). Differential privacy-based social network detection over spatio-temporal proximity for secure poi recommendation. SN Comput. Sci. 4:252. doi: 10.1007/s42979-023-01683-7

Crossref Full Text | Google Scholar

Acharya, M., Yadav, S., and Mohbey, K. K. (2023). How can we create a recommender system for tourism? A location centric spatial binning-based methodology using social networks. Int. J. Inf. Manage. Data Insights. 3:100161. doi: 10.1016/j.jjimei.2023.100161

Crossref Full Text | Google Scholar

Adamic, L. A., and Adar, E. (2003). Friends and neighbors on the web. Soc. Netw. 25, 211–30. doi: 10.1016/S0378-8733(03)00009-1

Crossref Full Text | Google Scholar

Adamic, L. A., and Huberman, B. A. (2000). Power-law distribution of the world wide web. Science 287, 2115–2115. doi: 10.1126/science.287.5461.2115a

Crossref Full Text | Google Scholar

Bordbar, J., Mohammadrezaie, M., Ardalan, S., and Shiri, M. E. (2022). Detecting fake accounts through generative adversarial network in online social media. arXiv preprint arXiv:2210.15657.

Google Scholar

Cai, L., Xu, J., Liu, J., and Pei, T. (2018). Integrating spatial and temporal contexts into a factorization model for poi recommendation. Int. J. Geogr. Inf. Sci. 32, 524–46. doi: 10.1080/13658816.2017.1400550

Crossref Full Text | Google Scholar

Cai, Z., Yuan, G., Qiao, S., Qu, S., Zhang, Y., Bing, R., et al. (2022). Fg-cf: friends-aware graph collaborative filtering for poi recommendation. Neurocomputing 488, 107–19. doi: 10.1016/j.neucom.2022.02.070

Crossref Full Text | Google Scholar

Chen, L., Cao, J., Liang, W., Wu, J., and Ye, Q. (2022). Keywords-enhanced deep reinforcement learning model for travel recommendation. ACM Trans. Web. 17, 1–21. doi: 10.1145/3570959

Crossref Full Text | Google Scholar

Chen, L., Cao, J., Tao, H., and Wu, J. (2023a). Trip reinforcement recommendation with graph-based representation learning. ACM Trans. Knowl. Discov. Data. 17, 1–20. doi: 10.1145/3564609

Crossref Full Text | Google Scholar

Chen, L., Zhu, G., Liang, W., and Wang, Y. (2023b). Multi-objective reinforcement learning approach for trip recommendation. Expert. Syst. Appl. 226:120145. doi: 10.1016/j.eswa.2023.120145

Crossref Full Text | Google Scholar

Chen, X., Zeng, Y., Cong, G., Qin, S., Xiang, Y., and Dai, Y. (2015). “On information coverage for location category based point-of-interest recommendation,” in Proceedings of the AAAI Conference on Artificial Intelligence, 29. doi: 10.1609/aaai.v29i1.9191

Crossref Full Text | Google Scholar

Cheng, X., Li, N., Rysbayeva, G., Yang, Q., and Zhang, J. (2023). Influence-aware successive point-of-interest recommendation. World Wide Web. 26, 615–629. doi: 10.1007/s11280-022-01055-w

Crossref Full Text | Google Scholar

Cho, E., Myers, S. A., and Leskovec, J. (2011). “Friendship and mobility: user movement in location-based social networks,” in Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 1082–1090. doi: 10.1145/2020408.2020579

Crossref Full Text | Google Scholar

Dai, S., Yu, Y., Fan, H., and Dong, J. (2022). Spatio-temporal representation learning with social tie for personalized poi recommendation. Data Sci. Eng. 7, 44–56. doi: 10.1007/s41019-022-00180-w

Crossref Full Text | Google Scholar

Dong, L., Li, Y., Yin, H., Le, H., and Rui, M. (2013). The algorithm of link prediction on social network. Mathem. Problems Eng. 2013:125123. doi: 10.1155/2013/125123

Crossref Full Text | Google Scholar

Duan, Z., Gao, Y., Feng, J., Zhang, X., and Wang, J. (2020). “Personalized tourism route recommendation based on user's active interests,” in 2020 21st IEEE International Conference on Mobile Data Management (MDM) (IEEE), 729–734. doi: 10.1109/MDM48529.2020.00071

Crossref Full Text | Google Scholar

Feng, L., Wang, H., Jin, B., Li, H., Xue, M., Wang, L., et al. (2018). Learning a distance metric by balancing kl-divergence for imbalanced datasets. IEEE Trans. Syst. Man Cybern. 49, 2384–2395. doi: 10.1109/TSMC.2018.2790914

Crossref Full Text | Google Scholar

Gan, M., and Tan, C. (2023). Mining multiple sequential patterns through multi-graph representation for next point-of-interest recommendation. World Wide Web. 26, 1345–1370. doi: 10.1007/s11280-022-01094-3

Crossref Full Text | Google Scholar

Griesner, J-. B., Abdessalem, T., and Naacke, H. (2015). “Poi recommendation: towards fused matrix factorization with geographical and temporal influences,” in Proceedings of the 9th ACM Conference on Recommender Systems, 301–304. doi: 10.1145/2792838.2799679

Crossref Full Text | Google Scholar

Guo, Y., Liu, F., Cai, Z., Zeng, H., Chen, L., Zhou, T., et al. (2021). “Prefer: point-of-interest recommendation with efficiency and privacy-preservation via federated edge learning,” in Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies, 1–25. doi: 10.1145/3448099

Crossref Full Text | Google Scholar

Haldar, N. A. H., Li, J., Ali, M. E., Cai, T., Chen, Y., Sellis, T., et al. (2022). Top-k socio-spatial co-engaged location selection for social users. IEEE Trans. Knowl. Data Eng. 35, 5325–5340. doi: 10.1109/TKDE.2022.3151095

Crossref Full Text | Google Scholar

Hao, P-. Y., Cheang, W-. H., and Chiang, J. H. (2019). Real-time event embedding for poi recommendation. Neurocomputing 349, 1–11. doi: 10.1016/j.neucom.2019.04.022

Crossref Full Text | Google Scholar

He, X., Liao, L., Zhang, H., Nie, L., Hu, X., and Chua, T. S. (2017). “Neural collaborative filtering,” in Proceedings of the 26th International Conference on World Wide Web, 173–182. doi: 10.1145/3038912.3052569

Crossref Full Text | Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9, 1735–80. doi: 10.1162/neco.1997.9.8.1735

PubMed Abstract | Crossref Full Text | Google Scholar

Huang, L., Fu, M., Li, F., Qu, H., Liu, Y., Chen, W., et al. (2021). A deep reinforcement learning based long-term recommender system. Knowl. Based Syst. 213:106706. doi: 10.1016/j.knosys.2020.106706

Crossref Full Text | Google Scholar

Huang, L., Ma, Y., Liu, Y., and He, K. (2020). Dan-snr: a deep attentive network for social-aware next point-of-interest recommendation. ACM Trans. Internet Technol. 21, 1–27. doi: 10.1145/3430504

Crossref Full Text | Google Scholar

Javed, M. A., Younis, M. S., Latif, S., Qadir, J., and Baig, A. (2018). Community detection in networks: a multidisciplinary review. J. Netw. Comput. Applic. 108, 87–111. doi: 10.1016/j.jnca.2018.02.011

Crossref Full Text | Google Scholar

Kumar, S., Mallik, A., Khetarpal, A., and Panda, B. (2022). Influence maximization in social networks using graph embedding and graph neural network. Inf. Sci. 607, 1617–1636. doi: 10.1016/j.ins.2022.06.075

Crossref Full Text | Google Scholar

Kusupati, A., Singh, M., Bhatia, K., Kumar, A., Jain, P., Varma, M., et al. Fastgrnn: a fast, accurate, stable and tiny kilobyte sized gated recurrent neural network. Adv. Neural Inf. Process Syst. (2018) 31.

Google Scholar

Li, X., Cong, G., Li, X-. L., Pham, T-. A. N., and Krishnaswamy, S. (2015). “Rank-geofm: a ranking based geographical factorization method for point of interest recommendation,” in Proceedings of the 38th International ACM SIGIR Conference on Research and Development in Information Retrieval, 433–442. doi: 10.1145/2766462.2767722

Crossref Full Text | Google Scholar

Lian, D., Zhao, C., Xie, X., Sun, G., Chen, E., Rui, Y., et al. (2014). “Geomf: joint geographical modeling and matrix factorization for point-of-interest recommendation,” in Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 831–840. doi: 10.1145/2623330.2623638

Crossref Full Text | Google Scholar

Liu, B., Fu, Y., Yao, Z., and Xiong, H. (2013). “Learning geographical preferences for point-of-interest recommendation,” in Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 1043–1051. doi: 10.1145/2487575.2487673

Crossref Full Text | Google Scholar

Liu, Q., Mu, L., Sugumaran, V., Wang, C., and Han, D. (2021). Pair-wise ranking based preference learning for points-of-interest recommendation. Knowl. Based Syst. 225:107069. doi: 10.1016/j.knosys.2021.107069

Crossref Full Text | Google Scholar

Liu, S. (2018). User modeling for point-of-interest recommendations in location-based social networks: the state of the art. Mobile Inf. Syst. 2018, 1–13. doi: 10.1155/2018/1904636

Crossref Full Text | Google Scholar

Liu, W., Lai, H., Wang, J., Ke, G., Yang, W., Yin, J., et al. (2020). Mix geographical information into local collaborative ranking for poi recommendation. World Wide Web. 23, 131–152. doi: 10.1007/s11280-019-00681-1

Crossref Full Text | Google Scholar

Long, J., Chen, T., Nguyen, Q. V. H., and Yin, H. (2023). Decentralized collaborative learning framework for next poi recommendation. ACM Trans. Inf. Syst. 41, 1–25. doi: 10.1145/3555374

Crossref Full Text | Google Scholar

Luo, Y., Liu, Q., and Liu, Z. (2021). “Stan: spatio-temporal attention network for next location recommendation,” in Proceedings of the Web Conference, 2177–2185. doi: 10.1145/3442381.3449998

Crossref Full Text | Google Scholar

Massimo, D., and Ricci, F. (2021). Popularity, novelty and relevance in point of interest recommendation: an experimental analysis. Inf. Technol. Tour. 23, 473–508. doi: 10.1007/s40558-021-00214-5

Crossref Full Text | Google Scholar

Miller, H. J. (2004). Tobler's first law and spatial analysis. Ann. Assoc. Am. Geogr. 94, 284–289. doi: 10.1111/j.1467-8306.2004.09402005.x

Crossref Full Text | Google Scholar

Ning, W., Cheng, R., Shen, J., Haldar, N. A. H., Kao, B., Yan, X., et al. (2022). “Automatic meta-path discovery for effective graph-based recommendation,” in Proceedings of the 31st ACM International Conference on Information &Knowledge Management, 1563–1572. doi: 10.1145/3511808.3557244

Crossref Full Text | Google Scholar

Pan, Z., Cui, L., Wu, X., Zhang, Z., Li, X., Chen, G., et al. (2019). Deep potential geo-social relationship mining for point-of-interest recommendation. IEEE Access. 7, 99496–99507. doi: 10.1109/ACCESS.2019.2930311

Crossref Full Text | Google Scholar

Qin, Y., Wang, Y., Sun, F., Ju, W., Hou, X., Wang, Z., et al. (2023). “Disenpoi: disentangling sequential and geographical influence for point-of-interest recommendation,” in Proceedings of the Sixteenth ACM International Conference on Web Search and Data Mining, 508–516. doi: 10.1145/3539597.3570408

Crossref Full Text | Google Scholar

Rahmani, H. A., Aliannejadi, M., Ahmadian, S., Baratchi, M., Afsharchi, M., Crestani, F., et al. (2020). “Lglmf: local geographical based logistic matrix factorization model for poi recommendation,” in Information Retrieval Technology: 15th Asia Information Retrieval Societies Conference, AIRS 2019, Hong Kong, China (Springer), 66–78. doi: 10.1007/978-3-030-42835-8_7

Crossref Full Text | Google Scholar

Rahmani, H. A., Deldjoo, Y., Tourani, A., and Naghiaei, M. (2022). “The unfairness of active users and popularity bias in point-of-interest recommendation,” in International Workshop on Algorithmic Bias in Search and Recommendation (Springer), 56–68. doi: 10.1007/978-3-031-09316-6_6

Crossref Full Text | Google Scholar

Rios, C., Schiaffino, S., and Godoy, D. (2018). A study of neighbour selection strategies for poi recommendation in lbsns. J. Inf. Sci. 44, 802–17. doi: 10.1177/0165551518761000

Crossref Full Text | Google Scholar

Roick, O., and Heuser, S. (2013). Location based social networks-definition, current state of the art and research agenda. Trans. GIS. 17, 763–84. doi: 10.1111/tgis.12032

Crossref Full Text | Google Scholar

Rostami, M., Muhammad, U., Forouzandeh, S., Berahmand, K., Farrahi, V., Oussalah, M., et al. (2022). An effective explainable food recommendation using deep image clustering and community detection. Intell. Syst. Applic. 16:200157. doi: 10.1016/j.iswa.2022.200157

Crossref Full Text | Google Scholar

Rostami, M., Oussalah, M., Berahmand, K., and Farrahi, V. (2023). Community detection algorithms in healthcare applications: a systematic review. IEEE Access. 11, 30247–30272. doi: 10.1109/ACCESS.2023.3260652

Crossref Full Text | Google Scholar

Safavi, S., and Jalali, M. (2021). Recpoid: Poi recommendation with friendship aware and deep cnn. Fut. Internet 13:79. doi: 10.3390/fi13030079

Crossref Full Text | Google Scholar

Safavi, S., and Jalali, M. (2022). Deepof: a hybrid approach of deep convolutional neural network and friendship to point-of-interest (poi) recommendation system in location-based social networks. Concurr. Comput. 34:e6981. doi: 10.1002/cpe.6981

Crossref Full Text | Google Scholar

Song, C., Wen, J., and Li, S. (2019). “Personalized poi recommendation based on check-in data and geographical-regional influence,” in Proceedings of the 3rd International Conference on Machine Learning and Soft Computing, 128–133. doi: 10.1145/3310986.3311034

Crossref Full Text | Google Scholar

Sun, L. (2021). Poi recommendation method based on multi-source information fusion using deep learning in location-based social networks. J. Inf. Proc. Syst. 17, 352–368. doi: 10.3745/JIPS.01.0068

Crossref Full Text | Google Scholar

Wang, D., Chen, C., Di, C., and Shu, M. (2023). Exploring behavior patterns for next-poi recommendation via graph self-supervised learning. Electronics 12:1939. doi: 10.3390/electronics12081939

Crossref Full Text | Google Scholar

Wang, D., Wang, X., Xiang, Z., Yu, D., Deng, S., Xu, G., et al. (2021). Attentive sequential model based on graph neural network for next poi recommendation. World Wide Web. 24, 2161–84. doi: 10.1007/s11280-021-00961-9

Crossref Full Text | Google Scholar

Wang, K., Wang, X., and Lu, X. (2023). Poi recommendation method using lstm-attention in lbsn considering privacy protection. Complex Intell. Syst. 9, 2801–2812. doi: 10.1007/s40747-021-00440-8

Crossref Full Text | Google Scholar

Wang, Q., Yin, H., Chen, T., Huang, Z., Wang, H., Zhao, Y., et al. (2020). “Next point-of-interest recommendation on resource-constrained mobile devices,” in Proceedings of the Web Conference 2020, 906–916. doi: 10.1145/3366423.3380170

Crossref Full Text | Google Scholar

Wei, X., Liu, C., Liu, Y., Li, Y., and Zhang, K. (2023). Next location recommendation: a multi-context features integration perspective. World Wide Web. 26, 2051–74. doi: 10.1007/s11280-022-01126-y

Crossref Full Text | Google Scholar

Xi, D., Zhuang, F., Liu, Y., Gu, J., Xiong, H., He, Q., et al. (2019). “Modelling of bi-directional spatio-temporal dependence and users' dynamic preferences for missing poi check-in identification,” in Proceedings of the AAAI Conference on Artificial Intelligence, 5458–5465. doi: 10.1609/aaai.v33i01.33015458

Crossref Full Text | Google Scholar

Xu, C., Ding, A. S., and Zhao, K. (2021a). A novel poi recommendation method based on trust relationship and spatial-temporal factors. Electron. Commer. Res. Appl. 48:101060. doi: 10.1016/j.elerap.2021.101060

Crossref Full Text | Google Scholar

Xu, C., Liu, D., and Mei, X. (2021b). Exploring an efficient poi recommendation model based on user characteristics and spatial-temporal factors. Mathematics 9:2673. doi: 10.3390/math9212673

Crossref Full Text | Google Scholar

Yang, D., Fankhauser, B., Rosso, P., and Cudre-Mauroux, P. (2020). “Location prediction over sparse user mobility traces using rnns,” in Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, 2184–2190. doi: 10.24963/ijcai.2020/302

Crossref Full Text | Google Scholar

Yin, F., Liu, Y., Shen, Z., Chen, L., Shang, S., Han, P., et al. (2023). “Next poi recommendation with dynamic graph and explicit dependency,” in Proceedings of the AAAI Conference on Artificial Intelligence, volume 37, 4827–4834. doi: 10.1609/aaai.v37i4.25608

Crossref Full Text | Google Scholar

Yu, D., Wanyan, W., and Wang, D. (2021). Leveraging contextual influence and user preferences for point-of-interest recommendation. Multimed. Tools Appl. 80, 1487–14501. doi: 10.1007/s11042-020-09746-0

Crossref Full Text | Google Scholar

Yu, D., Yu, T., Wang, D., and Shen, Y. (2022). Ngpr: a comprehensive personalized point-of-interest recommendation method based on heterogeneous graphs. Multimed Tools Appl. 81, 39207–39228. doi: 10.1007/s11042-022-13088-4

Crossref Full Text | Google Scholar

Yu, F., Cui, L., Guo, W., Lu, X., Li, Q., Lu, H., et al. (2020). “A category-aware deep model for successive poi recommendation on sparse check-in data,” in Proceedings of the web conference 2020, 1264–1274. doi: 10.1145/3366423.3380202

Crossref Full Text | Google Scholar

Yue, C., Zhu, J., Zhang, S., and Ma, X. (2020). “Poi recommendations using self-attention based on side information,” in Data Science: 6th International Conference of Pioneering Computer Scientists, Engineers and Educators, ICPCSEE 2020, Taiyuan, China, Proceedings, Part II (Springer), 62–76. doi: 10.1007/978-981-15-7984-4_5

Crossref Full Text | Google Scholar

Zhang, Z., Liu, Y., Zhang, Z., and Shen, B. (2019). Fused matrix factorization with multi-tag, social and geographical influences for poi recommendation. World Wide Web. 22, 1135–150. doi: 10.1007/s11280-018-0579-9

Crossref Full Text | Google Scholar

Zhao, J., Li, H., Qu, L., Zhang, Q., Sun, Q., Huo, H., et al. (2022). Dcfgan: An adversarial deep reinforcement learning framework with improved negative sampling for session-based recommender systems. Inf. Sci. 596, 222–235. doi: 10.1016/j.ins.2022.02.045

Crossref Full Text | Google Scholar

Zhao, K., Cong, G., Yuan, Q., and Zhu, K. Q. (2015). “Sar: a sentiment-aspect-region model for user preference analysis in geo-tagged reviews,” in 2015 IEEE 31st International Conference on Data Engineering (IEEE), 675–686. doi: 10.1109/ICDE.2015.7113324

Crossref Full Text | Google Scholar