The hidden ontological variable in quantum harmonic oscillators

The standard quantum mechanical harmonic oscillator has an exact, dual relationship with a completely classical system: a classical particle running along a circle. Duality here means that there is a one-to-one relation between all observables in one model, and the observables of the other model. Thus the duality we find, appears to be in conflict with the usual assertion that classical theories can never reproduce quantum effects as observed in many quantum models. We suggest that there must be more of such relationships, but we study only this one as a prototype. It reveals how classical hidden variables may work. The classical states can form the basis of Hilbert space that can be adopted in describing the quantum model. Wave functions in the quantum system generate probability distributions in the classical one. One finds that, where the classical system always obeys the rule probability in = probability out, the same probabilities are quantum probabilities in the quantum system. It is shown how the quantum x and p operators in a quantum oscillator can be given a classical meaning. It is explained how an apparent clash with quantum logic can be rationalized.

1 Introduction

It has become customary to investigate quantum theories by proving that they cannot be represented in terms of ontological variables. These ontological variables, known as “local hidden variables” (LHV), are assumed to reproduce the results of all experiments that can be performed on a given quantum system, which is subsequently shown to lead to logical contradictions.

However, when the outcome of an extensively examined quantum experiment is compared with a classical theory, it is often the classical dynamics that is finished off in one short sentence: “This cannot be the result of a classical theory.” One may however suspect that the assumptions made concerning these LHV are too strict, so that there could be loopholes.¹ Many investigations are aimed at closing these loopholes by making further assumptions (Bell, 1964; Bell, 1982; Bell, 1987; Conway and Kochen, 2008; Clauser et al., 1969; Greenberger et al., 1990).

This, we claim, may not be the only way to improve our understanding of quantum mechanics. Here, we approach the question concerning the interpretation of quantum mechanics from the other end: which quantum systems do allow for classical variables, and can these models be extended to include physically useful ones? Can these models be demanded to obey (some form of) locality? Can we use them as building blocks? We claim that this is a rich field for further investigation (Brans, 1988; Vervoort, 2013; ’t Hooft, 2016; ’t Hoofta, 2023).

Here, a very important example is exhibited: the quantum harmonic oscillator. As we shall see, it contains a variable that can explain everything we see in a quantum harmonic oscillator, in terms of completely classical mathematical logic. Our variables are not hidden at all, and completely ontological; therefore we call our variable “COV”, standing for “Classical Ontological Variable.” The letter $L$ is omitted, since locality may not be guaranteed, and anyway, we do not intend to contradict earlier no-go theorems, but rather search for ways out.² Understanding the COV may be an important pathway that could lead us to new insights, perhaps even in model building (Jegerlehner, 2021; ’t Hooft, 2022).

The most important part of this paper is Section 2. Here we show how any quantum harmonic oscillator, contains an ontological degree of freedom. Using modern jargon, we observe that the quantum harmonic oscillator is dual to a classical particle on a circle.

Questions asked after a talk I presented at the Lindau Meeting, June/July 2024, made me realise that the features discussed below are not very well-known and therefore this short publication may be useful.

2 The harmonic oscillator

In one space-like dimension, consider the Hamiltonian³ $H$ of an elementary quantum harmonic oscillator in terms of the variables $x$ and $p$,

$\left[x,p\right]=i,H=\frac{1}{2}\left(p^2+x^2-1\right).(1)$

Planck’s constant will always be set as $\hslash =1$, and as such it merely relates the units of energy to the units of frequencies. Also the angular frequency $\omega$ is set to 1. The operator equations are

$\frac{\mathrm{d}x}{\mathrm{d}t}=i\left[H,x\right]=p,\frac{\mathrm{d}p}{\mathrm{d}t}=i\left[H,p\right]=-x.(2)$

We shall need the annihilation operator $a$ and the creation operator $a^{†}$, defined by

$\begin{array}{llllll}\hfill a& =\frac{1}{\sqrt{2}}\left(x+ip\right),\hfill & \hfill a^{†}& =\frac{1}{\sqrt{2}}\left(x-ip\right),\hfill & \hfill \left[a,a^{†}\right]& =1,\hfill \\ \hfill x& =\frac{1}{\sqrt{2}}\left(a+a^{†}\right),\hfill & \hfill p& =\frac{i}{\sqrt{2}}\left(a^{†}-a\right),\hfill & \hfill \left[x,p\right]& =i.\hfill \end{array}(3)$

(For practical reasons, the signs chosen in our definitions, deviate from the signs chosen in other work). The eigenstates $|{n\rangle }^E$ of $H$, and their eigenvalues $E_n$, are found as usual to obey:

$H|{n\rangle }^E=a^{†}a|{n\rangle }^E=E_n|{n\rangle }^E ,E_n=n=\mathrm{0,1},\cdots (4)$

This, of course, is a completely standard, quantum mechanical procedure applied to the harmonic oscillator, but now we claim that it is dually related to a completely classical model. The classical system we have in mind is a particle moving on the unit circle, with fixed velocity $v=1$, and period $=2\pi$. The solution of its e.o.m. is:

$\phi \left(t\right)=\phi \left(0\right)+t\mathrm{mod}2\pi ;(5)$

$\phi$ is constrained to the interval $\left[0 ,2\pi \right)$, where the boundary conditions are periodic.

To make our point, it is important to introduce (temporarily) a large integer $N$, and a variable $s=0 ,\dots ,N-1$, discretising the allowed values of $\phi$, as follows:

$\phi =2\pi s/N ,s=0 ,1 ,\cdots ,N-1.$

This matches with the introduction of small, finite time steps $\delta t=2\pi /N$. The $\phi$ states span an $N$-dimensional vector space $\{|{s\rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}}\}$, where the superscript “ont” stands for ontological.

The energy eigenstates $|{n\rangle }^E ,n=0 ,\cdots ,N-1$, of this rotating particle are superpositions of the ontological states:

$|{n\rangle }^E=\frac{1}{\sqrt{N}}{\displaystyle \sum _{s=0}^{N-1}}{e}^{\frac{2\pi }{N}ins}|{s\rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}},(6)$

with the inverse:

$|{s\rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}}=\frac{1}{\sqrt{N}}{\displaystyle \sum _{n=0}^{N-1}}{e}^{-\frac{2\pi }{N}ins}|{n\rangle }^E.(7)$

Note that these equations are merely discrete Fourier transformations. By checking the time dependence of $|{n\rangle }^E$ and $|{s\rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}}$, we see that

$|{n\rangle }^E\left(t\right)=e^{-int}|{n\rangle }^E\left(0\right).(8)$

$\text{and}|{s\rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}}\left(t\right)=|s-t/2\pi {N\rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}}\left(0\right).$

We now note that the first $N$ energy eigenstates of the harmonic oscillator, Equation 4, obey exactly the same Equation 8, and therefore Equations 6, 7 define $N$ states, obeying (Equation 5). There is an important reason to start with a finite number $N$. We see that, in these equations, the energy spectrum not only has a lowest energy state, $|{0\rangle }^E$, but also a highest energy state, $|N-{1\rangle }^E$. With strictly continuous angular variables $|{\phi \rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}}$, we could postulate an energy spectrum running from $-\infty$ to $+\infty$. This would not dually correspond to a harmonic oscillator.⁴ In this paper, we keep the lowest energy to be $E=0$, while the highest energy will be unbounded. This enables us to take the limit $N\to \infty$, where we can write:

$\phi =2\pi s/N ,\mathrm{d}\phi =\frac{2\pi }{N} ,\text{and}|{\phi \rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}}=|{s\rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}}/\sqrt{\mathrm{d}\phi };$

This turns Equations 6, 7 into

$|{n\rangle }^E=\frac{1}{\sqrt{2\pi }}\oint \mathrm{d}\phi e^{i\phi n}|{\phi \rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}} ,|{\phi \rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}}=\frac{1}{\sqrt{2\pi }}{\displaystyle \sum _{n=0}^{\infty }}{e}^{-i\phi n}|{n\rangle }^E.$

Thus we proved that harmonic oscillators can be described in terms of variables $|{\phi \rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}}$ that evolve deterministically. It is easy to see that, due to Equation 5, the wave function in terms of the $s$ variable (or the $\phi$ variable) does not spread. However, the wave function may not have been chosen to collapse. In that case, the probability distribution $\varrho \left({\phi }_1\right)={\left|\langle {\phi }_1|{\phi \rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}}\right|}^2$ can be seen to rotate along the circle in the same way as $\phi$ itself, so that we easily conclude that this probability distribution merely reflects the probabilities of the initial state.

This is a typical feature of the COV in a theory: these variables can be projected on the basis states of any Hilbert space, in which case the theory reproduces the probability distribution of the final states in terms of that of the initial states. It is very important, however, that this identification between Hilbert space and the space of classical probability distributions, only applies to the ontological basis of Hilbert space, that is, the basis spanned by all ontological states (the states $|{\phi \rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}}$ in the case of the harmonic oscillator).

Thus we emphasise: any quantum harmonic oscillator is mathematically equivalent to a periodically moving particle on a unit circle, and the wave function of a quantum harmonic oscillator merely reflects the probability distribution on this circle, if the initial state is not known with infinite precision.

Some useful auxiliary functions are

$G\left(z\right)\equiv {\displaystyle \sum _{n=1}^{\infty }}\sqrt{n}{z}^n ,\text{and}g\left(\phi \right)=G\left(e^{i\phi }\right).(9)$

Since the annihilation operator $a$, defined in Equation 3 obeys

$a|{n\rangle }^E=\sqrt{n}|n-{1\rangle }^E ,$

we can derive the matrix elements

${}^{\mathrm{o}\mathrm{n}\mathrm{t}}\langle {\phi }_1|a|{\phi }_2\rangle ^{\mathrm{o}\mathrm{n}\mathrm{t}}=\frac{1}{2\pi }{e}^{-i{\phi }_1}g({\phi }_1-{\phi }_2) ,$

$\text{and}{}^{\mathrm{o}\mathrm{n}\mathrm{t}}\langle {\phi }_1|a^{†}|{\phi }_2\rangle ^{\mathrm{o}\mathrm{n}\mathrm{t}}=\frac{1}{2\pi }{e}^{i{\phi }_2}g({\phi }_1-{\phi }_2) ,$

and from this, using Equation 3, we find the matrix elements of the operators $x$ and $p$ of the original quantum harmonic oscillator, in terms of the basis states $|{\phi \rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}}$:

$\langle {\phi }_1|x|{\phi }_2\rangle =\frac{1}{2\pi \sqrt{2}}\left(e^{-i{\phi }_1}+e^{i{\phi }_2}\right)g({\phi }_1-{\phi }_2);(10)$

$\langle {\phi }_1|p|{\phi }_2\rangle =\frac{i}{2\pi \sqrt{2}}\left(e^{-i{\phi }_1}-e^{i{\phi }_2}\right)g({\phi }_1-{\phi }_2).(11)$

It is possible to combine $N$ oscillators with different frequencies ${\omega }_i$, requiring us to generalise Equations 1–4 as

$H={\displaystyle \sum _{i=i}^N}{H}_i;H_i=\frac{1}{2}({\omega }_i^2{x}_i^2+p_i^2-{\omega }_i)={\omega }_i{a^{†}}_i{a}_i ,$

$a_i=\frac{1}{\sqrt{2}}({\omega }_i^{1/2}x+i{\omega }_i^{-1/2}p) ,$

$E_n^i=n_i{\omega }_i.$

This system of $N$ quantum harmonic oscillators, gives us $N$ variables of the COV type,

${\phi }_i(t)={\phi }_i(0)+{\omega }_{i}t\mathrm{mod}2\pi .\text{etc.}$

Ideas of treating quantized field theories as systems in a box with periodic boundary conditions were investigated by Dolce (2023). The wave equation then fixes the timelike component of the periodicities, and systems of this kind may then be regarded as multiple systems of COV variables.

3 On the analytic structure of the auxiliary function $G(z)$

The auxiliary function $G(z)$ is defined by Equation 9, but this only converges for values of $z$ within the unit circle, that is, $|z|<1$. Also, on the unit circle, this definition seems to diverge. Usually, expansions that oscillate wildly at some distance from the origin, can be defined by slightly smearing the coefficients, but here, this procedure is tricky. Indeed, the mathematics needed to show that the probabilities generated by applying $g(\phi )$ are uniquely defined and real, is rather delicate, an understatement, as shown in this section.

This section is intended only for mathematically minded readers. Their comments would be appreciated.

At finite $N$ the function

$G_N(z)={\displaystyle \sum _{n=1}^N}\sqrt{n}{z}^n(12)$

has $N$ zeros. Most of these will be close to the unit circle, $|z{|}_n\to 1$. The questions we would like to see answered are:

1. What will be the analytic structure of Equation 12 in the limit $N\to \infty$?

2. Is it possible at all to define and compute an analytic continuation for the function $G_N$ for $|z|>1$?

3. Where are the zeros and the poles of this analytic function?

4. Can one prove that

$G^{*}(z)\stackrel{?}{=}G(z^{*}),(13)$

so that the operators $x$ and $p$ defined in Equations 10, 11 can be seen to be Hermitian?

The last question is not quite trivial because one must first redefine the limit function $g(\phi )$, but by careful study of the equations, we found that Equation 13 is true, due to the fact that the coefficients $\sqrt{n}$ are all real, see Figure 2.

Figure 1

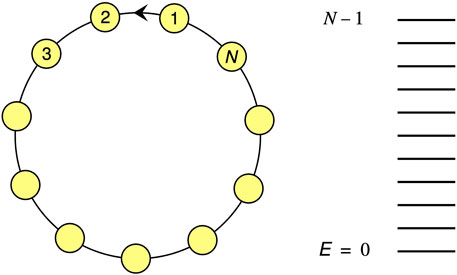
Figure 1. The ontological states $|{s\rangle }^{\mathrm{o}\mathrm{n}\mathrm{t}}$ when time is discrete, $\delta t=\frac{2\pi }{N}$. In this picture, the choice $N=11$ was made. The energy spectrum is shown; the energies form the same sequence as in harmonic oscillators, in particular if we take the limit $N\to \infty$.

Figure 2

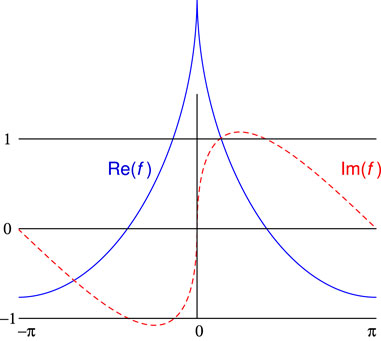
Figure 2. An accurate calculation of the function $f(\phi )$, defined in Equation 14. Blue solid line: its real part, dashed red line: its imaginary part. Both real part and imaginary part have a divergence in their first and second derivatives, apparently only at the origin, $\phi \to 0$.

First, we find that $G(z)$ is the second derivative of a function $F(z)$ that stays strictly finite on the unit circle (where $|z|=1$):

$\begin{array}{ccc}\hfill G(z)={(z{\partial }_z)}^{2}F(z) ,& \hfill & F(z)={\displaystyle \sum _{n=1}^{\infty }}{z}^n/(n\sqrt{n});\hfill \\ \hfill g(\phi )=\frac{-{\partial }^2}{\partial {\phi }^2}f(\phi ) ,& \hfill & f(\phi )=F(e^{i\phi }).\hfill \end{array}(14)$

Therefore, $F(z)$ is also accurately defined on the unit circle, but before using it to recuperate $G(z)$, one must carefully choose the order of the limits $N\to \infty$ and $|z|\to 1$. In practice, one encounters no problems, see Figure 2. A useful transformation may be the following:

$y=\frac{4z}{{(1+z)}^2} ,(15)$

and its inverse:

$z=-1+\frac{2}{y}\left(1-\sqrt{1-y}\right)=\frac{1}{4}y+\frac{1}{8}{y}^2+\cdots .(16)$

This can also be written as

$\sqrt{y}=\frac{2}{\sqrt{z}+1/\sqrt{z}}.(17)$

The second Riemann sheet describes the solution with the opposite sign of the square root on Equation 16. There, we get the solution

$\tilde{z}=-1+\frac{2}{y}\left(1+\sqrt{1-y}\right)=1/z ,$

which is easiest to see in Equation 17.

$G_N(z)={\displaystyle \sum _{n=1}^N}\sqrt{n}{\tilde{z}}^n={\displaystyle \sum _{n=1}^N}\sqrt{n}{z}^{-n};$

Figure 3 shows how the unit circle (Figure 3A) is mapped on the first Riemann sheet (Figure 3B). by the function (Equation 15), and how the branch cut at the right connects the two sheets. The function G(z) does go to infinity where the branch cut begins; the function F stays finite. They are related through Equation 14. By using Cauchy’s theorem one may be able to use this branch cut to define faster converging nexpressions for the function f(φ), and with that, our auxiliary function g(φ). Our attempts to use these observations for obtaining more convergent expressions for G(z) were however unsuccessful; much more work must be done to realise this, but an excessive list of calculations on this matter was not the aim of this paper. The function $G(z)$ does go to infinity where the branch cut begins; the function $F$ stays finite. They are related through Equation 14. Question (4) is now obviously answered in the positive.

Figure 3

Figure 3. (A) $y$ space, regions where the function $G(z)$ converges: domains $|z|\le .05,.1,\dots ,1.0$ are shown. (B) After the transformation (Equation 15), these domains turn into the regions shown here, that is, the entire $z$ plane up to the branch cut, will be singularity free if expressed in the new $y$ variable.

4 Epilogue

We showed how one may consider the quantum harmonic oscillator as an ontological theory in disguise. This is important since it appears to contradict theorems claiming that such a behaviour in quantum theories is impossible. Of course those theories were assumed to be far more general than a single harmonic oscillator, or even a simple collection of harmonic oscillators, but this now is a question of principle. Where is the dividing line? Which other quantum systems allow for the definition of COV variables, variables that commute with themselves and others at all times? If for instance one considers the quantum field theory of bosonic free particles in a box of an arbitrary shape in multiple dimensions, one may observe that this is merely a collection of harmonic oscillators.

One would be tempted to conclude that, therefore, bosonic particles in a box should also contain COV states (’t Hooft, 2023), but there is a complication in such systems: it is not easy to restore locality in the COV, since they are defined in momentum space. Turning these into variables that are local in position space appears not to be impossible, but then there is another complication: the operators one obtains that way seem to violate Lorentz invariance. This happens since the box is not Lorentz invariant. It is conceivably possible to restore Lorentz invariance, but we presently do not know how to do this in the Standard Model.

Thus our observations do not imply that text books on quantum mechanics have to be rewritten, except where they state explicitly that classical ontological variables cannot exist. Are local ontological variables forbidden? Locality is a meaningless concept in a single quantum harmonic oscillator. In this paper we show exactly what an ontological variable is. Emphatically, the ontological variable may be assumed to have a probability distribution as in quantum mechanics and in classical theories:

All uncertainties in the final state merely reflect the uncertainties in the initial state.

As soon as we claim that the initial state is exactly given, the wave function of the final state will collapse. The harmonic oscillator requires no special axiom for the collapse of the wave function – provided that we stick to the observables in $\phi$ space. There, we do not need to assume the existence of many universes. Just one universe, ours, is all we need to understand.

We emphasise that what we found here as a modification of the usual picture of quantum mechanics, is presumably merely the tip of an iceberg. It will not only apply to pure harmonic quantum oscillators, but also to many systems that evolve and interact in more generic ways. It is the fact that harmonic oscillators are periodic that counts. Whenever we consider a simplified model of nature where variables become periodic (for instance if we consider a box with periodic boundary conditions), one may observe that the energy spectrum consists of regular sequences of spectral lines (see Figure 1), so that harmonically oscillating fields enter the picture. Time-periodic motion is always classical. All we then need to talk about is how the probability distributions evolve.

In all classical systems, probability distributions evolve in the same orbits as the classical variables do. Consequently: probability in = probability out. If, in $\phi$ space, the initial state is defined with infinite precision, the final state will also be infinitely precise. This implies that the “typically quantum feature” of the collapse of the wave function, has its counter part in ontological theories. In the model we presented, the variables $\phi$ may be assumed to be infinitely sharply defined, but then also the final states will still be completely sharply defined; they always come in a collapsed form.

The clash with usual findings concerning the “impossible” physical reality of quantum mechanical phenomena and calculations, lies in the fact that the duality transformation is only applicable in one basis of Hilbert space: the one consisting of the ontological states. Choosing the conventional basis elements does not modify the results. The fact that we wish to emphasise is that, this “ontological” basis also never needs to be departed from, other than in approximative calculations: both the initial states and the final, observed states of any quantum process will be totally determined by the probabilities in the genuinely ontological basis; therefore, other choices of basis will never be necessary from a strictly logical viewpoint.

And it seems as if this possibility has never been considered before; however, see Refs Brans (1988) and Vervoort (2013). As for the numerous “quantum paradoxes” that have been formulated in the literature, the procedure needed, to formulate the probability patterns in an ontological basis has been worked out in Ref. Hooft et al. (2021). The guiding principle: always stay in the ontological basis.

The author benefitted from many discussions, notably with T. Palmer, C. Wetterich, M. Welling and D. Dolce.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

G’tH: Writing–review and editing, Writing–original draft.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹A very important loophole, not discussed further in this paper, is that models such as the Standard Model of the elementary particles, require perturbation expansions, which are known to be fundamentally divergent. This procedure introduces uncertainties (Hooft et al., 2021) that can be studied further, under the suspicion that this could be the cause of the tendency of quantum wave functions to spread.

²Locality is not a meaningful concept for the single harmonic oscillator.

³For convenience, we set the ground state energy to zero; ground-state energies can be returned whenever this might be needed.

⁴At finite $N$, there is an exact, dual relationship to the $SU\left(2\right)$ algebra, with $N=2\ell +1$.

References

Bell, J. S. (1964). On the Einstein-Podolsky-Rosen paradox. Physics 1, 195–200. doi:10.1103/physicsphysiquefizika.1.195

CrossRef Full Text | Google Scholar

Bell, J. S. (1982). On the impossible pilot wave. Found. Phys. 12, 989–999. doi:10.1007/bf01889272

CrossRef Full Text | Google Scholar

Bell, J. S. (1987). Speakable and unspeakable in quantum mechanics. Cambridge: Cambridge Univ. Press.

Google Scholar

Brans, C. H. (1988). Bell’s theorem does not eliminate fully causal hidden variables. Int. J. Theor. Phys. 27 (2), 219–226. doi:10.1007/bf00670750

CrossRef Full Text | Google Scholar

Clauser, J. F., Horne, M. A., Shimony, A., and Holt, R. A. (1969). Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23 (15), 880–884. doi:10.1103/Phys.Rev.Lett.23.880

CrossRef Full Text | Google Scholar

Conway, J. H., and Kochen, S. (2008). The strong free will theorem. arXiv: Quant-Ph 56 (2), 226.

Google Scholar

Dolce, D. (2023). Internal times and how to second-quantize fields by means of periodic boundary conditions. Ann. Phys. 457, 169398. doi:10.1016/j.aop.2023.169398

CrossRef Full Text | Google Scholar

Greenberger, D., Horne, M., Shimony, A., and Zeilinger, A. (1990). Bell’s theorem without inequalities. Am. J. Phys. 58 (12), 1131–1143. Bibcode:1990AmJPh.58.1131G. doi:10.1119/1.16243

CrossRef Full Text | Google Scholar

Hooft, G. ’t (2021). “Explicit construction of Local Hidden Variables for any quantum theory up to any desired accuracy, arxiv:2103.04335,” in: Quantum mechanics and fundamentality: naturalizing quantum theory between scientific realism and ontological indeterminacy, Springer Nature, chapt. 13, V. Allori ed arxiv:2103.04335[quant-ph].

Google Scholar

Jegerlehner, F. (2021). The Standard Model of particle physics as a conspiracy theory and the possible role of the Higgs boson in the evolution of the Early Universe. Acta Phys. Pol. B 52, 575. doi:10.5506/aphyspolb.52.575

CrossRef Full Text | Google Scholar

’t Hooft, G. (2023). An ontological description for relativistic, massive bosons. doi:10.48550/arXiv.2306.09885(quant-ph)09885

CrossRef Full Text | Google Scholar

’t Hooft, G. (2022). Projecting local and global symmetries to the Planck scale, dedicated to Prof. Chen Ning Yang at the occasion of his 100th birthday. ArXiv. Available at: http://arxiv.org/abs/2202.05367 (Accessed February 2022).

Google Scholar

’t Hooft, G. (2016). “The cellular automaton interpretation of quantum mechanics,” in Fundamental theories of physics (Springer International Publishing), 185. eBook ISBN 978-3-319-41285-6, Hardcover ISBN 978-3- 319-41284-9, Series ISSN 0168-1222, Edition Number 1. doi:10.1007/978-3-319-41285-6

CrossRef Full Text | Google Scholar

Vervoort, L. (2013). Bell’s theorem: two neglected solutions. Found. Phys. 43, 769–791. doi:10.1007/s10701-013-9715-7

CrossRef Full Text | Google Scholar