Single and entangled photon pair generation using atomic vapors for quantum communication applications

Significant progress has been achieved in leveraging atomic systems for the effective operation of quantum networks, which are essential for secure and long-distance quantum communication protocols. The key elements of such networks are quantum nodes that can store or generate both single and entangled photon pairs. The primary mechanisms leading to the production of single and entangled photon pairs revolve around established techniques such as parametric down-conversion, four-wave mixing, and stimulated Raman scattering. In contrast to solid-state platforms, atomic platforms offer a more controlled approach to the generation of single and entangled photon pairs, owing to the progress made in atom manipulation techniques such as trapping, cooling, and precise excitation schemes facilitated by the use of lasers. This review article delves into the techniques implemented for generating single and entangled photon pairs in atomic platforms, starting with a detailed discussion of the fundamental concepts associated with single and entangled photons and their characterization techniques. The aim is to evaluate the strengths and limitations of these methodologies and offer insights into potential applications. Additionally, the article will review the extent to which these atomic-based systems have been integrated into operational quantum communication networks.

1 Introduction

The emergence of quantum information science is set to revolutionize the field of quantum technologies. The development of secure quantum communication (Kimble, 2008) is a major part of it. Such schemes reduced eavesdropping and hacking owing to quantum phenomena like the superposition principle (Bouwmeester and Zeilinger, 2000), no-cloning theorem (Wootters and Zurek, 1982), and entanglement (Horodecki et al., 2009). The intrinsic security features enabled by these principles make quantum information science critically important for a wide array of applications in sectors such as finance, healthcare, telecommunications, defense, and supply chain management, to name a few. In this new era of quantum-enabled information technology, the fundamental bits of information transfer, known as qubits, are redefined. They are entirely different from the known conventional classical bit (0 and 1) (Dür and Heusler, 2016). Qubits are basically linear combinations of two independent states (0 and 1) realized in a quantum object like an atom and photon. The quantum mechanical representation of a qubit in Dirac notation is expressed as follows:

$|\psi \rangle =c_1|0\rangle +c_2|1\rangle .(1)$

In this Equation 1, $|\psi \rangle$ is the state of the qubit, and $c_1$ and $c_2$ represent complex probability amplitudes associated with the states $|0\rangle$ and $|1\rangle$, respectively. This conceptual framework underpins the revolutionary features of quantum communication and highlights its pivotal role in enabling secure information exchange through quantum networks. The primary objective of quantum communication is the reliable transmission of qubits from one location to another while preserving their quantum states. This task is notably arduous due to the susceptibility of quantum states to environmental noise. This tends to disrupt the fragile quantum coherence (Schlosshauer, 2019) between these states, altering the complex probability amplitudes $c_1$ and $c_2$ that define them. Photons are uniquely suited to this role due to their minimal interaction with the environment, high velocity of propagation, and the ease with which they can be manipulated using linear optics. These properties make photons an ideal candidate to transfer (“flying” qubits). These flying qubits are capable of traveling long distances without experiencing significant decoherence (Cirac et al., 1997).

However, the transmission of flying qubits is only one aspect of a larger system. A comprehensive quantum communication network also requires mechanisms for local encoding, retrieving, and storing information from these flying qubits. In this context, “matter qubits,” which are qubits stored in quantum materials, are essential. Matter nodes may be realized using trapped atoms and ions (Keller, 2022), nitrogen-vacancy (NV) centers (Kurtsiefer et al., 2000), quantum dots (Michler et al., 2000), etc. They serve as the stationary counterpart to flying qubits. The interaction between photons (flying qubits) and matter qubits necessitates an interfacing architecture that enables the quantum state transfer between matter and photons. The successful integration of this interface relies on the entanglement generation between photon qubits and matter qubits. Ultimately, establishing entanglement across distant matter nodes fulfills the fundamental aim of secure quantum communication, providing a robust platform for exchanging information securely across long distances.

Entanglement has predominantly been explored within the realms of quantum mechanics and philosophical inquiry. It is recognized that entanglement alone does not suffice for the instantaneous transmission of information between remotely situated entities, as this would contradict Einstein’s theory of relativity, which dictates that the speed of information transfer must not exceed that of light. Furthermore, encoding information within an entangled state is rendered impracticable by the inherent randomness of these quantum states, a principle central to quantum mechanics. Any manipulation of a qubit’s state within an entangled system, whether by measurement or other intervention, invariably leads to either the disintegration of the entanglement or a significant loss of systemic information, thereby undermining the primary aim of communication. Nevertheless, entanglement remains invaluable in enhancing the security of information transfer, underpinning several quantum communication techniques such as superdense coding (Bennett and Wiesner, 1992), quantum teleportation (Bennett et al., 1993), and quantum key distribution (QKD) (Yu, 2021), which do not require the entities to be in a maximally entangled state. These methods have been successfully implemented by various groups, who have distributed entangled states over significant distances $(248\mathrm{K}\mathrm{m})$ (Neumann et al., 2022).

The primary focus of this review does not involve diving into the distribution of entanglement between distant nodes. It centers on generating entangled photons or photon pairs, a fundamental step in establishing entanglement across distant nodes. Specifically, the discussion narrows down to utilizing atomic platforms for this purpose. The rationales behind these choices are the unique advantages offered by single atoms or atomic vapors compared to other solid-state platforms such as semiconductor quantum dots or NV centers in diamond. These advantages include their ease of isolation from the environment through trapping and the possibility of coherent manipulation using electromagnetic fields.

The section-wise distributions are as follows: In Section 2, we delve into the concept of single photons, supplemented by detailed mathematical descriptions, various generation methods, and different characterization techniques, accompanied by a brief overview of recent advancements in this domain. In Section 3, we explore the fundamentals of quantum entanglement with mathematical frameworks, delving into the generation techniques and characterization methods, along with a brief review of advances in entangled photon generation across different atomic platforms. In Section 4, we briefly discuss the alternative platforms for generating single and entangled photons. Section 5 offers a concise discussion on the impact of non-Markovian effects in these processes. In Section 6, we propose a designing consideration of the real experiments on the single and entangled photon pair generation. In Section 7, we discuss the applications and prospects of single and entangled photons. Section 8 contains the conclusion and outlook. This review article is structured to cater to both non-expert readers and seasoned experts, facilitating an accessible entry point for newcomers while providing nuanced technical insights for specialists in the field of single and entangled photon generation and their applications in quantum communication.

2 Single photons

The particle nature of light first arose with the discovery of the photoelectric effect Einstein (1905) and the Compton effect (Compton, 1923). In 1926, G. N. Lewis introduced the term “photon,” not precisely by the light quanta but as a carrier of radiation energy. While the term “photon” has been employed broadly, its underlying concept is significantly complex and demands a thorough comprehension. Rather than exploring the fundamental nature of photons in this review, we have taken a different approach that involves examining how different sources exhibit photon-specific behaviors. A primary distinction is evident: classical light sources adhere to classical electrodynamics, whereas single-photon sources exhibit quantum behaviors. The subsequent section will detail methods to differentiate these source types, providing mathematical justifications to underscore their distinct operational frameworks.

2.1 Mathematical descriptions

The fundamental understanding of single-photon behavior is rooted in the quantization of the electromagnetic (EM) field. When an EM field propagates through free space, it can be broken down into many modes. These modes undergo quantization, resembling a quantum harmonic oscillator whose elementary excitations are photons. A detailed and rigorous discussion of this process of field quantization can be found in Gerry and Knight (2005) and Walls and Milburn (2008). This quantization and its significance in comprehending the behavior of single photons will be discussed briefly in the following section.

Let us consider a single mode of an EM wave, characterized by an angular frequency $\omega$, confined along the z-axis within a perfectly conducting cavity of length L. At $z=0$ and $z=L$, the field must vanish in order to fulfill the boundary conditions. An EM field satisfying Maxwell’s equation and adhering to the above boundary conditions can be expressed as follows:

$\mathit{E}\left(z,t\right)={\left(\frac{2{\omega }^2}{V{ϵ}_0}\right)}^{\frac{1}{2}}\tilde{q}\left(t\right)\sin kz\widehat{x},(2)$

$\mathit{B}\left(z,t\right)=\frac{{\mu }_0{ϵ}_0}{k}{\left(\frac{2{\omega }^2}{V{ϵ}_0}\right)}^{\frac{1}{2}}\tilde{p}\left(t\right)\cos kz\widehat{y},(3)$

where $\tilde{q}(t)$ and $\tilde{p}(t)=\dot{\stackrel{̃}{q}}(t)$ can initially be treated as some functions of time, whose underlying physical meaning will be made clear in the subsequent discussion. $V$ represents the effective mode volume of the cavity. The above choice of EM fields does not cause any loss in the context of generality. It simplifies the mathematical complexity without compromising the rigor of the physics. The total energy of this single-mode EM field in the Hamiltonian form can be formulated as

$\widehat{H}=\frac{1}{2}\int \left({ϵ}_0{\mathit{E}}^2\left(z,t\right)+\frac{1}{{\mu }_0}{\mathit{B}}^2\left(z,t\right)\right)dV.(4)$

This Equation 4 can be further simplified with the help of Equations 2, 3 as

$\widehat{H}=\frac{1}{2}\left({\tilde{p}}^2+{\omega }^2{\tilde{q}}^2\right).(5)$

Here, we obtained the Hamiltonian, which is similar to that of the classical harmonic oscillator. We can then map $\tilde{p}$ and $\tilde{q}$ to resemble the momentum and position coordinates of the harmonic oscillator, respectively. Following the same formalism as of the quantum harmonic oscillator, the Hamiltonian in Equation 5 can be expressed in terms of the annihilation $(\widehat{a})$ and creation operator $({\widehat{a}}^{†})$ as

$\widehat{H}=\left({\widehat{a}}^{†}\widehat{a}+\frac{1}{2}\right)\hslash \omega ,(6)$

where $[\widehat{a},{\widehat{a}}^{†}]=1$ must be satisfied for the above equation. Intriguingly, the single mode Hamiltonian expressed in Equation 6 is identical to that of a quantum harmonic oscillator. Such equivalence is a hallmark of the quantization of the EM field, commonly referred to as the second quantization. Within this quantized framework, the EM field can be outlined as

$\mathit{E}\left(z,t\right)={\left(\frac{\hslash \omega }{V{ϵ}_0}\right)}^{\frac{1}{2}}\left(\widehat{a}+{\widehat{a}}^{†}\right)\sin kz\widehat{x},(7)$

$\mathit{B}\left(z,t\right)=\left(\frac{{\mu }_0}{k}\right){\left(\frac{\hslash {\omega }^3{ϵ}_0}{V}\right)}^{\frac{1}{2}}\left(\widehat{a}-{\widehat{a}}^{†}\right)\cos kz\widehat{y}.(8)$

In general, for an arbitrary propagation direction with arbitrary polarization, and considering all possible modes, the quantized electromagnetic field represents in Equations 7, 8 can be explicitly expressed as

$\mathit{E}\left(\mathit{r},t\right)=i{\displaystyle \sum _{\mathit{k}\sigma }}{\left(\frac{\hslash {\omega }_k}{2{ϵ}_{0}V}\right)}^{\frac{1}{2}}{\mathit{e}}_{\mathit{k}\sigma }\left[{\widehat{a}}_{\mathit{k}\sigma }{e}^{i\left(\mathit{k}\cdot \mathit{r}-{\omega }_{k}t\right)}-{\widehat{a}}_{\mathit{k}\sigma }^{†}{e}^{-i\left(\mathit{k}\cdot \mathit{r}-{\omega }_{k}t\right)}\right],(9)$

$\mathit{B}\left(\mathit{r},t\right)=\frac{i}{c}{\displaystyle \sum _{\mathit{k}\sigma }}\left(\mathit{k}\times {\mathit{e}}_{\mathit{k}\sigma }\right){\left(\frac{\hslash {\omega }_k}{2{ϵ}_{0}V}\right)}^{\frac{1}{2}}{\mathit{e}}_{\mathit{k}\sigma }\left[{\widehat{a}}_{\mathit{k}\sigma }{e}^{i\left(\mathit{k}\cdot \mathit{r}-{\omega }_{k}t\right)}-{\widehat{a}}_{\mathit{k}\sigma }^{†}{e}^{-i\left(\mathit{k}\cdot r-{\omega }_{k}t\right)}\right],(10)$

where $\sigma =\mathrm{1,2}$ defines the two orthogonal polarizations and ${\mathit{e}}_{\mathit{k}\sigma }$ is the polarization direction. The total Hamiltonian of the system is obtained by aggregating the Hamiltonians of the individual harmonic oscillators corresponding to each mode of EM field expressed in Equations 9, 10, which is expressed as

${\widehat{H}}_{\mathit{tot}}={\displaystyle \sum _{\mathit{k}\sigma }}\hslash {\omega }_k\left({\widehat{a}}_{\mathit{k}\sigma }^{†}{\widehat{a}}_{\mathit{k}\sigma }+\frac{1}{2}\right)={\displaystyle \sum _{\mathit{k}\sigma }}\hslash {\omega }_k\left({\widehat{n}}_{\mathit{k}\sigma }+\frac{1}{2}\right),(11)$

where

${\widehat{n}}_{\mathit{k}\sigma }={\widehat{a}}_{\mathit{k}\sigma }^{†}{\widehat{a}}_{\mathit{k}\sigma }.(12)$

Here, ${\widehat{n}}_{\mathit{k}\sigma }$ is the number operator for the $\mathit{k}\sigma$^th mode. This number operator in Equation 12 operates on the eigenstate $(|n_{\mathit{k}\sigma }\rangle )$ of the total Hamiltonian $({\widehat{H}}_{\mathit{tot}})$ (Equation 11) and yields the photon number present in the mode, that is,

${\widehat{n}}_{\mathit{k}\sigma }\left|n_{\mathit{k}\sigma }\right.⟩=n_{\mathit{k}\sigma }\left|n_{\mathit{k}\sigma }\right.⟩.(13)$

Here, $|n_{\mathit{k}\sigma }\rangle$ is also known as the Fock state. A remarkable result can be obtained by using Equation 13; the expectation value of the variance of the photon number $(\mathrm{\Delta }{\widehat{n}}_{\lambda }^2)$ is found to be 0:

$⟨\mathrm{\Delta }{\widehat{n}}_{\lambda }^2⟩=⟨n_{\lambda }\left|\mathrm{\Delta }{\widehat{n}}_{\lambda }^2\right|n_{\lambda }⟩=0.(14)$

In this context, $\lambda =\mathit{k}\sigma$ specifies a particular mode, and the zero expectation value for the photon number (Equation 14) signifies the absence of variance or fluctuations in the photon count within a Fock state. Thus, if a Fock state is explicitly created to contain precisely one photon $\left(n_{\lambda }=1\right.$), it will consistently maintain this photon number, neither accumulating additional photons nor devolving to a zero-photon state. This characteristic is crucial for applications in quantum cryptographic protocols, which require a single photon at a given instance to mitigate the risk of photon-splitting attacks. In such scenarios, an eavesdropper could potentially intercept one photon from a multiphoton state, allowing the remaining photons to proceed to the intended recipient, thus compromising the security of the communication. Therefore, a single-photon source that reliably produces a Fock state with a photon number of 1 is indispensable in maintaining the integrity and security of quantum communications.

Another striking feature of a Fock state is that, regardless of the photon count in a particular mode, the expectation values for both the electric $({\mathit{E}}_{\lambda }(r,t))$ and magnetic $({\mathit{B}}_{\lambda }(r,t))$ fields are 0:

$⟨n\left|{\mathit{E}}_{\lambda }\left(r,t\right)\right|n⟩=⟨n\left|{\mathit{B}}_{\lambda }\left(r,t\right)\right|n⟩=0.(15)$

Here, $|n\rangle$ denotes the Fock state corresponding to a specific mode. Henceforth, this notation will be strictly adhered to describe the Fock states. The outcome of Equation 15 can be attributed to the fact that the electric and magnetic fields are formulated as linear combinations of ${\widehat{a}}^{†}$ and $\widehat{a}$. Notably, the expectation values of these operators in a Fock state are 0, as indicated by $⟨n|{\widehat{a}}^{†}|n⟩=⟨n|\widehat{a}|n⟩=0$. In contrast, classical fields exhibit sinusoidal oscillations and do not vanish when observed from any fixed point in space. This difference highlights the fundamental disconnect between quantum and classical descriptions of fields. This underpins unique aspects of quantum behavior that do not have direct analogs to the classical world.

Experimentally generating a Fock state with precisely one photon presents significant challenges. In practice, no perfect deterministic single-photon source can produce precisely one photon upon each click (Reimer and Cher, 2019). However, certain sources do emit light that diverges significantly from classical light. In contrast, their behavior more closely resembles a Fock state. Consequently, the ability to distinguish clearly between these types of sources is essential. This distinction is typically achieved through the analysis of photon statistics or correlation parameters such as $g^{(2)}$. The methodologies and implications of these distinctions are discussed in the following sections.

The coherent states draw the boundary line between these two types of sources. Unlike the Fock state, coherent states are states for which a classical description can be drawn, considering some limiting cases. A coherent state, by definition, is an eigenstate of $\widehat{a}$, with eigenvalues that are complex due to the non-Hermitian property of $\widehat{a}$. Consequently, writing the eigenvalue equation for the operator $\widehat{a}$ gives

$\widehat{a}|\alpha \rangle ={\alpha }_0|\alpha \rangle ,(16)$

where ${\alpha }_0$ represents the complex eigenvalue and $|\alpha \rangle$ denotes the coherent state, which is further expressed as follows:

$|\alpha \rangle =\exp \left(-\frac{1}{2}|{\alpha }_0{|}^2\right){\displaystyle \sum _{n=0}^{\infty }}\frac{{\alpha }_0^n}{\sqrt{n!}}|n\rangle .(17)$

Thus Equations 16, 17 inferred that, a coherent state represents the superposition of numerous Fock states. In this state, both the mean electric field as well as the variance in the photon number are significant and non-zero. The mean electric field is expressed in Equation 18 as:

$⟨\alpha \left|{\mathit{E}}_x\left(\mathit{r},t\right)\right|\alpha ⟩=i{\left(\frac{\hslash \omega }{2{ϵ}_{0}V}\right)}^{\frac{1}{2}}\left[{\alpha }_0{e}^{i\left(\mathit{k}\cdot \mathit{r}-\omega t\right)}-{\alpha }_0^{*}{e}^{-i\left(\mathit{k}\cdot \mathit{r}-\omega t\right)}\right],(18)$

and the variance in photon number is expressed in Equation 19 as:

$\langle \alpha |\widehat{n}|\alpha \rangle =⟨\alpha \left|{\left(\mathrm{\Delta }\widehat{n}\right)}^2\right|\alpha ⟩=|{\alpha }_0{|}^2.(19)$

Consequently, for a coherent state, the photon number exhibits variability, indicating its unsuitability as a deterministic single-photon source and its limited utility in quantum communication or cryptography. Instead, a coherent source functions as a purely classical light source, exemplified by laser light. Crucially, the distinction between various types of light sources can often be made based on photon number statistics.

For a coherent source, the photon numbers adhere to Poissonian statistics, providing a crucial reference point for discriminating between three types of sources, which can be expressed as

$P_n\left({\alpha }_0\right)=|⟨n\mid \alpha ⟩{|}^2=\frac{|{\alpha }_0{|}^{2n}}{n!}\exp \left(-|{\alpha }_0{|}^2\right).(20)$

In accordance with Equation 19, a distinctive characteristic of Poissonian statistics (Equation 20) is the equivalence of the mean and the variance of the distribution, denoted as $\left(⟨\widehat{n}⟩=⟨\mathrm{\Delta }{\widehat{n}}^2⟩\right)$. Deviations from this equality suggest non-Poissonian behavior, manifesting in two distinct scenarios:

1. When the mean is less than the variance $\left(⟨\widehat{n}⟩<⟨\mathrm{\Delta }{\widehat{n}}^2⟩\right)$, the distribution is termed super-Poissonian. This condition indicates a higher level of noise than that expected under Poissonian statistics.

2. Conversely, if the mean exceeds the variance $\left(⟨\widehat{n}⟩>⟨\mathrm{\Delta }{\widehat{n}}^2⟩\right)$, the resulting distribution is classified as sub-Poissonian, indicative of reduced statistical fluctuations relative to a Poisson distribution.

A comparison of the photon statistics is illustrated in Figure 1. The photon number distributions offer a fundamental criterion for classifying light sources: those that display sub-Poissonian statistics are typically considered non-classical sources, whereas classical light sources generally exhibit super-Poissonian distributions (Fox, 2006). Single-photon sources are a special case of sub-Poissonian sources with $\mathrm{\Delta }n=0$. This statistical categorization is pivotal in distinguishing between various types of photon sources.

Figure 1

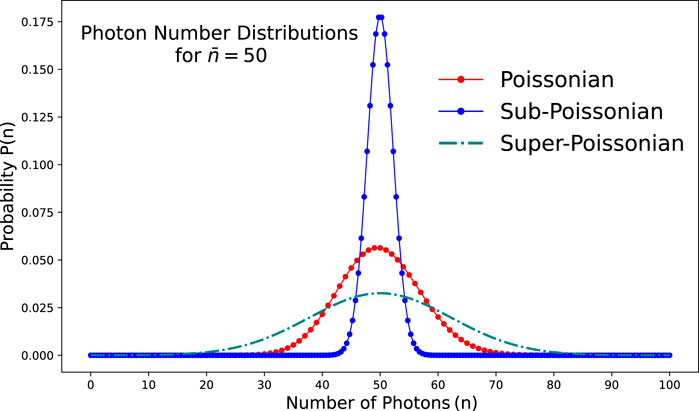
Figure 1. A comparison of the photon statistics for light with a Poisson distribution and those for super-Poissonian and sub-Poissonian light. The distributions have been graphically represented under the condition of an equivalent mean photon number, denoted as $\bar{n}=50$.

Beyond mere statistical distributions, photon anti-bunching and the second-order correlation function $g^{(2)}(\tau )$ serve as critical metrics for the characterization of single-photon sources (Woolley et al., 2013; Huang et al., 2018). Photon anti-bunching is an observable phenomenon where a definitive temporal and spatial gap exists between consecutive photons emitted by a source, a characteristic not found in classical black body radiation sources, which exhibit photon bunching where photons cluster together at a given point in time and space, as depicted in Figure 2. In contrast, a true single-photon source exhibits anti-bunching, a behavior confirmed through coincidence measurements in the Hanbury Brown–Twiss (HBT) experiment, detailed further in Section 2.3.1. Coherent sources display intermediate characteristics, manifesting both bunching and anti-bunching behaviors depending on the experimental conditions. The $g^{(2)}$ correlation measurement, integral to the HBT experiment, quantifies anti-bunching and is defined as the normalized intensity–intensity correlation function at different time intervals $\tau$, represented mathematically as (Fischer et al., 2018)

$g^{\left(2\right)}\left(\tau \right)=\frac{\langle I\left(t\right)I\left(t+\tau \right)\rangle }{⟨I^2\left(t\right)⟩},(21)$

where $I(t)$ is the instantaneous intensity and $⟨.⟩$ represents the ensemble average. In terms of $\widehat{a}$ and ${\widehat{a}}^{†}$, this $g^{(2)}$ correlation can be expressed as (Zhou et al., 2015)

$g^{\left(2\right)}\left(\tau \right)=\frac{⟨{\widehat{a}}^{†}\left(t\right){\widehat{a}}^{†}\left(t+\tau \right)\widehat{a}\left(t+\tau \right)\widehat{a}\left(t\right)⟩}{{⟨{\widehat{a}}^{†}\widehat{a}⟩}^2}.(22)$

Figure 2

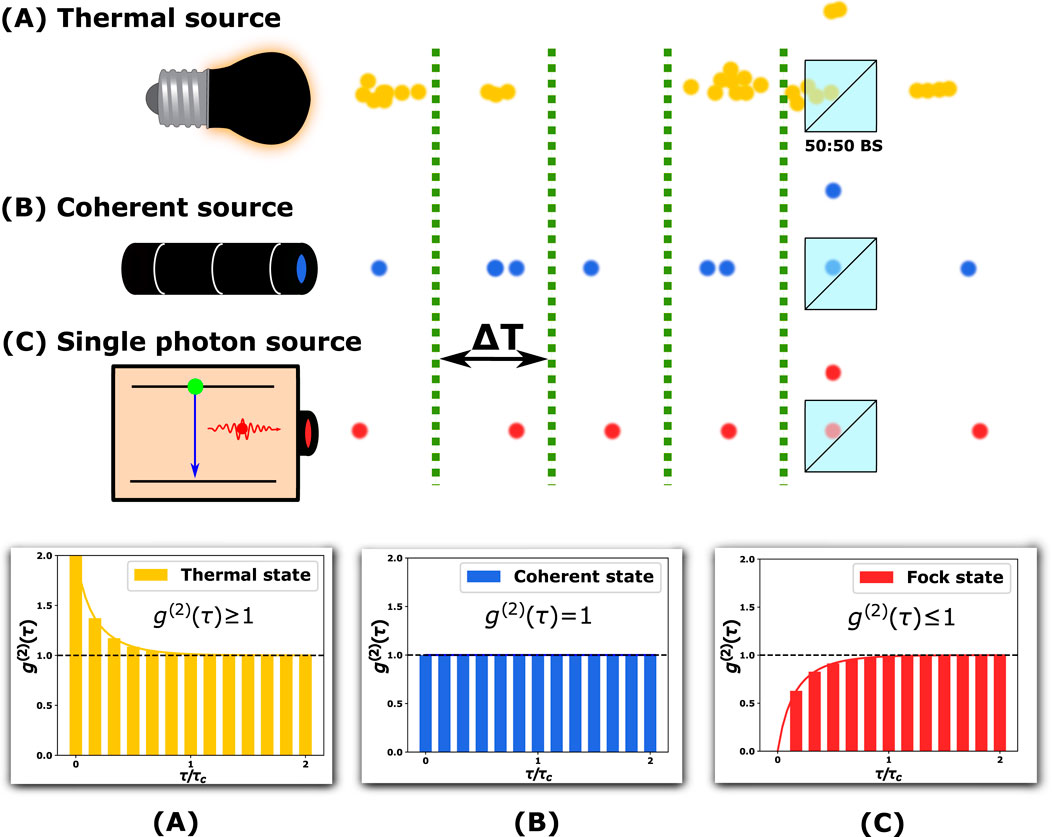
Figure 2. A schematic of the distinction between three types of light sources. A suitable time interval $\mathrm{\Delta }T$ is defined to characterize the temporal behavior of photons. (A) In the case of a thermal source, photons are emitted in bunches, resulting in more than one photon always within $\mathrm{\Delta }T$ and the maximum $g^{(2)}(0)$ value. (B) Multiphoton emission is possible for a coherent source, yet the number of photons within each interval remains relatively constant, resulting in a consistent value for $g^{(2)}(0)$. (C) In the case of a single-photon source, only one photon is emitted during each interval $\mathrm{\Delta }T$, resulting in a second-order correlation $(g^{(2)}(0))$ of 0.

The pivotal measure obtained from this correlation function in Equation 22 occurs at $\tau =0$ $(g^{(2)}(0))$, which is basically an equal time correlation function, quantifying simultaneous photon emission and providing crucial insights into the nature of the photon source (Shen et al., 2014; Shen et al., 2015; Shen et al., 2020). Distinct values of $g^{(2)}(0)$ for different sources enable straightforward categorization, as illustrated in Figure 2. Alongside $g^{(2)}$ correlation and anti-bunching, two additional indicators of photon nonclassicality are the Mandel parameter (Short and Mandel, 1983) and the Wigner function (Dahl, 1982). The Mandel parameter is expressed mathematically as given in Equation 23,

$Q=\frac{{\left(\mathrm{\Delta }\widehat{n}\right)}^2}{⟨\widehat{n}⟩}-1,(23)$

which indicates coherence for a coherent source (where Q = 0) and typically resides between −1 and 0 for a single-photon source, with −1 representing a perfect single-photon source emitting photons at regular intervals. Conversely, the Wigner function, representing the wave function in systems with classical counterparts, is positive by default, and its negativity strongly suggests non-classical behavior (Kenfack and Życzkowski, 2004). Table 1 contrasts these three types of light sources based on various parameters. However, achieving non-classical behavior or values close to the ideal for these parameters does not guarantee the reliability of a photon source for direct implementation in a quantum network. A truly deterministic photon source requires not only non-classical behavior but also high repeatability in photon generation with perfect indistinguishability.

Table 1

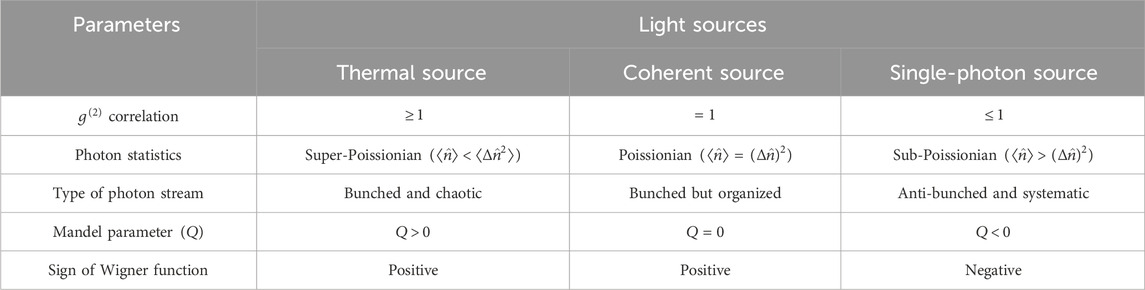
Table 1. Comparative table for three types of light sources. Each row except the first column represents the values of different characterization parameters. The characterization parameters are defined in the first column. The other three columns represent different types of light sources.

2.2 Generation processes

An excellent single-photon source exhibits significant coherence time, the capability to maintain well-defined qubit states, near-perfect indistinguishability, high repeatability, high brightness, and on-demand generation. In atomic systems, single photons are mainly generated through processes such as spontaneous parametric down-conversion (SPDC), Raman process, and four-wave mixing (FWM).

SPDC and FWM are nonlinear processes that are mainly used to generate entangled photon pairs. These processes also enable the use of such photon pair sources as heralded single-photon sources, where the detection of one photon invariably indicates the existence of the other. SPDC is extensively used for generating single photons, especially within systems that utilize solid-state nonlinear crystals (Harris et al., 1967; Burnham and Weinberg, 1970; Mosley et al., 2008; Bruno et al., 2014). Consequently, an in-depth discussion of SPDC falls beyond the scope of this manuscript; a brief overview can be found in Section 3.2.1. A thorough description of FWM within the context of generating entangled photon pairs is provided in Section 3.2.3.

Another major technique of single-photon generation is the Raman process, which enables both probabilistic and deterministic generation of single photons. The following section discusses the single-photon generation techniques, encompassing various Raman scattering processes such as spontaneous Raman scattering, stimulated Raman scattering, and cavity-mediated Raman transition.

2.2.1 Raman process

Inelastic Raman scattering serves as a fundamental interaction between light and matter. During this phenomenon, the interaction of an intense light field with matter produces both a higher-energy anti-Stokes field and a lower-energy Stokes field (Raman and Krishnan, 1928). The early investigations into Raman scattering, encompassing its introduction and initial experiments, were exclusively focused on elucidating the interplay between light and atoms, particularly addressing the rotational and vibrational levels of molecules (Gaubatz et al., 1990). Subsequently, Raman scattering found practical utility at the single-atom–photon level, gaining prominence for generating both individual and entangled photons.

2.2.1.1 Spontaneous Raman scattering

Raman scattering serves as a versatile tool for producing both single and entangled photons. In contrast to elastic scatterings such as Rayleigh scattering, the phenomenon of spontaneous Raman scattering requires a minimum of three energy levels in the $\mathrm{\Lambda }$ configuration, including two ground states and one excited state.

To understand the Raman scattering process, let us consider the atom is initialized to the state $|u\rangle$. Subsequently, a pump field is applied to excite the atom to the excited state $|e\rangle$, from which the atom spontaneously decays back to another ground state $|g\rangle$ (see Figure 3). The initial state of the system, denoted as $(|{\psi }_i\rangle )$, is explicitly defined as the tensor product of the atom’s initial state $(|u\rangle )$ and the state of the pump photon mode $(|l_{{\omega }_p}\rangle )$, expressed in Equation 24 as

$\left|{\psi }_i\right.⟩=|u\rangle \otimes \left|l_{{\omega }_p}\right.⟩.(24)$

Figure 3

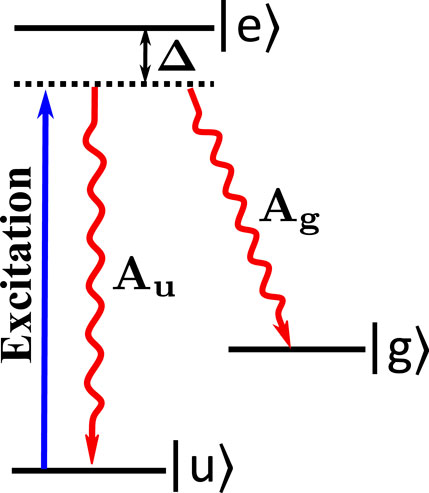
Figure 3. The representation of the spontaneous Raman scattering process involves excitation from the $|u\rangle$ level, followed by the atom returning to the same level or transitioning to another state. The coefficients $A_u$ and $A_g$ represent the Einstein $A$ coefficients for the respective transitions. For generalization, a detuning $\mathrm{\Delta }$ is considered.

Upon excitation, there is a finite probability for the atom to decay any one of the ground states. A successful event is registered by a spontaneously decaying atom to the other ground state $(|g\rangle )$ while emitting one photon $(|l_{{\omega }_s}\rangle )$. Equation 25 represents the final state |ψf〉 as,

$\left|{\psi }_f\right.⟩=|g\rangle \otimes \left|l_{{\omega }_s}\right.⟩.(25)$

The process of Raman scattering can be modeled by a three-level system interacting with an external field. The Hamiltonian can be decomposed into two parts: the field-independent bare Hamiltonian $({\widehat{H}}_0)$ of the atom and the atom-field interaction Hamiltonian $({\widehat{H}}_{\mathit{int}})$. Thus, the total Hamiltonian can be written as

${\widehat{H}}_{\mathit{tot}}\left(t\right)={\widehat{H}}_0\left(t\right)+{\widehat{H}}_{\mathit{int}}\left(t\right).(26)$

The bare Hamiltonian in the rotational frame of the laser, taking level $|u\rangle$ as the reference, can be explicitly written in Equation 27 as

${\widehat{H}}_0=\hslash \mathrm{\Delta }{\widehat{\sigma }}_{ee}+\hslash \tilde{\omega }{\widehat{\sigma }}_{gg},(27)$

where $\tilde{\omega }=({\mathcal{E}}_g-{\mathcal{E}}_u)/\hslash$, and ${\widehat{\sigma }}_{ii}=|i\rangle \langle i|$. Here, $\mathrm{\Delta }$ is the laser detuning, and ${\mathcal{E}}_g$ and ${\mathcal{E}}_u$ are the absolute energy of the level $|g\rangle$ and $|u\rangle$, respectively. The interaction Hamiltonian can be modeled using a semi-classical approach, wherein a classical EM field (E) interacts with an electric dipole (d) defined between two discrete atom states. In this context, the interaction Hamiltonian can be expressed as follows:

$H_{\mathit{int}}=-\mathit{d}\cdot \mathit{E}.(28)$

By considering the same rotational frame of laser and applying the rotating wave approximation (RWA), the interaction Hamiltonian takes the form

${\widehat{H}}_{int}=\hslash \left(\frac{\mathrm{\Omega }\left(t\right)}{2}{\widehat{\sigma }}_{e,u}+H.C.\right).(29)$

Here, $\mathrm{\Omega }$ is Rabi frequency, and ${\widehat{\sigma }}_{e,u}=|e\rangle \langle u|$ is the projection operator. The Hamiltonian in the matrix form can be represented in Equation 30 as (Müller et al., 2017)

${\widehat{H}}_{\mathit{tot}}=\hslash \left(\begin{array}{ccc}\hfill 0\hfill & \hfill {\mathrm{\Omega }}^{*}/2\hfill & \hfill 0\hfill \\ \hfill \mathrm{\Omega }/2\hfill & \hfill \mathrm{\Delta }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\tilde{\omega }\hfill \end{array}\right).(30)$

The transition amplitudes ($A_u$ and $A_g$ as depicted in Figure 3) may be determined using this Hamiltonian. The emission spectrum arises from the modulus square of these transition amplitudes. A detailed discussion of this process is outlined in Müller et al. (2017). A successful Raman process with single-photon excitation may be obtained by integrating the emission spectrum (Müller, 2021) and is expressed as

$P_{\text{scatter\hspace{0.17em}}}=\frac{A_u{A}_g}{\mathrm{\Gamma }}\frac{\mathrm{\Gamma }+\mathrm{\Delta }{\omega }_P}{{\mathrm{\Delta }}^2+{\left(\frac{\mathrm{\Gamma }+\mathrm{\Delta }{\omega }_P}{2}\right)}^2}.(31)$

Here, $A_u$ and $A_g$ denote the Einstein’s $A$ coefficient for transitions $|e\rangle \to |u\rangle$ and $|e\rangle \to |g\rangle$, respectively. The term $\mathrm{\Gamma }=A_u+A_g$ represents the full atomic linewidth, whereas $\mathrm{\Delta }{\omega }_P$ and $\mathrm{\Delta }$ represent the linewidth and detuning of the pump laser, respectively. For resonant excitation $(\mathrm{\Delta }\to 0)$ assisted by a very narrow linewidth laser $\left(\mathrm{\Delta }{\omega }_P\to 0\right)$ and considering multiphoton excitation, the success probability (Equation 31) modifies to Equation 32, as follows:

$P_{\text{scatter\hspace{0.17em}}}\cong \frac{A_g}{\mathrm{\Gamma }}{\left(\frac{A_u}{\mathrm{\Gamma }}\right)}^n.(32)$

Here, $n$ represents the average number of failures, indicating the occurrences of de-excitation to the same initial state before a successful event occurs. Hence, the occurrence of a successful single-photon generation cannot be guaranteed with each excitation. Furthermore, photons are only captured within a limited angle from the spontaneously emitted photons, which are distributed across the entire solid angle accessible. These factors render spontaneous Raman scattering a probabilistic single-photon generation process that is nevertheless useful due to its simplistic scheme.

Building upon the probabilistic nature of Raman scattering, L. Duan, M. Lukin, J.I. Cirac, and P. Zoller prescribed an innovative technique for enhancing single-photon generation from a cold atomic ensemble, leveraging collective atomic excitations (Duan et al., 2001). In their recipe utilizing collective excitations, a weak off-resonant laser pulse (commonly referred to as the “write pulse”) is applied to the atomic ensemble. This selectively induces a single atom within the ensemble to transition from one ground state to another via the spontaneous Raman process, subsequently emitting a single photon.

2.2.1.2 Stimulated Raman scattering process

It is possible to precisely control the single-photon generation via the stimulated Raman process. In this process, the Stokes or anti-Stokes fields are externally applied, contrasting with the spontaneous scattering process described in the previous section. This method, known as stimulated Raman adiabatic passage (STIRAP), also requires a three-level system in $\mathrm{\Lambda }$ configuration. This approach facilitates the transfer of population between the two ground states, effectively circumventing any transitions to the excited state, thereby minimizing the probability of spontaneous emissions (as shown in Figure 4). The Hamiltonian description is almost similar to Equation 26, in addition to the fact that for the laser–atom interaction, we must consider both the pump and Stokes field. By taking level $|u\rangle$ as a reference, the bare Hamiltonian can be expressed by invoking rotating wave approximation (RWA) (Rabi et al., 1954) as

${\widehat{H}}_0=\mathrm{\Delta }\left(t\right){\widehat{\sigma }}_{e,e}+\delta \left(t\right){\widehat{\sigma }}_{g,g}.(33)$

Here, ${\widehat{\sigma }}_{i,j}=|i\rangle \langle j|$ is the projection operator from state $|j\rangle$ to $|i\rangle$. $\mathrm{\Delta }(t)$ denotes the detuning of the pump field $({\mathrm{\Delta }}_P(t))$, while $\delta (t)$ represents (Equation 34) an additional detuning applied to the Stokes field $({\mathrm{\Delta }}_S)$ relative to the pump field,

$\delta \left(t\right)={\mathrm{\Delta }}_P\left(t\right)-{\mathrm{\Delta }}_S\left(t\right).(34)$

Figure 4

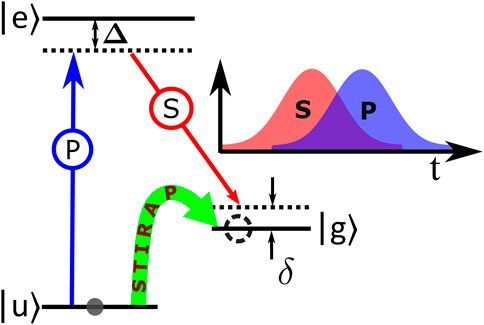
Figure 4. Schematic representation of the STIRAP process. Initially, the atom is in ground state $|u\rangle$. Pump and Stokes fields are applied in a counterintuitive manner, as shown in the top-right corner. A pump field is applied between level $|u\rangle$ and $|e\rangle$ with detuning $\mathrm{\Delta }$. A Stokes field is applied between $|e\rangle$ and $|g\rangle$ with detuning $(\mathrm{\Delta }+\delta )$.

The pump and Stokes laser detuning having frequencies ${\omega }_P$, and ${\omega }_S$ may be further decomposed in Equation 35 as

$\begin{array}{c}{\mathrm{\Delta }}_P\left(t\right)={\mathcal{E}}_e-{\mathcal{E}}_u-\hslash {\omega }_P\left(t\right);\\ {\mathrm{\Delta }}_S\left(t\right)={\mathcal{E}}_e-{\mathcal{E}}_g-\hslash {\omega }_S\left(t\right),\end{array}(35)$

where ${\mathcal{E}}_u$, ${\mathcal{E}}_e$, and ${\mathcal{E}}_g$ are the absolute energy of the unperturbed Hamiltonian corresponding to the states $|u\rangle ,|e\rangle$ and $|g\rangle$, respectively.

For the interaction Hamiltonian, we take the same approach as was derived for spontaneous Raman scattering (Equations 28, 29). By considering both Stokes and pump field interaction, employing the treatment of RWA and dipole approximation, the interaction Hamiltonian operator can be expanded as (Shore, 2017)

${\widehat{H}}_{int}=\hslash \left(\frac{{\mathrm{\Omega }}_S\left(t\right)}{2}{\widehat{\sigma }}_{e,g}+H.C.\right)+\hslash \left(\frac{{\mathrm{\Omega }}_P\left(t\right)}{2}{\widehat{\sigma }}_{e,u}+H.C.\right),(36)$

Here, ${\mathrm{\Omega }}_{S,P}(t)$ denotes the Rabi frequencies for the Stokes and pump laser, respectively. From Equation 33 and Equation 36, the matrix representation of the total Hamiltonian is articulated as follows (Vitanov et al., 2017):

${\widehat{H}}_{\mathit{tot}}=\hslash \left(\begin{array}{ccc}\hfill 0\hfill & \hfill \frac{{\mathrm{\Omega }}_P^{*}\left(t\right)}{2}\hfill & \hfill 0\hfill \\ \hfill \frac{{\mathrm{\Omega }}_P\left(t\right)}{2}\hfill & \hfill \mathrm{\Delta }\hfill & \hfill \frac{{\mathrm{\Omega }}_S\left(t\right)}{2}\hfill \\ \hfill 0\hfill & \hfill \frac{{\mathrm{\Omega }}_S^{*}\left(t\right)}{2}\hfill & \hfill \delta \left(t\right)\hfill \end{array}\right).(37)$

STIRAP demands Stokes and pump field detuning must be equal, that is, $\delta (t)=0$, which implies

$\mathrm{\Delta }={\mathrm{\Delta }}_P={\mathrm{\Delta }}_S.(38)$

From Equation 38, one of the eigenvalues of this total Hamiltonian (Equation 37) becomes 0. The corresponding eigenvector may be stated as

$|{\psi }_0\left(t\right)\rangle =\cos \mathrm{\Theta }|u\rangle -\sin \mathrm{\Theta }|g\rangle .(39)$

Here, $\mathrm{\Theta }$ represents the mixing angle, which can be represented in terms of ${\mathrm{\Omega }}_P$ and ${\mathrm{\Omega }}_S$ as

$\tan \mathrm{\Theta }=\frac{{\mathrm{\Omega }}_P\left(t\right)}{{\mathrm{\Omega }}_S\left(t\right)}.(40)$

The state $|{\psi }_0(t)\rangle$ is independent of the excited state $|e\rangle$, referred to as the dark state or the coherent population trapping state (CPT) (Gray et al., 1978). A successful realization of a STIRAP process may be explained in the following manner using the temporal evolution of the state $|{\psi }_0(t)\rangle$:

Step 1: Initially, the atom is considered to be in state $|u\rangle$, denoting the mixing angle, $\mathrm{\Theta }=0$ (from Equation 39), and also additionally implying ${\mathrm{\Omega }}_P(t)/{\mathrm{\Omega }}_S(t)=0$ (from Equation 40). Thus, this process is initiated by applying the Stokes field between the two unpopulated states ($|e\rangle$ and $|g\rangle$), causing Autler–Townes splitting between those two levels (Autler and Townes, 1955).

Step 2: In the next step, the pump field is applied, leading to an increase in the mixing angle. The initial state ${\psi }_0$ evolves into a superposition of state $|u\rangle$ and $|g\rangle$. This is accompanied by the temporal evolution of the population for the levels $|u\rangle$, $|g\rangle$, and $|e\rangle$. While the population for level $|u\rangle$ starts to diminish with time, the level $|g\rangle$ population increases without causing any change in level $|e\rangle$. This facilitates an adiabatic transfer of population from state $|u\rangle$ to $|g\rangle$.

Step 3: Ultimately, at the end of this process, the entire population is transferred coherently from level $|u\rangle$ to level $|g\rangle$. This condition demands the mixing angle, $\mathrm{\Theta }=\pi /2$ in Equation 39, which implies ${\mathrm{\Omega }}_S(t)/{\mathrm{\Omega }}_P(t)=0$.

A STIRAP process employs a counterintuitive sequence of fields applied. It is initiated by applying the Stokes field prior to the pump field while maintaining equal detuning for both fields from the upper state. Any deviation from these prescribed conditions leads to a population transfer to the excited state, which in turn may result in population loss in the state $|g\rangle$ due to the spontaneous decay from state $|e\rangle$. STIRAP holds substantial significance in applications such as the generation of single and entangled photons, thereby going beyond its usual predominant application, enabling coherent population transfer between two states.

2.2.1.3 Cavity-mediated Raman transition (CMRT)

A cavity-mediated Raman transition (CMRT) represents a unique adaptation of the STIRAP technique, employing the cavity field to enable the Stokes branch. The inclusion of a cavity utilizes the principles of cavity quantum electrodynamics (cQED), transforming the atom–cavity system into a completely quantized entity wherein both the atom and the field undergo quantization. This transformation is accurately captured by the Jaynes–Cummings Hamiltonian (Jaynes and Cummings, 1963). In this context, the states of the atom and photons become intricately connected, requiring an accurate representation within the dressed state framework.

To elucidate with an example, let us consider an atom–photon state labeled as $|g,n\rangle$. Such a composite state illustrates the atom to be in state $|g\rangle$ along with $n$ photons (Bina, 2012). Moreover, the presence of the cavity field induces an increase in the stimulated emission rate, causing the atom to emit photons more likely along the cavity mode, a phenomenon that is reminiscent of the Purcell effect (Purcell, 1995). Furthermore, the strong interaction between an atom and a cavity field is a hallmark of the strong coupling regime and results in a periodic exchange of energy in terms of re-emission and absorption of photons in the cavity mode. This condition is identified as the strong coupling regime (Kimble et al., 1992), characterized by a cooperativity factor $(C)$ (Goto et al., 2019) greater than 1. The cooperativity factor is formally defined in Equation 41 as

$C=\frac{g_0^2}{\kappa \gamma },(41)$

where $\gamma$, $\kappa$, and $g_0$ are the spontaneous emission rate, cavity decay rate, and atom–cavity coupling factor, respectively. The weak coupling regime is defined by $C<1$, which is also useful for describing the interaction with multiple atoms, where the coupling is enhanced by the presence of multi-atoms (Brecha et al., 1995).

The initiation of single-photon generation via CMRT involves the establishment of a strong coupling regime within the Stokes branch, fulfilling the STIRAP criterion. This dictates the Stokes field is applied before the pump field in a counterintuitive manner.

The procedure is initiated by preparing the atom–photon state at $|u,0\rangle$. Subsequently, the pump field, which is tuned to the same detuning as that of the cavity field from the excited level $(|e,0\rangle )$, is applied. The process follows a similar state transfer protocol as described in the STIRAP process. The population is transferred from $|u,0\rangle$ to the $|g,0\rangle$ state while accumulating one photon. Consequently, the final state will become $|g,1\rangle$. The accumulated photon is subsequently emitted into the cavity field and culminates in the final state $|g,0\rangle$ (as shown in Figure 5).

Figure 5

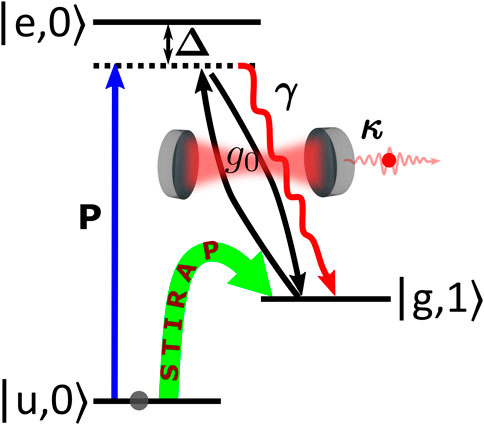
Figure 5. The cavity-mediated Raman transition process. The parameter $\kappa$ is the decay rate of the cavity, and $\gamma$ represents the spontaneous decay rate. The cavity is coupled with the $|g\rangle$ to $|e\rangle$ transition with coupling factor $g_0$.

The $|g,0\rangle$ state is generally chosen to be a metastable state with a higher lifetime. After the emission of one photon, the subsequent photon emission is delayed by the lifetime of the final state. To minimize this delay time, the atom can be pumped back to the ground state by the application of a repumping laser, which acts between the $|g\rangle$ and $|e\rangle$ states. This prepares the atom for the next cycle of single-photon generation. By repeating this pumping and repumping process multiple times at will, a deterministic single-photon generation is possible with greater collection efficiency due to channelized emission.

2.3 Experimental characterization

Experimental characterization is paramount in evaluating the suitability of single photons for quantum communication applications. This section delves into a comprehensive exploration of techniques utilized to assess and quantify the properties of single photons, with particular emphasis on their purity, indistinguishability, and quantum statistical behavior. Among the plethora of techniques available, two prominent methods, the Hanbury Brown–Twiss (HBT) and Hong–Ou–Mandel (HOM) interferometries, are extensively discussed.

2.3.1 Hanbury Brown–Twiss (HBT) interferometer

The HBT interferometer is pivotal for examining the statistical nature of light (Brown and Twiss, 1956), specifically to determine whether a light source emits single photons or photon bunches by measuring the second-order correlation $(g^{(2)}(\tau ))$. The schematic is illustrated in Figure 6. The interferometer setup contains a couple of single-photon detectors (A and B), a 50:50 beam splitter (BS), and a coincidence counter. In this experimental configuration, light is emitted from a source and directed toward a BS. After passing through the beam splitter, the light beam is split into two separate streams: one stream is directed toward detector A, while the other travels to detector B. Subsequently, the coincidence counter measures the number of photons that arrive at both detectors simultaneously. For a pure single-photon source, the BS encounters only one photon at a time. So there is no way to get simultaneous photon detection in both detectors A and B. Thus, for pure single-photon sources, $g^{(2)}(\tau =0)=0$. A time tagging unit inside a coincidence counter can log the instances of photon detection events. The recorded data are subsequently processed to generate histograms of multi-start, multi-stop correlation that faithfully replicate the $g^{(2)}(\tau )$ (see Figure 2).

Figure 6

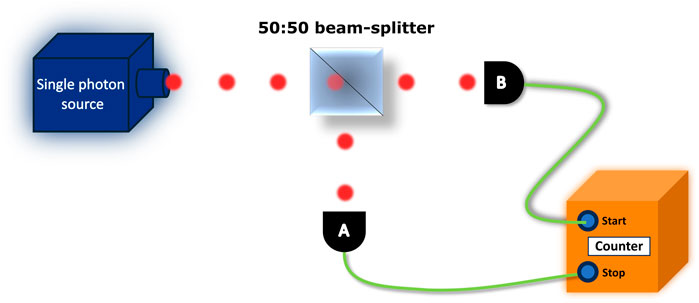
Figure 6. A schematic of the HBT interferometer setup for measuring the degree of second-order temporal coherence of the light source.

2.3.2 Hong–Ou–Mandel (HOM) interferometer

The HOM interferometry (Hong et al., 1987) is one of the elementary quantum optic experimental techniques exploring the principles of quantum interference between two indistinguishable photons. The indistinguishability of photons is characterized by their spatial, temporal, and spectral properties, in addition to identical polarization, indicating their existence in the same quantum state (Kosen, 2014). The experimental configuration is delineated in Figure 7A. This configuration involves a pair of identical photons, which may either emanate from a single-photon source or from two separate single-photon sources. These photons are subsequently introduced into the two input ports of a 50:50 beam splitter (BS), where interference occurs. The photons emerging from the output ports of the BS are then detected by two single-photon detectors. A coincidence counter is employed to measure the simultaneous detection events across these two detectors. The phenomenon of quantum interference has been rigorously utilized to characterize single photons generated from various platforms, such as quantum dots (Santori et al., 2002; Patel et al., 2010), nonlinear crystals (Hong et al., 1987; Riedmatten et al., 2003; Kaltenbaek et al., 2006), color centers in diamond (Bernien et al., 2012), trapped single neutral atoms (Legero et al., 2004; Beugnon et al., 2006), trapped single ions (Maunz et al., 2007), trapped atomic ensembles (Chanelière et al., 2007), and single molecules (Kiraz et al., 2005; Lettow et al., 2010). From most of these studies, it can be concluded that these two identical photons, originating from either the same source or two distinct sources, undergo similar generation processes. This ensures coherent interaction and subsequent interference of these two photons.

Figure 7

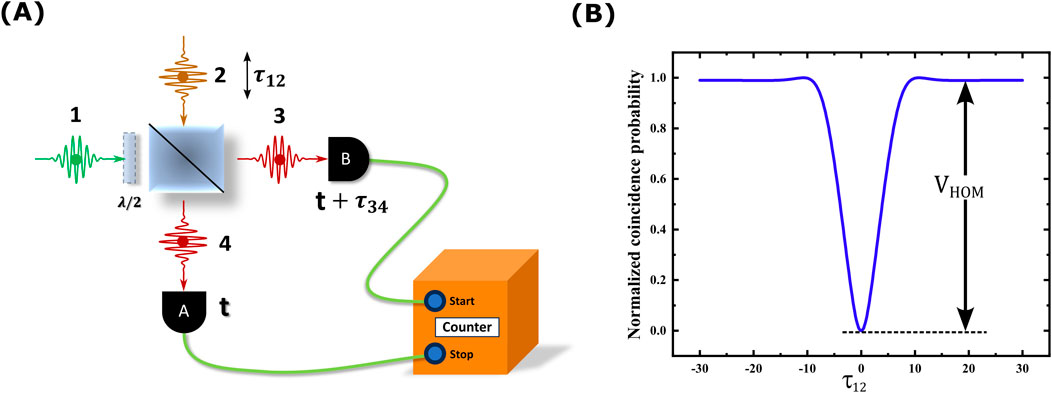
Figure 7. (A) The experimental schematic of a HOM interferometer. The time delay ${\tau }_{12}$ is the difference between the arrival time of photons 1 and 2 at the BS, and the time delay ${\tau }_{34}$ corresponds to the time interval between the detection of one photon at detector A and the detection of the other photon at detector B. (B) Plot of the HOM dip for $V_{\mathit{HOM}}=0.99$.

Figure 8 depicts the different pathways that two identical single photons may follow upon encountering a BS. Despite the indistinguishable nature of the photons, they are represented in different colors to indicate their paths. Scenarios (A) and (B) illustrate the outcomes where one photon is transmitted while the other is reflected, leading both of them to leave through the same port and rendering the other port vacant. This phenomenon effectively eliminates the possibility of coincidental detections. In cases (C) and (D), the photons exit through separate output ports, with one being transmitted and the other being reflected. Notably, the amplitudes associated with paths (C) and (D) exhibit opposing phases. Therefore, they interfere destructively and lead to the cancellation of the photon amplitudes. This mechanism guarantees that when two indistinguishable photons are directed onto a 50:50 BS, they invariably exit together through a single output port. When two indistinguishable single photons, each in a pure state, are directed toward a BS, the transformation is outlined as (Kosen, 2014)

$|{1\rangle }_1|{1\rangle }_2\to \left(|{2\rangle }_3|{0\rangle }_4+|{0\rangle }_3|{2\rangle }_4\right)/\sqrt{2}.(42)$

Figure 8

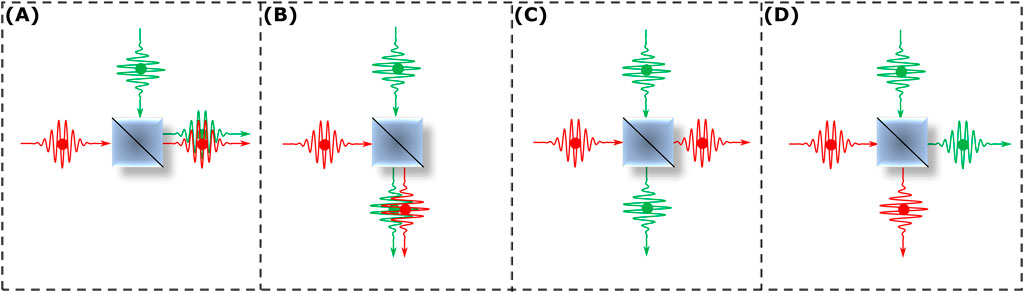
Figure 8. Various possible paths that two indistinguishable photons could take when passing through a BS. In cases (A,B), one photon is reflected while the other is transmitted. In case (C), both photons are transmitted, while in case (D), both photons are reflected.

Equation 42 implies that the two indistinguishable photons consistently exit through the same ports of the BS, although the choice of port is randomly determined. As a result, detectors A and B have zero coincidence. The photon indistinguishability can be investigated by adjusting the arrival times $({\tau }_{12})$ of the photon at the beam splitter (BS) and monitoring the coincidence event between the detectors A and B. A noticeable disparity in arrival times $({\tau }_{12})$ leads to random coincidence counts across both outputs. However, as this time gap narrows, photon interference emerges, subsequently decreasing correlation counts. Maximum interference, that is, the lowest coincidence, is observed when photons reach the BS simultaneously. This manifests as a HOM dip (Hong et al., 1987) in the coincidence count (as illustrated in Figure 7B), signifying zero simultaneous detections at both output ports. The degree of indistinguishability can be modified by manipulating parameters such as temporal overlap or polarization, thereby influencing the coincidence rate. In instances where indistinguishability is compromised by temporal misalignment or polarization mismatch, the coincidence rate increases accordingly. The HOM visibility is determined by comparing the coincidence probability of perfectly indistinguishable photons and the perfectly distinguishable photons. Perfectly distinguishable photons can be easily generated by changing the polarization state of one photon orthogonal to the other. Assuming all the incoming photons are linearly polarized, the insertion of a half-wave plate $(\lambda /2)$ before one of the input ports of BS ensures that two incoming photons are orthogonally polarized, rendering them perfectly distinguishable. Mathematically, the HOM visibility is defined as (Flagg et al., 2010)

$V_{\mathit{HOM}}=\frac{\left(P_c\left(\perp \right)-P_c\left(\Vert \right)\right)}{\left(P_c\left(\perp \right)\right)},(43)$

where $P_c(\perp )$ and $P_c(\Vert )$ are the coincidence probabilities of perpendicular polarization and parallel polarization, respectively. From Equation 43, the HOM visibility attains its maximum value of unity when three essential conditions are satisfied: (1) the presence of more than one photon in either input port must be precluded, (2) the two photons must exhibit indistinguishability, and (3) both photons must exist in pure states.

Together, the HBT and HOM techniques provide comprehensive tools for characterizing the quantum statistical properties and the quality of coherence in single-photon sources, ascertaining the suitability of single photons for quantum communication endeavors.

2.4 Summary of single-photon generation schemes in various atomic platforms

The pursuit of efficient and reliable single-photon sources has led to significant advancements across various atomic platforms. Each platform offers unique advantages and challenges, influenced by the underlying atomic properties and the interaction mechanisms employed. In this section, we explore the developments in single-photon generation, categorizing the discussion into single-atom platforms and ensembles of atoms. This bifurcation allows us to appreciate the nuanced approaches taken by researchers to harness atomic systems for applications in cutting-edge quantum technologies.

2.4.1 Single atoms

Trapped single atoms or ions stand at the forefront of quantum technology, offering unparalleled control over their quantum states. These platforms are pivotal for high-precision experiments, serving as a gateway to explore fundamental quantum mechanics and their potential applications in quantum communication technologies. The capability to isolate and manipulate individual atoms or ions has significantly expanded the possibilities within quantum optics and beyond (Keller, 2022). Such systems ensure that consecutive photon emission events adhere to the minimal temporal intervals dictated by spontaneous emission lifetimes, thus acting as natural single-photon sources.

The non-classical emission behavior has been extensively documented in various studies, revealing the potential of these systems for advanced quantum application experiments (Schubert et al., 1992; Diedrich and Walther, 1987; Darquié et al., 2005; Maunz et al., 2007; Gerber et al., 2009; Maiwald et al., 2012; Higginbottom et al., 2016). Nevertheless, the efficiency of these photon sources is hindered by the challenges in capturing spontaneously emitted fluorescence photons, which are emitted in random directions. Significant advancements have been achieved in enhancing the collection of fluorescence using indigenous techniques that employ high numerical aperture (NA) lenses, as demonstrated in Almendros et al. (2009), Streed et al. (2011), and Higginbottom et al. (2016), with maximum reported efficiencies reaching approximately 12% (Higginbottom et al., 2016). Moreover, integrating spherical mirrors (Shu et al., 2010) and parabolic mirrors (Maiwald et al., 2012) with high NA lenses has led to substantial improvements in fluorescence collection efficiency, achieving approximately 24% and 54%, respectively.

An alternative strategy employing a cavity to house a single atom represents a significant departure from traditional methods of single-atom fluorescence collection. The presence of the cavity alters the behavior of the atoms, resulting in strong interactions and subsequent photon emission along the cavity mode itself, thereby enhancing photon collection efficiency, as detailed in Subsection 2.2. Initial proposals for single-photon generation using a cavity considered the passage of slowly moving atoms, one by one, through the cavity mode. At the time of its passage, each atom interacts and emits a photon into the cavity mode (Law and Kimble, 1997; Kuhn et al., 1999). This method of single-photon generation has been successfully demonstrated in multiple experiments (Hennrich et al., 2000; Kuhn et al., 2002; McKeever et al., 2004). Furthermore, advancements in trapping technologies for both single atoms and ions have enhanced this photon generation technique by substantially mitigating the constraints associated with limited interaction times.

Single-photon generation employing the CMRT process with a ${}^{40}\mathrm{C}\mathrm{a}^{+}$ ion was initially demonstrated by Guthöhrlein et al. (2001) and Keller et al. (2004). Subsequently, Barros et al. achieved a photon detection efficiency of approximately 5% (Barros et al., 2009). In 2007, another study demonstrated the successful creation of single photons within a specific spatiotemporal mode exhibiting alternating circular polarization (Wilk et al., 2007c; Wilk et al., 2007a). A unique approach was adopted by Kimball’s group, leveraging a strong interaction between atoms and fields via the evanescent field from microtoroidal resonators, as reported by Dayan et al. (2008) and Aoki et al. (2009). Another study reported a method for trapping single ⁸⁷Rb atoms using a fiber-pigtailed optical tweezer, enabling the generation of photons from single atoms. This setup incorporated an optical cavity to enhance the collection of fluorescence from single atoms, achieving a remarkably low $g^{(2)}(0)$ value of approximately 0.0001 (Garcia et al., 2013).

As both trapped ion and single-atom technologies advance, their integration continues to improve the capabilities and efficiencies of single-photon sources. Josef Schupp et al. have experimentally achieved a photon generation probability of 0.72, nearing the theoretical limit of 0.73 for the CMRT process (Schupp et al., 2021). In contrast, another experiment reported single-photon generation with high fidelity (nearly unity), albeit with a reduced efficiency of 0.27%. Additionally, there have been efforts to enhance atom–cavity coupling using fiber-based cavities with smaller mode volumes, aiming to minimize the dielectric effects on ions (Harlander et al., 2010), as demonstrated in several studies (Steiner et al., 2013; Kobel et al., 2021).

A novel approach is explored by several groups utilizing the quantum Zeno effect (Misra and Sudarshan, 1977), where the cavity QED, along with electromagnetically induced transparency (EIT), is used for single-photon generation (Villas-Boas et al., 2020; Tolazzi et al., 2021). In this scheme, the atom remains in a dark state throughout the process. A continuous photon generation cycle is initiated using a combination of an excitation laser and a cavity field, along with another laser coupled to the atom’s two ground states. Remarkably, this method has achieved a photon generation rate of approximately 67,000 photons per second. Although this discussion has highlighted several significant advancements in single-photon generation from trapped single atoms, it is essential to note that the entangled photon sources described in Subsection 3.4 also function as single-photon generators. For a comparative analysis of various experiments on single-photon generation using trapped single atoms and their outcomes, refer to Table 2 in the accompanying text.

Table 2

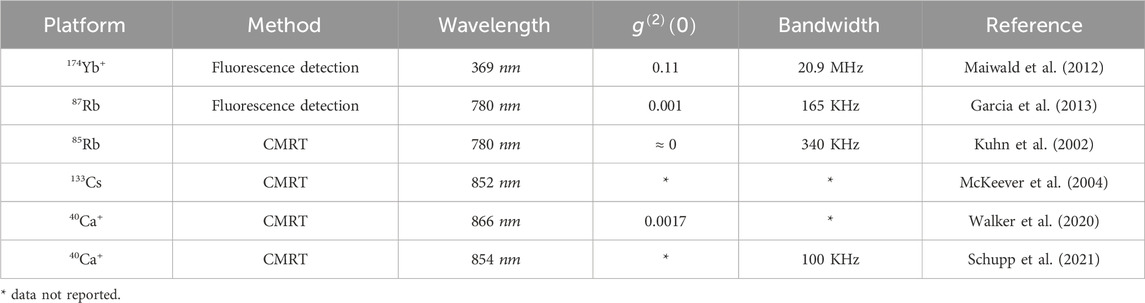
Table 2. A summary of significant experiments involving single atoms for single-photon generation and their outcomes.

2.4.2 Ensembles of atoms

While single atomic platforms highlight the potential of individual quantum systems, ensembles of atoms leverage collective effects to achieve enhanced performance in photon generation. These approaches seek a harmonious balance between the precision of individual control and the power of collective dynamics, striving to capture the optimal benefits from each strategy. Within this section, our attention is directed toward exploring single-photon generation within both cold and warm atomic ensemble platforms.

Cold atomic ensembles leverage atoms cooled to near absolute zero temperatures, where quantum phenomena become prominently observable, ideal for studying collective quantum effects. The reduced kinetic energy at these temperatures permits prolonged interaction times, enabling a deeper exploration of quantum-optical processes. In 2004, the first successful demonstration of generating single photons from a trapped cold cesium atomic vapor was conducted employing the DLCZ protocol (Duan et al., 2001), achieving a coherence time of several hundred nanoseconds (Chou et al., 2004). By controlling the de-coherence mechanism in the same experimental setup, Felinto et al. reported the coherence times longer than $10\mu$s (Felinto et al., 2005). Instead of using cold Cs atoms, Chen et al. demonstrated the controlled and storable generation of single photons from a trapped cold rubidium (Rb) atomic ensemble (Chen et al., 2006). By improving the compensation for residual magnetic fields in the magneto-optical trap (MOT) (Raab et al., 1987), they achieved a coherence time for the collective state of $300\mu$s. Some research groups also demonstrated the coherence time for single excitation to 1 ms (Zhao et al., 2008a; Zhao et al., 2008b). Farrera et al. demonstrated a heralded single-photon source from a trapped ⁸⁷Rb with a controllable emission time (Farrera et al., 2016). Interestingly, one experiment observed instances of photon anti-bunching in ion crystals comprising more than 1,000 ions, with measured $g^{(2)}(0)$ value approximately 0.032 (Obšil et al., 2018). Many experiments have successfully reported sources of correlated photon pairs (see Section 3.4.2), which act as heralded single-photon sources.

In contrast, warm atomic vapor systems operate at room temperature or higher, simplifying the operational complexities associated with ultra-cold environments and offering improved scalability for quantum networks. However, the primary challenge in warm atomic vapors is reducing the effect of thermal motion, which reduces the atom–field interaction time. Subsequently, it affects the efficiency of the photon generation rate. Strategies to overcome this issue include employing faster interaction times, during which the atoms are effectively treated as stationary (Podhora et al., 2017).

Another promising platform for single-photon generation involves the use of Rydberg atoms. This method capitalizes on the Rydberg blockade mechanism to suppress multiple excitations within a finite ensemble size (Saffman et al., 2010; Lukin et al., 2001; Urban et al., 2009; Gaëtan et al., 2009). The efficient application of this approach has been demonstrated in wedge-shaped microfabricated vapor cells where the stimulated FWM process occurs in less than 1 ns due to strong interactions between Rydberg atoms (Ripka et al., 2018).

Additionally, the motional averaging technique has been applied to neutralize the effects of thermal motion, effectively mimicking conditions where atoms remain in the interaction zone (Borregaard et al., 2016). This has led to the development of quantum memories with significant memory times in warm cesium atomic vapor, reinforcing the role of atom-based quantum memories as reliable single-photon sources (Zugenmaier et al., 2018).

A comparative analysis of different milestone experiments toward single-photon generation in the atomic ensembles is represented in Table 3 through different characterization parameters. Through this exploration of single-photon generation across different atomic platforms, we observe a rich landscape of technological innovation. Each platform, whether focusing on single atoms or ensembles in cold or warm conditions, contributes uniquely to our understanding and capability in quantum photonics. The continued advancement in these areas holds the key to unlocking the full potential of quantum technologies in communication, computation, and beyond.

Table 3

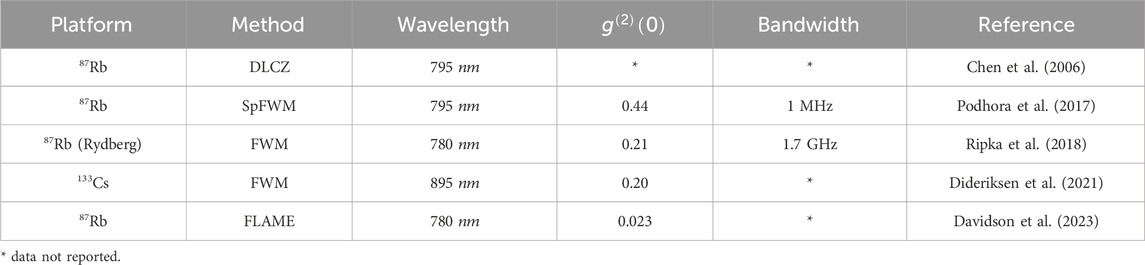
Table 3. A summary table of significant experiments involving atomic vapors for single-photon generation and their outcomes.

3 Entangled photons

Entanglement, a phenomenon at the heart of quantum mechanics, presents one of the most profound and intriguing concepts in modern physics. It describes a peculiar correlation between quantum particles—a mysteriously strong connection regardless of the distance between them. In the realm of quantum mechanics, the phenomenon known as entanglement manifests when the characteristics of individual particles or subsystems are intertwined to the extent that their descriptions become inseparable. The concept of entanglement first emerged from the quantum theory developed in the early 20th century, challenging the classical views of separate, well-defined states and local realism.

In 1935, Albert Einstein, Boris Podolsky, and Nathan Rosen introduced the EPR paradox (Einstein et al., 1935), challenging the completeness of quantum mechanics by criticizing entanglement as a “spooky action at a distance.” This paradox set the stage for decades of debate and continues to inspire research on the foundational aspects of quantum mechanics to date (Nath et al., 2024). Einstein, Podolsky, and Rosen proposed the local hidden-variable theory to explain quantum correlations through predetermined properties that do not rely on non-local interactions (Einstein et al., 1935). However, Bell’s theorem, formulated in 1964, fundamentally changed the understanding of quantum entanglement by postulating an inequality known as Bell’s inequality (Bell, 1964), which provides a way to test the predictions of quantum mechanics against the local hidden-variable theories (Bell, 1966). Bell’s work addressed the concerns raised by the EPR paradox by demonstrating that no local realistic hidden-variable theory could reproduce all the predictions of quantum mechanics with regard to entanglement. The violation of Bell’s inequality indicates a non-local behavior, confirming quantum entanglement. This framework provided a measurable test, paving the way for experiments that distinguish between classical and quantum entanglement.

Following Bell’s theorem, Carl A. Kocher and Eugene D. Commins conducted the first experimental demonstration of quantum entanglement using optical photons in 1967 at the University of California, Berkeley (Kocher and Commins, 1967). In this experiment, they exploited a two-stage cascade emission in calcium vapor to generate entangled photon pairs. While this seminal experiment demonstrated the generation of entangled photon pairs for the first time, it did not conclusively prove the nonexistence of the local hidden-variable theory or demonstrate Bell’s inequality violation. Kocher’s subsequent work on temporal correlations in successively emitted photons further strengthened the significance of the cascaded emission as a mechanism to demonstrate quantum entanglement (Kocher, 1971). His pioneering experimental setup directly influenced future experimental techniques and laid the foundation for modern entanglement-based protocols. His work inspired experimental investigations by J. Clauser (Freedman and Clauser, 1972) and A. Aspect (Aspect et al., 1980; Aspect et al., 1981) aimed at understanding and quantifying quantum entanglement. Building upon Kocher’s experimental setup, J. Clauser further refined the measurements pertaining to entanglement quantification (Kocher, 2024). He introduced crucial improvements by incorporating polarization-based measurements of the entangled photons and designing a more rigorous test of Bell’s inequality violation (Freedman and Clauser, 1972). Clauser’s modifications allowed for the measurement of quantum correlations at different angles (polarization states), providing the necessary statistical data to conclusively demonstrate the violation of Bell’s inequality (Clauser, 1976). We refer readers interested in the historical perspective and technical details of experiments performed by Kocher to his recent publication, where he reflects on the simplicity and elegance of his approach (Kocher, 2024).

While Bell’s inequality violation is a prominent method of demonstrating entanglement, it is not the only approach to visualize entanglement. The Leggett–Garg inequality (LGI) (Leggett and Garg, 1985), for instance, tests for quantum coherence in systems where the assumption of macroscopic realism is challenged (Leggett and Garg, 1985; Emary et al., 2013; Nath et al., 2024). It is analogous to Bell’s inequality, but instead of dealing with spatially separated systems (as in Bell’s theorem), the LGI focuses on measurements of a single system at different times. Recent experiments by U. Sinha and colleagues have explored violations of the LGI in more complex quantum systems (Nath et al., 2024). Furthermore, techniques such as entanglement witnesses (Horodecki et al., 2001) and quantum state tomography (Lvovsky and Raymer, 2009) offer alternative pathways to detect and quantify entanglement, broadening the tools available for verifying quantum correlations in both discrete and continuous variable systems.

In 2022, the Nobel Prize in Physics was awarded to Alain Aspect, John Clauser, and Anton Zeilinger in recognition of their pioneering contributions to the study of quantum entanglement, with a particular focus on their work involving entangled photon pairs. John Clauser’s earlier work (Clauser et al., 1969) established the experimental framework necessary for testing Bell’s theorem, which challenged the compatibility of quantum mechanics with local hidden-variable theories. In the early 1980s, Alain Aspect’s experiments (Aspect et al., 1982) provided the first strong empirical violation of Bell’s inequalities using entangled photon pairs to demonstrate quantum entanglement over significant distances. Subsequently, Anton Zeilinger’s contributions (Bouwmeester et al., 1997) advanced these ideas further by developing novel methods for producing entangled photon pairs and utilizing them in groundbreaking quantum teleportation experiments. Together, their research has not only validated quantum theory at its most counterintuitive but also laid the foundational work for future technologies in quantum computing and cryptography.

Quantum entanglement is not limited to discrete two-level systems such as qubits, which are represented by electron spins or photon polarization, as demonstrated in the pioneering experiments of Clauser, Aspect, and Zeilinger. It can also be extended to more complex continuous variable systems, where entanglement manifests through correlations in continuous quantities. These continuous variables include relationships such as energy and time (Mei et al., 2020; MacLean et al., 2018), position and momentum (Howell et al., 2004), or the coupling of angular position to angular momentum (Leach et al., 2010; Vaidman, 1994), as initially outlined in the EPR paradox. Research in continuous variable entanglement has opened new avenues for implementing quantum technologies, particularly in quantum communication and cryptography, where entangled states can be utilized in novel protocols (Braunstein and Kimble, 1998).

3.1 Mathematical descriptions

A comprehensive grasp of entangled photons necessitates a foundational understanding supported by mathematical expressions. Thus, we embark on an exploration starting with characterizing single and two-particle pure and mixed states. Subsequently, we delve into the representation of Bell states, particularly within the framework of photon polarization bases, as their significance lays the groundwork for further discussion.

3.1.1 Representation of single-particle pure and mixed states

In quantum mechanics, the pure state of a single particle is represented by a state vector, denoted as $|\psi \rangle$, which exists within a Hilbert space of dimensions equivalent to that of the state. This state vector can be articulated as a linear combination of the system’s specific observable operator’s (e.g., position $(x)$, momentum $(p)$, or energy $(E)$) basis vectors (eigenstates) that span the Hilbert space. For an N-dimensional system, a single-particle pure state can be expressed in Equation 44 as

$|\psi \rangle ={\displaystyle \sum _{i=1}^N}{d}_i\left|{\varphi }_i\right.⟩,(44)$

where $\left|{\varphi }_i\right.⟩$ represents the eigenstates, and $d_i$ are complex coefficients representing the amplitude for each basis state, satisfying the normalization condition: ${\sum }_{i=1}^N|d_i{|}^2=1.$ Similarly, for a two-dimensional system, representation of single-particle pure state takes the form

$|\psi \rangle =a|0\rangle +b|1\rangle =a\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right]+b\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \end{array}\right]=\left[\begin{array}{c}\hfill a\hfill \\ \hfill b\hfill \end{array}\right],(45)$

where $|a{|}^2+|b{|}^2=1$. In contrast to a pure state, which imparts complete knowledge of a system, a mixed state conveys only partial system knowledge. It furnishes a probability distribution encompassing multiple potential states. This scenario often arises within larger quantum systems or situations where state uncertainty is induced by decoherence. Distinguishable from pure states by their statistical nature, mixed states are written as composites of pure states. The density matrix, or density operator $\rho$, serves as the standard representation for a mixed state, defining a single-particle mixed state accordingly in Equation 46 as follows:

$\rho ={\displaystyle \sum _i}{p}_i\left|{\psi }_i\right.⟩\left.⟨{\psi }_i\right|,(46)$

where $\left|{\psi }_i\right.⟩$ are the single-particle state vectors, and $p_i$ are the associated probabilities satisfying $0\le p_i\le 1$ and ${\sum }_i{p}_i=1$.

3.1.2 Representation of two-particle pure and mixed state

The mathematical representation of a two-particle pure state in quantum mechanics extends the formalism used for single particles, incorporating the principles of superposition and entanglement. A two-particle state vector can be depicted as the tensor product of the Hilbert spaces corresponding to individual particles if they are not entangled. Let us label these two particles as 1 and 2 and assume both particles are in distinct pure states, with state vectors $|{\psi }_1\rangle$ and $|{\psi }_2\rangle$ situated in their unique Hilbert spaces $H_1$ and $H_2$, respectively. Therefore, the joint state of these two particles can be expressed as

$|\mathrm{\Psi }\rangle =\left|{\psi }_1\right.⟩\otimes \left|{\psi }_2\right.⟩.(47)$

In Equation 47, the notation $\otimes$ means the tensor product between $|{\psi }_1\rangle$ and $|{\psi }_2\rangle$. Thus, for an N-dimensional system, a two-particle state can be described in Equation 48 as a superposition of product states:

$|\mathrm{\Psi }\rangle ={\displaystyle \sum _{i,j=1}^N}{d}_{ij}\left|{\psi }_{1i}⟩\otimes ⟨{\psi }_{2j}\right|,(48)$

where $\left|{\psi }_{1i}\right.⟩$ and $\left.⟨{\psi }_{2j}\right|$ are basis states for particles 1 and 2, respectively, and $d_{ij}$ are complex coefficients that satisfy the normalization condition, as shown in Equation 49, is:

${\displaystyle \sum _{i,j=1}^N}{\left|d_{ij}\right|}^2=1.(49)$

Given a two-dimensional system comprising two distinct particles denoted as A and B, the expression delineating the pure state as presented in Equation 45 can be formulated as follows:

$\begin{array}{c}|{\psi \rangle }_A=\mathrm{a}|{0\rangle }_A+\mathrm{b}|{1\rangle }_A,\\ |{\psi \rangle }_B=\mathrm{c}|{0\rangle }_B+\mathrm{d}|{1\rangle }_B,\end{array}(50)$

where $|{0\rangle }_A,|{1\rangle }_A$ and $|{0\rangle }_B,|{1\rangle }_B$ of Equation 50 are the orthogonal bases for system A and B, respectively, and $|a{|}^2+|b{|}^2=|c{|}^2+|d{|}^2=1$. Then, the two-qubit state is described by

$\begin{array}{cc}\hfill |\psi \rangle & =|{\psi \rangle }_A\otimes |{\psi \rangle }_B;\hfill \\ \hfill |\psi \rangle & =ac|{0\rangle }_A|{0\rangle }_B+bd|{1\rangle }_A|{1\rangle }_B+ad|{0\rangle }_A|{1\rangle }_B+bc|{1\rangle }_A|{0\rangle }_B;\hfill \\ \hfill |\psi \rangle & =ac|00\rangle +bd|11\rangle +ad|01\rangle +bc|10\rangle .\hfill \end{array}(51)$

On the other hand, the mathematical representation of a two-particle mixed state utilizes the density matrix formalism. Mixed states act as statistical combinations of pure states, reflecting situations in which the system might exist in multiple potential states, each associated with a distinct probability. However, in contrast to pure states, mixed states lack coherence among these possibilities. Within a two-particle framework, the density matrix, $\rho$, encapsulates the complete statistical description of states (both pure and mixed) in which the system can be found. The density matrix representation for a two-particle mixed state in N-dimension can be written as

$\rho ={\displaystyle \sum _{k=1}}{p}_k\left|{\mathrm{\Psi }}_k\right.⟩\left.⟨{\mathrm{\Psi }}_k\right|,(52)$

where $\left|{\mathrm{\Psi }}_k\right.⟩$ in Equation 52 are the arbitrary pure states of the two-particle system and $p_k$ are the probabilities associated with each pure state, satisfying $0\le p_k\le 1$ and ${\sum }_k{p}_k=1$. The summation is over all the pure states $\left|{\mathrm{\Psi }}_k\right.⟩$ contributing to the mixed state, not only the dimensionality $N$ of the Hilbert space.

3.1.3 Bell states

It is evident that not every two-qubit state can be expressed as a straightforward combination of individual single-qubit states. Consider a two-qubit state $|\psi \rangle =\frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )$ as an illustration. By comparing it with the general form presented in Equation 51, it becomes evident that all coefficients $(a,b,c,d)$ must equate to 0, rendering an impractical representation. Conversely, the quantum state denoted by $\frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )$ is recognized as a valid quantum state. Notably, such a state is categorized as an entangled state. The entangled state reveals the absence of independence between systems A and B, underscoring the existence of quantum correlations between these entities. Remarkably, four such states are possible that exhibit complete entanglement, commonly referred to as Bell states or Bell bases,

$\begin{array}{cc}\hfill & \left|{\mathrm{\Phi }}^{\pm }\right.⟩=\frac{1}{\sqrt{2}}\left(|00\rangle \pm |11\rangle \right),\hfill \\ \hfill & |{\mathrm{\Psi }}^{\pm }\rangle =\frac{1}{\sqrt{2}}\left(|01\rangle \pm |10\rangle \right).\hfill \end{array}(53)$

These four states possess the highest level of entanglement, which qualifies them as maximally entangled states. Such a categorization implies that knowing the outcomes of measuring one qubit allows for precisely predicting the other qubit’s state, irrespective of their spatial separation. Conversely, consider a state defined by

$|\psi \rangle =\sqrt{1-a}|00\rangle +\sqrt{a}|11\rangle ,(54)$

where $a\ne 1/2$ and $\in [\mathrm{0,1}]$. In Equation 54, the state, |ψ〉 exhibits a lesser degree of entanglement. Therefore, it is referred to as a non-maximally entangled state, which means the correlation between subsystems is less than in the maximally entangled case. If $a=1$ or 0, the state is not entangled at all.

The four Bell states constitute a comprehensive basis for the two-qubit state space, indicating that any two-qubit state can be represented by a linear combination of the Bell states. Notably, within these four states, $\left|{\mathrm{\Psi }}^{-}\right.⟩$ is distinguished by its antisymmetry upon interchanging systems A and B, known as singlet or EPR states. The other three states in the Bell set are characterized by their symmetry and are commonly referred to as triplets.

3.1.4 Density matrix representation of the Bell states

Deeper insight into a qubit’s state can be gained through its density matrix representation. This representation serves as a robust framework in quantum mechanics, offering a detailed description of both pure and mixed quantum states. For Bell states, which are pure states, the density matrix can be derived directly from their state vectors. For example, let us consider the $\left|{\mathrm{\Phi }}^{+}\right.⟩$ state from Equation 53. The density matrix for this state can be expressed as

$\begin{array}{cc}\hfill {\rho }_{{\mathrm{\Phi }}^{+}}& =|{\mathrm{\Phi }}^{+}\rangle \langle {\mathrm{\Phi }}^{+}|=\frac{1}{2}\left(|00\rangle +|11\rangle \right)\left(\langle 00|+\langle 11|\right);\hfill \\ \hfill {\rho }_{{\mathrm{\Phi }}^{+}}& =\frac{1}{2}\left(|00\rangle \langle 00|+|00\rangle \langle 11|+|11\rangle \langle 00|+|11\rangle \langle 11|\right);\hfill \\ \hfill {\rho }_{{\mathrm{\Phi }}^{+}}& =\frac{1}{2}\left(\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right).\hfill \end{array}(55)$

The diagonal entries of the density matrix denote the probabilities or populations of the system existing within specific basis states. In contrast, the non-diagonal entries indicate the level of coherence across these states. Therefore, analyzing the density matrix of the $|{\mathrm{\Phi }}^{+}\rangle$ state, symbolized as ${\rho }_{{\mathrm{\Phi }}^{+}}$ in Equation 55, it is observed that the non-diagonal components $|00\rangle \langle 11|$ and $|11\rangle \langle 00|$ match the values of the diagonal components $|00\rangle \langle 00|$ and $|11\rangle \langle 11|$. This observation leads to the conclusion of full coherence between the states $|00\rangle$ and $|11\rangle$. A visual representation of the density matrices for the entire Bell basis is provided in Figure 9. Similarly, we can write the density matrices for the other three Bell states given in Equation 56 as:

${\rho }_{{\mathrm{\Phi }}^{-}}=\frac{1}{2}\left(\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right);{\rho }_{{\mathrm{\Psi }}^{+}}=\frac{1}{2}\left(\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right);{\rho }_{{\mathrm{\Psi }}^{-}}=\frac{1}{2}\left(\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill -1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),(56)$

Figure 9

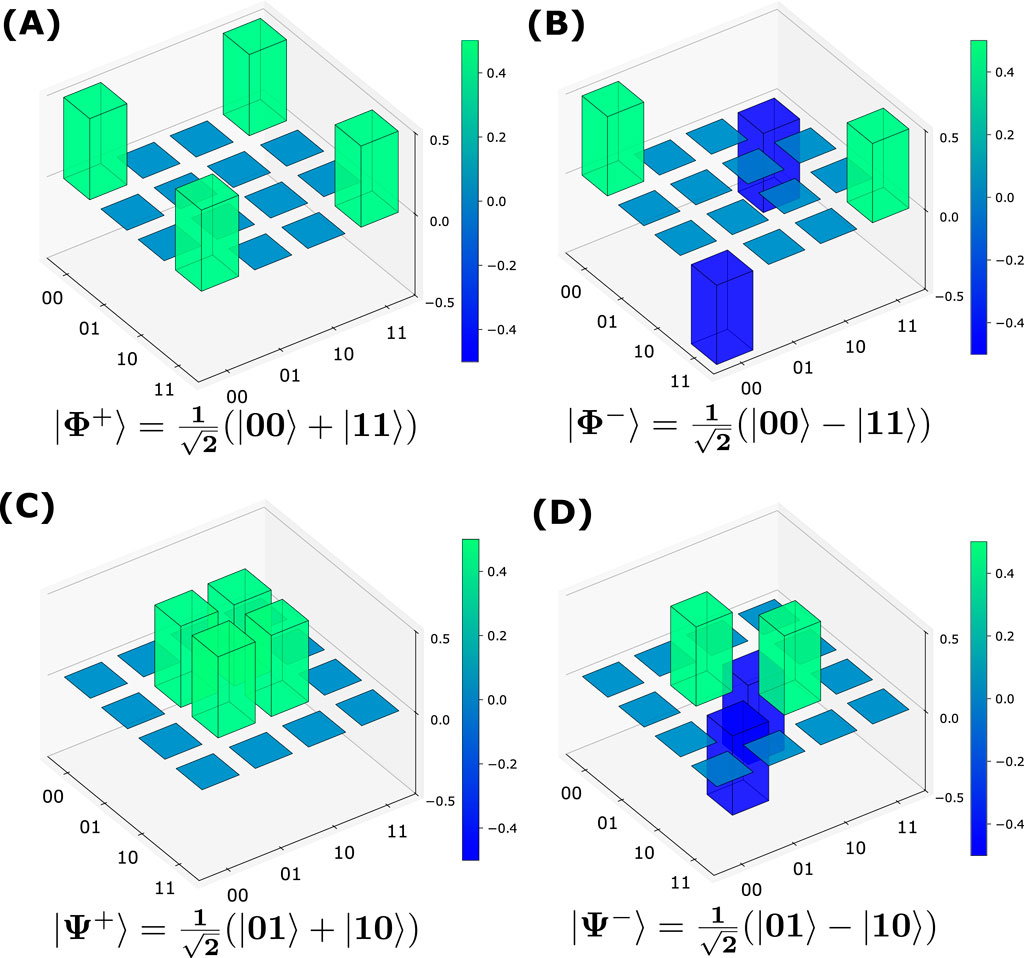
Figure 9. Density matrix representation for the (A) $|{\mathrm{\Phi }}^{+}\rangle$, (B) $|{\mathrm{\Phi }}^{-}\rangle$, (C) $|{\mathrm{\Psi }}^{+}\rangle$, and (D) $|{\mathrm{\Psi }}^{-}\rangle$ Bell states. The presence of non-zero elements in the off-diagonal terms signifies entanglement within the states. Uniformity in the height of all bars across the matrices indicates that these states are maximally entangled.

3.1.5 Polarization-entangled Bell states

Expressing Bell states in terms of photon polarization proves more convenient for practical applications as it is comparatively simpler to generate and analyze the entangled state using photon polarization. From the concept of Jones vector formalism (Kliger et al., 1990), the horizontal and vertical polarized light can be expressed as

$|H\rangle =\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right),|V\rangle =\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \end{array}\right).(57)$

Left and right circular polarized light can be written as

$|L\rangle =\frac{1}{\sqrt{2}}\left(\begin{array}{c}\hfill 1\hfill \\ \hfill i\hfill \end{array}\right),|R\rangle =\frac{1}{\sqrt{2}}\left(\begin{array}{c}\hfill 1\hfill \\ \hfill -i\hfill \end{array}\right).(58)$

Diagonal $\left(\pm 45°\right)$ polarized light can be written as

$|+\rangle =\frac{1}{\sqrt{2}}\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \end{array}\right),|-\rangle =\frac{1}{\sqrt{2}}\left(\begin{array}{c}\hfill 1\hfill \\ \hfill -1\hfill \end{array}\right).(59)$

The polarization states of two photons can be utilized to establish a two-qubit system. The fundamental basis states for this two-photon system include $|HH\rangle ,|HV\rangle ,|VH\rangle$, and $|VV\rangle$. In this notation, $\left|{\psi }_1{\psi }_2\right.⟩$ denotes the configuration where the first and second photons exhibit polarization states $\left|{\psi }_1\right.⟩$ and $\left|{\psi }_2\right.⟩$, respectively. Leveraging these basis states of Equations 57–59, the Bell states are articulated as follows:

$\begin{array}{cc}\hfill |{\mathrm{\Phi }}^{+}\rangle & =\frac{1}{\sqrt{2}}\left(|HH\rangle +|VV\rangle \right)=\frac{1}{\sqrt{2}}\left(|LR\rangle +|RL\rangle \right),\hfill \\ \hfill |{\mathrm{\Phi }}^{-}\rangle & =\frac{1}{\sqrt{2}}\left(|HH\rangle -|VV\rangle \right)=\frac{1}{\sqrt{2}}\left(|LL\rangle +|RR\rangle \right),\hfill \\ \hfill |{\mathrm{\Psi }}^{+}\rangle & =\frac{1}{\sqrt{2}}\left(|HV\rangle +|VH\rangle \right)=\frac{1}{\sqrt{2}}\left(|LL\rangle -|RR\rangle \right),\hfill \\ \hfill |{\mathrm{\Psi }}^{-}\rangle & =\frac{1}{\sqrt{2}}\left(|HV\rangle -|VH\rangle \right)=\frac{1}{\sqrt{2}}\left(|LR\rangle -|RL\rangle \right).\hfill \end{array}(60)$

In general, photons can be polarized at various angles, and their quantum states can be described in terms of these polarization angles. For a single photon polarized at an arbitrary angle $\theta$ relative to the horizontal axis, its state can be represented as

$|\theta \rangle =\cos \left(\theta \right)|H\rangle +\sin \left(\theta \right)|V\rangle .(61)$

Using the same convention as Equation 61, when dealing with two photons polarized at angles $\alpha$ and $\beta$, and both are measured in the linear polarization basis ($|V\rangle$ and $|H\rangle$), their states can be expressed as

$\begin{array}{cc}\hfill |\alpha \rangle & =\cos \left(\alpha \right)|H\rangle +\sin \left(\alpha \right)|V\rangle ,\hfill \\ \hfill |\beta \rangle & =\cos \left(\beta \right)|H\rangle +\sin \left(\beta \right)|V\rangle .\hfill \end{array}(62)$

If the system occupies the joint state $|\alpha \beta \rangle$, we can calculate the probability of obtaining specific Bell states (Equation 60). This will help to understand the role of polarization states in quantum entanglement and the resulting probabilities of obtaining different Bell states. The probability of obtaining the system in one of the Bell states is calculated with the help of Equation 62 as follows:

$p_{a\beta }=\left\{\begin{array}{cc}\frac{1}{2}{\cos }^2\left(\alpha \mp \beta \right)\hfill & \text{\hspace{0.17em}for\hspace{0.17em}}|\mathrm{\Phi }\pm \rangle \hfill \\ \frac{1}{2}{\sin }^2\left(\alpha \pm \beta \right)\hfill & \text{\hspace{0.17em}for\hspace{0.17em}}|\mathrm{\Psi }\pm \rangle \hfill \end{array}\right\}.(63)$

3.2 Generation processes

Most experiments that generate entangled photons rely on one of three fundamental processes: FWM, Raman scattering, and SPDC. The SPDC process stands out as the most widely accepted and utilized technique for producing correlated photon pairs from nonlinear crystals (Couteau, 2018). However, in the context of atomic platforms, FWM or Raman processes are employed for the controlled generation of entangled photons. In this review, we will provide a concise overview of all three processes, with a particular emphasis on FWM and Raman processes, as they are more pertinent to the topic under discussion.

3.2.1 SPDC process

SPDC is a nonlinear process (Harris et al., 1967) where a higher-energy pump photon spontaneously splits into two lower-energy daughter photons, namely, idler and signal photons (Burnham and Weinberg, 1970). This process occurs in materials with non-zero second-order nonlinearity $({\chi }^{(2)})$ (Mandel and Wolf, 1995), specifically for difference frequency generation (DFG) and parametric down-conversion (PDC). Examples of such second-order nonlinear crystals include potassium dihydrogen phosphate (KDP), beta barium borate (BBO), periodically poled lithium niobate (PPLN), and potassium titanyl phosphate (KTP). These crystals are employed across diverse optical applications, as evidenced by studies such as those referenced in Burnham and Weinberg (1970) and Edamatsu (2007). The Hamiltonian of this SPDC process can be formulated as follows (Mandel and Wolf, 1995):

$H=\hslash g\left({\widehat{a}}_s^{†}{\widehat{a}}_i^{†}{\widehat{a}}_p+{\widehat{a}}_p^{†}{\widehat{a}}_i{\widehat{a}}_s\right).(64)$

In this context, ${\widehat{a}}_{s,i,p}^{†}$ and ${\widehat{a}}_{s,i,p}$ symbolize the creation and annihilation operators for the signal, idler, and pump photons, respectively. The constant $g$ signifies the interaction strength, while $\hslash$ denotes the reduced Planck’s constant. The first and second terms of Equation 64 correspond to the process of parametric down-conversion and its complex conjugate, respectively. Under the continuous wave approximation, the energy conservation leads to the frequency of the pump being equal to the sum of the frequencies of the idler and signal photons. Additionally, a phase-matching condition is essential to ensure the coherent phase alignment of each generated light wave within the nonlinear crystal. These prerequisites are detailed as follows:

$\begin{array}{c}{\vec{\mathrm{k}}}_p={\vec{\mathrm{k}}}_s+{\vec{\mathrm{k}}}_i,\\ {\omega }_p={\omega }_s+{\omega }_i.\end{array}(65)$

Here, ${\omega }_{s,i,p}$ and $k_{s,i,p}$ represent the frequencies and wave vectors for the signal, idler, and pump photons, respectively. Due to the conservation principles (followed by Equation 65), the idler and signal photons are emitted in a cone shape (see Figure 10). If we consider the idler and signal photons to be on a horizontal (H) and vertical (V) basis at the intersection point of these two cones, there is no way to know which basis the photons are on without detecting them. However, detecting one photon ensures its existence and reveals the state of the other. Therefore, photons in these intersection points are considered to be entangled.

Figure 10

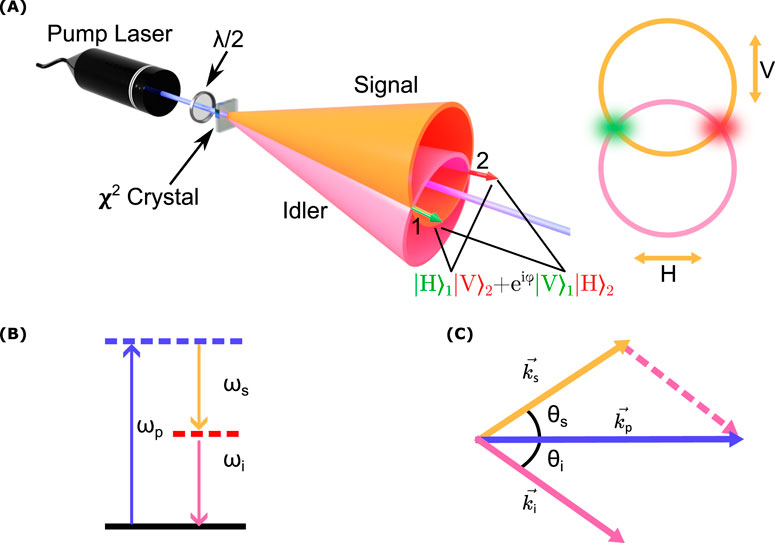
Figure 10. Entangled photon generation from the SPDC process. (A) Schematic representation of SPDC where a signal and idler photons on a vertical and horizontal basis are emitted from the ${\chi }^2$ crystal in a cone shape upon excited by a UV pump laser. (B) Representation of energy conservation. (C) Representation of momentum conservation.

3.2.2 Raman process

The realization of atom–photon entanglement is an essential part of state transfer between the atom and photon and is useful for long-distance quantum communication (Müller and Eschner, 2014). The establishment of atom–photon entanglement can be achieved by employing Raman scattering processes with two possible decay channels, as shown in Figure 11. A detailed discussion of the Raman scattering process in the context of single-photon generation can be found in Section 2.2.1. Therefore, this section will focus specifically on utilizing Raman scattering for entangled photon generation.

Figure 11

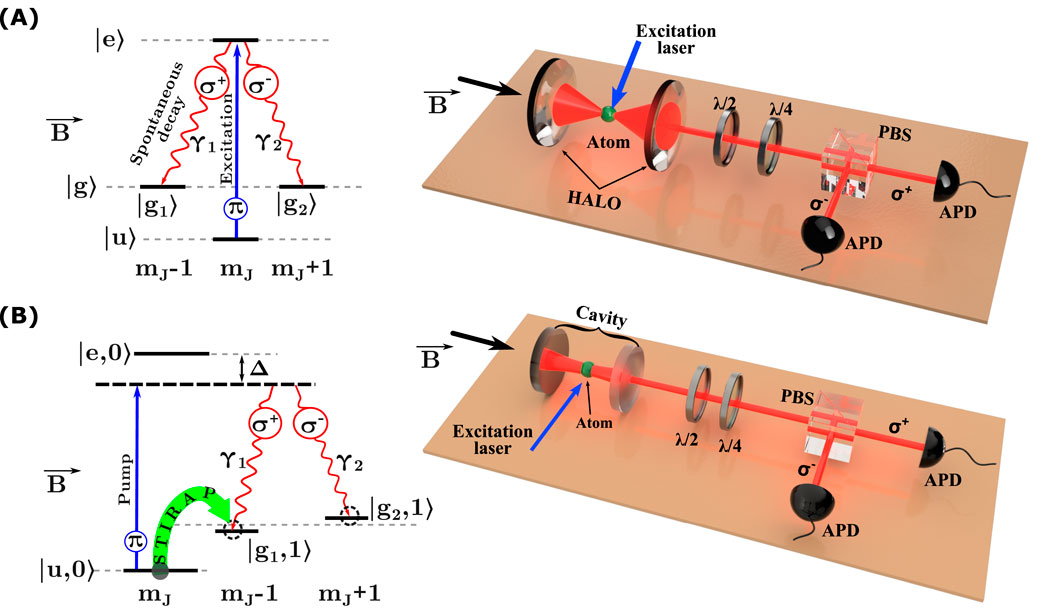
Figure 11. A schematic representation of atom–photon entanglement via the Raman process. (A) Generation of atom–photon entanglement through spontaneous Raman scattering. The emitted photons are collected by two high numeric aperture objectives (HALOs) and subsequently measured to establish an entangled state. In this depiction, photons are collected along the quantization axis (along the direction of the magnetic field, $\vec{B}$) direction, resulting in the presence of only ${\sigma }^{+}$ and ${\sigma }^{-}$ photons, which can be separated using combination of a half-wave plate $(\lambda /2)$, a quarter-wave plate $(\lambda /4)$, and a polarizing beam splitter (PBS). (B) Atom–photon entanglement is facilitated by the CMRT process. This method operates on the same principle described above, with the additional presence of a cavity field enabling the Stokes or anti-Stokes branch for stimulated scattering.

From the discussion in Subsection 3.1, it is evident that the presence of phase correlation or coherence between states is the key factor distinguishing an entangled state from a mixed state. The conservation of angular momentum in light–atom interactions results in polarization-selective transitions that establish a phase correlation between atomic and photon states. These polarization-selective transitions can be achieved by lifting the degeneracy of the magnetic sublevels ($m_J$ levels) through the application of a magnetic field. The selection rules can be defined as follows:

1. For the transitions where $\mathrm{\Delta }{m}_J=0$, the $\pi$-polarized light will be absorbed or emitted.

2. For the transitions where $\mathrm{\Delta }{m}_J=\pm 1$, the ${\sigma }^{\pm }$-polarized light will be absorbed or emitted.

Eventually, a phase correlation persists based on such polarization-selective transitions, which sets the base for the atom–photon entanglement. When there is no magnetic field present, the angular momentum levels will degenerate. Consequently, no phase correlation exists between the components of the final state, which can be expressed as (Volz, 2006)

$\left|{\psi }_F\right.⟩=C_e\left(t\right)|e\rangle |0\rangle +{\displaystyle \sum _{\omega ,\mathit{k}}}{C}_{\omega \mathit{k}}\left(t\right)|g\rangle |1_{\omega \mathit{k}}\rangle .(66)$

Here, $C_e(t)$ denotes the amplitude of the excited state $|e\rangle$, whereas $C_{\omega ,\mathit{k}}(t)$ are the amplitudes of the ground state while emitting one photon in the $\omega \mathit{k}$^th mode.

Along with the polarization-selective transitions, the transverse nature of radiation is also crucial for comprehending the atom–photon entangled state. Based on this transverse nature, the polarization of photons, stemming from transitions between specific magnetic sublevels ($m_J$ levels), exhibits a spatial distribution. If we choose the quantization axis along the direction of the magnetic field, the $\pi$-polarized light is absent along that direction, with ${\sigma }^{\pm }$-polarized light predominantly observed. Conversely, $\pi$-polarized light predominates perpendicular to the quantization axis (Bransden and Joachain, 2003). Incorporating this spatial distribution, modification to the polarization states can be made as delineated below:

$\begin{array}{c}|\pi \rangle \to \sin \theta |\pi \rangle ;\\ \left|{\sigma }^{\pm }\right.⟩\to \sqrt{\frac{1}{2}\left(1+{\cos }^2\theta \right)}\left|{\sigma }^{\pm }\right.⟩.\end{array}(67)$

Here, $\theta$ is the angle subtended by the emitted photon with the quantization axis. Considering the transition from the $\left|m_J\right.⟩$ level, the joint atom–photon state, $|{\psi }_{\text{joint\hspace{0.17em}}}\rangle$ can be expressed using Equation 67 as

$\begin{array}{cc}\hfill \left|{\psi }_{\text{joint\hspace{0.17em}}}\right.⟩=& \left[C_{J,m_J}^{J,m_J-1}\sqrt{\frac{1}{2}\left(1+{\cos }^2\theta \right)}\left|J,m_J-1\right.⟩\left|{\sigma }^{+}\right.⟩\right.\hfill \\ \hfill & \left.+C_{J,m_J}^{J,m_J+1}\sqrt{\frac{1}{2}\left(1+{\cos }^2\theta \right)}\left|J,m_J+1\right.⟩\left|{\sigma }^{-}\right.⟩+C_{J,m_J}^{J,m_J}\sin \theta \left|J,m_J\right.⟩|\pi \rangle \right],\hfill \end{array}(68)$

where $C_{J,m_J}^{J^{\prime },m_J^{\prime }}$ are the Clebsch–Gordan (CG) coefficients of the respective transitions. The resultant joint state is inherently entangled, albeit in practical scenarios, the complete state is never directly observable due to the transverse nature of photons. Upon photon detection along the quantization axis direction $(\theta =0)$, the state described by Equation 68 undergoes reduction to

$|{\psi }_{\text{joint\hspace{0.17em}}}⟩=\frac{1}{\sqrt{2}}\left[C_{J,m_J}^{J,m_J-1}\left|J,m_J-1\right.⟩\left|{\sigma }^{+}\right.⟩+C_{J,m_J}^{J,m_J+1}\left|J,m_J+1\right.⟩\left|{\sigma }^{-}\right.⟩\right].(69)$

The state |ψ_joint⟩ in Equation 69 represents a maximally entangled state, with the CG coefficients defining the phase relationships between the components. Figure 11 illustrates a simplified generic scheme of how entanglement can be generated through spontaneous and stimulated Raman scattering. The entanglement produced via this Raman process is inherently probabilistic, leading to potential compromises in both the generation rate and fidelity. However, a method known as bichromatic Raman transition (Stute et al., 2012b) allows for the amplitude-tunable generation of atom–photon entanglement. This technique utilizes two different pump fields to carry out two Raman transitions. By adjusting the Rabi frequencies and detunings of the pump field, the deterministic generation of entangled states with different probability amplitudes is possible.

3.2.3 FWM process

FWM is a nonlinear optical process (Yariv and Pepper, 1977) that originates from a third-order nonlinear effect (Boyd and Prato, 2008) involving the interaction among four light fields within a nonlinear medium. The application of an external optical field to a nonlinear dielectric medium induces the dipole moment, which causes the polarization of the medium. The medium’s response to this external optical field can be quantified by the equation

$\mathcal{P}={ϵ}_0\left[{\chi }^{\left(1\right)}\mathcal{E}+{\chi }^{\left(2\right)}{\mathcal{E}}^2+{\chi }^{\left(3\right)}{\mathcal{E}}^3+\cdots \right].(70)$

In Equation 70, $\mathcal{P}$ signifies the polarization of the medium; ${ϵ}_0$ denotes the free space permittivity; $\mathcal{E}$ represents the applied optical field; ${\chi }^{(1)}$ refers to the linear susceptibility that affects the medium’s refractive index, expressed as $n=\sqrt{1+{\chi }^{(1)}}$; and ${\chi }^{(2)}$, ${\chi }^{(3)}$ are the second- and third-order nonlinear susceptibilities, respectively. Typically, the contributions from higher-order terms are minor and often disregarded. Nevertheless, in situations involving higher field strengths or specific types of nonlinear materials, these contributions become significant. FWM can be exploited in a range of platforms, such as optical fiber (Aso et al., 2000; Sharping et al., 2001; Thompson and Roy, 1991), semiconductor optical amplifiers (Diez et al., 1997; Li et al., 2024), photonic crystal waveguides (Li et al., 2011; Monat et al., 2010; Wang et al., 2024), quantum dots (Nielsen and Chuang, 2010; Borri and Langbein, 2007; Kosionis and Paspalakis, 2024), and atomic and molecular mediums (Deng et al., 1999). This FWM process provides functionalities such as wavelength conversion (Bahar et al., 2018), optical parametric amplification (Luo et al., 2023; Zhang et al., 2015), and the entangled photon pair generation for quantum communication (Camacho et al., 2009; Srivathsan et al., 2013). This section concentrates on using FWM in atomic platforms to produce entangled photon pairs.

In the FWM process (see Figure 12A), two pump beams, labeled pump 1 and pump 2, interact non-linearly with a centrally symmetric atomic ensemble and generate two daughter photon signal (s) and the idler (i), which are detected by the avalanche photodetectors D1 and D2 (depicted in Figure 12B). To provide deeper insights, let us consider two pump electric fields $E_{p1}$ and $E_{p2}$, which can be expressed in terms of plane wave modes,

$\begin{array}{cc}\hfill E_{pj}& =\frac{1}{2}\left(E_{pj}^{\left(+\right)}+E_{pj}^{\left(-\right)}\right)=\frac{1}{2}\left(E_{pj}^{\left(+\right)}+C.C\right);\hfill \\ \hfill E_{pj}^{\left(+\right)}\left(r,t\right)& =E_{pj}{e}^{i\left[k_{pj}r-{\omega }_{pj}t\right]},\hfill \\ \hfill E_{pj}^{\left(-\right)}\left(r,t\right)& =E_{pj}^{*}{e}^{-i\left[k_{pj}r-{\omega }_{pj}t\right]},\hfill \end{array}(71)$

where $E_{pj}^{(+)}$ and $E_{pj}^{(-)}$ in Equation 71 represent the electric field with positive and negative frequency parts and $j\in \{\mathrm{1,2}\}$. Both the pump 1 $(E_{p1})$ and pump 2 $(E_{p2})$ with angular frequency ${\omega }_{p1}$ and ${\omega }_{p2}$, and wave vector $k_{p1}$ and $k_{p2}$ are so strong that one can represent them classically. Nonetheless, for a more comprehensive understanding of operations at the single-photon level, employing the quantization of the electric field (see Subsection 2.1) presents a superior approach. The generated signal and idler fields are represented with the help of a quantized electric field,

${\widehat{E}}_{s,i}^{\left(+\right)}\left(r,t\right)=\frac{1}{\sqrt{2\pi }}\int d{\omega }_{s,i}\sqrt{\frac{\hslash {\omega }_{s,i}}{2{ϵ}_{0}V}}{\widehat{a}}_{s,i}\left({\omega }_{s,i}\right)e^{i\left[{\vec{k}}_{s,i}\left({\omega }_{s,i}\right)\cdot \vec{r}-{\omega }_{s,i}t\right]},(72)$

where $V$ in Equation 72 denotes the volume of the medium, and ${\omega }_{s,i}$, ${\vec{k}}_{s,i}$, and ${\widehat{a}}_{s,i}$ represent the angular frequency, wave vector, and annihilation operator of the signal and idler photons respectively. In the time domain, the annihilation operator can be expressed as

${\widehat{a}}_{s,i}\left(z,t\right)=\frac{1}{\sqrt{2\pi }}\int d{\omega }_{s,i}^{\prime }{\widehat{a}}_{s,i}\left({\omega }_{s,i}^{\prime }\right)e^{i\left[{\vec{k}}_{s,i}\left({\omega }_{s,i}^{\prime }\right)\cdot \vec{r}-{\omega }_{s,i}^{\prime }t\right]},(73)$

which satisfies the commutation relation,

$\left[{\widehat{a}}_{s,i}\left(z,t\right),{\widehat{a}}_{s,i}^{†}\left(z,t^{\prime }\right)\right]=\delta \left(t-t^{\prime }\right).(74)$

Figure 12

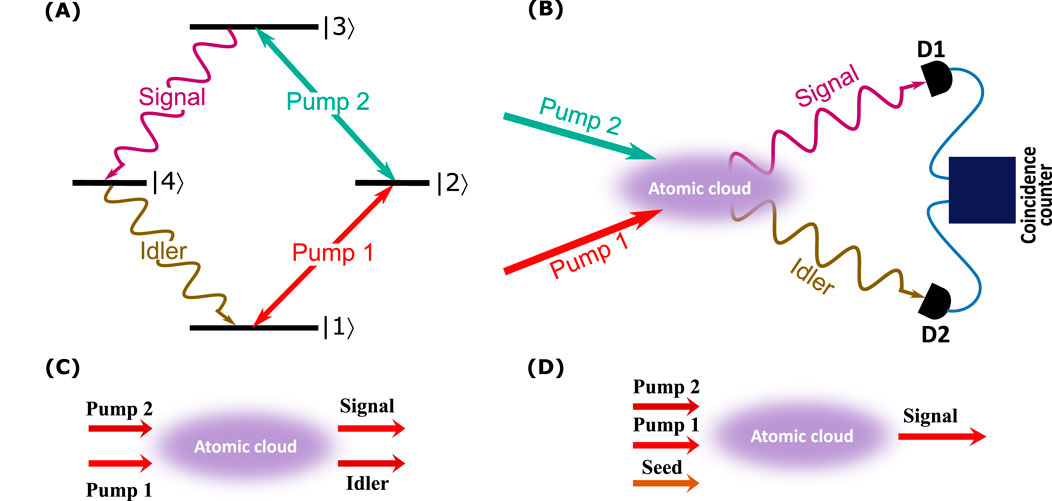
Figure 12. (A) The generic scheme for entangled photon pair generation through the FWM process. (B) Schematic experimental configuration for the FWM process. (C) Spontaneous FWM scheme. (D) Stimulated FWM scheme.

Similarly, the commutation relation (Equation 74) in the frequency domain can be written as

$\left[{\widehat{a}}_{s,i}\left(\omega \right),{\widehat{a}}_{s,i}^{†}\left({\omega }^{\prime }\right)\right]=\delta \left(\omega -{\omega }^{\prime }\right).(75)$

As FWM is a third-order nonlinear process, the effective interaction Hamiltonian of the system in terms of ${\chi }^{(3)}$ and the four electric fields is expressed as (Wen and Rubin, 2006)

${\widehat{H}}_I=\frac{{ϵ}_0}{4}{\displaystyle \sum _{jklm}}{\int }_{V}dr{\chi }_{jklm}^{\left(3\right)}{\left(E_{p1}^{\left(+\right)}\right)}_k{\left(E_{p2}^{\left(+\right)}\right)}_l{\left({\widehat{E}}_s^{\left(-\right)}\right)}_m{\left({\widehat{E}}_i^{\left(-\right)}\right)}_j+H.C.(76)$

where $dr$ in Equation 76 represents the differential of volume $V$ at which four fields overlap. Similar to the SPDC process, FWM is also a parametric process, where the medium’s state remains unchanged before and after the interaction. This means that neither the incident light nor the medium experiences any overall changes in energy or momentum. The energy conservation in the FWM process is described as follows:

${\omega }_{p1}+{\omega }_{p2}={\omega }_s+{\omega }_i.(77)$

Furthermore, the presence of a spatially extensive atomic ensemble ensures translational symmetry, which is crucial for conserving momentum or achieving phase matching (Gulati, 2014), which affects the direction in which photons are generated. The condition for phase matching is defined as follows:

${\vec{\mathrm{k}}}_{p1}+{\vec{\mathrm{k}}}_{p2}={\vec{\mathrm{k}}}_s+{\vec{\mathrm{k}}}_i.(78)$

Equation 78 indicates that the emitted signal and idler photons conform to spatial modes determined by these phase-matching conditions. Additionally, for the FWM process to effectively generate entangled photon pairs in their polarization states, it is imperative that it strictly adheres to energy and momentum conservation (Equations 77, 78). Meeting these conservation laws is both necessary and sufficient for generating entangled photon pairs in terms of their polarization degree of freedom.

Based on the frequency relationships between input pump beams, FWM can be categorized into two types: degenerate FWM (DFWM) (Bondurant et al., 1984) and non-degenerate FWM (NDFWM) (Pooser et al., 2009; Shahriar and Hemmer, 1998). DFWM involves four light waves of the same frequency in a nonlinear optical setting, where two incoming photons merge to produce two new photons at the same frequency. Conversely, NDFWM involves light waves of differing frequencies. FWM can be further classified into spontaneous FWM (SpFWM) (Liao et al., 2014) and stimulated FWM (StFWM) (Zhang W.-H. et al., 2022), contingent upon the configuration of the pump beam. In SpFWM, the interaction of two pump beams with an atomic medium results in the production of a temporally correlated photon pair, known as the signal and idler photons (as illustrated in Figure 12C). For StFWM, an extra seed beam is added to the initial two pump beams within the medium (see Figure 12D). This leads to the coherent generation of a signal photon. FWM in atomic platforms enables diverse schemes for generating entangled photon pairs, each tailored for specific quantum communication applications. The double-$\mathrm{\Lambda }$ configuration utilizes two coupled Lambda systems sharing a common ground state, enabling controlled photon bandwidth and wavelength (Du et al., 2008b). In contrast, the cascade configuration employs a sequential four-level system to produce time-correlated photon pairs, which is ideal for testing quantum mechanical principles such as Bell’s inequalities (Park et al., 2021). On the other hand, the ladder configuration, involving a direct excitation from the ground state to the higher excited state followed by a step-wise decay, offers high efficiency and control over photon emission properties (Ding et al., 2012). Lastly, the triangle configuration uses a unique triangular arrangement of energy levels, facilitating cyclic transitions that generate photon pairs with complex entanglement properties suitable for advanced quantum protocols (Marino et al., 2009). Each configuration leverages atomic transitions to produce photon pairs under controlled conditions, which is crucial for developing quantum communication systems.

3.3 Experimental verification and characterization

Researchers employ specific inequality violations as benchmarks to affirm the existence and quantify the degree of quantum entanglement. These violations are not merely theoretical curiosities but are essential for confirming entanglement in practical scenarios. One of the fundamental tests for entanglement verification involves examining the Cauchy–Schwarz inequality, which serves as a benchmark for distinguishing classical from quantum correlations. On the other hand, the Clauser–Horne–Shimony–Holt (CHSH)–Bell inequality offers a quantifiable measure for the non-local interactions characteristic of entangled states.

3.3.1 Violation of the Cauchy–Schwarz inequality

In quantum optics, particularly when discussing photon statistics, the Cauchy–Schwarz (CS) inequality (Walls and Milburn, 2008; Reid and Walls, 1986; Thompson et al., 2006) is often utilized to distinguish between classical and non-classical light states, especially when examining correlations between two photons emitted from a single source. Assuming a single source emits two photons, labeled as idler $(I)$ and signal $(S)$, we define $g_{II}^{(2)}$ and $g_{SS}^{(2)}$ as the second-order intensity-intensity correlation functions for the idler and signal photons, respectively. These correlations are defined between photons originating from the same sources and are also referred to as auto-correlation functions. In the context of entangled photon pairs, the auto-correlation function measures the correlation between the detection events of photons from the same pair. Unlike the $g^{(2)}$ function discussed in Subsection 2.1, which deals with single photons, the auto-correlation function exclusively addresses the correlations between photons constituting entangled pairs. In the scenario of entangled photon pairs, the auto-correlation function, particularly at zero time delay $(\tau =0)$, prominently exhibits anti-correlation. This distinctive characteristic underscores that the probability of simultaneously detecting two photons along one branch is minimized. Such anti-correlation is a hallmark of the non-classical nature of the correlation inherent in entangled pairs. The auto-correlation function in entangled photon pairs is crucial for verifying the presence of entanglement and assessing the quality of the entangled state. Additionally, $g_{SI}^{(2)}$ is defined as the second-order cross-correlation function between two different types of photons, namely, idler and signal. These correlations are derived from intensity measurements of the photon fields and correspond to the probability of photon detection at varying times or locations. From Equation 21, the second-order auto-correlation function can be expressed as

$g_{XX}^{\left(2\right)}\left(\tau \right)=\frac{⟨I_X\left(t\right)I_X\left(t+\tau \right)⟩}{{⟨I_X\left(t\right)⟩}^2}.(79)$

in Equation 79, $I_X(t)$ denotes the intensity operator for photon type $X$ (either $S$ or $I$) at time $t$, and $⟨\cdot ⟩$ symbolizes the ensemble average. At $\tau =0$, $g_{XX}^{(2)}(0)$ reveals the chance of simultaneous two-photon detection. Meanwhile, the cross-correlation function for distinct photon types, $S$ and $I$, is described as follows:

$g_{SI}^{\left(2\right)}\left(\tau \right)=\frac{⟨I_S\left(t\right)I_I\left(t+\tau \right)⟩}{⟨I_S\left(t\right)⟩⟨I_I\left(t\right)⟩}.(80)$

In the context of quantum optics, the CS inequality states that for any classical light sources, the square of the cross-correlation function (Equation 80) between two different sources should not exceed the product of their auto-correlation functions (Clauser and John, 1974):

$\begin{array}{cc}\hfill & {\left[g_{SI}^{\left(2\right)}\left(\tau \right)\right]}^2\le g_{SS}^{\left(2\right)}\left(\tau \right)g_{II}^{\left(2\right)}\left(\tau \right);\hfill \\ \hfill \Rightarrow & R=\frac{{\left[g_{SI}^{\left(2\right)}\left(\tau \right)\right]}^2}{g_{SS}^{\left(2\right)}\left(\tau \right)g_{II}^{\left(2\right)}\left(\tau \right)}\le 1.\hfill \end{array}(81)$

The inequality defined in Equation 81 must hold for any classical field due to the properties of classical EM waves and their intensities. A violation of this inequality is a strong indicator of non-classical light, suggesting quantum entanglement between two photons.

3.3.2 The violation of the CHSH–Bell inequality

The Clauser–Horne–Shimony–Holt (CHSH) (Clauser et al., 1969; Aspect et al., 1982) interpretation of Bell’s inequality offers a comprehensive method for evaluating the non-local characteristics of quantum entanglement, contrasting it with local hidden-variable theories (LHVTs) (Clauser et al., 1969). The CHSH inequality is a special mathematical inequality that local hidden-variable theories must satisfy. It involves measuring the correlations between measurement results obtained from two entangled photons polarized in different directions. The measurements are chosen from a set of four possible orientations, labeled as $(\theta ,\varphi ,{\theta }^{\prime },{\varphi }^{\prime })$. The inequality is given by

$S\left(\theta ,\varphi ,{\theta }^{\prime },{\varphi }^{\prime }\right)=\left|E\left(\theta ,\varphi \right)-E\left(\theta ,{\varphi }^{\prime }\right)+E\left({\theta }^{\prime },{\varphi }^{\prime }\right)+E\left({\theta }^{\prime },\varphi \right)\right|<2,(82)$

where $E(X,Y)$ represents the normalized expectation value of correlation between the measurement outcomes $X$ and $Y$. Mathematically, $E(\theta ,\varphi )$ can be expressed as

$E\left(\theta ,\varphi \right)=p_{\theta \varphi }+p_{{\theta }_{\perp }{\varphi }_{\perp }}-p_{\theta {\varphi }_{\perp }}-p_{{\theta }_{\perp }\varphi },(83)$

where $p_{\theta \varphi }$ represents the probability of the system existing in the state $|\theta \varphi \rangle$ (see Equation 63), and $\left({\theta }_{\perp },{\varphi }_{\perp }\right)=\left(\theta +90°,\varphi +90°\right)$. These probability terms can be experimentally estimated through coincidence counts in accordance with the modified expression of $E(\theta ,\varphi )$ in Equation 83 as articulated below:

$E\left(\theta ,\varphi \right)=\frac{C\left(\theta ,\varphi \right)-C\left(\theta ,{\varphi }_{\perp }\right)-C\left({\theta }_{\perp },\varphi \right)+C\left({\theta }_{\perp },{\varphi }_{\perp }\right)}{C\left(\theta ,\varphi \right)+C\left(\theta ,{\varphi }_{\perp }\right)+C\left({\theta }_{\perp },\varphi \right)+C\left({\theta }_{\perp },{\varphi }_{\perp }\right)},(84)$

where $\mathrm{C}(\theta ,\varphi )$ represents the rate of coincidences measured for the polarizer orientations $\theta$ and $\varphi$. Any values for the angles $(\theta ,\varphi ,{\theta }^{\prime },{\varphi }^{\prime })$ may be chosen such that the value of $S(\theta ,\varphi ,{\theta }^{\prime },{\varphi }^{\prime })$ is maximized. Let us consider a particular set of values for these angles:

$\left(\theta ,\varphi ,{\theta }^{\prime },{\varphi }^{\prime }\right)=\left(0+\delta ,\frac{\pi }{8}+\delta ,\frac{2\pi }{8}+\delta ,\frac{3\pi }{8}+\delta \right),(85)$

where $\delta \in \mathbb{R}$. For any value of $\delta$, the value of $S\left(\theta ,\varphi ,{\theta }^{\prime },{\varphi }^{\prime }\right)=2\sqrt{2}$ for all Bell states. This is the quantum mechanical upper bound, known as Tsirelson’s bound (Cirel’son, 1980). Remarkably, this bound exceeds the upper limit set by Bell’s inequality (as given in Equation 82), indicating the presence of entanglement.

In experimental setups, quantifying the standard deviation $(\mathrm{\Delta }S)$ associated with $S$ becomes essential for evaluating the precision and reliability of measurements. A smaller standard deviation indicates more precise measurements, suggesting a higher degree of confidence in the observed violations of Bell inequalities and the presence of non-classical correlations. Conversely, a larger standard deviation signifies greater uncertainty and variability in the experimental results. It necessitates meticulous consideration of measurement errors and inherent imperfections in the experimental setup. The mathematical expression governing the calculation of the standard deviation linked to the experimental determination of the Bell parameter $S$ is as follows:

$\mathrm{\Delta }S\left(\theta ,{\theta }^{\prime },\varphi ,{\varphi }^{\prime }\right)=\sqrt{{\displaystyle \sum _{x=\theta ,{\theta }^{\prime }}}{\displaystyle \sum _{y=\varphi ,{\varphi }^{\prime }}}\mathrm{\Delta }E{\left(x,y\right)}^2},(86)$

where $\mathrm{\Delta }E(x,y)$ denotes the error associated with each correlation coefficient, calculated through the application of Gaussian error propagation (Negre et al., 2023). $\mathrm{\Delta }E(x,y)$ can be expressed as

$\begin{array}{cc}\hfill \mathrm{\Delta }E\left(x,y\right)=& 2\frac{\left[C\left(x,y\right)+C\left(x_{\perp },y_{\perp }\right)\right]\left[C\left(x,y_{\perp }\right)+C\left(x_{\perp },y\right)\right]}{{\left(C\left(x,y\right)+C\left(x_{\perp },y_{\perp }\right)+C\left(x,y_{\perp }\right)+C\left(x_{\perp },y\right)\right)}^2}\hfill \\ \hfill & \times \sqrt{\frac{1}{C\left(x,y\right)+C\left(x_{\perp },y_{\perp }\right)}+\frac{1}{C\left(x,y_{\perp }\right)+C\left(x_{\perp },y\right)}}.\hfill \end{array}(87)$

The degree of violation is quantified by the number of standard deviations that the experimental $S$ value exceeds the local realistic threshold of 2. This is mathematically articulated using Equations 86, 87 as follows:

${\eta }_{\mathrm{\Delta }}=\frac{S\left(\theta ,\varphi ,{\theta }^{\prime },{\varphi }^{\prime }\right)-2}{\mathrm{\Delta }S\left(\theta ,\varphi ,{\theta }^{\prime },{\varphi }^{\prime }\right)}.(88)$

To verify the violation of the CHSH–Bell inequality, it is necessary to record the coincidence counts for each combination of $\theta ,\varphi ,{\theta }^{\prime },{\varphi }^{\prime }$. To simplify the process, at least 16 different combinations of these angles (four for each $E(\theta ,\varphi )$) in Equation 84, adhering to Equation 85, should be measured. For instance, these could include $\left(\theta =0^{°},{45}^{°},{90}^{°},{135}^{°}\right)$ and $\left(\varphi ={22.5}^{°},{67.5}^{°},{112.5}^{°},{157.5}^{°}\right)$. Recently, H. S. Moon’s group reported the value of the Bell–CHSH parameter, $S=2.753\pm 0.007$ (Park and Moon, 2022), which is greater than 2 and thus breaches Bell’s inequality by $\sim 107$ standard deviations $(\mathrm{\Delta }S)$ (using Equation 88).

3.3.3 Quantum state tomography

Understanding the density matrix of a system in real time, particularly when the system’s state is indeterminate, provides comprehensive probabilistic information about the measurable properties of the system. Quantum state tomography (QST) is a widely recognized technique employed to reconstruct the density matrix based on measurements from identically prepared quantum systems. In the context of bi-photon polarization states, polarization correlation measurements play a pivotal role in the density matrix reconstruction process. Subsequent sections delve into the intricacies of these measurements, elucidating their significance and application in the reconstruction of density matrix for bi-photon polarization states.

3.3.3.1 Polarization correlation measurement

According to Stokes formalism (Hecht and Zając, 1974), one must perform $4^n$ projection measurements to measure the state of an n-qubits system. Thus, for a 2-qubit system (two-photon polarization state), one must perform $4^2=16$ projection measurements (James et al., 2001). Figure 13 presents the experimental schematic for measuring the polarization correlation. In this setup, a photon pair is emitted from a source, and each photon passes through a polarization analyzer, sequentially encountering a quarter-wave plate (QWP) and a half-wave plate (HWP) and then being detected by a single-photon detector after being divided by a polarizing beam splitter (PBS). In Jones calculus, the representation of the QWP and HWP is (James et al., 2001)

$\begin{array}{cc}\hfill {\widehat{T}}_{QWP}\left(\tilde{q}\right)& =\frac{1}{\sqrt{2}}\left(\begin{array}{cc}\hfill i-\cos \left(2\tilde{q}\right)\hfill & \hfill \sin \left(2\tilde{q}\right)\hfill \\ \hfill \sin \left(2\tilde{q}\right)\hfill & \hfill i+\cos \left(2\tilde{q}\right)\hfill \end{array}\right);\hfill \\ \hfill {\widehat{T}}_{HWP}\left(\tilde{p}\right)& =\left(\begin{array}{cc}\hfill \cos \left(2\tilde{p}\right)\hfill & \hfill -\sin \left(2\tilde{p}\right)\hfill \\ \hfill -\sin \left(2\tilde{p}\right)\hfill & \hfill -\cos \left(2\tilde{p}\right)\hfill \end{array}\right),\hfill \end{array}(89)$

where $\tilde{q}$ and $\tilde{p}$ are the orientations of the fast axes of the QWP and HWP relative to the vertical axis, respectively. Thus, for one of the beams, the projection state is expressed with the help of Equation 89 as

$\begin{array}{cc}\hfill |{\varphi }_{proj}^{\left(1\right)}\left(\tilde{p},\tilde{q}\right)⟩& ={\widehat{T}}_{QWP}\left(\tilde{q}\right)\cdot {\widehat{T}}_{HWP}\left(\tilde{p}\right)\cdot |V\rangle \hfill \\ \hfill & =\eta \left(\tilde{p},\tilde{q}\right)|H\rangle +\xi \left(\tilde{p},\tilde{q}\right)|V\rangle ,\hfill \end{array}(90)$

where $|H\rangle$ and $|V\rangle$ are the horizontal and vertical states of polarized light (see Equation 57) and $\eta (\tilde{p},\tilde{q})$ and $\xi (\tilde{p},\tilde{q})$ are defined as follows:

$\begin{array}{cc}\hfill \eta \left(\tilde{p},\tilde{q}\right)& =\frac{1}{\sqrt{2}}\left\{\sin \left(2\tilde{p}\right)-i\sin \left[2\left(\tilde{p}-\tilde{q}\right)\right]\right\};\hfill \\ \hfill \xi \left(\tilde{p},\tilde{q}\right)& =-\frac{1}{\sqrt{2}}\left\{\cos \left(2\tilde{p}\right)+i\cos \left[2\left(\tilde{p}-\tilde{q}\right)\right]\right\}.\hfill \end{array}(91)$

Figure 13

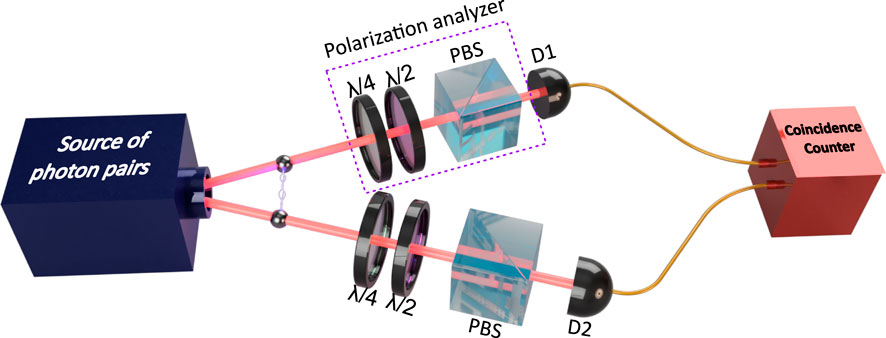
Figure 13. The schematic for measuring polarization correlation includes utilizing a quarter-wave plate (QWP), half-wave plate (HWP), and polarizing beam splitter (PBS) in each photon path to align the photons’ polarization into specific states. The coincidence counts for every polarization combination are recorded using two single-photon detectors (D1 and D2) connected to a coincidence counter.

As shown in Equation 92, the projection state for the two beams is expressed (using Equations 90, 91) as:

$\begin{array}{cc}\hfill |{\varphi }_{proj}^{\left(2\right)}\left({\tilde{p}}_1,{\tilde{q}}_1,{\tilde{p}}_2,{\tilde{q}}_2\right)⟩& =|{\varphi }_{proj}^{\left(1\right)}\left({\tilde{p}}_1,{\tilde{q}}_1\right)⟩\otimes |{\varphi }_{proj}^{\left(1\right)}\left({\tilde{p}}_2,{\tilde{q}}_2\right)⟩\hfill \\ \hfill & =\eta \left({\tilde{p}}_1,{\tilde{q}}_1\right)\eta \left({\tilde{p}}_2,{\tilde{q}}_2\right)|HH\rangle +\xi \left({\tilde{p}}_1,{\tilde{q}}_1\right)\xi \left({\tilde{p}}_2,{\tilde{q}}_2\right)|VV\rangle \hfill \\ \hfill & +\xi \left({\tilde{p}}_1,{\tilde{q}}_1\right)\eta \left({\tilde{p}}_2,{\tilde{q}}_2\right)|VH\rangle +\eta \left({\tilde{p}}_1,{\tilde{q}}_1\right)\xi \left({\tilde{p}}_2,{\tilde{q}}_2\right)|HV\rangle .\hfill \end{array}(92)$

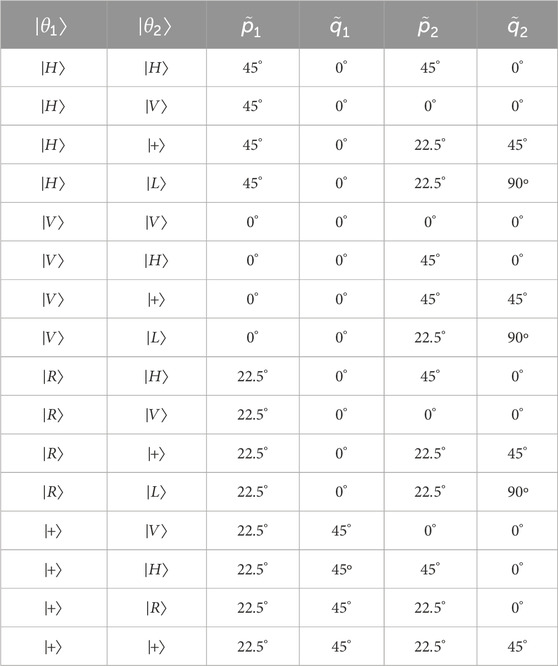
The orientation of the fast axes of both wave plates relative to the vertical polarization axis can be adjusted to any chosen angle (refer to Table 4), allowing for the projection of any arbitrary quantum state. Let us denote the polarization state of the photon in one arm as $\left|{\theta }_1\right.⟩$ and in the other arm as $\left|{\theta }_2\right.⟩$, where $\left|{\theta }_1\right.⟩$ and $\left|{\theta }_2\right.⟩$ can belong to the set $\{|H\rangle ,|V\rangle ,|L\rangle ,|R\rangle ,|+\rangle ,|-\rangle \}$. Then, the probability of detecting the two-photon polarization state in $\left|{\theta }_1{\theta }_2\right.⟩$ can be expressed in Equation 93 as:

$p_{{\theta }_1{\theta }_2}=\mathrm{Tr}\left\{\rho \left|{\theta }_1{\theta }_2\right.⟩\left.⟨{\theta }_1{\theta }_2\right|\right\}.(93)$

Table 4

Table 4. Sixteen sets of angles of QWP and HWP for different projection measurements.

Reconstruction of the density matrix can be achieved by utilizing three distinct protocols: linear inversion, maximum likelihood estimation (MLE), and Bayesian estimation (BE). Linear inversion is the most straightforward approach to QST, where the density matrix is directly calculated from the inverse of the linear equations relating the state to the measurement outcomes. This method, however, often results in unphysical states due to experimental noise and finite statistics (James et al., 2001). MLE improves upon linear inversion by optimizing a likelihood function, which finds a density matrix that best fits the experimental data constrained by the physical requirements of a density matrix. MLE is widely used due to its robustness against noise and its ability to produce physical states consistently (Hradil, 1997). Bayesian methods incorporate prior knowledge into the tomography process and update this knowledge based on the measurement outcomes, offering a probabilistic interpretation of the quantum state. This approach provides not only the most probable state but also quantifies the uncertainty of the estimation (Blume-Kohout, 2010).

In 2011, Shengwang Du’s group (Yan et al., 2011) experimentally generated the $|{\mathrm{\Phi }}^{+}\rangle$ Bell state using the SpFWM method. For complete characterization of the generated entangled state, they performed an extensive polarization correlation measurement on all 16 projection states and employed the MLE method to reconstruct the density matrix, which is given as

${\rho }_r=\left[\begin{array}{cccc}\hfill 0.03\hfill & \hfill 0.04\hfill & \hfill 0.06+0.01i\hfill & \hfill -0.01i\hfill \\ \hfill 0.04\hfill & \hfill 0.47\hfill & \hfill 0.44-0.02i\hfill & \hfill -0.05-0.02i\hfill \\ \hfill 0.06-0.01i\hfill & \hfill 0.44+0.02i\hfill & \hfill 0.47\hfill & \hfill -0.03-0.01i\hfill \\ \hfill 0.01i\hfill & \hfill -0.05+0.02i\hfill & \hfill -0.03+0.01i\hfill & \hfill 0.03\hfill \end{array}\right].(94)$

Figure 14 illustrates the reconstructed density matrix from Equation 94. To determine the similarity or identity between the reconstructed and target density matrix, it is essential to evaluate the quantity called fidelity, which is expressed as (Jozsa, 1994)

$F\left({\rho }_t,{\rho }_r\right)={\left[Tr\left(\sqrt{\sqrt{{\rho }_t}{\rho }_r\sqrt{{\rho }_t}}\right)\right]}^2,(95)$

where ${\rho }_t$ symbolizes the target density matrix, while ${\rho }_r$ stands for the reconstructed one. The value of fidelity, F (expressed in Equation 95), ranges from 0 to 1, where $F=0$ indicates no similarity between ${\rho }_t$ and ${\rho }_r$, and $F=1$ signifies that they are identical. A fidelity of 0.5 marks the classical boundary for any classical state’s fidelity to a maximally entangled state. According to Equation 94, the observed fidelity of $F=0.908$ surpasses the classical limit, clearly demonstrating entanglement in the state produced by the experiment.

Figure 14

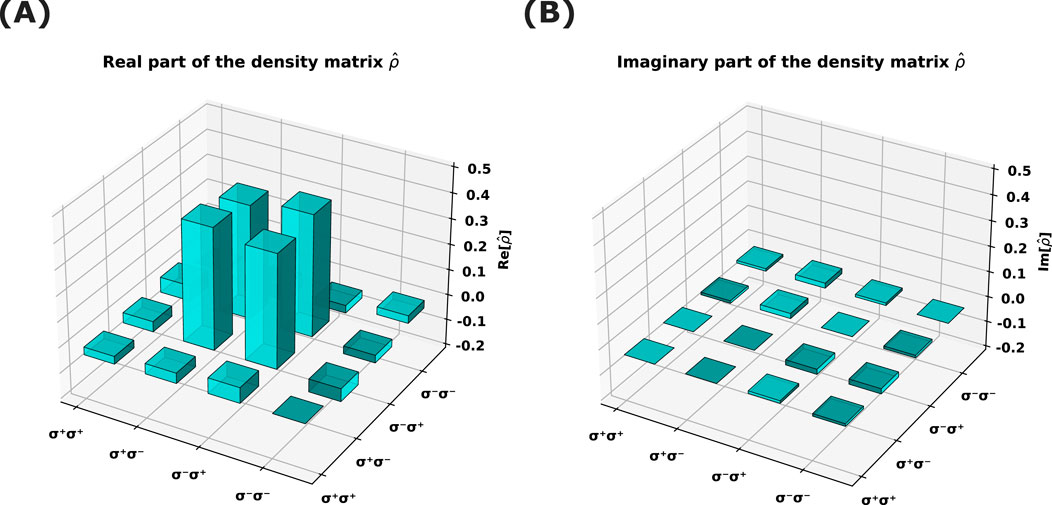
Figure 14. (A) Real part and (B) imaginary part of the reconstructed density matrix for polarization-entangled photon pairs. The figure is recreated from Yan et al. (2011).

The entanglement can also be measured in terms of other quantities; one is “concurrence,” defined as $C$, which quantifies the degree of entanglement between two qubits. It indicates the strength of entanglement, ranging from 0 (no entanglement) to 1 (maximal entanglement). Given a two-qubit density matrix $\rho$, the concurrence $(C)$ takes the form

$C\left(\rho \right)=\max \left\{0,\sqrt{{\mathrm{\Lambda }}_1}-\sqrt{{\mathrm{\Lambda }}_2}-\sqrt{{\mathrm{\Lambda }}_3}-\sqrt{{\mathrm{\Lambda }}_4}\right\},(96)$

where ${\mathrm{\Lambda }}_i$ represents the eigenvalues of a special matrix $R$, which is obtained by performing a specific matrix operation on $\rho$. To get the matrix $R$, it is necessary to calculate the spin-flipped version of the density matrix, denoted as $\tilde{\rho }$. This involves reversing the sequence of the basis states in the original density matrix $\rho$ and taking the complex conjugate of each element. The formula to define $R$ is as follows (Coffman et al., 2000):

$R=\rho \ast \left({\sigma }_y\otimes {\sigma }_y\right)\ast \tilde{\rho }\ast \left({\sigma }_y\otimes {\sigma }_y\right).(97)$

In Equation 97, ${\sigma }_y$ represents the Pauli spin matrix for the y coordinate, and $\otimes$ represents the tensor product.

Furthermore, the “tangle” is defined as $\tau$, which is the square of the concurrence and offers a quantitative measure of entanglement. Specifically, it quantifies the entanglement for two-qubit systems. For a state $\rho$, the tangle $\tau (\rho )$ is defined as

$\tau \left(\rho \right)=C{\left(\rho \right)}^2.(98)$

In Equation 98, $\tau =0$ indicates that there is no entanglement in the system. The state is a separable state. $\tau =1$ signifies maximum entanglement. Such states are often referred to as maximally entangled states, such as the Bell states in a two-qubit system. Values between 0 and 1 indicate partial entanglement. The closer the tangle is to 1, the higher the degree of entanglement.

Additionally, “entanglement of formation” is defined as $E$, which represents the entanglement cost or resources required to create a specific entangled state from separable states. It provides insights into the amount of entanglement needed to generate and manipulate entangled states in a given system. Mathematically, $E$ is defined as (Wootters, 1998)

$E\left(\rho \right)=\min \left(\sum p_{i}S\left({\psi }_i\right)\right).(99)$

In this context, $p_i$ represents the probabilities associated with each pure state $\left|{\psi }_i\right.⟩$ in the decomposition, and $S\left({\psi }_i\right)$ represents the von Neumann entropy of the reduced density matrix $({\rho }_i)$ of either subsystem when the entire system is in the state $\left|{\psi }_i\right.⟩$. The calculation of von Neumann entropy proceeds as follows:

$S\left({\psi }_i\right)=-\mathrm{tr}\left({\rho }_i{\log }_2\left({\rho }_i\right)\right).(100)$

In 2015, Gulati et al. (2015) experimentally produced the $\left|{\mathrm{\Phi }}^{+}\right.⟩$ state from a cold-trapped ⁸⁷Rb atom using the FWM technique. They reported a concurrence (using Equations 96, 97) value of $C=0.94\pm 0.01$ and an entanglement of formation (using Equations 99, 100) of $E=0.98\pm 0.01$, demonstrating the high quality of the entanglement achieved.

Furthermore, the concept of an “entanglement witness” (Tóth and Gühne, 2005a) offers a practical approach to discerning entangled states from separable (non-entangled) ones. The witness operator is defined for all the Bell states (see Equation 53) as (Tóth and Gühne, 2005b)

$\begin{array}{cc}\hfill {\widehat{W}}_{\left|{\varphi }^{\pm }\right.⟩}& =\frac{1}{4}\mathrm{I}\mp \frac{1}{4}\left(X_1{X}_2\pm Z_1{Z}_2\right);\hfill \\ \hfill {\widehat{W}}_{\left|{\psi }^{\pm }\right.⟩}& =\frac{1}{4}\mathrm{I}\mp \frac{1}{4}\left(X_1{X}_2\pm Z_1{Z}_2\right),\hfill \end{array}(101)$

where $X_i,Z_i$ is the Pauli-X and Pauli-Z operator acting on the i^th photon. In more technical terms, an entanglement witness $\widehat{W}$ is an operator represented in Equation 101 satisfying the following condition:

$\underset{|\mathrm{\Psi }\rangle \in \left\{\left|{\psi }^{\pm }\right.⟩,\left|{\varphi }^{\pm }\right.⟩\right\}}{\min }\left\{\mathrm{Tr}\left[{\widehat{\mathrm{W}}}_{|\mathrm{\Psi }\rangle }{\rho }_r\right]\right\}<0.(102)$

If the inequality represented in Equation 102 holds, the state is entangled; otherwise, it is separable. Recently, Hwang et al. demonstrated the entanglement witness value of $-0.23\pm 0.09$ (Hwang et al., 2023), which is less than 0, thereby validating the quantum entanglement present in the system under investigation.

3.4 Summary of entangled photon generation schemes in diverse atomic platforms

The generation of entangled photon pairs is fundamental to the field of quantum information science, facilitating advancements in quantum computing, secure communication, and fundamental tests of quantum mechanics. Various atomic platforms have been developed, each uniquely contributing to the advancement of entangled photon pair generation. These platforms can be broadly categorized into single-atom platforms and atomic ensemble-based platforms, each leveraging distinct physical processes to produce entanglement with varying efficiency, fidelity, and scalability. This section provides a comprehensive review of the development and recent progress within these categories.

3.4.1 Single atomic platforms

Establishing entanglement between the atom and photon is a crucial milestone in developing an atom–photon interface for long-distance quantum communication. Atoms can store qubits for a longer period of time, whereas photons are suitable for transferring quantum information with minimal loss. The atom–photon interface generates entanglement between atom and photon and provides a way to map photonic qubit state to atomic qubit and vice versa. The entangling operation between a single-trapped ¹¹¹Cd⁺ ion and its emitted photon was first demonstrated by Blinov et al. (2004). They achieved atom–photon entanglement through spontaneous decay via Raman scattering with a fidelity of 0.87, where the emitted photons are collected by a high numeric aperture lens objective (HALO lens). The emitted photon can be polarization-entangled (Moehring et al., 2007), frequency-entangled (Matsukevich et al., 2008), or photon number-entangled (Olmschenk et al., 2009) with the atom’s internal state. Such entanglement generation via spontaneous emission is limited by the photon collection efficiency of HALO.

Atom–photon entanglement has also been realized with a single neutral ⁸⁷Rb atom trapped inside a dipole trap (Metcalf and Van der Straten, 1999), where a major limitation arises in the success probability of entanglement from the trapping time of the neutral atom (Volz et al., 2006). In this experiment, a STIRAP-based detection scheme is used, where a superposition state is prepared with the help of two STIRAP processes. Atom–photon entanglement visibility around 0.85 with a fidelity of 0.87 has been reported. Limitations in photon collection can be overcome by using an optical cavity, where photons are prone to emit inside the cavity mode. One study shows a way to generate entangled photon pairs (reported fidelity, 0.86) from a single trapped atom using a cavity-based approach (Wilk et al., 2007b). First, atom–photon entanglement is created with a measured fidelity of approximately 0.83. Then, the entanglement is transferred to the second photon with a measured success probability of 0.6%.

Deterministic generation of entanglement is possible by the use of the STIRAP process instead of the usual Raman scattering, demonstrated by Stute et al. with trapped ⁴⁰Ca⁺ ion inside a high-finesse optical cavity (Stute et al., 2012a). Furthermore, the tunability in the amplitude of the entanglement can be achieved by the use of a bichromatic Raman transition involving two different Raman pump beams, where the Rabi frequency and polarization of the pump beam determine the amplitudes of the final entangled state (Stute et al., 2012b). Different entangled states with amplitudes $(1/\sqrt{2},1/\sqrt{2})$, $(1/\sqrt{3},\sqrt{2/3})$, and $(1/\sqrt{8},\sqrt{7/8})$ have been generated with fidelity of 96.3%, 96.8%, and 98%, respectively. Another important milestone toward long-distance quantum communication is achieved when an entangled photon is generated in telecom wavelength (at telecom O-band, 1,310 nm) with a reported fidelity of 98% (Bock et al., 2018). Telecom photons are particularly advantageous for long-distance transfer due to their lesser decay probability than visible photons. Further significant improvement in entanglement repeatability has been achieved using a fiber cavity of smaller mode volume, with a 62 Hz entanglement rate and fidelities of approximately 90% (Kobel et al., 2021). Table 5 provides a comparative analysis of various experiments on entangled photon generation from single trapped atoms.

Table 5

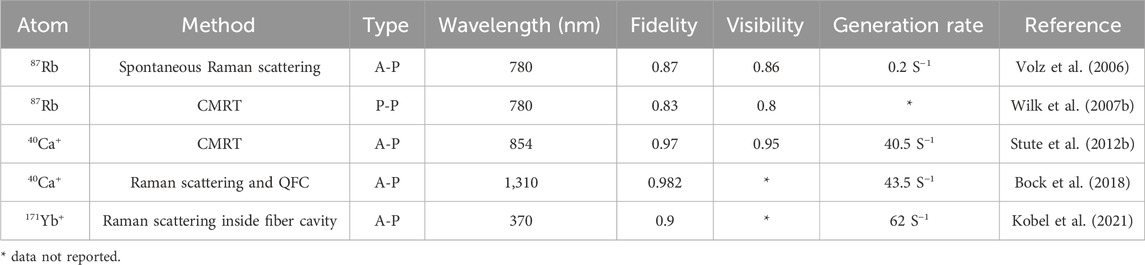
Table 5. Summary of key parameters of entangled photon platforms or entangled photon pair generation schemes using single atoms. Here, P-P signifies photon–photon entanglement, and A-P signifies atom–photon entanglement. In the case of multiple measurements, the best result is reported.

3.4.2 Atomic ensemble-based platforms

In addition to serving as a promising source of single photons, an ensemble of neutral atoms proves to be a reliable source of correlated photons or photon pairs, whether trapped and cooled to ultra-cold temperatures or present as atomic vapors at room temperature. The interaction between atoms and photons, facilitated by collective excitations of atoms, makes it a reliable storage of quantum information as well as the source of narrow-band entangled photons.

In 2005, Balić et al. employed a 3D MOT (Metcalf and Van der Straten, 1999) containing ⁸⁷Rb atoms, characterized by an optical depth (OD) (Srivathsan, 2014) of approximately 10, to facilitate the generation of counter-propagating photon pairs by using the FWM technique (Balić et al., 2005). These photon pairs exhibited a coherence time of approximately 50 ns and were generated at a rate of 12,000 pairs/s, corresponding to a photon linewidth of nearly 9 MHz. Notably, this experiment demonstrated the CS inequality violation by a factor of 400. Subsequently, in 2006, Kolchin et al. made significant progress in the field by employing a single retro-reflected titanium-sapphire (Ti:sapphire) laser, serving simultaneously as the coupling, pump, and driving fields (Kolchin et al., 2006). This innovative approach led to the narrow-band photon pair production characterized by a 5 ns coherence time and a generation rate of 600 pairs/s. Impressively, this method results in a CS inequality violation by a factor of 2,000. Further exploiting the retro-reflected geometric configuration, Du et al. demonstrated the production of bi-photons within a two-level system, achieving a maximum generation rate of $2\times 10^5$ pairs/s (Du et al., 2007).

It was postulated that the photon pair generation rate could be enhanced by extending the interaction duration between the trapped atoms and the pump fields. This enhancement was predicted to be achievable by employing a 2D MOT (Dieckmann et al., 1998) with a higher OD in lieu of a 3D MOT. Validating this prediction, in 2008, Du et al. successfully generated bi-photons from a 2D MOT characterized by an OD of 62, which exhibited a temporal linewidth ranging from 50 ns to 900 ns and an estimated photon generation linewidth of 0.75 MHz (Du et al., 2008a). This experiment marked a significant milestone by demonstrating the CS inequality violation by a factor of 11,600. These sequential advancements underscore a consistent trend toward increased photon pair generation rates with higher ODs.

The efficiency of nonlinear optical processes can be enhanced by narrowing the photon linewidth below the natural linewidth. However, this improvement is ultimately limited by the dephasing rate of the forbidden transition (Du et al., 2008a). Several research groups contributed a phenomenal effort to generate the narrow-band bi-photon source using the FWM technique (Xiao-Song et al., 2009; Ding et al., 2012; Chen et al., 2011), which has various applications in quantum memory (Ding et al., 2013). Most of these photon pairs are entangled in energy-time degrees of freedom. In 2011, Yan et al. first demonstrated the time-frequency-entangled and polarization-entangled photon pair generation from the 2D MOT of Rb using the SpFWM technique (Yan et al., 2011). The experiment achieved a two-photon coherence time of 30 ns and an estimated photon pair generation rate of 320 pairs/s, corresponding to a bandwidth of 6 MHz. In this work, they reported the violation of CS inequality by a factor of 100 for the OD of approximately 10 along with the Bell–CHSH parameter, $S=2.47\pm 0.15$.

In 2014, Liao et al. demonstrated a groundbreaking method for producing polarization-entangled photon pairs with subnatural linewidths and adjustable temporal lengths, leveraging the coherent integration of two SpFWM pathways within a Mach–Zehnder interferometer (Liao et al., 2014). By precisely adjusting the phase discrepancy between these SpFWM pathways and the driving laser’s polarization, they successfully generated all four Bell states with more than $91\%$ fidelity and a Bell–CHSH parameter exceeding 2.19. This technique facilitated the creation of narrow-band, polarization-entangled photon pairs, boasting a coherence time of 900 ns and an estimated bandwidth of around 1 MHz, alongside a generation rate of approximately 9,800 photon pairs/s. Utilizing a dark-line 2D MOT (Zhang et al., 2012) with an OD reaching 130 (Zhao et al., 2014), a subsequent study highlighted that these entangled photon pairs exhibited an extended coherence time up to $1.7\mu$s. In 2015, using laser-cooled dark-line 2D MOT of Rb atoms with OD of approximately 100 in the EIT-based SpFWM process, some research groups achieved a bi-photon source with a coherence time of $2.34\mu$s (Han et al., 2015) with a linewidth of 380 kHz (Zhao et al., 2016). By using similar laser-cooled dark-line 2D MOT of Rb atoms with an OD around 110 in the EIT-based SpFWM process, Wang et al. demonstrated the bi-photon generation of linewidth 50 kHz corresponding coherence time of $13.4\mu$s with a 4.8-fold violation of CS inequality (Wang et al., 2022).

Entangled photon pair generation using the SpFWM process is also demonstrated in warm atomic vapor (Shu et al., 2016; Podhora et al., 2017; Ren et al., 2022). Many experiments have achieved a significant violation factor of the CS inequality and achieved an excellent repetition rate using the SpFWM process in a ladder-type Doppler-broadened warm ⁸⁷Rb atomic ensemble (Park et al., 2019; Wang et al., 2020; Park et al., 2021). Different groups that have created significant milestones in entangled photon pair generation through atomic vapors are highlighted in Table 6.

Table 6

Table 6. Summary of key parameters of entangled photon pair generation schemes using atomic vapors. Here, P-P signifies photon–photon entanglement, and A-P signifies atom–photon entanglement. In the case of multiple measurements, the best result is reported.

4 Generation of single and entangled photons from other sources

We have thoroughly examined the generation of single and entangled photons via atomic platforms, which aligns with the primary objective of this article. However, numerous techniques utilizing various platforms are also emerging as promising candidates. A summary of these alternatives would give readers a more comprehensive understanding of the field. Solid-state platforms represent a leading frontier in this area, as evidenced by various studies (Aharonovich et al., 2016; Awschalom et al., 2018; Meng et al., 2024). These platforms encompass diverse technologies such as color centers in diamond (Ruf et al., 2021), quantum dots (Mohammadnejad et al., 2022; Liu et al., 2019), semiconductor nanocrystals (Choi et al., 2014), carbon nanotubes (He et al., 2018), and rare-earth doped crystals (Thiel et al., 2011). Extensive research has been conducted on diamond color centers, revealing their efficacy as sources of both single (Aharonovich et al., 2009; Neu and Becher, 2014) and entangled photons (Michaels, 2023), even at room temperature. Additionally, organic molecules isolated in solid states have emerged as another active area of investigation (Toninelli et al., 2021).

5 Effect of non-Markovianity in single and entangled photon generation

Thus far, the discussion about single and entangled photon generation has typically assumed the Born–Markov approximation, where decoherence due to the environment of a quantum system is considered irreversible, suggesting that quantum states are generally fragile. Systems such as trapped atoms, ions, or atomic vapors are examples of open quantum systems, where the environment can disrupt the generation of single and entangled photons, causing the system to lose its quantum information to the environment. In the Markovian regime, the environment does not retain any information about the system’s state prior to decoherence, leading to an eventual loss of information (Breuer and Petruccione, 2002).

In reality, this is not always the case. In non-Markovian systems, the environment retains some information about the system’s state, exhibiting a memory effect. This phenomenon, known as information backflow, can feed information back into the system, potentially altering predicted behaviors in ways that can be either detrimental or advantageous, depending on the property under study (Shrikant and Mandayam, 2023; Breuer et al., 2016).

In the context of single-photon generation, non-Markovian effects can significantly influence key properties such as emission rates and the coherence time of emitted photons. For example, feedback from the environment in a non-Markovian regime can lead to the re-excitation of the quantum emitter, thereby affecting the temporal correlations of the emitted photons (Shen et al., 2013). This feedback can either enhance or suppress photon emission rates, depending on the specifics of the system–environment coupling and the environmental spectral density. Furthermore, non-Markovian dynamics can impact the purity and indistinguishability of the generated photons, which are crucial for applications in quantum information processing and communication. The retention of past state information can influence the coherence properties of the photons, potentially reducing dephasing and improving their purity (Shen et al., 2023; Shen et al., 2022).

One study involving stimulated Raman adiabatic passage (STIRAP) shows that even with a large decay rate, the process of adiabatic state transfer can still be feasible, and the influence of decoherence diminishes with an increasing number of coupled environments (Zeng et al., 2019). The non-Markovian framework can also explain phenomena such as the sudden death of entanglement. In a non-Markovian regime, entanglement between two qubits coupled to different environments can transfer to the reservoirs, leading to the sudden death of entanglement. This can also lead to the phenomenon of sudden birth of entanglement (Zhang et al., 2009).

Experimentally, controlling the environmental degrees of freedom in non-Markovian quantum systems remains challenging, and such experiments are still in their early stages. However, with current control mechanisms, non-Markovian effects can be detected experimentally through parameters such as laser field detuning, cavity parameters, and the optimal number of atoms coupled with the cavity field. Moreover, non-Markovianity can be directly assessed experimentally, provided one can perform tomographic measurements of different initial states at various times during the evolution. A structured reservoir that offers greater control allows observation of non-Markovian effects. For example, an electromagnetic field within a lossy cavity for an atom–cavity system can serve as such an environment. In this scenario, the non-Markovian regime can be defined by the spectral width of the reservoir spectrum: if the width is smaller than the vacuum Rabi frequency, the system is in the non-Markovian regime, and vice versa (Zhang et al., 2009).

Non-Markovian systems, particularly within the scope of this article, are still largely unexplored, although many theoretical proposals exist. For instance, one study indicates that in a non-Markovian regime, the amplitude of the driving field depends only on the detuning of the cavity field, not the driving field itself (Shen et al., 2013). Another study explores the behavior of the dispersive readout of quantum states in a non-Markovian regime for atom–cavity systems (Shen et al., 2022). Further investigation in this area is crucial, as it directly impacts quantum communication, especially in developing communication channels. In quantum communication, the primary goal is often to minimize environmental effects and isolate the quantum system. In this context, controlled non-Markovianity could potentially simplify and reduce the cost of developing quantum channels.

6 Design considerations for realistic experiments

Throughout this article, we have explored various experimental realizations of single and entangled photon pair sources using atomic platforms. However, a practical guide on experiment design would be invaluable for researchers looking to develop experiments in this field. While optimal parameters will vary depending on the specific goals of the study, this section aims to provide a concise overview of key considerations for the experimental design process.

Selecting single-trapped atomic and ionic platforms is advantageous due to their enhanced control capabilities. When trapping single atoms, special attention must be given to designing the trap to ensure that, once laser-cooled, the trapped atoms do not experience any additional perturbations from the trapping technique that could cause unwanted heating. The trap depth is another crucial parameter; it should be sufficiently large (5–10 times $k_{B}T$) to effectively capture atoms at a given temperature.

For trapped ions, the choice of electrode geometry is critical as it helps minimize anharmonicity in the trap potential and ensures better optical access for imaging and laser application. To achieve deterministic generation of single or entangled photons, placing the atom in an optical cavity is preferable to free-space interaction. Achieving strong coupling between the atom and the field requires a cavity with a sufficiently high finesse ($>$20,000). However, increasing the finesse beyond a certain point can be counterproductive, as photons generated inside the cavity may not escape due to the high reflectivity of the mirrors, thereby reducing the overall photon generation probability. A finesse range of 40,000–80,000 is generally suitable, but the exact choice should be made judiciously based on specific requirements.

An important consideration is the challenge of manufacturing high-reflective cavity mirrors at UV or near-UV wavelengths. Thus, selecting the optimal transition to couple the cavity while considering these experimental limitations is crucial. Operating a cavity in the infrared or near-infrared region is typically more efficient and cost-effective. Regarding cavity geometry, a confocal configuration is often preferred due to the relative ease of coupling light. However, a near-concentric configuration offers a smaller mode waist at the center, maximizing atom-cavity coupling, although it requires careful alignment and additional design precautions.

Several critical parameters must be meticulously optimized to achieve optimal results when developing an experiment for generating entangled photon pairs using atomic ensemble-based platforms. For ultra-cold atomic ensembles, maintaining temperatures in the range of tens of $\mu$K is essential to minimize thermal noise and extend photon coherence times. The selection of an atomic ensemble with a high optical depth (OD), such as a 2D MOT or dark-line 2D MOT with ODs exceeding 100, will significantly enhance interaction duration and photon pair generation rates. Efficient photon collection methods, including high numerical aperture lenses or optical cavities, should be employed to maximize photon capture. Precise control over laser field parameters, such as detuning, Rabi frequency, and polarization, is crucial for optimizing the spontaneous four-wave mixing (SpFWM) process. Additionally, exact phase control between the SpFWM pathways and the driving laser’s polarization is necessary to achieve the desired entangled states, enabling the generation of narrow-band, high-fidelity entangled photon pairs with extended coherence times and high generation rates.

Conversely, key parameters must also be carefully controlled for warm atomic ensembles. The atomic number density should be in the range of $10^{10}$-$10^{12}$ atoms/${\mathrm{c}\mathrm{m}}^3$ to ensure effective photon pair generation while balancing interaction strength and Doppler broadening. The optical depth (OD) should ideally be between 1 and 10, and the temperature of the atomic vapor should be maintained between ${40}^{°}C$ and ${100}^{°}C$. This temperature range supports a high atomic density and manages Doppler broadening effectively. Proper optimization of these parameters is essential for achieving high-fidelity entangled photon pairs in warm atomic ensembles.

7 Applications of single and entangled photons with future prospective

A worldwide, all-encompassing effort to generate single and entangled photons aims to make them applicable to solving real-world problems, particularly in quantum communication. In this section, we aim to offer a concise overview of the present and forthcoming applications of both single and entangled photons across various domains within the realm of quantum communication.

7.1 Quantum repeaters

The concept of quantum repeaters, which is analogous to classical repeaters used in conventional internet communication, emerges to address the challenge associated with quantum communication over long distances. The approach involves dividing a lengthy quantum channel into smaller segments, each shorter than the photon dephasing length. These segments are then interconnected using quantum repeaters (Briegel et al., 1998; Munro et al., 2015). Quantum repeaters function by capturing photons at a particular state, encoding them into the atomic state, and subsequently transferring this atom’s state back into the state of the following photon (Sangouard et al., 2011). This process necessitates a quantum memory operation (Wei et al., 2022). The transfer of state between atom and photon relies on the entanglement established between them. When an incoming photon of a specific polarization interacts with an atom, it creates an entangled state (see Equation 68). By detecting the polarization of the entangled photon at a particular angle, the atomic state is projected into a superposition of atomic basis states, with coefficients determined by the incoming photon’s polarization. This establishes a correspondence between the atomic state and the photon’s polarization state. The atomic state is preserved until a read pulse is initiated. This read pulse reverses the writing process, generating a subsequent photon with a polarization state corresponding to the atom’s state. Thus, a deterministic generation of single and entangled photons is essential for the quantum repeater protocol. Furthermore, quantum repeaters facilitate the creation of entanglement between remote nodes by enabling the simultaneous presence of photons required for the entanglement swapping process (see Figure 15) (Azuma et al., 2023; Short et al., 2006), thanks to their storage and on-demand retrieval capability.

Figure 15

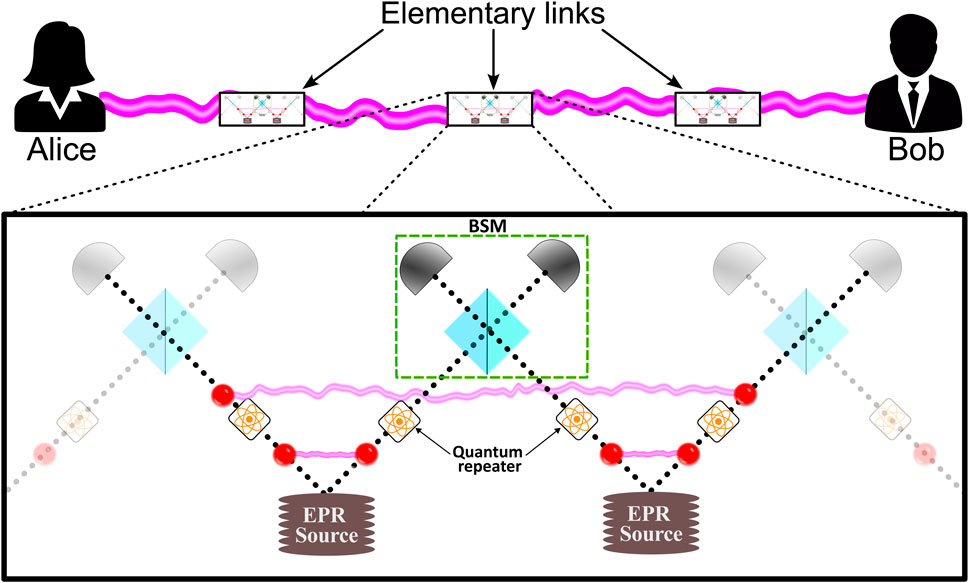
Figure 15. A protocol for establishing entanglement between two distant parties, such as Alice and Bob, involves segmenting the communication channel into multiple elementary links. Within each link, photons originating from two sources undergo entanglement through the Bell state measurement (BSM) process. Quantum repeaters are deployed prior to each BSM process to guarantee the simultaneous presence of photons. Employing the same procedure, the elementary links are entangled to facilitate the distribution of entanglement between the two distant nodes.

7.2 Long-distance quantum communication

Establishing long-distance quantum communication (Kozlowski and Wehner, 2019) is critically dependent on creating entanglement across far-apart nodes, which is essential for enabling technologies such as teleportation (Olmschenk et al., 2009), cryptography (Zhang W. et al., 2022; Nadlinger et al., 2022), and dense coding (Guo et al., 2019). The primary hurdle lies in entangling remote nodes without direct interaction. The ingenious technique of entanglement swapping is employed to overcome this challenge (Briegel et al., 1998; Żukowski et al., 1993). This approach involves a Bell state measurement (BSM) (Braunstein and Mann, 1995; Michler et al., 1996) on photons arriving from two separate, un-entangled nodes. The process, aided by quantum repeaters and the simultaneous detection of these photons, results in the entanglement of the previously independent nodes (refer to Figure 15). BSM has been successfully demonstrated on various platforms, including atomic (Riebe et al., 2004; González-Gutiérrez and Torres, 2019; Welte et al., 2021) and solid-state systems (Reyes et al., 2022), with a success rate of approximately 50%. Recently, one study has reported a higher success rate of 57.9$\pm$1.4% using linear optics and additional ancillary photons (Bayerbach et al., 2023). This improved BSM technique enables the creation of entanglement between distant nodes by recursively entangling intermediate nodes. Notably, recent experiments have achieved entanglement between atoms separated by 33 km (van Leent et al., 2022) and ions separated by 230 m (Krutyanskiy et al., 2023). Likewise, the trend in research in this field aims toward increasing the distances between entangled inter-node pairs as well as the number of entangled nodes, bringing these advancements closer to real-world applications.

7.3 Quantum teleportation

Quantum teleportation involves transmitting the state of a qubit from one node to another without transferring the physical particle itself, with the help of entanglement and classical communication. This groundbreaking technique, first proposed by Asher Peres and William K. Wootters, leverages the peculiar properties of entanglement and classical information to achieve state reconstruction (Bennett et al., 1993). Following the theoretical groundwork, numerous experimental demonstrations have successfully realized teleportation (Bouwmeester et al., 1997; Sherson et al., 2006; Ren et al., 2017). To execute quantum teleportation, initially, entanglement is established between the distant nodes between which the teleportation is intended. This entanglement distribution requires previously discussed methods of entangled photon generation, along with the entanglement swapping technique. Sequential measurements are then performed to transfer the quantum state. Notably, entanglement’s role is not in transmitting the information itself but in ensuring the complete security of the transfer. A classical channel is utilized to convey the security verification outcomes acquired from a Bell state measurement process (Liu, 2020). As envisioned, future endeavors in teleportation may prioritize extending the range of teleportation while also advancing the capability to teleport more intricate quantum states.

7.4 Quantum cryptography

Like classical cryptographic methods like RSA (Rivest, Shamir, and Adleman) (Rivest et al., 1978), quantum cryptography also involves encrypting, transmitting, and decrypting messages to remote locations. Quantum key distribution (QKD) (Bennett and Brassard, 2014; Bennett et al., 1992) emerges as the leading method within the realm of quantum cryptography (Lo et al., 2012; Cao et al., 2022). In this process, a secure key is used to encrypt the original message, which is subsequently sent over a classical channel in its encrypted form. Meanwhile, the secret key is shared through a quantum channel, which is subsequently utilized for decryption (Xu et al., 2020). These keys are basically a stream of single photons carrying the information. Hence, it is imperative to have a deterministic single-photon source with minimal multiphoton generation probabilities to thwart potential eavesdropping attempts. Regarding security concerns, entanglement offers an avenue for achieving unconditional security in a more streamlined manner (Ribordy et al., 2000). If entanglement is established between parties, it inherently provides complete security, periodically verified through the measurement of Bell’s inequality whenever necessary (Zhang W. et al., 2022; Nadlinger et al., 2022). Hence, quantum cryptography becomes a crucial aspect of secure quantum communication. The ongoing scope for improvement encompasses enhancing scalability, achieving QKD between multiple nodes simultaneously, and extending the distance of state transfer while effectively mitigating dephasing effects (Zhang et al., 2023).

8 Summary and conclusion

Single and entangled photon pair sources are an essential part of the development of quantum technologies. Trapped cooled atoms and warm atomic vapors serve as reliable platforms for single and entangled photon generation. We endeavor to provide a comprehensive review of the generation, verification, and characterization methods of both single and entangled photon pairs across different atomic platforms. First, we discuss the fundamental concepts related to single and entangled photons and the generation of single photons through processes such as the Raman process, STIRAP, and CMRT. Following those discussions, an experimental characterization of single photons using HBT and HOM interferometry techniques is explored. The article also explores entangled photon pair generation via SPDC and FWM processes and discusses methodologies for creating entangled states. Additionally, entanglement verification methods, including the violation of Cauchy–Schwarz and CHSH–Bell inequalities, and characterization techniques such as quantum state tomography, fidelity, entanglement of formation, and concurrence are addressed. The review emphasizes the significance of continued research and innovation in this rapidly evolving field to realize practical and robust quantum technologies. We briefly discuss the applications and future possibilities of single and entangled photons within the realm of quantum communication.

Deterministic single-photon generation at telecom wavelengths is critical yet technically challenging for advancing quantum communication. The importance of room temperature sources for single and entangled photons cannot be overstated, as they significantly enhance the feasibility of practical quantum communications. Employing cQED presents a strategic approach for efficiently producing single and entangled photons. Future applications in quantum communication necessitate miniaturized, chip-scale operations for these photon sources. Furthermore, reliable and deterministic generation of these photons at high rates will be crucial not only for quantum communication but also for future developments in quantum computing.

Hence, considering the importance of these emerging technologies, we hope this review will provide a basic understanding of the underlying concepts and an overview of the developments. We also believe that the review discusses some critical aspects of single and entangled photon generation and will be helpful for researchers developing experiments.

Author contributions

SA: writing–original draft. AK: writing–original draft. AC: writing–review and editing. AS: writing–review and editing and supervision.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. SA gratefully acknowledges financial support from the Council of Scientific and Industrial Research (CSIR, Govt. of India) through a Senior Research Fellowship (SRF) (File No: 09/1326(13149)/2021-EMR-I). AC gratefully acknowledges financial support from the Technology Innovation I-Hub Quantum Technology Foundation, IISER Pune, through the Chanakya Postdoctoral Fellowship (Project no: PHY2122002IHUBARIJ). AS and AK acknowledge financial support from IIT Tirupati through the CAMOST grant and Institute Fellowship respectively enabled through the OH35 grant received from the Ministry of Education, Government of India.

Acknowledgments

We express our special gratitude to Mr. Gyanendra Pratap Roy for his exceptional assistance in illustrating figures within this article. We owe a considerable debt of gratitude to Mr. Himanshu Miriyala for his meticulous efforts in graph construction, which significantly enhanced the analytical depth of this work. Furthermore, we are thankful for the insightful suggestions and assistance from Mr. Vikrant Yadav and Mr. Rishabh Pal, which have substantially improved the quality of this manuscript. We also acknowledge Ms. Poorvisha C and Mr. Shivam Sinha for their diligent collection of the critical data points that underpin our research findings. The combined endeavors of these individuals were pivotal in the realization of this study, and we express our sincere thanks for their invaluable contributions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aharonovich, I., Englund, D., and Toth, M. (2016). Solid-state single-photon emitters. Nat. Phot. 10, 631–641. doi:10.1038/nphoton.2016.186

CrossRef Full Text | Google Scholar

Aharonovich, I., Zhou, C., Stacey, A., Orwa, J., Castelletto, S., Simpson, D., et al. (2009). Enhanced single-photon emission in the near infrared from a diamond color center. Phys. Rev. B 79, 235316–2353165. doi:10.1103/PhysRevB.79.235316

CrossRef Full Text | Google Scholar

Almendros, M., Huwer, J., Piro, N., Rohde, F., Schuck, C., Hennrich, M., et al. (2009). Bandwidth-tunable single-photon source in an ion-trap quantum network. Phys. Rev. Lett. 103, 213601–2136014. doi:10.1103/PhysRevLett.103.213601

PubMed Abstract | CrossRef Full Text | Google Scholar

Aoki, T., Parkins, A. S., Alton, D. J., Regal, C. A., Dayan, B., Ostby, E., et al. (2009). Efficient routing of single photons by one atom and a microtoroidal cavity. Phys. Rev. Lett. 102, 083601–0836014. doi:10.1103/PhysRevLett.102.083601

PubMed Abstract | CrossRef Full Text | Google Scholar

Aso, O., Tadakuma, M., and Namiki, S. (2000). Four-wave mixing in optical fibers and its applications. Furukawa Rev. 1, 63–68.

Google Scholar

Aspect, A., Dalibard, J., and Roger, G. (1982). Experimental test of bell’s inequalities using time-varying analyzers. Phys. Rev. Lett. 49, 1804–1807. doi:10.1103/PhysRevLett.49.1804

CrossRef Full Text | Google Scholar

Aspect, A., Grangier, P., and Roger, G. (1981). Experimental tests of realistic local theories via bell’s theorem. Phys. Rev. Lett. 47, 460–463. doi:10.1103/PhysRevLett.47.460

CrossRef Full Text | Google Scholar

Aspect, A., Imbert, C., and Roger, G. (1980). Absolute measurement of an atomic cascade rate using a two photon coincidence technique. application to the 4p21s0 -4s4p 1p1 -4s21s0 cascade of calcium excited by a two photon absorption. Opt. Commun. 34, 46–52. doi:10.1016/0030-4018(80)90157-1

CrossRef Full Text | Google Scholar

Autler, S. H., and Townes, C. H. (1955). Stark effect in rapidly varying fields. Phys. Rev. 100, 703–722. doi:10.1103/PhysRev.100.703

CrossRef Full Text | Google Scholar

Awschalom, D. D., Hanson, R., Wrachtrup, J., and Zhou, B. B. (2018). Quantum technologies with optically interfaced solid-state spins. Nat. Phot. 12, 516–527. doi:10.1038/s41566-018-0232-2

CrossRef Full Text | Google Scholar

Azuma, K., Economou, S. E., Elkouss, D., Hilaire, P., Jiang, L., Lo, H.-K., et al. (2023). Quantum repeaters: from quantum networks to the quantum internet. Rev. Mod. Phys. 95, 045006–04500666. doi:10.1103/RevModPhys.95.045006

CrossRef Full Text | Google Scholar

Bahar, E., Ding, X., Dahan, A., Suchowski, H., and Moses, J. (2018). Adiabatic four-wave mixing frequency conversion. Opt. Express 26, 25582–25601. doi:10.1364/OE.26.025582

PubMed Abstract | CrossRef Full Text | Google Scholar

Balić, V., Braje, D. A., Kolchin, P., Yin, G. Y., and Harris, S. E. (2005). Generation of paired photons with controllable waveforms. Phys. Rev. Lett. 94, 183601–1836014. doi:10.1103/PhysRevLett.94.183601

PubMed Abstract | CrossRef Full Text | Google Scholar

Barros, H., Stute, A., Northup, T., Russo, C., Schmidt, P., and Blatt, R. (2009). Deterministic single-photon source from a single ion. New J. Phys. 11, 103004–10300410. doi:10.1088/1367-2630/11/10/103004

CrossRef Full Text | Google Scholar

Bayerbach, M. J., D’Aurelio, S. E., Loock, P. V., and Barz, S. (2023). Bell-state measurement exceeding 50% success probability with linear optics. Sci. Adv. 9, eadf4080. doi:10.1126/sciadv.adf4080

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, J. S. (1964). On the einstein podolsky rosen paradox. Phys. Phys. Fiz. 1, 195–200. doi:10.1103/PhysicsPhysiqueFizika.1.195

CrossRef Full Text | Google Scholar

Bell, J. S. (1966). On the problem of hidden variables in quantum mechanics. Rev. Mod. Phys. 38, 447–452. doi:10.1103/RevModPhys.38.447

CrossRef Full Text | Google Scholar

Bennett, C. H., Bessette, F., Brassard, G., Salvail, L., and Smolin, J. (1992). Experimental quantum cryptography. J. Cryptol. 5, 3–28. doi:10.1007/BF00191318

CrossRef Full Text | Google Scholar

Bennett, C. H., and Brassard, G. (2014). Quantum cryptography: public key distribution and coin tossing. Theor. Comput. Sci. 560, 7–11. doi:10.1016/j.tcs.2014.05.025

CrossRef Full Text | Google Scholar

Bennett, C. H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A., and Wootters, W. K. (1993). Teleporting an unknown quantum state via dual classical and einstein-podolsky-rosen channels. Phys. Rev. Lett. 70, 1895–1899. doi:10.1103/PhysRevLett.70.1895

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, C. H., and Wiesner, S. J. (1992). Communication via one- and two-particle operators on einstein-podolsky-rosen states. Phys. Rev. Lett. 69, 2881–2884. doi:10.1103/PhysRevLett.69.2881

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernien, H., Childress, L., Robledo, L., Markham, M., Twitchen, D., and Hanson, R. (2012). Two-photon quantum interference from separate nitrogen vacancy centers in diamond. Phys. Rev. Lett. 108, 043604–0436045. doi:10.1103/PhysRevLett.108.043604

PubMed Abstract | CrossRef Full Text | Google Scholar

Beugnon, J., Jones, M. P., Dingjan, J., Darquié, B., Messin, G., Browaeys, A., et al. (2006). Quantum interference between two single photons emitted by independently trapped atoms. Nature 440, 779–782. doi:10.1038/nature04628

PubMed Abstract | CrossRef Full Text | Google Scholar

Bina, M. (2012). The coherent interaction between matter and radiation: a tutorial on the jaynes-cummings model. Eur. Phys. J. Spec. Top. 203, 163–183. doi:10.1140/epjst/e2012-01541-3

CrossRef Full Text | Google Scholar

Blinov, B. B., Moehring, D. L., Duan, L.-M., and Monroe, C. (2004). Observation of entanglement between a single trapped atom and a single photon. Nature 428, 153–157. doi:10.1038/nature02377

PubMed Abstract | CrossRef Full Text | Google Scholar

Blume-Kohout, R. (2010). Optimal, reliable estimation of quantum states. New J. Phys. 12, 043034. doi:10.1088/1367-2630/12/4/043034

CrossRef Full Text | Google Scholar

Bock, M., Eich, P., Kucera, S., Kreis, M., Lenhard, A., Becher, C., et al. (2018). High-fidelity entanglement between a trapped ion and a telecom photon via quantum frequency conversion. Nat. Commun. 9, 1998. doi:10.1038/s41467-018-04341-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Bondurant, R. S., Kumar, P., Shapiro, J. H., and Maeda, M. (1984). Degenerate four-wave mixing as a possible source of squeezed-state light. Phys. Rev. A 30, 343–353. doi:10.1103/PhysRevA.30.343

CrossRef Full Text | Google Scholar

Borregaard, J., Zugenmaier, M., Petersen, J., Shen, H., Vasilakis, G., Jensen, K., et al. (2016). Scalable photonic network architecture based on motional averaging in room temperature gas. Nat. Commun. 7, 11356. doi:10.1038/ncomms11356

PubMed Abstract | CrossRef Full Text | Google Scholar

Borri, P., and Langbein, W. (2007). Four-wave mixing dynamics of excitons in ingaas self-assembled quantum dots. J. Phys. Condens. Matter. 19, 295201–29520120. doi:10.1088/0953-8984/19/29/295201

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouwmeester, D., Pan, J.-W., Mattle, K., Eibl, M., Weinfurter, H., and Zeilinger, A. (1997). Experimental quantum teleportation. Nature 390, 575–579. doi:10.1038/37539

CrossRef Full Text | Google Scholar

Bouwmeester, D., and Zeilinger, A. (2000). The physics of quantum information: basic concepts. Berlin, Heidelberg: Springer Berlin Heidelberg.

Google Scholar

Boyd, R., and Prato, D. (2008). Nonlinear optics. Elsevier Science.

Google Scholar

Bransden, B., and Joachain, C. (2003). Physics of atoms and molecules. United Kingdom: Prentice Hall, Pearson Education.

Google Scholar

Braunstein, S. L., and Kimble, H. J. (1998). Teleportation of continuous quantum variables. Phys. Rev. Lett. 80, 869–872. doi:10.1103/PhysRevLett.80.869

CrossRef Full Text | Google Scholar

Braunstein, S. L., and Mann, A. (1995). Measurement of the bell operator and quantum teleportation. Phys. Rev. A 51, R1727–R1730. doi:10.1103/PhysRevA.51.R1727

PubMed Abstract | CrossRef Full Text | Google Scholar

Brecha, R., Orozco, L., Raizen, M., Xiao, M., and Kimble, H. (1995). Observation of oscillatory energy exchange in a coupled-atom–cavity system. JOSA B 12, 2329–2339. doi:10.1364/JOSAB.12.002329

CrossRef Full Text | Google Scholar

Breuer, H., and Petruccione, F. (2002). The theory of open quantum systems. Oxford University Press.

Google Scholar

Breuer, H.-P., Laine, E.-M., Piilo, J., and Vacchini, B. (2016). Colloquium: non-markovian dynamics in open quantum systems. Rev. Mod. Phys. 88, 021002. doi:10.1103/RevModPhys.88.021002

CrossRef Full Text | Google Scholar

Briegel, H.-J., Dür, W., Cirac, J. I., and Zoller, P. (1998). Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935. doi:10.1103/PhysRevLett.81.5932

CrossRef Full Text | Google Scholar

Brown, R. H., and Twiss, R. Q. (1956). Correlation between photons in two coherent beams of light. Nature 177, 27–29. doi:10.1038/177027a0

CrossRef Full Text | Google Scholar

Bruno, N., Martin, A., Guerreiro, T., Sanguinetti, B., and Thew, R. T. (2014). Pulsed source of spectrally uncorrelated and indistinguishable photons at telecom wavelengths. Opt. Express 22, 17246–17253. doi:10.1364/OE.22.017246

PubMed Abstract | CrossRef Full Text | Google Scholar

Burnham, D. C., and Weinberg, D. L. (1970). Observation of simultaneity in parametric production of optical photon pairs. Phys. Rev. Lett. 25, 84–87. doi:10.1103/PhysRevLett.25.84

CrossRef Full Text | Google Scholar

Camacho, R. M., Vudyasetu, P. K., and Howell, J. C. (2009). Four-wave-mixing stopped light in hot atomic rubidium vapour. Nat. Phot. 3, 103–106. doi:10.1038/nphoton.2008.290

CrossRef Full Text | Google Scholar

Cao, Y., Zhao, Y., Wang, Q., Zhang, J., Ng, S. X., and Hanzo, L. (2022). The evolution of quantum key distribution networks: on the road to the qinternet. IEEE Commun. Surv. Tutor. 24, 839–894. doi:10.1109/COMST.2022.3144219

CrossRef Full Text | Google Scholar

Chanelière, T., Matsukevich, D. N., Jenkins, S. D., Lan, S.-Y., Zhao, R., Kennedy, T. A. B., et al. (2007). Quantum interference of electromagnetic fields from remote quantum memories. Phys. Rev. Lett. 98, 113602–1136024. doi:10.1103/PhysRevLett.98.113602

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, P., Zhou, S.-Y., Xu, Z., Duan, Y.-F., Cui, G.-D., Hong, T., et al. (2011). Narrowband biphoton generation with four-wave mixing in a far-detuning three-level system. Chin. Phys. Lett. 28, 074214. doi:10.1088/0256-307X/28/7/074214

CrossRef Full Text | Google Scholar

Chen, S., Chen, Y., Strassel, T., Yuan, Z. S., Zhao, B., Schmiedmayer, J., et al. (2006). Deterministic and storable single-photon source based on a quantum memory. Phys. Rev. Lett. 97, 173004–1730044. doi:10.1103/PhysRevLett.97.173004

PubMed Abstract | CrossRef Full Text | Google Scholar

Choi, S., Johnson, B. C., Castelletto, S., Ton-That, C., Phillips, M. R., and Aharonovich, I. (2014). Single photon emission from zno nanoparticles. Appl. Phys. Lett. 104, 261101. doi:10.1063/1.4872268

CrossRef Full Text | Google Scholar

Chou, C. W., Polyakov, S. V., Kuzmich, A., and Kimble, H. J. (2004). Single-photon generation from stored excitation in an atomic ensemble. Phys. Rev. Lett. 92, 213601. doi:10.1103/PhysRevLett.92.213601

PubMed Abstract | CrossRef Full Text | Google Scholar

Cirac, J. I., Zoller, P., Kimble, H. J., and Mabuchi, H. (1997). Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 78, 3221–3224. doi:10.1103/PhysRevLett.78.3221

CrossRef Full Text | Google Scholar

Cirel’son, B. S. (1980). Quantum generalizations of bell’s inequality. Lett. Math. Phys. 4, 93–100. doi:10.1007/BF00417500

CrossRef Full Text | Google Scholar

Clauser, J., and John, F. (1974). Experimental distinction between the quantum and classical field-theoretic predictions for the photoelectric effect. Phys. Rev. D. 9, 853–860. doi:10.1103/PhysRevD.9.853

CrossRef Full Text | Google Scholar

Clauser, J. F. (1976). Experimental investigation of a polarization correlation anomaly. Phys. Rev. Lett. 36, 1223–1226. doi:10.1103/PhysRevLett.36.1223

CrossRef Full Text | Google Scholar

Clauser, J. F., Horne, M. A., Shimony, A., and Holt, R. A. (1969). Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880–884. doi:10.1103/PhysRevLett.23.880

CrossRef Full Text | Google Scholar

Coffman, V., Kundu, J., and Wootters, W. K. (2000). Distributed entanglement. Phys. Rev. A 61, 052306. doi:10.1103/PhysRevA.61.052306

CrossRef Full Text | Google Scholar

Compton, A. H. (1923). A quantum theory of the scattering of x-rays by light elements. Phys. Rev. 21, 483–502. doi:10.1103/PhysRev.21.483

CrossRef Full Text | Google Scholar

Couteau, C. (2018). Spontaneous parametric down-conversion. Contemp. Phys. 59, 291–304. doi:10.1080/00107514.2018.1488463

CrossRef Full Text | Google Scholar

Dahl, J. (1982). The wigner function. Phys. A Stat. Mech. 114, 439–444. doi:10.1016/0378-4371(82)90328-4

CrossRef Full Text | Google Scholar

Darquié, B., Jones, M. P. A., Dingjan, J., Beugnon, J., Bergamini, S., Sortais, Y., et al. (2005). Controlled single-photon emission from a single trapped two-level atom. Science 309, 454–456. doi:10.1126/science.1113394

PubMed Abstract | CrossRef Full Text | Google Scholar

Davidson, O., Yogev, O., Poem, E., and Firstenberg, O. (2023). Single-photon synchronization with a room-temperature atomic quantum memory. Phys. Rev. Lett. 131, 033601. doi:10.1103/PhysRevLett.131.033601

PubMed Abstract | CrossRef Full Text | Google Scholar

Dayan, B., Parkins, A. S., Aoki, T., Ostby, E. P., Vahala, K. J., and Kimble, H. J. (2008). A photon turnstile dynamically regulated by one atom. Science 319, 1062–1065. doi:10.1126/science.1152261

PubMed Abstract | CrossRef Full Text | Google Scholar

Deng, L., Hagley, E. W., Wen, J., Trippenbach, M., Band, Y., Julienne, P. S., et al. (1999). Four-wave mixing with matter waves. Nature 398, 218–220. doi:10.1038/18395

CrossRef Full Text | Google Scholar

Dideriksen, K. B., Schmieg, R., Zugenmaier, M., and Polzik, E. S. (2021). Room-temperature single-photon source with near-millisecond built-in memory. Nat. Commun. 12, 3699. doi:10.1038/s41467-021-24033-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Dieckmann, K., Spreeuw, R. J. C., Weidemüller, M., and Walraven, J. T. M. (1998). Two-dimensional magneto-optical trap as a source of slow atoms. Phys. Rev. A 58, 3891–3895. doi:10.1103/PhysRevA.58.3891

CrossRef Full Text | Google Scholar

Diedrich, F., and Walther, H. (1987). Nonclassical radiation of a single stored ion. Phys. Rev. Lett. 58, 203–206. doi:10.1103/PhysRevLett.58.203

PubMed Abstract | CrossRef Full Text | Google Scholar

Diez, S., Schmidt, C., Ludwig, R., Weber, H. G., Obermann, K., Kindt, S., et al. (1997). Four-wave mixing in semiconductor optical amplifiers for frequency conversion and fast optical switching. IEEE J. Sel. Top. Quantum Electron. 3, 1131–1145. doi:10.1109/2944.658587

CrossRef Full Text | Google Scholar

Ding, D. S., Zhou, Z. Y., Shi, B. S., and Guo, G. C. (2013). Single-photon-level quantum image memory based on cold atomic ensembles. Nat. Commun. 4, 2527. doi:10.1038/ncomms3527

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, D.-S., Zhou, Z.-Y., Shi, B.-S., Zou, X.-B., and Guo, G.-C. (2012). Generation of non-classical correlated photon pairs via a ladder-type atomic configuration: theory and experiment. Opt. Express 20, 11433–11444. doi:10.1364/OE.20.011433

PubMed Abstract | CrossRef Full Text | Google Scholar

Du, S., Kolchin, P., Belthangady, C., Yin, G. Y., and Harris, S. E. (2008a). Subnatural linewidth biphotons with controllable temporal length. Phys. Rev. Lett. 100, 183603. doi:10.1103/PhysRevLett.100.183603

PubMed Abstract | CrossRef Full Text | Google Scholar

Du, S., Wen, J., and Rubin, M. H. (2008b). Narrowband biphoton generation near atomic resonance. J. Opt. Soc. Am. B 25, C98–C108. doi:10.1364/JOSAB.25.000C98

CrossRef Full Text | Google Scholar

Du, S., Wen, J., Rubin, M. H., and Yin, G. Y. (2007). Four-wave mixing and biphoton generation in a two-level system. Phys. Rev. Lett. 98, 053601. doi:10.1103/PhysRevLett.98.053601

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, L., Lukin, M. D., Cirac, J. I., and Zoller, P. (2001). Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418. doi:10.1038/35106500

PubMed Abstract | CrossRef Full Text | Google Scholar

Dür, W., and Heusler, S. (2016). The qubit as key to quantum physics part ii: physical realizations and applications. Phys. Teach. 54, 156–159. doi:10.1119/1.4942137

CrossRef Full Text | Google Scholar

Edamatsu, K. (2007). Entangled photons: generation, observation, and characterization. JJAP 46, 7175. doi:10.1143/JJAP.46.7175

CrossRef Full Text | Google Scholar

Einstein, A. (1905). Zur elektrodynamik bewegter körper. Ann. Phys. 322, 891–921. doi:10.1002/andp.19053221004

CrossRef Full Text | Google Scholar

Einstein, A., Podolsky, B., and Rosen, N. (1935). Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780. doi:10.1103/PhysRev.47.777

CrossRef Full Text | Google Scholar

Emary, C., Lambert, N., and Nori, F. (2013). Leggett–garg inequalities. Rep. Prog. Phys. 77, 016001. doi:10.1088/0034-4885/77/1/016001

CrossRef Full Text | Google Scholar

Farrera, P., Heinze, G., Albrecht, B., Ho, M., Chávez, M., Teo, C., et al. (2016). Generation of single photons with highly tunable wave shape from a cold atomic ensemble. Nat. Commun. 7, 13556. doi:10.1038/ncomms13556

PubMed Abstract | CrossRef Full Text | Google Scholar

Felinto, D., Chou, C. W., de Riedmatten, H., Polyakov, S. V., and Kimble, H. J. (2005). Control of decoherence in the generation of photon pairs from atomic ensembles. Phys. Rev. A 72, 053809. doi:10.1103/PhysRevA.72.053809

CrossRef Full Text | Google Scholar

Fischer, K. A., Müller, K., Lagoudakis, K. G., and Vučković, J. (2018). Corrigendum: dynamical modeling of pulsed two-photon interference (2016 new j. phys. 18 113053). New J. Phys. 20, 039502–039520. doi:10.1088/1367-2630/aab32a

CrossRef Full Text | Google Scholar

Flagg, E. B., Muller, A., Polyakov, S. V., Ling, A., Migdall, A., and Solomon, G. S. (2010). Interference of single photons from two separate semiconductor quantum dots. Phys. Rev. Lett. 104, 137401. doi:10.1103/PhysRevLett.104.137401

PubMed Abstract | CrossRef Full Text | Google Scholar

Fox, M. (2006). Quantum optics: an introduction. United Kingdom: OUP Oxford.

Google Scholar

Freedman, S. J., and Clauser, J. F. (1972). Experimental test of local hidden-variable theories. Phys. Rev. Lett. 28, 938–941. doi:10.1103/PhysRevLett.28.938

CrossRef Full Text | Google Scholar

Gaëtan, A., Miroshnychenko, Y., Wilk, T., Chotia, A., Viteau, M., Comparat, D., et al. (2009). Observation of collective excitation of two individual atoms in the rydberg blockade regime. Nat. Phys. 5, 115–118. doi:10.1038/nphys1183

CrossRef Full Text | Google Scholar

Garcia, S., Maxein, D., Hohmann, L., Reichel, J., and Long, R. (2013). Fiber-pigtailed optical tweezer for single-atom trapping and single-photon generation. Appl. Phys. Lett. 103, 114103. doi:10.1063/1.4821160

CrossRef Full Text | Google Scholar

Gaubatz, U., Rudecki, P., Schiemann, S., and Bergmann, K. (1990). Population transfer between molecular vibrational levels by stimulated Raman scattering with partially overlapping laser fields. a new concept and experimental results. J. Chem. Phys. 92, 5363–5376. doi:10.1063/1.458514

CrossRef Full Text | Google Scholar

Gerber, S., Rotter, D., Hennrich, M., Blatt, R., Rohde, F., Schuck, C., et al. (2009). Quantum interference from remotely trapped ions. New J. Phys. 11, 013032. doi:10.1088/1367-2630/11/1/013032

CrossRef Full Text | Google Scholar

Gerry, C., and Knight, P. (2005). Introductory quantum optics. Cambridge University Press.

Google Scholar

González-Gutiérrez, C. A., and Torres, J. M. (2019). Atomic bell measurement via two-photon interactions. Phys. Rev. A 99, 023854. doi:10.1103/PhysRevA.99.023854

CrossRef Full Text | Google Scholar

Goto, H., Mizukami, S., Tokunaga, Y., and Aoki, T. (2019). Figure of merit for single-photon generation based on cavity quantum electrodynamics. Phys. Rev. A 99, 053843. doi:10.1103/PhysRevA.99.053843

CrossRef Full Text | Google Scholar

Gray, H., Whitley, R., and Stroud, C. (1978). Coherent trapping of atomic populations. Opt. Lett. 3, 218–220. doi:10.1364/OL.3.000218

PubMed Abstract | CrossRef Full Text | Google Scholar

Gulati, G. K. (2014). Narrowband photon pairs from A cold atomic vapour for interfacing with A single atom. Singapore: National University of Singapore. Ph.D. thesis.

Google Scholar

Gulati, G. K., Srivathsan, B., Chng, B., Cerè, A., and Kurtsiefer, C. (2015). Polarization entanglement and quantum beats of photon pairs from four-wave mixing in a cold 87rb ensemble. New J. Phys. 17, 093034. doi:10.1088/1367-2630/17/9/093034

CrossRef Full Text | Google Scholar

Guo, Y., Liu, B.-H., Li, C.-F., and Guo, G.-C. (2019). Advances in quantum dense coding. Adv. Quantum Technol. 2, 1900011. doi:10.1002/qute.201900011

CrossRef Full Text | Google Scholar

Guthöhrlein, G. R., Keller, M., Hayasaka, K., Lange, W., and Walther, H. (2001). A single ion as a nanoscopic probe of an optical field. Nature 414, 49–51. doi:10.1038/35102129

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, Z., Qian, P., Zhou, L., Chen, J. F., and Zhang, W. (2015). Coherence time limit of the biphotons generated in a dense cold atom cloud. Sci. Rep. 5, 9126. doi:10.1038/srep09126

PubMed Abstract | CrossRef Full Text | Google Scholar

Harlander, M., Brownnutt, M., Hänsel, W., and Blatt, R. (2010). Trapped-ion probing of light-induced charging effects on dielectrics. New J. Phys. 12, 093035. doi:10.1088/1367-2630/12/9/093035

CrossRef Full Text | Google Scholar

Harris, S. E., Oshman, M. K., and Byer, R. L. (1967). Observation of tunable optical parametric fluorescence. Phys. Rev. Lett. 18, 732–734. doi:10.1103/PhysRevLett.18.732

CrossRef Full Text | Google Scholar

He, X., Htoon, H., Doorn, S., Pernice, W., Pyatkov, F., Krupke, R., et al. (2018). Carbon nanotubes as emerging quantum-light sources. Nat. Mater. 17, 663–670. doi:10.1038/s41563-018-0109-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Hecht, E., and Zając, A. (1974). Optics. Addison-Wesley series in physics. Addison-Wesley Publishing Company.

Google Scholar

Hennrich, M., Legero, T., Kuhn, A., and Rempe, G. (2000). Vacuum-stimulated Raman scattering based on adiabatic passage in a high-finesse optical cavity. Phys. Rev. Lett. 85, 4872–4875. doi:10.1103/PhysRevLett.85.4872

PubMed Abstract | CrossRef Full Text | Google Scholar

Higginbottom, D. B., Slodička, L., Araneda, G., Lachman, L., Filip, R., Hennrich, M., et al. (2016). Pure single photons from a trapped atom source. New J. Phys. 18, 093038. doi:10.1088/1367-2630/18/9/093038

CrossRef Full Text | Google Scholar

Hong, C. K., Ou, Z. Y., and Mandel, L. (1987). Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046. doi:10.1103/PhysRevLett.59.2044

PubMed Abstract | CrossRef Full Text | Google Scholar

Horodecki, M., Horodecki, P., and Horodecki, R. (2001). Separability of n-particle mixed states: necessary and sufficient conditions in terms of linear maps. Phys. Lett. A 283, 1–7. doi:10.1016/S0375-9601(01)00142-6

CrossRef Full Text | Google Scholar

Horodecki, R., Horodecki, P., Horodecki, M., and Horodecki, K. (2009). Quantum entanglement. Rev. Mod. Phys. 81, 865–942. doi:10.1103/RevModPhys.81.865

CrossRef Full Text | Google Scholar

Howell, J. C., Bennink, R. S., Bentley, S. J., and Boyd, R. W. (2004). Realization of the einstein-podolsky-rosen paradox using momentum- and position-entangled photons from spontaneous parametric down conversion. Phys. Rev. Lett. 92, 210403. doi:10.1103/PhysRevLett.92.210403

PubMed Abstract | CrossRef Full Text | Google Scholar

Hradil, Z. (1997). Quantum-state estimation. Phys. Rev. A 55, R1561–R1564. doi:10.1103/PhysRevA.55.R1561

CrossRef Full Text | Google Scholar

Huang, R., Miranowicz, A., Liao, J.-Q., Nori, F., and Jing, H. (2018). Nonreciprocal photon blockade. Phys. Rev. Lett. 121, 153601. doi:10.1103/PhysRevLett.121.153601

PubMed Abstract | CrossRef Full Text | Google Scholar

Hwang, K., Seong, J., Park, K., Kim, J., Pramanik, T., Bae, J., et al. (2023). Entanglement witness measurement of time-bin two-qubit states using fiber-based franson interferometers. Front. Phys. 11, 1254044. doi:10.3389/fphy.2023.1254044

CrossRef Full Text | Google Scholar

James, D. F. V., Kwiat, P. G., Munro, W. J., and White, A. G. (2001). Measurement of qubits. Phys. Rev. A 64, 052312. doi:10.1103/PhysRevA.64.052312

CrossRef Full Text | Google Scholar

Jaynes, E. T., and Cummings, F. W. (1963). Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 51, 89–109. doi:10.1109/PROC.1963.1664

CrossRef Full Text | Google Scholar

Jozsa, R. (1994). Fidelity for mixed quantum states. J. Mod. Opt. 41, 2315–2323. doi:10.1080/09500349414552171

CrossRef Full Text | Google Scholar

Kaltenbaek, R., Blauensteiner, B., Żukowski, M., Aspelmeyer, M., and Zeilinger, A. (2006). Experimental interference of independent photons. Phys. Rev. Lett. 96, 240502. doi:10.1103/PhysRevLett.96.240502

PubMed Abstract | CrossRef Full Text | Google Scholar

Keller, M. (2022). Cavity-qed with single trapped ions. Contemp. Phys. 63, 1–14. doi:10.1080/00107514.2022.2118385

CrossRef Full Text | Google Scholar

Keller, M., Lange, B., Hayasaka, K., Lange, W., and Walther, H. (2004). Continuous generation of single photons with controlled waveform in an ion-trap cavity system. Nature 431, 1075–1078. doi:10.1038/nature02961

PubMed Abstract | CrossRef Full Text | Google Scholar

Kenfack, A., and Życzkowski, K. (2004). Negativity of the wigner function as an indicator of non-classicality. J. Opt. B Quantum Semiclass. Opt. 6, 396–404. doi:10.1088/1464-4266/6/10/003

CrossRef Full Text | Google Scholar

Kimble, H. (2008). The quantum internet. Nature 453, 1023–1030. doi:10.1038/nature07127

PubMed Abstract | CrossRef Full Text | Google Scholar

Kimble, H. J., Polzik, E., Rempe, G., and Thompson, R. (1992). “Structure and dynamics in cavity quantum electrodynamics,” in Quantum electron. Laser sci. Conf. (United States: Optica Publishing Group).QTuA2.

Google Scholar

Kiraz, A., Ehrl, M., Hellerer, T., Müstecaplıoğlu, O. E., Bräuchle, C., and Zumbusch, A. (2005). Indistinguishable photons from a single molecule. Phys. Rev. Lett. 94, 223602. doi:10.1103/PhysRevLett.94.223602

PubMed Abstract | CrossRef Full Text | Google Scholar

Kliger, D. S., Lewis, J. W., and Randall, C. E. (1990). “Chapter 4 - introduction to the jones calculus, mueller calculus, and poincaré sphere,” in Polarized light in optics and spectroscopy. Editors D. S. Kliger, J. W. Lewis, and C. E. Randall (Boston: Academic Press), 59–101. doi:10.1016/B978-0-08-057104-1.50007-7

CrossRef Full Text | Google Scholar

Kobel, P., Breyer, M., and Köhl, M. (2021). Deterministic spin-photon entanglement from a trapped ion in a fiber Fabry–Perot cavity. Quantum Inf. 7, 6. doi:10.1038/s41534-020-00338-2

CrossRef Full Text | Google Scholar

Kocher, C. A. (1971). Time correlations in the detection of successively emitted photons. Ann. Phys. (N. Y.) 65, 1–18. doi:10.1016/0003-4916(71)90159-X

CrossRef Full Text | Google Scholar

Kocher, C. A. (2024). Quantum entanglement of optical photons: the first experiment, 1964–67. Front. Quantum Sci. Technol. 3, 1451239. doi:10.3389/frqst.2024.1451239

CrossRef Full Text | Google Scholar

Kocher, C. A., and Commins, E. D. (1967). Polarization correlation of photons emitted in an atomic cascade. Phys. Rev. Lett. 18, 575–577. doi:10.1103/PhysRevLett.18.575

CrossRef Full Text | Google Scholar

Kolchin, P., Du, S., Belthangady, C., Yin, G. Y., and Harris, S. E. (2006). Generation of narrow-bandwidth paired photons: use of a single driving laser. Phys. Rev. Lett. 97, 113602. doi:10.1103/PhysRevLett.97.113602

PubMed Abstract | CrossRef Full Text | Google Scholar

Kosen, S. (2014). Quantum interference between single photons from a single atom and a cold atomic ensemble. Singapore: National University of Singapore. Ph.D. thesis.

Google Scholar

Kosionis, S. G., and Paspalakis, E. (2024). Pump-probe response and four-wave mixing in quantum dot exciton-biexciton–metal nanoparticle hybrid. Phys. E Low. Dimens. Syst. Nanostruct. 157, 115845. doi:10.1016/j.physe.2023.115845

CrossRef Full Text | Google Scholar

Kozlowski, W., and Wehner, S. (2019). “Towards large-scale quantum networks,” in Proceedings of the sixth annual ACM international conference on nanoscale computing and communication (New York, NY, USA: Association for Computing Machinery), 1–7. NANOCOM ’19. doi:10.1145/3345312.3345497

CrossRef Full Text | Google Scholar

Krutyanskiy, V., Galli, M., Krcmarsky, V., Baier, S., Fioretto, D. A., Pu, Y., et al. (2023). Entanglement of trapped-ion qubits separated by 230 meters. Phys. Rev. Lett. 130, 050803. doi:10.1103/PhysRevLett.130.050803

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuhn, A., Hennrich, M., Bondo, T., and Rempe, G. (1999). Controlled generation of single photons from a strongly coupled atom-cavity system. Appl. Phys. B 69, 373–377. doi:10.1007/s003400050822

CrossRef Full Text | Google Scholar

Kuhn, A., Hennrich, M., and Rempe, G. (2002). Deterministic single-photon source for distributed quantum networking. Phys. Rev. Lett. 89, 067901. doi:10.1103/PhysRevLett.89.067901

PubMed Abstract | CrossRef Full Text | Google Scholar

Kurtsiefer, C., Mayer, S., Zarda, P., and Weinfurter, H. (2000). Stable solid-state source of single photons. Phys. Rev. Lett. 85, 290–293. doi:10.1103/PhysRevLett.85.290

PubMed Abstract | CrossRef Full Text | Google Scholar

Law, C., and Kimble, H. (1997). Deterministic generation of a bit-stream of single-photon pulses. J. Mod. Opt. 44, 2067–2074. doi:10.1080/09500349708231869

CrossRef Full Text | Google Scholar

Leach, J., Jack, B., Romero, J., Jha, A. K., Yao, A. M., Franke-Arnold, S., et al. (2010). Quantum correlations in optical angle–orbital angular momentum variables. Science 329, 662–665. doi:10.1126/science.1190523

PubMed Abstract | CrossRef Full Text | Google Scholar

Legero, T., Wilk, T., Hennrich, M., Rempe, G., and Kuhn, A. (2004). Quantum beat of two single photons. Phys. Rev. Lett. 93, 070503. doi:10.1103/PhysRevLett.93.070503

PubMed Abstract | CrossRef Full Text | Google Scholar

Leggett, A. J., and Garg, A. (1985). Quantum mechanics versus macroscopic realism: is the flux there when nobody looks? Phys. Rev. Lett. 54, 857–860. doi:10.1103/PhysRevLett.54.857

PubMed Abstract | CrossRef Full Text | Google Scholar

Lettow, R., Rezus, Y. L. A., Renn, A., Zumofen, G., Ikonen, E., Götzinger, S., et al. (2010). Quantum interference of tunably indistinguishable photons from remote organic molecules. Phys. Rev. Lett. 104, 123605. doi:10.1103/PhysRevLett.104.123605

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., O’Faolain, L., Rey, I. H., and Krauss, T. F. (2011). Four-wave mixing in photonic crystal waveguides: slow light enhancement and limitations. Opt. Express 19, 4458–4463. doi:10.1364/OE.19.004458

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Z., Xie, Q., Zhang, Y., Zhang, H., Huang, C., and Shu, C. (2024). Four-wave mixing based spectral Talbot amplifier for programmable purification of optical frequency combs. Apl. Photonics 9, 036101. doi:10.1063/5.0190398

CrossRef Full Text | Google Scholar

Liao, K., Yan, H., He, J., Du, S., Zhang, Z.-M., and Zhu, S.-L. (2014). Subnatural-linewidth polarization-entangled photon pairs with controllable temporal length. Phys. Rev. Lett. 112, 243602. doi:10.1103/PhysRevLett.112.243602

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, J., Su, R., Wei, Y., Yao, B., Silva, S. F. C. d., Yu, Y., et al. (2019). A solid-state source of strongly entangled photon pairs with high brightness and indistinguishability. Nat. Nanotechnol. 14, 586–593. doi:10.1038/s41565-019-0435-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, T. (2020). The applications and challenges of quantum teleportation. J. Phys. Conf. Ser. 1634, 012089. doi:10.1088/1742-6596/1634/1/012089

CrossRef Full Text | Google Scholar

Lo, H.-K., Curty, M., and Qi, B. (2012). Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 108, 130503. doi:10.1103/PhysRevLett.108.130503

PubMed Abstract | CrossRef Full Text | Google Scholar

Lukin, M. D., Fleischhauer, M., Cote, R., Duan, L. M., Jaksch, D., Cirac, J. I., et al. (2001). Dipole blockade and quantum information processing in mesoscopic atomic ensembles. Phys. Rev. Lett. 87, 037901. doi:10.1103/PhysRevLett.87.037901

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, B., Yan, J., Jiang, Y., Li, S., Li, Y., Zhang, S., et al. (2023). Experimental realization of multimode nonlinear parametric amplification from cascading four-wave mixing of dressed atoms. Opt. Express 31, 6982–6995. doi:10.1364/OE.483374

PubMed Abstract | CrossRef Full Text | Google Scholar

Lvovsky, A. I., and Raymer, M. G. (2009). Continuous-variable optical quantum-state tomography. Rev. Mod. Phys. 81, 299–332. doi:10.1103/RevModPhys.81.299

CrossRef Full Text | Google Scholar

MacLean, J.-P. W., Donohue, J. M., and Resch, K. J. (2018). Direct characterization of ultrafast energy-time entangled photon pairs. Phys. Rev. Lett. 120, 053601. doi:10.1103/PhysRevLett.120.053601

PubMed Abstract | CrossRef Full Text | Google Scholar

Maiwald, R., Golla, A., Fischer, M., Bader, M., Heugel, S., Chalopin, B., et al. (2012). Collecting more than half the fluorescence photons from a single ion. Phys. Rev. A 86, 043431. doi:10.1103/PhysRevA.86.043431

CrossRef Full Text | Google Scholar

Mandel, L., and Wolf, E. (1995). Optical coherence and quantum optics. EBL-Schweitzer Cambridge University Press.

Google Scholar

Marino, A., Pooser, R., Boyer, V., and Lett, P. (2009). Tunable delay of einstein–podolsky–rosen entanglement. Nature 457, 859–862. doi:10.1038/nature07751

PubMed Abstract | CrossRef Full Text | Google Scholar

Matsukevich, D., Maunz, P., Moehring, D. L., Olmschenk, S., and Monroe, C. (2008). Bell inequality violation with two remote atomic qubits. Phys. Rev. Lett. 100, 150404. doi:10.1103/PhysRevLett.100.150404

PubMed Abstract | CrossRef Full Text | Google Scholar

Maunz, P., Moehring, D., Olmschenk, S., Younge, K. C., Matsukevich, D., and Monroe, C. (2007). Quantum interference of photon pairs from two remote trapped atomic ions. Nat. Phys. 3, 538–541. doi:10.1038/nphys644

CrossRef Full Text | Google Scholar

McKeever, J., Boca, A., Boozer, A. D., Miller, R., Buck, J. R., Kuzmich, A., et al. (2004). Deterministic generation of single photons from one atom trapped in a cavity. Science 303, 1992–1994. doi:10.1126/science.1095232

PubMed Abstract | CrossRef Full Text | Google Scholar

Mei, Y., Zhou, Y., Zhang, S., Li, J., Liao, K., Yan, H., et al. (2020). Einstein-podolsky-rosen energy-time entanglement of narrow-band biphotons. Phys. Rev. Lett. 124, 010509. doi:10.1103/PhysRevLett.124.010509

PubMed Abstract | CrossRef Full Text | Google Scholar

Meng, R.-R., Liu, X., Jin, M., Zhou, Z.-Q., Li, C.-F., and Guo, G.-C. (2024). Solid-state quantum nodes based on color centers and rare-earth ions coupled with fiber fabry-pérot microcavities. Chip 3, 100081. doi:10.1016/j.chip.2023.100081

CrossRef Full Text | Google Scholar

Metcalf, H., and Van der Straten, P. (1999). Laser Cooling and Trapping. Graduate texts in contemporary physics. Springer.

Google Scholar

Michaels, C. (2023). Group-IV colour centres in diamond for multi-photon entangled state generation. England: University of Cambridge Repository. Ph.D. thesis. doi:10.17863/CAM.101822

CrossRef Full Text | Google Scholar

Michler, M., Mattle, K., Weinfurter, H., and Zeilinger, A. (1996). Interferometric bell-state analysis. Phys. Rev. A 53, R1209–R1212. doi:10.1103/PhysRevA.53.R1209

PubMed Abstract | CrossRef Full Text | Google Scholar

Michler, P., Kiraz, A., Becher, C., Schoenfeld, W., Petroff, P., Zhang, L., et al. (2000). A quantum dot single-photon turnstile device. science 290, 2282–2285. doi:10.1126/science.290.5500.2282

PubMed Abstract | CrossRef Full Text | Google Scholar

Misra, B., and Sudarshan, E. C. G. (1977). The Zeno’s paradox in quantum theory. J. Math. Phys. 18, 756–763. doi:10.1063/1.523304

CrossRef Full Text | Google Scholar

Moehring, D. L., Maunz, P., Olmschenk, S., Younge, K. C., Matsukevich, D. N., Duan, L.-M., et al. (2007). Entanglement of single-atom quantum bits at a distance. Nature 449, 68–71. doi:10.1038/nature06118

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohammadnejad, S., Mahmoudi, A., and Arab, H. (2022). A new iii–v nanowire-quantum dot single photon source with improved purcell factor for quantum communication. Opt. Quant. Electron. 54, 220. doi:10.1007/s11082-022-03567-1

CrossRef Full Text | Google Scholar

Monat, C., Ebnali-Heidari, M., Grillet, C., Corcoran, B., Eggleton, B. J., White, T., et al. (2010). Four-wave mixing in slow light engineered silicon photonic crystal waveguides. Opt. express 18, 22915–22927. doi:10.1364/OE.18.022915

PubMed Abstract | CrossRef Full Text | Google Scholar

Mosley, P. J., Lundeen, J. S., Smith, B. J., Wasylczyk, P., U’Ren, A. B., Silberhorn, C., et al. (2008). Heralded generation of ultrafast single photons in pure quantum states. Phys. Rev. Lett. 100, 133601. doi:10.1103/PhysRevLett.100.133601

PubMed Abstract | CrossRef Full Text | Google Scholar

Müller, P., and Eschner, J. (2014). Single calcium-40 ion as quantum memory for photon polarization: a case study. App. Phys. B 114, 303–306. doi:10.1007/s00340-013-5681-1

CrossRef Full Text | Google Scholar

Müller, P., Tentrup, T., Bienert, M., Morigi, G., and Eschner, J. (2017). Spectral properties of single photons from quantum emitters. Phys. Rev. A 96, 023861. doi:10.1103/PhysRevA.96.023861

CrossRef Full Text | Google Scholar

Müller, P. C. (2021). Raman scattering of single photons and its use for quantum networks and high-precision measurements. Germany: Saarland University. Ph.D. thesis. doi:10.22028/D291-35347

CrossRef Full Text | Google Scholar

Munro, W. J., Azuma, K., Tamaki, K., and Nemoto, K. (2015). Inside quantum repeaters. IEEE J. Sel. Top. Quantum Electron 21, 78–90. doi:10.1109/JSTQE.2015.2392076

CrossRef Full Text | Google Scholar

Nadlinger, D. P., Drmota, P., Nichol, B. C., Araneda, G., Main, D., Srinivas, R., et al. (2022). Experimental quantum key distribution certified by bell’s theorem. Nature 607, 682–686. doi:10.1038/s41586-022-04941-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Nath, P. P., Saha, D., Home, D., and Sinha, U. (2024). Single-system-based generation of certified randomness using leggett-garg inequality. Phys. Rev. Lett. 133, 020802. doi:10.1103/PhysRevLett.133.020802

PubMed Abstract | CrossRef Full Text | Google Scholar

Negre, A., Mathevet, R., Chalopin, B., and Massenot, S. (2023). Unexpected optimal measurement protocols in Bell’s inequality violation experiments. Am. J. Phys. 91, 64–73. doi:10.1119/5.0102516

CrossRef Full Text | Google Scholar

Neu, E., and Becher, C. (2014). “6 - diamond-based single-photon sources and their application in quantum key distribution,” in Quantum information processing with diamond. Editors S. Prawer, and I. Aharonovich (United Kingdom: Woodhead Publishing Ltd.), 127–159. doi:10.1533/9780857096685.2.127

CrossRef Full Text | Google Scholar

Neumann, S. P., Buchner, A., Bulla, L., Bohmann, M., and Ursin, R. (2022). Continuous entanglement distribution over a transnational 248 km fiber link. Nat. Commun. 13, 6134. doi:10.1038/s41467-022-33919-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Nielsen, D., and Chuang, S. L. (2010). Four-wave mixing and wavelength conversion in quantum dots. Phys. Rev. B 81, 035305. doi:10.1103/PhysRevB.81.035305

CrossRef Full Text | Google Scholar

Obšil, P., Lachman, L., Pham, T., Lešundák, A., Hucl, V., Čížek, M., et al. (2018). Nonclassical light from large ensembles of trapped ions. Phys. Rev. Lett. 120, 253602. doi:10.1103/PhysRevLett.120.253602

PubMed Abstract | CrossRef Full Text | Google Scholar

Olmschenk, S., Matsukevich, D., Maunz, P., Hayes, D., Duan, L.-M., and Monroe, C. (2009). Quantum teleportation between distant matter qubits. Science 323, 486–489. doi:10.1126/science.1167209

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, J., Bae, J., Kim, H., and Moon, H. S. (2021). Direct generation of polarization-entangled photons from warm atomic ensemble. Appl. Phys. Lett. 119, 074001. doi:10.1063/5.0045567

CrossRef Full Text | Google Scholar

Park, J., Kim, H., and Moon, H. S. (2019). Polarization-entangled photons from a warm atomic ensemble using a sagnac interferometer. Phys. Rev. Lett. 122, 143601. doi:10.1103/PhysRevLett.122.143601

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, J., and Moon, H. S. (2022). Generation of a bright four-photon entangled state from a warm atomic ensemble via inherent polarization entanglement. Appl. Phys. Lett. 120. 0240011–7. doi:10.1063/5.0076851

CrossRef Full Text | Google Scholar

Patel, R. B., Bennett, A. J., Farrer, I., Nicoll, C. A., Ritchie, D. A., and Shields, A. J. (2010). Two-photon interference of the emission from electrically tunable remote quantum dots. Nat. Phot. 4, 632–635. doi:10.1038/nphoton.2010.161

CrossRef Full Text | Google Scholar

Podhora, L., Obšil, P., Straka, I., Ježek, M., and Slodička, L. (2017). Nonclassical photon pairs from warm atomic vapor using a single driving laser. Opt. Express 25, 31230–31238. doi:10.1364/OE.25.031230

PubMed Abstract | CrossRef Full Text | Google Scholar

Pooser, R. C., Marino, A. M., Boyer, V., Jones, K. M., and Lett, P. D. (2009). Quantum correlated light beams from non-degenerate four-wave mixing in an atomic vapor: the D1 and D2 lines of ^{^}85Rb and ^{^}87Rb. Opt. Express 17, 16722–16730. doi:10.1364/OE.17.016722

PubMed Abstract | CrossRef Full Text | Google Scholar

Purcell, E. M. (1995). “Spontaneous emission probabilities at radio frequencies,” in Confined electrons and photons: new physics and applications (Springer), 839. doi:10.1007/978-1-4615-1963-8_40

CrossRef Full Text | Google Scholar

Raab, E. L., Prentiss, M., Cable, A., Chu, S., and Pritchard, D. E. (1987). Trapping of neutral sodium atoms with radiation pressure. Phys. Rev. Lett. 59, 2631–2634. doi:10.1103/PhysRevLett.59.2631

PubMed Abstract | CrossRef Full Text | Google Scholar

Rabi, I. I., Ramsey, N. F., and Schwinger, J. (1954). Use of rotating coordinates in magnetic resonance problems. Rev. Mod. Phys. 26, 167–171. doi:10.1103/RevModPhys.26.167

CrossRef Full Text | Google Scholar

Raman, C. V., and Krishnan, K. S. (1928). A new type of secondary radiation. Nature 121, 501–502. doi:10.1038/121501c0

CrossRef Full Text | Google Scholar

Reid, M. D., and Walls, D. F. (1986). Violations of classical inequalities in quantum optics. Phys. Rev. A 34, 1260–1276. doi:10.1103/PhysRevA.34.1260

PubMed Abstract | CrossRef Full Text | Google Scholar

Reimer, M. E., and Cher, C. (2019). The quest for a perfect single-photon source. Nat. Phot. 13, 734–736. doi:10.1038/s41566-019-0544-x

CrossRef Full Text | Google Scholar

Ren, J.-G., Xu, P., Yong, H.-L., Zhang, L., Liao, S.-K., Yin, J., et al. (2017). Ground-to-satellite quantum teleportation. Nature 549, 70–73. doi:10.1038/nature23675

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, Y., Wang, X., Lou, Y., Liu, S., Zhong, Y., and Jing, J. (2022). Violation of high-dimensional bell inequality using narrowband orbital-angular-momentum entanglement from warm atomic vapor. Phys. Rev. A 105, 013721. doi:10.1103/PhysRevA.105.013721

CrossRef Full Text | Google Scholar

Reyes, R., Nakazato, T., Imaike, N., Matsuda, K., Tsurumoto, K., Sekiguchi, Y., et al. (2022). Complete Bell state measurement of diamond nuclear spins under a complete spatial symmetry at zero magnetic field. Appl. Phys. Lett. 120, 194002. doi:10.1063/5.0088155

CrossRef Full Text | Google Scholar

Ribordy, G., Brendel, J., Gautier, J.-D., Gisin, N., and Zbinden, H. (2000). Long-distance entanglement-based quantum key distribution. Phys. Rev. A 63, 012309. doi:10.1103/PhysRevA.63.012309

CrossRef Full Text | Google Scholar

Riebe, M., Häffner, H., Roos, C. F., Hänsel, W., Benhelm, J., Lancaster, G. P., et al. (2004). Deterministic quantum teleportation with atoms. Nature 429, 734–737. doi:10.1038/nature02570

PubMed Abstract | CrossRef Full Text | Google Scholar

Riedmatten, H. d., Marcikic, I., Tittel, W., Zbinden, H., and Gisin, N. (2003). Quantum interference with photon pairs created in spatially separated sources. Phys. Rev. A 67, 022301. doi:10.1103/PhysRevA.67.022301

CrossRef Full Text | Google Scholar

Ripka, F., Kübler, H., Löw, R., and Pfau, T. (2018). RETRACTED: a room-temperature single-photon source based on strongly interacting Rydberg atoms. Science 362, 446–449. doi:10.1126/science.aau1949

PubMed Abstract | CrossRef Full Text | Google Scholar

Rivest, R. L., Shamir, A., and Adleman, L. (1978). A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 21, 120–126. doi:10.1145/359340.359342

CrossRef Full Text | Google Scholar

Ruf, M., Wan, N. H., Choi, H., Englund, D., and Hanson, R. (2021). Quantum networks based on color centers in diamond. J. Appl. Phys. 130, 070901. doi:10.1063/5.0056534

CrossRef Full Text | Google Scholar

Saffman, M., Walker, T. G., and Mølmer, K. (2010). Quantum information with rydberg atoms. Rev. Mod. Phys. 82, 2313–2363. doi:10.1103/RevModPhys.82.2313

CrossRef Full Text | Google Scholar

Sangouard, N., Simon, C., de Riedmatten, H., and Gisin, N. (2011). Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33–80. doi:10.1103/RevModPhys.83.33

CrossRef Full Text | Google Scholar

Santori, C., Fattal, D., Vučković, J., Solomon, G. S., and Yamamoto, Y. (2002). Indistinguishable photons from a single-photon device. Nature 419, 594–597. doi:10.1038/nature01086

PubMed Abstract | CrossRef Full Text | Google Scholar

Schlosshauer, M. (2019). Quantum decoherence. Phys. Rep. 831, 1–57. doi:10.1016/j.physrep.2019.10.001

CrossRef Full Text | Google Scholar

Schubert, M., Siemers, I., Blatt, R., Neuhauser, W., and Toschek, P. (1992). Photon antibunching and non-poissonian fluorescence of a single three-level ion. Phys. Rev. Lett. 68, 3016–3019. doi:10.1103/PhysRevLett.68.3016

PubMed Abstract | CrossRef Full Text | Google Scholar

Schupp, J., Krcmarsky, V., Krutyanskiy, V., Meraner, M., Northup, T., and Lanyon, B. (2021). Interface between trapped-ion qubits and traveling photons with close-to-optimal efficiency. PRX Quantum 2, 020331. doi:10.1103/PRXQuantum.2.020331

CrossRef Full Text | Google Scholar

Shahriar, M., and Hemmer, P. (1998). Generation of squeezed states and twin beams via non-degenerate four-wave mixing in a λ system. Opt. Commun. 158, 273–286. doi:10.1016/S0030-4018(98)00528-8

CrossRef Full Text | Google Scholar

Sharping, J. E., Fiorentino, M., Coker, A., Kumar, P., and Windeler, R. S. (2001). Four-wave mixing in microstructure fiber. Opt. Lett. 26, 1048–1050. doi:10.1364/OL.26.001048

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, H. Z., Chen, Y., Luan, T. Z., and Yi, X. X. (2023). Multiple single-photon generations in three-level atoms coupled to a cavity with non-markovian effects. Phys. Rev. A 107, 053705. doi:10.1103/PhysRevA.107.053705

CrossRef Full Text | Google Scholar

Shen, H. Z., Qin, M., and Yi, X. X. (2013). Single-photon storing in coupled non-markovian atom-cavity system. Phys. Rev. A 88, 033835. doi:10.1103/PhysRevA.88.033835

CrossRef Full Text | Google Scholar

Shen, H. Z., Wang, Q., Wang, J., and Yi, X. X. (2020). Nonreciprocal unconventional photon blockade in a driven dissipative cavity with parametric amplification. Phys. Rev. A 101, 013826. doi:10.1103/PhysRevA.101.013826

CrossRef Full Text | Google Scholar

Shen, H. Z., Wang, Q., and Yi, X. X. (2022). Dispersive readout with non-markovian environments. Phys. Rev. A 105, 023707. doi:10.1103/PhysRevA.105.023707

CrossRef Full Text | Google Scholar

Shen, H. Z., Zhou, Y. H., and Yi, X. X. (2014). Quantum optical diode with semiconductor microcavities. Phys. Rev. A 90, 023849. doi:10.1103/PhysRevA.90.023849

CrossRef Full Text | Google Scholar

Shen, H. Z., Zhou, Y. H., and Yi, X. X. (2015). Tunable photon blockade in coupled semiconductor cavities. Phys. Rev. A 91, 063808. doi:10.1103/PhysRevA.91.063808

CrossRef Full Text | Google Scholar

Sherson, J. F., Krauter, H., Olsson, R. K., Julsgaard, B., Hammerer, K., Cirac, I., et al. (2006). Quantum teleportation between light and matter. Nature 443, 557–560. doi:10.1038/nature05136

PubMed Abstract | CrossRef Full Text | Google Scholar

Shore, B. W. (2017). Picturing stimulated Raman adiabatic passage: a stirap tutorial. Adv. Opt. Phot. 9, 563–719. doi:10.1364/AOP.9.000563

CrossRef Full Text | Google Scholar

Short, A. J., Popescu, S., and Gisin, N. (2006). Entanglement swapping for generalized nonlocal correlations. Phys. Rev. A 73, 012101. doi:10.1103/PhysRevA.73.012101

CrossRef Full Text | Google Scholar

Short, R., and Mandel, L. (1983). Observation of sub-poissonian photon statistics. Phys. Rev. Lett. 51, 384–387. doi:10.1103/PhysRevLett.51.384

CrossRef Full Text | Google Scholar

Shrikant, U., and Mandayam, P. (2023). Quantum non-markovianity: overview and recent developments. Front. Quantum Sci. Technol. 2, 1134583. doi:10.3389/frqst.2023.1134583

CrossRef Full Text | Google Scholar

Shu, C., Chen, P., Chow, T. K. A., Zhu, L., Xiao, Y., Loy, M., et al. (2016). Subnatural-linewidth biphotons from a Doppler-broadened hot atomic vapour cell. Nat. Commun. 7, 12783. doi:10.1038/ncomms12783

PubMed Abstract | CrossRef Full Text | Google Scholar

Shu, G., Kurz, N., Dietrich, M., and Blinov, B. (2010). Efficient fluorescence collection from trapped ions with an integrated spherical mirror. Phys. Rev. A 81, 042321. doi:10.1103/PhysRevA.81.042321

CrossRef Full Text | Google Scholar

Srivathsan, B. (2014). Heralded single photons for efficient interaction with single atoms. Singapore: National University of Singapore. Ph.D. thesis.

Google Scholar

Srivathsan, B., Gulati, G. K., Chng, B., Maslennikov, G., Matsukevich, D., and Kurtsiefer, C. (2013). Narrow band source of transform-limited photon pairs via four-wave mixing in a cold atomic ensemble. Phys. Rev. Lett. 111, 123602. doi:10.1103/PhysRevLett.111.123602

PubMed Abstract | CrossRef Full Text | Google Scholar

Steiner, M., Meyer, H. M., Deutsch, C., Reichel, J., and Köhl, M. (2013). Single ion coupled to an optical fiber cavity. Phys. Rev. Lett. 110, 043003. doi:10.1103/PhysRevLett.110.043003

PubMed Abstract | CrossRef Full Text | Google Scholar

Streed, E. W., Norton, B. G., Jechow, A., Weinhold, T. J., and Kielpinski, D. (2011). Imaging of trapped ions with a microfabricated optic for quantum information processing. Phys. Rev. Lett. 106, 010502. doi:10.1103/PhysRevLett.106.010502

PubMed Abstract | CrossRef Full Text | Google Scholar

Stute, A., Casabone, B., Brandstätter, B., Habicher, D., Barros, H., Schmidt, P., et al. (2012a). Toward an ion-photon quantum interface in an optical cavity. Appl. Phys. B 107, 1145–1157. doi:10.1007/s00340-011-4861-0

CrossRef Full Text | Google Scholar

Stute, A., Casabone, B., Schindler, P., Monz, T., Schmidt, P., Brandstätter, B., et al. (2012b). Tunable ion–photon entanglement in an optical cavity. Nature 485, 482–485. doi:10.1038/nature11120

PubMed Abstract | CrossRef Full Text | Google Scholar

Thiel, C., Böttger, T., and Cone, R. (2011). Rare-earth-doped materials for applications in quantum information storage and signal processing. J. Lumin. 131, 353–361. doi:10.1016/j.jlumin.2010.12.015

CrossRef Full Text | Google Scholar

Thompson, J. K., Simon, J., Loh, H., and Vuletić, V. (2006). A high-brightness source of narrowband, identical-photon pairs. Science 313, 74–77. doi:10.1126/science.1127676

PubMed Abstract | CrossRef Full Text | Google Scholar

Thompson, J. R., and Roy, R. (1991). Nonlinear dynamics of multiple four-wave mixing processes in a single-mode fiber. Phys. Rev. A 43, 4987–4996. doi:10.1103/PhysRevA.43.4987

PubMed Abstract | CrossRef Full Text | Google Scholar

Tolazzi, K. N., Wang, B., Ianzano, C., Neumeier, J., Villas-Boas, C. J., and Rempe, G. (2021). Continuous quantum light from a dark atom. Commun. Phys. 4, 57. doi:10.1038/s42005-021-00559-7

CrossRef Full Text | Google Scholar

Toninelli, C., Gerhardt, I., Clark, A., Reserbat-Plantey, A., Götzinger, S., Ristanović, Z., et al. (2021). Single organic molecules for photonic quantum technologies. Nat. Mater. 20, 1615–1628. doi:10.1038/s41563-021-00987-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Tóth, G., and Gühne, O. (2005a). Detecting genuine multipartite entanglement with two local measurements. Phys. Rev. Lett. 94, 060501. doi:10.1103/PhysRevLett.94.060501

PubMed Abstract | CrossRef Full Text | Google Scholar

Tóth, G., and Gühne, O. (2005b). Entanglement detection in the stabilizer formalism. Phys. Rev. A 72, 022340. doi:10.1103/PhysRevA.72.022340

CrossRef Full Text | Google Scholar

Urban, E., Johnson, T. A., Henage, T., Isenhower, L., Yavuz, D., Walker, T., et al. (2009). Observation of rydberg blockade between two atoms. Nat. Phys. 5, 110–114. doi:10.1038/nphys1178

CrossRef Full Text | Google Scholar

Vaidman, L. (1994). Teleportation of quantum states. Phys. Rev. A 49, 1473–1476. doi:10.1103/PhysRevA.49.1473

PubMed Abstract | CrossRef Full Text | Google Scholar

van Leent, T., Bock, M., Fertig, F., Garthoff, R., Eppelt, S., Zhou, Y., et al. (2022). Entangling single atoms over 33 km telecom fibre. Nature 607, 69–73. doi:10.1038/s41586-022-04764-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Villas-Boas, C. J., Tolazzi, K. N., Wang, B., Ianzano, C., and Rempe, G. (2020). Continuous generation of quantum light from a single ground-state atom in an optical cavity. Phys. Rev. Lett. 124, 093603. doi:10.1103/PhysRevLett.124.093603

PubMed Abstract | CrossRef Full Text | Google Scholar

Vitanov, N. V., Rangelov, A. A., Shore, B. W., and Bergmann, K. (2017). Stimulated Raman adiabatic passage in physics, chemistry, and beyond. Rev. Mod. Phys. 89, 015006. doi:10.1103/RevModPhys.89.015006

CrossRef Full Text | Google Scholar

Volz, J. (2006). Atom-photon entanglement. Germany: Ludwig-Maximilians-Universität München. Ph.D. thesis. doi:10.5282/edoc.5635

CrossRef Full Text | Google Scholar

Volz, J., Weber, M., Schlenk, D., Rosenfeld, W., Vrana, J., Saucke, K., et al. (2006). Observation of entanglement of a single photon with a trapped atom. Phys. Rev. Lett. 96, 030404. doi:10.1103/PhysRevLett.96.030404

PubMed Abstract | CrossRef Full Text | Google Scholar

Walker, T., Kashanian, S. V., Ward, T., and Keller, M. (2020). Improving the indistinguishability of single photons from an ion-cavity system. Phys. Rev. A 102, 032616. doi:10.1103/PhysRevA.102.032616

CrossRef Full Text | Google Scholar

Walls, D., and Milburn, G. (2008). Quantum optics. Springer Berlin Heidelberg.

Google Scholar

Wang, C., Lee, C.-H., Kim, Y., and Kim, Y.-H. (2020). Generation of hyper-entangled photons in a hot atomic vapor. Opt. Lett. 45, 1802–1805. doi:10.1364/OL.384567

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Zeng, Q., Ma, H., and Yuan, Z. (2024). Progress on chip-based spontaneous four-wave mixing quantum light sources. Adv. Devices Instrum. 5, 0032. doi:10.34133/adi.0032

CrossRef Full Text | Google Scholar

Wang, Y.-S., Li, K.-B., Chang, C.-F., Lin, T.-W., Li, J.-Q., Hsiao, S.-S., et al. (2022). Temporally ultralong biphotons with a linewidth of 50 kHz. Apl. Photonics 7, 126102. doi:10.1063/5.0102393

CrossRef Full Text | Google Scholar

Wei, S.-H., Jing, B., Zhang, X.-Y., Liao, J.-Y., Yuan, C.-Z., Fan, B.-Y., et al. (2022). Towards real-world quantum networks: a review. Laser Photonics Rev. 16, 2100219. doi:10.1002/lpor.202100219

CrossRef Full Text | Google Scholar

Welte, S., Thomas, P., Hartung, L., Daiss, S., Langenfeld, S., Morin, O., et al. (2021). A nondestructive bell-state measurement on two distant atomic qubits. Nat. Phot. 15, 504–509. doi:10.1038/s41566-021-00802-1

CrossRef Full Text | Google Scholar

Wen, J., and Rubin, M. H. (2006). Transverse effects in paired-photon generation via an electromagnetically induced transparency medium. i. perturbation theory. Phys. Rev. A 74, 023808. doi:10.1103/PhysRevA.74.023808

CrossRef Full Text | Google Scholar

Wilk, T., Specht, H. P., Webster, S. C., Rempe, G., and Kuhn, A. (2007a). Scheme for generating a sequence of single photons of alternating polarization. J. Mod. Opt. 54, 1569–1580. doi:10.1080/09500340600736777

CrossRef Full Text | Google Scholar

Wilk, T., Webster, S. C., Kuhn, A., and Rempe, G. (2007b). Single-atom single-photon quantum interface. Science 317, 488–490. doi:10.1126/science.1143835

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilk, T., Webster, S. C., Specht, H. P., Rempe, G., and Kuhn, A. (2007c). Polarization-controlled single photons. Phys. Rev. Lett. 98, 063601. doi:10.1103/PhysRevLett.98.063601

PubMed Abstract | CrossRef Full Text | Google Scholar

Woolley, M. J., Lang, C., Eichler, C., Wallraff, A., and Blais, A. (2013). Signatures of hong–ou–mandel interference at microwave frequencies. New J. Phys. 15, 105025–105044. doi:10.1088/1367-2630/15/10/105025

CrossRef Full Text | Google Scholar

Wootters, W., and Zurek, W. H. (1982). A single quantum cannot be cloned. Nature 299, 802–803. doi:10.1038/299802a0

CrossRef Full Text | Google Scholar

Wootters, W. K. (1998). Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245–2248. doi:10.1103/PhysRevLett.80.2245

CrossRef Full Text | Google Scholar

Xiao-Song, L., Qun-Feng, C., Bao-Sen, S., and Guang-Can, G. (2009). Generation of a non-classical correlated photon pair via spontaneous four-wave mixing in a cold atomic ensemble. Chin. Phys. Lett. 26, 064204. doi:10.1088/0256-307X/26/6/064204

CrossRef Full Text | Google Scholar

Xu, F., Ma, X., Zhang, Q., Lo, H.-K., and Pan, J.-W. (2020). Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 92, 025002. doi:10.1103/RevModPhys.92.025002

CrossRef Full Text | Google Scholar

Yan, H., Zhang, S., Chen, J. F., Loy, M. M. T., Wong, G. K. L., and Du, S. (2011). Generation of narrow-band hyperentangled nondegenerate paired photons. Phys. Rev. Lett. 106, 033601. doi:10.1103/PhysRevLett.106.033601

PubMed Abstract | CrossRef Full Text | Google Scholar

Yariv, A., and Pepper, D. M. (1977). Amplified reflection, phase conjugation, and oscillation in degenerate four-wave mixing. Opt. Lett. 1, 16–18. doi:10.1364/OL.1.000016

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, Y. (2021). Advancements in applications of quantum entanglement. J. Phys.Conf. Ser. 2012, 012113. doi:10.1088/1742-6596/2012/1/012113

CrossRef Full Text | Google Scholar

Zeng, Y.-X., Gebremariam, T., Ding, M.-S., and Li, C. (2019). The influence of non-markovian characters on quantum adiabatic evolution. Ann. Phys. 531, 1800234. doi:10.1002/andp.201800234

CrossRef Full Text | Google Scholar

Zhang, C.-X., Wu, D., Cui, P.-W., Ma, J.-C., Wang, Y., and An, J.-M. (2023). Research progress in quantum key distribution. Chin. Phys. B 32, 124207. doi:10.1088/1674-1056/acfd16

CrossRef Full Text | Google Scholar

Zhang, S., Chen, J. F., Liu, C., Zhou, S., Loy, M. M. T., Wong, G. K. L., et al. (2012). A dark-line two-dimensional magneto-optical trap of ⁸⁵Rb atoms with high optical depth. Rev. Sci. Instrum. 83, 073102. doi:10.1063/1.4732818

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, W., van Leent, T., Redeker, K., Garthoff, R., Schwonnek, R., Fertig, F., et al. (2022a). A device-independent quantum key distribution system for distant users. Nature 607, 687–691. doi:10.1038/s41586-022-04891-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, W.-H., Peng, J.-Y., Li, E.-Z., Ye, Y.-H., Zeng, L., Dong, M.-X., et al. (2022b). Detection of infrared light through stimulated four-wave mixing process. Front. Quantum Sci. Technol. 1, 984638 01–07. doi:10.3389/frqst.2022.984638

CrossRef Full Text | Google Scholar

Zhang, Y., Man, Z., and Xia, Y. (2009). Non-markovian effects on entanglement dynamics in lossy cavities. Eur. Phys. J. D. 55, 173–179. doi:10.1140/epjd/e2009-00226-2

CrossRef Full Text | Google Scholar

Zhang, Z., Wen, F., Che, J., Zhang, D., Li, C., Zhang, Y., et al. (2015). Dressed gain from the parametrically amplified four-wave mixing process in an atomic vapor. Sci. Rep. 5, 15058. doi:10.1038/srep15058

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, B., Chen, Y. A., Bao, X. H., Straßel, T., Chuu, C. S., Jin, X., et al. (2008a). A millisecond quantum memory for scalable quantum networks. Nat. Phys. 5, 95–99. doi:10.1038/nphys1153

CrossRef Full Text | Google Scholar

Zhao, L., Guo, X., Liu, C., Sun, Y., Loy, M. M. T., and Du, S. (2014). Photon pairs with coherence time exceeding 1  μs. Optica 1, 84–88. doi:10.1364/OPTICA.1.000084

CrossRef Full Text | Google Scholar

Zhao, L., Su, Y., and Du, S. (2016). Narrowband biphoton generation in the group delay regime. Phys. Rev. A 93, 033815. doi:10.1103/PhysRevA.93.033815

CrossRef Full Text | Google Scholar

Zhao, R., Dudin, Y. O., Jenkins, S. D., Campbell, C. J., Matsukevich, D. N., Kennedy, T. A. B., et al. (2008b). Long-lived quantum memory. Nat. Phys. 5, 100–104. doi:10.1038/nphys1152

CrossRef Full Text | Google Scholar

Zhou, Y. H., Shen, H. Z., and Yi, X. X. (2015). Unconventional photon blockade with second-order nonlinearity. Phys. Rev. A 92, 023838. doi:10.1103/PhysRevA.92.023838

CrossRef Full Text | Google Scholar

Zugenmaier, M., Dideriksen, K. B., Sørensen, A. S., Albrecht, B., and Polzik, E. S. (2018). Long-lived non-classical correlations towards quantum communication at room temperature. Commun. Phys. 1, 76. doi:10.1038/s42005-018-0080-x

CrossRef Full Text | Google Scholar

Żukowski, M., Zeilinger, A., Horne, M. A., and Ekert, A. K. (1993). “event-ready-detectors” bell experiment via entanglement swapping. Phys. Rev. Lett. 71, 4287–4290. doi:10.1103/PhysRevLett.71.4287

PubMed Abstract | CrossRef Full Text | Google Scholar