- 1State Key Laboratory of Coal Conversion, Institute of Coal Chemistry, Chinese Academy of Sciences, Taiyuan, Shanxi, China
- 2SynCat@Beijing, Synfuels China Co., Ltd., Beijing, China
- 3Hong Kong Quantum AI Laboratory Ltd., Hong Kong Science Park, Hong Kong, Hong Kong SAR, China
- 4Synfuels China Co., Ltd., Beijing, China
- 5Department of Chemistry, The University of Hong Kong, Pokfulam, Hong Kong SAR, China
Over the past decade many researchers have applied machine learning algorithms with computational chemistry and materials science tools to explore properties of catalysts. There is a rapid increase in publications demonstrating the use of machine learning for rational catalyst design. In our perspective, targeted tools for rational catalyst design will continue to make significant contributions. However, the community should focus on developing high-throughput simulation tools that utilize molecular dynamics capabilities for thorough exploration of the complex potential energy surfaces that exist, particularly in heterogeneous catalysis. Catalyst-specific databases should be developed to contain enough data to represent the complex multi-dimensional space that defines structure-function relationships. Machine learning tools will continue to impact rational catalyst design; however, we believe that more sophisticated pattern recognition algorithms would yield better understanding of structure-function relationships for heterogeneous catalysis.
Introduction
The “magic” of catalysts is in the ability of these materials to transform the chemical world around us through a complex collective behavior. The rate of a chemical reaction is determined by a kinetic process that describes how molecules react via intermediates to an eventual product. A catalyst accelerates the rate of a reaction without being consumed in the process. There are several factors that enable a catalyst to perform its role; some factors are microscopic or mesoscopic in nature which are defined by material processing and some factors are macroscopic in nature as defined by industrial processing. Hence, the catalysts’ ability to energetically reduce the overall barrier for a reaction cannot be defined by a single factor, or feature, but rather many features working collectively to enable chemical conversion via an exceptionally complex route. From a fundamental viewpoint, the researcher struggles with trying to understand structure-function relationships of catalysts, and from an industrial viewpoint, the engineer struggles with finding industrial processes that maximize efficiency. Similarly, there are significant challenges to continuously find “green” or earth-abundant catalysts operating at lower temperature environments without reducing turn-over frequency, selectivity, or yield (Roger et al., 2017; Schneider and Thomas, 2020).
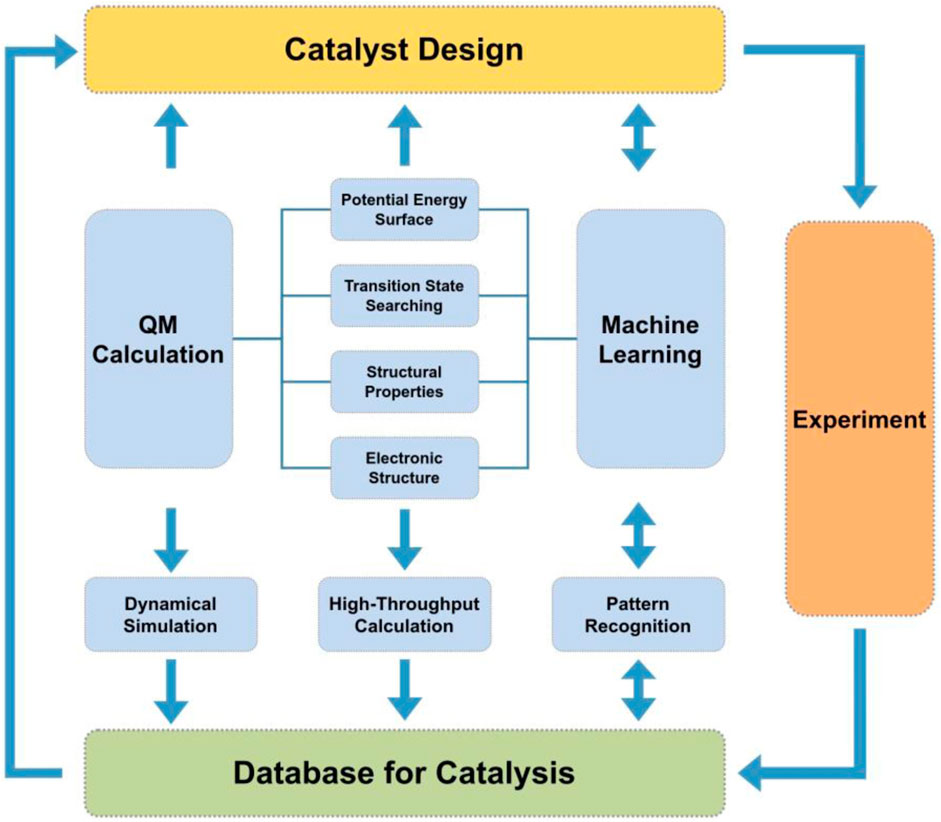
The role of computational chemistry and materials science calculations in catalysis is to find correlations between microscopic structure and performance in the hopes of understanding features that lead to rational catalyst design. Catalytic reactions mainly occur at some special sites on the surface, called active centers. From the microscopic viewpoint, the catalyst structure determines the electronic structure and reactivity of these active centers. The performance of the catalyst encompasses the reactivity, selectivity, and stability as well as other factors that define the structure-function relationships targeted to a specific reaction. Evaluation of structure-function relationships require collecting sets of features that describe a catalyst’s structure with its corresponding properties and further examining correlations between these features and performance (Norskov et al., 2009; Vojvodic and Nørskov, 2015). Structure-related features are based on structural parameters such as element types and geometry (bond lengths, angles, and dihedrals). Bond valence descriptions, proposed by Pauling, are also structure based as these features solely depend on element type and bond length (Ma et al., 2020a). Property-related features are based on the properties of a particular catalyst, for example, electronic structure, densities, electrostatic potentials, as well as the energetics of the reaction profiles (Li et al., 2017; Giordano et al., 2022). Computational chemistry and materials science calculations are an extremely useful tool for calculating the catalyst’s properties and evaluating property-related features. In the world of machine learning finally meets quantum chemistry in catalysis (see Figure 1) the interface between structure and functions is complex in that there are many iterations between structure properties, predicted function from machine learning algorithms, and the influence on reactivity and selectivity of the catalyst.
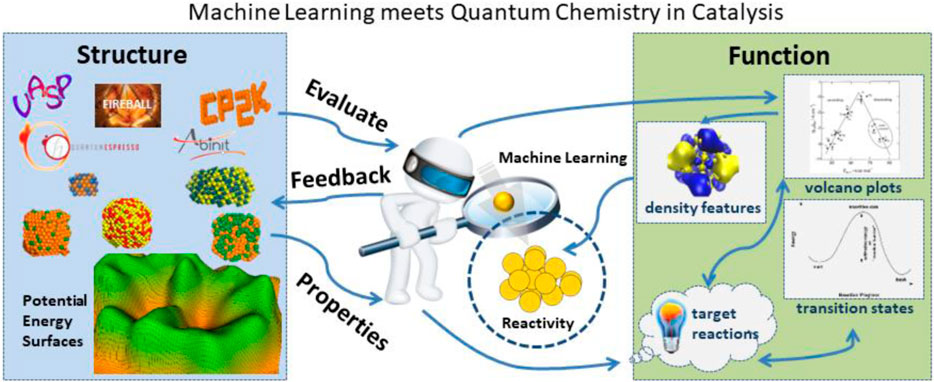
FIGURE 1. Future machine learning projects must be able to evaluate many different aspects of material properties from the underlying potential energy surfaces. The corresponding evaluation of reactivity must include understanding many underlying functional properties of the catalyst.
Quantum chemistry contributions to catalysis
Computational chemistry and materials science calculations for catalysts are roughly grouped into two classes–calculations of structural properties and calculations of energy profiles to evaluate selectivity/reactivity function. Both are dependent on the potential energy surface. The potential energy surface and hence, the corresponding electronic structure plays a central role for the structure of the catalysts just as in any other computational chemistry and materials science exploration. The potential energy surface is multi-dimensional information that will offer many details about how reactants and products will bind to the catalysts and define a catalyst’s selectivity and reactivity. For heterogeneous catalysts, the potential energy surfaces are largely dependent on surface changes due to the environmental conditions, the stoichiometry of the catalyst, and the morphology of the catalyst which is most certainly affected by the substrate where the catalysts are deposited. Properties based on the electronic structure include the very popular d-band center theory, Fermi softness, Fukui functions, to name a few, all which depend significantly on the catalyst structure and the corresponding electronic structure and potential energy surface. Calculation of catalyst’s structures should thereby primarily focus on the surface properties, particularly the defect or interfacial sites or undercoordinated sites which are highly reactive.
Computational models should incorporate hundreds, if not thousands, of atoms to reasonably probe physically and chemically meaningful active sites. The calculation of a catalyst for exploring its corresponding potential energy surface is therefore quite time consuming. Developing efficient and accurate computational methodologies that pertain to more relevant computational models (i.e., scale to 1000s of atoms) is an urgent prospect for the catalyst community. Many computational chemistry and materials science tools based on density functional theory exist. One such tool developed by Lewis et al. is the efficient FIREBALL method, a standard density functional code based on pseudo-potentials and a numerical local-orbital basis set (Lewis et al., 2011). An important feature of FIREBALL is the flexibility of constructing real-space-based localized basis functions to take advantage of fundamental chemistry in atomic bonding. Over the previous years, Lewis et al. has invested significant time and effort to develop high-throughput and machine-learning algorithms for heterogenous catalysts (Haycock et al., 2014a; Haycock et al., 2014b; Wang et al., 2015; Ranasingha et al., 2016; Wang et al., 2016; Senty et al., 2017; Panapitiya et al., 2018; Tavadze et al., 2018; Panapitiya et al., 2019).
Machine learning improves quantum chemistry accuracy
Over the past few decades, density functional theory has been a proven approach for quantum chemistry calculations of catalyst’s potential energy surfaces. Unfortunately, many functionals give incorrect dissociation energy limits which are critical for exploring the energy barriers between reactants and products. Slowly, improvements have been made with hybrid functionals, but these approaches add significant computational time to quantum chemistry calculations. Many researchers have developed machine learning methods to reduce the computational time by replacing the calculation expense of hybrid functionals with neural network potentials fit to high level quantum chemistry data (Liu et al., 2017; Zhou et al., 2019). These approaches are yielding some promising results that will greatly improve the accuracy and computational time for evaluating potential energy surfaces and corresponding properties of catalysts. Unfortunately, challenges for the quantum chemistry community to reduce the computational costs and increase accuracy will continue.
Machine learning meets quantum chemistry in reaction pathways
Evaluating accurate energy barriers relies on correctly calculating potential energy surfaces along a variety of primary reaction coordinates. Transition State Theory is the predominant tool for obtaining the reaction rate corresponding to a specific reaction mechanism. Two approaches are considered for these kinetic simulations–mean field theory and kinetic Monte Carlo (Salciccioli et al., 2011); the former is more efficient but neglects the heterogeneity of active sites and diffusion effects. Both methods require calculating transition states which is a bottleneck for obtaining energy barriers as it required searching for saddle points on the multi-dimensional potential energy surface. Calculating saddle points adds extra computational loops and nuances to the overall computational costs and therefore are expensive to calculate. Unfortunately, traditional transition state searching will not always accurately portray the full picture of reactivity and selectivity. Most transition state searching algorithms follow a single reaction pathway to one saddle point; whereas many saddle points are likely to exist within the potential energy surface.
One approach to simplify searching for transition states is Brønsted-Evans-Polanyi theory - there is a linear relationship between intermediate binding energies and activation barriers (Bligaard et al., 2004). This relationship can be utilized to reduce some of the computational costs in transition state searching and is quite accurate for many elemental reactions in transition metal catalysts. Brønsted-Evans-Polanyi theory is also found to be relevant for situations with two different intermediates (Calle-Vallejo et al., 2012). Reducing errors in calculating saddle points is a challenge for quantum chemistry calculations. Our perspective is that rational catalysts design by the computational catalyst community will require more sensitivity analysis of the energy barriers to generate more robust kinetic models. The concept of degree of rate control by Campbell et al. is one approach to quantify the contributions from intermediate adsorption energies and barriers to overall reaction rates which will provide fruitful understanding of the reaction mechanism for complex networks (Campbell, 2017).
Recently, Margraf et al. have also discussed the current state of machine learning for exploring catalytic reaction networks and have expressed their assessment that computational approaches are insightful; but, the predictive power is uncertain due to the underlying approximations and the utilization of idealized structures to obtain results (Margraf et al., 2023). While current approaches are not extremely accurate in predictability, the data generated can still be beneficial. We believe that despite the failings of computational approaches, the data produced will be greatly beneficial in exploiting correlation trends that cannot otherwise be obtained from any experimental approach. Therefore, high-throughput simulations of many structures and systems can more fully explore potential energy surfaces and subsequently provide information on short-lived intermediate states that would otherwise be unknown from experimental probing as also noted by Margraf et al. It is our perspective that challenges for the quantum chemistry community to reduce the computational costs and increase accuracy will always exist; however, machine learning tools that recognize patterns in the current data availability will still yield “nuggets” of information.
Machine learning meets quantum chemistry in volcano plots
In the early stages of catalysis research, Sabatier, in the 1920s, proposed a simple and intuitive principle that the interaction between the reactants and catalyst should be moderate for enhanced performance. Interactions that are either too strong or too weak will hinder the catalytic activity. Weak interactions will not induce enough change in the reactant density to break covalent bonds of the reactant and subsequently form products. Strong interactions will covalently bind the reactant and any potential products to the catalysts thereby trapping these molecules on the surface. According to Sabatier’s principle, the interaction energy between the reactant and the catalyst is an energy-based descriptor and is represented by a volcano-shape curve. Chemists will frequently utilize quantum chemistry calculations to evaluate these interaction energy descriptors and investigate one-dimensional volcano plots to predict optimal catalysts (Zhong et al., 2020; Liu et al., 2022). A qualitative example of a three-dimensional volcano plot for different types of catalysts is shown in Figure 2. The reality is that more effective searching of optimal catalysts will require multi-dimensional volcano plots that explore resulting properties as a function of several features (Lai et al., 2022).
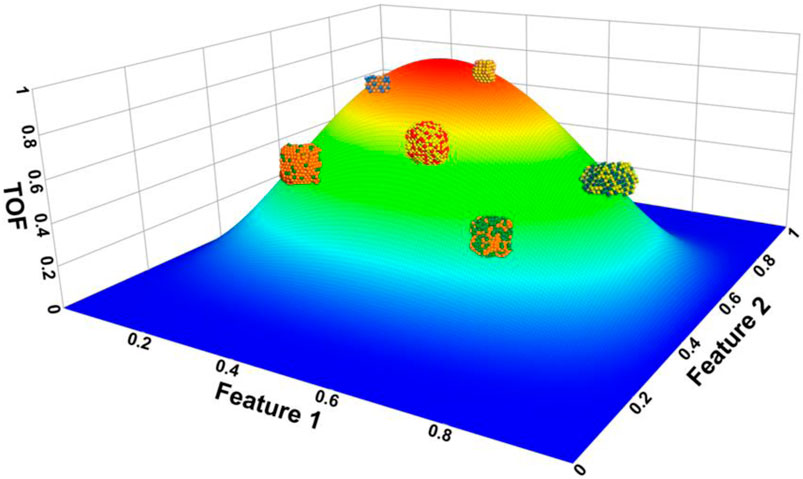
FIGURE 2. Proposed example of three-dimensional volcano plot for several representative bimetallic catalysts. The reaction barriers of different catalysts can be calculated from quantum chemistry calculations and their results plotted versus different features. This approach will produce much data that enables machine learning algorithms to hunt for optimal catalysts and target specific reactions.
As energy-based features mainly result from transition barriers, binding of intermediates, etc., then the calculation results for volcano plots can also be utilized to examine elementary rate-limiting reaction steps. Such features directly come from the reaction potential surface, so volcano plots can only yield enhanced predictability with affordable computational costs. Corminboeuf’s et al. applied machine learning concept for homogeneous catalyst screening by constructing a thermodynamics-only volcano plot for the Suzuki cross-coupling reaction and constructed a library of potential catalysts (or metal-ligand combinations). They have successfully demonstrated that exploring volcano plots using machine learning is an efficient approach for screening catalysts (Meyer et al., 2018). However, for heterogeneous catalysts, the screening would require multi-dimensional volcano plots with a much greater complexity than what has been explored by the community. Only machine learning algorithms can effectively explore the complexities between descriptors and catalyst properties to thereby observe patterns found within the data of multi-dimensional volcano plots.
Exploring rational catalyst design
Machine learning applied to materials science has perhaps made its greatest impact in two areas–structure prediction and data analysis for materials searching of a specific optimal property (e.g., band gaps). In structure prediction, many neural networks algorithms have been developed and machine learning potentials have already made a significant impact in structural prediction (Behler and Parrinello, 2007; Bartók and Csányi, 2015; Ryan et al., 2018; Xie and Grossman, 2018; Ma et al., 2020a). Despite that neural network potentials are commonly used; such potentials are not rigorously proven as the most ideal for supervised learning in structure prediction. Catalysts, particularly heterogeneous catalysts are very sophisticated complex systems where one should proceed with caution when using black box approaches. Machine learning is based on statistical algorithms. The features defined by users in the scientific community are often based on physical/chemical properties which unfortunately are not the most effective features from a statistical point of view. It is our perspective that machine learning should be considered physics and chemistry agnostic. Physically defined features will often lead to overlapping information within a given set of features as many physical properties stem from some common underlying characteristic (i.e., the structural properties all correspond to some underlying potential energy surface). Overlapping information within features leads to highly correlated features resulting in overfit data with increased requirements for training data.
Certainly, deep learning approaches can improve machine learning and optimize machine efficiency; however, researchers can greatly improve their models by first exploring feature analysis through Pearson correlation or mutual information techniques. The computational catalyst community should only develop efficient machine learning tools with the understanding that there is no “free lunch” within machine learning. Statistical models will work more efficiently if the features are “engineered” to reduce information sharing between features.
The potential energy surface is a multi-dimensional function based on the size of the system. Exploring the full potential energy surface is a significant challenge due to the variety of pathways resulting from the dimensionality. Additional challenges to this dimensionality are the effects of temperature, solvation effects, and many other environmental factors that will contribute to the multi-dimensionality of the potential energy surface. High throughput approaches using faster and efficient quantum chemistry codes are required to explore fully the properties of the potential energy surfaces. Many high-throughput tools have been developed that have benefited the community (Curtarolo et al., 2012; Ong et al., 2013; Jain et al., 2015; Hjorth Larsen et al., 2017). However, many of these tools are materials specific for searching a specific property and are geared towards structure optimizations; few can address the variety of structure-function relationships that are associated with catalysts. Many databases exist that provide results from these high-throughput calculations, for example, the Materials Project (Jain et al., 2013). These databases provide a framework by which machine learning can be used to evaluate important features of the potential energy surface that are generated from these high-throughput calculations. Only recently the Materials Project has started to build databases of materials for specific applications (e.g., Battery Explorer or Catalysis Explorer), but a catalyst specific database that focuses on structure-function relationships including data from reaction pathways, volcano plots or d-band information, etc., Would be more meaningful to the catalyst community.
Machine learning potentials will improve the exploration and prediction of high-throughput calculations by utilizing pattern recognition of the data (Ong et al., 2013; Jain et al., 2015; Pizzi et al., 2016). Machine learning approaches can explore subtle features and patterns in the potential energy surface that may go unnoticed through visual inspection of data. The importance of dynamics in catalysis warrants the development of high-throughput tools centered on analyzing ensembles of 100s of molecular dynamics trajectories, not only geometry optimizations, and incorporating these results into databases. From these ensembles one could utilize machine learning methods that increasingly explore statistical patterns of the potential energy surface and evaluate transition state pathways for catalysts and targeted reactions (Ma et al., 2019). Although there are several tools for performing high-throughput calculations of materials, it is our perspective that the computational catalyst community should build more specific tools targeting rational catalyst design. More specifically, develop high-throughput simulation tools that utilize efficient computational materials science software with molecular dynamics capabilities with data stored in large databases for ready access by machine-learning algorithms. We propose a rational catalyst design platform should be represented by something similar as Figure 3.
Incorporating experimental results will certainly improve rational catalyst design. Unfortunately, there is typically a disconnect between computational results and experimental data. This disconnect is based on several reasons. First, experimental data is by default based on an ensemble, one sample will contain within it a statistical distribution of properties because there is a distribution of configurations. For example, in a prepared sample of metal catalysts deposited on a substrate many different-sized clusters within one sample. A distribution of interfacial properties, stoichiometries (for alloyed metallic clusters), morphologies will exist leading to a distribution of reactivity and selectivity; experimental measurements are observations of the distribution average rather than specific configurations. Computational results focus rather on singular conditions and cannot represent the variety of distributions found within experiments. Machine learning methods can incorporate both experimental data as well as quantum chemistry data and including the former improves the predictability of the latter. Chen and coworkers have employed the limited experimental data to calibrate the first principles calculation results to match the corresponding experimental results, and have applied the method to compute the heat of formation of organic molecules (Hu et al., 2003; Zheng et al., 2004; Yang et al., 2022). The catalyst community should further explore high-throughput calculations coupled with machine learning methods that also incorporate experimental data. Furthermore, the interpretation of experimental data will be enhanced by calculating a large variety of systems to bridge the disconnect between computational results and experimental results. An ensemble of calculations can be assembled by evaluating 100s or 1000s of computational results. This computational ensemble can be organized with statistical approaches such as building partition functions, etc., to compare to the experimental data more directly.
The importance of the interface between the catalyst and substrate for determining catalytic performance is critical for rational catalysts design. Statistical learning by O’Connor et al. demonstrated that correlations of the quality of interactions between single atom catalysts and the substrate support determine catalytic activity (O’Connor et al., 2018). More complex systems of catalysts, such as including the interface, will require larger and larger systems of calculations which will make quantum chemistry simulations including molecular dynamics computationally expensive. In these situations, the call for more efficient quantum chemistry codes is greater as high-throughput calculations will require 100s of atoms and perhaps 1000s of atoms to represent complex systems more accurately. Even quantum chemistry packages that can scale on parallel machines will be undesirable as these simulations will occupy vast amounts of computational resources. The average research group does not have access to such resources. High-throughput calculations using highly efficient quantum chemistry packages coupled with machine learning methods is the best approach to achieving the necessary calculation of properties for developing a complete database of structure-function relationships.
Will quantum computing contribute to rational catalyst design?
Quantum computers are expected to perform exponentially faster than classical computers for solving electronic interactions because the curse of dimensionality in many-particle quantum mechanics will be overcome. Particularly, quantum computing will yield greater efficiency for simulations of strongly correlated material systems which is a quagmire for traditional electronic structure methods. Perhaps the plethora of potential applications make chemistry and materials science sound like the “killer application” for quantum computing (Bourzac, 2017). And, there has been progress - the present quantum computers have on the order of 100 qubits. This progress has renewed excitement for the quantum algorithms development and applications in chemistry and material science (Bauer et al., 2020; Ma et al., 2020b; Becerra et al., 2021; Paudel et al., 2022; von Burg et al., 2021). Specifically, for catalytic system simulation, von Burg et al. presented a quantum algorithm on the homogeneous ruthenium catalyst that transforms carbon dioxide to methanol (von Burg et al., 2021). Despite the advances reported in these works, the simulation on heterogeneous systems is still just a dream for the researcher. The number of qubits limits the simulations of catalysts which usually includes hundreds of atoms and thousands to millions of electronic wavefunctions. The tiny number of available quantum computers currently limits access for the average researcher. Quantum computers have the potential to fundamentally change the future of computational chemistry and materials science. However, realistically, it will require at least a decade and more likely 2–3 decades before any significant impact can be realized due to the complete infrastructure changes that are required–both in hardware and software.
Summary
The community is continuing to make significant strides in utilizing computational chemistry and materials science approaches for rational catalyst design. Machine-learning approaches are making some impact as well; however, the premise that there is no free lunch in machine learning should be more closely heeded. Simulations of very complex systems and properties of catalysts are better managed using high throughput approaches to generate large amounts of data for machine learning. Properties that evolve from molecular dynamics simulations are more important for incorporating kinetic effects–static-property calculations are becoming less meaningful for the future of rational catalyst design. Large databases should be developed to store not only static electronic structure properties, but also to store time-dependent properties as they evolve during molecular dynamics simulations. These types of databases will enable machine learning algorithms to recognize patterns that emerge from the molecular dynamics simulations - kinetic effects influencing multi-dimensional volcano plots, reaction pathway profiles from fully explored potential energy surfaces, density-related features, as well as other time-dependent properties.
Experimental data provides a means for further validating computational results. More impact will be gained from hypothesis testing the calculated data using statistical approaches. High throughput microreactor testing is already being utilized by academic researchers and can be incorporated easily into machine learning algorithms driven by computational chemistry and materials science simulations. Even better, data from catalytic reactors at the industrial testing level would make the impact of quantum chemistry even more meaningful if this data is incorporated as well. Databases that incorporate data from industrial processes would bring a dose of realism to computational chemistry and materials science approaches.
The community would benefit from the development of more robust approaches and algorithms in machine learning without making the mistake of treating machine learning approaches as a black box. Machine learning publications have largely addressed minor research questions in the field of catalysis; a more serious pursuit of structure-function relationships will require serious machine learning applied to vast complex systems that more accurately represent heterogeneous catalysis. A successful approach will include much feedback with further calculations, experimental, and industrial data. It is an exciting time to be engaged in rational catalyst design with the luring attraction of machine learning using much data that can be generated efficiently from computational chemistry and materials science software.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of interest
Some of the authors are affiliated with companies - JL, PR, XW, and YL are affiliated with Synfuels China; JL and GC are affiliated with the Hong Kong Quantum AI Laboratory.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bartók, A. P., and Csányi, G. (2015). Gaussian approximation potentials: A brief tutorial introduction. Int. J. Quantum Chem. 115 (16), 1051–1057. doi:10.1002/qua.24927
Bauer, B., Bravyi, S., Motta, M., and Chan, G. K.-L. (2020). Quantum algorithms for quantum chemistry and quantum materials science. Chem. Rev. 120 (22), 12685–12717. doi:10.1021/acs.chemrev.9b00829
Becerra, A., Prabhu, A., Rongali, M. S., Velpur, S. C. S., Debusschere, B., and Walker, E. A. (2021). How a quantum computer could quantify uncertainty in microkinetic models. J. Phys. Chem. Lett. 12 (29), 6955–6960. doi:10.1021/acs.jpclett.1c01917
Behler, J., and Parrinello, M. (2007). Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 98 (14), 146401. doi:10.1103/PhysRevLett.98.146401
Bligaard, T., Nørskov, J. K., Dahl, S., Matthiesen, J., Christensen, C. H., and Sehested, J. (2004). The brønsted–evans–polanyi relation and the volcano curve in heterogeneous catalysis. J. Catal. 224 (1), 206–217. doi:10.1016/j.jcat.2004.02.034
Bourzac, K. (2017). Chemistry is quantum computing’s killer app. Washington, United States: C&E News. Available at: https://cen.acs.org/articles/95/i43/Chemistry-quantum-computings-killer-app.html.
Calle-Vallejo, F., Martínez, J. I., García-Lastra, J. M., Rossmeisl, J., and Koper, M. T. M. (2012). Physical and chemical nature of the scaling relations between adsorption energies of atoms on metal surfaces. Phys. Rev. Lett. 108 (11), 116103. doi:10.1103/PhysRevLett.108.116103
Campbell, C. T. (2017). The degree of rate control: A powerful tool for catalysis research. ACS Catal. 7, 2770–2779. doi:10.1021/acscatal.7b00115
Curtarolo, S., Setyawan, W., Hart, G. L. W., Jahnatek, M., Chepulskii, R. V., Taylor, R. H., et al. (2012). Aflow: an automatic framework for high-throughput materials discovery. Comput. Mater. Sci. 58, 218–226. doi:10.1016/j.commatsci.2012.02.005
Giordano, L., Akkiraju, K., Jacobs, R., Vivona, D., Morgan, D., and Shao-Horn, Y. (2022). Electronic structure-based descriptors for oxide properties and functions. Acc. Chem. Res. 55, 298–308. doi:10.1021/acs.accounts.1c00509
Haycock, B. J., Kylee Rice, M., and Lewis, J. P. (2014a). High-throughput calculations of alloyed delafossite materials: application to CuGa1−xFexO2. Comput. Mater. Sci. 86, 155–164. doi:10.1016/j.commatsci.2014.01.024
Haycock, B. J., Lander, G., Rice, M. K., Prasai, K., Prasai, B., Drabold, D. A., et al. (2014b). High-throughput evaluation in nitrogen doping of amorphous titanium dioxide: high-throughput evaluation in nitrogen doping of a TiO 2. Phys. Status Solidi B 251 (6), 1225–1230. doi:10.1002/pssb.201451010
Hjorth Larsen, A., Jørgen Mortensen, J., Blomqvist, J., Castelli, I. E., Christensen, R., Dułak, M., et al. (2017). The atomic simulation environment—A Python library for working with atoms. J. Phys. Condens. Matter 29 (27), 273002. doi:10.1088/1361-648X/aa680e
Hu, L., Wang, X., Wong, L., and Chen, G. (2003). Combined first-principles calculation and neural-network correction approach for heat of formation. J. Chem. Phys. 119 (22), 11501–11507. doi:10.1063/1.1630951
Jain, A., Ong, S. P., Chen, W., Medasani, B., Qu, X., Kocher, M., et al. (2015). FireWorks: A dynamic workflow system designed for high-throughput applications. Concurrency Comput. Pract. Exp. 27 (17), 5037–5059. doi:10.1002/cpe.3505
Jain, A., Ong, S. P., Hautier, G., Chen, W., Richards, W. D., Dacek, S., et al. (2013). Commentary: the materials project: a materials genome approach to accelerating materials innovation. Apl. Mater. 1 (1), 011002. doi:10.1063/1.4812323
Lai, Z., Chen, J., Jia, M., Hu, P., and Wang, H. (2022). Universal skeleton feature of the three-dimensional volcano surface and the thermodynamic rule in locating the catalyst in heterogeneous catalysis. ACS Catal. 12 (1), 247–258. doi:10.1021/acscatal.1c04567
Lewis, J. P., Jelínek, P., Ortega, J., Demkov, A. A., Trabada, D. G., Haycock, B., et al. (2011). Advances and applications in the F IREBALL ab initio tight-binding molecular-dynamics formalism: F IREBALL molecular-dynamics formalism. Phys. Status Solidi B 248 (9), 1989–2007. doi:10.1002/pssb.201147259
Li, Z., Ma, X., and Xin, H. (2017). Feature engineering of machine-learning chemisorption models for catalyst design. Catal. Today 280, 232–238. doi:10.1016/j.cattod.2016.04.013
Liu, Q., Wang, J., Du, P., Hu, L., Zheng, X., and Chen, G. (2017). Improving the performance of long-range-corrected exchange-correlation functional with an embedded neural network. J. Phys. Chem. A 121 (38), 7273–7281. doi:10.1021/acs.jpca.7b07045
Liu, X., Cai, C., Zhao, W., Peng, H.-J., and Wang, T. (2022). Machine learning-assisted screening of stepped alloy surfaces for C1 catalysis. ACS Catal. 12, 4252–4260. doi:10.1021/acscatal.2c00648
Ma, H., Govoni, M., and Galli, G. (2020b). Quantum simulations of materials on near-term quantum computers. npj Comput. Mater 6 (1), 85–88. doi:10.1038/s41524-020-00353-z
Ma, H., Jiao, Y., Guo, W., Liu, X., Li, Y., and Wen, X.-D. (2020a). Predicting crystal morphology using a geometric descriptor: A comparative study of elemental crystals with high-throughput dft calculations. J. Phys. Chem. C 124 (29), 15920–15927. doi:10.1021/acs.jpcc.0c03537
Ma, S., Shang, C., and Liu, Z.-P. (2019). Heterogeneous catalysis from structure to activity via SSW-NN method. J. Chem. Phys. 151 (5), 050901. doi:10.1063/1.5113673
Margraf, J. T., Jung, H., Scheurer, C., and Reuter, K. (2023). Exploring catalytic reaction networks with machine learning. Nat. Catal. 6 (2), 112–121. doi:10.1038/s41929-022-00896-y
Meyer, B., Sawatlon, B., Heinen, S., von Lilienfeld, O. A., and Corminboeuf, C. (2018). Machine learning meets volcano plots: computational discovery of cross-coupling catalysts. Chem. Sci. 9 (35), 7069–7077. doi:10.1039/C8SC01949E
Norskov, J. K., Bligaard, T., Rossmeisl, J., and Christensen, C. H. (2009). Towards the computational design of solid catalysts. Nat. Chem. 1 (1), 37–46. doi:10.1038/nchem.121
O’Connor, N. J., Jonayat, A. S. M., Janik, M. J., and Senftle, T. P. (2018). Interaction trends between single metal atoms and oxide supports identified with density functional theory and statistical learning. Nat. Catal. 1 (7), 531–539. doi:10.1038/s41929-018-0094-5
Ong, S. P., Richards, W. D., Jain, A., Hautier, G., Kocher, M., Cholia, S., et al. (2013). Python materials genomics (pymatgen): A robust, open-source Python library for materials analysis. Comput. Mater. Sci. 68, 314–319. doi:10.1016/j.commatsci.2012.10.028
Panapitiya, G., Avendaño-Franco, G., and Lewis, J. P. (2019). Structural and electronic properties of Fe-doped silver delafossites: AgAl1−xFexO2 and AgGa1−xFexO2 (x = 1–5%). Comput. Mater. Sci. 170, 109173. doi:10.1016/j.commatsci.2019.109173
Panapitiya, G., Avendaño-Franco, G., Ren, P., Wen, X., Li, Y., and Lewis, J. P. (2018). Machine-learning prediction of CO adsorption in thiolated, Ag-alloyed Au nanoclusters. J. Am. Chem. Soc. 140 (50), 17508–17514. doi:10.1021/jacs.8b08800
Paudel, H. P., Syamlal, M., Crawford, S. E., Lee, Y.-L., Shugayev, R. A., Lu, P., et al. (2022). Quantum computing and simulations for energy applications: review and perspective. ACS Eng. Au 2 (3), 151–196. doi:10.1021/acsengineeringau.1c00033
Pizzi, G., Cepellotti, A., Sabatini, R., Marzari, N., and Kozinsky, B. (2016). AiiDA: automated interactive infrastructure and database for computational science. Comput. Mater. Sci. 111, 218–230. doi:10.1016/j.commatsci.2015.09.013
Ranasingha, O., Wang, H., Zobač, V., Jelínek, P., Panapitiya, G., Neukirch, A. J., et al. (2016). Slow relaxation of surface plasmon excitations in Au 55: the key to efficient plasmonic heating in Au/TiO 2. J. Phys. Chem. Lett. 7 (8), 1563–1569. doi:10.1021/acs.jpclett.6b00283
Roger, I., Shipman, M. A., and Symes, M. D. (2017). Earth-abundant catalysts for electrochemical and photoelectrochemical water splitting. Nat. Rev. Chem. 1 (1), 0003. doi:10.1038/s41570-016-0003
Ryan, K., Lengyel, J., and Shatruk, M. (2018). Crystal structure prediction via deep learning. J. Am. Chem. Soc. 140 (32), 10158–10168. doi:10.1021/jacs.8b03913
Salciccioli, M., Stamatakis, M., Caratzoulas, S., and Vlachos, D. G. (2011). A review of multiscale modeling of metal-catalyzed reactions: mechanism development for complexity and emergent behavior. Chem. Eng. Sci. 66 (19), 4319–4355. doi:10.1016/j.ces.2011.05.050
Senty, T. R., Haycock, B., Lekse, J., Matranga, C., Wang, H., Panapitiya, G., et al. (2017). Optical absorption and disorder in delafossites. Appl. Phys. Lett. 111 (1), 012102. doi:10.1063/1.4991388
Tavadze, P., Avendaño Franco, G., Ren, P., Wen, X., Li, Y., and Lewis, J. P. (2018). A machine-driven hunt for global reaction coordinates of azobenzene photoisomerization. J. Am. Chem. Soc. 140 (1), 285–290. doi:10.1021/jacs.7b10030
U. Schneider, and S. Thomas (Editors) (2020). Catalysis with earth-abundant elements (Cambridge: Royal Society of Chemistry). Catalysis Series. doi:10.1039/9781788012775
Vojvodic, A., and Nørskov, J. K. (2015). New design paradigm for heterogeneous catalysts. Natl. Sci. Rev. 2 (2), 140–143. doi:10.1093/nsr/nwv023
von Burg, V., Low, G. H., Häner, T., Steiger, D. S., Reiher, M., Roetteler, M., et al. (2021). Quantum computing enhanced computational catalysis. Phys. Rev. Res. 3 (3), 033055. doi:10.1103/PhysRevResearch.3.033055
Wang, L., Wang, H., Rice, A. E., Zhang, W., Li, X., Chen, M., et al. (2015). Design and preparation of supported Au catalyst with enhanced catalytic activities by rationally positioning Au nanoparticles on anatase. J. Phys. Chem. Lett. 6 (12), 2345–2349. doi:10.1021/acs.jpclett.5b00655
Wang, L., Zhang, J., Wang, H., Shao, Y., Liu, X., Wang, Y.-Q., et al. (2016). Activity and selectivity in nitroarene hydrogenation over Au nanoparticles on the edge/corner of anatase. ACS Catal. 6 (7), 4110–4116. doi:10.1021/acscatal.6b00530
Xie, T., and Grossman, J. C. (2018). Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120 (14), 145301. doi:10.1103/PhysRevLett.120.145301
Yang, G., Chiu, W. Y., Wu, J., Zhou, Y., Chen, S., Zhou, W., et al. (2022). Predicting experimental heats of formation via deep learning with limited experimental data. J. Phys. Chem. A 126 (36), 6295–6300. doi:10.1021/acs.jpca.2c02957
Zheng, X., Hu, L., Wang, X., and Chen, G. (2004). A generalized exchange-correlation functional: the neural-networks approach. Chem. Phys. Lett. 390 (1–3), 186–192. doi:10.1016/j.cplett.2004.04.020
Zhong, M., Tran, K., Min, Y., Wang, C., Wang, Z., Dinh, C.-T., et al. (2020). Accelerated discovery of CO2 electrocatalysts using active machine learning. Nature 581 (7807), 178–183. doi:10.1038/s41586-020-2242-8
Keywords: machine learning, catalysts, high-throughput, reaction coordinates, structure-function relationships
Citation: Lewis JP, Ren P, Wen X, Li Y and Chen G (2023) Machine learning meets quantum mechanics in catalysis. Front. Quantum Sci. Technol. 2:1232903. doi: 10.3389/frqst.2023.1232903
Received: 01 June 2023; Accepted: 04 August 2023;
Published: 31 August 2023.
Edited by:
Abolfazl Alizadeh Sahraei, Laval University, CanadaReviewed by:
Yuhua Duan, National Energy Technology Laboratory (DOE), United StatesCopyright © 2023 Lewis, Ren, Wen, Li and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: James P. Lewis, amFtZXMucC5sZXdpcy5waGRAZ21haWwuY29t
 James P. Lewis
James P. Lewis Pengju Ren1,4
Pengju Ren1,4