QREChem: quantum resource estimation software for chemistry applications

As quantum hardware continues to improve, more and more application scientists have entered the field of quantum computing. However, even with the rapid improvements in the last few years, quantum devices, especially for quantum chemistry applications, still struggle to perform calculations that classical computers could not calculate. In lieu of being able to perform specific calculations, it is important have a systematic way of estimating the resources necessary to tackle specific problems. Standard arguments about computational complexity provide hope that quantum computers will be useful for problems in quantum chemistry but obscure the true impact of many algorithmic overheads. These overheads will ultimately determine the precise point when quantum computers will perform better than classical computers. We have developed QREChem to provide logical resource estimates for ground state energy estimation in quantum chemistry through a Trotter-based quantum phase estimation approach. QREChem provides resource estimates which include the specific overheads inherent to problems in quantum chemistry by including heuristic estimates of the number of Trotter steps and number of necessary ancilla, allowing for more accurate estimates of the total number of gates. We utilize QREChem to provide logical resource estimates for a variety of small molecules in various basis sets, obtaining estimates in the range of 10⁷–10¹⁵ for total number of T gates. We also determine estimates for the FeMoco molecule and compare all estimates to other resource estimation tools. Finally, we compare the total resources, including hardware and error correction overheads, demonstrating the need for fast error correction cycle times.

1 Introduction

Quantum chemistry is often quoted as a potential “killer app” for quantum computers, with grand targets such as solving nitrogen fixation (Reiher et al., 2017). While there is much promise for quantum computers in quantum chemistry, due to a potential for an exponential speed up in eigenvalue estimation in quantum chemistry via the quantum phase estimation (QPE) algorithm (Kitaev, 1997; Abrams and Lloyd, 1999), realistic resource estimates, both at the logical and physical level, point to extremely large numbers of quantum gates and qubits necessary for even small systems (Reiher et al., 2017; Kim et al., 2022). Alternate algorithms, more suited to near-term, noisy intermediate scale quantum (NISQ) (Preskill, 2018) devices, such as the variational quantum eigensolver (VQE) (Peruzzo et al., 2014), provide a potential reduction in gate depth, but add additional complexity in optimization (Menickelly et al., 2023) and still require substantial gate depth for more interesting, classically intractable systems. With fault-tolerant, error-corrected quantum computers capable of the required gate depth and numbers of qubits still potentially years away, accurate resource estimates will play a key role in understanding the progress of quantum algorithms and the trade-offs of various architectural choices. There already exists several tools for estimating resources to varying degrees of precision. For example, TFermion (Casares et al., 2022) provides estimates of a wide variety of quantum algorithms for quantum chemistry but relies on strict error bounds, sometimes greatly overestimating the resources for certain algorithms, while OpenFermion provides estimates of certain specific quantum chemistry methods and also provides some tools for estimating surface code overhead (McClean et al., 2020). Microsoft has released a ‘full-stack’ resource estimation framework and tool (Beverland et al., 2022), which allows for a more general resource estimation, including many potential hardware overheads.

Here, we detail QREChem, which provides accurate logical and physical resource estimates with a specific focus on quantum chemistry. Within QREChem we have implemented a detailed resource estimation of the Trotter algorithm (Ortiz et al., 2001; Babbush et al., 2015), using heuristic, rather than worst-case, estimates for various algorithmic overheads. We have also included minimal implementations of error correction and hardware overheads. To benchmark our method, we compare our logical resource estimates to both TFermion (Casares et al., 2022) and OpenFermion (McClean et al., 2020) by estimating the total number of logical T gates for various small molecules and for the larger FeMoco molecule (Reiher et al., 2017). We additionally estimate the total physical resources needed, assuming various hardware and error correction parameters, for QREChem’s Trotter resource estimates.

QREChem was developed in mind as a tool for providing realistic estimations of resources to simulate ab initio quantum chemistry calculations on various quantum computers, both existing and future ones. It serves multiple purposes, with a primary goal of eventual co-design of future quantum computers and development of new quantum algorithms. For example, given a molecule, QREChem will be able to predict the resources (the number of qubits, gates, fidelities, sampling rate) required to accurately estimate the ground state energy. Or another way around given quantum hardware and molecule, QREChem could calculate a potential success rate. The current version of QREChem focuses on the algorithmic implementations; further development will involve adding more detailed implementations for the hardware and error correction overheads to provide more precise estimates.

2 Methods

2.1 Design of QREChem

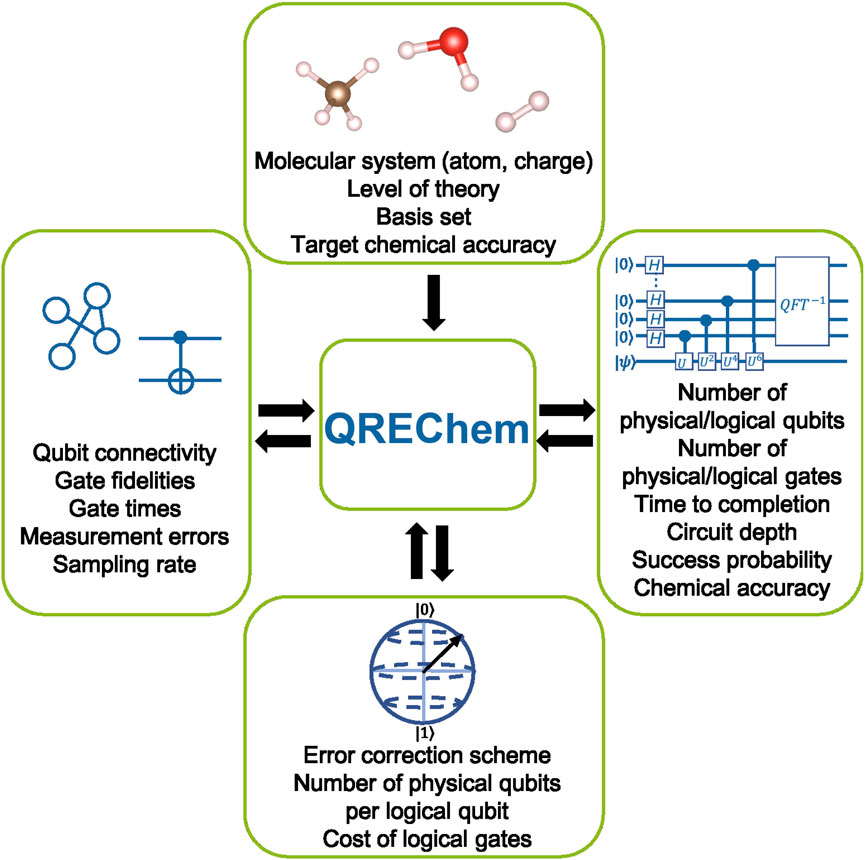
QREChem is designed to allow for efficient and accurate logical resource estimates of ground state energy calculations in quantum chemistry problems. Figure 1 details the overall design. QREChem consists of several modules: the ‘Chemistry’ module, which defines the chemical system of interest; the ‘Algorithm’ module, which defines the quantum algorithm to be used; the ‘Hardware’ module, which defines the target hardware; and the ‘Error Correction’ module, which defines the quantum error correcting code. These modules work in tandem to produce the final resource estimates. Our primary focus in this work was to provide detailed implementations of the ‘Chemistry’ and ‘Algorithm’ (focusing on Trotterization algorithms (Ortiz et al., 2001; Babbush et al., 2015)) modules; the ‘Hardware’ and ‘Error Correction’ modules are relatively simple, by comparison. In the following sections, we provide detailed descriptions of each module, as implemented in the initial version QREChem, as well as ways in which each module can be further developed.

FIGURE 1

FIGURE 1. Schematic diagram of QREChem.

2.1.1 Chemistry module

The first step in performing quantum chemistry calculations is to generate the chemical Hamiltonian, which describes the energy operator of the molecular system in terms of the positions of its constituent atoms. In the Chemistry module of QREChem, we generate the Hamiltonian using the self-consistent field (SCF) methods implemented in the PySCF program (Sun et al., 2018; Sun et al., 2020).

The Hamiltonian matrix elements, which represent the contributions of the various terms in the Hamiltonian, are defined in terms of one-electron integrals, h_pq, and two-electron integrals, h_pqrs (Low et al., 2019). These integrals depend on the molecular properties such as the atomic coordinates, the charge, and the choice of basis set. SCF calculations, such as the restricted Hartree-Fock (RHF) method, are performed to obtain the one- and two-electron integrals for the chosen molecular system. QREChem requires the definition of the chemical system of interest, in terms of the atomic coordinates, the charge, and the target basis set.

It is important to note that the SCF calculations can be time-consuming, especially for larger numbers of atoms and larger basis sets, and can be tricky to properly converge. However, QREChem supports the standard fcidump file format, which stores the one- and two-electron integrals, allowing a user to generate these integrals using a different program and then interface with the other modules of QREChem. The fcidump file format is a widely used format for storing quantum chemistry Hamiltonians (Knowles and Handy, 1989) and can be produced by other quantum chemistry packages, such as Gaussian (Foresman and Frish, 1996), MolPro (Werner et al., 2012), or Psi4 (Smith et al., 2020). Once the one- and two-electron integrals are obtained, the data is available to other modules within QREChem.

2.1.2 Algorithm module

There are many proposed quantum algorithms for solving for the ground state energy in chemical problems, including quantum phase estimation (QPE) (Kitaev, 1997; Abrams and Lloyd, 1999), the variational quantum eigensolver (VQE) (Peruzzo et al., 2014), combinations of the two (Otten et al., 2022; D’Cunha et al., 2023), and quantum machine learning methods (Xia and Kais, 2018). Within each of these families of algorithms, there are a substantial number of possible variations. In this work, we focus on QPE using Trotterization (Ortiz et al., 2001; Babbush et al., 2015). Here, we provide a brief overview of QPE using Trotterization.

QPE solves for the eigenvalue, λ_k, for an eigenvector |v_k⟩ of some unitary matrix, U. Aside from its use in ground state energy estimation in quantum chemistry, it also finds use in Shor’s prime number factoring algorithm (Shor, 1999) and the Hassidim–Harrow–Lloyd algorithm for matrix inversion (Harrow et al., 2009). Given a Hamiltonian generated by the Chemistry module, the unitary matrix, U is can be written as:

$U|v_k\rangle =e^{i\widehat{H}\tau }|v_k\rangle =e^{i2\pi \varphi }|v_k\rangle ,(1)$

where τ is a scale factor to map the eigenvalues of Hτ onto (0, 2π] or (-π, π]. Assuming |v_k⟩ is the ground state, the ground state energy is then mapped to the phase acquired, E = 2πϕ/τ, where units have been chosen such that ℏ = 1. The computational complexity of QPE is dependent on how the unitary matrix of Eq. 1 is implemented. In QREChem, we focus on Trotterization (Ortiz et al., 2001; Babbush et al., 2015), but many other strategies, such as Taylorization (Berry et al., 2015) and qubitization (Low and Chuang, 2019) have been proposed. The Trotterized version of the propagator, U, is

$U=\underset{n\to \infty }{\lim }{\left(\prod _j{e}^{i{H}_j\tau /n}\right)}^n.(2)$

By choosing some finite number of Trotter steps, n, U is only represented approximately. A first-order Trotter formula truncates Eq. (2) at some number of steps. Choosing a sufficient number of Trotter steps for a given accuracy is important for obtaining an accurate estimate of the total resources. Higher-order Trotter-Suzuki formulas (Suzuki, 1993) can be used to decrease the number of steps at the cost of increasing the complexity of each step. The standard fermionic quantum chemistry Hamiltonian has O(N⁴) terms. A fermion-to-spin mapping is required to implement each fermionic term on qubits. Using the Jordan–Wigner (Jordan and Wigner, 1993) transformation introduces an O(N) overhead, leading to a total complexity of O(N⁵) for the Trotterized evolution. The evolution of the phase is mapped to an ancilla register (introducing limits on the precision, based upon the number of ancilla) and, using the quantum Fourier transform (QFT) (Shor, 1994), the ground state energy can be read out. In realistic settings, the true eigenstate |v_k⟩ is unknown and an approximation must be used. This introduces an additional overhead in the success probability which scales as the overlap of the approximate state, |ϕ⟩, with the true eigenstate, i.e., |⟨ϕ|v_k⟩|².

Within QREChem, we provide resource estimates for Trotterized QPE by first estimating the resources required for a single Trotter time step and then estimating the total number of Trotter steps. The resource estimation tools within Microsoft Quantum Development Kit (QDK) (Svore et al., 2018; Low et al., 2019) are able to efficiently provide such logical gate estimates, even for very large systems. We estimate the total number of Trotter steps necessary as $n_o^{3/2}$, where n_o is the number of orbitals used in the Hamiltonian which is based on heuristic estimates (Poulin et al., 2015; Reiher et al., 2017). Beyond number of Trotter steps, we also need to accurately compute the number of ancilla necessary to reach the a user-defined desired precision ϵ_p (which, by default, we take to be 1 mHa). This allows us to calculate the base number of binary digits necessary, n_b = −log₂(ϵ_p/ΔE_R), where ΔE_R is a scaling factor that estimates the spectral range (i.e., ΔE_R ≈ E_max − E_min) (D’Cunha et al., 2023) and is taken to be 1 Ha (a number chosen heuristically to cover all studied molecules). The phase resulting from a QPE is given as a binary fraction and the number of bits in this fraction (the precision) is determined by the number of ancilla qubits used in the QPE algorithm. If the eigenvalue is not exactly representable with n_b bits of precision, the returned value will, instead, be mapped into the finite precision of n_b bits, causing a chance for error. To increase the QPE success probability, additional ancilla can be used. If the eigenvector is known precisely, the total number of ancilla, n_a, is a function of the desired failure probability, p_f (Nielsen and Chuang, 2000),

$n_a=n_b+{\log }_2\left(2+\frac{1}{2p_f}\right).(3)$

It is very unlikely to know the true eigenstate a priori. More accurate formulas can be derived which take into account errors in the Trotterization, ϵ_t, as well as the true gap ΔE = E₁ − E₀ (Li, 2022)

$n_a=n_b+{\log }_2\left(2+\frac{{\mathit{ϵ}}_{\mathit{t}}^2}{2p_f{\left(\mathrm{\Delta }E\right)}^2}\right).(4)$

Since the true gap, ΔE, is generally unknown, we instead use equation-of-motion (EOM) coupled-cluster with singles and doubles (CCSD) as implemented in PySCF (Sun et al., 2018) to estimate the gap. In cases where CCSD becomes too expensive, other methods with tunable cost and accuracy, such as selected configuration interaction (Chien et al., 2018) (which can be as cheap as Hartree-Fock) can be used. We also use a target Trotter error of chemical accuracy (ϵ_t = 1.6 mHa), rather than an observed Trotter error.

To calculate the total number of rotation gates, CNOT gates, and the total depth, we combine the estimates for a single Trotter step (using Q# and the Microsoft QDK) with the estimate of the total number of Trotter steps $(n_o^{3/2})$ and multiply that by the number of ancilla, n_a, as each ancilla will require evolution to some long time, giving, for example, the total number of rotation gates

$n_{r,tot}=n_r{n}_o^{2/3}{n}_a,(5)$

where n_r is the number of rotation gates for a single Trotter step. Similar equations are used for the total depth and total number of CNOTs.

Using the same Hamiltonians generated in the Chemistry module, we utilized TFermion (Casares et al., 2022) and OpenFermion (McClean et al., 2020) to provide comparison logical resource estimates. TFermion provides estimates of a variety of quantum algorithms, including variants of Trotterization (Campbell, 2019) and Taylorization (Babbush et al., 2016), among others. It uses properties of the computed Hamiltonians, such as the 1-norm, combined with analytic formulas derived from the literature. OpenFermion provides estimation of more advanced algorithms, such as qubitization with low rank factorization (Berry et al., 2019).

Future improvements to the Algorithm module would involve the implementation of resource estimates for other evolution algorithms with explicit circuit constructions, such as qubitization and Taylorization, as well as other algorithms, such as VQE. Furthermore, overheads relating to the preparation of sufficient overlap initial states will also be implemented.

2.1.3 Error correction module

Quantum error correction (QEC) is an essential feature of any viable quantum computing system due to the intrinsic susceptibility of quantum systems to errors. These errors can be caused by a variety of factors, including decoherence and operational imperfections. In simple terms, QEC codes encode a logical qubit into several physical qubits, and through the process of measurement and classical post-processing, corrects the inevitable errors, extending the effective processing time before errors destroy the quantum state.

There are many proposed codes within QEC. Among them, the surface code (Fowler et al., 2012) stands out due to its high error threshold, relative ease of implementation, and planar geometry, which matches many proposed quantum architectures. Like any QEC code, the implementation of surface code necessitates a large number of physical qubits to encode a single logical qubit and presents a significant overhead in terms of resource requirements. Various implementations of the surface code have a given distance, d, which refers to the minimum number of physical qubits that must be affected by errors in order to cause a logical error. Within QREChem, we provide estimates of the QEC space and time overheads of the surface code using OpenFermion (McClean et al., 2020). The surface code cost estimator takes in the number of Toffoli gates, the number of logical qubits, a physical error rate, and the estimated surface code cycle time. It then estimates the total error, including error contributions from both magic state distillation (which is necessary to produce the Toffoli gates) (Litinski, 2019a) and due to the physical error rate. The physical error rate, p_P, logical error rate, p_L, and distance are approximately related via (Fowler and Gidney, 2018; Webber et al., 2022)

$p_L=0.1{\left(100p_P\right)}^{\left(d+1\right)/2}.(6)$

The total error and space-time (number of qubits times number of seconds) is estimated for a various distances d of the surface code. The best, in terms of space-time, distance d estimate which has total error below a threshold ϵ_sc (which we by default take to be 0.1) is returned as the optimal surface code.

QREChem allows a user to input the desired total algorithmic success probability. Along with the total depth, which is estimated in the Algorithm module, and the physical error rate and cycle time, which is provided by the Hardware module, the error correction module provides the best surface code distance d. This provides an initial estimate of the QEC overhead in terms of the number of physical qubits and total runtime. Future module development will include more accurate estimates of the overhead in numbers of gates needed for the surface code (via, for example, the methods in Ref (Litinski, 2019b).), as well as estimates for other QEC codes (such as color codes (Litinski et al., 2017)).

2.1.4 Hardware module

The underlying quantum computing architecture plays a pivotal role in the overall resource estimates. Various quantum hardware can have vastly different error rates, gate times, connectivities, native gate sets, etc (Menickelly et al., 2023). The Hardware module captures several hardware-specific factors that can significantly affect the performance and resources of quantum algorithms. Within the initial release of QREChem, the Hardware module consists of a high-level description of the underlying hardware, including gate times and physical error rates. With this simplistic Hardware module, we estimate the logical depth by assuming that all single qubit gates can be performed in parallel batches using n_o, the number of orbitals, qubits, and the CNOT gates cannot be performed in parallel ($d=\frac{n_r}{n_o}+n_c$, where n_r is the number of rotation gates and n_c is the number of CNOTs). To estimate the number of T gates n_t, which are likely to be the most expensive gate for fault-tolerant, error-corrected quantum computers (Bravyi and König, 2013; Beverland et al., 2016), we use estimates of the circuit synthesis cost of arbitrary rotations from Clifford + T gates (Selinger, 2015)

$n_t=n_r\left(10+12{\log }_2\left({ϵ}_{ss}^{-1}\right)\right),(7)$

where ϵ_ss is the synthesis error, which we take to be 10^–9. We choose this value of the threshold to keep the synthesis error well below the standard $1/\sqrt{N_g}$ bound, where N_g is the number of gates (Hastings, 2016), for all circuits studied. This is a tunable parameter which can be varied by a user. Total runtime is computed by interfacing with the Error Correction module, which requires a surface code cycle time, physical error rate, number of Toffoli gates (which is related to the number of T gate) and number of logical qubits. In the initial release of QREChem, we use experimentally demonstrated cycle times to abstract away the hardware details.

Future development of this module will incorporate underlying connectivity, specific noise models, and compilation to native gate sets, along with gate times, to computer the surface code cycle time, as it is evident from the results of this work that a fault-tolerant quantum computer will be required to execute QPE quantum circuits.

3 Results

3.1 Benchmark molecules

Using QREChem, TFermion, and OpenFermion, we estimated the required logical quantum resources for the Trotter-based QPE algorithm to compute the ground state properties of various small molecules, including H₂, HF, H₂O, NH₃, CH₄, Be₂, and C₂. The geometries of these molecules were taken from the NIST database (Johnson, 2022). For these molecules, we investigated the relationship between the number of orbitals and the quantum resources by considering several Gaussian-type orbital basis sets for the smaller molecules (STO-6G, 6-31G*, cc-pVDZ, and cc-pVTZ). All orbitals were included in the active space. These small molecule benchmarks represent some of the most commonly found molecules, while stressing different types of molecular bonding. The choice of basis sets follows a progression of complexity, starting from where Gaussian orbitals are fit to a single Slater orbital (STO-6G) (Stewart, 1970), to more complete basis functions (6-31G*) (Ditchfield et al., 1971) to more consistent basis sets designed for converging post-Hartree-Fock calculations (cc-pVDZ, cc-pVTZ) (Dunning, 1989) to the complete basis set limit.

We also consider the much larger FeMoco molecule, also known as the iron-molybdenum cofactor, which is crucial for biological nitrogen fixation; however, its fixation mechanism is not fully understood (Reiher et al., 2017). FeMoco is a well-known benchmark molecule that has been used in previous resource estimations. To compare our results with those of other studies, we used the same Hamiltonians (i.e., active spaces) as used in (Reiher et al., 2017) and (Li et al., 2019).

3.2 Resource estimates

Using QREChem, we obtained the total number of logical T gates necessary for various algorithms for each molecule at different basis set levels. The data for all molecules is shown in Figure 2. “This Work” represents the QREChem estimate of number of Trotter gates, as described above. “SF” uses OpenFermion’s resource estimation tools for the single factorization algorithm (Berry et al., 2019) to estimate the number of Toffoli gates, which is then scaled by 4, as that is the number of T gates necessary for one Toffoli gate (Berry et al., 2019). “TF-Trot” uses TFermion (Casares et al., 2022) to estimate the number of T gates in the qDRIFT algorithm (Campbell, 2019) and “TF-SF” uses TFermion to estimate the single factorization algorithm. Most striking is the comparison between TFermion’s Trotter algorithm (“TF-Trot”) and the one estimated in QREChem (“This Work”). This is likely due to the fact the qDRIFT estimates use worst-case error bounds to calculate the total number of operations. In QREChem’s Trotter estimates, we instead use heuristic estimates, which result in orders of magnitude lower number of necessary Trotter steps and, thus, orders of magnitude lower resource estimates. Furthermore, QREChem uses explicit gate counting provided by the Microsoft QDK, rather than the more pessimistic estimates used in the formula of TFermion. These more realistic estimates put Trotter close to the estimates of the more advanced single factorization algorithm (which requires additional ancilla qubits).

FIGURE 2

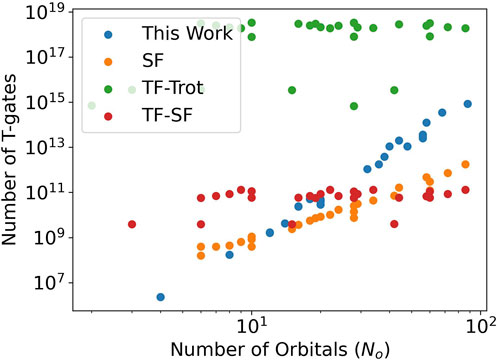
FIGURE 2. Estimated total numbers of logical T gates for various algorithms over many molecules at many basis set levels. See text for the definitions of the algorithms.

We further compare the resource estimates of the number of logical T gates for various algorithms using FeMoco, which is the standard benchmark molecule for evaluation of quantum algorithms. We used the same Hamiltonian as in previous studies (Reiher et al., 2017; Li et al., 2019) to obtain a precise comparison with other works. Table 1 shows the comparison of the number of T gates between QREChem’s Trotter estimation (“This Work”) and others from (Reiher et al., 2017; Berry et al., 2019; Casares et al., 2022). Ref (Reiher et al., 2017). provided the first theoretical estimates for FeMoco, which were approximately 10¹⁵ T gates. Again, we see that QREChem’s Trotter estimation lines up with the estimation from Ref. (Reiher et al., 2017), which is reasonable, given that both works used similar heuristic estimates. The single factorization algorithm (Berry et al., 2019) performs the best out of those studied.

TABLE 1

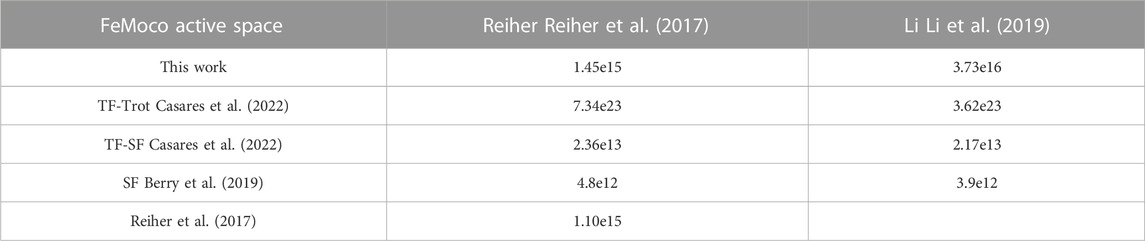
TABLE 1. The number of T gates for FeMoco molecule as estimated by various sources. The Hamiltonians were taken from the repository of (Lee et al., 2021) used in (Reiher et al., 2017) and (Li et al., 2019). See text for definitions of the algorithms.

All estimates presented in Figure 2 and Table 1 are only for the number of logical T gates required, not including additional overheads from hardware or error correction. To provide more realistic estimates, we estimated the surface code overhead for two benchmark systems: a superconducting qubit system and a trapped ion system. To parameterize the hardware, we use slight variations of parameters from recent demonstrations of error correction in each system (Chen et al., 2021; Ryan-Anderson et al., 2021), which are summarized in Table 2. The results are plotted in Figure 3 for our benchmark small molecules. The much lower error rates of the trapped ion system used (3e-5 vs. 5e-4 for the superconducting qubit system) allow for smaller surface code distances, d, and, hence, smaller numbers of physical qubits. The total runtime is several orders of magnitude higher, due to the increased cycle time (70 ms vs. 1μs for the superconducting qubit system). This leads to several orders of magnitude increase in the total space-time (measured in qubit-seconds) of the algorithm. These results point to the need for fast cycle times to achieve reasonable runtimes for quantum chemistry algorithms on quantum computers. Tabulated data for both physical qubit count and total runtime can be found in the Supplementary Materials for both architectures.

TABLE 2

TABLE 2. Hardware parameters used in the error correction calculations. *Error rates used are two orders of magnitude lower than reported in Refs. (Chen et al., 2021; Ryan-Anderson et al., 2021), due to the need to be below the standard surface code threshold of 1e-3. ^†The cycle time of 70 ms for the trapped ion is a third of that reported in Ref (Ryan-Anderson et al., 2021), as their protocol was a more complicated color code protocol.

FIGURE 3

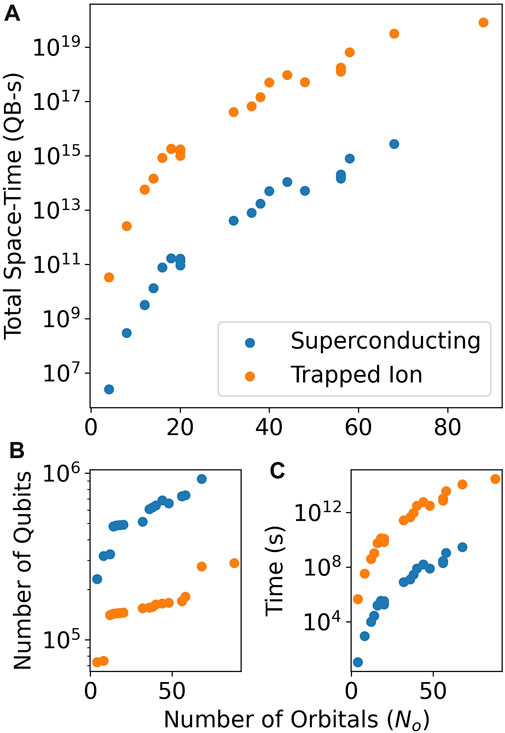
FIGURE 3. Estimated total resources with hardware and surface code error correction overheads included for QREChem’s Trotter algorithm. The total space-time volume (shown in (A)), in qubit-seconds, is larger for a trapped ion system compared with a superconducting qubit system. While the number of physical qubits is smaller for a trapped ion system due to the lower error rates (see (B)), the total time (see (C)) is much higher due to the slower error correction cycle time.

The data used in Figure 2 in collated in tabular form in the Supplementary Materials. Further tables, including our parameter settings, the number of rotation and CNOT gates and the number of physical qubits and runtime assuming a surface code error correction scheme on both superconducting qubit and trapped ion hardware can also be found in the Supplementary Materials as can details about the code and how to reproduce the results. The code is available from https://github.com/Argonne-QIS/QREChem/.

4 Discussion

We utilized the QREChem to provide accurate logical and physical resource estimations of a simple Trotter based algorithm over a broad range of molecules. Our heuristic-based Trotter estimates offers a more realistic estimate of the true cost of using Trotter, compared with more pessimistic estimates based on worst case bounds. On large systems such as the FeMoco molecule, the resource estimates are still large and do not include the necessary overheads of initial state preparation. The initial estimates of the overheads of quantum error correction and hardware limitations are significant and point to the need to have fast operations.

Accurate logical resource estimates, as currently implemented in QREChem, is a necessary first step for the larger goal of co-desiging future fault-tolerant quantum quantum computers capable of executing high-depth quantum chemistry circuits. Co-design allows for the optimization of both the hardware and algorithmic aspects of future quantum computers to facilitate the optimization of performance, scalability, accuracy, and energy efficiency. Moreover, co-design using a future version of QREChem will ensure that the simulation algorithms are tailored to the specific characteristics of the target quantum computers, ultimately enabling more effective and realistic quantum simulations. Future developments will include a detailed examination and implementation of advanced features in the Hardware and Error Correction modules, as well as inclusion of additional quantum algorithms. These enhancements will allow QREChem to continue to provide accurate, comprehensive, and actionable resource estimates for quantum chemistry.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author contributions

MO, BK, and DF performed the simulations. MO, BK, DF, and YA contributed to the code. All authors contributed to the article and approved the submitted version.

Funding

This research used resources of the Argonne Leadership Computing Facility, which is a U.S. Department of Energy Office of Science User Facility operated under contract DE-AC02-06CH11357. This material is based upon work supported by the Defense Advanced Research Projects Agency under Contract No. HR001122C0074. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the Defense Advanced Research Projects Agency. This research was supported by the quantum computing technology development program of the National Research Foundation of Korea (NRF) funded by the Korean government (Ministry of Science and ICT(MSIT)) (No. 2021M3H3A103657313) and by the National Research Foundation of Korea (NRF) grant funded by the Korea government(MOE) (No. 2020R1I1A2074957). This research is based on work supported by Laboratory Directed Research and Development (LDRD) funding from Argonne National Laboratory, provided by the Director, Office of Science, of the U.S. Department of Energy under Contract no. DE-AC0206CH11357. Work performed at the Center for Nanoscale Materials, a U.S. Department of Energy Office of Science User Facility, was supported by the U.S. DOE, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abrams, D. S., and Lloyd, S. (1999). Quantum algorithm providing exponential speed increase for finding eigenvalues and eigenvectors. Phys. Rev. Lett. 83, 5162–5165. doi:10.1103/PhysRevLett.83.5162

CrossRef Full Text | Google Scholar

Babbush, R., Berry, D. W., Kivlichan, I. D., Wei, A. Y., Love, P. J., and Aspuru-Guzik, A. (2016). Exponentially more precise quantum simulation of fermions in second quantization. New J. Phys. 18, 033032. doi:10.1088/1367-2630/18/3/033032

CrossRef Full Text | Google Scholar

Babbush, R., McClean, J., Wecker, D., Aspuru-Guzik, A., and Wiebe, N. (2015). Chemical basis of Trotter–Suzuki errors in quantum chemistry simulation. Phys. Rev. A 91, 022311. doi:10.1103/PhysRevA.91.022311

CrossRef Full Text | Google Scholar

Berry, D. W., Childs, A. M., Cleve, R., Kothari, R., and Somma, R. D. (2015). Simulating Hamiltonian dynamics with a truncated taylor series. Phys. Rev. Lett. 114, 090502. doi:10.1103/PhysRevLett.114.090502

PubMed Abstract | CrossRef Full Text | Google Scholar

Berry, D. W., Gidney, C., Motta, M., McClean, J. R., and Babbush, R. (2019). Qubitization of arbitrary basis quantum chemistry leveraging sparsity and low rank factorization. Quantum 3, 208. doi:10.22331/q-2019-12-02-208

CrossRef Full Text | Google Scholar

Beverland, M. E., Buerschaper, O., Koenig, R., Pastawski, F., Preskill, J., and Sijher, S. (2016). Protected gates for topological quantum field theories. J. Math. Phys. 57, 022201. doi:10.1063/1.4939783

CrossRef Full Text | Google Scholar

Beverland, M. E., Murali, P., Troyer, M., Svore, K. M., Hoeffler, T., Kliuchnikov, V., et al. (2022). Assessing requirements to scale to practical quantum advantage. arXiv preprint arXiv:2211.07629.

Google Scholar

Bravyi, S., and König, R. (2013). Classification of topologically protected gates for local stabilizer codes. Phys. Rev. Lett. 110, 170503. doi:10.1103/physrevlett.110.170503

PubMed Abstract | CrossRef Full Text | Google Scholar

Campbell, E. (2019). Random compiler for fast Hamiltonian simulation. Phys. Rev. Lett. 123, 070503. doi:10.1103/physrevlett.123.070503

PubMed Abstract | CrossRef Full Text | Google Scholar

Casares, P. A., Campos, R., and Martin-Delgado, M. A. (2022). Tfermion: a non-Clifford gate cost assessment library of quantum phase estimation algorithms for quantum chemistry. Quantum 6, 768. doi:10.22331/q-2022-07-20-768

CrossRef Full Text | Google Scholar

Chen, Z., Satzinger, K. J., Atalaya, J., Korotkov, A. N., Dunsworth, A., Sank, D., et al. (2021). Exponential suppression of bit or phase flip errors with repetitive error correction. arXiv preprint arXiv:2102.06132.

Google Scholar

Chien, A. D., Holmes, A. A., Otten, M., Umrigar, C. J., Sharma, S., and Zimmerman, P. M. (2018). Excited states of methylene, polyenes, and ozone from heat-bath configuration interaction. J. Phys. Chem. A 122, 2714–2722. doi:10.1021/acs.jpca.8b01554

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Cunha, R., Otten, M., Hermes, M. R., Gagliardi, L., and Gray, S. K. (2023). State preparation in quantum algorithms for fragment-based quantum chemistry. arXiv preprint arXiv:2305.18110.

Google Scholar

Ditchfield, R., Hehre, W. J., and Pople, J. A. (1971). Self-consistent molecular-orbital methods. IX. An extended Gaussian-type basis for molecular-orbital studies of organic molecules. J. Chem. Phys. 54, 724–728. doi:10.1063/1.1674902

CrossRef Full Text | Google Scholar

Dunning, T. H. (1989). Gaussian basis sets for use in correlated molecular calculations. i. the atoms boron through neon and hydrogen. J. Chem. Phys. 90, 1007–1023. doi:10.1063/1.456153

CrossRef Full Text | Google Scholar

Foresman, J., and Frish, E. (1996). Exploring chemistry. Pittsburg, USA: Gaussian Inc.

Google Scholar

Fowler, A. G., and Gidney, C. (2018). Low overhead quantum computation using lattice surgery. arXiv preprint arXiv:1808.06709.

Google Scholar

Fowler, A. G., Mariantoni, M., Martinis, J. M., and Cleland, A. N. (2012). Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324. doi:10.1103/physreva.86.032324

CrossRef Full Text | Google Scholar

Harrow, A. W., Hassidim, A., and Lloyd, S. (2009). Quantum algorithm for linear systems of equations. Phys. Rev. Lett. 103, 150502. doi:10.1103/PhysRevLett.103.150502

PubMed Abstract | CrossRef Full Text | Google Scholar

Hastings, M. B. (2016). Turning gate synthesis errors into incoherent errors. arXiv preprint arXiv:1612.01011.

Google Scholar

Johnson, R. D. (2022). NIST computational chemistry and comparison and benchmark database, NIST standard reference database number 101, release 22. Avaliable at: https://cccbdb.nist.gov.

Google Scholar

Jordan, P., and Wigner, E. P. (1993). über das paulische äquivalenzverbot The Collected Works of Eugene Paul Wigner Heidelberg: Springer Berlin, 109–129.

CrossRef Full Text | Google Scholar

Kim, I. H., Liu, Y. H., Pallister, S., Pol, W., Roberts, S., and Lee, E. (2022). Fault-tolerant resource estimate for quantum chemical simulations: case study on li-ion battery electrolyte molecules. Phys. Rev. Res. 4, 023019. doi:10.1103/physrevresearch.4.023019

CrossRef Full Text | Google Scholar

Kitaev, A. Y. (1997). Quantum computations: algorithms and error correction. Russ. Math. Surv. 52, 1191–1249. doi:10.1070/RM1997v052n06ABEH002155

CrossRef Full Text | Google Scholar

Knowles, P. J., and Handy, N. C. (1989). A determinant based full configuration interaction program. Comput. Phys. Commun. 54, 75–83. doi:10.1016/0010-4655(89)90033-7

CrossRef Full Text | Google Scholar

Lee, J., Berry, D. W., Gidney, C., Huggins, W. J., McClean, J. R., Wiebe, N., et al. (2021). Even more efficient quantum computations of chemistry through tensor hypercontraction. PRX Quantum 2, 030305. doi:10.1103/PRXQuantum.2.030305

CrossRef Full Text | Google Scholar

Li, X. (2022). Some error analysis for the quantum phase estimation algorithms. J. Phys. A Math. Theor. 55, 325303. doi:10.1088/1751-8121/ac7f6c

CrossRef Full Text | Google Scholar

Li, Z., Li, J., Dattani, N. S., Umrigar, C., and Chan, G. K. L. (2019). The electronic complexity of the ground-state of the femo cofactor of nitrogenase as relevant to quantum simulations. J. Chem. Phys. 150, 024302. doi:10.1063/1.5063376

PubMed Abstract | CrossRef Full Text | Google Scholar

Litinski, D. (2019a). Magic state distillation: not as costly as you think. Quantum 3, 205. doi:10.22331/q-2019-12-02-205

CrossRef Full Text | Google Scholar

Litinski, D. (2019b). A game of surface codes: large-scale quantum computing with lattice surgery. Quantum 3, 128. doi:10.22331/q-2019-03-05-128

CrossRef Full Text | Google Scholar

Litinski, D., Kesselring, M. S., Eisert, J., and von Oppen, F. (2017). Combining topological hardware and topological software: color-code quantum computing with topological superconductor networks. Phys. Rev. X 7, 031048. doi:10.1103/physrevx.7.031048

CrossRef Full Text | Google Scholar

Low, G. H., Bauman, N. P., Granade, C. E., Peng, B., Wiebe, N., Bylaska, E. J., et al. (2019). Q# and nwchem: tools for scalable quantum chemistry on quantum computers. arXiv preprint arXiv:1904.01131.

Google Scholar

Low, G. H., and Chuang, I. L. (2019). Hamiltonian simulation by qubitization. Quantum 3, 163. doi:10.22331/q-2019-07-12-163

CrossRef Full Text | Google Scholar

McClean, J. R., Rubin, N. C., Sung, K. J., Kivlichan, I. D., Bonet-Monroig, X., Cao, Y., et al. (2020). OpenFermion: the electronic structure package for quantum computers. Quantum Sci. Technol. 5, 034014. doi:10.1088/2058-9565/ab8ebc

CrossRef Full Text | Google Scholar

Menickelly, M., Ha, Y., and Otten, M. (2023). Latency considerations for stochastic optimizers in variational quantum algorithms. Quantum 7, 949. doi:10.22331/q-2023-03-16-949

CrossRef Full Text | Google Scholar

Nielsen, M. A., and Chuang, I. L. (2000). Quantum computation and quantum information Cambridge: Cambridge University Press.

Google Scholar

Ortiz, G., Gubernatis, J. E., Knill, E., and Laflamme, R. (2001). Quantum algorithms for fermionic simulations. Phys. Rev. A 64, 022319. doi:10.1103/PhysRevA.64.022319

CrossRef Full Text | Google Scholar

Otten, M., Hermes, M. R., Pandharkar, R., Alexeev, Y., Gray, S. K., and Gagliardi, L. (2022). Localized quantum chemistry on quantum computers. J. Chem. Theory Comput. 18, 7205–7217. doi:10.1021/acs.jctc.2c00388

PubMed Abstract | CrossRef Full Text | Google Scholar

Peruzzo, A., McClean, J., Shadbolt, P., Yung, M. H., Zhou, X. Q., Love, P. J., et al. (2014). A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213. doi:10.1038/ncomms5213

PubMed Abstract | CrossRef Full Text | Google Scholar

Poulin, D., Hastings, M. B., Wecker, D., Wiebe, N., Doberty, A. C., and Troyer, M. (2015). The Trotter step size required for accurate quantum simulation of quantum chemistry. Quantum info. comput. 15, 361–384. doi:10.26421/qic15.5-6-1

CrossRef Full Text | Google Scholar

Preskill, J. (2018). Quantum computing in the nisq era and beyond. Quantum 2, 79. doi:10.22331/q-2018-08-06-79

CrossRef Full Text | Google Scholar

Reiher, M., Wiebe, N., Svore, K. M., Wecker, D., and Troyer, M. (2017). Elucidating reaction mechanisms on quantum computers. Proc. Natl. Acad. Sci. 114, 7555–7560. doi:10.1073/pnas.1619152114

PubMed Abstract | CrossRef Full Text | Google Scholar

Ryan-Anderson, C., Bohnet, J. G., Lee, K., Gresh, D., Hankin, A., Gaebler, J., et al. (2021). Realization of real-time fault-tolerant quantum error correction. Phys. Rev. X 11, 041058. doi:10.1103/physrevx.11.041058

CrossRef Full Text | Google Scholar

Selinger, P. (2015). Efficient Clifford+T approximation of single-qubit operators. Quantum info. comput. 15, 159–180. doi:10.26421/qic15.1-2-10

CrossRef Full Text | Google Scholar

Shor, P. (1994). “Algorithms for quantum computation: discrete logarithms and factoring,” in Proceedings 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20-22 November 1994 (IEEE), 124–134. doi:10.1109/SFCS.1994.365700

CrossRef Full Text | Google Scholar

Shor, P. W. (1999). Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 41, 303–332. doi:10.1137/S0036144598347011

CrossRef Full Text | Google Scholar

Smith, D. G., Burns, L. A., Simmonett, A. C., Parrish, R. M., Schieber, M. C., Galvelis, R., et al. (2020). Psi4 1.4: open-source software for high-throughput quantum chemistry. J. Chem. Phys. 152, 184108. doi:10.1063/5.0006002

PubMed Abstract | CrossRef Full Text | Google Scholar

Stewart, R. F. (1970). Small Gaussian expansions of slater-type orbitals. J. Chem. Phys. 52, 431–438. doi:10.1063/1.1672702

CrossRef Full Text | Google Scholar

Sun, Q., Berkelbach, T. C., Blunt, N. S., Booth, G. H., Guo, S., Li, Z., et al. (2018). PySCF: the Python-based simulations of chemistry framework. Wiley Interdiscip. Rev. Comput. Mol. Sci. 8, e1340. doi:10.1002/wcms.1340

CrossRef Full Text | Google Scholar

Sun, Q., Zhang, X., Banerjee, S., Bao, P., Barbry, M., Blunt, N. S., et al. (2020). Recent developments in the pyscf program package. J. Chem. Phys. 153, 024109. doi:10.1063/5.0006074

PubMed Abstract | CrossRef Full Text | Google Scholar

Suzuki, M. (1993). Improved trotter-like formula. Phys. Lett. A 180, 232–234. doi:10.1016/0375-9601(93)90701-z

CrossRef Full Text | Google Scholar

Svore, K., Geller, A., Troyer, M., Azariah, J., Granade, C., Heim, B., et al. (2018). “Q#: enabling scalable quantum computing and development with a high-level dsl,” in Proceedings of the real world domain specific languages workshop 2018 (New York, NY, USA: Association for Computing Machinery), RWDSL2018. doi:10.1145/3183895.3183901

CrossRef Full Text | Google Scholar

Webber, M., Elfving, V., Weidt, S., and Hensinger, W. K. (2022). The impact of hardware specifications on reaching quantum advantage in the fault tolerant regime. AVS Quantum Sci. 4, 013801. doi:10.1116/5.0073075

CrossRef Full Text | Google Scholar

Werner, H. J., Knowles, P. J., Knizia, G., Manby, F. R., and Schütz, M. (2012). Molpro: a general-purpose quantum chemistry program package. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2, 242–253. doi:10.1002/wcms.82

CrossRef Full Text | Google Scholar

Xia, R., and Kais, S. (2018). Quantum machine learning for electronic structure calculations. Nat. Commun. 9, 4195. doi:10.1038/s41467-018-06598-z

PubMed Abstract | CrossRef Full Text | Google Scholar