Impact of non-Markovian evolution on characterizations of quantum thermodynamics

Here, we study the impact of non-Markovian evolution on prominent characteristics of quantum thermodynamics such as ergotropy and power. These are benchmarked by the behavior of the quantum speed limit time. We make use of both geometric-based, particularly the quantum Fisher and Wigner–Yanase information metric, and physical properties-based measures, particularly the relative purity measure and relative entropy of coherence measure, to compute the quantum speed limit time. A simple non-Markovian model of a qubit in a bosonic bath exhibiting non-Markovian amplitude damping evolution is considered, which, from the quantum thermodynamic perspective with finite initial ergotropy, can be envisaged as a quantum battery. To this end, we explore the connections between the physical properties-based measures of the quantum speed limit time and the coherent component of ergotropy. The non-Markovian evolution is shown to impact the recharging process of the quantum battery. Furthermore, a connection between the discharging–charging cycle of the quantum battery and the geometric measures of the quantum speed limit time is observed.

1 Introduction

A realistic quantum system is subjected to the influence of the environment. The dynamics of the system are altered by this, and as a consequence, information is lost from the system to the external environment. A paradigm for examining how the ambient environment affects a quantum system is provided by the theory of open quantum systems (OQS) (Weiss, 1999; Breuer and Petruccione, 2002; Banerjee, 2018). Ideas pertaining to open quantum systems are applicable to a number of scenarios (Caldeira and Leggett, 1983; Grabert et al., 1988; Louisell, 1990; Hu and Matacz, 1994; Banerjee and Ghosh, 2000; Banerjee and Ghosh, 2003; Srikanth and Banerjee, 2008; Hughes et al., 2009; Huelga and Plenio, 2013; Iles-Smith et al., 2014; Banerjee et al., 2016; Omkar et al., 2016; Banerjee et al., 2017; Naikoo et al., 2018; Dixit et al., 2019; Tanimura, 2020). A Markovian approximation, which implies that the environment instantly recovers from its contact with the system, can be used to describe the evolution of an OQS in many situations. This results in a constant movement of information from the system to the environment. However, research has been pushed into domains beyond the Markovian evolution due to increasing technical and technological advancements. In many of these situations, a clean division between system and environment timescales cannot be anticipated, leading to non-Markovian behavior (Breuer et al., 2004; Laine et al., 2010; Lu et al., 2010; Rivas et al., 2010; Chruściński et al., 2011; Vasile et al., 2011; Breuer, 2012; Luo et al., 2012; Fanchini et al., 2014; Hall et al., 2014; Haseli et al., 2014; de Vega and Alonso, 2017; Bhattacharya et al., 2018; Kumar et al., 2018; Shrikant et al., 2018; Filippov et al., 2020; Utagi et al., 2020; Hakoshima et al., 2021; Li et al., 2023). Non-Markovian behavior, such as that caused by strong system–bath coupling, can delay decay and sometimes even cause a rebirth of quantum effects (Wang and Chen, 2013; Kumar et al., 2018; Tiwari et al., 2023). The dynamics of the quantum speed limit time, introduced below, can demonstrate how the evolution of the system of interest might alter owing to the nature of the bath (Pfeifer and Fröhlich, 1995; Deffner and Campbell, 2017).

One of the cornerstones of quantum physics is Heisenberg’s uncertainty principle. The uncertainty principle for position and momentum demonstrates that it is impossible to measure both position and momentum at the same time accurately; however, the meaning of the energy–time uncertainty relation in this statement is not immediately clear. The energy–time uncertainty principle (Δt ≥ ℏ/ΔE) is a statement about the intrinsic time in which a quantum system develops, as demonstrated by Mandelstam and Tamm (1945). Using the Fubini–Study metric on the space of quantum pure states, the concept of the quantum speed limit (QSL) time, or the speed at which a quantum system can evolve, was first presented in (Anandan and Aharonov, 1990). Margolus and Levitin (1998) gave a different QSL time depending on the mean energy. Combining the MT and ML bounds results in a tighter QSL time for unitary dynamics, limited to orthogonal pure states. QSL time alludes to the shortest period of time needed for a quantum system to evolve from one state to another. It plays a crucial role in the development of quantum technologies such as quantum computing and quantum communication. Over the years, many measures to quantify the QSL time have emerged. Here, we use geometric-based measures, particularly the Fisher and Wigner–Yanase (WY) information metrics-based measures, and the inherent dynamics-based measures, particularly relative entropy, as well as the entropy of coherence-based measures to compute the QSL time. The design and execution of quantum information processing algorithms are significantly impacted by the expansion of the QSL time to open quantum systems (Deffner and Campbell, 2017; Deffner and Lutz, 2013; del Campo et al., 2013; Pires et al., 2016). Due to its applicability to other technical areas, this has been a subject of considerable recent research (Wei et al., 2016; O’Connor et al., 2021; Aggarwal et al., 2022; Mohan et al., 2022; Paulson and Banerjee, 2022; Baruah et al., 2023; Shahri et al., 2023; Tiwari et al., 2023). Furthermore, the idea of the lower bound for the time required to transform an initial state to a final state in a non-Markovian environment is an important area to explore from the perspective of quantum thermodynamics (Funo et al., 2019; Das et al., 2021).

The fundamental laws of thermodynamic equilibrium and non-equilibrium in the quantum regime are the subject of quantum thermodynamics (Gemmer et al., 2004; Vinjanampathy and Anders, 2016; Binder et al., 2019; Deffner and Campbell, 2019; Ali et al., 2020). The emerging field of quantum thermodynamics has grown rapidly over the last decade. The main objective of quantum thermodynamics is to extend classical thermodynamics to incorporate quantum effects and tiny ensemble sizes. This is facilitated by the rapid experimental control of quantum systems and the engineering of small environments. Effect of memory on a quantum thermodynamic system has been a recent area of interest (Thomas et al., 2018; Whitney, 2018; Czartowski et al., 2023). The extraction of maximal work from a system is an old problem in thermodynamics. It was shown (Allahverdyan et al., 2004; Çakmak, 2020) that in quantum systems, this can be quantified by the ergotropy of the system. Ergotropy has been established as an important quantity in the emerging field of quantum thermodynamics (Kosloff, 2013; Goold et al., 2016; Mitchison, 2019; Francica et al., 2020; Sone and Deffner, 2021) and has recently been measured experimentally (Van Horne et al., 2020; von Lindenfels et al., 2019).

Quantum batteries are quantum mechanical energy storage devices (Alicki and Fannes, 2013; Binder et al., 2019). The role of quantum effects on the issue of energy storage has been extensively studied in recent years (Binder et al., 2015; Andolina et al., 2018; Ferraro et al., 2018; Le et al., 2018; Kanti Konar et al., 2022; Konar et al., 2022; Mazzoncini et al., 2023). The problem of quantum battery charging and discharging has been studied in an open quantum system setting (Farina et al., 2019) along with the impact of non-Markovian evolution (Thomas et al., 2018; Kamin et al., 2020). In recent years, research on quantum batteries has gained much attention, and various methods have been employed to realize a practical quantum battery (Seah et al., 2021; Salvia et al., 2023). To this end, we aim to study a simple OQS model exhibiting non-Markovian behavior, viz., a non-Markovian amplitude damping (NMAD) evolution. We exploit characterizers of quantum thermodynamics, particularly ergotropy, along with instantaneous and average powers, to study this model from the perspective of a quantum battery. This is benchmarked by the QSL time of the evolution of the system, where we use geometric and inherent dynamics-based measures of QSL time.

This paper is organized as follows. In Section 2, we discuss the preliminaries used throughout the paper, including the discussion of QSL time, an OQS model with NMAD evolution, and ergotropy, as well as instantaneous and average powers. Section 3 discusses a direct connection between the physical properties-based measure of QSL time and the coherent component of ergotropy. We study the connection of geometrical-based measures of QSL time with ergotropy, instantaneous and average powers, and the impact of non-Markovian evolution on the discharging–charging process of quantum batteries in Section 4. This is followed by conclusion.

2 Preliminaries

This section briefly discusses the different bounds on the quantum speed limit time, a single qubit model with non-Markovian evolution modeled by the non-Markovian amplitude damping (NMAD) master equation, and ergotropy, followed by instantaneous and average powers.

2.1 Quantum speed limit (QSL) time

Here, we discuss four forms of the quantum speed limit (QSL) time. The first two are related to the geometric QSL time, where we use the quantum Fisher information and Wigner–Yanase (WY) information metrics for the geodesic distance between the initial and final state at time t. The other two measures depend on the inherent dynamics of the system, one of which is a definition of QSL time using the relative purity measure of a quantum state between the initial and final states, and the other is a QSL time based on the coherence of the initial and final states.

2.1.1 Using quantum Fisher information metric

Mandelstam and Tamm (MT)-and Margolus and Levitin (ML)-type bounds on speed limit time (Mandelstam and Tamm, 1945; Margolus and Levitin, 1998) are estimated by using the geometric approach, using the Bures angle, to quantify the closeness between the initial and final states. This approach is used to provide a bound for the initial pure state ρ₀ = |ψ₀⟩⟨ψ₀| on the quantum speed limit time (τ_QSL) (Deffner and Lutz, 2013) as

${\tau }_{\mathit{QSL}}=\max \left\{\frac{1}{{\mathrm{\Lambda }}_t^{\text{op}}},\frac{1}{{\mathrm{\Lambda }}_t^{\text{tr}}},\frac{1}{{\mathrm{\Lambda }}_t^{\text{hs}}}\right\}{\sin }^2\left[\mathcal{B}\right],(1)$

where $\mathcal{B}({\rho }_0,{\rho }_t)=\arccos \left({\left\{\mathrm{Tr}\left[\sqrt{\sqrt{{\rho }_0}{\rho }_t\sqrt{{\rho }_0}}\right]\right\}}^2\right)$, and

${\mathrm{\Lambda }}_t^{\text{op,tr,hs}}=\frac{1}{t}{\int }_0^{t}ds||\mathcal{L}\left({\rho }_s\right)|{|}_{\text{op,tr,hs}}.(2)$

The three norms ||⋅||_op, ||⋅||_tr, and ||⋅||_hs are the operator, trace, and Hilbert–Schmidt norms, respectively. $\mathcal{L}$ is the Liouvillian superoperator acting on ρ. From the norm inequalities, it can be shown that the operator norm of the generator provides a tighter bound on the quantum speed limit time.

2.1.2 Using Wigner–Yanase information metric

Here, we make use of the Wigner–Yanase information metric given by

$\mathcal{B}\left({\rho }_0,{\rho }_t\right)=\arccos \left(\mathrm{Tr}\left[\sqrt{{\rho }_0}\sqrt{{\rho }_t}\right]\right),(3)$

in the expression of the QSL time given in Eq. 1. The QSL time obtained using this metric is ${\tilde{\tau }}_{\mathit{QSL}}$. In (Pires et al., 2016), it was shown that by using this metric, one can obtain an upper bound on the QSL time in the case of mixed states.

2.1.3 QSL time using relative purity measure

A bound on the QSL time for the open quantum systems can be given based on the relative purity measure given in (del Campo et al., 2013). The bound to the required time of evolution, in this case, is given as

$t\ge {\tau }_{\mathit{QSL}}^{\prime }=\frac{4{\theta }^2\mathrm{Tr}\left({\rho }_0^2\right)}{{\pi }^2\stackrel{̄}{\sqrt{\mathrm{Tr}\left[{\left({\mathcal{L}}^{†}{\rho }_0\right)}^2\right]}}},(4)$

where θ = cos⁻¹[f(t)]. $f(t)=\mathrm{Tr}({\rho }_t{\rho }_0)/\mathrm{Tr}({\rho }_0^2)$ is the relative purity measure, ρ₀ is the initial state, and ρ_t is the state evolved to time t. In the denominator, we have $\overline{(\cdot )}=t^{-1}{\int }_0^t(\cdot )ds$.

2.1.4 QSL time for the coherence

There are several widely known (basis dependent) quantum coherence measures, such as the relative entropy of coherence, the l₁ norm of coherence, the geometric coherence, and the robustness of coherence. The relative entropy of coherence is used because of its operational meaning as distillable coherence. In addition, it is also easier to work and compute compared to some other measures of coherence. For a given state ρ, the relative entropy of coherence C(ρ) defined as

$C\left(\rho \right)=S\left({\rho }^D\right)-S\left(\rho \right),(5)$

where ρ^D = ∑_i⟨i|ρ|i⟩|i⟩⟨i| is the density operator that is diagonal in the reference basis, obtained by dephasing off-diagonal elements of ρ, and S(ρ) = − Tr[ρ log  ρ] is the von Neumann entropy of the state ρ.

For an arbitrary quantum dynamics of a finite-dimensional quantum system describable as the time evolution of its state, the minimum time needed for the state ρ_t to attain coherence C(ρ_t), starting with the initial coherence C(ρ₀), is lower bounded by the quantum speed limit time for coherence (τ_CSL) given by (Mohan et al., 2022)

$t\ge {\tau }_{\mathit{CSL}}=\frac{|C\left({\rho }_t\right)-C\left({\rho }_0\right)|}{{\mathrm{\Lambda }}_t^{\text{rms},D}\overline{||\ln {\rho }_s^D|{|}_{HS}^2}+{\mathrm{\Lambda }}_t^{\text{rms}}\overline{||\ln {\rho }_s|{|}_{HS}^2}},(6)$

where ${\mathrm{\Lambda }}_t^{\text{rms},D}=\sqrt{\frac{1}{t}{\int }_0^t||{\mathcal{L}}_s({\rho }_s^D)|{|}_{HS}^{2}ds}$, ${\mathrm{\Lambda }}_t^{\text{rms}}=\sqrt{\frac{1}{t}{\int }_0^t||{\mathcal{L}}_s({\rho }_s)|{|}_{HS}^{2}ds}$, $\overline{||\ln {\rho }_s^D|{|}_{HS}^2}=\sqrt{\frac{1}{t}{\int }_0^t||\ln {\rho }_s^D|{|}_{HS}^{2}ds}$, and $\overline{||\ln {\rho }_s|{|}_{HS}^2}=\sqrt{\frac{1}{t}{\int }_0^t||\ln {\rho }_s|{|}_{HS}^{2}ds}$. ||⋅||_HS is the Hilbert–Schmidt norm, and ${\mathcal{L}}_s$ is the Liouvillian superoperator acting on ρ.

2.2 The model

We consider an example of the decay of a two-state atom into a bosonic reservoir (Breuer, 2012). The general form of the total Hamiltonian is given as

$H=H_S\otimes {\mathbb{I}}_B+{\mathbb{I}}_S\otimes H_B+H_I,(7)$

where H_S is the system’s Hamiltonian, H_B is the Hamiltonian of the reservoir, and the interaction between the system and the reservoir is given by the Hamiltonian H_I. The form of the system’s Hamiltonian is

$H_S={\omega }_0{\sigma }_{+}{\sigma }_{-},(8)$

where σ₊ = |1⟩⟨0| and σ₋ = |0⟩⟨1| are the atomic raising and lowering operators, respectively, with |0⟩(|1⟩) denoting the ground (excited) state. The environment is represented by a reservoir of harmonic oscillators given as

$H_B={\displaystyle \sum _k}{\omega }_k{a}_k^{†}{a}_k,(9)$

where a_k and $a_k^{†}$ are the bosonic creation and annihilation operators, respectively, satisfying the commutation relation $[a_k,a_{k^{\prime }}^{†}]={\delta }_{k,k^{\prime }}$. The form of the interaction Hamiltonian can be given as

$H_I={\displaystyle \sum _k}\left(g_k{\sigma }_{+}\otimes a_k+g_k^{*}{\sigma }_{-}\otimes a_k^{†}\right),(10)$

where g_k is the coupling constant. In this case, the total number of excitations in the system $N={\sigma }_{+}{\sigma }_{-}+{\sum }_k{a}_k^{†}{a}_k$ is a conserved quantity due to the rotating wave approximation. The dynamical map of the evolution of the reduced state of the system, with the bath initially in the vacuum state, was derived in (Breuer et al., 1999) and is given by the quantum master equation

$\frac{d}{dt}{\rho }_s\left(t\right)=\frac{-i}{2}S\left(t\right)\left[{\sigma }_{+}{\sigma }_{-},{\rho }_s\right]+\gamma \left(t\right)\left[{\sigma }_{-}{\rho }_s{\sigma }_{+}-\frac{1}{2}\left\{{\sigma }_{+}{\sigma }_{-},{\rho }_s\right\}\right],(11)$

where $\gamma (t)=-2\mathfrak{R}\left(\frac{\dot{G}(t)}{G(t)}\right)$, $S(t)=-2\mathfrak{I}\left(\frac{\dot{G}(t)}{G(t)}\right)$, and $\mathfrak{R}$ and $\mathfrak{I}$ represent the real and imaginary parts of the quantity inside the brackets, respectively. For a Lorentzian spectral density of the environment in resonance with the transition frequency of the qubit, the expression for the function G(t) can be given as

$G\left(t\right)=e^{-\lambda t/2}\left[\cosh \left(\frac{lt}{2}\right)+\frac{\lambda }{l}\sinh \left(\frac{lt}{2}\right)\right],(12)$

where $l=\sqrt{{\lambda }^2-2{\gamma }_0\lambda }$. Here, γ₀ describes the strength of the system–environment coupling, and λ is the spectral width related to the environment. The quantities S(t) and γ(t) in Eq. 11 provide the time-dependent frequency shift and decay rates, respectively. Furthermore, the quantity $-2\left(\frac{\dot{G}(t)}{G(t)}\right)$ can be written as

$-2\frac{\dot{G}\left(t\right)}{G\left(t\right)}=2\left(\frac{{\gamma }_0}{\sqrt{1-\frac{2{\gamma }_0}{\lambda }\coth \left(\frac{1}{2}\lambda t\sqrt{1-\frac{2{\gamma }_0}{\lambda }}\right)+1}}\right).(13)$

In the limit λ < 2γ₀, the decay rate becomes negative for certain intervals, giving rise to non-Markovian evolution, referred to as the non-Markovian amplitude damping (NMAD) evolution. In the limit λ > 2γ₀, the dynamics become time-dependent Markovian. It can also be noted that for λ ≫ γ₀, the decay rate γ(t) = γ₀, that is, it becomes time independent, and the evolution corresponds to the standard AD channel. Furthermore, using the Bloch vector representation of the single qubit density matrix, we can write the density matrix of the system at any time t as

$\rho \left(t\right)=\frac{1}{2}\left(\begin{array}{cc}\hfill 1+z\left(t\right)\hfill & \hfill x\left(t\right)-iy\left(t\right)\hfill \\ \hfill x\left(t\right)+iy\left(t\right)\hfill & \hfill 1-z\left(t\right)\hfill \end{array}\right),(14)$

where x(t) = Tr[σ_xρ(t)], y(t) = Tr[σ_yρ(t)], and z(t) = Tr[σ_zρ(t)]. For the case considered above, the analytical expression for the dynamical map was derived in (Breuer et al., 1999), which is given by

$\begin{array}{ll}\hfill {\rho }_{00}\left(t\right)& =\left(1-|G\left(t\right){|}^2\right){\rho }_{11}\left(0\right)+{\rho }_{00}\left(0\right),\hfill \\ \hfill {\rho }_{01}\left(t\right)& ={\rho }_{01}\left(0\right)G^{*}\left(t\right),\hfill \\ \hfill {\rho }_{10}\left(t\right)& ={\rho }_{10}\left(0\right)G\left(t\right),\hfill \\ \hfill {\rho }_{11}\left(t\right)& ={\rho }_{11}\left(0\right)|G\left(t\right){|}^2,\hfill \end{array}(15)$

where ρ_ij is the element of the density matrix ρ(t), which we obtain as the solution of Eq. 11 A straightforward comparison between Eqs. 15, 14 gives us x(t), y(t), and z(t) in terms of the function G(t). Thus, the Bloch vectors are given by

$\begin{array}{ll}\hfill x\left(t\right)& =2\mathfrak{R}\left[{\rho }_{10}\left(0\right)G\left(t\right)\right],\hfill \\ \hfill y\left(t\right)& =-2\mathfrak{I}\left[{\rho }_{10}\left(0\right)G\left(t\right)\right],\hfill \\ \hfill z\left(t\right)& =2{\rho }_{11}\left(0\right)|G\left(t\right){|}^2-1.\hfill \end{array}(16)$

One may note that the function G(t) in Eq. 12 produces only real values due to its structure in both regimes when l is real or imaginary. Therefore, the value of y(t) in the above equation is zero for a real initial state ρ(0).

We can envisage the system as a quantum battery in the model studied here. The battery discharges when the ergotropy (discussed in the next subsection) of the system dissipates to the environment. We start with a state with finite ergotropy, and the ergotropy vanishes due to interaction with the environment during the evolution of the system. However, due to the system’s P-indivisible non-Markovian evolution (Utagi et al., 2020), the battery recharges again as the ergotropy revives. This is highlighted in the subsequent sections.In Figure 1, we compare the QSL time obtained using the Fisher information metric (τ_QSL), Wigner–Yanase (WY) information metric $({\tilde{\tau }}_{\mathit{QSL}})$, and the relative purity measure $({\tau }_{\mathit{QSL}}^{\prime })$. The evolution of the quantum state is through the NMAD master equation defined in Eq. 11 Here, we note that the QSL time using the Fisher information metric for this model was studied in (Deffner and Lutz, 2013; Paulson et al., 2022). The initial state, in this case, is subsequently taken to be ρ(0) = |ψ₀⟩⟨ψ₀|, where $|{\psi }_0\rangle =\frac{\sqrt{3}}{2}|0\rangle +\frac{1}{2}|1\rangle$, with |0⟩ and |1⟩ being the ground and excited state of the system, respectively. It can be observed that qualitatively the QSL times obtained using the WY and Fisher information metrics are similar, with WY information giving a tighter bound on the QSL time. This is consistent with the comparison of both metrics in (Pires et al., 2016).

FIGURE 1

FIGURE 1. Comparison between QSL time obtained using Fisher information metric (τ_QSL), WY information metric $({\tilde{\tau }}_{\mathit{QSL}})$, and relative purity measure $({\tau }_{\mathit{QSL}}^{\prime })$ under the evolution of state through NMAD master equation. The parameters are ω₀ = 1, λ = 0.5, and γ₀ = 10.

2.3 Ergotropy and instantaneous and average power

Here, we define the ergotropy, followed by the instantaneous and average powers. The categorization of ergotropy as a sum of incoherent and coherence ergotropies is also defined.

2.3.1 Ergotropy

Ergotropy refers to the maximum amount of work that can be extracted from a quantum system through a cyclic unitary transformation of the initial state. The problem of maximal extraction of work was discussed in (Allahverdyan et al., 2004). For a state governed with a time-dependent Hamiltonian H_S + V(t), the time-dependent potential V(t) corresponds to the transfer of work to external sources. The process is cyclic when the external source is connected at time t = 0 and disconnected at time t = t₀, i.e., the time-dependent potential has the form V(0) = V(t₀) = 0. One then looks out for the maximum work that can be extracted from the system for an arbitrary V(t). To this effect, among all final states ${\rho }_{t_0}$ reached from the initial state ρ₀, we look for the state with the lowest final energy $E_f=\mathrm{Tr}[{\rho }_{t_0}{H}_S]$. The thermal equilibrium state ${\rho }_{t_0}^{eq}=\exp (-\beta H_S)/\mathrm{Tr}[\exp (-\beta H_S)]$ (where β = T⁻¹, with T being the Temperature) under invariant von Neumann entropy is the standard answer to this problem. The largest amount of work that can be extracted in this case is ${\mathcal{W}}_{th}=E({\rho }_0)-TS({\rho }_0)+T\log (Z)$ (Allahverdyan et al., 2004), where S(⋅) is the von Neumann entropy, and Z = Tr[exp(−βH_S)] is the partition function.

Above, two arguments are made: one where we assume that the initial state can be brought to a thermal equilibrium state, and the other is that the entropy of the system is invariant during this evolution. This is allowed for the macroscopic systems where dissipative processes within the system may occur while the system evolves under the influence of V(t). However, in the case of the finite systems, in general, the action of only the potential V(t) is not sufficient for a state to reach the thermal state in time t₀. Here, for the unitary evolution of the finite systems, not only the von Neumann entropy but also the eigenvalues of ρ are conserved. Unlike thermodynamic systems, finite systems have the memory of their initial state, and relaxation mechanisms are not involved. Therefore, in these systems, the maximum amount of work extracted $\mathcal{W}$, called ergotropy, is generally smaller than ${\mathcal{W}}_{th}$. Below, we outline the method to obtain ergotropy of the system. We assume that we are given a quantum state ρ₀ with its internal Hamiltonian H_S such that they have the following spectral decomposition:

${\rho }_0={\displaystyle \sum _i}{r}_i|r_i\rangle \langle r_i|,(17)$

and

$H_S={\displaystyle \sum _i}{\epsilon }_i|{\epsilon }_i\rangle \langle {\epsilon }_i|,(18)$

where ordering of the eigenvalues for ρ₀ and H_S is in the decreasing, r₁ ≥ r₂ ≥…, and increasing, ɛ₁ ≤ ɛ₂ ≤ …, order, respectively. Since unitary dynamics is considered, any decrease in the internal energy of the system at hand, with respect to its self-Hamiltonian H_S, will be extracted as work. Thus, in order to find the ergotropy, one aims to minimize the internal energy of the final state:

$\mathcal{W}\left({\rho }_0\right)=\mathrm{Tr}\left({\rho }_0{H}_S\right)-\min \left\{\mathrm{Tr}\left(U\rho U^{†}{H}_S\right)\right\},(19)$

where minimization is performed over all possible unitaries.

It can be shown that the final state, ${\rho }_{t_0}={\rho }_f=U\rho U^{†}$, that achieves this minimum should commute with H_S and have the same eigenvalues as ρ₀, that is, ρ_f = ∑_jr_j|ɛ_j⟩⟨ɛ_j|. This is known as the passive state because no work can be extracted from this state. The intuition for the order of eigenvalues comes from the interpretation that the highest occupation fraction r₁ of ρ₀ should occupy the lowest level. A unitary operator that performs such a transformation is U = ∑_j|ɛ_j⟩⟨r_j|. Now we can rewrite Eq. 19 as

$\mathcal{W}\left({\rho }_0\right)={\displaystyle \sum _{j,i}}{r}_j{\epsilon }_i\left(|\left.⟨r_j\right|{\epsilon }_i\rangle {|}^2-{\delta }_{ij}\right).(20)$

The ergotropy $\mathcal{W}$ depends only on the initial state and Hamiltonian of the system. The upper bound on ergotropy is given by ${\mathcal{W}}_{th}\ge \mathcal{W}\ge 0$, where ${\mathcal{W}}_{th}$ is equal to $\mathcal{W}$ when r_j = −βɛ_j − log(Z). Furthermore, ergotropy has already been studied for open quantum systems in (Kamin et al., 2020; Çakmak, 2020; Touil et al., 2021). In the previous section, we discussed a simple open quantum system modeling a non-Markovian amplitude damping channel. To calculate the ergotropy of the system, we make use of the solution ρ(t) obtained after solving Eq. 11 for any time t, and we supply it as the initial state in the Eq. 19 to find the maximum work that can be extracted from this state after a cyclic unitary transformation. Physically, the work is extracted from the system after it is detached from the bath and is now subjected to the transformation stated above.

For the state ρ(t) given in Eq. 14, one can analytically calculate the ergotropy of the system with the inherent system Hamiltonian H_S defined by Eq. 8. To this end, the eigenvalues of the state ρ(t) are $\frac{1}{2}(1\pm |a(t)|)$, where $|a(t)|=\sqrt{x{(t)}^2+z{(t)}^2}$. Note that we have dropped y(t) from the calculations because it is zero for the case considered here, as given in Eq. 16 The spectral decomposition of the $H_S={\omega }_0\left|1\right.⟩\left.⟨1\right|+0\left|0\right.⟩\left.⟨0\right|$ can now be used to find the passive state ${\rho }_f(t)=r_1\left|0\right.⟩\left.⟨0\right|+r_2\left|1\right.⟩\left.⟨1\right|$, where $2r_1=1+|a(t)|\ge 1-|a(t)|=2r_2$. The ergotropy of the system now boils down to

$\begin{array}{ll}\hfill \mathcal{W}\left(\rho \left(t\right)\right)& =\mathrm{Tr}\left(\rho \left(t\right)H_S\right)-\mathrm{Tr}\left({\rho }_f\left(t\right)H_S\right),\hfill \\ \hfill & ={\omega }_0\left(\frac{1+z\left(t\right)}{2}\right)-{\omega }_0\left(\frac{1-|a\left(t\right)|}{2}\right)=\frac{{\omega }_0}{2}\left[|a\left(t\right)|+z\left(t\right)\right],\hfill \\ \hfill & =\frac{{\omega }_0}{2}\left(\sqrt{x{\left(t\right)}^2+z{\left(t\right)}^2}+z\left(t\right)\right).\hfill \end{array}(21)$

In the above equation, z(t) denotes the population terms, and x(t) denotes the coherence terms of the state at any time t Eq. 14 The value of the ergotropy is non-zero whenever the coherence term x(t) is present in the state. It becomes zero only when x(t) is zero and z(t) is less than or equal to zero. Using the Eq. 16 and the initial state ρ(0) = |ψ₀⟩⟨ψ₀|, where $|{\psi }_0\rangle =\frac{\sqrt{3}}{2}|0\rangle +\frac{1}{2}|1\rangle$, we can write the ergotropy in terms of the function G(t) as

$\mathcal{W}\left(\rho \left(t\right)\right)=\frac{{\omega }_0}{4}\left(-2+G{\left(t\right)}^2+\sqrt{4-G{\left(t\right)}^2+G{\left(t\right)}^4}\right).(22)$

It was recently recognized (Francica et al., 2020; Sone and Deffner, 2021) that quantum ergotropy can be separated into two different (coherent and incoherent) contributions:

$\mathcal{W}={\mathcal{W}}_i+{\mathcal{W}}_c.(23)$

The incoherent ergotropy ${\mathcal{W}}_i$ denotes the maximal work that can be extracted from ρ without changing its coherence, which is defined as

${\mathcal{W}}_i\left(\rho \right)=\mathrm{Tr}\left\{\left(\rho -\sigma \right)H_S\right\},(24)$

where σ is the coherence invariant state of ρ, which has property:

$\mathrm{Tr}\left\{\sigma H_S\right\}=\underset{\mathcal{U}{\in \mathcal{U}}^{\left(i\right)}}{\min }\mathrm{Tr}\left\{\mathcal{U}\rho {\mathcal{U}}^{†}{H}_S\right\},(25)$

where ${\mathcal{U}}^{(i)}$ is the set of unitary operations without changing the coherence of ρ. Alternatively, the incoherent ergotropy can be calculated using the state ρ after erasing all its coherence terms by applying a dephasing map and then using the same method used in calculating the full ergotropy for this dephased state. That is, consider the state ρ^D = ∑_i⟨i|ρ|i⟩|i⟩⟨i|; the incoherent ergotropy ${\mathcal{W}}_i(\rho )$ for state ρ is equivalent to the ergotropy $\mathcal{W}$ of the state ρ^D. The passive state ${\rho }_f^D$, in this case, can be found in a similar way to that done previously for the calculation of ergotropy. Therefore,

${\mathcal{W}}_i\left(\rho \right)=\mathcal{W}\left({\rho }^D\right)=\mathrm{Tr}\left[\left({\rho }^D-{\rho }_f^D\right)H_S\right].(26)$

The dephased state ρ^D(t) for the state ρ(t) in Eq. 14 is given by $\frac{1}{2}\left[(1+z(t))|1\rangle \langle 1|+(1-z(t))|0\rangle \langle 0|\right]$, and the corresponding passive state ${\rho }_f^D(t)$ depends on the sign of z(t). Considering the case z(t) < 0, we find that 1 + z(t) is lesser than 1 − z(t). To this end, the passive state ${\rho }_f^D(t)$ is found to be the same as ρ^D(t); therefore, the incoherent ergotropy ${\mathcal{W}}_i(\rho (t))$ becomes zero. However, if z(t) ≥ 0, then 1 + z(t) is greater than 1 − z(t) and ${\rho }_f^D(t)=\frac{1}{2}\left[(1-z(t))|1\rangle \langle 1|+(1+z(t))|0\rangle \langle 0|\right]$. In this case, for the system Hamiltonian H_S = ω₀|1⟩⟨1|, the incoherent ergotropy is given by

${\mathcal{W}}_i\left(\rho \left(t\right)\right)=\left\{\begin{array}{cc}{\omega }_{0}z\left(t\right).\hfill & \text{for\hspace{0.17em}}z\left(t\right)\ge 0\hfill \\ 0.\hfill & \text{for\hspace{0.17em}}z\left(t\right)<0\hfill \end{array}\right.(27)$

Upon comparing the above equation with Eq. 21, we observe that for the positive z(t) and zero coherence term x(t)/2, the incoherent ergotropy ${\mathcal{W}}_i$ becomes equal to the ergotropy $\mathcal{W}$. Furthermore, the incoherent ergotropy is always positive here and obtains contribution only from the population terms of ρ(t). The incoherent ergotropy in terms of the function G(t) and the initial state ρ(0) defined above Eq. 22 is given by

${\mathcal{W}}_i\left(\rho \left(t\right)\right)=\left\{\begin{array}{cc}{\omega }_0\frac{G{\left(t\right)}^2-2}{2}.\hfill & \text{for\hspace{0.17em}}G{\left(t\right)}^2\ge 2\hfill \\ 0.\hfill & \text{for\hspace{0.17em}}G{\left(t\right)}^2<2\hfill \end{array}\right.(28)$

Moreover, it is straightforward now to obtain the expression for the coherent ergotropy ${\mathcal{W}}_c=\mathcal{W}-{\mathcal{W}}_i$ for the state ρ(t) given in Eq. 14 and system Hamiltonian H_S in Eq. 8. This is given by

${\mathcal{W}}_c\left(\rho \left(t\right)\right)=\left\{\begin{array}{cc}\frac{{\omega }_0}{2}\left(\sqrt{x{\left(t\right)}^2+z{\left(t\right)}^2}-z\left(t\right)\right).\hfill & \text{for\hspace{0.17em}}z\left(t\right)\ge 0\hfill \\ \frac{{\omega }_0}{2}\left(\sqrt{x{\left(t\right)}^2+z{\left(t\right)}^2}+z\left(t\right)\right).\hfill & \text{for\hspace{0.17em}}z\left(t\right)<0\hfill \end{array}\right.(29)$

The coherent ergotropy ${\mathcal{W}}_c$ is the work that is exclusively stored in the coherence. This can be verified from the above equation. We note here that whenever the coherence term x(t)/2 of the state ρ(t) is zero, the coherent ergotropy of the system also becomes zero. Moreover, the coherent ergotropy becomes the full ergotropy for the negative values of z(t). The expression of coherent ergotropy ${\mathcal{W}}_c$ in terms of the function G(t) and for the initial state ρ(0) can be obtained in a similar manner to that for ergotropy and incoherent ergotropy using Eq. 16 Furthermore, we outline the relationship between the coherent ergotropy and the relative entropy of coherence C(ρ) defined in Eq. 5. The expression was derived in (Francica et al., 2020) and can be given via quantum relative entropy as

$\beta {\mathcal{W}}_c\left(\rho \right)=C\left(\rho \right)+D\left({\rho }_f^D||{\rho }^{eq}\right)-D\left({\rho }_f||{\rho }^{eq}\right),(30)$

where $D(\sigma \Vert \rho )=\mathrm{Tr}\left[\sigma \left(\log \sigma -\log \rho \right)\right]$ is the quantum relative entropy, ${\rho }_f^D$ is the passive state of the dephased state ρ^D, and ρ_f is the passive state of ρ. The state ρ^eq is the Gibbs state

${\rho }^{eq}=\frac{\exp \left(-\beta H_S\right)}{Z}\text{with}Z=\mathrm{Tr}\left\{\exp \left(-\beta H_S\right)\right\},(31)$

and β = 1/k_BT, with T being the temperature. Despite the fact that in Eq. 30, temperature T is present explicitly, upon substituting the values of all the terms in the right-hand side using Eq. 14 and dividing with β, we get the same expression as in Eq. 29, i.e., free of T.

We next establish a relation between the coherent ergotropy and another quantifier of the coherence of a quantum state given by the l₁ norm of coherence (Streltsov et al., 2017), defined as

${\mathcal{C}}_{l_1}\left(\rho \right)={\displaystyle \sum _{i,j,i\ne j}}|{\rho }_{i,j}|,(32)$

For the state of the form of Eq. 14 with y(t) being zero, the value of ${\mathcal{C}}_{l_1}(\rho (t))$ is given by

${\mathcal{C}}_{l_1}\left(\rho \left(t\right)\right)=|x\left(t\right)|.(33)$

Using the above equation and Eq. 29, for the case studied here, we can write a coherent ergotropy ${\mathcal{W}}_c$ in terms of ${\mathcal{C}}_{l_1}(\rho (t))$ as

${\mathcal{W}}_c\left(\rho \left(t\right)\right)=\left\{\begin{array}{cc}\frac{{\omega }_0}{2}\left(\sqrt{{\mathcal{C}}_{l_1}{\left(\rho \left(t\right)\right)}^2+z{\left(t\right)}^2}-z\left(t\right)\right).\hfill & \text{for\hspace{0.17em}}z\left(t\right)\ge 0\hfill \\ \frac{{\omega }_0}{2}\left(\sqrt{{\mathcal{C}}_{l_1}{\left(\rho \left(t\right)\right)}^2+z{\left(t\right)}^2}+z\left(t\right)\right).\hfill & \text{for\hspace{0.17em}}z\left(t\right)<0\hfill \end{array}\right.(34)$

We note that in case the value of z(t) becomes zero, the coherent ergotropy ${\mathcal{W}}_c$ becomes directly proportional to the value of ${\mathcal{C}}_{l_1}(\rho (t))$.

2.3.2 Average and instantaneous power

The instantaneous charging power is defined by available work in the battery as

$\mathcal{P}\left(t\right)=\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{\mathcal{W}\left(t+\mathrm{\Delta }t\right)-\mathcal{W}\left(t\right)}{\mathrm{\Delta }t}=\frac{d\mathcal{W}}{dt}.(35)$

Using Eq. 21, we can write the instantaneous power $\mathcal{P}(t)$ as

$\mathcal{P}\left(t\right)=\frac{{\omega }_0}{2}\left(\frac{x\left(t\right)\dot{x}\left(t\right)+z\left(t\right)\dot{z}\left(t\right)}{\sqrt{x{\left(t\right)}^2+z{\left(t\right)}^2}}+\dot{z}\left(t\right)\right).(36)$

It is also possible to define the average power-to-energy transfer given by

${\mathcal{P}}_{av}=\frac{\mathcal{W}\left(t\right)-\mathcal{W}\left(t_0\right)}{t-t_0},(37)$

where t − t₀ refers to the charging time of the battery.

We will now see the connection between various forms of the quantum speed limit, particularly the QSL time for coherence and using the relative purity measure, and the ergotropy, with the dynamics being generated by the NMAD model.

3 Connection of the quantum speed limits with the coherent ergotropy

This section first discusses the connection between the QSL for coherence and coherent ergotropy. Furthermore, we connect the QSL time obtained using the relative purity measure and the coherent ergotropy.

3.1 Connection between the QSL for coherence and the coherent ergotropy

We can rewrite Eq. 30 for the relative entropy of coherence in terms of coherent ergotropy as

$C\left(\rho \right)=\beta {\mathcal{W}}_c\left(\rho \right)-D\left({\rho }_f^D||{\rho }^{eq}\right)+D\left({\rho }_f||{\rho }^{eq}\right).(38)$

Plugging the above equation in Eq. 6 for the state ρ(t) at time t and at time t = 0, we obtain the following relation between the QSL time for coherence τ_CSL and the coherent ergotropy ${\mathcal{W}}_c$:

${\tau }_{\mathit{CSL}}=\frac{|\beta {\mathcal{W}}_c\left(\rho \left(t\right)\right)-D\left({\rho }_f^D\left(t\right)||{\rho }^{eq}\right)+D\left({\rho }_f\left(t\right)||{\rho }^{eq}\right)-C\left(\rho \left(0\right)\right)|}{{\mathrm{\Lambda }}_t^{\text{rms},D}\overline{||\ln {\rho }_s^D|{|}_{HS}^2}+{\mathrm{\Lambda }}_t^{\text{rms}}\overline{||\ln {\rho }_s|{|}_{HS}^2}},(39)$

where $C(\rho (0))=\beta {\mathcal{W}}_c(\rho (0))-D\left({\rho }_f^D(0)||{\rho }^{eq}\right)+D\left({\rho }_f(0)||{\rho }^{eq}\right)$. Here and in the next sections, we take the initial state to be ρ(0) = |ψ₀⟩⟨ψ₀|, where $|{\psi }_0\rangle =\frac{\sqrt{3}}{2}|0\rangle +\frac{1}{2}|1\rangle$. The value of C(ρ(0)) for this initial state is around 0.56. Using the Bloch vector representation of the state ρ(t) Eq. 14, the relative entropy of coherence C(ρ(t)) is given by

$\begin{array}{ll}\hfill C\left(\rho \left(t\right)\right)& =-\left(\frac{1+z\left(t\right)}{2}\right)\log \left(\frac{1+z\left(t\right)}{2}\right)-\left(\frac{1-z\left(t\right)}{2}\right)\log \left(\frac{1-z\left(t\right)}{2}\right)\hfill \\ \hfill & +\left(\frac{1+|a\left(t\right)|}{2}\right)\log \left(\frac{1+|a\left(t\right)|}{2}\right)+\left(\frac{1-|a\left(t\right)|}{2}\right)\log \left(\frac{1-|a\left(t\right)|}{2}\right),\hfill \end{array}(40)$

where $|a(t)|=\sqrt{x{(t)}^2+z{(t)}^2}$, as y(t) is zero for the case considered here. We note here that for the given initial state ρ(0) above, the value of z(t) remains negative for the whole dynamic. Interestingly, in this case, the values of ergotropy $\mathcal{W}$ and coherent ergotropy ${\mathcal{W}}_c$ are exactly the same. Therefore, the relationship between the coherent ergotropy ${\mathcal{W}}_c$ and τ_CSL corresponds to a relationship between ergotropy $\mathcal{W}$ and τ_CSL too. Furthermore, the relative entropy of coherence C(ρ(t)) vanishes whenever x(t) is zero, and at those points in time, the ergotropy $\mathcal{W}$ and coherence ergotropy ${\mathcal{W}}_c$ are also zero. This is depicted in Figure 2. At these points in time, the τ_CSL achieves a local maximum, which is intuitive because the numerator of τ_CSL is locally maximum.In Figure 2, we can see the variation of the QSL time for coherence (τ_CSL) and the characterizers of quantum thermodynamics, particularly ergotropy $(\mathcal{W})$, coherent ergotropy $({\mathcal{W}}_C)$, and instantaneous $(\mathcal{P}(t))$ and average $({\mathcal{P}}_{av})$ powers. The region in the ergotropy curve is denoted by the brown “+” symbols, which indicate the battery’s charging process, while the black “|” symbols depict the discharging process in the given cycle from time t = 1 to 3. During the charging process, the instantaneous power is positive and negative while the battery is discharging. Furthermore, in this case, we observe that the maxima and minima of the τ_CSL are in contrast with the ergotropy and coherent ergotropy’s maxima and minima. This shows that the speed of evolution of the coherence of the state during the discharging process is getting slower. This speed hits its minimum when the ergotropy is zero. However, during the charging process, when ergotropy again becomes non-zero, the speed of evolution of the coherence increases and reaches its maximum when the battery is fully charged. We also point out here that one can take a different initial state ρ(0) and obtain some contribution to the ergotropy from the incoherent ergotropy too. However, the dynamics of the system characterized by the NMAD master equation quickly drive the system’s state in such a way that the value of z(t) becomes negative. In this case, at longer times, the coherent ergotropy eventually becomes equal to the ergotropy of the system.

FIGURE 2

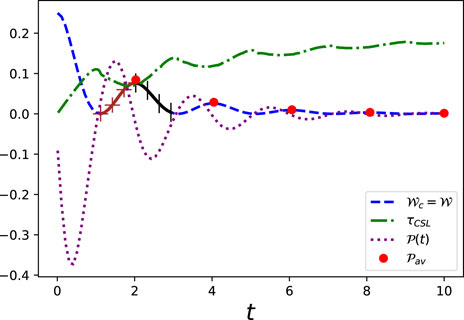
FIGURE 2. Variation of the QSL time for coherence τ_CSL, ergotropy $\mathcal{W}$, coherent ergotropy ${\mathcal{W}}_C$, instantaneous and average powers, $\mathcal{P}(t)$ and ${\mathcal{P}}_{av}$ with time. The state is evolved through the NMAD master equation. The parameters are chosen to be ω₀ = 1, λ = 0.5, and γ₀ = 10.

3.2 QSL time for relative purity measure and coherent ergotropy

Here, we start with Eq. 4 using the initial state ρ(0) used in the previous section and the Bloch vector form of the system’s state ρ(t) given in Eq. 14 at any time t. To this end, the value of Tr[ρ(0)²] is one as we have considered an initial pure state. The value of the relative purity f(t) = Tr[ρ(t)ρ(0)]/Tr[ρ(0)²] is now given by

$f\left(t\right)=\frac{1}{4}\left(2-z\left(t\right)+\sqrt{3}x\left(t\right)\right).(41)$

Furthermore, the value of the term $\sqrt{\mathrm{Tr}\left[{\left({\mathcal{L}}^{†}\rho (0)\right)}^2\right]}$ present in the denominator of Eq. 4 becomes $\sqrt{\frac{11}{8}}\left|\frac{G(s)}{\dot{G}(s)}\right|$, where the function G(s) is given in Eq. 12 Now, the QSL time obtained using the relative purity measure ${\tau }_{\mathit{QSL}}^{\prime }$ boils down to

${\tau }_{\mathit{QSL}}^{\prime }=\frac{8\sqrt{\frac{2}{11}}{\left[{\cos }^{-1}\left(\frac{1}{4}\left(2-z\left(t\right)+\sqrt{3}x\left(t\right)\right)\right)\right]}^2}{\frac{{\pi }^2}{t}{\int }_0^t\left|\frac{G\left(s\right)}{\dot{G}\left(s\right)}\right|dt}.(42)$

Here, we again mention that the value of z(t) for the given initial state ρ(0) is always negative. Therefore, the incoherent ergotropy is zero, and the coherent ergotropy is equal to the ergotropy of the system. Furthermore, we observe that in contrast to τ_CSL’s variation of the numerator, in this case, when the coherence term x(t), and the ergotropy and coherent ergotropy goes to zero, the numerator obtains a minimum value.

Figure 3 depicts the connection between the QSL time using the relative purity measure $({\tau }_{\mathit{QSL}}^{\prime })$ with ergotropy $(\mathcal{W})$, coherent ergotropy $({\mathcal{W}}_c)$ and the instantaneous $(\mathcal{P}(t))$ and average $({\mathcal{P}}_{av})$ powers. It can be observed that, in this case, the peaks and valleys of ${\tau }_{\mathit{QSL}}^{\prime }$ are in contrast with the peaks and valleys of instantaneous power. This indicates that changes in the ${\tau }_{\mathit{QSL}}^{\prime }$ pick up the maximal rate of charging or discharging of the battery—with a maximum in ${\tau }_{\mathit{QSL}}^{\prime }$ corresponding to the maximum discharging rate of the battery and a minimum in ${\tau }_{\mathit{QSL}}^{\prime }$ corresponding to the maximum charging rate—in a given charging and discharging cycle.

FIGURE 3

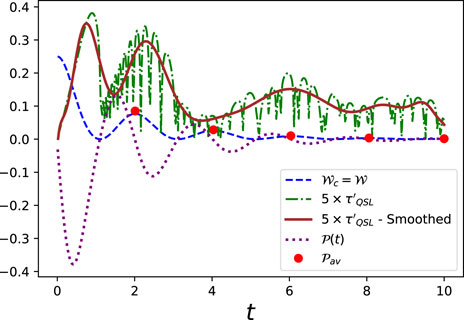
FIGURE 3. Variation of QSL time with relative purity measure $({\tau }_{\mathit{QSL}}^{\prime })$, ergotropy $(\mathcal{W})$, coherent ergotropy $({\mathcal{W}}_c)$, and instantaneous $(\mathcal{P}(t))$ and average $({\mathcal{P}}_{av})$ powers with evolution time t. The evolution is through the NMAD master equation. The parameters are taken to be ω₀ = 1, λ = 0.5, and γ₀ = 10. Note that we have scaled the value of ${\tau }_{\mathit{QSL}}^{\prime }$ by multiplying a constant factor of 5 for a better comparison of its variation with other quantities in the figure.

4 Quantum speed limit and ergotropy in non-Markovian evolution

Now, we discuss the impact of the non-Markovian evolution on the charging and discharging process of the quantum battery together with its impact on the QSL time, particularly those obtained using geometric measures. In Figure 4, the evolution of the system under Markovian evolution is depicted.Here, we observe that the system (qubit) keeps on discharging, but due to the Markovian evolution, there is no revival in the ergotropy or charging of the battery. This brings out the fact that in the present qubit–bath setup, the non-Markovian nature of the evolution plays a crucial role in highlighting the role of the system as a battery. Furthermore, the QSL time obtained using the Fisher information metric (τ_QSL) is also monotonically increasing; that is, the speed of evolution of the system keeps slowing down with time.

FIGURE 4

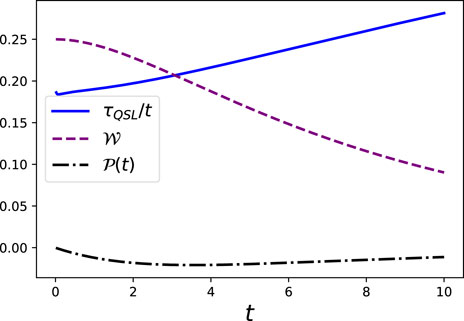
FIGURE 4. Variation of QSL time using Fisher information metric (τ_QSL), ergotropy $(\mathcal{W})$, and instantaneous $(\mathcal{P}(t))$ and average $({\mathcal{P}}_{av})$ powers with time. The evolution of the state is through the Markovian AD channel. The parameters are taken to be ω₀ = 1, λ = 0.5, and γ₀ = 0.1.

Figures 5, 6 show the variation of the QSL time obtained using the geometric measures (using Fisher and Wigner–Yanase information metrics), ergotropy, and instantaneous and average powers with time.Qualitatively, the QSL times obtained using the Fisher (τ_QSL) and WY $({\tilde{\tau }}_{\mathit{QSL}})$ information metrics show a similar pattern. In both cases, we observe that either of the peaks or valleys of the τ_QSL and ${\tilde{\tau }}_{\mathit{QSL}}$ occurs exactly at the points when a cycle of complete discharging and recharging to a maximum value is completed. This coincides with the points where the average power is calculated. The revivals in the ergotropy (or recharging of the battery) are completely due to the non-Markovian nature of the system in both figures. This also brings out a difference between the QSL time obtained using the inherent dynamics of the system, particularly the QSL time for coherence (τ_CSL in Figure 2) and the relative purity measure (${\tau }_{\mathit{QSL}}^{\prime }$ in Figure 3), and the QSL time obtained using geometric measures in Figures 5, 6. The peaks and valleys of the τ_CSL and ${\tau }_{\mathit{QSL}}^{\prime }$ specify the discharging and charging processes, being exact for τ_CSL. However, the peaks and valleys of τ_QSL and ${\tilde{\tau }}_{\mathit{QSL}}$ specify the completion of a discharging–charging cycle. This thus brings out a difference between the geometric and physical properties-based measures of the QSL time from the perspective of discharging–charging processes. It can also be seen that the speed of evolution first decreases and then increases, oscillating around a fixed point later. This again benchmarks the non-Markovian nature of the system.

FIGURE 5

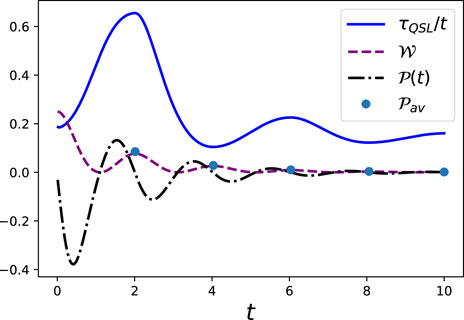
FIGURE 5. Variation of QSL time using Fisher information metric (τ_QSL), ergotropy $(\mathcal{W})$, and instantaneous $(\mathcal{P}(t))$ and average $({\mathcal{P}}_{av})$ powers with time. The evolution of the state is through the NMAD channel. The parameters are taken to be ω₀ = 1, λ = 0.5, and γ₀ = 10.

FIGURE 6

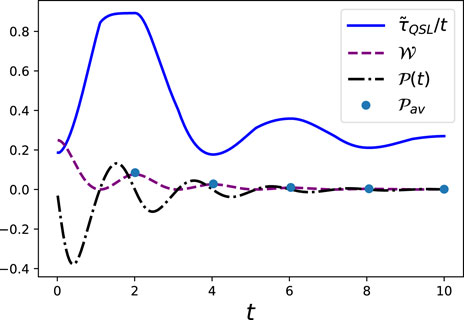
FIGURE 6. Variation of QSL time using Wigner–Yanase information metric $({\tilde{\tau }}_{\mathit{QSL}})$, ergotropy $(\mathcal{W})$, and instantaneous $(\mathcal{P}(t))$ and average $({\mathcal{P}}_{av})$ powers with time. The evolution of the state is through the NMAD channel. The parameters are taken to be ω₀ = 1, λ = 0.5, and γ₀ = 10.

5 Conclusion

Here, we have studied the impact of non-Markovian evolution on the quantities characterizing quantum thermodynamics, particularly ergotropy and its components and instantaneous and average powers. We explored the connection of these quantities with the quantum speed limit (QSL) time of evolution. The characterization of the QSL time was performed using both geometric and physical properties-based measures. Fisher and Wigner–Yanase information metrics were used for the geometric-based measures (τ_QSL and ${\tilde{\tau }}_{\mathit{QSL}}$, respectively), and relative purity and relative entropy of coherence were used for the physical properties-based measure (τ_CSL and ${\tau }_{\mathit{QSL}}^{\prime }$, respectively) of the QSL time. We considered the evolution of a single qubit system interacting with the bosonic bath through the non-Markovian amplitude damping (NMAD) master equation. Having an initial finite ergotropy, we proposed that the system could be envisaged as a quantum battery discharging into the bosonic environment.

The coherent and incoherent components of ergotropy were discussed. It was observed that due to the nature of the non-Markovian amplitude damping evolution of the state, the contribution to the ergotropy in the form of incoherent ergotropy quickly vanishes, and the coherent ergotropy becomes equivalent to the ergotropy of the system. Furthermore, direct connections between the coherent ergotropy and QSL time using relative purity and relative entropy of coherence measures were explored. It was observed that the QSL time obtained using physical properties-based measures identified the discharging and charging process of the quantum battery. This was different from the geometric-based measures that brought out the connection between the completion of the discharging–charging cycle and the change in the speed of evolution of the system. The revivals in the ergotropy of the system (or recharging of the battery) only occurred in the non-Markovian limit. It was observed that in the Markovian limit, the battery only discharged, and the speed of evolution was monotonically decreasing (the QSL time was monotonically increasing). Therefore, the non-Markovian evolution is crucial when modeling the system as a quantum battery.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

DT contributed to the methodology, software, validation, formal analysis, investigation, resources, data curation, writing—original draft, and visualization. SB contributed to the conceptualization, validation, formal analysis, investigation, resources, data curation, writing—review and editing, supervision, project administration, and funding acquisition. All authors contributed to the article and approved the submitted version.

Acknowledgments

SB acknowledges support from the Interdisciplinary Cyber-Physical Systems (ICPS) programme of the Department of Science and Technology (DST), India, grant no. DST/ICPS/QuST/Theme-1/2019/13. SB also acknowledges support from the Interdisciplinary Research Platform (IDRP) on Quantum Information and Computation (QIC) at IIT Jodhpur.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author SB declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aggarwal, S., Banerjee, S., Ghosh, A., and Mukhopadhyay, B. (2022). Non-uniform magnetic field as a booster for quantum speed limit: Faster quantum information processing. New J. Phys. 24, 085001. doi:10.1088/1367-2630/ac84f9

CrossRef Full Text | Google Scholar

Ali, M. M., Huang, W. M., and Zhang, W. M. (2020). Quantum thermodynamics of single particle systems. Sci. Rep. 10, 13500. doi:10.1038/s41598-020-70450-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Alicki, R., and Fannes, M. (2013). Entanglement boost for extractable work from ensembles of quantum batteries. Phys. Rev. E 87, 042123. doi:10.1103/physreve.87.042123

PubMed Abstract | CrossRef Full Text | Google Scholar

Allahverdyan, A. E., Balian, R., and Nieuwenhuizen, T. M. (2004). Maximal work extraction from finite quantum systems. Europhys. Lett. 67, 565–571. doi:10.1209/epl/i2004-10101-2

CrossRef Full Text | Google Scholar

Anandan, J., and Aharonov, Y. (1990). Geometry of quantum evolution. Phys. Rev. Lett. 65, 1697–1700. doi:10.1103/physrevlett.65.1697

PubMed Abstract | CrossRef Full Text | Google Scholar

Andolina, G. M., Farina, D., Mari, A., Pellegrini, V., Giovannetti, V., and Polini, M. (2018). Charger-mediated energy transfer in exactly solvable models for quantum batteries. Phys. Rev. B 98, 205423. doi:10.1103/physrevb.98.205423

CrossRef Full Text | Google Scholar

Banerjee, S., Alok, A. K., and MacKenzie, R. (2016). Eur. Phys. J. Plus 131, 1.

Banerjee, S., and Ghosh, R. (2003). General quantum Brownian motion with initially correlated and nonlinearly coupled environment. Phys. Rev. E 67, 056120. doi:10.1103/physreve.67.056120

PubMed Abstract | CrossRef Full Text | Google Scholar

Banerjee, S., and Ghosh, R. (2000). Quantum theory of a Stern-Gerlach system in contact with a linearly dissipative environment. Phys. Rev. A 62, 042105. doi:10.1103/physreva.62.042105

CrossRef Full Text | Google Scholar

Banerjee, S., Kumar Alok, S., Omkar, S., and Srikanth, S. (2017). Characterization of Unruh channel in the context of open quantum systems. J. High Energy Phys. 1, 82. doi:10.1007/JHEP02082

CrossRef Full Text | Google Scholar

Banerjee, S. (2018). Open quantum systems. Singapore: Springer.

Google Scholar

Baruah, R., Paulson, K. G., and Banerjee, S. (2023). Phase covariant channel: Quantum speed limit of Evolution. Ann. Phys. 535, 2200199. doi:10.1002/andp.202200199

CrossRef Full Text | Google Scholar

Bhattacharya, S., Banerjee, S., and Pati, A. K. (2018). Evolution of coherence and non-classicality under global environmental interaction. Quantum Inf. Process. 17, 236. doi:10.1007/s11128-018-1989-4

CrossRef Full Text | Google Scholar

Binder, F., Correa, L., Gogolin, C., Anders, J., and Adesso, G. (2019). Thermodynamics in the quantum regime: Fundamental aspects and new directions, fundamental theories of physics. Switzerland: Springer International Publishing.

Google Scholar

Binder, F. C., Vinjanampathy, S., Modi, K., and Goold, J. (2015). Quantacell: Powerful charging of quantum batteries. New J. Phys. 17, 075015. doi:10.1088/1367-2630/17/7/075015

CrossRef Full Text | Google Scholar

Breuer, H. P., Burgarth, D., and Petruccione, F. (2004). Non-Markovian dynamics in a spin star system: Exact solution and approximation techniques. Phys. Rev. B 70, 045323. doi:10.1103/physrevb.70.045323

CrossRef Full Text | Google Scholar

Breuer, H. P. (2012). Foundations and measures of quantum non-Markovianity. J. Phys. B Atomic, Mol. Opt. Phys. 45, 154001. doi:10.1088/0953-4075/45/15/154001

CrossRef Full Text | Google Scholar

Breuer, H. P., Kappler, B., and Petruccione, F. (1999). Stochastic wave-function method for non-Markovian quantum master equations. Phys. Rev. A 59, 1633–1643. doi:10.1103/physreva.59.1633

CrossRef Full Text | Google Scholar

Breuer, H. P., and Petruccione, F. (2002). The theory of open quantum systems. England: Oxford University Press, Great Clarendon Street.

Google Scholar

Çakmak, B. (2020). Phys. Rev. E 102, 042111.

PubMed Abstract |

Caldeira, A., and Leggett, A. (1983). Quantum tunnelling in a dissipative system. Ann. Phys. 149, 374–456. doi:10.1016/0003-4916(83)90202-6

CrossRef Full Text | Google Scholar

Chruściński, D., Kossakowski, A., and Rivas, A. (2011). Measures of non-Markovianity: Divisibility versus backflow of information. Phys. Rev. A 83, 052128. doi:10.1103/physreva.83.052128

CrossRef Full Text | Google Scholar

Czartowski, J., Junior, A., and Korzekwa, K. (2023). Entanglement properties of multipartite informationally complete quantum measurements. arXiv preprint arXiv:2303.12840. doi:10.48550/arXiv.2303.12840

CrossRef Full Text | Google Scholar

Das, A., Bera, A., Chakraborty, S., and Chruściński, D. (2021). Thermodynamics and the quantum speed limit in the non-Markovian regime. Phys. Rev. A 104, 042202. doi:10.1103/physreva.104.042202

CrossRef Full Text | Google Scholar

de Vega, I., and Alonso, D. (2017). Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 89, 015001. doi:10.1103/revmodphys.89.015001

CrossRef Full Text | Google Scholar

Deffner, S., and Campbell, S. (2017). Quantum speed limits: From Heisenberg’s uncertainty principle to optimal quantum control. J. Phys. A Math. Theor. 50, 453001. doi:10.1088/1751-8121/aa86c6

CrossRef Full Text | Google Scholar

Deffner, S., and Campbell, S. (2019). “Quantum thermodynamics,” in An introduction to the thermodynamics of quantum information, IOP (series) (United States: Morgan and Claypool Publishers).

CrossRef Full Text | Google Scholar

Deffner, S., and Lutz, E. (2013). Quantum speed limit for non-markovian dynamics. Phys. Rev. Lett. 111, 010402. doi:10.1103/physrevlett.111.010402

PubMed Abstract | CrossRef Full Text | Google Scholar

del Campo, A., Egusquiza, I. L., Plenio, M. B., and Huelga, S. F. (2013). Quantum speed limits in open system dynamics. Phys. Rev. Lett. 110, 050403. doi:10.1103/physrevlett.110.050403

PubMed Abstract | CrossRef Full Text | Google Scholar

Dixit, K., Naikoo, J., Banerjee, S., and Alok, A. K. (2019). Study of coherence and mixedness in meson and neutrino systems. Eur. Phys. J. C 79, 1. doi:10.1140/epjc/s10052-019-6609-7

CrossRef Full Text | Google Scholar

Fanchini, F. F., Karpat, G., Çakmak, B., Castelano, L. K., Aguilar, G. H., Farías, O. J., et al. (2014). Non-markovianity through accessible information. Phys. Rev. Lett. 112, 210402. doi:10.1103/physrevlett.112.210402

CrossRef Full Text | Google Scholar

Farina, D., Andolina, G. M., Mari, A., Polini, M., and Giovannetti, V. (2019). Charger-mediated energy transfer for quantum batteries: An open-system approach. Phys. Rev. B 99, 035421. doi:10.1103/physrevb.99.035421

CrossRef Full Text | Google Scholar

Ferraro, D., Campisi, M., Andolina, G. M., Pellegrini, V., and Polini, M. (2018). High-power collective charging of a solid-state quantum battery. Phys. Rev. Lett. 120, 117702. doi:10.1103/physrevlett.120.117702

PubMed Abstract | CrossRef Full Text | Google Scholar

Filippov, S. N., Glinov, A. N., and Leppäjärvi, L. (2020). Phase covariant qubit dynamics and divisibility. Lobachevskii J. Math. 41, 617–630. doi:10.1134/s1995080220040095

CrossRef Full Text | Google Scholar

Francica, G., Binder, F. C., Guarnieri, G., Mitchison, M. T., Goold, J., and Plastina, F. (2020). Quantum coherence and ergotropy. Phys. Rev. Lett. 125, 180603. doi:10.1103/physrevlett.125.180603

PubMed Abstract | CrossRef Full Text | Google Scholar

Funo, K., Shiraishi, N., and Saito, K. (2019). Speed limit for open quantum systems. New J. Phys. 21, 013006. doi:10.1088/1367-2630/aaf9f5

CrossRef Full Text | Google Scholar

Gemmer, J., Michel, M., and Mahler, G. (2004). “Quantum thermodynamics: Emergence of thermodynamic behavior within composite quantum systems,” in Lecture notes in physics (Berlin Heidelberg: Springer).

Google Scholar

Goold, J., Huber, M., Riera, A., del Rio, L., and Skrzypczyk, P. (2016). The role of quantum information in thermodynamics—A topical review. J. Phys. A Math. Theor. 49, 143001. doi:10.1088/1751-8113/49/14/143001

CrossRef Full Text | Google Scholar

Grabert, H., Schramm, P., and Ingold, G. L. (1988). Quantum Brownian motion: The functional integral approach. Phys. Rep. 168, 115–207. doi:10.1016/0370-1573(88)90023-3

CrossRef Full Text | Google Scholar

Hakoshima, H., Matsuzaki, Y., and Endo, S. (2021). Relationship between costs for quantum error mitigation and non-Markovian measures. Phys. Rev. A 103, 012611. doi:10.1103/physreva.103.012611

CrossRef Full Text | Google Scholar

Hall, M. J. W., Cresser, J. D., Li, L., and Andersson, E. (2014). Canonical form of master equations and characterization of non-Markovianity. Phys. Rev. A 89, 042120. doi:10.1103/physreva.89.042120

CrossRef Full Text | Google Scholar

Haseli, S., Karpat, G., Salimi, S., Khorashad, A. S., Fanchini, F. F., Çakmak, B., et al. (2014). Non-Markovianity through flow of information between a system and an environment. Phys. Rev. A 90, 052118. doi:10.1103/physreva.90.052118

CrossRef Full Text | Google Scholar

Hu, B. L., and Matacz, A. (1994). Quantum brownian motion in a bath of parametric oscillators: A model for system-field interactions. Phys. Rev. D. 49, 6612–6635. doi:10.1103/physrevd.49.6612

PubMed Abstract | CrossRef Full Text | Google Scholar

Huelga, S., and Plenio, M. (2013). Vibrations, quanta and biology. Contemp. Phys. 54, 181–207. doi:10.1080/00405000.2013.829687

CrossRef Full Text | Google Scholar

Hughes, K. H., Christ, C. D., and Burghardt, I. (2009). Effective-mode representation of non-markovian dynamics: A hierarchical approximation of the spectral density. II. Application to environment-induced nonadiabatic dynamics. J. Chem. Phys. 131, 124108. doi:10.1063/1.3226343

PubMed Abstract | CrossRef Full Text | Google Scholar

Iles-Smith, J., Lambert, N., and Nazir, A. (2014). Environmental dynamics, correlations, and the emergence of noncanonical equilibrium states in open quantum systems. Phys. Rev. A 90, 032114. doi:10.1103/physreva.90.032114

CrossRef Full Text | Google Scholar

Kamin, F. H., Tabesh, F. T., Salimi, S., Kheirandish, F., and Santos, A. C. (2020). Non-Markovian effects on charging and self-discharging process of quantum batteries. New J. Phys. 22, 083007. doi:10.1088/1367-2630/ab9ee2

CrossRef Full Text | Google Scholar

Kanti Konar, T., Patra, A., Gupta, R., Ghosh, S., and De, A. S. (2022). Multimode advantage in continuous variable quantum battery. arXiv:2210.16528.

Google Scholar

Konar, T. K., Lakkaraju, L. G. C., Ghosh, S., and Sen(De, A. (2022). Quantum battery with ultracold atoms: Bosons versus fermions. Phys. Rev. A 106, 022618. doi:10.1103/physreva.106.022618

CrossRef Full Text | Google Scholar

Kosloff, R. (2013). Quantum thermodynamics: A dynamical viewpoint. Entropy 15, 2100–2128. doi:10.3390/e15062100

CrossRef Full Text | Google Scholar

Kumar, N. P., Banerjee, S., Srikanth, R., Jagadish, V., and Petruccione, F. (2018). Non-markovian evolution: A quantum walk perspective. Open Syst. Inf. Dyn. 25, 1850014. doi:10.1142/s1230161218500142

CrossRef Full Text | Google Scholar

Laine, E. M., Piilo, J., and Breuer, H. P. (2010). Measure for the non-Markovianity of quantum processes. Phys. Rev. A 81, 062115. doi:10.1103/physreva.81.062115

CrossRef Full Text | Google Scholar

Le, T. P., Levinsen, J., Modi, K., Parish, M. M., and Pollock, F. A. (2018). Spin-chain model of a many-body quantum battery. Phys. Rev. A 97, 022106. doi:10.1103/physreva.97.022106

CrossRef Full Text | Google Scholar

Li, Y., Li, X., and Jin, J. (2023). Quantum nonstationary phenomena of spin systems in collision models. Phys. Rev. A 107, 042205. doi:10.1103/physreva.107.042205

CrossRef Full Text | Google Scholar

Louisell, W. H. (1990). Quantum statistical properties of radiation. New York: Wiley.

Google Scholar

Lu, X. M., Wang, X., and Sun, C. P. (2010). Quantum Fisher information flow and non-Markovian processes of open systems. Phys. Rev. A 82, 042103. doi:10.1103/physreva.82.042103

CrossRef Full Text | Google Scholar

Luo, S., Fu, S., and Song, H. (2012). Quantifying non-Markovianity via correlations. Phys. Rev. A 86, 044101. doi:10.1103/physreva.86.044101

CrossRef Full Text | Google Scholar

Mandelstam, L., and Tamm, I. (1945). The uncertainty relation between energy and time in non-relativistic quantum mechanics. J. Phys. 9, 249. doi:10.1007/978-3-642-74626-0_8

CrossRef Full Text | Google Scholar

Margolus, N., and Levitin, L. B. (1998). The maximum speed of dynamical evolution. Phys. D. Nonlinear Phenom. 120, 188–195. doi:10.1016/s0167-2789(98)00054-2

CrossRef Full Text | Google Scholar

Mazzoncini, F., Cavina, V., Andolina, G. M., Erdman, P. A., and Giovannetti, V. (2023). Optimal control methods for quantum batteries. Phys. Rev. A 107, 032218. doi:10.1103/physreva.107.032218

CrossRef Full Text | Google Scholar

Mitchison, M. T. (2019). Quantum thermal absorption machines: Refrigerators, engines and clocks. Contemp. Phys. 60, 164–187. doi:10.1080/00107514.2019.1631555

CrossRef Full Text | Google Scholar

Mohan, B., Das, S., and Pati, A. K. (2022). Quantum speed limits for information and coherence. New J. Phys. 24, 065003. doi:10.1088/1367-2630/ac753c

CrossRef Full Text | Google Scholar

Naikoo, J., Alok, A. K., and Banerjee, S. (2018). Study of temporal quantum correlations in decoheringBandKmeson systems. Phys. Rev. D. 97, 053008. doi:10.1103/physrevd.97.053008

CrossRef Full Text | Google Scholar

O’Connor, E., Guarnieri, G., and Campbell, S. (2021). Action quantum speed limits. Phys. Rev. A 103, 022210. doi:10.1103/physreva.103.022210

CrossRef Full Text | Google Scholar

Omkar, S., Banerjee, S., Srikanth, R., and Alok, A. K. (2016). The Unruh effect interpreted as a quantum noise channel. Quantum Inf. Comput. 16, 757–770. doi:10.26421/qic16.9-10-2

CrossRef Full Text | Google Scholar

Paulson, K. G., and Banerjee, S. (2022). Quantum speed limit time: Role of coherence. J. Phys. A Math. Theor. 55, 505302. doi:10.1088/1751-8121/acaadb

CrossRef Full Text | Google Scholar

Paulson, K. G., Banerjee, S., and Srikanth, R. (2022). The effect of quantum memory on quantum speed limit time for CP-(in)divisible channels. Quantum Inf. Process. 21, 335. doi:10.1007/s11128-022-03675-7

CrossRef Full Text | Google Scholar

Pfeifer, P., and Fröhlich, J. (1995). Generalized time-energy uncertainty relations and bounds on lifetimes of resonances. Rev. Mod. Phys. 67, 759–779. doi:10.1103/revmodphys.67.759

CrossRef Full Text | Google Scholar

Pires, D. P., Cianciaruso, M., Céleri, L. C., Adesso, G., and Soares-Pinto, D. O. (2016). Generalized geometric quantum speed limits. Phys. Rev. X 6, 021031. doi:10.1103/physrevx.6.021031

CrossRef Full Text | Google Scholar

Rivas, A., Huelga, S. F., and Plenio, M. B. (2010). Entanglement and non-markovianity of quantum evolutions. Phys. Rev. Lett. 105, 050403. doi:10.1103/physrevlett.105.050403

PubMed Abstract | CrossRef Full Text | Google Scholar

Salvia, R., Perarnau-Llobet, M., Haack, G., Brunner, N., and Nimmrichter, S. (2023). Quantum advantage in charging cavity and spin batteries by repeated interactions. Phys. Rev. Res. 5, 013155. doi:10.1103/physrevresearch.5.013155

CrossRef Full Text | Google Scholar

Seah, S., Perarnau-Llobet, M., Haack, G., Brunner, N., and Nimmrichter, S. (2021). Quantum speed-up in collisional battery charging. Phys. Rev. Lett. 127, 100601. doi:10.1103/physrevlett.127.100601

PubMed Abstract | CrossRef Full Text | Google Scholar

Shahri, Y., Hadipour, M., Haddadi, S., Dolatkhah, H., and Haseli, S. (2023). Quantum speed limit of Jaynes-Cummings model with detuning for arbitrary initial states. Phys. Lett. A 470, 128783. doi:10.1016/j.physleta.2023.128783

CrossRef Full Text | Google Scholar

Shrikant, U., Srikanth, R., and Banerjee, S. (2018). Non-Markovian dephasing and depolarizing channels. Phys. Rev. A 98, 032328. doi:10.1103/physreva.98.032328

CrossRef Full Text | Google Scholar

Sone, A., and Deffner, S. (2021). Quantum and classical ergotropy from relative entropies. Entropy 23, 1107. doi:10.3390/e23091107

PubMed Abstract | CrossRef Full Text | Google Scholar

Srikanth, R., and Banerjee, S. (2008). Squeezed generalized amplitude damping channel. Phys. Rev. A 77, 012318. doi:10.1103/physreva.77.012318

CrossRef Full Text | Google Scholar

Streltsov, A., Adesso, G., and Plenio, M. B. (2017). Colloquium: Quantum coherence as a resource. Rev. Mod. Phys. 89, 041003. doi:10.1103/revmodphys.89.041003

CrossRef Full Text | Google Scholar

Tanimura, Y. (2020). Numerically “exact” approach to open quantum dynamics: The hierarchical equations of motion (HEOM). J. Chem. Phys. 153, 020901. doi:10.1063/5.0011599

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomas, G., Siddharth, N., Banerjee, S., and Ghosh, S. (2018). Thermodynamics of non-Markovian reservoirs and heat engines. Phys. Rev. E 97, 062108. doi:10.1103/physreve.97.062108

PubMed Abstract | CrossRef Full Text | Google Scholar

Tiwari, D., Paulson, K. G., and Banerjee, S. (2023). Quantum correlations and speed limit of central spin systems. Ann. Phys. 535, 2200452. doi:10.1002/andp.202200452

CrossRef Full Text | Google Scholar

Touil, A., Çakmak, B., and Deffner, S. (2021). Ergotropy from quantum and classical correlations. J. Phys. A Math. Theor. 55, 025301. doi:10.1088/1751-8121/ac3eba

CrossRef Full Text | Google Scholar

Utagi, S., Srikanth, R., and Banerjee, S. (2020). Temporal self-similarity of quantum dynamical maps as a concept of memorylessness. Sci. Rep. 10, 15049. doi:10.1038/s41598-020-72211-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Horne, N., Yum, D., Dutta, T., Hänggi, P., Gong, J., Poletti, D., et al. (2020). Single-atom energy-conversion device with a quantum load. npj Quantum Inf. 6, 37. doi:10.1038/s41534-020-0264-6

CrossRef Full Text | Google Scholar

Vasile, R., Maniscalco, S., Paris, M. G. A., Breuer, H. P., and Piilo, J. (2011). Quantifying non-Markovianity of continuous-variable Gaussian dynamical maps. Phys. Rev. A 84, 052118. doi:10.1103/physreva.84.052118

CrossRef Full Text | Google Scholar

Vinjanampathy, S., and Anders, J. (2016). Quantum thermodynamics. Contemp. Phys. 57, 545–579. doi:10.1080/00107514.2016.1201896

CrossRef Full Text | Google Scholar

von Lindenfels, D., Gräb, O., Schmiegelow, C. T., Kaushal, V., Schulz, J., Mitchison, M. T., et al. (2019). Spin heat engine coupled to a harmonic-oscillator flywheel. Phys. Rev. Lett. 123, 080602. doi:10.1103/physrevlett.123.080602

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C., and Chen, Q. H. (2013). Exact dynamics of quantum correlations of two qubits coupled to bosonic baths. New J. Phys. 15, 103020. doi:10.1088/1367-2630/15/10/103020

CrossRef Full Text | Google Scholar

Wei, Y. B., Zou, J., Wang, Z. M., and Shao, B. (2016). Quantum speed limit and a signal of quantum criticality. Sci. Rep. 6, 19308. doi:10.1038/srep19308

PubMed Abstract | CrossRef Full Text | Google Scholar

Weiss, U. (1999). “Quantum dissipative systems,” in Series in modern condensed matter physics (Singapore: World Scientific).

CrossRef Full Text | Google Scholar

Whitney, R. S. (2018). Non-Markovian quantum thermodynamics: Laws and fluctuation theorems. Phys. Rev. B 98, 085415. doi:10.1103/physrevb.98.085415

CrossRef Full Text | Google Scholar