NV-centers in SiC: A solution for quantum computing technology?

Spin S = 1 centers in diamond and recently in silicon carbide, have been identified as interesting solid-state qubits for various quantum technologies. The largely-studied case of the nitrogen vacancy center (NV) in diamond is considered as a suitable qubit for most applications, but it is also known to have important drawbacks. More recently it has been shown that divacancies (V_SiV_C)° and NV (V_SiN_C)^- centers in SiC can overcome many of these drawbacks such as compatibility with microelectronics technology, nanostructuring and n- and p-type doping. In particular, the 4H-SiC polytype is a widely used microelectronic semiconductor for power devices for which these issues are resolved and large-scale substrates (300mmm) are commercially available. The less studied 3C polytype, which can host the same centers (VV, NV), has an additional advantage, as it can be epitaxied on Si, which allows integration with Si technology. The spectral range in which optical manipulation and detection of the spin states are performed, is shifted from the visible, 632 nm for NV centers in diamond, to the near infrared 1200–1300 nm (telecom wavelength) for divacancies and NV centers in SiC. However, there are other crucial parameters for reliable information processing such as the spin-coherence times, deterministic placement on a chip and controlled defect concentrations. In this review, we revisit and compare some of the basic properties of NV centers in diamond and divacancies and NV centers in 4H and 3C-SiC.

1 Introduction

In the search for a system which can provide technologically implementable, cost-effective and easy-to-deploy platform for various quantum technology applications, some paramagnetic point defects (Weber et al., 2010) in semiconductor materials seem to stand heads and shoulders above other candidates such as cold atoms (Beterov, 2020), trapped ions (Bruzewicz et al., 2019), and even technologically implemented superconductor-based systems (Arute et al., 2019); it seems that they yet have not been given the attention they deserve in the field of information technology.

These solid-state qubits, based on point defects with levels in the band gap of their host, are characterized by degenerate electronic ground states, the degeneracy of which can be removed either by the application of a magnetic field or via electric fields and spin-orbit interaction giving rise to the zero-field splitting (ZFS) (Lommer et al., 1988). These defects have to be in a specific charge state obtained by Fermi level engineering in order to have the required spin state S<=1; then the manipulation of their spin states via the application of appropriate microwave and optical pulses is considered as a practical route for information registration and processing. A key property is the presence of excited states within the band gap of the material, which allow the optical manipulation of the spin states and an optical read-out via the photoluminescence intensity (Weber et al., 2010). The spin-selective recombination from the excited state to the ground state spin state is a mean to readout the registered information. Combined with the possibility of optical re-initialization of the qubit after each readout through recombination through intermediate singlet states (Chakraborty et al., 2017), such solid-state qubits satisfy the well-known criteria proposed by Divincenzo for the realization of a quantum information system (DiVincenzo, 2000). More interestingly, all these processes, in the case of defect-based spin-qubits, are achievable through relatively simple experimental setups such as optically detected magnetic resonance and as shown recently also by photoelectric magnetic resonance (ODMR and PDMR respectively) measurements (Falk et al., 2013; Bourgeois et al., 2020).

Solid-state qubits in semiconductor materials are by far more advantageous over other solid-state qubits, due to their compatibility with the present microelectronic technology (de Leon et al., 2021). Large band gap semiconductors such as SiC and diamond are known as optimal matrices to host qubits in an electronically isolated environments (Balasubramanian et al., 2009), compared to vacuum chambers required to for implementation of trapped ions (Kaufmann et al., 2017). Also, compared to quantum dots where the physical properties considerably vary from one center to the other, isolated point defects in a specific host have close to identical characteristics (Kloeffel and Loss, 2013). This makes them reliable candidates for qubit applications which require defects with identical properties when addressing them optically or with microwaves.

While several color centers in both diamond and SiC have been identified as suitable, the focus of the research, in the past few years has mainly been upon the negatively charged NV center in diamond (Pezzagna and Meijer, 2021) and the neutral di-vacancy VV in SiC (Anderson et al., 2022). These defects have intrinsic properties based on their electronic structure, groundstate/first excited state, and interesting spin coherence times, Debye factors and second order correlation factors. Meanwhile the analogue of the NV center in diamond, the NV center in SiC, have been discovered and investigated in detail in different SiC polytypes (3C, 4H, 6H) (von Bardeleben et al., 2016). We will show that for practical applications, apparently NV centers in SiC are more advantageous (Figure 1) over the two former centers. In this manuscript, we revisit the previous studies on each of these systems, and show why the NV centers in SiC are favored.

FIGURE 1

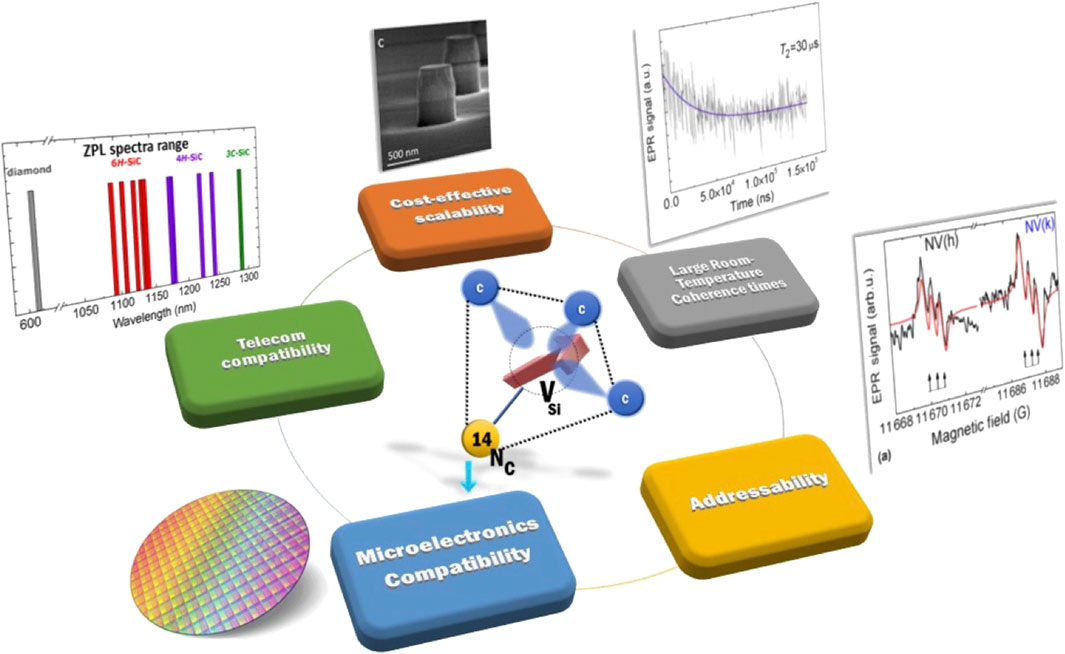
FIGURE 1. The determining parameters in comparison between the various solid-state spin qubits with the highest potential to be applied in the future quantum computing and related technologies.

2 Defect formation and electronic configurations

The NV center in diamond is a point defect with a 0/- level deep in the band gap of diamond (5.5eV). It is formed by a carbon substituted nitrogen atom in the nearest neighbor position of a carbon vacancy. Nitrogen doping is generally performed by ion implantation which at the same time introduces carbon monovacancies, the second ingredient to form NV centers, with energies of keV to MeV giving a yield of NV formation <50% (Pezzagna et al., 2010). Post-implantation thermal treatment at temperatures around 600°C–800°C is then required to induce diffusion of the vacancies and the formation of nitrogen vacancy pairs. As in the annealing considerable number of vacancies can be captured by other type defects (other than nitrogen ions), electron irradiation at kinetic energies of 1 MeV can enhance their concentration and improve the yield of NV formation (Newton et al., 2002). It has trigonal C_3v symmetry oriented along the [111] direction of the diamond structure (Walker, 1979). Among the various stable charge states, namely, NV⁰, NV⁺¹ and NV⁻¹, it is only the latter which is of interest for qubit applications. The NV- center is characterized by a triplet ground state, ³A, with total spin S = 1 and a charge transition level at E = 2.545 eV from the top of the valance band (Subedi et al., 2019). The Hamiltonian H of a spin S = 1 center is given by:

$\mathit{H}={\mathit{D}\mathit{S}}_{\mathit{z}}+{\mathit{\gamma }}_{\mathit{S}}\overrightarrow{\mathit{S}}\overrightarrow{\mathit{B}}+\overrightarrow{\mathit{S}}\stackrel{═}{\mathit{A}}\overrightarrow{\mathit{B}}+{\mathit{\gamma }}_{\mathit{I}}\overrightarrow{\mathit{I}}\overrightarrow{\mathit{B}}(1)$

For the NV⁻ center in diamond the zero-field splitting D of the ground-state levels m_s = 0, and m_s = ±1 is D = 2.87 GHz (Wrachtrup and Jelezko, 2006). The first excited state (³E triplet) is at 1.94 eV, which situates the zero phonon lines (ZPL) at λ = 637 nm (Chen et al., 2011). Of crucial importance is the existence of intermediate singlet states, ¹A₁,¹E₁ below the ³E state (Goldman et al., 2015), which allow to optically polarize the spins of the ground-state (Tetienne et al., 2012). To obtain the NV centers in the negative charge state the control of the Fermi level is required (Deák et al., 2014). Donor doping of the samples (Lühmann et al., 2019), hydrogen passivation (Mittiga et al., 2018), and electric field gating of the samples (Schreyvogel et al., 2016) have been shown to solve this problem. While the deep electronic level of the NV center in insulating matrix of diamond is a determining parameter to isolate them from environmental disturbance, still the readout of the qubits at room temperature is a limiting problem. In this context, one of the proposed strategies is the information transfer from electron spins to nuclear spins trough electron-nuclear spins interaction, using SWAP gates (Dolde et al., 2014). In this single shot process, using the relevant microwave pulse sequences, the spin state of the electrons are transferred to doublet nuclear spins prior to readout and then retransferred to them in order to prevent state modification upon quantum measurement. Electron-nuclear spins interactions are achieved, due to their short-range effectiveness, wherever the defect is in the vicinity of a non-zero nuclear spin. This is achieved either by the coupling to naturally present ¹³C isotopes (Smeltzer et al., 2011) or the implanted ones (Haruyama et al., 2019); their location is obviously uncontrollable (even though the interaction is very strong), or via ¹⁴N (I = 1) and ¹⁵N (I = 1/2) implantation (Rabeau et al., 2006) and doping (Felton et al., 2009). The dipolar hyperfine interaction has a 1/r³ distant dependence and its strength is only a few MHz (between 2 and 5 MHz) for nearest neighbor nitrogen atoms (Gali et al., 2008).

It was pointed out that several color centers in SiC present similar properties as NV center in diamond. In fact, the most studied polytypes of SiC, namely 3C and 4H have large indirect band gaps (E_G = 2.2 eV and 3.2 eV) respectively (Zhao and Bagayoko, 2000; Gali, 2009) in which the defect states can be well isolated. Color centers, such as the silicon/carbon divacancy pairs, V_SiV_C, in hexagonal 4H-SiC, have particularly been in the center of the research (Christle et al., 2017). This defect has been observed as a native defect at low 10¹⁵cm⁻³ concentrations in bulk 4H-SiC substrates (Koehl et al., 2011); but by high energy electron irradiation a large concentrations (>10¹⁸cm⁻³) can be generated in a controlled way (Hazdra and Vobecký, 2019; Crook et al., 2020). Here, again, post-irradiation annealing, at typical temperatures T = 850°C–1,050°C, is required for silicon monovacancy diffusion and V_SiV_C pair formation (Son and Ivanov, 2021). However, contrary to diamond, different type of NV centers can be formed depending on the lattice site of the carbon vacancy - 4H-SiC has two non-equivalent carbon sites with hexagonal (h) or quasi-cubic (k) neighboring symmetries and the location of the N atom, on-axis or in the (0001) plane (Davidsson et al., 2018). Thus we have two axial NV centers (kk,hh) and two basal NV centers (hk, kh). In addition, divacancy centers in the vicinity of stacking faults generate an additional variety, which results in the possible formation of seven distinct VV centers with slightly different magneto-optical properties (Ivády et al., 2019). For instance, the photoluminescence peaks (PL 1–7) vary from 1,037 to 1,132 nm in the near-infrared range, increasing their selectivity and addressability as distinguishable color centers. Their Debye-Waller factor of 5.3% (Christle et al., 2017) for isolated defects in epitaxial non-enriched layers, can be significantly increased to 75% using nanocavities (Gordon et al., 2015). The relatively small electron-phonon interaction is also reflected in the negligible Stokes shift of the optical absorption and photoluminescence spectra (60 nm) (Gordon et al., 2015). The VV centers has various stable charge states in 4H-SiC, among which the neutral state with S = 1 is of interest. Its groundstate zero-field splitting varies between 1.14 GHz and 1.365 GHz for the four distinct divacancies in 4H-SiC (Falk et al., 2013). The temperature dependence of the ZFS parameter D has been interpreted in the Debye model (Lin et al., 2021). Further, each divacancy defect, has its specific hyperfine structure related to ¹³C (I =1/2) and ²⁹Si (I = 1/2) neigbours. This increases the scalability of the defect and the number of addressable qubit states. In the case of proximity to ²⁹Si isotopes the so-called PL1-PL4 defects (kk,hh,hk,kh) have hyperfine splittings ranging from 9 to 13 MHz (Falk et al., 2015). The swap and CNOT gates between the nuclear and electronic spins for transferring the polarization states (information) have been realized via various MW pulse sequences (Bourassa et al., 2020). The time required to perform the gate is of the order of µs whereas the coherence time of the defect in the presence of electron-nuclear spin interaction is in the order of ms (1,000 operations); sufficient for error correction deployment.

While the divacancy color centers in 4H-SiC has gained a lot of attention for quantum technology applications, the NV center, i.e., the V_SiN_C pair defect, was also identified in the three main polytypes 3C,4H, 6H (Zargaleh et al., 2018a; von Bardeleben et al., 2015; Khazen et al., 2019; Csóré et al., 2017) and shown to combine the advantages of both systems. Similar to diamond, the center is formed by a nitrogen substitutional (N_C) defect paired to a vacancy (V_Si), and similar to divacancies in SiC, depending on the polytype in which it is formed, it exists in various configurations with non-equivalent magneto-optical properties. For instance, in 4H we have four and in 6H in six distinct NV center configurations. The nitrogen impurity in SiC is a low concentration native defect (Nashiyamal et al., 1992) and higher concentrations can be obtained by doping during the growth (Slack and Scace, 1965; Ivanov et al., 1996) or by ion implantation (Hirano and Inada, 1995; Gimbert et al., 1999). Silicon and carbon monovacancies can be generated by electron irradiation at energies E > 100 keV and it is again the post irradiation annealing at T = 700°C, which finalize the pair formation. For NV centers in SiC it is the negative charge state–as in diamond-which produces the interesting qubit. The spin-photon interface has already been demonstrated in the case of negatively charged NV centers with a S = 1 ground state and a ZFS parameter D of 1.3GHz; is numerical value is polytype-, symmetry- and temperature dependent (see Table 1) (Csóré et al., 2017). The first excited state E₁ is located within the band gap for all NV center and polytypes. The lowest energy optical transition is in the infrared range (1100–1300 nm) (see Table 1 for details) (Zargaleh et al., 2018b; Khazen et al., 2019; von Bardeleben et al., 2021) and interestingly due to this energy range, contrary to NV center in diamond, the photoexcitation, does not lead to a simultaneous photoionization (Fu et al., 2010; Löfgren et al., 2020). This eliminates blinking effects, making the NV centers much more practical for quantum information applications. As for NV centers in diamond and VV in SiC the presence of an intermediate singlet state allows optically induced ground state spin polarization. The NV center in SiC has been shown both theoretically and experimentally to be a single photon emitter with a small second order correlation factor g² = 0.03 (Wang et al., 2020a). The NV centers are also expected to present high quantum efficiency due to their small Huang-Rhys factor of 2.64 and 2.85 for 4H and 3C-SiC respectively (Hashemi et al., 2021; von Bardeleben et al., 2021), and the larger Debye-Waller factor at both low and high temperatures (two-fold enhancement) (von Bardeleben et al., 2021). Their weak electron-phonon interactions with the lattice shows up in the low temperature photoluminescence spectra. They present high intensity ZPL photoluminescence lines observable up to T = 100K (Zargaleh et al., 2018a). At higher temperatures (T = 300K) the phonon sidebands are clearly dominating and can be used for optical readout of the spin state (Wang et al., 2020b), again in analogy to the NV center in diamond and the divacancy centers in SiC. A further important parameter is the count rate of the collected photons; it does not only depend on the physical properties (quantum efficiency) of the defect itself, but also on the total reflection of the surface (sample dependence), interference of other defects and the collection efficiency (measurement setup dependence). In the case of NV center in diamond it has been shown that the photoluminescence emission reaches a saturated value of the order of 10⁸ counts/s as a function of laser power. Due to experimental and sample dependent limitations, the experimental count rates are often only a few percent of this value decreasing the sensitivity of this system. However, using photocurrents as a probe of the spin state, one can increase the sensitivity by two orders of magnitude (Bourgeois et al., 2020). The reported count rates for single NV center in 4H-SiC are in the same range as for NV centers in diamond (30kc/s) (Zargaleh et al., 2016); up to now, no PDMR measurements have yet been reported for NV centers in SiC. From EPR measurements the hyperfine interaction between the spin of electronic states and the neighboring ¹³C and ¹⁴N nuclear spins has been determined (Csóré et al., 2017). It was pointed out that this property is essential for storage of the information, prior to its readout process, which eventually would destroy the information written in the electronic states. Hence, even though the application of any intra-atomic quantum gate, such as SWAP, has not yet been demonstrated for NV centers in SiC, they have all the potential to be efficient. Moreover, a major advantage of NV center compared to divacancies is that they benefit from the presence an on-site nuclear spin with 14N atoms. This, indeed largely facilitates the control over the location and magnitude of the interactions, particularly in isotopically purified samples, where one eliminate the randomly distributed nuclear spins.

TABLE 1

TABLE 1. List of the measured determining parameters used for comparing the candidate defects.

3 Coherence times

Spin coherence times, T1 and T2 (or T2*), have been obtained via ODMR from Ramsey oscillation and Hahn echo measurements. They correspond to the spin–lattice relaxation times between two electron states and the time the superposed states persist before dephasing occurs, respectively. Hence, they determine the time during which various quantum gates and readout procedures can be applied in a reliable way. The determination of intrinsic T1 and T2 times is rather complicated, as they are highly sensitive to the presence of spins in the defect environment. The spin coherence can be disturbed via interactions with the neighboring defects via spin-spin interactions, via nuclear spin-electronic spin interactions, structural defects, electron-spin interactions with surrounding charges, environmental noises as inhomogeneous electric and magnetic fields, and also with spin-phonon interactions, which become particularly important at high temperatures. This, on one hand led to numerous reports with different experimentally determined coherence times for the same defect, and on the other hand, has led to new approaches to minimize these effects. The very first of these attempts concerned the isolation of the defects and the use of isotopically modified material to reduce the influence of ²⁹Si with a nuclear spin I = 1/2 (Christle et al., 2014). Other protocols include specific decoupling microwave pulse sequences and microwave dressings to extrinsically isolate the defects during the gate applications (Miao et al., 2020). To date, the highest reported values for NV centers in diamond, are T₁ > 1 h and T₂ = 1s at 4K (Abobeih et al., 2018). The dephasing time T₂ is the limiting parameter of the coherence as T₁ is orders of magnitude larger at low temperatures (where the contribution of the phonons is small enough). Even at high temperatures, as the phonon contribution to dephasing increases significantly, both the coherence times and their differences are reduced (they can become comparable). For instance, at room temperature the values for NV in diamond reach T1 = 6 ms and T2 = 3.3 ms, as determined by multiple decoupling pulse sequences (Bar-Gill et al., 2013). Knowing that each gate operation requires a few ns and for each operation several thousand error correction operations are necessary, the minimum coherence times for quantum computing applications are of the order of few ms. This has indeed been largely achieved for the NV center in diamond even at room temperature. Interestingly, the coherence times of the divacancies in SiC have shown to be more promising. Very recently, a value of T2 = 5s at T = 5K for the neutral divacancy in isotopically purified 4H-SiC, using microwave dressing protocols, has been reported (Anderson et al., 2022). This is the highest recorded value among for solid state qubits. Yet, it should be noted that for room-temperature applications this value is expected to reduce significantly to a few tens of milliseconds. Among the many studies, which have been dedicated to the optimization of the coherence times for the aforementioned defects, it is surprising that only very few are reported for the case of NV centers in SiC. The only reported values correspond to ¹²C-implanted isotopically natural 4H-SiC samples; there at low-temperature (T = 15K) dephasing time for basal and axial defects are in the range of 1 ms, in agreement with DFT calculations (Zhu et al., 2021). The measurement of the coherence time on a similar sample at room-temperature has presented T₂ ≈ 20µs using conventional Hahn-echo measurement without defect isolation (Li et al., 2021). It is very important to note that, when comparing results for these three defects, one should take into account the similar sample conditions. The initial reports concerning the dephasing times in NV centers in diamond and divacancies in SiC at room temperature have shown values ranging from 6 μs at room temperature to few hundreds of µs at T = 20K (Falk et al., 2013). These values are nearly one order of magnitude smaller than the reported value for NV center in 4H-SiC. Hence, although the coherence times for NV centers in SiC have not been measured in detail and using various defect isolation procedures, a simple comparison between the presented values and their extrapolation to NV centers under optimized conditions, lead us to expect coherence at least as large as the other two systems.

4 Spectral range

The possibility to select a particular defect for information registration, processing and readout relies on two parameters. The first one is the electronic structure (electron and nuclear), which is specific for each defect and each addressed state. For all of the aforementioned defects, its value is comparable and of the order of MHz to GHz, hence addressable via microwave pulses. The second one is the spectral range for optical excitation/recombination. Due to the weak electron-phonon interactions in the host materials, the Stokes shift is small and the spectral range has been measured precisely from the photoluminescence experiments at various temperatures. At low temperatures, where the zero phonon lines (ZPL) dominate the optical absorption and emission spectra, high resolution measurements of the relevant excitation wavelengths are possible. In the case of the NV center in diamond the absorption ZPL is at λ = 637 nm and can still be observed at temperatures above room temperature (Zhao et al., 2012); this is one of the parameters why this defect is applicable for practical quantum technology applications. However, due to Franck-Condon shift in optical absorption/emission transitions of NV center, the excitation should be performed at higher energies (Gali et al., 2011). This results in the photoionization of the center due to simultaneous defect to band transitions (Razinkovas et al., 2021). Usually, photoexcitation with λ = 583 nm is used for initializing the spin state of the NV center in diamond (Aslam et al., 2013). Several defects in SiC can also be spin polarized by optical excitation. However, the spectral range (near infrared) for VV and NV centers in 3C,4H,6H-SiC polytypes is advantageous over NV in diamond. It is situated in the range (1000–1300 nm) more compatible for information transfer through optical fibers, generally used in the present state of the art of telecommunication (Wang et al., 2018; Cao et al., 2019). Further, each defect (hh,kk,hk,kh) (VV, NV) in the different polytypes of SiC (3C, 4H,6H) has a distinct ZPL, depending on their local symmetries, which increases the selectivity and flexibility of the qubits depending on the application and technical resources. For the neutral divacancy centers VV with ZPL named PL1-PL4 and VV-X complexes (PL5 and 6) in 4H-SiC, six different ZPL have been observed, with wavelength from 1,000 nm to 1,260 nm (Table 1) (Koehl et al., 2011). The ZPL of the NV center in SiC (Csóré et al., 2017) and particularly in 3C-SiC (1,289 nm) (Felton et al., 2009) is well suited for transition in the telecom O-band. By this technology the information, transferred to flying qubits from the localized electronic qubits, can be transported easily over long distances using quantum repeaters embedded inside the fibers (Buterakos et al., 2017) and quantum entanglement (Whiteley et al., 2019; Bourassa et al., 2020) at large distances are feasible.

5 Fabrication process

Apart from the intrinsic properties of the solid-state spin-qubits, their efficient and cost-effective scalability and addressability are determining factors for their implementation as practical technological information systems. These factors are mainly governed by the host matrix and defect generation process. It is worth mentioning that these points are different to the intrinsic capability of the qubits to be scaled or addressed which were discussed in previous sections.

5.1 Cost-effective scalability

The present information technology stands on the microelectronics infrastructure. The future of quantum technology, whatever it would be, should either establish a novel industrial infrastructure which requires years of development and optimization and huge financial investments, or to use the currently well-established infrastructures of material fabrication and device processing in microelectronics, which relies on more than 60 years of research and development. In this context, cost-effective diamond structures are fabricated either in the form of nano-powders (Qin et al., 2021), which face the same problems of size and uniformity as quantum dots, or via thin films obtained by CVD growth (Chakraborty et al., 2019). The latter approach, although have enabled its integration into the current CMOS technology (Kim et al., 2019), is still in an early stage and requires further developments for achieving an standardized industrial approach, particularly from defect generation and device processing (e.g., lithography) points of view. Meanwhile, high quality silicon carbide epitaxial layers are already widely applied in industries such as power-electronics. Particularly, 3C-SiC/Si and 4H-SiC wafers, with controlled conductivity, impurity concentration and thickness can be commercially obtained. Moreover, the defect generation of Si and C monovacancies in 4H-SiC using high energy (100keV-1 MeV) electron irradiation, which was formerly developed for carrier concentration control of these layers (Storasta et al., 2004; Danno and Kimoto, 2006), as well as nitrogen implantation (Moscatelli et al., 2008) are standard procedures. In consequence, one can consider that all qubits in the SiC polytypes are more advantageous compared to diamond due to the material properties and the microelectronic background of this material.

5.2 Addressability

Localizing the qubits on a chip in an ordered and hence technologically addressable manner, is the key to achieve technologically practical memory and information processing units. The possibility of nano-structurization of silicon carbide via nanolithography is another major advantage of this material compared to diamond. Although there have been reports concerning the local implantation of nitrogen in diamond, yet this approach cannot achieve the required nanometer lateral resolution and the inter-defect distances required for state-superpositions. Optimized inter-defect distances to allow the required interaction (coupled qubits), and yet not reducing the coherence times is around 100 nm; this is easily achievable by e-beam lithography in industrial environments. Specifically, nanolithography possibility in epitaxial SiC has paved all the way for fabrication of various crucial devices and structures from ordered arrays of nanostructures (high-resolution addressability) (Castelletto et al., 2019) and resonant nanocavities (significant Purcell factor and DWF enhancement) (Lohrmann et al., 2017; Song et al., 2019; Crook et al., 2020) to on-chip nanowaveguides (Babin et al., 2021) which will facilitate the realization of semiconductor-based on-chip entangled photon sources for quantum computers and quantum networks (Matthews et al., 2009; Feng et al., 2019). Industrially developed processing technologies once more present the advantages of silicon carbide-based qubits over the NV center in diamond.

While both divacancy and NV color centers in silicon carbide benefit from the advantages of the host matrix, yet the former suffers from the challenges regarding formation process of divacancy defects. It was mentioned earlier that the divacancy centers are formed by the post-irradiation annealing procedures at T = 700°C at which Si monovacancies become mobile and diffuse and may form divacancies with the stable C vacancies. This leads to the important issue of the precise localization of these defects. This is not the case for NV centers, as nitrogen atom on the C lattice site will not diffuse at this temperature and hence the pair is formed exactly where the nitrogen has been implanted. Very recently, a local annealing process using a focused laser beam has been proposed to overcome this issue (Almutairi et al., 2022). However, once again on one hand the spatial resolution on the patterned annealing will not satisfy the required nanometric distances and in addition, in the annealed regions one would expect the presence of several type of defects other than divacancies. Hence once more the NV centers in SiC show advantages over the VV centers in SiC.

6 Conclusion

In Table 1, we have summarized the main conclusions of our discussions. It is surprising that despite the clear advantages of NV centers in SiC over divacancies in SiC and NV center in diamond, much less attention and work has been dedicated to development of this high potential qubit. There are several other potential qubit are presently under examination and investigation and there is an ever-growing number of reports regarding the achievements in elucidation of, both, their fundamental properties and devices and technologies, which are designed based on them. This includes all systems from trapped ions¹, superconductors², quantum dots³, and neutral atoms⁴ to the very recently developed 2D systems such as h-BN (Li and Gali, 2022). They have even been successful to receive significant financial supports to build technology startup units. In this context, it is a surprise that the case of NV center in SiC, with its high potential suffers from the lack of attention. NV centers in 4H-SiC not only dispose of properties adapted to quantum computing, but also for other applications functioning at room-temperature such as quantum sensing, metrology, and communication applications; further they are biocompatible, have a large natural abundance of its constituent elements, are suitable for industrial fabrication and processing, and cost efficient.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Examples of such companies are: IonQ (www.ionq.com), Honeywell (www.honeywell.com), Infineon Technologies (www.infenoin.com), Alpine Quantum Technologies, EleQtron (www.eleqtron.com), Quantinuum (www.quantimuum.com), Universal Quantum (www.universalquantum.com).

²Examples of such companies are: Google (www.google.com), IBM, IMEC (www.imec.com), BBN Technologies (www.bbn.com), Rigetti, and Intel (www.intel.com).

³For example, Quandela company (www.quandela.com).

⁴For example, Pasqual company (www.pasqual.com).

References

Abobeih, M. H., Cramer, J., Bakker, M. A., Kalb, N., Markham, M., Twitchen, D. J., et al. (2018). One-second coherence for a single electron spin coupled to a multi-qubit nuclear-spin environment. Nat. Commun. 9 (1), 2552. doi:10.1038/s41467-018-04916-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Alkauskas, A., Buckley, B. B., Awschalom, D. D., and Van de Walle, C. G. (2014). First-principles theory of the luminescence lineshape for the triplet transition in Diamond NV Centres. New J. Phys. 16 (7), 073026. doi:10.1088/1367-2630/16/7/073026

CrossRef Full Text | Google Scholar

Almutairi, A. F., Partridge, J. G., Xu, C., Cole, I. S., and Holland, A. S. (2022). Direct writing of divacancy centers in silicon carbide by femtosecond laser irradiation and subsequent thermal annealing. Appl. Phys. Lett. 120 (1), 014003. doi:10.1063/5.0070014

CrossRef Full Text | Google Scholar

Anderson, C. P., Glen, E. O., Zeledon, C., Bourassa, A., Jin, Y., Zhu, Y., et al. (2022). Five-second coherence of a single spin with single-shot readout in Silicon Carbide. Sci. Adv. 8 (5), eabm5912. doi:10.1126/sciadv.abm5912

PubMed Abstract | CrossRef Full Text | Google Scholar

Arute, F., Arya, K., Babbush, R., Bacon, D., Bardin, J. C., Barends, R., et al. (2019). Quantum supremacy using a programmable superconducting processor. Nature 574 (7779), 505–510. doi:10.1038/s41586-019-1666-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Aslam, N., Waldherr, G., Neumann, P., Jelezko, F., and Wrachtrup, J. (2013). Photo-induced ionization dynamics of the nitrogen vacancy defect in diamond investigated by single-shot charge state detection. New J. Phys. 15 (1), 013064. doi:10.1088/1367-2630/15/1/013064

CrossRef Full Text | Google Scholar

Babin, C., Stohr, R., Morioka, N., Linkewitz, T., Steidl, T., Wornle, R., et al. (2021). Fabrication and nanophotonic waveguide integration of silicon carbide colour centres with preserved spin-optical coherence. Nat. Mater. 21 (1), 67–73. doi:10.1038/s41563-021-01148-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Balasubramanian, G., Neumann, P., Twitchen, D., Markham, M., Kolesov, R., Mizuochi, N., et al. (2009). Ultralong spin coherence time in isotopically engineered diamond. Nat. Mater. 8 (5), 383–387. doi:10.1038/nmat2420

PubMed Abstract | CrossRef Full Text | Google Scholar

Bar-Gill, N., Pham, L., Jarmola, A., Budker, D., and Walsworth, R. (2013). Solid-state electronic spin coherence time approaching one second. Nat. Commun. 4 (1), 1743. doi:10.1038/ncomms2771

PubMed Abstract | CrossRef Full Text | Google Scholar

Beterov, I. I. (2020). Quantum computers based on cold Atoms. Instrum. Data Process. 56 (4), 317–324. doi:10.3103/s8756699020040020

CrossRef Full Text | Google Scholar

Bourassa, A., Anderson, C. P., Miao, K. C., Onizhuk, M., Ma, H., Crook, A. L., et al. (2020). Entanglement and control of single nuclear spins in isotopically engineered silicon carbide. Nat. Mater. 19 (12), 1319–1325. doi:10.1038/s41563-020-00802-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Bourgeois, E., Gulka, M., and Nesladek, M. (2020). Photoelectric detection and quantum readout of nitrogen-vacancy center spin states in Diamond. Adv. Opt. Mater. 8 (12), 1902132. doi:10.1002/adom.201902132

CrossRef Full Text | Google Scholar

Bruzewicz, C. D., Chiaverini, J., McConnell, R., and Sage, J. M. (2019). Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 6 (2), 021314. doi:10.1063/1.5088164

CrossRef Full Text | Google Scholar

Buterakos, D., Barnes, E., and Economou, S. E. (2017). Deterministic generation of all-photonic quantum repeaters from solid-state emitters. Phys. Rev. X 7 (4), 041023. doi:10.1103/physrevx.7.041023

CrossRef Full Text | Google Scholar

Cao, X., Zopf, M., and Ding, F. (2019). Telecom wavelength single photon sources. J. Semicond. 40 (7), 071901. doi:10.1088/1674-4926/40/7/071901

CrossRef Full Text | Google Scholar

Castelletto, S., Al Atem, A. S., Inam, F. A., Bardeleben, H. J. v., Hameau, S., Almutairi, A. F., et al. (2019). Deterministic placement of ultra-bright near-infrared color centers in arrays of silicon carbide micropillars. Beilstein J. Nanotechnol. 10, 2383–2395. doi:10.3762/bjnano.10.229

PubMed Abstract | CrossRef Full Text | Google Scholar

Chakraborty, T., Lehmann, F., Zhang, J., Borgsdorf, S., Wohrl, N., Remfort, R., et al. (2019). CVD growth of ultrapure diamond, generation of NV centers by ion implantation, and their spectroscopic characterization for quantum technological applications. Phys. Rev. Mater. 3 (6), 065205. doi:10.1103/physrevmaterials.3.065205

CrossRef Full Text | Google Scholar

Chakraborty, T., Zhang, J., and Suter, D. (2017). Polarizing the electronic and nuclear spin of the NV-center in diamond in arbitrary magnetic fields: Analysis of the optical pumping process. New J. Phys. 19 (7), 073030. doi:10.1088/1367-2630/aa7727

CrossRef Full Text | Google Scholar

Chen, X.-D., Dong, C. H., Sun, F. W., Zou, C. L., Cui, J. M., Han, Z. F., et al. (2011). Temperature dependent energy level shifts of nitrogen-vacancy centers in Diamond. Appl. Phys. Lett. 99 (16), 161903. doi:10.1063/1.3652910

CrossRef Full Text | Google Scholar

Christle, D. J., Falk, A. L., Andrich, P., Klimov, P. V., Hassan, J. U., Son, N., et al. (2014). Isolated electron spins in silicon carbide with millisecond coherence times. Nat. Mater. 14 (2), 160–163. doi:10.1038/nmat4144

PubMed Abstract | CrossRef Full Text | Google Scholar

Christle, D. J., Klimov, P. V., de las Casas, C. F., Szasz, K., Ivady, V., Jokubavicius, V., et al. (2017). Isolated spin qubits in SiC with a high-fidelity infrared spin-to-photon interface. Phys. Rev. X 7 (2), 021046. doi:10.1103/physrevx.7.021046

CrossRef Full Text | Google Scholar

Crook, A. L., Anderson, C. P., Miao, K. C., Bourassa, A., Lee, H., Bayliss, S. L., et al. (2020). Purcell enhancement of a single silicon carbide color center with coherent spin control. Nano Lett. 20 (5), 3427–3434. doi:10.1021/acs.nanolett.0c00339

PubMed Abstract | CrossRef Full Text | Google Scholar

Csóré, A., Ivanov, I. G., Son, N. T., and Gali, A. (2022). Fluorescence spectrum and charge state control of divacancy qubits via illumination at elevated temperatures in 4H silicon carbide. Phys. Rev. B 105, 165108. doi:10.1103/PhysRevB.105.165108

CrossRef Full Text | Google Scholar

Csóré, A., von Bardeleben, H. J., Cantin, J. L., and Gali, A. (2017). Characterization and formation of NV centers in 3C, 4H, and 6H SiC: An ab initio study. Phys. Rev. B 96 (8), 085204. doi:10.1103/physrevb.96.085204

CrossRef Full Text | Google Scholar

Danno, K., and Kimoto, T. (2006) Investigation of deep levels in n-type 4H-SiC epilayers irradiated with low-energy electrons. J. Appl. Phys. 100, 113728. doi:10.1063/1.2401658

CrossRef Full Text | Google Scholar

Davidsson, J., Ivady, V., Armiento, R., Son, N. T., Gali, A., and Abrikosov, I. A. (2018). First principles predictions of magneto-optical data for semiconductor point defect identification: The case of divacancy defects in 4H–SiC. New J. Phys. 20 (2), 023035. doi:10.1088/1367-2630/aaa752

CrossRef Full Text | Google Scholar

de Leon, N. P., Itoh, K. M., Kim, D., Mehta, K. K., Northup, T. E., Paik, H., et al. (2021). Materials challenges and opportunities for quantum computing hardware. Science 372 (6539), eabb2823. doi:10.1126/science.abb2823

PubMed Abstract | CrossRef Full Text | Google Scholar

Deák, P., Aradi, B., Kaviani, M., Frauenheim, T., and Gali, A. (2014). formation of NV centers in diamond: A theoretical study based on calculated transitions and migration of nitrogen and vacancy related defects. Phys. Rev. B 89 (7), 075203. doi:10.1103/physrevb.89.075203

CrossRef Full Text | Google Scholar

DiVincenzo, D. P. (2000). The physical implementation of quantum computation. Fortschr. Phys. 48 (9-11), 771–783. doi:10.1002/1521-3978(200009)48:9/11<771::aid-prop771>3.0.co;2-e

CrossRef Full Text | Google Scholar

Dolde, F., Bergholm, V., Wang, Y., Jakobi, I., Naydenov, B., Pezzagna, S., et al. (2014). High-fidelity spin entanglement using Optimal Control. Nat. Commun. 5 (1), 3371. doi:10.1038/ncomms4371

PubMed Abstract | CrossRef Full Text | Google Scholar

Falk, A. L., Buckley, B. B., Calusine, G., Koehl, W. F., Dobrovitski, V. V., Politi, A., et al. (2013). Polytype control of spin qubits in silicon carbide. Nat. Commun. 4 (1), 1819. doi:10.1038/ncomms2854

PubMed Abstract | CrossRef Full Text | Google Scholar

Falk, A. L., Klimov, P. V., Ivady, V., Szasz, K., Christle, D. J., Koehl, W., et al. (2015). Optical polarization of nuclear spins in silicon carbide. Phys. Rev. Lett. 114 (24), 247603. doi:10.1103/physrevlett.114.247603

PubMed Abstract | CrossRef Full Text | Google Scholar

Felton, S., Edmonds, A. M., Newton, M. E., Martineau, P. M., Fisher, D., Twitchen, D. J., et al. (2009). Hyperfine interaction in the ground state of the negatively charged nitrogen vacancy center in Diamond. Phys. Rev. B 79 (7), 075203. doi:10.1103/physrevb.79.075203

CrossRef Full Text | Google Scholar

Feng, L.-T., Zhang, M., Xiong, X., Chen, Y., Wu, H., Li, M., et al. (2019). On-chip transverse-mode entangled photon pair source. npj Quantum Inf. 5 (1), 2. doi:10.1038/s41534-018-0121-z

CrossRef Full Text | Google Scholar

Fu, K.-M. C., Santori, C., Barclay, P. E., and Beausoleil, R. G. (2010). Conversion of neutral nitrogen-vacancy centers to negatively charged nitrogen-vacancy centers through selective oxidation. Appl. Phys. Lett. 96 (12), 121907. doi:10.1063/1.3364135

CrossRef Full Text | Google Scholar

Gali, A., Fyta, M., and Kaxiras, E. (2008). ab initio supercell calculations on nitrogen-vacancy center in Diamond: Electronic Structure and hyperfine tensors. Phys. Rev. B 77 (15), 155206. doi:10.1103/physrevb.77.155206

CrossRef Full Text | Google Scholar

Gali, A. (2009). Identification of individual ¹³C isotopes of nitrogen-vacancy center in diamond by combining the polarization studies of nuclear spins and first-principles calculations. Phys. Rev. B 80 (24), 241204(R). doi:10.1103/physrevb.80.241204

CrossRef Full Text | Google Scholar

Gali, A., Simon, T., and Lowther, J. E. (2011). Anab initiostudy of local vibration modes of the nitrogen-vacancy center in Diamond. New J. Phys. 13 (2), 025016. doi:10.1088/1367-2630/13/2/025016

CrossRef Full Text | Google Scholar

Gimbert, J., Billon, T., Ouisse, T., Grisolia, J., Ben-Assayag, G., and Jaussaud, C. (1999). Nitrogen implantation in 4H and 6H–SiC. Mater. Sci. Eng. B 61-62, 368–372. doi:10.1016/s0921-5107(98)00536-4

CrossRef Full Text | Google Scholar

Goldman, M. L., Sipahigil, A., Doherty, M., Yao, N., Bennett, S., Markham, M., et al. (2015). Phonon-induced population dynamics and intersystem crossing in nitrogen-vacancy centers. Phys. Rev. Lett. 114 (14), 145502. doi:10.1103/physrevlett.114.145502

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordon, L., Janotti, A., and Van de Walle, C. G. (2015). Defects as qubits in 3C− and 4H−SiC. Phys. Rev. B 92 (4), 045208. doi:10.1103/physrevb.92.045208

CrossRef Full Text | Google Scholar

Haruyama, M., Onoda, S., Higuchi, T., Kada, W., Chiba, A., Hirano, Y., et al. (2019). Triple nitrogen-vacancy centre fabrication by C₅N₄H_n Ion Implantation. Nat. Commun. 10 (1), 2664. doi:10.1038/s41467-019-10529-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Hashemi, A., Linderälvet, C., Krasheninnikov, A. V., Ala-Nissila, T., Erhart, P., and Komsa, H. P. (2021) Photoluminescence line shapes for color centers in silicon carbide from density functional theory calculations. Phys. Rev. B 103 (12), 125203. doi:10.1103/PhysRevB.103.125203

CrossRef Full Text | Google Scholar

Hazdra, P., and Vobecký, J. (2019). Radiation defects created in n-type 4H-SiC by electron irradiation in the energy range of 1–10 MeV. Phys. status solidi (a) 216 (17), 1900312. doi:10.1002/pssa.201900312

CrossRef Full Text | Google Scholar

Herbschleb, E. D., Kato, H., Maruyama, Y., Danjo, T., Makino, T., Yamasaki, S., et al. (2019). Ultra-long coherence times amongst room-temperature solid-state spins. Nat. Commun. 10 (1), 3766. doi:10.1038/s41467-019-11776-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Hirano, Y., and Inada, T. (1995). Nitrogen implantation in (100)-β-SiC layers grown on si substrate. J. Appl. Phys. 77 (3), 1020–1028. doi:10.1063/1.358960

CrossRef Full Text | Google Scholar

Ivády, V., Davidsson, J., Delegan, N., Falk, A. L., Klimov, P. V., Whiteley, S. J., et al. (2019). Stabilization of point-defect spin qubits by quantum Wells. Nat. Commun. 10 (1), 5607. doi:10.1038/s41467-019-13495-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Ivanov, I. G., Hallin, C., Henry, A., Kordina, O., and Janzen, E. (1996). Nitrogen doping concentration as determined by photoluminescence in 4H– and 6H–SiC. J. Appl. Phys. 80 (6), 3504–3508. doi:10.1063/1.363221

CrossRef Full Text | Google Scholar

Kaufmann, H., Ruster, T., Schmiegelow, C., Luda, M., Kaushal, V., Schulz, J., et al. (2017). Scalable creation of long-lived multipartite entanglement. Phys. Rev. Lett. 119 (15), 150503. doi:10.1103/physrevlett.119.150503

PubMed Abstract | CrossRef Full Text | Google Scholar

Khazen, K., von Bardeleben, H. J., Zargaleh, S. A., Cantin, J. L., Zhao, M., Gao, W., et al. (2019). High-resolution resonant excitation of NV centers in 6H−SiC: A matrix for quantum technology applications. Phys. Rev. B 100 (20), 205202. doi:10.1103/physrevb.100.205202

CrossRef Full Text | Google Scholar

Kim, D., Ibrahim, M. I., Foy, C., Trusheim, M. E., Han, R., and Englund, D. R. (2019). A CMOS-integrated quantum sensor based on nitrogen–vacancy centres. Nat. Electron. 2 (7), 284–289. doi:10.1038/s41928-019-0275-5

CrossRef Full Text | Google Scholar

Kloeffel, C., and Loss, D. (2013). Prospects for spin-based quantum computing in Quantum Dots. Annu. Rev. Condens. Matter Phys. 4 (1), 51–81. doi:10.1146/annurev-conmatphys-030212-184248

CrossRef Full Text | Google Scholar

Koehl, W. F., Buckley, B. B., Heremans, F. J., Calusine, G., and Awschalom, D. D. (2011). Room temperature coherent control of defect spin qubits in silicon carbide. Nature 479 (7371), 84–87. doi:10.1038/nature10562

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Q., Wang, J. F., Yan, F. F., Zhou, J. Y., Wang, H. F., Liu, H., et al. (2021). Room-temperature coherent manipulation of single-spin qubits in silicon carbide with a high readout contrast. Natl. Sci. Rev. 9 (5), nwab122. doi:10.1093/nsr/nwab122

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S., and Gali, A. (2022). Bistable carbon-vacancy defects in h-BN. Front. Quantum Sci. Technol. 1, 1. doi:10.3389/frqst.2022.1007756

CrossRef Full Text | Google Scholar

Lin, W.-X., Yan, F. F., Li, Q., Wang, J. f., Hao, Z. H., Zhou, J. Y., et al. (2021). Temperature dependence of divacancy spin coherence in implanted silicon carbide. Phys. Rev. B 104 (12), 125305. doi:10.1103/physrevb.104.125305

CrossRef Full Text | Google Scholar

Löfgren, R., Öberg, S., and Larsson, J. A. (2020). A theoretical study of de-charging excitations of the NV-center in diamond involving a nitrogen donor. J. Phys. 22 (12), 123042. doi:10.1088/1367-2630/abd1ae

CrossRef Full Text | Google Scholar

Lohrmann, A., Karle, T. J., Sewani, V. K., Laucht, A., Bosi, M., Negri, M., et al. (2017). Integration of single-photon emitters into 3C-SiC microdisk resonators. ACS Photonics 4 (3), 462–468. doi:10.1021/acsphotonics.6b00913

CrossRef Full Text | Google Scholar

Lommer, G., Malcher, F., and Rossler, U. (1988). Spin splitting in semiconductor heterostructures for B→0. Phys. Rev. Lett. 60 (8), 728–731. doi:10.1103/physrevlett.60.728

PubMed Abstract | CrossRef Full Text | Google Scholar

Lühmann, T., John, R., Wunderlich, R., Meijer, J., and Pezzagna, S. (2019). Coulomb-driven single defect engineering for scalable qubits and spin sensors in Diamond. Nat. Commun. 10 (1), 4956. doi:10.1038/s41467-019-12556-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Matthews, J. C., Politi, A., Stefanov, A., and O'Brien, J. L. (2009). Manipulation of multiphoton entanglement in waveguide quantum circuits. Nat. Photonics 3 (6), 346–350. doi:10.1038/nphoton.2009.93

CrossRef Full Text | Google Scholar

Miao, K. C., Blanton, J. P., Anderson, C. P., Bourassa, A., Crook, A. L., Wolfowicz, G., et al. (2020). Universal coherence protection in a solid-state spin qubit. Science 369 (6510), 1493–1497. doi:10.1126/science.abc5186

PubMed Abstract | CrossRef Full Text | Google Scholar

Mittiga, T., Hsieh, S., Zu, C., Kobrin, B., Machado, F., Bhattacharyya, P., et al. (2018). Imaging the local charge environment of nitrogen-vacancy centers in Diamond. Phys. Rev. Lett. 121 (24), 246402. doi:10.1103/physrevlett.121.246402

PubMed Abstract | CrossRef Full Text | Google Scholar

Moscatelli, F., Poggi, A., Solmi, S., and Nipoti, R. (2008). Nitrogen implantation to improve electron channel mobility in 4H-SiC MOSFET. IEEE Trans. Electron Devices 55 (4), 961–967. doi:10.1109/ted.2008.917107

CrossRef Full Text | Google Scholar

Mu, Z., Zargaleh, S. A., von Bardeleben, H. J., Froch, J. E., Nonahal, M., Cai, H., et al. (2020). Coherent manipulation with resonant excitation and single emitter creation of nitrogen vacancy centers in 4H Silicon Carbide. Nano Lett. 20 (8), 6142–6147. doi:10.1021/acs.nanolett.0c02342

PubMed Abstract | CrossRef Full Text | Google Scholar

Nashiyamal, I. (1992). “Nitrogen impurities in 3C-SiC epilayers,” in Amorphous and crystalline silicon carbide IV. Editors Cary Y. Yang, M. Mahmudur Rahman, and Gary L. Harris (Berlin, Germany: Springer), 136–142. Proceedings of the 4th International ConferenceSanta Clara, CAOctober 9–11, 1991

CrossRef Full Text | Google Scholar

Newton, M. E., Campbell, B., Twitchen, D., Baker, J., and Anthony, T. (2002). Recombination-enhanced diffusion of self-interstitial atoms and vacancy–interstitial recombination in Diamond. Diam. Relat. Mater. 11 (3-6), 618–622. doi:10.1016/s0925-9635(01)00623-9

CrossRef Full Text | Google Scholar

Pezzagna, S., and Meijer, J. (2021). Quantum computer based on color centers in Diamond. Appl. Phys. Rev. 8 (1), 011308. doi:10.1063/5.0007444

CrossRef Full Text | Google Scholar

Pezzagna, S., Naydenov, B., Jelezko, F., Wrachtrup, J., and Meijer, J. (2010). Creation efficiency of nitrogen-vacancy centres in Diamond. New J. Phys. 12 (6), 065017. doi:10.1088/1367-2630/12/6/065017

CrossRef Full Text | Google Scholar

Qin, J.-X., Yang, X. G., Lv, C. F., Li, Y. Z., Liu, K. K., Zang, J. H., et al. (2021). Nanodiamonds: Synthesis, properties, and applications in nanomedicine. Mater. Des. 210, 110091. doi:10.1016/j.matdes.2021.110091

CrossRef Full Text | Google Scholar

Rabeau, J. R., Reichart, P., Tamanyan, G., Jamieson, D. N., Prawer, S., Jelezko, F., et al. (2006). Implantation of labelled single nitrogen vacancy centers in Diamond using N₁₅. Appl. Phys. Lett. 88 (2), 023113. doi:10.1063/1.2158700

CrossRef Full Text | Google Scholar

Radko, I. P., Boll, M., Israelsen, N. M., Raatz, N., Meijer, J., Jelezko, F., et al. (2016). Determining the internal quantum efficiency of shallow-implanted nitrogen-vacancy defects in bulk diamond. Opt. Express. 24 (24), 27715–27725. doi:10.1364/OE.24.027715

PubMed Abstract | CrossRef Full Text | Google Scholar

Razinkovas, L., Maciaszek, M., Reinhard, F., Doherty, M. W., and Alkauskas, A. (2021) Photoionization of negatively charged NV centers in diamond: Theory and ab initio calculations. Phys. Rev. B 104 (23), 235301. doi:10.1103/PhysRevB.104.235301

CrossRef Full Text | Google Scholar

Schreyvogel, C., Polyakov, V., Burk, S., Fedder, H., Denisenko, A., Favaro de Oliveira, F., et al. (2016). Active and fast charge-state switching of single NV centres in Diamond by in-plane al-Schottky junctions. Beilstein J. Nanotechnol. 7, 1727–1735. doi:10.3762/bjnano.7.165

PubMed Abstract | CrossRef Full Text | Google Scholar

Slack, G. A., and Scace, R. I. (1965). Nitrogen incorporation in SiC. J. Chem. Phys. 42 (2), 805–806. doi:10.1063/1.1696022

CrossRef Full Text | Google Scholar

Smeltzer, B., Childress, L., and Gali, A. (2011). 13C hyperfine interactions in the nitrogen-vacancy centre in Diamond. New J. Phys. 13 (2), 025021. doi:10.1088/1367-2630/13/2/025021

CrossRef Full Text | Google Scholar

Son, N. T., Carlsson, P., ul Hassan, J., Janzen, E., Umeda, T., Isoya, J., et al. (2006). Divacancy in 4H-SiC. Phys. Rev. Lett. 96 (5), 055501. doi:10.1103/physrevlett.96.055501

PubMed Abstract | CrossRef Full Text | Google Scholar

Son, N. T., and Ivanov, I. G. (2021). Charge state control of the silicon vacancy and divacancy in silicon carbide. J. Appl. Phys. 129 (21), 215702. doi:10.1063/5.0052131

CrossRef Full Text | Google Scholar

Song, B.-S., Asano, T., Jeon, S., Kim, H., Chen, C., Kang, D. D., et al. (2019). Ultrahigh-Q photonic crystal nanocavities based on 4H Silicon Carbide. Optica 6 (8), 991. doi:10.1364/optica.6.000991

CrossRef Full Text | Google Scholar

Storasta, L., Bergman, J. P., Janzen, E., Henry, A., and Lu, J. (2004). Deep levels created by low energy electron irradiation in 4H-SiC. J. Appl. Phys. 96 (9), 4909–4915. doi:10.1063/1.1778819

CrossRef Full Text | Google Scholar

Su, Z., Ren, Z., Bao, Y., Lao, X, Zhang, J., Zhang, J., et al. (2019) Luminescence landscapes of nitrogen-vacancy centers in diamond: quasi-localized vibrational resonances and selective coupling. J. Mat. Chem. C 7, 8086–8091. doi:10.1039/C9TC01954E

CrossRef Full Text | Google Scholar

Subedi, S. D., Fedorov, V. V., Peppers, J., Martyshkin, D. V., Mirov, S. B., Shao, L., et al. (2019). Laser spectroscopic characterization of negatively charged nitrogen-vacancy (NV⁻) centers in Diamond. Opt. Mater. Express 9 (5), 2076. doi:10.1364/ome.9.002076

CrossRef Full Text | Google Scholar

Tetienne, J.-P., Rondin, L., Spinicelli, P., Chipaux, M., Debuisschert, T., Roch, J. F., et al. (2012). Magnetic-field-dependent photodynamics of single NV defects in diamond: An application to qualitative all-optical magnetic imaging. New J. Phys. 14 (10), 103033. doi:10.1088/1367-2630/14/10/103033

CrossRef Full Text | Google Scholar

von Bardeleben, H. J., Cantin, J. L., Csore, A., Gali, A., Rauls, E., and Gerstmann, U. (2016). NV centers in3C,4H, and6Hsilicon carbide: A variable platform for solid-state qubits and nanosensors. Phys. Rev. B 94 (12), 121202. doi:10.1103/physrevb.94.121202

CrossRef Full Text | Google Scholar

von Bardeleben, H. J., Cantin, J. L., Gerstmann, U., Schmidt, W. G., and Biktagirov, T. (2021). Spin polarization, electron–phonon coupling, and zero-phonon line of the NV Center in 3C-SiC. Nano Lett. 21 (19), 8119–8125. doi:10.1021/acs.nanolett.1c02564

PubMed Abstract | CrossRef Full Text | Google Scholar

von Bardeleben, H. J., Cantin, J. L., Rauls, E., and Gerstmann, U. (2015). Identification and magneto-optical properties of the NV center in 4H−SiC. Phys. Rev. B 92 (6), 064104. doi:10.1103/physrevb.92.064104

CrossRef Full Text | Google Scholar

Walker, J. (1979). Optical absorption and luminescence in Diamond. Rep. Prog. Phys. 42 (10), 1605–1659. doi:10.1088/0034-4885/42/10/001

CrossRef Full Text | Google Scholar

Wang, J.-F., Liu, Z. H., Yan, F. F., Li, Q., Yang, X. G., Guo, L., et al. (2020a). Experimental optical properties of single nitrogen vacancy centers in silicon carbide at room temperature. ACS Photonics 7 (7), 1611–1616. doi:10.1021/acsphotonics.0c00218

CrossRef Full Text | Google Scholar

Wang, J.-F., Yan, F. F., Li, Q., Liu, Z. H., Liu, H., Guo, G. P., et al. (2020b). Coherent control of nitrogen-vacancy center spins in silicon carbide at room temperature. Phys. Rev. Lett. 124 (22), 223601. doi:10.1103/physrevlett.124.223601

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Zhou, Y., Wang, Z., Rasmita, A., Yang, J., Li, X., et al. (2018). Bright room temperature single photon source at Telecom Range in cubic silicon carbide. Nat. Commun. 9 (1), 4106. doi:10.1038/s41467-018-06605-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Weber, J. R., Koehl, W. F., Varley, J. B., Janotti, A., Buckley, B. B., Van de Walle, C. G., et al. (2010). Quantum computing with defects. Proc. Natl. Acad. Sci. 107 (19), 8513–8518. doi:10.1073/pnas.1003052107

PubMed Abstract | CrossRef Full Text | Google Scholar

Whiteley, S. J., Wolfowicz, G., Anderson, C. P., Bourassa, A., Ma, H., Ye, M., et al. (2019). Spin–phonon interactions in silicon carbide addressed by Gaussian acoustics. Nat. Phys. 15 (5), 490–495. doi:10.1038/s41567-019-0420-0

CrossRef Full Text | Google Scholar

Wrachtrup, J., and Jelezko, F. (2006). Processing quantum information in diamond. J. Phys. Condens. Matter 18 (21), S807. doi:10.1088/0953-8984/18/21/s08

CrossRef Full Text | Google Scholar

Zargaleh, S. A., Eble, B., Hameau, S., Cantin, J. L., Legrand, L., Bernard, M., et al. (2016). Evidence for near-infrared photoluminescence of nitrogen vacancy centers in 4H-SiC. Phys. Rev. B 94 (6), 060102. doi:10.1103/physrevb.94.060102

CrossRef Full Text | Google Scholar

Zargaleh, S. A., Hameau, S., Eble, B., Margaillan, F., von Bardeleben, H. J., Cantin, J. L., et al. (2018a). Nitrogen vacancy center in cubic silicon carbide: A promising qubit in the 1.5 μm spectral range for photonic quantum networks. Phys. Rev. B 98 (16), 165203. doi:10.1103/physrevb.98.165203

CrossRef Full Text | Google Scholar

Zargaleh, S. A., von Bardeleben, H. J., Cantin, J. L., Gerstmann, U., Hameau, S., Eble, B., et al. (2018b). Electron paramagnetic resonance tagged high-resolution excitation spectroscopy of NV-centers in 4H-SiC. Phys. Rev. B 98 (21), 214113. doi:10.1103/physrevb.98.214113

CrossRef Full Text | Google Scholar

Zhao, G. L., and Bagayoko, D. (2000). Electronic structure and charge transfer in 3C- and 4H-SiC. New J. Phys. 2, 16. doi:10.1088/1367-2630/2/1/316

CrossRef Full Text | Google Scholar

Zhao, H.-Q., Fujiwara, M., and Takeuchi, S. (2012). Suppression of fluorescence phonon sideband from nitrogen vacancy centers in diamond nanocrystals by substrate effect. Opt. Express 20 (14), 15628. doi:10.1364/oe.20.015628

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, Y., Kovos, B., Onizhuk, M., Awschalom, D., and Galli, G. (2021). Theoretical and experimental study of the nitrogen-vacancy center in 4H-SiC. Phys. Rev. Mater. 5 (7), 074602. doi:10.1103/physrevmaterials.5.074602

CrossRef Full Text | Google Scholar