Theoretical development of discrete-modulated continuous-variable quantum key distribution

Continuous-variable quantum key distribution offers simple, stable and easy-to-implement key distribution systems. The discrete modulation scheme further reduces the technical difficulty. The main regret is that the security of discrete modulation schemes has not been sufficiently demonstrated. Schemes with different signal state distributions use various physical conditions to obtain the key rate formula, resulting in different security levels, computation complexities and implementation difficulties. Therefore, a relatively systematic and logically consistent security proof against most general attacks is worth exploring. On the other hand, extending the discrete modulation scheme and its variants to different applications, such as satellite-to-earth communication, can further activate and advance this field. Here, we briefly review the achievements that have been made in discrete-modulated continuous-variable quantum key distribution, and openly discuss some issues worthy of further research.

1 Introduction

Quantum private communication is a practical direction of the application of quantum mechanics. It offers chances to communicate securely against the art-of-state techniques and predictably powerful technologies, such as quantum computers. Various forms of communication are carried out according to cryptographic tasks (Gu et al., 2021; Li et al., 2021a), such as quantum private query (Liu B. et al., 2022) and quantum digital signatures (Lu et al., 2021). The most basic one is quantum key distribution (QKD) (Zhou et al., 2016; Pirandola et al., 2020; Wang et al., 2020; Xu et al., 2020; Kwek et al., 2021) that does not involve the transmission of information, but only shares a string of identical and secure keys for both parties against quantum attacks. For this symmetric encryption, the one-time pad (Shannon, 1949) ensures that if each key generated from QKD is used only once, the theoretical security of information can be achieved.

Continuous-variable QKD (CV-QKD) (Su et al., 2009; Diamanti and Leverrier, 2015; Guo et al., 2021; Su et al., 2022; Zhao et al., 2022) is an important direction of QKD, which encodes keys in continuous degrees of freedom. Another notable choice is to encode keys in discrete degrees of freedom on single photon, which is called discrete-variable QKD (Yin et al., 2021; Xie et al., 2022; Zeng et al., 2022). In general, CV-QKD has advantages in experimental implementation (Karinou et al., 2018). The intensity of signals in CV-QKD is usually stronger to resist channel loss, increasing the amount of measurement outcomes and improving the key rates. Measurement devices are homodyne detectors or heterodyne detectors (Liu J. et al., 2022) that are compatible with classical optical communication and inexpensive to manufacture and maintain, compared to the single-photon detector in discrete-variable QKD (Zhao et al., 2006; Yin et al., 2020; Jiang et al., 2021).

For key encoding, discrete modulation (Ralph, 1999) is proposed earlier than Gaussian modulation, but Gaussian modulation (Grosshans and Grangier, 2002; Grosshans et al., 2003) pushes the CV-QKD to the hot spot. The Gaussian modulation scheme achieves security against general attacks (Leverrier et al., 2010; Leverrier, 2015; Pirandola, 2021), which is based on U(N) symmetry by sampling and estimating quadratures from a Gaussian distribution. However, the U(N) symmetry of the Gaussian distribution requires signal continuity, while we can only prepare finite kinds of signal states (Lupo, 2020). It is necessary to propose a stricter security proof for the discreteness of prepared states. The preparation step can be further simplified by sending a few coherent states and 1 bit value for each coherent state. This encoding manner is similar to discrete variables, which facilitates simplified postprocessing.

Discrete-modulated continuous-variable quantum key distribution (DM-CV-QKD) is now easy to realize in terms of preparation and measurement (Aguiar et al., 2022; Wang H. et al., 2022). However, many problems remain to be solved, such as security (Shao et al., 2022), key rate calculation, and fast postprocessing methods (Gyongyosi and Imre, 2018; Zhou et al., 2021). This work reviews the theoretical achievements that have been made in DM-CV-QKD, and openly discusses the issues worthy of further research.

2 Protocol and variants

We discuss the prepare-and-measure type protocols with two users Alice and Bob and an adversary Eve. The first binary-modulated scheme (Silberhorn et al., 2002), which sends states with a Gaussian distribution but interprets a state as logical 0 or one according to the displacement direction (Heid and Lütkenhaus, 2007), is the early form of discrete modulation. Later, schemes with different signal states or different probability distributions evolved (Zhao et al., 2020a; Dias and de Assis, 2021; Kaur et al., 2021).

The phase-shift-keying (PSK) type prepares different signal states by changing phases. Concretely, the M-PSK type scheme (Sych and Leuchs, 2010; Papanastasiou et al., 2018) prepares M kinds of signals represented by $\left|\alpha e^{2\pi ik/M}\right.⟩$, where k ∈ {0, 1, …, M − 1}. Signals have the same amplitude α > 0 but different phases. The value of M can be taken as 2 (Zhao et al., 2009), 3 (Brádler and Weedbrook, 2018), 4 (Leverrier and Grangier, 2009) or 8 (Becir et al., 2012; Guo et al., 2018, 2020). M = 4 is the most popular choice in the investigation (Xuan et al., 2009; Hirano et al., 2017; Liao et al., 2018; Ghorai et al., 2019; Lin et al., 2019; Liu et al., 2021).

The quadrature amplitude modulation (QAM) type (Denys et al., 2021) is a practical implementation of Gaussian modulation, using limited kinds of signal states to approximate the Gaussian distribution. Each quadrature has m choices, and there are M = m² signal states in total. The state that takes the kth $\widehat{q}$ quadrature and the lth $\widehat{p}$ quadrature can be denoted by $\left|{\alpha }_{k,l}\right.⟩$, where ${\alpha }_{k,l}=\frac{\alpha \sqrt{2}}{\sqrt{m-1}}\left(k-\frac{m-1}{2}\right)+i\frac{\alpha \sqrt{2}}{\sqrt{m-1}}\left(l-\frac{m-1}{2}\right)$ and α > 0 is the amplitude. The probability distribution is $P_{k,l}=\frac{1}{2^{2(m-1)}}\left(\genfrac{}{}{0ex}{}{m-1}{k}\right)\left(\genfrac{}{}{0ex}{}{m-1}{l}\right)$. Signal states are arranged in a coordinate system formed by two quadratures as a square lattice.

The amplitude and phase shift keying (APSK) type (Almeida et al., 2021) is likely a multi-ring of PSK type. The states in each ring have the same amplitude, and adjacent states have the same phase difference. It has 4, 12, 16, 32, 64, 128, and 256 states in the first ring to the seventh ring, respectively. For instance, 16-APSK has two rings, and 32-APSK has three rings. To approach the Gaussian modulation, the probability of a state in ring p is P_p = 1/(RM_p), where R is the total number of rings and M_p is the total number of states in ring p.

For detector selection, homodyne detection is more precise and simpler than heterodyne detection (Caves and Drummond, 1994; Laudenbach et al., 2018) in principle. However, if there are too many types of signal states, it is better to use heterodyne detection to distinguish them accurately. It is worth noting that more states can improve key rates but complicate postprocessing, especially because error correction is difficult due to the high error rate caused by the difficulty of distinguishing different states.

3 Security analysis

Security is the deciding factor in whether a protocol should exist or not. In this section, we briefly summarize some art-of-state security analysis methods. In general, security analysis starts from the Devetak-Winter formula (Igor and Andreas, 2005), which reads

$K=I\left({\mathbf{S}}_A;{\mathbf{S}}_B\right)-\max \chi \left({\mathbf{S}}_B:\mathbf{E}\right),(1)$

where I(S_A; S_B) is the mutual information between Alice and Bob’s measurement outcomes S_A and S_B that are used to distil keys, and χ(S_B: E) is the Holevo bound between Bob’s outcome S_B and the quantum register E of Eve. The search range for the maximal solution of χ(S_B: E) is any possible attack that matches the statistics of experimental parameters obtained by Alice and Bob.

Discrete modulation schemes cannot be directly applied to Gaussian attack optimization and quantum de Finetti theory due to insufficient symmetry of the prepared signal states. Estimation of the Holevo bound χ(S_B: E) is an admittedly difficult problem.

3.1 Analytical method

Based on physical conditions, analytical methods scale the objective function by various inequalities until a bound that can be directly calculated with known experimental parameters is found. Therefore, the key rate formula obtained by the analytical method has the advantage of being easy to compute.

Considering universality, one method (Denys et al., 2021) is constructing the covariance matrix according to the security analysis of Gaussian modulation schemes. χ(S_B: E) can be explicitly bounded by taking the value of the Holevo information for a Gaussian state with the covariance matrix

$\left[\begin{array}{cc}\hfill V{\mathbb{I}}_2\hfill & \hfill Z{\sigma }_Z\hfill \\ \hfill Z{\sigma }_Z\hfill & \hfill W{\mathbb{I}}_2\hfill \end{array}\right](2)$

where V and W can be directly given by experimental parameters, but Z is linearly related to the density operator of both parties and is influenced by Eve. σ_Z is the pauli-Z matrix and ${\mathbb{I}}_2$ is two-dimensional identity matrix. Under constraints of the experimental outcomes, we can find a scaling that gives upper and lower bounds on the parameter Z of the covariance matrix. The lower bound of the secret key rate of CV-QKD with an arbitrary modulation is secure against collective attacks under the asymptotic regime. (Almeida et al., 2021) applies this method to the M-QPSK type considering finite-size effects.

It is worth noting that a binary-modulated CV-QKD protocol has achieved the highest security against general coherent attacks in the finite-key-size regime (Matsuura et al., 2021). The security is based on the fidelity of an optical pulse to a coherent state. For this purpose, a tight and robust method of estimating fidelity via heterodyne detection has been proposed. The drawbacks of this method are not tight and not universal, since the key rate is small, and the transmission distance is short.

3.2 Numerical method

Numerical methods usually have the advantage of being tight, since the lower bound of the key rate can be calculated directly according to the experimental parameters with less scaling. One method (Ghorai et al., 2019) is based on the covariance matrix and is the predecessor of the universal analytical method (Denys et al., 2021) mentioned above. The difference is how to calculate the parameter Z of the covariance matrix. In the numerical method, we directly search the optimal value of Z under the constraints using semidefinite programming. The numerical solution and the analytical solution of the key rate are consistent, but neither is as high as the numerical solution of the nonlinear method (Lin et al., 2019).

In this nonlinear method, the secret key rate K against collective attacks in the asymptotic limit from Devetak-Winter formula (Igor and Andreas, 2005) is rewritten as

$K=\underset{\rho \in \mathbf{S}}{\min }f\left(\rho \right)-{\text{leak}}_{\text{obs}}^{\text{EC}},(3)$

where the first term is associated with privacy amplification and ${\text{leak}}_{\text{obs}}^{\text{EC}}$ is information leakage during error correction. ρ is the density operator shared by Alice, Bob, and possibly other parties involved in the protocol. S = {ρ ∈ H₊|Tr(Γ_iρ = γ_i, ∀i)} denotes the set of states satisfying linear constraints from asymptotic experimental data, where H₊ is the set of positive semidefinite operators, {Γ_i} is the set of Hermitian operators and {γ_i} is the corresponding set of expectation values. χ(S_B: E) is implicit in f(ρ) (Winick et al., 2018)

$f\left(\rho \right)=D\left(\mathcal{G}\left(\rho \right)\Vert \mathcal{Z}\left(\mathcal{G}\left(\rho \right)\right)\right),(4)$

where D(σ‖τ)≔Tr(σ log  σ) − Tr(σ log  τ) is the quantum relative entropy, $\mathcal{G}$ is a completely positive map related to the postselection and $\mathcal{Z}$ is a completely positive trace preserving map related to the key map. Since the relative entropy is jointly convex, $\mathcal{G}$ and $\mathcal{Z}$ are linear maps, S is convex, f(ρ) is convex in ρ and min_ρ∈Sf(ρ) is a convex optimization problem. A two-step numerical method is developed for calculating a reliable lower bound on the convex optimization problem min_ρ∈Sf(ρ) (Winick et al., 2018). We first need to find a ρ close to the minimum ρ* of Eq. 4 with feasible convex optimization methods such as the Frank-Wolfe method (Frank and Wolfe, 1956). Subsequently, we solve the dual problem of the linearization of f about ρ and obtain the reliable lower bound.

This method has been used for 4-PSK type schemes (Lin et al., 2019; Lin and Lütkenhaus, 2020; Liu et al., 2021), in which the constraints S include the statistics of experimental outcomes, the definition of density operator and the requirement that Eve cannot modify Alice’s system A. The optical mode Bob received is in an infinite-dimensional Hilbert space; thus, a photon-number cutoff assumption is imposed (Lin et al., 2019) and latter removed by (Upadhyaya et al., 2021).

3.3 Neural network method

Although numerical methods offer a tight key rate bound of DM-CV-QKD, the high requirement of time and computational resources in solving semidefinite programming remains a key challenge (Hu et al., 2021). Machine learning (Zdeborová, 2017; Mehta et al., 2019) can efficiently learn complex patterns, thus potentially speeding up the computation of key rates. Recently, several works have taken a solid step in this direction (Liu Z.-P. et al., 2022; Zhou et al., 2022).

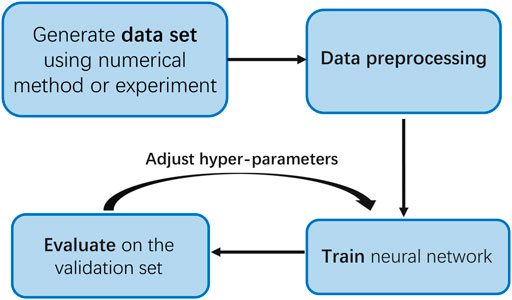
A brief workflow of the neural network method is illustrated in Figure 1. The architectures of neural networks are chosen by considering the complexity of protocols and the scale of the data sets collected. The data set composed of the training set and test set is collected from numerical simulations or experiments. Each entry in the data set consists of the input features and an output label. Data preprocessing is necessary to significantly improve the prediction accuracy of the key rates. Then, the neural network is trained on the training set and evaluated on a validation set. A critical ingredient is a loss function including two adjustable hyperparameters designed specifically, which keeps the predicted key rates reliable and tight. It usually costs several trials to find the hyperparameters that make the neural network perform best. After completing this stage, the trained-well neural network is tested on the test set and can be deployed on certain devices in quantum networks to infer key rates online in real-time.

FIGURE 1

FIGURE 1. Schematic diagram of the brief workflow of the neural network method.

With the set of values {γ_i} (Lin et al., 2019) mentioned above as the input features and the corresponding key rates as the output labels, this method can be introduced into DM-CV-QKD to reduce the time and computational resource waste of solving semidefinite programming (Zhou et al., 2022). It yields a speedup of approximately six or seven orders of magnitude compared with numerical methods, which means it can infer key rates in milliseconds when given new inputs.

In addition, (Liu Z.-P. et al., 2022), introduced Bayesian optimization into the neural network method to automatically search the best structure and hyperparameters. This improved automatic neural network method has calculated the key rates of two variants of DM-CV-QKD protocols (Lin et al., 2019; Liu et al., 2021) with high reliability, considerable tightness and great efficiency.

4 Satellite-to-ground DM-CV-QKD

In the past few decades, the communication distance of QKD has been extended to several hundreds of kilometers (Yin et al., 2016; Chen et al., 2021; Pittaluga et al., 2021; Wang S. et al., 2022) due to progress in experimental technology and protocol design. Unfortunately, the amount of secret bits distributed through a lossy ground-based channel per use cannot exceed the repeaterless bound proposed by Pirandola et al (Pirandola et al., 2017). Quantum repeaters, relying on entanglement distribution, entanglement swapping and quantum memories, are a solution to mitigate the problem of fundamental limits in the lossy channel. However, such technology is currently far from practical for the large-scale deployment of quantum networks. Satellites provide an alternative opportunity for long distance QKD due to less decibels of loss in a satellite-to-ground channel compared with ground-based fiber connections. The milestone in this field is the first complete satellite-to-ground QKD experiment realized with Micius (Liao et al., 2017a; Liao et al., 2017c; Yin et al., 2017b). In the same year, QKD was implemented in a small payload on-board of the Tiangong-2 space laboratory (Liao et al., 2017b). Apart from QKD, entanglement distribution (Yin et al., 2017a) and quantum teleportation (Ren et al., 2017) have been realized.

An important aspect in a global QKD network is developing stable, high-throughput QKD links from a constellation of satellites to a network of ground stations. CV-QKD exploits the heritage of classical optical communication in terms of high-speed components and space qualification and may bring a breakthrough in this field. Currently, the progress in satellite CV-QKD mainly focuses on the investigation of feasibility theoretically considering the fluctuation effects in realistic satellite-to-ground links and calculating the secret key rate of Gaussian modulation CV-QKD (Kish et al., 2020; Villasenor et al., 2020; Dequal et al., 2021). The preliminary experimental study was implemented in terms of signal measurement in satellite-to-ground links (Günthner et al., 2017). Further efforts can be made to investigate the theoretical feasibility of DM-CV-QKD (Wang T.-L. et al., 2019), and the demonstration of satellite CV-QKD is expected.

5 Measurement-device-independent DM-CV-QKD

If one wants to extend the advantages of CV QKD to the condition of longer transmission distance, constructing a measurement-device-independent (MDI) type variant (Pirandola et al., 2015; Wang P. et al., 2019; Ye et al., 2020; Tian et al., 2022) is a reasonable choice. With efficient reconciliation error correction, an MDI type DM-CV-QKD protocol can transmit longer than the MDI type Gaussian-modulated CV-QKD protocol (Ma et al., 2019; Zhao et al., 2020b). At the same time, MDI protocols (Huang et al., 2022) close the loophole of detectors (Ma et al., 2014; Zhang et al., 2014), which offers higher security than protocols trusting both senders and detectors. Additionally, MDI protocols naturally facilitate scenarios in which two users Alice and Bob are in different media, such as fiber-to-water (Yu et al., 2022) and space-to-water (Peng et al., 2022). The intermediate party, Charlie, can be placed at the junction of the two media, so that each signal is transmitted in only one medium.

6 Discussion

DM-CV-QKD is a vibrant research direction with great potential for development. Compared with traditional discrete-variable systems, continuous-variable systems have indisputable low-cost advantages. In terms of preparation, discrete modulation is also simpler than Gaussian modulation, and eases the interpretation, error correction and privacy amplification of measurement outcomes during the postprocessing. Relaxing the requirements for experimental conditions inevitably increases the difficulty of security analysis.

The quality of security analysis should be evaluated from four aspects: security levels, tightness, universality and computation complexity. Most security analysis methods can only resist collective attacks under the asymptotic regime, which is still some distance from security against coherent attacks under the finite-size regime. Recently, analytical and numerical methods that can be widely applied to different discrete modulation schemes have been proposed. Analytical methods are usually easy to compute but not tight enough for long distance transmission. Numerical methods, especially nonlinear methods, can find the tight lower bound of the key rate but consume considerable computational resources and time. There is still room for improvement in terms of tightness of key rate bounds, security level and postprocessing speed.

Imposing the idea of machine learning in DM-CV-QKD is a promising way to enhance the practicality (Li et al., 2018). For instance, the neural network can reduce time consumption in predicting the secret key rate (Liu Z.-P. et al., 2022; Zhou et al., 2022). Ensemble learning has been used to predict communication failure caused by channel disturbance (Li et al., 2021b). Additionally, some technical means can be applied to further improve the performance (Li and Cvijetic, 2018), such as quantum catalysis (Guo et al., 2020; Ye et al., 2021) and quantum scissors (Ghalaii et al., 2020; Li Y. et al., 2021), multicarrier (Gyongyosi, 2020).

While mastering the basic protocol of DM-CV-QKD, its application range can be expanded according to its characteristics. It has the potential for communications in free-space channels (Hill et al., 2017; Mélen et al., 2017), satellite-to-earth channels (Liao et al., 2017a) and seawater channels (Ruan et al., 2019). In addition, MDI protocols against side-channel attacks and device-independent protocols with higher security are also worthy of further study.

Author contributions

C-LL arranged and wrote the section of numerical method and the satellite-to-ground protocol. Z-PL and M-GZ organized and wrote the section on the neural network method. W-BL wrote other parts and integrated all the content. H-LY and Z-BC supervised the project.

Funding

We gratefully acknowledge support from the Natural Science Foundation of Jiangsu Province (No. BK20211145), the Fundamental Research Funds for the Central Universities (No. 020414380182), the Key Research and Development Program of Nanjing Jiangbei New Area (No. ZDYD20210101), and the Program for Innovative Talents and Entrepreneurs in Jiangsu (No. JSSCRC2021484).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aguiar, L. d. S., Borelli, L. F., Roversi, J. A., and Vidiella-Barranco, A. (2022). Performance analysis of continuous-variable quantum key distribution using non-gaussian states. Quant. Inf. Process. 21, 304.doi:10.1007/s11128-022-03645-z

CrossRef Full Text | Google Scholar

Almeida, M., Pereira, D., Muga, N. J., ao, M. F., Pinto, A. N., and Silva, N. A. (2021). Secret key rate of multi-ring m-apsk continuous variable quantum key distribution. Opt. Express 29, 38669–38682. doi:10.1364/oe.439992

PubMed Abstract | CrossRef Full Text | Google Scholar

Becir, A., El-Orany, F. A. A., and Wahiddin, M. R. B. (2012). Continuous-variable quantum key distribution protocols with eight-state discrete modulation. Int. J. Quantum Inf. 10, 1250004. doi:10.1142/s0219749912500049

CrossRef Full Text | Google Scholar

Brádler, K., and Weedbrook, C. (2018). Security proof of continuous-variable quantum key distribution using three coherent states. Phys. Rev. A 97, 022310. doi:10.1103/physreva.97.022310

CrossRef Full Text | Google Scholar

Caves, C. M., and Drummond, P. D. (1994). Quantum limits on bosonic communication rates. Rev. Mod. Phys. 66, 481–537. doi:10.1103/revmodphys.66.481

CrossRef Full Text | Google Scholar

Chen, J.-P., Zhang, C., Liu, Y., Jiang, C., Zhang, W.-J., Han, Z.-Y., et al. (2021). Twin-field quantum key distribution over a 511 km optical fibre linking two distant metropolitan areas. Nat. Photonics 15, 570–575. doi:10.1038/s41566-021-00828-5

CrossRef Full Text | Google Scholar

Denys, A., Brown, P., and Leverrier, A. (2021). Explicit asymptotic secret key rate of continuous-variable quantum key distribution with an arbitrary modulation. Quantum 5, 540. doi:10.22331/q-2021-09-13-540

CrossRef Full Text | Google Scholar

Dequal, D., Trigo Vidarte, L., Roman Rodriguez, V., Vallone, G., Villoresi, P., Leverrier, A., et al. (2021). Feasibility of satellite-to-ground continuous-variable quantum key distribution. npj Quantum Inf. 7, 3. doi:10.1038/s41534-020-00336-4

CrossRef Full Text | Google Scholar

Diamanti, E., and Leverrier, A. (2015). Distributing secret keys with quantum continuous variables: Principle, security and implementations. Entropy 17, 6072–6092. doi:10.3390/e17096072

CrossRef Full Text | Google Scholar

Dias, M. A., and de Assis, F. M. (2021). The impact of constellation cardinality on discrete unidimensional cvqkd protocols. Quantum Inf. process. 20, 284. doi:10.1007/s11128-021-03222-w

CrossRef Full Text | Google Scholar

Frank, M., and Wolfe, P. (1956). An algorithm for quadratic programming. Nav. Res. Logist. 3, 95–110. doi:10.1002/nav.3800030109

CrossRef Full Text | Google Scholar

Ghalaii, M., Ottaviani, C., Kumar, R., Pirandola, S., and Razavi, M. (2020). Discrete-modulation continuous-variable quantum key distribution enhanced by quantum scissors. IEEE J. Sel. Areas Commun. 38, 506–516. doi:10.1109/jsac.2020.2969058

CrossRef Full Text | Google Scholar

Ghorai, S., Grangier, P., Diamanti, E., and Leverrier, A. (2019). Asymptotic security of continuous-variable quantum key distribution with a discrete modulation. Phys. Rev. X 9, 021059. doi:10.1103/physrevx.9.021059

CrossRef Full Text | Google Scholar

Grosshans, F., and Grangier, P. (2002). Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 88, 057902. doi:10.1103/physrevlett.88.057902

PubMed Abstract | CrossRef Full Text | Google Scholar

Grosshans, F., Van Assche, G., Wenger, J., Brouri, R., Cerf, N. J., and Grangier, P. (2003). Quantum key distribution using gaussian-modulated coherent states. Nature 421, 238–241. doi:10.1038/nature01289

PubMed Abstract | CrossRef Full Text | Google Scholar

Gu, J., Xie, Y.-M., Liu, W.-B., Fu, Y., Yin, H.-L., and Chen, Z.-B. (2021). Secure quantum secret sharing without signal disturbance monitoring. Opt. Express 29, 32244–32255. doi:10.1364/oe.440365

PubMed Abstract | CrossRef Full Text | Google Scholar

Günthner, K., Khan, I., Elser, D., Stiller, B., Bayraktar, Ö., Müller, C. R., et al. (2017). Quantum-limited measurements of optical signals from a geostationary satellite. Optica 4, 611–616. doi:10.1364/optica.4.000611

CrossRef Full Text | Google Scholar

Guo, Y., Li, R., Liao, Q., Zhou, J., and Huang, D. (2018). Performance improvement of eight-state continuous-variable quantum key distribution with an optical amplifier. Phys. Lett. A 382, 372–381. doi:10.1016/j.physleta.2017.12.011

CrossRef Full Text | Google Scholar

Guo, Y., Ding, J., Mao, Y., Ye, W., Liao, Q., and Huang, D. (2020). Quantum catalysis-based discrete modulation continuous variable quantum key distribution with eight states. Phys. Lett. A 384, 126340. doi:10.1016/j.physleta.2020.126340

CrossRef Full Text | Google Scholar

Guo, H., Li, Z., Yu, S., and Zhang, Y. (2021). Toward practical quantum key distribution using telecom components. Fundam. Res. 1, 96–98. doi:10.1016/j.fmre.2020.12.002

CrossRef Full Text | Google Scholar

Gyongyosi, L., and Imre, S. (2018). Low-dimensional reconciliation for continuous-variable quantum key distribution. Appl. Sci. (Basel). 8, 87. doi:10.3390/app8010087

CrossRef Full Text | Google Scholar

Gyongyosi, L. (2020). Multicarrier continuous-variable quantum key distribution. Theor. Comput. Sci. 816, 67–95. doi:10.1016/j.tcs.2019.11.026

CrossRef Full Text | Google Scholar

Heid, M., and Lütkenhaus, N. (2007). Security of coherent-state quantum cryptography in the presence of gaussian noise. Phys. Rev. A 76, 022313. doi:10.1103/physreva.76.022313

CrossRef Full Text | Google Scholar

Hill, A. D., Chapman, J., Herndon, K., Chopp, C., Gauthier, D. J., and Kwiat, P. (2017). Drone-based quantum key distribution. Urbana 51, 61801–63003.

Google Scholar

Hirano, T., Ichikawa, T., Matsubara, T., Ono, M., Oguri, Y., Namiki, R., et al. (2017). Implementation of continuous-variable quantum key distribution with discrete modulation. Quantum Sci. Technol. 2, 024010. doi:10.1088/2058-9565/aa7230

CrossRef Full Text | Google Scholar

Hu, H., Im, J., Lin, J., Lütkenhaus, N., and Wolkowicz, H. (2021). Robust interior point method for quantum key distribution rate computation. arXiv preprint arXiv:2104.03847

Google Scholar

Hu, H., Im, J., Lin, J., Lütkenhaus, N., and Wolkowicz, H. (2022). Robust interior point method for quantum key distribution rate computation. Quantum 6, 792. doi:10.22331/q-2022-09-08-792

CrossRef Full Text | Google Scholar

Huang, P., Wang, T., Huang, D., and Zeng, G. (2022). Phase-matching continuous-variable measurement-device-independent quantum key distribution. Symmetry 14, 568. doi:10.3390/sym14030568

CrossRef Full Text | Google Scholar

Igor, D., and Andreas, W. (2005). Distillation of secret key and entanglement from quantum states. Proc. R. Soc. A 461, 207–235. doi:10.1098/rspa.2004.1372

CrossRef Full Text | Google Scholar

Jiang, C., Hu, X.-L., Yu, Z.-W., and Wang, X.-B. (2021). Composable security for practical quantum key distribution with two way classical communication. New J. Phys. 23, 063038. doi:10.1088/1367-2630/ac0285

CrossRef Full Text | Google Scholar

Karinou, F., Brunner, H. H., Fung, C.-H. F., Comandar, L. C., Bettelli, S., Hillerkuss, D., et al. (2018). Toward the integration of cv quantum key distribution in deployed optical networks. IEEE Phot. Technol. Lett. 30, 650–653. doi:10.1109/lpt.2018.2810334

CrossRef Full Text | Google Scholar

Kaur, E., Guha, S., and Wilde, M. M. (2021). Asymptotic security of discrete-modulation protocols for continuous-variable quantum key distribution. Phys. Rev. A 103, 012412. doi:10.1103/physreva.103.012412

CrossRef Full Text | Google Scholar

Kish, S. P., Villaseñor, E., Malaney, R., Mudge, K. A., and Grant, K. J. (2020). Feasibility assessment for practical continuous variable quantum key distribution over the satellite-to-Earth channel. Quantum Eng. 2, e50. doi:10.1002/que2.50

CrossRef Full Text | Google Scholar

Kwek, L.-C., Cao, L., Luo, W., Wang, Y., Sun, S., Wang, X., et al. (2021). Chip-based quantum key distribution. AAPPS Bull. 31, 15. doi:10.1007/s43673-021-00017-0

CrossRef Full Text | Google Scholar

Laudenbach, F., Pacher, C., Fung, C.-H. F., Poppe, A., Peev, M., Schrenk, B., et al. (2018). Continuous-variable quantum key distribution with gaussian modulation - the theory of practical implementations. Adv. Quantum Technol. 1, 1800011. doi:10.1002/qute.201800011

CrossRef Full Text | Google Scholar

Leverrier, A., and Grangier, P. (2009). Unconditional security proof of long-distance continuous-variable quantum key distribution with discrete modulation. Phys. Rev. Lett. 102, 180504. doi:10.1103/physrevlett.102.180504

PubMed Abstract | CrossRef Full Text | Google Scholar

Leverrier, A., Grosshans, F., and Grangier, P. (2010). Finite-size analysis of a continuous-variable quantum key distribution. Phys. Rev. A 81, 062343. doi:10.1103/physreva.81.062343

CrossRef Full Text | Google Scholar

Leverrier, A. (2015). Composable security proof for continuous-variable quantum key distribution with coherent states. Phys. Rev. Lett. 114, 070501. doi:10.1103/physrevlett.114.070501

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, M., and Cvijetic, M. (2018). Continuous-variable quantum key distribution with self-reference detection and discrete modulation. IEEE J. Quantum Electron. 54, 1–8. doi:10.1109/jqe.2018.2867651

CrossRef Full Text | Google Scholar

Li, J., Guo, Y., Wang, X., Xie, C., Zhang, L., and Huang, D. (2018). Discrete-modulated continuous-variable quantum key distribution with a machine-learning-based detector. Opt. Eng. 57, 1. doi:10.1117/1.oe.57.6.066109

CrossRef Full Text | Google Scholar

Li, Z., Cao, X.-Y., Li, C.-L., Weng, C.-X., Gu, J., Yin, H.-L., et al. (2021a). Finite-key analysis for quantum conference key agreement with asymmetric channels. Quantum Sci. Technol. 6, 045019. doi:10.1088/2058-9565/ac1e00

CrossRef Full Text | Google Scholar

Li, Z., Zhang, H., Liao, Q., Mao, Y., and Guo, Y. (2021b). Ensemble learning for failure prediction of underwater continuous variable quantum key distribution with discrete modulations. Phys. Lett. A 419, 127694. doi:10.1016/j.physleta.2021.127694

CrossRef Full Text | Google Scholar

Li, Y., Guo, Y., Ruan, X., and Zhao, W. (2021). Improving the discrete-modulated continuous-variable measurement-device-independent quantum key distribution with quantum scissors. Int. J. Theor. Phys. 60, 1949–1962. doi:10.1007/s10773-021-04813-0

CrossRef Full Text | Google Scholar

Liao, S.-K., Cai, W.-Q., Liu, W.-Y., Zhang, L., Li, Y., Ren, J.-G., et al. (2017a). Satellite-to-ground quantum key distribution. Nature 549, 43–47. doi:10.1038/nature23655

PubMed Abstract | CrossRef Full Text | Google Scholar

Liao, S.-K., Lin, J., Ren, J.-G., Liu, W.-Y., Qiang, J., Yin, J., et al. (2017b). Space-to-ground quantum key distribution using a small-sized payload on tiangong-2 space lab. Chin. Phys. Lett. 34, 090302. doi:10.1088/0256-307x/34/9/090302

CrossRef Full Text | Google Scholar

Liao, S.-K., Yong, H.-L., Liu, C., Shentu, G.-L., Li, D.-D., Lin, J., et al. (2017c). Long-distance free-space quantum key distribution in daylight towards inter-satellite communication. Nat. Photonics 11, 509–513. doi:10.1038/nphoton.2017.116

CrossRef Full Text | Google Scholar

Liao, Q., Guo, Y., Huang, D., Huang, P., and Zeng, G. (2018). Long-distance continuous-variable quantum key distribution using non-gaussian state-discrimination detection. New J. Phys. 20, 023015. doi:10.1088/1367-2630/aaa8c4

CrossRef Full Text | Google Scholar

Lin, J., and Lütkenhaus, N. (2020). Trusted detector noise analysis for discrete modulation schemes of continuous-variable quantum key distribution. Phys. Rev. Appl. 14, 064030. doi:10.1103/physrevapplied.14.064030

CrossRef Full Text | Google Scholar

Lin, J., Upadhyaya, T., and Lütkenhaus, N. (2019). Asymptotic security analysis of discrete-modulated continuous-variable quantum key distribution. Phys. Rev. X 9, 041064. doi:10.1103/physrevx.9.041064

CrossRef Full Text | Google Scholar

Liu, W.-B., Li, C.-L., Xie, Y.-M., Weng, C.-X., Gu, J., Cao, X.-Y., et al. (2021). Homodyne detection quadrature phase shift keying continuous-variable quantum key distribution with high excess noise tolerance. PRX Quantum 2, 040334. doi:10.1103/prxquantum.2.040334

CrossRef Full Text | Google Scholar

Liu, B., Xia, S., Xiao, D., Huang, W., Xu, B., and Li, Y. (2022a). Decoy-state method for quantum-key-distribution-based quantum private query. Sci. China Phys. Mech. Astron. 65, 240312. doi:10.1007/s11433-021-1843-7

CrossRef Full Text | Google Scholar

Liu, J., Cao, Y., Wang, P., Liu, S., Lu, Z., Wang, X., et al. (2022b). Impact of homodyne receiver bandwidth and signal modulation patterns on the continuous-variable quantum key distribution. Opt. Express 30, 27912–27925. doi:10.1364/oe.461235

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z.-P., Zhou, M.-G., Liu, W.-B., Li, C.-L., Gu, J., Yin, H.-L., et al. (2022c). Automated machine learning for secure key rate in discrete-modulated continuous-variable quantum key distribution. Opt. Express 30, 15024–15036. doi:10.1364/oe.455762

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, Y.-S., Cao, X.-Y., Weng, C.-X., Gu, J., Xie, Y.-M., Zhou, M.-G., et al. (2021). Efficient quantum digital signatures without symmetrization step. Opt. Express 29, 10162–10171. doi:10.1364/oe.420667

PubMed Abstract | CrossRef Full Text | Google Scholar

Lupo, C. (2020). Towards practical security of continuous-variable quantum key distribution. Phys. Rev. A 102, 022623. doi:10.1103/physreva.102.022623

CrossRef Full Text | Google Scholar

Ma, X.-C., Sun, S.-H., Jiang, M.-S., Gui, M., and Liang, L.-M. (2014). Gaussian-modulated coherent-state measurement-device-independent quantum key distribution. Phys. Rev. A 89, 042335. doi:10.1103/physreva.89.042335

CrossRef Full Text | Google Scholar

Ma, H.-X., Huang, P., Bai, D.-Y., Wang, T., Wang, S.-Y., Bao, W.-S., et al. (2019). Long-distance continuous-variable measurement-device-independent quantum key distribution with discrete modulation. Phys. Rev. A 99, 022322. doi:10.1103/physreva.99.022322

CrossRef Full Text | Google Scholar

Matsuura, T., Maeda, K., Sasaki, T., and Koashi, M. (2021). Finite-size security of continuous-variable quantum key distribution with digital signal processing. Nat. Commun. 12, 252. doi:10.1038/s41467-020-19916-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Mehta, P., Bukov, M., Wang, C.-H., Day, A. G., Richardson, C., Fisher, C. K., et al. (2019). A high-bias, low-variance introduction to machine learning for physicists. Phys. Rep. 810, 1–124. doi:10.1016/j.physrep.2019.03.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Mélen, G., Freiwang, P., Luhn, J., Vogl, T., Rau, M., Sonnleitner, C., et al. (2017). “Handheld quantum key distribution,” in Quantum information and measurement (Optica Publishing Group). QT6A–57.

Google Scholar

Papanastasiou, P., Lupo, C., Weedbrook, C., and Pirandola, S. (2018). Quantum key distribution with phase-encoded coherent states: Asymptotic security analysis in thermal-loss channels. Phys. Rev. A 98, 012340. doi:10.1103/physreva.98.012340

CrossRef Full Text | Google Scholar

Peng, Q., Guo, Y., Liao, Q., and Ruan, X. (2022). Satellite-to-submarine quantum communication based on measurement-device-independent continuous-variable quantum key distribution. Quantum Inf. process. 21, 61. doi:10.1007/s11128-022-03413-z

CrossRef Full Text | Google Scholar

Pirandola, S., Ottaviani, C., Spedalieri, G., Weedbrook, C., Braunstein, S. L., Lloyd, S., et al. (2015). High-rate measurement-device-independent quantum cryptography. Nat. Photonics 9, 397–402. doi:10.1038/nphoton.2015.83

CrossRef Full Text | Google Scholar

Pirandola, S., Laurenza, R., Ottaviani, C., and Banchi, L. (2017). Fundamental limits of repeaterless quantum communications. Nat. Commun. 8, 15043. doi:10.1038/ncomms15043

PubMed Abstract | CrossRef Full Text | Google Scholar

Pirandola, S., Andersen, U. L., Banchi, L., Berta, M., Bunandar, D., Colbeck, R., et al. (2020). Advances in quantum cryptography. Adv. Opt. Phot. 12, 1012–1236. doi:10.1364/aop.361502

CrossRef Full Text | Google Scholar

Pirandola, S. (2021). Limits and security of free-space quantum communications. Phys. Rev. Res. 3, 013279. doi:10.1103/physrevresearch.3.013279

CrossRef Full Text | Google Scholar

Pittaluga, M., Minder, M., Lucamarini, M., Sanzaro, M., Woodward, R. I., Li, M.-J., et al. (2021). 600-km repeater-like quantum communications with dual-band stabilization. Nat. Photonics 15, 530–535. doi:10.1038/s41566-021-00811-0

CrossRef Full Text | Google Scholar

Ralph, T. C. (1999). Continuous variable quantum cryptography. Phys. Rev. A 61, 010303. doi:10.1103/physreva.61.010303

CrossRef Full Text | Google Scholar

Ren, J.-G., Xu, P., Yong, H.-L., Zhang, L., Liao, S.-K., Yin, J., et al. (2017). Ground-to-satellite quantum teleportation. Nature 549, 70–73. doi:10.1038/nature23675

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruan, X., Zhang, H., Zhao, W., Wang, X., Li, X., and Guo, Y. (2019). Security analysis of discrete-modulated continuous-variable quantum key distribution over seawater channel. Appl. Sci. (Basel). 9, 4956. doi:10.3390/app9224956

CrossRef Full Text | Google Scholar

Shannon, C. E. (1949). Communication theory of secrecy systems. Bell Syst. Tech. J. 28, 656–715. doi:10.1002/j.1538-7305.1949.tb00928.x

CrossRef Full Text | Google Scholar

Shao, Y., Li, Y., Wang, H., Pan, Y., Pi, Y., Zhang, Y., et al. (2022). Phase-reference-intensity attack on continuous-variable quantum key distribution with a local local oscillator. Phys. Rev. A 105, 032601. doi:10.1103/physreva.105.032601

CrossRef Full Text | Google Scholar

Silberhorn, C., Ralph, T. C., Lütkenhaus, N., and Leuchs, G. (2002). Continuous variable quantum cryptography: Beating the 3 db loss limit. Phys. Rev. Lett. 89, 167901. doi:10.1103/physrevlett.89.167901

PubMed Abstract | CrossRef Full Text | Google Scholar

Su, X., Wang, W., Wang, Y., Jia, X., Xie, C., and Peng, K. (2009). Continuous variable quantum key distribution based on optical entangled states without signal modulation. Europhys. Lett. 87, 20005. doi:10.1209/0295-5075/87/20005

CrossRef Full Text | Google Scholar

Su, Z., Cai, D., Jiang, H., Wang, J., Wang, D., Guo, X., et al. (2022). Optical injection locking based local oscillator regeneration for continuous variable quantum key distribution. Opt. Lett. 47, 1287–1290. doi:10.1364/ol.451670

PubMed Abstract | CrossRef Full Text | Google Scholar

Sych, D., and Leuchs, G. (2010). Coherent state quantum key distribution with multi letter phase-shift keying. New J. Phys. 12, 053019. doi:10.1088/1367-2630/12/5/053019

CrossRef Full Text | Google Scholar

Tian, Y., Wang, P., Liu, J., Du, S., Liu, W., Lu, Z., et al. (2022). Experimental demonstration of continuous-variable measurement-device-independent quantum key distribution over optical fiber. Optica 9, 492–500. doi:10.1364/optica.450573

CrossRef Full Text | Google Scholar

Upadhyaya, T., van Himbeeck, T., Lin, J., and Lütkenhaus, N. (2021). Dimension reduction in quantum key distribution for continuous- and discrete-variable protocols. PRX Quantum 2, 020325. doi:10.1103/prxquantum.2.020325

CrossRef Full Text | Google Scholar

Villasenor, E., Malaney, R., Mudge, K. A., and Grant, K. J. (2020). “Atmospheric effects on satellite-to-ground quantum key distribution using coherent states,” in GLOBECOM 2020 - 2020 IEEE Global Communications Conference (IEEE).

CrossRef Full Text | Google Scholar

Wang, P., Wang, X., and Li, Y. (2019a). Continuous-variable measurement-device-independent quantum key distribution using modulated squeezed states and optical amplifiers. Phys. Rev. A 99, 042309. doi:10.1103/physreva.99.042309

CrossRef Full Text | Google Scholar

Wang, T.-L., Djordjevic, I. B., and Nagel, J. (2019b). Laser beam propagation effects on secure key rates for satellite-to-ground discrete modulation cv-qkd. Appl. Opt. 58, 8061–8068. doi:10.1364/ao.58.008061

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X.-B., Wang, J.-T., Qin, J.-Q., Jiang, C., and Yu, Z.-W. (2020). Guessing probability in quantum key distribution. npj Quantum Inf. 6, 45. doi:10.1038/s41534-020-0267-3

CrossRef Full Text | Google Scholar

Wang, H., Li, Y., Pi, Y., Pan, Y., Shao, Y., Ma, L., et al. (2022a). Sub-gbps key rate four-state continuous-variable quantum key distribution within metropolitan area. Commun. Phys. 5, 162. doi:10.1038/s42005-022-00941-z

CrossRef Full Text | Google Scholar

Wang, S., Yin, Z.-Q., He, D.-Y., Chen, W., Wang, R.-Q., Ye, P., et al. (2022b). Twin-field quantum key distribution over 830-km fibre. Nat. Photonics 16, 154–161. doi:10.1038/s41566-021-00928-2

CrossRef Full Text | Google Scholar

Winick, A., Lütkenhaus, N., and Coles, P. J. (2018). Reliable numerical key rates for quantum key distribution. Quantum 2, 77. doi:10.22331/q-2018-07-26-77

CrossRef Full Text | Google Scholar

Xie, Y.-M., Lu, Y.-S., Weng, C.-X., Cao, X.-Y., Jia, Z.-Y., Bao, Y., et al. (2022). Breaking the rate-loss bound of quantum key distribution with asynchronous two-photon interference. PRX Quantum 3, 020315. doi:10.1103/prxquantum.3.020315

CrossRef Full Text | Google Scholar

Xu, F., Ma, X., Zhang, Q., Lo, H.-K., and Pan, J.-W. (2020). Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 92, 025002. doi:10.1103/revmodphys.92.025002

CrossRef Full Text | Google Scholar

Xuan, Q. D., Zhang, Z., and Voss, P. L. (2009). A 24 km fiber-based discretely signaled continuous variable quantum key distribution system. Opt. Express 17, 24244. doi:10.1364/oe.17.024244

PubMed Abstract | CrossRef Full Text | Google Scholar

Ye, W., Zhong, H., Wu, X., Hu, L., and Guo, Y. (2020). Continuous-variable measurement-device-independent quantum key distribution via quantum catalysis. Quantum Inf. process. 19, 346. doi:10.1007/s11128-020-02859-3

CrossRef Full Text | Google Scholar

Ye, W., Guo, Y., Zhang, H., Zhong, H., Mao, Y., and Hu, L. (2021). Enhancing discrete-modulated continuous-variable measurement-device-independent quantum key distribution via quantum catalysis. J. Phys. B At. Mol. Opt. Phys. 54, 045501. doi:10.1088/1361-6455/abdac9

CrossRef Full Text | Google Scholar

Yin, H.-L., Chen, T.-Y., Yu, Z.-W., Liu, H., You, L.-X., Zhou, Y.-H., et al. (2016). Measurement-device-independent quantum key distribution over a 404 km optical fiber. Phys. Rev. Lett. 117, 190501. doi:10.1103/physrevlett.117.190501

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, J., Cao, Y., Li, Y.-H., Liao, S.-K., Zhang, L., Ren, J.-G., et al. (2017a). Satellite-based entanglement distribution over 1200 kilometers. Science 356, 1140–1144. doi:10.1126/science.aan3211

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, J., Cao, Y., Li, Y.-H., Ren, J.-G., Liao, S.-K., Zhang, L., et al. (2017b). Satellite-to-ground entanglement-based quantum key distribution. Phys. Rev. Lett. 119, 200501. doi:10.1103/physrevlett.119.200501

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, H.-L., Liu, P., Dai, W.-W., Ci, Z.-H., Gu, J., Gao, T., et al. (2020). Experimental composable security decoy-state quantum key distribution using time-phase encoding. Opt. Express 28, 29479–29485. doi:10.1364/oe.401829

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, Z.-Q., Lu, F.-Y., Teng, J., Wang, S., Chen, W., Guo, G.-C., et al. (2021). Twin-field protocols: Towards intercity quantum key distribution without quantum repeaters. Fundam. Res. 1, 93–95. doi:10.1016/j.fmre.2020.11.001

CrossRef Full Text | Google Scholar

Yu, C., Li, Y., Ding, J., Mao, Y., and Guo, Y. (2022). Photon subtraction-based continuous-variable measurement-device-independent quantum key distribution with discrete modulation over a fiber-to-water channel. Commun. Theor. Phys. 74, 035104. doi:10.1088/1572-9494/ac5320

CrossRef Full Text | Google Scholar

Zdeborová, L. (2017). New tool in the box. Nat. Phys. 13, 420–421. doi:10.1038/nphys4053

CrossRef Full Text | Google Scholar

Zeng, P., Zhou, H., Wu, W., and Ma, X. (2022). Mode-pairing quantum key distribution. Nat. Commun. 13, 3903. doi:10.1038/s41467-022-31534-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y.-C., Li, Z., Yu, S., Gu, W., Peng, X., and Guo, H. (2014). Continuous-variable measurement-device-independent quantum key distribution using squeezed states. Phys. Rev. A 90, 052325. doi:10.1103/physreva.90.052325

CrossRef Full Text | Google Scholar

Zhao, Y., Qi, B., Ma, X., Lo, H.-K., and Qian, L. (2006). Experimental quantum key distribution with decoy states. Phys. Rev. Lett. 96, 070502. doi:10.1103/physrevlett.96.070502

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y.-B., Heid, M., Rigas, J., and Lütkenhaus, N. (2009). Asymptotic security of binary modulated continuous-variable quantum key distribution under collective attacks. Phys. Rev. A 79, 012307. doi:10.1103/physreva.79.012307

CrossRef Full Text | Google Scholar

Zhao, W., Shi, R., Feng, Y., and Huang, D. (2020a). Unidimensional continuous-variable quantum key distribution with discrete modulation. Phys. Lett. A 384, 126061. doi:10.1016/j.physleta.2019.126061

CrossRef Full Text | Google Scholar

Zhao, W., Shi, R., Shi, J., Ruan, X., Guo, Y., and Huang, D. (2020b). Phase-noise estimation using bayesian inference for discretely modulated measurement-device-independent continuous-variable quantum key distribution. Phys. Rev. A 102, 022621. doi:10.1103/physreva.102.022621

CrossRef Full Text | Google Scholar

Zhao, W., Shi, R., Ruan, X., Guo, Y., Mao, Y., and Feng, Y. (2022). Monte Carlo-based security analysis for multi-mode continuous-variable quantum key distribution over underwater channel. Quantum Inf. process. 21, 186. doi:10.1007/s11128-022-03533-6

CrossRef Full Text | Google Scholar

Zhou, Y.-H., Yu, Z.-W., and Wang, X.-B. (2016). Making the decoy-state measurement-device-independent quantum key distribution practically useful. Phys. Rev. A 93, 042324. doi:10.1103/physreva.93.042324

CrossRef Full Text | Google Scholar

Zhou, C., Wang, X., Zhang, Z., Yu, S., Chen, Z., and Guo, H. (2021). Rate compatible reconciliation for continuous-variable quantum key distribution using raptor-like ldpc codes. Sci. China Phys. Mech. Astron. 64, 260311. doi:10.1007/s11433-021-1688-4

CrossRef Full Text | Google Scholar

Zhou, M.-G., Liu, Z.-P., Liu, W.-B., Li, C.-L., Bai, J.-L., Xue, Y.-R., et al. (2022). Neural network-based prediction of the secret-key rate of quantum key distribution. Sci. Rep. 12, 8879. doi:10.1038/s41598-022-12647-x

PubMed Abstract | CrossRef Full Text | Google Scholar