Phase-dependent strategy to mimic quantum phase transitions

This study proposes a hybrid quantum system of an ensemble of collective spins coupled to a surface acoustic wave (SAW) cavity through a sideband design. Assisted by a dichromatic optical drive with a phase-dependent control, this spin ensemble can effectively mimic different types of long-range Lipkin–Meshkov–Glick (LMG) interactions and then undergo quantum phase transitions (QPTs) due to phase-induced spontaneous symmetry breaking (SSB). In addition, this phase-controlled scheme also ensures the dynamical preparation of the spin-squeezed state (SSS), which may be a useful application in quantum measurement. This study is a fresh attempt at quantum manipulation based on acoustic control and also provides a promising route toward useful applications in quantum information processing, especially the adiabatic preparation of multiparticle-entangled ground states via QPTs; i.e., the Greenberger–Horne–Zeilinger (GHZ) or W-type states.

1 Introduction

In the field of quantum information processing (QIP) and quantum manipulation (QM), the quantized electromagnetic field has always been considered the most reliable medium and means, such as in cavity quantum electrodynamics (QED) system and the superconducting circuits (SC) system (Xiang et al., 2013; Blais et al., 2020; Carusotto et al., 2020; Clerk et al., 2020; Haroche et al., 2020; Blais et al., 2021). However, with the rapid development of cryogenic and micro-nano processing technologies, traditional mechanical or acoustic devices have gradually re-entered the quantum world (O’Connell et al., 2010; Aspelmeyer et al., 2014; Forn-Díaz et al., 2019). In particular, quantum acoustic devices (QADs) have become among the most valuable quantum units owing to their unique advantages (Naber et al., 2006; Gustafsson et al., 2014; Schuetz et al., 2015). First, for the suppression of quantum noise, QADs can isolate environmental phononic noise at a much higher efficiency compared to other electromagnetic systems. Second, QADs are more convenient to design and fabricate because of their inherent larger dimensions (Schuetz et al., 2015; Kuzyk and Wang, 2018). Third, they originate from mature magnetostrictive or piezoelectric technologies, which can further improve their adaptive capacity to establish various hybrid quantum systems (Manenti et al., 2016; Knörzer et al., 2018). Finally, QADs can induce strong coupling to different qubits; this coupling mechanism is mainly similar to the ion (or atom) trap system and is naturally applicable to multiple QIP schemes, which were first proposed in ion trap systems (Andrew Golter et al., 2016a; Andrew Golter et al., 2016b). Therefore, an acoustic-based hybrid system can provide a promising platform to implement QIP and QM targets to ensure the efficient tailoring of spin–phonon and spin–spin interactions (Rabl et al., 2009; Bennett et al., 2013). Working as a quantum data bus or transducer, QADs can provide strong interactions in a wide range of qubits, especially at the single-quantum level (Li et al., 2020; Zhou et al., 2021; Leng et al., 2022; Zhou et al., 2022). Taking the surface acoustic wave (SAW) cavity, for example, strong coupling to different qubits can be achieved, with an estimated cooperativity C ∼ g²/(γκ) of C ∼ 10–100 (Schuetz et al., 2015).

Recently, other kinds of artificial qubits, including nitrogen-vacancy (NV), silicon-vacancy (SiV), and hexagonal boron nitride (hBN) color centers have been introduced into the field of quantum science (Gao et al., 2015; Lemonde et al., 2018; Tan et al., 2022; Zhao et al., 2022). Without an additional trap, a SAW-based device may also induce strong stressful interactions directly to this type of solid-state spin, which increased interest for QIP and QM. This study proposes a general hybrid quantum system of an ensemble of collective spins coupled to a surface acoustic wave (SAW) cavity through a sideband design. Assisted by a dichromatic optical drive with a phase-dependent control, this spin ensemble effectively mimicked different types of long-range spin–spin interactions, namely the Lipkin–Meshkov–Glick (LMG) model with different types (Lipkin et al., 1965; Castaños et al., 2006; Morrison and Parkins, 2008; Ma and Wang, 2009; Zhang et al., 2017). Through a phase-dependent modification of this optical drive, this ensemble of spins undergoes quantum phase transitions (QPTs) because of the so-called spontaneous symmetry breaking (SSB). In addition, this phase-controlled scheme can also supply both the dynamical preparation of spin-squeezed state (SSS) (Kitagawa and Ueda, 1993; Wineland et al., 1994) and the adiabatic preparation of the multiparticle entangled ground states via QPTs (Vidal et al., 2004a; Vidal et al., 2004b); i.e., the Greenberger–Horne–Zeilinger (GHZ) or W-type states (Anders and Mølmer, 1999; Mølmer and Anders, 1999; Zheng, 2001; Unanyan and Fleischhauer, 2003). Given the goal of performing realistic QIP and QM, the results of our investigations are a fresh attempt using an acoustic control and may also provide general and useful applications.

2 Setup and Hamiltonian

Here we consider the basic proposal for this hybrid system and the coupling mechanism, which are illustrated in Figures 1A, B, C. Without a loss of generality, we take an ensemble of the NV centers as an example. In Figure 1A, an ensemble of solid-state spins is set near the surface of the SAW cavity with a fundamental frequency ω_m/2π ∼ 0.1–1.0 GHz. A phase-dependent dichromatic field (λ ∼ 700 nm) is applied to transmit the optional classical field (θ₁, ω₁, Ω₁) or (θ₂, ω₂, Ω₂). According to the previous investigation, this type of spin–phonon coupling is analogous to the ion trap system, and this SAW mode is similar to a harmonic oscillator potential as shown in Figure 1B. For an NV center, the energy-level design is plotted in Figure 1C, where |e(g)⟩ denotes the excited (ground) state with the energy split ω₀ ≫ ω_m. We can obtain only the longitudinal coupling to each NV center via the SAW cavity, based on the expression ${\widehat{H}}_L\sim \hslash g_0(\widehat{a}+{\widehat{a}}^{†})|e\rangle \langle e|$ and coupling strength g₀ (Andrew Golter et al., 2016b). Meanwhile, we apply the dichromatic optical drive to each NV spin obtain to the transition process |e⟩ ⇌|g⟩ near-resonantly. This sideband design is illustrated in Figure 1C. The identical red and blue detuning satisfies Δ ≡ ω₂−ω₀ ≡ ω₀−ω₁ ∼ ω_m.

FIGURE 1

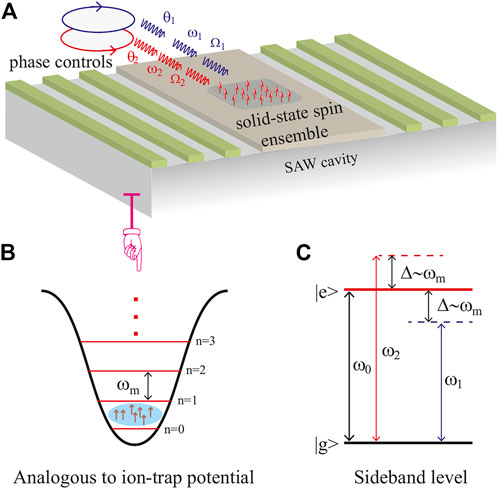
FIGURE 1. (Color online) Scheme diagrams. (A) An ensemble of solid-state spins is set near the surface of the SAW cavity with the phonon annihilation (creation) operator $\widehat{a}$ $({\widehat{a}}^{†})$ and mode frequency ω_m. The phase modulators are applied to transmit the optional and controllable optical fields with tunable phase θ_1,2, frequency ω_1,2, and driving strength Ω_1,2. (B) This type of sideband spin–phonon coupling system can be analogous to the ion trap system. (C) Energy-level schematic and sideband design, where the two-tune classical fields are applied to the solid-state spins via additional phase controls, thereby ensuring an optional drive to the spins with the red (blue) detuning Δ ∼ ω_m.

Therefore, the systemic Hamiltonian for each NV spin (i.e., we consider the jth NV spin) is expressed as (ℏ = 1)

${\widehat{H}}_j={\omega }_0{\widehat{\sigma }}_z^j/2+{\omega }_m{\widehat{a}}^{†}\widehat{a}+g_0\left(\widehat{a}+{\widehat{a}}^{†}\right){\widehat{\sigma }}_z^j+{\widehat{\sigma }}_j^{+}\left({\mathrm{\Omega }}_1{e}^{-i{\omega }_{1}t}+{\mathrm{\Omega }}_2{e}^{-i{\omega }_{2}t}\right)+\text{H.c.},(1)$

where ${\widehat{\sigma }}_z^j\equiv |e{\rangle }_j{⟨e|-|g⟩}_j\langle g|$, ${\widehat{\sigma }}_j^{+}\equiv |e{\rangle }_j\langle g|$. For simplicity, we assume here that the collective spins are homogenous, and write the Hamiltonian of this whole system as

$\widehat{H}={\omega }_0{\widehat{S}}_z+{\omega }_m{\widehat{a}}^{†}\widehat{a}+g\left(\widehat{a}+{\widehat{a}}^{†}\right){\widehat{S}}_z+{\widehat{S}}^{+}\left({\mathrm{\Omega }}_1{e}^{-i{\omega }_{1}t}+{\mathrm{\Omega }}_2{e}^{-i{\omega }_{2}t}\right)+\text{H.c.}(2)$

in which the collective spin operators are defined as ${\widehat{S}}_{x,y,z}={\sum }_{j=1}^N{\widehat{\sigma }}_{x,y,z}^j/2$ and ${\widehat{S}}^{\pm }={\sum }_{j=1}^N{\widehat{\sigma }}_j^{\pm }$, with the basic commutation relation: $[{\widehat{S}}_i,{\widehat{S}}_j]=i{\epsilon }_{\mathit{ijk}}{\widehat{S}}_k$, $[{\widehat{S}}^{+},{\widehat{S}}^{-}]=2{\widehat{S}}^z$, and $[{\widehat{S}}_z,{\widehat{S}}^{\pm }]=\pm {\widehat{S}}^{\pm }$. We apply the unitary Schrieffer–Wolff transformation ${\widehat{U}}_{\text{SW}}=e^{-i\widehat{p}}$ to Eq. 2, with the Hermitian operator $\widehat{p}\equiv i\eta ({\widehat{a}}^{†}-\widehat{a}){\widehat{S}}_z$ and the Lamb–Dicke-like parameter η = g/ω_m ∼ 0.1–0.2 (Rabl et al., 2010; Zhou et al., 2018; Li et al., 2020). We assume that the SAW is cooled sufficiently at extremely low ambient temperature so that this hybrid system satisfies the so-called Lamb–Dicke limit $(\bar{n}+1){\eta }^2\ll 1$, where $\bar{n}=1/(e^{\hslash {\omega }_m/k_{B}T}-1)$ is the average number of the phonon for this acoustic mode for the environmental temperature T. For example, we assume that ω_m/2π ∼ 1.0 GHz; once T ≈ 1.0 K, we get $\bar{n}\approx 20.3$; if T ≈ 0.1 K, we also get $\bar{n}\approx 1.6$. Therefore, the thermal phonon number can be compressed effectively as long as this hybrid system is at a low temperature. Applying the approximate relation $e^{\pm \eta ({\widehat{a}}^{†}-\widehat{a})}\simeq 1\pm \eta ({\widehat{a}}^{†}-\widehat{a})$ to Eq. 2 we acquire the Hamiltonian in the interaction picture. As η ≪ 1, we can effectively rewrite the Hamiltonian in the interaction picture (IP)

${\widehat{H}}_{\text{IP}}\simeq {\widehat{S}}^{+}{e}^{i{\omega }_{0}t}\times \left[1+\eta \left({\widehat{a}}^{†}{e}^{i{\omega }_{m}t}-\widehat{a}{e}^{-i{\omega }_{m}t}\right)\right]\times \left({\mathrm{\Omega }}_1{e}^{-i{\omega }_{1}t}+{\mathrm{\Omega }}_2{e}^{-i{\omega }_{2}t}\right)+\text{H.c.}(3)$

In this scheme, we assume the following relations: ν ≫ λ, |Δ|≫|Ω_1,2|, and {ν, |Δ|, |Δ ± ν|}≫ η|Ω_1,2| and can then eliminate this phonon mode adiabatically (according to Appendix A) (James, 1998; James and Jerke, 2012). Ignoring the items for the energy shift caused by this acoustic mode ($\sim {\widehat{a}}^{†}\widehat{a}{\widehat{S}}_z$), we can get the general LMG model with the long-range spin–spin interactions.

${\widehat{H}}_{\text{Total}}^{\text{eff}}\approx A{\widehat{S}}_z+B{\widehat{S}}_x^2+C{\widehat{S}}_y^2+D\left({\widehat{S}}_x{\widehat{S}}_y+{\widehat{S}}_y{\widehat{S}}_x\right),(4)$

where the relevant coefficients are

$\begin{array}{ll}\hfill A& =\left(\frac{2}{\mathrm{\Delta }}-\frac{2{\eta }^2\mathrm{\Delta }}{{\delta }_2{\delta }_3}\right)\left(r_1^2-r_2^2\right),\hfill \\ \hfill B& =\frac{2{\omega }_m{\eta }^2}{{\delta }_2{\delta }_3}\left(2r_1{r}_2\cos \mathrm{\Theta }-r_1^2-r_2^2\right),\hfill \\ \hfill C& =\frac{2{\omega }_m{\eta }^2}{{\delta }_2{\delta }_3}\left(-2r_1{r}_2\cos \mathrm{\Theta }-r_1^2-r_2^2\right),\hfill \\ \hfill D& =\frac{-4{\omega }_m{\eta }^2}{{\delta }_2{\delta }_3}{r}_1{r}_2\sin \mathrm{\Theta }.\hfill \end{array}$

3 LMG model

The Lipkin–Meshkov–Glick (LMG) model was first proposed in the area of nuclear physics to describe monopole-monopole interactions and is one kind of solvable long-range spin–spin model (Lipkin et al., 1965). This model, not only obeys the conservation of angular momentum but also satisfies the ${\mathbb{Z}}_2$ symmetry. Thus, many theoretical proposals have been described for simulating this spin model to explore new topics in physics. Different physical systems such as the ion-trap system (Zheng, 2001; Unanyan and Fleischhauer, 2003), the cavity QED system (Morrison and Parkins, 2008; Zhang et al., 2017), and the superconducting system (Tsomokos et al., 2008) have presented theoretical schemes and reported interesting results. The general LMG model may be expressed as

$\widehat{H}=ϵ{\widehat{S}}_z+V\left({\widehat{S}}_x^2-{\widehat{S}}_y^2\right)+W\left({\widehat{S}}_x^2+{\widehat{S}}_y^2\right),(5)$

and the relevant tunable parameters are ϵ, V, and W, respectively (Lipkin et al., 1965). Here, Eq. 5 satisfies the conservation of angular momentum, namely, $[\widehat{H},{\mathbf{S}}^2]$ with ${\mathbf{S}}^2\equiv {\widehat{S}}_x^2+{\widehat{S}}_y^2+{\widehat{S}}_z^2=S(S+1)$. In addition, we can achieve several types of LMG models by modifying the aforementioned parameters. For example, once V = 0 and W ≠ 0, we can first obtain isotropy-type interactions with ${\widehat{H}}_I=ϵ{\widehat{S}}_z+W({\mathbf{S}}^2-{\widehat{S}}_z^2)$. This type of LMG Hamiltonian can be solved exactly in the representation of ${\widehat{S}}_z$; i.e., ${\widehat{S}}_z|m_z\rangle =m_z|m_z\rangle$, −S ≤ m_z ≤ S and |m_z⟩ denote the eigenstate of ${\widehat{S}}_z$. We can, therefore, obtain the relation ${\widehat{H}}_I|m_z\rangle =E_{m_z}|m_z\rangle$ and $E_{m_z}=ϵm_z+W[S(S+1)-m_z^2]$. This model mainly indicates the ferromagnetic order, with a ground state of |m_z = S⟩ or |m_z = −S⟩. When ϵ = 0 and V = W ≠ 0 (or V = −W ≠ 0), we obtain the one-axis twisting LMG model; i.e., ${\widehat{H}}_{x,y}=C_{x,y}{\widehat{S}}_{x,y}^2$ with C_x = W + V and C_y = W−V. Here, ${\widehat{H}}_{x,y}$ belongs to the ferromagnetic order when C_x,y < 0; conversely, when C_x,y > 0, it obeys the antiferromagnetic order. Furthermore, when V ≠ W ≠ 0, we obtain the two-axis twisting LMG model; i.e., ${\widehat{H}}_T=ϵ{\widehat{S}}_z+C_x{\widehat{S}}_x^2+C_y{\widehat{S}}_y^2$.

4 Discussion of the phase-dependent control

First, according to the previous investigation of this long-range spin model, the isotropy LMG model is (see Appendix B)

${\widehat{H}}_{\text{Isotropy}}^{\mathrm{1,2}}=A_0^{\mathrm{1,2}}{\widehat{S}}_z-B_0^{\mathrm{1,2}}{\widehat{S}}_z^2+B_0^{\mathrm{1,2}}{\mathbf{S}}^2.(6)$

In this Hamiltonian, ${\mathbf{S}}^2\equiv {\widehat{S}}_x^2+{\widehat{S}}_y^2+{\widehat{S}}_z^2=S(S+1)$ is a conserved quantity, S = N/2 represents the maximum total angular momentum, and ${\widehat{H}}_{\text{Isotropy}}^{\mathrm{1,2}}$ corresponds to a phase-independent model. This also belongs to the ferromagnetic- (FM-) order Hamiltonian, with the unique and non-degenerate ground state namely, |Ψ⟩_u = |↑↑⋯⟩ ≡|m_z = S⟩ or |Ψ⟩_d = |↓↓⋯⟩ ≡|m_z = −S⟩, with spin number N (Zheng, 2001). Here, the coefficient $A_0^{\mathrm{1,2}}$ breaks the original symmetry and eliminates the degeneracy of item $-B_0^{\mathrm{1,2}}{\widehat{S}}_z^2$. The unique ground state |Ψ⟩_u or |Ψ⟩_d is decided mainly by the parameter $A_0^{\mathrm{1,2}}$. For example, if we can obtain ${\widehat{H}}_{\text{Isotropy}}^2$ and $A_0^2>0$, the ground state is |Ψ⟩_u; however, for ${\widehat{H}}_{\text{Isotropy}}^1$ and $A_0^1>0$, the ground state is |Ψ⟩_d.

Second, the more interesting and novel point lies in the phase-dependent control of this proposal, which we discuss briefly. Here, we assume ${\mathrm{\Omega }}_{\mathrm{1,2}}=r_{\mathrm{1,2}}{e}^{i{\theta }_{\mathrm{1,2}}}$ and Θ = θ₁+θ₂. To study the effects caused by the phase of this dichromatic optical drive, we assume r₁ = r₂ = r for simplicity, to get

${\widehat{H}}_{\text{General}}^{\text{LMG}}\approx -G_T\left[\left(1-\cos \mathrm{\Theta }\right){\widehat{S}}_x^2+\left(1+\cos \mathrm{\Theta }\right){\widehat{S}}_y^2+\sin \mathrm{\Theta }\left({\widehat{S}}_x{\widehat{S}}_y+{\widehat{S}}_y{\widehat{S}}_x\right)\right],(7)$

with $G_T=\frac{4{\omega }_m{r}^2{\eta }^2}{{\delta }_2{\delta }_3}$.

For single solid-state spin, we first define $|\pm {\rangle }_x=(|\uparrow \rangle \pm |\downarrow \rangle )/\sqrt{2}$ and $|\pm {\rangle }_y=(|\uparrow \rangle \pm i|\downarrow \rangle )/\sqrt{2}$. We can then make the brief list shown in Table 1. For example, for the first case, namely, case (1), with Θ = 0, we obtain the one-axis twisting LMG model along the y direction,

${\widehat{H}}_y^{\text{LMG}}=-G_y{\widehat{S}}_y^2.(8)$

When $G_y=\frac{8{\omega }_m{r}^2{\eta }^2}{{\delta }_2{\delta }_3}>0$, the Hamiltonian ${\widehat{H}}_y^{\text{LMG}}$ presents the ferromagnetic (FM) order, with a ground state corresponding to |m_y = ±N/2⟩ = |±±⋯⟩_y ≡|±⟩_y|±⟩_y⋯|±⟩_y; however, when G_y < 0, the Hamiltonian ${\widehat{H}}_y^{\text{LMG}}$ is the antiferromagnetic (AFM) order, with a ground state of |m_y = 0⟩ (N is an even number) or |m_y = ±1/2⟩ (N is an odd number). In addition, according to our previous investigation on this type of interaction, we can obtain an adiabatic transition process from the initial disentangled ground state (governed by ${\widehat{H}}_{\text{Isotropy}}^{\mathrm{1,2}}$) to the N-particle Greenberger–Horne–Zeilinger (GHZ)-type entangled state (Zhou et al., 2018).

TABLE 1

TABLE 1. Phase-dependent LMG models and ground states (GS) (Zhou et al., 2018).

While for case (2), when Θ = π, we can also get another one-axis twisting LMG model along the x direction,

${\widehat{H}}_x^{\text{LMG}}=-G_x{\widehat{S}}_x^2.(9)$

Equivalently, when $G_x=\frac{8{\omega }_m{r}^2{\eta }^2}{{\delta }_2{\delta }_3}>0$, the Hamiltonian ${\widehat{H}}_x^{\text{LMG}}$ also shows the ferromagnetic (FM) order, with a ground state of |m_x = ±N/2⟩ = |±±⋯⟩_x ≡|±⟩_x|±⟩_x⋯|±⟩_x; however, when G_x < 0, the Hamiltonian ${\widehat{H}}_x^{\text{LMG}}$ is of the antiferromagnetic (AFM) order, with a ground state of |m_x = 0⟩ (N is an even number) or |m_x = ±1/2⟩ (N is an odd number).

Then, for case (3), as illustrated in the third and fourth lines of Table 1, when Θ = ±π/2, we obtain a novel transverse-type LMG model (in the x−y plane) as follows:

${\widehat{H}}_T^{\pm }=-G_T{\left({\widehat{S}}_x\pm {\widehat{S}}_y\right)}^2.(10)$

This type of spin–spin interaction belongs to the one-axis twisting model. For example, if we define a linear transformation in this model; i.e., ${\widehat{\mathcal{S}}}^{+}=\sqrt{2}{\widehat{S}}^{+}{e}^{i\vartheta }$, ${\widehat{\mathcal{S}}}^{-}=\sqrt{2}{\widehat{S}}^{-}{e}^{-i\vartheta }$, and ${\widehat{\mathcal{S}}}_{\mathbf{x}}=({\widehat{\mathcal{S}}}^{+}+{\widehat{\mathcal{S}}}^{-})/2$, we get ${\widehat{H}}_T^{\pm }=-G_T{\widehat{\mathcal{S}}}_{\mathbf{x}}^2$, with the “±” signs ϑ = ∓π/4, respectively. In this new x representation, we can also obtain an equivalent one-axis twisting LMG model along the x direction. The physical mechanism of this model is also similar to that in case (2), and its FM and AFM phases are governed by the sign of G_T; i.e., G_T > 0, the Hamiltonian ${\widehat{H}}_T^{\pm }$ denotes the FM order, with a ground state of |m_x = ±N/2⟩ = |±±⋯⟩_x; but while G_T < 0, ${\widehat{H}}_{\mathbf{x}}^{\pm }$ stands for the AFM order, with a ground state of |m_x = 0⟩ (N is an even number) or |m_x = ±1/2⟩ (N is an odd number).

Thus, despite the different representations, we can always get the one-axis twisting LMG model, which can also lead to the preparation of the spin-squeezed state (SSS) through a dynamic process. Two main definitions have been proposed to describe the squeezed degree of this spin ensemble, (Sidles et al., 1995). First, Masahiro Kitagawa and Masahito Ueda defined ${\xi }_S^2=\frac{4\min (\mathrm{\Delta }{\widehat{J}}_{\vec{n}\perp }^2)}{N}$ in 1993. Another similar definition, the metrological spin-squeezing parameter ${\xi }_R^2=\frac{N{(\mathrm{\Delta }{\widehat{J}}_{\perp })}^2}{{⟨{\widehat{J}}_S⟩}^2}$, was introduced by Wineland et al. in 1992 and 1994 (Wineland et al., 1992; Wineland et al., 1994). According to our previous investigation, both definitions are valid and reliable for describing the SSS; moreover, we also reported that ${\xi }_S^2\le {\xi }_R^2$ (Li et al., 2020). For simplicity, we plot the dynamical ${\xi }_R^2$ (Kitagawa and Ueda, 1993) in Figure 2, by solving the following master equation numerically. Under the realistic condition considering both decay and dephasing factors (Γ_dc and Γ_dp), the corresponding dynamical process of this whole system is dominated by the master equation:

$\frac{d\widehat{\varrho }}{dt}=i\left[\widehat{\varrho },{\widehat{H}}_{\text{General}}^{\text{LMG}}\right]+{\mathrm{\Gamma }}_{\text{dc}}\left(2{\widehat{S}}^{-}\widehat{\varrho }{\widehat{S}}^{+}-{\widehat{S}}^{+}{\widehat{S}}^{-}\widehat{\varrho }-\widehat{\varrho }{\widehat{S}}^{+}{\widehat{S}}^{-}\right)+{\mathrm{\Gamma }}_{\text{dp}}\left(2{\widehat{S}}_z\widehat{\varrho }{\widehat{S}}_z-{\widehat{S}}_z{\widehat{S}}_z\widehat{\varrho }-\widehat{\varrho }{\widehat{S}}_z{\widehat{S}}_z\right).(11)$

FIGURE 2

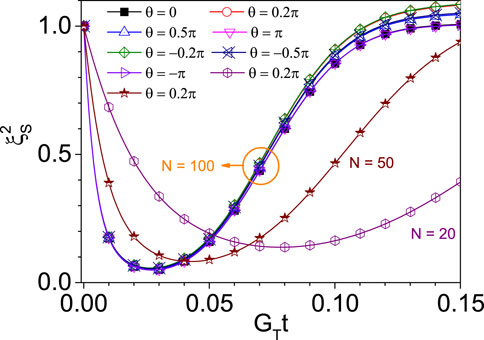
FIGURE 2. (Color online) Dynamical squeezing parameter ${\xi }_S^2$ for different Θ = 0, ± π/2, ± π, ± 0.2π, with γ_dp ≈ 0.1γ_dc ≈ 0.001G_T and N = 100, 50, 20.

From which we note that this general LMG model can always engineer collective spins into the SSS dynamically at time $\sim \frac{0.03}{G_T}$ (N = 100), or $\sim \frac{0.05}{G_T}$ (N = 50), or $\sim \frac{0.08}{G_T}$ (N = 20). In addition, governed by this general LMG model, no matter the special phase Θ or general Θ, the collective spins will be equivalently and efficiently engineered into the SSS.

5 Quantum phase transitions (QPTs)

Utilizing the standard average-field approximation, we can determine the expected value of the collective spin components via the definition $⟨{\widehat{S}}_i⟩=\mathrm{Tr}(\rho {\widehat{S}}_i)$ and then write a group of time-dependent differential equations for the total angular momentum through the basic relation $d⟨{\widehat{S}}_i⟩/dt=\mathrm{Tr}(\dot{\rho }{\widehat{S}}_i)$. We introduce an equivalent normalization transformation: $⟨{\widehat{S}}_x⟩=NX$, $⟨{\widehat{S}}_y⟩=NY$, and $⟨{\widehat{S}}_z⟩=NZ$ to this proposal. To achieve the theoretical results, we also rewrite Eq. 11 for simplicity.

$\frac{d\widehat{\rho }}{dt}=i\left[\widehat{\rho },{\widehat{H}}_{\mathrm{\Theta }}\right]+{\gamma }_{\text{dc}}\left(2{\widehat{S}}^{-}\rho {\widehat{S}}^{+}-{\widehat{S}}^{+}{\widehat{S}}^{-}\rho -\rho {\widehat{S}}^{+}{\widehat{S}}^{-}\right)+{\gamma }_{\text{dp}}\left(2{\widehat{S}}_z\rho {\widehat{S}}_z-{\widehat{S}}_z{\widehat{S}}_z\rho -\rho {\widehat{S}}_z{\widehat{S}}_z\right),(12)$

in which we assume that all spins are homogenous and that their relative dephasing and decay rates are uniform factors; i.e., we assume that γ_dc ∼Γ_dc/(−G_T) and γ_dp ∼Γ_dp/(−G_T). By discarding the quantum fluctuations of ${\widehat{S}}_{x,y,z}$, we effectively obtain a group of semiclassical equations:

$\begin{array}{cc}\hfill \dot{X}& =2\left(\cos \mathrm{\Theta }+1\right)YZ+\left(2\sin \mathrm{\Theta }-{\gamma }_{\text{dc}}\right)XZ-{\gamma }_{\text{dp}}X/2,\hfill \\ \hfill \dot{Y}& =2\left(\cos \mathrm{\Theta }-1\right)XZ+\left(-2\sin \mathrm{\Theta }-{\gamma }_{\text{dc}}\right)YZ-{\gamma }_{\text{dp}}Y/2,\hfill \\ \hfill \dot{Z}& =-4\cos \mathrm{\Theta }XY+\left(-2\sin \mathrm{\Theta }+{\gamma }_{\text{dc}}\right)X^2+\left(2\sin \mathrm{\Theta }+{\gamma }_{\text{dc}}\right)Y^2.\hfill \end{array}(13)$

Together with the total spins’ conservation relation X²+Y²+Z² = 1, we obtain the analytical solutions of the relevant order parameters, i.e., X, Y, and Z, by solving this group of equations. Then, we can determine the analytical solutions as (1) the trivial solution X = Y = 0, and Z = ±1 for the normal phase; and (2) the non-trivial solutions

$\begin{array}{cc}\hfill Z& =-\frac{{\gamma }_{\text{dp}}}{2{\gamma }_{\text{dc}}},\hfill \\ \hfill X& =\pm \sqrt{\frac{\left(1-Z^2\right)\left(\cos \mathrm{\Theta }+1\right)}{2}},\hfill \\ \hfill Y& =-X\frac{\sin \mathrm{\Theta }}{\cos \mathrm{\Theta }+1}.\hfill \end{array}(14)$

Assuming γ_dp ≈ 0.1γ_dc, we get Z = −0.05 and plot the numerical average-value order parameters X and Y in Figure 3. Owing to the Z₂ symmetry of this general LMG model ${\widehat{H}}_{\mathrm{\Theta }}$, we can obtain the positive and negative values symmetrically with X_± and Y_±. From which, we first note several critical points among the varying region [−2π, 2π].

FIGURE 3

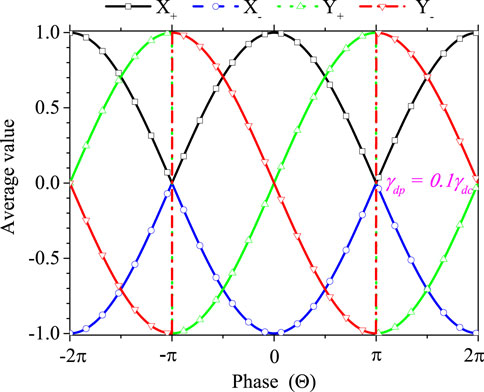
FIGURE 3. (Color online) Steady-state order parameters X and Y varying with Θ ∈ [−2π, 2π], with γ_dp ≈ 0.1γ_dc.

More specifically, when Θ approaches points such as 0, ± 2π, and even 2kπ (k is any integer number), X₊ → 1, X₋ → −1, and Y_± → 0 simultaneously. This type of QPT is mainly induced by the transformation of the representation; i.e., z ↔ x or x ↔ y. We consider this to correspond to phase-induced spontaneous symmetry breaking (SSB). When Θ → ±π, we get a different QPT effect, namely, X_± → 0; however, its n-order derivative at this point ${({\partial }^n{X}_{\pm }/\partial {\mathrm{\Theta }}^n)}_{\pm \pi }$ is discontinuous with n ≥ 1. More interestingly, around these points, Y₊ and Y₋ will suddenly turn over to each other and both Y_± and ${({\partial }^n{Y}_{\pm }/\partial {\mathrm{\Theta }}^n)}_{\pm \pi }$ are discontinuous at this type of critical point. Finally, regarding other critical points, when Θ is modified near points such as ± π/2, ± 3π/2, ⋯, a synchronous crossing phenomenon will occur; i.e., X₊ = Y₊ and X₋ = Y₋. This result corresponds to the mixture-type LMG model (10), and it is also basically induced by the so-called SSB.

6 Applications for engineering multiparticle entanglement

Therefore, no matter in case (1) and in cases (2) and (3), these long-range spin–spin interactions belong to the one-axis twisting LMG model under their different y, x, and x representations. This type of spin model can also play an important role in the preparation of multiparticle entanglement. Starting from the original and general LMG model (4), we briefly discuss this topic.

Initially, we can easily get the isotropy LMG model such as Eq. 6, which belongs to the FM order. Its ground state is the disentangled and unique state |m_z = S⟩ or |m_z = −S⟩, which is also decided by the sign of $A_0^{\mathrm{1,2}}$. The relevant results are plotted in Figure 4. Next, when we modify the amplitude of this classical field adiabatically with r_1,2 → r and select the phase θ_1,2 with Θ = θ₁+θ₂, we obtain not only the SSB-induced QPTs but also efficient adiabatic passage for engineering collective spins into the entangled ground state; i.e., the GHZ or W states. As illustrated in Figure 4, if this GS transition corresponds to the FM↦FM, we can get the entanglement passage for the GHZ state. However, when the GS transition is FM↦AFM, we get another entanglement strategy for the W-type GS. Because these types of investigations have been performed previously, these results confirm the feasibility of this scheme for the preparation of entanglement (Zhou et al., 2018).

FIGURE 4

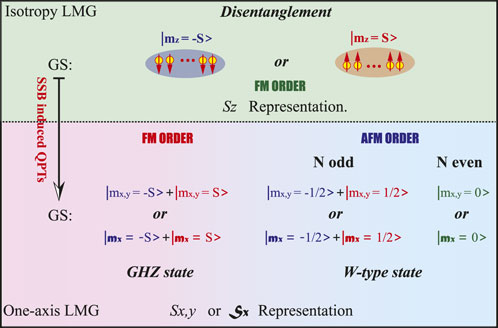
FIGURE 4. (Color online) Basic transformation schematic for generating the multiparticle entanglement via QPTs induced by SSB.

7 Experimental considerations

In this proposal, we first considered an ensemble of solid-state spins located on the surface of the SAW cavity with a fundamental frequency of ω_m/2π ∼ 0.1–1.0 GHz (Schuetz et al., 2015). SAW-based quantum devices can induce strong or ultra-strong interactions in many kinds of atoms, spins, and even other artificial atoms, as shown in Table 2. Taking the nitrogen-vacancy (NV) spins for example, we can define the ground state |0⟩ ≡|g⟩ and excited state |E_y⟩ ≡|e⟩, with energy-splitting ω₀/2π ∼ 470 THz. The estimated coherent spin–phonon coupling at the single-quantum level is approximately g₀/2π ∼ 100 kHz; thus, we can determine the collective coupling strength $g\approx \sqrt{N}{g}_0$ (Andrew Golter et al., 2016a; Andrew Golter et al., 2016b). The coherent spin–phonon coupling at the single-quantum level of a single quantum dot (QD) can reach g₀/2π ∼ 100 MHz. For both different solid-state spins, their cooperativity in a SAW-based hybrid system is C ∼ g²/(γκ) ∼ 10–100, which also belongs to the strong-coupling region (Schuetz et al., 2015).

TABLE 2

TABLE 2. Basic coupling of the SAW-based platform to different qubits (Schuetz et al., 2015).

8 Conclusion

Utilizing a hybrid system of collective spins coupled to a SAW cavity, we study a proposal for simulating the general long-range LMG model with a phase-dependent control. Our analysis and discussion show that this scheme can not only ensure the generation of the SSS via a dynamical evolution governed by the general one-axis twisting interactions but also supply a potential route toward multiparticle GHZ or W-type states through their FM or AFM phase transitions. We also studied the open-system critical behavior of this general LMG model by using the average-field method. For the target of carrying out realistic QIP and QM, our findings may be considered a fresh attempt by using an acoustic control, especially a phase-dependent control. Moreover, this proposed system might have various applications.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

YZ propose the proposal and write the whole paper; Q-LW support this investigation and provide the necessary financial assistance; L-ZC, C-SH, Z-CZ, WX, and Q-LW participate in the discussions.

Funding

This investigation was supported by the National Key Research and Development Program of China (NKRD) (2020YFC2200500), Natural National Science Foundation (NSFC) (11774285, 12047524, and 11774282); the China Postdoctoral Science Foundation (2021M691150); the Natural Science Foundation of Hubei Province (2020CFB748); the Natural Science Foundation of Shandong Province (ZR2021MA042 and ZR2021MA078); the Research Project of Hubei Education Department (B2020079); the Doctoral Scientific Research Foundation of Hubei University of Automotive Technology (HUAT) (BK201906, BK202113, and BK202008); the Innovation Project of University Students in HUAT (DC2022097, DC2022100, DC2021107, and DC2021108); an Open Fund of HUAT (QCCLSZK 2021A07); and the Foundation of Discipline Innovation Team of HUAT. Part of the simulations is coded in Python using the QuTiP library (Johansson et al., 2012; Johansson et al., 2013).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anders, S., and Mølmer, K. (1999). Quantum computation with ions in thermal motion. Phys. Rev. Lett. 82, 1971–1974. doi:10.1103/physrevlett.82.1971

CrossRef Full Text | Google Scholar

Andrew Golter, D., Oo, T., Amezcua, M., Stewart, K. A., and Wang, H. (2016). Optomechanical quantum control of a Nitrogen-Vacancy center in diamond. Phys. Rev. Lett. 116, 143602. doi:10.1103/physrevlett.116.143602

PubMed Abstract | CrossRef Full Text | Google Scholar

Andrew Golter, D., Oo, T., Amezcua, M., Lekavicius, I., Stewart, K. A., and Wang, H. (2016). Coupling a surface acoustic wave to an electron spin in diamond via a dark state. Phys. Rev. X 6, 041060. doi:10.1103/physrevx.6.041060

CrossRef Full Text | Google Scholar

Aspelmeyer, M., Tobias, J., and Marquardt, F. (2014). Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452. doi:10.1103/revmodphys.86.1391

CrossRef Full Text | Google Scholar

Bennett, S. D., Yao, N. Y., Otterbach, J., Zoller, P., Rabl, P., and Lukin, M. D. (2013). Phonon-induced spin-spin interactions in diamond nanostructures: Application to spin squeezing. Phys. Rev. Lett. 110, 156402. doi:10.1103/physrevlett.110.156402

PubMed Abstract | CrossRef Full Text | Google Scholar

Blais, A., Girvin, S. M., and Oliver, W. D. (2020). Quantum information processing and quantum optics with circuit quantum electrodynamics. Nat. Phys. 16, 247–256. doi:10.1038/s41567-020-0806-z

CrossRef Full Text | Google Scholar

Blais, A., Arne, L., and Grimsmo, S. M. (2021). Circuit quantum electrodynamics. Rev. Mod. Phys. 93, 025005. doi:10.1103/revmodphys.93.025005

CrossRef Full Text | Google Scholar

Carusotto, I., Houck, A. A., Kollár, A. J., Roushan, P., and Simon, J. (2020). Photonic materials in circuit quantum electrodynamics. Nat. Phys. 16, 268–279. doi:10.1038/s41567-020-0815-y

CrossRef Full Text | Google Scholar

Castaños, O., López-Peña, R., Hirsch, J. G., and López-Moreno, E. (2006). Classical and quantum phase transitions in the Lipkin-Meshkov-Glick model. Phys. Rev. B 74, 104118. doi:10.1103/physrevb.74.104118

CrossRef Full Text | Google Scholar

Clerk, A. A., Lehnert, K. W., Bertet, P., Petta, J. R., and Nakamura, Y. (2020). Hybrid quantum systems with circuit quantum electrodynamics. Nat. Phys. 16, 257–267. doi:10.1038/s41567-020-0797-9

CrossRef Full Text | Google Scholar

Forn-Díaz, P., Lamata, L., Rico, E., Kono, J., and Solano, E. (2019). Ultrastrong coupling regimes of light-matter interaction. Rev. Mod. Phys. 91, 025005. doi:10.1103/revmodphys.91.025005

CrossRef Full Text | Google Scholar

Gao, W. B., Imamoglu, A., Bernien, H., and Hanson, R. (2015). Coherent manipulation, measurement and entanglement of individual solid-state spins using optical fields. Nat. Photonics 9, 363–373. doi:10.1038/nphoton.2015.58

CrossRef Full Text | Google Scholar

Gustafsson, M. V., Aref, T., Kockum, A. F., Ekström, M. K., and Johansson, G. (2014). Propagating phonons coupled to an artificial atom. Science 346, 207–211. doi:10.1126/science.1257219

PubMed Abstract | CrossRef Full Text | Google Scholar

Haroche, S., Brune, M., and Raimond, J. M. (2020). From cavity to circuit quantum electrodynamics. Nat. Phys. 16, 243–246. doi:10.1038/s41567-020-0812-1

CrossRef Full Text | Google Scholar

James, D. F. V., and Jerke, J. (2012). Effective Hamiltonian theory and its applications in quantum information. Can. J. Phys. 85 (8), 625–632. doi:10.1139/p07-060

CrossRef Full Text | Google Scholar

James, D. F. V. (1998). Quantum dynamics of cold trapped ions with application to quantum computation. Appl. Phys. B Lasers Opt. 66, 181–190. doi:10.1007/s003400050373

CrossRef Full Text | Google Scholar

Johansson, J. R., Nation, P. D., and Nori, F. (2012). QuTiP: An open-source Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 183, 1760–1772. doi:10.1016/j.cpc.2012.02.021

CrossRef Full Text | Google Scholar

Johansson, J. R., Nation, P. D., and Nori, F. (2013). Qutip 2: A python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 184, 1234–1240. doi:10.1016/j.cpc.2012.11.019

CrossRef Full Text | Google Scholar

Kitagawa, M., and Ueda, M. (1993). Squeezed spin states. Phys. Rev. A 47, 5138–5143. doi:10.1103/physreva.47.5138

PubMed Abstract | CrossRef Full Text | Google Scholar

Knörzer, J., Schuetz, M. J. A., Giedke, G., Huebl, H., Weiler, M., Lukin, M. D., et al. (2018). Solid-state magnetic traps and lattices. Phys. Rev. B 97, 235451. doi:10.1103/physrevb.97.235451

CrossRef Full Text | Google Scholar

Kuzyk, M. C., and Wang, H. (2018). Scaling phononic quantum networks of solid-state spins with closed mechanical subsystems. Phys. Rev. X 8, 041027. doi:10.1103/physrevx.8.041027

CrossRef Full Text | Google Scholar

Lemonde, M. A., Meesala, S., Sipahigil, A., Schuetz, M. J. A., Lukin, M. D., Loncar, M., et al. (2018). Phonon networks with silicon-vacancy centers in diamond waveguides. Phys. Rev. Lett. 120, 213603. doi:10.1103/physrevlett.120.213603

PubMed Abstract | CrossRef Full Text | Google Scholar

Leng, S-Y., Lü, D-Y., Yang, S-L., Ma, M., Dong, Y-Z., Zhou, B-F., et al. (2022). Simulating the dicke lattice model and quantum phase transitions using an array of coupled resonators. J. Phys. Condens. Matter 34, 415402. doi:10.1088/1361-648x/ac84bd

CrossRef Full Text | Google Scholar

Li, P-B., Zhou, Y., Gao, W-B., and Nori, F. (2020). Enhancing spin-phonon and spin-spin interactions using linear resources in a hybrid quantum system. Phys. Rev. Lett. 125, 153602. doi:10.1103/physrevlett.125.153602

PubMed Abstract | CrossRef Full Text | Google Scholar

Lipkin, H. J., Meshkov, N., and Glick, A. J. (1965). Validity of many-body approximation methods for a solvable model:(i). exact solutions and perturbation theory. Nucl. Phys. 62, 188–198. doi:10.1016/0029-5582(65)90862-x

CrossRef Full Text | Google Scholar

Ma, J., and Wang, X. (2009). Fisher information and spin squeezing in the Lipkin-Meshkov-Glick model. Phys. Rev. A 80, 012318. doi:10.1103/physreva.80.012318

CrossRef Full Text | Google Scholar

Manenti, R., Peterer, M. J., Nersisyan, A., Magnusson, E. B., Patterson, A., and Leek, P. J. (2016). Surface acoustic wave resonators in the quantum regime. Phys. Rev. B 93, 041411. doi:10.1103/physrevb.93.041411

CrossRef Full Text | Google Scholar

Mølmer, K., and Anders, S. (1999). Multiparticle entanglement of hot trapped ions. Phys. Rev. Lett. 82, 1835–1838. doi:10.1103/physrevlett.82.1835

CrossRef Full Text | Google Scholar

Morrison, S., and Parkins, A. S. (2008). Dynamical quantum phase transitions in the dissipative Lipkin-Meshkov-Glick model with proposed realization in optical cavity QED. Phys. Rev. Lett. 100, 040403. doi:10.1103/physrevlett.100.040403

PubMed Abstract | CrossRef Full Text | Google Scholar

Naber, W. J. M., Fujisawa, T., Liu, H. W., and van der Wiel, W. G. (2006). Surface-acoustic-wave-induced transport in a double quantum dot. Phys. Rev. Lett. 96, 136807. doi:10.1103/physrevlett.96.136807

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Connell, A. D., Hofheinz, M., Ansmann, M., Bialczak, R. C., Lenander, M., Lucero, E., et al. (2010). Quantum ground state and single-phonon control of a mechanical resonator. Nature 464, 697–703. doi:10.1038/nature08967

PubMed Abstract | CrossRef Full Text | Google Scholar

Rabl, P., Cappellaro, P., Gurudev Dutt, M. V., Jiang, L., Maze, J. R., and Lukin, M. D. (2009). Strong magnetic coupling between an electronic spin qubit and a mechanical resonator. Phys. Rev. B 79, 041302. doi:10.1103/physrevb.79.041302

CrossRef Full Text | Google Scholar

Rabl, P., Kolkowitz, S. J., Koppens, F. H. L., Harris, J. G. E., Zoller, P., and Lukin, M. D. (2010). A quantum spin transducer based on nanoelectromechanical resonator arrays. Nat. Phys. 6, 602–608. doi:10.1038/nphys1679

CrossRef Full Text | Google Scholar

Schuetz, M. J. A., Kessler, E. M., Giedke, G., Vandersypen, L. M. K., Lukin, M. D., and Cirac, J. I. (2015). Universal quantum transducers based on surface acoustic waves. Phys. Rev. X 5, 031031. doi:10.1103/physrevx.5.031031

CrossRef Full Text | Google Scholar

Sidles, J. A., Garbini, J. L., Bruland, K. J., Rugar, D., Züger, O., Hoen, S., et al. (1995). Magnetic resonance force microscopy. Rev. Mod. Phys. 67, 249–265. doi:10.1103/revmodphys.67.249

CrossRef Full Text | Google Scholar

Tan, Q., Lai, J-M., Liu, X-L., Guo, D., Xue, Y., Dou, X., et al. (2022). Donor-acceptor pair quantum emitters in hexagonal boron nitride. Nano Lett. 22, 1331–1337. doi:10.1021/acs.nanolett.1c04647

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsomokos, D. I., Ashhab, S., and Nori, F. (2008). Fully connected network of superconducting qubits in a cavity. New J. Phys. 10, 113020. doi:10.1088/1367-2630/10/11/113020

CrossRef Full Text | Google Scholar

Unanyan, R. G., and Fleischhauer, M. (2003). Decoherence-free generation of many-particle entanglement by adiabatic ground-state transitions. Phys. Rev. Lett. 90, 133601. doi:10.1103/physrevlett.90.133601

PubMed Abstract | CrossRef Full Text | Google Scholar

Vidal, J., Palacios, G., and Mosseri, R. (2004). Entanglement in a second-order quantum phase transition. Phys. Rev. A 69, 022107. doi:10.1103/physreva.69.022107

CrossRef Full Text | Google Scholar

Vidal, J., Mosseri, R., and Dukelsky, J. (2004). Entanglement in a first-order quantum phase transition. Phys. Rev. A 69, 054101. doi:10.1103/physreva.69.054101

CrossRef Full Text | Google Scholar

Wineland, D. J., Bollinger, J. J., Itano, W. M., Moore, F. L., and Heinzen, D. J. (1992). Spin squeezing and reduced quantum noise in spectroscopy. Phys. Rev. A 46, R6797–R6800. doi:10.1103/physreva.46.r6797

PubMed Abstract | CrossRef Full Text | Google Scholar

Wineland, D. J., Bollinger, J. J., Itano, W. M., and Heinzen, D. J. (1994). Squeezed atomic states and projection noise in spectroscopy. Phys. Rev. A 50, 67–88. doi:10.1103/physreva.50.67

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiang, Z-L., Ashhab, S., You, J. Q., and Nori, F. (2013). Hybrid quantum circuits: Superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 85, 623–653. doi:10.1103/revmodphys.85.623

CrossRef Full Text | Google Scholar

Zhang, Y-C., Zhou, X-F., Guo, G. C., and Zhou, Z. W. (2017). Cavity-assisted single-mode and two-mode spin-squeezed states via phase-locked atom-photon coupling. Phys. Rev. Lett. 118, 083604. doi:10.1103/physrevlett.118.083604

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, M., Cai, H., Chen, D., Kenny, J., Jiang, Z., Ru, S., et al. (2022). Excited-state optically detected magnetic resonance of spin defects in hexagonal boron nitride. Phys. Rev. Lett. 128, 216402. doi:10.1103/PhysRevLett.128.216402

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, S-B. (2001). One-step synthesis of multiatom Greenberger-Horne-Zeilinger states. Phys. Rev. Lett. 87, 230404. doi:10.1103/physrevlett.87.230404

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, Y., Li, B., Li, X-X., Li, F-L., and Li, P-B. (2018). Preparing multiparticle entangled states of nitrogen-vacancy centers via adiabatic ground-state transitions. Phys. Rev. A 98, 052346. doi:10.1103/physreva.98.052346

CrossRef Full Text | Google Scholar

Zhou, Y., Lü, D-Y., Wang, G-H., Fu, Y-H., He, M-Y., and Ren, H-T. (2021). Improvement on the manipulation of a single nitrogen-vacancy spin and microwave photon at single-quantum level. Commun. Theor. Phys. 73, 065101. doi:10.1088/1572-9494/abec3a

CrossRef Full Text | Google Scholar

Zhou, Y., Hu, C-S., Lü, D-Y., Li, X-K., Huang, H-M., Xiong, Y-C., et al. (2022). Synergistic enhancement of spin-phonon interaction in a hybrid system. Phot. Res. 10, 1640–1649. doi:10.1364/prj.459794

CrossRef Full Text | Google Scholar

Appendix A: Derivation of the effective Hamiltonian

According to Eq. 3, we can rewrite

$\begin{array}{ll}\hfill H_{\text{IP}}& \simeq {\widehat{S}}^{+}{e}^{i{\omega }_{0}t}\times \left[1+\eta \left({\widehat{a}}^{†}{e}^{i{\omega }_{m}t}-\widehat{a}{e}^{-i{\omega }_{m}t}\right)\right]\times \left({\mathrm{\Omega }}_1{e}^{-i{\omega }_{1}t}+{\mathrm{\Omega }}_2{e}^{-i{\omega }_{2}t}\right)+\text{H.c.}\hfill \\ \hfill & =\left[1+\eta \left({\widehat{a}}^{†}{e}^{i{\omega }_{m}t}-\widehat{a}{e}^{-i{\omega }_{m}t}\right)\right]\times \left({\mathrm{\Omega }}_1{\widehat{S}}^{+}{e}^{i\mathrm{\Delta }t}+{\mathrm{\Omega }}_2{\widehat{S}}^{+}{e}^{-i\mathrm{\Delta }t}\right)+\text{H.c.}\hfill \\ \hfill & ={\widehat{H}}_1\left(\mathrm{\Delta }\right)+{\widehat{H}}_2\left({\delta }_2\right)+{\widehat{H}}_3\left({\delta }_3\right),\hfill \end{array}(\mathrm{A1})$

where δ₂ = ω_m+Δ, δ₃ = ω_m−Δ, and

${\widehat{H}}_1={\mathrm{\Omega }}_1{\widehat{S}}^{+}{e}^{i\mathrm{\Delta }t}+{\mathrm{\Omega }}_2{\widehat{S}}^{+}{e}^{-i\mathrm{\Delta }t}+{\mathrm{\Omega }}_1^{*}{\widehat{S}}^{-}{e}^{-i\mathrm{\Delta }t}+{\mathrm{\Omega }}_2^{*}{\widehat{S}}^{-}{e}^{i\mathrm{\Delta }t},(\mathrm{A2})$

${\widehat{H}}_2=\eta {\mathrm{\Omega }}_1{\widehat{a}}^{†}{\widehat{S}}^{+}{e}^{i{\delta }_{2}t}-\eta {\mathrm{\Omega }}_2\widehat{a}{\widehat{S}}^{+}{e}^{-i{\delta }_{2}t}+\eta {\mathrm{\Omega }}_1^{*}\widehat{a}{\widehat{S}}^{-}{e}^{-i{\delta }_{2}t}-\eta {\mathrm{\Omega }}_2^{*}{\widehat{a}}^{†}{\widehat{S}}^{-}{e}^{i{\delta }_{2}t},(\mathrm{A3})$

${\widehat{H}}_3=\eta {\mathrm{\Omega }}_2{\widehat{a}}^{†}{\widehat{S}}^{+}{e}^{i{\delta }_{3}t}-\eta {\mathrm{\Omega }}_1\widehat{a}{\widehat{S}}^{+}{e}^{-i{\delta }_{3}t}+\eta {\mathrm{\Omega }}_2^{*}\widehat{a}{\widehat{S}}^{-}{e}^{-i{\delta }_{3}t}-\eta {\mathrm{\Omega }}_1^{*}{\widehat{a}}^{†}{\widehat{S}}^{-}{e}^{i{\delta }_{3}t}.(\mathrm{A4})$

Utilizing the method of effective Hamiltonian, we get (James, 1998; James and Jerke, 2012)

${\widehat{H}}_1\to {\widehat{H}}_1^{\text{eff}}=\frac{{\mathrm{\Omega }}_1{\mathrm{\Omega }}_1^{*}}{\mathrm{\Delta }}\left[{\widehat{S}}^{+},{\widehat{S}}^{-}\right]+\frac{{\mathrm{\Omega }}_2{\mathrm{\Omega }}_2^{*}}{\mathrm{\Delta }}\left[{\widehat{S}}^{-},{\widehat{S}}^{+}\right]=\frac{2\left(|{\mathrm{\Omega }}_1{|}^2-|{\mathrm{\Omega }}_2{|}^2\right)}{\mathrm{\Delta }}{\widehat{S}}_z,(\mathrm{A5})$

$\begin{array}{ccc}\hfill {\widehat{H}}_2& \to \hfill & {\widehat{H}}_2^{\text{eff}}\hfill \\ \hfill & =\hfill & {\eta }^2\left\{-{\mathrm{\Omega }}_1{\mathrm{\Omega }}_2\left[{\widehat{a}}^{†}{\widehat{S}}^{+},\widehat{a}{\widehat{S}}^{+}\right]+{\mathrm{\Omega }}_1{\mathrm{\Omega }}_1^{*}\left[{\widehat{a}}^{†}{\widehat{S}}^{+},\widehat{a}{\widehat{S}}^{-}\right]+{\mathrm{\Omega }}_2{\mathrm{\Omega }}_2^{*}\left[{\widehat{a}}^{†}{\widehat{S}}^{-},\widehat{a}{\widehat{S}}^{+}\right]-{\mathrm{\Omega }}_1^{*}{\mathrm{\Omega }}_2^{*}\left[{\widehat{a}}^{†}{\widehat{S}}^{-},\widehat{a}{\widehat{S}}^{-}\right]\right\}/{\delta }_2\hfill \\ \hfill & \approx \hfill & {\eta }^2\left[{\mathrm{\Omega }}_1{\mathrm{\Omega }}_2{\left({\widehat{S}}^{+}\right)}^2+{\mathrm{\Omega }}_1^{*}{\mathrm{\Omega }}_2^{*}{\left({\widehat{S}}^{-}\right)}^2-|{\mathrm{\Omega }}_1{|}^2{\widehat{S}}^{-}{\widehat{S}}^{+}-|{\mathrm{\Omega }}_2{|}^2{\widehat{S}}^{+}{\widehat{S}}^{-}\right]/{\delta }_2,\hfill \end{array}(\mathrm{A6})$

$\begin{array}{ccc}\hfill {\widehat{H}}_3& \to \hfill & {\widehat{H}}_3^{\text{eff}}\hfill \\ \hfill & =\hfill & {\eta }^2\left\{-{\mathrm{\Omega }}_1{\mathrm{\Omega }}_2\left[{\widehat{a}}^{†}{\widehat{S}}^{+},\widehat{a}{\widehat{S}}^{+}\right]+{\mathrm{\Omega }}_2{\mathrm{\Omega }}_2^{*}\left[{\widehat{a}}^{†}{\widehat{S}}^{+},\widehat{a}{\widehat{S}}^{-}\right]+{\mathrm{\Omega }}_1{\mathrm{\Omega }}_1^{*}\left[{\widehat{a}}^{†}{\widehat{S}}^{-},\widehat{a}{\widehat{S}}^{+}\right]-{\mathrm{\Omega }}_1^{*}{\mathrm{\Omega }}_2^{*}\left[{\widehat{a}}^{†}{\widehat{S}}^{-},\widehat{a}{\widehat{S}}^{-}\right]\right\}/{\delta }_3\hfill \\ \hfill & \approx \hfill & {\eta }^2\left[{\mathrm{\Omega }}_1{\mathrm{\Omega }}_2{\left({\widehat{S}}^{+}\right)}^2+{\mathrm{\Omega }}_1^{*}{\mathrm{\Omega }}_2^{*}{\left({\widehat{S}}^{-}\right)}^2-|{\mathrm{\Omega }}_2{|}^2{\widehat{S}}^{-}{\widehat{S}}^{+}-|{\mathrm{\Omega }}_1{|}^2{\widehat{S}}^{+}{\widehat{S}}^{-}\right]/{\delta }_3.\hfill \end{array}(\mathrm{A7})$

Thus, we can rewrite the total systemic Hamiltonian with an effective form

${\widehat{H}}_{\text{Total}}^{\text{eff}}\approx {\widehat{H}}_1^{\text{eff}}+{\widehat{H}}_2^{\text{eff}}+{\widehat{H}}_3^{\text{eff}}.(\mathrm{A8})$

Utilizing the relation ${\widehat{S}}^{\pm }={\widehat{S}}_x\pm i{\widehat{S}}_y$, we get ${({\widehat{S}}^{\pm })}^2={\widehat{S}}_x^2-{\widehat{S}}_y^2\pm i({\widehat{S}}_x{\widehat{S}}_y+{\widehat{S}}_y{\widehat{S}}_x)$, ${\widehat{S}}^{+}{\widehat{S}}^{-}={\widehat{S}}_x^2+{\widehat{S}}_y^2+{\widehat{S}}_z$, and ${\widehat{S}}^{-}{\widehat{S}}^{+}={\widehat{S}}_x^2+{\widehat{S}}_y^2-{\widehat{S}}_z$. Then, the total Hamiltonian is mainly expressed as

${\widehat{H}}_{\text{Total}}^{\text{eff}}\approx A{\widehat{S}}_z+B{\widehat{S}}_x^2+C{\widehat{S}}_y^2+D{\widehat{S}}_x{\widehat{S}}_y+E{\widehat{S}}_y{\widehat{S}}_x,(\mathrm{A9})$

with the coefficients

$\begin{array}{cc}\hfill A& =\left(\frac{2}{\mathrm{\Delta }}-\frac{2{\eta }^2\mathrm{\Delta }}{{\delta }_2{\delta }_3}\right)\left(|{\mathrm{\Omega }}_1{|}^2-|{\mathrm{\Omega }}_2{|}^2\right),\hfill \\ \hfill B& =\frac{2{\omega }_m{\eta }^2}{{\delta }_2{\delta }_3}\left({\mathrm{\Omega }}_1{\mathrm{\Omega }}_2+{\mathrm{\Omega }}_1^{*}{\mathrm{\Omega }}_2^{*}-|{\mathrm{\Omega }}_1{|}^2-|{\mathrm{\Omega }}_2{|}^2\right),\hfill \\ \hfill C& =\frac{2{\omega }_m{\eta }^2}{{\delta }_2{\delta }_3}\left(-{\mathrm{\Omega }}_1{\mathrm{\Omega }}_2-{\mathrm{\Omega }}_1^{*}{\mathrm{\Omega }}_2^{*}-|{\mathrm{\Omega }}_1{|}^2-|{\mathrm{\Omega }}_2{|}^2\right),\hfill \\ \hfill D& =E=\frac{2i{\omega }_m{\eta }^2}{{\delta }_2{\delta }_3}\left({\mathrm{\Omega }}_1{\mathrm{\Omega }}_2-{\mathrm{\Omega }}_1^{*}{\mathrm{\Omega }}_2^{*}\right).\hfill \end{array}(\mathrm{A10})$

In general, if we may assume ${\mathrm{\Omega }}_{\mathrm{1,2}}\equiv r_{\mathrm{1,2}}{e}^{i{\theta }_{\mathrm{1,2}}}$ and Θ ≡θ₁+θ₂, then we can get

$\begin{array}{cc}\hfill A& =\left(\frac{2}{\mathrm{\Delta }}-\frac{2{\eta }^2\mathrm{\Delta }}{{\delta }_2{\delta }_3}\right)\left(r_1^2-r_2^2\right),\hfill \\ \hfill B& =\frac{2{\omega }_m{\eta }^2}{{\delta }_2{\delta }_3}\left(r_1{r}_2{e}^{i\mathrm{\Theta }}+r_1{r}_2{e}^{-i\mathrm{\Theta }}-r_1^2-r_2^2\right),\hfill \\ \hfill C& =\frac{2{\omega }_m{\eta }^2}{{\delta }_2{\delta }_3}\left(-r_1{r}_2{e}^{i\mathrm{\Theta }}-r_1{r}_2{e}^{-i\mathrm{\Theta }}-r_1^2-r_2^2\right),\hfill \\ \hfill D& =E=\frac{2i{\omega }_m{\eta }^2}{{\delta }_2{\delta }_3}\left(r_1{r}_2{e}^{i\mathrm{\Theta }}-r_1{r}_2{e}^{-i\mathrm{\Theta }}\right).\hfill \end{array}(\mathrm{A11})$

Appendix B: Isotropy LMG model

From Eqs. A9, A11, we assume r₁ = 0, r₂ ≠ 0 or r₂ = 0, r₁ ≠ 0; thus, the isotropy LMG model is

${\widehat{H}}_{\text{Isotropy}}^{\mathrm{1,2}}=A_0^{\mathrm{1,2}}{\widehat{S}}_z+B_0^{\mathrm{1,2}}\left({\widehat{S}}_x^2+{\widehat{S}}_y^2\right)=A_0^{\mathrm{1,2}}{\widehat{S}}_z-B_0^{\mathrm{1,2}}{\widehat{S}}_z^2+B_0^{\mathrm{1,2}}{\mathbf{S}}^2,(\mathrm{B1})$

with coefficients (η ∼ 0.1–0.2)

$\begin{array}{ccc}\hfill A_0^1& =\hfill & \left(\frac{2}{\mathrm{\Delta }}-\frac{2{\eta }^2\mathrm{\Delta }}{{\delta }_2{\delta }_3}\right)r_1^2\approx \frac{2r_1^2}{\mathrm{\Delta }},\hfill \\ \hfill A_0^2& =\hfill & -\left(\frac{2}{\mathrm{\Delta }}-\frac{2{\eta }^2\mathrm{\Delta }}{{\delta }_2{\delta }_3}\right)r_2^2\approx -\frac{2r_2^2}{\mathrm{\Delta }},\hfill \\ \hfill B_0^{\mathrm{1,2}}& =\hfill & -\frac{2{\omega }_m{\eta }^2}{{\delta }_2{\delta }_3}{r}_{\mathrm{1,2}}^2.\hfill \end{array}$