Bistable carbon-vacancy defects in h-BN

Introduction

Point defects as emerging single-photon emitters (SPEs) in two-dimensional (2D) hexagonal boron nitride (hBN) have been intensively studied for possible applications in quantum sensing, computing, and nanophotonics (Tran et al., 2016a; Bourrellier et al., 2016; Tran et al., 2016b; Bommer and Becher, 2019; Gottscholl et al., 2020; Hayee et al., 2020; Chejanovsky et al., 2021; Mendelson et al., 2021). The wide band gap (∼6 eV) and small spin-orbital coupling of hBN manifest as the ideal host to accommodate color centers in a wide region of emission wavelength. The spatial confinement and dielectric screening of 2D defects enable them to show desirable properties, for example, bright luminescence, ease of manipulation, tunable emission through strain (Grosso et al., 2017; Hayee et al., 2020; Mendelson et al., 2020), and electric fields (Noh et al., 2018), motivating researchers to investigate the underlying physical and chemical nature of the structures in detail. However, direct mapping or characterization of the defects in experiment is still a challenge. This might be partially related to the various defect types and unintentional impurities during hBN sample fabrication and post-processing.

Photoluminescence data reveal that there are strong emission bands in the ultraviolet region with zero-phonon-line (ZPL) energy at 4.1 eV (Museur et al., 2008; Du et al., 2015; Bourrellier et al., 2016; Vuong et al., 2016) and in the visible region from 1.6 to 2.2 eV (Tran et al., 2016a; Tran et al., 2016b; Gottscholl et al., 2020; Li et al., 2020; Sajid et al., 2020; Chejanovsky et al., 2021; Mendelson et al., 2021). Based on this, many kinds of point defects have been proposed and analyzed theoretically through density functional theory (DFT) calculations. Several of them could match the experimental result well, such as the boron vacancy (V_B) (Abdi et al., 2018; Ivády et al., 2020; Reimers et al., 2020), nitrogen vacancy (V_N) (Sajid et al., 2018), and Stone–Wales defect (Wang et al., 2016; Hamdi et al., 2020). V_B has been identified experimentally (Jin et al., 2009; Kianinia et al., 2020; Gottscholl et al., 2021; Liu et al., 2021), and single spins of other defects could be coherently manipulated (Chejanovsky et al., 2021; Stern et al., 2022). In addition, defect complexes and impurities deliberately incorporated during synthesis or ion implantation could also serve as potential candidates (Sajid et al., 2018; Weston et al., 2018; Wu et al., 2019; Gottscholl et al., 2020; Chejanovsky et al., 2021; Mendelson et al., 2021). Among them, carbon impurity in hBN has been extensively considered and investigated. A previous study indicated that the recombination from C_N as a donor–acceptor pair with V_N donor (Du et al., 2015) should not be related to 4.1-eV emission line due to the deep donor level of V_N, whereas the C_B might be a possible source with charge transition level (0/+) at 3.71 eV (Weston et al., 2018). Later, carbon dimer C_NC_B was also associated to this emission with a calculated ZPL at 4.3 eV (Mackoit-Sinkevičienė et al., 2019; Li S. et al., 2022). For the visible emission, both V_NC_B and C_NV_B are considered depending on their charge states and spin multiplicity. Our study already revealed that the positively charged V_NC_B(+) has ZPL about 1.5 eV which could be classified to the so called “Group-2” SPE (Abdi et al., 2018). In the triplet electronic configuration of its neutral-charge state, the two defects have ZPL optical transitions at 1.58 and 1.54 eV, respectively (Sajid et al., 2018). A recent study has indicated that the quartet state of the negatively charged C_NV_B(−) is the origin of the SPEs in carbon-doped hBN (Mendelson et al., 2021).

The robust emission features from carbon defects in hBN samples grown with different techniques and environments indicate that they come from very stable configurations. However, considering the fact that the carbon atom in V_NC_B and C_NV_B structures can migrate easily under external perturbation, it is necessary to investigate the relative stability and transformation of the two defects in detail. Formation energy and energy barrier calculation can help to identify the possible structures. The experimentally observed ZPL emission is about 1.6–2.2 eV with the Huang–Rhys factor less than 2. Here, we use these criteria to examine the possibility of V_NC_B and C_NV_B as single-photon emitter candidates. In this study, we employ plane-wave supercell DFT calculations to study the energetic and electronic properties of V_NC_B and C_NV_B at different charge states and spin multiplicities. We find that the charge states influence the relative stability of the two proposed defects. Although the ZPL energy of C_NV_B(−) with quartet spin multiplicity is in the experimental range of interest, the calculated formation energy and charge transition level (CTL) indicate that the quartet state is not stable. Our results imply that the charge states of defects can dramatically affect their relative stability and provide further evidence for the identification of quantum emitters in the visible region.

Methods

We performed the spin-polarized DFT calculation within the Kohn–Sham scheme as implemented in the VASP code (Kresse and Furthmüller, 1996a,b). Standard projector augmented wave (PAW) formalism (Blöchl, 1994; Kresse and Joubert, 1999) is used to separate the valence electrons from the nuclei. The convergence threshold is 0.01 eV/Å for force acting on each atom, and energy cutoff for the expansion of the plane-wave basis set is 450 eV. The screened hybrid density functional of Heyd, Scuseria, and Ernzerhof (HSE) (Heyd et al., 2003) is used to calculate the electronic structure and localize bound states. In this approach, we could mix part of non-local Hartree–Fock exchange with the generalized gradient approximation of Perdew, Burke, and Ernzerhof (PBE) with fraction α. α = 0.32 can reproduce the experimental band gap about 6 eV. We embedded the carbon defects in a $9\times 5\sqrt{3}$ monolayer supercell with 162 atoms which is sufficient to avoid the periodic defect–defect interaction; a vacuum layer of 12 Å is applied to separate the periodic layer images. The single Γ-point scheme is converged for the k-point sampling for the Brillouin zone. The excited states were calculated using the ΔSCF method (Gali et al., 2009). For the formation energy calculation, a bulk model with two hBN layers is used to include the interlayer interaction and decreases the artificial influence induced by a vacuum layer. The charge correction term is computed by the SXDEFECTALIGN code from the Freysoldt method (Freysoldt and Neugebauer, 2018). During the NEB calculation, for V_NC_B to C_NV_B transition, the threshold of force is set to 0.02 eV/Å, whereas for n-C_NV_B to sw-C_NV_B transition, it is 0.1 eV/Å due to the numerical challenges. The electron paramagnetic resonance (EPR) simulation is performed with EASYSPIN software at the X band region (9.45 GHz) (Stoll and Schweiger, 2006).

The total HR factor is defined as the number of an effective phonon participating in the optical transition which is a key parameter of the absorption and fluorescence spectra. The total HR factor can be readily calculated within the Franck–Condon approximation which assumes that the vibrational modes in the ground and excited states are identical. The associated phonon overlap spectral function can be derived from the overlap between the phonon modes in the electronic ground and excited states (Gali et al., 2009; Alkauskas et al., 2014).

Results

The ground state electronic structures are calculated for V_NC_B and C_NV_B in −1, 0, and +1 charged states with the high-spin (HS) and low-spin (LS) states included. Previous results about the spin multiplicity of the ground state varied with the applied calculation methods (Sajid et al., 2018; Mendelson et al., 2021). For neutral V_NC_B(0), Cheng et al. (2017) predicted a triplet ground state; however, further comprehensive calculations indicated that the ¹A₁ singlet is the most favorable one (Reimers et al., 2018). Our calculation shows that the singlet (LS) state of V_NC_B(0) has lower energy considering the symmetry reduction caused by the pseudo-Jahn–Teller (JT) distortion in the singlet state, while it does not occur in the triplet state. The C_s symmetry configuration is lower in energy by 1.87 eV over that of C_2v symmetry configuration. In the following calculation, we remove the symmetry constrain and investigate the electronic structure. We find that the C_2v symmetry is the most stable one in the positive charge state regardless of the spin multiplicity, and V_NC_B(+) prefers the low-spin doublet (LS). Meanwhile, V_NC_B(−) exhibits the doublet state with C_s symmetry.

For the C_NV_B defect (n-C_NV_B in this study), the triplet state is predicted to have lower energy than singlet for C_NV_B(0) with transition energy in experimental value (Sajid et al., 2018). However, a recent report indicates that this configuration suffers from multiple low-energy minima, and none of them have significant oscillator strength (Mendelson et al., 2021). Notably, we find that the C_NV_B could form a Stone–Wales-like (sw-C_NV_B) configuration, as shown in Figure 1, which could have lower formation energy. The multireference character still exists here which is manifested as the unrestricted spin-polarized calculation which yields different energy for spin-up and spin-down channels. We speculate that this phenomenon is due to the spin contamination from the triplet ground state, and indeed, the calculated energy of the singlet is almost identical to that of the triplet. Although these states are not spin eigenstates, the unrestricted DFT orbitals provide more realistic total energies. Except for the HSs of C_NV_B(−), other electronic states prefer the sw-C_NV_B configuration. In the following discussion, the most stable configuration is always discussed for C_NV_B defects in the context. LSs always have lower energy, whereas the CCSD methods pointed out that the HS quartet for C_NV_B(−) could be the ground state (Mendelson et al., 2021). This controversy motivated us to further investigate the relative stability of carbon impurity in these two defects.

FIGURE 1

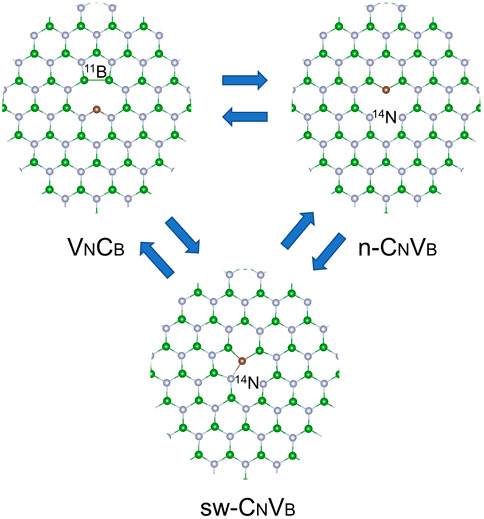
FIGURE 1. Schematic view of carbon-vacancy complexes in hBN. The carbon atom can migrate to the antisite-vacancy configuration. Gray-, green-, and brown-colored balls represent nitrogen, boron, and carbon atoms, respectively. The usual C_NV_B considered before is denoted as n-C_NV_B.

The energy-level diagrams for the two defects are shown in Figure 2. V_NC_B(−) at both HS and LS states do not have empty localized states; therefore, only defect-to-conduction band (CB) excitation occurs which results in a relatively dim emission. The experimental observed bright luminescence should come from defect states in the fundamental band gap, and neither of the vertical transition energies is in line with the experimental PL energies. The V_NC_B(0) HS state with C_2v symmetry has been studied (Sajid and Thygesen, 2020); the defect demonstrates suitable ZPL energy and 1.5 HR factor. However, the HR factor of the more stable LS state in C_s is 7.25, much larger than the experimental value at 1.45. The ZPL of V_NC_B(+) LS is 1.51 eV (Abdi et al., 2018), which agrees relatively well with the experimental data for the Group-2 emitters. Despite that, the corresponding HR factor is about 24, so we can also disregard it as a good candidate for the observed visible emitters. C_NV_B(−) with both HS and LS states have defect-to-defect transitions. The singlet C_NV_B(0) has ZPL of 1.98 eV, and we believe this value is still in the range of interest even taking into account the possible error due to the multireference character of the ground state; however, the HR factor is 8.17. There are no occupied defect states in the gap for C_NV_B(+), and the allowed transition is between valence band maximum and defect states which should result in, again, a relatively dim optical transition.

FIGURE 2

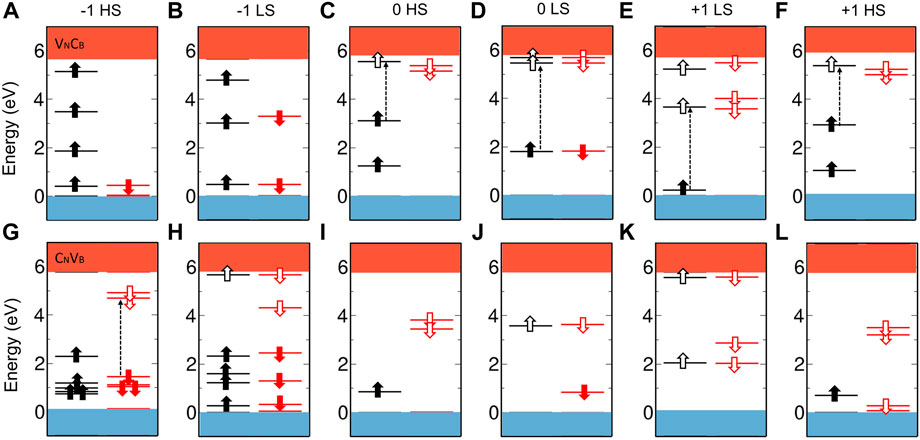
FIGURE 2. Energy-level diagram of V_NC_B (A–F) and C_NV_B (G–L) with different charge states and spin multiplicities. The filled and empty arrows indicate the occupied and unoccupied defect states in the spin-up and spin-down channels. Resonant defect levels below valence band maximum are not shown here. The dash lines represent the allowed optical transition in the visible wavelength region. We use the most stable configurations at every charge and spin states. Here, the C_NV_B(−2) and HSs of C_NV_B(−) have n-C_NV_B configuration, and the others are calculated with sw-C_NV_B.

We summarized the calculated lowest vertical excitation energies in Table 1. For defects in the negative-charge state, the C_NV_B(−) with the HS state is the only possible candidate for the bright visible emitters, and the defects in other charge states have either too small transition energy or large phonon side band. The calculated ZPL is 1.89 eV which is close to that obtained in the flake model (Mendelson et al., 2021).

TABLE 1

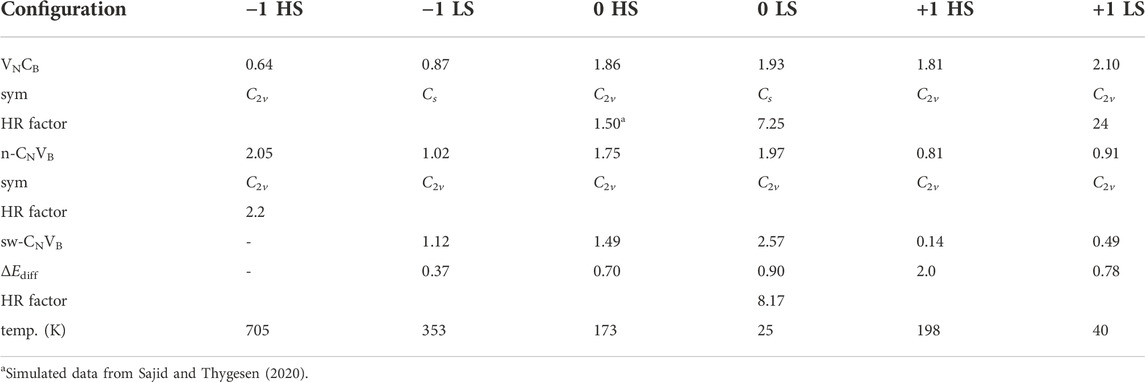
TABLE 1. The lowest vertical transition energy for two defects in hBN. The energy unit is eV. The simulated annealing temperature (temp.) is also listed as obtained from the calculated barrier energies (see text). For C_NV_B defect, except for the C_NV_B(−) HSs, other charge states have lower total energy with sw-C_NV_B configuration. The ΔE_diff indicates energy difference between these two configurations and defined as ΔE_diff = E (n-C_NV_B)-E (sw-C_NV_B).

The defect formation energies E_f are calculated to determine the charge stability with the following equation,

$E_f^q=E_d^q-E_{\text{per}}-{\mu }_{\text{C}}+{\mu }_{\text{B}}+{\mu }_{\text{N}}+q\left({ϵ}_{\text{VBM}}^{\text{per}}+{ϵ}_{\text{Fermi}}\right)+E_{\text{corr}}\left(q\right)\text{,}(1)$

where $E_d^q$ is the total energy of the hBN model with defect at q charge state and E_per is the total energy of the hBN layer without defect. μ_C is the chemical potential of carbon and can be derived from pure graphite. The Fermi-level ϵ_Fermi represents the chemical potential of electron reservoir, and it is aligned to the valence band maximum (VBM) energy of perfect hBN, ${ϵ}_{\text{VBM}}^{\text{per}}$. The $E_{\text{corr}}\left(q\right)$ is the correction term for the charged system due to the existence of electrostatic interactions of the periodic images of the defect. V_NC_B and C_NV_B always prefer LS state for different charge states. As shown in Figure 3, in the fundamental gap, the CTL of V_NC_B for (+1/0) is 2.88 eV and it is 5.30 eV for (0/−1) with respect to VBM. These CTLs are far from conduction band minimum (CBM) and VBM, respectively, making V_NC_B a hyper-deep donor and acceptor. For C_NV_B, the (+1/0) and (0/−1) levels are at 1.51 and 3.19 eV, respectively. We notice that the +2 charge state of V_NC_B and −2 charge state of C_NV_B are also stable as reported previously (Maciaszek et al., 2022). V_NC_B(+2) has C_2v symmetry and the C_NV_B(−2) has n-C_NV_B configuration. However, the calculated CTLs are relatively close to the band edge. (+2/+ 1) is at 1.11 eV for V_NC_B, while the (−1/−2) is at 4.49 eV for C_NV_B. Optical excitation results in photoionization to other charge states, and thus cannot have optical transition energies in fluorescence close to the experimental values. V_NC_B is generally more stable with lower formation energy than C_NV_B when ϵ_Fermi < 4.75 eV. The C_NV_B(−2) has lower formation energy with the Fermi level close to CBM which is not a typical experimental condition.

FIGURE 3

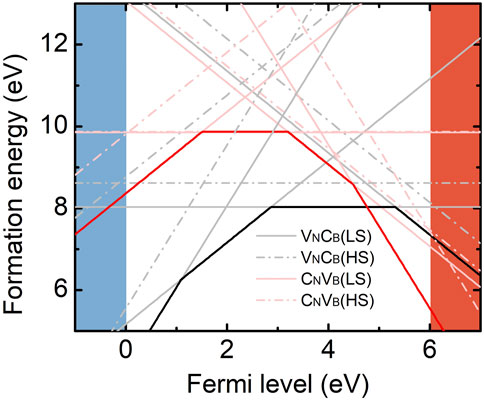
FIGURE 3. Formation energies of V_NC_B (black) and C_NV_B (red) as a function of the Fermi level. The slope of line segment corresponds to the charge state. The solid and dash lines indicate the LS and HS state, respectively. Crossing of the lines denote the charge transition level. Here, the C_NV_B(−2) and HSs of C_NV_B(−) have n-C_NV_B configuration, and the others are calculated with sw-C_NV_B.

Next, we calculated the defect migration with the climbing-image nudged-elastic-band method (Henkelman et al., 2000; Henkelman and Jónsson, 2000) as shown in Figure 4. The n-C_NV_B and sw-C_NV_B are both considered here. The carbon atom can migrate between boron site and nitrogen site, and this transition rate Γ can be simply expressed as (Weston et al., 2018),

$\mathrm{\Gamma }={\mathrm{\Gamma }}_0\exp \left(-\frac{E_b}{k_{B}T}\right)\text{,}(2)$

where E_b is the reaction barrier energy, k_B is the Boltzmann constant, T is the temperature, and Γ₀ is typical phonon frequency in hBN which is about 10¹⁴s⁻¹ (Geick et al., 1966). The calculated T can be regarded as the annealing temperature at which the defect becomes mobile as listed in Table 1. Usually, the temperature is estimated when the jump rate Γ is 1/s (Janotti and Van de Walle, 2007). Above this temperature, the reaction barrier can be passed to reach an equilibrium point. In the negative-charge state, the reaction barrier energies for LSs and HSs are 0.98 and 1.96 eV, respectively, for carbon migration from boron site to nitrogen site. The large barrier energies indicate that the carbon atom cannot jump from one site to another; therefore, the two defects could exist simultaneously. The annealing temperature are 353 and 705 K; therefore, V_NC_B would transform into C_NV_B if the sample is grown or annealed above these temperatures. However, the barrier energies are quite small in the neutral- and positive-charge states. The barrier energies are generally less than 0.6 eV, especially for LSs in the neutral state, manifesting the carbon that can move freely from nitrogen site to boron site. The calculated annealing temperature is lower than room temperature; hence, the V_NC_B defect will dominate in these two charge states and the C_NV_B can only be stabilized through low-temperature irradiation.

FIGURE 4

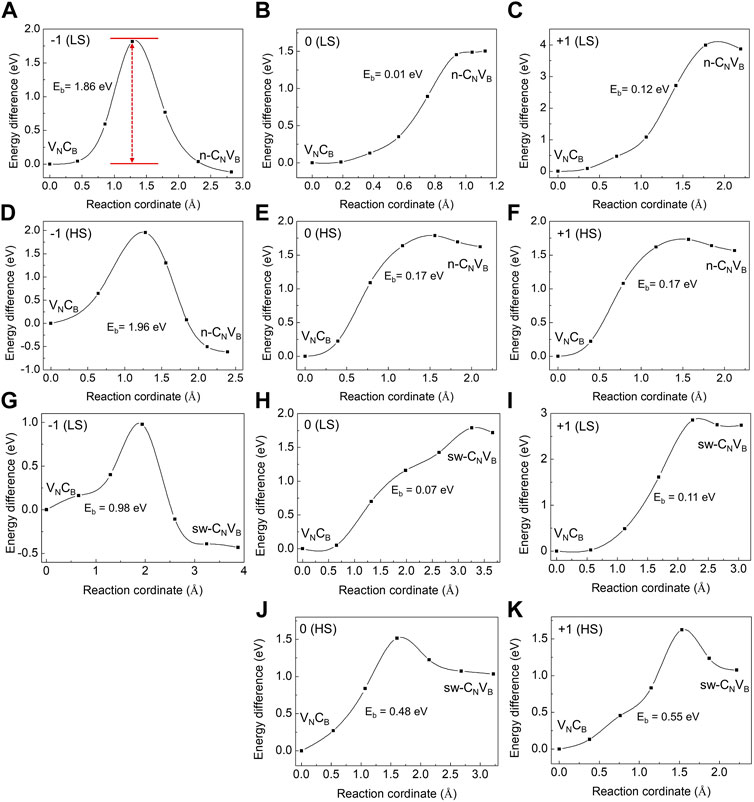
FIGURE 4. Reaction barrier for the carbon atom from initial-state V_NC_B to final-state C_NV_B in different charge states. Transitions from V_NC_B to n-C_NV_B (A–F) and from V_NC_B to sw-C_NV_B(G–K) are shown here. The red arrow indicates the reaction barrier E_b. The HSs of C_NV_B does not have sw-C_NV_B configuration.

The reaction barrier energies and migration paths depend on the charge state. We tentatively associate the low stability of C_NV_B(0) and C_NV_B(+) to the unoccupied localized states in the gap. Filling these defect levels by electrons could stabilize the defect.

Discussion

We calculated the formation energies and the barrier energy of transformation of carbon-vacancy complexes depending on the symmetry and spin multiplicities. We note that the geometry distortions from the planar structure was found for certain carbon-vacancy complexes as the common Jahn–Teller distortion effect where the atoms farther from the core of the defect structure remain in the sheet of hBN layer. This is different from recently proposed geometry containing dramatically out-of-plane warping calculated by CAM-B3LYP DFT functional (Mendelson et al., 2021). This warping might be induced by the hydrogen termination of the model or the freezing of atoms during optimization. In addition, the large-scale distortion might yield the opposite result. In our model, the relaxation energy of HS C_NV_B(−) is 0.16 eV and the HR factor is 2.2, which are close to the experimental data (Mendelson et al., 2021). However, the formation energy difference between the HS and LS for n-C_NV_B(−) is 0.4 eV, where the LS configuration exhibits C_2v symmetry. Our NEB calculation shows there is no barrier for n-C_NV_B to transform into sw-C_NV_B at LSs for three charge states which indicates that the n-C_NV_B might not exist at all. Recent work indicates that n-C_NV_B is dynamically unstable and it quickly relaxes to V_NC_B defect (Ortigoza and Stolbov, 2022). This is consistent with our present data for the neutral-charge state. We show here that sw-C_NV_B occurs in the other charge states too; thus, this behavior is independent of the position of the Fermi level of hBN.

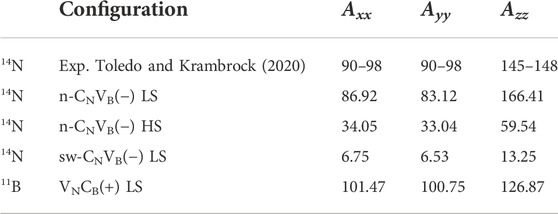
Similar to V_B (Gottscholl et al., 2020), hyperfine interaction-related features may be a unique fingerprint of the C_NV_B(−) defect observed by electron spin resonance techniques. Recently, an electron paramagnetic resonance (EPR) center has been observed in hBN (Toledo and Krambrock, 2020). The experimental data clearly show splitting pattern of five peaks with relative intensities of 1:2:3:2:1. This is due to the hyperfine coupling between one electron spin and two equivalent nitrogen nuclear spin of I = 1; therefore, the EPR center has been tentatively associated with the spin doublet of n-C_NV_B(−) defect (Toledo and Krambrock, 2020). Although our calculations indicate that n-C_NV_B(−) does not exist in hBN, we still simulated its EPR spectrum after calculation of the hyperfine tensors of the defect (see Table 2). Indeed, the simulated EPR spectrum of n-C_NV_B(−) agrees with the experimental one (Toledo and Krambrock, 2020) (Table 2). We note that the hyperfine signatures of the HSs configuration significantly differ. The stable sw-C_NV_B(−) has very different spin density distributions with localization on two boron ions; thus, its EPR spectrum significantly deviates from that of the observed EPR center. However, n-C_NV_B(−) is not a stable structure; therefore, we conclude that it cannot account for the EPR center as tentatively proposed by Toledo and Krambrock (2020), despite the agreement between the simulated and observed hyperfine related features in the EPR spectra.

TABLE 2

TABLE 2. Hyperfine constants for carbon-vacancy complexes in hBN. The unit is in MHz.

We found that the most stable form of the carbon-vacancy complex in hBN is V_NC_B; thus, we plot the simulated EPR spectrum for the paramagnetic V_NC_B(+) in Figure 5B which may occur in hBN. The EPR spectrum shows seven peaks due to two neighboring boron atoms (I = 3/2 for ¹¹B). Further experimental data are needed to confirm the existence of this kind of defect.

FIGURE 5

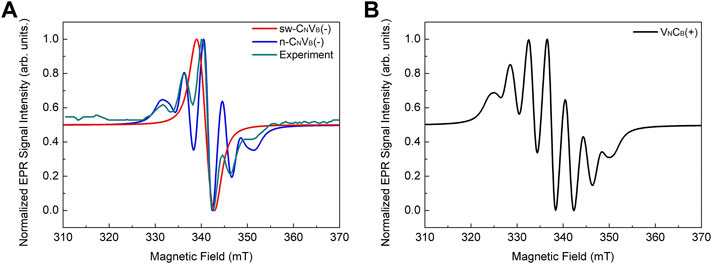
FIGURE 5. Simulated EPR spectrum of defects considered. (A) Experimental data are (Toledo and Krambrock, 2020) recorded at 550 °C to clearly show the line splitting. sw-C_NV_B has relatively small hyperfine coupling so there is no line splitting. The experimental spectrum is shifted 4 mT toward left to match simulation result. (B) EPR spectrum of V_NC_B(+).

We note that there is a metastable triplet state for V_NC_B(0). The triplet state may be accessed by optical pumping of the system from the singlet ground state to the singlet excited state followed by an intersystem crossing from the excited singlet state toward the metastable triplet state. However, the large singlet-triplet energy gap makes this process inefficient; thus, we do not consider the triplet of V_NC_B(0) to be observed by photo-EPR studies.

Summary and conclusions

In this study, we performed density functional theory calculations on the carbon-vacancy complexes in hBN. The analyzed relative stability of these complexes could reveal the origin of the single-photon emitters observed in experiments in the visible wavelength region. sw-C_NV_B is always more stable than n-C_NV_B, and n-C_NV_B transforms into sw-C_NV_B without any barrier in three charge states. Hence, previously reported n-C_NV_B is not the origin of visible SPEs in hBN. sw-C_NV_B is metastable and can transform into V_NC_B with some barrier energies depending on the charge states. In addition, neither V_NC_B nor C_NV_B is a potential candidate for the SPEs associated with the carbon impurities. The formation energies for V_NC_B and C_NV_B complexes imply that these complexes cannot account for the experiments claiming that the number of C-B bond is larger than that of the C-N bond in carbon-contaminated hBN (Mendelson et al., 2021). Further investigation is needed for finding the microscopic origin of SPEs associated with the carbon impurities. Recent studies proposed the C₂C_N configuration (Auburger and Gali, 2021; Li K. et al., 2022; Golami et al., 2022), of which optical properties well reproduce the experimental data. We also found that the recently reported EPR center (Toledo and Krambrock, 2020) is not associated with the unstable V_NC_B defect. Further investigation is needed to identify this EPR center in hBN. We provide the EPR spectrum for the most stable carbon-vacancy complex in hBN that might be found in future EPR studies of carbon contaminated hBN layers.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

AG acknowledges the Hungarian NKFIH grant No. KKP129866 of the National Excellence Program of Quantum-coherent materials project and the support for the Quantum Information National Laboratory from the Ministry of Innovation and Technology of Hungary.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdi, M., Chou, J.-P., Gali, A., and Plenio, M. B. (2018). Color centers in hexagonal boron nitride monolayers: A group theory and ab initio analysis. ACS Photonics 5, 1967–1976. doi:10.1021/acsphotonics.7b01442

CrossRef Full Text | Google Scholar

Alkauskas, A., Buckley, B. B., Awschalom, D. D., and Van de Walle, C. G. (2014). First-principles theory of the luminescence lineshape for the triplet transition in diamond nv centres. New J. Phys. 16, 073026. doi:10.1088/1367-2630/16/7/073026

CrossRef Full Text | Google Scholar

Auburger, P., and Gali, A. (2021). Towards ab initio identification of paramagnetic substitutional carbon defects in hexagonal boron nitride acting as quantum bits. Phys. Rev. B 104, 075410. doi:10.1103/physrevb.104.075410

CrossRef Full Text | Google Scholar

Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50, 17953–17979. doi:10.1103/physrevb.50.17953

CrossRef Full Text | Google Scholar

Bommer, A., and Becher, C. (2019). New insights into nonclassical light emission from defects in multi-layer hexagonal boron nitride. Nanophotonics 8, 2041–2048. doi:10.1515/nanoph-2019-0123

CrossRef Full Text | Google Scholar

Bourrellier, R., Meuret, S., Tararan, A., Stéphan, O., Kociak, M., Tizei, L. H., et al. (2016). Bright uv single photon emission at point defects in h-bn. Nano Lett. 16, 4317–4321. doi:10.1021/acs.nanolett.6b01368

PubMed Abstract | CrossRef Full Text | Google Scholar

Chejanovsky, N., Mukherjee, A., Geng, J., Chen, Y.-C., Kim, Y., Denisenko, A., et al. (2021). Single-spin resonance in a van der waals embedded paramagnetic defect. Nat. Mat. 20, 1079–1084. doi:10.1038/s41563-021-00979-4

CrossRef Full Text | Google Scholar

Cheng, G., Zhang, Y., Yan, L., Huang, H., Huang, Q., Song, Y., et al. (2017). A paramagnetic neutral cbvn center in hexagonal boron nitride monolayer for spin qubit application. Comput. Mater. Sci. 129, 247–251. doi:10.1016/j.commatsci.2016.12.032

CrossRef Full Text | Google Scholar

Du, X., Li, J., Lin, J., and Jiang, H. (2015). The origin of deep-level impurity transitions in hexagonal boron nitride. Appl. Phys. Lett. 106, 021110. doi:10.1063/1.4905908

CrossRef Full Text | Google Scholar

Freysoldt, C., and Neugebauer, J. (2018). First-principles calculations for charged defects at surfaces, interfaces, and two-dimensional materials in the presence of electric fields. Phys. Rev. B 97, 205425. doi:10.1103/physrevb.97.205425

CrossRef Full Text | Google Scholar

Gali, A., Janzén, E., Deák, P., Kresse, G., and Kaxiras, E. (2009). Theory of spin-conserving excitation of theN−V−Center in diamond. Phys. Rev. Lett. 103, 186404. doi:10.1103/physrevlett.103.186404

PubMed Abstract | CrossRef Full Text | Google Scholar

Geick, R., Perry, C., and Rupprecht, G. (1966). Normal modes in hexagonal boron nitride. Phys. Rev. 146, 543–547. doi:10.1103/physrev.146.543

CrossRef Full Text | Google Scholar

Golami, O., Sharman, K., Ghobadi, R., Wein, S. C., Zadeh-Haghighi, H., da Rocha, C. G., et al. (2022). Ab initio and group theoretical study of properties of a carbon trimer defect in hexagonal boron nitride. Phys. Rev. B 105, 184101. doi:10.1103/physrevb.105.184101

CrossRef Full Text | Google Scholar

Gottscholl, A., Diez, M., Soltamov, V., Kasper, C., Sperlich, A., Kianinia, M., et al. (2021). Room temperature coherent control of spin defects in hexagonal boron nitride. Sci. Adv. 7, eabf3630. doi:10.1126/sciadv.abf3630

PubMed Abstract | CrossRef Full Text | Google Scholar

Gottscholl, A., Kianinia, M., Soltamov, V., Orlinskii, S., Mamin, G., Bradac, C., et al. (2020). Initialization and read-out of intrinsic spin defects in a van der waals crystal at room temperature. Nat. Mat. 19, 540–545. doi:10.1038/s41563-020-0619-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Grosso, G., Moon, H., Lienhard, B., Ali, S., Efetov, D. K., Furchi, M. M., et al. (2017). Tunable and high-purity room temperature single-photon emission from atomic defects in hexagonal boron nitride. Nat. Commun. 8, 705–708. doi:10.1038/s41467-017-00810-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamdi, H., Thiering, G., Bodrog, Z., Ivády, V., and Gali, A. (2020). Stone–wales defects in hexagonal boron nitride as ultraviolet emitters. npj Comput. Mat. 6, 178–187. doi:10.1038/s41524-020-00451-y

CrossRef Full Text | Google Scholar

Hayee, F., Yu, L., Zhang, J. L., Ciccarino, C. J., Nguyen, M., Marshall, A. F., et al. (2020). Revealing multiple classes of stable quantum emitters in hexagonal boron nitride with correlated optical and electron microscopy. Nat. Mat. 19, 534–539. doi:10.1038/s41563-020-0616-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Henkelman, G., and Jónsson, H. (2000). Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 113, 9978–9985. doi:10.1063/1.1323224

CrossRef Full Text | Google Scholar

Henkelman, G., Uberuaga, B. P., and Jónsson, H. (2000). A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904. doi:10.1063/1.1329672

CrossRef Full Text | Google Scholar

Heyd, J., Scuseria, G. E., and Ernzerhof, M. (2003). Hybrid functionals based on a screened coulomb potential. J. Chem. Phys. 118, 8207–8215. doi:10.1063/1.1564060

CrossRef Full Text | Google Scholar

Ivády, V., Barcza, G., Thiering, G., Li, S., Hamdi, H., Chou, J.-P., et al. (2020). Ab initio theory of the negatively charged boron vacancy qubit in hexagonal boron nitride. npj Comput. Mat. 6, 41–46. doi:10.1038/s41524-020-0305-x

CrossRef Full Text | Google Scholar

Janotti, A., and Van de Walle, C. G. (2007). Native point defects in zno. Phys. Rev. B 76, 165202. doi:10.1103/physrevb.76.165202

CrossRef Full Text | Google Scholar

Jin, C., Lin, F., Suenaga, K., and Iijima, S. (2009). Fabrication of a freestanding boron nitride single layer and its defect assignments. Phys. Rev. Lett. 102, 195505. doi:10.1103/physrevlett.102.195505

PubMed Abstract | CrossRef Full Text | Google Scholar

Kianinia, M., White, S., Froch, J. E., Bradac, C., and Aharonovich, I. (2020). Generation of spin defects in hexagonal boron nitride. ACS Photonics 7, 2147–2152. doi:10.1021/acsphotonics.0c00614

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996a). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50. doi:10.1016/0927-0256(96)00008-0

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996b). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186. doi:10.1103/physrevb.54.11169

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775. doi:10.1103/physrevb.59.1758

CrossRef Full Text | Google Scholar

Li, K., Smart, T. J., and Ping, Y. (2022a). Carbon trimer as a 2 ev single-photon emitter candidate in hexagonal boron nitride: A first-principles study. Phys. Rev. Mat. 6, L042201. doi:10.1103/physrevmaterials.6.l042201

CrossRef Full Text | Google Scholar

Li, S., Chou, J.-P., Hu, A., Plenio, M. B., Udvarhelyi, P., Thiering, G., et al. (2020). Giant shift upon strain on the fluorescence spectrum of vnnb color centers in h-bn. npj Quantum Inf. 6, 85–87. doi:10.1038/s41534-020-00312-y

CrossRef Full Text | Google Scholar

Li, S., Pershin, A., Thiering, G., Udvarhelyi, P., and Gali, A. (2022b). Ultraviolet quantum emitters in hexagonal boron nitride from carbon clusters. J. Phys. Chem. Lett. 13, 3150–3157. doi:10.1021/acs.jpclett.2c00665

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W., Li, Z.-P., Yang, Y.-Z., Yu, S., Meng, Y., Wang, Z.-A., et al. (2021). Rabi oscillation of vb- spin in hexagonal boron nitride. arXiv preprint arXiv:2101.11220.

Google Scholar

Maciaszek, M., Razinkovas, L., and Alkauskas, A. (2022). Thermodynamics of carbon point defects in hexagonal boron nitride. Phys. Rev. Mat. 6, 014005. doi:10.1103/physrevmaterials.6.014005

CrossRef Full Text | Google Scholar

Mackoit-Sinkevičienė, M., Maciaszek, M., Van de Walle, C. G., and Alkauskas, A. (2019). Carbon dimer defect as a source of the 4.1 ev luminescence in hexagonal boron nitride. Appl. Phys. Lett. 115, 212101. doi:10.1063/1.5124153

CrossRef Full Text | Google Scholar

Mendelson, N., Chugh, D., Reimers, J. R., Cheng, T. S., Gottscholl, A., Long, H., et al. (2021). Identifying carbon as the source of visible single-photon emission from hexagonal boron nitride. Nat. Mat. 20, 321–328. doi:10.1038/s41563-020-00850-y

CrossRef Full Text | Google Scholar

Mendelson, N., Doherty, M., Toth, M., Aharonovich, I., and Tran, T. T. (2020). Strain-induced modification of the optical characteristics of quantum emitters in hexagonal boron nitride. Adv. Mat. 32, 1908316. doi:10.1002/adma.201908316

CrossRef Full Text | Google Scholar

Museur, L., Feldbach, E., and Kanaev, A. (2008). Defect-related photoluminescence of hexagonal boron nitride. Phys. Rev. B 78, 155204. doi:10.1103/physrevb.78.155204

CrossRef Full Text | Google Scholar

Noh, G., Choi, D., Kim, J.-H., Im, D.-G., Kim, Y.-H., Seo, H., et al. (2018). Stark tuning of single-photon emitters in hexagonal boron nitride. Nano Lett. 18, 4710–4715. doi:10.1021/acs.nanolett.8b01030

PubMed Abstract | CrossRef Full Text | Google Scholar

Ortigoza, M. A., and Stolbov, S. (2022). Thermodynamic stability and optical properties of c-doping-induced defects in hexagonal boron nitride as potential single-photon emitters. Phys. Rev. B 105, 165306. doi:10.1103/physrevb.105.165306

CrossRef Full Text | Google Scholar

Reimers, J. R., Sajid, A., Kobayashi, R., and Ford, M. J. (2018). Understanding and calibrating density-functional-theory calculations describing the energy and spectroscopy of defect sites in hexagonal boron nitride. J. Chem. Theory Comput. 14, 1602–1613. doi:10.1021/acs.jctc.7b01072

PubMed Abstract | CrossRef Full Text | Google Scholar

Reimers, J. R., Shen, J., Kianinia, M., Bradac, C., Aharonovich, I., Ford, M. J., et al. (2020). Photoluminescence, photophysics, and photochemistry of the VB− defect in hexagonal boron nitride. Phys. Rev. B 102, 144105. doi:10.1103/physrevb.102.144105

CrossRef Full Text | Google Scholar

Sajid, A., Ford, M. J., and Reimers, J. R. (2020). Single-photon emitters in hexagonal boron nitride: A review of progress. Rep. Prog. Phys. 83, 044501. doi:10.1088/1361-6633/ab6310

PubMed Abstract | CrossRef Full Text | Google Scholar

Sajid, A., Reimers, J. R., and Ford, M. J. (2018). Defect states in hexagonal boron nitride: Assignments of observed properties and prediction of properties relevant to quantum computation. Phys. Rev. B 97, 064101. doi:10.1103/physrevb.97.064101

CrossRef Full Text | Google Scholar

Sajid, A., and Thygesen, K. S. (2020). Vncb defect as source of single photon emission from hexagonal boron nitride. 2D Mat. 7, 031007. doi:10.1088/2053-1583/ab8f61

CrossRef Full Text | Google Scholar

Stern, H. L., Gu, Q., Jarman, J., Eizagirre Barker, S., Mendelson, N., Chugh, D., et al. (2022). Room-temperature optically detected magnetic resonance of single defects in hexagonal boron nitride. Nat. Commun. 13, 618–619. doi:10.1038/s41467-022-28169-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Stoll, S., and Schweiger, A. (2006). Easyspin, a comprehensive software package for spectral simulation and analysis in epr. J. magnetic Reson. 178, 42–55. doi:10.1016/j.jmr.2005.08.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Toledo, J., and Krambrock, K. (2020). Identification and thermal stability of point defects in neutron-irradiated hexagonal boron nitride (h-bn). J. Phys. D. Appl. Phys. 54, 065303. doi:10.1088/1361-6463/abc37c

CrossRef Full Text | Google Scholar

Tran, T. T., Bray, K., Ford, M. J., Toth, M., and Aharonovich, I. (2016a). Quantum emission from hexagonal boron nitride monolayers. Nat. Nanotechnol. 11, 37–41. doi:10.1038/nnano.2015.242

PubMed Abstract | CrossRef Full Text | Google Scholar

Tran, T. T., Elbadawi, C., Totonjian, D., Lobo, C. J., Grosso, G., Moon, H., et al. (2016b). Robust multicolor single photon emission from point defects in hexagonal boron nitride. ACS Nano 10, 7331–7338. doi:10.1021/acsnano.6b03602

PubMed Abstract | CrossRef Full Text | Google Scholar

Vuong, T., Cassabois, G., Valvin, P., Ouerghi, A., Chassagneux, Y., Voisin, C., et al. (2016). Phonon-photon mapping in a color center in hexagonal boron nitride. Phys. Rev. Lett. 117, 097402. doi:10.1103/physrevlett.117.097402

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, R., Yang, J., Wu, X., and Wang, S. (2016). Local charge states in hexagonal boron nitride with stone–wales defects. Nanoscale 8, 8210–8219. doi:10.1039/c5nr09099g

PubMed Abstract | CrossRef Full Text | Google Scholar

Weston, L., Wickramaratne, D., Mackoit, M., Alkauskas, A., and Van de Walle, C. (2018). Native point defects and impurities in hexagonal boron nitride. Phys. Rev. B 97, 214104. doi:10.1103/physrevb.97.214104

CrossRef Full Text | Google Scholar

Wu, F., Smart, T. J., Xu, J., and Ping, Y. (2019). Carrier recombination mechanism at defects in wide band gap two-dimensional materials from first principles. Phys. Rev. B 100, 081407. doi:10.1103/physrevb.100.081407

CrossRef Full Text | Google Scholar