
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Robot. AI, 22 June 2022
Sec. Robotic Control Systems
Volume 9 - 2022 | https://doi.org/10.3389/frobt.2022.878364
This article is part of the Research TopicCurrent Challenges and Future Developments in Robot GraspingView all 6 articles
Two sub-problems are typically identified for the replication of human finger motions on artificial hands: the measurement of the motions on the human side and the mapping method of human hand movements (primary hand) on the robotic hand (target hand). In this study, we focus on the second sub-problem. During human to robot hand mapping, ensuring natural motions and predictability for the operator is a difficult task, since it requires the preservation of the Cartesian position of the fingertips and the finger shapes given by the joint values. Several approaches have been presented to deal with this problem, which is still unresolved in general. In this work, we exploit the spatial information available in-hand, in particular, related to the thumb-finger relative position, for combining joint and Cartesian mappings. In this way, it is possible to perform a large range of both volar grasps (where the preservation of finger shapes is more important) and precision grips (where the preservation of fingertip positions is more important) during primary-to-target hand mappings, even if kinematic dissimilarities are present. We therefore report on two specific realizations of this approach: a distance-based hybrid mapping, in which the transition between joint and Cartesian mapping is driven by the approaching of the fingers to the current thumb fingertip position, and a workspace-based hybrid mapping, in which the joint–Cartesian transition is defined on the areas of the workspace in which thumb and fingertips can get in contact. The general mapping approach is presented, and the two realizations are tested. In order to report the results of an evaluation of the proposed mappings for multiple robotic hand kinematic structures (both industrial grippers and anthropomorphic hands, with a variable number of fingers), a simulative evaluation was performed.
The mapping of finger motions on multi-articulated robot hands is nowadays an open problem in the robotics community (Shahbazi et al., 2018; Carfì et al., 2021). Indeed, a general mapping solution for the replication of human primary hand (PH) motions onto a robotic target hand (TH), ensuring ease of use and good motion reproducibility, is a very challenging target to be achieved. The presence, in real situations, of unavoidable kinematic dissimilarities between PH and TH does not allow to precisely replicate PH finger motions onto TH fingers with a direct identity mapping, and some adaptation and/or interpretation must be adopted (Gioioso et al., 2012). Therefore, despite several advances during the last years, it results from evidence that developing TH to RH mapping strategies is a non-trivial and both conceptual and analytical problem (Meeker et al., 2018).
The two principal fields in which human-to-robot hand mapping methods used are teleoperation and learning by demonstration (Dillmann et al., 2000). In teleoperation applications, data measured from the operator’s human hand are used to control in real-time motion of a robot hand. Differently, in learning by demonstration applications, motion measurements from the human hand are exploited as a source of human skill information to improve the dexterity and the behavior of autonomous robot hands. In the literature, several works have attempted to design mapping solutions such that to obtain correct and predictable behaviors on the TH. Two fundamental sub-problems have been considered for human-to-robot hand mapping: 1) the measurement of human PH motions using appropriate kinematic modeling and sensor equipment and 2) the design of a mapping algorithm to obtain a proper imitation of PH motions on the robot TH. In this study, we will not focus on the former sub-problem, which has been extensively addressed using sensorized gloves (Cobos et al., 2010; Geng et al., 2011; Bianchi et al., 2013), vision systems (Gupta and Ma, 2001; Infantino et al., 2005; Wachs et al., 2005), hand exoskeletons (Bergamasco et al., 2007), and advanced calibration procedures (Rohling and Hollerbach, 1993). We will instead focus on the second sub-problem, for the reason that it is still lacking a general solution (Colasanto et al., 2012).
Among the many approaches that have been presented in the literature for PH to TH motion mapping, the simplest realization is the direct joint mapping (Speeter, 1992), in which joint angles of the PH are directly imposed onto the robot TH. Direct joint mapping presents the advantage of being rapidly implementable, while preserving PH finger shapes on anthropomorphic TH, allowing better reproduction of gestures and power grasps (Cerulo et al., 2017). Additionally, it generally permits an increased predictability of TH behaviors, allowing the human operator to more easily compensate for inaccurate behaviors by moving ones hand (Speeter, 1992). The second simplest mapping approach is the direct Cartesian mapping (Rohling and Hollerbach, 1993), which consists in computing Cartesian positions and orientations of the PH fingertips (i.e., the fingertip poses) by means of forward kinematics, and directly imposing them on the TH fingertips, followed by the computation of the TH joint angles via inverse kinematics. Direct Cartesian mapping is more appropriate for the execution of precision grasps and in-hand manipulation since it preserves the PH fingertip positions on the TH. However, on the other hand, it does not guarantee, in general, the preservation of the PH finger shapes, making difficult the correct execution of power grasps, non-prehensile manipulation, and gestures (Chattaraj et al., 2014). More advanced mapping approaches are based on attenuating the problem of PH-TH kinematic dissimilarities by using a suitable task-oriented description of the finger motions. This is the case of the object-based mapping method (Gioioso et al., 2013), in which PH finger motion information is encapsulated within a virtual object defined in the PH workspace, which is then reported in the TH workspace in order to impose coordinated finger motions. This mapping presents the advantage of being implementable for non-anthropomorphic TH, in which case direct joint and direct Cartesian mappings are particularly unsatisfactory. However, when the precision of single fingertips is required, or purposes different from grasping objects are desired, the object-oriented mapping can produce highly unintuitive behaviors of the TH (Meeker et al., 2018) critically affecting its applicability, even when the object-oriented mapping algorithm is abstracted from defining a specific virtual object shape (Salvietti et al., 2014). In an interesting more recent mapping approach denoted as DexPilot (Handa et al., 2020), PH fingertip poses are obtained via a marker-less vision, and, thereafter, a cost function based on the distance and orientation among fingertips in the TH workspace is designed in order to optimize the final TH finger configurations. Other types of mapping are based on recognizing the PH posture in order to reproduce it on the TH (Ekvall and Kragic, 2004; Pedro et al., 2012; Ficuciello et al., 2021). In this kind of approach, the functions of the TH are limited to a discrete set of predefined grasps/motions and, thereafter, based on the output of the PH posture recognition process (mostly based on machine learning techniques (Dillmann et al., 2000; Yoshimura and Ozawa, 2012)), one of the available TH motions is selected and executed. In this case, the operator can easily learn how to configure ones own hand in order to activate specific actions of the robot hand, whereas the lack of continuous control, and the fact that the number of predefined TH grasps/motions increases with the complexity of the applications, de facto make this mapping method difficult to be applied for several applications (e.g., precision grasps and gestures/grasps not included in the predefined TH motions.) Furthermore, types of PH-to-TH mapping approaches can be found in the literature, for example, based on dimensionality reduction of the TH input space (Ciocarlie et al., 2007; Salvietti, 2018), deep learning architectures (Gomez-Donoso et al., 2019; Li et al., 2019), or shared control (Song et al., 1999; Hu et al., 2005). However, in general, state-of-the-art mapping solutions do not take into account the necessity of preserving on the TH, within a single method, both PH finger shapes and fingertip Cartesian positions. Instead, these aspects are essential to ensure acceptable levels of intuitiveness and predictability of TH motions during a hand motion mapping (Fischer et al., 1998), and we therefore claim that they should be carefully considered for novel advances in the research problem of mapping motions on robot hands.
In the light of these concepts, in this study, we introduce a hybrid approach combining joint and Cartesian mappings in a single solution. Specifically, the proposed hybrid joint–Cartesian mapping exploits specific spatial information that we denote as “available in-hand,” which means that is available a priori just once certain hand kinematics is given because they can be systematically derived from geometrical considerations and forward/inverse kinematics computations. We therefore exploit spatial in-hand information to enforce a smooth and continuous transition between joint and Cartesian mappings. In particular, in this study, we present and evaluate two specific realizations of this mapping paradigm. The first one is denoted as distance-based hybrid mapping, in which the spatial in-hand information related to the distance between the fingertips of the thumb and opposite fingers is exploited to realize the transition between joint and Cartesian mappings. In the second realization, denoted as workspace-based hybrid mapping, the spatial in-hand information used to enforce the transition between joint and Cartesian mappings is related to the areas of the workspace in which the thumb and opposite fingertips can get in contact. In the article, these hybrid mapping realizations are thoroughly presented, and simulation experiments are conducted on a series of well-known multi-articulated robot hands, both anthropomorphic and non-anthropomorphic, in order to evaluate and compare the proposed mapping paradigm.
We are interested in having a mapping algorithm to realize a smooth transition based on in-hand spatial information between two types of basic mappings, the joint mapping and the Cartesian mapping. Also, the transition has to be continuous in order to avoid any discontinuity during the PH-to-TH motion mapping. Therefore, we here introduce the general concept underlying the joint–Cartesian hybrid mapping based on spatial in-hand information and, thereafter, we will describe two specific realizations, the distance-based hybrid mapping and the workspace-based hybrid mapping, which characterize the usage of two different kinds of spatial in-hand information. To this aim, let us consider the block diagram of Figure 1, illustrating the general joint–Cartesian hybrid mapping approach. According to Figure 1, we will consider, here and in the following of this section, only the thumb and the index finger, since the algorithm can immediately be extended to the consideration of all PH and TH fingers. Furthermore, we assume in this section that the joint and Cartesian mappings results are already available, while their specific formulations for the distance-based realization and workspace-based realization are reported later in Section 2.2 and Section 2.3, respectively. Let us then consider
for the TH thumb and index fingertips, respectively. Therefore, applying the forward kinematics it holds that
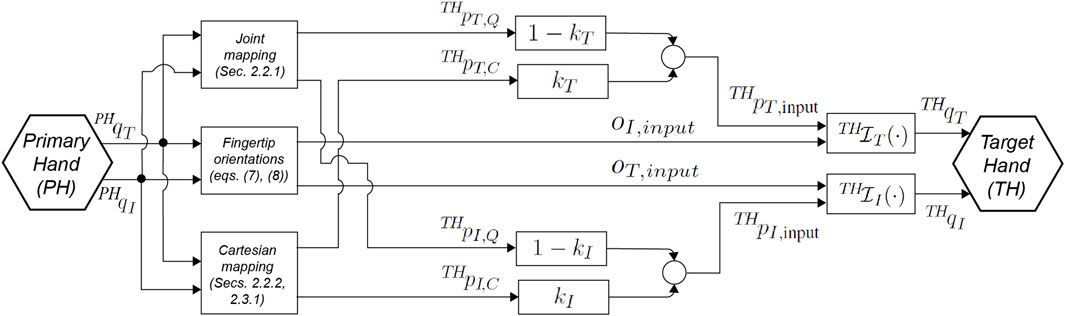
FIGURE 1. Block diagram of the proposed hybrid joint–Cartesian mapping approach, for thumb (subscript i = T) and index (subscript i = I) fingers only (extension to other fingers is straightforward.) The PH joints
In a similar manner, if instead of the joint mapping we consider the case of the Cartesian mapping, we can write the TH thumb and index fingertip poses as:
respectively, where the fingertip Cartesian positions
where
with
In Eq. 6, kT and kI are smooth, sigmoidal gains governing the transition between joint and Cartesian mappings. Since we want our hybrid mapping to be based on spatial information, it follows that the definition of kT, kI has to be founded on such spatial information, and therefore they will be introduced in the next subsection, with different formulations for the distance-based (see Section 2.2.3) and workspace-based (see Section 2.3.2) hybrid mapping realizations. Now that we have introduced how the Cartesian position inputs for the TH thumb and index fingertips are imposed by the proposed mapping algorithm, we are going to describe the fingertips' orientation inputs (see also Figure 1) we imposed.
where
In the distance-based realization of the proposed hybrid mapping, we consider the spatial in-hand information given by the module of the distance vector between the thumb and opposite fingertips. The idea is that, during a wide variety of precise actions, the thumb fingertip is closer in space to opposite fingertips. Thus, when the distance between the PH thumb and index fingertips (the algorithm can be immediately extended to any thumb-finger couple) is lower than a given threshold, a transition between joint and Cartesian mappings is imposed on the TH. In the following joint mapping, Cartesian mapping and transition behavior are illustrated.
Let us denote with
Where m, n, l, and p are TH thumb, TH index, PH thumb, and PH index number of joints, respectively. In other words, Eqs. 9, 10 describe that, to each single joint of the TH thumb and index fingers (denoted by the subscripts i and j in Eqs. 9, 10) is arbitrarily imposed the angular value related to a single specific joint of the PH thumb or index fingers (denoted by the subscripts h and k in Eqs. 9, 10). According to Eq. 10,
Within the distance-based hybrid mapping realization, the Cartesian mapping is implemented considering differently the thumb and the opposite fingers. Taking into account the index finger, as representative of the opposite fingers without loss of generality, its Cartesian mapping is realized according to the following relation:
where
and the PH thumb position relative to the base frame of the opposite finger m is:
where the subscripts l, t, and m are equal to {l, t} = {{I, M}, {M, R}, {R, P}}, and m = {I, M, R}, with I, M, R, and P indicating the index, middle, ring, and little fingers, and
Where the [a]b indicates the component along the b axis of the vectorial expression a,
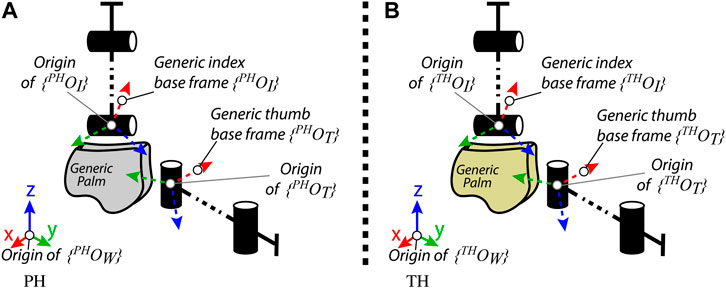
FIGURE 2. Generic representations of the (A) PH and (B) TH thumb and index finger, for the distance-based hybrid mapping realization.
In order to define the joint–Cartesian mapping transition of the distance-based hybrid mapping realization, it is necessary to properly impose the gains kT and kI previously introduced in Eq. 6 in Section 2.1 (see also Figure 1.) To this purpose, let rin and rout (rin < rout) be the radii of two spheres centered in the PH thumb fingertip. For the TH index finger, we want to obtain that: 1) the joint mapping (see Section 2.2.1) is applied if the inequality
with
In the workspace-based realization, the spatial in-hand information exploited for the implementation of the joint–Cartesian hybrid mapping is related to the areas of the PH and TH workspaces in which the thumb and index can get in contact (as before, we keep considering only the thumb and index finger without the loss of generality). Indeed, the consideration of the fingertip contact areas within robot hands has not been investigated in previous mapping methods, while the intersection between finger workspaces has been demonstrated to be a key descriptor in dexterous manipulations (Kuo et al., 2009), and therefore we want to explore its usage as spatial information within the proposed hybrid mapping approach. In the following description of the workspace-based mapping realization, the joint mapping is not illustrated because its formulation has no differences from the joint mapping already described in Section 2.2.1 for the distance-based mapping realization. Therefore, in the following, only the specific implementation of the Cartesian mapping and joint–Cartesian mapping transition is provided.
Let us consider the PH workspace region delimited by the convex hull
The Cartesian mapping is finally imposed for the TH thumb and index finger as
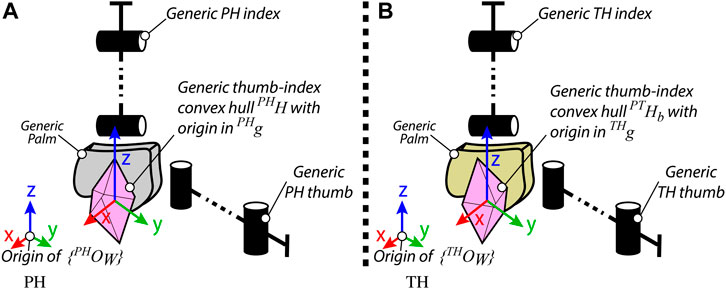
FIGURE 3. Generic representations of the (A) PH and (B) TH thumb and index finger, for the workspace-based hybrid mapping realization.
For the description of the joint–Cartesian mapping transition for the workspace-based realization of the proposed hybrid mapping, let us define
which can also be simply indicated as fTI. We can now finally describe the gains kT and kI, as necessary to impose a desired joint–Cartesian transition (see Eq. 6 in Section 2.1 and Figure 1), which are given according to
According to Eq. 22, the Cartesian mapping is enforced if
For the evaluation of the proposed PH-to-TH mapping strategies, we performed a series of simulation experiments using both non-anthropomorphic and anthropomorphic robot hands. As PH, we used the paradigmatic hand model, available from the open-source SynGrasp MATLAB toolbox (Malvezzi et al., 2015) (see Figure 4.) As TH, we simulated, via SynGrasp, four types of well-known multi-articulated robot hands: a 3-fingered hand inspired to the Barrett hand (Townsend, 2000), the 4-fingered anthropomorphic Allegro hand (WonikRobotics, 2015), the anthropomorphic DLR-Hit II hand (Butterfaß et al., 2001), and the anthropomorphic University of Bologna Hand IV (UBHand) (Melchiorri et al., 2013) (Figure 4).
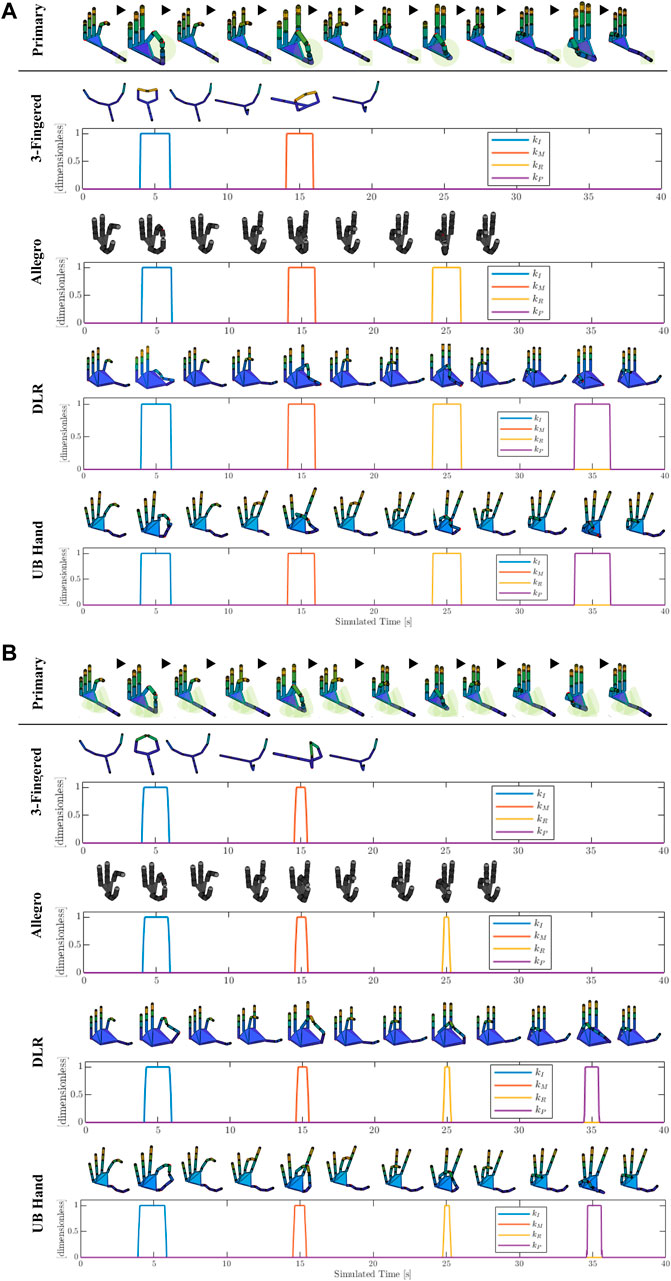
FIGURE 4. Mapping of the tip-to-tip motion of the PH on the different types of TH and related transition gains between joint and Cartesian mappings (kI, kM, kR, and kP for the index, middle, ring, and pinkie fingers, respectively) for the (A) distance-based and (B) workspace-based proposed approaches. The sphere of the distance-based mapping and the convex hull of the workspace-based mapping (see Section 2) are reported only on the PH for better visualization. Note that a color-coded shading of the simulated robot hand is applied for improving the visualization.
Specifically, for the first simulation experiment, a particular motion was generated for the PH, referred to as tip-to-tip motion, in which the fingertips of the thumb and opposite fingers get in contact in a sequence, as shown in Figure 4. Furthermore, Figure 4 also reports the results of the distance-based (Figure 4A) and workspace-based mappings (Figure 4B) on the different simulated robot hands, along with the relative behavior of the gains for the transition between joint and Cartesian mappings (kI, kM, kR, and kP for the index, middle, ring, and pinkie fingers, respectively.) Note that for the 3-fingered hand we mapped only the PH thumb, index, and middle fingers, whereas for the Allegro hand we mapped only the PH thumb, index, middle, and ring fingers. From Figure 4, first of all, it is possible to see how both the distance-based and workspace-based mappings allow the TH to conserve the shape of the PH fingers (i.e., their joint configuration) when the fingers are not close to the thumb, and, at the same time, to perform a correct thumb–fingers tip-to-tip contact, thanks to the switching to the Cartesian mapping according to the related transition gains.
In Figure 6A we reported, for each different TH, the mean joint error—that is the mean of the norm of the error between the joint angle vectors of the PH and the TH—during the enforcing of the Cartesian mapping (top graph, for both distance-based and workspace-based approaches), and the mean thumb–finger fingertip Cartesian position error during the enforcing of the joint mapping (bottom graph, for both distance-based and workspace-based approaches). Note that the latter Cartesian error was normalized by the value of the distance between thumb and index fingertips in the open hand configuration, for each respective robot hand. This made the Cartesian error between the different robot hands comparable, taking into account the different TH sizes. Looking at the top graph of Figure 6A, it is possible to observe that for the workspace-based mapping the Allegro hand presented a clearly higher joint error when the workspace-based mapping was used, due to the fact that the Allegro hand presents a workspace geometrically less compatible with the one of the PHs (the paradigmatic hand.) Also, it is possible to see how 5-fingered anthropomorphic robot hands showed a lower joint error. Looking at the bottom graph of Figure 6A, it is worth highlighting that, using the workspace-based approach, the 3-fingered hand and the Allegro hand showed a substantially higher thumb–finger Cartesian error. This was due to the fact that, since these two TH present more pronounced kinematic differences with respect to the PH anthropomorphic structure and therefore more different workspaces, the distance-based mapping enforces the Cartesian mapping for a larger part of the motion, reducing the reported Cartesian error (which is reported when the joint mapping is enforced). Differently, the workspace-based approach required that both the thumb and opposite finger enter the convex hull region which enables the transition to the Cartesian mapping.
The second simulation experiment, visible in Figure 5, consisted in performing the grasp of a sphere requiring to use the joint mapping for the preservation of the PH finger shapes and a thin cylinder requiring precise positioning of the fingertip in order to preserve the fingertips–object contact point locations. For the grasping of the sphere, the PH fingers were closed uniformly along all joints producing the finger flexions. Then, the motion was mapped on the different simulated robot hands (distance-based and workspace-based mappings coincide, in this case, because only joint mapping was enforced in both mappings), and each PH finger was stopped when the relative TH finger got in contact with the object surface. The result of the sphere grasping can be seen in the left part of Figure 5 for the different robot hands, and the Cartesian error is reported in the top graph of Figure 6B. In the latter graph, it can be observed how the 3-fingered hand showed the higher Cartesian error, due to the fact that it presents the less anthropomorphic-like kinematic structure. For the grasping of the thin cylinder, the tip-to-tip motion only for the thumb and index finger was performed on the PH and then mapped with the distance-based and workspace-based approaches on the TH. The PH thumb and index were stopped when the TH counterpart got in contact with the object's surface. As can be seen in the right part of Figure 5, both proposed mapping methods were able to map the precision grasp on the different robot hands (the position of the cylinder was adjusted based on the specific TH because we reasonably assumed that, during the thumb–index approaching motion, the object location could be adjusted with respect to the robot hand accordingly). The bottom graph of Figure 6B reports the joint error when the cylinder is grasped. It is possible to see that, for the different robot hands, the distance-based and workspace-based mappings showed comparable joint errors, with the workspace-based mapping presenting lower error values for the 3-fingered, DLR, and UBHand robot hands. This latter aspect can also be seen in the right part of Figure 5, where the workspace-based approach was able to put the TH fingers in contact with the object with a more similar shape with respect to the PH. A video of the simulation results reported in Figures 4, 5 is available at the link: https://bit.ly/3OUcqaa.
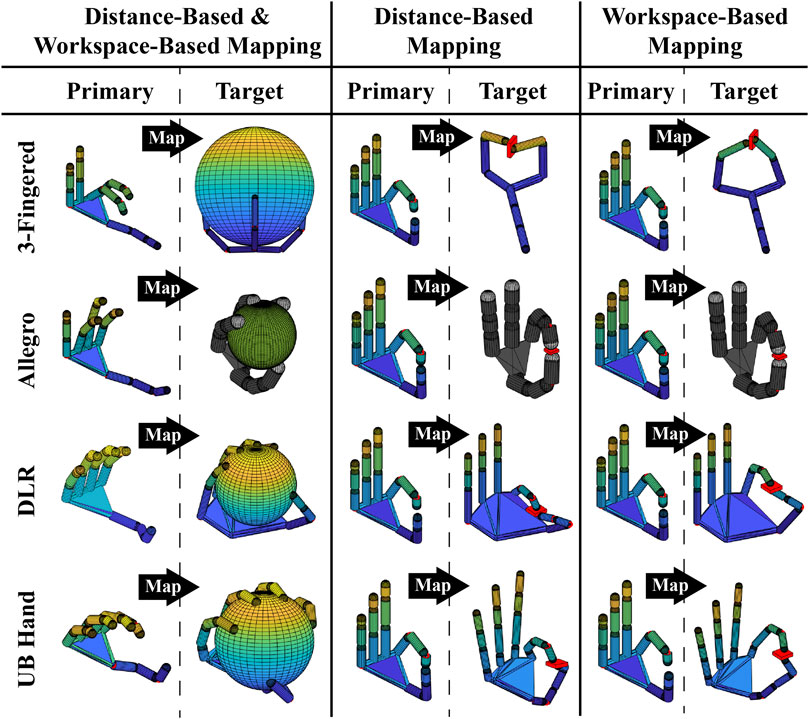
FIGURE 5. Proposed mapping approaches applied for the simulated grasp of a sphere (left part) and a thin cylinder (right part). Note that a color-coded shading of the simulated robot hand is applied for improving the visualization.
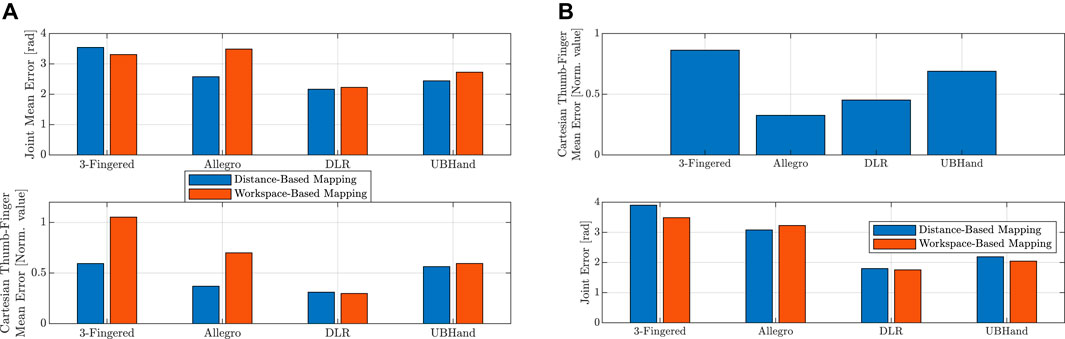
FIGURE 6. (A) Top graph: mean joint error for the tip-to-tip motion during the enforcing of the Cartesian mapping. (A) Bottom graph: mean Cartesian error for the tip-to-tip motion during the enforcing of the joint mapping. (B) Top graph: Cartesian error for the grasping of the spherical objects. (B) Bottom graph: joint error for the grasping of the thin cylinder object.
Finally, in order to contextualize the proposed hybrid mapping approaches with respect to other mapping methods presented in the literature, we report a qualitative comparison. Specifically, in Table 1, we report a comparison between the proposed mapping, standard joint/Cartesian mappings, and two recent advanced mappings. The considered mappings are the following: a standard direct joint mapping in accordance with Speeter (1992), a standard direct Cartesian mapping as presented by Rohling and Hollerbach, (1993), a virtual-object-based mapping Gioioso et al. (2013), and the DexPilot mapping (Handa et al., 2020). Specifically, the qualitative comparison was made with respect to the following features: 1) PH-to-TH preservation of the finger shapes, 2) PH-to-TH preservation of the distance between thumb and opposite fingertips, 3) applicability to anthropomorphic TH, 4) applicability to non-anthropomorphic TH, 5) evaluation on multiple hands (with different kinematic structures and number of fingers), and 6) evaluation metrics (see Table 1). Looking at the table, it can be observed how only the proposed mappings and the DexPilot mapping (Handa et al., 2020) have the capability to preserve both PH finger shapes and fingertip positions on the TH. In our approaches, different from the others, in Table 1, we also evaluated these capabilities on different robot hand kinematic structures, both anthropomorphic and non-anthropomorphic, by means of the simulation study presented in this section.
Two realizations of a joint–Cartesian hybrid mapping for robot hands, based on spatial in-hand information, have been presented in this article: the distance-based and workspace-based approaches. By performing several simulation experiments of PH-to-TH mapping, we evaluated the proposed approaches on four well-known robot hands: a 3-fingered hand inspired by Barrett hand, the 4-fingered anthropomorphic Allegro hand, the anthropomorphic DLR-Hit II hand, and the anthropomorphic UBHand. We evaluated both a free motion of the PH including thumb–fingers tip-to-tip contacts and the grasping of a sphere (requiring finger shape preservation) and a thin cylinder (requiring fingertip position preservation.) The results show that both approaches were capable of successfully performing the mapping of PH finger shapes and TH fingertip positions, on both anthropomorphic and non-anthropomorphic robot hands, and the differences between the distance-based and workspace-based approaches have been discussed. Future developments will be devoted to performing experiments with real robot hands, focusing the study on the investigation of specific telemanipulation performance using the proposed mapping, instead of a simulative evaluation of multiple different robot hands.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
RM, DC, GP, and CM planned the study. RM developed the concept, wrote the manuscript, and created the figures. DC performed the experiments and collected the experimental data. All authors reviewed the manuscript for important intellectual content and approved the submitted version.
This work was supported by the European Commission’s Horizon 2020 Framework Programme with the project REMODEL—Robotic tEchnologies for the Manipulation of cOmplex DeformablE Linear objects—under Grant 870133.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frobt.2022.878364/full#supplementary-material
Bergamasco, M., Frisoli, A., and Avizzano, C. A. (2007). “Exoskeletons as Man-Machine Interface Systems for Teleoperation and Interaction in Virtual Environments,” in Advances in Telerobotics (Springer), 61–76. doi:10.1007/978-3-540-71364-7_5
Bianchi, M., Salaris, P., and Bicchi, A. (2013). Synergy-based Hand Pose Sensing: Optimal Glove Design. Int. J. Robotics Res. 32, 407–424. doi:10.1177/0278364912474079
Butterfaß, J., Grebenstein, M., Liu, H., and Hirzinger, G. (2001). “Dlr-hand Ii: Next Generation of a Dextrous Robot Hand,” in Proceedings 2001 ICRA. IEEE International Conference on Robotics and Automation (Cat. No. 01CH37164), Seoul, Korea (South), May 21–26, 2001 (IEEE), 109.
Carfì, A., Patten, T., Kuang, Y., Hammoud, A., Alameh, M., Maiettini, E., et al. (2021). Hand-object Interaction: From Human Demonstrations to Robot Manipulation. Front. Robotics AI 316, 316. doi:10.3389/frobt.2021.714023
Cerulo, I., Ficuciello, F., Lippiello, V., and Siciliano, B. (2017). Teleoperation of the Schunk S5fh Under-actuated Anthropomorphic Hand Using Human Hand Motion Tracking. Robotics Aut. Syst. 89, 75–84. doi:10.1016/j.robot.2016.12.004
Chattaraj, R., Bepari, B., and Bhaumik, S. (2014). “Grasp Mapping for Dexterous Robot Hand: A Hybrid Approach,” in 2014 Seventh International Conference on Contemporary Computing (IC3), Noida, India, August 07–November 09, 2014 (IEEE), 242–247. doi:10.1109/ic3.2014.6897180
Chen, C., Hon, Y., and Schaback, R. (2005). Scientific Computing with Radial Basis Functions. Hattiesburg: Department of Mathematics, University of Southern Mississippi.
Ciocarlie, M., Goldfeder, C., and Allen, P. (2007). “Dimensionality Reduction for Hand-independent Dexterous Robotic Grasping,” in 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, October 29–November 02, 2007 (IEEE), 327.
Cobos, S., Ferre, M., Ángel Sánchez-Urán, M., Ortego, J., and Aracil, R. (2010). Human Hand Descriptions and Gesture Recognition for Object Manipulation. Comput. methods biomechanics Biomed. Eng. 13, 305–317. doi:10.1080/10255840903208171
Colasanto, L., Suárez, R., and Rosell, J. (2012). Hybrid Mapping for the Assistance of Teleoperated Grasping Tasks. IEEE Trans. Syst. Man, Cybern. Syst. 43, 390. doi:10.1109/TSMCA.2012.2195309
Dillmann, R., Rogalla, O., Ehrenmann, M., Zöliner, R., and Bordegoni, M. (2000). “Learning Robot Behaviour and Skills Based on Human Demonstration and Advice: the Machine Learning Paradigm,” in Robotics Research (Springer), 229–238. doi:10.1007/978-1-4471-0765-1_28
Ekvall, S., and Kragic, D. (2004). “Interactive Grasp Learning Based on Human Demonstration,” in IEEE International Conference on Robotics and Automation, 2004 Proceedings. ICRA’04. 2004, New Orleans, LA, April 26–May 01, 2004 (IEEE), 3519–3524. doi:10.1109/robot.2004.13087984
Ficuciello, F., Villani, A., Lisini Baldi, T., and Prattichizzo, D. (2021). A Human Gesture Mapping Method to Control a Multi-Functional Hand for Robot-Assisted Laparoscopic Surgery: The Musha Case. Front. Robot. AI 8, 741807. doi:10.3389/frobt.2021.741807
Fischer, M., van der Smagt, P., and Hirzinger, G. (1998). “Learning Techniques in a Dataglove Based Telemanipulation System for the Dlr Hand,” in Proceedings. 1998 IEEE International Conference on Robotics and Automation (Cat. No. 98CH36146), Leuven, Belgium, May 20–20, 1998 (IEEE), 1603.
Geng, T., Lee, M., and Hülse, M. (2011). Transferring Human Grasping Synergies to a Robot. Mechatronics 21, 272–284. doi:10.1016/j.mechatronics.2010.11.003
Gioioso, G., Salvietti, G., Malvezzi, M., and Prattichizzo, D. (2012). “An Object-Based Approach to Map Human Hand Synergies onto Robotic Hands with Dissimilar Kinematics,” in Robotics: Science and Systems VIII (Sydney, NSW: The MIT Press), 97–104. doi:10.15607/rss.2012.viii.013
Gioioso, G., Salvietti, G., Malvezzi, M., and Prattichizzo, D. (2013). Mapping Synergies from Human to Robotic Hands with Dissimilar Kinematics: an Approach in the Object Domain. IEEE Trans. Robot. 29, 825–837. doi:10.1109/tro.2013.2252251
Gomez-Donoso, F., Orts-Escolano, S., and Cazorla, M. (2019). Accurate and Efficient 3d Hand Pose Regression for Robot Hand Teleoperation Using a Monocular Rgb Camera. Expert Syst. Appl. 136, 327–337. doi:10.1016/j.eswa.2019.06.055
Gupta, L., and Suwei Ma, S. (2001). Gesture-based Interaction and Communication: Automated Classification of Hand Gesture Contours. IEEE Trans. Syst. Man. Cybern. C 31, 114–120. doi:10.1109/5326.923274
Handa, A., Van Wyk, K., Yang, W., Liang, J., Chao, Y.-W., Wan, Q., et al. (2020). “Dexpilot: Vision-Based Teleoperation of Dexterous Robotic Hand-Arm System,” in 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, May 31–August 31, 2020 (IEEE). doi:10.1109/icra40945.2020.9197124
Hu, H., Li, J., Xie, Z., Wang, B., Liu, H., and Hirzinger, G. (2005). “A Robot Arm/hand Teleoperation System with Telepresence and Shared Control,” in Proceedings, 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, CA, July 24–28, 2005 (IEEE), 1312.
Infantino, I., Chella, A., Dindo, H., and Macaluso, I. (2005). A Cognitive Architecture for Robotic Hand Posture Learning. IEEE Trans. Syst. Man. Cybern. C 35, 42–52. doi:10.1109/tsmcc.2004.840043
Kuo, L.-C., Chiu, H.-Y., Chang, C.-W., Hsu, H.-Y., and Sun, Y.-N. (2009). Functional Workspace for Precision Manipulation between Thumb and Fingers in Normal Hands. J. Electromyogr. Kinesiol. 19, 829–839. doi:10.1016/j.jelekin.2008.07.008
Li, S., Ma, X., Liang, H., Görner, M., Ruppel, P., Fang, B., et al. (2019). “Vision-based Teleoperation of Shadow Dexterous Hand Using End-To-End Deep Neural Network,” in 2019 International Conference on Robotics and Automation, Montreal, QC, May 20–24, 2019 (ICRA IEEE), 416–422. doi:10.1109/icra.2019.8794277
Malvezzi, M., Gioioso, G., Salvietti, G., and Prattichizzo, D. (2015). Syngrasp: A Matlab Toolbox for Underactuated and Compliant Hands. IEEE Robot. Autom. Mag. 22, 52–68. doi:10.1109/mra.2015.2408772
Meeker, C., Rasmussen, T., and Ciocarlie, M. (2018). Intuitive Hand Teleoperation by Novice Operators Using a Continuous Teleoperation Subspace,” in 2018 IEEE International Conference on Robotics and Automation (ICRA) (IEEE), Brisbane, QLD, May 21–25, 2018, doi:10.1109/icra.2018.8460506
Melchiorri, C., Palli, G., Berselli, G., and Vassura, G. (2013). Development of the Ub Hand Iv: Overview of Design Solutions and Enabling Technologies. IEEE Robot. Autom. Mag. 20, 72–81. doi:10.1109/mra.2012.2225471
Pedro, L. M., Caurin, G. A., Belini, V. L., Pechoneri, R. D., Gonzaga, A., Neto, I., et al. (2012). Hand Gesture Recognition for Robot Hand Teleoperation. ABCM Symposium Ser. Mechatronics 5, 1065.
Rohling, R. N., and Hollerbach, J. M. (1993). “Optimized Fingertip Mapping for Teleoperation of Dextrous Robot Hands,” in 1993 Proceedings IEEE International Conference on Robotics and Automation, Atlanta, GA, May 02–06, 1993 (IEEE), 769.
Salvietti, G., Malvezzi, M., Gioioso, G., and Prattichizzo, D. (2014). “On the Use of Homogeneous Transformations to Map Human Hand Movements onto Robotic Hands,” in 2014 IEEE International Conference on Robotics and Automation (ICRA) (IEEE), 5352–5357. doi:10.1109/icra.2014.6907646
Salvietti, G. (2018). Replicating Human Hand Synergies onto Robotic Hands: A Review on Software and Hardware Strategies. Front. Neurorobot. 12, 27. doi:10.3389/fnbot.2018.00027
Shahbazi, M., Atashzar, S. F., and Patel, R. V. (2018). A Systematic Review of Multilateral Teleoperation Systems. IEEE Trans. Haptics 11, 338–356. doi:10.1109/toh.2018.2818134
Siciliano, B., Sciavicco, L., Villani, L., and Oriolo, G. (2010). Robotics: Modelling, Planning and Control. London: Springer Science & Business Media.
Song, Y., Tianmiao, W., Jun, W., Fenglei, Y., and Qixian, Z. (1999). “Share Control in Intelligent Arm/hand Teleoperated System,” in Proceedings 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C), Detroit, MI, May 10–15, 1999 (IEEE), 2489.
Speeter, T. H. (1992). Transforming Human Hand Motion for Telemanipulation. Presence Teleoperators Virtual Environ. 1, 63–79. doi:10.1162/pres.1992.1.1.63
Sugihara, T. (2009). “Solvability-unconcerned Inverse Kinematics Based on Levenberg-Marquardt Method with Robust Damping,” in 2009 9th IEEE-RAS International Conference on Humanoid Robots (IEEE), Paris, France, December 07–10, 2009, 555.
Townsend, W. (2000). The Barretthand Grasper–Programmably Flexible Part Handling and Assembly. Industrial Robot Int. J. 27 (3 ), 181–188.
Wachs, J. P., Stern, H., and Edan, Y. (2005). Cluster Labeling and Parameter Estimation for the Automated Setup of a Hand-Gesture Recognition System. IEEE Trans. Syst. Man. Cybern. A 35, 932–944. doi:10.1109/tsmca.2005.851332
WonikRobotics (2015). Allegro Hand by Wonik Robotics. Available at: http://www.simlab.co.kr/Allegro-Hand.
Yoshimura, Y., and Ozawa, R. (2012). “A Supervisory Control System for a Multi-Fingered Robotic Hand Using Datagloves and a Haptic Device,” in 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, October 07–12, 2012 (IEEE), 5414. doi:10.1109/iros.2012.6385486
Keywords: multifingered hands, human-centered robotics, grasping, dexterous manipulation, telerobotics and teleoperation
Citation: Meattini R, Chiaravalli D, Palli G and Melchiorri C (2022) Simulative Evaluation of a Joint-Cartesian Hybrid Motion Mapping for Robot Hands Based on Spatial In-Hand Information. Front. Robot. AI 9:878364. doi: 10.3389/frobt.2022.878364
Received: 17 February 2022; Accepted: 06 May 2022;
Published: 22 June 2022.
Edited by:
Beatriz Leon, Shadow Robot, United KingdomCopyright © 2022 Meattini, Chiaravalli, Palli and Melchiorri. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Roberto Meattini, cm9iZXJ0by5tZWF0dGluaTJAdW5pYm8uaXQ=; Davide Chiaravalli, ZGF2aWRlLmNoaWFyYXZhbGxpMkB1bmliby5pdA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.