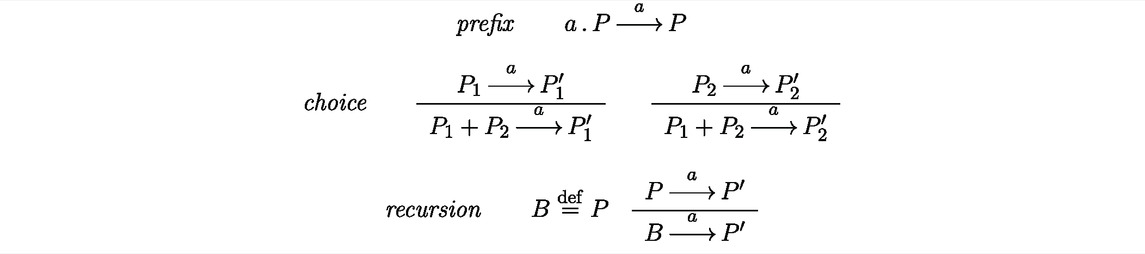On the Modeling and Verification of Collective and Cooperative Systems

The formal description and verification of networks of cooperative and interacting agents is made difficult by the interplay of several different behavioral patterns, models of communication, scalability issues. In this paper, we will explore the functionalities and the expressiveness of a general-purpose process algebraic framework for the specification and model checking based analysis of collective and cooperative systems. The proposed syntactic and semantic schemes are general enough to be adapted with small modifications to heterogeneous application domains, like, e.g., crowdsourcing systems, trustworthy networks, and distributed ledger technologies.

1 Introduction

Cooperation activities and collective behaviors are widespread phenomena in several environments, ranging from nature to human social relationships and artificial systems. Therefore, they have cross-cutting implications in different specific fields of knowledge, including, just to cite a few, biology (Crall et al., 2019; Glen et al., 2019; Romanov et al., 2022), sociology (Takano and Ichinose, 2018; Will et al., 2020), and robotics (Dai et al., 2016; Rausch et al., 2020; Mehmood et al., 2021). Although different levels of abstraction are involved, information sharing mechanisms form the base for the evolution of biological, social, and engineering systems exhibiting the behaviors specified above. In particular, the efficiency of these mechanisms determines not only the success of individuals but also the fitness of systems of communities of such individuals. This is even more critical whenever:

1. The systems need to be adaptive with respect to dynamically changing environments;

2. A multiplicity of different types of agents collaborate (or compete) to engage in community decision processes (or to achieve individual goals to survive and emerge);

3. Complex tasks are interleaved with frequent mutual interactions.

In this respect, one of the main aspects to pay attention to is given by the communication and cooperation models, with a specific emphasis on the information exchange policies, the allocation of tasks and of resources, the synchronization of activities converging to group goals. Moreover, it is worth distinguishing the nature and use of the information that may be subject to exchange, which can derive from the external environment, be processed by every agent in isolation, and/or represent community-based shares.

All these considerations play a role when devising techniques to model, verify, and develop collective and cooperative systems - see, e.g., De Nicola et al. (2020) and the references therein for a comprehensive overview. In this paper, we concentrate on the issues related to the formal modeling and verification of such systems. To this aim, we propose a general-purpose process algebraic framework that can be instantiated to the various and heterogeneous application domains surveyed above. The basic ingredients of this framework focus on the specification of the autonomous behavior of the agents, the handling of data collected from the environment and shared with the neighbours, the mode of interaction within communities of agents, the topology of the interacting communities, the dynamically changing external environment and system configuration. The flexibility of the approach is the main contribution provided by the framework, which makes it adequate to model and verify both natural and socially collective systems (including social networks as well as crowdsourcing systems), and artificial networks (including P2P and GRID systems, multi-agent systems, and sensor networks).

The kernel of the specification language is based on process algebra and relies only on a few, basic set of operators for the description of the behavioral pattern of agents in isolation. The syntax is left as simple as possible and abstracts away from the overwhelming details of standard parallel composition operators, thus making the process of composing even large networks of agents easy and scalable.

The semantics of the language encodes the mode of communication among agents, through rule schemes that support flexibility and adaptiveness with respect to the specific application domain of interest. Moreover, the framework includes the capability of grouping agents into dynamic communities, and to model local information stored by agents as well as global information shared within a given community of agents. Such an agent/community-oriented modeling framework is equipped with a temporal logic for the specification of properties of agents, communities, and networks. Thus, the flexibility of the modeling paradigm is inherited also by the property specification framework, enabling the definition of various property patterns, ranging from safety to performance.

The rest of the paper is organized as follows. In the next section, the basic syntax and semantics of the modeling framework are presented, by emphasizing the way in which customized semantics rules can be devised depending on the application domain. Section 3 defines the temporal logic for property specification. The applicability of this framework to various application domains is illustrated in Section 4 via some real-world references and examples. Finally, a discussion on related and future work is the topic of Section 5.

2 Modeling Agents and Networks

A key aspect for simplifying as much as possible the description of complex networks of agents is the clear separation between the description of each agent in isolation and the definition of the network of agents. This is even more crucial for formal paradigms like process algebra, which are typically based on a set of algebraic operators that join together the two levels of descriptions surveyed above, i.e., the agent level and the network level.

The separation of concerns between the definition of the system topology and of the behavioral pattern of the agents forming such a topology is a typical approach of architectural description languages–see, e.g., Aldini et al. (2010)—and is indeed motivated by usability and scalability issues. Therefore, we base the modeling framework on such a separation.

2.1 Modeling Behavioral Patterns and Agents

As a first step, we start with the presentation of a basic calculus–see, e.g., Fokkink, (2007)—for the description of the isolated behavior of sequential processes.

Let Act be the set of actions, ranged over by a, b, … , including also the special internal action τ. The set $\mathcal{L}$ of process terms of the basic calculus for sequential processes is generated through the following syntax:

$\begin{array}{c}P⩴\underline{0}\mid a.P\mid P+P\mid B\hfill \end{array}$

where we have the constant $\underline{0}$ for the inactive process, the classical algebraic operators for prefix and nondeterministic choice, and a constant based mechanism for expressing recursive processes, such that a set of constants defining equations of the form $B\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}P$ is assumed. As standard, we consider only guarded and closed process terms. The semantics of process terms is expressed in terms of labeled transition systems.

Definition 1. A labeled transition system (LTS) is a tuple (Q, q₀, L, R), where Q is a finite set of states (with q₀ the initial one), L is a finite set of labels, and R ⊆ Q × L × Q is a finitely-branching transition relation.

As a shorthand, (q, a, q′) ∈ R is denoted by $q\stackrel{a}{\to }{q}^{\prime }$. Then, the behavior of process term P is defined by the smallest LTS $(\mathcal{L},P,Act,R)$, where the transitions in R are obtained through the application of the operational semantics rules of Table 1. The prefix rule is at the base of the sequential behavior of processes, stating that a. P executes a and then behaves as P. The two choice rules express the nondeterministic choice between P₁ and P₂. The winning process proceeds with its execution, thus disabling once and for all the other one. The recursion rule establishes that the process term named B and defined as P, behaves as P itself; naming enables the definition of recursive behaviors.

TABLE 1

TABLE 1. Semantics rules of the basic calculus.

Example 1.

As a first running example, we consider a social network in which various agents contribute to the spreading of (possibly fake) news. A detailed version of this system is modeled and analyzed in Aldini, (2022), by using a formal framework that turns out to be an instance of that proposed in this work. Here, we start considering a simple, process term:

$F\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}nbr.\left(re-evaluate.F+forget.\underline{0}\right)$

which models the behavior of a fact checker in such a network. Action nbr denotes the gathering of shared news from the neighbourhood, action forget expresses that any shared news is forgotten once and for all, and action re-evaluate denotes that the process of news evaluation is repeated again.

As another running example, we will consider a trustworthy network of communities, where agents exchange services and the interactions among agents are enabled/disabled by trust/distrust relations. A detailed version of this system is modeled and analyzed in Aldini, (2018) through an alternative framework that, similarly as above, is generalized by the current proposal. Here, we start considering a simple, process term:

$T\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}snd\text{\_}\mathit{req}.\left(rec\text{\_}\mathit{acc}.T+rec\text{\_}\mathit{ref}.T\right)+leave\text{\_}\mathit{com}.\underline{0}$

describing the behavior of a trustor, which may ask for services from the unique provider operating in the community to which the trustor belongs. Action snd_req denotes a service request sent to such a provider, which in fact represents the trustee subject of trust evaluation by the trustor; the request can be either accepted (action rec_acc) or refused (action rec_ref). Alternatively, the trustor may decide to abandon the community (action leave_com).

In the following, an agent is any instance of a given process term P, which is referred to as the behavioral type (or pattern) of the agent. In other words, an agent represents an element exhibiting the behavior associated with a process term. Agents are associated with a unique identity, which in the following we denote with a natural number for the sake of simplicity. Moreover, each agent is equipped with a local data repository, used to store local parameters as well as data retrieved from sensors or received from the neighborhood. Such a repository is represented as a set of local atomic predicates. By assuming a standard first-order logic interpretation, predicates are of the form v = d, with v ∈ VNames a local variable and d a value of the corresponding domain.

Formally, an agent is described by a triple of elements ⟨id, P, V⟩, where:

• $id\in \mathbb{N}$ is the identity of the agent;

• process term $P\in \mathcal{L}$ is its behavioral type;

• function V: VNames↦D is the mapping from local variables to values in their corresponding domain D.¹

Given the triple ⟨id, P, V⟩, as a shorthand we sometimes use the classical dot notation id. P to denote the local behavior of agent id, id. a to denote an action a enabled by the local behavior P of agent id, and id. v to denote the value V(v) of the local variable v in the local data repository of agent id.

Example 2. A fact checker named id of behavioral type F is described by the triple ⟨id, F, V⟩. The local variables are: type, which expresses the level of susceptibility of the agent to accept shared news; accept, which is a Boolean modeling whether the news is accepted and in turn shared by the agent; threshold, which expresses the minimum number of neighbours that must share the same news in order to consider the news for acceptance.

A trustor named id of behavioral type T is described by the triple ⟨id, T, V⟩. The local variables are: α and β, reporting the number of accepted (respectively, refused) requests, and θ, which represents the trust threshold employed by the trustor for the trust-based evaluation of the trustee.

While it is easy to see that the agent local semantics is given by the semantics of its behavioral type, it is less obvious to determine the agent’s behavior in the context of the environment. Such a context affects also the updates applied by the agent to its local repository. Therefore, we need to define formally the interaction semantics for a network of communicating agents.

2.2 Modeling Networks of Interacting Agents

A network is a set of agents, which are grouped to form (possibly dynamic) communities. Basically, direct interactions among agents are possible only within the same community. However, each agent, in general, may belong to several different communities at the same time. Similarly as in the case of single agents, each community is associated with a global data repository, storing data that can be shared by all the community participants. Such a repository is modeled as a set of global atomic predicates of the form w = d, with w ∈ WNames² a global variable and d a value of the corresponding domain.

Formally, a network is a triple of elements $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$, where:

• $\mathcal{S}$ is the finite set ${\bigcup }_{i=1}^n⟨{id}_i,P_i,V_i⟩$ of n agents in the network, such that id_j ≠ id_k for every pair of indexes j, k;

• function $\mathcal{G}:CNames\to 2^{\mathbb{N}}$ maps every community (with CNames being the set of community names) to the set of agents identities forming it, thus representing the network topology;

• function $\mathcal{W}:CNames\to (WNames\mapsto D)$ maps every community to the related mapping from global variables to values in their corresponding domain.

The semantics of a network and, in particular, the way in which the constituting agents cooperate and evolve, depend on requirements of the specific scenario under consideration. Hence, (almost all) the rules we are going to introduce are actually schemes of rules including customizable elements. The first, fundamental modeling choice is related to the mode of execution, for which we distinguish two classical, alternative cases: asynchronous mode, where every agent may execute an autonomous action while all the others remain idle, and synchronous mode, where all the agents involved simultaneously execute one of their enabled actions.

The general semantic rule scheme for the asynchronous mode is as follows:

$(async)\frac{P\stackrel{a}{\to }{P}^{\prime }\wedge \mathtt{c}\mathtt{o}\mathtt{n}\mathtt{d}}{\langle \left\{\langle id,P,V\rangle \right\}\cup \mathcal{S},\mathcal{G},\mathcal{W}\rangle \stackrel{a}{\to }\langle \left\{\langle id,P^{\prime },V^{\prime }\rangle \right\}\cup \mathcal{S},\mathcal{G},{\mathcal{W}}^{\prime }\rangle }$

where the side condition $\mathtt{c}\mathtt{o}\mathtt{n}\mathtt{d}$ stands for a Boolean formula composed of logical predicates over any combination of identities, communities, local variables, and global variables taken from the current network triple $⟨\{⟨id,P,V⟩\}\cup \mathcal{S},\mathcal{G},\mathcal{W}⟩$, and stating whether the action a offered by the local behavior P of agent id is enabled in the network environment. Hence, the side condition is actually of the form $\mathtt{c}\mathtt{o}\mathtt{n}\mathtt{d}(a,id,V,\mathcal{S},\mathcal{G},\mathcal{W},V^{\prime },{\mathcal{W}}^{\prime })$. The additional terms V′ and ${\mathcal{W}}^{\prime }$ depend on V and $\mathcal{W}$, respectively, and represent their updated versions by virtue of the execution of the action a. More details about these terms and the definition of the side condition will be provided through examples. Notice that, for the sake of readability, in the rule scheme above and in the following ones, the side condition $\mathtt{c}\mathtt{o}\mathtt{n}\mathtt{d}$ is reported without making the list of arguments explicit.

Example 3. We present three typical formats for the atomic predicates that can be combined through logical connectives to define the side condition $\mathtt{c}\mathtt{o}\mathtt{n}\mathtt{d}$ in the rule scheme async:

1. id. v⋈k, with ⋈ any arithmetic comparison operator and k a scalar value belonging to the domain of the local variable v: such a condition is purely local as it does not depend on the context in which agent ⟨id, P, V⟩ operates;

2. $\exists G\in CNames:id\in \mathcal{G}(G)\wedge id.v\bowtie (\mathcal{W}(G))(w)$, which compares the local variable v of the agent to the global variable w of a community G to which the agent belongs $(id\in \mathcal{G}(G))$;

3. id. v⋈f(X), where f is a scalar function (e.g., min, sum, count) applied to a set X of local/global variables filtered in a certain way, and returning a value belonging to the domain of variable v.

Analogous patterns can be envisioned by defining conditions over id rather than over id. v.

Later on we will show some exemplifying conditions specifically adapted to the application domains of interest. As stated above, the rule scheme async expresses also potential side effects of the execution of the action a over the local variables of the agent id and/or over the global variables of the network. Formally, the terms V′ and ${\mathcal{W}}^{\prime }$ represent the updated versions of the terms V and $\mathcal{W}$, respectively. On one hand, they may be equal to V and $\mathcal{W}$, respectively, to express that no change occurs. On the other hand, they may be defined in terms of updates occurring in V and $\mathcal{W}$. To this aim, in the following examples we will use the standard notation s′ = s[x↦d] to express a mapping s′ equal to s in every point but x, where s′(x) = d.

Summarizing, the rule format states that if the agent of the network defined as ⟨id, P, V⟩ enables locally a move, and such a move is permitted by the environmental conditions, then the agent is allowed to evolve and change accordingly the variables under its control.

We point out that, as a special case, ad-hoc actions can be envisioned to model movements to or from communities, which is typical of dynamic scenarios–see, e.g., Aldini, (2022) for a possible semantic characterization. Just notice that such a kind of actions would affect the structure $\mathcal{G}$ of the tuple describing the network configuration. As an example, the general semantic rule scheme describing the action of leaving a group is as follows:

$(leave)\frac{P\stackrel{leave\text{\_}\mathit{com}}{\to }{P}^{\prime }\wedge \mathtt{c}\mathtt{o}\mathtt{n}\mathtt{d}}{\langle \left\{\langle id,P,V\rangle \right\}\cup \mathcal{S},\mathcal{G},\mathcal{W}\rangle \stackrel{a}{\to }\langle \left\{\langle id,P^{\prime },V^{\prime }\rangle \right\}\cup \mathcal{S},{\mathcal{G}}^{\prime },{\mathcal{W}}^{\prime }\rangle }$

where leave_com is the name of such an action, the side condition $\mathtt{c}\mathtt{o}\mathtt{n}\mathtt{d}$ specifies the enabling situation and the identification of the community G ∈ CNames that the agent id is leaving, V′ and ${\mathcal{W}}^{\prime }$ express possible updates to the local/global repositories V and $\mathcal{W}$ due to such a move, and ${\mathcal{G}}^{\prime }=\mathcal{G}(G)\backslash \{id\}$ represents the update of the involved community. We can reason analogously for a corresponding action join_com modeling the entry into a community G, in which case we have ${\mathcal{G}}^{\prime }=\mathcal{G}(G)\cup \{id\}$.

From the cooperation model standpoint, the rule scheme async enables forms of knowledge-based communication. Indeed, if the local repository modification (and/or the side condition $\mathtt{c}\mathtt{o}\mathtt{n}\mathtt{d}$) depends on some content deriving from the environment, then a data-driven communication from the environment to such an agent is actually modeled. Analogously, writing to the global repository, to which any other agent may have access, represents a form of community-based multicast communication. Sometimes, these forms of (asynchronous) communication are not enough as two (or more) agents have to synchronize over a certain event. To model such a kind of interaction, the following general semantic rule scheme is needed:

$(sync)\frac{P\stackrel{a}{\to }{P}^{\prime }Q\stackrel{b}{\to }{Q}^{\prime }\exists G\in CNames.{id}_1,{id}_2\in \mathcal{G}\left(G\right)\wedge \mathtt{c}\mathtt{o}\mathtt{n}\mathtt{d}}{\langle \left\{\langle {id}_1,P,V_1\rangle ,\langle {id}_2,Q,V_2\rangle \right\}\cup \mathcal{S},\mathcal{G},\mathcal{W}\rangle \stackrel{a\times b}{\to }\langle \left\{\langle {id}_1,P^{\prime },V_1^{\prime }\rangle ,\langle {id}_2,Q^{\prime },V_2^{\prime }\rangle \right\}\cup \mathcal{S},\mathcal{G},{\mathcal{W}}^{\prime }\rangle }$

where the action a × b expresses the simultaneous execution of the actions a and b, so that the two involved agents evolve synchronously. The form of the side conditions is as discussed above, with the additional constraint that the two agents involved in the (synchronous) communication must be members of the same community, which is formally expressed by the predicate $\exists G\in CNames.{id}_1,{id}_2\in \mathcal{G}(G)$. As a special case, it is possible to define an ad-hoc semantic rule scheme modeling a multicast synchronous communication from an agent of a community to the other agents of the same community–see, e.g., Aldini, (2018) for a possible characterization.

We now discuss the case of a purely synchronous mode of execution, which requires a slightly different approach relying on a two-steps semantics. In the first step, the local actions of the agents that are enabled by the environment according to the given side conditions are determined. In the second step, one action per agent is sampled nondeterministically and the system performs a move by simultaneously executing all the sampled actions. By assuming that the network of agents $\mathcal{S}$ includes the agent ⟨id, P, V⟩, the general semantic rule scheme implementing the first step is as follows:

$(global)\frac{P\stackrel{a}{\to }{P}^{\prime }\wedge \mathtt{c}\mathtt{o}\mathtt{n}\mathtt{d}}{\langle id,P,V{\rangle }_{\langle \mathcal{S},\mathcal{G},\mathcal{W}\rangle }\stackrel{a}{\to }\langle id,P^{\prime },V^{\prime }{\rangle }_{\langle \left(\mathcal{S}\backslash \left\{\langle id,P,V\rangle \right\}\right)\cup \left\{\langle id,P^{\prime },V^{\prime }\rangle \right\},\mathcal{G},{\mathcal{W}}^{\prime }\rangle }}$

Notice that in the conclusion of the rule scheme, the triple of elements describing the agent is decorated with the subscripted context expressing the environment with respect to which the side condition must be evaluated. More precisely, the rule scheme global expresses whether the network $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ enables the execution of the action a offered in isolation by the agent represented by ⟨id, P, V⟩. This is done through the verification of the side condition $\mathtt{c}\mathtt{o}\mathtt{n}\mathtt{d}$, parameterized by the elements of the triple $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ representing the environment of ⟨id, P, V⟩. The rule scheme expresses also what would be the effect of such an execution upon the agent and upon the network. Thus, the same considerations related to the asynchronous case apply as well, the unique difference being that the global semantics defines what actions can be potentially performed by the agents in the network. Since every agent is expected to enable at least one action to not block the synchronous evolution of the network, we assume also the following rule:

$\begin{array}{c}\hfill (idle)\frac{\langle id,P,V{\rangle }_{\langle \mathcal{S},\mathcal{G},\mathcal{W}\rangle }\to }{\langle id,P,V{\rangle }_{\langle \mathcal{S},\mathcal{G},\mathcal{W}\rangle }\stackrel{\tau }{\to }\langle id,P,V{\rangle }_{\langle \mathcal{S},\mathcal{G},\mathcal{W}\rangle }}\hfill \end{array}$

the effect of which is to allow the agent to stay idle without blocking the network.

Then, in the second step, the network semantics must express the simultaneous execution of one action per agent. By assuming $\mathcal{S}={\bigcup }_{i=1}^n⟨{id}_i,P_i,V_i⟩$, the semantic rule for the second step is as follows:

$\begin{array}{c}\hfill (network)\frac{{\bigwedge }_{i=1}^n\langle {id}_i,P_i,V_i{\rangle }_{\langle \mathcal{S},\mathcal{G},\mathcal{W}\rangle }\stackrel{a_i}{\to }\langle {id}_i,P_i^{\prime },V_i^{\prime }{\rangle }_{\langle {\mathcal{S}}_i,\mathcal{G},{\mathcal{W}}_i\rangle }}{\langle {\bigcup }_{i=1}^n\langle {id}_i,P_i,V_i\rangle ,\mathcal{G},\mathcal{W}\rangle \stackrel{\tau }{\to }\langle {\bigcup }_{i=1}^n\langle {id}_i,P_i^{\prime },V_i^{\prime }\rangle ,\mathcal{G},\prod {\mathcal{W}}_i\rangle }\hfill \end{array}$

In practice, in the premise of the rule each agent (indexed by i) offers a transition labeled with a_i that derives from the application of the rule scheme global or idle. Then, the conclusion establishes that all these moves are performed synchronously, as modeled by the τ action. ³ The proposed scheme is intentionally general. More sophisticated variants of the network semantic rule are however possible. For instance, only specific agents (e.g., of selected communities) could be engaged in the synchronization and perform a move. Alternatively, each a_i in the premise may be replaced by a unique action a, expressing that the involved agents must synchronize on the specific action. Such a condition may be too strong, as some agents may be not available to execute the action a, thus blocking all the others. However, similarly as discussed above, it is sufficient to use an ad-hoc version of the idle semantic rule that adds the action information as a negative premise on a and decorates the τ action with a subscripted a. Then, the network semantic rule may enable the synchronization of the involved agents that offer either a or τ_a. These variants emphasize the flexibility and the expressiveness of the approach, which make it adequate to deal with even very specific requirements of various application domains.

In any case, independently from the chosen mode of execution, the semantics of a system $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ will be given by the smallest LTS with initial state $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ and transitions deriving from the application of the SOS rules at hand. We observe that the proposed rule schemes express a general format that may potentially guide the definition of a library of several, alternative rules. Such rules can be customized to deal with a comprehensive set of behavioral models and application domains. Obviously, a tradeoff exists between such an expressive power and the efficiency issues that may arise when checking complex side conditions in order to build the underlying LTS.

Example 4.

Assume a social network $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ of agents adopting the synchronous mode of execution and including the agent ⟨id, F, V⟩ of the previous example. One specific instance of the global rule scheme, which is related to the execution of action a = nbr, may establish that cautious agents (identified by type 2) accept the news whenever the number of neighbours accepting the news is greater than the agent’s threshold. This rule can be formalized easily, first of all by setting the following side conditions:

$\left(id.type=2\right)\wedge \left(id.threshold<\mid \left\{{id}^{\prime }\mid {id}^{\prime }\ne id\wedge {id}^{\prime }.accept=true\wedge \exists G.{id}^{\prime },id\in \mathcal{G}\left(G\right)\right\}\mid \right)$

Notice that the neighbours of the agent id are those agents, different from id, belonging to communities of which id is a member. Then, as a side effect, we would also need to update V with the mapping accept = true, i.e., V′ = V[accept↦true].

As another use case, assume that $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ is a trustworthy network including the trustor ⟨id, T, V⟩ of the previous example. In such a scenario, let us assume the asynchronous mode of execution. In particular, assume by hypothesis that the action snd_req of the trustor must synchronize with a corresponding action rcv_req of the trustee in the same community of the trustor. Therefore, we need one specific instance of the sync rule scheme with a = snd_req and b = rcv_req. Then, if the interaction must be enabled only if the trustor trusts the trustee, we would need a side condition as follows:

${id}_1.\theta \le f\left({id}_1.\alpha ,{id}_1.\beta \right)$

where f is the specific trust function, like, e.g., the probability expectation of the Beta distribution, $\frac{\alpha }{\alpha +\beta }$(Jøsang and Ismail, 2002). Another instance of such a rule scheme is related to the synchronization involving action rec_acc, the consequence of which would be the update α = α + 1 in the local repository of the trustor. We can argue analogously in the case of action rec_ref and the related update involving β. Finally, one instance of the rule scheme async would be associated to the execution of action leave_com. If the agent is expected to leave the community whenever the trustee is not trusted anymore, then a side condition of such a rule would be the predicate idθ > f(id.α, id. β). Moreover, two side effects would be given by the corresponding update of the community $\mathcal{G}(G)$ to which the agent belongs and, possibly, the updates α = β = 0.

3 Model Checking Temporal Properties

The verification of the properties of networks of agents is conducted through model checking (Clarke et al., 1999). Therefore, we need to define a sufficiently expressive and intuitive logic to reason about the various levels of information that our framework can express. To this aim, in this section we present a temporal logic for the specification of properties of networks, which is an instance of action/state-based logics à la CTL (De Nicola and Vaandrager, 1990; ter Beek et al., 2008). The logic is rather standard and its main novelties are concerned with the treatment of the atomic formulas, in a way that recalls and favors the agent/community perspective of the modeling language.

The set of formulas $\mathcal{N}$ of the network logic we propose is generated through the following syntax:

$\begin{array}{c}\mathrm{\Phi }⩴true\mid id.a\mid z\bowtie r\mid \mathrm{\Phi }\wedge \mathrm{\Phi }\mid \neg \mathrm{\Phi }\mid A\pi \mid E\pi \hfill \\ \pi ⩴\mathrm{\Phi }U\mathrm{\Phi }\mid \mathrm{\Phi }{U}^{\le k}\mathrm{\Phi }\hfill \end{array}$

where:

• $r\in \mathbb{R}$, $k\in \mathbb{N}$, and ⋈ is any arithmetic comparison operator;

• id. a is the action-based atomic formula, and is satisfied by any state enabling the execution of action a ∈ Act by agent id;

• z⋈r is the state-based atomic formula, and is satisfied by any state in which the evaluation of variable z satisfies the condition ⋈r;

• Aπ and Eπ express the classical universally and existentially quantified path formulas;

• the two flavours of the until operator represent the unique type of path formulas; basically a path satisfies Φ₁ U Φ₂ if it begins with a finite sequence of states satisfying Φ₁ followed by a state satisfying Φ₂ (the k-bounded version adds a requirement on the length of such a finite sequence).

As mentioned above, the main peculiarities of the logic are given by the atomic formulas, while the composite formulas are standard. The atomic formulas are action-based (id.a), denoting the execution of an action a by the agent id, and state-based (z⋈r), denoting that the state variable z satisfies a certain condition parameterized by r.

As far as the semantics of the action-based formula id. a is concerned, we have to distinguish between the two modes of execution. In the asynchronous setting, id. a holds in $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$, denoted by ${⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩\vDash }_{\mathcal{N}}id.a$, if either agent $⟨id,P,V⟩\in \mathcal{S}$ can execute action a in $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ by virtue of a semantic rule of scheme async, or agent $⟨id,P,V⟩\in \mathcal{S}$ contributes, by offering action a, to the execution of a synchronized action a × b in $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ by virtue of a semantic rule of scheme sync. In the synchronous setting, id. a holds in $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ if agent $⟨id,P,V⟩\in \mathcal{S}$ contributes, by executing action a locally, to the execution of the global, synchronous action τ enabled in $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ by virtue of the semantic rule network.

As far as the semantics of the state-based formula z⋈r is concerned, we point out that, in our framework, any state of the LTS modeling a network is labeled with different types of information: the identities of the agents forming the system communities, their local repositories, and the global repositories. Hence, in order to allow for the definition of any kind of state-based requirement, we admit z to represent combinations of different types of values filtered in a certain way. To this aim, we distinguish the following three cases.

The first case refers to the state-based formulas over global variables. In this case, let z≔f{w | ϕ_g}, such that f is a scalar function, w ∈ WNames, and ϕ_g is a logic formula filtering communities. The intuition is that the values of the global variable w taken from those communities that satisfy ϕ_g are combined through f to obtain the result z. The logic formula ϕ_g obeys the following syntax:

${\varphi }_g⩴true\mid c\bowtie k\mid w\bowtie r\mid \neg {\varphi }_g\mid {\varphi }_g\wedge {\varphi }_g$

where $k\in \mathbb{N}$, w ∈ WNames, and $r\in \mathbb{R}$. A formula ϕ_g is a Boolean predicate used to select communities based on conditions over their identity (c⋈k, where c stands for community)⁴, conditions over the value of their global variables (w⋈r), and logical combinations of such atomic conditions. Semantically, the evaluation of z≔f{w | ϕ_g} in a network state $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ is given by:

$f\left\{|\left(\mathcal{W}\left(G\right)\right)\left(w\right)|G\in CNames\wedge {\left(\mathcal{W},G\right)\vDash }_g{\varphi }_g|\right\}(1)$

where f works on values of a multiset and the satisfiability relation ⊧_g for the atomic formulas generated by ϕ_g is defined as follows (the case of the composite formulas is standard):

$\begin{array}{cc}\left(\mathcal{W},G\right)\vDash true\hfill & holdsalways\hfill \\ \left(\mathcal{W},G\right)\vDash c\bowtie k\hfill & \mathrm{iff}G\bowtie k\hfill \\ \left(\mathcal{W},G\right)\vDash w\bowtie r\hfill & \mathrm{iff}\left(\mathcal{W}\left(G\right)\right)\left(w\right)\bowtie r\hfill \end{array}$

If the evaluation of z≔f{w | ϕ_g} satisfies the condition ⋈r, then we have that z⋈r holds in $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$, denoted by ${⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩\vDash }_{\mathcal{N}}z\bowtie r$. Summarizing, f combines the values of the global variable w extracted from those communities that satisfy the community predicate ϕ_g; then the resulting value is compared to r.

The second case refers to the state-based formulas over local variables. In this case, let z≔f{v | ϕ_l}, such that f is a scalar function, v ∈ VNames, and ϕ_l is a logic formula filtering agents. The intuition is that the values of the local variable v taken from those agents that satisfy ϕ_l are combined through f to obtain the result z. The logic formula ϕ_l obeys the following syntax:

${\varphi }_l⩴true\mid ide\bowtie k\mid ide\in G\mid v\bowtie r\mid v\bowtie z\mid \neg {\varphi }_l\mid {\varphi }_l\wedge {\varphi }_l$

where $k\in \mathbb{N}$, G ∈ CNames, v ∈ VNames, $r\in \mathbb{R}$, and z≔f{w | ϕ_g} is any combination of global variables as previously defined. A formula ϕ_l is a Boolean predicate used to select agents based on their identity (ide⋈k)⁵, community membership (ide ∈ G), evaluation of their local variables compared to constant values (v⋈r) or combinations of global variables (v⋈z), and logical combinations of such atomic conditions. Semantically, the evaluation of z≔f{v | ϕ_l} in a network state $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ is given by:

$f\left\{{|V\left(v\right)|⟨id,P,V⟩\in \mathcal{S}\wedge ⟨id,P,V⟩}_{⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩}{\vDash }_l{\varphi }_l|\right\}(2)$

The satisfiability relation ⊧_l for the atomic formulas generated by ϕ_l is defined as follows (the case of the composite formulas is standard):

$\begin{array}{cc}\langle id,P,V{\rangle }_{\langle \mathcal{S},\mathcal{G},\mathcal{W}\rangle }\vDash true\hfill & holdsalways\hfill \\ \langle id,P,V{\rangle }_{\langle \mathcal{S},\mathcal{G},\mathcal{W}\rangle }\vDash ide\bowtie k\hfill & \mathrm{iff}id\bowtie k\hfill \\ \langle id,P,V{\rangle }_{\langle \mathcal{S},\mathcal{G},\mathcal{W}\rangle }\vDash ide\in G\hfill & \mathrm{iff}id\in \mathcal{G}\left(G\right)\hfill \\ \langle id,P,V{\rangle }_{\langle \mathcal{S},\mathcal{G},\mathcal{W}\rangle }\vDash v\bowtie r\hfill & \mathrm{iff}V\left(v\right)\bowtie r\hfill \\ \langle id,P,V{\rangle }_{\langle \mathcal{S},\mathcal{G},\mathcal{W}\rangle }\vDash v\bowtie z\hfill & \mathrm{iff}V\left(v\right)\bowtie \left(1\right)\hfill \end{array}$

Notice that, for the semantics of v⋈z, with z≔f{w | ϕ_g}, the evaluation of v in $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ is compared to the evaluation of z in the same state, which is computed as stated by Eq. 1. Then, as in the first case, if the evaluation of z≔f{v | ϕ_l} in $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ satisfies the condition ⋈r, we have that z⋈r holds in $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$. Summarizing, f combines the values of the local variable v extracted from those agents that satisfy the local predicate ϕ_l; then the resulting value is compared to r.

The third case is similar to the previous one and refers to the state-based formulas over identities. In this case, let z≔f{ide | ϕ_l}. The intuition is that the values of the identities of those agents that satisfy ϕ_l are combined through f to obtain the result z. Similarly as in the case of Eq. 2, the evaluation of f{ide | ϕ_l} in a network state $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ is given as follows:

$f\left\{{id|⟨id,P,V⟩\in \mathcal{S}\wedge ⟨id,P,V⟩}_{⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩}{\vDash }_l{\varphi }_l\right\}(3)$

Notice that f applies to identities, which, by their uniqueness, do not form multisets.

Now the semantics for the atomic formulas of $\mathcal{N}$ is clarified. Hence, we are ready to define the satisfiability relation, denoted by ${\vDash }_{\mathcal{N}}$, for the non-atomic operators of the network logic. For this purpose, given a LTS (Q, q₀, L, R) we need to define the notion of a path. A path σ is a (possibly infinite) sequence of transitions of the form:

$\sigma ≔q_0\stackrel{a_0}{\to }{q}_1\dots q_{j-1}\stackrel{a_{j-1}}{\to }{q}_j\dots$

where $q_{j-1}\stackrel{a_{j-1}}{\to }{q}_j\in R$ for each j > 0. Every state q_j in the path is denoted by σ(j). Moreover, we denote with Path(q) the set of paths starting in state q ∈ Q. The notion of path is needed to formalize the quantified path operators. In particular, the semantics of formula Φ U Φ′ states that a path satisfies the formula if it reaches a state that satisfies Φ′, while satisfying Φ in each intermediate state; note that the path could be empty if its initial state satisfies Φ′. As far as the k-bounded version of U is concerned, an additional condition must be applied, which expresses that the length of the prefix of the path terminating in the state satisfying Φ′ must be $\le k$. The formal semantics of the composite operators of our network logic is presented in Table 2.

TABLE 2

TABLE 2. Satisfiability relation of the network logic.

Example 5. Let us consider the social network $⟨\mathcal{S},\mathcal{G},\mathcal{W}⟩$ of the previous example. The following state-based atomic formula Φ:

$count\left\{ide|\left(ide\in 1\right)\wedge \left(accept=true\right)\wedge \left(type=2\right)\right\}>3$

is true if and only if the number of agents of type 2 belonging to the community 1 of the social network and that are accepting (and sharing) the news, is greater than 3. Then, through formula E true U Φ we can evaluate whether a state is reachable that satisfies Φ.On the other hand, let us consider the case of the trustworthy network example. Given n the identity of the trustor of interest, the following composite formula Φ:

$n.leave\text{\_}\mathit{com}\wedge \left(\min \left\{\alpha |\left(ide=n\right)\right\}\ge k\right)$

checks whether the agent n is available to leave the community (since the action n. leave_com is enabled) even if the value of its local variable α is $\ge k$. Again, through formula E true U Φ we check whether such a state is reachable.

4 Use Cases and Quantitative Extensions

The objective of the proposed framework is to generalize various approaches to the same problem, which differ from each other for the requirements of the application domain. Hence, it would be useful to have a general-purpose approach, with high-level rules and policies, that can be refined and adapted to each specific case.

For example, an instance of the presented general-purpose modeling approach was proposed in previous work (Aldini, 2016, Aldini, 2018), in the specific domain of trustworthy networks, in which trust and reputation models are used to govern the interactions among trustors and trustees. Notice that the examples reported in the previous section illustrate a simplification of a trustor agent and associated behavioral rules. As in such examples, the mode of execution is asynchronous and the most interesting rules are those related to the semantic rule scheme sync, as it is used to describe trust-based interactions between agents. More precisely, the side conditions of the semantic rules of such a scheme describe both the trust-based communication policies (e.g., a certain interaction from trustor A to trustee B is enabled if and only if the trust of A towards B is higher/lower than the trust threshold applied by A) and the policies behind the computation of trust values (e.g., the trust from A to B is computed by combining several variables, including the dispositional trust of A, the previous experience with B, and the reputation of B). The local repositories include any local trust-based information needed to govern the policies above (e.g., the dispositional trust of A towards unknown trustees, the trust threshold applied by A, and the scores used to adjust trust after each satisfactory/unsatisfactory interaction). The community-based global repositories are used to collect the opinions shared by the agents within each community to form the reputation scores feeding the trust model.

Then, through model checking, properties expressed in our network logic are used to analyze, e.g., how the trust towards a trustee as perceived by a community is determined depending on the services delivered by such an agent. Variants of such properties allow also to investigate the impact of attacks performed, e.g., by injecting false recommendations. The analysis of real-world case studies, like the Trust-Incentive Service Management by Zhang et al. (2007), the Reputation-based Framework for Sensor Networks by Ganeriwal et al. (2008), and the Robust Reputation System by Buchegger and Boudec, (2004), was conducted automatically through the model checker NuSMV (Cimatti et al., 2002), thanks to a mapping from our specification language to the model of finite state machines used by the software tool.

The proposed modeling approach is general enough to allow for standard extensions to, e.g., probabilistic and stochastic models. For instance, in Aldini, (2022), it is extended with probabilities in order to model and analyze the spread of fake news in social networks. The network is divided into communities of agents, which in turn may exhibit different attitudes to share unchecked news or to conduct some fact checking. The examples reported in the previous section illustrate the non-probabilistic behavior of a type of agent susceptible to stimuli from the environment. The local repositories include the variables characterizing the agent’s attitute to believe, check, and share news.

The reference model underlying the approach of Aldini, (2022) is that of fully probabilistic LTSs (PTSs, for short) obeying the generative model of probabilities (Van Glabbeek et al., 1995). Analogously, our basic calculus is enriched with probabilistic information, similarly as done, e.g., in Baeten et al. (1992). For instance, in a. P action a is executed with probability 1, while the choice operator P + Q is replaced by the probabilistic choice operator P + ^pQ, with $p\in \left.\right]\mathrm{0,1}\left[\right.$, stating that an action of P (respectively, Q) is chosen with probability p (respectively, 1 − p). The mode of execution is synchronous: the global and network semantic rule schemes are extended accordingly to deal properly with such quantitative information in respect of the underlying model of probabilities.⁶.

The verification of PTSs relies on model checking of probabilistic temporal logic formulas (Kwiatkowska et al., 2011; Chen et al., 2013), which are described in a version of our logic that replaces the quantified path operators with the PCTL probabilistic (reachability) operator ${\mathcal{P}}_{\bowtie p}(\pi )$ (Hansson and Jonsson, 1994; Bianco and de Alfaro, 1995). The automated analysis was possible through a mapping to the PRISM model checker (Kwiatkowska et al., 2011). The goal of the analysis was to estimate the propagation of fake news over the whole network, depending on the topology of the system and the presence of reliable fact checkers.

In the following, we complete such an overview of potential applications, by considering an example based on another instance of our framework.

4.1 Use Case: Blockchain Efficiency

In order to show the flexibility of our approach, here we discuss a case study requiring to deal with stochastically timed events. In such a way, our basic process calculus becomes a stochastic process calculus, in which actions are enriched with rates of exponentially distributed random variables that represent the action duration. Thus, such models give rise to stochastic processes in the form of (action-labeled) Continuous Time Markov chains (Clark et al., 2007). Technically, the operators of our basic calculus are still the same, with the trick of adopting the additional syntax and semantics of the stochastic process algebra PEPA (Hillston, 1996; Tribastone et al., 2009). In particular, actions are pairs of the form (a, λ), where a ∈ Act and $\lambda \in {\mathbb{R}}^{+}$ is a positive rate representing the parameter of an exponential probability distribution governing the duration of the timed action. In this setting, the choice operator captures a notion of competition solved via the race policy: the action to execute is the one that samples the least duration. We refer to the citations above for all the details about the semantics of stochastic processes. In our use case, we assume the fully asynchronous mode of execution, so that in the following we have to specify the instances of the rule async tailored to the given use case.

The objective of the case study is to model a network of peers (P2P network) exchanging information about the blocks of a blockchain, which are generated by special agents called miners - see, e.g., Gamage et al. (2020) for a comprehensive overview of this distributed ledger technology. The blockchain model under consideration is permissionless and based on the proof-of-work mechanism (as in the case, e.g., of Bitcoin). Basically, any peer can mine a new block by solving a cryptographic puzzle called proof-of-work. To this aim, it is essential for the miner to learn information about the most recent block added to the blockchain and the data with which a new block is compiled, which depend on the specific application domain (e.g., virtual currency transactions in the case of Bitcoin). Here, we abstract away from the application domain and we concentrate on the blockchain management.

Peers acting as miners have the following behavioral pattern:

$\begin{array}{ccc}\hfill Miner\hfill & \hfill \stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\hfill & \hfill \left(obs\text{\_}\mathit{block},prop\text{\_}\mathit{rate}\right).Miner+\left(mine,mining\text{\_}\mathit{rate}\right).{Miner}^{\prime }\hfill \\ \hfill {Miner}^{\prime }\hfill & \hfill \stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\hfill & \hfill \left(obs\text{\_}\mathit{block},resume\text{\_}\mathit{rate}\right).Miner+\left(add\text{\_}\mathit{block},prop\text{\_}\mathit{rate}\right).Miner\hfill \end{array}$

A mining node can notice that a new block was mined and propagated through the miner’s community (action obs_block) and, at the same time, tries to solve the proof-of-work that would allow him to mine the next block (action mine) to be added to the blockchain and propagated to the network (action add_block). The other ordinary peers advertise and relay to their reference communities any new block added to the blockchain. Hence, they simply act as forwarder nodes:

$\begin{array}{ccc}\hfill Peer& \hfill \stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\hfill & \left(obs\text{\_}\mathit{block},prop\text{\_}\mathit{rate}\right).Peer+\left(prop\text{\_}\mathit{block},prop\text{\_}\mathit{rate}\right).Peer\hfill \end{array}$

A peer can notice that a new block was mined (action obs_block) and can propagate newly received blocks (action prop_block).

As far as the local repositories are concerned, every node shall maintain a local copy of the blockchain; for the sake of simplicity we limit each node to store the last block of the blockchain, which is abstractedly represented by a local counter block_id initially set to 0 for every node of the network. As far as the community-based global repositories are concerned, we use a global variable last_block_id storing the most recent block propagated in the community. With such additional information in view–used to define the local mapping V of each node and the global mappings $\mathcal{W}$ for the communities–we now define the several instances of the semantic rule scheme async. For each instance, we specify the action of interest, the enabling conditions, and the side effects:

1. case a = obs_block:

• $\exists G\in CNames:id\in \mathcal{G}(G)\wedge id.block\text{\_}\mathit{id}<(\mathcal{W}(G))(last\text{\_}\mathit{block}\text{\_}\mathit{id})$

• $V^{\prime }=V[block\text{\_}\mathit{id}\mapsto (\mathcal{W}(G))(last\text{\_}block\text{\_}id)]$

• ${\mathcal{W}}^{\prime }=\mathcal{W}$

2. case a = prop_block:

• $\exists G\in CNames:id\in \mathcal{G}(G)\wedge id.block\text{\_}\mathit{id}>(\mathcal{W}(G))(last\text{\_}block\text{\_}id)$

• V′ = V

• ${\mathcal{W}}^{\prime }(G)=\mathcal{W}(G)[last\text{\_}block\text{\_}id\mapsto V(block\text{\_}\mathit{id})]$

3. case a = add_block:

• $\exists G\in CNames:id\in \mathcal{G}(G)\wedge (id.block\text{\_}\mathit{id}+1)>(\mathcal{W}(G))(last\text{\_}block\text{\_}id)$

• V′ = V[block_id↦V(block_id) + 1]

• ${\mathcal{W}}^{\prime }(G)=\mathcal{W}(G)[last\text{\_}block\text{\_}id\mapsto V(block\text{\_}\mathit{id})+1]$

The first case, which refers to the observation of a new block by a node in one of its communities, requires the node to update its local copy of the blockchain. The second case, which refers to the propagation of a new block by a node to one of its communities, requires the node to update the global repository of that community. The third case, which refers to the upload of a new block to the blockchain, requires the miner to update its local copy and to propagate the block. Notice that, by the presence of several potential communities (see the existential quantifier over G ∈ CNames), such cases may enable several different outgoing transitions, one per involved community. Any other action, like action mine in our example, does not require side conditions and/or effects, i.e., the async rule scheme is applied with $\mathtt{c}\mathtt{o}\mathtt{n}\mathtt{d}≔true$ and no variation of the local/global repositories.

Essentially, the specification requires just to define the behavioral pattern of the node types (Miner and Peer) and the pre/post-conditions associated with the execution of the relevant actions. Analogously, we now show through a simple example how it is easy to model properties of interest.

Block propagation delays may potentially impair the correctness of the blockchain sharing process, because a miner could mine and propagate a block before learning of a newly mined block that has been added to the blockchain. Such a misalignment problem is known as blockchain fork. To solve the issue, the network abandons the blocks that are not in the longest chain. Hence, performance and correctness are tightly connected, as the speed at which peers learn of new blocks is related to the likelihood of forks in the blockchain. Recently, in Chandrasekaran et al. (2022) an empirical study of the information propagation delays between nodes in blockchain P2P networks was proposed that emphasizes how the likelihood of forks drastically diminished since 2013. In particular, block propagation delays are estimated in the top four blockchain-based applications, including Bitcoin.

Here, we propose a formal and automated verification of the analysis mentioned above, based on the use of the PRISM model checker⁷. For analysis purposes, we decided to instantiate the rates of the timed actions according to the Bitcoin related estimates of Chandrasekaran et al. (2022): the expected time to mine is about 10 min, while the mean (respectively, median) end-to-end propagation delay is about 4 s (respectively, about 0.4 s). Moreover, we modeled various configurations, represented by the topology shown in Figure 1, in which the P2P network radius - represented by the number of involved communities, depicted as clouds - is equal to 6. When a block is advertised in a community, all the members of the community react by experiencing the same delay, so that the overall end-to-end delay of the network depends on the network radius. Two miners are present in the network, while the other peers are either members of a single community or belonging to the intersection of many of them.

FIGURE 1

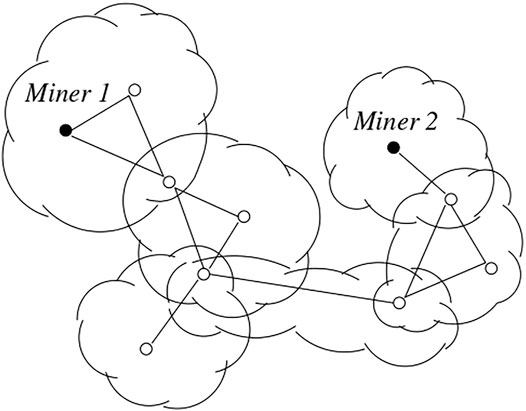
FIGURE 1. Example of P2P network with 6 communities; some representative peers are depicted, including 2 miners.

For the purpose of model checking, we consider a probabilistic reachability property of the form ${\mathcal{P}}_{\bowtie p}(\pi )$, where π is an until formula expressing the reachability of a state in which a peer mines a new block and uses it to extend an obsolete version of the blockchain, thus causing a fork. Formally, if we concentrate on the miner with id = 1, such a condition is a mixture of action and state based formulas defined as follows:

$\left(1.add\text{\_}\mathit{block}\right)\wedge \left(count\left\{ide|ide=1\wedge block\text{\_}\mathit{id}<\max \left\{last\text{\_}\mathit{block}\text{\_}\mathit{id}|true\right\}\right\}=1\right).$

The first conjunct holds when the first miner is enabled to update the blockchain. The second conjunct holds when such an update is obsolete as a more recent block is circulating in the network. We can reason analogously for the other miner, and then join the result of the two properties.

In Figure 2, we show the results of such an analysis by considering the four combinations deriving from two different configuration choices. The first dimension is given by the topology specification: in scenarios A and B we have exactly the representative nodes depicted in Figure 1, while in scenarios C and D only the miners and the peers in the intersecting areas between the communities are modeled. Then, in the first two scenarios we measure the fork likelihood in a period of time equal to 100 min, while in the other two scenarios we refer to a 1 day interval. The second dimension is given by the propagation delay between each pair of peers, which is chosen to correspond to the mean end-to-end delay measured in Chandrasekaran et al. (2022) for scenarios A and C, and to the median end-to-end delay measured in Chandrasekaran et al. (2022) for scenarios B and D. Moreover, each figure presents the results obtained in three different cases: in case (1) both miners experience the same mining delay (10 min), in case (2) the second miner is slower (15 min), while in the third case the second miner is faster (5 min).

FIGURE 2

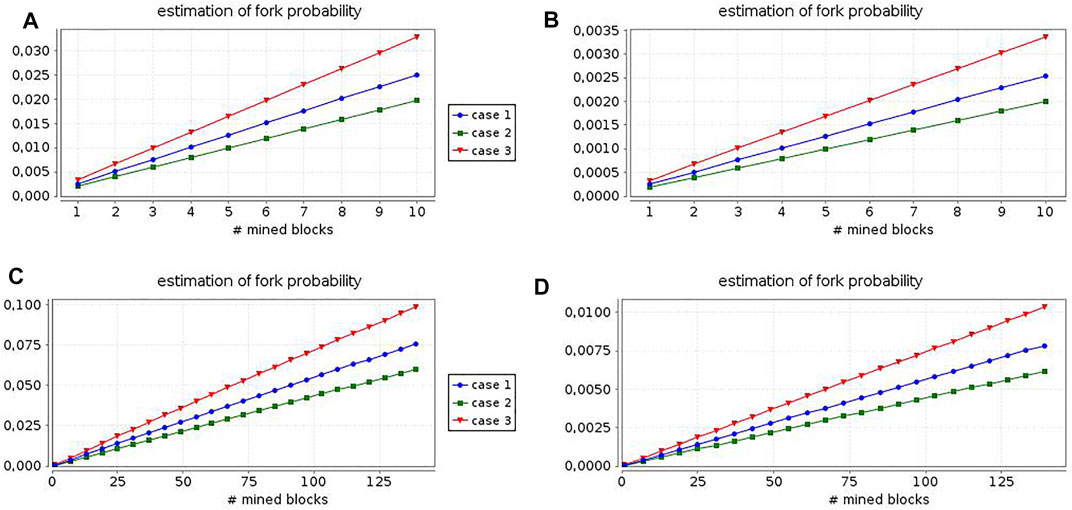
FIGURE 2. Relation between blockchain length and fork likelihood: analysis for 4 different scenarios.

In general, case (1) emphasizes that the fork probability is negligible, especially in cases (b) and (d). These results confirm the performance shown in Chandrasekaran et al. (2022). In detail, cases (2) and (3) reveal that the monitoring of the proof-of-work expected time is critical to maintain the fork likelihood at the desired level. Summarizing, already this simple case study illustrates that our framework is flexible and easy-to-use both from the modeling and the verification standpoints, also in the quantitative setting.

5 Related Work and Conclusions

The aim of the proposed approach is to provide a modeling and analysis framework that can be instantiated to specific application domains. The common feature of such domains is that they are characterized by collections of autonomous, dynamic, and interactive agents exhibiting a wide spectrum of cooperation patterns, as well as both reactive and proactive behaviors. The reported examples emphasize that the considered systems may express social relations of human agents in virtual environments, human–computer interactions, and also machine to machine communication. These include online services for smart and sustainable environments, and computer supported cooperative networks.

The verification of coordination and control strategies for cooperative multi-agent systems is of paramount importance even in the setting of inter-robot communications. To this aim, several formal approaches to the design of coordination for robotics emerged in the literature. For instance, the design method proposed in Dai et al. (2016) employs concurrent finite automata and is based on a top-down approach recalling the separation of concerns adopted in our framework at a higher abstraction level. In Gu et al. (2020), the specific problem of synthesising and verifying collision-free paths for autonomous multi-agent systems is dealt with formally through stochastic timed automata and statistical model checking. The verification is conducted automatically through the software tool UPPAAL. In Abd Alrahman and Piterman, (2021), reconfigurable multi-agent systems are modeled via finite automata and model checked using a variant of the Linear Temporal Logic (LTL). The authors emphasize that formal paradigms for modeling dynamic multi-agent systems cannot rely (only) on point-to-point communication. Instead, group-based communication is more appropriate, which is exactly one of the principles behind our framework. By following the same basic ideas, formal modeling paradigms and probabilistic model checking techniques are adopted for the analysis of autonomous agents by Sekizawa et al. (2015) and by Al-Nuaimi et al. (2018). Both approaches use the software tool PRISM for the automated analysis, similarly as done in the quantitative extensions of our framework. In general, all the formal approaches mentioned above rely directly on paradigms that are also at the base of our framework, on top of which we defined a high-level process algebraic specification language. The need for high-level languages in this setting is emphasized, e.g., by De Nicola et al. (2018); Abd Alrahman and Piterman (2021). For instance, we mention the languages ISPL (Lomuscio et al., 2009) and SCEL (De Nicola et al., 2015). The semantics of the former is based on concurrent labeled transition systems, which specifically adopt a form of synchronous communication. Interestingly, model checking is based on an epistemic logic encompassing a knowledge operator. On the other hand, the latter naturally supports knowledge-based communication for dynamic systems, in a way that recalls the method used in our framework to support uni/multi-cast communication via local/global repositories. The full semantics of SCEL is not trivial to export to a runtime environment; tool support is given, e.g., by the model checker SPIN and the MAUDE framework.

In the literature, it is worth mentioning that formal, process-algebraic approaches (Loreti and Hillston, 2016), semi-formal, architectural description approaches (Ozkaya and Kloukinas, 2013), and combinations of both (Basu et al., 2011; Hennicker et al., 2014; Bures et al., 2016) have been proposed to model and analyze dynamic reconfigurable architectures (De Nicola et al., 2020) and (self-)adaptive systems (Gabor et al., 2020). In particular, the language CARMA (Loreti and Hillston, 2016) is specifically defined to model collective adaptive systems and shares several features with our framework, such as the separation of concerns advocated in Section 2, support for local/global views, and a formal semantics in operational style. The process calculus of CARMA is stochastic and has a Markovian semantics, on which numerical analysis based on simulation can be conducted. Moreover, CARMA is equipped with an architectural-style specification language on top of the calculus. By virtue of its modeling capabilities, CARMA is an ideal candidate for representing an instance of the modeling framework proposed in this paper. The BIP framework of Basu et al. (2011) proposes synchronous priority-based communication and a rigorous semantics based on finite-state automata and Petri nets. Compositional verification methods are based on static analysis of local/global invariants. For instance, deadlock-freedom is checked for a robot controller. Interestingly, BIP can be part of a software design flow culminating in deployable code generation. The HELENA approach of Hennicker et al. (2014) formalises the modeling of ensembles (i.e., groups of dynamic collaborating entities) through a class of automata. A mapping towards Promela allows for model checking verification through the SPIN model checker (Klarl, 2015). The modeling of ensembles is also the goal of the DEECo approach of Bures et al. (2016), the operational semantics of which is defined in terms of labeled transition systems. Tool support is provided to enable the verification of reachability properties.

In many of the cases discussed above, classical temporal logics, like LTL and PCTL, support, via model checking, the formal verification of dynamic, multi-agent systems. Sometimes, ad-hoc extensions are used to model specific properties of cyber-physical systems, such as spatial-based conditions (Ciancia et al., 2018; Platzer et al., 2019). The property specification language proposed in our work encompasses the features of CTL-like logics, with a specific emphasis on the separation of concerns and local/global views that characterize the modeling style of our framework.

The key factor of the proposed approach that represents the novelty of this paper is given by the flexibility of a high-level framework combining an action-based formalism with data-driven communication mechanisms based on which different, customized semantics can be provided and supported by several automated tools. So, with respect to the state-of-the-art, by itself the proposed approach does not add new theoretical insights and results. Together with the ease of use in modeling both behavioral patterns and property specifications, the flexibility mentioned above makes our framework adequate to model collective adaptive systems and to support those programming frameworks (Beal et al., 2015; Berndtsson and Mellin, 2018; Casadei et al., 2018) used to develop them.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

As unique author of the manuscript, AA contributed to all its parts, including design of the study, case study modeling and verification, and writing of all sections.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹This can be generalized to consider a separate domain for each variable. By the way, in this paper we assume that D is a finite, numerical domain.

²For the sake of simplicity we a ssume that WNames and VNames are disjoint.

³We point out that $\prod {\mathcal{W}}_i$ is a shorthand expressing the combination of updates ${\mathcal{W}}_i$ applied to the global data repository $\mathcal{W}$ by virtue of the moves performed locally by the n agents. It is worth noticing that concurrent accesses to the same global variable may occur whenever no mutual exclusion mechanisms are used explicitly by the agents. It is known that this leads to nondeterministic behaviors. This is reflected correctly by the network semantic rule, which, in such a case, would enable multiple outgoing transitions, depending on the nondeterminism influencing the way in which $\mathcal{W}$ can be updated. However, if the system at hand implements mutual exclusion mechanisms, these would be modeled at the level of the agents’ behavior and of the semantics of the global rule scheme, so that no nondeterminism about the update of $\mathcal{W}$ would emerge by applying the rule network.

⁴For the sake of simplicity, here we are assuming that $CNames\subseteq \mathbb{N}$ and the condition c⋈k applies to the natural i representing the community identity, i.e., i⋈k. If using another domain for community names (e.g., strings) then the elements of the term ⋈k would change accordingly.

⁵We recall that, similarly as argued for the case of communities identities, we have that agents identities are expressed as naturals. While an obvious condition identifying a specific agent is of the form ide = n, with $n\in \mathbb{N}$, we could also envision the use of inequality operators if, e.g., the identities are ordered according to some criteria.

⁶Models combining nondeterminism and probabilities, like in Markov Decision Processes, can be adopted as well in our approach, by adapting accordingly the semantics.

⁷The PRISM source file resulting from our specification is available at: https://github.com/aldinia/prism-bc-specs.

References

Abd Alrahman, Y., and Piterman, N. (2021). Modelling and Verification of Reconfigurable Multi-Agent Systems. Auton. Agent Multi Agent Syst. 35, 47. doi:10.1007/s10458-021-09521-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Al-Nuaimi, M., Qu, H., and Veres, S. M. (2018). “A Stochastically Verifiable Decision Making Framework for Autonomous Ground Vehicles,” in 2018 IEEE International Conference on Intelligence and Safety for Robotics (ISR), 26–33. doi:10.1109/iisr.2018.8535911

CrossRef Full Text | Google Scholar

Aldini, A. (2016). “A Formal Framework for Modeling Trust and Reputation in Collective Adaptive Systems,” in Workshop on FORmal Methods for the Quantitative Evaluation of Collective Adaptive SysTems, FORECAST 2016 (Electronic Proceedings in Theoretical Computer Science), 19–30. doi:10.4204/eptcs.217.4

CrossRef Full Text | Google Scholar

Aldini, A., Bernardo, B., and Corradini, F. (2010). A Process Algebraic Approach to Software Architecture Design. London: Springer.

Google Scholar

Aldini, A. (2018). Design and Verification of Trusted Collective Adaptive Systems. Trans. Model. Comput. Simul. (TOMACS) 28, 1–27. doi:10.1145/3155337

CrossRef Full Text | Google Scholar

Aldini, A. (2022). “On the Modeling and Verification of the Spread of Fake News, Algebraically,” in Journal of Logic and Computation, Special Issue on Reasoning about Social Networks. doi:10.1093/logcom/exac015

CrossRef Full Text | Google Scholar

Baeten, J. C. M., Bergstra, J. A., and Smolka, S. A. (1992). “Axiomatizing Probabilistic Processes: ACP with Generative Probabilities,” in CONCUR’92. Editor W. Cleaveland (Springer), 472–485. doi:10.1007/bfb0084810

CrossRef Full Text | Google Scholar

Basu, A., Bensalem, B., Bozga, M., Combaz, J., Jaber, M., Nguyen, T.-H., et al. (2011). Rigorous Component-Based System Design Using the BIP Framework. IEEE Softw. 28, 41–48. doi:10.1109/MS.2011.27

CrossRef Full Text | Google Scholar

Beal, J., Pianini, D., and Viroli, M. (2015). Aggregate Programming for the Internet of Things. Computer 48, 22–30. doi:10.1109/MC.2015.261

CrossRef Full Text | Google Scholar

Berndtsson, M., and Mellin, J. (2018). “ECA Rules,” in Encyclopedia of Database Systems. Editors L. Liu,, and M. T. Özsu. Second Edition (Springer). doi:10.1007/978-1-4614-8265-9_504

CrossRef Full Text | Google Scholar

Bianco, A., and de Alfaro, L. (1995). “Model Checking of Probabilistic and Nondeterministic Systems,” in Foundations of Software Technology and Theoretical Computer Science. Editor P. S. Thiagarajan (Springer), 499–513. doi:10.1007/3-540-60692-0_70

CrossRef Full Text | Google Scholar

Buchegger, S., and Boudec, J.-Y. L. (2004). “A Robust Reputation System for Peer-To-Peer and Mobile Ad-Hoc Networks,” in 2nd Workshop on the Economics of Peer-to-Peer Systems (P2PEcon).

Google Scholar

Bures, T., Plasil, F., Kit, M., Tuma, P., and Hoch, N. (2016). Software Abstractions for Component Interaction in the Internet of Things. Computer 49, 50–59. doi:10.1109/mc.2016.377

CrossRef Full Text | Google Scholar

Casadei, R., Aldini, A., and Viroli, M. (2018). Towards Attack-Resistant Aggregate Computing Using Trust Mechanisms. Sci. Comput. Program. 167, 114–137. doi:10.1016/j.scico.2018.07.006

CrossRef Full Text | Google Scholar

Chandrasekaran, B., Makkes, M. X., and Fechner, J. (2022). “Calibrating the Performance and Security of Blockchains via Information Propagation Delays,” in 37th ACM/SIGAPP Symposium On Applied Computing - Track on Decentralized Applications with Blockchain, DLT and Crypto-Currencies (ACM).

CrossRef Full Text | Google Scholar

Chen, T., Forejt, V., Kwiatkowska, M., Parker, D., and Simaitis, A. (2013). “PRISM-games: a Model Checker for Stochastic Multi-Player Games,” in Procs. of the 19th Int. Conf. on Tools and Algorithms for the Construction and Analysis of Systems (TACAS’13) (Springer). doi:10.1007/978-3-642-36742-7_13

CrossRef Full Text | Google Scholar

Ciancia, V., Gilmore, S., Grilletti, G., Latella, D., Loreti, M., and Massink, M. (2018). Spatio-temporal Model Checking of Vehicular Movement in Public Transport Systems. Int. J. Softw. Tools Technol. Transf. 20, 289–311. doi:10.1007/s10009-018-0483-8

CrossRef Full Text | Google Scholar

Cimatti, A., Clarke, E., Giunchiglia, E., Giunchiglia, F., Pistore, M., Roveri, M., et al. (2002). “Nusmv 2: An Opensource Tool for Symbolic Model Checking,” in 14th Conf. on Computer Aided Verification (LNCS), 359–364. doi:10.1007/3-540-45657-0_29

CrossRef Full Text | Google Scholar

Clark, A., Gilmore, S., Hillston, J., and Tribastone, M. (2007). “Stochastic Process Algebras,” in Formal Methods for Performance Evaluation: 7th International School on Formal Methods for the Design of Computer, Communication, and Software Systems, SFM 2007 (Bertinoro, Italy: Springer), 132–179.

Google Scholar

Clarke, E. M., Grumberg, O., and Peled, D. A. (1999). Model Checking. Cambridge, MA: MIT Press.

Google Scholar

Crall, J. D., de Bivort, B. L., Dey, B., and Ford Versypt, A. N. (2019). Social Buffering of Pesticides in Bumblebees: Agent-Based Modeling of the Effects of Colony Size and Neonicotinoid Exposure on Behavior within Nests. Front. Ecol. Evol. 7, 51. doi:10.3389/fevo.2019.00051

CrossRef Full Text | Google Scholar

Dai, J., Benini, A., Lin, H., Antsaklis, P. J., Rutherford, M. J., and Valavanis, K. P. (2016). “Learning-based Formal Synthesis of Cooperative Multi-Agent Systems with an Application to Robotic Coordination,” in 2016 24th Mediterranean Conference on Control and Automation (MED), 1008–1013. doi:10.1109/med.2016.7536071

CrossRef Full Text | Google Scholar

De Nicola, R., Di Stefano, L., and Inverso, O. (2018). Toward Formal Models and Languages for Verifiable Multi-Robot Systems. Front. Robot. AI 5, 94. doi:10.3389/frobt.2018.00094

PubMed Abstract | CrossRef Full Text | Google Scholar

De Nicola, R., Jähnichen, S., and Wirsing, M. (2020). Rigorous Engineering of Collective Adaptive Systems: Special Section. Int. J. Softw. Tools Technol. Transf. 22, 389–397. doi:10.1007/s10009-020-00555-2

CrossRef Full Text | Google Scholar

De Nicola, R., Latella, D., Lafuente, A. L., Loreti, M., Margheri, A., Massink, M., et al. (2015). The SCEL Language: Design, Implementation, Verification. Cham: Springer, 3–71.

CrossRef Full Text | Google Scholar

Fokkink, W. (2007). Introduction to Process Algebra. Berlin, Heidelberg: Springer.

Google Scholar

Gabor, T., Sedlmeier, A., Phan, T., Ritz, F., Kiermeier, M., Belzner, L., et al. (2020). The Scenario Coevolution Paradigm: Adaptive Quality Assurance for Adaptive Systems. Int. J. Softw. Tools Technol. Transf. 22, 457–476. doi:10.1007/s10009-020-00560-5

CrossRef Full Text | Google Scholar

Gamage, H., Weerasinghe, H., and Dias, N. (2020). A Survey on Blockchain Technology Concepts, Applications, and Issues. SN Comput. Sci. 1, 114. doi:10.1007/s42979-020-00123-0

CrossRef Full Text | Google Scholar

Ganeriwal, S., Balzano, L. K., and Srivastava, M. B. (2008). Reputation-based Framework for High Integrity Sensor Networks. ACM Trans. Sen. Netw. 4, 1–37. doi:10.1145/1362542.1362546

CrossRef Full Text | Google Scholar

Glen, C. M., Kemp, M. L., and Voit, E. O. (2019). Agent-based Modeling of Morphogenetic Systems: Advantages and Challenges. PLoS Comput. Biol. 15, e1006577–31. doi:10.1371/journal.pcbi.1006577

PubMed Abstract | CrossRef Full Text | Google Scholar

Gu, R., Enoiu, E., Seceleanu, C., and Lundqvist, K. (2020). “Probabilistic Mission Planning and Analysis for Multi-Agent Systems,” in Leveraging Applications of Formal Methods, Verification and Validation: Verification Principles. Editors T. Margaria,, and B. Steffen (Springer), 350–367. doi:10.1007/978-3-030-61362-4_20

CrossRef Full Text | Google Scholar

Hansson, H., and Jonsson, B. (1994). A Logic for Reasoning about Time and Reliability. Form. Asp. Comput. 6, 512–535. doi:10.1007/bf01211866

CrossRef Full Text | Google Scholar

Hennicker, R., Klarl, A., Iida, S., Meseguer, J., and Ogata, K. (2014). “Foundations for Ensemble Modeling - the Helena Approach,” in Specification, Algebra, and Software: Essays Dedicated to Kokichi Futatsugi (Springer), 359–381. doi:10.1007/978-3-642-54624-2_18

CrossRef Full Text | Google Scholar

Hillston, J. (1996). A Compositional Approach to Performance Modelling. Cambridge: Cambridge University Press.

Google Scholar

Jøsang, A., and Ismail, R. (2002). “The Beta Reputation System,” in 15th Bled Conference on Electronic Commerce.

Google Scholar

Klarl, A. (2015). “From Helena Ensemble Specifications to Promela Verification Models,” in 22nd International Symposium on Model Checking Software (Springer), 39–45. doi:10.1007/978-3-319-23404-5_4

CrossRef Full Text | Google Scholar

Kwiatkowska, M., Norman, G., and Parker, D. (2011). “PRISM 4.0: Verification of Probabilistic Real-Time Systems,” in Proc. Of the 23rd Int. Conf. on Computer Aided Verification (CAV’11). Editors G. Gopalakrishnan,, and S. Qadeer (Springer). doi:10.1007/978-3-642-22110-1_47

CrossRef Full Text | Google Scholar

Lomuscio, A., Qu, H., and Raimondi, F. (2009). “Mcmas: A Model Checker for the Verification of Multi-Agent Systems,” in Computer Aided Verification. Editors A. Bouajjani,, and O. Maler (Springer), 682–688. doi:10.1007/978-3-642-02658-4_55

CrossRef Full Text | Google Scholar

Loreti, M., and Hillston, J. (2016). “Modelling and Analysis of Collective Adaptive Systems with CARMA and its Tools,” in Formal Methods for the Quantitative Evaluation of Collective Adaptive Systems: 16th International School on Formal Methods for the Design of Computer, Communication, and Software Systems, SFM 2016 (Springer), 83–119. doi:10.1007/978-3-319-34096-8_4

CrossRef Full Text | Google Scholar

Mehmood, U., Stoller, S. D., Grosu, R., Roy, S., Damare, A., and Smolka, S. A. (2021). “A Distributed Simplex Architecture for Multi-Agent Systems,” in Dependable Software Engineering. Theories, Tools, and Applications. Editors S. Qin, J. Woodcock, and W. Zhang (Springer), 239–257. doi:10.1007/978-3-030-91265-9_13

CrossRef Full Text | Google Scholar

De Nicola, R., Maggi, A., and Sifakis, J. (2020). The Dream Framework for Dynamic Reconfigurable Architecture Modelling: Theory and Applications. Int. J. Softw. Tools Technol. Transf. 22, 437–455.

CrossRef Full Text | Google Scholar

De Nicola, R., and Vaandrager, F. (1990). “Action versus State Based Logics for Transition Systems,” in Semantics of Systems of Concurrent Processes. Editor I. Guessarian (Springer), 407–419. doi:10.1007/3-540-53479-2_17

CrossRef Full Text | Google Scholar

Ozkaya, M., and Kloukinas, C. (2013). “Are We There yet? Analyzing Architecture Description Languages for Formal Analysis, Usability, and Realizability,” in 2013 39th Euromicro Conference on Software Engineering and Advanced Applications, 177–184. doi:10.1109/SEAA.2013.34

CrossRef Full Text | Google Scholar

Platzer, A., Parker, D., and Wolf, V. (2019). “The Logical Path to Autonomous Cyber-Physical Systems,” in Quantitative Evaluation of Systems (Springer), 25–33. doi:10.1007/978-3-030-30281-8_2

CrossRef Full Text | Google Scholar

Rausch, I., Simoens, P., and Khaluf, Y. (2020). Adaptive Foraging in Dynamic Environments Using Scale-free Interaction Networks. Front. Robot. AI 7, 86. doi:10.3389/frobt.2020.00086

PubMed Abstract | CrossRef Full Text | Google Scholar

Romanov, G. P., Smirnova, A. A., Zamyatin, V. I., Mukhin, A. M., Kazantsev, F. V., Pshennikova, V. G., et al. (2022). Agent-based Modeling of Autosomal Recessive Deafness 1a (Dfnb1a) Prevalence with Regard to Intensity of Selection Pressure in Isolated Human Population. Biol. (Basel) 11, 257. doi:10.3390/biology11020257

CrossRef Full Text | Google Scholar

Sekizawa, T., Otsuki, F., Ito, K., and Okano, K. (2015). “Behavior Verification of Autonomous Robot Vehicle in Consideration of Errors and Disturbances,” in 2015 IEEE 39th Annual Computer Software and Applications Conference, 550–555. doi:10.1109/compsac.2015.2683

CrossRef Full Text | Google Scholar

Takano, M., and Ichinose, G. (2018). Evolution of Human-like Social Grooming Strategies Regarding Richness and Group Size. Front. Ecol. Evol. 6, 8. doi:10.3389/fevo.2018.00008

CrossRef Full Text | Google Scholar

ter Beek, M. H., Fantechi, A., Gnesi, S., and Mazzanti, F. (2008). “An Action/state-Based Model-Checking Approach for the Analysis of Communication Protocols for Service-Oriented Applications,” in 12th Workshop on Formal Methods for Industrial Critical Systems (LNCS), 133–148. doi:10.1007/978-3-540-79707-4_11

CrossRef Full Text | Google Scholar

Tribastone, M., Duguid, A., and Gilmore, S. (2009). The PEPA Eclipse Plugin. ACE SIGMETRICS Perform. Eval. Rev. 36, 28–33. doi:10.1145/1530873.1530880

CrossRef Full Text | Google Scholar

Van Glabbeek, R. J., Smolka, S. A., and Steffen, B. (1995). Reactive, Generative, and Stratified Models of Probabilistic Processes. Inf. Comput. 121, 59–80. doi:10.1006/inco.1995.1123

CrossRef Full Text | Google Scholar

Will, M., Groeneveld, J., Frank, K., and Müller, B. (2020). Combining Social Network Analysis and Agent-Based Modelling to Explore Dynamics of Human Interaction: A Review. Socio-Environmental Syst. Model. 2, 16325. doi:10.18174/sesmo.2020a16325

CrossRef Full Text | Google Scholar

Zhang, Y., Lin, L., and Huai, J. (2007). Balancing Trust and Incentive in Peer-To-Peer Collaborative System. J. Netw. Secur. 5, 73–81.

Google Scholar