
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Robot. AI , 02 November 2022
Sec. Bio-Inspired Robotics
Volume 9 - 2022 | https://doi.org/10.3389/frobt.2022.1030515
This article is part of the Research Topic Soft Aerial Robots: Design, Control, and Applications of Morphologically Adaptive Flyers View all 6 articles
This work focuses on catching safely an aerial micro-robot in mid-air using another aerial robot that is equipped with a universal soft gripper. To avoid aerodynamic disturbances such as downwash, that would push the target robot away, we follow a horizontal grasping approach. To this end, the article introduces a gripper design based on soft actuators that can stay horizontally straight with a single fixture and maintain sufficiently compliance in order to bend when air pressure is applied. Further, we develop the Soft Aerial Gripper (SoAG), an open-source aerial robot equipped with the developed soft end-effector and that features an onboard pneumatic regulation system. Experimental results show that the developed low-cost soft gripper has fast opening and closing responses despite being powered by lightweight air pumps, responses that are comparable to those of a commercially available end-effector tested we test against. Static grasping tests study the soft gripper’s robustness in capturing aerial micro-robots under aerodynamic disturbances. We experimentally demonstrated the feasibility of using the SoAG robot to catch a hovering micro-robot with or without propeller guards. The feasibility of dynamic catching is also shown by capturing a moving aerial micro-robot with a velocity of 0.2 m/s. The free flight performance of the SoAG robot is studied against a conventional quadrotor and in different gripper and payload status.
Grasping with aerial robots attracts increasing interest from both research institutes and companies across industry sectors, owing to these robots’ unique capability to operate in 3-dimensional (3D) space while avoiding terrain constraints that often limit access to ground robots (and humans) Ruggiero et al. (2018). Grasping can be defined as a sequence of three key consecutive steps: 1) approaching a target, 2) establishing contact with the object, and 3) securing and holding the object firmly Meng et al. (2021). Grasping is also a crucial ability for aerial robots to interact with the environment and facilitate several key applications such as inspection Yüksel et al. (2015), search and rescue Gómez-de Gabriel et al. (2018), transportation Fiaz et al. (2018), and construction Augugliaro et al. (2014).
The most common way to achieve aerial grasping is to directly mount robotic manipulators onto appropriate aerial robots. Notable examples include multirotor aerial vehicles with mostly servo-driven robotic arms Korpela et al. (2013); Jimenez-Cano et al. (2013); Ruggiero et al. (2015); Garimella and Kobilarov (2015); Baizid et al. (2015); Kim et al. (2016); Zhang et al. (2018); Staub et al. (2018). To overcome payload limitations, unmanned helicopters have been utilized to carry industry manipulators Pounds et al. (2011a); Kondak et al. (2013); Bejar et al. (2019). Aerial robots have also been equipped with dual robotic arms for precise manipulation Korpela et al. (2014); Suarez et al. (2017) as well as parallel manipulators Danko and Oh (2013); Fumagalli et al. (2014); Danko et al. (2015). Multi-link robotic arms can provide precise position control of the end-effector with improved reachability. However, mounting robotic arms on aerial robots requires larger scales thereby leading increasing costs and compromising mobility in confined environments. Such aerial manipulators often employ ordinary multi-finger end-effectors; studying the ability to grasp irregularly-shaped micro-objects has received less attention. A fixed-wing aerial vehicle is equipped with a passive claw for high-speed grasping Stewart et al. (2022). However, the robot is still constrained to grasping regular objects such as poles. In a different line of work, multi-robot systems can be leveraged to grasp and move objects Ritz et al. (2012); Zhao et al. (2017); Gabrich et al. (2018); Shi et al. (2020). However, cooperative grasping increases the computational effort on control and planning, and requires significant system integration efforts to be practical. The aerial grippers are often constrained to vertical grasping, which limits potential applications.
Distinctly from rigid aerial robot grasping, soft (compliant) grasping has been receiving increased attention due to its advantages of being robust and safe to irregularly-shaped objects Shintake et al. (2018). Several micro aerial vehicles (MAVs) have been equipped with soft (compliant) end-effectors, including but not limited to impactive and ingressive Mellinger et al. (2011), compliant multi-fingered Ghadiok et al. (2011); Pounds et al. (2011b); Kruse and Bradley (2018); McLaren et al. (2019); Zhang et al. (2019); Appius et al. (2022); Chen G. et al. (2022), closed-structure compliant Lee et al. (2021), origami-inspired Kim et al. (2018), wasp-pedal-carrying Zhao et al. (2018), soft cable-driven Ramon-Soria et al. (2019); Fishman et al. (2021), and soft pneumatic Mishra et al. (2018) grippers. However, these aerial grippers have been limited to vertical grasps directly underneath the robot, which, besides limiting applicability, is also impacted by aerodynamic disturbances.
In recent years, there is a growing interest in developing non-military tools to capture aerial robots in mid-air with applications to recover malfunctioning aerial robots and intercept and contain unidentified flying targets Park et al. (2021). Physically catching flying robots in mid-air is challenging due to their irregular shapes and self-propulsion. Notable attempts include a soft gripper fixed on a ground manipulator to catch flying micro-robots Fedoseev et al. (2021). However, the solution is limited by vertical grasping, as well as the workspace of the ground manipulator. The most common way to catch flying robots in mid-air is using nets, such as net bullets Meng et al. (2018); DroneCatcher (2022), top nets Rodriguez-Ramos et al. (2021); DroGone (2022), side nets Vidyadhara et al. (2022), and nets carried by cooperative vehicles Klausen et al. (2018); Rothe et al. (2019). Despite the proved effectiveness, these solutions primarily focus on catching aerial robots with diagonal sizes (including propellers) over 500 mm (e.g., DJI1 Mavic Pro and Phantom 4). However, little attention is paid to capturing flying micro-robots such as Crazyflie2 2.1 with diagonal sizes around 100 mm, which are relatively more challenging to detect and intercept Park et al. (2021). In addition, capturing by nets involve relative motion to targets that will inevitably create impact and possibly damage target robots. Flying robots with nets are usually unable to grasp, move and release objects compared to ones with conventional grippers. A recent work studies catching aerial micro-robots with a passive gripper Chen T. G. et al. (2022). However, the capture relies on contact with the propeller guard of the target, which is usually missing with commercially available aerial vehicles. After capturing, the suspending target will compromise the free fly performance of the catcher Kim et al. (2016). Similarly, the method requires relative velocities to the target, and creates impact.
In this work, we aim to address the challenge of catching aerial micro-robots safely in mid-air using flying robots with a universal soft gripper. To this end, we introduce a soft actuator and pneumatic four-fingered end-effector designs to enable horizontal grasps. As shown in Figure 1, we develop a quadrotor MAV equipped with a soft end-effector named Soft Aerial Gripper (SoAG). The hardware design of SoAG is introduced, as well as the dynamic modeling and control. Piecewise-polynomial-based optimal planning is studied to facilitate catching of flying targets. Static grasping results are compared to a commercially-available gripper to validate the efficacy of grasping irregular objects. Experimental trials also demonstrate the feasibility of using the SoAG robot to catch a target aerial micro-robot while both agents are flying without relative velocities to mimimize impact. We study the robustness of the soft gripper with catching tests of flying targets with or without propeller guards. Furthermore, we study the feasibility of dynamic catching by capturing a moving aerial micro-robot in the mid-air. Lastly, free flight performance of the SoAG robot is studied and compared to a conventional quadrotor to validate the design and evaluate the effect of the gripper on flight mechanics, control, and energetics. The project is open-sourced to facilitate rapid replication of the developed robot.

FIGURE 1. Bio-inspiration and prototype of the project. (A) An eagle is horizontally catching a small bird in mid-air. (B) To enable horizontal grasping, we develop an open-source micro-aerial vehicle (MAV) equipped with a soft end-effector and onboard pneumatic regulation named Soft Aerial Gripper (SoAG).
This project exploits soft robotic grippers to catch flying micro-robots safely. However, horizontal grasps are challenging for most soft grippers because they cannot stay horizontally straight with a single fixture. As mentioned earlier, horizontal captures are critical to avoid aerodynamic disturbance (downwash), which can make targets crash. Thus, this paper revises the Pneumatic Network (PneuNet) design Polygerinos et al. (2013); Mosadegh et al. (2014) to enable horizontal grasps.
Two improvements to the PneuNet design are made to achieve horizontal grasps. To minimize deformation by gravity and keep the softness for safe interactions, appropriate stiffness of the actuators is achieved by combining two materials with different shore hardness. As shown in Figure 2A, the main body (white) is made of Smooth-On Dragon Skin 20 silicone with shore hardness of 20A (A here meaning the type A indenter and scale) to maintain the softness for adaptive grasps. In the PneuNet design, there is an inextensible layer to assist bending, which is made of thin fabric or paper Polygerinos et al. (2013). However, the thin inextensible layer fails to increase the stiffness sufficiently for horizontal grasps. In this work, we replace the thin inextensible layer with a solid flexible cuboid base (part shown in red in Figure 2A), which is 3D-printed using the Formlabs flexible 80A resin. The base has a shore hardness of 80A. Despite increased hardness, the actuators still maintain enough compliance to bend relatively fast under pneumatic inflation. Moreover, the actuator’s width is reduced and base thickness is increased to accelerate actuation response and support the horizontal-grasping potential. Details of the revised dimensions can be found in Figure 2A, where parts in yellow denote the implanted air chambers.
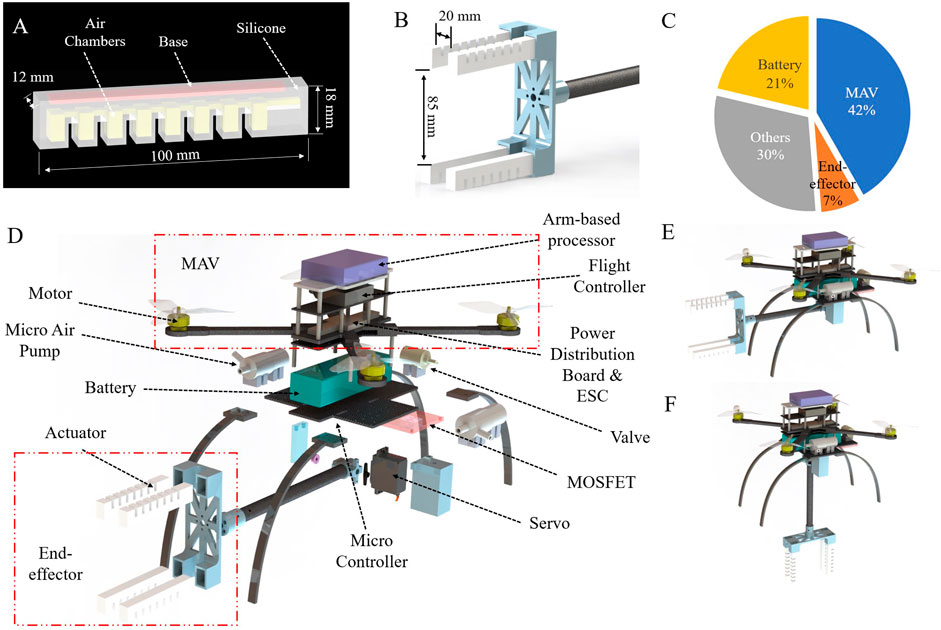
FIGURE 2. Details of the system design. (A) Actuator design. (B) End-effector design. (C) Weight distribution of the SoAG robot. (D) An exploded view of the SoAG robot. (E,F) The robot with the arm up and down.
The fabrication of actuators follows the conventional method of casting with molds. The custom molds are 3D-printed in polylactic acid (PLA) while bases are directly 3D-printed with flexible 80A resin as mentioned earlier. With molds and bases ready, we mix the elastomer and process it using a degassing chamber. After cured, the two casted parts of the actuator (chamber and base layers) are bonded with an adhesive (Sil-Poxy). Note that the flexible 80A base should be surrounded by silicone in the manufacturing of the base layer. We open-source all mold design files to enable rapid replication of the actuator.
Similar to conventional grippers, our four-fingered soft end-effector consists of two opposing claws. When inflated, the tips come together on opposite sides (top and bottom) of flying micro-robots to grasp them. Each claw of the gripper has two actuators in parallel with a gap of 20 mm while the two opposite sides have a distance of 85 mm as shown in Figure 2B. All actuators are fixed by a 3D-printed adapter connecting to the aerial platform using a carbon fiber rod. The end-effector weighs 0.115 kg, accounting for only 7% of the total weight (see Figure 2C). Similarly, we open-source all files to fabricate the end-effector. The total cost of fabrication is about $40. We evaluated the end-effector performance by comparing it to a commercially available gripper, as detailed in Section 3.
We mount the end-effector on a custom quadcopter MAV to develop the SoAG robot. The robot has a total weight of 1.64 kg, which consists of four types of components: MAV, battery, end-effector, and other parts (see Figure 2C). A hardware overview of SoAG is shown in Figure 2D. The custom-made MAV features frames that are fabricated with lightweight carbon fiber sheets (tensile strength 120, 000–175, 000 psi) using a Stepcraft D.600 CNC router with enclosure and milling bath. The MAV measures 380 mm from the motor tip to tip. It integrates a flight controller (Pixhawk 4 Mini) running the corresponding open-source autopilot system. The vehicle also includes an ARM-based multi-core processor (Odroid XU4) for high-level computing tasks.
In addition to the MAV and end-effector (highlighted in red boxes in Figure 2D), the robot also includes pneumatic regulating components necessary to power the soft gripper. The onboard pneumatic regulation consists of two micro air pumps, one solenoid valve, and one MOSFET module. The air pumps have a flow rate of 2.0 L/min with a low weight of about 0.07 kg. When the robot tries to catch a target, the two pumps will inflate four actuators to bend (one pump per two actuators) and close the gripper. All actuators are also connected to the normally-closed solenoid valve, of which the other side is directly open to the atmosphere air. When pumps are off and the valve is on, the pressure values inside the actuators will decrease to the atmospheric one so that the gripper will open. The MOSFET module reads PWM signals and regulates the DC voltages of the pumps and valves. SoAG has one revolute joint to move the position of the end-effector to the main robot (see Figures 2E,F). A MG 996R servo motor controls the angle of the revolute joint between the vehicle and the arm. We use a micro-controller (Arduino Nano) to control both the pneumatic actuation and the arm angle.
We considered NWU (X North, Y West, Z Up) as the world frame, denoted with
where c denotes the cosine, s stands for sine, and Euler angles ϕ, θ, and ψ denote rotating angles along the axis x, y and z, respectively.
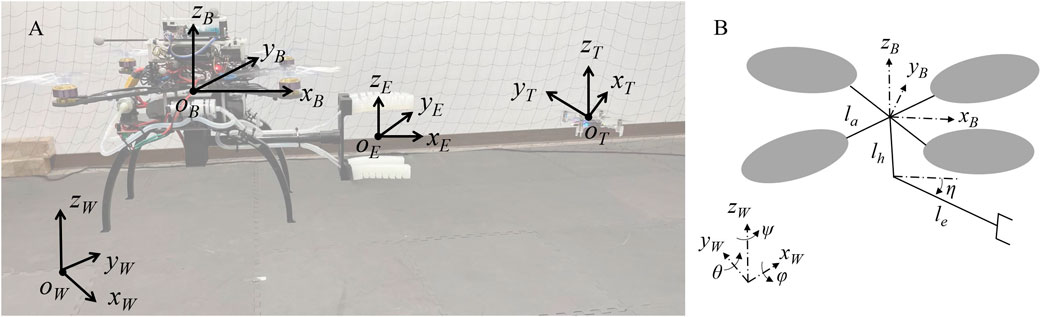
FIGURE 3. Frames and modeling description. (A) Four frames are defined in this work: world, robot, end-effector and target frames. (B) Dynamic model of the system.
The generalized coordinate variables comprise the position of
As shown in Figure 3B, the revolute joint lies along the axis
Using the Euler-Lagrange formulation, we can derive the equations of motion as
where
where
with
where
By combining the equations above, we can rewrite the dynamic modeling of the entire system as
where
As detailed in Figure 4, the controller reads desired states of the end-effector
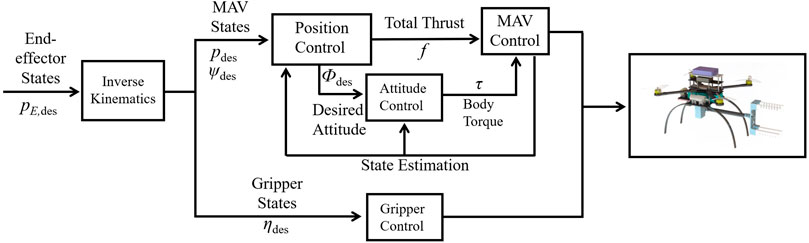
FIGURE 4. A cascaded tracking controller is used in this work to regulate both the vehicle and gripper.
To eliminate the assumption of small angles near hovering states, we adopt a nonlinear cascaded tracking control method based on geometric constraints as in Lee et al. (2010); Mellinger and Kumar (2011); Thomas et al. (2016). As shown in Figure 4, the cascaded control method includes position and attitude controllers. The position controller reads the desired position pdes, velocity
where
Since the aerial vehicle can only generate thrust along the
where the operator × denotes the cross product. Note that a singularity exists when calculating
We adopt a nonlinear attitude control method as in Brescianini et al. (2013). The attitude controller reads the estimated actual and desired attitude, and outputs the desired angular velocity to the low-level PID bodyrate controller. The nonlinear controller is asymptotically stable, and readers are referred to the report Brescianini et al. (2013) for a thorough analysis. The low-level bodyrate controller is implemented in the open-source PX4 firmware Meier et al. (2015).
Aerial micro-robots are vulnerable to aerodynamic disturbances (e.g., downwash and ground effect) generated by other aerial vehicles Preiss et al. (2017) or rigid surfaces Karydis et al. (2015); Karydis and Hsieh (2016). Thus, planning for the catching task seeks to generate smooth trajectories that satisfy catching constraints, without producing downwash effect that may destabilize the target aerial robot and while remaining out of ground effect regions that depend on the robot size, propeller length and forward velocity Kan et al. (2019). Trajectory generation for aerial robots has been extensively studied (e.g., Hehn and D’Andrea, (2011); Kreciglowa et al. (2017); Mohta et al. (2018)). The planner generates smooth desired trajectories for the end-effector based on piecewise polynomials as in Mellinger and Kumar (2011); Richter et al. (2016). Assuming the path has m segments (and therefore we have m + 1 key frames to apply constraints t ∈ {t0, t1, … , tm}), we use nth order polynomial functions to describe the segment i on axis μ ∈ {x, y, z}, considering the desired yaw always set to zero (ψdes = 0). That is,
where
Following the minimum-snap formulation Mellinger and Kumar (2011), we minimize the snap along the trajectory, so k = 4 and n = 8. Then, the trajectory generation can be reformulated as a quadratic program
where
The constraint Ac ≤ b in Eq. 14 is described next. As shown in Figure 5, the target aerial robot is assumed to follow a constant velocity
In the close segment (t ∈ [t1, t2]), the end-effector moves from
and t2 = t1 + τ1, t3 = t2 + τ2, where α,
Results are categorized based on three types of tests: grasping, catching, and flyability. In the grasping test, the soft gripper is studied against a commercially available gripper, mounted on a Kinova Gen3-lite robot for response and static catching tests. In the catching experiment, the target aerial robots hovers at a fixed position with tracking errors. After taking off manually, the developed SoAG robot generates and tracks a trajectory automatically to catch the flying target as described in Section 2.4. Finally, we study the free flight tracking performance of the robot with different arm and gripper states compared to a conventional quadrotor.
All experiments rely on motion capture camera systems (VICON and OptiTrack) for odometry feedback. The feedback is only used to estimate the states of the robots, which can also be achieved by cameras or laser sensors in outdoor environments. The Crazyflie 2.1 with MoCap deck is used as the target aerial robot, with a total weight of 0.035 kg. The developed SoAG robot measures 0.38 m from the motor tip to tip, with a total weight of 1.64 kg. A 3-cell 5200 mAh LiPo battery is used to power the entire system. Key parameters for different tasks can be found in Table 1.
In this experiment, both grippers are placed vertically at the same 3D position, as shown in Figures 6A,B. The position of both claw tips is measured using the OptiTrack motion capture feedback in 100 Hz. We use gaps in millimeter to denote the position difference along the
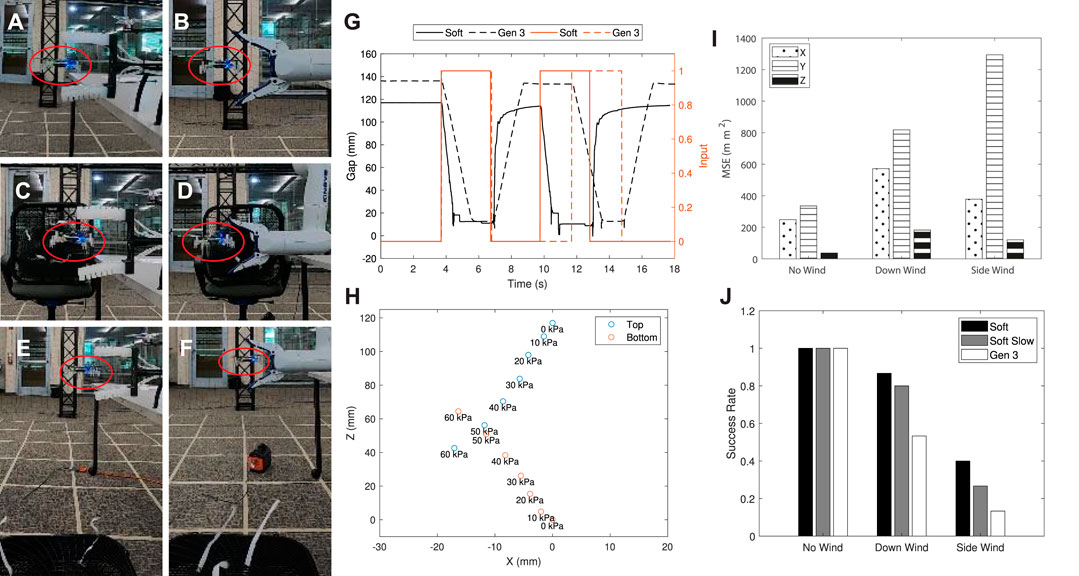
FIGURE 6. Grasping test for the soft and Gen3-lite grippers. (A–F) Both grippers are placed vertically at the same 3D position and studied in three cases: no-wind, down-wind, and side-wind. (G) Step response for both grippers. (H) Relative positions of the soft gripper’s two claws with respect to different pressure values. (I) Mean squared error for a hovering micro-robot under disturbances. (J) Success rates for horizontal grasping of a flying micro-robot using both grippers.
As shown in Figure 6G, we command the soft gripper to close and open for 3 s, while the Gen3-lite gripper is controlled to close for 3 s and open for 5 s. The Gen3-lite gripper has an initial opening of 136 mm, larger than the one of the soft gripper (117 mm). However, the soft gripper completely closes after 0.72 s, while it takes 1.90 s for Gen3-lite gripper to do so, with closing velocities 162.50 and 71.58 mm/s for the soft and Gen3-lite grippers, respectively. Large amounts of noise are observed when the soft gripper completely closes. The noise comes from the rigid-body-based motion capture system model, and the fact that inflated soft actuators have shape changes which introduce measuring errors. On the other hand, unlike the same speeds of the Gen3-lite gripper, the soft gripper has a much faster response for opening, with only 0.24 s to reach 85% of the initial gap. The normally-straight actuators with the flexible 80A support recover very fast with basic ventilation. Admittedly, the response of both grippers can be improved by having more powerful motors or inflators. However, the low-cost soft gripper introduced in this work has good performance powered by lightweight air pumps, compared to commercially available end-effectors like the Gen3-lite gripper.
Second, positions of the soft gripper’s two claws (top and bottom) are studied with respect to different pressure values 3. The end-effector is placed vertically along
In the catching test, both grippers aim to grasp an aerial micro-robot that is hovering. In addition to irregular shapes, micro aerial robots can have comparably larger tracking errors in the hover state, thus making it a challenge to grasp by grippers. To further investigate the robustness of catches, three cases are studied in this test: no-wind, down-wind, and side-wind. As shown in Figures 6C–F, the target aerial micro-robot hovers under disturbance in down-wind and side-wind modes. Specifically, we use a fan to create aerodynamic disturbances at a distance of 1 m along
Figure 6I presents the mean squared error (MSE) between actual and desired hovering positions in three cases. Results show that the hovering micro-robot has larger tracking errors under these disturbances, especially along
Lastly, we study the maximum force applied by both grippers to validate the catching safety. A digital force gauge is used to measure vertical force along
In this test, we study the feasibility of using the developed SoAG robot to catch an aerial micro-robot that is hovering. The target
A sample trial is presented in Figure 7, where images depict events when the SoAG robot approaches the target (A), grasps the target (B), and returns (C) with the target. Figure 7D shows the state tracking for the end-effector and target, where black solid and dashed curves denote the actual and desired positions of the end-effector in
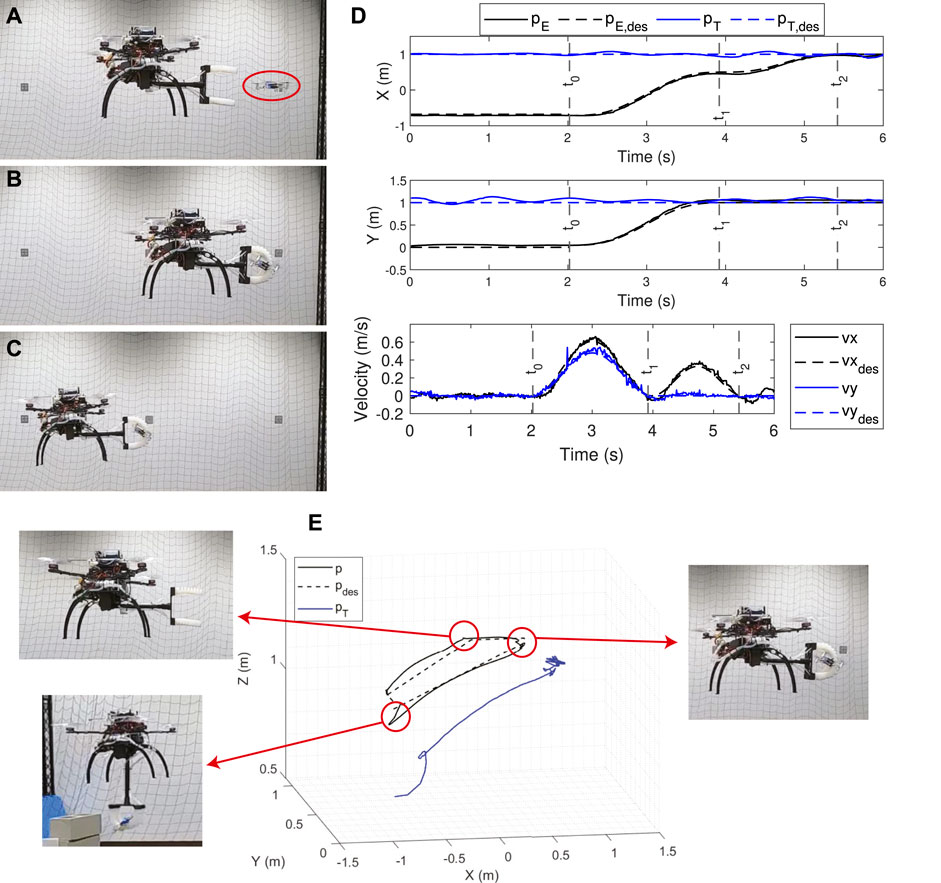
FIGURE 7. A sample trial of the static catching test. (A–C) The SoAG robot approaches the target, grasps the target, and returns with the target. (D) State tracking for the end-effector and target. (E) 3D positions of the SoAG robot and the target aerial robot.
The actual and desired 3D positions of the SoAG robot are plotted in Figure 6E, as well as the target’s 3D position. The robot has larger tracking errors during the chase segment, and smaller errors for the close part. The results back up the planning method in piecewise polynomials to achieve small tracking errors before the grasping. Note that random noise is still present in the target’s hovering position, which makes aerial catching more challenging. Owing to the robustness of the soft gripper, the catcher robot manages to grasp the target and return with it. At the end of the trajectory, SoAG rotates the arm to place the target at a lower position and gets ready to drop the target safely.
While the related work Chen T. G. et al. (2022) relies on the contact with the propeller guards, our method can catch flying micro-robots with or without protective frames. In this part, we study the robustness of the soft gripper by introducing the catching test of flying targets with propeller guards. Figure 8 shows close-up images of the flying targets used in the tests with (B) or without (A) propeller guards. The flying micro-robot with the protective frame has a dimension of 130 × 130 × 40 mm, and a total mass of 40 g. The custom propeller guard is 3D-printed using the Form 3 in clear resin, which has the post-cured ultimate tensile strength 65 MPa. We repeat the static catching tests on flying targets, and the robot can successfully capture hovering micro-robots regardless of the propeller guards. Figure 8 presents side and first-person views of the aerial catching in both cases, where red ellipses mark hovering micro-robots. As shown in first-person views, the robot can catch flying targets even though the gripper is not in align with the center of the target, thanks to the robustness of the soft grasping. In the meantime, the observation that aerial catching does not damage the fragile propeller guards further support the safety of our method.

FIGURE 8. Close-up images of the flying targets without (A) or with (B) propeller guards, as well as side views and first-person views of the aerial captures.
In this test, we study the feasibility of dynamically catching an aerial micro-robot that is following a path. The flying target takes off at the position [−1.0,0,1.0]T and moves along
A sample dynamic catching trial is shown in Figure 9, where the SoAG robot triggers the catching (A), starts inflating (B), finishes grasping (C), and enters hovering state (D). Figure 9E visualizes the actual and desired states tracking of both the catcher and target robots. Due to the limited space of the experimental area, the catcher robot hovers at a position relatively close to the flying target, thus the planning skips the chase segment. The results show that the planner generates a smooth trajectory for t ∈ [t0, t2] = [1.1, 5.2] to reach the same position and velocity of the target. At time t2, the SoAG robot starts inflating the end-effector to grasp the target, and keeps the constant velocity for another 4 s before the hovering state.
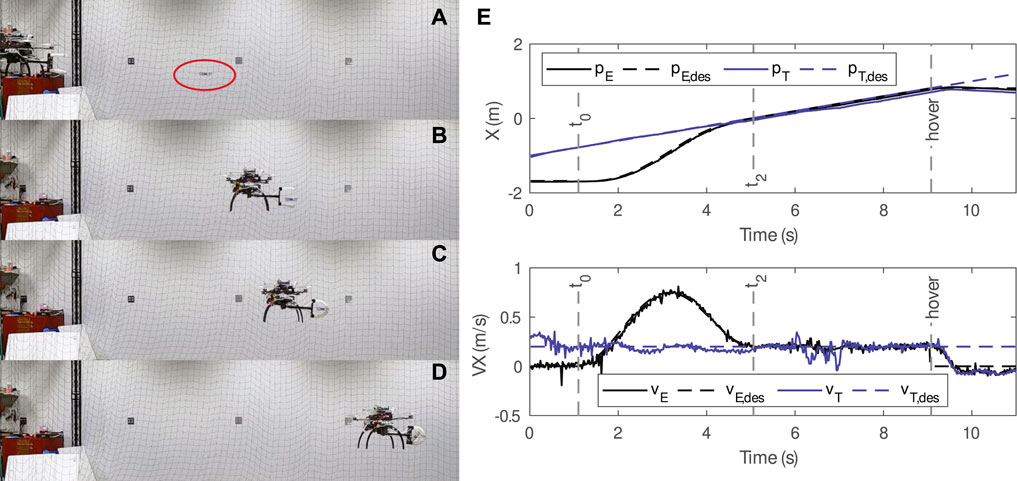
FIGURE 9. A sample trial of the dynamic catching test. (A–D) The SoAG robot chases, reaches and grasps the moving aerial target. (E) State tracking for the end-effector and moving target. Note that the planning skips the chase segment due relatively close starting positions.
The position profile in Figure 9E shows that the robot is tracking the desired trajectory well. After the grasping, the target’s position has a small deviation from the desired one. Both the catcher and target robots remain the same position during the hovering. On the other hand, velocities tracking shows that the target has relatively larger tracking errors compared to the catcher, especially after the grasping. The catcher robot follows the smooth desired velocities well to reach and maintain the target velocity
In this experiment, we study the effect of the arm and target on the free flight tracking performance of the catcher. As shown in Figures 10A–E, five cases are considered in the test: conventional quadrotor (Quad), SoAG with arm up and without target (Up w/o), SoAG with arm up and seized target (Up w/o), SoAG with arm down and without target (Down w/o), and SoAG with arm down and seized target (Down w/). The angle η = 0 when the arm is up, and η is
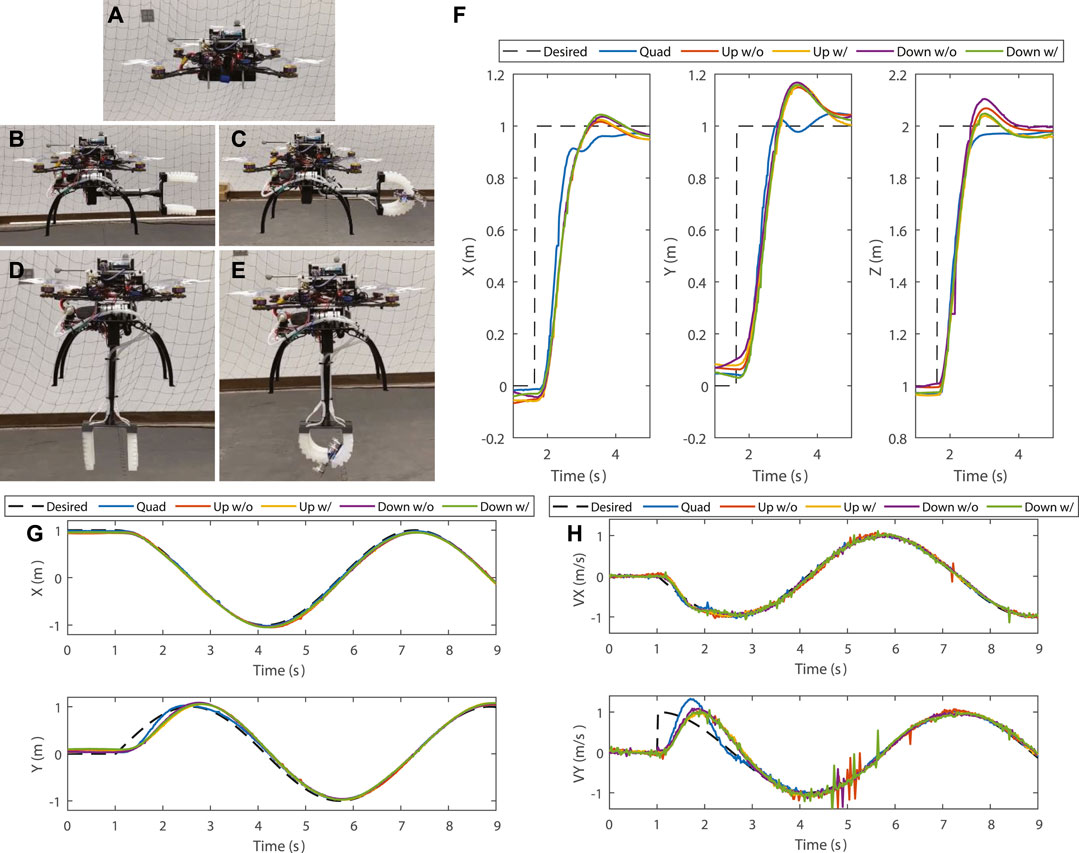
FIGURE 10. Free flight tracking test. (A–E) Five cases are considered in the test: conventional quadrotor (Quad), SoAG robot with arm up without target (Up w/o), SoAG robot with arm up with target (Up w/), and SoAG robot with arm down without target (Down w/o). (F) States for all robots in the step response test. (G) Positions and (H) Velocities on
Figure 10F shows the states for all robots in the step response test. Green dashed curves show desired states from the planner, and black dashed and solid curves show the response of the SoAG robot with the arm lifted. Blue dashed and solid curves denote the response of the robot when the arm is down. Note that the time is synchronized solely in the visualization for better comparison. The results show that Quad has a faster rising time compared to the other four cases in both
In this work, we focus on addressing the challenge of catching a aerial micro-robot in mid-air using another MAV equipped with a soft gripper. Specifically, we introduce a gripper design based on soft actuators that keep a horizontally straight shape with a single fixture and maintain sufficiently compliance when bending. To enable horizontal grasping, we further develop an open-source MAV equipped with the end-effector and onboard pneumatic regulation named Soft Aerial Gripper (SoAG). The hardware design is introduced, as well as the dynamic modeling and control. We present a planning method based on piecewise polynomial optimization to catch the flying micro-robots without generating aerodynamic disturbances detrimental to the target’s stability.
Experimental results show the low-cost soft gripper, powered by light weight air pumps that are onboard the robot, has fast opening and closing responses as compared to commercially available end-effectors. Static grasping tests study the soft gripper’s robustness in capturing aerial micro-robots under the influence of aerodynamic disturbances. We experimentally demonstrate the feasibility of using the SoAG robot to catch a hovering micro-robot and return with the target. The free flight performance of the SoAG robot is studied against a conventional quadrotor and in different gripper and payload status to validate the design. To the authors’ knowledge, the SoAG robot is the first MAV to demonstrate the feasibility of catching a flying micro-robot with a soft gripper. The robot can be used in search and rescue of aerial robots or seize unidentified flying targets without damage. In the meantime, the robot can move fragile objects as a conventional aerial gripper, with potential applications in aerial transportation and construction.
With the introduction and validation of the SoAG robot in this paper, several directions for future work can be enabled. For instance, small aerial robots have limited flight time so one way to improve their energetics besides other means currently at the forefront of research Karydis and Kumar (2017) would be to be caught and released in mid-air safely via larger aerial robots. Another direction of interest includes safe multi-robot co-manipulation for transportation and assembly. The compliance afforded by the soft gripper can help account for positioning errors of the robots and thus help relax some of the optimization constraints in aerial co-manipulation. Furthermore, at the current stage of development, the flying target’s weight in this work is very small. To enable grasping and transportation of heavier objects, we plan to upgrade the MAV hardware and incorporate the target’s mass onto the system’s modeling as in Mellinger et al. (2011), as well as robust or adaptive controlling methods to address changes in mass and inertia. While the aerial vehicle has a maximum payload of 1.2 kg, the proposed soft gripper can only grasp objects with masses up to 280 g. To scale up the solution, we plan to strengthen the grasping capacity by using stronger materials and pneumatic actuation. Third, the project uses the basic on-off control for the gripper with constant inflating rates. It is of interest to incorporate feedback control of the soft end-effector as in Mucchiani et al. (2022). Fourth, we aim to deploy the robot in outdoor or confined environments without a motion capture system, thus enabling vision guidance as in Kim et al. (2016) and impact resilience as in Liu and Karydis (2021b). Lastly, it is of interest to discover the possibility of combining aerial-ground robots by including pneumatic legged mobility as in Liu et al. (2020); Liu and Karydis (2021a).
The files for developing the robot can be found in the repository https://github.com/UCR-Robotics/SoAG. The raw data supporting the conclusion of this article will be made available by the authors. Inquiries can be directed to the corresponding author.
ZL conceived and developed the system with support from CM and KY. ZL designed and carried out the experiments with support from KY and CM. ZL, CM, and KK prepared and edited the manuscript. KK supervised all aspects of the project. All authors discussed the results, provided feedback, and contributed to the final manuscript preparation.
We gratefully acknowledge the support of NSF award numbers #IIS-1724341, #IIS-1901379, and #IIS-1910087, ARL award number #W911NF-18-1-0266, and ONR award number #N00014-18-1-2252.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the funding agencies.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frobt.2022.1030515/full#supplementary-material
Appius, A., Bauer, E., Blöchlinger, M., Kalra, A., Oberson, R., Raayatsanati, A., et al. (2022). Raptor: Rapid aerial pickup and transport of objects by robots. IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, October 23–37, 2022 (In press).
Augugliaro, F., Lupashin, S., Hamer, M., Male, C., Hehn, M., Mueller, M. W., et al. (2014). The flight assembled architecture installation: Cooperative construction with flying machines. IEEE Control Syst. Mag. 34, 46–64. doi:10.1109/MCS.2014.2320359
Baizid, K., Giglio, G., Pierri, F., Trujillo, M. A., Antonelli, G., Caccavale, F., et al. (2015). “Experiments on behavioral coordinated control of an unmanned aerial vehicle manipulator system,” in IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26-30 May 2015 (IEEE), 4680–4685.
Bejar, M., Ollero, A., and Kondak, K. (2019). Helicopter based aerial manipulators aerial robotic manipulation. Berlin, Germany: Springer, 35–52.
Brescianini, D., Hehn, M., and D’Andrea, R. (2013). Nonlinear quadrocopter attitude control: Technical report. Tech. Rep. ETH Zurich. doi:10.3929/ethz-a-009970340
Chen, G., Zhou, J., Wang, L., Wang, Y., Yin, Y., and Ding, Z. (2022a). “Modeling and adaptive controlling of quadrotor uav with flexible gripper,” in IEEE Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 17-19 June 2022 (IEEE), 1991–1998.
Chen, T. G., Hoffmann, K. A., Low, J. E., Nagami, K., Lentink, D., and Cutkosky, M. R. (2022b). Aerial grasping and the velocity sufficiency region. IEEE Robot. Autom. Lett. 7, 10009–10016. doi:10.1109/lra.2022.3192652
Danko, T. W., Chaney, K. P., and Oh, P. Y. (2015). “A parallel manipulator for mobile manipulating uavs,” in IEEE International Conference on Technologies for Practical Robot Applications (TePRA), Woburn, MA, USA, 11-12 May 2015 (IEEE), 1–6.
Danko, T. W., and Oh, P. Y. (2013). “A hyper-redundant manipulator for mobile manipulating unmanned aerial vehicles,” in IEEE International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 28-31 May 2013 (IEEE), 974–981.
DroGone (2022). Drogone autonomous counter drone systems. [online] available at: https://www.drogone.com/ (Accessed Sep 14, 2022).
DroneCatcher (2022). Dronecatcher a delft dynamics product. [online] available at: https://dronecatcher.nl/ (Accessed Sep 14, 2022).
Fedoseev, A., Serpiva, V., Karmanova, E., Cabrera, M. A., Shirokun, V., Vasilev, I., et al. (2021). “Dronetrap: Drone catching in midair by soft robotic hand with color-based force detection and hand gesture recognition,”IEEE International Conference on Soft Robotics (RoboSoft), New Haven, CT, USA, 12-16 April 2021 (IEEE), 261–266.
Fiaz, U. A., Abdelkader, M., and Shamma, J. S. (2018). “An intelligent gripper design for autonomous aerial transport with passive magnetic grasping and dual-impulsive release,” in IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, New Zealand, 09-12 July 2018 (IEEE), 1027–1032.
Fishman, J., Ubellacker, S., Hughes, N., and Carlone, L. (2021). “Dynamic grasping with a” soft” drone: From theory to practice,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September 2021 - 01 October 2021 (IEEE), 4214–4221.
Fumagalli, M., Naldi, R., Macchelli, A., Forte, F., Keemink, A. Q., Stramigioli, S., et al. (2014). Developing an aerial manipulator prototype: Physical interaction with the environment. IEEE Robot. Autom. Mag. 21, 41–50. doi:10.1109/mra.2013.2287454
Gabrich, B., Saldana, D., Kumar, V., and Yim, M. (2018). “A flying gripper based on cuboid modular robots,” in IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21-25 May 2018 (IEEE), 7024–7030.
Garimella, G., and Kobilarov, M. (2015). “Towards model-predictive control for aerial pick-and-place,” in IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26-30 May 2015 (IEEE), 4692–4697.
Ghadiok, V., Goldin, J., and Ren, W. (2011). “Autonomous indoor aerial gripping using a quadrotor,” in IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25-30 September 2011 (IEEE), 4645–4651.
Gómez-de Gabriel, J. M., Gandarias, J. M., Pérez-Maldonado, F. J., García-Núñcz, F. J., Fernández-García, E. J., and García-Cerezo, A. J. (2018). “Methods for autonomous wristband placement with a search-and-rescue aerial manipulator,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 01-05 October 2018 (IEEE), 7838–7844.
Hehn, M., and D’Andrea, R. (2011). Quadrocopter trajectory generation and control. IFAC Proc. Vol. 44, 1485–1491. doi:10.3182/20110828-6-it-1002.03178
Jimenez-Cano, A. E., Martin, J., Heredia, G., Ollero, A., and Cano, R. (2013). “Control of an aerial robot with multi-link arm for assembly tasks,” in IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 06-10 May 2013 (IEEE), 4916–4921.
Kan, X., Thomas, J., Teng, H., Tanner, H. G., Kumar, V., and Karydis, K. (2019). Analysis of ground effect for small-scale uavs in forward flight. IEEE Robot. Autom. Lett. 4, 3860–3867. doi:10.1109/lra.2019.2929993
Karydis, K., and Hsieh, M. A. (2016). “Uncertainty quantification for small robots using principal orthogonal decomposition,” in International Symposium on Experimental Robotics (ISER), Berlin, Germany, 21 March 2016 (IEEE), 33–42.
Karydis, K., and Kumar, V. (2017). Energetics in robotic flight at small scales. Interface focus 7, 20160088. doi:10.1098/rsfs.2016.0088
Karydis, K., Poulakakis, I., Sun, J., and Tanner, H. G. (2015). Probabilistically valid stochastic extensions of deterministic models for systems with uncertainty. Int. J. Robotics Res. 34, 1278–1295. doi:10.1177/0278364915576336
Kim, S.-J., Lee, D.-Y., Jung, G.-P., and Cho, K.-J. (2018). An origami-inspired, self-locking robotic arm that can be folded flat. Sci. Robot. 3, eaar2915. doi:10.1126/scirobotics.aar2915
Kim, S., Seo, H., Choi, S., and Kim, H. J. (2016). Vision-guided aerial manipulation using a multirotor with a robotic arm. Ieee. ASME. Trans. Mechatron. 21, 1912–1923. doi:10.1109/tmech.2016.2523602
Klausen, K., Fossen, T. I., and Johansen, T. A. (2018). Autonomous recovery of a fixed-wing uav using a net suspended by two multirotor uavs. J. Field Robot. 35, 717–731. doi:10.1002/rob.21772
Kondak, K., Krieger, K., Albu-Schaeffer, A., Schwarzbach, M., Laiacker, M., Maza, I., et al. (2013). Closed-loop behavior of an autonomous helicopter equipped with a robotic arm for aerial manipulation tasks. Int. J. Adv. Robotic Syst. 10, 145. doi:10.5772/53754
Korpela, C., Orsag, M., and Oh, P. (2014). “Towards valve turning using a dual-arm aerial manipulator,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 14-18 September 2014 (IEEE), 3411–3416.
Korpela, C., Orsag, M., Pekala, M., and Oh, P. (2013). “Dynamic stability of a mobile manipulating unmanned aerial vehicle,” in IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 06-10 May 2013 (IEEE), 4922–4927.
Kreciglowa, N., Karydis, K., and Kumar, V. (2017). “Energy efficiency of trajectory generation methods for stop-and-go aerial robot navigation,” in IEEE International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13-16 June 2017 (IEEE), 656–662.
Kruse, L., and Bradley, J. (2018). “A hybrid, actively compliant manipulator/gripper for aerial manipulation with a multicopter,” in IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Philadelphia, PA, USA, 06-08 August 2018 (IEEE), 1–8.
Lee, L. Y., Syadiqeen, O. A., Tan, C. P., and Nurzaman, S. G. (2021). Closed-structure compliant gripper with morphologically optimized multi-material fingertips for aerial grasping. IEEE Robot. Autom. Lett. 6, 887–894. doi:10.1109/lra.2021.3052420
Lee, T., Leok, M., and McClamroch, N. H. (2010). “Geometric tracking control of a quadrotor uav on se (3),” in IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15-17 December 2010 (IEEE), 5420–5425.
Liu, Z., and Karydis, K. (2021a). “Position control and variable-height trajectory tracking of a soft pneumatic legged robot,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 03 August 2021 (IEEE), 1708–1709.
Liu, Z., and Karydis, K. (2021b). “Toward impact-resilient quadrotor design, collision characterization and recovery control to sustain flight after collisions,” in IEEE International Conference on Robotics and Automation (ICRA), Xi'an, China, 30 May 2021 - 05 June 2021 (IEEE), 183–189.
Liu, Z., Lu, Z., and Karydis, K. (2020). “Sorx: A soft pneumatic hexapedal robot to traverse rough, steep, and unstable terrain,” in IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May 2020 - 31 August 2020 (IEEE), 420–426.
McLaren, A., Fitzgerald, Z., Gao, G., and Liarokapis, M. (2019). “A passive closing, tendon driven, adaptive robot hand for ultra-fast, aerial grasping and perching,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 03-08 November 2019 (IEEE), 5602–5607.
Meier, L., Honegger, D., and Pollefeys, M. (2015). “Px4: A node-based multithreaded open source robotics framework for deeply embedded platforms,” in IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26-30 May 2015 (IEEE), 6235–6240.
Mellinger, D., and Kumar, V. (2011). “Minimum snap trajectory generation and control for quadrotors,” in IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 09-13 May 2011 (IEEE), 2520–2525.
Mellinger, D., Lindsey, Q., Shomin, M., and Kumar, V. (2011). “Design, modeling, estimation and control for aerial grasping and manipulation,” in IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25-30 September 2011 (IEEE), 2668–2673.
Meng, J., Buzzatto, J., Liu, Y., and Liarokapis, M. (2021). On aerial robots with grasping and perching capabilities: A comprehensive review. Front. Robot. AI 8, 739173. doi:10.3389/frobt.2021.739173
Meng, X., Ding, X., and Guo, P. (2018). “A net-launching mechanism for uav to capture aerial moving target,” in IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 05-08 August 2018 (IEEE), 461–468.
Mishra, S., Yang, D., Thalman, C., Polygerinos, P., and Zhang, W. (2018). “Design and control of a hexacopter with soft grasper for autonomous object detection and grasping,” in Dynamic Systems and Control Conference, Atlanta, USA, September 30 - October 3, 2018 (American Society of Mechanical Engineers (ASME)), 9.
Mohta, K., Watterson, M., Mulgaonkar, Y., Liu, S., Qu, C., Makineni, A., et al. (2018). Fast, autonomous flight in gps-denied and cluttered environments. J. Field Robot. 35, 101–120. doi:10.1002/rob.21774
Mosadegh, B., Polygerinos, P., Keplinger, C., Wennstedt, S., Shepherd, R. F., Gupta, U., et al. (2014). Pneumatic networks for soft robotics that actuate rapidly. Adv. Funct. Mat. 24, 2163–2170. doi:10.1002/adfm.201303288
Mucchiani, C., Liu, Z., Sahin, I., Dube, J., Vu, L., Kokkoni, E., et al. (2022). “Closed-loop position control of a pediatric soft robotic wearable device for upper extremity assistance,” in IEEE International Conference on Robot & Human Interactive Communication (RO-MAN), Macau, China, 16 June 2022 (IEEE), 6.
Park, S., Kim, H. T., Lee, S., Joo, H., and Kim, H. (2021). Survey on anti-drone systems: Components, designs, and challenges. IEEE Access 9, 42635–42659. doi:10.1109/access.2021.3065926
Polygerinos, P., Lyne, S., Wang, Z., Nicolini, L. F., Mosadegh, B., Whitesides, G. M., et al. (2013). “Towards a soft pneumatic glove for hand rehabilitation,” in IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 03-07 November 2013 (IEEE), 1512–1517.
Pounds, P. E., Bersak, D. R., and Dollar, A. M. (2011a). “Grasping from the air: Hovering capture and load stability,” in IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 09-13 May 2011 (IEEE), 2491–2498.
Pounds, P. E., Bersak, D. R., and Dollar, A. M. (2011b). “Practical aerial grasping of unstructured objects,” in IEEE Conference on Technologies for Practical Robot Applications, Woburn, MA, USA, 11-12 April 2011 (IEEE), 99–104.
Preiss, J. A., Hönig, W., Ayanian, N., and Sukhatme, G. S. (2017). “Downwash-aware trajectory planning for large quadrotor teams,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24-28 September 2017 (IEEE), 250–257.
Ramon-Soria, P., Gomez-Tamm, A. E., Garcia-Rubiales, F. J., Arrue, B. C., and Ollero, A. (2019). “Autonomous landing on pipes using soft gripper for inspection and maintenance in outdoor environments,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 03-08 November 2019 (IEEE), 5832–5839.
Richter, C., Bry, A., and Roy, N. (2016). Polynomial trajectory planning for aggressive quadrotor flight in dense indoor environments Robotics research. Berlin, Germany: Springer, 649–666.
Ritz, R., Müller, M. W., Hehn, M., and D’Andrea, R. (2012). “Cooperative quadrocopter ball throwing and catching,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura-Algarve, Portugal, 07-12 October 2012 (IEEE), 4972–4978.
Rodriguez-Ramos, A., Bavle, A. A.-F. H., Rodriguez-Vazquez, J., Fernandez-Cortizas, L. L. M., Fernandez, R. A. S., Rodelgo, A., et al. (2021). Autonomous aerial robot for high-speed search and intercept applications. Berlin, Germany: Springer.
Rothe, J., Strohmeier, M., and Montenegro, S. (2019). “A concept for catching drones with a net carried by cooperative uavs,” in IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Würzburg, Germany, 02-04 September 2019 (IEEE), 126–132.
Ruggiero, F., Lippiello, V., and Ollero, A. (2018). Aerial manipulation: A literature review. IEEE Robot. Autom. Lett. 3, 1957–1964. doi:10.1109/lra.2018.2808541
Ruggiero, F., Trujillo, M. A., Cano, R., Ascorbe, H., Viguria, A., Peréz, C., et al. (2015). “A multilayer control for multirotor uavs equipped with a servo robot arm,” in IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26-30 May 2015 (IEEE), 4014–4020.
Shi, F., Zhao, M., Murooka, M., Okada, K., and Inaba, M. (2020). “Aerial regrasping: Pivoting with transformable multilink aerial robot,” in IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May 2020 - 31 August 2020 (IEEE), 200–207.
Shintake, J., Cacucciolo, V., Floreano, D., and Shea, H. (2018). Soft robotic grippers. Adv. Mat. 30, 1707035. doi:10.1002/adma.201707035
Sreenath, K., Lee, T., and Kumar, V. (2013). “Geometric control and differential flatness of a quadrotor uav with a cable-suspended load,” in IEEE Conference on Decision and Control (CDC), Firenze, Italy, 10-13 December 2013 (IEEE), 2269–2274.
Staub, N., Bicego, D., Sablé, Q., Arellano, V., Mishra, S., and Franchi, A. (2018). “Towards a flying assistant paradigm: The othex,” in IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21-25 May 2018 (IEEE), 6997–7002.
Stewart, W., Ajanic, E., Müller, M., and Floreano, D. (2022). How to swoop and grasp like a bird with a passive claw for a high-speed grasping. Ieee. ASME. Trans. Mechatron. 5, 1–9. doi:10.1109/tmech.2022.3143095
Suarez, A., Jimenez-Cano, A., Vega, V., Heredia, G., Rodriguez-Castaño, A., and Ollero, A. (2017). “Lightweight and human-size dual arm aerial manipulator,” in IEEE International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13-16 June 2017 (IEEE), 1778–1784.
Thomas, J., Pope, M., Loianno, G., Hawkes, E. W., Estrada, M. A., Jiang, H., et al. (2016). Aggressive flight with quadrotors for perching on inclined surfaces. J. Mech. Robotics 8, 051007. doi:10.1115/1.4032250
Vidyadhara, B., Tony, L. A., Gadde, M. S., Jana, S., Varun, V., Bhise, A. A., et al. (2022). Design and integration of a drone based passive manipulator for capturing flying targets. Robotica 40, 2349–2364. doi:10.1017/s0263574721001673
Yüksel, B., Mahboubi, S., Secchi, C., Bülthoff, H. H., and Franchi, A. (2015). “Design, identification and experimental testing of a light-weight flexible-joint arm for aerial physical interaction,” in IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26-30 May 2015 (IEEE), 870–876.
Zhang, G., He, Y., Dai, B., Gu, F., Yang, L., Han, J., et al. (2018). “Grasp a moving target from the air: System & control of an aerial manipulator,” in IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21-25 May 2018 (IEEE), 1681–1687.
Zhang, H., Sun, J., and Zhao, J. (2019). “Compliant bistable gripper for aerial perching and grasping,” in IEEE International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20-24 May 2019 (IEEE), 1248–1253.
Zhao, M., Kawasaki, K., Chen, X., Noda, S., Okada, K., and Inaba, M. (2017). “Whole-body aerial manipulation by transformable multirotor with two-dimensional multilinks,” in IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May 2017 - 03 June 2017 (IEEE), 5175–5182.
Keywords: aerial systems, biologically-inspired robots, soft robots, grasping, manipulation planning, field robots
Citation: Liu Z, Mucchiani C, Ye K and Karydis K (2022) Safely catching aerial micro-robots in mid-air using an open-source aerial robot with soft gripper. Front. Robot. AI 9:1030515. doi: 10.3389/frobt.2022.1030515
Received: 29 August 2022; Accepted: 14 October 2022;
Published: 02 November 2022.
Edited by:
Pham Huy Nguyen, Imperial College London, United KingdomReviewed by:
Karishma Patnaik, Arizona State University, United StatesCopyright © 2022 Liu, Mucchiani, Ye and Karydis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Konstantinos Karydis, a2thcnlkaXNAZWNlLnVjci5lZHU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.