Identification of COM Controller of a Human in Stance Based on Motion Measurement and Phase-Space Analysis

This article proposes a process to identify the standing stabilizer, namely, the controller in humans to keep upright posture stable against perturbations. We model the controller as a piecewise-linear feedback system, where the state of the center of mass (COM) is regulated by coordinating the whole body so as to locate the zero-moment point (ZMP) at the desired position. This was developed for humanoid robots and is possibly able to elaborate the fundamental control scheme used by humans to stabilize themselves. Difficulties lie on how to collect motion trajectories in a wide area of the state space for reliable identification and how to identify the piecewise-affine dynamical system. For the former problem, a motion measurement protocol is devised based on the theoretical phase portrait of the system. Regarding the latter problem, some clustering techniques including K-means method and EM (Expectation-and-Maximization) algorithm were examined. We found that a modified K-means method produced the most accurate result in this study. The method was applied to the identification of a lateral standing controller of a human subject. The result of the identification quantitatively supported a hypothesis that the COM-ZMP regulator reasonably models the human’s controller when deviations of the angular momentum about the COM are limited.

1 Introduction

Standing stabilization control, namely, the control to keep upright posture stable against perturbations, is one of the fundamental functions in humans and has been studied, through which the ankle and hip strategies have been hypothesized (Nashner and McCollum, 1985; Mueller et al., 1994; Gatev et al., 1999; Vette et al., 2007). The discussions mainly focused on a coordination of a couple of joints in the sagittal plane under specific conditions in the beginning, and has been extended to a control scheme in more generalized situations at various postures against various types of perturbations, where the lower and upper bodies move in-phase in the lower frequency domain and counter-phase in the higher domain (Goodworth and Peterka, 2010). Some works to implement the ankle/hip strategies on humanoid robots (Atkeson and Stephens, 2007; Lippi et al., 2016) have also been made.

How humans synthesize behaviors on their complex musculo-skeletal system into such control strategies has been of great interest to researchers in the field of body science and studied in depth for decades. Advanced technology has enabled precise motion measurements and a large-scale simulation of a detailed neuro-musculo-skeletal model of a human (Murai et al., 2008). However, the identification of human’s motor controller is still challenging. On the other hand, comprehensive studies of the whole-body dynamics have been made in the field of humanoid robotics, where some key aspects such as floating-base dynamics (Yoshida et al., 1995; Fujimoto and Kawamura, 1998) and the structure-varying nature (Nakamura and Yamane, 2000) have been discussed. It was also shown to be effective to focus on the macroscopic relationship between the center of mass (COM) and the center of pressure (COP), to which the zero-moment point (ZMP) (Vukobratović and Stepanenko, 1972) was given as an alias in the context of the motion synthesis. Although it omits the complex control that exploits counter-phase movements of the upper body, it plays a fundamental role in the stabilization in the reduced-order dynamics that can be visually analyzed in the phase space. Several controllers for humanoid robots were developed based on it (Mitobe et al., 2000; Sugihara et al., 2002; Kajita et al., 2003; Morimoto et al., 2008; Sugihara, 2009) In particular, a control scheme to regulate the COM by manipulating the ZMP was discussed (Sugihara, 2009). This enabled an intuitive understanding of the relationship between the response to perturbations and the stability performance under the limited supporting region compared with another scheme to manipulate the distribution of ground reaction forces (Hyon, 2009; Henze et al., 2016). It was also found to be related to the extrapolated center of mass (XCOM) (Hof, 2008) studied in the field of biomechanics. This suggests a possible hypothesis that human’s standing controller can be modeled by the COM-ZMP regulator. A study to compare it with the humans’ standing controller was also made (Peterka, 2009).

A problem that arises when applying the system identification to the human controller based on the model is that it is difficult to collect a sufficient number of motion trajectories since humans in general unconsciously stabilize themselves and hardly show behaviors in a distance from the point of equilibrium. A particular protocol to observe such behaviors has to be devised for this purpose. Another difficulty is that the system is piecewise, namely, the state space of the COM is divided into some regions described by different equations of motions due to the unilaterality of contact forces. It is a chicken-and-egg problem to identify such a system since the equation of description has to be provided to identify system parameters, while the system parameters are required to choose the equation of description (Bemporad et al., 2003; Ferrari-Trecate et al., 2003; Vidal et al., 2003).

The contributions of this article are twofold. First, we propose a method to collect motion trajectories in a wide area of the state space. The behaviors to be observed in each region can be predicted based on the dynamics of the COM-ZMP regulator in a phase portrait. Then, we add preparatory motion to each trial to accelerate the COM to preferable initial states. The preparatory phase in each motion trajectory is detected and discarded in the data processing based on the profile of the ground reaction force. Second, we propose methods to identify parameters of the piecewise system from the measured motion data. We examined K-means method (MacQueen, 1967; Duda and Hart, 1973) and EM (Expectation-and-Maximization) algorithm (Dempster et al., 1977) to cluster points in the state space into consistent regions and identify the system parameters in an iterative way. It was verified that both methods successfully output consistent results of the identification and a modified K-means method produced the most accurate result in this study. The entire process in which the above methods were combined was applied to the stabilization motion in the lateral direction of a human subject. Although the number of subjects was only one, the result supported the hypothesis that the human’s behavior can be modeled by the COM-ZMP regulator when deviations of the angular momentum about the COM are limited and thereby the translational movement of the COM is dominant. To the best of the authors’ knowledge, this is the first work that identified the standing controller of a human based on the model. Notice that the objective of this article is to propose the process, and to validate the hypothesis based on a number of results is outside the scope of this article.

Earlier versions of this work were presented at 2012 IEEE-RAS International Conference on Humanoid Robots (Kaneta et al., 2012), 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (Kaneta et al., 2013; Murai et al., 2013), and The 8th IEEE RAS/EMBS International Conference on Biomedical Robotics and Biomechatronics (Murai and Sugihara, 2020).

2 Dynamics Model of the COM-ZMP Regulator

The dynamics of a humanoid, which could be either a real human or a humanoid robot, is represented by a large-scale equation of motion and many inequalities originated from the limitation of contact forces. However, macroscopic characteristics embedded in the dynamics can be abstracted by focusing on the relationship between the COM and the ZMP (Sugihara and Morisawa, 2020). Let us consider lateral motion of a humanoid as shown in Figure 1. Suppose the vertical movement of the COM and the torque about the COM are both negligibly small, the equation of motion of the COM is obtained as

$\begin{array}{ll}\hfill \ddot{x}& ={\zeta }^2(x-x_{\mathrm{Z}})\hfill \end{array}(1)$

$\begin{array}{ll}\hfill \zeta & \stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\sqrt{\frac{g}{\mathrm{z}}}\hfill \end{array}(2)$

where x is the lateral position of the COM, x_Z is the lateral position of the ZMP, z is the height of the COM with respect to the nominal ground, and g = 9.8m/s² is the acceleration due to the gravity. Note that z is assumed to be constant, and thus, ζ is also constant. The ZMP is naturally constrained within the supporting region due to the unilaterality of the contact forces as

$x_{\text{Zmin}}\le x_{\mathrm{Z}}\le x_{\text{Zmax}},(3)$

where x_Zmin and x_Zmax are the right and the left boundaries of the supporting region in the x-axis, respectively.

FIGURE 1

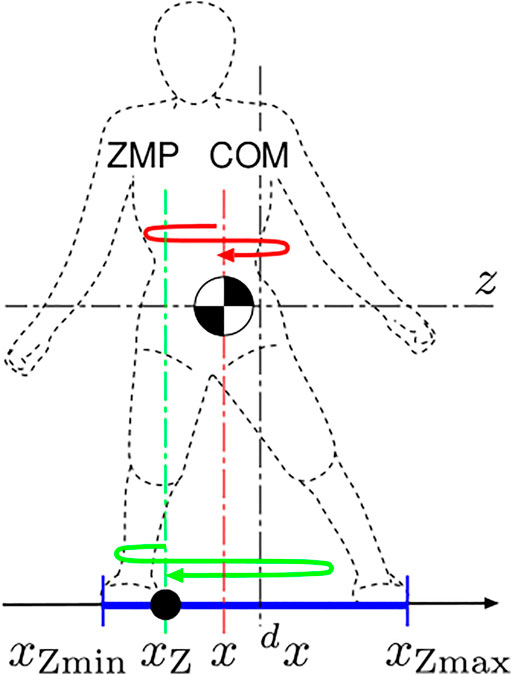
FIGURE 1. The COM-ZMP model of lateral standing motion. z is the height of the COM with respect to the nominal ground, x is the lateral position of the COM, ^dx is the referential position of the COM, x_Z is the lateral position of the ZMP, and x_Zmin and x_Zmax are the minimum and maximum boundaries of the supporting region, respectively.

The COM-ZMP regulator (Sugihara, 2009) is a standing stabilization controller designed for humanoid robots, in which the desired location of the ZMP ^dx_Z is decided based on a piecewise-linear feedback of the COM state as

$\begin{array}{ll}\hfill {}^{d}x_{\mathrm{Z}}& =\left\{\begin{array}{cc}{x}_{\text{Zmax}}\hfill & (\mathrm{S}1:{\tilde{x}}_{\mathrm{Z}}\ge x_{\text{Zmax}})\hfill \\ {\tilde{x}}_{\mathrm{Z}}\hfill & (\mathrm{S}2:x_{\text{Zmin}}<{\tilde{x}}_{\mathrm{Z}}<x_{\text{Zmax}})\hfill \\ x_{\text{Zmin}}\hfill & (\mathrm{S}3:{\tilde{x}}_{\mathrm{Z}}\le x_{\text{Zmin}})\hfill \end{array}\right.\hfill \end{array}(4)$

$\begin{array}{ll}\hfill {\tilde{x}}_{\mathrm{Z}}& \stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}{}^{d}x+k_1(x-{}^{d}x)+k_2\dot{x},\hfill \end{array}(5)$

where ^dx is the referential position of the COM, and k₁ and k₂ are feedback gains. Suppose the actual ZMP is manipulated to track the desired ZMP without delay, i.e., x_Z =^dx_Z. The closed-loop system becomes

$\ddot{x}=\left\{\begin{array}{cc}{\zeta }^{2}x-{\zeta }^2{x}_{\text{Zmax}}\hfill & \left(\text{S1}\right)\hfill \\ -{\zeta }^2(k_1-1)(x-x^d)-{\zeta }^2{k}_2\dot{x}\hfill & \left(\text{S2}\right)\hfill \\ {\zeta }^{2}x-{\zeta }^2{x}_{\text{Zmin}}\hfill & \left(\text{S3}\right)\hfill \end{array}\right..(6)$

This is a piecewise-affine system. The gains k₁ and k₂ are related to the system poles − ζq₁ and − ζq₂ in (S2) as

$k_1=q_1{q}_2+1,k_2=\frac{q_1+q_2}{\zeta }.(7)$

Figure 2 shows the phase portraits of Eq. 6 with respect to some different sets of q₁ and q₂. Four lines that characterize the system in the figure are

$\begin{array}{ll}\hfill & l_1:x+\frac{\dot{x}}{\zeta }=x_{\text{Zmin}}\hfill \end{array}(8)$

$\begin{array}{ll}\hfill & l_2:x+\frac{\dot{x}}{\zeta }=x_{\text{Zmax}}\hfill \end{array}(9)$

$\begin{array}{ll}\hfill & l_a:{}^{d}x+k_1(x-{}^{d}x)+k_2\dot{x}=x_{\text{Zmin}}\hfill \end{array}(10)$

$\begin{array}{ll}\hfill & l_b:{}^{d}x+k_1(x-{}^{d}x)+k_2\dot{x}=x_{\text{Zmax}},\hfill \end{array}(11)$

where l₁ and l₂ are asymptotic lines in states (S1) and (S3). l_a and l_b in the portraits are the switching lines between (S1), (S2), and (S3); (S1) and (S2) are separated by l_a, and (S2) and (S3) by l_b, respectively. The blue areas are the stable regions, where $(x,\dot{x})$ stably converges to (^dx, 0). It was also figured out that the controller with q₁ = 1 satisfies the capturability condition (Pratt et al., 2006; Koolen et al., 2012), which is a sufficient condition for the standing stability (Hof, 2008).

FIGURE 2

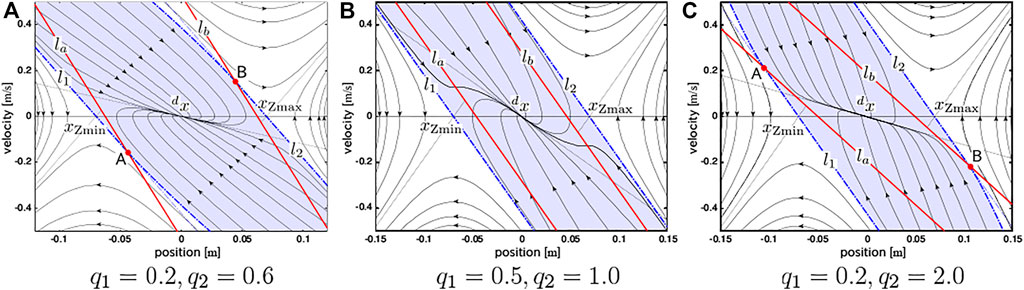
FIGURE 2. Phase portraits of the COM-ZMP model and the piecewise-linear controller with respect to different eigenvalues. (A) q₁ = 0.2, q₂ = 0.6 (B) q₁ = 0.5, q₂ = 1.0 (C) q₁ = 0.2, q₂ = 2.0.

The above controller does not assume any particular body constitution but highlights the dominant dynamics and constraint due to the unilaterality of contact forces, which is hard to be seen when focusing on only some joints.

3 Motion Measurement Protocol to Collect Trajectories in the State Space

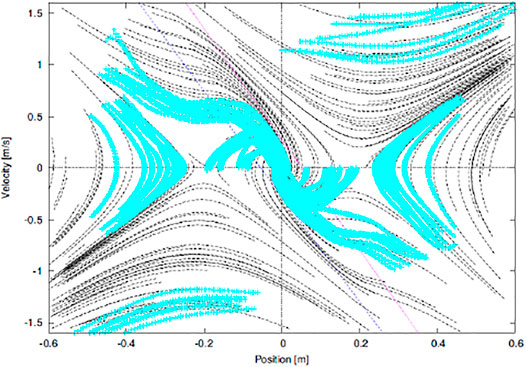
Now, we aim to see if the system represented by Eq. 6 fits the actual human behavior in stance, which is achieved by applying the system identification to measured motion data and evaluating the error of the identified parameters. It is important to collect motion trajectories from as broad area of the state space as possible for a reliable identification. However, it is not easy since a subject can start his or her motion only from a stable resting state, meaning that he or she can start motion only from points on the line x = 0 between x_Zmin and x_Zmax. The motion trajectories that we can observe in regular situations exist within a narrow area near the point of equilibrium in the state space as depicted in Figure 3. To measure motions in a distance from the point of equilibrium, we have to devise a protocol.

FIGURE 3

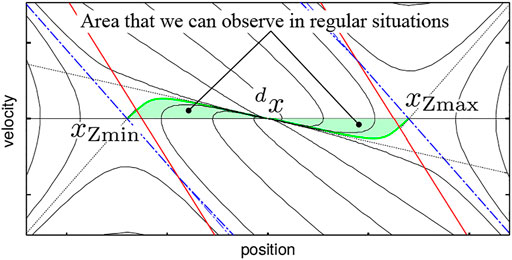
FIGURE 3. In normal situations, motion trajectories that we can observe exist within a narrow (green) area near the point of equilibrium (^dx, 0).

We know the phase portrait in the theory as Figure 2 and can associate it with the following four typical behaviors:

A) regulatory motions to the referential position against a perturbation

B) regulatory motions from a far posture to the referential position

C) falling-down motions over the referential position

D) failure motions to recover to the referential position

Our idea is to cover the regions that correspond to the above behaviors in the state space by adding preparatory motions to each trial to accelerate the COM to the target initial states as depicted in Figure 4 with helps of a holding platform (a ladder) and an assistant person who perturbs the subject.

FIGURE 4

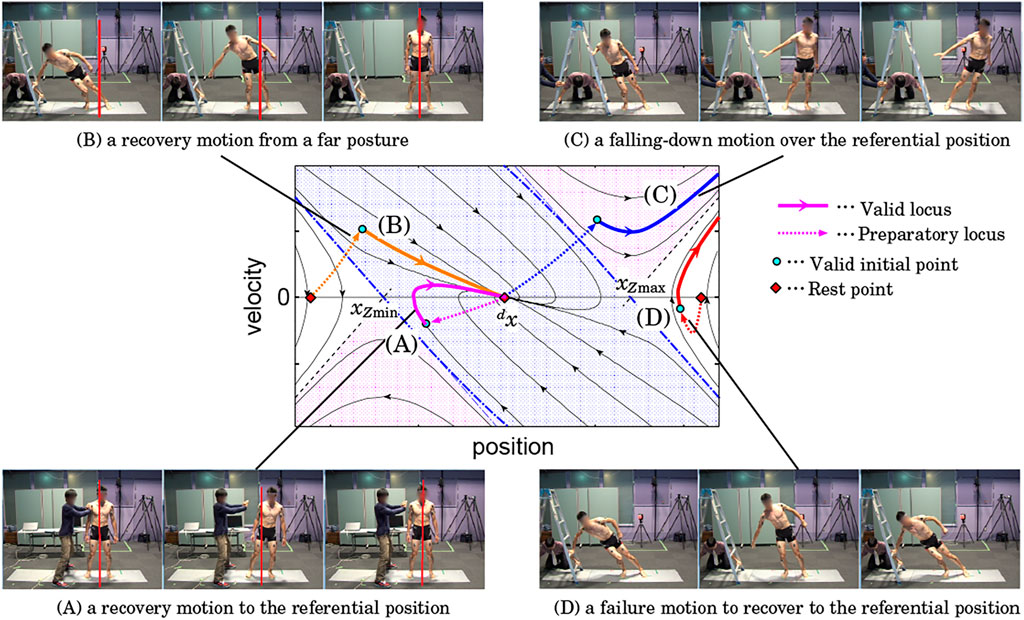
FIGURE 4. A set of motions to visualize standing stabilization behavior of a human. The labels (A) – (D) are corresponding to the groups of loci in the center figure.

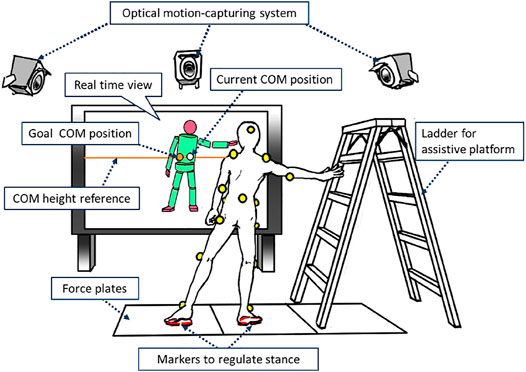
We conducted motion measurement experiments based on the above protocol. The subject was a 21-year-old male, who was 181 cm tall and weighed 70 kg. His kinematics parameters and mass properties were identified before the experiments based on a method proposed by Ayusawa et al. (2011). The subject was informed about the objective and risk of the experiment and understood them in advance. Figure 5 illustrates the setup for the motion measurement. The referential point was set at the same position and visually presented to the subject on a monitor in front of him in every trial. The point was defined as the origin, i.e., ^dx = 0. An optical motion capture system (MAC3D System; Motion Analysis Corp.) was used to acquire 3D trajectories of retroreflective markers attached to the subject’s body every 5ms. They were converted to the trajectory of the whole-body configuration through the inverse kinematics. Then, the trajectory of the COM was computed through the forward kinematics based on the mass property identified before the experiment. Measurement noises were reduced by a second-order Butterworth filter with 2Hz of cutoff frequency. A history of the velocity and acceleration of the COM were computed by numerically differentiating it. The trajectory of the ZMP was also computed from a history of the reaction forces. The partial trajectories of preparatory motions were detected and discarded in a postprocess. In the case of (A), the phases in which the subject was pushed by the assistant person were segmented by referring the recorded scenes. Regarding the types (B), (C), and (D), distinct profiles of the reaction force from the ladder were found since the subject strongly pushed it to accelerate himself. It should be also noted that this does not require severely accurate segmentations since reliable identifications are possible if sufficient length of the trajectories is provided. In this way, 8 × 2 trajectories for the above types (A)–(D) of motions were collected in symmetric manners with respect to the point of equilibrium. Hence, the total number of trajectories was 64.

FIGURE 5

FIGURE 5. Motion measurement system setup.

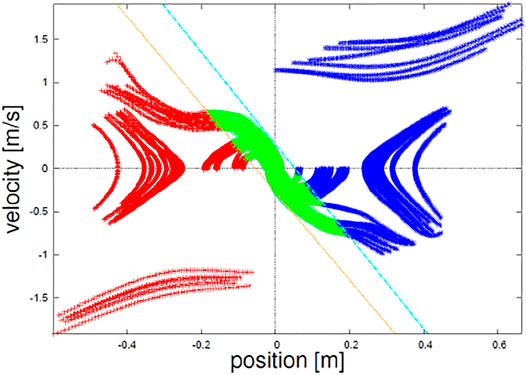
Figure 6 shows the trajectories of the COM reproduced based on the above-proposed protocol and plotted in the state space. The same types of trajectories are grouped by color. This qualitatively shows a similarity to the theoretical phase portrait (Figure 2).

FIGURE 6

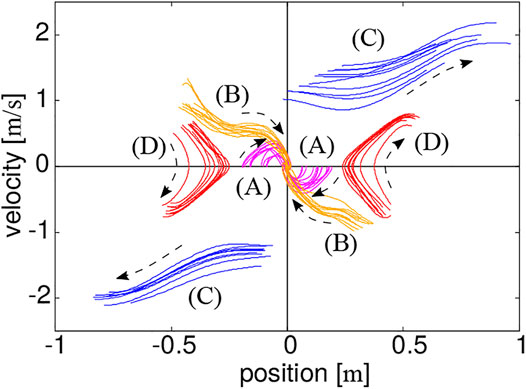
FIGURE 6. Trajectories of the COM measured based on the proposed protocol, where their directions are indicated by dashed arrows.

4 Identification of the System Based on Clustering Techniques

Methods for the parameter identification from the measured trajectories are described in this section. Let us redescribe the system in a general form of a piecewise-affine differential equation as

$\ddot{x}=\left\{\begin{array}{cc}{c}_{11}x+c_{12}\dot{x}+c_{13}\hfill & \left(\text{S1}\right)\hfill \\ c_{21}x+c_{22}\dot{x}+c_{23}\hfill & \left(\text{S2}\right)\hfill \\ c_{31}x+c_{32}\dot{x}+c_{33}\hfill & \left(\text{S3}\right)\hfill \end{array}\right.,(12)$

where {c_ij} (i, j = 1, 2, 3) are constant coefficients. The above is equivalent to Eq. 6 if

$\begin{array}{llllll}\hfill c_{11}& ={\zeta }^2,\hfill & \hfill c_{12}& =0,\hfill & \hfill c_{13}& =-{\zeta }^2{x}_{\text{Zmax}},\hfill \end{array}(13)$

$\begin{array}{llllll}\hfill c_{21}& =-{\zeta }^2(k_1-1),\hfill & \hfill c_{22}& =-{\zeta }^2{k}_2,\hfill & \hfill c_{23}& ={\zeta }^2(k_1-1){}^{d}x,\hfill \end{array}(14)$

$\begin{array}{llllll}\hfill c_{31}& ={\zeta }^2,\hfill & \hfill c_{32}& =0,\hfill & \hfill c_{33}& =-{\zeta }^2{x}_{\text{Zmin}}.\hfill \end{array}(15)$

The idea here is to cluster all the samples of the discretized motion loci so that they result in the most likely identification of {c_ij}. As shown in Eq. 4, the switching condition is whether the ZMP is inside of the supporting region or not. It may seem to be possible to know which of (S1), (S2), and (S3) the sampled state belongs to by checking the location of the measured ZMP with respect to the measured supporting region. This approach, however, does not work well since the human’s feet are neither rigid nor adhered to the ground, and the boundaries of the supporting region x_Zmin and x_Zmax are not clearly defined in the actual motions, although their nominal values are available. We examined K-means method (MacQueen, 1967; Duda and Hart, 1973) and EM algorithm (Dempster et al., 1977) for the clustering, the former of which also provided the initial guess of the latter.

Given a set of discretized position, velocity, and acceleration {(x_k, v_k, a_k)} (k = 1, …, N) of the motion trajectories, the algorithm based on the K-means method is summarized as follows.

1) Divide all samples into three groups as the initial guess of {S_i} (i = 1, 2, 3), where S_i belongs to (Si).

2) Identify {c_ij} from S_i (i, j = 1, 2, 3) through the least square minimization.

3) Reassociate each sample {(x_k, v_k, a_k)} with S_i such that the error $e_{ik}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}|a_k-c_{i1}{x}_k-c_{i2}{v}_k-c_{i3}|$ is the minimum of {e_jk} (j = 1, 2, 3).

4) Repeat the above 2–3 until all the samples are settled into invariant groups.

Let us name the above method (M1).

A fact that Eq. 12 forms three planes in x-$\dot{x}$-$\ddot{x}$ space and the dividing lines l_a and l_b are intersections of those planes suggests another idea to alter the above step 3 to

3^') Find the dividing lines l_a and l_b from the tentatively identified {c_ij}, and regroup all the samples based on them.

Let us name the above modified K-means method (M2).

The result of the above algorithms might be improved in terms of accuracy by conducting EM algorithm, which does not explicitly divide the samples into groups but estimates the most likely parameters through a stochastic computation. It goes with the Gaussian mixture model assumption as follows.

1) Let the result of (M1) be the initial guess of {c_ij}, and compute the corresponding initial covariance matrices {Σ_i} and mixing factors {π_i}.

2) Compute the (tentative) responsibilities {γ_ik} of each sample based on the prior probability of the corresponding sample to be produced from the current guess. (Expectation step)

3) Update {c_ij}, {Σ_i}, and {π_i} from {γ_ik}. (Maximization step)

4) Repeat the above 2–3 until the guess is settled into invariant values.

Refer to the original paper for more details. Let us name the above method (M3).

The identification based on the three methods (M1) ∼ (M3) described in the previous section was conducted with respect to the trajectories acquired in the previous section. The following techniques were additionally adopted for preprocess due to practical reasons.

• The samples {(x_k, v_k, a_k)} were offset by the referential position (^dx, 0, 0), and each component was scaled by the minimum and maximum values of all the samples.

• Instead of Eq. 12, the following equation was assumed:

$x=\left\{\begin{array}{cc}{c}_{11}^{\prime }\ddot{x}+c_{12}^{\prime }\dot{x}+c_{13}^{\prime }\hfill & \left(\text{S1}\right)\hfill \\ c_{21}^{\prime }\ddot{x}+c_{22}^{\prime }\dot{x}+c_{23}^{\prime }\hfill & \left(\text{S2}\right)\hfill \\ c_{31}^{\prime }\ddot{x}+c_{32}^{\prime }\dot{x}+c_{33}^{\prime }\hfill & \left(\text{S3}\right)\hfill \end{array}\right.,(16)$

where $\{c_{ij}^{\prime }\}$ were also constant coefficients. This coordinate transformation worked for separations of the planar clusters and was necessary for success. $\{c_{ij}^{\prime }\}$ were converted to the equivalent set {c_ij} afterward.

• The KKZ method (Katsavounidis et al., 1994) was applied for the initialization of (M1) and (M2).

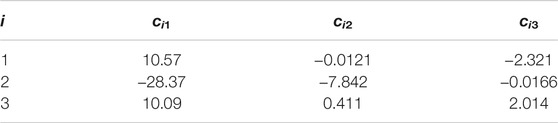
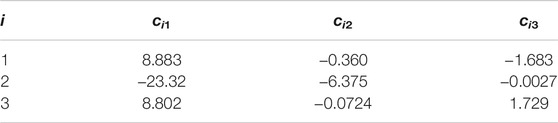
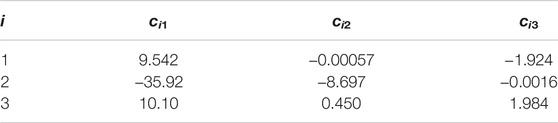
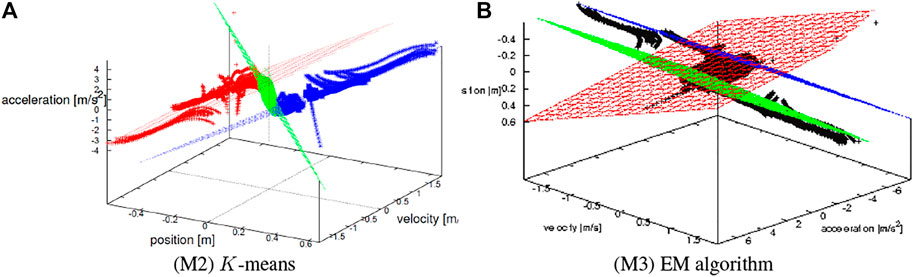
Tables 1, 2, and 3 show the identified parameters by (M1), (M2), and (M3), respectively.

TABLE 1

TABLE 1. Result of parameter identification by (M1).

TABLE 2

TABLE 2. Result of parameter identification by (M2).

TABLE 3

TABLE 3. Result of parameter identification by (M3).

5 Discussion

We can estimate some values of c₁₁, c₁₂, c₁₃, c₂₃, c₃₁, c_32, and c₃₃ from nominal values of ζ, ^dx, x_Zmin, and x_Zmax before the identification based on Eqs 13–15.

• c₁₂ ≃ 0, c₃₂ ≃ 0

• c₂₃ ≃ 0 since ^dx = 0

• c₁₁ ≃ c₃₁ ≃ 10 based on the nominal height of the COM

• − c₁₃ ≃ c₃₃ ≃ 2 based on the nominal height of the COM, the nominal width of the foot, and the nominal stance width

The results conform to the above. On the other hand, c₁₂ and c₃₂ in any result are different from each other by an order of magnitudes. It means that the time constants of the outward and inward falling movements are different in the case of a human. This cannot be explained when assuming a symmetric COM-ZMP model.

The standard deviations of (M1), (M2), and (M3) were 1.041, 0.764, and 1.026, respectively. Surprisingly, (M2) achieved the best result even over (M3) from this viewpoint. A possible reason is that the K-means method explicitly associates each sample with any of the divided regions (S1) ∼ (S3) so that the estimation accuracy is increased if the association is correct, while EM algorithm remains nonzero possibilities for all the regions which the samples are associated with.

As noted in the previous section, Eq. 12 forms three planes in x-$\dot{x}$-$\ddot{x}$ space. Figures 7A,B visualize the planes identified by (M2) and (M3), respectively. The samples in (a) are drawn in the same color with the associated plane, while those in (b) are not since EM algorithm does not explicitly associate each sample with the planes. It is confirmed that they are correctly identified in a qualitative sense and the planes in (S2) fit more than the others in particular. Figure 8 shows the top view of Figure 7A, from which it is seen that the samples are consistently grouped with respect to the dividing lines.

FIGURE 7

FIGURE 7. Identified planes in x-$\dot{x}$-$\ddot{x}$ space. (A) (M2) K-means. (B) (M3) EM algorithm.

FIGURE 8

FIGURE 8. Result of division of the state space by (M2).

The trajectories of the identified dynamical system by (M2) are overlaid on the measured loci in Figure 9. It seems almost consistent, though a part around the initial phase of the falling-down motion over the referential position (type (C)) is deviated from the trajectories. It might be because the human subject unconsciously pushed himself outward too much. How to control the subject’s behavior more finely or discard such preparatory trajectories should be discussed in the future.

FIGURE 9

FIGURE 9. Result of the system identification by (M2).

Overall, the hypothesis that the piecewise-linear feedback scheme of the state of the COM to the manipulation of the ZMP reasonably models a human’s standing stabilization controller was supported at least with respect to the measured subject through the above discussions, although there are some points of improvement of the model.

6 Conclusion

An identification process of a human’s standing stabilization behavior modeled as a piecewise-linear feedback control, i.e., the COM-ZMP regulator, was proposed. The contributions of this article are summarized into the following two points.

1) A protocol to collect motion data for reliable system identification was presented based on the expected phase portrait of the system.

2) Some computation methods based on clustering techniques were proposed for the identification of the piecewise-affine dynamical system.

A model of a human’s standing controller was identified by combining the above protocol and the computation method. The result quantitatively supported a hypothesis that the COM-ZMP regulator, which had been originally designed for humanoid robots, models a human’s standing control scheme. We additionally pointed out and discussed some differences of the actual human’s behavior from the model.

Note again that this study does not aim to make statistics of the identified parameters to generalize the humans’ control scheme but to develop a method to identify an individual controller. Hence, the number of subjects does not concern at the current stage, although the validity of the model should be investigated carefully by accumulating case studies.

We noticed that the studied behavior was not a “natural” but rather a “defensive” standing. We know reports of some cases (Moretto et al., 2016; Lim and Park, 2018; Neptune and Vistamehr, 2019) that humans’ behaviors are not necessarily approximated well by the COM-ZMP representation. On the other hand, we needed to pose some conditions on the subject to control his behavior for reliable identification as the first step. We need to relax the conditions by extending the model to elaborate more natural human behaviors that require hip-strategy-like counter-phase coordination of joints. Such a model may be retransferred to a whole-body control scheme for humanoid robots. This is one of the important future works.

The parameters of controllers for humanoid robots are designed in general based on the stabilization performance and the hardware responsivity against perturbations. We think that this knowledge is directly utilized in an evaluation of humans’ body control abilities. Namely, the abilities to coordinate the whole body, which are hardly seen in a single physical performance such as the muscle strength and the lung capacity, can be measured based on the identified parameters as well as other holistic approaches (Torricelli et al., 2020).

Data Availability Statement

The datasets presented in this article are not readily available because it includes personal information. Requests to access the datasets should be directed to zhidao@ieee.org.

Ethics Statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. The participants provided their orally informed consent to participate in this study.

Author Contributions

Conception and design of study: TS. Acquisition of data: TS, DK, and NM. Analysis and/or interpretation of data: TS, DK, and NM. Drafting the manuscript: TS and DK. Revising the manuscript critically for important intellectual content: TS. Approval of the version of the manuscript to be published: TS, DK, and NM.

Funding

This work was supported by Grant-in-Aid for Young Scientists (A) #22680018, Japan Society for the Promotion of Science.

Conflict of Interest

Author TS is employed by OMRON Corporation. Authors DK and NM are employed by Kawada Robotics Corporation.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors cordially express our gratitude to Prof. Yoshihiko Nakamura, Dr. Ko Ayusawa, Dr. Akihiko Murai, Dr. Yosuke Ikegami and other members of Nakamura-Takano laboratory in the University of Tokyo for their cooperation on the experiments.

References

Atkeson, C. G., and Stephens, B. (2007). “Multiple Balance Strategies from One Optimization Criterion,” in Proceedings of the 2007 IEEE-RAS International Conference on Humanoid Robots, Pittsburgh, USA, November 29–December 1, 2007, 57–64. doi:10.1109/ichr.2007.4813849

CrossRef Full Text | Google Scholar

Ayusawa, K., Venture, G., and Nakamura, Y. (2011). “Real-Time Implementation of Physically Consistent Identification of Human Body Segments,” in Proceedings of 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, May 9–13, 2011, 6282–6287. doi:10.1109/icra.2011.5979903

CrossRef Full Text | Google Scholar

Bemporad, A., Garulli, A., Paoletti, S., and Vicino, A. (2003). “Set Membership Identification of Piecewise Affine Models,” in Proceedings of 13th IFAC Symposium on System Identification, Rotterdam, Netherlands, August 27–29, 2003, 1826–1831. doi:10.1016/s1474-6670(17)35019-x

CrossRef Full Text | Google Scholar

Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977). Maximum Likelihood from Incomplete Data via theEMAlgorithm. J. R. Stat. Soc. Ser. B (Methodological) 39, 1–22. doi:10.1111/j.2517-6161.1977.tb01600.x

CrossRef Full Text | Google Scholar

Duda, R. O., and Hart, P. E. (1973). Pattern Classication and Scene Analysis. New York: John Wiley & Sons.

Google Scholar

Ferrari-Trecate, G., Muselli, M., Liberati, D., and Morari, M. (2003). A Clustering Technique for the Identification of Piecewise Affine Systems. Automatica 39, 205–217. doi:10.1016/s0005-1098(02)00224-8

CrossRef Full Text | Google Scholar

Fujimoto, Y., and Kawamura, A. (1998). Simulation of an Autonomous Biped Walking Robot Including Environmental Force Interaction. IEEE Robot. Automat. Mag. 5, 33–42. doi:10.1109/100.692339

CrossRef Full Text | Google Scholar

Gatev, P., Thomas, S., Kepple, T., and Hallett, M. (1999). Feedforward Ankle Strategy of Balance during Quiet Stance in Adults. J. Physiol. 514, 915–928. doi:10.1111/j.1469-7793.1999.915ad.x

CrossRef Full Text | Google Scholar

Goodworth, A. D., and Peterka, R. J. (2010). Influence of Stance Width on Frontal Plane Postural Dynamics and Coordination in Human Balance Control. J. Neurophysiol. 104, 1103–1118. doi:10.1152/jn.00916.2009

CrossRef Full Text | Google Scholar

Henze, B., Roa, M. A., and Ott, C. (2016). Passivity-Based Whole-Body Balancing for Torque-Controlled Humanoid Robots in Multi-Contact Scenarios. Int. J. Robotics Res. 35, 1522–1543. doi:10.1177/0278364916653815

CrossRef Full Text | Google Scholar

Hof, A. L. (2008). The 'Extrapolated Center of Mass' Concept Suggests a Simple Control of Balance in Walking. Hum. Move. Sci. 27, 112–125. doi:10.1016/j.humov.2007.08.003

CrossRef Full Text | Google Scholar

Hyon, S.-H. (2009). Compliant Terrain Adaptation for Biped Humanoids without Measuring Ground Surface and Contact Forces. IEEE Trans. Robot. 25, 171–178. doi:10.1109/tro.2008.2006870

CrossRef Full Text | Google Scholar

Kajita, S., Kanehiro, F., Kaneko, K., Fujiwara, K., Harada, K., Yokoi, K., et al. (2003). “Biped Walking Pattern Generation by Using Preview Control of Zero-Moment Point,” in Proceedings of the 2003 IEEE International Conference on Robotics & Automation, Taipei, Taiwan, September 14–19, 2003, 1620–1626.

Google Scholar

Kaneta, D., Murai, N., and Sugihara, T. (2012). “Visualization and Identification of Macroscopic Dynamics of a Human Motor Control Based on the Motion Measurement,” in Proceedings of the 2012 IEEE-RAS International Conference on Humanoid Robots, Osaka, Japan, November 29–December 12, 2012, 767–772. doi:10.1109/humanoids.2012.6651606

CrossRef Full Text | Google Scholar

Kaneta, D., Murai, N., and Sugihara, T. (2013). “Reassessment of COM-ZMP Model for the Identification of Lateral Standing Controller of a Human,” in Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, November 3–8, 2013, 2351–2356. doi:10.1109/iros.2013.6696686

CrossRef Full Text | Google Scholar

Katsavounidis, I., Jay Kuo, C.-C., and Zhen Zhang, Z. (1994). A New Initialization Technique for Generalized Lloyd Iteration. IEEE Signal. Process. Lett. 1, 144–146. doi:10.1109/97.329844

CrossRef Full Text | Google Scholar

Koolen, T., de Boer, T., Rebula, J., Goswami, A., and Pratt, J. (2012). Capturability-Based Analysis and Control of Legged Locomotion, Part 1: Theory and Application to Three Simple Gait Models. Int. J. Robotics Res. 31, 1094–1113. doi:10.1177/0278364912452673

CrossRef Full Text | Google Scholar

Lim, H., and Park, S. (2018). Kinematics of Lower Limbs during Walking Are Emulated by Springy Walking Model with a Compliantly Connected, Off-Centered Curvy Foot. J. Biomech. 71, 119–126. doi:10.1016/j.jbiomech.2018.01.031

CrossRef Full Text | Google Scholar

Lippi, V., Mergner, T., Szumowski, M., Zurawska, M. S., and Zielińska, T. (2016). “Human-Inspired Humanoid Balancing and Posture Control in Frontal Plane,” in Proceedings of ROMANSY 21 - Robot Design, Dynamics and Control. Editors V Parenti-Castelli, and W Schiehlen (Cham: Springer), 285–292. doi:10.1007/978-3-319-33714-2_32

CrossRef Full Text | Google Scholar

MacQueen, J. B. (1967). “Some Methods for Classication and Analysis of Multivariate Observations,” in Proceedings of the fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, USA, June 21–July 18, 1967 (University of California Press), 1.

Google Scholar

Mitobe, K., Capi, G., and Nasu, Y. (2000). Control of Walking Robots Based on Manipulation of the Zero Moment point. Robotica 18, 651–657. doi:10.1017/s0263574700002708

CrossRef Full Text | Google Scholar

Moretto, P., Villeger, D., Costes, A., and Watier, B. (2016). Elastic Energy in Locomotion: Spring-Mass vs. Poly-Articulated Models. Gait & Posture 48, 183–188. doi:10.1016/j.gaitpost.2016.05.015

CrossRef Full Text | Google Scholar

Morimoto, J., Endo, G., Nakanishi, J., and Cheng, G. (2008). A Biologically Inspired Biped Locomotion Strategy for Humanoid Robots: Modulation of Sinusoidal Patterns by a Coupled Oscillator Model. IEEE Trans. Robot. 24, 185–191. doi:10.1109/tro.2008.915457

CrossRef Full Text | Google Scholar

Mueller, M. J., Sinacore, D. R., Hoogstrate, S., and Daly, L. (1994). Hip and Ankle Walking Strategies: Effect on Peak Plantar Pressures and Implications for Neuropathic Ulceration. Arch. Phys. Med. Rehabil. 75, 1196–1200. doi:10.1016/0003-9993(94)90004-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Murai, N., and Sugihara, T. (2020). “Identification of COM Control Behavior of a Human in Stance as a Dynamical System,” in The 8th IEEE RAS/EMBS International Conference on Biomedical Robotics and Biomechatronics, online, November 29–December 1, 2020, 95–100. doi:10.1109/biorob49111.2020.9224431

CrossRef Full Text | Google Scholar

Murai, A., Yamane, K., and Nakamura, Y. (2008). Modeling and Identification of Human Neuromusculoskeletal Network Based on Biomechanical Property of Muscle. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2008, 3706–3709. doi:10.1109/IEMBS.2008.4650014

PubMed Abstract | CrossRef Full Text | Google Scholar

Murai, N., Kaneta, D., and Sugihara, T. (2013). “Identification of a Piecewise Controller of Lateral Human Standing Based on Returning Recursive-Least-Square Method,” in Proceedings of 2013 IEEE International Conference on Intelligent Robots and Systems, Tokyo, Japan, November 3–8, 2013, 96–101. doi:10.1109/iros.2013.6696338

CrossRef Full Text | Google Scholar

Nakamura, Y., and Yamane, K. (2000). Dynamics Computation of Structure-Varying Kinematic Chains and its Application to Human Figures. IEEE Trans. Robot. Automat. 16, 124–134. doi:10.1109/70.843167

CrossRef Full Text | Google Scholar

Nashner, L. M., and McCollum, G. (1985). The Organization of Human Postural Movements: A Formal Basis and Experimental Synthesis. Behav. Brain Sci. 8, 135–150. doi:10.1017/s0140525x00020008

CrossRef Full Text | Google Scholar

Neptune, R. R., and Vistamehr, A. (2019). Dynamic Balance during Human Movement: Measurement and Control Mechanisms. ASME J. Biomechanical Eng. 141, 0708011–07080110. doi:10.1115/1.4042170

CrossRef Full Text | Google Scholar

Peterka, R. J. (2009). Comparison of Human and Humanoid Robot Control of Upright Stance. J. Physiology-Paris 103, 149–158. doi:10.1016/j.jphysparis.2009.08.001

CrossRef Full Text | Google Scholar

Pratt, J., Carff, J., Drakunov, S., and Goswami, A. (2006). “Capture Point: A Step toward Humanoid Push Recovery,” in Proceeding of the 2006 IEEE-RAS International Conference on Humanoid Robots, Genoa, Italy, December 4–6, 2012, 200–207. doi:10.1109/ichr.2006.321385

CrossRef Full Text | Google Scholar

Sugihara, T., and Morisawa, M. (2020). A Survey: Dynamics of Humanoid Robots. Adv. Robotics 34, 1353–1369. doi:10.1080/01691864.2020.1778524

CrossRef Full Text | Google Scholar

Sugihara, T., Nakamura, Y., and Inoue, H. (2002). “Realtime Humanoid Motion Generation through ZMP Manipulation Based on Inverted Pendulum Control,” in Proceedings of the 2002 IEEE International Conference on Robotics & Automation, Washington DC, USA, May 11–15, 2002, 1404–1409.

Google Scholar

Sugihara, T. (2009). “Standing Stabilizability and Stepping Maneuver in Planar Bipedalism Based on the Best COM-ZMP Regulator,” in Proceedings of the 2009 IEEE International Conference on Robotics & Automation, Kobe, Japan, May 12–17, 2009, 1966–1971. doi:10.1109/robot.2009.5152284

CrossRef Full Text | Google Scholar

Torricelli, D., Mizanoor, R. S. M., Lippi, V., Weckx, M., Mathijssen, G., Vanderborght, B., et al. (2020). “Benchmarking Human Likeness of Bipedal Robot Locomotion: State of the Art and Future Trends,” in Cognitive Systems Monographs (Cham: Springer), 36, 147–166. doi:10.1007/978-3-030-14126-4_8

CrossRef Full Text | Google Scholar

Vette, A. H., Masani, K., and Popovic, M. R. (2007). Implementation of a Physiologically Identified PD Feedback Controller for Regulating the Active Ankle Torque during Quiet Stance. Neural Syst. Rehabil. Eng. 15, 235–243. doi:10.1109/tnsre.2007.897016

PubMed Abstract | CrossRef Full Text | Google Scholar

Vidal, R., Soatto, S., Ma, Y., and Sastry, S. (2003). “An Algebraic Geometric Approach to the Identification of a Class of Linear Hybrid Systems,” in Proceedings of 42nd IEEE Conference on Decision and Control, Maui, USA, December 9–12, 2003, 167–172.

Google Scholar

Vukobratović, M., and Stepanenko, J. (1972). On the Stability of Anthropomorphic Systems. Math. Biosciences 15, 1–37. doi:10.1016/0025-5564(72)90061-2

CrossRef Full Text | Google Scholar

Yoshida, K., Nenchev, D. N., and Uchiyama, M. (1995). “Moving Base Robotics and Reaction Management Control,” in Proceedings of The Seventh International Symposium of Robotics Research, Herrsching, Germany, October 21–24, 1995, 100–109.

Google Scholar