- 1Department of Mechanical Engineering and Material Science, University of Pittsburgh, Pittsburgh, PA, United States
- 2Neuromuscular Control and Robotics Lab, Joint Department of Biomedical Engineering, North Carolina State University and the University of North Carolina Chapel-Hill, Raleigh, NC, United States
- 3Department of Biomedical Engineering at University of Wisconsin-Milwaukee, Milwaukee, WI, United States
- 4Department of Physical Medicine and Rehabilitation, School of Medicine and Department of Bioengineering, University of Pittsburgh, Pittsburgh, PA, United States
A hybrid exoskeleton comprising a powered exoskeleton and functional electrical stimulation (FES) is a promising technology for restoration of standing and walking functions after a neurological injury. Its shared control remains challenging due to the need to optimally distribute joint torques among FES and the powered exoskeleton while compensating for the FES-induced muscle fatigue and ensuring performance despite highly nonlinear and uncertain skeletal muscle behavior. This study develops a bi-level hierarchical control design for shared control of a powered exoskeleton and FES to overcome these challenges. A higher-level neural network–based iterative learning controller (NNILC) is derived to generate torques needed to drive the hybrid system. Then, a low-level model predictive control (MPC)-based allocation strategy optimally distributes the torque contributions between FES and the exoskeleton’s knee motors based on the muscle fatigue and recovery characteristics of a participant’s quadriceps muscles. A Lyapunov-like stability analysis proves global asymptotic tracking of state-dependent desired joint trajectories. The experimental results on four non-disabled participants validate the effectiveness of the proposed NNILC-MPC framework. The root mean square error (RMSE) of the knee joint and the hip joint was reduced by 71.96 and 74.57%, respectively, in the fourth iteration compared to the RMSE in the 1st sit-to-stand iteration.
1 Introduction
Functional electrical stimulation (FES) is often prescribed to reanimate standing and walking functions in people with spinal cord injury (SCI) and other gait disorders due to stroke, multiple sclerosis, etc. (Chang et al. (2016); Nagai et al. (2016); Bulea et al. (2013)). FES is usually applied transcutaneously via adhesive electrode pads that deliver electrical currents to the skeletal muscles’ motor units. Electrical stimulation of the lower-limb muscles, when coordinated, can produce desired standing and walking movements. However, FES causes a rapid onset of muscle fatigue (Bickel et al. (2011)), which reduces the muscle’s ability to sustain or produce contraction force and significantly decreases the duration of FES-elicited tasks.
FES can be combined with a passive orthosis (Sharma et al. (2014); Bao et al. (2016); Alouane et al. (2019)) to alleviate the effects of FES-induced muscle fatigue. These hybrid devices lock knee joints during stance or standing to reduce FES stimulation duration but may not provide additional torque to the knee joints. Battery-operated powered exoskeletons (Strausser and Kazerooni (2011); Neuhaus et al. (2011); Farris et al. (2014)) can also supplement FES-elicited joint torque (del Ama et al., 2014); Ha et al. (2015); Kirsch et al. (2014); Alibeji et al. (2018b)). This combination, which is also known as a hybrid exoskeleton, can overcome FES limitations. Supplementing FES-induced muscle contractions with robotic assistance reduces the overall stimulation duty cycle, delaying the onset of muscle fatigue during high torque–demanding physical exercises like sit-to-stand tasks. The shared use may also reduce actuator size and power consumption in the powered exoskeleton. More importantly, unlike powered exoskeletons that passively move the limbs, FES-induced active muscle contractions contribute to neuroplasticity that may recover the lost limb function (Popovic et al. (2012)). The use of FES also promotes or improves bone health, overall limb elasticity, and cardiovascular and metabolic benefits (Peckham and Knutson (2005)). Thus, its integration with an exoskeleton system is likely to maintain or enhance the therapeutic benefits.
Despite its promising benefits, the hybrid exoskeleton’s dynamic shared control is an open research topic. Actuation redundancy due to FES and electrical motors’ simultaneous use and modulation of the shared effort to compensate for FES-induced fatigue dynamics are challenging control problems. Recent research efforts in this direction certainly inform ways to implement shared control in a hybrid exoskeleton, but these control designs did not explicitly account for FES-induced fatigue dynamics in functionally relevant and multi-DOF lower-limb movements. In the study by Quintero et al. (2012), the authors used an adaptive control method to allocate inputs to motors and FES. In studies by both (del Ama et al., 2014) and (Ha et al. (2015), a combination of feed-forward learning control and proportional-integral-derivative (PID) feedback controlled electric motors and FES. Optimal control is also a suitable approach for cooperative control of FES and an electric motor in the hybrid exoskeleton. Kirsch et al. (2018), Bao et al. (2016), and Bao et al. (2019) optimally controlled a one–degree-of-freedom (DOF) hybrid leg extension machine using a nonlinear model predictive control (NMPC) method to modulate FES and electric motor assistance as per the FES-induced fatigue dynamics. However, a muscle fatigue–based dynamic effort distribution between FES and an electric motor has not been attempted in functionally relevant and multi-DOF lower-limb movements. As a step toward this direction, this study aims to show the feasibility of a low-level optimal MPC strategy to dynamically distribute a higher-level knee torque between FES and the electric motor during sit-to-stand tasks.
For controlling different muscle groups and multiple electric motors during walking or swing-like leg movements, a muscle synergy–inspired controller used a set of synergy blocks in the works of Alibeji et al. (2017), Alibeji et al. (2015), and Alibeji et al. (2018a). Each synergy acted as a set of allocation ratios for different actuators. A modified PD controller provided robustness to modeling uncertainties, and a robust adaptive term modified the coefficients of a combination of synergies to compensate for the muscle fatigue. The muscle synergy–inspired controllers in the studies by Alibeji et al. (2017, 2015, 2018a) enabled automatic allocation of effort between the powered exoskeleton and FES and have been shown to provide good performance. However, the muscle synergy–inspired control design did not employ a real-time optimal control approach, and even then, it is not yet shown if an optimal control allocation can be embedded into a robust control framework that guarantees desired joint torque levels or system stability despite modeling uncertainties and disturbances.
Due to a lack of optimal control allocation strategies for the hybrid exoskeleton for sit-to-stand, or any functional task in general, this study explored the use of an MPC strategy to allocate FES and electric motor torques. The MPC strategy in this study hinges on a higher-level desired torque generator. However, unlike the techniques discussed in the study by Zhang et al. (2015) that generate torque based on predetermined angles, electromyography, or time, we use a novel neural network (NN)-based position tracking control approach to generate desired joint torques. The NN-based control approach and the associated NN update laws use a discrete Lyaupunov-like stability analysis that shows asymptotic error convergence for the first time for iterative sit-to-stand tasks. The NN-based control approach is robust to modeling uncertainties and time-varying disturbances in the FES-driven musculoskeletal dynamics. Notably, the NN-based control approach is derived to iteratively increase the feed-forward learning component and decrease the high-level torque generator’s high gain feedback component. The feed-forward learning is an improvement over our recent approach that used a high-gain position tracking controller for high-level torque generation for an experimental study on sit-to-stand tasks (Bao et al. (2020a)). Unlike most exoskeleton controllers that follow a time-dependent desired joint trajectory (Ha et al. (2012); Contreras-Vidal et al. (2016); Alibeji et al. (2018b); Bae and Tomizuka (2012)) or a desired time-dependent or EMG-generated torque trajectory (Zhang et al. (2015)), the designed NN-based approach follows state-dependent desired joint trajectories known as virtual constraints (Westervelt et al. (2007); Gregg and Sensinger (2014)).
Compared to our previous simulation studies by Molazadeh et al. (2019), Bao et al. (2020b), and Molazadeh et al. (2018a,b), the study presents a more detailed derivation of the controller, improved robustness to modeling uncertainties, and supporting stability analysis. Furthermore, extensive sit-to-stand experiments with a hybrid exoskeleton validated the approach on four participants with no disabilities. The experiments validated the proposed bi-level control framework for sharing control between the powered exoskeleton and FES dynamically.
The article is organized as follows. Section 2 describes the overall shared control design, which is followed by Section 3, which presents the experimental results, followed by discussion in Section 4 and the conclusion in Section 5. Supplementary Appendices A–D provide a more detailed open-loop and closed-loop error dynamics development, the stability analysis, virtual constraint design, and the MPC allocation algorithm, respectively.
2 Shared Control Framework
The main task of our control framework is to implement a learning control approach that estimates unknown/uncertain dynamics in an iterative fashion and then use the estimates in a controller that outputs stabilizing torques for a desired movement. Therefore, in the first subsection, an NNILC method is presented as a top-level controller. The NNILC method estimates the unknown/uncertain dynamics, and based on these estimates, it provides robust and stabilizing torques for a low-level controller. Furthermore, in the next subsection, a model predictive approach is used as the low-level controller to distribute the NNILC-designed torque among FES and the powered exoskeleton. This control framework can be used for repetitive movements including repeated sit-to-stand and walking. Below, we first present a general hybrid exoskeleton model.
An N-DOF hybrid exoskeleton that comprises Nf muscles where FES is applied, Nm electric motors, and a powered exoskeleton is modeled as follows:
where
2.1 Top-Level Control Structure
In this subsection, a top-level controller is presented. Its detailed derivation using the open-loop and closed-loop error dynamics are provided in Supplementary Appendix A.
The control objective is to ensure that the independent joint angle function,
which must be driven to zero. Subscription k shows the value of the variables in the kth iteration (e.g., in a repetitive sit-to-stand task, each sit-to-stand can be considered as one iteration).
The sliding surface
where λ1 and λ2 are positive constants and e1,k = − yk,
Based on the stability analysis provided in Supplementary Appendix B, the top-level controller, Uk, is designed as given below:
where
where
where
Fk in Eq. 4 is designed as follows:
where
where β1 and β2 are positive constants. The term Fk has been added to the top-level control input to keep the closed-loop system stable when considerable estimation errors may be present during initial iterations.
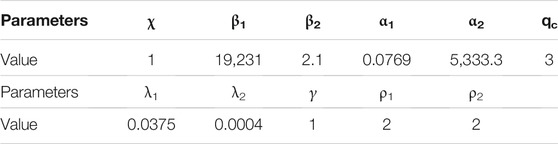
Remark 1. Because the top-level controller is based on NNs and updates itself every iteration, we call it the NN-based ILC. Choosing its control parameters has significant effect on the learning speed in each iteration and the closed-loop control system performance. For example, the speed of learning of σ can be changed by qc in Eq. 5. Similarly the speed of learning of f2 can be changed by changing the learning gains in the weight update laws. These gains are subsequently defined as ρ1 and ρ2 in (29) and (28) in Supplementary Appendix A. Please note that the speed of learning must not be chosen to be so high that it causes destabilization of the closed-loop control system and/or noise accumulation.
2.2 Predictive Allocation Strategy
In this subsection, a lower-level controller is formulated that determines the allocation of control between motors and FES. Mainly, the objective of the low-level controller is to constrain the optimized FES and the electric motor torque values to the desired torque level that is dictated by the top-level controller in the first subsection. An MPC allocation strategy is used for this purpose. A strategy is also designed to consider the muscle fatigue level by including a fatigue variable as a weighting variable in the cost function. The optimization objective is to minimize a cost function.
where the terms with a bar, for example,
where
where
where
The objective index
Control Distribution Between Functional Electrical Stimulation and Motor
The distribution of the control effort between FES and the powered motor is described in this subsection. Based on the calculated optimal normalized FES virtual input, uF,k, through the MPC algorithm and (11), the motor input can be calculated using the following:
where Uk is defined in Eq. 4, Bm is a known vector of motor constant gains, and ψk is given by the following:
where the spectral radius of
where
where
2.3 Overall Bi-Level Control Structure
The control schematic is depicted in Figure 1.
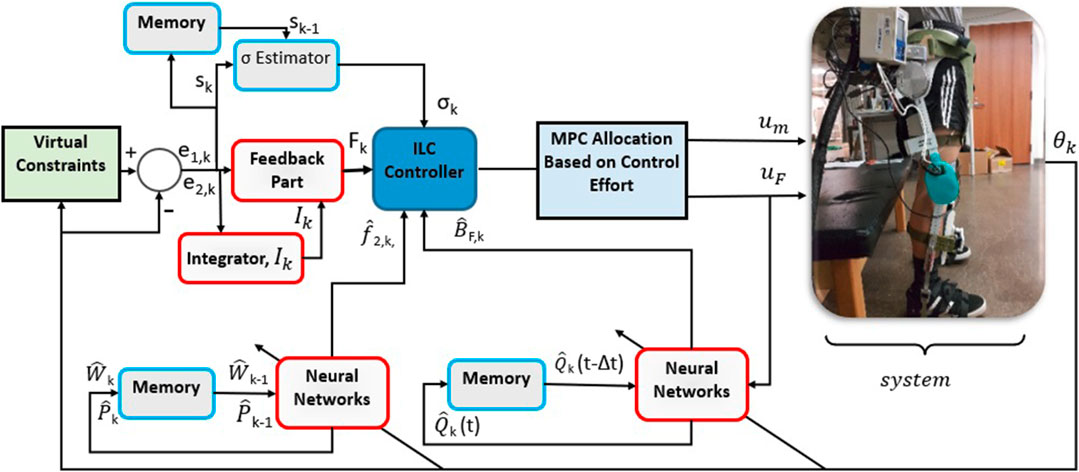
FIGURE 1. Structure of the proposed controller and the test bed that are used during experiments for the controller validation.
As can be seen in this figure, the top-level ILC controller block uses three inputs: the NN estimates
3 Experiments
We implemented the proposed controller for repetitive sit-to-stand tasks with a hybrid exoskeleton. The exoskeleton that is shown in Figure 1 was developed in our laboratory (Alibeji et al. (2018b)). The hip joints of the powered exoskeleton are actuated by two LPA-17–100-SP electric motors (Harmonic Drive, United States). These two motors have a maximum speed of 30 revolutions per minute (RPM) and a peak torque of 54 Nm. Two 90-W EC Flat Maxon motors (Maxon Motor, Sachseln, Switzerland) actuate the knee joints of the exoskeleton. The gearbox ratio for both knee and hip joints is 100:1. In the experiments, FES was applied on the quadriceps muscle group for the sit-to-stand task. The NNILC method was used to compute the stabilizing torques for the hip and knee joints during the task, while the MPC method was used to distribute inputs between FES and the electric motors at the knee joints.
The study was approved by the Institutional Review Board (IRB) at the University of Pittsburgh (IRB approval number: PRO 14040419) and the IRB of North Carolina State University (IRB approval number: 20553). Four male participants without any neurological disorders (listed in Table 1) were recruited for the study. Before each experiment, every participant signed an informed consent form.
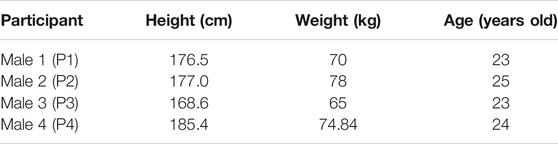
TABLE 1. Anthropometric characteristics of the participants. P1, P2, P3, and P4 represent the first, second, third, and fourth participant.
Before doing the control validation experiments, a set of trials were conducted on each participant to estimate the knee musculoskeletal model. These experiments were conducted while participants were seated in a leg extension machine. This model identification is needed for the execution of the MPC allocator. The model parameters of the participants, like the fatigue model parameters like the fatigue time constant,
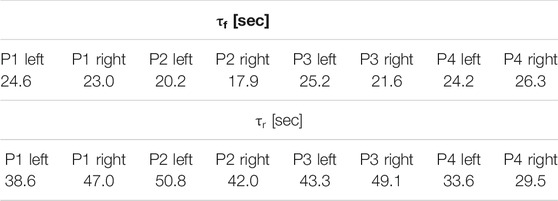
TABLE 2. Fatigue and recovery time constants τf and τr for participants 1, 2, 3, and 4 on both legs.
3.1 Sit-to-Stand Experiment Protocol
A real-time target machine (Speedgoat, Inc., Liebefeld, Switzerland) running at a control frequency of 400 Hz was used to control the exoskeleton and FES. The control implementation was programmed in Simulink (MathWorks, Inc., United States). The control parameters were programmed based on the following rules: γ = 1, β2 > 2, and
Stimulation Parameters: A pair of FES electrodes (size: 2 inches × 3.5 inches, Chattanooga Medical Supply, Inc., United States) were placed on the participant’s thighs, after shaving and cleaning the area. The distal electrode was placed on the medial side near the knee joint, while the proximal electrode was placed either at midline or slightly to the lateral side. A biphasic pulse train was delivered to the electrodes using an FES stimulator (RehaStim 8-channel stimulator, Hasomed, Inc., DE). The threshold and saturation current amplitude of the stimulation are defined as the minimal current amplitude that generates observable knee extension torque and the maximal current amplitude that cannot increase knee extension torque, respectively. Both the threshold and saturation current amplitudes were determined by using a set of prior tests (Bao et al. (2020a)). Due to the large current amplitude range between the threshold level and the saturation level (around 50 mA), a current amplitude modulating protocol with a stimulation frequency of 35 Hz and a pulse width of 400 μs was chosen in this work.
Since none of the participants had experienced FES or had used an exoskeleton before they were enrolled in the experiments, the participants were trained to properly use the hybrid exoskeleton. During the sit-to-stand task, a walker was used to assist the participant’s balance. There were multiple trials for each participant, and there were four iterations per trial. Between each iteration, we waited for a minute to provide each participant some rest. The trials conducted after the training were chosen for analysis to minimize any unexpected influence of the participants’ unfamiliarity with the hybrid device.
3.2 Results
Figure 2 demonstrates the snapshots of the sit-to-stand experiment from one of the trials for Participant 2.
The trajectory tracking results on both knee and hip joints for Participant 2 are illustrated in Figure 3. The figure includes the desired trajectories that are based on the virtual constraint function and the actual trajectories on both legs in the 1st and 4th iterations. The joint angle tracking errors of Participant 2 in the 1st iteration and the 4th iteration are shown in Figure 4. Left and right legs have different desired profiles. In general, the trajectory tracking errors and the resultant input torques of the left knee joint are lower than those of the right knee joint because the virtual constraints, used as the desired profile for the left knee joint, take the right knee joint actual angular position as the base. However, the desired profile of the right knee joint is pre-designed. Therefore, the right knee joint leads the left knee joint at the initiation of the task and during the movement. Because the right knee joint is the joint that initiates the task, it needs higher torque, and the tracking is more challenging for this joint.
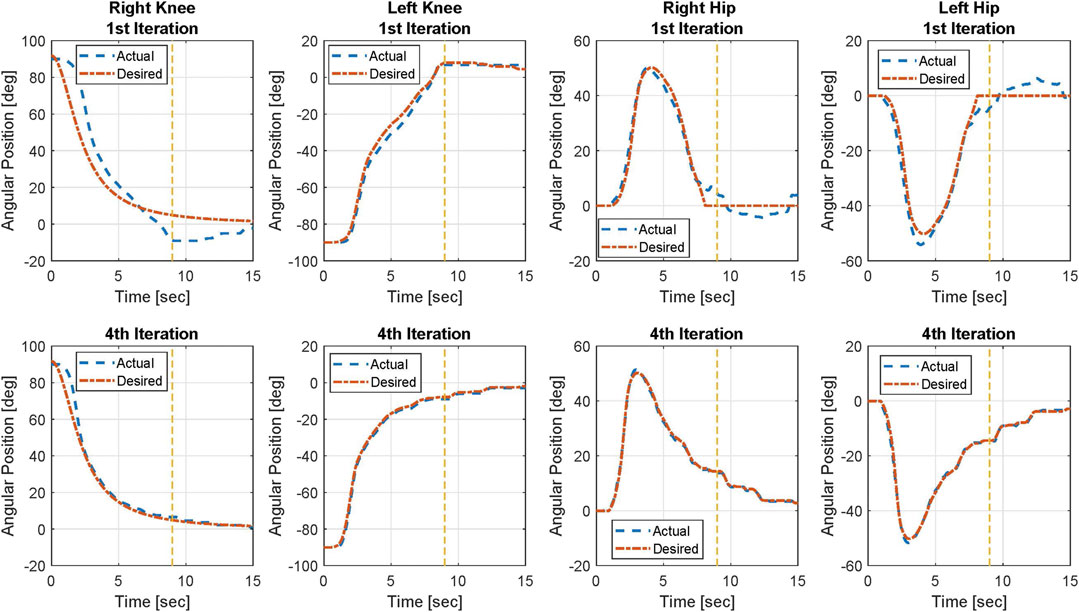
FIGURE 3. Knee and hip joint angular position tracking results of Participant 2 in the 1st and 4th iterations. Yellow dashed line shows the approximate time in which the sit-to-stand movement is mainly done.
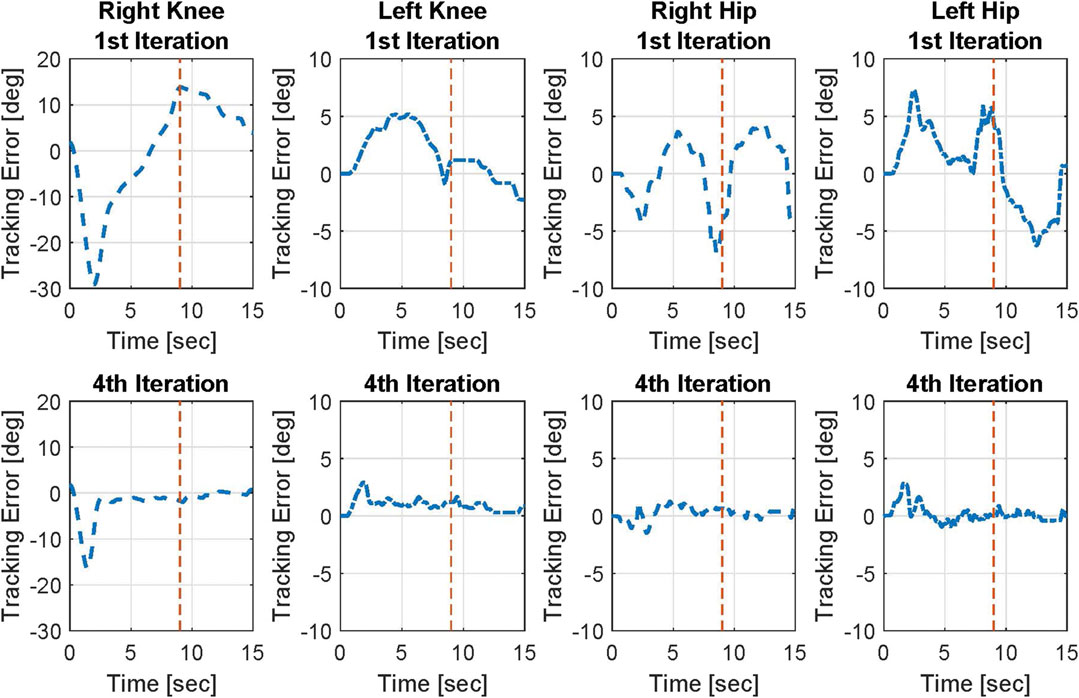
FIGURE 4. Angular position tracking errors on both knee and hip joints of Participant 2 in the 1st and 4th iterations. Red dashed line shows the approximate time in which the sit-to-stand movement is mainly done.
The improvement percentage of the RMSE of the joints’ trajectories’ tracking performance for the four participants is plotted in Figure 5. The improvement percentage of the RMSE is calculated based on the following equation:
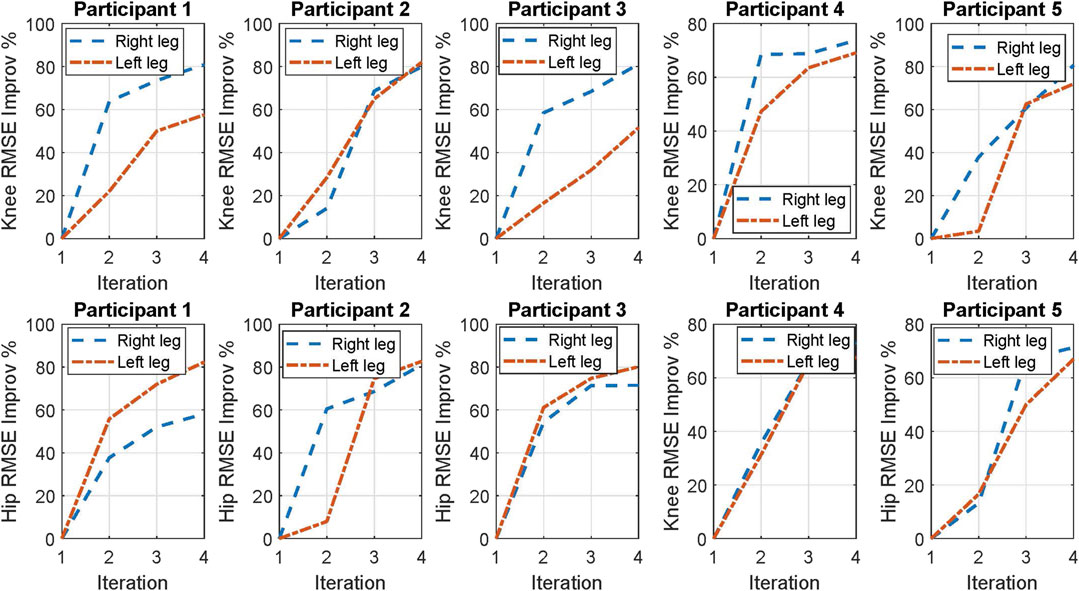
FIGURE 5. RMSE improvement percentage of both knee and hip joints from the 1st to the 4th iterations for each participant.
The results show that from the 1st iteration to the 4th iteration, for each participant, the RMSE improvement values for both knee and hip joints are increasing. These results indicate that the ILC method improves the joint trajectory tracking performance in successive iterations.
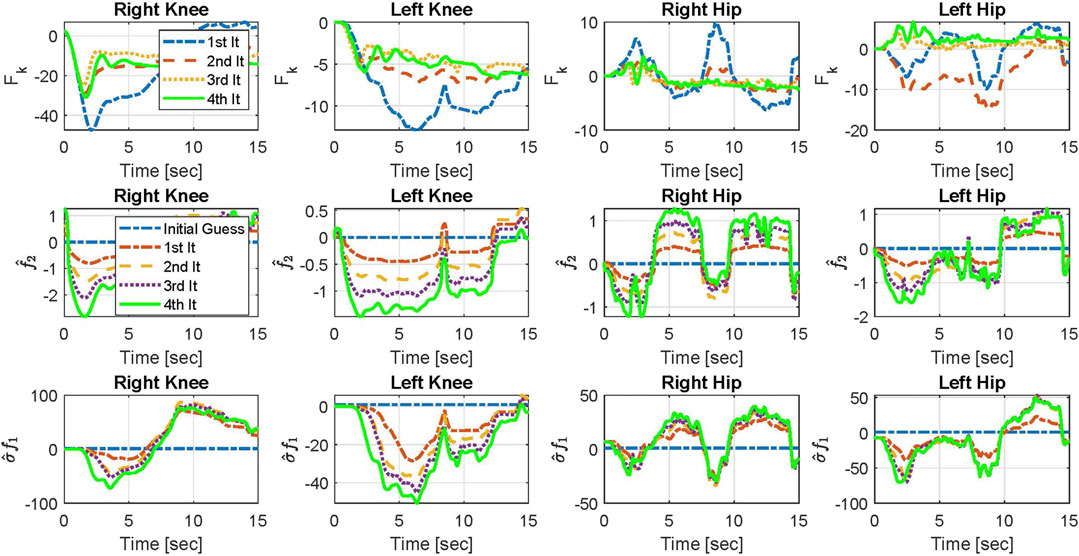
In Figure 6, components of the top-level controller, Uk, in Eq. 4 for Participant 2 in four iterations are shown. The components include Fk,
The bottom-level control inputs for the 1st and 4th iterations for Participant 2 are shown in Figure 7. In this figure, the allocation ratio for FES is shown in the kth iteration. The allocation ratio shows how much of the top-level control input is allocated to FES by the model predictive allocator. At t = 10 s in the 1st iteration, the knee motor torque magnitude is 0 and the allocation ratio for FES is one.
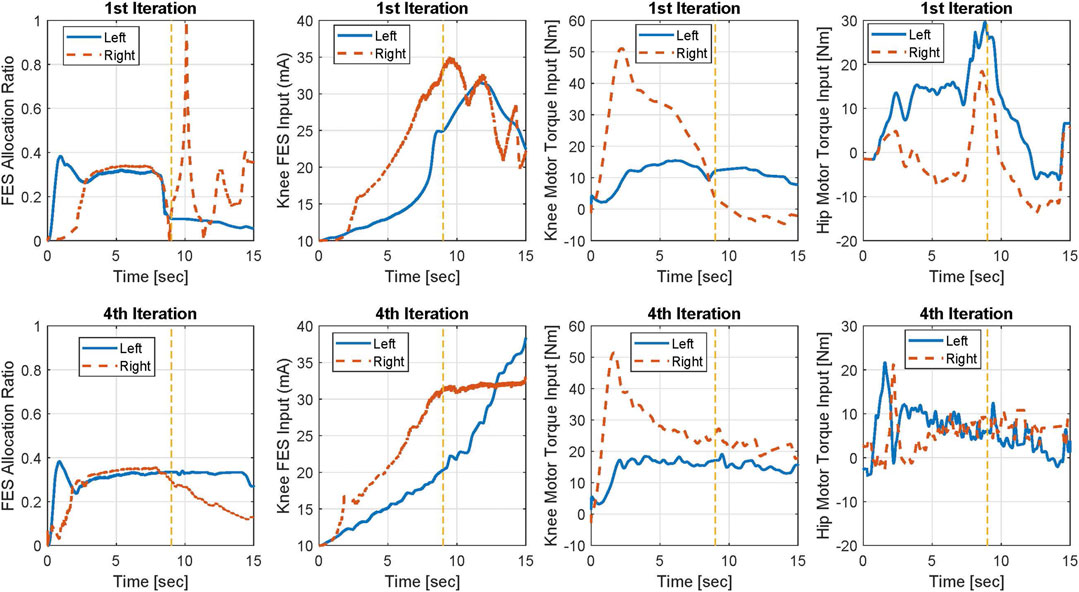
FIGURE 7. Bottom-level control inputs for Participant 2 allocated by MPC in the 1st and 4th iterations. Yellow dashed line shows the approximate time in which the sit-to-stand movement is mainly done.
Detailed experimental results for all 4 participants are provided in Table 4, where
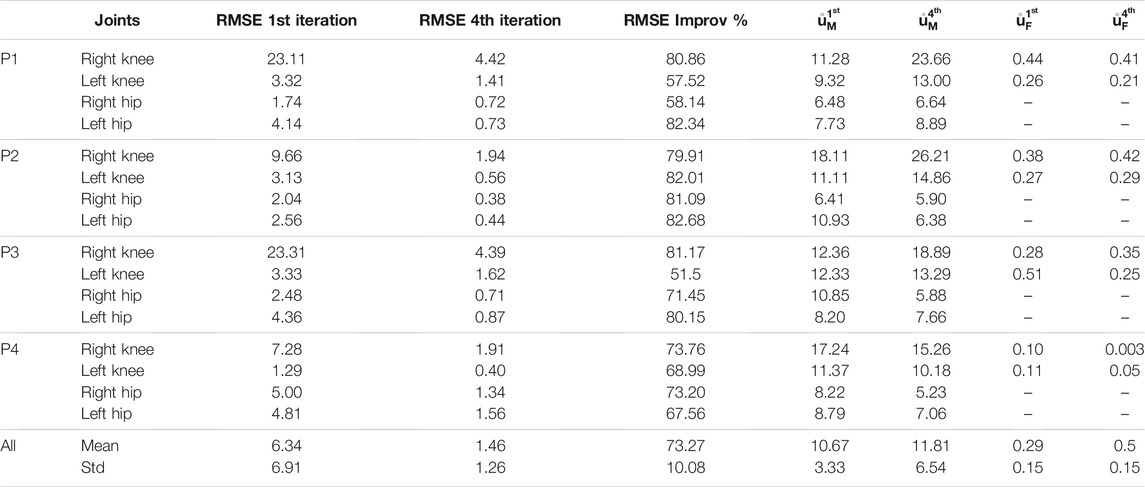
TABLE 4. RMSE of trajectory tracking and inputs from motors and FES on each participant in the 1st and 4th iterations.
According to Figure 8, the novel NNILC method was able to improve the right-knee, left-knee, right-hip, and left-hip RMSEs, 78.92, 65.02, 70.93, and 78.19%, respectively, on average for all participants. For statistical analysis of the novel controller, we focused on the RMSE reduction percentage of each iteration across the four participants and compared the reduction performance between the left knee/hip joint and the right knee/hip joint. For each joint in an individual iteration, there were four RMSE values across participants. A Shapiro–Wilk test was used to determine the normality of the data. The results did not show a normal distribution of RMSE results on each joint. Therefore, a Wilcoxon rank sum test was used to determine if there was a significant difference among the left and right joints’ RMSE reduction percentage in the second, third, and fourth iterations, respectively. We observed significant difference between the left and right knee joints in the third iteration (p = 0.029). Other than this, there was no significant difference between the left and right joints in each iteration (detailed p values are shown in Figure 8), which indicates a comparative and symmetric performance of the proposed controller on the left and right knee/hip joints.
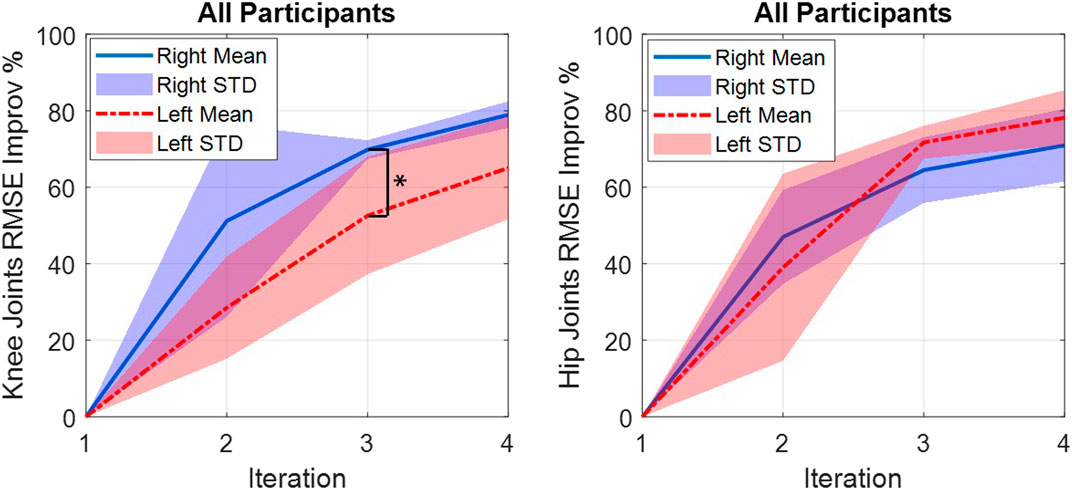
FIGURE 8. Improvements in the mean RMSE for all participants. Solid and dashed lines show the mean, and the shaded areas show the standard deviation.
4 Discussion
A hybrid system that combines FES and the powered exoskeleton is a promising rehabilitation intervention to assist people with mobility disorders. Motivated by an ILC approach that improves a system’s transient performance in multiple iterations, the study presented derivation and experimental results of a novel NN-based ILC method. The optimal low-level MPC-based allocator automates the need to specify an allocation ratio between the powered exoskeleton and FES. The allocation process has coupled performance effects. Thus, in a manual tuning involving trial and error, a clinician/physical therapist may lack the relevant control engineering experience to guarantee stability and performance of the system. The proposed bi-level control framework potentially contrasts the manual allocation process, which could be daunting to a clinician/physical therapist. Also, the optimization framework determines optimal allocation ratios instead of static/ad hoc nonoptimal allocation, which potentially increases the device efficiency.
The results show that the iterative learning process improves tracking performance by increasing a feed-forward learning part while decreasing the control’s feedback component. The NN-based ILC potentially facilitates the control implementation despite inter-person and day-to-day variations in a user’s FES-driven musculoskeletal dynamics. Most model-based optimal control approaches often involve a tedious process of identifying the model (Stein et al. (1996); Kirsch et al. (2018)), which hinders their control implementation. Instead, nonlinear robust control methods, for example, discontinuous sliding mode control (Bkekri et al. (2018)) and continuous RISE control (Sharma et al. (2009)), have been explicitly designed to address uncertainties in the nonlinear musculoskeletal model. However, these approaches inherently rely on the high frequency or high gain control to compensate for the modeling uncertainties and cause overstimulation. A feed-forward control strategy is usually recommended along with feedback control to reduce overall control effort. Therefore, the FES controllers in the studies by Ajoudani and Erfanian (2009), Lujan and Crago (2009), and Cousin et al. (2019) used neural networks as feed-forward controllers. The NN-based control approach’s advantage is its universal approximation property that helps to capture unstructured uncertainties in the musculoskeletal dynamics (Sharma et al. (2012)). NN-based control, however, requires training to obtain the desired performance. Both offline (Kim et al. (2008); Yu and Rosen (2013)) and online (Sharma et al. (2012)) NN training methods have been used for FES control. In this study, the NN approach uses a combination of online gradient update laws that tune NN weights after every task iteration or at every time instant. A Lyapunov-like stability analysis facilitates the design of these update laws and guarantees the bi-level hierarchical control method’s stability.
Compared to a predetermined higher-level input generator, the NN-based ILC method’s torque generation is more robust to disturbances. Zhang et al. (2015) investigated multiple predetermined higher torque generation techniques based on a limb angle, time, or an EMG signal. A low-level controller then matched the desired torque trajectory. However, the predetermined desired torque may not be robust to perturbations such as spasticity. The robustness to perturbations is essential in situations where the goal is to enable a person with absent motor control to verticalize from sitting. The bi-level control approach used in our study produces robust torque that tracks the desired trajectory. Unlike kinematic tracking, torque-based control of a wearable robot may be more useful in situations where a user may need some torque assistance to control stiffness/impedance or torque. Our focus was on people with completely absent volitional control. Thus, the control design focused on kinematic control instead of torque control.
Repetitive movements such as walking are a good benchmark to test an ILC control method’s performance. For sit-to-stand, each sit-to-stand movement is considered as one iteration, and for the case of walking, each gait cycle is considered as one iteration. We, however, used sit-to-stand experiments to show the feasibility of the NN-based ILC method. Sit-to-stand movement has a very high torque demand, which makes it even more challenging than walking. These tasks are significant as they facilitate a sit-to-stand, a basic movement, a precursor to walking. Also, enabling people with SCI to perform repeated upright standing tasks is beneficial for their musculoskeletal and cardiovascular health. While we do not underestimate the significance of walking, which is critical to mobility and is our ultimate goal, we emphasize sit-to-stand as an equally challenging control problem and actively pursued research on it, for example, in the studies by Alouane et al. (2019), Huo et al. (2016), and Jatsun et al. (2015).
In this work, state-dependent manifolds are used as reference trajectories. This desired trajectory design approach differs from our previous work in the study by Alibeji et al. (conditionally accepted, 2018a) that used time-dependent reference trajectories. Some SCI participants may exhibit asymmetric left and right leg movements during the sit-to-stand task. The time-dependent desired trajectories in this situation may not correct themselves and may produce an uncoordinated movement, potentially uncomfortable and unsafe for a user. In our current approach, the joint reference profiles adapt based on the current state of the system. The state-dependent desired trajectory design coordinates both legs’ hip and knee joints, enabling the users to achieve a more stable and natural movement.
Two limitations in the study deserve discussion. First, we could have used pulse width (PW) modulation, instead of current amplitude (CA) modulation, for FES control. Although both PW and CA modulation have the same function of increasing and decreasing muscle fiber recruitment, the stimulator (Rehastim, Hasomed, Inc.) used in the study has a higher resolution for PW modulation than the current modulation. We will be switching our future work to the PW mode.
Furthermore, the results from subjects with no disability verified the proposed bi-level NNILC-MPC framework’s feasibility to optimally allocate FES and the powered exoskeleton. The experimental results on the participants with no disabilities here are preliminary and more experiments on participants with SCI will be performed to validate the benefits of the control framework further.
5 Conclusion
A novel NNILC augmented with an MPC-based allocation strategy was developed to control a hybrid exoskeleton in this work. A Lyapunov-like stability analysis proved that the unified control framework yielded asymptotic tracking performance despite uncertain dynamics and disturbances. State-dependent trajectories were used as desired joint trajectories. The experimental results of four participants without a disability demonstrated that the controller enabled sit-to-stand tasks. The tracking performance showed improvement in each iteration. The results also showed that the MPC strategy could achieve the optimal allocation between FES and the powered exoskeleton.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics Statement
The study was approved by the Institutional Review Board (IRB) at the University of Pittsburgh (IRB approval number: PRO 14040419) and the IRB of North Carolina State University (IRB approval number: 20553). The patients/participants provided their written informed consent to participate in this study.
Author Contributions
VM wrote the manuscript, developed the iterative learning control system and trajectory design, conducted experiments, and analyzed the experimental results. QZ helped in the experiments and edited the manuscript. XB helped in the design and implementation of the MPC algorithm. BD helped in the participant recruitment, provided medical oversight, and edited the manuscript. NS conceptualized the study, advised in control design and development, and edited the manuscript.
Funding
This work was supported in part by the National Science Foundation (NSF) under Award # 1646009 and NSF CAREER Award # 2002261.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors would like to thank Albert Dodson for his help in the experiment.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frobt.2021.711388/full#supplementary-material
References
Ajoudani, A., and Erfanian, A. (2009). A Neuro-Sliding-Mode Control with Adaptive Modeling of Uncertainty for Control of Movement in Paralyzed Limbs Using Functional Electrical Stimulation. IEEE Trans. Biomed. Eng. 56, 1771–1780. doi:10.1109/tbme.2009.2017030
Alibeji, N. A., Molazadeh, V., Dicianno, B. E., and Sharma, N. (2018a). A Control Scheme that Uses Dynamic Postural Synergies to Coordinate a Hybrid Walking Neuroprosthesis: Theory and Experiments. Front. Neurosci. 12, 159. doi:10.3389/fnins.2018.00159
Alibeji, N. A., Molazadeh, V., Moore-Clingenpeel, F., and Sharma, N. (2018b). A Muscle Synergy-Inspired Control Design to Coordinate Functional Electrical Stimulation and a Powered Exoskeleton: Artificial Generation of Synergies to Reduce Input Dimensionality. IEEE Control. Syst. 38, 35–60. doi:10.1109/mcs.2018.2866603
Alibeji, N., Kirsch, N., and Sharma, N. (2015). A Muscle Synergy-Inspired Adaptive Control Scheme for a Hybrid Walking Neuroprosthesis. Front. Bioeng. Biotechnol.3, 203. doi:10.3389/fbioe.2015.00203
Alibeji, N., Kirsch, N., and Sharma, N. (2017). An Adaptive Low-Dimensional Control to Compensate for Actuator Redundancy and Fes-Induced Muscle Fatigue in a Hybrid Neuroprosthesis. Control. Eng. Pract. 59, 204–219. doi:10.1016/j.conengprac.2016.07.015
Alouane, M. A., Huo, W., Rifai, H., Amirat, Y., and Mohammed, S. (2019). Hybrid Fes-Exoskeleton Controller to Assist Sit-To-Stand Movement. IFAC-PapersOnLine 51, 296–301. doi:10.1016/j.ifacol.2019.01.032
Bae, J., and Tomizuka, M. (2012). A Gait Rehabilitation Strategy Inspired by an Iterative Learning Algorithm. Mechatronics 22, 213–221. doi:10.1016/j.mechatronics.2012.01.009
Bao, X., Kirsch, N., Dodson, A., and Sharma, N. (2019). Model Predictive Control of a Feedback-Linearized Hybrid Neuroprosthetic System with a Barrier Penalty. J. Comput. Nonlinear Dyn. 14, 101009–1010097. doi:10.1115/1.4042903
Bao, X., Kirsch, N., and Sharma, N. (2016). Dynamic Control Allocation of a Feedback Linearized Hybrid Neuroprosthetic System. 2016 American Control Conference (ACC). 6-8 July 2016. Boston, USA. IEEE, 3976–3981. doi:10.1109/acc.2016.7525534
Bao, X., Molazadeh, V., Dodson, A., Dicianno, B. E., and Sharma, N. (2020a). Using Person-specific Muscle Fatigue Characteristics to Optimally Allocate Control in a Hybrid Exoskeleton-Preliminary Results. IEEE Trans. Med. Robot. Bionics 2, 226–235. doi:10.1109/tmrb.2020.2977416
Bao, X., Molazadeh, V., Dodson, A., and Sharma, N. (2020b). Model Predictive Control-Based Knee Actuator Allocation during a Standing-Up Motion with a Powered Exoskeleton and Functional Electrical Stimulation. Adv. Mot. Neuroprostheses, 89–100. doi:10.1007/978-3-030-38740-2_6
Bickel, C. S., Gregory, C. M., and Dean, J. C. (2011). Motor Unit Recruitment during Neuromuscular Electrical Stimulation: a Critical Appraisal. Eur. J. Appl. Physiol. 111, 2399–2407. doi:10.1007/s00421-011-2128-4
Bkekri, R., Benamor, A., Alouane, M. A., Fried, G., and Messaoud, H. (2018). Robust Adaptive Sliding Mode Control for a Human-Driven Knee Joint Orthosis. Ir 45, 379–389. doi:10.1108/ir-11-2017-0205
Bulea, T. C., Kobetic, R., Audu, M. L., Schnellenberger, J. R., and Triolo, R. J. (2013). Finite State Control of a Variable Impedance Hybrid Neuroprosthesis for Locomotion after Paralysis. IEEE Trans. Neural Syst. Rehabil. Eng. 21, 141–151. doi:10.1109/tnsre.2012.2227124
Chang, S. R., Nandor, M. J., Kobetic, R., Foglyano, K. M., Quinn, R. D., and Triolo, R. J. (2016). Improving Stand-To-Sit Maneuver for Individuals with Spinal Cord Injury. J. Neuroeng. Rehabil. 13, 27. doi:10.1186/s12984-016-0137-6
Chen, W., Chen, Y.-Q., and Yeh, C.-P. (2012). Robust Iterative Learning Control via Continuous Sliding-Mode Technique with Validation on an Srv02 Rotary Plant. Mechatronics 22, 588–593. doi:10.1016/j.mechatronics.2011.12.005
Contreras-Vidal, J. L., A Bhagat, N., Brantley, J., Cruz-Garza, J. G., He, Y., Manley, Q., et al. (2016). Powered Exoskeletons for Bipedal Locomotion after Spinal Cord Injury. J. Neural Eng. 13, 031001. doi:10.1088/1741-2560/13/3/031001
Cousin, C. A., Deptula, P., Rouse, C. A., and Dixon, W. E. (2019). Cycling with Functional Electrical Stimulation and Adaptive Neural Network Admittance Control. IEEE ACC., 1742–1747. doi:10.23919/acc.2019.8814619
del-Ama, A. J., Gil-Agudo, Á., Pons, J. L., and Moreno, J. C. (2014). Hybrid Fes-Robot Cooperative Control of Ambulatory Gait Rehabilitation Exoskeleton. J. NeuroEngineering Rehabil. 11, 27. doi:10.1186/1743-0003-11-27
Farris, R. J., Quintero, H. A., Murray, S. A., Ha, K. H., Hartigan, C., and Goldfarb, M. (2014). A Preliminary Assessment of Legged Mobility provided by a Lower Limb Exoskeleton for Persons with Paraplegia. IEEE Trans. Neural Syst. Rehabil. Eng. 22, 482–490. doi:10.1109/TNSRE.2013.2268320
Graichen, K., and Kugi, A. (2010). Stability and Incremental Improvement of Suboptimal MPC without Terminal Constraints. IEEE Trans. Automat. Contr. 55, 2576–2580. doi:10.1109/tac.2010.2057912
Gregg, R. D., and Sensinger, J. W. (2014). Towards Biomimetic Virtual Constraint Control of a Powered Prosthetic Leg. IEEE Trans. Contr. Syst. Technol. 22, 246–254. doi:10.1109/tcst.2012.2236840
Ha, K. H., Quintero, H. A., Farris, R. J., and Goldfarb, M. (2012). Enhancing Stance Phase Propulsion during Level Walking by Combining FES with a Powered Exoskeleton for Persons with Paraplegia. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2012, 344–347. doi:10.1109/EMBC.2012.6345939
Ha, K., Murray, S., and Goldfarb, M. (2015). An Approach for the Cooperative Control of FES with a Powered Exoskeleton during Level Walking for Persons with Paraplegia. IEEE Trans. Neural Syst. Rehabil. Eng. 24, 455–466. doi:10.1109/TNSRE.2015.2421052
Huo, W., Mohammed, S., Amirat, Y., and Kong, K. (2016). Active Impedance Control of a Lower Limb Exoskeleton to Assist Sit-To-Stand Movement. Robotics and Automation (ICRA), 2016 IEEE International Conference on. 16-21 May 2016. Stockholm, Sweden. IEEE, 3530–3536. doi:10.1109/icra.2016.7487534
Jatsun, S., Savin, S., Yatsun, A., and Turlapov, R. (2015). Adaptive Control System for Exoskeleton Performing Sit-To-Stand Motion. Mechatronics and its Applications (ISMA), 2015 10th International Symposium on. 8-10 Dec. 2015. Sharjah, United Arab. IEEE, 1–6. doi:10.1109/isma.2015.7373462
Kim, S. J., Fairchild, M. D., Iarkov Yarkov, A., Abbas, J. J., and Jung, R. (2008). Adaptive Control of Movement for Neuromuscular Stimulation-Assisted Therapy in a Rodent Model. IEEE Trans. Biomed. Eng. 56, 452–461. doi:10.1109/TBME.2008.2008193
Kirsch, N. A., Bao, X., Alibeji, N. A., Dicianno, B. E., and Sharma, N. (2018). Model-based Dynamic Control Allocation in a Hybrid Neuroprosthesis. IEEE Trans. Neural Syst. Rehabil. Eng. 26, 224–232. doi:10.1109/tnsre.2017.2756023
Kirsch, N., Alibeji, N., Dicianno, B. E., and Sharma, N. (2016). Switching Control of Functional Electrical Stimulation and Motor Assist for Muscle Fatigue Compensation. ACC (IEEE), 4865–4870. doi:10.1109/acc.2016.7526123
Kirsch, N., Alibeji, N., Fisher, L., Gregory, C., and Sharma, N. (2014). A Semi-active Hybrid Neuroprosthesis for Restoring Lower Limb Function in Paraplegics. In 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26-30 Aug. 2014. doi:10.1109/embc.2014.6944144
Kirsch, N., Sharma, N., Alibeji, N., and Sharma, N. (2017). Nonlinear Model Predictive Control of Functional Electrical Stimulation. Control. Eng. Pract. 58, 319–331. doi:10.1016/j.conengprac.2016.03.005
Lewis, F. L., Selmic, R., and Campos, J. (2002). Neuro-Fuzzy Control of Industrial Systems with Actuator Nonlinearities. Philadelphia, PA, USA: Society for Industrial and Applied Mathematics).
Lujan, J. L., and Crago, P. E. (2009). Automated Optimal Coordination of Multiple-Dof Neuromuscular Actions in Feedforward Neuroprostheses. IEEE Trans. Biomed. Eng. 56, 179–187. doi:10.1109/tbme.2008.2002159
Mingxuan Sun, M. (2009). A Barbalat-like Lemma with its Application to Learning Control. IEEE Trans. Automat. Contr. 54, 2222–2225. doi:10.1109/tac.2009.2026849
Molazadeh, V., Sheng, Z., Bao, X., and Sharma, N. (2018a). A Robust Iterative Learning Switching Controller for Following Virtual Constraints: Application to a Hybrid Neuroprosthesis. CPHS IFAC 51, 28–33. doi:10.1016/j.ifacol.2019.01.011
Molazadeh, V., Sheng, Z., and Sharma, N. (2018b). A Within-Stride Switching Controller for Walking with Virtual Constraints: Application to a Hybrid Neuroprosthesis. ACC (IEEE), 5286–5291. doi:10.23919/acc.2018.8431436
Molazadeh, V., Zhang, Q., Bao, X., and Sharma, N. (2019). Neural-network Based Iterative Learning Control of a Hybrid Exoskeleton with an Mpc Allocation Strategy. ASME DSCC. Park City, Utah: ASME, 7. doi:10.1115/DSCC2019-9191
Mou Chen, M., Shuzhi Sam Ge, S. S., and How, B. (2010). Robust Adaptive Neural Network Control for a Class of Uncertain Mimo Nonlinear Systems with Input Nonlinearities. IEEE Trans. Neural Netw. 21, 796–812. doi:10.1109/tnn.2010.2042611
Nagai, M. K., Marquez-Chin, C., and Popovic, M. R. (2016). Why Is Functional Electrical Stimulation Therapy Capable of Restoring Motor Function Following Severe Injury to the central Nervous System? Translational Neuroscience. Springer, 479–498. doi:10.1007/978-1-4899-7654-3_25
Neuhaus, P. D., Noorden, J. H., Craig, T. J., Torres, T., Kirschbaum, J., and Pratt, J. E. (2011). Design and Evaluation of mina: A Robotic Orthosis for Paraplegics. IEEE Int. Conf. Rehabil. Robot 2011, 5975468–8. doi:10.1109/ICORR.2011.5975468
Peckham, P. H., and Knutson, J. S. (2005). Functional Electrical Stimulation for Neuromuscular Applications. Annu. Rev. Biomed. Eng. 7, 327–360. doi:10.1146/annurev.bioeng.6.040803.140103
Popovic, D., Stein, R. B., Namik Oguztoreli, M., Lebiedowska, M., and Jonic, S. (1999). Optimal Control of Walking with Functional Electrical Stimulation: a Computer Simulation Study. IEEE Trans. Rehab. Eng. 7, 69–79. doi:10.1109/86.750554
Popovic, M. R., Masani, K., and Micera, S. (2012). Functional Electrical Stimulation Therapy: Recovery of Function Following Spinal Cord Injury and Stroke. London: Springer London, 105–121. doi:10.1007/978-1-4471-2277-7_7
Quintero, H. A., Farris, R. J., Ha, K., and Goldfarb, M. (2012). Preliminary Assessment of the Efficacy of Supplementing Knee Extension Capability in a Lower Limb Exoskeleton with FES. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2012, 3360–3363. doi:10.1109/EMBC.2012.6346685
Riener, R., Quintern, J., and Schmidt, G. (1996). Biomechanical Model of the Human Knee Evaluated by Neuromuscular Stimulation. J. Biomech. 29, 1157–1167. doi:10.1016/0021-9290(96)00012-7
Sharma, N., Gregory, C. M., Johnson, M., and Dixon, W. E. (2012). Closed-loop Neural Network-Based NMES Control for Human Limb Tracking. IEEE Trans. Contr. Syst. Technol. 20, 712–725. doi:10.1109/tcst.2011.2125792
Sharma, N., Mushahwar, V., and Stein, R. (2014). Dynamic Optimization of FES and Orthosis-Based Walking Using Simple Models. IEEE Trans. Neural Syst. Rehabil. Eng. 22, 114–126. doi:10.1109/tnsre.2013.2280520
Sharma, N., Stegath, K., Gregory, C. M., and Dixon, W. E. (2009). Nonlinear Neuromuscular Electrical Stimulation Tracking Control of a Human Limb. IEEE Trans. Neural Syst. Rehabil. Eng. 17, 576–584. doi:10.1109/tnsre.2009.2023294
Stein, R. B., Zehr, E. P., Lebiedowska, M. K., Popovic, D. B., Scheiner, A., and Chizeck, H. J. (1996). Estimating Mechanical Parameters of Leg Segments in Individuals with and without Physical Disabilities. IEEE Trans. Rehab. Eng. 4, 201–211. doi:10.1109/86.536776
Strausser, K., and Kazerooni, H. (2011). The Development and Testing of a Human Machine Interface for a mobile Medical Exoskeleton. 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems. 25-30 Sept. 2011. San Francisco, CA, USA. IEEE, 4911–4916. doi:10.1109/iros.2011.6095025
Sun, Z., Bao, X., and Sharma, N. (2018). Lyapunov-based Model Predictive Control of an Input Delayed Functional Electrical Simulation. In 2nd IFAC CPHS, Miami, FL, USA. 51, 290–295. doi:10.1016/j.ifacol.2019.01.037
Wen Yu, W., and Rosen, J. (2013). Neural Pid Control of Robot Manipulators with Application to an Upper Limb Exoskeleton. IEEE Trans. Cybern. 43, 673–684. doi:10.1109/tsmcb.2012.2214381
Westervelt, E. R., Grizzle, J. W., Chevallereau, C., Choi, J. H., and Morris, B. (2007). Feedback Control of Dynamic Bipedal Robot Locomotion, 28. Boca Raton, Florida: CRC Press, 528.
Xu, J.-X., and Yan, R. (2004). Iterative Learning Control Design without A Priori Knowledge of the Control Direction. Automatica 40, 1803–1809. doi:10.1016/j.automatica.2004.05.010
Keywords: exoskeleton, wearable robot, shared control, iterative learning, functional electrical stimulation (FES)
Citation: Molazadeh V, Zhang Q, Bao X, Dicianno BE and Sharma N (2021) Shared Control of a Powered Exoskeleton and Functional Electrical Stimulation Using Iterative Learning. Front. Robot. AI 8:711388. doi: 10.3389/frobt.2021.711388
Received: 18 May 2021; Accepted: 27 September 2021;
Published: 03 November 2021.
Edited by:
Noman Naseer, Air University, PakistanReviewed by:
Reza Sharif Razavian, Northeastern University, United StatesThomas Schauer, Technical University of Berlin, Germany
Copyright © 2021 Molazadeh , Zhang , Bao , Dicianno and Sharma . This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nitin Sharma , bnNoYXJtMjNAbmNzdS5lZHU=
 Vahidreza Molazadeh
Vahidreza Molazadeh  Qiang Zhang
Qiang Zhang  Xuefeng Bao
Xuefeng Bao  Brad E. Dicianno 4
Brad E. Dicianno 4 Nitin Sharma
Nitin Sharma