- Living Machines Laboratory, School of Information Science and Technology, ShanghaiTech University, Shanghai, China
Model-Based Reinforcement Learning (MBRL) algorithms have been shown to have an advantage on data-efficiency, but often overshadowed by state-of-the-art model-free methods in performance, especially when facing high-dimensional and complex problems. In this work, a novel MBRL method is proposed, called Risk-Aware Model-Based Control (RAMCO). It combines uncertainty-aware deep dynamics models and the risk assessment technique Conditional Value at Risk (CVaR). This mechanism is appropriate for real-world application since it takes epistemic risk into consideration. In addition, we use a model-free solver to produce warm-up training data, and this setting improves the performance in low-dimensional environments and covers the shortage of MBRL’s nature in the high-dimensional scenarios. In comparison with other state-of-the-art reinforcement learning algorithms, we show that it produces superior results on a walking robot model. We also evaluate the method with an Eidos environment, which is a novel experimental method with multi-dimensional randomly initialized deep neural networks to measure the performance of any reinforcement learning algorithm, and the advantages of RAMCO are highlighted.
1 Introduction
The controllers of robots are primarily designed and tuned by human engineers through tiresome iterations and require extensive experience and a high degree of expertize (Deisenroth et al., 2013). The resulting programmed controllers are built upon assuming rigorous models of both the robot’s behavior and its environment. As a consequence, hard-coded controllers for robots have its limitations when a robot needs to adapt to a new situation or when the robot/environment cannot be precisely modeled. Machine learning and, particularly, deep learning, have made ground-breaking success in various domains, such as speech recognition (Hinton et al., 2012), computer vision (Krizhevsky et al., 2012), video games (Mnih et al., 2015), or medicine (Xu et al., 2020) in recent years. However, unlike other machine learning branches, RL is still not widely applied to real-world engineering products, especially in the field of robotics. Overall, the main obstacles on the application of RL to such problems are 1) data inefficiency, 2) lack of robustness, and 3) lack of practical advantage over hand-tuned controllers.
It can be easily stated that most of the successful and famous methods up to now (Lillicrap et al., 2015; Schulman et al., 2015, 2017; Haarnoja et al., 2018) require millions of steps to find the best policy, which is acceptable in simulators but impractical in a real-world application. Data-efficiency is an important consideration when applying machine learning techniques in a real robot (Chatzilygeroudis et al., 2020). Unlike applications in video games or images processing, it is unrealistic to train a robot in the real world with millions of trials, since implementation in real-world can suffer from mechanical wearing and prohibitive wall-clock time.
Safety is another consideration when it comes to some applications, such as self-driving cars, surgical robots, or assistive robots. In these applications, the loss is not only a number like in a simulator but a clear threat to human life. The finance literature differentiates between three risk-related types of behavior, namely risk-neutral, risk-averse and risk-seeking. Decision making by RL agents typically involves the optimization of a risk-neutral performance objective, namely the expected total discounted reward. This approach neither takes into account the variability of the cost or the modeling errors and hence becomes another barrier for the application of machine learning on robotics. Furthermore, the gap between implementation and mathematical theories shown by Engstrom et al. (Engstrom et al., 2020) reveals the unreliability of using RL in risk-sensitive problems, which implies that decision-making algorithms should be more conservative when they are designed for real-world applications.
The current state-of-the-art for robotic control is vastly model-based and human-designed, with simulators being used to calculate paths and find solutions before deployment (Mouret and Chatzilygeroudis, 2017). Unlike some applications such as playing video games, it is very difficult for an RL agent to produce better performance than human experts. While most of the successful learning-based controllers still produce peculiar locomotion gaits on legged robots, the most impressive works in robot control do not include machine learning algorithms for control design (Fabisch et al., 2019; Kim et al., 2020). We claim that the learning-based controllers can be essential and outperform human-designed controllers when the agent faces an unknown environment, where even humans would not know the optimum, instead of learning trivial control tasks.
The motivation behind this work is to take a step towards narrowing the gap between academic advances and industrial applications by handling the aforementioned problems. First, we focus on model-based reinforcement learning (MBRL) with a probabilistic dynamics model, as incorporating uncertainties into our dynamics model usually prevents overfitting with insufficient data. Second, we consider the risk based on this uncertainty to protect real-world applications from dramatic loss due to model uncertainty. Prior works on Robust Markov Decision Processes have traditionally dealt with risk due to uncertainty in the transition and reward parameters (Givan et al., 2000; Mannor et al., 2012). However, most of these works assume inherent stochasticity of the environment, while model uncertainty due to lack of data should, in fact, be regarded as a bigger issue from an engineering standpoint. Finally, we expect that the RL environment in our simulator can equally evaluate the performance of the agent in real-world applications, even dealing with some unknown problems.
Our primary contribution is a novel MBRL algorithm called Risk-Aware Model-Based Control (RAMCO). We employ model-free solvers to produce warm-up data, train a Bayesian dynamics model based on these data, and do the planning based on Conditional Value at Risk (CVaR) measurement. The overall results are shown to be competitive when compared to other successful state-of-the-art RL algorithms. In addition, to better evaluate and compare the performances of different RL algorithms, we propose a real-world-inspired walking robot model called AntX and a novel pseudo-environment method called Eidos that can emulate an RL environment with any complexity.
2 Related Work
Reinforcement Learning has contributed to the machine learning community with a wide variety of applications, ranging from robotics to finance. It is a computational approach for solving goal-oriented decision-making problems (Sutton and Barto, 2018), described as a process of interaction between an agent and an environment (Figure 1).
Most current research on RL is built on the theoretical framework of Markov Decision Process (MDPs) (Puterman, 1994), which is a general formalism for the study of decision-making problem. In this classic theoretical framework, an agent takes actions typically in a discrete-time sequence. In each time step, it is said that the agent is in a state, representing the information needed from the environment. Then according to a policy, an agent would take a specific action in each state. After that, the agent would be transited into the next state and receive a reward signal. The unknown function that map a tuple (state, action) to the next state is usually called the transition function. Some algorithms try to model this transition function as a dynamics model and hence are called model-based method.
2.1 Model-free Reinforcement Learning
Popular RL algorithms, such as Deep Q learning and Deep Deterministic Policy Gradient (DDPG) (Lillicrap et al., 2015), do not assume any transition model on the environment, and hence they can also be called model-free methods. These methods have shown great promise as a general-purpose solver for complex learning problems. We take some other popular advanced model-free algorithms as examples: Distributed Distributional Deterministic Policy Gradients (D4PG) (Barth-Maron et al., 2018) is a variant of DDPG, and it uses multiple actors to collect samples in parallel and store the collected data into a shared replay buffer. A distributional value function is used in the Critic part, while experiment shows that this trick improves the performance. Twin Delayed Deep Deterministic policy gradient (TD3) (Fujimoto et al., 2018) is another variant of DDPG, using two critic networks to overcome the overestimation bias. Instead of using Q function
2.2 Model-Based Reinforcement Learning
Compared with model-free approaches, MBRL algorithms are generally considered as being more data-efficient since they are able to model the transition function and hence train on the modeled environment. Once the transition function is learned, the reinforcement learning problem indeed becomes a Dynamic Programming function. MBRL methods could be categorized based on whether an explicit policy exists. The method of Probabilistic Ensembles with Trajectory Sampling (PETS) (Chua et al., 2018) is a recent successful example for the ones without a policy. It uses a deep neural network with ensembles (Lakshminarayanan et al., 2017) to model the environment dynamics taking the uncertainty in consideration, and does open-loop planning on this model. The PETS method is also successfully applied to real robots in (Nagabandi et al., 2019). The model-based control method introduced in (Nagabandi et al., 2018) is similar, but with a deterministic dynamics model. Deep Planning Network (PlaNet) (Hafner et al., 2019) is another successful method without policy. It uses a recurrent state-space model and shows its advantage of image-based control. As for MBRL with an explicit policy, Probabilistic Inference for Learning Control (PILCO) (Deisenroth and Rasmussen, 2011) is one of the most popular methods. It uses Gaussian Process to model the transition function of the environment and lowers the model bias by taking the uncertainty of the input into consideration, leading to a more accurate long-term prediction. Cutler et al. successfully applied the PILCO method to an inverted pendulum model (Cutler and How, 2015) and Englert et al. applied it to an imitation learning problem (Englert et al., 2013). Nonetheless, PILCO relies on Gaussian Process, which limits its applicability for complex problems that need more trials to be solved. Furthermore, ignorance of the temporal correlation in model uncertainty between successive states can lead to underestimation of state uncertainty at future time steps (Deisenroth et al., 2015). Deep PILCO (Gal et al., 2016) is proposed to make up for these drawbacks by replacing the Gaussian Process component with a Bayesian neural network dynamics model but still suffers from lack of scalability.
2.3 Combination of Model-free and Model-Based Methods
Many previous works also try to combine advantages from both model-free and model-based RL. A control pipeline proposed in the work (Nagabandi et al., 2018) uses random-shooting and model predictive control (MPC) method to find an optimal action at each state based on a dynamics model and then produces multiple sub-optimum rollouts. These rollouts are severed as training data for a neural network to learn a closed-loop policy, using a DAGGER (Ross et al., 2011) method. Finally, the weights of this network are used as the initialization of the policy network in a TRPO method. It is shown that this framework can improve the data efficiency of pure model-free methods. Another way for hybridizing model-based and model-free methods is Dyna algorithm, which uses a model to generate synthetic samples for model-free policy optimiser. The original Dyna-Q algorithm (Sutton, 1990) use a model to have a better Q function estimation based on Q-learning method. Recently proposed Dyna-style methods including Model-Based Acceleration (MBA) (Gu et al., 2016), Model-Based Value Expansion (MVE) (Feinberg et al., 2018), Model-Based Policy Optimization (MBPO) (Janner et al., 2019) and so on. These methods usually differ from whether the training is based on real-world rollout or predicted rollout, or whether using predicted rollouts to estimate target value or to train the whole Q function. The experiment of the MBPO method shows that it can obtain better sample efficiency than prior model-based methods and asymptotic performance of the state-of-the-art model-free algorithms.
2.4 Risk-Sensitive Reinforcement Learning
There is another aspect we can evaluate an RL method: whether or not it is risk-aware. All the works we have mentioned above are risk-neutral. There are also works applying reinforcement learning to robust MDP setting, which has traditionally dealt with risk due to uncertainty in the transition and reward parameters. Tamar et al. (Tamar et al., 2014) use approximate dynamic programming (ADP) to scale up the robust MDP paradigm with larger state space. Roy et al. (Roy et al., 2017) propose a robust counterpart to Q-Learning, which is robust to model misspecification, while Derman et al. (Derman et al., 2019) propose a robust version of DQN for higher dimensional domains. Tessler et al. (Tessler et al., 2019) propose a robust variant of DDPG, training two deterministic policy networks, the Actor and the Adversary. The Adversary is a potentially adversarial policy. Similar to DDPG, a critic is trained to update the joint-policy. It is shown that robust-oriented RL can do better in generalization, although it is still not clear how the connection between robustness and generalization holds in RL (Tessler et al., 2019). While the works mentioned above are dealing with uncertainty due to inherent stochasticity of the environment, a. k.a. aleatory uncertainty, it is usually not the most important source of risk occurs in engineering. It is because systems in engineering are nearly deterministic, and most uncertainty is due to the lack of information about the environment (Eriksson and Dimitrakakis, 2020). Therefore, Depeweg et al. (Depeweg et al., 2017) focus on decomposition in aleatory and epistemic risk. They employ a Bayesian neural network to model the underlying dynamics and utility function to do a trade-off between expected return and each risk. The work by Eriksson et al. (Eriksson and Dimitrakakis, 2020) is also developed in a Bayesian framework, using policy gradient and utility function to leverage preferences between risk and expected return based on a model-free setting.
3 Preliminaries
We formularize our control problem as a continuous state space Markov Decision Process, written as a tuple
In MBRL, the transition function is usually expressed as a dynamics model. Throughout this paper, we consider a dynamics model
The dynamics model does not directly output the predicted successive state
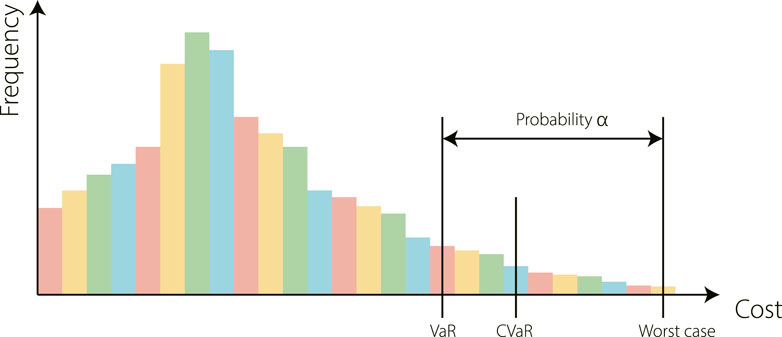
FIGURE 2. An example to illustrate three risk metrics: Value at Risk (VaR), Conditional Value at Risk (CVaR), and the worst case. Intuitively, Var is the
In Eq. 2,
Overall, we want to find an (implicit) policy π that can maximize the cumulative reward starting from the first state
The transformation of this objective function to relate it with the risk evaluation functions would be discussed in the next section.
4 Risk-Aware Model-Based Control
In this work, we propose a model-based method with a probabilistic dynamics model, and our main objective is to learn a safe and scalable policy efficiently. We combine it with an MPC, taking a CVaR into consideration, to perform planning using this dynamics model. Overall, the core contribution of this work is a risk-sensitive model-based control framework, which uses a Bayesian neural network to capture aleatoric and epistemic uncertainty and uses CVaR to trade between risk and return. The overview of our method is illustrated in Figure 3. We now detail our control framework.
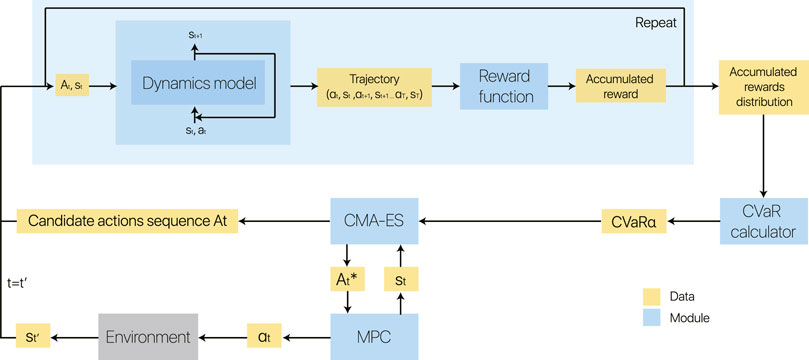
FIGURE 3. Block diagram of our model-based reinforcement learning method on run time. For each state
4.1 Dynamics Model: Transition Function as a Gaussian Process
First, predicting the next state. Any MBRL algorithm has to select some mechanism to model the environment dynamics. This selection is generally of significance for an MBRL algorithm, since even small error can considerably affect the quality of the corresponding controlled results (Abbeel et al., 2006). There are lots of choices for the function
This means that we can implement this stochastic dynamics model based on a structure of deep neural networks, with dropout layers. Compared to common deterministic neural networks, all the dropout layers are not only activated during the back-propagation phase but also when making an inference.
4.2 Training the Dynamics Model
4.2.1 Training Data Collection and Pre-processing
Initially, we collect warm-up training data by having agents take actions from a sampled initial state
4.2.2 Model Training
To optimize the objective function (4), we build a network with three dense layers and dropout layers. In the l-th pair of layers, we have
Note that the optimization objective of our network, which is just the minimization objective of the loss function Eq. 5 and Eq. 4 would both converge to the same limit. We minimize the loss function using an Adam optimiser.
4.2.3 Model Validation
For validation, similar to some other supervised learning method in machine learning, we can calculate the mean square error (MSE) between the expectation of the predicted result and the true data given by a validation data set:
where
where the expectation of state
4.3 Policy Evaluation
Then, evaluating the predicted consequences. While this is a stochastic dynamic model, in each state, we are able to generate K next state samples, moment-match these samples as a Gaussian distribution, and sample from this distribution. Previous works show that this moment-matching could benefit data efficiency by penalizing multi-modal distributions through smoothing of the loss surface (Deisenroth and Rasmussen, 2011). The step-wize prediction can hence be expressed as
Given a sequence of actions starting from step t:
with standard deviation
4.4 Optimization
Finding the best action. The calculation of the exact optimum of Eq. 10 can be challenging, as the transition and reward functions are both nonlinear. In this work, we use an evolutionary algorithm called Covariance Matrix Adaptation Evolution Strategy (CMA-ES) (Hansen, 2006). In each generation, it samples N-many candidate solutions from a multivariate Gaussian distribution
Each candidate solution is evaluated according to the objective function (10). Parameters mean vector
where the component
It was shown previously that CMA-ES could be served as an efficient tool for solving ill-conditioned functions and optimal control problems (Maki et al., 2020). For instance, to solve a quadratic function, it is proven that it can approximate the inverse Hessian empirically (Hansen and Auger, 2014) and theoretically (Akimoto, 2012). However, the problem of this method is that it would be computationally expensive for solving high-dimensional problems (10). Therefore, a variant of CMA-ES is used in our work. Inspired by VkD-CMA (Akimoto and Hansen, 2016b) which involves a simplification of the covariance matrix and an online-adapting simplification rule (Akimoto and Hansen, 2016a), we simplify the evolutionary path for computational efficiency.
Overall, we use a variant of CMA-ES as a black-box optimiser for the objective (10). For each generation, we sample N candidate solutions from a Gaussian distribution, calculate the CVaR of each candidate solutions, update the distribution and repeat.
4.5 Model-Based Control
We have shown how to solve Eqn. 10 and find an approximately optimal solution
5 Experimental Setup
5.1 AntX: A Real-World-Inspired Robot Model
The main robot model we use to test our RAMCO algorithm is AntX model, which is modified from the MuJoCo Ant-v2 benchmark model in OpenAI gym library. The original model contains a state space of 111 dimensions and action space of eight dimensions, while our model contains 29 dimensions of state space and also eight dimensions of action space. The modification is based on two reasons: First, we assume that the reward function
5.2 Eidos: A Pseudo Experimental RL Environment
As we claim that RL should show its advantage over solving unknown problems, we propose a novel experimental platform using a pseudo environment, named Eidos (a term coined by Plato as a permanent reality that defines a thing as what it is). We use Eidos to simulate an MDP with arbitrary state and action dimensionality. In this pseudo environment, we use a deep neural network with randomly initialized weights to represent the ground-truth dynamics function
When the number of observation dimensions
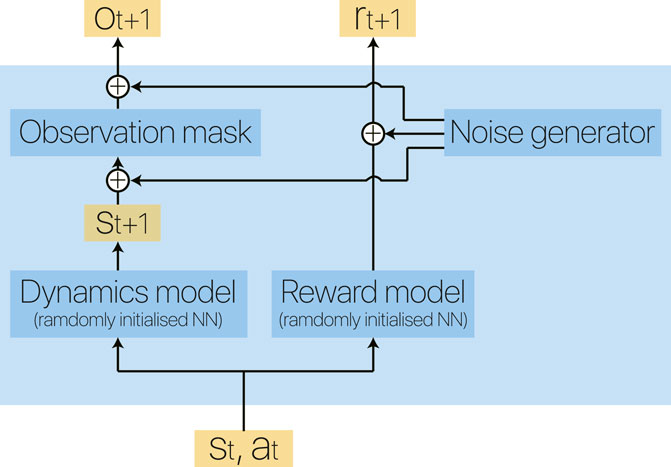
FIGURE 4. Block diagram of our Eidos environment. Two randomly initialized deep neural networks represent the dynamics model and reward model of an environment, making it flexible to vary the complexity of the corresponding MDP.
6 Experimental Results
In this section, we aim to answer the following questions:
Can the dynamics model predict trajectories precisely?
Is the Eidos environment effective as an evaluation method?
How is the overall performance of RAMCO in terms of accumulated reward?
Our initial experiments aimed to test the trajectories from the dynamics model. Then, we stack up RAMCO against other state-of-the-art algorithms on a simulation of a walking robot. Finally, we briefly introduce our novel RL testing environment called Eidos and perform another comparison.
6.1 Dynamics Model
We first train the dynamics model on 11 benchmark environments and a simulated walking robot AntX (improved from Ant-v2) with the simulators MuJoCo (Todorov et al., 2012), PyBullet (Coumans and Bai, 2020), and Box2D (Catto, 2010), which are introduced in the supplementary material.
To estimate the effectiveness of using different policies as the back-end to generate training data, we compare training curves based on
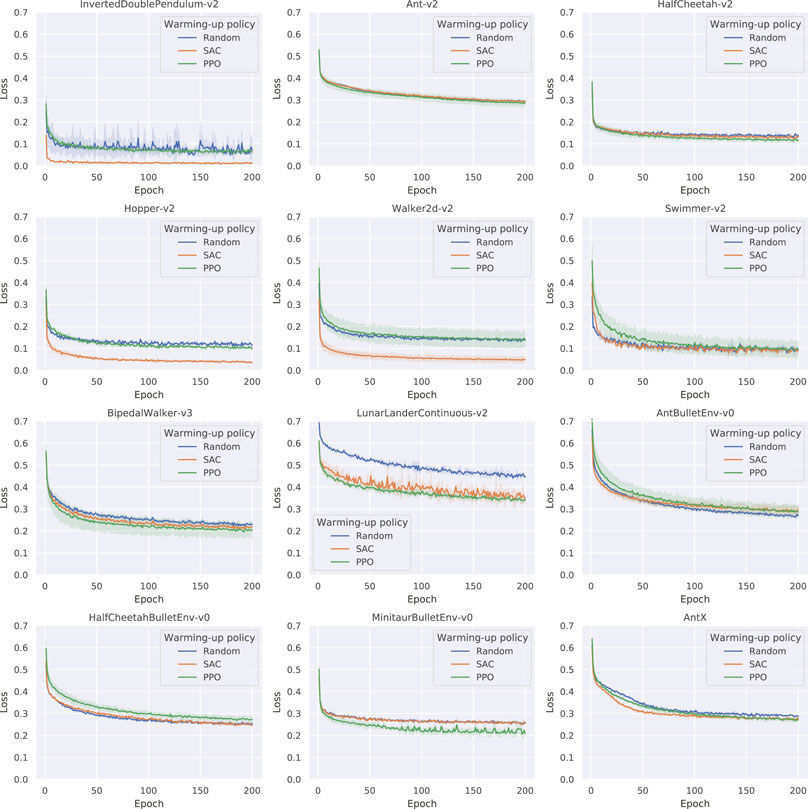
FIGURE 5. Learning curves of the dynamics model based on different warm-up data (Average of three trials), where the metric of loss is the sum of squared errors (SSE) with L2 regularization. In most cases, model-free methods significantly improve the dynamics model learning.
Based on the trained dynamics model, we then estimate the prediction performance of the model. We plot the output from the trained model with random warm-up data and with different training iterations (20, 60, 200). For visualization purposes, we average over all the dimensions of a state to a scalar. We generate a random sequence of actions and predict each state recursively with the dynamics model for 1,000 times. Some visualization results are shown in Figure 6 and the others are shown in the supplementary material. We can see a strong prediction from our algorithm with the baseline dots approaching the average prediction even when stretching the prediction horizon to 90 steps.
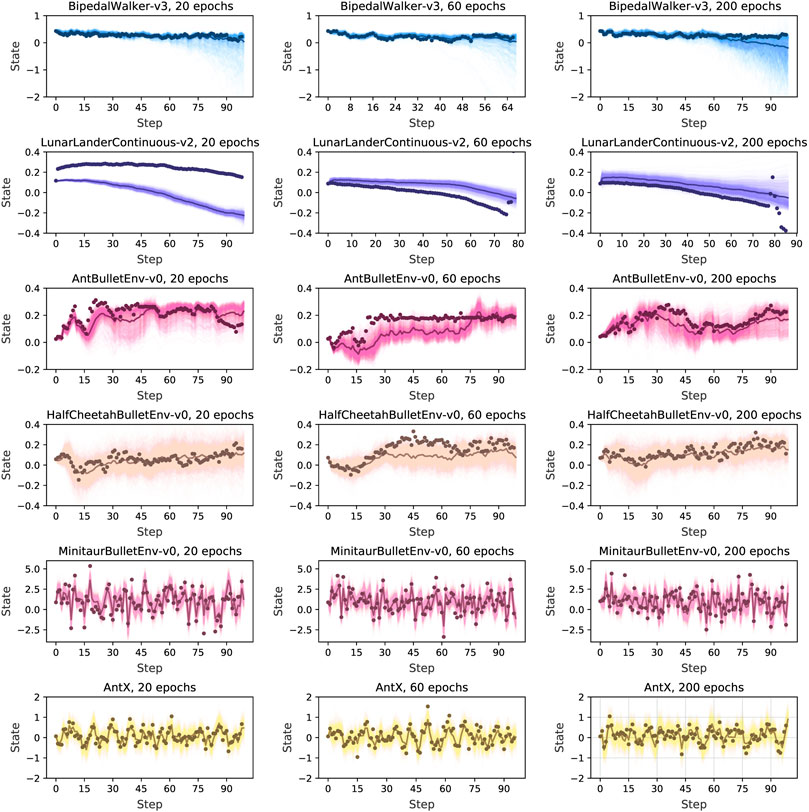
FIGURE 6. Predicted trajectories with RAMCO, with all dimensions of a state averaged over to a scalar. After a random warm-up we predict states recursively with the dynamics model. Each prediction and predictions average are in light and dark colors, and the baseline in dots. Through this visualization of predictive trajectories, we claim that this dynamics model meets the requirements of our control framework and can support our system to produce risk-aware control.
It is usually not good for a dynamics model if only the average output is close to the baseline but with high variance. This variance of prediction is unavoidable in real-world applications because of aleatory and epistemic uncertainty. For example, it is easy to observe from the case of BipedalWalker-v3 in Figure 6 that high prediction variance occurs when the prediction horizon is longer than 60 steps. However, our control framework can still deal with this variance in a risk-aware way. It is because we can observe from the figure that our sample-based dynamics model can always produce at least one accurate prediction. If this accurately predicted trajectory is dangerous, (i.e. with a very low return), our CVaR-based optimiser will take this into consideration and avoid performing the corresponding dangerous actions in the real world. In this case, our system can successfully detect and avoid the worst cases using CVaR, statistically eliminating risks and reducing losses, even though the predictions are noisy. Therefore, we claim that this dynamics model meets the requirements of our control framework and can support our system to produce risk-aware control.
In order to estimate the prediction accuracy quantitively and hence verify the effectiveness of our prediction, we then calculate the exact validation loss according to Eq. 7 for 1-step, 5-steps, 10-steps, 50-steps, and 100-steps prediction length
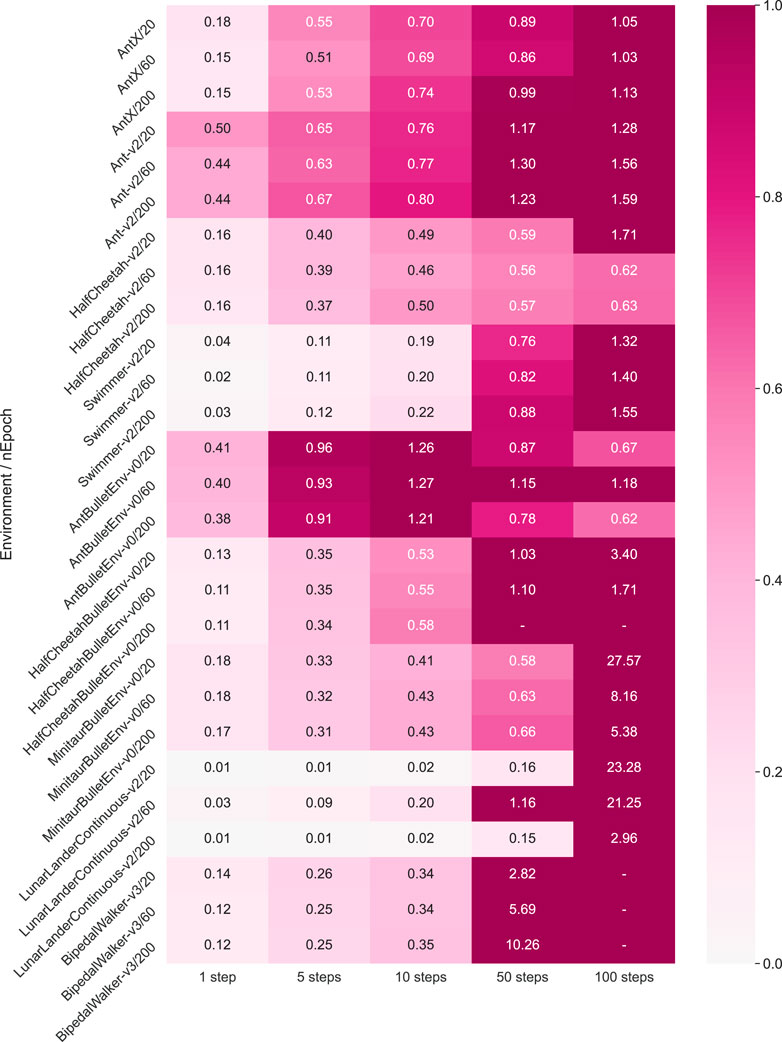
FIGURE 7. Dynamics model multi-step prediction error, with different RL environments (introduced in the supplementary material) and training epochs (20, 60, 200). We calculate the validation loss in Eq. 7 for one step, five steps, 10 steps, 50 steps, and 100 steps of prediction length. The smaller the value is, the more accurate the prediction makes, and the lighter color is shown. All the results are averaged after three trials.
6.2 RAMCO on AntX
We test our RAMCO method with different warm-up policies (SAC, PPO and random) on our AntX model with the hyperparameters shown in the supplementary material, and these results are shown in Figure 8. All the result data are an average of three runs. We compare our results with RL algorithms listed below:
Proximal Policy Optimization (PPO) (Schulman et al., 2017): PPO is one of the most popular and successful model-free RL algorithms. As introduced in Section 2, essentially it is a policy-gradient-based RL method.
Deep Deterministic Policy Gradient (DDPG) (Lillicrap et al., 2015): DDPG is another model-free RL algorithm with an actor-critic structure.
Soft Actor-Critic (SAC) (Haarnoja et al., 2018): SAC adds entropy as part of its objective function for better exploration. It reports better data efficiency than DDPG on MuJoCo benchmarks.
Model-Based Model-Free hybrid (MBMF) (Nagabandi et al., 2018): The model-based part of the method MBMF is implemented. It is an deterministic model-based method using random shooting method as the optimiser.
Model-Based Policy Optimization (MBPO) (Nagabandi et al., 2018): MBPO uses a probabilistic dynamics model to generate additional data to a replay buffer for training a SAC-based model-free agent. It is reported that this can highly improve data efficiency.
Probabilistic Ensembles with Trajectory Sampling (PETS) (Chua et al., 2018): PETS is a recent pure model-based method. It uses deep neural networks with ensembles to model the environment dynamics taking the uncertainty in consideration, and does open-loop planning based on this model.
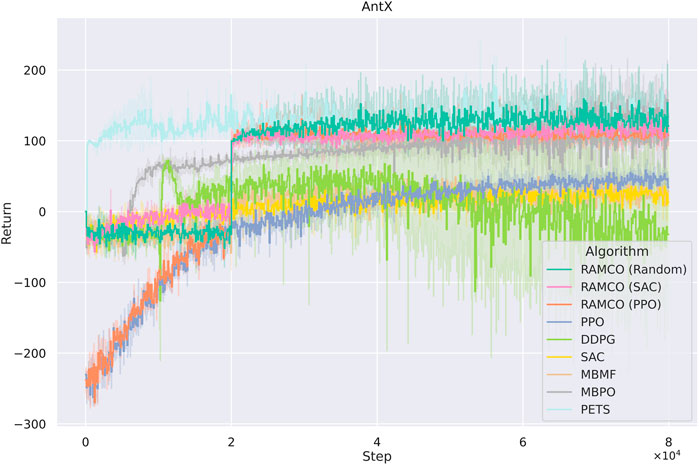
FIGURE 8. Accumulated rewards from each episode of AntX for different algorithms. RAMCO (SAC) and RAMCO (PPO) stand for using SAC and PPO as training data generators in our RAMCO control framework, respectively. These two model-free agents are trained from scratch. RAMCO (Random) means RAMCO with random data for training of the dynamics model. Although our method uses
In addition, the first four methods use the implementation from TF2RL package (Kei Ohta, 2020) with all default hyperparameters. MBPO uses its official implementation and PETS uses the implementation from (Vuong, 2020). We run all these methods for
It is noticed that some specially designed risk-sensitive metric is not used in the comparison but the final returns are shown since this is fairer for other algorithms. Furthermore, we consider that users will focus more on the final performance in their applications and this also meets with our assumption in Section 3 that the negative of total discounted future reward is equivalent to the value of loss. In order to highlight the superior of our risk-aware framework, we plot a histogram showing the distribution of final returns (after the warm-up phase of RAMCO and the corresponding period of other methods) among different algorithms in Figure 9. It can be obtained from the figure that not only the average of our returns is outstanding, but also the variance. While the random-based RAMCO has shown an exceptional average return, the PPO-based RAMCO shows the lowest variance among all the methods. RAMCO based on SAC warm-up policy produces a variance between the two.
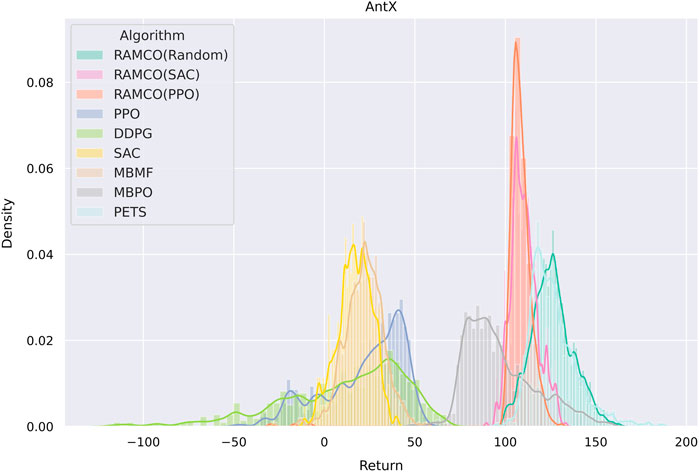
FIGURE 9. A histogram showing the distribution of final returns among different algorithms. Data of the warm-up phase of RAMCO and the corresponding period of other methods are dropped. We can see from the figure that not only the average of our returns is outstanding, but also the variance. While the random-based RAMCO has shown an exceptional average return, the PPO-based RAMCO shows the lowest variance among all the algorithms, which could be a very useful property in risk-sensitive applications. The SAC-based RAMCO has a variance between the two.
Compared to another state-of-the-art model-based method PETS, it is observed from Figures 8, 9 that our methods are highly competitive with respects to the average and variance. While the random-based RAMCO shows a similar average return to PETS, the use of SAC and PPO as the warm-up policy can further reduce the variance and hence risk. This means that the choice of the back-end warm-up policy can be used for trading between risk and return. This feature comes from our risk-awareness nature and more flexible framework compared to PETS. On the one hand, our CVaR decision-making mechanism tends to perform conservative strategies; on the other hand, we can choose the back-end warm-up policy (random policy, SAC, or PPO) to meet users’ requirement of performance and robustness. We will discuss more on the differences between our method and PETS in Section 7.1 and our advantages on generalization and risk aversion over PETS in sections 7.2 and 7.3.
6.3 RAMCO on Eidos
Based on the fact that Eidos is a very efficient method to evaluate RL algorithms, which is shown in the supplementary material, we benchmark different algorithms on Eidos with state dimensions of 10,
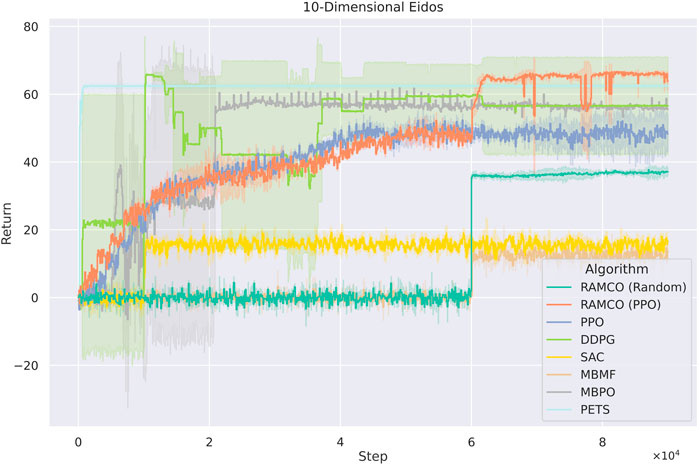
FIGURE 10. Training curves for Eidos with 10 state dimensionality. The PPO-version of RAMCO outperforms all other methods after
In the 100 dimensions case (Figure 11), PPO-version of RAMCO still shows advantages over all other model-based and model-free methods. In this case, model-free methods such as PPO begin to show its advantages on scalability while other model-based methods start to show their limit of applications. However, RAMCO based on PPO-generated training data still shows a jump in its training curve after the warm-up phase, which makes it outperforms other state-of-the-art model-free methods including PPO, DDPG and SAC and model-based methods including PETS, MBMF and MBPO. The random-based RAMCO seems to have a lower return than the one based on PPO, while still produces a competitive result compared to SAC, PETS, and MBMF.
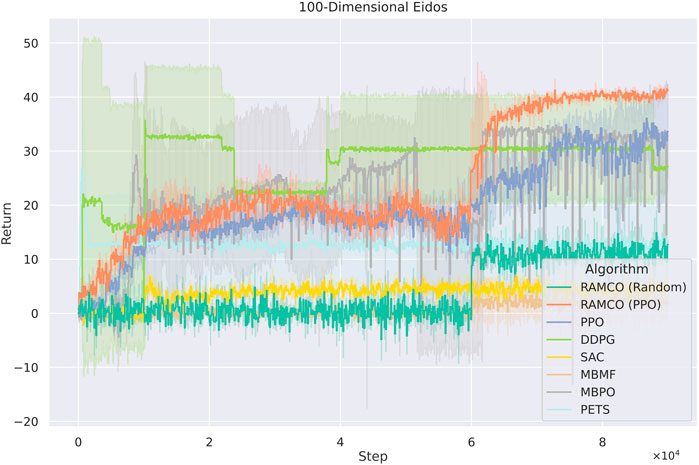
FIGURE 11. Training curves for Eidos with 100 state dimensionality. The PPO-version of RAMCO continuous to show its advantages over all other model-based and model-free methods. In this case, model-free methods begin to show its advantages on scalability while other model-based methods start to show their shortage. However, RAMCO based on PPO-generated training data still outperforms other state-of-the-art model-free methods including PPO, DDPG and SAC and model-based methods including PETS, MBMF and MBPO after the warm-up phase.
As for the cases with 1,000 dimensions (Figure 12), RAMCO (Random) shows performance similar to PETS, which are still better than the model-based method MBMF and MBPO. The PPO-warm-up version of RAMCO reached its highest returns during the warm-up phase, and its performance degrades afterwards. While RAMCO excels in low dimensionality data efficiency, even when the warm-up is taken into consideration, it still suffers from the curse of dimensionality. Nonetheless, its flexible control framework makes it a good candidate for real-world applications by directly deploying the underneath warm-up policy for solving problems.
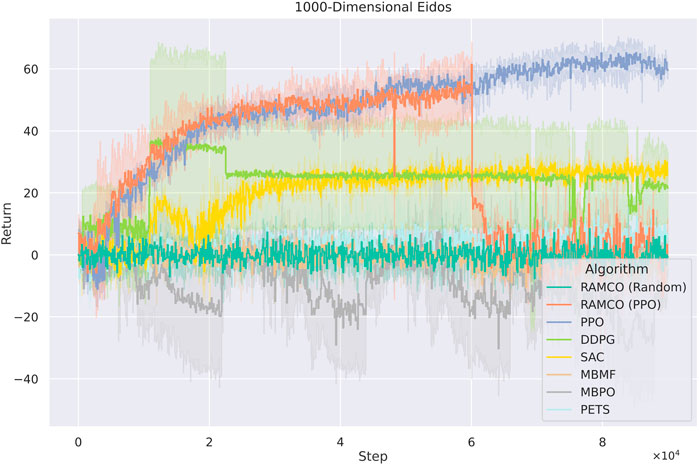
FIGURE 12. Training curves for Eidos with 1,000 state dimensionality. RAMCO (Random) shows performance similar to PETS, which are still better than the model-based method MBMF and hybrid method MBPO. The PPO-warm-up version of RAMCO reached its highest returns during the warm-up phase, and its performance degrades afterwards. Therefore, PPO-warm-up RAMCO excels while dealing with scalability with its flexible control framework in real-world applications where the back-end warm-up policy can be adopted directly.
Overall, in the 10-dimension case, our RAMCO method (with a back-end PPO policy) shows its advantages on both performance and robustness over all other model-based and model-free methods. In the case with
7 Discussion
This paper proposes a novel algorithm called RAMCO. It uses a probabilistic dynamics model to model the transition function whose initial training data can be produced by a random policy or model-free agents. Within this method, we use CVaR as a metric to evaluate the predicted trajectories, and once the optimum action sequence is found by CMA-ES, the first action of the sequence is taken to interact with the environment. To be consistent with our comparisons, we also propose a novel RL environment called Eidos. In short, Eidos is a pseudo environment consisting of two randomly initialized deep neural networks: one representing the ground-truth dynamics model and one regarded as a reward function. After showing the effectiveness of this Eidos environment, we show that our method achieves a remarkable trade-off between data efficiency, generalization, and risk aversion.
7.1 Data Efficiency
Data inefficiency can lead to a heavy human workload during real-world applications, which ironically contradicts the original motivation behind using learning algorithms. However, such inefficiency can still be found in most model-free algorithms (Chatzilygeroudis, 2018). As we show in Figures 8,10, all the model-free algorithms, including PPO, DDPG, and SAC, do not perform well in these two cases, mostly because of their data-inefficiency:
The model-based method PETS benefits from its probabilistic dynamics model and shows a competitive result when compared to our RAMCO method. This success presented by PETS can be explained from its nonconsideration of risk. First, PETS does not distinguish the warm-up phase and application phase and has a higher update frequency of the dynamics model, which makes the improvement of policies more aggressive. However, this also leads to a higher risk of being constrained to a local optimum, which can be proven by the results of the 10-dimensional case, where the returns of our methods surpass the ones from PETS. The second reason for the advantage of PETS in the AntX case is that its evaluation only takes into consideration the average returns. Compared to the conservative policy of RAMCO, PETS performs a risky strategy which outputs higher mean returns but also a higher variance. We will further discuss the negative impact of this trade-off in Section 7.3. As for another model-based method MBMF, the random-shooting optimiser used for the MPC is not enough to find an optimum solution effectively in all cases. Overall, our method shows its advantage in data efficiency as an MBRL algorithm, which makes it competitive on the AntX and 10-dimensional Eidos environments.
7.2 Generalization
The generalization of an RL algorithm can be characterized in two aspects: robustness and scalability, both of which attract less attention from the MBRL communities, but still crucial for real-world application. When in situations where humans themselves cannot predict what the best policies/actions are, RL algorithms require a certain degree of insensitivity to hyperparametric choices and environment complexity. In this sense, our proposed Eidos environment is an efficient tool to evaluate the generalization of RL algorithms, and RAMCO still proves to be efficient following this metric.
As it can be seen from Figures 11, 12, model-free RL algorithms have natural advantages on scalability. For instance, DDPG begins to show a higher return than RAMCO on the 100-dimensional Eidos environment and all the model-free methods achieve higher returns than RAMCO based on random rollouts on the 1000-dimensional Eidos. Conversely, scalability is a common problem for model-based methods focusing on data efficiency. Since it is challenging to learn a precise dynamics model in a complex environment even with neural networks, the model bias can often lead to failed decision making. This can be proven by the last two cases, where the problem dimensionality expands to 100 and 1,000. As we can see, while the dimensionality of the environment increases, model-based methods (including PETS and MBMF, and hybrid methods like MBPO) begin to suffer from model bias and hence produce much worse results than model-free methods. Other model-based methods, such as black-box optimisers (Hansen et al., 2015) to find a closed-loop policy (Chatzilygeroudis et al., 2017) or using policy gradient to find an optimum policy with respect to a Bayesian neural network (Gal et al., 2016), suffer from time complexity, so they mostly focus on simple tasks like cart-pole-swing-up or double-pendulum swing-up with lower dimensionalities (typically less than 10). As mentioned in Section 2, modeling the transition function with Gaussian Process (Deisenroth and Rasmussen, 2011; Kamthe and Deisenroth, 2018) is also a barrier for applying some MBRL methods to more complex environments.
As for RAMCO, we solve this problem with the flexibility of the warm-up policy. In the case of 100-dimensional Eidos, the RAMCO method based on PPO rollouts can still produce successful results compared with other methods, supported by our MC-dropout-based probabilistic dynamics model. In the case of 1000-dimensional Eidos, although our methods also suffer from model bias, in practice, we can directly adopt the warm-up policy to make up for this generalization problem of model-based methods. Therefore, the PPO-rollouts version is recommended for all environments with any dimensionality.
7.3 Risk Aversion
When compared to other methods, RAMCO is the only one taking calculated risks on its trials and hence producing much smoother training curves in most cases. By preventing drastic fluctuations, such as shown by the training returns produced by DDPG in the AntX case, it shows its excellence towards real-world application to avoid catastrophic loss. Compared to PETS on the AntX environment, although the PPO-version of our strategies causes a lower mean return, it shows a lower variance in the controlled phase, which is also meaningful for risk-sensitive real-world applications where expectable output is required.
In term of risk-sensitive control, most of the prior works are based on assuming a stochastic MDP (Tamar et al., 2014; Roy et al., 2017; Derman et al., 2019) and trying to reduce risk due to aleatory uncertainty, as we have introduced in Section 2. Since we believe that the risk assessment should take into consideration the epistemic uncertainty within an engineering application, we focus on the epistemic risk and maintain a regular environment setting. Depeweg et al. (Depeweg et al., 2017) decompose aleatory and epistemic uncertainty and propose a risk-sensitive RL algorithm to attain a balance between expected reward and risk. However, their consideration of risk is solely with respect to individual rewards, instead of the total return of each episode. Work with a very similar risk-control objective to ours can be found in (Eriksson and Dimitrakakis, 2020). There, the goal is to control the epistemic risk by a model-free RL algorithm and utility function. However, they only show experimental results on Gridworld and option pricing but not locomotion control. In addition, since it is based on a model-free structure, the data inefficiency limits its real-world application, which is inconsistent with the motivation of using a risk-sensitive model. In order to solve the problem of data inefficiency, there are also works on risk-sensitive batch-RL algorithms (Thomas et al., 2015; Levine et al., 2020), which return incremental policies based on historical data with probabilistic guarantees about the quality of generated policies. Their problem setting is closer to applications such as marketing and therapies.
It can be seen that there exists a broad diversity within the field of risk-sensitive RL. Therefore, specific settings and improvements of our Eidos environment should be our further work when building upon a general benchmark for risk-aware RL. At the same time, instead of using a constant α parameter for the CVaR component at RAMCO, an alternative path for our future work is to study the effects of this variable on the risk-sensitive performance on different Eidos settings. Furthermore, based on the flexibility of the Eidos environment, interesting and valuable experiments involving concepts of epistemic value, epistemic action, and active perception can be further designed in future work. The epistemic cost in these experiments can be further evaluated on both warm-up and application phases, which could be a significant metric in real-world risk-sensitive applications.
8 Conclusion
In this work, we propose an MBRL algorithm called RAMCO and an RL environment called Eidos, both motivated by the need from real-world applications to quickly converge to an optimal solution without incurring in catastrophic failures. While RAMCO is a risk-sensitive and data-efficient algorithm, Eidos is an environment which allows us to simulate a multitude of unknown/multi-dimensional problems which could be faced by an RL agent in the real-world. Compared to other works in MBRL methods (Deisenroth and Rasmussen, 2011; Nagabandi et al., 2018; Chua et al., 2018), we assign more attention to risk-awareness, robustness, and scalability; while compared to other works in robust MDP (Tamar et al., 2014; Roy et al., 2017; Derman et al., 2019), we innovate by considering epistemic uncertainty and data efficiency. We empirically show that the dynamics model in our RAMCO method can meet the requirements of our setting and the overall performance is competitive to state-of-the-art model-based and model-free RL algorithms. The results are encouraging as a step towards bringing RL into safe industrial applications.
9 Broader Impact
Robots in our daily life are gradually transitioning from a utopic “sci‐fi” concept to a concrete reality, and the capacity to adapt within very few trials to disturbances and malfunctions is crucial. Our work concentrates on risk-awareness and data efficiency, specifically, to address this problem. Unlike other works which rely on the abundance of data to find solutions (big data approaches), our solution deviates from this trend to follow a micro data approach. The reason for this is because trials can be very expensive, and failures can result in property damage (robotics) or loss of lives (therapeutics).
Our proposed algorithm excels on problems with less than 100 dimensions, finding excellent solutions right in its first trial after finishing its warming up phase. Although it has a higher computational cost per episode than its counterparts (which is convenient, in juxtaposition to the very nature of problems that it aims to solve, as “expensive trials” shouldn’t be quickly repeated), the exponential advances in computer architectures and cloud computing will make such strategies more preferable in the long run, quickly taking in consideration real-world inputs to output better strategies to physical machines directly.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
CY and AR conceived of the presented idea. CY developed the theory and carried out the experiment. AR verified the proposed methods and supervised the findings of this work. Both authors discussed the results and contributed to the final manuscript.
Funding
This work was supported by the National Natural Science Foundation of China, project number 61850410527, and the Shanghai Young Oriental Scholars, project number 0830000081.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frobt.2021.617839/full#supplementary-material.
References
Abbeel, P., Quigley, M., and Ng, A. Y. (2006). Using inaccurate models in reinforcement learning. Proceedings of the 23rd international conference on Machine learning, Pittsburgh, PA, United States, January 2006, 1–8. doi:10.1145/1143844.1143845
Akimoto, Y. (2012). Analysis of a natural gradient algorithm on monotonic convex-quadratic-composite functions. Proceedings of the 14th international conference on Genetic and evolutionary computation conference—GECCO, Philadelphia, PA, United States, 7-11 July 2012 12. doi:10.1145/2330163.2330343
Akimoto, Y., and Hansen, N. (2016a). “Online model selection for restricted covariance matrix adaptation,” Parallel problem solving from nature – PPSN XIV. Editors J. Handl, E. Hart, P. R. Lewis, M. López-Ibáñez, G. Ochoa, and B. Paechter (Cham, Switzerland: Springer International Publishing), 3–13.
Akimoto, Y., and Hansen, N. (2016b). Projection-based restricted covariance matrix adaptation for high dimension. GECCO. Proceedings of the Genetic and Evolutionary Computation Conference 2016, Denver, CO, United States, 20–24 July 2016. New York, NY, United States: Association for Computing Machinery). 16, 197–204. doi:10.1145/2908812.2908863
Barth-Maron, G., Hoffman, M. W., Budden, D., Dabney, W., Horgan, D., Tb, D., et al. (2018). Distributed distributional deterministic policy gradients. ICLR, 2018, Vancouver, BC, Canada, April 30 2018.
Blundell, C., Cornebise, J., Kavukcuoglu, K., and Wierstra, D. (2015). Weight uncertainty in neural networks. ICML’15: Proceedings of the 32nd International Conference on International Conference on Machine Learning—Volume, Lille, France, 6-11 July 2015, 37, 1613–1622.
Catto, E. (2010). Box2d: a 2d physics engine for games. Accessed 2020-05-01: https://box2d.org/. doi:10.1063/1.3460168
Chatzilygeroudis, K. (2018). Micro-data reinforcement learning for adaptive robots. Nancy, France: Theses, Universite de Lorraine.
Chatzilygeroudis, K., Rama, R., Kaushik, R., Goepp, D., Vassiliades, V., and Mouret, J. (2017). Black-box data-efficient policy search for robotics. 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September, 2017, 51–58.
Chatzilygeroudis, K., Vassiliades, V., Stulp, F., Calinon, S., and Mouret, J.-B. (2020). A survey on policy search algorithms for learning robot controllers in a handful of trials. IEEE Trans. Robot. 36, 328–347. doi:10.1109/tro.2019.2958211
Chua, K., Calandra, R., McAllister, R., and Levine, S. (2018). “Deep reinforcement learning in a handful of trials using probabilistic dynamics models,” in Advances in neural information processing systems, December 2-8, Quebec, Canada. Editors S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett (Curran Associates, Inc.), 4754–4765. Available at: https://proceedings.neurips.cc/paper/2018/file/3de568f8597b94bda53149c7d7f5958c-Paper.pdf.
Coumans, E., and Bai, Y. (2020). Pybullet: a python module for physics simulation in robotics, games and machine learning. Accessed 2020-05-01: http://www.pybullet.org/
Cutler, M., and How, J. P. (2015). Efficient reinforcement learning for robots using informative simulated priors. ICRA. 2015, 2605–2612. doi:10.1109/ICRA.2015.7139550
Deisenroth, M. P., Fox, D., and Rasmussen, C. E. (2015). Gaussian processes for data-efficient learning in robotics and control. IEEE Trans. Pattern Anal. Mach. Intell. 37, 408–423. doi:10.1109/TPAMI.2013.218
Deisenroth, M. P., Neumann, G., and Peters, J. (2011). A survey on policy search for robotics. FNT in Robotics 2, 1–142. doi:10.1561/2300000021
Deisenroth, M. P., and Rasmussen, C. E. (2011). Pilco: a model-based and data-efficient approach to policy search. Proceedings of the 28th International Conference on International Conference on Machine Learning, ICML’11, Bellevue, DC, United States, 28-2 July, 2011. Madison, WI, United Status: Omnipress), 465–472.
Depeweg, S., Hernández-Lobato, J. M., Doshi-Velez, F., and Udluft, S. (2017). Decomposition of uncertainty in bayesian deep learning for efficient and risk-sensitive learning. Proccedings of the 35th International Conference on Machine Learning, ICML 2017, Stockholm, Sweden, 15 July 2017.
Derman, E., Mankowitz, D. J., Mann, T. A., and Mannor, S. (2019). “A bayesian approach to robust reinforcement learning,” in Proceedings of the thirty-fifth conference on uncertainty in artificial intelligence, UAI 2019, tel aviv, Israel, july 22-25, 2019. Editors A. Globerson, and R. Silva (Arlington, VA, United States: AUAI Press), 228.
Englert, P., Paraschos, A., Peters, J., and Deisenroth, M. P. (2013). Model-based imitation learning by probabilistic trajectory matching. 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6-10 May 2013. doi:10.1109/ICRA.2013.6630832
Engstrom, L., Ilyas, A., Santurkar, S., Tsipras, D., Janoos, F., Rudolph, L., et al. (2020). Implementation matters in deep rl: a case study on ppo and trpo. Iclr
Eriksson, H., and Dimitrakakis, C. (2020). “Epistemic risk-sensitive reinforcement learning,” in 28th European symposium on artificial neural networks, computational intelligence and machine learning, Bruges, Belgium, October 2–4, 2020, 339–344. Available at: https://www.esann.org/sites/default/files/proceedings/2020/ES2020-84.pdf.
Fabisch, A., Petzoldt, C., Otto, M., and Kirchner, F. (2019). A survey of behavior learning applications in robotics - state of the art and perspectives. CoRR. [arXiv. 1906.01868] (Accessed February 4, 2021).
Feinberg, V., Wan, A., Stoica, I., Jordan, M. I., Gonzalez, J. E., and Levine, S. (2018). Model-based value estimation for efficient model-free reinforcement learning. CoRR. [arXiv. 1803.00101]. Available at: https://arxiv.org/abs/1803.00101 (Accessed February 4, 2021).
Fujimoto, S., van Hoof, H., and Meger, D. (2018). “Addressing function approximation error in Actor-Critic Methods,” in Proceedings of the 35th international conference on machine learning, Stockholm, Sweden, July 10–15. Editors J. Dy and A. Krause (PMLR), 1587–1596. Available at: http://proceedings.mlr.press/v80/fujimoto18a/fujimoto18a.pdf.
Gal, Y., and Ghahramani, Z. (2015). Dropout as a Bayesian approximation: appendix. CoRR. [arXiv. 1506.02157]. Available at: https://arxiv.org/abs/1506.02157 (Accessed February 4, 2021).
Gal, Y., and Ghahramani, Z. (2016). “Dropout as a bayesian approximation: representing model uncertainty in deep learning,” in Proceedings of the 33rd international conference on machine learning, New York, NY, June 20 –22. Editors M. F. Balcan and K. Q. Weinberger (PMLR), 1050–1059. Available at: http://proceedings.mlr.press/v48/gal16.pdf.
Gal, Y., McAllister, R., and Rasmussen, C. E. (2016). Improving pilco with bayesian neural network dynamics models. Data-efficient machine learning workshop, 4. New York, NY, United States: ICML.
Givan, R., Leach, S., and Dean, T. (2000). Bounded-parameter Markov decision processes. Artif. Intell. 122, 71–109. doi:10.1016/s0004-3702(00)00047-3
Gu, S., Lillicrap, T., Sutskever, I., and Levine, S. (2016). Continuous deep q-learning with model-based acceleration. Proceedings of the 33rd International Conference on International Conference on Machine Learning—ICML’16, New York, NY, United States, 19-24 June 2016, 48, 2829–2838.
Haarnoja, T., Zhou, A., Abbeel, P., and Levine, S.PMLR (2018). “Soft actor-critic: off-policy maximum entropy deep reinforcement learning with a stochastic actor,”. Proceedings of the 35th international conference on machine learning, ICML 2018. Editors J. G. Dy, and A. Krause (Stockholmsmässan, Stockholm, Sweden: of Proceedings of Machine Learning Research), vol. 80.
Hafner, D., Lillicrap, T., Fischer, I., Villegas, R., Ha, D., Lee, H., et al. (2019). “Learning latent dynamics for planning from pixels,” in Proceedings of the 36th international conference on machine learning, June 9–15. Editors K. Chaudhuri and R. Salakhutdinov (PMLR). 2555–2565. Available at: http://proceedings.mlr.press/v97/hafner19a/hafner19a.pdf.
Hansen, N., Arnold, D. V., and Auger, A. (2015). “Evolution strategies,” in Springer handbook of computational intelligence. Editors J. Kacprzyk, and W. Pedrycz (Berlin, Germany: Springer Berlin Heidelberg), 871–898. doi:10.1007/978-3-662-43505-244
Hansen, N., and Auger, A. (2014). “Principled design of continuous stochastic search: from theory to practice,” Natural Computing Series. Theory and principled methods for the design of metaheuristics. Editors Y. Borenstein, and A. Moraglio (Berlin, Germany: Springer), 145–180. doi:10.1007/978-3-642-33206-78
Hansen, N. (2006). “The CMA evolution strategy: a comparing review,” in Towards a new evolutionary computation—advances in the estimation of distribution algorithms. Of studies in fuzziness and Soft computing. Editors J. A. Lozano, P. Larrañaga, I. Inza, and E. Bengoetxea (Berlin, Germany: Springer), vol. 192, 75–102. doi:10.1007/3-540-32494-14
Hinton, G., Deng, L., Yu, D., Dahl, G., Mohamed, A.-r., Jaitly, N., et al. (2012). Deep neural networks for acoustic modeling in speech recognition: the shared views of four research groups. IEEE Signal Process. Mag. 29, 82–97. doi:10.1109/msp.2012.2205597
Janner, M., Fu, J., Zhang, M., and Levine, S. (2019). “When to trust your model: model-based policy optimization,” in Advances in neural information processing systems (Vancouver, CANADA: Curran Associates, Inc.), 12519–12530.
Kamthe, S., and Deisenroth, M. (2018). “Data-efficient reinforcement learning with probabilistic model predictive control,” in International conference on artificial intelligence and statistics (Beijing, China: PMLR), 1701–1710.
Kim, D., Carballo, D., Di Carlo, J., Katz, B., Bledt, G., Lim, B., et al. (2020). Vision aided dynamic exploration of unstructured terrain with a small-scale quadruped robot. IEEE International Conference on Robotics and Automation (ICRA) 2020, 2464–2470. doi:10.1109/ICRA40945.2020.9196777
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). “Imagenet classification with deep convolutional neural networks,” in Advances in neural information processing systems 25. Editors F. Pereira, C. J. C. Burges, L. Bottou, and K. Q. Weinberger (New York, NY, United States: Curran Associates, Inc.), 1097–1105.
Lakshminarayanan, B., Pritzel, A., and Blundell, C. (2017). “Simple and scalable predictive uncertainty estimation using deep ensembles,” in Advances in neural information processing systems. Editors I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett (Long Beach, CA: Curran Associates, Inc.), Vol. 30. 6402–6413.
Levine, S., Kumar, A., Tucker, G., and Fu, J. (2020). Offline reinforcement learning: tutorial, review, and perspectives on open problems. arXiv preprint arXiv:2005.01643
Li, H., Liu, D., and Wang, D. (2017). Manifold regularized reinforcement learning. IEEE Trans Neural Netw Learn Syst 2017, 3043–3052. doi:10.1109/TNNLS.2017.2650943
Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N. M. O., Erez, T., Tassa, Y., et al. (2015). Continuous control with deep reinforcement learning. [arXiv. 1509.02971]. Available at: https://arxiv.org/abs/1509.02971 (Accessed February 4, 2021).
Majumdar, A., and Pavone, M. (2020). “How should a robot assess risk? towards an axiomatic theory of risk in robotics,” in Robotics research. Editors N. M. Amato, G. Hager, S. Thomas, and M. Torres-Torriti (Cham: Springer International Publishing), 75–84. doi:10.1007/978-3-030-28619-4_10
Maki, A., Sakamoto, N., Akimoto, Y., Nishikawa, H., and Umeda, N. (2020). Application of optimal control theory based on the evolution strategy (cma-es) to automatic berthing. J. Mar. Sci. Technol. 25, 221–233. doi:10.1007/s00773-019-00642-3
Mannor, S., Mebel, O., and Xu, H. (2012). Lightning does not strike twice: robust mdps with coupled uncertainty. Proceedings of the 29th International Coference on International Conference on Machine Learning, ICML, Edinburgh, Scotland, June 26–July 1, 2012. 12. Madison, WI, United States: Omnipress), 451–458.
Mansour, M., and Abdel-Rahman, T. (1984). Non-linear var optimization using decomposition and coordination. IEEE Trans. Power Apparatus Syst. 103, 246–255. doi:10.1109/tpas.1984.318223
Puterman, M. L. (1994). Markov decision Processes (Hoboken, NJ, United States: John Wiley and Sons). doi:10.1002/9780470316887
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., et al. (2015). Human-level control through deep reinforcement learning. Nature 518, 529–533. doi:10.1038/nature14236
Mouret, J.-B., and Chatzilygeroudis, K. (2017). 20 years of reality gap: a few thoughts about simulators in evolutionary robotics, Proceedings of the genetic and evolutionary computation conference companion. GECCO’17. (New York, NY, United States: Association for Computing Machinery). 1121–1124. doi:10.1145/3067695.3082052
Nagabandi, A., Kahn, G., Fearing, R. S., and Levine, S. (2018). “Neural network dynamics for model-based deep reinforcement learning with model-free fine-tuning,” in 2018 {IEEE} international conference on robotics and Automation, {ICRA} 2018, Brisbane, Australia, May 21–25, 2018 (IEEE), 7559–7566. doi:10.1109/ICRA.2018.8463189
Nagabandi, A., Konolige, K., Levine, S., and Kumar, V. (2019). “Deep dynamics models for learning dexterous manipulation,” 3rd Annual Conference on Robot Learning, CoRL 2019 (PMLR), Osaka, Japan, October 30—November 1, 2019. Editors L. P. Kaelbling, D. Kragic, and K. Sugiura, 100, 1101–1112.
Osiński, B., Jakubowski, A., Zięcina, P., Miłoś, P., Galias, C., Homoceanu, S., et al. (2020). Simulation-based reinforcement learning for real-world autonomous driving. IEEE International Conference on Robotics and Automation (ICRA) 2020, 6411–6418. doi:10.1109/ICRA40945.2020.9196730
Righi, M. B., and Ceretta, P. S. (2016). Shortfall deviation risk: an alternative for risk measurement. J. Risk 19, 81–116. doi:10.21314/jor.2016.349
Ross, S., Gordon, G. J., and Bagnell, D. (2011). “A reduction of imitation learning and structured prediction to no-regret online learning,”. Proceedings of the 14th International Conference on Artificial Intelligence and Statistics AISTATS 2011 of JMLR, Fort Lauderdale, FL, United States, 11-13 April, 2011. Editors G. J. Gordon, D. B. Dunson, and M. Dudík, 15, 627–635.
Schoettler, G., Nair, A., Luo, J., Bahl, S., Ojea, J. A., Solowjow, E., et al. (2020). “Deep reinforcement learning for industrial insertion tasks with visual inputs and natural rewards,” 2in International Conference on Intelligent Robots and Systems (IROS), October 25–29, Las Vegas, NV (IEEE), 5548–5555. Available at: https://ras.papercept.net/proceedings/IROS20/1872.pdf.
Schulman, J., Levine, S., Abbeel, P., Jordan, M. I., and Moritz, P. (2015). “Trust region policy optimization,” Proceedings of the 32nd International Conference on Machine Learning.of JMLR Workshop and Conference, ICML 2015, Lille, France, 6-11 July 2015. Editors F. R. Bach, and D. M. Blei, 37, 1889–1897.
Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and Klimov, O. (2017). Proximal policy optimization algorithms. CoRR. [arXiv. 1707.06347]. Available at: https://arxiv.org/abs/1707.06347 (Accessed February 4, 2021).
Sutton, R. S., and Barto, A. G. (2018). Reinforcement learning: an introduction. 2nd edn. Cambridge, MA, United States: The MIT Press.
Sutton, R. S. (1990). Integrated architectures for learning, planning, and reacting based on approximating dynamic programming. In Proceedings of the seventh international conference on machine learning (Burlington, MA, United States: Morgan Kaufmann), 216–224.
Tamar, A., Mannor, S., and Xu, H. (2014). “Scaling up robust mdps using function approximation,” Proceedings of the 31st International Conference on International Conference on Machine Learning ICML 2014 32, 181–189. doi:10.5555/3044805.3044913
Tessler, C., Efroni, Y., and Mannor, S. (2019). Action robust reinforcement learning and applications in continuous control. In Proceedings of the 36th International Conference on Machine Learning, ICML 2019, Long Beach, CA, United States, 9-15 June 2019, eds. K. Chaudhuri, and R. Salakhutdinov (PMLR), vol. 97, 6215–6224.
Thomas, P. S., Theocharous, G., and Ghavamzadeh, M. (2015). High confidence policy improvement. In Proceedings of the 32nd International Conference on Machine Learning, ICML 2015, Lille, France, 6-11 July 2015, eds. F. R. Bach, and D. M. Blei. 37, 2380–2388.
Todorov, E., Erez, T., and Tassa, Y. (2012). Mujoco: a physics engine for model-based control. IEEE/RSJ International Conference on Intelligent Robots and Systems 2012, 5026–5033. doi:10.1109/IROS.2012.6386109
Wu, Y., Mansimov, E., Liao, S., Grosse, R., and Ba, J. (2017). Scalable trust-region method for deep reinforcement learning using kronecker-factored approximation. Proceedings of the 31st international conference on neural information processing systems, NIPS’17. Red Hook, NY, United States: Curran Associates Inc.), 5285–5294.
Xu, X., Jiang, X., Ma, C., Du, P., Li, X., Lv, S., et al. (2020). A deep learning system to screen novel coronavirus disease 2019 pneumonia. Engineering 6, 1122–1129. doi:10.1016/j.eng.2020.04.010
Keywords: machine learning, reinforcement learning, dynamics model, risk awareness, conditional value at risk, data efficiency, eidos, mujoco
Citation: Yu C and Rosendo A (2021) Risk-Aware Model-Based Control. Front. Robot. AI 8:617839. doi: 10.3389/frobt.2021.617839
Received: 15 October 2020; Accepted: 14 January 2021;
Published: 11 March 2021.
Edited by:
Sheri Marina Markose, University of Essex, United KingdomReviewed by:
Dimitri Ognibene, University of Milano-Bicocca, ItalyRabie A. Ramadan, Cairo University, Egypt
Copyright © 2021 Yu and Rosendo.. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andre Rosendo, YXJvc2VuZG9Ac2hhbmdoYWl0ZWNoLmVkdS5jbg==
 Chen Yu
Chen Yu Andre Rosendo
Andre Rosendo