Swarm-Enabling Technology for Multi-Robot Systems

Swarm robotics has experienced a rapid expansion in recent years, primarily fueled by specialized multi-robot systems developed to achieve dedicated collective actions. These specialized platforms are, in general, designed with swarming considerations at the front and center. Key hardware and software elements required for swarming are often deeply embedded and integrated with the particular system. However, given the noticeable increase in the number of low-cost mobile robots readily available, practitioners and hobbyists may start considering to assemble full-fledged swarms by minimally retrofitting such mobile platforms with a swarm-enabling technology. Here, we report one possible embodiment of such a technology—an integrated combination of hardware and software—designed to enable the assembly and the study of swarming in a range of general-purpose robotic systems. This is achieved by combining a modular and transferable software toolbox with a hardware suite composed of a collection of low-cost and off-the-shelf components. The developed technology can be ported to a relatively vast range of robotic platforms—such as land and surface vehicles—with minimal changes and high levels of scalability. This swarm-enabling technology has successfully been implemented on two distinct distributed multi-robot systems, a swarm of mobile marine buoys and a team of commercial terrestrial robots. We have tested the effectiveness of both of these distributed robotic systems in performing collective exploration and search scenarios, as well as other classical cooperative behaviors. Experimental results on different swarm behaviors are reported for the two platforms in uncontrolled environments and without any supporting infrastructure. The design of the associated software library allows for a seamless switch to other cooperative behaviors—e.g., leader–follower heading consensus and collision avoidance, and also offers the possibility to simulate newly designed collective behaviors prior to their implementation onto the platforms. This feature greatly facilitates behavior-based design, i.e., the design of new swarming behaviors, with the possibility to simulate them prior to physically test them.

1. Introduction

A swarm robotics system consists of autonomous robots with local sensing and communication capabilities, lacking centralized control or access to global information, situated in a possibly unknown environment performing a collective action (Brambilla et al., 2013). Based on this definition, one can easily distinguish swarm robotics systems from other multi-robot approaches (Iocchi et al., 2001). It is not uncommon for multi-robot systems to lack some form of decentralization at the computation, communication, and/or operation levels (Vásárhelyi et al., 2014). Swarm robotics systems are often inspired by natural systems in which large numbers of simple agents perform complex collective behaviors—e.g., schooling fish, flocking birds—through repeated local interactions between themselves and their environment (Bouffanais, 2016). The swarm robotics design paradigm allows a multi-robot system to overcome the aforementioned limitations (local sensing, lack of centralized control, etc.) and operate autonomously in a coordinated fashion.

One main challenge in artificial swarming is the design of systems that, while maintaining decentralized control, have agents capable of (i) acquiring local information through sensing, (ii) communicating with at least some subset of agents, and (iii) making decisions based on the dynamically gathered sensed data. While decentralization denies the agents the benefits of a large central computation and/or communication hub, it affords the system robustness. The system is thus capable of performing global collective actions under a wide range of group sizes (scalability), despite the possible sudden loss of multiple agents (robustness), and under unknown and dynamic circumstances (flexibility) (Brambilla et al., 2013).

There have been a number of notable efforts to design robotic swarms. The kilobit (Rubenstein et al., 2012), e-puck (Mondada et al., 2009), Swarm-bots (Dorigo et al., 2004), marXbot (Bonani et al., 2010), Alice (Caprari and Siegwart, 2005), iAnt (Hecker et al., 2012), Scarab (Michael et al., 2008), I-Swarm (Woern et al., 2006), r-one (McLurkin et al., 2013), and Pi Swarm (Hilder et al., 2014) are only a few examples of different swarm/distributed multi-robot platforms that have been developed. Each platform explores the potential and feasibility of a few aspects of swarming and not all of them fulfill all requirements of a robotic swarm system—according to the definition above—or are capable of operating in real and uncontrolled environments without any supporting infrastructure. The technological advances implemented on each platform make it challenging to port to others due to the specificities of each robot. Indeed, these platforms have been conceived with swarming considerations at the core of their design. As a consequence, the central components necessary to enable swarming are fully integrated inside the robots. Moreover, the software layer is often highly dependent on the hardware specifications owing to the original co-design process of both hardware and software. Although this deep technical integration lacking modularity provides platforms that can easily swarm, it also is a serious impediment to its portability to other mobile platforms.

Practitioners with access to multiple units of an existing autonomous robotic platform—including commercial ones—and seeking to study swarming have currently no other option than devising their own custom-made framework. A common alternative used by a number of research groups consists in simply devising swarming experiments that can be achieved with existing commercial swarm robotics platform (e.g., kilobot, e-puck, etc.). Although this alternative has the advantage of piggybacking on well-tested platforms, thereby saving a significant amount of time, it nonetheless limits the ability to design very original experiments. Our proposed technological solution aims at filling this gap by offering a platform-agnostic framework—an integrated combination of a hardware suite with a software layer—easily portable to a host of hardware platforms and facilitating the implementation of various swarm algorithms, while reducing the burden associated with platform-dependent interfacing.

Here, we report a unified platform-agnostic hardware/software tool capable of: (i) assembling and transforming a collection of basic mobile robots into full-fledged swarms and (ii) achieving versatile swarming behaviors using an easily programmable software library. The modular nature of both the hardware suite and software layer allows for possible evolution, upgrade, and extension of the technology independently from the specifications of the mobile platform. We present some preliminary results validating the technology on two vastly different swarming systems. This swarm-enabling technology is a combination of hardware/software that allows a wide range of multi-robot platforms to perform versatile and responsive swarming. This is achieved by providing each agent with an additional interface hardware built from low-cost and off-the-shelf components, which are integrated with a specifically developed general purpose software library. We believe that this technology that decouples swarming considerations from robotics ones could be of interest to both researchers and educators primarily interested in the study of artificial swarming.

The software—written in Python, but also tested in C++—is designed in a modular way so as to make the technology portable between platforms as seamlessly as possible, i.e., with minimal hardware/software changes. To assess the effectiveness of the proposed technology, we used it on two different platforms operating in uncontrolled environments: a differential drive robot and a water surface platform (sensing mobile buoy). Furthermore, a number of collective behaviors such as heading consensus, perimeter defense, and collective marching are tested on these platforms, thereby confirming the versatility of our swarm-enabling technology.

2. Materials and Methods

To enable swarming, it is essential to achieve distributed communication and decentralized decision-making (Hamann et al., 2014; Valentini et al., 2014, 2015, 2017; Vigelius et al., 2014). For instance, natural swarms achieve self-organizing behaviors and decentralized decision-making by means of distributed information exchanges through local signaling (Camazine et al., 2001) associated with sometimes sophisticated signaling mechanisms and trophic interactions (Dusenbery, 1992). Note that signaling refers to communication involving sensory capabilities. Swarm robotics systems mimic natural swarms in that communications between units is restricted to local information exchanges through short-range interactions (Brambilla et al., 2013). More generally, locality of communication in space and time between individual platforms leads to distributed communication. Therefore, platforms should be able to establish a dynamic and possibly switching communication networks and process information locally, using solely the computation capabilities onboard each individual agent.

2.1. Computational Unit

Most multi-robot platforms have limited computational resources only to read sensors data from the robot and send them to a remote central unit. The remote processor makes appropriate decisions based on its supervisory control algorithm and sends commands back to the robot. Since we need the technology to be easily portable to many different robotic platforms, we use a dedicated processing unit independent from the robot’s sensing and actuation processor as the “brain” of each agent. In our setup, computations are performed by Raspberry Pi/BeagleBone, single-board computers (SBCs) equipped with a number of multi-purpose inputs and outputs. These two SBCs provide ample computational resources for their size given the tasks at hand. Note that one can also consider using a different SBC such as Gumstix¹ to serve the same purpose. The recently released Raspberry Pi “0” (resp. “3”) offers a very low-cost solution at half-credit card size (resp. high computational power and increased interfacing possibilities). If even more computational power is required, one may consider the Odroid SBC or ultimately the GIGABYTE.

This computational unit receives all sensor data from the robot and neighbors’ information through the communication network in order to make appropriate decision based on the swarm algorithm, which is embedded in the software toolkit detailed below; this latter part is preloaded onto each platform prior to any collective operation.

2.2. Distributed Communication

From a theoretical viewpoint, distributed communication can be better analyzed and understood using network theoretical concepts—even in the absence of a real physical communication network as in the case of flocking birds and schooling fish (Bouffanais, 2016). Recently, studies of such signaling networks in swarms have revealed the need for specific structural properties of the network—in terms of degree distribution, shortest path, and clustering coefficient—in order to achieve effective consensus-reaching dynamics (Shang and Bouffanais, 2014; Sekunda et al., 2016) and high dynamic controllability of the swarm by a given subset of driving agents (Komareji and Bouffanais, 2013).

From a practical viewpoint, platforms should be able to establish a dynamic—i.e., switching—communication network. Recently, studies of such temporal networks (Holme and Saramäki, 2012) in swarms have revealed the need for specific structural properties of the network—in terms of degree distribution, shortest path, and clustering coefficient—in order to achieve effective consensus-reaching dynamics (Shang and Bouffanais, 2014; Sekunda et al., 2016) and high dynamic control of the swarm by a given subset of driving agents (Komareji and Bouffanais, 2013). With a mesh network, all agents are identical (from the network viewpoint) and can exchange information with a specific set of neighbors (e.g., metric, topological, Voronoi neighborhoods) directly without involving a third agent or going through a central hub or router. This grants the system robustness, as the loss of a subset of agents does not have a critical impact on the operation of the rest, assuming the nodes are within the limited communication range. This stands in stark contrast with the star network configuration, where the loss of the routing agent will halt the operation of the whole system. The same scenario would hold if the agents communicate in a mesh network but rely on a centralized computational hub to process information as is actually the case with many multi-robot systems, see Vásárhelyi et al. (2014) for further discussion.

The crucial component required to achieve a fully decentralized system is the communication device. We use XBee modules (XBee, 2010) to establish a mesh network. The communication network is based on a metric interaction in which information is being communicated between agents within the communication range of one another (typically 300 m line of sight). The device is configured in broadcast mode in which the information sent by each agent is received by all neighbors within the communication range. The range of communication depends on various factors such as the output power of the module and the type of obstacles blocking the radio frequency wave. The hardware block diagram of this swarm-enabling unit (SEU) is shown in Figure 1.

FIGURE 1

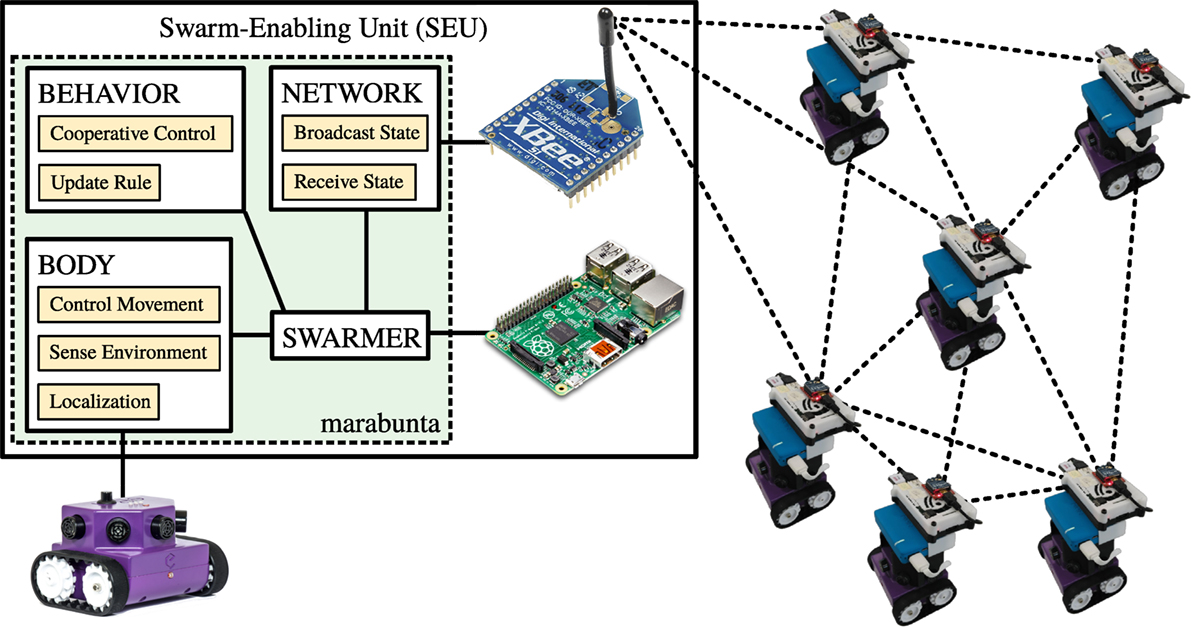
Figure 1. Block diagram of the swarm-enabling unit (SEU). The SEU serves as a bridge between a particular robot and the swarm and is composed of a communication module and a processing unit running code using the marabunta module. At the software level, each agent (or swarmer) is composed of three elements. First, the “body” interacts with the robot to control its movement and gather information from its state and sensed environmental data. Second, the “network” interacts with the communication module to broadcast the current state of the agent to the swarm and to gather information from other agents’ state. Third, the “behavior” contains the cooperative control strategy. In its most elementary form, the behavior is implemented by an update rule that defines the movement of the robot for a certain time window, given the current state of the robot and these data gathered from the body and the network.

FIGURE 2

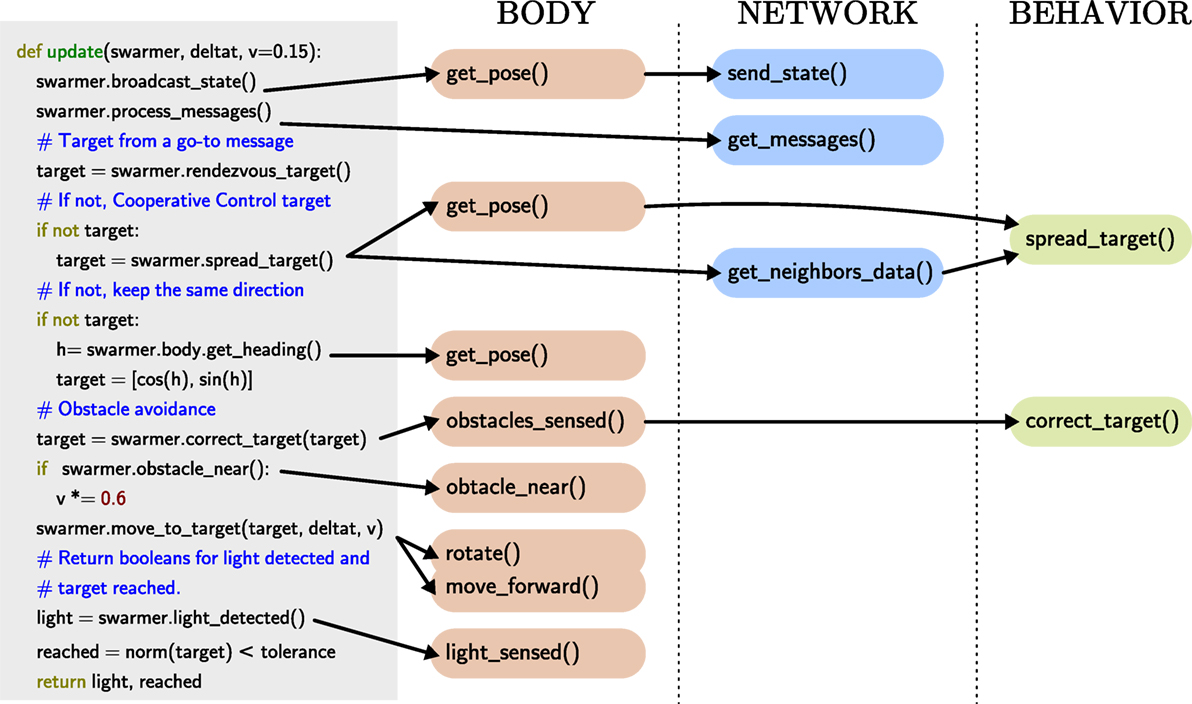
Figure 2. An example of the behavior of the agents defined with an update function that is called in a loop. The update function calls different method of the body (red), network (blue), and behavior (green) of the agent.

A natural concern with such a dynamic and distributed communication network is its effectiveness in maintaining a sustained flow of information among swarming agents. This was analyzed and quantified during swarming experiments with the BoB system with buoys continuously broadcasting their state at 0.1 Hz. The expected communication range is about 310 m and the modules are capable of relaying messages through multiple hops in the network, which means that, in principle, any module can broadcast their state globally to all the agents in the collective. However, our experiments show that when tens of buoys are operating, the communication is far from perfect, and the effective communication range is significantly smaller. The ratio of successful communications obtained during a typical field experiment is presented in Table 1. These results provide a measure of the effective communication range in a large and dynamic network of mobile XBee units. As one increases the number of buoys deployed, interferences between them will cause more messages to drop. This presents a clear example of why the distributed control algorithm should be designed to provide a robust collective behavior against imperfect communication.

TABLE 1

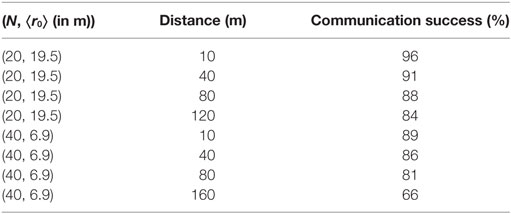
Table 1. Relative successful communications established between two buoys separated by a certain distance inside a dynamic collective of N buoys spread with a mean nearest-neighbor distance of ⟨r₀⟩.

2.3. Cooperative Control Strategy

The achievement of effective collective behaviors by a multi-robot system requires fully decentralized control algorithms. Such cooperative control strategies have received particular attention from different scientific communities with different aims and goals: first by the computer graphics community (Reynolds, 1987), then followed by the physics community (Vicsek and Zafeiris, 2012). The control community subsequently established a formal framework (Jadbabaie et al., 2003a; Olfati-Saber et al., 2007; Ren and Beard, 2008), which has been put into practice and expanded by multi-robot systems and swarm robotics community (Turgut et al., 2008; Brambilla et al., 2013). Recently, Virágh et al. (2014) have established the connection between dynamical update rules of locally interacting agents and cooperative control strategies for flocks of autonomous flying robots. This endeavor was fueled by an intense research activity from biologists and physicists who have sought to identify local update rules at the agent level, which result into observed collective animal behavior (Vicsek and Zafeiris, 2012; Bouffanais, 2016). This acquired knowledge-enabled novel biologically inspired approaches to the design of cooperative control strategies. Such an approach has been successfully implemented and tested on a small flock of 10 quadcopters (Vásárhelyi et al., 2014), using GPS for localization, and the same distributed communication paradigm as the one reported here. Using the taxonomy introduced by Brambilla et al. (2013), our decentralized cooperative control strategy follows a behavior-based design approach in a similar vein as Vicsek et al. (Virágh et al., 2014).

In what follows, we discuss several swarm algorithms coded and tested on different platforms.

2.3.1. Consensus

In a consensus algorithm, the participating agents seek to have their state variable—in the present case, their heading—converging toward a common value; this latter value is not known a priori and is entirely the outcome of this self-organizing process (Ren et al., 2005).

In the particular case of collective motion, agents can aim at aligning their direction of travel, leading a well-aligned flock of agents all traveling in the same direction. Another common example is aggregation. As its name implies, this dynamical behavioral rule leads the agents to collectively undergo an aggregation process. Such collective aggregation is extremely common and important in natural swarms (e.g., insects and microorganisms such as amoebae (Bouffanais and Yue, 2010)) and is also very useful with distributed multi-robot systems during certain phases of deployment in the field.

Denote the set of agents whose information is available to agent i as ${\mathcal{N}}_i$, a consensus protocol can be summarized as

$x_i[k+1]={\displaystyle \sum _{j\in {\mathcal{N}}_i\cup \left\{i\right\}}}{\alpha }_{ij}[k]x_j[k],$ (1)

where x_i[k] ∈ℝ is the state of agent i at time k and α_ij[k] > 0 is a desired weighting factor. Considering the heading ${{\displaystyle \stackrel{}{\widehat{\theta }}}}_i=(cos{\theta }_i,sin{\theta }_i)$ and choosing ${\alpha }_{ij}=\frac{1}{N_i+1}$ where $N_i=\left|{\mathcal{N}}_i\right|$, equation (1) reads

${{\displaystyle \stackrel{}{\widehat{\theta }}}}_i[k+1]={\displaystyle \sum _{j\in {\mathcal{N}}_i[k]\cup \left\{i\right\}}}\frac{1}{N_i+1}{{\displaystyle \stackrel{}{\widehat{\theta }}}}_j[k].$ (2)

Essentially, the target heading at k + 1 is defined as the average heading of the agent itself and its neighbors at time k. This protocol only involves local information exchange and is guaranteed to generate a global common consensus if the swarm is connected (Jadbabaie et al., 2003b).

2.3.2. Perimeter Defense

The perimeter defense, or all round defense algorithm, for swarming agents consists in having them self-organize so as to maximize the perimeter covered in an unknown dynamic two-dimensional environment. To obtain this result over local information transfers, the agents maximize the distance between themselves and their neighbors, giving a larger weight to the closer agents. This can be encoded as the dynamical rule

$p_i[k+1]={\displaystyle \sum _{j\in {\mathcal{N}}_i}}\frac{p_j[k]-p_i[k]}{|p_j[k]-p_i[k]{|}^2},$ (3)

where p_i[k] = (x_i[k], y_i[k]) is the position of agent i in Cartesian coordinates at time k. In equation (3), the target heading is obtained from p_i[k + 1], and it is designed such that a larger weight is given the closer the neighbor is. Note that equations (2) and (3) are purely Markovian, involving only local information in both space and time without any assumption of information about prior or future states. Thus, any such algorithm comes with implicit flexibility, as the swarm can operate under dynamic environments.

2.3.3. Environment Exploration

For the purposes of environment exploration, we combine heading consensus and a modified attraction–repulsion behavior with individually manifested heading goals. Unlike the perimeter defense, the goal here is to provide a dynamic two-dimensional spatial coverage for sensing and environment reconstruction and prediction purposes. Each member has the autonomy to diverge from collective behaviors in order to investigate their surroundings, yet maintain underlying neighbor-to-neighbor interactions.

Self-assembling within a group relies on three basic aspects: equilibrium distance between neighbors, center of mass (members), and collective heading. The agents move according to p_i[k + 1] = p_i[k] + δv_i[k], where v_i[k] is the scaled velocity of agent i

$\begin{array}{c}{v}_i[k]=H_i{{\displaystyle \widehat{\beta }}}_i[k]+\frac{1}{N_i}{\displaystyle \sum _{j\in {\mathcal{N}}_i}}\left[{{\displaystyle \widehat{\gamma }}}_{ij}[k]\left((1-H_i)-\frac{p_0^2}{|p_i[k]-p_j[k]{|}^2}\right)\right]\\ +\frac{H_i}{N_i}{\displaystyle \sum _{j\in {ℛ}_i\cup \left\{i\right\}}}{{\displaystyle \stackrel{}{\widehat{\theta }}}}_j[k].\end{array}$ (4)

Here, ${{\displaystyle \stackrel{}{\widehat{\beta }}}}_i=(cos{\beta }_i,sin{\beta }_i)$ is the bearing vector toward the goal, ${{\displaystyle \widehat{\gamma }}}_{ij}=(cos{\gamma }_{ij},sin{\gamma }_{ij})$ the azimuth vector of agent i toward agent j, and ${{\displaystyle \widehat{\theta }}}_j$ the heading of agent j as defined before. The heading consensus is achieved here on a subset of agents ${ℛ}_i$ that are within a distance p₀ from agent i, making the heading consensus localized. The binary heading consensus weight H_i determines whether the agent moves toward a goal (H_i = 1), or purely positions itself with respect to the other members of the swarm (H_i = 0). Leader–follower behavior is established by setting the position of agent i (leader) as the goal for the other agents in the swarm. The scaling factor of ${{\displaystyle \widehat{\gamma }}}_{ij}$ is more influenced by close spacing, leading to strong repulsion and collision avoidance. When the distance between two agents is the equilibrium distance p₀, the corresponding scaling factor of ${{\displaystyle \widehat{\gamma }}}_{ij}$ is 0. The time constant δ is a parameter that depends on the update rate and the overall speed scaling. In general, the formulation [equation (4)] results in lattice-like swarm arrangements, with different types of avoidance strategies (see Figure 3).

FIGURE 3

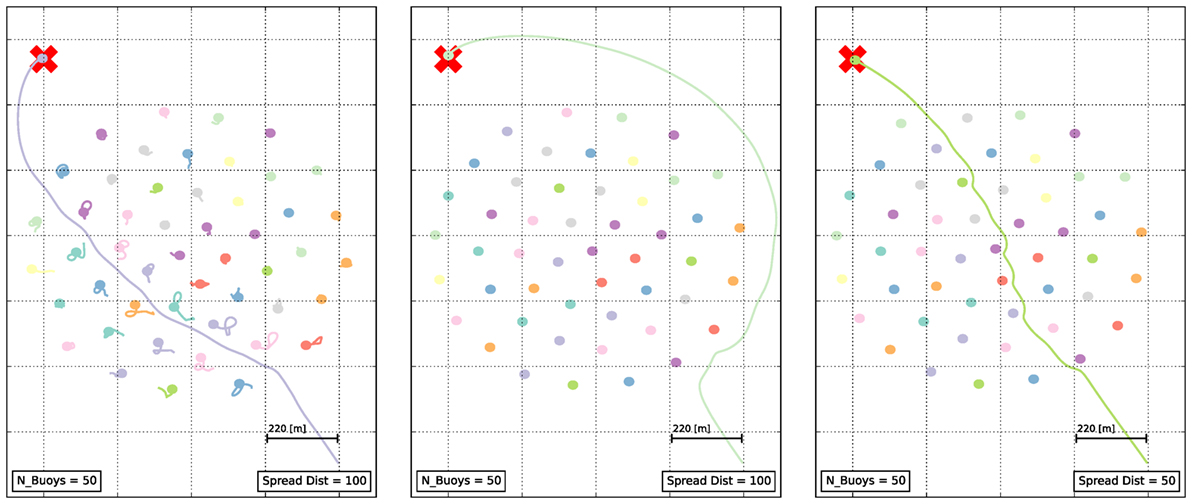
Figure 3. Examples of simulated avoidance behaviors based on equation (4), with H_i = 1, H_j = 0, (p₀)_j = 100 m, j ≠ i. The mission of agent i is to reach the goal (red cross) when the path is blocked by other agents in the swarm (starting from a position at the lower right corner). Left: yielding behavior. The equilibrium distance (p₀)_i = 100 m of agent i is too large for it to go through the swarm without reconfiguration. In response, the agents in the swarm yield as agent i moves toward the goal through the swarm, only to circle back to their equilibrium positions based on equation (4). Center: swarm fixed in place (ν_j ≡ 0). The equilibrium distance (p₀)_i = 100 m is too large for the agent i to go through the swarm, so it goes around. Right: swarm fixed in place (ν_j ≡ 0). The equilibrium distance (p₀)_i = 50 m is small enough for the agent i to go through the swarm.

2.4. Robotic Platforms

We tested the technology on two different platforms detailed below.

2.4.1. eBot

The eBot is a commercial small-size differential drive robot developed by EdgeBotix,² a spin-off company developing educational robots based on research robots developed by the SUTD MEC Laboratory.³ It is equipped with 6 ultrasonic or infrared range finders, inertial measurement unit (IMU), two wheel encoders, and two light sensors (see Figure 4). The maximum velocity of the platform is 20 cm/s. We developed an extended Kálmán filter (included in the eBot’s API) to localize the robot in real time based on its IMU and wheel encoders.

FIGURE 4

Figure 4. Right: the eBot with ultrasound sensors crowned with the swarm-enabling technology. A 3D printed structure is hosting the Raspberry Pi and XBee module, along with a power bank serving as the power source. The WiFi module is used exclusively for monitoring and updating purposes and is not required for the autonomous operation of the robot. Left: swarm of 15 eBots with IR sensors.

2.4.2. Autonomous Surface Vehicle

The “BoB” (for “Bunch of Buoys”) system is a distributed multi-robots effort based on a small developmental surface craft (Figure 5) initially developed at MIT to perform collective environmental sensing. (Videos of the collective sensing with more than 50 U during a field test are available online.^4,5,6) It is equipped with a global positioning satellite (GPS) receiver, MEMS compass, and 3-axis accelerometer. Omnidirectional design concepts lead to the vectored propulsion system, allowing for maximum agility with near instantaneous direction changes. The maximum velocity of the platform is up to 1 m/s, although design considerations are more concerned with positioning than transit.

FIGURE 5

Figure 5. A cast aluminum hull mitigates magnetic interference with sensitive MEMS sensory elements used to reference buoy orientation. Many standard expansion ports along the perimeter allow for the addition of environmental measuring devices seamlessly in the field. A large access cover at the top provides easy access for maintenance as needed. All components are housed securely within the watertight hull and can be seen on the top view (top right corner).

Finally, the buoy may be equipped with multiple sensors in order to monitor its environment. The fleet of buoys (BoB) (Figure 6) is not constrained to homogeneity, and some units may be equipped with various sensors in order to provide varying levels knowledge about the surrounding waters.

FIGURE 6

Figure 6. A small fleet of autonomous surface vehicles: (top panel) 25 buoys collectively operating at Bedok Reservoir, Singapore; (bottom left panel) Buoys stacked up during transportation to the field site; (bottom right panel) 48 buoys lined up before deployment.

2.5. Software

The connection between robot control, distributed communications management, and collective behavior is established by means of a Python module called marabunta⁷ that we designed with modular development of swarming behaviors in mind and that emphasizes portability and ease of deployment in different platforms.

With this module, the interaction with the robot is abstracted at a low-level through a platform-dependent class (the “body” of the agent). In the same fashion, the management of communications is also handled by another low-level and platform-dependent “network” class. Both of these classes are independent from one another and are also independent from the high-level behavior of the swarm, defined as the “behavior” class.

Each different robot platform requires its own body class. This is designed following the assumption that the processor running the code has the capacity to interact with the robot such that it can (i) send commands to move it in space, (ii) request these data needed for localization of the unit, and (iii) access the information gathered by the robot about its local environment typically by means of a sensor suite. The swarm-enabling unit (SEU for short and shown in Figure 1) does not require total access to the inner workings of the robot or deep knowledge of its specifications. For instance, if one is using commercial robots such as the eBot or e-puck (Mondada et al., 2009), establishing a Bluetooth connection and using the provided API to send commands to the robot is enough to use this technology to deploy a swarm of robots. The body classes for both the eBot and the e-puck are included in marabunta.

The communication between agents is handled by a separate network class. Separating this from the control of the body allows to pair different robot platforms with different communication protocols. This implementation assumes that the processor has the capacity to interact with a communication module capable of (i) broadcasting messages to nearby agents and (ii) reading the messages broadcast by other agents. There is no need for the communication module to be able to handle directed communication or recognition of nearby nodes. The marabunta module provides a network class for the Digimesh protocol, so that one can connect an XBee module in serial to the computer running the software to get out-of-the-box distributed communications between agents afforded with the present technology.

The collective behavior of the swarm is a result of the agents’ individual behavior, implemented in a separate behavior class that is hardware-agnostic. Since the behavior is independent of the robot used, this technology allows to have heterogeneous swarming where different robots perform the collective behaviors described in the previous section. Additionally, since the behavior is also independent of the communication between agents, a swarm can have heterogeneous behaviors where different agents follow different behaviors. A friction-less platform to experiment with heterogeneous swarming can yield interesting novel emergent behaviors arising from the combination of behaviors (for example, combining some ratio of agents performing consensus with others performing perimeter defense makes the swarm split in sub-groups).

The modular design of the technology allows for fast experimentation. One can use the included MockBody and MockNetwork to design collective behaviors iteratively using simulations. From there, one can change the body to the proper robot controller and do some preliminary tests from a single, central control terminal (by keeping a “mock network” in the terminal). Finally, by affording each robot with a SEU with the desired behavior and a proper communication module, the system is ready to perform swarming experiments in a truly decentralized fashion.

2.6. Integration

In order to illustrate and exemplify the full integration of our SEU, we detail in this subsection the actual implementation used for the search and exploration experiments whose results are presented in Sec. 3.2.

The natural starting point is implementing the cooperative control algorithm described in Sec. 2.3.2 as a behavioral behavior class. By generating some artificial data for walls and position of the target to locate, one can readily simulate the behavior of the swarm and iterate the design of the algorithm by providing the behavior with a MockBody and network classes. For the search and exploration experiment, the behavior of a swarming agent is defined by the update rule presented in Figure 2. This figure highlights the dependencies with the methods implemented in the body, network, and behavior classes.

After iterating the design of the behavior via simulation, we equip a fleet of 10 eBots with a “swarming-enabling unit” (SEU) consisting of a Raspberry Pi with Python and the marabunta module loaded on it, an XBee module, a Bluetooth module, and a power bank. To operate these robots, one has to establish a Bluetooth connection and send simple commands (such as activate wheels with a certain power or read the values of each sensor) through their dedicated Python API. Implementing a body class for the eBot is, in practice, a matter of expanding the provided API to obtain a comprehensive interface to interact with the robot and return the sensor data in a convenient, hardware-agnostic format (e.g., giving the estimated coordinates of the obstacles detected, as opposed to these raw sensor data).

For this kind of experiments, one does not need most of the features of the communication module; the XBee can be set in transparent mode and interfaced purely by writing the messages to be sent and reading the received ones through a serial connection. This makes the network class implementation for an XBee module quite straightforward. The main task of this class is to translate the received messages and properly structure these data so that the other elements of the module can access it.

By switching the MockBody for the eBotBody and the MockNetwork by the XbeeNetwork, the code used for simulation can run on the SEU and make the swarm to autonomously perform search and exploration.

3. Results

3.1. Perimeter Defense

Experimental results regarding the perimeter defense algorithm discussed in Section 2.3.2 for different number of robots are shown in Figure 7. One can observe the dynamic decision-making feature of the swarm algorithm in Figures 7A–D. Each individual decides on its target heading based on the information received from other agents in the network. For this reason, the target direction of robots are vastly different with different number of robots. We also remark that one of the most important features of a swarm is its scalability. This feature can be observed in Figure 7 that by reducing the number of robots from 10 to 5, the swarm is still capable of covering the perimeter in the best possible manner. Robustness has been tested with the same scenario with the forced removal of a number of units while performing the experiment. In such a case, the whole swarm dynamically reacts to this change and tries to cover the area the removed robots were supposed to cover. As mentioned earlier, the Markovian nature of the swarming algorithms enables the swarm to adapt instantaneously to any change in the environment or configuration, including the addition or removal of agents and modifications of the experimental arena.

FIGURE 7

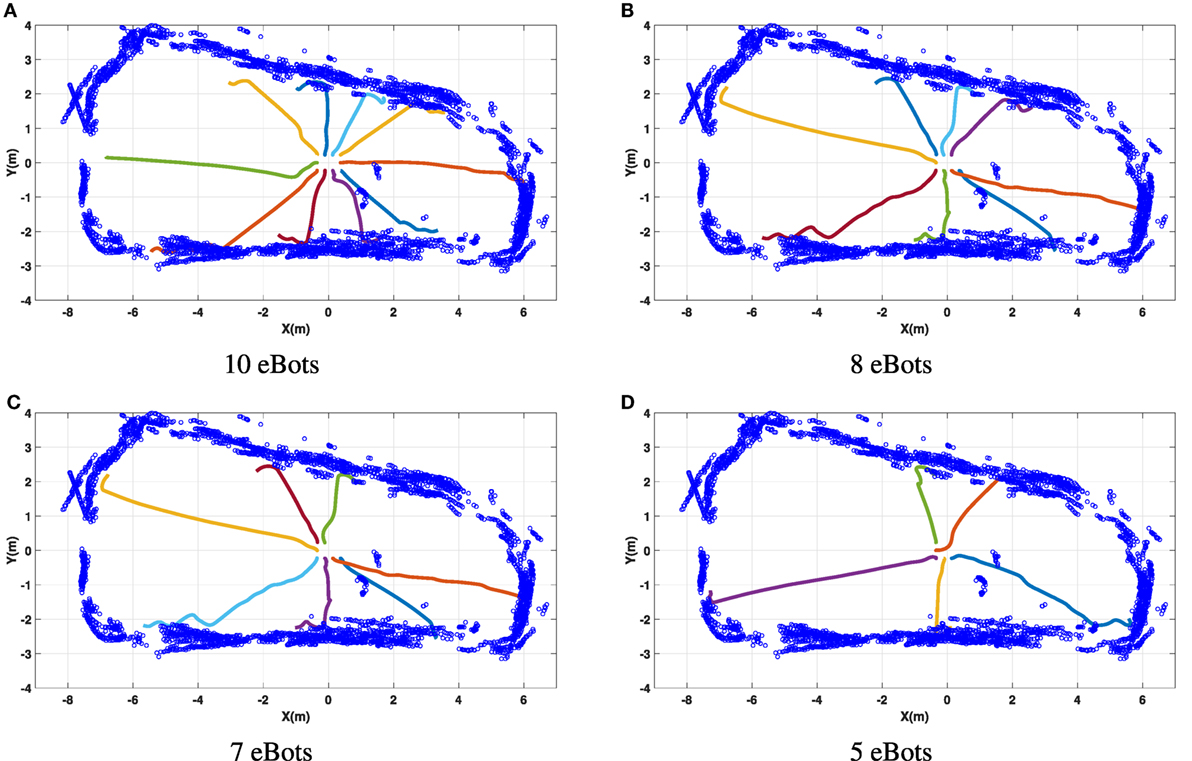
Figure 7. Perimeter defense algorithm using 5, 7, 8, and 10 eBots. The experiment is performed in a room with approximate dimension of 13.5 m × 6.2 m. All robots start with zero initial heading and information about all initial positions and headings. Each robot uses an extended Kálmán Filter to estimate its position and heading based on onboard sensors. This information is shared among neighbors leading to the decentralized computation of a target heading based on equation (3). (A) 10 eBots, (B) 8 eBots, (C) 7 eBots, and (D) 5 eBots.

3.2. Search and Exploration

The second experiment is regarding a search and exploration task in which robots try to collectively find a target in the environment. The target in our setup is a light source in an unknown environment. This experiment is divided into two phases: (i) the robots perform a perimeter defense until one finds the light source and informs its neighbors about the location of the target and (ii) the robots perform a rendezvous in space to collectively navigate to the location of the detected light source. The algorithm was tested with up to 10 eBots. We ran ten experiments for each number of agents to better quantify the effectiveness of the swarming behavior. Figure 8 shows the convergence speed—inverse of the time it takes to find the target and navigate to its location—with respect to the number of robots. Scalability of the swarm can be seen from the upward trend of the graphs in Figure 8: in most cases, incorporating more agents in the experiment speeds up the search and exploration task (watch video online⁸). The same experiment was expanded to allow for 14 robots swarming in 5 distinct rooms (watch video online⁹).

FIGURE 8

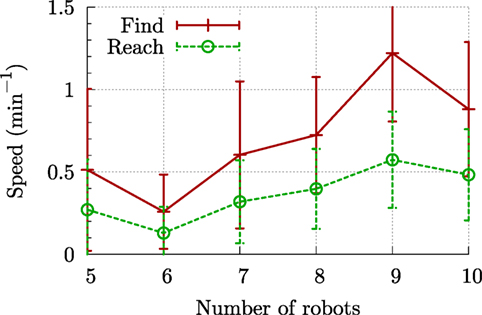
Figure 8. Speed at which one agent finds the target (solid red) and at which the swarm reaches the target (dashed green) as a function of the number of agents in the swarm. Each data point is averaged over 10 runs. The error bars show the variance over these runs.

3.3. Heading Consensus

Figure 9 presents the experimental results of the heading consensus algorithm discussed in subsection 2.3.1 using 10 agents. This experiment consists of two parts: (1) robots with random initial heading converge to a common heading, and (2) a robot is forced not to follow the swarm heading. This can be interpreted as a leader–follower configuration where the forced robot plays the role of the leader in the swarm and forces the swarm to follow its heading.

FIGURE 9

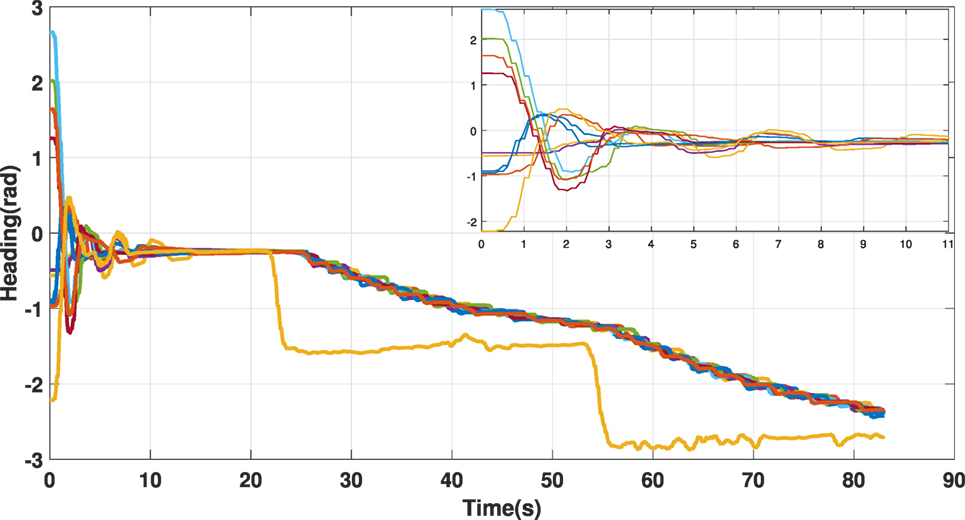
Figure 9. Heading consensus algorithm tested with a swarm of 10 eBots. Each robot starts with a random heading. After a number of iterations, the swarm agrees on a common value for its heading. At time t = 22 s, one of the robots stops participating to the consensus algorithm and we are in the presence of a leader–follower swarm, thereby forcing the swarm to converge to the leader’s heading. The sub-figure is a zoomed-in view of the swarm heading from t = 0 to t = 11 s.

3.4. Aggregation and Leader–Follower

Figure 10 shows some preliminary results of the aggregation behavior and Figure 11 of a leader–follower behavior according to equation (4) for a swarm of N = 45 buoys. For the aggregation test (H_i ≡ 0, i = 1, …, N), the buoys are initially self-assembled in a loose arrangement, and then the equilibrium distance p₀ is reduced; the spreading follows by enlarging p₀. For the leader–follower behavior (H_i ≡ 1, i = 1, …, N), one buoy is driven along a given path, and its position is given as the goal for all other buoys in the swarm. The experiments show that lattice-like arrangement is persistent. They further confirm that the mesh network strategy scales robustly for a swarm of this size (videos of these experiments are available online^10,11,12).

FIGURE 10

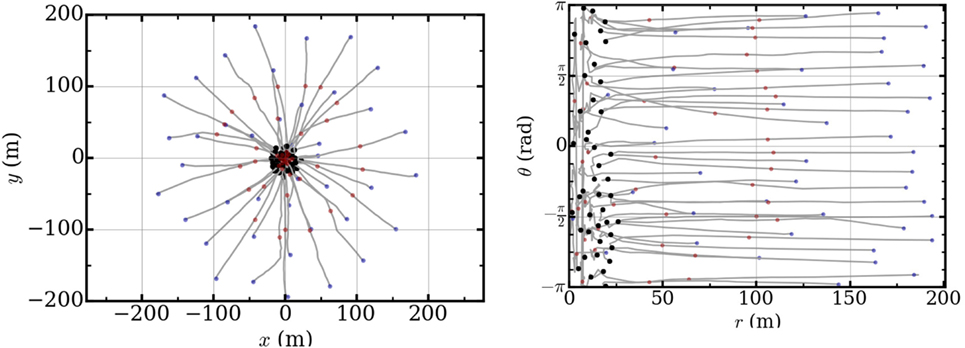
Figure 10. Field tests of aggregation behavior of a swarm of 45 buoys, conducted on a ~1 km² body of water on a moderately windy day. Left: buoy trajectories for aggregation behavior. The aggregation test consisted of a single aggregation event (p₀ from 50 to 5 m), where the relative bearing to the group center is maintained. The entire aggregation event takes just over 8 min, in which time the coverage area is decreased from ≈125, 000 m² to 1, 250 m². Right: buoy heading ${\widehat{\theta }}_i$ as a function of distance ${{\displaystyle \widehat{r}}}_i$ from the group center for the same aggregation event. Blue dots indicate the initiation position of the buoys, while red and black indicate the 50% and terminal positions, respectively.

FIGURE 11

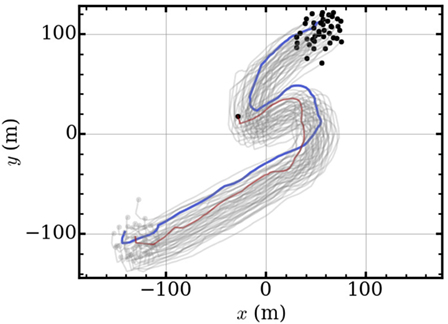
Figure 11. Field tests of leader–follower behavior of a swarm of 45 buoys with p₀ = 5 m. The group traverses ~400 m in calm seas. The trajectory of the leader buoy is marked with a blue trail and that of the followers with a gray trail. The red trail highlights the trajectory of a buoy lagging behind due to low battery. Even though there are a number of degraded members, the system successfully executes the intended behavioral exercise.

4. Conclusion

In this report, we presented the design of integrated hardware and software tools enabling a wide range of multi-robot systems to collectively operate in a fully distributed manner. Although our proposed swarm-enabling technology requires some work to develop a basic interfacing with the selected mobile platform, it nonetheless offers a general framework to assemble full-fledged swarms from virtually any set of mobile robots. As already mentioned and shown in the particular case of the e-puck, this basic interface can be extremely simple and straightforward to put in place. In particular, this technology adds decentralization features to the robotic platforms, which is a key element in a swarm and distributed robotics systems. Modular design of the software library allows a swift transfer of the hardware toolkit onto vastly different platforms. Moreover, the overall modular design of this swarm-enabling technology facilitates possible future upgrade and evolution depending on the particular requirements of any given swarm experiment, e.g., more powerful computing unit to run swarming behaviors requiring on-the-fly machine learning. We reported experimental results regarding various swarm algorithms on land and water surface platforms equipped with this swarm-enabling technology.

Future research directions are toward including further swarm algorithms in the software library and also the possibility to simulate newly designed collective behaviors prior to their implementation onto the platforms. This feature greatly facilitates the design and testing of new swarming behaviors. Last, given the fact that our swarm-enabling technology can seamlessly function with a host of different mobile robots, it should, therefore, facilitate studies of heterogeneous swarming.

Author Contributions

RB and EW initiated the study and the development of the technology. All authors designed the technology. MC, DM, GT, and BZ implemented the technology and carried out the field tests. DM developed the software pack. All authors analyzed the results, wrote the main text, and reviewed the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

This work was supported by grants from the Temasek Lab (TL@SUTD) under a Seed grant #IGDS S15 01021, from the Singapore Ministry of Education (MOE Tier 1) grant #SUTDT12015003, and by the National Research Foundation Singapore under its Campus for Research Excellence and Technological Enterprise programme. The Center for Environmental Sensing and Modeling is an interdisciplinary research group of the Singapore MIT Alliance for Research and Technology.

Footnotes

1. ^https://www.gumstix.com/.
2. ^http://www.edgebotix.com/.
3. ^http://people.sutd.edu.sg/~erikwilhelm/.
4. ^Dynamic Environmental Monitoring using Swarming Mobile Sensing Buoys: https://youtu.be/Qe-wZOi3ONs.
5. ^51 Networked Buoys Swarming: https://youtu.be/fhg1rIX_y3A.
6. ^Dynamic Area Coverage (Geofencing) Field Test: https://youtu.be/hlBNjHS_Q7s.
7. ^See http://www.github.com/david-mateo/marabunta.
8. ^Swarm Robotics: Collective Search & Exploration: https://www.youtube.com/watch?v=JzbWV1sfZ-A.
9. ^Simultaneous Collective Exploration of 5 rooms by a Swarm of 14 Terrestrial Robots: https://www.youtube.com/watch?v=0tsAx6TDy-Q.
10. ^Dynamic Environmental Monitoring using Swarming Mobile Sensing Buoys: https://youtu.be/Qe-wZOi3ONs.
11. ^51 Networked Buoys Swarming: https://youtu.be/fhg1rIX_y3A.
12. ^Dynamic Area Coverage (Geofencing) Field Test: https://youtu.be/hlBNjHS_Q7s.

References

Bonani, M., Longchamp, V., Magnenat, S., Rétornaz, P., Burnier, D., Roulet, G., et al. (2010). “The marxbot, a miniature mobile robot opening new perspectives for the collective-robotic research,” in 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE), 4187–4193.

Google Scholar

Bouffanais, R. (2016). Design and Control of Swarm Dynamics. Springer Briefs in Complexity. Singapore: Springer.

Google Scholar

Bouffanais, R., and Yue, D. K. (2010). Hydrodynamics of cell-cell mechanical signaling in the initial stages of aggregation. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 81, 041920. doi: 10.1103/PhysRevE.81.041920

PubMed Abstract | CrossRef Full Text | Google Scholar

Brambilla, M., Ferrante, E., Birattari, M., and Dorigo, M. (2013). Swarm robotics: a review from the swarm engineering perspective. Swarm Intell. 7, 1–41. doi:10.1007/s11721-012-0075-2

CrossRef Full Text | Google Scholar

Camazine, S., Deneubourg, J.-L., Franks, N. R., Sneyd, J., Theraulaz, G., and Bonabeau, E. (2001). Self-Organization in Biological Systems. Princeton, NJ: Princeton University Press.

Google Scholar

Caprari, G., and Siegwart, R. (2005). “Mobile micro-robots ready to use: Alice,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IEEE), 3295–3300.

Google Scholar

Dorigo, M., Tuci, E., Groß, R., Trianni, V., Labella, T., Nouyan, S., et al. (2004). “The swarm-bots project,” in International Workshop on Swarm Robotics (Berlin, Heidelberg: Springer), 31–44.

Google Scholar

Dusenbery, D. B. (1992). Sensory Ecology: How Organisms Acquire and Respond to Information. New York, NY: WH Freeman and Co.

Google Scholar

Hamann, H., Valentini, G., Khaluf, Y., and Dorigo, M. (2014). “Derivation of a micro-macro link for collective decision-making systems,” in Parallel Problem Solving from Nature – PPSN XIII. PPSN 2014. Lecture Notes in Computer Science, Vol 8672, eds T. Bartz-Beielstein, J. Branke, B. Filipič, and J. Smith (Cham: Springer), 181–190.

Google Scholar

Hecker, J. P., Letendre, K., Stolleis, K., Washington, D., and Moses, M. E. (2012). “Formica ex machina: ant swarm foraging from physical to virtual and back again,” in Swarm Intelligence. ANTS 2012. Lecture Notes in Computer Science, Vol 7461, eds M. Dorigo, M. Birattari, C. Blum, A. L. Christensen, A. P. Engelbrecht, R. Groß, et al. (Berlin, Heidelberg: Springer), 252–259.

Google Scholar

Hilder, J., Naylor, R., Rizihs, A., Franks, D., and Timmis, J. (2014). “The pi swarm: a low-cost platform for swarm robotics research and education,” in Advances in Autonomous Robotics Systems. TAROS 2014. Lecture Notes in Computer Science, Vol 8717, eds M. Mistry, A. Leonardis, M. Witkowski, and C. Melhuish (Cham: Springer), 151–162.

Google Scholar

Holme, P., and Saramäki, J. (2012). Temporal networks. Phys. Rep. 519, 97–125. doi:10.1016/j.physrep.2012.03.001

CrossRef Full Text | Google Scholar

Iocchi, L., Nardi, D., and Salerno, M. (2001). “Reactivity and deliberation: a survey on multi-robot systems,” in Balancing Reactivity and Social Deliberation in Multi-Agent Systems. BRSDMAS 2000. Lecture Notes in Computer Science, Vol 2103, eds M. Hannebauer, J. Wendler, and J. Pagello (Berlin, Heidelberg: Springer), 9–32.

Google Scholar

Jadbabaie, A., Lin, J., and Morse, A. S. (2003a). Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Automat. Contr. 48, 988–1001. doi:10.1109/TAC.2003.817537

CrossRef Full Text | Google Scholar

Jadbabaie, A., Lin, J., and Morse, A. (2003b). Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Automat. Contr. 48, 988–1001. doi:10.1109/TAC.2003.817537

CrossRef Full Text | Google Scholar

Komareji, M., and Bouffanais, R. (2013). Resilience and controllability of dynamic collective behaviors. PLoS ONE 8:e82578. doi:10.1371/journal.pone.0082578

PubMed Abstract | CrossRef Full Text | Google Scholar

McLurkin, J., Lynch, A., Rixner, S., Barr, T., Chou, A., Foster, K., et al. (2013). “A low-cost multi-robot system for research, teaching, and outreach,” in Distributed Autonomous Robotic Systems, eds A. Martinoli, F. Mondada, N. Correll, G. Mermoud, M. Egerstedt, M. A. Hsieh, et al. (Berlin Heidelberg: Springer), 597–609.

Google Scholar

Michael, N., Fink, J., and Kumar, V. (2008). Experimental testbed for large multirobot teams. IEEE Robot. Autom. Mag. 15, 53–61. doi:10.1109/M-RA.2007.914924

CrossRef Full Text | Google Scholar

Mondada, F., Bonani, M., Raemy, X., Pugh, J., Cianci, C., Klaptocz, A., et al. (2009). “The e-puck, a robot designed for education in engineering,” in Proceedings of the 9th Conference on Autonomous Robot Systems and Competitions, Vol. 1, Castelo Branco, 59–65.

Google Scholar

Olfati-Saber, R., Fax, J. A., and Murray, R. M. (2007). Consensus and cooperation in networked multi-agent systems. Proc. IEEE 95, 215–233. doi:10.1109/JPROC.2006.887293

CrossRef Full Text | Google Scholar

Ren, W., and Beard, R. (2008). Distributed Consensus in Multi-vehicle Cooperative Control. London: Springer.

Google Scholar

Ren, W., Beard, R., and Atkins, E. (2005). “A survey of consensus problems in multi-agent coordination,” in Proceedings of American Control Conference (IEEE), 1859–1864.

Google Scholar

Reynolds, C. W. (1987). Flocks, herds, and schools: a distributed behavioral model. Comput. Graph. 21, 25–34. doi:10.1145/37402.37406

CrossRef Full Text | Google Scholar

Rubenstein, M., Ahler, C., and Nagpal, R. (2012). “Kilobot: a low cost scalable robot system for collective behaviors,” in Proceedings 2012 IEEE International Conference on Robotics and Automation (ICRA), (IEEE) 3293–3298.

Google Scholar

Sekunda, A., Komareji, M., and Bouffanais, R. (2016). Interplay between signaling network design and swarm dynamics. Netw. Sci. (Camb. Univ. Press) 4, 244–265. doi:10.1017/nws.2016.5

CrossRef Full Text | Google Scholar

Shang, Y., and Bouffanais, R. (2014). Influence of the number of topologically interacting neighbors on swarm dynamics. Sci. Rep. 4, 1–7. doi:10.1038/srep04184

PubMed Abstract | CrossRef Full Text | Google Scholar

Turgut, A. E., Çelikkanat, H., Gökçe, F., and Şahin, E. (2008). Self-organized flocking in mobile robot swarms. Swarm Intell. 2, 97–120. doi:10.1007/s11721-008-0016-2

CrossRef Full Text | Google Scholar

Valentini, G., Ferrante, E., and Dorigo, M. (2017). The best-of-n problem in robot swarms: formalization, state of the art, and novel perspectives. Front. Robot. A.I. 4:9. doi:10.3389/frobt.2017.00009

CrossRef Full Text | Google Scholar

Valentini, G., Hamann, H., and Dorigo, M. (2014). “Self-organized collective decision making: the weighted voter model,” in Proceedings of the 2014 International Conference on Autonomous Agents and Multi-Agent Systems (International Foundation for Autonomous Agents and Multiagent Systems), 45–52.

Google Scholar

Valentini, G., Hamann, H., and Dorigo, M. (2015). “Self-organized collective decision-making in a 100-robot swarm,” in Twenty-Ninth AAAI Conference on Artificial Intelligence, Paris, 4216–4217.

Google Scholar

Vásárhelyi, G., Virágh, C., Somorjai, G., Tarcai, N., Szorenyi, T., Nepusz, T., et al. (2014). “Outdoor flocking and formation flight with autonomous aerial robots,” in Proceedings 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), (IEEE), 3866–3873.

Google Scholar

Vicsek, T., and Zafeiris, A. (2012). Collective motion. Phys. Rep. 517, 71–140. doi:10.1016/j.physrep.2012.03.004

CrossRef Full Text | Google Scholar

Vigelius, M., Meyer, B., and Pascoe, G. (2014). Multiscale modelling and analysis of collective decision making in swarm robotics. PLoS ONE 9:e111542. doi:10.1371/journal.pone.0111542

PubMed Abstract | CrossRef Full Text | Google Scholar

Virágh, C., Vásárhelyi, G., Tarcai, N., Szörényi, T., Somorjai, G., Nepusz, T., et al. (2014). Flocking algorithm for autonomous flying robots. Bioinspir. Biomim. 9, 025012. doi:10.1088/1748-3182/9/2/025012

PubMed Abstract | CrossRef Full Text | Google Scholar

Woern, H., Szymanski, M., and Seyfried, J. (2006). “The i-swarm project,” in Proceedings 15th IEEE International Symposium on Robot and Human Interactive Communication, 2006, 492–496.

Google Scholar

XBee. (2010). Product Manual and DigiMesh, XBee-PRO: 2.4 OEM RF Modules. Digi International.

Google Scholar