The Best-of-n Problem in Robot Swarms: Formalization, State of the Art, and Novel Perspectives

The ability to collectively choose the best among a finite set of alternatives is a fundamental cognitive skill for robot swarms. In this paper, we propose a formal definition of the best-of-n problem and a taxonomy that details its possible variants. Based on this taxonomy, we analyze the swarm robotics literature focusing on the decision-making problem dealt with by the swarm. We find that, so far, the literature has primarily focused on certain variants of the best-of-n problem, while other variants have been the subject of only a few isolated studies. Additionally, we consider a second taxonomy about the design methodologies used to develop collective decision-making strategies. Based on this second taxonomy, we provide an in-depth survey of the literature that details the strategies proposed so far and discusses the advantages and disadvantages of current design methodologies.

1. Introduction

Collective decision-making refers to the phenomenon whereby a collective of agents makes a choice in a way that, once made, it is no longer attributable to any of the individual agents. This phenomenon is widespread across natural and artificial systems and is studied in a number of different disciplines including psychology (Moscovici and Zavalloni, 1969; Hirokawa and Poole, 1996), biology (Camazine et al., 2001; Conradt and List, 2009; Couzin et al., 2011), and physics (Galam, 2008; Castellano et al., 2009). For example, social insects such as honeybees and ants are able to collectively choose and commit to a single suitable nest site using collective and distributed information processing (Franks et al., 2002). In a similar way, schools of fish, flocks of birds, and wild baboons are able to move coherently in a common direction using only local interactions with their neighbors (Okubo, 1986; Sumpter, 2010; Kao et al., 2014; Strandburg-Peshkin et al., 2015). A different situation arises in the context of other social insect colonies, where workers are able to collectively allocate themselves to a variety of tasks, such as foraging, brood care, and nest construction, and to change their allocation as a function of the colony needs (Pinter-Wollman et al., 2013; Gordon, 2016; Jandt and Gordon, 2016). The distinction between these two situations has been formalized in the context of swarm robotics by Brambilla et al. (2013) and organized in two categories: consensus achievement and task allocation (see Figure 1). The first category encompasses systems where agents aim at making a common decision on a certain matter (see Section 4 and Section 5), whereas the second category includes systems where agents allocate themselves to different tasks, with the objective to maximize the performance of the collective (Gerkey and Matarić, 2004; Liu et al., 2007; Correll, 2008; Berman et al., 2009). Understanding and designing both types of collective decision-making systems is pivotal for the development of robot swarms (Brambilla et al., 2013).

FIGURE 1

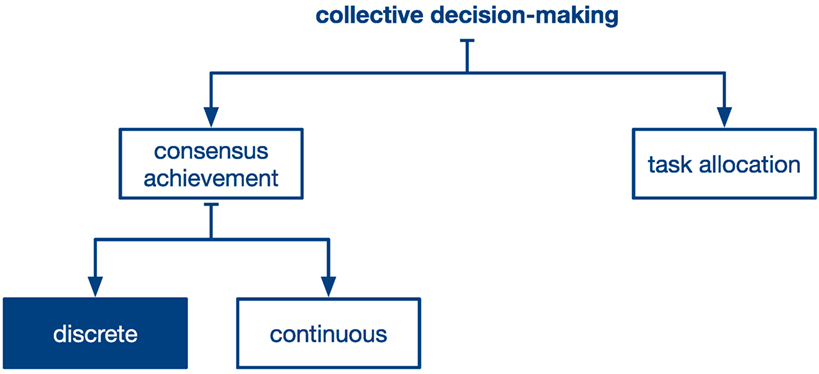
Figure 1. Taxonomy of collective decision-making processes with the focus of this survey highlighted in blue (i.e., discrete consensus achievement).

The field of swarm robotics aims at developing robotic systems that exhibit features similar to those that characterize natural self-organized systems (Brambilla et al., 2013; Dorigo et al., 2014). In particular, it aims at developing systems that are scalable to different swarm sizes (i.e., the number of robots), robust to a broad range of environmental conditions (e.g., same application but different environments), tolerant to failures of individual components (i.e., the robots), and offer flexible solutions to different goals (i.e., application scenarios). To obtain these features, swarm robotics systems are characterized by robots interacting only locally, without access to global information, and without a leader to coordinate the work activities. Similar to natural systems, swarm robotics systems achieve a desired collective behavior through self-organization.

Recent review articles have highlighted the intrinsic empirical nature of swarm robotics as one of the primary challenges of this field (Brambilla et al., 2013; Hamann et al., 2016). This fact is exacerbated by the lack of a formal engineering process that allows the designer to develop individual behaviors and interaction rules that generate a collective behavior with the desired characteristics. In our view, one important reason for this is the lack of agreement on the definition of what are the possible classes of problems for robot swarms and, consequently, we lack a formal understanding of each of these classes.

The goal of this article is to provide a contribution toward a formal understanding of swarm robotics problems. We focus on one specific class of problems, that is, on consensus achievement problems. This class of problems encompasses a wide set of application scenarios faced by robot swarms: whether the swarm needs to select the shortest path to traverse, the most suitable morphology to create, or the most favorable rendez-vous location, it first needs to address a consensus achievement problem (Christensen et al., 2007; Garnier et al., 2009; Montes de Oca et al., 2011). We further decompose this wide set of problems into two classes (cf. Figure 1), depending on the cardinality of the choices available to the swarm. When the possible choices of the swarm are finite and countable, we say that the consensus achievement problem is discrete. An example of a discrete problem is the selection of the shortest path connecting the entry of a maze to its exit (Szymanski et al., 2006). Alternatively, when the choices of the swarm are infinite and measurable, we say that the consensus achievement problem is continuous. For example, the selection of a common direction of motion by a swarm of agents flocking in a two- or three-dimensional space (Reynolds, 1987; Olfati-Saber et al., 2007) is a continuous problem.

In this article, we introduce the best-of-n problem, i.e., an abstraction capturing the structure and logic of discrete consensus achievement problems that need to be solved in several swarm robotics scenarios. First, we provide a taxonomy of possible variants of the best-of-n problem, irrespective of the specific application scenario and design solution. According to this taxonomy, we group together research studies in which the environment and the robot capabilities share common characteristics. In doing so, we identify which variants of the best-of-n problem have received less attention and thus require further research. Second, we provide a more in-depth review of the literature using an additional taxonomy that classifies research studies according to the design approach utilized to develop the collective decision-making strategy. This second classification of the literature allows us to discuss for each different design approach the domain of application and the level of portability of the resulting strategies.

2. Context of the Survey

Discrete consensus achievement problems similar to those faced by robot swarms have been studied in a number of different contexts. The community of artificial intelligence focused on decision-making approaches for cooperation in teams of agents and studied methods from the theory of decentralized partially observable Markov decision processes (Bernstein et al., 2002; Pynadath and Tambe, 2002). Discrete consensus achievement problems have been considered also in the context of the RoboCup soccer competition (Kitano et al., 1997). In this scenario, robots in a team are provided with a predefined set of plays and are required to agree on which play to execute. Different decision-making approaches have been developed to tackle this problem including centralized (Bowling et al., 2004) and decentralized (Kok and Vlassis, 2003; Kok et al., 2003) play-selection strategies. Other approaches to consensus achievement over discrete problems have been developed in the context of sensor fusion to perform distributed object classification (Kornienko et al., 2005a,b). These approaches, however, rely on sophisticated communication strategies and are suitable only for relatively small teams of agents. Finally, discrete consensus achievement problems are also studied by the community of statistical physics. Examples include models of collective motion in one-dimensional spaces (Czirók et al., 1999; Czirók and Vicsek, 2000; Yates et al., 2009) that describe the marching bands phenomenon of locust swarms (Buhl et al., 2006) as well as models of democratic voting and opinion dynamics (Galam, 2008; Castellano et al., 2009).

Continuous consensus achievement problems have been mainly studied in the context of collective motion, that is, flocking (Camazine et al., 2001). Flocking is the phenomenon whereby a collective of agents moves cohesively in a common direction. The selection of a shared direction of motion represents the consensus achievement problem. In swarm robotics, flocking has been studied in the context of both autonomous ground robots (Nembrini et al., 2002; Spears et al., 2004; Turgut et al., 2008; Ferrante et al., 2012, 2014) and unmanned aerial vehicles (Holland et al., 2005; Hauert et al., 2011) with a focus on developing control and communication strategies suitable for minimal and unreliable hardware. Apart from flocking, the swarm robotics community focused on spatial aggregation scenarios, where robots are required to aggregate in the same region of a continuous space (Trianni et al., 2003; Soysal and Şahin, 2007; Garnier et al., 2008; Gauci et al., 2014; Güzel and Kayakökü, 2017). Outside the swarm robotics community, the phenomenon of flocking is also studied within statistical physics (Szabó et al., 2006; Vicsek and Zafeiris, 2012) with the aim of defining a unifying theory of collective motion that equates several natural systems. A popular study is provided by the minimalist model of self-driven particles proposed by Vicsek et al. (1995). The community of control theory has intensively studied the problem of consensus achievement (Mesbahi and Egerstedt, 2010) with the objective of deriving optimal control strategies and proves their stability. In addition to flocking and tracking (Savkin and Teimoori, 2010; Cao and Ren, 2012), the consensus achievement problems studied in control theory include formation control (Ren et al., 2005), agreement on state variables (Hatano and Mesbahi, 2005), sensor fusion (Ren and Beard, 2008), as well as the selection of motion trajectories (Sartoretti et al., 2014). Continuous consensus achievement problems have been also studied in the context of wireless sensor networks with the aim of developing algorithms for distributed estimation of signals (Schizas et al., 2008a,b). More recently, continuous consensus achievement has been investigated using a network-theoretic perspective, which focuses on the signaling network emerging between interacting agents (Komareji and Bouffanais, 2013; Shang and Bouffanais, 2014).

3. The Best-of-n Problem

The best-of-n problem requires a swarm of robots to make a collective decision over which option, out of n available options, offers the best alternative to satisfy the current needs of the swarm. We use the term options to abstract domain-specific concepts that are related to particular application scenarios (e.g., foraging patches, aggregation areas, traveling paths). We refer to the different options of the best-of-n problem using natural numbers, 1, …, n. Given a swarm of N robots, we say that the swarm has found a solution to a particular instance of the best-of-n problem as soon as it makes a collective decision for any option i ∈ {1, …, n}. A collective decision is represented by the establishment of a large majority M ≥ (1 − δ)N of robots that favor the same option i, where δ, 0 ≤ δ ≪ 0.5, represents a threshold set by the designer. The constraint δ ≪ 0.5 requires the opinions within the swarm to form a cohesive collective decision for a single option (i.e., the opinions are not spread over different options of the best-of-n problem). In the boundary case with δ = 0, we say that the swarm has reached a consensus decision, i.e., all robots of the swarm favor the same option i.

The best-of-n problem requires a swarm of robots to make a collective decision for the option i ∈ {1, …, n} that maximizes the resulting benefits for the collective and minimizes its costs. Each option i is characterized by a quality and by a cost that are function of one or more attributes of the target environment (Reid et al., 2015). For example, when searching for a new nest site, honeybees instinctively favor candidate sites with a certain volume, exposure, and height from the ground (Camazine et al., 1999); however, their search is limited to sites within a certain distance from the current nest location. In this example, the volume, exposure, and height from the ground of a candidate site represent the option qualities, while the distance from the current nest location to the candidate site location represents the option cost.

Let ρ_i be the opinion quality associated with each option i ∈ {1, …, n}. Without loss of generality, we consider the quality of each option i to be normalized in the interval (0;1]. Option i is a maximum quality option if ρ_i = 1. We use the term option quality as an abstraction to represent the quality of domain-specific attributes of primary concern for the objective of the swarm. These attributes are defined by the designer for the specific application scenario. Robots are programmed to actively measure and estimate their quality and to prefer options whose attributes have certain characteristics. For example, in a collective construction scenario, the focus of the swarm is often on the dimension of a candidate site for construction; differently, in a foraging scenario, the swarm usually focuses on the type, quality, or availability of food in a foraging patch. Once evaluated, the information carried by the option quality is used by the robots to directly influence or modulate the collective decision-making process in favor of the best option (Garnier et al., 2007a; Valentini et al., 2016b).

We define the option cost σ_i > 0 associated with each option i ∈ {1, …, n} as the cost in terms of the average time needed by a robot to obtain one sample of the quality ρ_i of option i. The option cost is a function of the characteristics of one or more attributes of the target environment. We will use the term option cost as an abstraction for the cost resulting from these domain-specific features. These attributes depend on the target scenario, and robots are not required to perform measurements to evaluate them. Instead, this cost biases the collective decision-making process indirectly: the bias is induced by the environment and is not under the control of individual robots. For example, when foraging, certain species of ants find the shortest traveling path between a pair of locations as a result of pheromone trails being reinforced more often on the shortest path (Goss et al., 1989). These ants do not measure the length of each path individually and do not lay more or less pheromone depending on the path they are on. However, the length of a path indirectly influences the amount of pheromone laid over the path by the ants. Note that other sources of cost such as the amount of energy consumed or the risk involved in exploring a certain option need to be considered as option cost only when they affect the time necessary to explore a certain option while otherwise they need to be considered during the estimation of the option quality.

We classify instances of the best-of-n problem in five different categories depending on how the option quality and the option cost are configured in the application scenario and perceived by the robots (cf. Figure 2). In general, the best-of-n problem is either symmetric or asymmetric with respect to both the option quality and option cost. If all options have the same quality (respectively, cost), we say that the best-of-n problem is symmetric with respect to the option quality (option cost). If at least two options of different quality (cost) exist, we say that the best-of-n problem has asymmetric option qualities (costs). When both option qualities and option costs are symmetric, the options of the best-of-n problem are equivalent to each other and the objective of the swarm is to make a collective decision for any of them. This problem is known in the literature as the symmetry-breaking problem (de Vries and Biesmeijer, 2002; Hamann et al., 2012). When the option qualities are symmetric but the option costs are not, the objective of the swarm is to make a collective decision for the option of minimum cost. In the opposite situation, i.e., asymmetric qualities but symmetric costs, the best option for the swarm corresponds to the option of maximum quality. Finally, when both option qualities and option costs are asymmetric, we further distinguish between two situations: in the first situation, the option qualities and the option costs are synergic and the best option has both maximum quality and minimum costs; in the second situation, they are antagonistic and the best option is characterized by a trade-off between quality and cost.

FIGURE 2

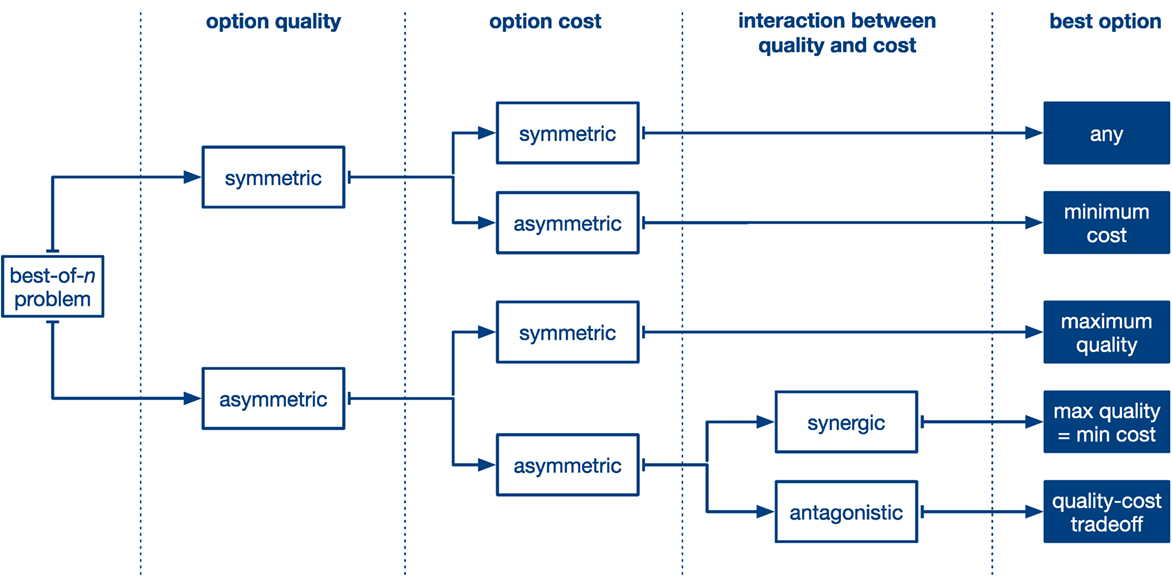
Figure 2. Taxonomy of possible discrete consensus achievement scenarios corresponding to different variants of the best-of-n problem. The schema illustrates how different combinations of option quality and option cost define the best option of the best-of-n problem.

Finally, the option quality and the option cost can be either static or dynamic. This feature is particularly relevant to guide the choices of designers during the design of a collective decision-making strategy. When the option quality is static, designers favor collective decision-making strategies that results in consensus decisions (Parker and Zhang, 2009; Montes de Oca et al., 2011; Scheidler et al., 2016). Differently, when the option quality is dynamic, i.e., a function of time, designers favor strategies that result in a large majority of robots in the swarm favoring the same option without converging to consensus (Parker and Zhang, 2010; Arvin et al., 2014). In this case, the remaining minority of agents that are not aligned with the current collective decision keep exploring other options and possibly discover new ones, making the swarm adaptive to changes in the environment (Schmickl et al., 2009b). Additionally, a consensus decision corresponding to a large majority rather than unanimity allows swarm systems to swiftly react to perturbations as in the case of fish schools (Calovi et al., 2015).

4. Problem-Based Classification

4.1. Symmetric Option Qualities and Costs: Symmetry Breaking

When the problem is symmetric with respect to both the option quality and option cost (i.e., there is no difference in the quality and there is no environmental bias toward any option), the best-of-n problem reduces to a symmetry-breaking problem. In this case, the objective of the swarm is to make a collective decision for any option of the best-of-n problem. The option that is ultimately favored by the swarm is usually selected arbitrarily as a result of the amplification of noise and random fluctuations.

Wessnitzer and Melhuish (2003) considered a prey-hunting scenario with moving preys. In this scenario, a swarm of robots needs to capture two preys (i.e., best-of-2 problem) that are moving in the environment and is required to choose which prey to hunt first. The two preys are equally valuable for the robots (i.e., their quality is symmetric) and are initially located at the same distance from the swarm (i.e., their cost is symmetric too). Although the distance of the preys is dynamic, the collective decision made by the swarm is based only on information about the initial preys’ position and therefore the cost of each option is constant in time.

Garnier et al. (2007b) considered a double-bridge scenario, similar to the one designed by Goss et al. (1989) and Deneubourg and Goss (1989), to study the foraging behavior of ant colonies. In this foraging scenario, a nest is connected to a foraging site by a pair of paths. The two paths have symmetric option quality because they both connect the nest to the foraging site and allow the swarm to fulfill its objective (i.e., foraging). Additionally, being the two paths equal in length, they are also characterized by the same traversal time and their cost is symmetric too.

Garnier et al. (2009) considered an aggregation scenario inspired by the collective selection of shelters by cockroaches (Amé et al., 2006; Halloy et al., 2007). In their application scenario, robots of a swarm are presented with two shelters (i.e., a best-of-2 problem) and are required to select one shelter under which the swarm should aggregate. The two shelters, which correspond to a pair of black-colored areas, are indistinguishable to the robots except for their size, which is varied by the authors between two different experimental setups. In the first scenario they considered, which is the only one of interest in this section, the two shelters have equal size and, therefore, are characterized by the same quality and by the same cost (see Section 4.4 for the description of the second scenario). The aggregation problem requires to break the symmetry between the two shelters of equal size. This aggregation scenario has also been investigated in more recent studies by Francesca et al. (2012, 2014) (see Figure 3) and by Brambilla et al. (2014).

FIGURE 3

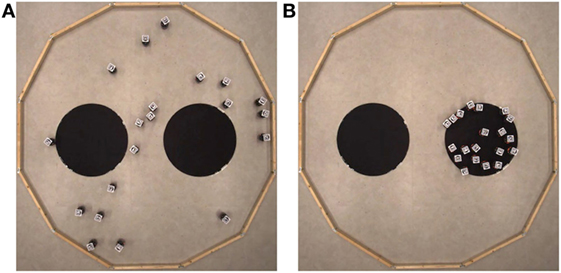
Figure 3. The aggregation scenario in Francesca et al. (2014) consists of a dodecagonal arena of 4.91 m² that contains a pair of circular aggregation spots of 0.35 m radius and 20 e-puck robots (Mondada et al., 2009). Panel (A) shows the initial distribution of robots in the arena; Panel (B) shows the robots aggregated over the chosen spot at the end of the experiment.

Finally, Hamann et al. (2012) considered a binary aggregation scenario that is similar to the one proposed by Garnier et al. (2009). The only difference is that, in the scenario of Hamann et al. (2012), the two aggregation spots are represented by projected light whose intensity determines the size of the aggregation spot rather than by colored areas as done in previous studies (Garnier et al., 2009; Francesca et al., 2012, 2014; Brambilla et al., 2014). In this symmetry-breaking scenario, both aggregation spots are characterized by the same level of brightness and therefore by the same option quality and by the same option cost.

4.2. Symmetric Option Qualities and Asymmetric Option Costs

When all options of the best-of-n problem have the same quality (i.e., symmetric option quality) but are subject to different environmental bias (i.e., asymmetric option cost), the best-of-n problem reduces to finding the option of minimum cost. This variant can be tackled using strategies that do not require robots to directly measure neither the quality nor the cost of each option.

Schmickl and Crailsheim (2006, 2008) studied a foraging scenario reminiscent of the double-bridge problem. In their scenario, a nest area is separated from a foraging patch by a wall with two gates, and the swarm needs to decide which gate to traverse in order to reach the foraging patch (the options of a best-of-2 problem). Both gates allow robots to forage between the foraging patch and the nest area (i.e., the objective of the swarm) and have therefore symmetric quality. However, the position of the two gates on the wall, which determines the length of the corresponding traveling path (i.e., the option cost), is different. The best-of-n problem is therefore characterized by asymmetric option cost.

Schmickl et al. (2007) considered a binary aggregation scenario with a pair of aggregation spots of different area size. In their study, the objective of the swarm is to form a cohesive aggregate in the proximity of any of the two spots. Each robot is only provided with the means to perceive whether it is over an aggregation spot or not and it cannot measure any other feature of the aggregation spots (i.e., symmetric option quality). Nonetheless, aggregation spots differ in their cost: having bigger area, the large spot is easier to discover by robots exploring the environment than the small spot; this spot is discovered sooner and more frequently and has therefore a lower cost (i.e., asymmetric option cost).

Campo et al. (2010b) focused on a navigation scenario in which the shortest between two paths needs to be found. In their scenario, paths are represented by chains of robots of different length that lead to two different locations. This scenario belongs to this category as the locations reachable following either of the two paths are indistinguishable by the robots (i.e., symmetric option quality) but the shorter path is faster to traverse (i.e., asymmetric option cost) and biases the collective decision. A similar setup was studied in the context of foraging by Reina et al. (2015a). In this case, the two foraging patches (of equal quality) are positioned in an open environment at different distances from the retrieval area.

An additional shortest-path problem inspired by the double-bridge problem (Goss et al., 1989) has been studied by Montes de Oca et al. (2011) and subsequent work (Brutschy et al., 2012; Scheidler et al., 2016). Two areas, a source area containing objects and a destination area where objects are to be delivered, are connected by two paths of different length (see Figure 4A). Robots do not measure the length or any other feature of the two paths (i.e., symmetric option quality). In contrast, the length of each path indirectly biases the collective decision-making process, which takes place at the source area, because robots traveling through the shortest (and fastest) path have higher chances to influence other members of the swarm (i.e., asymmetric option cost).

FIGURE 4

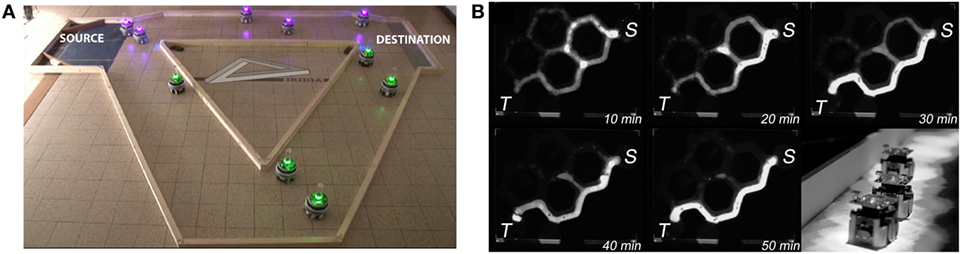
Figure 4. Two examples of scenarios with symmetric option qualities and asymmetric option costs. Panel (A) shows the double-bridge scenario used in Scheidler et al. (2016). 10 foot-bot robots (Dorigo et al., 2013) navigate an environment of size 4.5 m × 3.5 m, with a source location (left) and a destination location (right) connected by two paths of different length. Panel (B) shows the maze scenario used in Garnier et al. (2013) (Creative Commons Attribution, CC BY 3.0). Each corridor in this maze is 9 cm wide and its walls are 2.5 cm high. The starting (S, top right) and the target (T, bottom left) areas are hexagons of 22.5 cm diameter and there are 7 possible connecting paths of different lengths (shortest: 86 cm; longest: 178 cm). Robots used are Alice robots (Caprari et al., 2001), depicted in the bottom-right part of Panel (B).

Garnier et al. (2013) considered a foraging scenario that takes place in a maze. Similarly to the double-bridge scenario, a swarm of robots is located in an environment composed of corridors that connect a source area with a destination area. In the case of Garnier et al. (2013), corridors form a maze that provides the swarm with n = 7 different paths connecting the source area with the destination area (see Figure 4B). The robots in the swarm do not measure explicitly any feature of a foraging path, and the option quality is therefore symmetric. The option cost is still represented by the length of each path and is asymmetric due to the existence of a path shorter than all other paths (i.e., best option). In addition to the path length, Garnier et al. (2013) also showed that a second environmental factor that can bias the collective decision is the angle of branches in a bifurcation whereby the branch offering the smallest deviation from the current direction of motion has a lower cost.

4.3. Asymmetric Option Qualities and Symmetric Option Costs

When only the option quality is asymmetric while the option cost is symmetric, the best option of the best-of-n problem corresponds to that with the highest quality. In this variant of the best-of-n problem, the designer of a collective decision-making strategy is required to consider robots with means to directly measure the quality of each option. In the case in which this requirement is not respected, the swarm would not be able to collect the information necessary to discriminate the best option from other sub-optimal options.

Parker and Zhang (2009, 2011) considered a site-selection scenario, where a swarm of robots is required to discriminate the brightest between two sites. The two sites are symmetrically located at the borders of an hexagonal arena, have the same size, and are uniquely identified by colored light beacons (i.e., symmetric option costs). However, sites are also characterized by an overhead light whose intensity differs between the two sites. Since the objective of the swarm is to select the brightest site, the level of brightness of a site represents the site quality and option qualities are asymmetric due to their different level of brightness. Valentini et al. (2014, 2015, 2016b) investigated a similar site-selection scenario in which two sites of equal size are symmetrically positioned at the sides of a rectangular arena (i.e., no environmental bias and therefore symmetric costs). Rather than a physical feature as the level of brightness, the two sites are characterized by an abstract quality which has the form of a numeric value broadcast by beacons and perceived by robots. These values are different between the two sites and the option quality is therefore asymmetric.

Parker and Zhang (2010) considered a task-sequencing problem where a swarm of robots needs to work sequentially on different tasks (e.g., site preparation, collective construction of structures). The robots are required to collectively agree on the completion of a blind-bulldozing task (i.e., remove debris from a site) prior to begin working on the next task in the sequence. The task-sequencing problem is a best-of-2 problem whose options (i.e., “task complete” or “task incomplete”) are characterized by dynamic qualities (i.e., the task completion level changes over time). The task completion level, which represents the option quality, corresponds to the size of the cleared area. The option qualities are asymmetric and change over time as the size of the cleared area is complementary to the one of the area with debris. Moreover, there is no asymmetry in accessing this information, and therefore, the option costs are symmetric.

Mermoud et al. (2010) considered a scenario where robots of the swarm are required to monitor a certain environment, searching and destroying undesirable artifacts (e.g., pathogens, pollution). Specifically, artifacts correspond to colored spots that are projected on the surface of the arena and can be of two types: “good” or “bad” (see Figure 5A). The robots need to determine collectively whether each spot is good or bad. This scenario corresponds to an infinite series of best-of-2 problems (i.e., one for each spot) that are tackled in parallel by different subsets of robots of the swarm. Each spot type has a different color, and robots can measure the light intensity to determine the type of a spot. The quality of a spot is either maximal (e.g., ρ = 1), if the spot is good, or minimal (e.g., ρ = 0), if the spot is bad. Each best-of-2 problem is characterized therefore by asymmetric option qualities. Once again, as both spot types appear randomly in the environment, their positions do not bias the discovery of spots by robots and the option cost is symmetric.

FIGURE 5

Figure 5. Examples of robotic scenarios with asymmetric option qualities and symmetric option costs. Panel (A) shows the 50 cm sided square arena with five Alice robots (Caprari et al., 2001) and four differently colored light spots projected by an overhead projector used in the monitoring scenario in Mermoud et al. (2010). Panel (B) shows the collective perception scenario in Valentini et al. (2016a) characterized by a 2 m × 2 m square arena with 10 cm × 10 cm cells of different colors (black or white) and 20 epuck robots (Mondada et al., 2009).

Recently, Valentini et al. (2016a) proposed a collective perception scenario in which a closed environment is characterized by different features scattered around in different proportions. The objective of the swarm is to determine which feature is the most frequent in the environment. The authors considered a binary scenario in which the two features (i.e., options) are represented by different colors of the arena surface, respectively, black and white (see Figure 5B). The colors of the arena surface can be perceived by the robots; their corresponding covered area, i.e., the size of the arena surface covered with a certain color, represents the option quality which, in this case, is asymmetric. Moreover, the cost in terms of time necessary for a robot to perceive the color of the arena surface is the same for both the black and white colors. The option cost is therefore symmetric.

4.4. Asymmetric Option Qualities and Costs: Synergic Case

When both option qualities and option costs are asymmetric, we distinguish between the synergic case and the antagonistic case (cf. Section 3). In the following, we consider research studies where the interaction between the option quality, and the option cost is synergic and the best option of the best-of-n problem has both the highest quality and the lowest cost.

The aggregation scenario of Garnier et al. (2009) was characterized by two shelters which, in their first case study, were of equal size (see Section 4.1). In the second case study, one shelter is larger than the other and the objective of the swarm is to aggregate under the larger shelter. In this case, the size of a shelter acts both as the option quality and option cost. The shelter size represents the option quality. Robots are programmed to sense the number of neighbors under a shelter, use this information to estimate the shelter size, and prioritize shelters of larger size. The shelter size represents also the option cost. Larger shelters are easier to discover by robots and have therefore lower cost; being larger shelters also those where robots are required to aggregate into, the interaction between quality and cost is synergic.

Schmickl et al. (2009b) considered an aggregation scenario characterized by two spots (i.e., a best-of-2 problem) identified by two lamps with different levels of brightness (see Figure 6). The swarm is required to aggregate at the brightest spot, and therefore, the level of brightness represents the option quality which, being different between the two spots, is asymmetric. Additionally, the level of brightness of each lamp determines the size of the spot because brighter lights define larger spots. The size of each spot influences the probability for a robot to discover that spot (i.e., asymmetric option cost) and bias the collective decision toward larger spots. Due to the fact that larger spots are also brighter, the interaction between option quality and option cost is synergic.

FIGURE 6

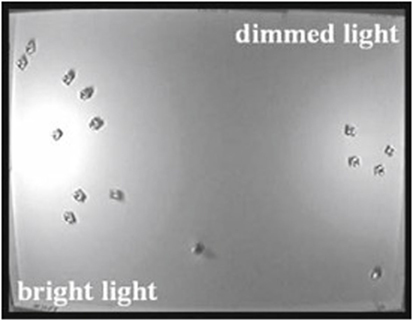
Figure 6. The 1.5 m × 1 m rectangular arena used in Schmickl et al. (2009b), containing 15 Jasmine-III robots and differently light-dimmed areas for robot aggregations.

Arvin et al. (2012, 2014) studied a dynamic aggregation problem, where robots need to aggregate in one of two available spots. Each spot is identified by a sound emitter. The sound magnitudes of the two spots are different and vary over time. The objective of the swarm is to decide, which spot has the highest level of magnitude. This feature can be measured by the robots using their sensors and represents an asymmetric option quality. The size of each aggregation spot is proportional to the magnitude of the emitted sound and different for the two spots (i.e., asymmetric option cost). Consequently, the option cost is asymmetric and its interaction with the option quality is synergic due to the fact that spots with louder sound (i.e., higher quality) also have larger area (i.e., lower cost) making them easier to discover by the robots.

Gutiérrez et al. (2010) studied a foraging scenario characterized by two foraging patches (i.e., a best-of-2 problem) positioned at different distances from a retrieval area. The objective of the swarm is to forage from the closest foraging patch. In this scenario, the distance between a patch and the retrieval area acts both as option quality and option cost: as option quality, because each robot can directly measure the distance and is programmed to favor closer foraging patches; as option cost because patches that are closer to the retrieval area are easier to discover by robots and are therefore of lower cost. Both the option quality and the option cost are asymmetric and their interaction produces a synergic effect.

4.5. Asymmetric Option Qualities and Costs: Antagonistic Case

Finally, the antagonistic case of asymmetric option qualities and option costs is characterized by application scenarios where the option cost bias negatively the collective decision toward options with sub-optimal quality. In this case, the best option of the best-of-n problem is characterized by a trade-off between the quality of an option and its cost. The target compromise between quality and cost driving the collective decision-making process of the swarm is determined by the designer at design time.

Campo et al. (2010a) considered an aggregation scenario similar to that of Garnier et al. (2009), where two shelters of different size are located in a closed arena. As in Garnier et al. (2009), the size of a shelter determines both the quality and the cost of a certain option. However, differently from Garnier et al. (2009), the objective of the swarm is to select the smallest shelter that can host the entire swarm. The larger shelter is still the one associated with the smaller cost; however, its quality is not necessarily the highest. Campo et al. (2010a) studied different experimental setups varying the size of the shelters. In one of these setups, the smallest of the two shelters can host the entire swarm, and the interaction between quality and cost of an option is therefore antagonistic.

Recently, Reina et al. (2015b) studied a binary foraging scenario, where the objective of the swarm is to decide which foraging patch offers the highest quality resource and to forage from that patch. The environment is characterized by a central retrieval area and two foraging patches. Each foraging patch contains resources of a certain quality that a robot can measure using its sensors. The two foraging patches differ in the quality of the contained resources (i.e., asymmetric option quality). Moreover, foraging patches are positioned at different distances from the retrieval area (i.e., asymmetric option cost) in a way that the foraging patch with highest quality resource is the farthest from the retrieval area. As a consequence, the best foraging patch is harder to discover by robots and, once discovered, requires longer traveling time. The interaction between the option quality and the option cost is therefore antagonistic.

4.6. Summary

We have distinguished research studies in the five different categories previously described. For each category, we have further grouped the literature in separate lines of research, where each line of research focuses on a specific combination of application scenario and collective decision-making strategy (as explained in Section 5). Each research line is characterized by a first seminal work (i.e., the research studies reviewed above) and by subsequent work that extended or continued that line of research in one or more directions (e.g., theoretical studies that will be surveyed in Section 5).

As shown in Table 1, the first three variants of the best-of-n problem, namely, symmetry-breaking problems and problems where either only the option cost or only the option quality is asymmetric, have been the subject of a large portion of the literature. This part of the literature is structured in several different research lines for each variant of the best-of-n problem.

TABLE 1

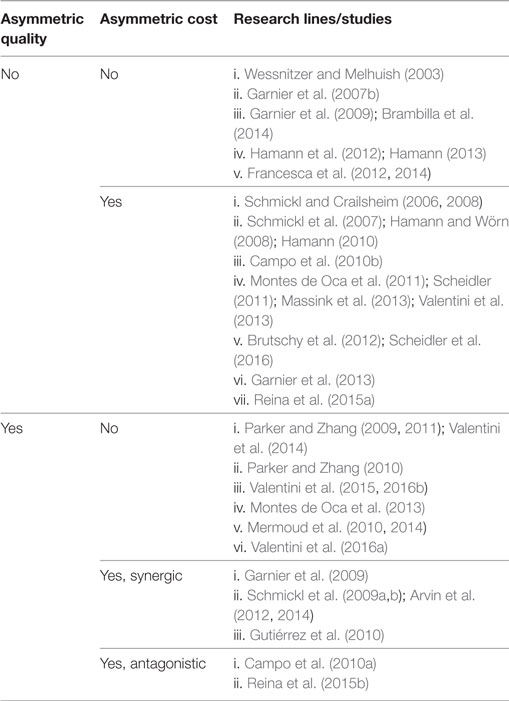
Table 1. Classification of swarm robotics literature according to the combination of factors that determines the quality and the cost of the options of the best-of-n problem.

Differently, a significantly smaller portion of the literature focused on the remaining two variants of the best-of-n problem, that is, when both the option quality and the option cost are asymmetric and their interaction is either synergic or antagonistic. Most of these studies considered the synergic case and resulted in 3 different research lines. The case where the interaction between quality and cost is antagonistic is the least developed area of study in the literature on discrete consensus achievement, with only two research contributions. A possible reason for this fact is that, from the perspective of the designer, this variant of the best-of-n problem represents application scenarios with the highest level of complexity and requires design solutions able to compensate the negative bias of environmental factors affecting the cost of each option.

An additional consideration that we can draw from our analysis is represented by the fact that nearly all reviewed studies focused on binary decision-making scenarios. The study of Garnier et al. (2013) provides the only experimental results over a problem with n = 7 options (see Section 4.2), while the study of Scheidler et al. (2016) provided a theoretical analysis for the case of n = 3 options (see Section 5.1.1).

5. Design-Based Classification

The efforts of researchers in the last decade resulted in research contributions that span over a number of different design approaches. Brambilla et al. (2013), who surveyed the field of swarm robotics focusing on design methodologies, organized research studies in two categories, behavior-based and automatic design methods. In this section, we make use of a similar taxonomy to classify research studies according to the methodology used by designers to derive their collective decision-making strategies (see Figure 7). Differently from Brambilla et al. (2013), our focus is not on the design methodology but on the structure and functioning of the designed strategies.

FIGURE 7

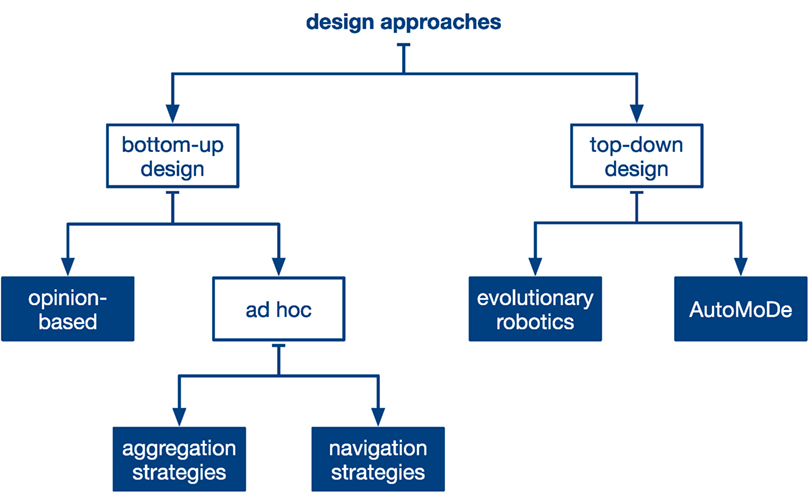
Figure 7. Taxonomy used to review research studies that consider a discrete consensus achievement scenario. Research studies are organized according to their design approach (i.e., bottom-up and top-down) and to how the control rules governing the interaction among robots have been defined.

We divide the design approaches used to address the best-of-n problem into two categories: bottom-up and top-down (Crespi et al., 2008). In a bottom-up approach, the designer develops the robot controller by hand, following a trial and error process where the robot controller is iteratively refined until the swarm behavior fulfills the requirements. Conversely, in a top-down approach, the controller for individual robots is derived directly from a high-level specification of the desired behavior of the swarm by means of automatic techniques, for example, as a result of an optimization process (Nolfi and Floreano, 2000; Bongard, 2013).

In a bottom-up approach (see Section 5.1), a typical design paradigm consists in defining different atomic behaviors that are combined together by the designer to obtain a probabilistic finite-state machine that represents the robot controller (Scheutz and Andronache, 2004). Each behavior used in the robot controller is implemented by a set of control rules that determine (i) how a robot works on a certain task and (ii) how it interacts with its neighbor robots and (iii) with the environment. We organize collective decision-making strategies designed by means of a bottom-up process in two categories (see Figure 7), according to how the control rules governing the interaction among robots have been defined. In the first category, that we call opinion-based approaches, robots have an explicit internal representation of their favored opinion, and the role of the designer is to define the control rules that determine how robots exchange opinions and how they change their own opinion. The main advantage of opinion-based approaches is that they result in strategies that are generic and can be applied to different application scenarios. In the second category, that we call ad hoc approaches, we consider research studies where the control rules governing the interaction between robots have been defined by the designer to address a specific task. As opposed to opinion-based approaches, control strategies belonging to this category are not explicitly designed to solve a consensus achievement problem; nonetheless, their execution by the robots of the swarm results in a collective decision. In this category, we consider research studies that focus on the problem of spatial aggregation and on the problem of navigation in unknown environments.

In a top-down approach (see Section 5.2), the robot controller is derived automatically from a high-level description of the desired swarm behavior. We organize research studies adopting a top-down approach in two categories: evolutionary robotics and automatic modular design (AutoMoDe). Evolutionary robotics (Nolfi and Floreano, 2000; Bongard, 2013) relies on evolutionary computation to obtain a neural network representing the robot controller. As a consequence, this design approach results in black-box controllers. In contrast, automatic modular design (Francesca et al., 2014) relies on optimization processes to combine behaviors chosen from a predefined set and obtain a robot controller that is represented by a probabilistic finite-state machine.

5.1. Bottom-Up Design

5.1.1. Opinion-Based Approaches

A large amount of research work has focused on the design of collective decision-making strategies characterized by robots having an explicit representation of their opinions. We refer to these collective decision-making strategies as opinion-based approaches. Using this design approach, robots are required to perform explicit information transfer, i.e., to purposely transmit information representing their current opinion to their neighbors. As a consequence, a collective decision-making strategy developed using an opinion-based approach requires robots to have communication capabilities (e.g., visual or infrared communication).

One of the first research studies developed with an opinion-based approach is that of Wessnitzer and Melhuish (2003), which tackled a prey-hunting scenario with moving prey. The authors proposed a collective decision-making strategy based on the majority rule. At the beginning of the experiment, each robot favors a prey chosen at random. At each time step, robots apply the majority rule over their neighborhood in order to reconsider and possibly change their opinions. Following this strategy, the swarm decides which prey to hunt first, captures the first prey, and successively focuses on the second.

Parker and Zhang (2009) developed a collective decision-making strategy by taking inspiration from the house-hunting behavior of social insects (Franks et al., 2002). The robots need to discriminate between two sites having different levels of brightness. The proposed control strategy is characterized by three phases. Initially, robots are in the search phase either exploring the environment or waiting in an idle state. Upon discovery of a site and estimating its quality, a robot transits to the deliberation phase. During the deliberation phase, a robot recruits other robots in the search phase by repeatedly sending recruitment messages. The frequency of these messages is proportional to the option quality. Meanwhile, robots estimate the popularity of their favored option and use this information to test if a quorum has been reached. Upon detection of a quorum, robots enter the commitment phase and eventually relocate to the chosen site. The strategy proposed by Parker and Zhang builds on a direct recruitment and a quorum-sensing mechanism inspired by the house-hunting behavior of ants of the Temnothorax species. Later, Parker and Zhang (2011) considered a simplified version of this strategy and proposed a rate equation model to study its convergence properties.

Parker and Zhang (2010) proposed a collective decision-making strategy for unary decisions and applied it to a task-sequencing problem (see Section 4.3). The authors proposed a quorum-sensing strategy to address this problem. Robots working on the current task monitor its level of completion: when a robot recognizes the completion of the task, it enters the deliberation phase during which it asks its neighbors if they recognized too the completion of the task. Once a deliberating robot perceives a certain number of neighbors in the deliberation phase (i.e., the quorum), it moves to the committed phase during which it sends commit messages to inform neighbor robots about the completion of the current task. Robots in the deliberation phase that receive a commit message enter the committed phases and respond with an acknowledgment message. Committed robots measure the time passed since the last received acknowledgment and, after a certain time, they begin working on the next task.

Montes de Oca et al. (2011) took advantage of the theoretical framework developed in the field of opinion dynamics (Krapivsky and Redner, 2003) to develop their own strategy. The authors extended the concept of latent voters introduced by Lambiotte et al. (2009) (i.e., voters stop participating to the decision-making process for a stochastic amount of time after changing opinion) and proposed a collective decision-making strategy referred to as majority rule with differential latency. They considered a double-bridge scenario where robots need to transport objects between two locations connected by two paths of different length. Objects are heavy and require a team of 3 robots to be transported. During the collective decision-making process, robots repeatedly form teams at the source location. Within a team, robots share with each other their opinion for their favored path and then apply the majority rule (Galam, 2008) to determine which path the team should traverse. Then, the team travels back-and-forth along the chosen path before dismantling once back in the source location. Due to its lower option cost, robots taking the shortest path appear more frequently at the source location and have a higher chance to influence other members of the swarm. This self-organized process biases the collective decision of the swarm toward the shortest path. The majority rule with differential latency has been the subject of an extensive theoretical analysis that includes deterministic macroscopic models (Montes de Oca et al., 2011), master equations (Scheidler, 2011), statistical model checking (Massink et al., 2013), and Markov chains (Valentini et al., 2013).

The same foraging scenario investigated in Montes de Oca et al. (2011) has been the subject of other research studies. Brutschy et al. (2012) and Scheidler et al. (2016) extended the control structure underlying the majority rule with differential latency introducing the k-unanimity rule. Instead of forming teams and applying the majority rule within each team, robots have a memory of size k, where they store the opinions of other robots as they encounter them. A robot using the k-unanimity rule changes its current opinion in favor of a different option only after consecutively encountering k other robots all favoring that other option. The primary benefit of the k-unanimity rule is that it allows the designer to adjust the speed and accuracy of the collective decision-making strategy by means of the parameter k (Scheidler et al., 2016). The authors studied the dynamics of the k-unanimity rule analytically when applied to decision-making problems with up to n = 3 options using a deterministic macroscopic model and a master equation.

Montes de Oca et al. (2013) built on the concept of differential latency and proposed a more complex individual decision mechanism that is motivated by the imitation behavior characteristic of many biological systems (Goss et al., 1989; Rendell et al., 2010). The authors replace the majority rule used in Montes de Oca et al. (2011) by means of a learning rule implemented through an exponential smoothing equation. Each agent has both an opinion for a particular option and an internal belief over the set of options. When an agent perceives the opinion of a different member of the swarm, it updates its internal belief as a weighted sum of both its current opinion and the perceived one. The agent then tests the value of its belief against a fixed threshold in order to decide whether to change its opinion or not.

Valentini et al. (2014) considered a binary site-selection scenario and proposed a collective decision-making strategy that is based on direct modulation of opinion dissemination and on the use of the voter model as decision mechanism. Robots alternate a period of option exploration to a period of opinion dissemination. In the exploration state, a robot samples the quality of the option associated to its current opinion. In the dissemination state, a robot advertises its current opinion for a time proportional to the sampled quality (i.e., direct modulation). Before moving to the exploration state, a robot switches opinion in favor of that of a randomly chosen neighbor (as in the voter model). The authors demonstrated the effectiveness of the method using multi-agent simulations as well as two mathematical models: an ordinary differential equation model to explore the asymptotic properties of the proposed strategy and a chemical reaction network model to quantify finite-size effects.

Valentini et al. (2015, 2016b) proposed a collective decision-making strategy similar to that in Valentini et al. (2014) but used a different decision rule to let robots change their opinion. As in Valentini et al. (2014), the robots sample the quality of the option associated to their opinions and disseminate their preferences for a time proportional to the sampled quality. In contrast to the voter model, robots use the majority rule (Galam, 2008) to change their opinion, whereby a robot adopts the opinion favored by the majority of its neighbors. This strategy has been validated with experiments with a hundred-robot swarm. Additionally, the performance of the proposed strategy has been investigated in a broad range of problem configurations using both an ordinary differential equation model and a chemical reaction network model. More recently, Kouvaros and Lomuscio (2016) studied the strategy proposed by Valentini et al. (2016b) using formal methods and symbolic model-checking methodologies showing that consensus is a guaranteed property of this strategy.

Reina et al. (2015a,b) proposed a collective decision-making strategy inspired by theoretical studies that unify the decision-making behavior of social insects with that of neurons in vertebrate brains (Marshall et al., 2009; Seeley et al., 2012). The authors considered the problem of finding the shortest path connecting a pair of locations in the environment. In their strategy, robots can be either uncommitted, i.e., without any opinion favoring a particular option, or committed to a certain option, i.e., with an opinion. Uncommitted robots might discover new options in which case they become committed to the discovered option. Committed robots can recruit other robots that have not yet an opinion (i.e., direct recruitment); inhibit the opinion of robots committed to a different option making them become uncommitted (i.e., cross-inhibition); or abandon their current opinion and become uncommitted (i.e., abandonment). The proposed strategy is supported by both deterministic and stochastic mathematical models that link the microscopic parameters of the system to the macroscopic dynamics of the swarm.

5.1.2. Ad Hoc Approaches

In this section, we consider research studies where control strategies were developed for specific tasks: spatial aggregation and navigation in unknown environments. As opposed to opinion-based approaches, the objective of the designers of these control strategies is not to tackle a consensus achievement problem directly but to address a specific need of the swarm (i.e., aggregation or navigation). Nonetheless, the control strategies reviewed in this section provide a swarm of robots with collective decision-making capabilities.

5.1.2.1. Aggregation-Based Control Strategies

Aggregation-based control strategies make the robots of the swarm aggregate in a common region of the environment forming a cohesive cluster. The opinion of a robot is represented implicitly by its position in space. Aggregation-based strategies have the advantage of not requiring communication due to the fact that the information regarding a robot opinion is transferred implicitly to nearby robots. Implicit information transfer can be implemented, for example, by means of neighbors observation without requiring any explicit communication. As a consequence, designers can simplify the hardware requirements of individual robots (Gauci et al., 2014).

Garnier et al. (2009) considered a behavioral model of self-organized aggregation and studied the emergence of collective decisions. The authors proposed a control strategy inspired by the behavior of young larvae of the German cockroach, Blattella germanica, Jeanson et al. (2003). Robots explore a bounded arena by executing a correlated random walk. When a robot detects the boundaries of the arena, it pauses the execution of the random walk and begins the execution of a wall-following behavior. The wall-following behavior is performed for an exponentially distributed period of time after which the robot turns randomly toward the center of the arena. When encountering a shelter, the robot decides whether to stop or not as well as whether to stop for a short or a long period of time as a function of the number of nearby neighbors. Given the number of perceived neighbors, this function returns the probability for a robot to stop and its value has been tuned by the designer to favor the selection of shelters with larger area. Correll and Martinoli (2011) studied this collective behavior with both Markov chains and difference equations and showed that a collective decision arises only when robots move faster than a minimum speed and are characterized by a sufficiently large communication range.

Campo et al. (2010a) considered the same aggregation scenario of Garnier et al. (2009) and developed a control strategy taking inspiration from theoretical studies of the aggregation behaviors of cockroaches (Amé et al., 2006). In their strategy, the robot controller is composed of three phases: exploration, stay under a shelter, and move back to the shelter. Initially, the robots explore the environment by performing a random walk. Once a robot discovers a shelter, it moves randomly within the shelter’s area and estimates the density of other robots therein. If during this phase a robot accidentally exits the shelter, it performs a U-turn aimed at reentering the original shelter. Differently from Garnier et al. (2009), the robots directly decide whether to stay under a shelter or to leave and return to the exploration phase. This decision is stochastic and the probability to leave the shelter is given by a sigmoid function of the estimated density of robots under the shelter. A similar aggregation strategy was proposed later by Brambilla et al. (2014) and studied in a binary symmetry-breaking setup. Differently from the sigmoid function used in Campo et al. (2010a), the authors considered a linear function of the number of neighbors to determine the probability with which a robot decides whether to leave a shelter or not.

Kernbach et al. (2009) took inspiration from the thermotactic aggregation behavior of young honeybees, Apis mellifera L., Grodzicki and Caputa (2005), and proposed the BEECLUST algorithm (Kernbach et al., 2009; Schmickl et al., 2009b). The goal of a swarm executing the BEECLUST algorithm is to aggregate around the brightest spot in the environment. For this purpose, a robot moves forward in the environment and, when it is encounter an obstacle, it turns in a random direction to avoid it. Upon encountering another robot, the robot stops moving and measures the local intensity of the ambient light. After waiting for a period of time proportional to the measured light, the robot resumes random walk. Schmickl et al. (2009b) studied the BEECLUST algorithm in a setup characterized by two spots of different brightness. Later, Hamann et al. (2012) studied the BEECLUST algorithm in a binary symmetry-breaking setup, where both spots are characterized by the same level of brightness. The BEECLUST algorithm has been the subject of an extensive theoretical analysis that includes both spatial and non-spatial macroscopic models (Schmickl et al., 2009a; Hereford, 2010; Hamann et al., 2012; Hamann, 2013). While the resulting decision-making process is robust, it is difficult to model due to the complex dynamics of cluster formation and cluster breakup (Hamann et al., 2012).

More recently, Arvin et al. (2012, 2014) extended the original BEECLUST algorithm by means of a fuzzy controller. In the original BEECLUST algorithm, after the expiration of the waiting period, a robot chooses randomly a new direction of motion. Differently, using the extension proposed by Arvin et al., the new direction of motion is determined using a fuzzy controller that maps the magnitude and the bearing of the input signal (in their case, a sound signal) to one out of five predetermined directions of motion (i.e., left, slightly left, straight, slightly right, right). The authors studied the extended version of the BEECLUST algorithm considering a dynamic, binary aggregation scenario with two aggregation areas identified by a sound emitter. The proposed extension has been shown to improve the aggregation performance of the BEECLUST algorithm (i.e., clusters last for a longer period of time) as well as its robustness to noisy perceptions of the environment.

Mermoud et al. (2010) considered a scenario where the task of the robots is to collectively classify colored spots in the environment as “good” or “bad.” The authors proposed an aggregation-based strategy that allows robots to collectively perceive the type of a spot and to destroy those spots that have been perceived as bad while safeguarding good spots. Each robot explores the environment by performing a random walk and avoiding obstacles. Once a robot enters a spot, it measures the light intensity to determine the type of the spot. Successively, the robot moves inside the spot area until it detects a border; at this point, the robot decides with a probability that depends on the estimated spot type whether to leave the spot or to remain inside it by performing a U-turn. Within the spot, a robot stops moving and starts to form an aggregate as soon as it perceives one or more other robots evaluating the same spot. When the aggregate reaches a certain size (which is predefined by the experimenter), the spot is collaboratively destroyed and robots resume the exploration of the environment. The achievement of consensus is detected using an external tracking infrastructure, which also emulates the destruction of the spot. The proposed strategy has been derived following a bottom-up, multi-level modeling methodology that encompasses physics-based simulations, chemical reaction networks, and continuous ODE approximation (Mermoud et al., 2010, 2014).

5.1.2.2. Navigation-Based Control Strategies

Navigation-based control strategies allow a swarm of robots to navigate an environment toward one or more regions of interest. Navigation strategies have been extensively studied in the swarm robotics literature. However, not all of them provide a swarm with collective decision-making capabilities. For examples, navigation strategies based on hop-count strategies have been proposed to find the shortest-path connecting a pair of locations (Payton et al., 2001; Szymanski et al., 2006). However, these strategies are incapable of selecting a unique path when there are two or more paths with equal length and thus fail to make a collective decision (Campo et al., 2010b).

Schmickl and Crailsheim (2006) took inspiration from the trophallactic behavior of honeybee swarms, Apis mellifera L. (Camazine et al., 1998), and proposed a virtual gradient and navigation strategy that provides a swarm of robots with collective decision-making capabilities. Trophallaxis refers to the direct, mouth-to-mouth exchange of food between two honeybees (or other social insects). Using the proposed strategy, the authors investigated an aggregation scenario (Schmickl et al., 2007) and a foraging scenario (Schmickl and Crailsheim, 2006, 2008). Robots explore their environment searching for resources (i.e., aggregation spots, foraging patches). Once a robot finds a resource, it loads a certain amount of virtual nectar. As the robot moves in the environment, it spreads and receives virtual nectar to and from other neighboring robots. This behavior allows robots to create a virtual gradient of nectar that can be used by robots to navigate back-and-forth a pair of locations following the shortest of two paths or to orient toward the largest of two aggregation areas. This trophallaxis-inspired strategy has been studied later using models of Brownian motion (Hamann and Wörn, 2008; Hamann, 2010). The authors defined both a Langevin equation (i.e., a microscopic model) to describe the motion of an individual agent and a Fokker–Planck equation (i.e., a macroscopic model) to model the motion of the entire swarm finding a good qualitative agreement with the simulated dynamics of the trophallaxis-inspired strategy.

Garnier et al. (2007b) considered the double-bridge problem and developed a robot control strategy based on a pheromone-laying behavior similar to that used by ants (Goss et al., 1989). During robot experiments, pheromone is emulated by means of an external tracking infrastructure interfaced with a light projector that manages both the laying of pheromone and its evaporation. The robots can perceive pheromone trails by means of a pair of light sensors and can recognize the two target areas by means of IR beacons. In the absence of a trail, a robot moves randomly in the environment avoiding obstacles. When perceiving a trail, the robot starts following the trail and depositing pheromone, which evaporates with an exponential decay. In their study, the authors show that using this strategy the robots of a swarm are capable to make a consensus decision for one of the two paths.

Campo et al. (2010b) proposed a solution to the above limitations of pheromone-inspired mechanisms for the case of chain-based navigation systems. In their work, the robots of the swarm form a pair of chains leading to 2 different locations. Similarly to Garnier et al. (2007b, 2013), the authors proposed a collective decision-making strategy to select the closest of the two locations that is based on virtual pheromones. However, rather than relying on an external infrastructure to emulate pheromone, robots in a chain communicate with their two immediate neighbors in order to form a communication network. The messages exchanged by robots represent virtual ants navigating through the network and depositing virtual pheromone over the nodes of the network (i.e., the robots). Eventually, this navigation strategy leads to the identification and to the selection of the closest location.

Gutiérrez et al. (2009) proposed a navigation strategy called social odometry that allows a robot of a swarm to keep an estimate of its current location with respect to a certain area of interest. A robot has an estimate of its current location and a measure of confidence about its belief that decreases with the traveled distance. Upon encountering a neighboring robot, they both exchange their location estimates and confidence measures. Successively, each of the two robots updates its current location estimate by averaging its current location with that of its neighbor weighted by the respective measures of confidence. Using social odometry, Gutiérrez et al. (2010) studied a foraging scenario characterized by two foraging patches each at a different distance from a central retrieval area. The authors found that the weighted mean underlying social odometry favors the selection by the swarm of the closest foraging patch due to the fact that robots traveling to that patch have higher confidence in their location estimates. Due to the presence of noise, social odometry allows a swarm of robots to find consensus on a common foraging patch also in a symmetric setup, where the two patches are positioned at the same distance from the retrieval area.

5.2. Top-Down Design

5.2.1. Evolutionary Robotics

As for most collective behaviors studied in swarm robotics (Brambilla et al., 2013), collective decision-making systems have also been developed by means of automatic design approaches. The typical automatic design approach is evolutionary robotics (Nolfi and Floreano, 2000; Bongard, 2013), where optimization methods based on evolutionary computation (Back et al., 1997) are used to evolve a population of robot controllers following the Darwinian principles of recombination, mutation, and natural selection. Generally, the individual robot controller is an artificial neural network that maps the sensory perceptions of a robot (i.e., input of the neural network) to appropriate actions of its actuators (i.e., output of the neural network). The parameters of the neural network are evolved to tackle a specific application scenario by opportunely defining a fitness function on a per-case base; the fitness function is then used to evaluate the quality of each controller and to drive the evolutionary optimization process.

Evolutionary robotics has been successfully applied to address a number of collective decision-making scenarios. Trianni and Dorigo (2005) evolved a collective behavior that allows a swarm of physically connected robots to discriminate the type of holes present on the arena surface based on their perceived width and to decide whether to cross the hole (i.e., the hole is sufficiently narrow to be safely crossed) or to avoid it by changing the motion direction (i.e., the hole is too risky to cross). Similarly, Trianni et al. (2007) considered a collective decision-making scenario, where a swarm of robots need to collectively evaluate the surrounding environment and determine whether there are physical obstacles that require cooperation in the form of a self-assembly or, alternatively, if robots can escape obstacles independently of each other.

Francesca et al. (2012, 2014) applied methods from evolutionary robotics to a binary aggregation scenario similar to the one studied in Garnier et al. (2008, 2009), Campo et al. (2010a) but with shelters of equal size (i.e., a symmetry-breaking problem). The authors compared the performance of the evolved controller with theoretical predictions of existing mathematical models (Amé et al., 2006); however, their results show a good agreement between the two models only for a small parameter range.

As shown by the above examples, evolutionary robotics can be successfully applied to the design of collective decision-making systems. However, its use as a design approach suffers of several drawbacks. For example, artificial evolution is a computationally intensive process that needs to be repeated for each newly considered scenario. Artificial evolution may suffer from over-fitting whereby a successfully evolved controller performs well in simulation but poorly on real robots. This phenomenon is also known as the reality gap (Jakobi et al., 1995; Koos et al., 2013). Moreover, artificial evolution does not provide guarantees on the optimality of the resulting robot controller (Bongard, 2013). The robot controller, being ultimately a black-box model, is difficult to model and analyze mathematically (Francesca et al., 2012). As a consequence, in general, the designer cannot maintain and improve the designed solutions (Matarić and Cliff, 1996; Trianni and Nolfi, 2011).

5.2.2. Automatic Modular Design

More recently, Francesca et al. (2014) proposed an automatic design method, called AutoMoDe, that provides a white-box alternative to evolutionary robotics. The robot controllers designed using AutoMoDe are behavior-based and have the form of a probabilistic finite-state machine. Robot controllers are obtained by combining a set of predefined modules (e.g., random walk, phototaxis) using an optimization process that, similarly to evolutionary robotics, is driven by an objective function defined by the designer for each specific scenario.

Using AutoMoDe, Francesca et al. (2014) designed an aggregation strategy for the same scenario as in Garnier et al. (2008, 2009), Campo et al. (2010a). In their experimental setup, the swarm needs to select one of two equally good aggregation spots. The resulting robot controller proceeds as follows. A robot starts in the attraction state in which its goal is to get close to other robots. When perceiving an aggregation spot, the robot stops moving. Once stopped, the robot has a fixed probability for time unit to return to the attraction state and start moving again. Additionally, the robot may transit to the attraction state in the case in which it has been pushed out of the aggregation spot by other robots.

6. Discussion and Conclusion

In this article, our aim was to improve our formal understanding of a given class of problems within swarm robotics. We divided collective decision-making problems in task allocation and consensus achievement, whereby the latter is further divided into discrete and continuous problems. We then focused on discrete consensus achievement. We formally defined the structure of the best-of-n problem and showed how this general framework covers a large number of specific application scenarios. We analyzed and surveyed the literature on discrete consensus achievement from two complementary points of view: the problem structure and the solution design.

In order to analyze the literature with a focus on the structure of the underlying cognitive problem, we first formalized the best-of-n problem. In the best-of-n problem, a swarm of robots is required to make a collective decision about which of a set of n available options offers the best alternative to satisfy its current needs. In the best-of-n problem, each option is characterized by an intrinsic quality and by a cost in terms of time necessary to evaluate that option. Depending on how quality and cost interact with each other, we distinguished between five different variants of the best-of-n problem and defined a problem-oriented taxonomy. Using this taxonomy, we surveyed the literature of swarm robotics and classified research studies according to the considered variant of the best-of-n problem.

As it emerged at the end of Section 4 and perhaps due to their simpler problem structure, the first three variants of the best-of-n problem have been the subject of a large portion of the literature. The first variant is the simplest form of best-of-n problem, whereby options have both equal quality and equal cost (i.e., symmetry-breaking problem), and the objective of the swarm is to make a decision for any of the available options. The second variant is characterized by options of equal quality but with different cost, and the objective of the swarm is to minimize the cost of the chosen option. We saw that, in this case, the environment has a key role in biasing the collective decision and no direct measurement by individual robots is required. In the third variant, options differ in their quality but have the same cost. A collective decision in favor of the best option requires individual robots of the swarm to measure (or sample) the quality of each option and to use this information to bias the collective decision-making process.

Less effort has been put in the study of the last two variants of the best-of-n problem. These two variants have asymmetries in both the option quality and the option cost and their interaction is either synergic or antagonistic. In the fourth variant, the interaction is synergic: options with higher quality have lower costs and the best option has both maximum quality and minimum cost. This is possibly the easiest type of best-of-n problem to solve from the perspective of the swarm because both the environment and the individual robots of the swarm bias the collective decision toward the best option. In the fifth variant, the interaction is antagonistic and the selection by the swarm of the option with highest quality is hindered by its cost. This variant of the best-of-n problem is the most challenging one. Probably because of its difficulty, it is the one that received the least attention from the swarm robotics community. For this reason, we encourage further research to tackle novel application scenarios within this variant of the best-of-n problem.

As discussed in Section 4.6, only a handful of research studies investigated application scenarios requiring the solution of a best-of-n problem with more than n = 2 options. While binary decision-making scenarios simplify the study and analysis of collective decision-making strategies, robot swarms will generally face best-of-n problems with a higher number of options. Moreover, some of the research results reviewed in this paper might not extend to the general case of n > 2 options. For this reason, we encourage further research to develop and study application scenarios characterized by more than 2 options.

In order to analyze the literature with a focus on the designed strategies, we divided research studies in two categories: bottom-up and top-down design approaches. We further organized each category in sub-categories. In the case of bottom-up design, we distinguished between opinion-based approaches and ad hoc control strategies (further organized in aggregation-based and navigation-based strategies). In the case of top-down design, we distinguished between evolutionary robotics and automatic modular design.

Aggregation-based strategies to collective decision-making have the advantage of functioning without the need of communication as they exploit implicit information transfer. However, aggregation as a means of communicating one’s own opinion provides a viable solution only when the options of the best-of-n problem are clearly separated in space from each other, which, as showed in Figure 5B, is not always the case. Similarly, navigation-based strategies can be applied only to scenarios in which the swarm is required to find the shortest-path connecting different locations. In contrast, automatic design approaches as evolutionary robotics and automatic modular design have the potential to be applicable to a larger set of consensus achievement scenarios. Evolutionary robotics, however, suffer from the reality gap between simulated and real robots. Moreover, it is difficult to derive predictive mathematical models for systems designed using artificial evolution. This latter limitation might also affect automatic modular design depending on the complexity of the resulting probabilistic finite-state machines. Opinion-based approaches offer a more general design methodology that can be applied and ported to different application scenarios. This higher level of generality, however, requires explicit information transfer and is obtained at the cost of allowing for robot-to-robot communication.

The work presented in this paper sets the basis for a principled understanding of discrete consensus agreement in robot swarms. The identified structure of the best-of-n problem provides designers with the means to understand, which design requirements characterize a certain application scenario, while the overview of the possible design approaches supports them in the selection of a design solution.

Author Contributions

GV, EF, and MD equally contributed to the conception of the work, to the writing of the paper, and to its critical revision concerning intellectual content. GV performed most of the preliminary bibliographic research.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank S. Garnier, G. Mermoud, and T. Schmickl for giving the permission to reproduce Figures 4B, 5A and 6.

Funding

This work was partially supported by the European Research Council through the ERC Advanced Grant “E-SWARM: Engineering Swarm Intelligence Systems” (contract 246939) to MD. GV acknowledges support from the National Science Foundation (grant 1505048). EF acknowledges support from the Fund for Scientific Research (FWO) Flanders (grant 12N7515N), the DIVINA Challenge Team framework of the Labex MS2T program, supported by the French Government through the program “Investments for the future” and managed by the National Agency for Research (Reference ANR-11-IDEX-0004-02), and the European Regional Development Fund (ERDF) of the Regional Council of Hauts de France. MD acknowledges support from the Belgian F.R.S.-FNRS, of which he is a Research Director.

References

Amé, J.-M., Halloy, J., Rivault, C., Detrain, C., and Deneubourg, J.-L. (2006). Collegial decision making based on social amplification leads to optimal group formation. Proc. Natl. Acad. Sci. U.S.A. 103, 5835–5840. doi: 10.1073/pnas.0507877103

PubMed Abstract | CrossRef Full Text | Google Scholar

Arvin, F., Turgut, A. E., Bazyari, F., Arikan, K. B., Bellotto, N., and Yue, S. (2014). Cue-based aggregation with a mobile robot swarm: a novel fuzzy-based method. Adapt. Behav. 22, 189–206. doi:10.1177/1059712314528009

CrossRef Full Text | Google Scholar

Arvin, F., Turgut, A. E., and Yue, S. (2012). “Fuzzy-based aggregation with a mobile robot swarm,” in Swarm Intelligence, Vol. 7461, eds M. Dorigo, M. Birattari, C. Blum, A. L. Christensen, A. P. Engelbrecht, R. Groß, and T. Stützle (Berlin, Heidelberg: Springer), 346–347.

Google Scholar

Back, T., Fogel, D. B., and Michalewicz, Z. (1997). Handbook of Evolutionary Computation. Bristol, UK: IOP Publishing Ltd.

Google Scholar

Berman, S., Halasz, A., Hsieh, M., and Kumar, V. (2009). Optimized stochastic policies for task allocation in swarms of robots. IEEE Trans. Robot. 25, 927–937. doi:10.1109/TRO.2009.2024997

CrossRef Full Text | Google Scholar

Bernstein, D. S., Givan, R., Immerman, N., and Zilberstein, S. (2002). The complexity of decentralized control of Markov decision processes. Math. Oper. Res. 27, 819–840. doi:10.1287/moor.27.4.819.297

CrossRef Full Text | Google Scholar

Bongard, J. C. (2013). Evolutionary robotics. Commun. ACM 56, 74–83. doi:10.1145/2493883

CrossRef Full Text | Google Scholar

Bowling, M. H., Browning, B., and Veloso, M. M. (2004). “Plays as effective multiagent plans enabling opponent-adaptive play selection,” in Proceedings of the 14th International Conference on Automated Planning & Scheduling (Whistler: AAAI Press), 376–383.

Google Scholar

Brambilla, M., Brutschy, A., Dorigo, M., and Birattari, M. (2014). Property-driven design for robot swarms: a design method based on prescriptive modeling and model checking. ACM Trans. Auton. Adapt. Syst. 9, 17:1–17:28. doi:10.1145/2700318

CrossRef Full Text | Google Scholar

Brambilla, M., Ferrante, E., Birattari, M., and Dorigo, M. (2013). Swarm robotics: a review from the swarm engineering perspective. Swarm Intell. 7, 1–41. doi:10.1007/s11721-012-0075-2

CrossRef Full Text | Google Scholar

Brutschy, A., Scheidler, A., Ferrante, E., Dorigo, M., and Birattari, M. (2012). “Can ants inspire robots?” Self-organized decision making in robotic swarms,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (Piscataway: IEEE Press), 4272–4273.

Google Scholar

Buhl, J., Sumpter, D. J. T., Couzin, I. D., Hale, J. J., Despland, E., Miller, E. R., et al. (2006). From disorder to order in marching locusts. Science 312, 1402–1406. doi:10.1126/science.1125142

PubMed Abstract | CrossRef Full Text | Google Scholar

Calovi, D. S., Lopez, U., Schuhmacher, P., Chaté, H., Sire, C., and Theraulaz, G. (2015). Collective response to perturbations in a data-driven fish school model. J. R. Soc. Interface 12, 20141362. doi:10.1098/rsif.2014.1362

PubMed Abstract | CrossRef Full Text | Google Scholar

Camazine, S., Crailsheim, K., Hrassnigg, N., Robinson, G. E., Leonhard, B., and Kropiunigg, H. (1998). Protein trophallaxis and the regulation of pollen foraging by honey bees (Apis mellifera l.). Apidologie 29, 113–126. doi:10.1051/apido:19980107

CrossRef Full Text | Google Scholar

Camazine, S., Deneubourg, J.-L., Franks, N. R., Sneyd, J., Theraulaz, G., and Bonabeau, E. (2001). Self-Organization in Biological Systems. Princeton, NJ: Princeton University Press.

Google Scholar

Camazine, S., Visscher, P. K., Finley, J., and Vetter, R. S. (1999). House-hunting by honey bee swarms: collective decisions and individual behaviors. Insectes Soc. 46, 348–360. doi:10.1007/s000400050156

CrossRef Full Text | Google Scholar

Campo, A., Garnier, S., Dédriche, O., Zekkri, M., and Dorigo, M. (2010a). Self-organized discrimination of resources. PLoS ONE 6:e19888. doi:10.1371/journal.pone.0019888

CrossRef Full Text | Google Scholar

Campo, A., Gutiérrez, Á, Nouyan, S., Pinciroli, C., Longchamp, V., Garnier, S., et al. (2010b). Artificial pheromone for path selection by a foraging swarm of robots. Biol. Cybern. 103, 339–352. doi:10.1007/s00422-010-0402-x

CrossRef Full Text | Google Scholar

Cao, Y., and Ren, W. (2012). Distributed coordinated tracking with reduced interaction via a variable structure approach. IEEE Trans. Automat. Contr. 57, 33–48. doi:10.1109/TAC.2011.2146830

CrossRef Full Text | Google Scholar

Caprari, G., Estier, T., and Siegwart, R. (2001). Fascination of down scaling – alice the sugar cube robot. J. Micromechatronics 1, 177–189. doi:10.1163/156856301760132097

CrossRef Full Text | Google Scholar

Castellano, C., Fortunato, S., and Loreto, V. (2009). Statistical physics of social dynamics. Rev. Mod. Phys. 81, 591–646. doi:10.1103/RevModPhys.81.591

CrossRef Full Text | Google Scholar

Christensen, A. L., O’Grady, R., and Dorigo, M. (2007). Morphology control in a multirobot system. IEEE Robot. Autom. Mag. 14, 18–25. doi:10.1109/M-RA.2007.908970

CrossRef Full Text | Google Scholar

Conradt, L., and List, C. (2009). Group decisions in humans and animals: a survey. Philos. Trans. R. Soc. Lond. B Biol. Sci. 364, 719–742. doi:10.1098/rstb.2008.0276

PubMed Abstract | CrossRef Full Text | Google Scholar

Correll, N. (2008). “Parameter estimation and optimal control of swarm-robotic systems: a case study in distributed task allocation,” in IEEE International Conference on Robotics and Automation (Piscataway), 3302–3307.

Google Scholar

Correll, N., and Martinoli, A. (2011). Modeling and designing self-organized aggregation in a swarm of miniature robots. Int. J. Robot. Res. 30, 615–626. doi:10.1177/0278364911403017

CrossRef Full Text | Google Scholar

Couzin, I. D., Ioannou, C. C., Demirel, G., Gross, T., Torney, C. J., Hartnett, A., et al. (2011). Uninformed individuals promote democratic consensus in animal groups. Science 334, 1578–1580. doi:10.1126/science.1210280

PubMed Abstract | CrossRef Full Text | Google Scholar

Crespi, V., Galstyan, A., and Lerman, K. (2008). Top-down vs bottom-up methodologies in multi-agent system design. Auton. Robots 24, 303–313. doi:10.1007/s10514-007-9080-5

CrossRef Full Text | Google Scholar

Czirók, A., Barabási, A.-L., and Vicsek, T. (1999). Collective motion of self-propelled particles: kinetic phase transition in one dimension. Phys. Rev. Lett. 82, 209–212. doi:10.1103/PhysRevLett.82.209

CrossRef Full Text | Google Scholar

Czirók, A., and Vicsek, T. (2000). Collective behavior of interacting self-propelled particles. Phys. A Stat. Mech. Appl. 281, 17–29. doi:10.1016/S0378-4371(00)00013-3

CrossRef Full Text | Google Scholar

de Vries, H., and Biesmeijer, J. C. (2002). Self-organization in collective honeybee foraging: emergence of symmetry breaking, cross inhibition and equal harvest-rate distribution. Behav. Ecol. Sociobiol. 51, 557–569. doi:10.1007/s00265-002-0454-6

CrossRef Full Text | Google Scholar

Deneubourg, J.-L., and Goss, S. (1989). Collective patterns and decision-making. Ethol. Ecol. Evol. 1, 295–311. doi:10.1080/08927014.1989.9525500

CrossRef Full Text | Google Scholar

Dorigo, M., Birattari, M., and Brambilla, M. (2014). Swarm robotics. Scholarpedia 9, 1463. doi:10.4249/scholarpedia.1463

CrossRef Full Text | Google Scholar

Dorigo, M., Floreano, D., Gambardella, L. M., Mondada, F., Nolfi, S., Baaboura, T., et al. (2013). Swarmanoid: a novel concept for the study of heterogeneous robotic swarms. IEEE Robot. Autom. Mag. 20, 60–71. doi:10.1109/MRA.2013.2252996

CrossRef Full Text | Google Scholar

Ferrante, E., Turgut, A. E., Huepe, C., Stranieri, A., Pinciroli, C., and Dorigo, M. (2012). Self-organized flocking with a mobile robot swarm: a novel motion control method. Adapt. Behav. 20, 460–477. doi:10.1177/1059712312462248

CrossRef Full Text | Google Scholar

Ferrante, E., Turgut, A. E., Stranieri, A., Pinciroli, C., Birattari, M., and Dorigo, M. (2014). A self-adaptive communication strategy for flocking in stationary and non-stationary environments. Nat. Comput. 13, 225–245. doi:10.1007/s11047-013-9390-9

CrossRef Full Text | Google Scholar

Francesca, G., Brambilla, M., Brutschy, A., Trianni, V., and Birattari, M. (2014). AutoMoDe: a novel approach to the automatic design of control software for robot swarms. Swarm Intell. 8, 89–112. doi:10.1007/s11721-014-0092-4

CrossRef Full Text | Google Scholar

Francesca, G., Brambilla, M., Trianni, V., Dorigo, M., and Birattari, M. (2012). “Analysing an evolved robotic behaviour using a biological model of collegial decision making,” in From Animals to Animats 12, Vol. 7426, eds T. Ziemke, C. Balkenius, and J. Hallam (Berlin, Heidelberg: Springer), 381–390.

Google Scholar

Franks, N. R., Pratt, S. C., Mallon, E. B., Britton, N. F., and Sumpter, D. J. T. (2002). Information flow, opinion polling and collective intelligence in house-hunting social insects. Philos. Trans. R. Soc. Lond. B Biol. Sci. 357, 1567–1583. doi:10.1098/rstb.2002.1066

PubMed Abstract | CrossRef Full Text | Google Scholar

Galam, S. (2008). Sociophysics: a review of Galam models. Int. J. Mod. Phys. C 19, 409–440. doi:10.1142/S0129183108012297

CrossRef Full Text | Google Scholar

Garnier, S., Combe, M., Jost, C., and Theraulaz, G. (2013). Do ants need to estimate the geometrical properties of trail bifurcations to find an efficient route? A swarm robotics test bed. PLoS Comput. Biol. 9:1–12. doi:10.1371/journal.pcbi.1002903

CrossRef Full Text | Google Scholar

Garnier, S., Gautrais, J., Asadpour, M., Jost, C., and Theraulaz, G. (2009). Self-organized aggregation triggers collective decision making in a group of cockroach-like robots. Adapt. Behav. 17, 109–133. doi:10.1177/1059712309103430

CrossRef Full Text | Google Scholar

Garnier, S., Gautrais, J., and Theraulaz, G. (2007a). The biological principles of swarm intelligence. Swarm Intell. 1, 3–31. doi:10.1007/s11721-007-0004-y

CrossRef Full Text | Google Scholar

Garnier, S., Tache, F., Combe, M., Grimal, A., and Theraulaz, G. (2007b). “Alice in pheromone land: an experimental setup for the study of ant-like robots,” in Proceedings of the IEEE Swarm Intelligence Symposium, SIS 2007 (Piscataway), 37–44.

Google Scholar

Garnier, S., Jost, C., Gautrais, J., Asadpour, M., Caprari, G., Jeanson, R., et al. (2008). The embodiment of cockroach aggregation behavior in a group of micro-robots. Artif. Life 14, 387–408. doi:10.1162/artl.2008.14.4.14400

PubMed Abstract | CrossRef Full Text | Google Scholar

Gauci, M., Chen, J., Li, W., Dodd, T. J., and Groß, R. (2014). Self-organized aggregation without computation. Int. J. Robot. Res. 33, 1145–1161. doi:10.1177/0278364914525244

CrossRef Full Text | Google Scholar

Gerkey, B. P., and Matarić, M. J. (2004). A formal analysis and taxonomy of task allocation in multi-robot systems. Int. J. Robot. Res. 23, 939–954. doi:10.1177/0278364904045564

CrossRef Full Text | Google Scholar

Gordon, D. M. (2016). From division of labor to the collective behavior of social insects. Behav. Ecol. Sociobiol. 70, 1101–1108. doi:10.1007/s00265-015-2045-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Goss, S., Aron, S., Deneubourg, J.-L., and Pasteels, J. M. (1989). Self-organized shortcuts in the Argentine ant. Naturwissenschaften 76, 579–581. doi:10.1007/BF00462870

CrossRef Full Text | Google Scholar

Grodzicki, P., and Caputa, M. (2005). Social versus individual behaviour: a comparative approach to thermal behaviour of the honeybee (Apis mellifera L.) and the American cockroach (Periplaneta americana L.). J. Insect Physiol. 51, 315–322. doi:10.1016/j.jinsphys.2005.01.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Gutiérrez, Á., Campo, A., Monasterio-Huelin, F., Magdalena, L., and Dorigo, M. (2010). Collective decision-making based on social odometry. Neural Comput. Appl. 19, 807–823. doi:10.1007/s00521-010-0380-x

CrossRef Full Text | Google Scholar

Gutiérrez, Á., Campo, A., Santos, F., Monasterio-Huelin, F., and Dorigo, M. (2009). Social odometry: imitation based odometry in collective robotics. Int. J. Adv. Robot. Syst. 6, 129–136. doi:10.5772/6794

CrossRef Full Text | Google Scholar

Güzel, M. S., and Kayakökü, H. (2017). “A collective behaviour framework for multi-agent systems,” in Mechatronics and Robotics Engineering for Advanced and Intelligent Manufacturing. Lecture Notes in Mechanical Engineering, eds D. Zhang and B. Wei (Cham: Springer), 61–71.

Google Scholar

Halloy, J., Sempo, G., Caprari, G., Rivault, C., Asadpour, M., Tâche, F., et al. (2007). Social integration of robots into groups of cockroaches to control self-organized choices. Science 318, 1155–1158. doi:10.1126/science.1144259

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamann, H. (2010). Space-Time Continuous Models of Swarm Robotic Systems: Supporting Global-to-Local Programming, Volume 9 of Cognitive Systems Monographs. Berlin, Heidelberg: Springer.

Google Scholar

Hamann, H. (2013). Towards swarm calculus: urn models of collective decisions and universal properties of swarm performance. Swarm Intell. 7, 145–172. doi:10.1007/s11721-013-0080-0

CrossRef Full Text | Google Scholar

Hamann, H., Khaluf, Y., Botev, J., Divband Soorati, M., Ferrante, E., Kosak, O., et al. (2016). Hybrid societies: challenges and perspectives in the design of collective behavior in self-organizing systems. Front. Robot. AI 3:14. doi:10.3389/frobt.2016.00014

CrossRef Full Text | Google Scholar

Hamann, H., Schmickl, T., Wörn, H., and Crailsheim, K. (2012). Analysis of emergent symmetry breaking in collective decision making. Neural Comput. Appl. 21, 207–218. doi:10.1007/s00521-010-0368-6

CrossRef Full Text | Google Scholar

Hamann, H., and Wörn, H. (2008). A framework of space–time continuous models for algorithm design in swarm robotics. Swarm Intell. 2, 209–239. doi:10.1007/s11721-008-0015-3

CrossRef Full Text | Google Scholar

Hatano, Y., and Mesbahi, M. (2005). Agreement over random networks. IEEE Trans. Automat. Contr. 50, 1867–1872. doi:10.1109/TAC.2005.858670

CrossRef Full Text | Google Scholar

Hauert, S., Leven, S., Varga, M., Ruini, F., Cangelosi, A., Zufferey, J. C., et al. (2011). “Reynolds flocking in reality with fixed-wing robots: communication range vs. maximum turning rate,” in Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS 2011 (Piscataway), 5015–5020.

Google Scholar

Hereford, J. M. (2010). “Analysis of a new swarm search algorithm based on trophallaxis,” in IEEE Congress on Evolutionary Computation, CEC (Piscataway: IEEE Press), 1–8.

Google Scholar

Hirokawa, R. Y., and Poole, M. S. (1996). Communication and Group Decision Making. Thousand Oaks: SAGE.

Google Scholar

Holland, O., Woods, J., Nardi, R. D., and Clark, A. (2005). “Beyond swarm intelligence: the ultraswarm,” in Proceedings of the 2005 IEEE Swarm Intelligence Symposium, SIS 2005 (Piscataway), 217–224.

Google Scholar

Jakobi, N., Husbands, P., and Harvey, I. (1995). “Noise and the reality gap: the use of simulation in evolutionary robotics,” in Proceedings of the Third European Conference on Advances in Artificial Life, Vol. 929, eds F. Morán, A. Moreno, J. J. Merelo, and P. Chacón (Berlin, Heidelberg: Springer), 704–720.

Google Scholar

Jandt, J. M., and Gordon, D. M. (2016). The behavioral ecology of variation in social insects. Curr. Opin. Insect Sci. 15, 40–44. doi:10.1016/j.cois.2016.02.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Jeanson, R., Blanco, S., Fournier, R., Deneubourg, J.-L., Fourcassié, V., and Theraulaz, G. (2003). A model of animal movements in a bounded space. J. Theor. Biol. 225, 443–451. doi:10.1016/S0022-5193(03)00277-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Kao, A. B., Miller, N., Torney, C., Hartnett, A., and Couzin, I. D. (2014). Collective learning and optimal consensus decisions in social animal groups. PLoS Comput. Biol. 10:e1003762. doi:10.1371/journal.pcbi.1003762

PubMed Abstract | CrossRef Full Text | Google Scholar

Kernbach, S., Thenius, R., Kernbach, O., and Schmickl, T. (2009). Re-embodiment of honeybee aggregation behavior in an artificial micro-robotic system. Adapt. Behav. 17, 237–259. doi:10.1177/1059712309104966

CrossRef Full Text | Google Scholar

Kitano, H., Asada, M., Kuniyoshi, Y., Noda, I., Osawa, E., and Matsubara, H. (1997). RoboCup: a challenge problem for AI. AI Mag. 18, 73–85.

Google Scholar

Kok, J. R., Spaan, M. T., and Vlassis, N. (2003). “Multi-robot decision making using coordination graphs,” in Proceedings of the 11th International Conference on Advanced Robotics (Piscataway: ICAR), 1124–1129.

Google Scholar

Kok, J. R., and Vlassis, N. (2003). “Distributed decision making of robotic agents,” in Proceedings of the 8th Annual Conference of the Advanced School for Computing and Imaging (Lochem), 318–325.

Google Scholar

Komareji, M., and Bouffanais, R. (2013). Resilience and controllability of dynamic collective behaviors. PLoS One 8:e82578. doi:10.1371/journal.pone.0082578

PubMed Abstract | CrossRef Full Text | Google Scholar

Koos, S., Mouret, J.-B., and Doncieux, S. (2013). The transferability approach: crossing the reality gap in evolutionary robotics. IEEE Trans. Evol. Comput. 17, 122–145. doi:10.1109/TEVC.2012.2185849

CrossRef Full Text | Google Scholar

Kornienko, S., Kornienko, O., Constantinescu, C., Pradier, M., and Levi, P. (2005a). “Cognitive micro-agents: individual and collective perception in microrobotic swarm,” in Proceedings of the IJCAI-05 Workshop on Agents in Real-Time and Dynamic Environments (Edinburgh, UK), 33–42.

Google Scholar

Kornienko, S., Kornienko, O., and Levi, P. (2005b). “Minimalistic approach towards communication and perception in microrobotic swarms,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (Piscataway), 2228–2234.

Google Scholar

Kouvaros, P., and Lomuscio, A. (2016). “Formal verification of opinion formation in swarms,” in Proceedings of the 15th International Conference on Autonomous Agents and Multiagent Systems, AAMAS ’16, eds J. Thangarajah, K. Tuyls, C. Jonker, and S. Marsella (Richland: IFAAMAS), 1200–1208.

Google Scholar

Krapivsky, P. L., and Redner, S. (2003). Dynamics of majority rule in two-state interacting spin systems. Phys. Rev. Lett. 90, 238701. doi:10.1103/PhysRevLett.90.238701

PubMed Abstract | CrossRef Full Text | Google Scholar

Lambiotte, R., Saramäki, J., and Blondel, V. D. (2009). Dynamics of latent voters. Phys. Rev. E Stat. Nonlin. Soft. Matter Phys. 79, 046107. doi:10.1103/PhysRevE.79.046107

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W., Winfield, A. F. T., Sa, J., Chen, J., and Dou, L. (2007). Towards energy optimization: emergent task allocation in a swarm of foraging robots. Adapt. Behav. 15, 289–305. doi:10.1177/1059712307082088

CrossRef Full Text | Google Scholar

Marshall, J. A. R., Bogacz, R., Dornhaus, A., Planqué, R., Kovacs, T., and Franks, N. R. (2009). On optimal decision-making in brains and social insect colonies. J. R. Soc. Interface 6, 1065–1074. doi:10.1098/rsif.2008.0511

PubMed Abstract | CrossRef Full Text | Google Scholar

Massink, M., Brambilla, M., Latella, D., Dorigo, M., and Birattari, M. (2013). On the use of bio-PEPA for modelling and analysing collective behaviours in swarm robotics. Swarm Intell. 7, 201–228. doi:10.1007/s11721-013-0079-6

CrossRef Full Text | Google Scholar

Matarić, M., and Cliff, D. (1996). Challenges in evolving controllers for physical robots. Rob. Auton. Syst. 19, 67–83. doi:10.1016/S0921-8890(96)00034-6

CrossRef Full Text | Google Scholar

Mermoud, G., Matthey, L., Evans, W. C., and Martinoli, A. (2010). “Aggregation-mediated collective perception and action in a group of miniature robots,” in Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems: Volume 2, AAMAS ’10 (Richland: IFAAMAS), 599–606.

Google Scholar

Mermoud, G., Upadhyay, U., Evans, W. C., and Martinoli, A. (2014). “Top-down vs. bottom-up model-based methodologies for distributed control: a comparative experimental study,” in Experimental Robotics, Volume 79 of STAR, eds O. Khatib, V. Kumar, and G. Sukhatme (Berlin, Heidelberg: Springer), 615–629.

Google Scholar

Mesbahi, M., and Egerstedt, M. (2010). Graph Theoretic Methods in Multiagent Networks. Princeton, NJ: Princeton Series in Applied Mathematics. Princeton University Press.

Google Scholar

Mondada, F., Bonani, M., Raemy, X., Pugh, J., Cianci, C., Klaptocz, A., et al. (2009). “The e-puck, a robot designed for education in engineering,” in Proceedings of the 9th Conference on Autonomous Robot Systems and Competitions, Vol. 1, eds P. J. S. Gonçalves, P. J. D. Torres, and C. M. O. Alves (Castelo Branco: IPCB: Instituto Politécnico de Castelo Branco), 59–65.

Google Scholar

Montes de Oca, M. A., Ferrante, E., Scheidler, A., Pinciroli, C., Birattari, M., and Dorigo, M. (2011). Majority-rule opinion dynamics with differential latency: a mechanism for self-organized collective decision-making. Swarm Intell. 5, 305–327. doi:10.1007/s11721-011-0062-z

CrossRef Full Text | Google Scholar

Montes de Oca, M. A., Ferrante, E., Scheidler, A., and Rossi, L. F. (2013). “Binary consensus via exponential smoothing,” in Complex Sciences, Volume 126 of LNICST, eds K. Glass, R. Colbaugh, P. Ormerod, and J. Tsao (Cham: Springer), 244–255.

Google Scholar

Moscovici, S., and Zavalloni, M. (1969). The group as a polarizer of attitudes. J. Pers. Soc. Psychol. 12, 125–135. doi:10.1037/h0027568

CrossRef Full Text | Google Scholar

Nembrini, J., Winfield, A., and Melhuish, C. (2002). “Minimalist coherent swarming of wireless networked autonomous mobile robots,” in Proceedings of the Seventh International Conference on Simulation of Adaptive Behavior: From Animals to Animats, ICSAB (Cambridge: MIT Press), 373–382.

Google Scholar

Nolfi, S., and Floreano, D. (2000). Evolutionary Robotics. The Biology, Intelligence, and Technology of Self-Organizing Machines. Cambridge, MA: MIT Press.

Google Scholar

Okubo, A. (1986). Dynamical aspects of animal grouping: swarms, schools, flocks, and herds. Adv. Biophys. 22, 1–94. doi:10.1016/0065-227X(86)90003-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Olfati-Saber, R., Fax, J. A., and Murray, R. M. (2007). Consensus and cooperation in networked multi-agent systems. Proc. IEEE 95, 215–233. doi:10.1109/JPROC.2006.887293

CrossRef Full Text | Google Scholar

Parker, C. A. C., and Zhang, H. (2009). Cooperative decision-making in decentralized multiple-robot systems: the best-of-n problem. IEEE/ASME Trans. Mechatron. 14, 240–251. doi:10.1109/TMECH.2009.2014370

CrossRef Full Text | Google Scholar

Parker, C. A. C., and Zhang, H. (2010). Collective unary decision-making by decentralized multiple-robot systems applied to the task-sequencing problem. Swarm Intell. 4, 199–220. doi:10.1007/s11721-010-0042-8

CrossRef Full Text | Google Scholar

Parker, C. A. C., and Zhang, H. (2011). Biologically inspired collective comparisons by robotic swarms. Int. J. Robot. Res. 30, 524–535. doi:10.1177/0278364910397621

CrossRef Full Text | Google Scholar

Payton, D., Daily, M., Estowski, R., Howard, M., and Lee, C. (2001). Pheromone robotics. Auton. Robots 11, 319–324. doi:10.1023/A:1012411712038

CrossRef Full Text | Google Scholar

Pinter-Wollman, N., Bala, A., Merrell, A., Queirolo, J., Stumpe, M. C., Holmes, S., et al. (2013). Harvester ants use interactions to regulate forager activation and availability. Anim. Behav. 86, 197–207. doi:10.1016/j.anbehav.2013.05.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Pynadath, D. V., and Tambe, M. (2002). The communicative multiagent team decision problem: analyzing teamwork theories and models. J. Artif. Intell. Res. 16, 389–423. doi:10.1613/jair.1024

CrossRef Full Text | Google Scholar

Reid, C. R., Garnier, S., Beekman, M., and Latty, T. (2015). Information integration and multiattribute decision making in non-neuronal organisms. Anim. Behav. 100, 44–50. doi:10.1016/j.anbehav.2014.11.010

CrossRef Full Text | Google Scholar

Reina, A., Miletitch, R., Dorigo, M., and Trianni, V. (2015a). A quantitative micro-macro link for collective decisions: the shortest path discovery/selection example. Swarm Intell. 9, 75–102. doi:10.1007/s11721-015-0105-y

CrossRef Full Text | Google Scholar

Reina, A., Valentini, G., Fernández-Oto, C., Dorigo, M., and Trianni, V. (2015b). A design pattern for decentralised decision making. PLoS ONE 10:e0140950. doi:10.1371/journal.pone.0140950

CrossRef Full Text | Google Scholar

Ren, W., and Beard, R. W. (2008). Distributed Consensus in Multi-Vehicle Cooperative Control: Theory and Applications. London, UK: Communications and Control Engineering. Springer.

Google Scholar

Ren, W., Beard, R. W., and Atkins, E. M. (2005). “A survey of consensus problems in multi-agent coordination,” in Proceedings of the 2005 American Control Conference, Vol. 3 (Piscataway: IEEE Press), 1859–1864.

Google Scholar

Rendell, L., Boyd, R., Cownden, D., Enquist, M., Eriksson, K., Feldman, M. W., et al. (2010). Why copy others? Insights from the social learning strategies tournament. Science 328, 208–213. doi:10.1126/science.1184719

PubMed Abstract | CrossRef Full Text | Google Scholar

Reynolds, C. W. (1987). Flocks, herds and schools: a distributed behavioral model. ACM SIGGRAPH Comput. Graph. 21, 25–34. doi:10.1145/37402.37406

CrossRef Full Text | Google Scholar

Sartoretti, G., Hongler, M.-O., de Oliveira, M., and Mondada, F. (2014). Decentralized self-selection of swarm trajectories: from dynamical systems theory to robotic implementation. Swarm Intell. 8, 329–351. doi:10.1007/s11721-014-0101-7

CrossRef Full Text | Google Scholar

Savkin, A. V., and Teimoori, H. (2010). Decentralized navigation of groups of wheeled mobile robots with limited communication. Trans. Robot. 26, 1099–1104. doi:10.1109/TRO.2010.2081430

CrossRef Full Text | Google Scholar

Scheidler, A. (2011). Dynamics of majority rule with differential latencies. Phys. Rev. E Stat. Nonlin. Soft. Matter Phys. 83, 031116. doi:10.1103/PhysRevE.83.031116

PubMed Abstract | CrossRef Full Text | Google Scholar

Scheidler, A., Brutschy, A., Ferrante, E., and Dorigo, M. (2016). The k-unanimity rule for self-organized decision-making in swarms of robots. IEEE Trans. Cybern. 46, 1175–1188. doi:10.1109/TCYB.2015.2429118

PubMed Abstract | CrossRef Full Text | Google Scholar

Scheutz, M., and Andronache, V. (2004). Architectural mechanisms for dynamic changes of behavior selection strategies in behavior-based systems. IEEE Trans. Syst. Man Cybern. B Cybern. 34, 2377–2395. doi:10.1109/TSMCB.2004.837309

PubMed Abstract | CrossRef Full Text | Google Scholar

Schizas, I., Giannakis, G., Roumeliotis, S., and Ribeiro, A. (2008a). Consensus in ad hoc WSNs with noisy links – part II: distributed estimation and smoothing of random signals. IEEE Trans. Signal Process. 56, 1650–1666. doi:10.1109/TSP.2007.908943

CrossRef Full Text | Google Scholar

Schizas, I., Ribeiro, A., and Giannakis, G. (2008b). Consensus in ad hoc WSNs with noisy links – part I: distributed estimation of deterministic signals. IEEE Trans. Signal Process. 56, 350–364. doi:10.1109/TSP.2007.906734

CrossRef Full Text | Google Scholar

Schmickl, T., and Crailsheim, K. (2006). “Trophallaxis among swarm-robots: a biologically inspired strategy for swarm robotics,” in The First IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics, BioRob 2006 (Piscataway), 377–382.

Google Scholar

Schmickl, T., and Crailsheim, K. (2008). Trophallaxis within a robotic swarm: bio-inspired communication among robots in a swarm. Auton. Robots 25, 171–188. doi:10.1007/s10514-007-9073-4

CrossRef Full Text | Google Scholar

Schmickl, T., Hamann, H., Wörn, H., and Crailsheim, K. (2009a). Two different approaches to a macroscopic model of a bio-inspired robotic swarm. Rob. Auton. Syst. 57, 913–921. doi:10.1016/j.robot.2009.06.002

CrossRef Full Text | Google Scholar

Schmickl, T., Thenius, R., Moeslinger, C., Radspieler, G., Kernbach, S., Szymanski, M., et al. (2009b). Get in touch: cooperative decision making based on robot-to-robot collisions. Auton. Agents Multi Agent Syst. 18, 133–155. doi:10.1007/s10458-008-9058-5

CrossRef Full Text | Google Scholar

Schmickl, T., Möslinger, C., and Crailsheim, K. (2007). “Collective perception in a robot swarm,” in Swarm Robotics, Volume 4433 of LNCS, eds E. Şahin, W. M. Spears, and A. F. Winfield (Berlin, Heidelberg: Springer), 144–157.

Google Scholar

Seeley, T. D., Visscher, P. K., Schlegel, T., Hogan, P. M., Franks, N. R., and Marshall, J. A. R. (2012). Stop signals provide cross inhibition in collective decision-making by honeybee swarms. Science 335, 108–111. doi:10.1126/science.1210361

PubMed Abstract | CrossRef Full Text | Google Scholar

Shang, Y., and Bouffanais, R. (2014). Influence of the number of topologically interacting neighbors on swarm dynamics. Sci. Rep. 4, 4184E. doi:10.1038/srep04184

PubMed Abstract | CrossRef Full Text | Google Scholar

Soysal, O., and Şahin, E. (2007). “A macroscopic model for self-organized aggregation in swarm robotic systems,” in Swarm Robotics, Volume 4433 of LNCS, eds E. Şahin, W. M. Spears, and A. F. T. Winfield (Berlin, Heidelberg: Springer), 27–42.

Google Scholar

Spears, W. M., Spears, D. F., Hamann, J. C., and Heil, R. (2004). Distributed, physics-based control of swarms of vehicles. Auton. Robots 17, 137–162. doi:10.1023/B:AURO.0000033970.96785.f2

CrossRef Full Text | Google Scholar

Strandburg-Peshkin, A., Farine, D. R., Couzin, I. D., and Crofoot, M. C. (2015). Shared decision-making drives collective movement in wild baboons. Science 348, 1358–1361. doi:10.1126/science.aaa5099

CrossRef Full Text | Google Scholar

Sumpter, D. J. T. (2010). Collective Animal Behavior. Princeton, NJ: Princeton University Press.

Google Scholar

Szabó, B., Szöllösi, G. J., Gönci, B., Jurányi, Z., Selmeczi, D., and Vicsek, T. (2006). Phase transition in the collective migration of tissue cells: experiment and model. Phys. Rev. E Stat. Nonlin. Soft. Matter Phys. 74, 061908. doi:10.1103/PhysRevE.74.061908

PubMed Abstract | CrossRef Full Text | Google Scholar

Szymanski, M., Breitling, T., Seyfried, J., and Wörn, H. (2006). “Distributed shortest-path finding by a micro-robot swarm,” in Ant Colony Optimization and Swarm Intelligence, Volume 4150 of LNCS, eds M. Dorigo, L. M. Gambardella, M. Birattari, A. Martinoli, R. Poli, and T. Stützle (Berlin, Heidelberg: Springer), 404–411.

Google Scholar

Trianni, V., Ampatzis, C., Christensen, A. L., Tuci, E., Dorigo, M., and Nolfi, S. (2007). “From solitary to collective behaviours: decision making and cooperation,” in Advances in Artificial Life, Volume 4648 of LNCS, eds F. Almeida Costa, L. M. Rocha, E. Costa, I. Harvey, and A. Coutinho (Berlin, Heidelberg: Springer), 575–584.

Google Scholar

Trianni, V., and Dorigo, M. (2005). “Emergent collective decisions in a swarm of robots,” in Proceedings of the IEEE Swarm Intelligence Symposium, SIS 2005 (Piscataway: IEEE Press), 241–248.

Google Scholar

Trianni, V., Groß, R., Labella, T. H., Şahin, E., and Dorigo, M. (2003). “Evolving aggregation behaviors in a swarm of robots,” in Advances in Artificial Life, Volume 2801 of LNCS, eds W. Banzhaf, J. Ziegler, T. Christaller, P. Dittrich, and J. T. Kim (Berlin, Heidelberg: Springer), 865–874.

Google Scholar

Trianni, V., and Nolfi, S. (2011). Engineering the evolution of self-organizing behaviors in swarm robotics: a case study. Artif. Life 17, 183–202. doi:10.1162/artl_a_00031

PubMed Abstract | CrossRef Full Text | Google Scholar

Turgut, A. E., Çelikkanat, H., Gökçe, F., and Şahin, E. (2008). Self-organized flocking in mobile robot swarms. Swarm Intell. 2, 97–120. doi:10.1007/s11721-008-0016-2

CrossRef Full Text | Google Scholar

Valentini, G., Birattari, M., and Dorigo, M. (2013). “Majority rule with differential latency: an absorbing Markov chain to model consensus,” in Proceedings of the European Conference on Complex Systems 2012, eds T. Gilbert, M. Kirkilionis, and G. Nicolis (Cham: Springer), 651–658.

Google Scholar

Valentini, G., Brambilla, D., Hamann, H., and Dorigo, M. (2016a). “Collective perception of environmental features in a robot swarm,” in Swarm Intelligence, Volume 9882 of LNCS, eds M. Dorigo, M. Birattari, X. Li, M. López-Ibáñez, K. Ohkura, C. Pinciroli, and T. Stützle (Cham: Springer), 65–76.

Google Scholar

Valentini, G., Ferrante, E., Hamann, H., and Dorigo, M. (2016b). Collective decision with 100 kilobots: speed versus accuracy in binary discrimination problems. Auton. Agents Multi Agent Syst. 30, 553–580. doi:10.1007/s10458-015-9323-3

CrossRef Full Text | Google Scholar

Valentini, G., Hamann, H., and Dorigo, M. (2014). “Self-organized collective decision making: the weighted voter model,” in Proceedings of the 13th International Conference on Autonomous Agents and Multiagent Systems, AAMAS ’14, eds A. Lomuscio, P. Scerri, A. Bazzan, and M. Huhns (Richland: IFAAMAS), 45–52.

Google Scholar

Valentini, G., Hamann, H., and Dorigo, M. (2015). “Efficient decision-making in a self-organizing robot swarm: on the speed versus accuracy trade-off,” in Proceedings of the 14th International Conference on Autonomous Agents and Multiagent Systems, AAMAS ’15, eds R. Bordini, E. Elkind, G. Weiss, and P. Yolum (Richland: IFAAMAS), 1305–1314.

Google Scholar

Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I., and Shochet, O. (1995). Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 75, 1226–1229. doi:10.1103/PhysRevLett.75.1226

CrossRef Full Text | Google Scholar

Vicsek, T., and Zafeiris, A. (2012). Collective motion. Phys. Rep. 517, 71–140. doi:10.1016/j.physrep.2012.03.004

CrossRef Full Text | Google Scholar

Wessnitzer, J., and Melhuish, C. (2003). “Collective decision-making and behaviour transitions in distributed ad hoc wireless networks of mobile robots: target-hunting,” in Advances in Artificial Life, Volume 2801 of LNCS, eds W. Banzhaf, J. Ziegler, T. Christaller, P. Dittrich, and J. T. Kim (Berlin, Heidelberg: Springer), 893–902.

Google Scholar

Yates, C. A., Erban, R., Escudero, C., Couzin, I. D., Buhl, J., Kevrekidis, I. G., et al. (2009). Inherent noise can facilitate coherence in collective swarm motion. Proc. Natl. Acad. Sci. U.S.A. 106, 5464–5469. doi:10.1073/pnas.0811195106

PubMed Abstract | CrossRef Full Text | Google Scholar