- 1Center for Computer Games Research, IT University of Copenhagen, Copenhagen, Denmark
- 2Department of Computer Science, University of Southern California, Los Angeles, CA, USA
- 3Department of EECS, University of Central Florida, Orlando, FL, USA
An ambitious goal in evolutionary robotics (ER) is to evolve increasingly complex robotic behaviors with minimal human design effort. Reaching this goal requires evolutionary algorithms that can unlock from genetic encodings their latent potential for evolvability. One issue clouding this goal is conceptual confusion about evolvability that often obscures important or desirable aspects of evolvability. The danger from such confusion is that it may establish unrealistic goals for evolvability that prove unproductive in practice. An important issue separate from conceptual confusion is the common misalignment between selection and evolvability in ER. While more expressive encodings can represent higher-level adaptations (e.g. sexual reproduction or developmental systems) that increase long-term evolutionary potential (i.e. evolvability), realizing such potential requires gradients of fitness and evolvability to align. In other words, selection is often a critical factor limiting increasing evolvability. Thus, drawing from a series of recent papers, this article seeks to both (1) clarify and focus the ways in which the term evolvability is used within artificial evolution and (2) argue for the importance of one type of selection, i.e. divergent selection, for enabling evolvability. The main argument is that there is a fundamental connection between divergent selection and evolvability (on both the individual and population level) that does not hold for typical goal-oriented selection. The conclusion is that selection pressure plays a critical role in realizing the potential for evolvability and that divergent selection in particular provides a principled mechanism for encouraging evolvability in artificial evolution.
1. Introduction
Natural evolution is an unguided process that has produced organisms with functionalities far exceeding the products of current human engineering. Although biological evolution is well studied, the abstract mechanisms through which cascades of increasingly complex functionalities evolve are not deeply understood. Supporting this claim, artificial evolutionary processes so far cannot reproduce biological levels of behavioral complexity.
This problem is well known within the evolutionary robotics (ER) community, given its aim to create complex robotic behaviors through algorithmic evolution. Note that while this paper focuses on ER, the insights likely generalize to many applications of evolutionary algorithms (EAs) beyond the black box setting (Doncieux and Mouret, 2014); for this reason, the term EA assumes domains in which observable behavior results from an evaluation. While ER’s aims are ambitious, in practice evolved behaviors have remained simple relative to biological organisms, and ER does not compete commercially with mainstream robotics approaches. Thus, it is natural to seek the cause of the qualitative gulf between natural organisms and ER’s current products. One hypothesis is that evolvability, i.e. the speed of evolutionary innovation, stagnates in ER systems, whereas in biological evolution, second-order mechanisms (e.g. sexual reproduction or developmental systems) often evolve that accelerate innovation.
Accordingly, this paper argues that an important limiting factor in ER is bounded evolvability, which manifests on different structural levels. First, there are limits to the evolvability possible to attain within particular ER models, because the search space does not contain certain possibilities. For example, most encodings do not enable an organism to influence how its offspring are generated, even if such influence could increase evolvability. Second, there are limits in practice to what levels of evolvability will be attained, given how the chosen environment, form of selection pressure, and encoding interact. In particular, because the gradients of task performance and evolvability often fail to align conveniently, selection may prune hereditary pathways that lead to increased evolvability. This paper focuses on this latter factor, because while there exist many interesting proposals for more expressive encodings (Spector and Robinson, 2002; Risi et al., 2010; Lehman and Stanley, 2011b), in practice realizing their potential for evolvability remains difficult (Edmonds, 2001; Spector and Robinson, 2002; Clune et al., 2008). The position taken here is that this challenge largely results from applying selection pressure uncorrelated with evolvability.
A further issue is that the term evolvability is defined across ER studies in disjoint and conflicting ways, which conflates distinct concepts. The result is confusion over what challenges evolvability poses for ER and even over what outcomes are most desirable or possible. One particular source of confusion addressed here concerns the level of organization (e.g. the level of the individual or the population) in which it is most important to consider and encourage evolvability.
To address such confusion, this paper aggregates from an ongoing research agenda (Lehman and Stanley, 2011b; Wilder and Stanley, 2015) one coherent vision of evolvability. Rather than focus on an individual’s hereditary potential to achieve particular goals, the idea is to encourage the population’s hereditary potential for creative divergence. The argument is that this conception of evolvability is more realistic and productive than alternative visions, and that it aligns well with researchers’ expectations of ER and intuitions about natural evolution’s creativity.
Viewing evolvability from this perspective of accelerating creativity has consequences for algorithm design. In particular, this paper argues that divergent selection, i.e. selection that encourages simultaneous exploration of diverse solutions, aligns systematically with this type of evolvability; in contrast, more traditional objective-based selection, i.e. selection for improving objective performance, has no such consistent alignment. Thus, to create more prolific ER algorithms may require increasing the potential for evolvability in encodings, focusing on population-level evolvability instead of on individual-level evolvability, and guiding search through divergent selection.
2. Evolvability in Evolutionary Robotics
Because evolutionary computation (EC) as a whole struggles with evolvability (Wagner and Altenberg, 1996; Reisinger et al., 2005; Hu and Banzhaf, 2010), the subfield of ER naturally confronts the same issue (Lehman and Stanley, 2011b; Tarapore and Mouret, 2015). A distracting complication when discussing or quantifying evolvability is the lack of consensus on evolvability’s definition across biology (Pigliucci, 2008), EC in general (Altenberg, 1994; Reisinger et al., 2005), or ER in particular (Lehman and Stanley, 2011b; Tarapore and Mouret, 2015).
Overall, evolvability definitions largely can be divided into two main families. One focuses on the ability to respond to particular adaptive challenges (Reisinger et al., 2005; Pigliucci, 2008; Clune et al., 2013), while the other focuses more generally on future creative potential, i.e. the variety of phenotypes reachable from an individual or population (Wagner and Altenberg, 1996; Dichtel-Danjoy and Félix, 2004; Lehman and Stanley, 2011b). Encompassing these narrower viewpoints, a larger-scale conception of evolvability is the ability to create major phenotypic, behavioral, or morphological breakthroughs (Pigliucci, 2008), e.g. the de novo evolution of a developmental system. A unifying point is that this kind of large-scale evolvability is evident in natural evolution and is what researchers ultimately aspire to recreate. The hope is that studying and learning how to encourage lower levels of evolvability may aid this latter pursuit.
Such plurality of definitions is not inherently problematic; evolvability as an overarching concept may simply take on different meanings when considered across different functional goals (e.g. whether privileging adaptation to a specific target or potential for founding new niches through creative divergence) or levels of organization (e.g. whether considered over individuals, populations, or species) (Pigliucci, 2008). Thus, rather than absolute truth, the choice of evolvability definition may instead reflect the aims of a particular research agenda. That is, if one hopes to create an ER algorithm that directly solves any ambitious problem through optimization, the most fitting characterization of evolvability may be one aligned with increasing the value of a static fitness function. Yet when adopting a particular definition and devising a measure of it for ER, it is important that the resulting measure still respects what is ultimately realistic or possible. The measure can then identify limitations in current algorithms and highlight possible improvements, in service of a particular research agenda.
However, some overarching aims of ER may be more realistic than others. For example, while the optimization-based abstraction of evolution has long dominated ER (Lehman and Stanley, 2010), growing evidence suggests that such an approach is misaligned with how ambitious objectives are actually achieved (Doncieux and Mouret, 2014; Stanley and Lehman, 2015) and does not scale in practice (Lehman and Stanley, 2011c; Lehman et al., 2013; Nguyen et al., 2015). Thus, viewing evolvability through the lens of optimization (i.e. evolvability as the potential for solving particular adaptive challenges) may draw focus to desirable but ultimately unrealistic goals, like the design of an algorithm that can successfully optimize toward any arbitrarily complex robotic behavior. So while defining evolvability this way is valid, it may not fruitfully steer ER research.
In contrast, this paper instead frames evolvability by considering ER’s most ambitious creative goals (i.e. evolvability as future creative potential) where creativity is defined here as the ability to create novel functionally complex artifacts. The argument is that framing evolvability this way draws focus to more realistic goals, because it better reflects how complex behaviors evolve in practice. That is, evolution does not craft highly complex functionalities because such behaviors are an explicit engineering objective, but instead cobbles them together through opportunistic tinkering (Jacob, 1977). Indeed, according to one mainstream biological opinion, complexity in biological evolution results from exploratory diffusion through the space of complexity rather than from any pervasive selective advantage that such complexity provides (Miconi, 2008; McShea and Brandon, 2010; Gould, 2011; Stanley and Lehman, 2015). In this view, complex behavior emerges as evolution creatively expands through a growing space of ecological niches (Kauffman, 2000; Schluter, 2000; Kelly, 2010), driven by opportunistic exaptation (Gould and Vrba, 1982) or ecological pressures toward diversity such as competitive exclusion (Hardin, 1960). Empirically, this understanding is supported by studies showing that complex functionalities fail to evolve without the scaffolding of functionally simpler niches (Lenski et al., 2003; Arthur and Polak, 2004), that bacteria colonies tend naturally to generate and maintain vast phenotypic diversity (Saint-Ruf et al., 2014), and that biodiversity begets further biodiversity (Jousset et al., 2016). Furthermore, viewing evolution as an open-ended creative process aligns with a similar understanding of cultural processes such as technological growth (Arthur, 2009; Kelly, 2010; Stanley and Lehman, 2015). Thus, if evolution’s productivity largely derives from its capacity to diverge creatively, then accelerating such capacity is a logical aim for ER. This paper accordingly argues for measuring and encouraging evolvability as the potential for creative divergence, while acknowledging that other views may better fit alternative research agendas.
One representative such measure of divergent potential is to quantify the phenotypic variability of an individual (Dichtel-Danjoy and Félix, 2004; Pigliucci, 2008), i.e. the phenotypic diversity accessible within an individual’s mutational neighborhood. This measure is used in practice (Lehman and Stanley, 2011b) and captures an important facet of an individual’s potential for creative divergence. However, as explored in the next section, such individual-level focus neglects the greater possibilities enabled by considering the population as a whole (Wilder and Stanley, 2015).
3. Evolvability of Populations and Individuals
When evolvability is measured and encouraged in ER, most often it is considered a property of an individual (Clune et al., 2013; Lehman and Stanley, 2013; Velez and Clune, 2014), often aggregated across the population by taking the mean or maximum value. However, simple aggregations obscure important properties unique to the population level, such as to what extent the population contains a complementary diversity of evolvable individuals. An alternative approach is to consider evolvability explicitly as a property of a population (Wilder and Stanley, 2015). For example, one such measure is the diversity of phenotypes accessible within the mutational neighborhood of all individuals in the population.
Both conceptions are logically consistent, but they imply different goals for ER. That is, benchmarking methods by their production of individual-level evolvability sets the implicit goal of producing maximally evolvable individuals. Even if individual evolvability is aggregated over the population by considering mean or maximum evolvability, both common aggregations can be maximized by a population converged to a single maximally evolvable individual. In contrast, benchmarking on population-level evolvability stresses the need for maximally evolvable populations, which may result from a diversity of individuals with complementary and specialized evolutionary potentials.
The fundamental problem with guiding ER by individual-level evolvability stems from the logical conclusion of its maximization. For evolvability measures focused on adapting to new goals, maximization requires an individual that can very quickly evolve to achieve any possible goal. For evolvability measures focused on creative potential, maximization requires an individual who can quickly lead to any possible phenotype. While such outcomes are certainly desirable, neither of these extreme visions are realistic nor do they reflect intuitions about terrestrial evolvability.
To highlight the benefits of population-level evolvability for ER, consider two controllers for a biped robot, one that locomotes with a one-legged hop and the other that uses both legs to achieve a smooth walking gait. To achieve their distinct gaits, both controllers contain specialized knowledge and thus are only locally evolvable, e.g. mutating the hopping controller yields many hopping gait variations, while mutating the walking controller likewise generates many variations of walking. Through the lens of individual-level evolvability, if both controllers had equivalent quantities of evolvability, there is no preference to preserve both in a population. In contrast, population-level evolvability recognizes the greater span of evolutionary potential when the hopper and the walker are both viable leaping-off points (see Figure 1).
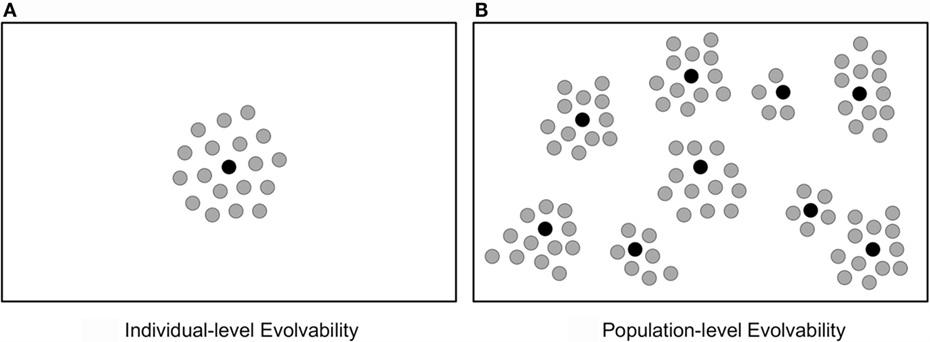
Figure 1. Encouraging evolvability on different levels of organization. Both figures show an abstract space of phenotypes, where black circles indicate individuals and gray circles indicate phenotypes accessible within an individual’s mutational neighborhood. Thus, a more expansive radius of gray circles indicates a more evolvable individual. When considering (A) individual-level evolvability, its maximization is achieved by a single highly evolvable individual. However, when considering (B) population-level evolvability, its maximization is achieved by accumulating a diversity of complementarily evolvable individuals. In this way, encouraging population-level evolvability is a more productive goal, because a broader set of phenotypes can be reached through mutations of the resulting population than through mutations of any singularly evolvable individual.
In this way, population-level evolvability may be a more principled guiding light for ER than individual-level evolvability. As a result, increased focus on population-level evolvability may have implications for improving the design and creativity of ER algorithms and may illuminate promising research trajectories. In this spirit, the next section argues that divergent selection is an important algorithmic feature for cultivating such population-level evolvability.
4. Divergent Selection and Evolvability
One necessary condition for the evolution of evolvability is that selection must encourage (or at minimum, not oppose) trajectories through the search space leading to evolvable genotypes. Even if highly evolvable individuals exist within the search space, they are unlikely to be discovered if selection and evolvability are completely decorrelated. Just as degeneracy is over-represented relative to functionality within complex search spaces (i.e. a mutation more often causes catastrophe than novel functionality), there is no reason to expect an arbitrary genome to be highly evolvable. Thus it is important to explore the relationship between different forms of selection pressure and evolvability. Note that a similar argument related to the evolution of complexity is provided by Miconi (2008).
The dominant form of selection pressure in ER is objective-based fitness: a heuristic measure of progress to some fixed objective. Search driven to optimize such a measure often converges, because as the population’s fitness rises the set of admissible improvements shrinks. This objective-based perspective derives from abstracting natural evolution as an optimization process (Lehman and Stanley, 2011a), i.e. from considering optimization as the key ingredient that enables impressive evolutionary products.
One might intuitively assume that evolvability will naturally increase with objective-based selection, because increased evolvability will hitchhike as a byproduct of selecting the adaptations such evolvability enables. That is, an evolvable individual will be more likely than an unevolvable one to produce useful adaptions (i.e. increases in fitness); therefore, evolvability will consistently be favored as a result of selecting high-fitness individuals. However, this intuition does not hold up to closer scrutiny or empirical studies (Lehman and Stanley, 2011b).
First, there is no necessary logical connection between narrowly increasing fitness and long-term potential. For example, in ER there may be many genomes with varying evolvability that express the same high-fitness behavior (e.g. a low-evolvability memorized list of motor commands vs. a higher evolvability generic wall following policy); yet short-term fitness optimization cannot distinguish between them. For more evolvable lineages to reliably distinguish themselves requires competition between sufficiently different lineages with differing potentials. Yet maintaining such diversity is in direct tension with objective-based selection’s tendency to converge. As a result, in most EAs an adaptation quickly propagates throughout the population, regardless if other reachable adaptations hold greater future potential.
A second more fundamental problem results from deception, i.e. the tendency in objective-based search for short-term fitness increases to themselves anticorrelate with long-term potential; such deception seems to increase in frequency and severity as problems scale in complexity (Zaera et al., 1996; Ficici and Pollack, 1998; Lehman and Stanley, 2011c; Stanley and Lehman, 2015). When objective-based fitness is itself a broken compass, then even if lineage-level selection could lead to evolutionary acceleration, the end effect would only be faster discovery of an ultimately unsatisfactory local optimum.
An alternative to objective-driven search is to explicitly abstract evolution as a creative process, reflecting that a key characteristic of biological evolution is its divergent accumulation of novelty. Practical examples of such selection in EAs are given by novelty search (Lehman and Stanley, 2011a), behavioral diversity (Mouret and Doncieux, 2012), and MAP-Elites (Mouret and Clune, 2015). In such algorithms, novelty or divergence is directly selected for, serving as a proxy for important creative processes in biology that are overlooked when evolution is treated only as an optimizer, e.g. negative frequency-dependent selection (Endler and Greenwood, 1988) and adaptive radiation (Schluter, 2000).
In contrast to objective-driven search, a consistent relationship often holds between divergent selection and evolvability (Lehman and Stanley, 2011b, 2013; Lehman and Miikkulainen, 2015; Wilder and Stanley, 2015; Mengistu et al., 2016). Importantly, unlike with static measures of progress, measures of divergence are relative to the current and past states of the search process. As a result, seeking divergence is self-defeating in a way that pursuing a fixed goal is not (see Figure 2). When objective-driven search is stuck within a local optimum, a high-fitness individual retains such fitness indefinitely; selection in such cases is antagonistic to evolvability, because phenotypic deviations are overwhelmingly unlikely to be adaptive. However, with divergent selection, a lineage must continually innovate to remain novel. Thus there is consistent pressure to diverge, meaning mechanisms that enhance the ability to diverge can hitchhike along with the divergences they enable. Furthermore, because divergent algorithms like novelty search and MAP-Elites are designed to simultaneously maintain many distinct lineages (Lehman et al., 2012; Gomes et al., 2015; Nguyen et al., 2015), evolvable lineages can therefore distinguish themselves by consistently producing novelty. In this way, divergent selection systematically aligns with evolvability. Note that the choice of how to measure divergence will significantly impact the evolvability generated by a divergent EA, similarly to how such choice significantly impacts algorithmic performance (Mouret and Doncieux, 2012; Doncieux and Mouret, 2013); how to best align behavioral distance metrics with evolvability without relying on human domain expertise remains an open research question.
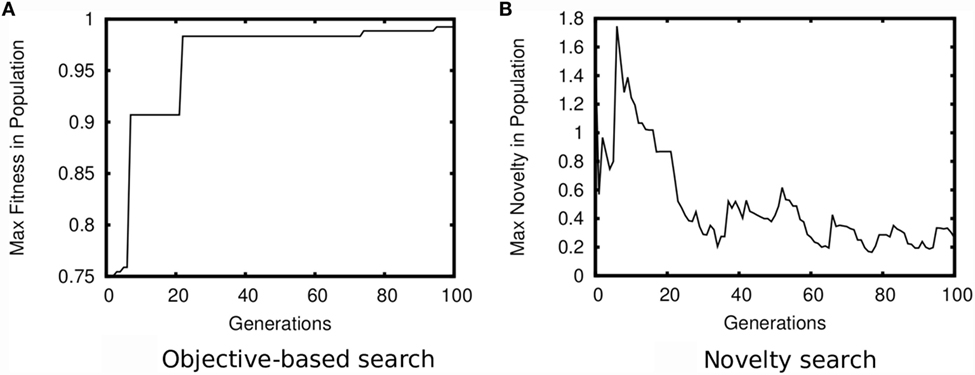
Figure 2. Contrast between optimizing absolute and relative measures. Both figures show a plot of the maximum of an optimization measure present in the population over generations. When optimizing a static measure of progress, as in (A) objective-driven search, a high-fitness individual remains so indefinitely. As a result, adaptations quickly sweep through the entire population. Such convergence precludes lineages from distinguishing themselves by producing adaptations at differential rates. In contrast, when optimizing a measure of divergence, as in (B) novelty search, novel innovations cause only a temporary spike in the maximum novelty of the population. In this way, selection can maintain many diverging lineages that can distinguish themselves by more consistently producing novelty than the other ones. Plots are the characteristic result from running search in the medium maze domain of Lehman and Stanley (2011a).
Importantly, this argument gracefully extends to the population level. Because divergence is the primary selection criteria, individuals are directly incentivized to diversify and spread over the space of possible phenotypes. The product is thus a diverse set of leaping-off points that enable a significant base level of population-level evolvability. At the same time, by the argument above, lineages are indirectly rewarded to consistently produce diversity, which encourages individual evolvability that is fit to an individual’s local phenotypic neighborhood. In this way, divergent selection encourages a population of individuals with complementary evolvabilities, resulting in a much wider range of reachable phenotypes than that would result from considering any single individual.
Beyond theoretical arguments, empirical studies have demonstrated that divergent search often results in higher evolvability than objective-based search (Lehman and Stanley, 2011b, 2013; Lehman and Miikkulainen, 2015; Wilder and Stanley, 2015; Mengistu et al., 2016). Other studies have highlighted that objective-based search often cannot fully exploit features that enable greater potential for evolvability, e.g. allowing individuals to control aspects of mutation (Clune et al., 2008; Lehman and Stanley, 2011b) or of reproduction (Spector and Robinson, 2002). One important caveat for interpreting these results is that nearly all such studies focus on individual-level evolvability (Wilder and Stanley, 2015), meaning that further studies focusing on population-level evolvability are needed to validate the theory. But, taken as a whole, evidence is accumulating that divergent selection is a critical ingredient for encouraging evolvability in ER.
5. Conclusion
This paper addressed two connected aspects of ER: (1) what is a coherent vision that realistically relates evolvability to the goals of ER, and (2) what algorithmic considerations align with achieving that vision. The idea is that it is both realistic and desirable to create divergent EAs that indirectly optimize population-level evolvability, formalized as the potential for a population to realize phenotypic variety. Such an approach agrees with intuitions about and understanding of natural evolution, and respects limitations about what ultimately is algorithmically possible.
While divergent search methods seem more aligned with evolvability than convergent search, a vast gulf still remains between the dynamics of such algorithms and those of natural evolution. One hope is that an explicit focus on population-level evolvability may lead to algorithmic improvements that enhance evolvability. However, a more fundamental problem is that existing measures of divergence in EAs are relatively simplistic and do not enable the seemingly endless and interesting innovation observed in natural evolution. Interesting proposals for more sophisticated divergent selection pressure are beginning to emerge (Liapis et al., 2013; Nguyen et al., 2015; Pugh et al., 2015), and are an important direction for future research.
Author Contributions
JL, BW, and KS, each contributed to the conception and writing of this article.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Funding
This work was supported by the National Science Foundation under grant no. IIS-1421925. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
References
Altenberg, L. (1994). The evolution of evolvability in genetic programming. Adv. Genet. Program. 3, 47–74.
Arthur, W. B. (2009). The Nature of Technology: What It Is and How It Evolves. New York, NY: Simon and Schuster.
Arthur, W. B., and Polak, W. (2004). The evolution of technology within a simple computer model. Complexity 11, 23–31. doi:10.1002/cplx.20130
Clune, J., Misevic, D., Ofria, C., Lenski, R. E., Elena, S. F., and Sanjun, R. (2008). Natural selection fails to optimize mutation rates for long-term adaptation on rugged fitness landscapes. PLoS Comput. Biol. 4:e1000187. doi:10.1371/journal.pcbi.1000187
Clune, J., Mouret, J. B., and Lipson, H. (2013). The evolutionary origins of modularity. Proc. Biol. Sci. 280, 20122863. doi:10.1098/rspb.2012.2863
Dichtel-Danjoy, M.-L., and Félix, M.-A. (2004). Phenotypic neighborhood and micro-evolvability. Trends Genet. 20, 268–276. doi:10.1016/j.tig.2004.03.010
Doncieux, S., and Mouret, J.-B. (2013). “Behavioral diversity with multiple behavioral distances,” in 2013 IEEE Congress on Evolutionary Computation (CEC) (Washington, DC: IEEE), 1427–1434.
Doncieux, S., and Mouret, J.-B. (2014). Beyond black-box optimization: a review of selective pressures for evolutionary robotics. Evol. Intell. 7, 71–93. doi:10.1007/s12065-014-0110-x
Edmonds, B. (2001). Meta-genetic programming: co-evolving the operators of variation. Turk. J. Elec. Engin. 9, 13–29.
Endler, J. A., and Greenwood, J. J. D. (1988). Frequency-dependent predation, crypsis and aposematic coloration [and discussion]. Philos. Trans. R. Soc. Lond. B Biol. Sci. 319, 505–523. doi:10.1098/rstb.1988.0062
Ficici, S., and Pollack, J. B. (1998). “Challenges in coevolutionary learning: arms-race dynamics, open-endedness, and mediocre stable states,” in Proceedings of the Sixth International Conference on Artificial Life (Cambridge, MA: MIT Press), 238–247.
Gomes, J., Mariano, P., and Christensen, A. L. (2015). “Devising effective novelty search algorithms: a comprehensive empirical study,” in Proceedings of the 2015 on Genetic and Evolutionary Computation Conference (New York, NY: ACM), 943–950.
Gould, S. J., and Vrba, E. S. (1982). Exaptationa missing term in the science of form. Paleobiology 8, 4–15. doi:10.1017/S0094837300004310
Hardin, G. (1960). The competitive exclusion principle. Science 131, 1292–1297. doi:10.1126/science.131.3409.1292
Hu, T., and Banzhaf, W. (2010). Evolvability and speed of evolutionary algorithms in light of recent developments in biology. J. Artif. Evol. Appl. 2010, 1. doi:10.1155/2010/568375
Jousset, A., Eisenhauer, N., Merker, M., Mouquet, N., and Scheu, S. (2016). High functional diversity stimulates diversification in experimental microbial communities. Sci. Adv. 2, e1600124. doi:10.1126/sciadv.1600124
Lehman, J., and Miikkulainen, R. (2015). “Enhancing divergent search through extinction events,” in Proceedings of the 2015 on Genetic and Evolutionary Computation Conference (New York, NY: ACM), 951–958.
Lehman, J., Risi, S., and Stanley, K. O. (2012). “On the benefits of divergent search for evolved representations,” in Proceedings of the EvoNet 2012 Workshop at ALIFE XIII. Cambridge, MA.
Lehman, J., and Stanley, K. O. (2010). “Revising the evolutionary computation abstraction: minimal criteria novelty search,” in Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2010) (New York, NY: ACM), 103–110.
Lehman, J., and Stanley, K. O. (2011a). Abandoning objectives: evolution through the search for novelty alone. Evol. Comput. 19, 189–223. doi:10.1162/EVCO_a_00025
Lehman, J., and Stanley, K. O. (2011b). “Improving evolvability through novelty search and self-adaptation,” in Proceedings of the 2011 Congress on Evolutionary Computation (CEC 2011) (Washington, DC: IEEE), 2693–2700.
Lehman, J., and Stanley, K. O. (2011c). “Novelty search and the problem with objectives,” in Genetic Programming Theory and Practice IX, eds T. McConaghy, E. Vladislavleva and R. Riolo (Berling, Heidelberg: Springer), 37–56.
Lehman, J., and Stanley, K. O. (2013). Evolvability is inevitable: increasing evolvability without the pressure to adapt. PLoS ONE 8:e62186. doi:10.1371/journal.pone.0062186
Lehman, J., Stanley, K. O., and Miikkulainen, R. (2013). “Effective diversity maintenance in deceptive domains,” in Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2013) (New York, NY: ACM), 215–222.
Lenski, R. E., Ofria, C., Pennock, R. T., and Adami, C. (2003). The evolutionary origin of complex features. Nature 423, 139–144. doi:10.1038/nature01568
Liapis, A., Martinez, H. P., Togelius, J., and Yannakakis, G. N. (2013). “Transforming exploratory creativity with delenox,” in Proceedings of the Fourth International Conference on Computational Creativity (Cambridge, MA: AAAI Press), 56–63.
McShea, D. W., and Brandon, R. N. (2010). Biology’s First Law: The Tendency for Diversity and Complexity to Increase in Evolutionary Systems. Chicago: University of Chicago Press.
Mengistu, H., Lehman, J., and Clune, J. (2016). “Evolvability search: directly selecting for evolvability in order to study and produce it,” in Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2016) (New York, NY: ACM).
Miconi, T. (2008). Evolution and complexity: the double-edged sword. Artif. Life 14, 325–344. doi:10.1162/artl.2008.14.3.14307
Mouret, J.-B., and Clune, J. (2015). Illuminating search spaces by mapping elites. arXiv preprint arXiv:1504.04909.
Mouret, J.-B., and Doncieux, S. (2012). Encouraging behavioral diversity in evolutionary robotics: an empirical study. Evol. Comput. 20, 91–133. doi:10.1162/EVCO_a_00048
Nguyen, A., Yosinski, J., and Clune, J. (2015). “Innovation engines: automated creativity and improved stochastic optimization via deep learning,” in Proceedings of the Genetic and Evolutionary Computation Conference. New York, NY.
Pugh, J. K., Soros, L., Szerlip, P. A., and Stanley, K. O. (2015). “Confronting the challenge of quality diversity,” in Proceedings of the Genetic and Evolutionary Computation Conference. New York, NY.
Reisinger, J., Stanley, K. O., and Miikkulainen, R. (2005). “Towards an empirical measure of evolvability,” in Genetic and Evolutionary Computation Conference (GECCO2005) Workshop Program (Washington, DC: ACM Press), 257–264.
Risi, S., Lehman, J., and Stanley, K. O. (2010). “Evolving the placement and density of neurons in the hyperneat substrate,” in Proceedings of the 12th Annual Conference on Genetic and Evolutionary Computation (New York, NY: ACM), 563–570.
Saint-Ruf, C., Garfa-Traoré, M., Collin, V., Cordier, C., Franceschi, C., and Matic, I. (2014). Massive diversification in aging colonies of Escherichia coli. J. Bacteriol. 196, 3059–3073. doi:10.1128/JB.01421-13
Spector, L., and Robinson, A. (2002). Genetic programming and autoconstructive evolution with the push programming language. Genet. Program. Evolvable Mach. 3, 7–40. doi:10.1023/A:1020945110902
Stanley, K. O., and Lehman, J. (2015). Why Greatness Cannot Be Planned. Berlin, Heidelberg: Springer Science Business Media, 978–983.
Tarapore, D., and Mouret, J.-B. (2015). Evolvability signatures of generative encodings: beyond standard performance benchmarks. Inf. Sci. 313, 43–61. doi:10.1016/j.ins.2015.03.046
Velez, R., and Clune, J. (2014). “Novelty search creates robots with general skills for exploration,” in Proceedings of the 2014 Conference on Genetic and Evolutionary Computation (New York, NY: ACM), 737–744.
Wagner, G., and Altenberg, L. (1996). Complex adaptations and the evolution of evolvability. Evolution 50, 967–976. doi:10.2307/2410639
Wilder, B., and Stanley, K. (2015). Reconciling explanations for the evolution of evolvability. Adapt. Behav. 23, 171–179. doi:10.1177/1059712315584166
Keywords: evolutionary robotics, evolvability, divergent selection, encodings, evolution of complexity
Citation: Lehman J, Wilder B and Stanley KO (2016) On the Critical Role of Divergent Selection in Evolvability. Front. Robot. AI 3:45. doi: 10.3389/frobt.2016.00045
Received: 30 March 2016; Accepted: 08 July 2016;
Published: 02 August 2016
Edited by:
Stephane Doncieux, Pierre-and-Marie-Curie University, FranceReviewed by:
Jean-Baptiste Mouret, French Institute for Research in Computer Science and Automation, FranceAnders Lyhne Christensen, University Institute of Lisbon (ISCTE-IUL), Portugal
Copyright: © 2016 Lehman, Wilder and Stanley. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joel Lehman, amxlaEBpdHUuZGs=
 Joel Lehman
Joel Lehman Bryan Wilder
Bryan Wilder Kenneth O. Stanley
Kenneth O. Stanley