The Sensorimotor Loop as a Dynamical System: How Regular Motion Primitives May Emerge from Self-Organized Limit Cycles

We investigate the sensorimotor loop of simple robots simulated within the LPZRobots environment from the point of view of dynamical systems theory. For a robot with a cylindrical shaped body and an actuator controlled by a single proprioceptual neuron, we find various types of periodic motions in terms of stable limit cycles. These are self-organized in the sense that the dynamics of the actuator kicks in only, for a certain range of parameters, when the barrel is already rolling, stopping otherwise. The stability of the resulting rolling motions terminates generally, as a function of the control parameters, at points where fold bifurcations of limit cycles occur. We find that several branches of motion types exist for the same parameters, in terms of the relative frequencies of the barrel and of the actuator, having each their respective basins of attractions in terms of initial conditions. For low drivings stable limit cycles describing periodic and drifting back-and-forth motions are found additionally. These modes allow to generate symmetry breaking explorative behavior purely by the timing of an otherwise neutral signal with respect to the cyclic back-and-forth motion of the robot.

1. Introduction

Robots moving through an environment need to take the physical laws into account. This can be achieved either via classical control theory (de Wit et al., 2012), or by considering the full sensorimotor loop as an overarching dynamical system (Ay et al., 2012). This distinction could be cast, alternatively, into open-loop control, e.g., via central pattern generators (Ijspeert, 2008), and closed-loop schemes using feedback to control the states of an internal dynamical system (Dorf and Bishop, 1998). The presence of such feedback mechanisms capable of amplifying local instabilities are key components leading to the emergence of self-organization (Der and Martius, 2012). A closely related notion is that of embodiment (Ziemke, 2003), for which no need arises for an explicit modeling of the interactions between the robot and its surroundings. The agent situated in a given environment can be treated, in an embodied approach, as an overarching dynamical system, incorporating both the external dynamics (body–environment interaction) and the internal (controller body) processes. Thus, combining the closed-loop control with the embodied approach leads to movements generated through self-organizing processes. These may in turn be guided by generic, e.g., information-theoretical objective functions (Martius et al., 2013), such as predictive information (Ay et al., 2008), resulting in explorative or even playful behavior (Der and Martius, 2012).

Similar objective functions, such as the free energy (Friston, 2010), can also be considered for the brain as a whole (Baddeley et al., 2008) and in the context of adaptive behavior (Friston and Ao, 2012). Distinct control mechanisms for neural networks can also be derived from other information-theoretical generating functionals, such as the relative information entropy (Triesch, 2007), the mutual information (Toyoizumi et al., 2005), the Fisher information (Echeveste and Gros, 2014), and the recently introduced active information storage measure (Lizier et al., 2012; Dasgupta et al., 2013). Starting from first principles Hebbian learning rules have also been derived (Echeveste et al., 2015).

A parallel approach for studying the power of embodiment is provided by evolutionary robotics. Robots, selected through evolutionary processes (Nolfi and Floreano, 2000) take environmental feedback naturally into account, as they would otherwise not be positively selected. The notion of an acting agent in a reacting environment becomes blurry, to a certain extent, when the full sensorimotor loop is considered, with the motion coming to a standstill without a fully functional feedback cycle. Within other approaches to embodiment, the physical constraints acting on compliant real-world robots are studied (Pfeifer et al., 2007), or the flow of information, e.g., in terms of transfer entropy, through the sensorimotor loop (Schmidt et al., 2013). A related question is how to ground actions generically, i.e., without a priori knowledge, in sensorimotor perceptions (Olsson et al., 2006), or how to select actions from universal and agent-centric measures of control (Klyubin et al., 2005).

Abstracting from the sensorimotor loop, one may regard, from the point of view of dynamical system theory (Beer, 2000), motions as organized sequences of movement primitives in terms of attractor dynamics (Schaal et al., 2000), which the agent needs first to acquire by learning attractor landscapes (Ijspeert et al., 2002, 2013). These may be used later on for encoding the transients leading to periodic motions (Ernesti et al., 2012) or may furthermore self-organize into complex behaviors (Tani and Ito, 2003). In this context, the fully embodied approach may serve as an algorithmic first step to generate a palette of motion primitives. One may also observe that all regular motions are, per definition, attractors in terms of stable limit cycles in the overarching sensorimotor loop, which may be controlled either actively (Laszlo et al., 1996) or passively in terms of limit-cycle walking (Hobbelen, 2008). As an alternative approach for creating and controlling limit cycles, one could use prototype dynamical systems, a concept recently proposed for the study of complex bifurcation scenarios (Sándor and Gros, 2015).

In the present study, we examine in detail the notion of periodic movements as stable limit cycles, using the LPZRobots package (Der and Martius, 2012; Martius et al., 2013) for simulating robots (current development version), which are geometrically simple enough to allow for an at least partial modeling in terms of dynamical system theory (Gros, 2015). Our robots, see Figures 1 and 2, are controlled by a single proprioceptual neuron with a time-dependent threshold b = b(t). We find a region of parameters in which the motion is fully embodied, and where the movement v_b = v_b(t) of the robot and the threshold dynamics are mutually fully interdependent, vanishing when one of them, either b(t) or v_b(t), is clamped. In engineering terms, the engine db/dt powering the motion of the robot is turned on dynamically through the feedback of its very motion.

FIGURE 1

Figure 1. Screenshots from the LPZRobots simulation package, of the one and two rod barrel robots used (left and right panel, respectively).

FIGURE 2

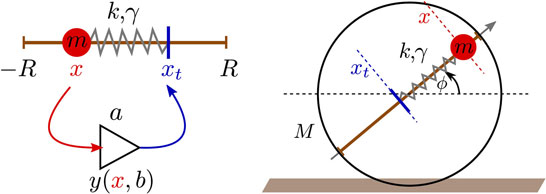
Figure 2. Left: illustration of the proprioceptual single-neuron controlled damped-spring actuator. The input x of the neuron [described by equation (1)] is given by the actual position x ∈ [−R, R] of the ball of mass m moving on the rod, while the output y being proportional, via equation (2), to the target position x_t of the ball. The PID controller then simulates the dynamics of a damped spring, with constant k and damping γ, between the current and the target positions of the mass. Right: sketch of the one-rod robot composed of a barrel of mass M and radius R, with a mass m moving along a rod, as illustrated in the left panel. Slipping is not allowed, the robot moves hence with a velocity v_b = Rω = R (dϕ∕dt), where ϕ measures the angle of the rod with respect to the horizontal.

We also find that a set of qualitatively distinct movements can arise for identical settings of the parameters in terms of stable limit cycles, having their own distinct basins of attraction in phase space. Control signals may hence switch between different motion primitives without the need to interfere with the parameter setting of the sensorimotor loop. Most modes found lead to regular motions with finite average velocities. We discovered, however, also a particular mode corresponding to a cyclic back-and-forth movement, without an average translational motion of the robot. When the parameter settings are changed in this mode, the robot will enter a rolling motion, either to the left or to the right, depending on the timing of the signal with respect to the phase of the cycle, allowing, as a matter of principle, for a truly explorative behavior.

A central result of the present study is that even very simple controller dynamics (a single differential equation, in our case) may lead via the sensorimotor loop to surprisingly rich repertoires of regular motion primitives, which may be selected in turn through higher order decision processes. This is due to the self-stabilization of motion patterns within the sensorimotor loop. Goal-oriented behavior would in this context be achieved not by optimizing motion directly, but by selecting from the many attracting states generated by an embodied controller within the overall sensorimotor loop.

2. Materials and Methods

We start by describing the one-neuron controller used together with the actuator in terms of a damped spring, and the actual setup of the robot.

2.1. Rate Encoding Neurons with Internal Adaption

In this paper, we consider actuators controlled by simple rate encoding neurons, characterized by a sigmoidal transfer function

$y\left(x,b\right)=\frac{1}{1+e^{a\left(b-x\right)}},\dot{b}=\epsilon a\left(2y-1\right)$ (1)

between the membrane potential x and the firing rate y, where a is the gain, taken to be fixed, and b = b(t) a time-dependent threshold. The dynamics $\dot{b}$ for the threshold in equation (1) would lead to b → x and y → 1/2 for any constant input x(t) = x, with a relaxation time being inversely proportional to the adaption rate ϵ. This adaption rate can also be motivated by information-theoretical considerations for the distribution of the firing rates (Triesch, 2005; Marković and Gros, 2010).

2.2. Damped-Spring Actuators

Our robots are controlled by actuators regulating the motion of the ball of mass m on a rod, as illustrated in Figure 2, from its actual position x on the rod, to its target position

$x_t=2R\left(y\left(x,b\right)-\frac{1}{2}\right),$ (2)

where R is the radius of the barrel containing the rod and where y(x, b) is the sigmoidal equation (1). We note that the input and the output of the neuron are, via equation (2), of the same dimensionality, namely positions. The force $F=m\ddot{x}$ moving the ball is evaluated by the PID controller

$F=g_P\left(x_t-x\right)+g_I{\int }_0^t\left(x_t-x\right)\mathit{dt}+g_D\frac{d\left(x_t-x\right)}{\mathit{dt}},$ (3)

provided by the LPZRobots simulation environment (Der and Martius, 2012), characterized by the standard PID-control parameters g_P, g_I, and g_D.

For our simulations, we considered the case g_I = 0, for which the PID controller reduces to a damped spring, see Figure 2,

$m\ddot{x}=-k\left(x-x_t\right)-\mathrm{\gamma }\frac{d\left(x-x_t\right)}{\mathit{dt}},$ (4)

with k = g_P and γ = g_D.

• Equation (4) represents only the contribution of the actuator to the force moving the ball along the rod. The gravitational pull acting on the mass m, and the centrifugal force resulting from the rolling motion of the barrel on the ground are to be added to the RHS of equation (4).

• The target position x_t = x_t(t) is time-dependent through equations (2) and (1).

• Equation (4) is strictly dissipative, due to the damping γ > 0. The same holds for the rolling motion of the barrel on the ground, which is also characterized by a finite rolling friction. Thus, the dynamics db/dt of the threshold in equation (1) can be considered as an engine, providing, by adjusting continuously the target position x_t of the ball, and hence the length of the spring, the energy dissipated by the physical motions.

2.3. Motion of a Mass on a Fixed Rod

As an example we consider a robot, for which we keep the angle ϕ between the rod and the horizontal fixed, ϕ = ϕ₀, by preventing it from rolling. We are then left with a self-coupled motion of a ball along a rod, as illustrated in the left panel of Figure 2, resulting in a dynamics similar to the one of a self coupled neuron (Marković and Gros, 2012; Gros et al., 2014). Using Ω² = k/m and $\mathrm{\Gamma }=\mathrm{\gamma }∕m$, we find in this case

$\begin{array}{cc}\dot{x}=v\hfill & {\dot{x}}_t=2\mathit{Ray}\left(1-y\right)\left(v-\dot{b}\right)\hfill \\ \dot{v}=-{\mathrm{\Omega }}^2\left(x-x_t\right)-\mathrm{\Gamma }\left(v-{\dot{x}}_t\right)-g\sin \left({\varphi }_0\right)\hfill & \dot{b}=2\epsilon a\left(y-1∕2\right)\hfill \end{array},$ (5)

when combining equations (1), (2), and (4). The gravitational term −g sin(ϕ₀) can be transformed away via

$x\to x-g∕{\mathrm{\Omega }}^2\sin {\varphi }_o,b\to b-g∕{\mathrm{\Omega }}^2\sin {\varphi }_o,$ (6)

and does hence not influence the phase diagram, which is shown in Figure 3 for Ω² = 200, Γ = 2Ω, and g = 9.81. We have used standard numerical methods (Clewley, 2012).

FIGURE 3

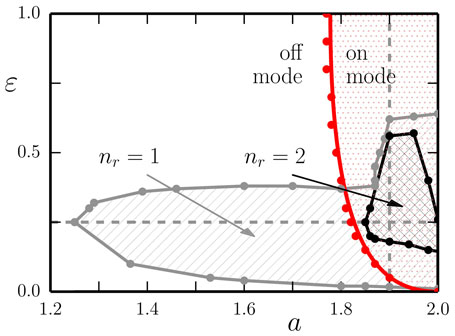
Figure 3. The phase diagram of the one-rod barrel, as a function of the gain a and of the adaption rate ϵ. The results are obtained using the LPZRobots package, apart from the red solid line separating the off- and the on-mode, which follows from equation (5), for a fixed but otherwise arbitrary angle ϕ = ϕ₀. The dashed vertical and horizontal gray lines indicate the cuts used for the phase diagrams presented in Figure 5. The number of stable limit cycles found in the respective parameter regions is denoted by n_r. Non-rolling modes: the red dots/lines indicate the locus of a Hopf bifurcation, where a stable non-rolling limit cycle (on mode) emerges from the trivial non-rolling fixpoint (off mode). In the off mode the “engine” db(t)/dt, see equation (1), kicks in only when the barrel is already moving. Rolling modes: shown are the regions containing n_r = 1 (enclosed by the solid gray line) and n_r = 2 (enclosed by the solid black line) attracting limit-cycles corresponding to a barrel moving with a finite velocity <v_b >. Note that the robot is able to move also in the off mode (of the engine). The stationary and the drifting back-and-forth modes, discussed in Figure 6, have been omitted, in order to avoid overcrowding.

We find a Hopf bifurcation line separating the stability regions for the trivial fixpoint and for a limit cycle, denoted, respectively, as off and on modes. This behavior is similar to the one observed for a self coupled neuron with intrinsic adaption (Marković and Gros, 2012; Gros et al., 2014).

3. Results

In Figure 1, the screenshots of the one- and two-rod robots simulated with the LPZRobots package (current development version) (Der and Martius, 2012; Martius et al., 2013) are presented. Throughout the simulations the control parameters Γ = 2Ω and Ω² = 200 for the actuator, Λ = 1 for the mass ratio m/M (ball to barrel), R = 1 for the radius for the barrel, and Ψ = 0.3 for the coefficient of the rolling friction have been held constant, varying only the adaption rate ϵ for the threshold of the neuron, and the gain a. For the simulations, a step size of 0.001 was used. In the figures (and in the rest of the paper), the parameters will be presented in dimensionless units, with SI units being implied: seconds/meter for the time and length, respectively, and g = 9.81 m/s² for the gravitational acceleration. Our barrel has a radius of 1 m and a moving mass of 1 kg, rolling typically at speeds of (1–4) m/s ≈ (3–12) km/h. A table of the parameters is given in the Supplementary Material.

3.1. One-Rod Barrel

The overall phase diagram of the one-rod barrel shown in Figure 3 contains regions of non-rolling fixpoints or limit cycles, and regions where one or more attracting limit cycles corresponding to a continuously rolling barrel are present, in part additionally. Depending on the initial conditions the system will eventually settle into one of the attracting states.

3.1.1. Coexisting Modes as Behavioral Primitives

Standard robot control aims at achieving a predefined outcome, and for this purpose it is indispensable that identical robot actions lead also to identical movements. This is not necessarily the case for robots controlled by self-organized processes, as investigated here.

In Figure 4, we illustrate the time series and the corresponding phase-space plots of the dominant modes of the one-rod barrel shown in Figure 1. The simulation parameters a = 1.9 for the gain, and the ϵ = 0.25 adaption rate are close to the Hopf bifurcation line shown in Figure 3, but in the on mode, which means that the ball moves both for fixed horizontal and vertical rods.

FIGURE 4

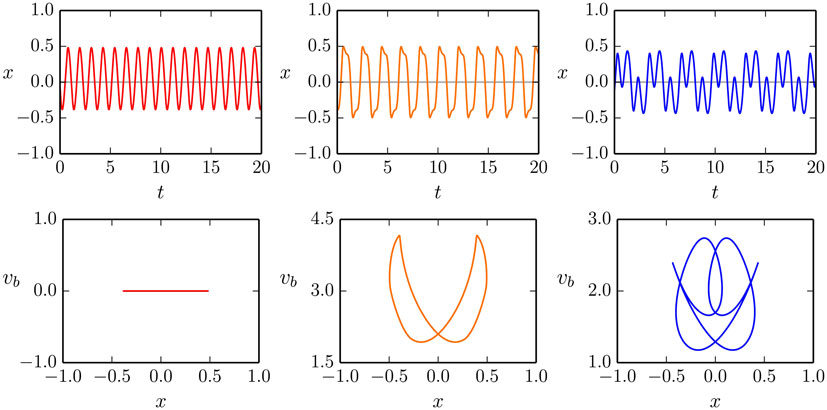
Figure 4. The motion x(t) of the mass along the rod of the one-rod barrel (top row), together with the corresponding phase-plane trajectories (x(t), v_b(t)) (bottom row), compare Figure 2. The gain and the adaption rate are a = 1.9 and ϵ = 0.25, respectively. Shown are the 0:1, 1:1, and 1:3 modes (left/middle/right column). Note that the velocity v_b(t) of the barrel vanishes for the 0:1 mode, oscillating but remaining otherwise positive for the 1:1 and the 1:3 mode. For the corresponding videos, see the Supplementary Material.

The first of the three coexisting stable limit cycles, illustrated in Figure 4, corresponds to the non-moving barrel with the ball oscillating vertically along the rod (first column). For the second, 1:1 mode, the average rolling frequency of the barrel and of the oscillation of the ball along the rod match (second column). For the 1:3 mode, the corresponding ratio of frequencies is, however, 1:3 (third column).

The occurrence of several distinct limit cycles for identical parameters can be interpreted in terms of behavioral primitives, potentially allowing an agent to switch rapidly between different types of motions, by shortly destabilizing the currently active limit cycle.

Note that the self-coupled neuron, controlling the dynamics of the ball along the horizontally fixed rod, has only two possible stable states (a fixpoint and a limit cycle). Considering, however, the fully embodied rolling robot, coexisting states are arising, which can lead to different behavioral patterns purely as a result of the environmental context. An external force applied to the robot can qualitatively change its behavior, indicating the sign of multifunctionality (Williams and Beer, 2013).

3.1.2. Embodiment as Self-Organized Motion

Most robots are autonomously active in the sense that the motion is not essentially dependent on the feedback of the environment. For the case of self-organized motion, as considered here, there would be, on the other side, no motion when the sensorimotor loop would be interrupted.

We present in the left plot of Figure 5, the evolution of the self-sustained rolling modes, in terms of the averaged measured velocity, for a = 1.9 and as a function of adaption rate ϵ. The dashed black line indicates, as a guide to the eye, that the velocity increases roughly $\propto \sqrt{\epsilon }$ for the 1:1 mode. The two branches are stable for ϵ ∈ [0.018, 0.55] and ϵ ∈ [0.19, 0.61], respectively, for the 1:1 and the 1:3 mode, and terminate (presumably) through saddle node bifurcations of limit cycles. We have indicated this scenario by adding by hand in Figure 5, as guides to the eye, the respective unstable branches.

FIGURE 5

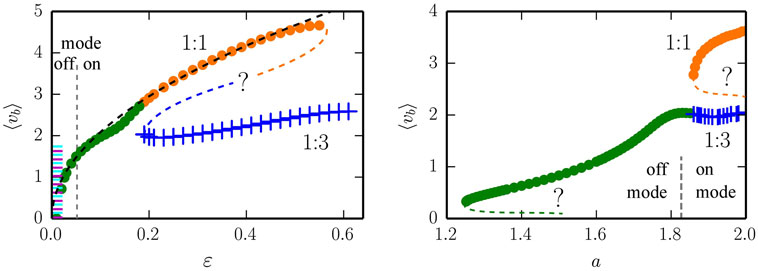
Figure 5. The average speed <v_b> of the one-rod barrel for the 1:1 (green/orange dots) and for 1:3 (blue crosses) mode. The vertical dashed line denotes the locus of the Hopf bifurcation line shown in Figure 3. In the off mode (on mode), the attracting state for the non-rolling mode is a stable fixpoint (limit cycle), respectively. Presumably existing unstable limit cycles are indicated by dashed lines (labeled with question marks). Left: for a gain a = 1.9. The colored region for very small adaption rates ϵ indicates a region with both stable and drifting back-and-forth modes, further described in Figure 6. Right: for an adaption rate ϵ = 0.25.

The locus of the Hopf bifurcation shown in Figure 3, at ϵ ≈ 0.05, is indicated in (the left panel of) Figure 5 by the dashed vertical line, separating the off from the on mode. In the off and on modes, the non-rolling attractors are a fixpoint and a limit cycle, respectively. Note that self-sustained rolling modes exist in the off mode as well, where the “engine” db(t)/dt of the barrel only kicks in, through amplifying local fluctuations (damped oscillations around the fixpoint), when the barrel is already moving. This underlines the embodied nature of the motion, which arises in a truly self-organized fashion [in terms of dynamical systems theory (Gros, 2015)] through the bidirectional feedback between environment and both the body and the controller of the robot.

However, in the absence of feedback mechanisms (such as centrifugal- and Coriolis-forces), the neuron controlled actuator could only generate a single regular rolling motion, similar to the ones achieved by sending motor signals generated by some central pattern generators (Der and Martius, 2012). This is not the case for our robot, which exhibits, as shown in Figure 5 (and in Figure 6, see Discussion below) a wide spectrum of possible rolling modes.

FIGURE 6

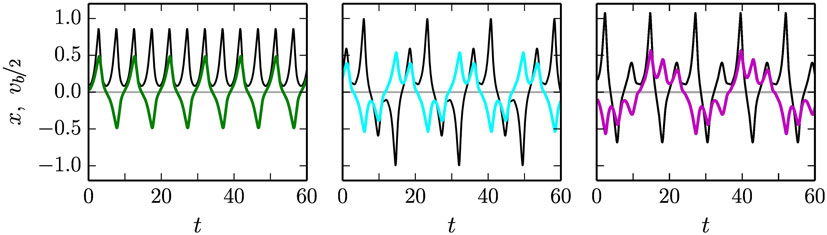
Figure 6. The time evolution of the position x (colored lines) of the mass along the rod, and of the (rescaled) speed v_b of the barrel (black lines), for a = 1.9 and ϵ = 0.019/0.017/0.015 (left/center/right), all in the off mode (compare Figure 5). The respective average velocities are <v_b > = 0.63/0.00/0.25 for the 1:1 mode (left), the stationary back-and-forth mode (middle), and the drifting back-and-forth mode (right). For the corresponding videos, see the Supplementary Material.

3.1.3. Avoided Pitchfork Bifurcations of Limit Cycles

In the right panel of Figure 5, we present the measured mean velocity <v_b > of the ball for ϵ = 0.25, as a function of the gain a. The Hopf bifurcation between the off- and on- non-rolling modes occurs at a_H ≈ 1.83, compare Figure 3.

For 1.23 < a < 1.83, the ball hence is moving in the off mode, with the engine kicking in only through the feedback from the environment, which we interpret as self-organized embodied motion, with the environment being an essential component of the overarching dynamical system.

Comparing both panels of Figure 5, one can notice that the low-velocity mode (green dots) connects either to the 1:1 mode (as in the left panel) or to the 1:3 mode (as in the right panel). The reason for the apparent discrepancy lies in the fact that the respective bifurcation line is oblique in the phase space plane (a,ϵ). The evolution of these modes suggests in any case that the low-velocity mode connects to the two higher-velocity modes via an avoided pitchfork transition of limit cycles (Gros, 2015).

3.1.4. Explorative Motion via Noise-Induced Directional Switching

Our robot contains a single dynamical variable, the threshold b(t), generating self-stabilizing motions via the sensorimotor loop. The palette of modes generated is, despite this apparent simplicity, surprisingly large and may be used to generate higher order behavior.

There are three dominant branches, the 0:1, 1:1, and 1:3 modes (in terms of the ratios of the respective barrel and mass frequencies), compare Figures 4 and 5, which are stable for a wide range of parameters. We found in addition also a parameter region for which different types of motions arise from minute changes of control parameters, such as the adaption rate ϵ.

In Figure 6, the motion x(t) of the ball along the rod and the velocity v_b(t) of the barrel are given for three closely spaced adaption rates ϵ = 0.019, 0.017, and 0.015, for which three qualitatively different types of motions are found (which have partially, but not completely overlapping stability regions).

• For ϵ = 0.019, the standard 1:1 rolling motion is recovered, with an average velocity <v_b > = 0.63.

• For ϵ = 0.017, a new mode arises, for which the ball rolls back-and-forth forever. The motion is exactly symmetric with respect to the left and to the right, and the average velocity <v_b > = 0.0 of the barrel hence vanishes exactly.

• For ϵ = 0.015, the ball also rolls back-and-forth, but asymmetrically, giving rise to a drifting motion with small but finite average velocity of <v_b > = 0.25.

The occurrence of a limit cycle corresponding to a symmetric back-and-forth rolling motion, sandwiched between symmetry breaking modes, gives rise to an interesting venue for the generation of explorative behaviors, as the robot will be sensitive to finite but otherwise very small perturbations influencing its internal control parameters. This behavior is illustrated in Figure 7. Depending on the timing of the perturbation with respect to the back-and-forth rolling cycle, the robot will settle into a left- or into a right-moving motion (in the 1:1 or in the back-and-forth drifting mode, respectively, for increasing/decreasing ϵ). It is hence possible to break spatial symmetries, in general, purely via the timing of a perturbation. The perturbation itself, here acting on the adaption rate ϵ, does not need to carry any information about the direction of motion.

FIGURE 7

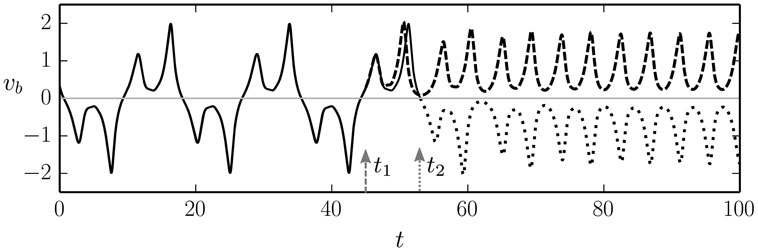
Figure 7. Two superimposed runs for the time evolution of the speed v_b of the barrel (black lines), for a = 1.9. In the first run, the adaption rate ϵ is changed discontinuously at time t₁ = 45 from ϵ = 0.017 (corresponding to the stationary back-and-forth mode, see Figure 6) to ϵ = 0.02 (corresponding to the 1:1 rolling mode). In the second run, identical initial conditions have been used and an identical change is made to the adaption rated ϵ, but now at time t₂ = 53. In both runs (dashed and dotted lines, respectively), the barrel settles into the 1:1 rolling motion, albeit in opposite directions (to the left/right with ⟨v_b⟩ > 0 and ⟨v_b⟩ < 0, respectively). For the corresponding videos, see the Supplementary Material.

3.2. Two-Rod Barrel

Adding a second actuator perpendicular to the first one, a neuron controlled ball moving along a rod, one can increase the complexity of the robot (see the right picture of Figure 1). Both actuators work, in our setup, independently, with the crosstalk being provided exclusively by the environmental feedback. Both actuators are identical to the rod used for the single-rod barrel, with each rod having its own adapting threshold b_α(t) and membrane potential x_α(t), with α = 1,2. The adaption rate ϵ, the gain a, and all other parameters are identical for the two rods.

In Figure 8, we show in the right panel the stability range, for a = 1.9 and as a function of the adaption rate ϵ, of the three most dominant rolling modes (1:1, 1:3, and 1:5) of the two-rod barrel. A large variety of higher order 1:M modes (with M being an integer) is found in addition. We did not carry out a systematic search of their stability range, which becomes progressively smaller with increasing M, and present here only exemplary parameter settings for which the respective modes have been found by trial-and-error (by randomly kicking the barrel). A blow-up is given in the right panel of Figure 8. Most values of M found are odd, but not exclusively. We cannot exclude, at this stage that an infinite cascade M → ∞ of higher order limit cycles may possibly occur.

FIGURE 8

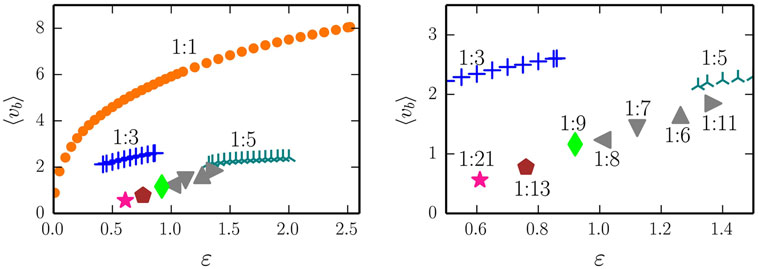
Figure 8. Left: the average speed <v_b> of the two-rod barrel for the 1:1/1:3/1:5 (orange dots, blue crosses, dark-cyan stars) modes. The gain is a = 1.9, all other parameters are identical to the ones used for the one-rod barrel. The respective time series and phase-space plots are presented in Figure 9. The filled symbols denote examples of additional higher order modes, of which the 1:21, 1:13, and 1:9 (pink star, maroon pentagon, and green rhombus) are illustrated in Figure 10. Right: a blow-up, showing the relative location of the 1:8, 1:7, 1:6, and 1:11 modes found at ϵ = 1.009, 1.122, 1.263, and 1.370, respectively.

The time series and the respective phase space trajectories (x₁(t), x₂(t)) of the 1:1, 1:3, and of the 1:5 modes are presented in Figure 9. As one can see in the time series plots, the two independent actuators, being only coupled through the dynamics of the barrel, self-organize themselves in a constant phase-shift, necessary for a consistent rolling. In the reduced phase space (x₁, x₂), the trajectories exactly close on themselves, needing, respectively, 1, 3, and 5 revolutions around the origin (0,0) to close, for, respectively, the 1:1, 1:3, and for the 1:5 limit cycles. In Figure 10, we show the corresponding phase-space trajectories of the M = 9, 13, and 21 limit cycles. These modes have progressively slower average velocities ⟨v_b⟩, compare Figure 8, and smaller basins of attractions, being otherwise regular stable limit cycles. Whether they arise through a bifurcation cascade of limit cycles (Sándor and Gros, 2015), or via some other mechanism, is, however, beyond the scope of the present study.

FIGURE 9

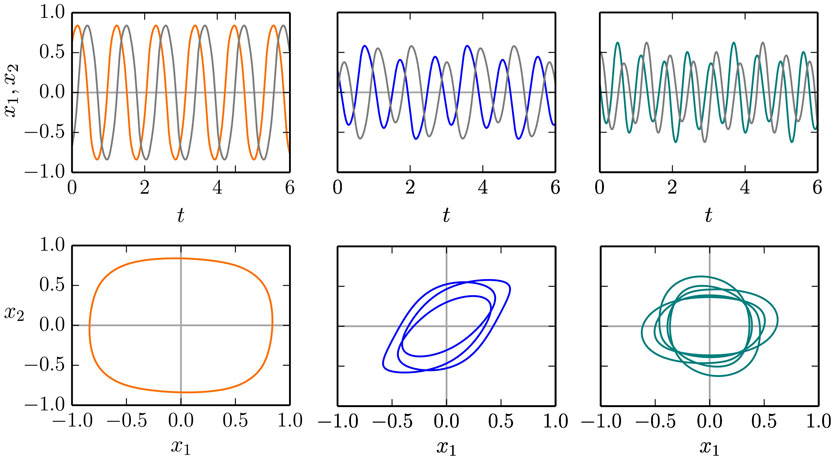
Figure 9. Time series x₁(t) and x₂(t) of the balls along the two rods of the two-rod barrel (top row), and the respective phase plots (x₁(t), x₂(t)). Shown are the 1:1/1:3/1:5 modes (left/middle/right column) for ϵ = 1.0/0.5/1.5, compare Figure 8, needing, respectively, 1/3/5 revolutions around the origin (x₁, x₂) = (0,0) in order to close. For the corresponding videos, see the Supplementary Material.

FIGURE 10

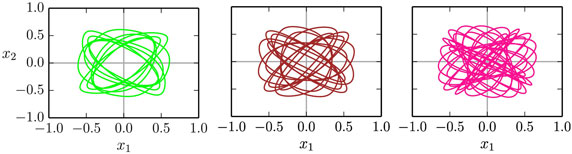
Figure 10. Examples of higher order limit cycles found for the two-rod barrel, closing (within numerical accuracy, viz the thickness of the lines) after 9/13/21 revolutions around the origin (x₁, x₂) = (0,0) (left/middle/right). The gain is a = 1.9 and the respective adaption rates are ϵ = 0.92, 0.76, and 0.61, compare Figure 8.

4. Discussion

It is, in a certain sense, a trivial statement, that the environment is part of the dynamical system a biological or artificial agent lives in. Little of the environmental dynamics is, however, in general accessible, or known, from the perspective of a robot, and it is hence often more suitable, as in closed-loop control (Dorf and Bishop, 1998), to consider the sensorimotor loop as a sequence of stimulus–response reactions of the agent, eliciting at every step the subsequent environmental signal. Here, we have considered simple barrel-shaped robots in a simulated environment, for which the sensorimotor loop constitutes truly a dynamical system, capable of generating, even in a simple setup, a very rich palette of dynamical modes and hence a wide range of qualitatively different types of motions.

The dominant rolling modes found are 1:M attractors, where the actuators cycle M = 1, 3, 5, … times during one revolution ϕ → ϕ + 2π of the barrel. These modes coexist with non-rolling modes, having their own respective basins of attractions, emerging from the mutual feedback of robot and environment. There exist, in addition, regions of phase space with stationary rolling modes (rolling periodically back-and-forth), and drifting back-and-forth modes. We have also found preliminary indications of rolling modes living on two or higher dimensional tori, with incommensurate revolution frequencies, which we did, however, not investigate in detail in the present study. There may additionally exist further attracting states, yet not discovered when performing numerical simulations within the LPZRobots environment.

All modes found are attracting dynamical states and hence robust against noise. This robustness varies, however, with the dominant 1:1 being the most stable, and higher order modes, like the 1:3 or the 1:21 limit cycles, being relatively less stable. There is, in addition, the need to overcome the dissipation, which is present in the simulated environment, by an appropriate energy intake of the actuator. As for all robots the question then arises, whether the observed behavior can be considered as dominantly driven, in the sense of actuator overpowering, or as self-organized, via an inherent and essential feedback loop through the environment [in this context, see Egbert et al. (2010) for an analogous discussion in the context of bacterial sensorimotor system involving chemotaxis].

Actuator-controlled behavior would generally lead, in our perspective, to rather stereotypical movements modes. The fact that our robots show a very large variety of modes upon changing the adaption rate ϵ, viz, the reaction time 1/ϵ of the actuator, indicates self-organization. These modes are also partially overlapping with several rolling modes possibly coexisting for the same settings. It is then a question of starting conditions, into which behavior the robot then settles.

We have also investigated the dynamics of the actuators employed, a damped-spring ball moving along a rod, when the rolling motion dϕ/dt → 0 of the barrel is turned off. In this setting, the environmental feedback from the rolling motion is not present. We find parameter regions where the engine is autonomously active and parameter regions, where the engine shuts itself off. In the later region, the engine may be kicked in again, when the barrel is given a kick, and allowed to roll normally. In this case, the environmental feedback is hence essential, and the motion of the robot is a consequence of self-organizing processes in the combined phase space of the internal degrees of freedom of the robot and of the physical environment.

Thus, the behavior of the robot can not be attributed to merely one of the subsystems, but it is a property of the coupled brain–body–environment system, a result also found in the context of minimally cognitive agents (Beer, 2003; Beer and Williams, 2015). Since we are not aiming here for the presence of higher level cognitive processes, our work can be seen as a purely dynamical systems approach for understanding embodiment directly within the sensorimotor loop.

Our work has been performed with the LPZRobots simulation package, which has been used extensively to investigate the emergence of “playful” behavior and sensorimotor intelligence in terms of intermittent chaotic motion patterns (Der and Martius, 2012; Martius et al., 2013). In this context, our investigation is embedded in the long-standing effort (Taga et al., 1991; Kelso, 1994; Pfeifer et al., 2007; Der and Martius, 2015) to reduce the demanding problem of programing robots by investigating the emergence of self-organized motions within the sensorimotor loop.

Author Contributions

Most data and figures where produced by BS, the paper written by CG and BS, with TJ and LM adding data and material.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Georg Martius for extensive discussions and for helping setting up the LPZRobots simulation environment.

Supplementary Material

The Supplementary Material for this article can be found online at http://journal.frontiersin.org/article/10.3389/frobt.2015.00031

References

Ay, N., Bernigau, H., Der, R., and Prokopenko, M. (2012). Information-driven self-organization: the dynamical system approach to autonomous robot behavior. Theory Biosci. 131, 161–179. doi: 10.1007/s12064-011-0137-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Ay, N., Bertschinger, N., Der, R., Güttler, F., and Olbrich, E. (2008). Predictive information and explorative behavior of autonomous robots. Eur. Phys. J. B 63, 329–339. doi:10.1140/epjb/e2008-00175-0

CrossRef Full Text | Google Scholar

Baddeley, R., Hancock, P., and Földiák, P. (2008). Information Theory and the Brain. New York: Cambridge University Press. p. 1.

Google Scholar

Beer, R. D. (2000). Dynamical approaches to cognitive science. Trends Cogn. Sci. 4, 91–99. doi:10.1016/S1364-6613(99)01440-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Beer, R. D. (2003). The dynamics of active categorical perception in an evolved model agent. Adaptive Behav. 11, 209–243. doi:10.1177/1059712303114001

CrossRef Full Text | Google Scholar

Beer, R. D., and Williams, P. L. (2015). Information processing and dynamics in minimally cognitive agents. Cogn. Sci. 39, 1–38. doi:10.1111/cogs.12142

PubMed Abstract | CrossRef Full Text | Google Scholar

Clewley, R. (2012). Hybrid models and biological model reduction with pydstool. PLoS Comput. Biol. 8:e1002628. doi:10.1371/journal.pcbi.1002628

PubMed Abstract | CrossRef Full Text | Google Scholar

Dasgupta, S., Wörgötter, F., and Manoonpong, P. (2013). Information dynamics based self-adaptive reservoir for delay temporal memory tasks. Evolving Syst. 4, 235–249. doi:10.1007/s12530-013-9080-y

CrossRef Full Text | Google Scholar

de Wit, C. C., Siciliano, B., and Bastin, G. (2012). Theory of Robot Control. London: Springer Science & Business Media.

Google Scholar

Der, R., and Martius, G. (2012). The Playful Machine: Theoretical Foundation and Practical Realization of Self-Organizing Robots, Volume 15. Berlin: Springer Science & Business Media.

Google Scholar

Der, R., and Martius, G. (2015). A novel plasticity rule can explain the development of sensorimotor intelligence. arXiv preprint arXiv 1505.00835.

Google Scholar

Dorf, R. C., and Bishop, R. H. (1998). Modern Control Systems. Menlo Park, CA: Pearson (Addison-Wesley).

Google Scholar

Echeveste, R., Eckmann, S., and Gros, C. (2015). The fisher information as a neural guiding principle for independent component analysis. Entropy 17, 3838–3856. doi:10.3390/e17063838

CrossRef Full Text | Google Scholar

Echeveste, R., and Gros, C. (2014). Generating functionals for computational intelligence: the fisher information as an objective function for self-limiting Hebbian learning rules. Front. Rob. AI 1. doi:10.3389/frobt.2014.00001

CrossRef Full Text | Google Scholar

Egbert, M. D., Barandiaran, X. E., and Di Paolo, E. A. (2010). A minimal model of metabolism-based chemotaxis. PLoS Comput. Biol. 6:e1001004. doi:10.1371/journal.pcbi.1001004

PubMed Abstract | CrossRef Full Text | Google Scholar

Ernesti, J., Righetti, L., Do, M., Asfour, T., and Schaal, S. (2012). “Encoding of periodic and their transient motions by a single dynamic movement primitive,” in 12th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2012) (Piscataway, NJ: IEEE), 57–64.

Google Scholar

Friston, K. (2010). The free-energy principle: a unified brain theory? Nat. Rev. Neurosci. 11, 127–138. doi:10.1038/nrn2787

PubMed Abstract | CrossRef Full Text | Google Scholar

Friston, K., and Ao, P. (2012). Free energy, value, and attractors. Comput. Math. Methods Med. 2012:937860. doi:10.1155/2012/937860

CrossRef Full Text | Google Scholar

Gros, C. (2015). Complex and Adaptive Dynamical Systems: A Primer. Heidelberg: Springer.

Google Scholar

Gros, C., Linkerhand, M., and Walther, V. (2014). “Attractor metadynamics in adapting neural networks,” in Artificial Neural Networks and Machine Learning–ICANN 2014 (Heidelberg: Springer-Verlag), 65–72.

Google Scholar

Hobbelen, D. G. (2008). Limit Cycle Walking. Delft: TU Delft, Delft University of Technology.

Google Scholar

Ijspeert, A. J. (2008). Central pattern generators for locomotion control in animals and robots: a review. Neural Networks 21, 642–653. doi:10.1016/j.neunet.2008.03.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Ijspeert, A. J., Nakanishi, J., Hoffmann, H., Pastor, P., and Schaal, S. (2013). Dynamical movement primitives: learning attractor models for motor behaviors. Neural Comput. 25, 328–373. doi:10.1162/NECO_a_00393

PubMed Abstract | CrossRef Full Text | Google Scholar

Ijspeert, A. J., Nakanishi, J., and Schaal, S. (2002). “Learning attractor landscapes for learning motor primitives,” in Advances in Neural Information Processing Systems (Cambridge, MA: MIT Press), 1547–1554.

Google Scholar

Kelso, J. (1994). The informational character of self-organized coordination dynamics. Hum. Mov. Sci. 13, 393–413. doi:10.1016/0167-9457(94)90047-7

CrossRef Full Text | Google Scholar

Klyubin, A. S., Polani, D., and Nehaniv, C. L. (2005). “Empowerment: a universal agent-centric measure of control,” in The 2005 IEEE Congress on Evolutionary Computation, 2005, Vol. 1 (Piscataway, NJ: IEEE), 128–135.

Google Scholar

Laszlo, J., van de Panne, M., and Fiume, E. (1996). “Limit cycle control and its application to the animation of balancing and walking,” in Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques (New York: ACM), 155–162.

Google Scholar

Lizier, J. T., Prokopenko, M., and Zomaya, A. Y. (2012). Local measures of information storage in complex distributed computation. Inf. Sci. 208, 39–54. doi:10.1016/j.ins.2012.04.016

CrossRef Full Text | Google Scholar

Marković, D., and Gros, C. (2010). Self-organized chaos through polyhomeostatic optimization. Phys. Rev. Lett. 105, 068702. doi:10.1103/PhysRevLett.105.068702

PubMed Abstract | CrossRef Full Text | Google Scholar

Marković, D., and Gros, C. (2012). Intrinsic adaptation in autonomous recurrent neural networks. Neural Comput. 24, 523–540. doi:10.1162/NECO_a_00232

PubMed Abstract | CrossRef Full Text | Google Scholar

Martius, G., Der, R., and Ay, N. (2013). Information driven self-organization of complex robotic behaviors. PLoS ONE 8:e63400. doi:10.1371/journal.pone.0063400

PubMed Abstract | CrossRef Full Text | Google Scholar

Nolfi, S., and Floreano, D. (2000). Evolutionary Robotics: The Biology, Intelligence, and Technology of Self-Organizing Machines. Cambridge, MA: MIT Press.

Google Scholar

Olsson, L. A., Nehaniv, C. L., and Polani, D. (2006). From unknown sensors and actuators to actions grounded in sensorimotor perceptions. Connection Sci. 18, 121–144. doi:10.1080/09540090600768542

CrossRef Full Text | Google Scholar

Pfeifer, R., Lungarella, M., and Iida, F. (2007). Self-organization, embodiment, and biologically inspired robotics. Science 318, 1088–1093. doi:10.1126/science.1145803

PubMed Abstract | CrossRef Full Text | Google Scholar

Sándor, B., and Gros, C. (2015). A versatile class of prototype dynamical systems for complex bifurcation cascades of limit cycles. Sci. Rep. 5, 12316. doi:10.1038/srep12316

PubMed Abstract | CrossRef Full Text | Google Scholar

Schaal, S., Kotosaka, S., and Sternad, D. (2000). “Nonlinear dynamical systems as movement primitives,” in IEEE International Conference on Humanoid Robotics (Cambridge, MA: CD-Proceedings), 1–11.

Google Scholar

Schmidt, N. M., Hoffmann, M., Nakajima, K., and Pfeifer, R. (2013). Bootstrapping perception using information theory: case studies in a quadruped robot running on different grounds. Adv. Complex Syst. 16, 1250078. doi:10.1142/S0219525912500786

CrossRef Full Text | Google Scholar

Taga, G., Yamaguchi, Y., and Shimizu, H. (1991). Self-organized control of bipedal locomotion by neural oscillators in unpredictable environment. Biol. Cybern. 65, 147–159. doi:10.1007/BF00198086

PubMed Abstract | CrossRef Full Text | Google Scholar

Tani, J., and Ito, M. (2003). Self-organization of behavioral primitives as multiple attractor dynamics: a robot experiment. IEEE Trans. Syst. Man Cybern. Part A Syst. Humans 33, 481–488. doi:10.1109/TSMCA.2003.809171

CrossRef Full Text | Google Scholar

Toyoizumi, T., Pfister, J.-P., Aihara, K., and Gerstner, W. (2005). Generalized Bienenstock-Cooper-Munro rule for spiking neurons that maximizes information transmission. Proc. Natl. Acad. Sci. U.S.A. 102, 5239–5244. doi:10.1073/pnas.0500495102

PubMed Abstract | CrossRef Full Text | Google Scholar

Triesch, J. (2005). “A gradient rule for the plasticity of a neurons intrinsic excitability,” in Artificial Neural Networks: Biological Inspirations ICANN 2005 (Berlin: Springer), 65–70.

Google Scholar

Triesch, J. (2007). Synergies between intrinsic and synaptic plasticity mechanisms. Neural Comput. 19, 885–909. doi:10.1162/neco.2007.19.4.885

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, P., and Beer, R. (2013). “Environmental feedback drives multiple behaviors from the same neural circuit,” in Advances in Artificial Life, ECAL 2013, Vol. 12 (Cambridge, MA: MIT Press), 268–275.

Google Scholar

Ziemke, T. (2003). “Whats that thing called embodiment,” in Proceedings of the 25th Annual Meeting of the Cognitive Science Society (Mahwah, NJ: Lawrence Erlbaum), 1305–1310.

Google Scholar