Transient electrophoresis of colloidal particles in a salt-free medium

A general theory is developed for the time dependent transient electrophoretic mobility of spherical colloidal particles in a salt-free liquid medium containing only counterions when a step external electric field is suddenly applied to the colloidal suspension. It is found that as in the case of the steady electrophoretic mobility in a salt-free medium, there is a certain critical value of the particle surface charge separating two cases, that is, the low-surface-charge case and the high-surface-charge case. In the latter case the counterion condensation takes place near the particle surface. For the low-surface charge case, the transient electrophoretic mobility agrees with that of a sphere in an electrolyte solution in the limit of very low electrolyte concentrations. For the high-surface-charge case, however, the transient mobility becomes independent of the particle surface charge because of the counterion condensation effects. A simple expression is derived for the ratio of the transient electrophoretic mobility to the steady electrophoretic mobility, which is found to take the same form irrespective of the magnitude of the particle surface charge. Using this equation, it is now possible to predict how the system will approach its final steady state.

1 Introduction

The fundamental theories of electrophoresis developed in colloid and interface science have recently attracted significant attention in micro- and nano-fluidic lab-on-a-chip systems for the manipulation of liquids and colloidal particles. According to the standard theories of electrophoresis (von Smoluchowski, 1921; Hückel, 1924; Henry, 1931; Overbeek, 1943; Booth, 1950; Wiersema et al., 1966; O’Brien and White, 1978; Ohshima et al., 1983; Delgado, 2001; Dukhin and Goetz, 2001; Spasic and Hsu, 2005; Masliyah and Bhattacharjee, 2006; Ohshima, 2006; Lee, 2018), the zeta potential of colloidal particles is crucial in determining the stability of colloidal suspensions (Derjaguin and Landau, 1941; Verwey and Overbeek, 1948). Usually, the zeta potential is calculated from the electrophoretic mobility of the particles under a constant electric field, known as steady electrophoresis. In contrast, transient electrophoresis involves the non-steady motion of colloidal particles in a liquid medium when subjected to a sudden step electric field. Over time, the transient electrophoretic mobility tends to its static value. Understanding this relaxation time is vital for designing effective electrophoresis measurement systems. The theory of transient electrophoresis originated from Morison (Morrison, 1969; Morrison, 1971) and Ivory (Ivory, 1983; Ivory, 1984), was expanded by Keh and others (Keh and Tseng, 2001; Huang and Keh, 2005; Keh and Huang, 2005; Chiang and Keh, 2015a; Lai and Keh, 2020; Li and Keh, 2020; Lai and Keh, 2021), and has been further developed by various researchers (Khair, 2012; Ohshima, 2022a; Ohshima, 2022b; Ohshima, 2022c; Ohshima, 2023b). Many studies cover different particle types and extend to transient dynamic electrophoresis and transient gel electrophoresis. A lot of theoretical studies exist on transient electrophoresis, covering various particle types such as spherical rigid particles (Morrison, 1971; Ivory, 1984; Huang and Keh, 2005; Keh and Huang, 2005; Chiang and Keh, 2015a; Lai and Keh, 2021; Ohshima, 2022a), cylindrical rigid particles (Morrison, 1971; Li and Keh, 2020; Ohshima, 2022b), porous particle (Chiang and Keh, 2015b; Lai and Keh, 2020; Yu and Keh, 2024), soft particles (Ohshima, 2022c) and particles with a slip surface (Ohshima, 2023b). Beyond the aforementioned transient free-solution electrophoresis theories, there are also theories on transient gel electrophoresis, which deal with the transient electrophoretic behavior of colloidal particles (Ivory, 1984) in a polymer gel medium (Saad, 2018; Saad and Faltas, 2018; Saad, 2019; Sherief et al., 2021; Ohshima, 2023c; Ragab, 2023; Ayman et al., 2024). In addition, there are theories on the transient dynamic electrophoresis, which refers to the transient dynamic electrophoresis of colloidal particles when a dynamic electric field is suddenly applied (Ohshima, 2023a; Ohshima, 2024a). Further, there are theories on transient electrophoresis of colloidal particles in a multi-particle suspension (Chiang and Keh, 2015a; Ohshima, 2024b).

The above-mentioned theories of transient electrophoresis deal with colloidal particles in an electrolyte solution, or, in a salt-containing medium. When colloidal particles are suspending in a liquid medium containing only counterions, that is, in a salt-free liquid medium, a remarkable phenomenon called the counterion condensation effect occurs, especially in the case of highly charged colloidal particles (Ohshima, 2002a; Ohshima, 2002b; Ohshima, 2003a; Ohshima, 2003b; Carrique et al., 2010; Delgado et al., 2016; Luo and Keh, 2021). Chang (Chang, 2009; Chang, 2010; Chang, 2012) presented theoretical studies on the transient electroosmotic flow of a salt-free solution in a cylindrical microcapillary and found that the counterion condensation effect occurs when the microcapillary wall is highly charged.

In the present paper we focus on the transient electrophoresis in a salt-free medium. In micro- and nano-fluidic lab-on-a-chip systems, the importance of understanding the electrophoresis theory of charged colloidal particles in a salt-free medium, compared to salt-containing systems, lies in the precision and control it offers. Salt-free conditions eliminate interference from electrolyte ions, enabling more accurate manipulation of particle behavior within confined channels. This advanced control is crucial for applications such as separation, sorting, and sensing within lab-on-a-chip platforms, where even small variations in mobility of colloidal particles can have a significantly impact on their performance. Moreover, insights gained from studying salt-free electrophoresis contribute to the development of novel techniques for precise particle manipulation and analysis in micro- and nano-fluidic devices, advancing their capabilities in various fields such as biotechnology, medicine, and environmental monitoring. We derive here a simple closed form expression for the time dependent transient electrophoretic mobility of spherical colloidal particles suspended in a salt-free medium when a step external electric field is suddenly applied to the colloidal suspension.

2 Theory

Let us consider a suspension of spherical colloidal particles of radius a, mass density ρ_p, and surface charge density σ or total surface charge Q = 4πa²σ in a salt-free liquid medium of relative permittivity ε_r, mass density ρ₀, and viscosity η containing only counterions. We employ Kuwabara’s cell model for a concentrated suspension of colloidal particles (Kuwabara, 1959). In addition to Kuwabara’s cell model, Happel’s cell model (Happel, 1958) is also known. The reason for adopting Kuwabara’s model is that in the steady electrophoresis problem, Kuwabara’s cell model correctly yields the Smoluchowski mobility equation in the limit of the dilute case. We thus assume that each spherical particle is surrounded by a spherical free volume of radius R, within which counterions are distributed so that electroneutrality is satisfied. The particle volume fraction ϕ is given by

$\varphi ={\left(\frac{a}{R}\right)}^3(1)$

We treat the dilute case, ϕ «1. Let the valence of the counterions and the average concentration (number density) in the absence of the applied electric field be −z and n₀, respectively. Then we have

$Q=\frac{4}{3}\pi \left(R^3-a^3\right)ze{n}_0(2)$

where e is the elementary electric charge. Eq. 2 is the electroneutrality condition. The right-hand side of Eq. 2 is the total amount of charge resulting from the counterions in the spherical free volume with a radius R.

We suppose that at time t = 0, a step electric field E(t) is suddenly applied to the particle suspension, viz.,

$\mathit{E}\left(t\right)=\left\{\begin{array}{c}0,t=0\\ {\mathit{E}}_0,t>0\end{array}\right.(3)$

where E₀ is constant. Then the particles start to move with a time-dependent transient electrophoretic velocity U(t) in the direction parallel to E₀. We define the transient electrophoretic mobility μ(t) of the particle as U(t)= μ(t)E(t) =μ(t)E₀. The origin of the spherical polar coordinate system (r, θ, ϕ) is held fixed at the center of the representative particle and the polar axis (θ = 0) is set parallel to E₀. Let λ_c be the drag coefficient of the counterions. The main assumptions in our analysis are as follows. (i) The applied field E(t) is weak so that U(t) is proportional to E(t) and terms of higher order in E(t) may be neglected. (i) The applied electric field E(t) is weak so that U(t) is proportional to E(t) and terms of higher order in E(t) may be neglected so that the convection term ρ₀ (u·∇)u involving the square of the liquid velocity u (r, t) in the Navier-Stokes equation can be neglected. (ii)The slipping plane (at which the liquid velocity relative to the particle becomes zero) is located on the particle surface (at r = a). (iii) Counterions cannot penetrate the particle surface. (iv) The fluid vorticity ω is zero at the outer surface of the free volume, following Kuwabara’s model (Kuwabara, 1959).

The fundamental electrokinetic equations for the flow velocity u (r, t) of the liquid at position r and time t and that of the counterions v(r, t) are similar to those for the dynamic electrophoresis of spherical colloidal particles in a salt free medium (Ohshima, 2003b), viz.,

${\rho }_{\mathrm{o}}\frac{\mathit{\partial }}{\mathit{\partial }\mathrm{t}}\left\{\mathit{u}\left(\mathit{r},\mathit{t}\right)+\mathit{U}\left(t\right)\right\}-\eta {\nabla }^2\mathit{u}\left(\mathit{r},\mathit{t}\right)+\nabla p\left(\mathit{r},\mathit{t}\right)+{\rho }_c\left(\mathit{r},\mathit{t}\right)\nabla \psi \left(\mathit{r},\mathit{t}\right)=\mathbf{0}(4)$

$\nabla ·\mathit{u}\left(\mathit{r},\mathit{t}\right)=0(5)$

$\mathit{v}\left(\mathit{r},t\right)=\mathit{u}\left(\mathit{r},t\right)-\frac{1}{{\lambda }_c}\nabla {\mu }_{\mathrm{c}}\left(\mathit{r},t\right)(6)$

$\frac{\partial n\left(\mathit{r},t\right)}{\partial t}+\nabla ·\left\{n\left(\mathit{r},t\right)v\left(\mathit{r},t\right)\right\}=0(7)$

${\rho }_{\mathrm{c}}\left(\mathit{r},t\right)=-zen\left(r,t\right)(8)$

${\mu }_{\mathrm{c}}\left(\mathit{r},t\right)={\mu }_{\mathrm{c}}^0-ze\psi \left(\mathit{r},t\right)+kT\ln n\left(\mathit{r},t\right)(9)$

$\Delta \psi \left(\mathit{r},t\right)=-\frac{{\rho }_{\mathrm{c}}\left(\mathit{r},t\right)}{{\epsilon }_{\mathrm{r}}{\epsilon }_0}(10)$

$\frac{4\pi a^3}{3}{\rho }_{\mathrm{p}}\frac{d\mathit{U}\left(t\right)}{dt}={\mathit{F}}_{\mathrm{H}}\left(t\right)+{\mathit{F}}_{\mathrm{E}}\left(t\right)(11)$

where p (r, t) is the pressure, ρ_c (r, t) is the charge density resulting from the counterions of concentration (number density) n(r, t), ψ(r, t) is the electric potential outside the sphere, μ_c(r, t)is the electrochemical potential of the counterions, μ_c⁰ is a constant term in μ_c(r, t), which corresponds to the standard electrochemical potential of counterions, F_H(t) and F_E(t) are, respectively, the hydrodynamic and electric forces acting on the particle, ε₀ is the permittivity of a vacuum, k is the Boltzmann constant, and T is the absolute temperature. Eq. 5 are the Navier-Stokes equation and the equations of continuity for an incompressible flow. Eq. 6 expresses that the flow v(r, t) of the counterions is caused by the liquid flow u(r, t) and the gradient of the electrochemical potential μ_c(r, t) given by Eq. 9 of the counterions. Eq. 7 is the continuity equation for the counterions. Eqs 10, 11 and are, respectively, the Poisson equation and the equation of motion of the particle.

The initial condition for u (r, t) is given by

$\mathit{u}\left(\mathit{r},t\right)=\mathbf{0}\text{\hspace{1em}at\hspace{0.5em}}t=0(12)$

The slipping plane (at which the liquid velocity u (r, t) relative to the particle is zero) is assumed to be located on the particle surface (at r = a), viz.,

$\mathit{u}\left(\mathit{r},t\right)=\mathbf{0}\text{\hspace{1em}at\hspace{0.5em}}r=a(13)$

According to Kuwabara’s cell model (Kuwabara, 1959), we assume that at the outer surface of the unit cell (r = R) the liquid velocity is parallel to the electrophoretic velocity U(t) of the particle, viz.,

$\mathit{u}\left(\mathit{r},t\right)·\widehat{\mathit{n}}=-U\left(t\right)\cos \theta \text{\hspace{0.17em}at\hspace{0.17em}}r=R(14)$

where $\widehat{\mathit{n}}$ is the unit normal outward from the particle surface, U(t) is the magnitude of U(t), and that the vorticity ω(r, t) is zero at r = R,

$\mathit{\omega }\left(\mathit{r},t\right)=\nabla \times \mathit{u}\left(\mathit{r},t\right)=\mathbf{0}\text{\hspace{1em}at\hspace{0.5em}}r=R(15)$

Also, we assume that on the outer surface of the unit cell (r = R) the gradient of the electric potential is parallel to the applied field E(t), viz.,

$\nabla \delta \psi \left(\mathit{r},t\right)·\widehat{\mathit{n}}=-E\left(t\right)\cos \theta \text{\hspace{0.17em}at\hspace{0.17em}}r=R(16)$

where E(t) is the magnitude of E(t). Finally, we adopt the boundary condition that no electrolyte ions can penetrate the particle surface, viz,

${\mathit{v}}_i\left(\mathit{r},t\right)·\widehat{\mathit{n}}=0\text{\hspace{0.17em}at\hspace{0.17em}}r=a(17)$

For a weak field E(t) [assumption (i)], we may write

$n\left(\mathit{r},t\right)=n^{\left(0\right)}\left(r\right)+\delta n\left(\mathit{r},\mathit{t}\right)(18)$

$\psi \left(\mathit{r},t\right)={\psi }^{\left(0\right)}\left(r\right)+\delta \psi \left(\mathit{r},t\right)(19)$

${\mu }_{\mathrm{c}}\left(\mathit{r},t\right)={\mu }_{\mathrm{c}}^{\left(0\right)}+\delta {\mu }_{\mathrm{c}}\left(\mathit{r},t\right)(20)$

${\rho }_{\mathrm{c}}\left(\mathit{r},t\right)={\rho }_{\mathrm{c}}^{\left(0\right)}\left(r\right)+\delta {\rho }_{\mathrm{c}}\left(\mathit{r},t\right)(21)$

where the quantities with superscript (0) refer to those at equilibrium, δn (r, t), δψ(r, t), δμ_c (r, t), δρ_c (r, t) are small quantities, and ${\mu }_{\mathrm{c}}^{\left(0\right)}$ is a constant independent of r. We assume that the equilibrium concentration n⁽⁰⁾ (r) of the counterions obeys the Boltzmann distribution and the equilibrium electric potential ψ⁽⁰⁾ (r) around the particle with a zeta potential ζ

$n^{\left(0\right)}\left(r\right)=n_0\exp \left(-\frac{-ze{\psi }^{\left(0\right)}\left(r\right)}{kT}\right)=n_0\exp \left(\frac{ze{\psi }^{\left(0\right)}\left(r\right)}{kT}\right)(22)$

and

$\frac{d^2{\psi }^{\left(0\right)}\left(r\right)}{d{r}^2}+\frac{2}{r}\frac{d{\psi }^{\left(0\right)}\left(r\right)}{dr}=-\frac{{\rho }_{\mathrm{c}}^{\left(0\right)}\left(r\right)}{{\epsilon }_{\mathrm{r}}{\epsilon }_0}(23)$

with

${\rho }_{\mathrm{c}}^{\left(0\right)}\left(r\right)=-ze{n}^{\left(0\right)}\left(r\right)={-zen}_0\exp \left(\frac{ze{\psi }^{\left(0\right)}\left(r\right)}{kT}\right)(24)$

Here we have set the equilibrium electric potential ψ^{(0) (}r) to be zero at points where the volume charge density ρ_c(r) resulting from counterions equals its average value (−zen₀). We define the equilibrium surface potential as ψ⁽⁰⁾ (a)−ψ⁽⁰⁾ (R). The boundary conditions for ψ⁽⁰⁾ (r) at the particle surface r = a and at the outer surface of the free volume r =R are

${\left.\frac{d{\psi }^{\left(0\right)}\left(r\right)}{dr}\right|}_{r=a}=-\frac{\sigma }{{\epsilon }_{\mathrm{r}}{\epsilon }_0}(25)$

${\left.\frac{d{\psi }^{\left(0\right)}\left(r\right)}{dr}\right|}_{r=R}=0(26)$

Further, symmetry considerations permit us to write

$\mathit{u}\left(\mathit{r},t\right)=\left(-\frac{2}{r}h\left(r,t\right)E\left(t\right)\cos \theta ,\frac{1}{r}\frac{\partial }{\partial r}\left(rh\left(r,t\right)\right)E\left(t\right)\sin \theta ,0\right)(27)$

$\delta {\mu }_{\mathrm{c}}\left(\mathit{r},t\right)=\mathrm{z}e\mathrm{\Phi }\left(r,t\right)E\left(t\right)\cos \theta (28)$

$\delta \psi \left(\mathit{r},t\right)=-Y\left(r,t\right)E\left(t\right)\cos \theta (29)$

Here Φ(r, t), Y(r, t), and h(r, t) are functions of r and t.

By substituting Eq. 27–29 into Eqs 4–7, and neglecting the products of the small quantities, we obtain the following equation for h(r, t), ϕ_i(r, t), and Y(r, t):

$L\left[Lh\left(r,t\right)-\frac{1}{\nu }\frac{\partial h\left(r,t\right)}{\partial t}\right]=G\left(r,t\right)(30)$

$L\mathrm{\Phi }\left(r,t\right)-\frac{{\lambda }_{\mathrm{c}}}{kT}\frac{\partial }{\partial t}\left\{\mathrm{\Phi }\left(r,t\right)-Y\left(r,t\right)\right\}=\frac{dy\left(r\right)}{dr}\left\{-z\frac{\partial \mathrm{\Phi }\left(r,t\right)}{\partial r}-\frac{2{\lambda }_{\mathrm{c}}}{e}\frac{h\left(r,t\right)}{r}\right\}(31)$

$LY\left(r,t\right)=\frac{1}{{\epsilon }_{\mathrm{r}}{\epsilon }_{0}kT}{z}^2{e}^2{n}^{\left(0\right)}\left(r\right)\left\{Y\left(r,t\right)-\mathrm{\Phi }\left(r,t\right)\right\}(32)$

with

$L=\frac{\partial }{\partial r}\frac{1}{r^2}\frac{\partial }{\partial r}{r}^2=\frac{{\partial }^2}{\partial r^2}+\frac{2}{r}\frac{\partial }{\partial r}-\frac{2}{r^2}(33)$

$G\left(r,t\right)=-\frac{ze{n}_0}{\eta r}\frac{dy}{dr}{e}^{y\left(r\right)}\mathrm{\Phi }\left(r,t\right)(34)$

$y\left(r\right)=\frac{ze}{kT}{\psi }^{\left(0\right)}\left(r\right)(35)$

$\nu =\frac{\eta }{{\rho }_0}(36)$

where y(r) is the scaled equilibrium electric potential, ν is the kinematic viscosity of the liquid.

The initial and boundary conditions (Eqs 12–16) and the equation of the motion of the particle (Eq. 11) can be rewritten as those for h(r, t) and Y(r, t) as follows.

$h\left(r,0\right)={\left.\frac{\partial }{\partial \mathrm{r}}h\left(r,t\right)\right|}_{t=0}=0(37)$

$h\left(a,t\right)={\left.\frac{\partial }{\partial \mathrm{r}}h\left(r,t\right)\right|}_{r=a}=0(38)$

$h\left(R,t\right)=\frac{RU\left(t\right)}{2E\left(t\right)}=\frac{R\mu \left(t\right)}{2}(39)$

${\left.Lh\left(r,t\right)\right|}_{r=R}=0(40)$

${\left.\eta \frac{\partial }{\partial r}\left[r\left(Lh\left(r,t\right)-\frac{1}{\nu }\frac{\partial h\left(r,t\right)}{\partial t}\right)\right]\right|}_{r=R}-{\rho }_{\text{el}}^{\left(0\right)}\left(R\right)Y\left(R,t\right)+{\rho }_{0}R\left(1-\varphi \frac{{\rho }_{\mathrm{p}}-{\rho }_0}{{\rho }_0}\right)\frac{d\mu \left(t\right)}{dt}=0(41)$

Eqs 16, 17 and give

${\left.\frac{\partial }{\partial r}\mathrm{Y}\left(r,t\right)\right|}_{r=R}=1(42)$

${\left.\frac{\partial }{\partial r}\mathrm{\Phi }\left(r,t\right)\right|}_{r=a}=0(43)$

The transient electrophoretic mobility μ(t) can be obtained from Eq. 39, viz.,

$\mu \left(t\right)=\frac{2h\left(R,t\right)}{R}(44)$

Eq. 31 for h(r, t) is most easily solved by using the Laplace transformation with respect to time t. We introduce the Laplace transforms $\widehat{h}\left(r,s\right)$, $\widehat{G}\left(r,s\right)$, Y (r, s), and $\widehat{\mu }\left(s\right)$ of h (r, t), G (r, t), Y (r, t), and μ(t), respectively, which are given by

$\widehat{h}\left(r,s\right)={\int }_0^{\infty }h\left(r,t\right)e^{-st}dt(45)$

$\widehat{G}\left(r,s\right)={\displaystyle {\int }_0^{\infty }}G\left(r,t\right)e^{-st}dt(46)$

$\widehat{Y}\left(r,s\right)={\displaystyle {\int }_0^{\infty }}Y\left(r,t\right)e^{-st}dt(47)$

$\widehat{\mu }\left(s\right)={\displaystyle {\int }_0^{\infty }}\mu \left(t\right)e^{-st}dt(48)$

and the Laplace transform of Eq. 42 is

$\widehat{\mu }\left(s\right)=\frac{2\widehat{h}\left(b,s\right)}{R}(49)$

The Laplace transform of Eq. 29 thus gives

$L\left[L\widehat{h}\left(r,s\right)-\frac{s}{\nu }\widehat{h}\left(r,s\right)\right]=\widehat{G}\left(r,s\right)(50)$

By solving Eq. 50 subject to Eqs 37–41 and using Eq. 49, we obtain the following general expression for the Laplace transform $\widehat{\mu }\left(s\right)$ of the transient electrophoretic mobility μ(t):

$\widehat{\mu }\left(s\right)=-\frac{2a^2}{3S\left\{M\left(a,S\right)+\mathrm{\Gamma }\mathrm{S}\right\}}\left[{\int }_a^R\left\{M\left(a,S\right)-M\left(r,S\right)\right\}\widehat{G}\left(r,S\right)dr+\frac{S{\rho }_{\text{el}}^{\left(0\right)}\left(R\right)\widehat{Y}\left(R,S\right)}{3\eta \varphi R}\right](51)$

where

$M\left(r,S\right)=\frac{H\left(r,S\right)-H^{*}\left(r,S\right)\mathrm{\Omega }\left(S\right)}{\left\{1-3\varphi S^{-1}H\left(a,S\right)\right\}-\left\{1-3\varphi S^{-1}{H}^{*}\left(a,S\right)\right\}\mathrm{\Omega }\left(S\right)}(52)$

$M\left(a,S\right)=\frac{H\left(a,S\right)-H^{*}\left(a,S\right)R\left(S\right)}{\left\{1-3\varphi S^{-1}H\left(a,S\right)\right\}-\left\{1-3\varphi S^{-1}{H}^{*}\left(a,S\right)\right\}R\left(S\right)}=\frac{H\left(a,S\right)+\frac{2\sqrt{S}\mathrm{\Omega }\left(S\right)}{1-\mathrm{\Omega }\left(S\right)}}{1-\varphi -3\varphi S^{-1}\left(1+\sqrt{S}\frac{1+\mathrm{\Omega }\left(S\right)}{1-\mathrm{\Omega }\left(S\right)}\right)}(53)$

$H\left(r,S\right)=\left(1+\sqrt{S}\frac{r}{a}\right)\exp \left[-\sqrt{S}\left(\frac{r}{a}-1\right)\right]+S\frac{r^3}{{3a}^3}(54)$

$H^{*}\left(r,S\right)=\left(1-\sqrt{S}\frac{r}{a}\right)\exp \left[\sqrt{S}\left(\frac{r}{a}-1\right)\right]+S\frac{r^3}{{3a}^3}(55)$

$H\left(a,S\right)=1+\sqrt{S}+\frac{S}{3}(56)$

$H^{*}\left(a,S\right)=1-\sqrt{S}+\frac{S}{3}(57)$

$\mathrm{\Omega }\left(S\right)=\frac{1+\sqrt{S}{\varphi }^{-1/3}}{1-\sqrt{S}{\varphi }^{-1/3}}\exp \left[-2\sqrt{S}\left({\varphi }^{-1/3}-1\right)\right](58)$

$S=\frac{\mathrm{s}}{\nu }{a}^2(59)$

$\mathrm{\Gamma }=\frac{2\left({\rho }_p-{\rho }_0\right)}{9{\rho }_0}(60)$

3 Results and discussion

Eq. 51 is the general expression Laplace transform of the transient electrophoretic mobility μ(t) of a spherical colloidal particle in a salt-free liquid medium. The transient mobility μ(t) can be obtained from Eq. 51 by the numerical inverse Laplace transformation. It can be shown that as in the case of steady electrophoresis in salt-free media, the electrophoretic mobility is determined almost solely by the second term of the right-hand side of Eq. 51 (Ohshima, 2002a; Ohshima, 2003a; Ohshima, 2003b), viz.,

$\widehat{\mu }\left(s\right)=-\frac{2a^2}{9\left\{M\left(a,S\right)+\mathrm{\Gamma }\mathrm{S}\right\}}\frac{{\rho }_{\text{el}}^{\left(0\right)}\left(R\right)\widehat{Y}\left(R,S\right)}{\eta \varphi R}(61)$

This term comes from the contribution of the pressure due to the counterions at the outer surface of the free volume (at r = R). Further, for the dilute case (ϕ ≪ 1) we may approximate $\widehat{Y}\left(R,S\right)$ by R/s and M(a, S) by H (a, S) so that Eq. 61 becomes

$\widehat{\mu }\left(s\right)=-\frac{2a^2}{9\left\{H\left(a,S\right)+\mathrm{\Gamma }\mathrm{S}\right\}}\frac{{\rho }_{\text{el}}^{\left(0\right)}\left(R\right)}{\eta \varphi s}(62)$

By substituting Eq. 25 into Eq. 43 and using Eq. 8, we have for the dilute case

$\widehat{\mu }\left(s\right)=\frac{Q}{6\pi \eta a\left\{H\left(a,S\right)+\mathrm{\Gamma }\mathrm{S}\right\}s}\exp \left[\frac{ze{\psi }^{\left(0\right)}\left(R\right)}{kT}\right](63)$

An accurate analytic expression for the equilibrium potential distribution around a spherical particle in a salt-free medium for the dilute case (ϕ ≪ 1) has already been derived (Ohshima, 2002a). The expressions for ψ⁽⁰⁾ (a) and ψ⁽⁰⁾ (R) are given below.

Case 1. (low-surface-charge case)

$\frac{Q}{{4\pi \epsilon }_{\mathrm{r}}{\epsilon }_{0}a}\frac{\text{ze}}{kT}\le \ln \left(\frac{1}{\varphi }\right)(64)$

is satisfied, then

${\psi }^{\left(0\right)}\left(a\right)=\frac{Q}{{4\pi \epsilon }_{\mathrm{r}}{\epsilon }_{0}a}(65)$

${\psi }^{\left(0\right)}\left(R\right)=0(66)$

If the zeta potential ζ is identified as the surface potential defined by ψ⁽⁰⁾ (a)−ψ⁽⁰⁾ (R), then we have

$\zeta ={\psi }^{\left(0\right)}\left(a\right)-{\psi }^{\left(0\right)}\left(R\right)=\frac{Q}{{4\pi \epsilon }_{\mathrm{r}}{\epsilon }_{0}a}(67)$

which is the Coulomb potential. That is, in the low-surface-charge case, the expression for the zeta potential ζ of a particle in a salt-free medium agrees with the limiting form of the zeta potential of a particle in an electrolyte solution with a very low electrolyte concentration.

Case 2. (high-surface-charge-case)

$\frac{Q}{{4\pi \epsilon }_{\mathrm{r}}{\epsilon }_{0}a}\frac{\text{ze}}{kT}>\ln \left(\frac{1}{\varphi }\right)(68)$

is satisfied, then

${\psi }^{\left(0\right)}\left(a\right)=\frac{kT}{ze}\ln \left[\frac{1}{6\varphi }\left(\frac{ze}{kT}\right)\left(\frac{\mathrm{Q}}{{4\pi \epsilon }_{\mathrm{r}}{\epsilon }_{0}a}\right)\right](69)$

${\psi }^{\left(0\right)}\left(R\right)=-\frac{kT}{ze}\ln \left[\frac{1}{6\varphi \ln \left(1/\varphi \right)}\left(\frac{ze}{kT}\right)\left(\frac{Q}{{4\pi \epsilon }_{\mathrm{r}}{\epsilon }_{0}a}\right)\right](70)$

from which

$\zeta ={\psi }^{\left(0\right)}\left(a\right)-{\psi }^{\left(0\right)}\left(R\right)=\frac{kT}{ze}\ln \left[\frac{1}{6\varphi \ln \left(1/\varphi \right)}{\left(\frac{ze}{kT}\right)}^2{\left(\frac{Q}{{4\pi \epsilon }_{\mathrm{r}}{\epsilon }_{0}a}\right)}^2\right](71)$

Eq. 71 demonstrates that in the high-surface-charge case, unlike in the low-surface-charge case, the zeta potential ζ is no longer given by the Coulomb potential (Eq. 67) but by a more complicated equation (Eq. 71). Eq. 71 depends less on Q than Eq. 67 and becomes a function of the particle volume fraction ϕ, as the counter ion condensation occurs in the vicinity of the particle surface.

By substituting the above results into Eq. 63, we obtain the following results:

Case 1. (low-surface- charge case)

$\widehat{\mu }\left(s\right)=\frac{Q}{6\pi \eta a\left\{H\left(a,S\right)+\mathrm{\Gamma }S\right\}s}=\frac{2{\epsilon }_{\mathrm{r}}{\epsilon }_0\zeta }{3\eta }\frac{1}{\left\{H\left(a,S\right)+\mathrm{\Gamma }S\right\}s}(72)$

Case 2. (high-surface- charge case)

$\widehat{\mu }\left(s\right)=\frac{Q}{6\pi \eta a\left\{H\left(a,S\right)+\mathrm{\Gamma }\mathrm{S}\right\}s}\left(\frac{kT}{ze}\right)\ln \left(\frac{1}{\varphi }\right)=\frac{2{\epsilon }_{\mathrm{r}}{\epsilon }_0}{3\eta }\frac{1}{\left\{H\left(a,S\right)+\mathrm{\Gamma }S\right\}s}\left(\frac{kT}{ze}\right)\ln \left(\frac{1}{\varphi }\right)(73)$

In the limit of s→0, Eqs 72, 73 become the steady electrophoretic mobility μ_s = μ(∞) at t = ∞ of spherical colloidal particles in a salt free medium (Ohshima, 2002a), that is,

Case 1. (low-surface- charge case)

${\mu }_{\mathrm{s}}=\mu \left(\infty \right)=\underset{s\to 0}{\lim }s\widehat{\mu }\left(S\right)=\frac{2{\epsilon }_{\mathrm{r}}{\epsilon }_0\zeta }{3\eta }(74)$

Case 2. (high-surface- charge case)

${\mu }_{\mathrm{s}}=\mu \left(\infty \right)=\underset{s\to 0}{\lim }s\widehat{\mu }\left(S\right)=\frac{2{\epsilon }_{\mathrm{r}}{\epsilon }_0}{3\eta }\left(\frac{kT}{ze}\right)\ln \left(\frac{1}{\varphi }\right)(75)$

The transient electrophoretic mobility μ(t) can be obtained analytically from Eqs 72, 73 by the inverse Laplace transformation. The result is

Case 1. (low-surface- charge case)

$\mu \left(t\right)=\frac{2{\epsilon }_{\mathrm{r}}{\epsilon }_{\mathrm{o}}\zeta }{3\eta }\left\{\frac{q_2}{q_2-q_1}M\left(\frac{q_1\sqrt{\nu t}}{a}\right)-\frac{q_1}{q_2-q_1}M\left(\frac{q_2\sqrt{\nu t}}{a}\right)\right\}(76)$

Case 2. (high-surface- charge case)

$\mu \left(t\right)=\frac{2{\epsilon }_{\mathrm{r}}{\epsilon }_{\mathrm{o}}}{3\eta }\left(\frac{kT}{ze}\right)\ln \left(\frac{1}{\varphi }\right)\left\{\frac{q_2}{q_2-q_1}M\left(\frac{q_1\sqrt{\nu t}}{a}\right)-\frac{q_1}{q_2-q_1}M\left(\frac{q_2\sqrt{\nu t}}{a}\right)\right\}(77)$

with

$q_1=\frac{9}{2\left(1+\frac{2{\rho }_{\mathrm{p}}}{{\rho }_{\mathrm{o}}}\right)}\left(1+\frac{1}{3}\sqrt{5-\frac{8{\rho }_{\mathrm{p}}}{{\rho }_{\mathrm{o}}}}\right)(78)$

$q_2=\frac{9}{2\left(1+\frac{2{\rho }_{\mathrm{p}}}{{\rho }_{\mathrm{o}}}\right)}\left(1-\frac{1}{3}\sqrt{5-\frac{8{\rho }_{\mathrm{p}}}{{\rho }_{\mathrm{o}}}}\right)(79)$

$M\left(z\right)=1-e^{z^2}\text{erfc}\left(z\right)(80)$

where erfc(z) is the complementary error function, defined by

$\text{erfc}\left(z\right)=\frac{2}{\sqrt{\pi }}{\int }_z^{\infty }{e}^{-x^2}dx(81)$

We see that Eq. 76 for the low-surface-charge case agrees with the low κa limiting form of the transient electrophoretic mobility μ(t) of a spherical colloidal particle of radius a in an electrolyte solution of the Debye-Hückel parameter κ (Ohshima, 2022a). For the high-surface-charge case, the transient electrophoretic mobility μ(t) deviates from Eq. 76 and given by Eq. 77, which is independent of Q. In other words, in the high-surface-charge case, as Q increases, the zeta potential ζ does not increase linearly with Q (Eq. 71). This is because the number of counterions condensed near the particle surface increases, which tends to suppress the rise in the zeta potential. Consequently, the particle zeta potential depends less on Q.

It follows from Eqs 74–77 that the ratio of the transient electrophoretic mobility μ(t) to the steady mobility μ_s = μ(∞) in a salt-free medium is always simply given by

$\frac{\mu \left(t\right)}{{\mu }_{\mathrm{s}}}=\frac{q_2}{q_2-q_1}M\left(\frac{q_1\sqrt{\nu t}}{a}\right)-\frac{q_1}{q_2-q_1}M\left(\frac{q_2\sqrt{\nu t}}{a}\right)(82)$

for both cases 1 (low-surface- charge case) and 2 (high-surface- charge case), irrespective of the magnitude of the particle surface charge Q.

Figure 1 illustrates the ratio μ(t)/μ_s calculated with Eq. 82 as a function of scaled time νt/a² for four values of the mass density ratio ρ_p/ρ₀, showing how μ(t) reaches the corresponding steady value μ_s. It is observed that the transient mobility μ(t) of heavier particles with larger mass density ρ_p requires a longer time to reach its steady value μ_s. Figure 2 gives a 3-D plot of the ratio μ(t)/μ_s calculated with Eq. 82 as a function of scaled time νt/a² and the mass density ratio ρ_p/ρ₀, which covers wider ranges of νt/a² and the mass density ratio ρ_p/ρ_0.

Figures 1, 2 show that the relaxation time required for μ(t) to reach its steady value μ_s becomes longer as the mass density ratio ρ_p/ρ₀ increases. An approximate expression for the relaxation time T can be derived as follows. As a crude approximation, Eq. 82 reduces to

$\frac{\mu \left(t\right)}{{\mu }_{\mathrm{s}}}=1-e^{-t/T}(83)$

with

$T=\frac{1}{9}\left(1+\frac{2{\rho }_{\mathrm{p}}}{{\rho }_0}\right)\frac{a^2}{\nu }(84)$

where T can be regarded as the relaxation time.

Figure 1

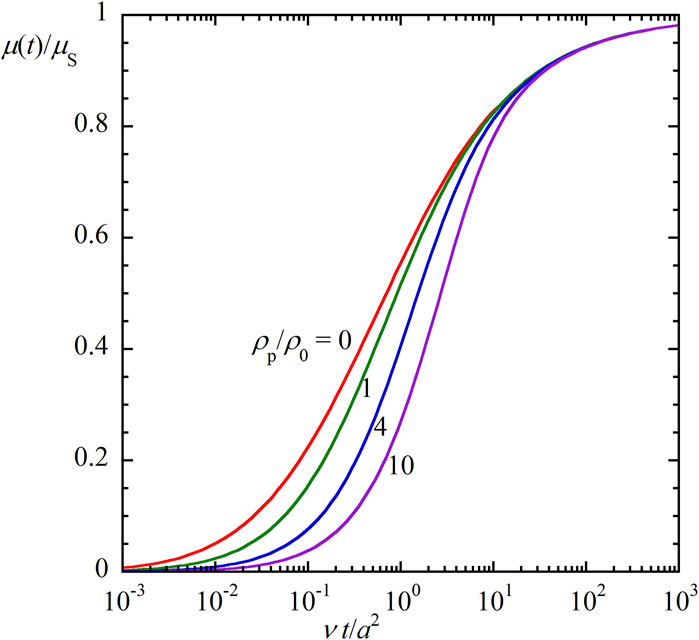
Figure 1. The ratio μ(t)/μ_s of the transient electrophoretic mobility μ(t) to the steady electrophoretic mobility μ_s for spherical colloidal particles of radius a and mass density ρ_p in a salt-free liquid medium of mass density ρ₀ and kinematic viscosity ν as a function of the scaled time νt/a² for four values of the mass density ratio ρ_p/ρ₀ (ρ_p/ρ₀ = 0, 1, 4, and 10).

Figure 2

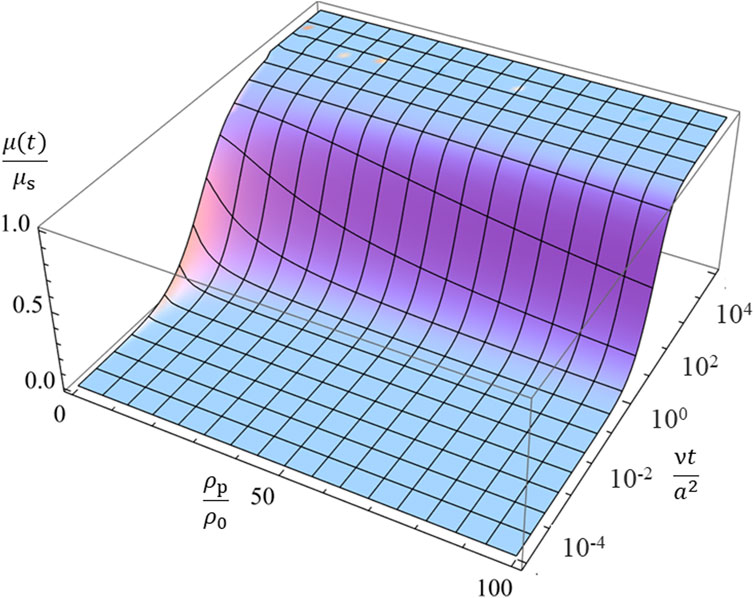
Figure 2. The 3-D plot of the ratio μ(t)/μ_s of the transient electrophoretic mobility μ(t) to the steady electrophoretic mobility μ_s for spherical colloidal particles of radius a and mass density ρ_p in a salt-free liquid medium of mass density ρ₀ and kinematic viscosity ν as a function of the scaled time νt/a² and the mass density ratio ρ_p/ρ₀.

4 Concluding remarks

We have developed a theory of the transient electrophoresis of colloidal particles in a salt-free medium, which provides vital information for designing effective electrophoresis measurement systems related to micro- and nano-fluidic lab-on-a-chip technologies. We first derived a general expression (Eq. 51 for the Laplace transform $\widehat{\mu }\left(s\right)$ of the time dependent transient electrophoretic mobility μ(t) of spherical colloidal particles in a salt-free liquid medium containing only counterions when a step external electric field is suddenly applied to the colloidal suspension. On the bases of this general expression for $\widehat{\mu }\left(s\right)$ , we derived an accurate analytic expression for μ(t), which takes the different forms for the low-surface-charge case (Eq. 76) and the high-surface-charge case (Eq. 77). Only for the low-surface-charge case, the transient electrophoretic mobility agrees with that of a sphere in an electrolyte solution in the limit of very low electrolyte concentrations. For the high-surface-charge case, however, the transient mobility becomes independent of the particle surface charge because of the counterion condensation effects. Finally, we derived a simple expression (Eq. 82) for the ratio of the transient electrophoretic mobility to the steady electrophoretic mobility, which is found to take the same form irrespective of the magnitude of the particle surface charge. Finaly, it is to be noted that since we have considered the transient motion of colloidal particles under a weak electric field, an overshoot phenomenon, which is sometimes observed in transient processes, is not observed.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

HO: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ayman, M., Saad, E. I., and Faltas, M. S. (2024). Transient electrophoresis of a conducting cylindrical colloidal particle suspended in a Brinkman medium. Z. fur Angew. Math. Phys. 75 (2), 53–23. doi:10.1007/s00033-023-02182-8

CrossRef Full Text | Google Scholar

Booth, F. (1950). The cataphoresis of spherical, solid non-conducting particles in a symmetrical electrolyte. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 203 (1075), 514–533. doi:10.1098/rspa.1950.0154

CrossRef Full Text | Google Scholar

Carrique, F., Ruiz-Reina, E., Arroyo, F. J., and Delgado, Á. V. (2010). Dynamic electrophoretic mobility of spherical colloidal particles in realistic aqueous salt-free concentrated suspensions. J. Phys. Chem. B 114 (18), 6134–6143. doi:10.1021/jp102350d

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, S. H. (2009). Transient electro-osmotic flow in cylindrical microcapillaries containing salt-free medium. Biomicrofluidics 3 (1), 12802. doi:10.1063/1.3064113

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, S. H. (2010). Electroosmotic flow in slit microchannel containing salt-free solution. Eur. J. Mech. B/Fluids 29 (5), 337–341. doi:10.1016/j.euromechflu.2010.04.003

CrossRef Full Text | Google Scholar

Chang, S. H. (2012). Electroosmotic flow in a dissimilarly charged slit microchannel containing salt-free solution. Eur. J. Mech. B/Fluids 34, 85–90. doi:10.1016/j.euromechflu.2012.01.020

CrossRef Full Text | Google Scholar

Chiang, C. C., and Keh, H. J. (2015a). Startup of electrophoresis in a suspension of colloidal spheres. Electrophoresis 36 (24), 3002–3008. doi:10.1002/elps.201500316

PubMed Abstract | CrossRef Full Text | Google Scholar

Chiang, C. C., and Keh, H. J. (2015b). Transient electroosmosis in the transverse direction of a fibrous porous medium. Colloids Surfaces A Physicochem. Eng. Aspects 481, 577–582. doi:10.1016/j.colsurfa.2015.06.021

CrossRef Full Text | Google Scholar

Delgado, A. V. (2001). in Interfacial electrokinetics and electrophoresis (New York: Dekker).

Google Scholar

Delgado, Á. V., Carrique, F., Roa, R., and Ruiz-Reina, E. (2016). Recent developments in electrokinetics of salt-free concentrated suspensions. Curr. Opin. Colloid and Interface Sci. 24, 32–43. doi:10.1016/j.cocis.2016.06.004

CrossRef Full Text | Google Scholar

Derjaguin, B. V., and Landau, D. L. (1941). Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes. Acta Physicochim. USSR 14, 633–662.

Google Scholar

Dukhin, A. S., and Goetz, J. P. (2001). Ultrasound for characterizing colloids. Particle sizing, zeta potential, rheology. Amsterdam: Elsevier.

Google Scholar

Happel, J. (1958). Viscous flow in multiparticle systems: slow motion of fluids relative to beds of spherical particles. AIChE J. 4 (2), 197–201. doi:10.1002/aic.690040214

CrossRef Full Text | Google Scholar

Henry, D. C. (1931) The cataphoresis of suspended particles. Part I.—the equation of cataphoresis, Proc. R. Soc. A Math. Phys. Eng. Sci., 133, 106–129. doi:10.1098/rspa.1931.0133

CrossRef Full Text | Google Scholar

Huang, Y. C., and Keh, H. J. (2005). Transient electrophoresis of spherical particles at low potential and arbitrary double-layer thickness. Langmuir 21 (25), 11659–11665. doi:10.1021/la051171q

PubMed Abstract | CrossRef Full Text | Google Scholar

Hückel, E. (1924). Die Kataphorese der Kugel. Phys. Z. 25, 204–210.

Google Scholar

Ivory, C. F. (1983). Transient electroosmosis: the momentum transfer coefficient. J. Colloid And Interface Sci. 96 (1), 296–298. doi:10.1016/0021-9797(83)90032-2

CrossRef Full Text | Google Scholar

Ivory, C. F. (1984). Transient electrophoresis of a dielectric sphere. J. Colloid And Interface Sci. 100 (1), 239–249. doi:10.1016/0021-9797(84)90432-6

CrossRef Full Text | Google Scholar

Keh, H. J., and Huang, Y. C. (2005). Transient electrophoresis of dielectric spheres. J. Colloid Interface Sci. 291 (1), 282–291. doi:10.1016/j.jcis.2005.04.108

PubMed Abstract | CrossRef Full Text | Google Scholar

Keh, H. J., and Tseng, H. C. (2001). Transient electrokinetic flow in fine capillaries. J. Colloid Interface Sci. 242 (2), 450–459. doi:10.1006/jcis.2001.7797

CrossRef Full Text | Google Scholar

Khair, A. S. (2012). Transient phoretic migration of a permselective colloidal particle. J. Colloid Interface Sci. 381 (1), 183–188. doi:10.1016/j.jcis.2012.05.038

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuwabara, S. (1959). The forces experienced by randomly distributed parallel circular cylinders or spheres in a viscous flow at small Reynolds numbers. J. Phys. Soc. Jpn. 14 (4), 527–532. doi:10.1143/JPSJ.14.527

CrossRef Full Text | Google Scholar

Lai, Y. C., and Keh, H. J. (2020). Transient electrophoresis of a charged porous particle. Electrophoresis 41 (3–4), 259–265. doi:10.1002/elps.201900413

PubMed Abstract | CrossRef Full Text | Google Scholar

Lai, Y. C., and Keh, H. J. (2021). Transient electrophoresis in a suspension of charged particles with arbitrary electric double layers. Electrophoresis 42 (21–22), 2126–2133. doi:10.1002/elps.202000336

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, E. (2018). Theory of electrophoresis and diffusiophoresis of highly charged colloidal particles. Amsterdam: Elsevier B.V.

Google Scholar

Li, M. X., and Keh, H. J. (2020). Start-Up electrophoresis of a cylindrical particle with arbitrary double layer thickness. J. Phys. Chem. B 124 (44), 9967–9973. doi:10.1021/acs.jpcb.0c07436

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, R. H., and Keh, H. J. (2021). Electrophoresis and electric conduction in a salt-free suspension of charged particles. Electrophoresis 42 (21–22), 2134–2142. doi:10.1002/elps.202100181

PubMed Abstract | CrossRef Full Text | Google Scholar

Masliyah, J. H., and Bhattacharjee, S. (2006). Electrokinetic and colloid transport phenomena. Hoboken: John Wiley and Sons.

Google Scholar

Morrison, F. A. (1969). Transient electrophoresis of a dielectric sphere. J. Colloid And Interface Sci. 29 (4), 687–691. doi:10.1016/0021-9797(69)90221-5

CrossRef Full Text | Google Scholar

Morrison, F. A. (1971). Transient electrophoresis of an arbitrarily oriented cylinder. J. Colloid And Interface Sci. 36 (1), 139–145. doi:10.1016/0021-9797(71)90250-5

CrossRef Full Text | Google Scholar

O’Brien, R. W., and White, L. R. (1978). Electrophoretic mobility of a spherical colloidal particle. J. Chem. Soc. Faraday Trans. Chem. Soc. Faraday Trans. 22 Mol. Chem. Phys. 74, 1607–1626. doi:10.1039/F29787401607

CrossRef Full Text | Google Scholar

Ohshima, H. (2002a). Electrophoretic mobility of a cylindrical colloidal particle in a salt-free medium. J. Colloid Interface Sci. 255 (1), 202–207. doi:10.1006/jcis.2002.8650

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohshima, H. (2002b). Electrophoretic mobility of a spherical colloidal particle in a salt-free medium. J. Colloid Interface Sci. 248 (1), 499–503. doi:10.1006/jcis.2002.8232

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohshima, H. (2003a). Dynamic electrophoretic mobility of spherical colloidal particles in a salt-free medium. J. Colloid Interface Sci. 265 (2), 422–427. doi:10.1016/S0021-9797(03)00470-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohshima, H. (2003b). Numerical calculation of the electrophoretic mobility of a spherical particle in a salt-free medium. J. Colloid Interface Sci. 262 (1), 294–297. doi:10.1016/S0021-9797(03)00190-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohshima, H. (2006). Theory of colloid and interfacial electric phenomena. Amsterdam: Elsevier B.V.

Google Scholar

Ohshima, H. (2022a). Approximate analytic expression for the time-dependent transient electrophoretic mobility of a spherical colloidal particle. Molecules 27 (16), 5108. doi:10.3390/molecules27165108

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohshima, H. (2022b). Transient electrophoresis of a cylindrical colloidal particle. Fluids 7 (11), 342. doi:10.3390/fluids7110342

CrossRef Full Text | Google Scholar

Ohshima, H. (2022c). Transient electrophoresis of a spherical soft particle. Colloid Polym. Sci. 300 (12), 1369–1377. doi:10.1007/s00396-022-05029-2

CrossRef Full Text | Google Scholar

Ohshima, H. (2023a). Transient dynamic electrophoresis of a spherical colloidal particle. Electrophoresis 45 (July), 706–711. doi:10.1002/elps.202300153

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohshima, H. (2023b). Transient electrophoresis of a spherical colloidal particle with a slip surface. Electrophoresis 44 (23), 1795–1801. doi:10.1002/elps.202200242

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohshima, H. (2023c). Transient gel electrophoresis of a spherical colloidal particle. Gels 9 (5), 356. doi:10.3390/gels9050356

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohshima, H. (2024a). Transient dynamic electrophoresis of a soft particle. Electrophoresis. doi:10.1002/elps.202300247

CrossRef Full Text | Google Scholar

Ohshima, H. (2024b). Transient electrophoresis of spherical colloidal particles in a multi-particle suspension. Colloid Polym. Sci. doi:10.1007/s00396-024-05269-4

CrossRef Full Text | Google Scholar

Ohshima, H., Healy, T. W., and White, L. R. (1983). Approximate analytic expressions for the electrophoretic mobility of spherical colloidal particles and the conductivity of their dilute suspensions. J. Chem. Soc. Faraday Trans. 2 79 (11), 1613. doi:10.1039/F29837901613

CrossRef Full Text | Google Scholar

Overbeek, J. T. G. (1943) Beih. Theor. Elektrophorese Relaxationseffekt, 54, 287–364. doi:10.1007/BF02556774

CrossRef Full Text

Ragab, K. E. (2023). An investigation of the transient electrophoresis of conducting colloidal particles in porous media using a cell model. Chin. J. Phys. 85 326–344. doi:10.1016/j.cjph.2023.07.024

CrossRef Full Text | Google Scholar

Saad, E. I. (2018). Start-up Brinkman electrophoresis of a dielectric sphere for Happel and Kuwabara models. Math. Methods Appl. Sci. 41 (18), 9578–9591. doi:10.1002/mma.5314

CrossRef Full Text | Google Scholar

Saad, E. I. (2019). Unsteady electrophoresis of a dielectric cylindrical particle suspended in porous medium. J. Mol. Liq. 289, 111050. doi:10.1016/j.molliq.2019.111050

CrossRef Full Text | Google Scholar

Saad, E. I., and Faltas, M. S. (2018). Time-dependent electrophoresis of a dielectric spherical particle embedded in Brinkman medium. Z. fur Angew. Math. Phys. 69 (2), 43–18. doi:10.1007/s00033-018-0939-4

CrossRef Full Text | Google Scholar

Sherief, H. H., Faltas, M. S., and Ragab, K. E. (2021). Transient electrophoresis of a conducting spherical particle embedded in an electrolyte-saturated Brinkman medium. Electrophoresis 42 (16), 1636–1647. doi:10.1002/elps.202100063

PubMed Abstract | CrossRef Full Text | Google Scholar

Spasic, A., and Hsu, J. P. (2005). Finely dispersed particles. Micro-. nano-, atto-engineering (Boca Raton: Taylor and Francis).

Google Scholar

Verwey, E. J. W., and Overbeek, J. T. G. (1948). Theory of the stability of lyophobic colloids. Amsterdam: Elsevier B.V.

Google Scholar

von Smoluchowski, M. (1921). “Elektrische endosmose und strömungsströme,” in Handbuch der Elektrizität und des Magnetismus, Band II Stationäre ströme. Editor E. Greatz (Leipzig: Barth).

Google Scholar

Wiersema, P. H., Loeb, A. L., and Overbeek, J. T. G. (1966). Calculation of the electrophoretic mobility of a spherical colloid particle. J. Colloid And Interface Sci. 22 (1), 78–99. doi:10.1016/0021-9797(66)90069-5

CrossRef Full Text | Google Scholar

Yu, C. W., and Keh, H. J. (2024). Transient slow motion of a porous sphere. Fluid Dyn. Res. 56 (1), 015503. doi:10.1088/1873-7005/ad220c

CrossRef Full Text | Google Scholar

Glossary