From classical to quantum machine learning: survey on routing optimization in 6G software defined networking

The sixth generation (6G) of mobile networks will adopt on-demand self-reconfiguration to fulfill simultaneously stringent key performance indicators and overall optimization of usage of network resources. Such dynamic and flexible network management is made possible by Software Defined Networking (SDN) with a global view of the network, centralized control, and adaptable forwarding rules. Because of the complexity of 6G networks, Artificial Intelligence and its integration with SDN and Quantum Computing are considered prospective solutions to hard problems such as optimized routing in highly dynamic and complex networks. The main contribution of this survey is to present an in-depth study and analysis of recent research on the application of Reinforcement Learning (RL), Deep Reinforcement Learning (DRL), and Quantum Machine Learning (QML) techniques to address SDN routing challenges in 6G networks. Furthermore, the paper identifies and discusses open research questions in this domain. In summary, we conclude that there is a significant shift toward employing RL/DRL-based routing strategies in SDN networks, particularly over the past 3 years. Moreover, there is a huge interest in integrating QML techniques to tackle the complexity of routing in 6G networks. However, considerable work remains to be done in both approaches in order to accomplish thorough comparisons and synergies among various approaches and conduct meaningful evaluations using open datasets and different topologies.

1 Introduction

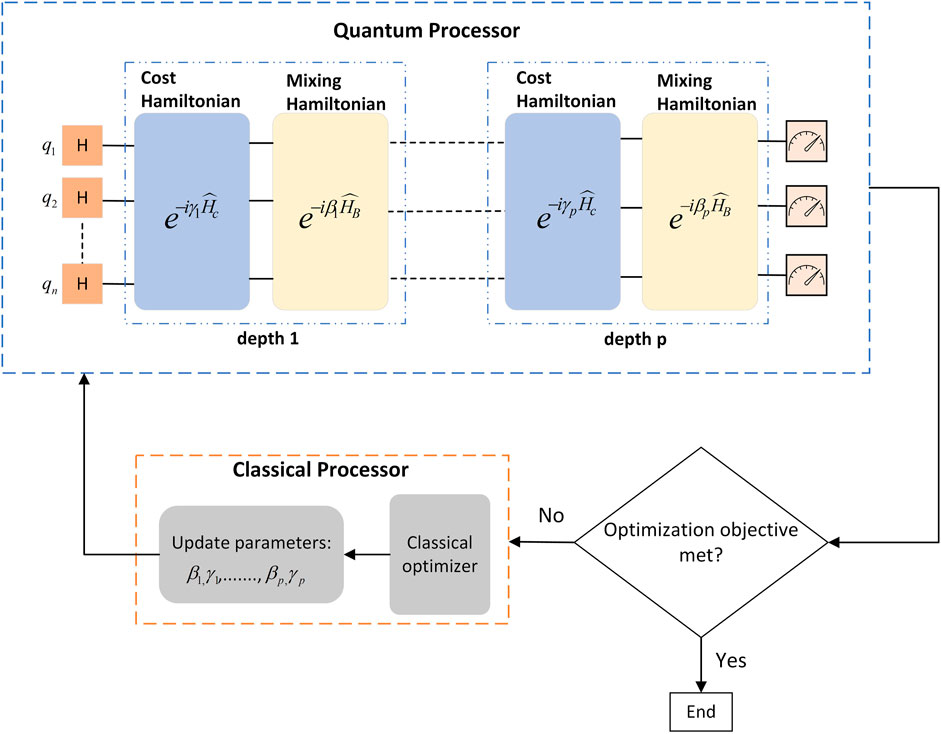
While the 5G era has just begun, the telecommunication industry and research community are already looking into what will be the next-generation of wireless communication, namely, 6G which is expected to outperform 5G by achieving outstanding Quality of Service (QoS) and enabling new applications beyond Internet of Things (IoT). However, such ambition will inevitably face multiple challenges and opportunities (Zhang et al., 2019b). Following this logic, 6G key performance indicators (KPIs) will increase by a factor of 10–100 (Banafaa et al., 2023). It is expected that 6G will be the first cellular generation that will support 1 Tbps peak data rates and connectivity density of 10 million devices/km². The latency requirement will take a range between 10 to 100 ms, traffic capacity will take a range between 1-10 Gbps2 and a reliability percentage up to 99,9999%. In Table 1, a comparison between 4G, 5G and 6G KPIs is represented. Moving beyond these metrics, one of the most marked evolutions in 6G will be its routing complexities, particularly concerning end-to-end routing, from user devices to destination services. Given the complexity and dynamicity of the topologies, the high degree of heterogeneity and the need for dynamic, adaptive, and intelligent networking systems. These aforementioned factors will contribute to the routing challenges in the following ways:

1) Dynamic and complex topologies: This refers to the changing structure of the network, where nodes (such as devices, cell towers and other network equipment) may frequently join or leave the network and connections between them may constantly change. Moreover, the topology may change rapidly with autonomous vehicles, drones, and mobile devices connected to the network. This continuous movement requires real-time updates to routing tables and paths, making static routing algorithms inefficient.

2) Higher degree of heterogeneity: With 6G potentially involving the integration of different types of networks (satellite, terrestrial, aerial) and integrating newer technologies, there is a high degree of heterogeneity that has to be taken into consideration. Ensuring smooth communication and efficient routing across such diverse networks can be very challenging (Chen et al., 2020; Cao et al., 2022).

3) Dense networks: 6G aims to support the growth of IoT devices, the device density is expected to grow exponentially, thus, managing connections between this massive number of devices requires robust routing strategies that can scale efficiently. Additionally, a higher density of devices can lead to congestion and interference, which might result in packet collision and delays. Furthermore, different devices and applications may have varying QoS requirements. Meeting these diverse demands in a network with this high number of devices would require more fine-tuned, sophisticated and dynamic routing strategies (Zhang et al., 2019b; Zhang et al., 2019b).

TABLE 1

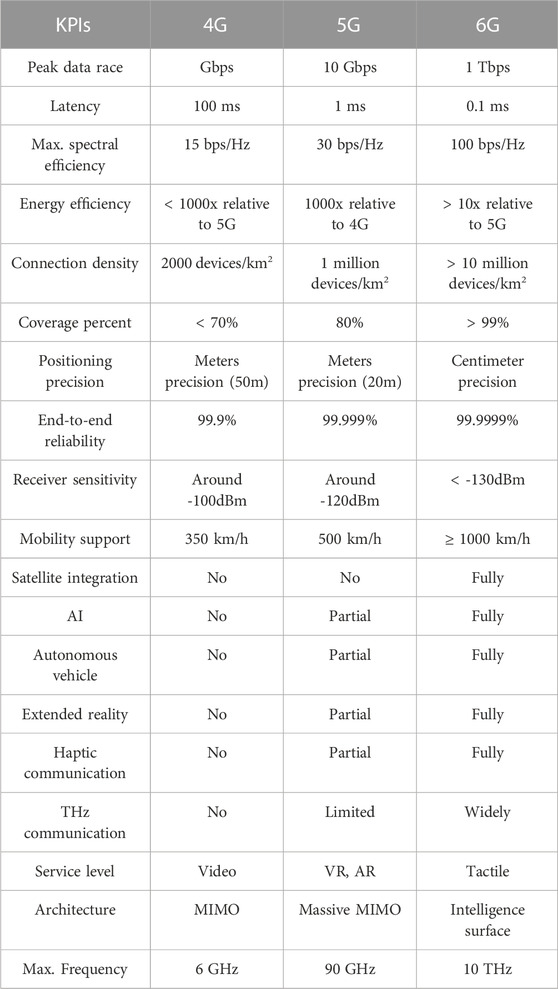
TABLE 1. 6G KPIs in comparison to 4G and 5G. Reproduced from Banafaa et al., 2023, licensed CC-BY-NC-ND 4.0.

On the other side, 5G technologies will still be valid for 6G, yet they will be extremely stressed. Such as Software Defined Networking (SDN).

In SDN (Lantz et al., 2010), the network intelligence is typically centralized in one network entity, the SDN controllers. These controllers are capable of configuring the different switching nodes of a network virtually and autonomously throughout the control plane, thanks to the global view and the centralized architecture of SDN. This is referred to as the decoupling of the data plane, which performs data processing, from the control plane that is responsible for allocating resources, defining the traffic routing policies and maintaining the network topology. This decoupling makes SDN solutions hardware and vendor-independent, thus enabling the efficient merging of different telecom equipment. In an SDN-based network architecture, the SDN controller holds information about the topology and the network status and periodically updates the routing table (the updates and the routing decisions are made in the control plane), instead of having each node update its own table, allowing for an adaptive network configuration, meeting diverse user requirements and maintaining an optimal network performance.

The efficiency of SDN is proven to be more evident in the case when the topology scale of the network grows ((Zhang and Yan, 2015; Gopi et al., 2017)). However, in 6G, the complexity and the density of network traffic flows are foreseen to bring an uneven load to the SDN controllers that must provide routing decisions constantly at a faster pace. Additionally, many applications require not only a high throughput but also need to ensure strict Quality of Service/Quality of Experience (QoS/QoE) requirements. In this context, SDN routing will become a critical problem in the large-scale and complex future 6G networks. SDN routing in 6G is a combinatorial optimization problem that falls under the non-deterministic polynomial-time hardness (NP-Hard) category (Van Mieghem et al., 2003), which can be defined, in computational complexity theory, as a category of problems that are at least as hard as the hardest problems in NP class (Hochba, 1997). Therefore, there is a clear need for real-time adaptive and customizable routing strategies to provide suitable network resources and the best service quality. For that reason, Machine Learning (ML) techniques have been studied to enhance SDN routing applications.

Since the seminal work of Boyan and Michael (Stampa et al., 2017), routing approaches based on Reinforcement Learning (RL) have gained special prominence since they do not require a supervision process and are optimal for dynamic networks that continuously change their topology, thus they require continuous updates of the routing tables. In 2019, the work of Kato et al. introduced the use of Deep Reinforcement Learning (DRL) as a solution more adapted to topologies of great dimension and high volatility (Zhao et al., 2019). Moreover, the advent of quantum computers makes it of interest to solve NP-Hard problems using quantum algorithms. An emerging effort to integrate ML and Quantum Computing (QC), referred to as Quantum Machine Learning (QML), was presented in (Nawaz et al., 2019). More recently, in 2021, the first optimal path calculation solutions through a QC-based technique has been obtained in (Harwood et al., 2021).

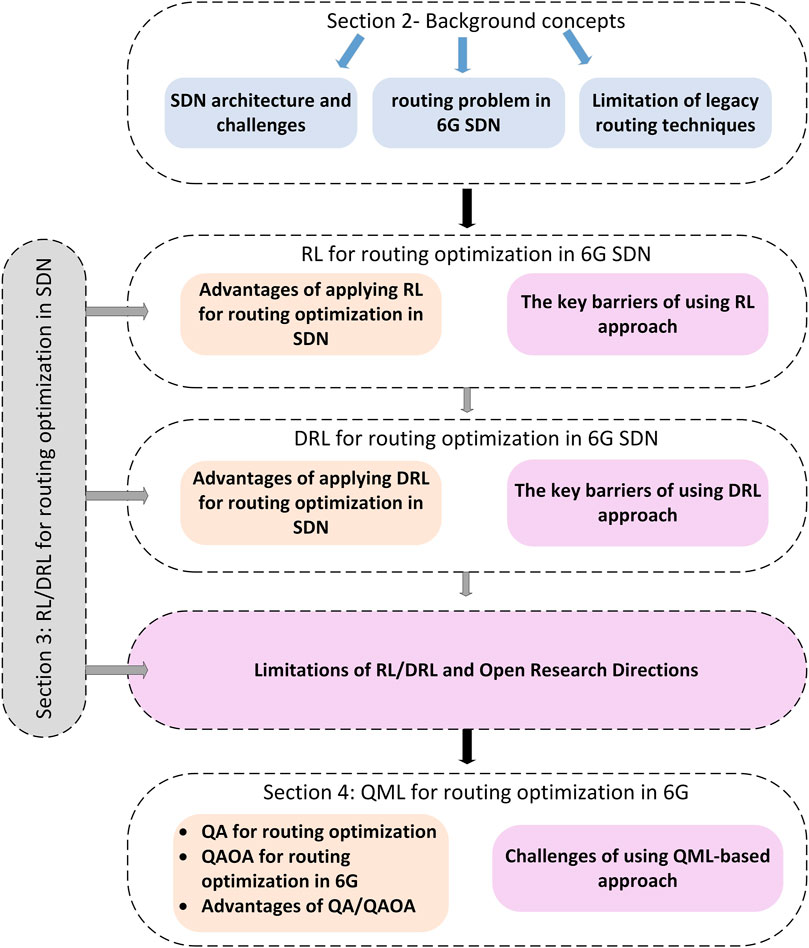
The objective of this paper is to survey the latest advances in the literature concerning routing optimization, starting with the emergent techniques based on RL/DRL and moving toward QML, its properties and the open research questions that come with it. The most recent studies using these three technologies are summarized and analyzed. The remainder of this paper is structured as follows: The background concepts related to SDN and routing and the limitations of legacy routing techniques in an SDN network are presented in Section 2. Section 3 is devoted to a literature review of the classical approach for routing optimization in SDN, including RL and DRL techniques. Section 4 presents an introduction to QC and QML, the challenges of applying QC are also discussed, then a discussion about Quantum Annealing (QA) and Quantum Approximate Optimization Algorithm (QAOA) based solution for routing optimization is presented. We review the latest works in this field and finally, Section 6 presents conclusions and open research directions. The structure of the paper is graphically represented in Figure 1.

FIGURE 1

FIGURE 1. Structure and Sections of the review paper.

2 Background concepts

In this section, we will explain three of the background concepts which are SDN, the routing problem in the SDN-6G scenario, and the limitation of legacy routing protocols in SDN. This brief introduction is intended to highlight the motivation and the key concepts behind the solutions presented in Section 3 and Section 4.

2.1 Software Defined Networking (SDN)

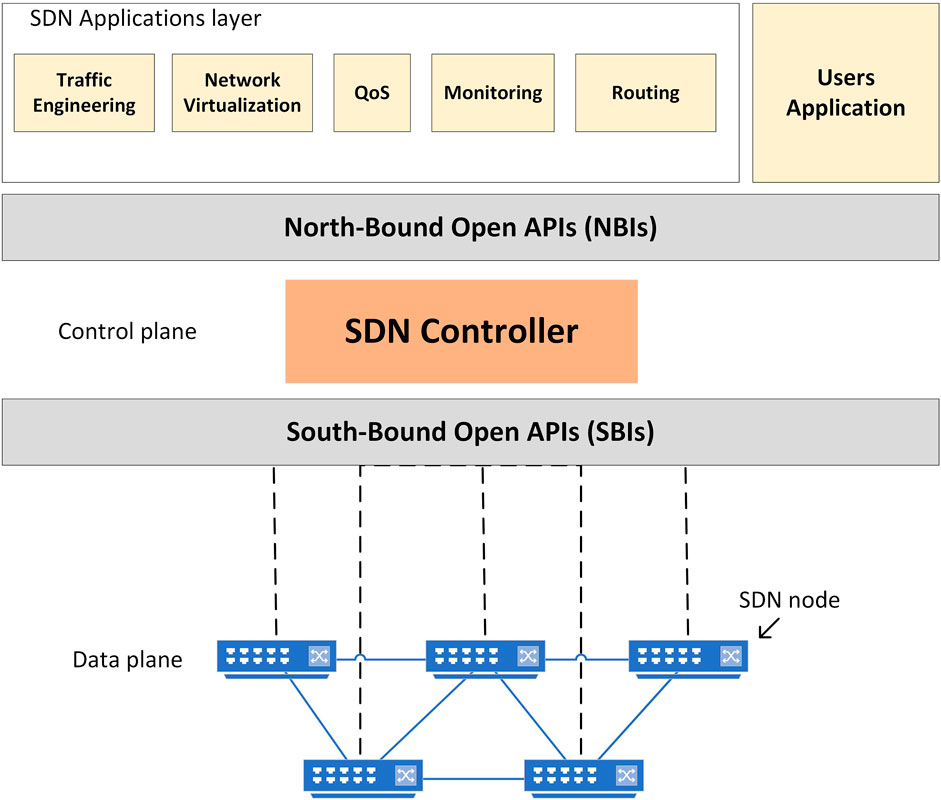
SDN is a network architecture that separates the control plane from the hardware plane, enabling more intelligent network programmability, flexibility and automation (Bosshart et al., 2013; Macedo et al., 2015). It is mainly composed of three layers connected via interfaces considered communication channels, as depicted in Figure 2.

FIGURE 2

FIGURE 2. Block diagram of SDN architecture.

The data plane layer is also known as the dummy devices (physical or virtual) layer. It is responsible for managing the user data traffic, handling the arriving frames (forward, modify or discard the frames) and providing network data to the control layer via Southbound Interfaces (SBIs). There are numerous SBIs protocols that can be implemented to connect the two layers, such as OpenFlow and Netconf (Macedo et al., 2015; Amin et al., 2021).

The control plane layer is considered the brain of the architecture, responsible for allocating resources, performing traffic management functions, routing and maintaining the network topology. Typical SDN controller platforms are Ryu, Open Network Operating System (ONOS) and OpenDaylight (ODL) (Macedo et al., 2015).

Above the control plane layer, the application layer executes the typical network functions such as routing and load balancing. The communication between these two layers is accomplished via Northbound Interfaces (NBIs) such as the RESTCONF protocol (Macedo et al., 2015). The main task of this layer is to define the global behavior of the network requested by the network administrator. Usually, SDN controllers are open-source frameworks containing application and control layers.

In summary, SDN differs from traditional networks by virtualizing the network components, giving the administrators a new level of visibility, which brings significant benefits like efficiency and agility to the network. Compared to The Open Systems Interconnection model (OSI model) (Figure 3) (Banjar et al., 2014). The OSI is a model that describes how computer systems communicate over a network using seven layers. As shown in Figure 3), the SDN model reduces the seven OSI layers to three: application, control and physical SDN layers.

FIGURE 3

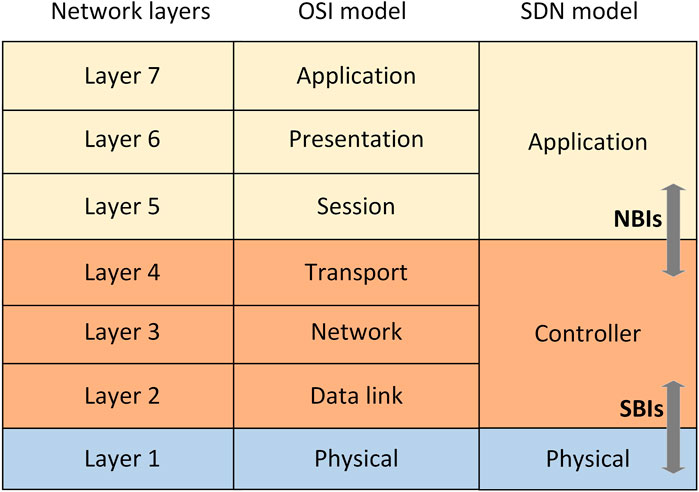
FIGURE 3. Comparison of OSI and SDN models. Reprinted, with permission, from Banjar et al., 2014. Copyright 2014 IEEE.

Traffic demand can change swiftly depending on the type of applications (Amin et al., 2021). This is where SDN comes in, its logically centralized view facilitates different routing aspects compared to legacy strategies. For example, it can easily extract the network topology and apply Shortest Path (SSP) algorithms, like Bellman-Ford (Goldberg and Radzik, 1993), to obtain the most efficient path. As a result, the routing problem becomes easily parameterized regarding resources, types of optimal routing, or cost functions. Nevertheless, even though SDN has been considered a key enabler technology for 5G and beyond and one of the prominent solutions for today’s enlarging network infrastructure, it is still immature. Indeed, benefits like enhanced configuration, automation and cost reduction, besides others, were presented in the literature (Thirupathi et al., 2019; Xie et al., 2019). Various critical challenges have been identified that affect the performance and the implementation of SDN (Shirmarz and Ghaffari, 2020). Those challenges can be divided into five categories: scalability, reliability and vulnerability, security, compatibility and performance optimization.

2.1.1 Scalability

In a centralized controller architecture, the risk of the controller becoming a network bottleneck is high. As the network enlarges the bottleneck becomes tighter, this will become a critical issue for 6G networks. Hence it is crucial to examine to what extent the network monitoring should be delegated to a single controller. Hierarchical SDN architectures were proposed as a possible solution to address this issue where the control plane is built from multiple layers of controllers and the load is shared between these layers (Ravuri et al., 2022). However, this solution suffers from the problem of the “synchronization between the controllers” and it is still an open research question that needs to be investigated (Zhang et al., 2019a; Domeke et al., 2022).

2.1.2 Reliability and vulnerability

A reliable system can be defined as a system that performs its tasks or functions without failure. In SDN, due to the separation between the control plane and the data plane, reliability relates to both layers which add extra precautions that have to be taken in advance to prevent any failures compared with traditional networks (Amin et al., 2021).

2.1.3 Security of the control layer

The control plane plays a decisive role in the SDN architecture, as it is the entity that manages and gives orders to the data plane devices, thus it has to be fully secured and protected which is not an effortless task. Moreover, with the advent of quantum computers, the control plane is more vulnerable to cyberattacks. One of the options that were proposed as a solution is Quantum Key Distributed (QKD) and Post-Quantum Cryptography (PQC) (Wang et al., 2019; García et al., 2023a). This research direction is still ongoing and there is a lot of room for investigations and research (García et al., 2023b).

2.1.4 Performance optimization of SDN

The main challenge of SDN is how it can handle high-level packet processing flows efficiently. Moreover, with the large number of connected devices and strict QoS requirements in 6G, it becomes even harder to ensure a satisfactory SDN performance. To tackle this issue, four scenarios are considered: routing optimization, resource management, QoS/QoE prediction and traffic classification (Xie et al., 2019). In this paper, we will focus on the routing optimization aspect and how it was addressed in the literature.

2.2 Routing optimization in 6G-SDN networks

In networking, routing can be defined as the problem of selecting paths to send packets from a source to destination nodes while fulfilling QoS requirements and optimizing network resources. The main concept behind routing optimization is to identify the best path between source and destination nodes in terms of a defined set of criteria and requirements. These criteria are represented as weights of a cost function used to determine the optimal path. Generally, defining a cost function depends on the technique chosen to address routing (i.e., Linear programming, and QML).

However, managing efficient connectivity between endpoint devices at first seems like a straightforward task, but the complexity quickly grows beyond what is possible to comprehend and manage with SDN when considering a scenario with thousands of endpoints where connections are dynamically changing. This picture becomes more complicated and challenging when point-to-multipoint connectivity, strict QoS requirements and a real-time decision scenario are considered, which is the 6G SDN routing situation. For this reason, routing in 6G becomes an NP-Hard problem (Puri and Tripakis, 2002), consequently, finding or designing a routing algorithm that can optimize the cost and reduce the complexity of the problem is becoming a prominent issue to be solved.

2.3 Limitation of legacy routing techniques in SDN environments

Conventional routing approaches do not perform well in SDN environments. For example, implementing the unaware-state techniques that follow fixed control methods such as shortest path algorithms (e.g., OSPF) (McKeown et al., 2008) will not be able to deal with dynamic topologies as they do not take advantage of SDN’s overall view to handle dynamic networks. Also, the Heuristic routing techniques that use specific algorithms to define quickly a good path to a destination node that is not always optimal in SDN (Xie et al., 2019), such as the Ant Colony Optimization algorithm. Moreover, the above approaches are computationally expensive and are not able to make real-time routing decisions in highly dynamic networks. In addition, the 6G network’s complexity will be difficult to predict, control and model. Thus, designing and implementing a routing optimization algorithm requires deep knowledge to establish mathematical models suitable for each type of application (Xu et al., 2018). Therefore, learning-based methods such as ML and QML have been introduced as promising solutions to routing optimization problems over the SDN architecture (Fadlullah et al., 2017; Mammeri, 2019; Nawaz et al., 2019).

In light of these routing challenges and the technological development that are coming with the development of 6G, the author’s goal in this survey is to point out the benefits and the limitations of classical ML and QML techniques for routing optimization in 6G-SDN networks and to highlight and discuss the open issues from a classical and a quantum perspective.

3 RL and DRL for routing optimization in SDN

In this Section, we will provide answers to four questions related to ML for SDN-routing optimization.

• Q1: How RL/DRL techniques can be applied to SDN-routing optimization?

• Q2: What are the tools and the performance metrics determined to show if the optimization technique fulfills the objective?

• Q3: What are the limitations of these methods?

• Q4: Can RL/DRL handle and fulfill the strict QoS requirements and the complexity of routing in 6G-SDN Networks?

In order to answer these questions, we present a summarized review focusing on some of the recent works (Table 2), limitations and open research questions.

TABLE 2

TABLE 2. Comparison of RL techniques for routing optimization in SDN.

3.1 RL concept for routing optimization in SDN

RL is an ML category concerned with mapping a situation to an action that can maximize/minimize the reward function. There are six main elements of a reinforcement learning system (Lewis and Vrabie, 2009).

• Agent: can be viewed as an AI algorithm that is perceiving its environment and trying to solve it.

• Policy: is the mapping between a perceived state s of the environment to action a π:s → a.

• Reward function: It tells the agent if the actions are correct or wrong by using rewards and penalties.

• State: It is the representation of the current environment in which the agent is.

• Action: It is the set of possible acts that the agent can take to change the current state.

• Environment: A simulation or a task that the agent is trying to solve (i.e., network) and it contains the set of actions, states, rewards and the final objective the agent needs to reach. Usually, we use Markov Decision Process (MDP) to describe the environment.

The process of the RL model can be summarized in three steps, the agent learns by interacting with the environment, 2) observing the resulting reward R_i, 3) modifying the action A_i accordingly to maximize the reward.

In order to map an RL framework into a routing problem, we can translate the components mentioned above as illustrated in Figure 4: the agent will be the RL algorithm chosen to be implemented, the reward function will be calculated depending on the chosen algorithm and the metrics taken into consideration (i.e., latency, throughput … ), the state presents the devices in the data plane layer, the actions are the links that we have between the devices and the environment is the overall network topology. RL takes advantage of the SDN architecture to obtain a centralized view and control, thereby, the RL agent can adjust the selected paths according to the network changes.

FIGURE 4

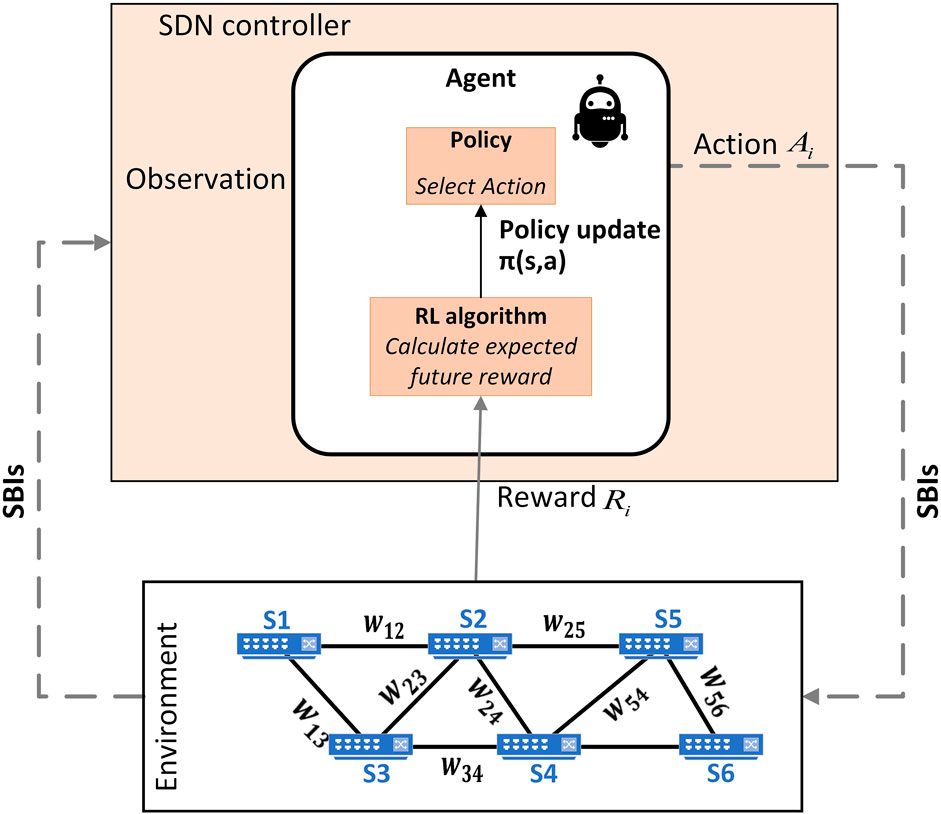
FIGURE 4. Schematic of a Reinforcement Learning approach for routing optimization in SDN where the SDN nodes represent the states (S_i) of the RL agent and w_ij represent the cost of the link.

Typically, RL algorithms are divided into the on-policy and off-policy models (Fakoor et al., 2020). In on-policy algorithms, given a state, the agent translates an action into a reward value and it uses this value for deciding future actions. i.e., the policy for updating and the one for taking action is the same. An example of an on-policy algorithm is the State-Action-Reward-State-Action algorithm (SARSA) (Qiang and Zhongli, 2011). While in the off-policy algorithms, the agent learns from observed actions (including past and exploratory actions), then it uses the accumulated knowledge to take future actions; this means that the policy for updating is different than the one for taking actions. An example of an off-policy is the Quality-Learning algorithm (Q-learning) (Mehta and Meyn, 2009). In general, for networking problems, off-policy algorithms are more suitable as they are able to learn from data collected by any given policy (more flexible), unlike off-policy algorithms which can not be used unless the learning data was collected using the same policy.

3.2 Related work on RL for routing optimization in SDN

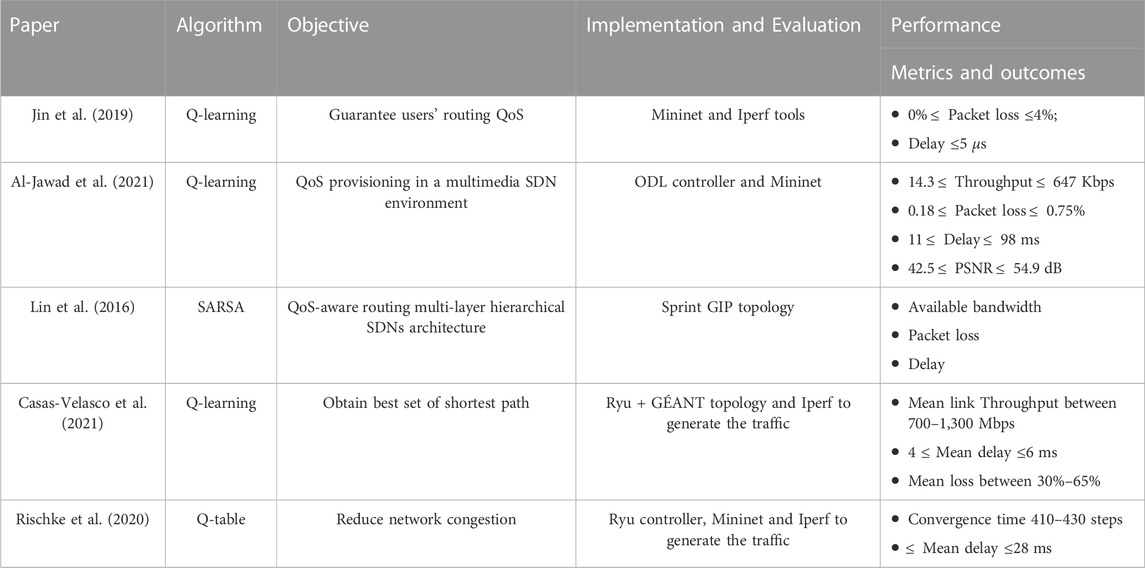
To put the contributions of this survey into context, the first step is to review some of the recent works related to RL techniques applied to SDN routing, which are summarized in Table 2. This table presents the reviewed studies, the algorithm used, the objective of the paper, implementation and evaluation tools, performance metrics and the limitation.

(Jin et al., 2019) introduced a routing QoS security method based on a Q-learning technique. The authors proposed path planning using four modules: link discovery, link classification processing, intensive training and the Q-value table sending module. The experimental topology consisted of 7 switches and 16 hosts, relying on the Mininet tool to build the underlying network. Moreover, the experimental result of Q-learning was compared with Equal-cost multi-path routing (ECMP) and colony algorithms. ECMP is a routing strategy that aims to increase available bandwidth by balancing the traffic load across multiple paths (Iselt et al., 2004). On the other hand, a colony algorithm solves computational problems by searching for optimal solutions in graphs within a set of possibilities, similar to how ants search and plot (Lin and Shao, 2010). The results showed that Q-learning outperforms the other two algorithms in terms of packet loss and delay for four different types of services (session, streaming media, interactive and data class service).

Al-Jawad et al. (2021) proposed an RL-based framework to improve QoS provisioning within a multimedia-based SDN environment. As a proof of concept, a comparison was made with four other algorithms, Minimum Hop Algorithm (MHA), which selects the optimal route regarding the number of hops between source and destination nodes, Shortest Widest Path (SWP) algorithm which chooses the optimal route that has the maximum available bandwidth, SWP finds the practical path with the shortest route. If there are various such routes, it selects the one with the maximum available bandwidth and the Minimum Interference Routing Algorithm (MIRA) that uses the concept of ingress-egress pairs to decrease the interference between the routes when new requests arrive. To evaluate the algorithms under study, (Al-Jawad et al., 2021), create a dynamic network considering three factors: Topology of the network in which three realistic topologies picked from Internet Topology Zoo was deployed: GetNet, a small scale- 7 nodes and eight links), Sprint (middle scale- 11 nodes and eight links) and AT&T (large scale—25 nodes and 56 links). Service type in which four types of traffic classes (live HD video streaming, SD video streaming, Web browsing and file transfer) were associated with two types of services (QoS and background traffic). The network load level was configured into three scales: low, medium and high load levels. Results reported in (Al-Jawad et al., 2021) show that the RL-based method reduces the packet loss by up to 0.75% and fulfills the Service Level Agreement (SLA) requirements based on QoS parameters, even in the case of a wide network with high traffic demands. On the other hand, the performance of the other algorithms dropped significantly.

Lin et al. (2016) consider the scenario of routing in a hierarchical control architecture, where they combined the work of (Hassas Yeganeh and Ganjali, 2012; McCauley et al., 2013) by proposing a QoS-Aware Adaptive Routing (QAR) technique based on RL and multi-layer control architecture. The proposed architecture contained three levels of controllers; a slave, a master and a super controller. The slave controllers dispatch the messages to the switches and provide some of the control functions. Each master controller is answerable for signaling inside its subnet, while the one-super controller is in charge of regulating the whole network functionalities and has full access to all the switches. The simulations showed that the QAR outperforms Q-learning with fast convergence when considering QoS provisioning.

Casas-Velasco et al. (2021) use the concept of Knowledge Defined Networking (KDN) to deploy their algorithm named Reinforcement Learning and Software-Defined Networking for Intelligent Routing (RSIR). This concept consists of adding one extra plane, the knowledge plane, to the traditional SDN architecture, which is fed by data collected by the management plane. More precisely, they propose an RL-based algorithm that works proactively by filling the flow tables of the switches beforehand for all the traffic matches. The evaluation was implemented in a prototype with real traffic matrices using GÉANT topology in Mininet and a comparison was made against the classical Dijkstra algorithm. The provided results showed that the mean loss values of the RSIR were on an average of 10%–50% lower than the loss ratio of Dijkstra and the mean link throughput was 26% lower than Dijkstra however, the mean link delay of RSIR was higher by 3% than Dijkstra.

Rischke et al. (2020) considered tackling a dynamic network where traffic loads vary significantly by creating a model-free framework based on RL entitled QR-SDN. The proposed approach uses the concept of different routing paths to distribute the traffic flows, i.e., the routing traffic will be sent/distributed over different routes sharing the same source-destination pairs during traffic peaks to avoid network congestion, thus decreasing the latencies and the convergence time. QR-SDN was compared against the classic Shortest Path First (SPF) algorithm where the Delay was set as the cost.

In Table 2, we provided a detailed comparison of the work related to RL techniques for routing optimization in SDN from perspectives of algorithms, objectives, implementation and evaluation, performance metrics and outcomes and limitations. From the concerning studies, we conclude that most of the studies:

• Used a Q-learning algorithm and this is due to the fact that Q-learning is an off-policy algorithm that is able to compare the expected rewards of available actions without the need for an environment model.

• Used Mininet for emulation and Ryu controller for their implementations and this is because they are easy to implement and better for prototyping.

Moreover, all the results suffer from the lack of scalability, as most of the proposals adopted simple and wired network topology (GÉANT, NSFNET) to evaluate their approaches, which imposes three research questions; how can we address the scalability issue in the case of larger networks? Why RL is disabled to manage high-dimension networks and how can we improve its performance?

To answer these questions, DRL techniques that combine RL and DL were introduced as an alternative solution for routing optimization in SDN.

3.3 DRL concept for routing optimization in SDN

The term “Deep” in Deep Reinforcement Learning (DRL) comes from the fact that we use Deep Learning (DL) within RL techniques (Arulkumaran et al., 2017). DL is a sub-field of ML that utilizes multiple Neural Network (NN) layers to extract a set of outputs from a set of inputs. The concept behind DRL is that instead of using RL algorithms to create the Q-tables that output the policy, a Neural Network (NN) is incorporated to approximate the policy π(s,a,θ), where θ is the weights of the neural network. Following the same Logic as what we explained in Section 3.1, mapping DRL elements to routing optimization in SDN is the same as RL, Figure 5.

FIGURE 5

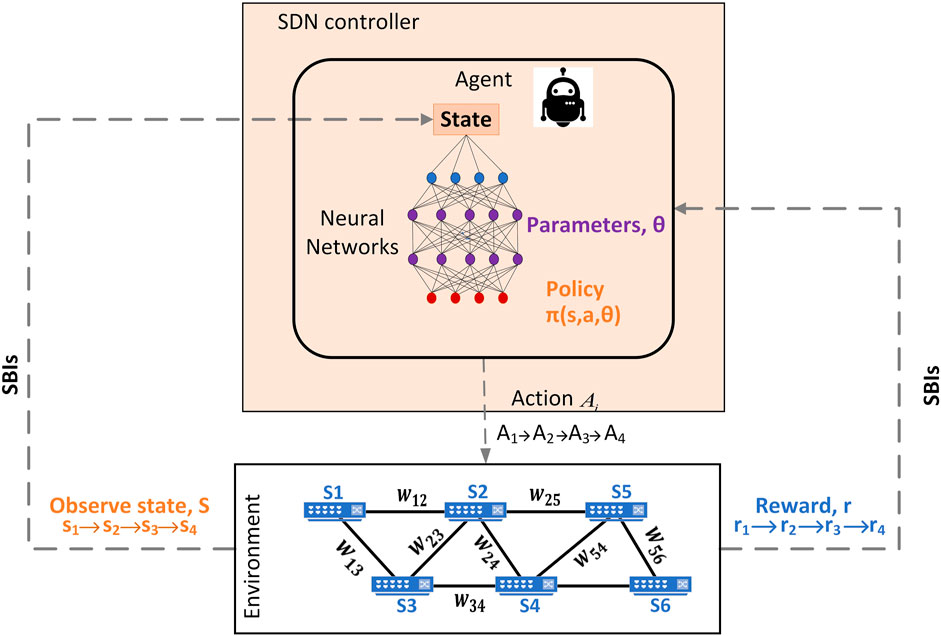
FIGURE 5. Schematic of a Deep Reinforcement Learning approach for routing optimization in SDN where the SDN nodes represent the states (S_i) of the RL agent and w_ij represent the cost of the link.

Similar to RL, DRL algorithms are also divided into two big categories: Model-based and Model-free algorithms. In the model-free category, we assume that we have a primary model for how the environment works and how it evolves according to the MDP. It uses NN/Deep NN to approximate the reward function. This approach is based on understanding the rules of the environment. Hence it does not require a long training process to achieve acceptable rewards. Unlike the model-based, DRL algorithms in the model-free category do not have a primary representation of the environment. To predict the best action of each state, NN and Deep NN are combined with trained parameters θ to express the policy. Usually, the amount of information gathered from one single action is not enough. For that, to improve the approximation of the action’s reward, we need to go through a massive.

3.4 Related work on DRL for routing optimization in SDN

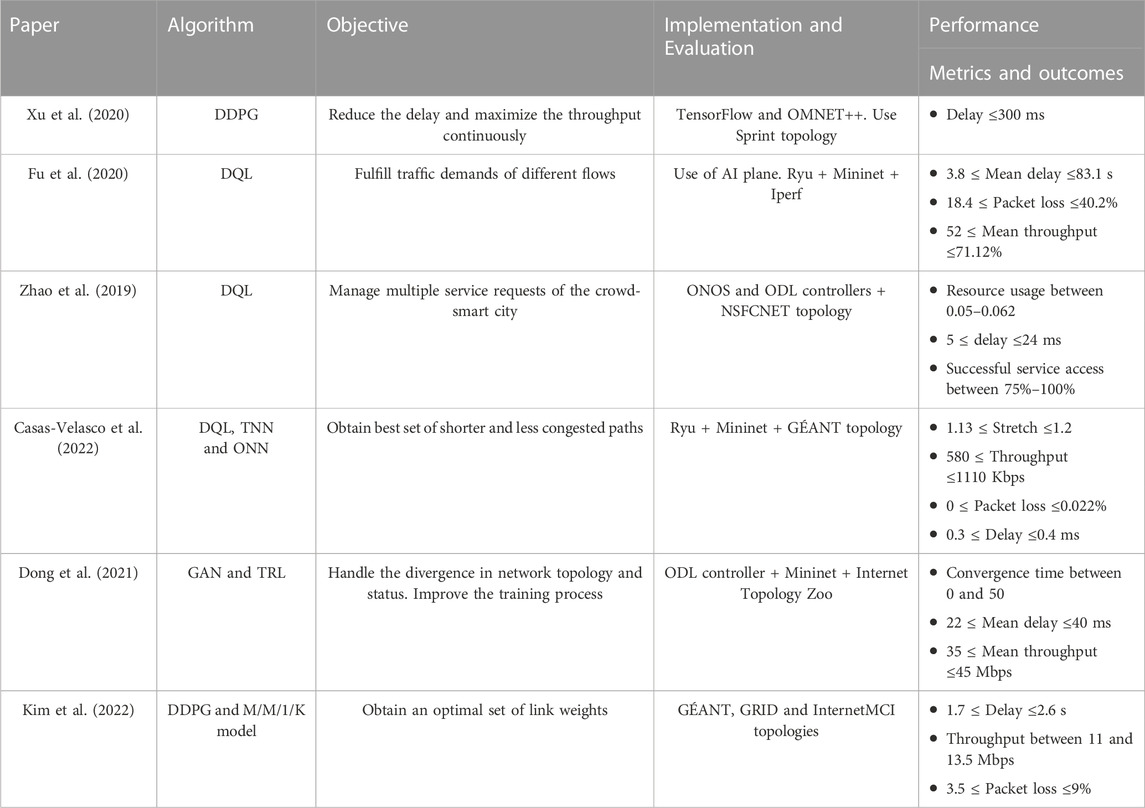
In decision-making problems, such as routing, representing the functions of classical RL such as the policy and Q values, might become extremely complex when the states and the actions of the MDP are high-dimensional (Haj-Ali et al., 2019). Unlike RL, DRL techniques are more scalable as they have the advantage of using DL to abstract the different levels of data and it represents the RL learned functions as a neural network, which makes them more suitable for high-dimension problems. In this respect, in this section, we review the works related to DRL for routing optimization in SDN which are summarized in Table 3.

TABLE 3

TABLE 3. Comparison of DRL techniques for routing optimization in SDN.

Xu et al. (2020) integrated a Deep Deterministic Policy Gradient (DDPG) mechanism that can continuously realize a black-box optimization, able to enhance network performance. To simulate the environment, a Sprint network topology that contains 25 nodes connected with 53 links was used. The proposed approach was compared to the conventional OSPF protocol and a randomly generated routing configurations technique regarding the delay in terms of traffic load for the random algorithm as well as packet transmission for OSPF. Results show that the performance of the DDPG algorithm exceeds the one of OSPF in terms of delay under different traffic loads.

Fu et al. (2020) addressed the problem of satisfying the demands of different flow types in SDN-base data center networks. The authors added an AI plane to the SDN architecture in which a Deep Q-learning (DQL) technique that uses neural networks instead of a Q-table was deployed, able to generate intelligent routing strategies for two types of flow: mice flow or elephant flow, where mice-flows transmit a small amount of data and last for a short time, while elephant flows do the reverse. DQL was compared to ECMP and Selective Randomize Load Balancing (SRL)+FlowFit algorithms on a Fat-tree topology with 16 servers and 20 switches.

Zhao et al. (2019) proposed a Deep Reinforcement Learning based smart (DRLS) routing algorithm to reduce network congestion and boost the network capacity to support smart city services and sectors (i.e., smart homes, smart transportation, smart building and smart healthcare). The authors analyzed SDN-enabled Ultra-Dense Networking (UDN) crowd management in smart cities with Mobile Edge Computing (MEC) technology. In (Zhao et al., 2019) the problem is defined in terms of managing the network resource considering the high cost of deploying the infrastructure and maintenance and balancing service access speed to guarantee a high QoE of the crowd. To validate the efficacy of DRLS, a comparison with the conventional OSPF and an enhanced version of OSPF (EOSPF) is made. The study results demonstrate the high performance of DRLS in terms of maximizing the successful service access rate and network resource usage with a different number of request aggregation spots.

As a follow-up of their previous work (Casas-Velasco et al., 2021; Casas-Velasco et al., 2022) used DL with RL for routing optimization in SDN. The approach entitled DRSIR, uses path-state metrics, a Deep Q-learning algorithm, experience memory delay, Target Neural Networks (TNN) and Online Neural Networks (ONN) to compute the best paths in SDN. ONN is an ML technique that trains the model over a consecutive dataset instead of using the entire dataset at one time, then, the model is used to predict future data. For evaluating the performance of DRSIR, the GÉANT topology of 23 nodes with 37 links and a 48-topology with 60 links that was generated using the Barbasi-Albert algorithm, were used, each switch in both topologies had a host for the recipient and forward traffic. However, the weight values (available bandwidth, path delay and packet loss ratio) in their reward function had the same preference, so different QoS requirements were not considered. Results reported in (Casas-Velasco et al., 2022) show that DRSIR outperforms the RSIR and the four variants of the Dijkstra algorithm in terms of stretch, link throughput, packet loss and delay.

Dong et al. (2021) introduced a DRL approach that makes use of Generative Adversarial Networks (GAN) and Transfer Reinforcement Learning (TRL) methods to tackle the three common challenges of routing: the varying networks status distribution, the inconstant network topology and the need of convergence speed. The GAN which is a DL technique that uses two NNs to produce new data instances similar to the training set was applied to speed up the training process and improve its efficiency. TRL, which is a method that exploits the knowledge from other sources of agents trained on similar tasks, was used to handle the changes in the network status or topology and to adapt the proposed model to the new environment. GAN-based TRL was evaluated over three real-world topologies: T-lex in Tokyo-Japan, NSFNET in the USA and HARNET in Hong Kong-China. The authors used ACKTR (Actor-Critic using Kronecker-factored Trust Region—pronounced “actor”) and naive transfer as their benchmark algorithms to evaluate the performance of the proposed model over different network sizes (from 15 to 50 nodes) regarding convergence time, average delay and throughput. For the GAN-based TRL model, the gap in the convergence time between a small network (15 nodes) and a large one (50 nodes) was minimal compared to the others. Moreover, GAN-based TRL maintained a decent average throughput value of up to 45 Mbps over the different network sizes. However, the average delay values of the GAN-based TRL and ACKTR were highly close.

Kim et al. (2022) addressed the issue of routing from a different angle by deploying an M/M/1/K queue-based network model to overcome network performance degradation during the DRL techniques’ learning process. In their approach, a DDPG algorithm was adopted to compute the optimal link weights to reduce end-to-end delay and packet losses of the network. The proposed method was compared to the naive and de facto hop-count-based routing methods and evaluated under three topologies (Grid, GÉANT and InternetMCI) regarding the delay, the packet loss, and the throughput concerning the number of iterations and the number of flows. The results indicate that the proposed approach outperforms the alternatives. However, the improvement was not substantial, as the outcomes were closely comparable to those derived from the naive and de facto hop-count-based strategies.

In Table 3, we summarized the work related to DRL techniques for routing optimization in SDN from perspectives of algorithms, objectives, implementation and evaluation, performance metrics, outcomes and limitations. From the related studies, we conclude that most of the studies.

• Compared the proposed approaches to OSPF or Dijkstra. Few works have made a comparison with other ML techniques (such as in Casas-Velasco et al. (2022), a comparison between Q-learning and deep Q-learning was made).

• Used DDPG and DQL algorithms that belong to the model-free category and this is due to the fact that model-free are computationally cheaper and the agents are easier to train compared to model-based algorithms.

3.5 Limitations summary of RL/DRL for routing optimization in SDN and open research directions

RL and DRL are powerful and advanced frameworks for decision-making problems. The idea behind these two approaches is that the agents take actions by interacting with the environment in order to maximize the reward and optimize its efficiency without labeled data. Moreover, because of their flexibility and adaptability, compared to conventional routing methods (including supervised and unsupervised learning), they are mostly adopted for routing scenarios, as they rely on the trial-and-error process that can set and adjust the routing decision based on current observed status (through the interaction with the environments). However, when specifically considering the demands and the challenges of 6G, there are reasons why these two approaches might not be entirely sufficient.

• The Convergence Time: Training a DRL model is time-consuming and does not scale efficiently because it requires a large space-action control that depends on the network size, thus making the algorithm difficult to converge (known as the Curse of Dimensionality (Chen, 2009)).

• Sample Efficiency: It refers to the amount of experience that the algorithm needs to generate during the training to reach a certain level of performance. However, an RL algorithm, especially DRL, requires a significant number of samples to learn an optimal policy.

• Non-stationarity: One fundamental assumption of RL is that the environment is not dynamic. However, 6G networks will be highly non-stationary/dynamic due to several factors such as user mobility, adaptive applications and integration of different types of networks (mentioned in section 1).

• Scalability issue of large tables: The Q-tables size in RL algorithms grows with the network size. A larger Q-table increases the complexity of the states, the execution and the convergence time

• Exploration vs Exploitation Dilemma: RL models, by nature, switch between exploring new and exploiting known actions to maximize the reward. When the size of the network increases, the cost of exploration may become prohibitive. Furthermore, in the scenario of a complex and dynamic network, exploration operations may become too slow to successfully react to any change in the environment.

Furthermore, our literature study on RL/DRL for optimal routing in SDN, reveals that most of the authors compared their proposal algorithms with shortest path algorithms (such as OSPF and Dijkstra) in terms of packet loss, delay and throughput. Additionally, most of the topologies selected for the evaluation are GÉANT and NSFNET (all wired networks). Our conclusion is that, in the case of small and simple topologies, RL is more suitable as it is easier to implement (compared to DRL) and gives prominent results. However, as the topology grows in complexity and size, DRL is preferable. On the other hand, there is still much work to be done in tackling SDN routing for large-scale and dynamic networks. Also, additional metrics such as node energy consumption and high robustness were not considered. On top of that, with the emergence of 6G, the complexity of the network will be even higher, accompanied by more restricted QoS requirements and constraints applications such as Massive-IoT (M-IoT), than the previous cellular generation.

In conclusion, while RL and DRL have demonstrated potential across various applications, their inherent limitations become more noticeable, especially within the dynamic, dense, and demanding context of 6G networks. This highlights the need to explore alternative and more powerful computing solutions that match 6G’s expected performance. In this light, the emergence of QC and QML-based techniques becomes particularly interesting. These quantum-based technologies, with their ability to address complex problems in high-dimensional spaces, offer a promising approach to address the routing challenges of 6G.

4 Quantum machine learning for 6G routing optimization

4.1 Introduction and motivation of QC and QML

Unlike classical computers that use bits to process information, quantum computers use quantum bits (qubits). Quantum computers, unlike classical ones, can rely on three quantum physics principles.

• Superposition: qubits can be in superposition which means they can represent from just two states 2ⁿ unique binary pattern in parallel, where n is the number of qubits in the quantum system.

• Entanglement: it is the state where two qubits are strongly correlated so that gaining information about one of them gives you immediate information about the other no matter how far these systems are (Steane, 1998).

• Quantum Parallelism: it is considered the most crucial characteristic in numerous quantum algorithms. This property allows quantum computers to process a large number of classical inputs in one single quantum computational step.

The power provided by combining the techniques of ML and the inherent features offered by QC led to a new framework called Quantum Machine Learning (QML). The main principle of QML is to encode classical data and classical algorithms into a manageable quantum language so that they can be processed by a quantum computer (Khan and Robles-Kelly, 2020). There are several encoding methods that were proposed such as Hamiltonian encoding, Qsample encoding and amplitude encoding (Sergioli, 2020; Sierra-Sosa et al., 2020). Because QML proved that it can outperform classical ML by decreasing the computational complexity of some heavy operations, reducing the learning process and providing an exponential speed-up (Nawaz et al., 2019; Bhat and Alqahtani, 2021), numerous scientific research propose it as a convenient solution for real-time optimization and computationally complex 6G applications such as Massive-IoT (M-IoT), robotics, unmanned vehicles, Virtual Reality (VR) and Augmented Reality (AR) (Nawaz et al., 2019; Akyildiz et al., 2020; Duong et al., 2022).

Moreover, several works presented QML as a potential solution that can reduce/break the complexity of NP-hard optimization problems (Zahedinejad and Zaribafiyan, 2017; Khumalo et al., 2022), more specifically, combinatorial optimization problems. One of the well-known applications of combinatorial optimization problems is routing optimization (Oliveira and Pardalos, 2005). With the huge surge in the number of connected devices (everything is connected to everything and everywhere), QML can be considered a potential solution for routing optimization, especially in M-IoT scenarios in 6G. In fact, when solving combinatorial optimization problems, Classical Parallelism (CP) with conventional hardware typically can reduce the complexity by order of O(P), where P is the number of parallel processes, while Quantum Parallelism (QP) reduces the complexity to the order of O$(\sqrt{N})$, where N is the size of the dataset. Therefore, in this section, we will survey the latest works related to QML for routing optimization.

4.2 Types of quantum computing

Many Industry and research institutes can already provide access to advanced cloud-based quantum hardware as well as gate-based quantum computers (James, 2022). In addition, fault-tolerance quantum computers are expected to become available within the upcoming years (Chow et al., 2021; Wang and Liu, 2022). Today, there are three designs of quantum computers based on the number and the type of qubits (Ladd et al., 2010), as represented in Table 4:

TABLE 4

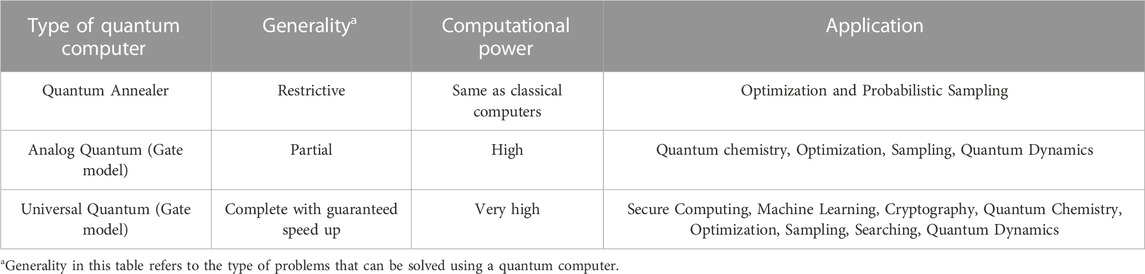
TABLE 4. Types of quantum computers. Based on data from Das and Chakrabarti (2008) and Tacchino et al. (2020).

• Quantum Annealers: They are a type of Adiabatic Quantum Computation (AQC) processors. Quantum annealers are the least powerful and most restrictive type of quantum computing. In order to use quantum annealer processors, the problem has to be expressed as an optimization task. D-wave and Fujitsu have made their quantum annealing computers publically available (Fijutsu, 2016; McGeoch et al., 2019).

• Analog Quantum simulators: They are able to simulate complex quantum systems. However, they are limited to solving specific types of problems. An example of this processor is the Ion Trap systems built by Harvard University and the National Institute of Standards and Technology (NIST) (NIST, 1995). These machines comprise between 50 and 100 qubits. Both quantum annealer and analog quantum computers are considered as Not-Universal Quantum Computers as they are built specifically to solve certain niche problems better than classical computers.

• Universal Gate Quantum Computers: They are the hardest to build and the most powerful as they can “theoretically” implement any quantum system (Tacchino et al., 2020). They are considered “universal” because they can execute all the quantum algorithms known till now (Stephen Jordan, 2011), and they can run any complex computation task and achieve the best solution faster than classical computers (Quantum Supremacy). In Universal Gate Quantum Computers, as the name indicate, the problem to solve has to be expressed in terms of quantum gates. Ideally, it is conjectured that Universal quantum computers will contain between 100,000 qubits to 1 M qubits. IBM, Google and Rigetti among others are trying to build quantum computers using this technology paradigm (Chow et al., 2021; James, 2022; Wang and Liu, 2022).

Generally, in Quantum Annealing (QA), the idea is to harness the natural evolution of quantum states without any control over that evolution. On the other hand, in gate model quantum computers, the aim is more ambitious. The goal is to control and manipulate the evolution of that quantum states over time using quantum gates; such a goal is difficult to achieve because quantum systems tend to be incredibly delicate to work with. However, having that amount of control enables solving a wider range of problems. These differences are the reason why it is been possible to scale up the quantum annealing-based processors to over thousands of qubits (D-Wave; 5640 qubits, Fujitsu; 8192 qubits), where the state-of-the-art in gate model quantum computing is around hundreds of qubits (IBM; 433 qubits, Google; 53 qubits).

4.3 Challenges of quantum machine learning

Despite many efforts toward building the first quantum computer, we are still in the Noisy-Intermediate-Scale Quantum (NISQ) era where we can run only hybrid algorithms. The core of hybrid algorithms is to use NISQ processors to compute and measure the results and the classical computer is used to improve these results by correcting some of the generated noise. Fully quantum-based algorithms face three main challenges.

• Complexity: Encoding and mapping a problem to a quantum computer require deep knowledge of mathematics, quantum physics and classical physics, especially for NP-Hard problems.

• Lack of standards: QML is still relatively a young field and there are not yet any general standards that can be followed in order to implement QML solutions for networking scenarios.

• Universal set of quantum gates: The type of algorithms that we can run on a quantum computer or a quantum simulator is bounded by the number and the quality of the quantum gates. Therefore, the type of problems we can solve using a quantum computer is still limited.

Researchers are trying to overcome these key barriers. Google and IBM for example, are targeting to build a “fault-tolerance-quantum computer” with one million qubits by 2030 (Lucero, 2021; IBM, 2022a) where more powerful quantum algorithms such as Grover’s algorithm for searching and Shor’s algorithm for factorization can be processed. Moreover, small-scale quantum computers with 50–100 qubits are already available and ready to be used and accessed via Quantum Cloud computing (Lucero, 2016). Furthermore, to standardize and facilitate the integration of QC techniques in 6G, researchers aim to design its architecture based on QC (Vista et al., 2021).

4.4 Benefits of QML over ML for routing optimization in 6G networks

The core of most ML algorithms is to repeat the computation of complex mathematical models, for example, DRL mostly consists of matrix operations such as matrix multiplication. However, with an ever-growing amount of data, ML techniques are getting closer to their limits (Ciliberto et al., 2018). In this sense, QML techniques are able to provide faster solutions to process data. Moreover, for high-dimension problems, the training and learning phases of most DL systems become extensive (as mentioned in Section 3.5). In this respect, QML can offer a speedup of the training time up to O$(\sqrt{N})$ (Biamonte et al., 2017).

QML can be implemented on both gate-based quantum computers/simulators and quantum annealing processors. Both techniques have their advantages and caveats. In the next section, we will survey the latest work from 2019 to 2022 and provide answers to four questions related to QML for routing optimization.

• Q1: How can QML techniques be applied to routing optimization?

• Q2: What are the tools to implement the proposed solutions?

• Q3: What are the limitations of these two methods?

• Q4: Can QML solve the problem of high-complex routing in 6G Networks?

4.5 Adiabatic Quantum Computation

A Hamiltonian in quantum physics is an operator that represents the total energy of a system (including the potential energy and the kinetic energy) (Odzijewicz, 2011). In general, in order to solve NP-Hard problems and more precisely, combinatorial optimization problems using quantum-based methods, we have to transform them into problems of characterization of a quantum Hamiltonian, in which the optimal solution corresponds to the ground energy state of the quantum system and this is one of the fundamentals of the Adiabatic Quantum Computation (AQC).

AQC was proposed in the early 2000s by Edward Farhi et al (Farhi et al., 2000; Farhi et al., 2001) based on the adiabatic theorem. The idea is that if a quantum system evolves slowly enough from an initial Hamiltonian H_init to a final Hamiltonian H_fin and if the system starts in the ground energy state of the H_init, then it will remain in the ground energy state of H_fin that will correspond to the optimal solution to the problem. This is known as the adiabatic transition and “adiabaticity” occurs only when a physical system remains close to or stays in its ground energy state of the initial Hamiltonian throughout the change/evolution (Kato, 1950). This change should be made with a speed limit of 1/min (Δ(t))², where Δ is the gap between the ground energy state and the first excited energy state (Bauch et al., 2006). One of the most advanced forms of AQC is Quantum Annealing (QA).

4.5.1 Quantum annealing based solution

Quantum Annealing (QA) was first introduced in the 1989 (Apolloni et al., 1988; Apolloni et al., 1989) as a combinatorial procedure based on the theory of using the time-dependent Schrödinger equation to find the global minimum of a specific objective function over a given set of candidate solutions, by decreasing the quantum fluctuations (Kadowaki and Nishimori, 1998). With the advent of quantum computing, QA was adopted by many high techs, such as D-Wave, as a metaheuristic optimization form of AQC to build their quantum machines (Quantum Annealers mentioned in section 4.2) to solve combinatorial optimization problems.

The procedure of QA for all the types of combinatorial optimization problems can be summarized in six steps (Santoro and Tosatti, 2006).

• Step 1, Formulating a Quadratic Unconstrained Binary Optimization (QUBO) function and graph representation: QUBO is the standard input format of quantum annealers that is used in order to convert a real-world problem into a mathematical formulation. After defining the QUBO, it has to be converted into a graph where each variable represents a node and the interactions between the variables are represented as the edges of the graph.

• Step 2, Minor Embedding: it is considered the most important and the hardest step in the process as it consists of mapping the graph that we had in step 1 into the physical hardware of the annealing machine (for example, fit the graph into chimera topology used by D-Wave 2000Q processor (Yang and Dinneen, 2016))

• Step 3, Programming the machine: it consists of setting the parameters that define the QUBO problem we need to solve, which is the final Hamiltonian, involving the weight of each qubit and the coupling strength to control interactions between qubits.

• Step 4, The Initialization: start the initial Hamiltonian (energy function) in a fully entangled set of N qubits (that represent the graph) in an equal superposition of all the possible states (the ground energy state of the system).

• Step 5, The annealing process: the system evolves into the Hamiltonian of the optimization problem following the time-dependent Schrödinger equation trying to minimize the energy.

• Step 6, Readout the solution: ideally and according to the principle of AQC, at the end of the annealing process, the slow evolution of the energy function allows the system to stay close to the ground energy state of the initial Hamiltonian, therefore, find the optimal solution to the problem we want to solve.

Computing by adiabatic evolution started in 2003 (Moser, 2003) with the first theoretical work that combines QC and the well-known routing problem, the Traveling Salesman Problem (TSP). (Martoňák et al., 2004). introduced the formulation of the TSP based on QA theorem. The authors evaluated their formulation by means of an experiment executed using some classical techniques and TSP models of sizes up to 1,200 nodes. In (Chen and Zhang, 2006), the authors proposed a substitutional formulation to the TSP that can improve the efficiency by escaping from local optima. In 2011, (Chen et al., 2011), presented one of the first experiments on simulated quantum hardware that was applied to a small TSP graph consisting of four nodes.

Most works in that time interval (2003 to late 2013) focused on addressing the routing problem from a theoretical point of view when quantum computers were not reachable. Nowadays, with the advent of quantum computers (especially quantum annealers), many works were published in the last few years that implemented QA-based solutions for different applications. In (Warren, 2013), the authors gave a very detailed and comprehensible explanation of TSP and how to translate it into a real adiabatic processor. In the same year, (Crispin and Syrichas, 2013), introduced the formulation of the Vehicle Routing Problem (VRP) for a Quantum Annealer processor. These two works gave inspiration to numerous subsequent studies such as (Feld et al., 2019; Irie et al., 2019; Mehta et al., 2019; Papalitsas et al., 2019; Dixit et al., 2021).

Turning our attention to the routing optimization problem for a network scenario, (Krauss and McCollum, 2020), used QA to solve the network Shortest Path Problem (SSP). In their work, they presented three approaches (Hope-based, Directed edge-based and undirected edge-based approaches). The time complexity of the proposed approaches was compared to one of Dijkstra and Bellman-Ford algorithms and they claim that if the degree of connectivity of the graph remains constant, the Directed edge-based and undirected edge-based approaches will be faster than the fastest known implementation of Dijkstra’s algorithm. To formulate the energy function of the optimization problem they used the QUBO technique and to evaluate the performance of the proposed formulas, they used D-Wave quantum annealers.

Dixit et al. (2021) proposed a QUBO formulation for the Scenario-based Least Expected Time (SLET) algorithm, to find the shortest path in Stochastic Time-Dependent networks (STDSP). For the implementation of the formula, they used the D-Wave Advantage quantum annealer and the quantum hybrid solver, they demonstrated that in the case of independent link costs where the size of the problem increases exponentially, their proposed approach provides a linear computational experience with respect to the problem size. To the best of our knowledge, these two works were the only ones that attempted to use QA for solving the lowest cost problem in a network scenario.

In Table 5, we present a general overview of reported applications of QA techniques to solve real-world optimization problems focusing on routing optimization. From these studies, we conclude that.

• Almost all the studies formulate the problem as a QUBO instance. This is due to the fact that the QUBO facilitates mapping the problem into a quantum annealer (step 2 mentioned in section 4.5.1).

• Boutique applications: Most of the practical work applied QA for small sizes of problems (boutique problems) and this is because of the immature state of the knowledge and the Hardware in this field.

TABLE 5

TABLE 5. Quantum Annealing for real-world routing optimization problems.

4.6 NISQ computing for routing optimization

In this section, we review the application of routing optimization in near-term gate-based quantum computers, referred to as the NISQ era (Noisy-Intermediate Scale Quantum) (Preskill, 2018). The term “Noisy” refers to the fact that these quantum devices are very sensitive to the external environment and they may collapse quickly (lack of stability), this is known as “Quantum Decoherence.” In order to overcome this problem, Peter Shor introduces the Quantum Error Correction method (Shor, 1995). However, this method -practically- is still under the scope of research due to the lack of enough qubits to implement it. The term “Intermediate-scale” refers to the quantum volume, which is the number of qubits and quantum gates that exist in this processor which is not too large, the largest quantum computer that exists nowadays is IBM’s 433-qubit Osprey which was released on the 9 of November 2022 (Fadelli, 2023), and when we talk about fault-tolerance quantum computers we refer to processors with more than one million qubits. In this regard and in order to benefit from the quantum speed-up given by those devices to solve nowadays complex problems, a new breed of algorithms has been developed specifically for these NISQ devices called Hybrid Quantum-Classical Algorithms. The main tactic behind those hybrid algorithms is combining quantum computers and classical computers to solve a specific problem (De Luca, 2022). In practice, the term “hybrid” can be defined as a technique that follows a process of back-and-forth cooperation where different parts of the problem under study are passed between the classical and the quantum devices best fit for each stage. To the best of our knowledge, there are three gate-based hybrid algorithms presented in the literature: the Quantum Approximate Optimization Algorithm (QAOA), the Variational Quantum Eigensolver (VQE) and the Multistate Contracted Variant of the Variational Quantum Eigensolver (MC-VQE) (Endo et al., 2021). VQE is used to compute the ground energy state of a given Hamiltonian (Tilly et al., 2022), while MC-VQE is used to derive the excited states of big molecules in high accuracy (Parrish et al., 2019). Both algorithms are mainly applied in quantum chemistry and condensed matter physics. On the other hand, QAOA is mostly used to solve combinatorial optimization problems, more precisely, 6G routing optimization (Nawaz et al., 2019).

4.6.1 QAOA for 6G routing optimization

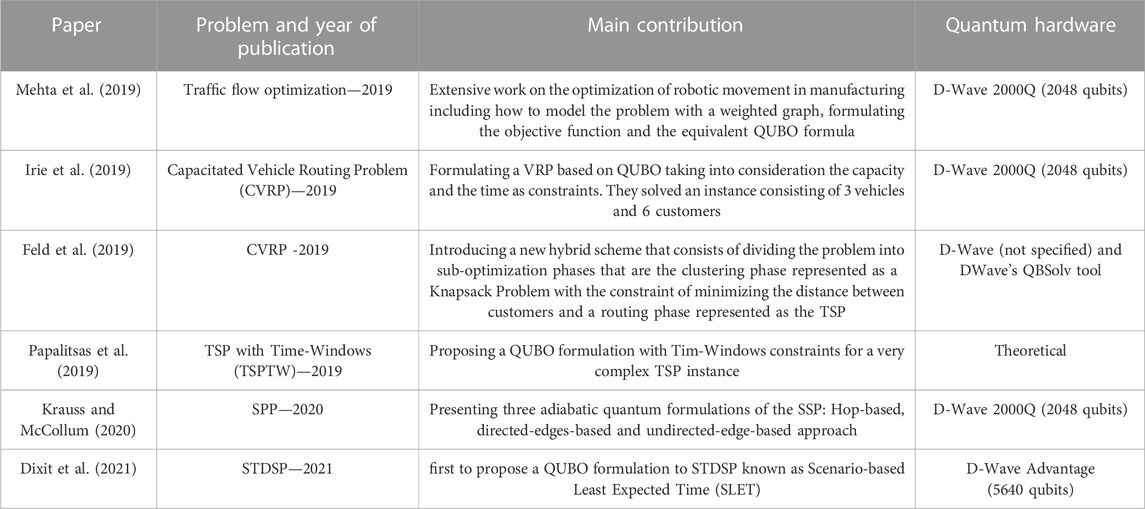
QAOA was introduced in 2014 by Edward Farhi to find a “good enough approximate” solution for combinatorial optimization problems (Farhi et al., 2014). It was designed to run on gate-based quantum computers. It takes a combinatorial optimization problem as input and outputs a string that maximizes/minimizes the objective function. Moreover, in (Farhi and Harrow, 2016), QAOA was proposed as a candidate for solving optimization problems and proving “Quantum Supremacy”. In order to use QAOA for an optimization problem, we need to translate the problem in a way that the gate-based quantum computer can understand it, meaning we have to encode the problem in terms of quantum gates. The most common technique is to translate the problem into unitary operators using the Hamiltonian encoding method (IBM, 2022b). For this reason, the QAOA applied to a combinatorial problem, in a general manner, will consist of two unitary operators, as depicted in Figure 6.

• The Mixing Unitary U(β) = $e^{-i\beta H_B}$

• The Cost/Problem Unitary U(γ) = $e^{-i\gamma H_C}$

Where H_B is the mixing Hamiltonian, H_C is the problem Hamiltonian and β and γ are angles used to rotate the state vector of the quantum circuit, where β represents the rotation around the x-axis applied to all the qubits and usually it has to be 0 ≤ β ≤ π while γ represents the rotation around the z-axis and it has to be 0 ≤ β ≤ 2π, making sure that H_B and H_C are anti-commute. These two unitaries form a quantum circuit, known as Variational Quantum Circuit (VQC), that works by alternating between the cost Hamiltonian and the Mixing Hamiltonian gates. Usually, the input of the VQC consists of the number of rounds of iterations p (depth of the circuit), βand γ.

FIGURE 6

FIGURE 6. p-depth of the Quantum-Classical hybrid loop of QAOA for optimization problems.

For the sake of simplicity, we summarized the hybrid process of QAOA in seven steps, as illustrated in Figure 6.

• Step 1: prepare the first part of the quantum circuit setting all the n-qubits in an equal superposition by applying the Hadamard gate to each qubit.

• Step 2: pick a p and initialize the parameters β and γ (angles for the quantum gates).

• Step 3: apply the set of gates corresponding to the cost and mix Hamiltonians.

• Step 4: the classical optimizer (such as COBYLA, ADAM) feeds the set of parameters (β and γ) to the quantum circuit.

• Step 5: then the outcome of the circuit (optimized objective function) is measured and it communicates back to the classical optimizer, completing one loop of the computational procedure.

• Step 6: the classical optimizer suggests a new set of parameters that may lead the quantum circuit to produce a new optimized objective function.

• Step 7: then the quantum circuit with the new parameters is executed and the outcome is measured again. The process is repeated until the objective function converges to its meaning (maximum or minimum).

Many works attempted to use QAOA to solve NP-hard problems, focusing more on the Max-Cut problem, from different angles (e.g., improving the approximation accuracy and reducing the quantum circuit depth) as the first time QAOA was introduced, it was formulated and evaluated over the Max-Cut problem. The results of these works are reported in (Crooks, 2018; Wang et al., 2018; Zhu et al., 2022) among others. However, there are very few works that addressed the problem of path-finding or routing using QAOA. One of these works was proposed by (Radzihovsky et al., 2019). The authors suggested using QAOA as a solution for the TSP, inspired by the work presented in (Srinivasan et al., 2018). The proposed formula was implemented using pyQuil, a Python library for quantum programming developed by Rigetti. Yet, details about the quantum circuit used or the achieved performance were not provided. The second one was from IBM where a deep explanation of how to formulate and solve the vehicle routing problem with time windows (VRPTW) on a quantum computer is presented (Harwood et al., 2021) and a comparison between QAOA and VQE performance was made using the Qiskit Qasm-Simulator backend. Moreover, In (Fitzek et al., 2021), the authors proposed QAOA as a solution to the heterogeneous vehicle routing problem (HVRP). A detailed study on how to map an HVRP formula into an Ising Hamiltonian to fit the QAOA structure and a deep analysis of how the quality of the solution found by the QAOA depends on the type of classical optimizer and the depth of the circuit, are presented.

One of the latest works regarding the QAOA for routing optimization was proposed in (Azad et al., 2022), where the authors gave, first, a representation of the QUBO formulation used to solve the VRP instances composed of 4 and 5 nodes, then the mapping into an Ising Hamiltonian. For evaluating their approach they use IBM Qiskit and they compared the QAOA using the different types of optimizers provided by the Qiskit platform and several circuit depths, with the CPLEX model, which is a classical optimization solver. The authors provide also a discussion about the impact of increasing the circuit depth on the optimization process. A summary of these studies from perspectives of problem and year of publication, main contribution and the quantum resources used for the implementation of the proposed approaches are represented in Table. 6.

TABLE 6

TABLE 6. QAOA for optimization problems.

Nevertheless and to the best of the author’s knowledge, there is no practical study yet that applied the QAOA to the routing optimization problem in networking. In this regard, the application of QAOA for routing optimization in a network scenario can be considered an interesting future research direction for the 6G routing optimization problem, as it can be implemented on current NISQ devices and is expected to reduce or even break the complexity of routing in 6G networks (Farhi and Harrow, 2016).

5 Open research directions

Routing optimization remains a dynamic and critical domain of research with significant scope for enhancement and exploration. In parallel, both classical ML and QML have already begun to impact in several areas such as face recognition, and biomedicine among others. For this reason, we aim to summarize our vision for some of the future research directions in these three domains, hoping it will serve as an inspiration for the research community.

• Modeling Complex and Dynamic Environment: 6G will feature highly complex and dynamic environments due to several factors (e.g., device mobility, dynamic spectrum, etc.). How RL and DRL can model and adapt to these ever-changing is a critical area of research.

• Scalability issues in RL and DRL: With the massive number of devices in 6G networks, the scalability issue of RL and DRL approaches becomes more serious, Techniques to make RL and DRL more scalable such as hierarchical RL or distributed RL, should be explored (Shin et al., 2020; Pateria et al., 2021). Moreover, the Multi-Agent RL (MARL) approach can be also adopted. This method involves multiple agents learning and making decisions simultaneously, potentially optimizing response times and decision-making processes (Zhang et al., 2021).

• Transfer-Learning and Meta-Learning: In dynamic networks, using meta-learning and transfer-learning techniques can significantly speed up the learning process of DRL by transferring knowledge from one task or environment to another. When integrated with SDN, these techniques can provide potential solutions to the routing optimization problem in 6G.

• Quantum Reinforcement Learning: Integrating QC principles with RL/DRL techniques can lead to new algorithms that could potentially outperform the classical versions, especially in terms of computation speed and handling vast state spaces (Dong et al., 2008; Bouchmal et al., 2023).

• Combining SDN and QML: An interesting future research direction that can fulfill 6G routing requirements such as the on-demand configuration, high-dynamic and heterogeneous networks, real-time routing decisions and high QoS obligations could be combining the flexibility and automation given by SDN and the power provided by QML algorithms.

6 Conclusion

This paper has reviewed the latest advances in the literature on ML routing optimization, starting with RL and DRL techniques for SDN routing optimization. As a potential solution for routing optimization with the advent of 6G, the Quantum Annealing and the hybrid QC-based mechanism have also been introduced. The analysis highlights that so far most researchers have focused on using DRL for routing optimization in SDN. However, most of the studies were based on simple topologies and particular network scenarios, such as centralized SDN architecture and wired networks. The reported classical algorithms were evaluated based on packet loss, delay, and throughput. Furthermore, in most cases, the proposed RL/DRL approaches outperform conventional routing methods (e.g., Dijkstra, OSPF), yet a comprehensive study on their scalability remains to be conducted. On the other hand, QML-based techniques appear as a potential solution that can reduce the complexity of routing, which is expected to increase with the advent of 6G. However, it is still a young and fertile field that needs to be explored and investigated in order to overcome the challenges that arise with it. Taking into account the growing interest in QML-based techniques to solve optimization problems, we presented a review that combines classical and quantum approaches that have been applied to routing optimization. Moreover, we provide some open research directions regarding RL, DRL and QML, that will, hopefully, serve as an inspiration for the research community.

Author contributions

OB contributed to the investigation and wrote the original draft. OB, BC, RS, JV, and IT contributed to the formal analysis, writing, reviewing, and editing. All authors contributed to the article and approved the submitted version.

Funding

This research was partially funded by Marie Skłodowska-Curie IoTalentum project ITN-ETN with grant number 953442 and the ECSEL-JU project BRAINE with grant number 876967.

Acknowledgments

This paper received support from the European Union Horizon 2020 research and innovation program within the framework of Marie Skłodowska-Curie Actions ITN-ETN with grant number 953442 and the ECSEL-JU project BRAINE with grant number 876967.

Conflict of interest

Author JV was employed by NVIDIA Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akyildiz, I. F., Kak, A., and Nie, S. (2020). 6G and beyond: the future of wireless communications systems. IEEE access 8, 133995–134030. doi:10.1109/ACCESS.2020.3010896

CrossRef Full Text | Google Scholar

Al-Jawad, A., Comşa, I.-S., Shah, P., Gemikonakli, O., and Trestian, R. (2021). An innovative reinforcement learning-based framework for quality of service provisioning over multimedia-based sdn environments. IEEE Trans. Broadcast. 67, 851–867. doi:10.1109/TBC.2021.3099728

CrossRef Full Text | Google Scholar

Amin, R., Rojas, E., Aqdus, A., Ramzan, S., Casillas-Perez, D., and Arco, J. M. (2021). A survey on machine learning techniques for routing optimization in SDN. IEEE Access 9, 104582–104611. doi:10.1109/ACCESS.2021.3099092

CrossRef Full Text | Google Scholar

Apolloni, B., Carvalho, C., and de Falco, D. (1989). Quantum stochastic optimization. Stoch. Process. their Appl. 33, 233–244. doi:10.1016/0304-4149(89)90040-9

CrossRef Full Text | Google Scholar

Apolloni, B., Cesa-Bianchi, N., and De Falco, D. (1988). A numerical implementation of “quantum annealing”. Tech. Rep. Bielef. Tu. Bielefeld-Bochum-Stochastik, Bielef.

Google Scholar

Arulkumaran, K., Deisenroth, M. P., Brundage, M., and Bharath, A. A. (2017). Deep reinforcement learning: a brief survey. IEEE Signal Process. Mag. 34, 26–38. doi:10.1109/MSP.2017.2743240

CrossRef Full Text | Google Scholar

Azad, U., Behera, B. K., Ahmed, E. A., Panigrahi, P. K., and Farouk, A. (2022). Solving vehicle routing problem using quantum approximate optimization algorithm. IEEE Trans. Intelligent Transp. Syst. 1, 7564–7573. doi:10.1109/TITS.2022.3172241

CrossRef Full Text | Google Scholar

Banafaa, M., Shayea, I., Din, J., Hadri Azmi, M., Alashbi, A., Ibrahim Daradkeh, Y., et al. (2023). 6G mobile communication technology: requirements, targets, applications, challenges, advantages, and opportunities. Alexandria Eng. J. 64, 245–274. doi:10.1016/j.aej.2022.08.017

CrossRef Full Text | Google Scholar

Banjar, A., Pupatwibul, P., Braun, R., and Moulton, B. (2014). “Analysing the performance of the openflow standard for software-defined networking using the omnet++ network simulator,” in 2014 Asia-Pacific Conference on Computer Aided System Engineering (APCASE), South Kuta, Indonesia, 10-12 February 2014, 31–37. doi:10.1109/APCASE.2014.6924467

CrossRef Full Text | Google Scholar

Bauch, T., Lindström, T., Tafuri, F., Rotoli, G., Delsing, P., Claeson, T., et al. (2006). Quantum dynamics of a D-wave josephson junction. Science 311, 57–60. doi:10.1126/science.1120793

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhat, J. R., and Alqahtani, S. A. (2021). 6G ecosystem: current status and future perspective. IEEE Access 9, 43134–43167. doi:10.1109/ACCESS.2021.3054833

CrossRef Full Text | Google Scholar

Biamonte, J., Wittek, P., Pancotti, N., Rebentrost, P., Wiebe, N., and Lloyd, S. (2017). Quantum machine learning. Nature 549, 195–202. doi:10.1038/nature23474

PubMed Abstract | CrossRef Full Text | Google Scholar

Bosshart, P., Gibb, G., Kim, H.-S., Varghese, G., McKeown, N., Izzard, M., et al. (2013). Forwarding metamorphosis: fast programmable match-action processing in hardware for sdn. SIGCOMM Comput. Commun. Rev. 43, 99–110. doi:10.1145/2534169.2486011

CrossRef Full Text | Google Scholar

Bouchmal, O., Cimoli, B., Stabile, R., Olmos, J. J. V., and Monroy, I. T. (2023). “Quantum-inspired network optimization in 6g: opportunities, challenges and open research directions,” in Distributed computing and artificial intelligence, special sessions I, 20th international conference (Cham: Springer Nature Switzerland), 480–488.

CrossRef Full Text | Google Scholar

Cao, X., Li, Y., Xiong, X., and Wang, J. (2022). Dynamic routings in satellite networks: an overview. Sensors 22, 4552. doi:10.3390/s22124552

PubMed Abstract | CrossRef Full Text | Google Scholar

Casas-Velasco, D. M., Rendon, O. M. C., and da Fonseca, N. L. S. (2021). Intelligent routing based on reinforcement learning for software-defined networking. IEEE Trans. Netw. Serv. Manag. 18, 870–881. doi:10.1109/TNSM.2020.3036911

CrossRef Full Text | Google Scholar

Casas-Velasco, D. M., Rendon, O. M. C., and da Fonseca, N. L. S. (2022). Drsir: a deep reinforcement learning approach for routing in software-defined networking. IEEE Trans. Netw. Serv. Manag. 19, 4807–4820. doi:10.1109/TNSM.2021.3132491

CrossRef Full Text | Google Scholar

Chen, H., Kong, X., Chong, B., Qin, G., Zhou, X., Peng, X., et al. (2011). Experimental demonstration of a quantum annealing algorithm for the traveling salesman problem in a nuclear-magnetic-resonance quantum simulator. Phys. Rev. A 83, 032314. doi:10.1103/PhysRevA.83.032314

CrossRef Full Text | Google Scholar

Chen, L. (2009). Curse of dimensionality. Boston, MA: Springer US, 545–546. doi:10.1007/978-0-387-39940-9_133

CrossRef Full Text | Google Scholar

Chen, S., Sun, S., and Kang, S. (2020). System integration of terrestrial mobile communication and satellite communication —the trends, challenges and key technologies in b5g and 6g. China Commun. 17, 156–171. doi:10.23919/JCC.2020.12.011

CrossRef Full Text | Google Scholar

Chen, Y., and Zhang, P. (2006). Optimized annealing of traveling salesman problem from the nth-nearest-neighbor distribution. Phys. A Stat. Mech. its Appl. 371, 627–632. doi:10.1016/j.physa.2006.04.052

CrossRef Full Text | Google Scholar

Chow, J., Dial, O., and Gambetta, J. (2021). Ibm quantum breaks the 100-qubit processor barrier. IBM Res. Blog.

Google Scholar

Ciliberto, C., Herbster, M., Ialongo, A. D., Pontil, M., Rocchetto, A., Severini, S., et al. (2018). Quantum machine learning: a classical perspective. Proc. R. Soc. A Math. Phys. Eng. Sci. 474, 20170551. doi:10.1098/rspa.2017.0551

PubMed Abstract | CrossRef Full Text | Google Scholar

Crispin, A., and Syrichas, A. (2013). “Quantum annealing algorithm for vehicle scheduling,” in 2013 IEEE International Conference on Systems, Man, and Cybernetics, Manchester, UK, 27 January 2014, 3523–3528. doi:10.1109/SMC.2013.601

CrossRef Full Text | Google Scholar

Crooks, G. E. (2018). Performance of the quantum approximate optimization algorithm on the maximum cut problem. arXiv preprint arXiv:1811.08419. doi:10.48550/arXiv.1811.08419

CrossRef Full Text | Google Scholar

Das, A., and Chakrabarti, B. K. (2008). Colloquium: quantum annealing and analog quantum computation. Rev. Mod. Phys. 80, 1061–1081. doi:10.1103/RevModPhys.80.1061

CrossRef Full Text | Google Scholar

De Luca, G. (2022). Survey of NISQ era hybrid quantum-classical machine learning research. J. Artif. Intell. Technol. 2, 9–15. doi:10.37965/jait.2021.12002

CrossRef Full Text | Google Scholar

Dixit, V., Rey, D., Waller, T. S., and Levin, M. (2021). Quantum computing to solve scenario-based stochastic time-dependent shortest path routing. Transp. Lett. doi:10.2139/ssrn.3977598

CrossRef Full Text | Google Scholar

Domeke, A., Cimoli, B., and Monroy, I. T. (2022). Integration of network slicing and machine learning into edge networks for low-latency services in 5G and beyond systems. Appl. Sci. 12, 6617. doi:10.3390/app12136617

CrossRef Full Text | Google Scholar

Dong, D., Chen, C., Li, H., and Tarn, T.-J. (2008). Quantum reinforcement learning. IEEE Trans. Syst. Man, Cybern. Part B Cybern. 38, 1207–1220. doi:10.1109/TSMCB.2008.925743

PubMed Abstract | CrossRef Full Text | Google Scholar

Dong, T., Qi, Q., Wang, J., Liu, A. X., Sun, H., Zhuang, Z., et al. (2021). Generative adversarial network-based transfer reinforcement learning for routing with prior knowledge. IEEE Trans. Netw. Serv. Manag. 18, 1673–1689. doi:10.1109/TNSM.2021.3077249

CrossRef Full Text | Google Scholar

Duong, T. Q., Nguyen, L. D., Narottama, B., Ansere, J. A., Huynh, D. V., and Shin, H. (2022). Quantum-inspired real-time optimization for 6G networks: opportunities, challenges, and the road ahead. IEEE Open J. Commun. Soc. 3, 1347–1359. doi:10.1109/OJCOMS.2022.3195219

CrossRef Full Text | Google Scholar

Endo, S., Cai, Z., Benjamin, S. C., and Yuan, X. (2021). Hybrid quantum-classical algorithms and quantum error mitigation. J. Phys. Soc. Jpn. 90, 032001. doi:10.7566/JPSJ.90.032001

CrossRef Full Text | Google Scholar

Fadelli, I. (2023). Exclusive—IBM shares details of its 400+ qubit quantum processor. Available at: https://www.allaboutcircuits.com/news/exclusive-ibm-shares-details-of-its-400-plus-qubit-quantum-processor/.

Google Scholar

Fadlullah, Z. M., Tang, F., Mao, B., Kato, N., Akashi, O., Inoue, T., et al. (2017). State-of-the-art deep learning: evolving machine intelligence toward tomorrow’s intelligent network traffic control systems. IEEE Commun. Surv. Tutorials 19, 2432–2455. doi:10.1109/COMST.2017.2707140

CrossRef Full Text | Google Scholar

Fakoor, R., Chaudhari, P., and Smola, A. J. (2020). “P3o: policy-on policy-off policy optimization,” in Uncertainty in artificial intelligence (Elsevier), 1017–1027.

Google Scholar

Farhi, E., Goldstone, J., and Gutmann, S. (2014). A quantum approximate optimization algorithm. arXiv preprint arXiv:1411.4028. doi:10.48550/arXiv.1411.4028

CrossRef Full Text | Google Scholar

Farhi, E., Goldstone, J., Gutmann, S., Lapan, J., Lundgren, A., and Preda, D. (2001). A quantum adiabatic evolution algorithm applied to random instances of an np-complete problem. Science 292, 472–475. doi:10.1126/science.1057726

PubMed Abstract | CrossRef Full Text | Google Scholar

Farhi, E., Goldstone, J., Gutmann, S., and Sipser, M. (2000). Quantum computation by adiabatic evolution. arXiv preprint quant-ph/0001106. doi:10.48550/arXiv.quant-ph/0001106

CrossRef Full Text | Google Scholar

Farhi, E., and Harrow, A. W. (2016). Quantum supremacy through the quantum approximate optimization algorithm. arXiv preprint arXiv:1602.07674. doi:10.48550/arXiv.1602.07674

CrossRef Full Text | Google Scholar

Feld, S., Roch, C., Gabor, T., Seidel, C., Neukart, F., Galter, I., et al. (2019). A hybrid solution method for the capacitated vehicle routing problem using a quantum annealer. Front. ICT 6, 13. doi:10.3389/fict.2019.00013

CrossRef Full Text | Google Scholar

Fijutsu (2016). Fujitsu digital annealer. Available at: https://www.fujitsu.com/global/services/business-services/digital-annealer/.

Google Scholar

Fitzek, D., Ghandriz, T., Laine, L., Granath, M., and Kockum, A. F. (2021). Applying quantum approximate optimization to the heterogeneous vehicle routing problem. arXiv preprint arXiv:2110.06799. doi:10.48550/arXiv.2110.06799

CrossRef Full Text | Google Scholar

Fu, Q., Sun, E., Meng, K., Li, M., and Zhang, Y. (2020). Deep Q-learning for routing schemes in SDN-based data center networks. IEEE Access 8, 103491–103499. doi:10.1109/ACCESS.2020.2995511

CrossRef Full Text | Google Scholar

García, C. R., Bouchmal, O., Stan, C., Giannakopoulos, P., Cimoli, B., Olmos, J. J. V., et al. (2023b). “Secure and agile 6g networking – quantum and ai enabling technologies,” in 2023 23rd International Conference on Transparent Optical Networks (ICTON), Bucharest, Romania, 02-06 July 2023, 1–4. doi:10.1109/ICTON59386.2023.10207418

CrossRef Full Text | Google Scholar

García, C. R., Rommel, S., Olmos, J. J. V., and Monroy, I. T. (2023a). “Enhancing the security of software defined networks via quantum key distribution and post-quantum cryptography,” in Distributed computing and artificial intelligence, special sessions I, 20th international conference. Editors R. Mehmood, V. Alves, I. Praça, J. Wikarek, J. Parra-Domínguez, R. Loukanovaet al. (Springer Nature Switzerland), 428–437.

Google Scholar

Goldberg, A. V., and Radzik, T. (1993). A heuristic improvement of the bellman-ford algorithm. Appl. Math. Lett. 6, 3–6. doi:10.1016/0893-9659(93)90022-F

CrossRef Full Text | Google Scholar

Gopi, D., Cheng, S., and Huck, R. (2017). “Comparative analysis of SDN and conventional networks using routing protocols,” in 2017 International Conference on Computer, Information and Telecommunication Systems (CITS), Dalian, China, 21-23 July 2017, 108–112. doi:10.1109/CITS.2017.8035305

CrossRef Full Text | Google Scholar

Haj-Ali, A., Ahmed, N. K., Willke, T., Gonzalez, J., Asanovic, K., and Stoica, I. (2019). A view on deep reinforcement learning in system optimization. arXiv preprint arXiv:1908.01275. doi:10.48550/arXiv.1908.01275

CrossRef Full Text | Google Scholar

Harwood, S., Gambella, C., Trenev, D., Simonetto, A., Bernal, D., and Greenberg, D. (2021). Formulating and solving routing problems on quantum computers. IEEE Trans. Quantum Eng. 2, 1–17. doi:10.1109/TQE.2021.3049230

CrossRef Full Text | Google Scholar

Hassas Yeganeh, S., and Ganjali, Y. (2012). “Kandoo: a framework for efficient and scalable offloading of control applications,” in Proceedings of the first workshop on hot topics in software defined networks, 19–24. doi:10.1145/2342441.2342446

CrossRef Full Text | Google Scholar

Hochba, D. S. (1997). Approximation algorithms for np-hard problems. SIGACT News 28, 40–52. doi:10.1145/261342.571216

CrossRef Full Text | Google Scholar

IBM (2022a). The IBM quantum development roadmap. Available at: https://www.ibm.com/quantum/roadmap.

Google Scholar

IBM (2022b). Solving combinatorial optimization problems using QAOA. Available at: https://qiskit.org/textbook/ch-applications/qaoa.html.

Google Scholar

Irie, H., Wongpaisarnsin, G., Terabe, M., Miki, A., and Taguchi, S. (2019). “Quantum annealing of vehicle routing problem with time, state and capacity,” in Quantum technology and optimization problems. Editors S. Feld,, and C. Linnhoff-Popien (Springer International Publishing), 145–156. doi:10.1007/978-3-030-14082-3_13

CrossRef Full Text | Google Scholar

Iselt, A., Kirstadter, A., Pardigon, A., and Schwabe, T. (2004). “Resilient routing using mpls and ecmp,” in 2004 Workshop on High Performance Switching and Routing, 2004. HPSR, 345–349. doi:10.1109/HPSR.2004.1303507

CrossRef Full Text | Google Scholar

James, D. (2022). The quantum insider. Available at: https://thequantuminsider.com/2022/09/05/quantum-computing-companies-ultimate-list-for-2022.

Google Scholar

Jin, Z., Zang, W., Jiang, Y., and Lan, J. (2019). A qlearning based business differentiating routing mechanism in sdn architecture. J. Phys. Conf. Ser. 1168, 022025. doi:10.1088/1742-6596/1168/2/022025

CrossRef Full Text | Google Scholar

Jordan, S. (2011). Quantum algorithm Zoo. https://quantumalgorithmzoo.org/.

Google Scholar

Kadowaki, T., and Nishimori, H. (1998). Quantum annealing in the transverse ising model. Phys. Rev. E 58, 5355–5363. doi:10.1103/PhysRevE.58.5355

CrossRef Full Text | Google Scholar

Kato, T. (1950). On the adiabatic theorem of quantum mechanics. J. Phys. Soc. Jpn. 5, 435–439. doi:10.1143/jpsj.5.435

CrossRef Full Text | Google Scholar

Khan, T. M., and Robles-Kelly, A. (2020). Machine learning: quantum vs classical. IEEE Access 8, 219275–219294. doi:10.1109/ACCESS.2020.3041719

CrossRef Full Text | Google Scholar

Khumalo, M. T., Chieza, H. A., Prag, K., and Woolway, M. (2022). An investigation of ibm quantum computing device performance on combinatorial optimisation problems. Neural Comput. Appl., 1–16. doi:10.1007/s00521-022-07438-4

CrossRef Full Text | Google Scholar

Kim, G., Kim, Y., and Lim, H. (2022). Deep reinforcement learning-based routing on software-defined networks. IEEE Access 10, 18121–18133. doi:10.1109/ACCESS.2022.3151081

CrossRef Full Text | Google Scholar

Krauss, T., and McCollum, J. (2020). Solving the network shortest path problem on a quantum annealer. IEEE Trans. Quantum Eng. 1, 1–12. doi:10.1109/TQE.2020.3021921

CrossRef Full Text | Google Scholar

Ladd, T. D., Jelezko, F., Laflamme, R., Nakamura, Y., Monroe, C., and O’Brien, J. L. (2010). Quantum computers. nature 464, 45–53. doi:10.1038/nature08812

PubMed Abstract | CrossRef Full Text | Google Scholar

Lantz, B., Heller, B., and McKeown, N. (2010). “A network in a laptop: rapid prototyping for software-defined networks,” in Proceedings of the 9th ACM SIGCOMM workshop on hot topics in networks (Monterey, California: Association for Computing Machinery), 1–6. doi:10.1145/1868447.1868466

CrossRef Full Text | Google Scholar

Lewis, F. L., and Vrabie, D. (2009). Reinforcement learning and adaptive dynamic programming for feedback control. IEEE Circuits Syst. Mag. 9, 32–50. doi:10.1109/MCAS.2009.933854

CrossRef Full Text | Google Scholar

Lin, N., and Shao, Z. (2010). “Improved ant colony algorithm for multipath routing algorithm research,” in 2010 International Symposium on Intelligence Information Processing and Trusted Computing, Huanggang, China, 28-29 October 2010, 651–655. doi:10.1109/IPTC.2010.162

CrossRef Full Text | Google Scholar

Lin, S.-C., Akyildiz, I. F., Wang, P., and Luo, M. (2016). “QoS-aware adaptive routing in multi-layer hierarchical software defined networks: a reinforcement learning approach,” in 2016 IEEE International Conference on Services Computing (SCC), San Francisco, CA, USA, 27 June 2016 - 02 July 2016, 25–33. doi:10.1109/SCC.2016.12

CrossRef Full Text | Google Scholar

Lucero, E. (2016). Unveiling our new Quantum AI campus. Available at: https://quantum-computing.ibm.com/.

Google Scholar

Lucero, E. (2021). Unveiling our new Quantum AI campus. Available at: https://blog.google/technology/ai/unveiling-our-new-quantum-ai-campus/.

Google Scholar

Macedo, D. F., Guedes, D., Vieira, L. F. M., Vieira, M. A. M., and Nogueira, M. (2015). Programmable networks—from software-defined radio to software-defined networking. IEEE Commun. Surv. Tutorials 17, 1102–1125. doi:10.1109/COMST.2015.2402617

CrossRef Full Text | Google Scholar

Mammeri, Z. (2019). Reinforcement learning based routing in networks: review and classification of approaches. IEEE Access 7, 55916–55950. doi:10.1109/ACCESS.2019.2913776

CrossRef Full Text | Google Scholar

Martoňák, R., Santoro, G. E., and Tosatti, E. (2004). Quantum annealing of the traveling-salesman problem. Phys. Rev. E 70, 057701. doi:10.1103/PhysRevE.70.057701

CrossRef Full Text | Google Scholar

McCauley, J., Panda, A., Casado, M., Koponen, T., and Shenker, S. (2013). Extending sdn to large-scale networks. Open Netw. Summit 1–2.

PubMed Abstract | Google Scholar

McGeoch, C. C., Harris, R., Reinhardt, S. P., and Bunyk, P. I. (2019). Practical annealing-based quantum computing. Computer 52, 38–46. doi:10.1109/MC.2019.2908836

CrossRef Full Text | Google Scholar

McKeown, N., Anderson, T., Balakrishnan, H., Parulkar, G., Peterson, L., Rexford, J., et al. (2008). Openflow: enabling innovation in campus networks. SIGCOMM Comput. Commun. Rev. 38, 69–74. doi:10.1145/1355734.1355746

CrossRef Full Text | Google Scholar

Mehta, A., Muradi, M., and Woldetsadick, S. (2019). “Quantum annealing based optimization of robotic movement in manufacturing,” in Quantum technology and optimization problems. Editors S. Feld,, and C. Linnhoff-Popien (Springer International Publishing), 136–144. doi:10.1007/978-3-030-14082-3_12

CrossRef Full Text | Google Scholar

Mehta, P., and Meyn, S. (2009). “Q-learning and pontryagin’s minimum principle,” in Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15-18 December 2009, 3598–3605. doi:10.1109/CDC.2009.5399753

CrossRef Full Text | Google Scholar

Moser, H. R. (2003). The quantum mechanical solution of the traveling salesman problem. Phys. E Low-dimensional Syst. Nanostructures 16, 280–285. doi:10.1016/S1386-9477(02)00928-1

CrossRef Full Text | Google Scholar

Nawaz, S. J., Sharma, S. K., Wyne, S., Patwary, M. N., and Asaduzzaman, M. (2019). Quantum machine learning for 6G communication networks: state-of-the-art and vision for the future. IEEE Access 7, 46317–46350. doi:10.1109/ACCESS.2019.2909490

CrossRef Full Text | Google Scholar

NIST (1995). Ion storage group. Available at: https://www.nist.gov/pml/time-and-frequency-division/ion-storage.

Google Scholar

Odzijewicz, A. (2011). “Hamiltonian and quantum mechanics,” in Lectures on Poisson geometry. Editors T. Ratiu, A. Weinstein, and T. Zung, 385–472. Geometry and Topology Monographs. doi:10.2140/gtm.2011.17.385

CrossRef Full Text | Google Scholar

Oliveira, C. A., and Pardalos, P. M. (2005). A survey of combinatorial optimization problems in multicast routing. Comput. Operations Res. 32, 1953–1981. doi:10.1016/j.cor.2003.12.007

CrossRef Full Text | Google Scholar

Papalitsas, C., Andronikos, T., Giannakis, K., Theocharopoulou, G., and Fanarioti, S. (2019). A qubo model for the traveling salesman problem with time windows. Algorithms 12, 224. doi:10.3390/a12110224

CrossRef Full Text | Google Scholar

Parrish, R. M., Hohenstein, E. G., McMahon, P. L., and Martínez, T. J. (2019). Quantum computation of electronic transitions using a variational quantum eigensolver. Phys. Rev. Lett. 122, 230401. doi:10.1103/PhysRevLett.122.230401

PubMed Abstract | CrossRef Full Text | Google Scholar

Pateria, S., Subagdja, B., Tan, A.-h., and Quek, C. (2021). Hierarchical reinforcement learning: a comprehensive survey. ACM Comput. Surv. 54, 1–35. doi:10.1145/3453160

CrossRef Full Text | Google Scholar

Preskill, J. (2018). Quantum computing in the NISQ era and beyond. Quantum 2, 79. doi:10.22331/q-2018-08-06-79

CrossRef Full Text | Google Scholar

Puri, A., and Tripakis, S. (2002). Algorithms for routing with multiple constraints. AIPS-02. 7.

Google Scholar

Qiang, W., and Zhongli, Z. (2011). “Reinforcement learning model, algorithms and its application,” in 2011 international conference on mechatronic science. Jilin, China (Electric Engineering and Computer MEC), 1143–1146. doi:10.1109/MEC.2011.6025669

CrossRef Full Text | Google Scholar

Radzihovsky, M., Murphy, J., and Swofford, M. (2019). A qaoa solution to the traveling salesman problem using pyquil. 199454617

Google Scholar

Ravuri, H. K., Vega, M. T., van der Hooft, J., Wauters, T., and De Turck, F. (2022). A scalable hierarchically distributed architecture for next-generation applications. J. Netw. Syst. Manag. 30, 1–32. doi:10.1007/s10922-021-09618-4

CrossRef Full Text | Google Scholar

Rischke, J., Sossalla, P., Salah, H., Fitzek, F. H. P., and Reisslein, M. (2020). Qr-sdn: towards reinforcement learning states, actions, and rewards for direct flow routing in software-defined networks. IEEE Access 8, 174773–174791. doi:10.1109/ACCESS.2020.3025432

PubMed Abstract | CrossRef Full Text | Google Scholar

Santoro, G. E., and Tosatti, E. (2006). Optimization using quantum mechanics: quantum annealing through adiabatic evolution. J. Phys. A Math. General 39, R393–R431. doi:10.1088/0305-4470/39/36/R01

CrossRef Full Text | Google Scholar

Sergioli, G. (2020). Quantum and quantum-like machine learning: a note on differences and similarities. Soft Comput. 24, 10247–10255. doi:10.1007/s00500-019-04429-x

CrossRef Full Text | Google Scholar

Shin, K.-S., Hwang, G.-H., and Jo, O. (2020). Distributed reinforcement learning scheme for environmentally adaptive iot network selection. Electron. Lett. 56, 462–464. doi:10.1049/el.2019.3891

CrossRef Full Text | Google Scholar

Shirmarz, A., and Ghaffari, A. (2020). Performance issues and solutions in sdn-based data center: a survey. J. Supercomput. 76, 7545–7593. doi:10.1007/s11227-020-03180-7

CrossRef Full Text | Google Scholar

Shor, P. W. (1995). Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52, R2493–R2496. doi:10.1103/PhysRevA.52.R2493

PubMed Abstract | CrossRef Full Text | Google Scholar

Sierra-Sosa, D., Telahun, M., and Elmaghraby, A. (2020). Tensorflow quantum: impacts of quantum state preparation on quantum machine learning performance. IEEE Access 8, 215246–215255. doi:10.1109/ACCESS.2020.3040798

CrossRef Full Text | Google Scholar

Srinivasan, K., Satyajit, S., Behera, B. K., and Panigrahi, P. K. (2018). Efficient quantum algorithm for solving travelling salesman problem: an ibm quantum experience. arXiv preprint arXiv:1805.10928. doi:10.48550/arXiv.1805.10928

CrossRef Full Text | Google Scholar

Stampa, G., Arias, M., Sánchez-Charles, D., Muntés-Mulero, V., and Cabellos, A. (2017). A deep-reinforcement learning approach for software-defined networking routing optimization. arXiv preprint arXiv:1709.07080. doi:10.48550/arXiv.1709.07080

CrossRef Full Text | Google Scholar

Steane, A. (1998). Quantum computing. Rep. Prog. Phys. 61, 117–173. doi:10.1088/0034-4885/61/2/002

CrossRef Full Text | Google Scholar

Tacchino, F., Chiesa, A., Carretta, S., and Gerace, D. (2020). Quantum computers as universal quantum simulators: state-of-the-art and perspectives. Adv. Quantum Technol. 3. doi:10.1002/qute.201900052

CrossRef Full Text | Google Scholar

Thirupathi, V., Sandeep, C., Kumar, S. N., and Kumar, P. P. (2019). A comprehensive review on sdn architecture, applications and major benefits of sdn. Int. J. Adv. Sci. Technol. 28, 607–614.

Google Scholar

Tilly, J., Chen, H., Cao, S., Picozzi, D., Setia, K., Li, Y., et al. (2022). The variational quantum eigensolver: a review of methods and best practices. Phys. Rep. 986, 1–128. doi:10.1016/j.physrep.2022.08.003

CrossRef Full Text | Google Scholar

Van Mieghem, P., Kuipers, F. A., Korkmaz, T., Krunz, M., Curado, M., Monteiro, E., et al. (2003). “Quality of service routing,” in Lecture notes in computer science (Berlin: Springer), 80–117. doi:10.1007/b13823

CrossRef Full Text | Google Scholar

Vista, F., Musa, V., Piro, G., Grieco, L. A., and Boggia, G. (2021). “Network intelligence with quantum computing in 6G and B6G: design principles and future directions,” in 2021 IEEE Globecom Workshops (GC Wkshps), Madrid, Spain, 07-11 December 2021, 1–6. doi:10.1109/GCWkshps52748.2021.9682045

CrossRef Full Text | Google Scholar

Wang, H., Zhao, Y., and Nag, A. (2019). Quantum-key-distribution (QKD) networks enabled by software-defined networks (SDN). Appl. Sci. 9, 2081. doi:10.3390/app9102081

CrossRef Full Text | Google Scholar

Wang, Y., and Liu, H. (2022). Quantum computing in a statistical context. Annu. Rev. Statistics Its Appl. 9, 479–504. doi:10.1146/annurev-statistics-042720-024040

CrossRef Full Text | Google Scholar

Wang, Z., Hadfield, S., Jiang, Z., and Rieffel, E. G. (2018). Quantum approximate optimization algorithm for maxcut: a fermionic view. Phys. Rev. A 97, 022304. doi:10.1103/PhysRevA.97.022304

CrossRef Full Text | Google Scholar

Warren, R. H. (2013). Adapting the traveling salesman problem to an adiabatic quantum computer. Quantum inf. Process. 12, 1781–1785. doi:10.1007/s11128-012-0490-8

CrossRef Full Text | Google Scholar

Xie, J., Yu, F. R., Huang, T., Xie, R., Liu, J., Wang, C., et al. (2019). A survey of machine learning techniques applied to software defined networking (sdn): research issues and challenges. IEEE Commun. Surv. Tutorials 21, 393–430. doi:10.1109/COMST.2018.2866942

CrossRef Full Text | Google Scholar

Xu, C., Zhuang, W., and Zhang, H. (2020). “A deep-reinforcement learning approach for sdn routing optimization,” in Proceedings of the 4th international conference on computer science and application engineering. Sanya, China (Association for Computing Machinery), 5. doi:10.1145/3424978.3425004

CrossRef Full Text | Google Scholar

Xu, Z., Tang, J., Meng, J., Zhang, W., Wang, Y., Liu, C. H., et al. (2018). “Experience-driven networking: a deep reinforcement learning based approach,” in IEEE INFOCOM 2018 - IEEE Conference on Computer Communications, Honolulu, HI, USA, April 16-19, 2018, 1871–1879. doi:10.1109/INFOCOM.2018.8485853

CrossRef Full Text | Google Scholar

Yang, Z., and Dinneen, M. J. (2016). “Graph minor embeddings for D-Wave computer architecture,”. Tech. rep. (New Zealand: Department of Computer Science, The University of Auckland).

Google Scholar

Zahedinejad, E., and Zaribafiyan, A. (2017). Combinatorial optimization on gate model quantum computers: a survey. arXiv preprint arXiv:1708. doi:10.48550/arXiv.1708.05294

CrossRef Full Text | Google Scholar

Zhang, H., and Yan, J. (2015). “Performance of sdn routing in comparison with legacy routing protocols,” in 2015 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery, Xi'an, China, 17-19 September 2015, 491–494. doi:10.1109/CyberC.2015.30

CrossRef Full Text | Google Scholar

Zhang, K., Yang, Z., and Başar, T. (2021). Multi-agent reinforcement learning: a selective overview of theories and algorithms. Cham: Springer International Publishing, 321–384. doi:10.1007/978-3-030-60990-0_12

CrossRef Full Text | Google Scholar

Zhang, Z., Ma, L., Poularakis, K., Leung, K. K., Tucker, J., and Swami, A. (2019a). “Macs: deep reinforcement learning based sdn controller synchronization policy design,” in 2019 IEEE 27th International Conference on Network Protocols (ICNP), Chicago, IL, USA, 08-10 October 2019, 1–11. doi:10.1109/ICNP.2019.8888034

CrossRef Full Text | Google Scholar

Zhang, Z., Xiao, Y., Ma, Z., Xiao, M., Ding, Z., Lei, X., et al. (2019b). 6G wireless networks: vision, requirements, architecture, and key technologies. IEEE Veh. Technol. Mag. 14, 28–41. doi:10.1109/MVT.2019.2921208

CrossRef Full Text | Google Scholar

Zhao, L., Wang, J., Liu, J., and Kato, N. (2019). Routing for crowd management in smart cities: a deep reinforcement learning perspective. IEEE Commun. Mag. 57, 88–93. doi:10.1109/MCOM.2019.1800603

CrossRef Full Text | Google Scholar

Zhu, L., Tang, H. L., Barron, G. S., Calderon-Vargas, F. A., Mayhall, N. J., Barnes, E., et al. (2022). Adaptive quantum approximate optimization algorithm for solving combinatorial problems on a quantum computer. Phys. Rev. Res. 4, 033029. doi:10.1103/PhysRevResearch.4.033029

CrossRef Full Text | Google Scholar