- 1Department of Electrical and Computer Engineering, University of Akron, Akron, OH, United States
- 2Air Force Research Laboratory, Kirtland Air Force Base, Albuquerque, NM, United States
In this work, we establish the sum-capacity-achieving signaling schemes and the sum-capacity of a 2-user multiple access Rayleigh fading channel with 1-bit output quantization in the presence of Gaussian-mixture co-channel interference. The considered Gaussian mixture channel is an accurate model to capture non-Gaussian co-channel interference plus noise in practical wireless networks under coexistence regimes, especially for those having heterogeneous structures and high frequency reuse factor. By first examining the phases of the optimal input signals, we demonstrate that these phases must be π/2 circularly symmetric. As a result, the problem of optimizing the sum-rate is equivalent to minimizing the conditional output entropy. By establishing the Kuhn-Tucker condition on the optimal amplitude input distributions, we then show that the optimal input amplitudes are bounded. Our proof relies on the convexity of the log of sum of Q functions. Then, given the linearity of the conditional entropy over the feasible set of bounded amplitude distributions, it is concluded that the optimal input signals must have constant amplitudes. Therefore, the use of any π/2 circularly symmetric signaling schemes with constant amplitudes and full power are sum-capacity-achieving. Using these optimal input signals, the sum-capacity can finally be calculated.
1 Introduction
Given the significant benefit in power and cost saving of 1-bit analog-digital-converter (ADC), considerable efforts have been dedicated to signal designs and processing techniques for this ultra-low resolution ADC in high-bandwidth and/or multi-antenna systems Liu et al. (2019); Jeon et al. (2019); Choi et al. (2020); Xu et al. (2018); Zhang et al. (2016); Mo et al. (2017); Mollen et al. (2017); Xiong et al. (2017); Jacobsson et al. (2017); Studer and Durisi (2016). Over the years, several interesting information-theoretical results have been obtained for both point-to-point and multi-user channels with 1-bit ADC under additive white Gaussian noise (AWGN). For example, it has been shown in Singh et al. (2009); Mo and Heath (2015) that Quadrature phase Shift Keying (QPSK) is capacity-achieving in point-to-point single- and multiple-antenna static channels. Optimal signaling schemes and fundamental limits of 1-bit ADC have also been established for point-to-point fading channels in Krone and Fettweis (2010); Mezghani and Nossek (2008); Vu et al. (2018), Vu et al. (2019). Recently, under the assumption of AWGN, signal design and fundamental limits of 1-bit ADC have also been extended to multi-user static channels Rassouli et al. (2018) and multi-user fading channels (Ranjbar et al., 2019; Ranjbar et al., 2020). Specifically, it was shown in Rassouli et al. (2018) that any point in the capacity region of a 2-user static Gaussian multiple access channel (MAC) can be achieved by input signals with bounded supports. Furthermore, an upper bound on the sum-capacity was also developed in Rassouli et al. (2018). However, to our knowledege, the detailed characteristics of the optimal signals for such static Gaussian MACs remain unknown. In Ranjbar et al. (2020), by exploiting the effect of fading, the detailed characteristics of optimal input signals on the boundary of the capacity region of a 2-user Gaussian fading MAC with 1-bit ADC were also addressed.
Current and future active wireless systems (AWSs) such as 5G and beyond cellular networks with their multi-tier heterogeneous architectures are being designed to operate in the same or adjacent spectrum to other existing wireless systems. For example, proliferation in the number of wireless users and devices fueled by emerging applications in e.g., Internet of Things (IoT), unmanned systems, wearable technology, remote sensing is leading to the design of active-active coexistence such as LTE-U and WiFi in unlicensed bands, and incumbent, priority and general authorized access in Citizens Broadband Radio Service (CBRS) bands FCC (2020). Such coexistence is intensifying concerns on co-channel and adjacent-channel interference and its management for wireless systems. Specifically, AWSs themselves need to cope with increased active co-channel interference, which is generated in different ways. For example, due to their heterogeneous structures and the high frequency reuse factor, future AWSs require sharing of time-frequency resources with existing users and this makes intercell interference no longer negligible Osseiran et al. (2014); Chen and Zhao (2014); Feng et al. (2014); Lin et al. (2014); Fodor et al. (2012). In addition, radio frequency interference (RFI) mitigation might not be perfect, which leads to residual interference. Such intermittence and asynchronism make the statistical properties of RFI at AWS complicated. In particular, the traditional approach of treating co-channel interference plus noise as Gaussian no longer holds Irio et al., 2020; Irio et al., 2019; ElSawy et al. (2013); Lin et al. (2014). For example, aggregate interference generated by small cells to macro cells are non-Gaussian. It is due to the effect of dominant interferers, and the central limit theorem no longer holds Quek et al. (2013). In many wireless networks, especially heterogeneous AWSs, co-channel interference plus noise can be accurately modeled as Gaussian mixture (GM) Irio et al. (2020); Quek et al. (2013); Gulati et al. (2010); Stein (1995); Middleton (1999); Wang and Poor (1999); MIT Lincoln Laboratory (Reynolds, 2009); Erseghe et al. (2008); Moghimi et al. (2011); Bayram and Gezici (2010); Nasri and Schober (2009); Kenarsari-Anhari and Lampe (2010); Bhatia and Mulgrew (2007).
During the last few years, there have been several contributions on fundamental limits and optimal signal designs for non-Gaussian AWSs Das (2000); Fahs et al. (2012); Tchamkerten (2004); Oettli (1974); Cao et al. (2014); Vu et al. (2015); Ranjbar et al. (2018); Dytso et al. (2017). However, the results are rather limited. It is because for non-Gaussian channels, the assumption of having Gaussian input signals is no longer valid. Due to the difficulty in studying the detailed properties of the optimal inputs and in establishing the capacity in closed-form for a non-Gaussian channel, numerical methods are usually need to find the capacity-achieving signal, even for a point-to-point channel Vu et al. (2015); Le et al. (2016). In our recent work in Rahman et al. (2020a), Rahman et al. (2020b), the detailed characteristics of a capacity-achieving scheme were studied for a point-to-point Gaussian mixture channel using 1-bit output quantization. In particular, it was shown in Rahman M. H. et al. (2020) that for a general GM channel, the maximum number of mass points in the optimal signal is four. In addition, under the special case of zero-mean GM components, QPSK is optimal. Unfortunately, at the network level, signal design and network information-theoretical results for non-Gaussian noise and interference are complete lacking. Therefore, considering non-Gaussian interference plus noise in multi-user AWSs presents new challenges.
Motivated by the above discussions, we investigate the network information-theoretical limits of a 2-user multiple access Rayleigh fading channel with 1-bit output quantization in the presence of Gaussian-mixture co-channel interference. Specifically, we establish the sum-capacity-achieving signaling schemes and the sum-capacity of the considered GM MAC, which is an accurate model to capture non-Gaussian co-channel interference plus noise in practical wireless networks under coexistence regimes, especially for those having heterogeneous structures and high frequency reuse factor. In general, the problem of maximizing the sum-rate over input signals to determine the sum-capacity is both analytically and computationally challenging, especially on the space of multi-dimensional probability distributions with a non-linear mapping from the inputs to the output and non-Gaussian noise plus interference. Therefore, the main contribution of this work lies in the explicit establishment of optimal signaling schemes for such non-linear and non-Gaussian multi-user channels. Our approach is to separate the phases and amplitudes of the input signals to study their effects to the main sum-rate optimization problem. The specific contributions of our work can be summarized as follows:
• In the first part of our work, we demonstrate that the phases of the optimal inputs must be π/2 circularly symmetric. While this property has been shown before over various 1-bit ADC single-user, it is not trivial to extend to multi-user channels in the presence GM noise. Given the π/2 circularly symmetric property, it is then demonstrated that the problem of optimizing the sum-rate is equivalent to minimizing the conditional output entropy.
• More importantly, in the second part of the paper, by establishing and examining the Kuhn-Tucker condition (KTC) on the optimal amplitude input distributions, we then show that the optimal input amplitudes are bounded. Towards this end, we exploit the convexity of the log of sum of Q functions to deal with the presence of a mixture of Gaussian components. Furthermore, since the main objective function is now linear over the feasible set of bounded amplitude distributions, it achieves the minimum value at an extreme point. As a result, we can conclude that the optimal input signals must have constant amplitudes. Therefore, the use of any π/2 circularly symmetric signaling schemes with constant amplitudes and full power are sum-capacity-achieving. Using these optimal input signals, the sum-capacity can finally be established
2 A 2-User Mac in Rayleigh Fading with 1-Bit adc and Achievable Sum-Rate
2.1 Channel Model
We consider a 2-user multiple access channel (MAC) under GM noise plus interference N as depicted in Figure 1. The two users transmit their own signals X1 and X2, respectively, to the base station being equipped with an 1-bit ADC. These two transmitted signals X1 and X2 are imposed by the power constraints
Here, the total noise plus interference N follows a GM distribution, which is a mixture of M Gaussian components, and its probability density function (PDF) is given as
In Eq. 2,
Furthermore, in Eq. 1, H1 and H2 are the complex fading gains from user 1 and user 2 to the base station, respectively. In this paper, we consider Rayleigh fading channels, where H1 and H2 are circular symmetric Gaussian random variables with mean zero and variance
In addition, the fading channel gains are assumed to be known at the base station, but not the users, and they change independently over time.
With 1-bit output quantization, the real and imaginary parts of the received signal Z will be fed through a 1-bit quantizer, which results in the following complex binary outputs:
where Quant (⋅) is the 1-bit quantization operation defined as:
It is then easy to see that the output Y can only take on one of the following values in
2.2 Ergodic Sum-Rate and Sum-Capacity
For a given set of input distributions
In Eq. 6, the expectation E [⋅] is performed over fading gains H1 and H2, and
In Eq. 7, the joint entropy
Note that
where
It should be mentioned that
For simplicity, hereafter, we shall use the notations
The ergodic sum-capacity Cs of the considered MAC is the maximum ergodic sum-rate over all feasible input distributions
3 Sum-Capacity Achieving Input Signals
In general, the problem of maximizing MI over input distributions under certain input constraints as in Eq. 12 has been extensively studied, but tractable solutions can only be obtained for very few specific cases when the mapping from the inputs to output is linear, and the noise is additive Gaussian. Unfortunately, for the considered non-Gaussian channel, we have a non-linear mapping from the inputs to the output under the presence of GM noise. Therefore, this optimization problem is not trivial. In the following, our approach to solve Eq. 12 is to first address the optimal phases. The optimal amplitude distributions are then investigated to determine the complete input distributions.
3.1 Optimal Phase Distributions
To examine the effect of the input phase distributions, we first re-write the conditional density function in Eq. 10 using the amplitudes and phases as:
The joint and output entropies in Eqs. 8, 11, respectively, can then be expressed as
and
In Eq. 15, ξ(⋅) is an entropy function of the distribution in Eq. 10, which is calculated as:
To determine the optimal phases of the input signals, for a given set of the inputs
It is not difficult to verify that the two new distributions are π/2 circularly symmetric. Note that a density function FX(X) is π/2 circularly symmetric if FX(X) = FX (Xejπ/2) for any integer j. As we demonstrate in Appendix A, the use of
Because we consider Rayleigh fading, and the channel is ergodic, the expectation over H1 and H2 in Eq. 18 can be written in terms of their amplitudes and phases as
Since the two conditional entropies are the same, it is then clear that the use of
where
3.2 Optimal Amplitude Distributions
Given the characteristic of the optimal phases established in the previous section, we now turn out attention to the optimality of the amplitude distributions.
To provide more insights on the solutions of Eq. 21, we first examine a simplified optimization problem by fixing the distribution
We know that the entropy function
where μ1 is the Lagrangian multiplier and D (⋅) is the directional derivative. Before examining further the above KTC, we state the following result regarding μ1.
Proposition 1. The Lagrangian multiplier μ1 in Eq. 23 is positive. Equivalently, for the optimization problem in Eq. 22, full-power P1 is used.
Proof. Let Ω1 is the set of the feasible set of
It can then be verified that when choosing t such as:
we have
With a positive μ1, we shall analyze the properties of the amplitude of
where
Then, the KTC in Eq. 23 can be re-written as:
with the equality being achieved for any mass point
Proposition 2.
Proof. The proof is straightforward. Specifically, it can be verified that
The result in Proposition 2 helps establish the finiteness
Lemma 1. For any
Proof. Because 0 ≤ p(y|x1, x2, h1, h2) ≤ 1, it is apparent that
As shown in Appendix B, we have:
Then, by applying the convexity property of
The finiteness of
Theorem 1. The optimal input distribution
Proof. The proof is done by contradiction. Specifically, assume that the amplitude of
Given Theorem 1, we can now focus on the set of bounded
A similar result as in Theorem 1 but for
Theorem 2. The optimal input distribution
Proof. The proof follows a similar procedure as before, and it can be summarized as follows. We can first establish the KTC for Eq. 31 as
where μ2 is the non-negative Lagrangian multiplier. It can then be verified that full-power power P2 is used, and μ2 > 0. Furthermore, we have:
In a similar manner as in the proof of Lemma 1, we can then show that
Now, by combining the results from Theorems 1 and 2, we can conclude the capacity-achieving input distributions
Since all input distributions are π/2 circularly symmetric, as similar to the analysis we made earlier, the objective function
Given the above results, we can conclude that the optimal distributions
Note that ξ(⋅) is an entropy function of the corresponding distribution.
It is not hard to verify that in the case of a single-user channel under power constraint P and fading H, the single-user capacity C can be obtained from Cs in 35 by setting P1 = P and P2 = 0, and it is given as:
Furthermore, C can be achieved by a π/2 circularly symmetric input having a constant input, e.g., QPSK.
As the final note, we would like to mention that the developed results above apply directly to the traditional Gaussian channel. It is because GM include Gaussian as a special case with M = 1.
4 Sum-Rate and Sum-Capacity: Numerical Examples
In the following, we will provide several examples to verify the optimality of
First, let consider a 1-bit ADC MAC under a 2-term GM noise with ɛ1 = 0.45, ɛ2 = 0.55 and
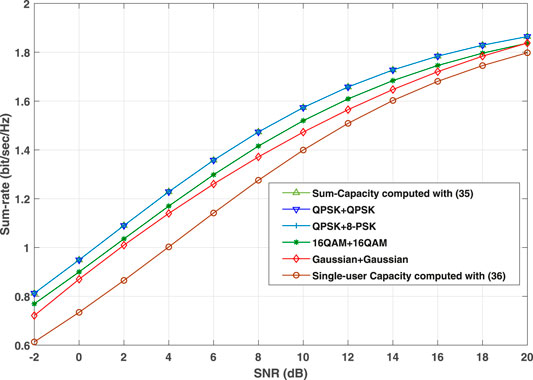
FIGURE 3. Sum-rates achieved by different pairs of input signals and Single-user capacity over the 2-term GM MAC. The two users are assumed to have equal transmit power P = P1= P2 and single-user has transmit power P.
The superiority of QPSK + QPSK and QPSK+8-PSK can clearly be seen from Figure 3. The reason for that is because such input signals are π/2 circularly symmetric with constant amplitudes, which are sum-capacity-achieving. It is also clear from Figure 3 that over the considered SNR range, the single user capacity C is always smaller than the sum-capacity Cs. While the single-user case corresponds to a corner point of the 2-user capacity-region, operating at this corner point is clearly sub-optimal. However, the results shown in Figure 3 indicates that both Cs and C asymptotically approach 2 bits/sec/Hz at a sufficiently high SNR. This fact can also be verified from Eqs. 35, 36.
Our results on the optimal signaling schemes also hold for a general GM channel having any number of Gaussian components. To demonstrate it, Figure 4 presents the sum-rates achieved by the same signaling schemes over a MAC under GM noise having three Gaussian components with ɛ1 = 0.9, ɛ2 = 0.05, ɛ3 = 0.05 and
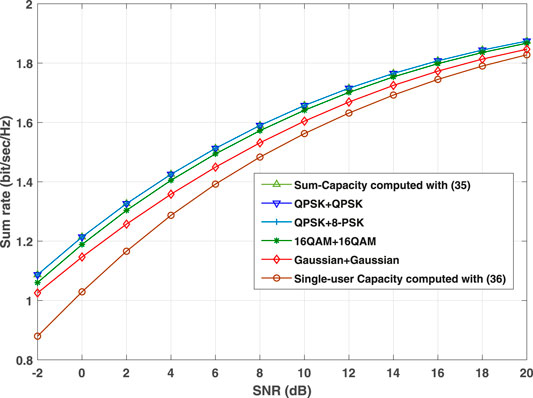
FIGURE 4. Sum-rates achieved by different pairs of input signals and Single-user capacity over the 3-term GM MAC. The two users are assumed to have equal transmit power P = P1= P2 and single-user has transmit power P.
In Figures 5, 6, the sum-rates are plotted for the considered 2-GM and 3-GM channels, respectively, but using un-equal transmit power with P1 = P and P2 = 3P. Note that in this case, we still define SNR as SNR =
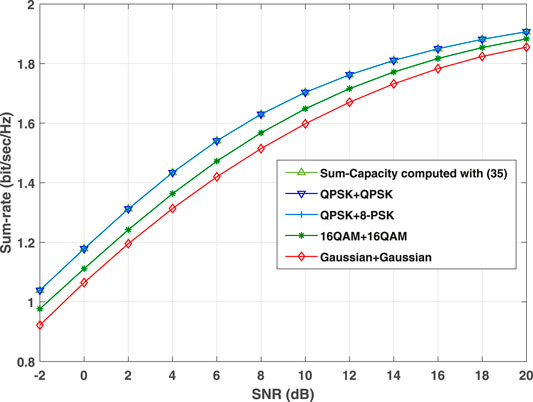
FIGURE 5. Sum-rates achieved by different pairs of input signals over the 2-term GM MAC. The two users are assumed to have unequal transmit power P1 = P and P2 = 3P.
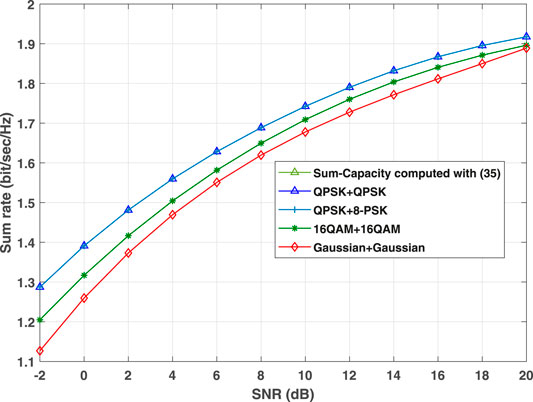
FIGURE 6. Sum-rates achieved by different pairs of input signals over the 3-term GM MAC. The two users are assumed to have unequal transmit power P1 = P and P2 = 3P.
Finally, Figure 7 compares the sum-capacities of three different channels: the Gaussian, 2-term GM, and 3-term GM channels. Note that we use the same 2-term and 3-term GMs as before. For simplicity, we assume the equal transmit power again with P1 = P and P2 = P, and use SNR =
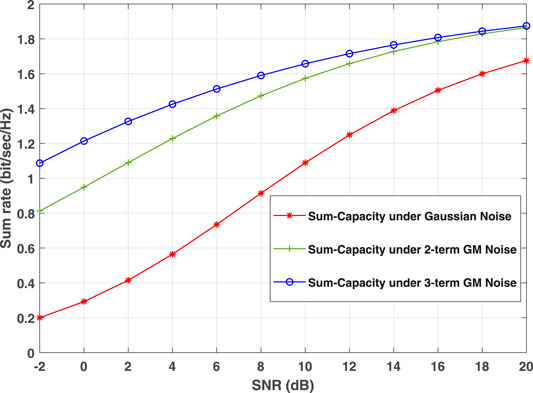
FIGURE 7. Sum-capacities of MACs under different types of noise: Gaussian, 2-term GM, and 3-term GM.
5 Conclusion
In this paper, we have addressed the optimal input distributions and the sum-capacity of a 2-user Rayleigh fading MAC under a general Gaussian-mixture noise plus interference with 1-bit ADC. The phases of the optimal inputs were first shown to be π/2 circularly symmetric. By exploiting this result, it was proved that the amplitudes of the optimal input distributions must only have a single mass point in order to minimize the conditional entropy. As a result, the sum-capacity achieving signaling schemes are π/2 circularly symmetric with a single mass point amplitude using full power. The advantages of the proposed signaling schemes in terms of the sum-rate were also clearly demonstrated.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was partially supported by Air Force Research Lab/Intelligent Fusion Technology under SBIR Grant No. IFT079-02.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abou-Faycal, I. C., Trott, M. D., and Shamai, S. (2001). The Capacity of Discrete-Time Memoryless Rayleigh-Fading Channels. IEEE Trans. Inform. Theor. 47, 1290–1301. doi:10.1109/18.923716
Bayram, S., and Gezici, S. (2010). On the Performance of Single-Threshold Detectors for Binary Communications in the Presence of Gaussian Mixture Noise. IEEE Trans. Commun. 58, 3047–3053. doi:10.1109/tcomm.2010.091710.090124
Bhatia, V., and Mulgrew, B. (2007). Non-parametric Likelihood Based Channel Estimator for Gaussian Mixture Noise. Signal. Process. 87, 2569–2586. doi:10.1016/j.sigpro.2007.04.006
Borwein, J., and Lewis, A. S. (2010). Convex Analysis and Nonlinear Optimization: Theory and Examples. Springer Science & Business Media.
Cao, J., Hranilovic, S., and Chen, J. (2014). Capacity-Achieving Distributions for the Discrete-Time Poisson Channel-Part I: General Properties and Numerical Techniques. IEEE Trans. Commun. 62, 194–202. doi:10.1109/tcomm.2013.112513.130142
Choi, J., Lee, G., Alkhateeb, A., Gatherer, N., and Evans, B. L. (2020). Advanced Receiver Architectures for Millimeter-Wave Communications with Low-Resolution ADCs. IEEE Commun. Mag. 58, 42–48. doi:10.1109/MCOM.001.2000122
Cover, T. M., and Thomas, J. A. (2006). Elements of Information Theory. 2nd edition. Wiley-Interscience.
Das, A. (2000). “Capacity-achieving Distributions for Non-gaussian Additive Noise,” in 2017 IEEE International Symposium on Information Theory (ISIT), Sorrento, Italy, June, 2000.
Dytso, A., Bustin, R., Poor, H. V., and Shitz, S. S. (2017). “On Additive Channels with Generalized Gaussian Noise,” in 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, June 25–30, 2017, 426–430. doi:10.1109/isit.2017.8006563
ElSawy, H., Hossain, E., and Haenggi, M. (2013). Stochastic Geometry for Modeling, Analysis, and Design of Multi-Tier and Cognitive Cellular Wireless Networks: A Survey. IEEE Commun. Surv. Tutorials 15, 996–1019. doi:10.1109/surv.2013.052213.00000
Erseghe, T., Cellini, V., and Donà, G. (2008). On UWB Impulse Radio Receivers Derived by Modeling MAI as a Gaussian Mixture Process. IEEE Trans. Wireless Commun. 7, 2388–2396. doi:10.1109/twc.2008.070133
Fahs, J., Ajeeb, N., and Abou-Faycal, I. (2012). “The Capacity of Average Power Constrained Additive Non-gaussian Noise Channels,” in International Conference on Telecommunications (ICT), Jounieh, Lebanon, April 23–25, 2012. doi:10.1109/ictel.2012.6221320
FCC (2020). 3.5 GHz Band Overview. Available at: https://www.fcc.gov/35-ghz-band-overview.
Feng, D., Lu, L., Yuan-Wu, Y., Li, G., Li, S., and Feng, G. (2014). Device-to-device Communications in Cellular Networks. IEEE Commun. Mag. 52, 49–55. doi:10.1109/mcom.2014.6807946
Fodor, G., Dahlman, E., Mildh, G., Parkvall, S., Reider, N., Miklós, G., et al. (2012). Design Aspects of Network Assisted Device-To-Device Communications. IEEE Commun. Mag. 50, 170–177. doi:10.1109/mcom.2012.6163598
Gulati, K., Evans, B. L., Andrews, J. G., and Tinsley, K. R. (2010). Statistics of Co-channel Interference in a Field of Poisson and Poisson-Poisson Clustered Interferers. IEEE Trans. Signal. Process. 58, 6207–6222. doi:10.1109/tsp.2010.2072922
Irio, L., Oliveira, R., da Costa, D. B., and Alouini, M.-S. (2020). Impact of Wireless-Powered Communications in Coexisting mobile Networks. IEEE Wireless Commun. Lett. 9, 1. doi:10.1109/LWC.2020.2980524
Irio, L., Oliveira, R., and da Costa, D. B. (2019). Highly Accurate Approaches for the Interference Modeling in Coexisting Wireless Networks. IEEE Commun. Lett. 23, 1652–1656. doi:10.1109/LCOMM.2019.2924887
Jacobsson, S., Durisi, G., Coldrey, M., Gustavsson, U., and Studer, C. (2017). Throughput Analysis of Massive MIMO Uplink with Low-Resolution ADCs. IEEE Trans. Wireless Commun. 16, 4038–4051. doi:10.1109/TWC.2017.2691318
Jeon, Y.-S., Do, H., Hong, S.-N., and Lee, N. (2019). Soft-output Detection Methods for Sparse Millimeter-Wave MIMO Systems with Low-Precision ADCs. IEEE Trans. Commun. 67, 2822–2836. doi:10.1109/tcomm.2019.2892048
Kenarsari-Anhari, A., and Lampe, L. (2010). Performance Analysis for BICM Transmission over Gaussian Mixture Noise Fading Channels. IEEE Trans. Commun. 58, 1962–1972. doi:10.1109/TCOMM.2010.07.090337
Krone, S., and Fettweis, G. (2010). “Fading Channels with 1-bit Output Quantization: Optimal Modulation, Ergodic Capacity and Outage Probability,” in 2010 IEEE Information Theory Workshop, Cairo, Egypt, January 6–8, 2010 (IEEE), 1–5. doi:10.1109/cig.2010.5592653
Le, D.-A., Vu, H. V., Tran, N. H., Gursoy, M. C., and Le-Ngoc, T. (2016). Approximation of Achievable Rates in Additive Gaussian Mixture Noise Channels. IEEE Trans. Commun. 64, 5011–5024. doi:10.1109/TCOMM.2016.2602342
Lin, X., Andrews, J., Ghosh, A., and Ratasuk, R. (2014). An Overview of 3GPP Device-To-Device Proximity Services. IEEE Commun. Mag. 52, 40–48. doi:10.1109/mcom.2014.6807945
Liu, T., Tong, J., Guo, Q., Xi, J., Yu, Y., and Xiao, Z. (2019). Energy Efficiency of Massive MIMO Systems with Low-Resolution ADCs and Successive Interference Cancellation. IEEE Trans. Wireless Commun. 18, 3987–4002. doi:10.1109/twc.2019.2920129
Mezghani, A., and Nossek, J. A. (2008). “Analysis of Rayleigh-Fading Channels with 1-bit Quantized Output,” in 2008 IEEE International Symposium on Information Theory (IEEE), Toronto, Canada, July 7–12, 2008, 260–264. doi:10.1109/isit.2008.4594988
Middleton, D. (1999). Non-Gaussian Noise Models in Signal Processing for Telecommunications: New Methods an Results for Class A and Class B Noise Models. IEEE Trans. Inform. Theor. 45, 1129–1149. doi:10.1109/18.761256
Mo, J., Alkhateeb, A., Abu-Surra, S., and Heath, R. W. (2017). Hybrid Architectures with Few-Bit ADC Receivers: Achievable Rates and Energy-Rate Tradeoffs. IEEE Trans. Wireless Commun. 16, 2274–2287. doi:10.1109/TWC.2017.2661749
Mo, J., and Heath, R. W. (2015). Capacity Analysis of One-Bit Quantized MIMO Systems with Transmitter Channel State Information. IEEE Trans. Signal. Process. 63, 5498–5512. doi:10.1109/tsp.2015.2455527
Moghimi, F., Nasri, A., and Schober, R. (2011). Adaptive L_p-Norm Spectrum Sensing for Cognitive Radio Networks. IEEE Trans. Commun. 59, 1934–1945. doi:10.1109/tcomm.2011.051311.090588
Mollen, C., Choi, J., Larsson, E. G., and Heath, R. W. (2017). Uplink Performance of Wideband Massive MIMO with One-Bit ADCs. IEEE Trans. Wireless Commun. 16, 87–100. doi:10.1109/TWC.2016.2619343
Nasri, A., and Schober, R. (2009). Performance of BICM-SC and BICM-OFDM Systems with Diversity Reception in Non-gaussian Noise and Interference. IEEE Trans. Commun. 57, 3316–3327. doi:10.1109/tcomm.2009.11.080180
Oettli, W. (1974). Capacity-achieving Input Distributions for Some Amplitude-Limited Channels with Additive Noise (corresp.). IEEE Trans. Inform. Theor. 20, 372–374. doi:10.1109/TIT.1974.1055225
Osseiran, A., Boccardi, F., Braun, V., Kusume, K., Marsch, P., Maternia, M., et al. (2014). Scenarios for 5G mobile and Wireless Communications: The Vision of the METIS Project. IEEE Commun. Mag. 52, 26–35. doi:10.1109/mcom.2014.6815890
Quek, T. Q. S., de la Roche, G., Güvenç, I., and Kountouris, M. (2013). Small Cell Networks: Deployment, PHY Techniques, and Resource Management. 1st edn. Cambridge University Press.
Rahman, M. H., Ranjbar, M., Tran, N. H., and Pham, K. (2020b). “Capacity-achieving Signal and Capacity of Gaussian Mixture Channels with 1-bit Output Quantization,” in ICC 2020 - 2020 IEEE International Conference on Communications (ICC), Virtual Conference, Jun 7–11, 2020, 1–6. doi:10.1109/ICC40277.2020.9149428
Rahman, M., Ranjbar, M., and Tran, N. (2020a). On the Capacity-Achieving Scheme and Capacity of 1-bit Adc Gaussian-Mixture Channels. EAI Endorsed Trans. Ind. Networks Intell. Syst. 7, 162830. doi:10.4108/eai.31-1-2020.162830
Ranjbar, M., Tran, N. H., Nguyen, T. V., Gursoy, M. C., and Nguyen-Le, H. (2018). Capacity-achieving Signals for point-to-point and Multiple-Access Channels under Non-gaussian Noise and Peak Power Constraint. IEEE Access 6, 30977–30989. doi:10.1109/access.2018.2837056
Ranjbar, M., Tran, N. H., Vu, M. N., Nguyen, T. V., and Cenk Gursoy, M. (2020). Capacity Region and Capacity-Achieving Signaling Schemes for 1-bit ADC Multiple Access Channels in Rayleigh Fading. IEEE Trans. Wireless Commun. 19, 6162–6178. doi:10.1109/twc.2020.3000610
Ranjbar, M., Vu, M., Tran, N., Pham, K., and Nguyen, D. (2019). “On the Sum-Capacity-Achieving Distributions and Sum-Capacity of 1-bit Adc Macs in Rayleigh Fading,” in ICC 2019-2019 IEEE International Conference on Communications (ICC), Shanghai, China, May 20–24, 2019 (IEEE), 1–6. doi:10.1109/icc.2019.8761097
Rassouli, B., Varasteh, M., and Gündüz, D. (2018). Gaussian Multiple Access Channels with One-Bit Quantizer at the Receiver. Entropy 20, 686. doi:10.3390/e20090686
Chen, S., and Zhao, J. (2014). The Requirements, Challenges, and Technologies for 5G of Terrestrial mobile Telecommunication. IEEE Commun. Mag. 52, 36–43. doi:10.1109/mcom.2014.6815891
Singh, J., Dabeer, O., and Madhow, U. (2009). On the Limits of Communication with Low-Precision Analog-To-Digital Conversion at the Receiver. IEEE Trans. Commun. 57, 3629–3639. doi:10.1109/TCOMM.2009.12.080559
Stein, D. W. J. (1995). Detection of Random Signals in Gaussian Mixture Noise. IEEE Trans. Inform. Theor. 41, 1788–1801. doi:10.1109/18.476307
Studer, C., and Durisi, G. (2016). Quantized Massive MU-MIMO-OFDM Uplink. IEEE Trans. Commun. 64, 2387–2399. doi:10.1109/TCOMM.2016.2558151
Tchamkerten, A. (2004). On the Discreteness of Capacity-Achieving Distributions. IEEE Trans. Inform. Theor. 50, 2773–2778. doi:10.1109/tit.2004.836662
Vu, H. V., Tran, N. H., Gursoy, M. C., Le-Ngoc, T., and Hariharan, S. I. (2015). Capacity-achieving Input Distributions of Additive Quadrature Gaussian Mixture Noise Channels. IEEE Trans. Commun. 63, 3607–3620. doi:10.1109/tcomm.2015.2451096
Vu, M. N., Tran, N. H., Wijeratne, D. G., Pham, K., Lee, K.-S., and Nguyen, D. H. N. (2019). Optimal Signaling Schemes and Capacity of Non-coherent Rician Fading Channels with Low-Resolution Output Quantization. IEEE Trans. Wireless Commun. 18, 2989–3004. doi:10.1109/twc.2019.2907952
Vu, M., Wijeratne, D., Tran, N., and Pham, K. (2018). “Optimal Signaling Scheme and Capacity of Non-coherent Rician Fading Channels with 1-bit Output Quantization,” in 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, May 20–24, 2018 (IEEE), 1–6. doi:10.1109/icc.2018.8422260
Winkler, G. (1988). Extreme Points of Moment Sets. Mathematics OR 13, 581–587. doi:10.1287/moor.13.4.581
Xiaodong Wang, X., and Poor, H. V. (1999). Robust Multiuser Detection in Non-gaussian Channels. IEEE Trans. Signal. Process. 47, 289–305. doi:10.1109/78.740103
Xiong, Y., Wei, N., Zhang, Z., Li, B., and Chen, Y. (2017). Channel Estimation and IQ Imbalance Compensation for Uplink Massive MIMO Systems with Low-Resolution ADCs. IEEE Access 5, 6372–6388. doi:10.1109/ACCESS.2017.2690439
Xu, J., Xu, W., Zhang, H., Li, G. Y., and You, X. (2018). Performance Analysis of Multi-Cell Millimeter Wave Massive MIMO Networks with Low-Precision ADCs. IEEE Trans. Commun. 67, 302–317. doi:10.1109/TCOMM.2018.2874963
Zhang, J., Dai, L., Sun, S., and Wang, Z. (2016). On the Spectral Efficiency of Massive MIMO Systems with Low-Resolution ADCs. IEEE Commun. Lett. 20, 842–845. doi:10.1109/LCOMM.2016.2535132
Appendix A
Proof that
From Eq. 13, it can be verified that
The third equality is based on the variable transformation and the fourth equality is due to the fact that
Appendix B
The Inequality
We Have
Note that the last inequality comes from the fact that Q(x) is a decreasing function of a positive x.
Keywords: 1-bit ADC, achievable rate, Gaussian-mixture interference, multiple access channel, rayleigh fading, sum-capacity
Citation: Rahman MH, Ranjbar M, Tran NH and Pham K (2021) Optimal Signaling Schemes and Sum-Capacity of 1-bit ADC Fading 2-User MACs under Gaussian-Mixture Interference. Front. Comms. Net 2:734165. doi: 10.3389/frcmn.2021.734165
Received: 30 June 2021; Accepted: 16 September 2021;
Published: 20 October 2021.
Edited by:
Ebrahim Bedeer, University of Saskatchewan, CanadaReviewed by:
Lukas T. N. Landau, Pontifical Catholic University of Rio de Janeiro, BrazilChinmoy Kundu, University College Dublin, Ireland
Copyright © 2021 Rahman, Ranjbar, Tran and Pham. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nghi H. Tran, bmdoaS50cmFuQHVha3Jvbi5lZHU=
 Md Hasan Rahman
Md Hasan Rahman Mohammad Ranjbar
Mohammad Ranjbar Nghi H. Tran
Nghi H. Tran Khanh Pham2
Khanh Pham2