OFDM-IM for Joint Communication and Radar-Sensing: A Promising Waveform for Dual Functionality

The demand for dual-functional wireless systems is on the rise as certain resources become more congested and scarce. Joint communication-radar (JCR) is a promising technology that is becoming very critical and growing in popularity, where communication and radar applications are serviced simultaneously sharing the same hardware/software and the frequency band resources. JCR and its alternatives need to be cleverly integrated into certain waveforms such as orthogonal frequency division multiplexing (OFDM) to function properly without degradation in the performance. With the aid of the promising concepts of index modulation (IM) and Golay complementary sequences, a novel JCR waveform is proposed to serve both communication and radar applications with the same resources. It has been shown by extensive computer simulations that the proposed OFDM with an index modulation (OFDM-IM) waveform outperforms the classical OFDM with fixed pilot design both in bit error rate (BER) performance and radar-based applications by introducing diversity among subcarriers and frequency agility over the whole frequency band.

1 Introduction

Future, 6G and beyond, wireless systems are evolving rapidly in terms of flexibility, interoperability, and coexistence of various wireless technologies. Due to the invaluable and scarce bandwidth, as researchers explore techniques to make efficient use of strict resources, different applications, systems, and waveforms are envisioned to coexist and operate together in harmony. On account of radar, wireless sensing and communication being eminently common and important radio frequency (RF) applications, the marriage of these concepts has recently attracted substantial attention. In the literature, radar-sensing and communicatio4n marriage have been given numerous names, such as radar-communication coexistence (RCC) and dual-functional radar-communication (DFRC) (Liu et al., 2020). In the first category, two systems share the same habitat (cohabitation), and they operate with efficient interference management techniques (cooperation). The second category can be seen as a codesign of a system having both radar and communication capabilities. The design approach of a DFRC system can be divided into three subgroups as follows: joint radar-communication (JRC), joint communication-radar (JCR) Mazahir et al. (2021), and unified architecture. JRC mainly focuses on the radar capability and performs communication as a secondary functionality. On the other hand, JCR refers to the systems whose essential design parameter is the communication capability of a DFRC system. Last but not least, a unified architecture proposes a codesign system that is designed for the application requirements from the scratch.

Moreover, DFRC provides hardware and software convergence of radar-sensing and communication applications to utilize scarce resources more efficiently and effectively. With these and upcoming considerable contributions, DFRC is envisioned to be implemented and provide service to many applications, some of which include intelligent vehicular transportation, aircraft traffic, and military applications whether it is in the air, sea, or space. JCR, which is a form of the DFRC system, creates a fusion of both functionalities in a unified platform, which is feasible since the gap between radar and communication systems is small. This unification not only grants a cost reduction but also enables an efficient spectrum usage, efficient power consumption, and a more compact system size. One major challenge of designing a JCR system is the performance criteria (Zheng et al., 2019); that is, both functionalities are desired to be designed cooperatively without performance degradation. Additional challenges include dedicated receiver algorithms and complication of the transmitter design.

JCR research has pushed significant efforts to share the spectrum between radar and communication without interference. Fundamental concepts and important performance metrics have been discussed, and resource management approaches have been analyzed for JCR in the study by Luong et al. (2021). Waveform design plays a critical role in the JCR concept, and a single novel waveform for both radar and communication functionalities, without a reduction in performance of either, is yet to exist. Orthogonal frequency division multiplexing (OFDM) is a very popular waveform integrated to JCR (Ozkaptan et al., 2018). Also, a JCR technique on the wireless system standard IEEE 802.11 employing OFDM is proposed in the study by Nguyen and Heath (2017) with dedicated OFDM-radar algorithms. However, for the dual-functionality of the system, it is not mandatory to have a single waveform. Different waveforms may be superimposed and transmitted simultaneously as in the study by Şahin and Arslan (2020), Şahin and Arslan (2021), where frequency-modulated continuous wave (FMCW) and OFDM are used. Additionally, millimeter wave (mmWave) communication provides large transmission bandwidth enabling large data rates and has a potential to collaborate with JCR. From the signal processing perspective, Mishra et al. (2019) dived in to mm-Wave JCR systems and waveform design. As a further note, Feng et al. (2020) explored state-of-the-art JCR evolution with a comprehensive survey on the DFRC technology.

On the other hand, index modulation (IM) is a simple, spectral, and energy efficient scheme that can be implemented by many waveforms and techniques, such as OFDM. OFDM with index modulation (OFDM-IM) is a very popular scheme that conveys information not only through quadrature amplitude modulated symbols but also through the indices of active subcarriers in the frequency domain Basar et al. (2013). It has been utilized in various ways to transmit additional bits, provide flexibility, improve reliability, and more, such as in the study by Basar (2015), Arslan et al. (2020a), Dogukan and Basar (2020), Arslan et al. (2020b). Superiorities of OFDM-IM over classical OFDM include efficient implementation and flexibility of active subcarriers, energy efficiency, a reduced peak-to-average power ratio (PAPR), robustness to inter-carrier interference (ICI), and improved bit error performance Basar et al. (2017). Recently, IM has even been applied to DFRC. In the study by Hoque and Şahin (2020), IM-aided circularly shifted chirps are proposed for DFRC systems. In the study by Huang et al. (2020), information is embedded on the DFRC system in an IM manner, where different frequency and antenna selections construct possible constellation space. However, to the best of our knowledge, there is no study focusing on the implementation and analysis of OFDM-IM in JCR systems.

This study sheds lights on the drawbacks of pilot-based OFDM in the JCR system such as a limited unambiguous radar range and channel estimation errors, and proposes a novel structure using OFDM-IM to overcome these problems. To perform radar functionality on the proposed structure, Golay complementary sequences (GCS) are inserted into the OFDM-IM waveform, which are explained in Section 2. Since GCS have suitable ambiguity function properties for radar functionality (Kumari et al., 2018), they are used as preknown radar symbols in our proposed scheme.

The contributions of this study can be summarized and highlighted as follows:

• A novel JCR waveform scheme is proposed using the OFDM-IM structure and GCS as radar symbols.

• The transmitter and receiver structures are introduced to improve both the communication and radar performance of the proposed waveform scheme.

• A novel channel estimation scheme is proposed for OFDM-IM utilizing its radar functionality.

• Superiority of the proposed scheme is analyzed compared to the conventional OFDM structure with comb-type pilots for JCR systems proposed in the study by Ozkaptan et al. (2018).

The rest of the article can be summarized as follows. In Section 2, the system model of the proposed JCR scheme is presented. In Sections 3 and 4, radar and communication functionalities of the proposed scheme are explained. Computer simulation results are presented in Section 5. Finally, Section 6 concludes the article.

2 System Model

In this section, the system model of the proposed OFDM-IM JCR scheme is provided. First, the transmitter architecture is presented, and then the channel model is explained.

2.1 Transmitter Design

The block diagram of the considered OFDM-IM JCR system is presented in Figure 1. As in classical OFDM-IM, the entire OFDM-IM symbol consisting of N subcarriers is split into total G subblocks. Since each subblock undergoes the same procedures, it is sufficient to consider the ξ^th subblock $\mathbf{x}(\xi )\in {\mathbb{C}}^{g\times 1}$, where ξ ∈ {1, … , G}. Each subblock has a length of g = N/G subcarriers with indices (i₁, … , i_n, … , i_g), where i_n is the n^th subcarrier index of the ξ^th subblock.

FIGURE 1

FIGURE 1. Transmitter structure for the m^th OFDM symbol of the proposed DFRC system.

For the ξ^th subblock, incoming b bits are split into b₁ and b₂ bits. The $b_1=\lfloor {\text{log}}_2\left(\genfrac{}{}{0.0pt}{}{g}{k}\right)\rfloor$ bits determine the indices of the k communication, r radar, and l null subcarriers of a subblock, via binary-to-decimal conversion, using a predefined look-up table. Then the remaining b₂ = klog₂(Q) bits assign quadrature amplitude modulation (QAM) symbols, which are chosen from the complex set $\mathbb{S}$, to the communication subcarriers of the subblock. Consequently, a total of

$b=b_1+b_2=\lfloor {\log }_2\left(\genfrac{}{}{0.0pt}{}{g}{k}\right)\rfloor +k{\log }_{2}Q,(1)$

bits can be transmitted per subblock. An example look-up table with a subblock size of four and two communication subcarriers (k = 2) per subblock with symbols C_o, where o ∈ {1, 2}, is shown in Figure 2A. In this example, there is one radar (r = 1) and one null subcarrier (l = 1) in a subblock. The number of total radar symbols in one OFDM symbol is denoted as R = rN/g. Figure 2B is presented to visualize the considered time–frequency lattice, according to Figure 2A. The flexible design of OFDM-IM allows the proposed scheme to utilize the whole bandwidth for radar processing such as frequency-agile radars. At the receiver side, the location of the radar symbol is found via estimation of the null subcarrier location, which will be explained in Section 3. Therefore, null subcarriers are distributed intelligently to find the locations of radar symbols.

FIGURE 2

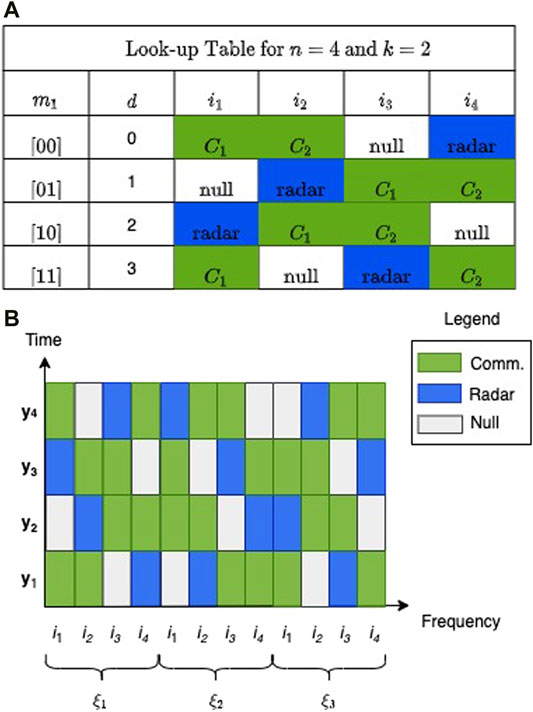
FIGURE 2. A case study for the proposed architecture. (A) Look-up table for two active subcarriers out of four subcarriers in a subblock. (B) Example of the transmitted OFDM-IM JCR frame.

Next, two complementary Golay sequences G_a and G_b, both with length R/2, are generated. In succession, the elements of G_a are placed into the first half of the OFDM-IM JCR block with N/2 subcarriers. Subsequently, the aforementioned procedure is repeated for the remaining N/2 subcarriers using G_b. After this point, the procedures as in OFDM are applied. The time domain m^th OFDM symbol x_m is generated by applying the inverse fast Fourier (IFFT) transformation on frequency domain samples X_m, as given below:

${\mathbf{x}}_m=\mathrm{I}\mathrm{F}\mathrm{F}\mathrm{T}\left\{{\mathbf{X}}_m\right\}={\left[\begin{array}{cccc}\hfill X_{m,1}\hfill & \hfill X_{m,2}\hfill & \hfill \cdots \hfill & \hfill X_{m,N}\hfill \end{array}\right]}^{\mathrm{T}}.(2)$

Let the matrix X ∈ C^M×N be the frame of frequency domain–transmitted symbols, where the element X_m,n is the mth symbol transmitted on subcarrier n, for m = 1, … , M and n = 1, … , N. After the IFFT operation, a cyclic prefix (CP) of length C samples ${\left[\begin{array}{cccc}\hfill x_{m,(N-C+1)},\hfill & \hfill \cdots ,\hfill & \hfill x_{m,(N-1)},\hfill & \hfill x_{m,N}\hfill \end{array}\right]}^{\mathrm{T}}$ is added to the beginning of the OFDM symbol. Then, the OFDM-IM frame $\mathbf{x}\in {\mathbb{C}}^{M(N+C)\times 1}$ including M OFDM symbols is generated by appending each OFDM symbol back to back.

Afterward, the baseband discrete signal x is processed with a digital-to-analog converter (DAC) and upconverted to the desired radio frequency (RF) band, where the transmitted passband analog signal becomes

$\tilde{\mathbf{x}}(t)=\mathfrak{R}\{\mathbf{x}(t)e^{j(2\pi f_{c}t+\bar{\theta })}\},(3)$

where $\mathfrak{R}\{.\}$ denotes the real part of a complex quantity. Here, f_c and $\bar{\theta }$ are the carrier frequency and the initial phase of the transmitted signal, respectively, where f_c is selected according to the 5G mm wave band.

2.2 Channel Model

Throughout the study, the communication receiver is also exploited as a radar receiver. Hence, the bistatic radar model is used, where the transmitter and the radar receiver are not colocated. The wireless channel is dedicated for both communication and radar operation, where the transmitted OFDM-IM JCR waveform propagates through. The channel model includes complex channel gain, Doppler shift, and delay for every path. It is also assumed that the transmission of the frame is long enough to be affected from time selectivity, but short enough such that the time variation can be accurately modeled as depending only on per-tap linear phase variations due to Doppler effects (Letzepis et al., 2011). Therefore, the linear time-variant channel in the time-delay domain, c(t, τ), can be modeled as follows (Hlawatsch and Matz, 2011):

$c(t,\tau )=\sum _{p=1}^P{\alpha }_p{e}^{j2\pi {\nu }_{p}t}\delta (\tau -{\tau }_p),(4)$

where α_p, τ_p, and ν_p denote the complex attenuation factor, bistatic time delay, and the Doppler frequency shift associated with the p^th target, respectively, where there are a total of P targets. The estimation of the complex gain, delay, and the Doppler shift from each tap of the multipath channel is performed via radar signal processing techniques as explained in Section 3. It is known that the frequency domain channel coefficients for an entire frame can be expressed as the superimposition of two-dimensional complex sinusoids, which allow us to use a periodogram-based delay and Doppler shift estimation. Down-converting the received passband signal into baseband and sampling with the frequency of F_s = NΔf, the discrete-time signal becomes

$y[n]=\sum _{p=1}^P{\alpha }_{p}x\left(\frac{n}{F_s}-{\tau }_p\right)e^{j2\pi n\frac{{\nu }_p}{F_s}}+w[n],n\in {\mathbb{N}}^{+},(5)$

where $w[n]\sim \mathcal{CN}\left(0,{\sigma }^2\right)$ denotes the sampled additive white Gaussian noise (AWGN). With the assumption that the channel components remains the same during transmission of an OFDM frame and the CP length (C) is larger than maximum bistatic delay eliminating inter-symbol interference (ISI), the received vector is given by

$\mathbf{y}={[y_1^T\cdots y_M^T]}^{\mathrm{T}}={\mathbf{H}}^t\mathbf{x}+\mathbf{w},(6)$

where ${\mathbf{H}}^t\in {\mathbb{C}}^{M(N+C)\times M(N+C)}$ is the time domain channel matrix and w is the noise vector. The signal-to-noise ratio (SNR) is defined as 1/σ².

The relation of Eq. 4 with the time domain channel matrix H^t can be represented as follows:

${\mathbf{H}}^t=\sum _{p=1}^P{\alpha }_p{\mathbf{\Pi }}^{n_{{\tau }_p}}\mathbf{\Delta }({\nu }_p),(7)$

where the delay matrix ${\mathbf{\Pi }}^{n_{{\tau }_p}}\in {\mathbb{C}}^{M(N+C)\times M(N+C)}$ is the forward cyclic shifted permutation matrix according to the delay of the pth path. It can be expressed as follows:

$\mathbf{\Pi }=\left[\begin{array}{ccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right],\text{and}{n}_{{\tau }_p}=\lfloor \frac{{\tau }_p}{N\mathrm{\Delta }f}\rfloor .(8)$

The Doppler shift matrix for the pth path, $\mathbf{\Delta }({\nu }_p)\in {\mathbb{C}}^{M(N+C)\times M(N+C)}$, can be written as follows:

$\mathbf{\Delta }({\nu }_p)=\mathrm{diag}\left(\left[e^{\frac{j2\pi {\nu }_p}{N\mathrm{\Delta }f}},e^{\frac{j2\pi {\nu }_{p}2}{N\mathrm{\Delta }f}},\dots ,e^{\frac{j2\pi {\nu }_p(N+C)M}{N\mathrm{\Delta }f}}\right]\right),(9)$

where there are total P paths with different delays and Doppler shifts.

The channel estimation and decoding processes are explained in the next sections.

3 Bistatic Radar and Channel Estimation

In this section, the bistatic radar signal processing scheme is introduced using the known Golay sequence on the transmitted OFDM-IM frame. The general structure of the steps followed both in this section and the next section can be seen in Figure 3. Revisiting (Eq. 6), the received signal can be written in frequency domain as follows:

$\mathbf{Y}={\mathbf{H}}^fʘ\mathbf{X}+\mathbf{Z},(10)$

where ʘ denotes the Hadamard product, $\mathbf{Y}\in {\mathbb{C}}^{M\times N}$ is the frequency domain received matrix, and $\mathbf{Z}\in {\mathbb{C}}^{M\times N}$ is the frequency domain representation of noise w. The elements of frequency domain channel matrix ${\mathbf{H}}^f\in {\mathbb{C}}^{M\times N}$ can be expressed as follows:

$H_{m,n}^f=\sum _{p=1}^P{\alpha }_p{e}^{-j2\pi {\nu }_p{T}_d(m-1)}{e}^{-j2\pi (n-1-\lfloor N/2\rfloor ){\tau }_p/T},(11)$

where T_d is the OFDM symbol duration after cyclic prefix (CP) in addition to the original duration $T=\frac{1}{\mathrm{\Delta }f}$.

FIGURE 3

FIGURE 3. Decoding process for an OFDM-IM frame of the proposed DFRC system.

3.1 Null Subcarrier Estimation

In this step, the entire Y matrix is processed to estimate the null subcarrier locations. Once the null subcarrier location is found for each subblock, the location of radar and communication subcarrier can also be found as it can be seen in Figure 2A. For each ξ subblock in the m^th OFDM symbol, the null subcarrier estimation ${(n_m^{\xi })}^{\star }$ is performed as follows:

${(n_m^{\xi })}^{\star }=\underset{n:n\in \{1,\dots ,N/g\}}{\min }|Y_{m,n}^{\xi }|{.}^2(12)$

Afterward, the vector ${\mathbf{n}}^{\star }\in {\mathbb{C}}^{1\times M\cdot R}$ indicating null subcarriers is constructed by gathering all estimated ${(n_m^{\xi })}^{\star }$. Once the null subcarrier location is estimated, locations of radar and communication subcarriers are also known due to the mapping scheme shown in Figure 2A.

3.2 De-Chirping

After the null subcarrier estimation, de-chirping of the received sequence is done. Also, it is followed by filling estimated communication subcarriers with zeros. In this step, the fast-time/slow-time coherent processing interval matrix $\mathbf{K}\in {\mathbb{C}}^{M\times N}$ is formed. Let the matrix $\tilde{\mathbf{X}}\in {\{-\mathrm{1,1}\}}^{M\times R}$ denote the known Golay sequences for all OFDM frames. Then, the elements K_m,n of matrix K become

$K_{m,n}=\left\{\begin{array}{c}\hfill Y_{m,n}/X_{m,\beta },whenn\in {\mathbf{n}}^{\star },\hfill \\ \hfill 0,otherwise,\hfill \end{array}\right.(13)$

where the index in the Golay sequence matrix is $\beta =\lceil \frac{n\cdot g}{N}\rceil$.

3.3 Delay and Doppler Shift Estimation

Delay and Doppler shift estimation of the proposed method is done via the 2D-periodogram method. The matrix K is utilized to perform periodogram-based radar processing. The output power of the periodogram at the ι^th Doppler and ς^th range bin is as follows:

$P(\iota ,\varsigma )=\frac{1}{NM}{\left|\underset{N\text{\hspace{0.17em}FFTs\hspace{0.17em}of\hspace{0.17em}length\hspace{0.17em}}M}{\underbrace{\sum _{m=0}^{M-1}\left(\stackrel{M\text{\hspace{0.17em}FFTs\hspace{0.17em}of\hspace{0.17em}length\hspace{0.17em}}N}{\underset{\sum _{n=0}^{N-1}{\mathbf{K}}_{m,n}{e}^{-j2\pi \frac{n\iota }{N}}}{︷}}\right)e^{-j2\pi \frac{m\varsigma }{M}}}}\right|}^2,(14)$

where sinusoids in K related to object’s distance and velocity lead to peaks in P (ι, ς). Then certain distance and velocity values can be found from the related range and the Doppler bin value of peaks. The threshold value is set according to the SNR of the system. Distance d and velocity ν of the paths are found as follows:

$d=\frac{\iota c}{\mathrm{\Delta }fN}\text{and}\nu =\frac{\varsigma c}{f_{c}T}(15)$

where c denotes the speed of light.

3.4 Complex Attenuation Estimation

In this step, the complex attenuation factor of the channel is estimated. It is assumed that the total number of targets is known in advance. The number of targets can be obtained by simply putting a threshold in Eq. 14. Let the vector $\tilde{\mathbf{Y}}\in {\mathbb{C}}^{M\cdot R\times 1}$ denote the complex symbols extracted from the estimated radar subcarrier locations, which are also affected by the noise $\tilde{\mathbf{Z}}\in {\mathbb{C}}^{M\cdot R\times 1}$. Considering the frequency domain channel shown in Eq. 11, $\tilde{\mathbf{Y}}$ can be written as follows:

$\tilde{\mathbf{Y}}=\mathbf{\Omega }(\mathit{\tau },\mathit{\nu },\tilde{\mathbf{X}})\mathit{\alpha }+\tilde{\mathbf{Z}},(16)$

and the MR × P matrix Ω as a function of $\mathit{\tau },\mathit{\nu },\tilde{\mathbf{X}}$ becomes

$\mathbf{\Omega }(\mathit{\tau },\mathit{\nu },\tilde{\mathbf{X}})=\left(\begin{array}{ccc}\hfill X_{\mathrm{1,1}}\mathrm{\Psi }(v_1)\mathrm{\Phi }({\tau }_1)\hfill & \hfill \dots \hfill & \hfill X_{\mathrm{1,1}}\mathrm{\Psi }(v_P)\mathrm{\Phi }{\tau }_P\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill X_{1,R}\mathrm{\Psi }(v_1)\mathrm{\Phi }({\tau }_1)\hfill & \hfill \dots \hfill & \hfill X_{1,R}\mathrm{\Psi }(v_P)\mathrm{\Phi }{\tau }_P\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill X_{M,1}\mathrm{\Psi }(v_1)\mathrm{\Phi }({\tau }_1)\hfill & \hfill \dots \hfill & \hfill X_{M,1}\mathrm{\Psi }(v_P)\mathrm{\Phi }{\tau }_P\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill X_{M,R}\mathrm{\Psi }(v_1)\mathrm{\Phi }({\tau }_1)\hfill & \hfill \dots \hfill & \hfill X_{M,R}\mathrm{\Psi }(v_P)\mathrm{\Phi }{\tau }_P\hfill \end{array}\right),(17)$

where $\mathrm{\Psi }({\nu }_p)=e^{-j2\pi {\nu }_p{T}_d(m-1)}$ and $\mathrm{\Phi }({\tau }_p)=e^{-j2\pi (n-1-\lfloor N/2\rfloor ){\tau }_p/T}.$ Then the estimation of complex attenuation factor vector $\widehat{\mathit{\alpha }}\in {\mathbb{C}}^{P\times 1}$ for all targets can be found as follows:

$\widehat{\mathit{\alpha }}={({\mathbf{\Omega }}^H\mathbf{\Omega })}^{-1}{\mathbf{\Omega }}^H\tilde{\mathbf{Y}},(18)$

where (⋅)^H denotes the Hermitian operator.

4 Communication Functionality and Decoding Algorithms

In this section, the decoding process of transmitted information is explained with two different options. Both options are numerically evaluated in Section 5.

4.1 Null Subcarrier Estimation–Based Decoding

Here, the null subcarrier estimation in the first step of radar processing is utilized to determine the location of communication symbols and the index bits b₁. The QAM symbols on estimated communication subcarrier locations are demodulated via well-known maximum likelihood (ML) QAM demodulation, which calculates the minimum Euclidean distance with the possible symbols in a complex symbol set.

4.2 Maximum-Likelihood–Based Decoding

The full-ML detector considers all possible subblock realizations by searching for all possible subcarrier index combinations, the signal constellation points, and corresponding radar symbol for each subblock in order to make a joint decision on the active indices and the constellation symbols. For the m^th OFDM symbol, the full-ML detector is employed in each subblock by minimizing the following metric:

$\begin{array}{lll}\hfill \left({\widehat{\mathbf{I}}}_{\xi },{\widehat{\mathbf{s}}}_{\xi }\right)& =\hfill & \hfill \underset{{\mathbf{I}}_{\xi },{\mathbf{s}}_{\xi }}{\mathrm{arg\; min}}\Vert {\mathbf{Y}}_m^{\xi }-{\mathbf{c}}^{\xi }{\Vert }^2,\end{array}(19)$

where c denotes all possible subblock realizations, including radar symbol, null subcarrier, and QAM symbols.

4.3 Soft Decoding With a Channel Decoder

This section includes the log-likelihood ratio (LLR) calculations of the proposed OFDM-IM structure. Calculated LLRs are sent to the channel decoder as input. For the sake of fair comparison, we have used the log-sum approximation technique (Caire et al., 1998) to calculate approximate LLR of the proposed OFDM-IM scheme and conventional OFDM with a comb-type pilot scheme (Ozkaptan et al., 2018). The LLR of the bit i ($b_{\xi }^m(i)$) of the proposed OFDM-IM JCR scheme at the ξ^th subblock of the m^th OFDM symbol ${\mathrm{\Lambda }}_{\xi }^m(i)$ is as follows:

$\begin{array}{ll}\hfill {\mathrm{\Lambda }}_{\xi }^m(i)& =\log \left(\frac{f({\mathbf{Y}}_m^{\xi }|b_{\xi }^m(i)=0)}{f({\mathbf{Y}}_m^{\xi }|b_{\xi }^m(i)=1)}\right)\hfill \\ \hfill & \approx \underset{{\mathbf{b}}_{\xi }^m:b_{\xi }^m(i)=1}{\min }\Vert {\mathbf{Y}}_m^{\xi }-{\mathbf{h}}_{\xi }^mʘ{\mathbf{b}}_{\xi }^m{\Vert }^2\hfill \\ \hfill & -\underset{{\mathbf{b}}_{\xi }^m:b_{\xi }^m(i)=0}{\min }\Vert {\mathbf{Y}}_m^{\xi }-{\mathbf{h}}_{\xi }^mʘ{\mathbf{b}}_{\mathit{\xi }}^{\mathbf{m}}{\Vert }^2,\hfill \end{array}(20)$

where ${\mathbf{h}}_{\xi }^m\in {\mathbb{C}}^{1\times g}$ denotes the channel state information (CSI) through ξ^th subblock of the m^th OFDM symbol. Also, ${\mathbf{b}}_{\xi }^m(i)\in {\mathbb{S}}^{\prime }=\{0,G_a,G_b,\mathbb{S}\}$ is the all possible symbol set that is inserted into the proposed OFDM-IM JCR structure.

4.4 Complexity Analysis

Here, the complexity analysis of the proposed decoding methods is performed to compare decoding schemes. The complexity of null subcarrier–based decoding becomes, in terms of complex multiplications, $\sim \mathcal{O}\left(k|S|\right)$, whereas the complexity of ML-based decoding is $\sim \mathcal{O}\left(2^{b_1}|S{|}^k\right)$. The complexity of LLR calculation, in terms of complex multiplications, is also $\sim \mathcal{O}\left(2^{b_1}|S{|}^k\right)$; however, this calculation is followed by the complex channel decoding process. Therefore, the overall complexity is higher than that of the previous two methods.

5 Simulation Results

This section demonstrates the applicability of the proposed OFDM-IM JCR waveform structure in the presence of multiple and mobile targets. Mean-square error (MSE) and the bit error rate (BER) metrics are used to demonstrate the radar-sensing and communication performance of the proposed scheme. Simulation parameters depending on radar and communication requirements are shown in Table 1. It is assumed that the maximum delay τ_max caused by targets is smaller than the CP length of each OFDM symbol. The total symbol energy is set the same for the proposed scheme and the conventional OFDM JCR scheme. For LDPC codes, NR LDPC codes with code rates 0.5 and 0.75 are implemented, where the code length is set to be 384, and the iteration number of decoding is 20. Interleaving after LDPC encoding is not implemented to have fair comparison between conventional OFDM JCR and the proposed OFDM-IM JRC scheme. The number of subcarriers in one OFDM symbol is 256 due to the code length and SE, and 180 OFDM symbols are transmitted with one OFDM frame. BER and MSE results are obtained with repeated 1,000 Monte Carlo simulations to get ensemble averages. To compare the proposed OFDM-IM JCR scheme, the conventional OFDM JCR scheme with comb-type pilot arrangement is implemented, which is proposed in Ozkaptan et al. (2018); one out of four subcarriers is assigned with a pilot symbol. For communication symbols, QPSK modulation is utilized. Therefore, the spectral efficiency of both schemes becomes 1.5 bit per subcarrier.

TABLE 1

TABLE 1. Simulation parameters.

The power delay profile (PDP) of the channel is determined as an exponentially decaying function where the power of complex channel coefficients is set as $\mathrm{E}{[{\alpha }_p(\gamma )]}^2=\eta e^{-p}$, where η denotes the normalization factor and p is the target index. Each tap amplitude follows the Rayleigh distribution.

After evaluating the complex attenuation factor α_p in Eq. 5, the estimation of channel matrix ${\widehat{\mathbf{H}}}^f$ is performed by using the obtained values of Doppler shifts and delays which is done previously via radar symbols on OFDM-IM. Finally, these estimates are used to demodulate communication symbols in the proposed OFDM-IM waveform structure. MSE is calculated with ${\widehat{\mathbf{H}}}^f$ and ${\mathbf{H}}^f$ matrices, ${\sigma }_e^2=\frac{\mathrm{E}[\Vert {\hat{\mathbf{H}}}^f-{\mathbf{H}}^f{\Vert }^2]}{\mathrm{E}[\Vert {\mathbf{H}}^f{\Vert }^2]}$, where E [⋅] denotes the expected value.

The proposed scheme is compared with the conventional OFDM scheme where the channel estimation is done with comb-type pilot arrangements explained in the study by Ozdemir and Arslan (2007). It is well known that the minimum MSE is obtained when the pilots are equi-spaced (comb-type arrangement), when the MSE of the least-square (LS) estimation is utilized. Also, the use of the same subcarriers for pilot allocation among subsequent OFDM symbols is a widely used pilot arrangement scheme Ozdemir and Arslan (2007). Simple LS estimate is employed to find initial channel estimates on pilot subcarriers, where the correlation across the OFDM carriers and OFDM symbols is not exploited. The channel frequency response (CFR) vector is obtained by implementing linear interpolation over all pilots. This is followed by replacing the samples after the length of the CP with zeros in the time domain by taking IFFT. The noise reduced signal is then transformed back into the frequency domain via FFT operation to obtain the estimated value of the channel over each OFDM symbol. The number of pilots, symbols, and subcarrier spacing (Δf) used in conventional OFDM for comparison are the same as those of the proposed OFDM-IM JCR structure. Figure 4 illustrates the radar functionality of the proposed scheme compared to conventional OFDM when SNR is 10 dB. It is obviously seen in Figure 4A that a fixed pilot design limits the unambiguous radar range, whereas it is not the case in the proposed scheme as seen in Figure 4B.

FIGURE 4

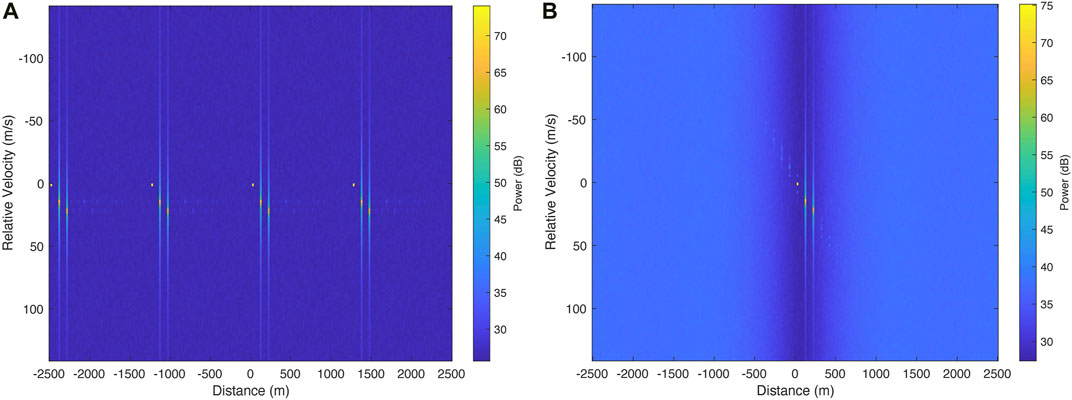
FIGURE 4. Distance–velocity plot of the three targets with velocities [0, 14.9, 21.2] (m/s) and distances [29.3, 127.3, 225.3] (m) where SNR is 10 dB. (A) Comb-type pilot-based OFDM and (B) proposed OFDM-IM JCR scheme.

Figure 5 shows the performance analysis for two stationary and one moving targets and their respective distances. In Figure 5A, conventional OFDM JCR with a comb-type pilot arrangement, OFDM-IM with interpolation of irregularly spaced pilots, and the proposed radar-based OFDM-IM waveform are compared considering their MSE of channel estimation. It can be observed that the proposed scheme significantly outperforms the two existing conventional schemes. As a channel decoder to perform BER simulations, LDPC (low-density parity check) is used with two different rates, which are 0.5 and 0.75. Figure 5B shows the benefit of the proposed scheme in terms of error performance compared to conventional OFDM with pilots. It also compares the proposed OFDM-IM JCR scheme with two different decoding types such as the null subcarrier–based and ML-based decoding explained in Section 4. It can be observed that our scheme outperforms the conventional schemes in both detection methods. The ML-based scheme provides better error performance than the proposed null-based decoding; however, it has a much higher complexity.

FIGURE 5

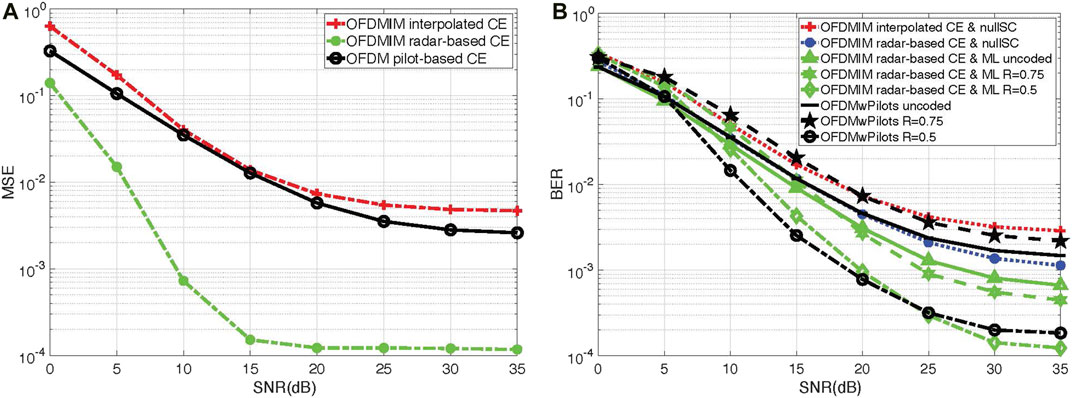
FIGURE 5. Performance analysis in the presence of three targets with velocities [0, 0, 14.9] (m/s) and distances [39, 136.6, 234.2] (m). (A) MSE vs. SNR and (B) BER vs. SNR.

Figure 6 shows the performance analysis for one stationary and three moving targets and their respective distances. From Figures 6A,B, the conventional OFDM scheme reaches error floor at ∼ 10^–3 BER, whereas proposed scheme exhibits promising performance reaching beyond 10^–4 BER. There exists a trade-off between complexity and performance for ML detection over null subcarrier–based detection. It is observed that since there are more active targets in Figure 5, due to multiple Doppler effects, the performance of the conventional OFDM scheme degrades. However, the performance of the proposed OFDM-IM JCR scheme is maintained the same as in Figure 5B, claiming the superiority of the proposed scheme against high Doppler effect. Also, it should be noted that the conventional OFDM with 0.75 code rate performs worse than the uncoded system in Figures 5B, 6B. It is the case because we do not implement interleaving after encoding the bit sequence for both the conventional OFDM JCR scheme and the proposed OFDM-IM JRC scheme. It is can be seen that the proposed OFDM-IM performs better and index bits inherently introduce diversity over one OFDM-IM symbol.

FIGURE 6

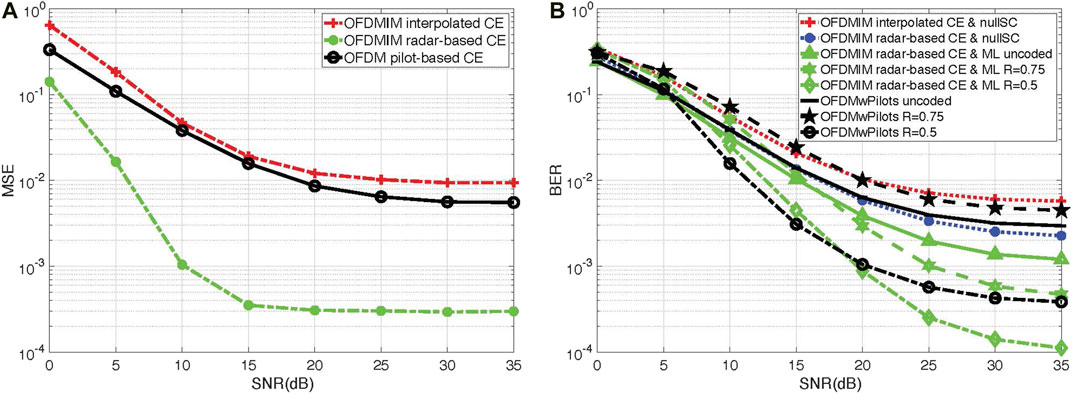
FIGURE 6. Performance analysis in the presence of four targets with velocities [0, 14.9, 21.2, 30.6] (m/s) and distances [29.3, 127.3, 225.3, 323.3] (m). (A) MSE vs. SNR and (B) BER vs. SNR.

6 Conclusion

In this study, a novel JCR waveform utilizing OFDM-IM and its promising properties has been proposed. The system model description along with numerical and computational evaluations has been provided. Computer simulations show that the proposed scheme provides not only improvement in error performance for communication but also enhanced radar performance when compared to OFDM-JCR schemes in terms of BER and MSE performance. Also, it is shown that the proposed scheme increases the maximum unambiguous radar range compared to conventional OFDM with a comb-type pilot design. For future research direction, generalization of the proposed OFDM-IM scheme for different subblocks and active subcarrier numbers will be studied.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

HA and EB guided the whole study, suggested the outline of the article, and revised it many times. MS, IG, and EA carried out numerical evaluations and wrote the article. As a PhD student, MMS is the corresponding author of the paper.

Funding

The work of HA was supported the National Science Foundation under award ECCS-1609581. The work of EB was supported by TUBITAK under Grant 218E035.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arslan, E., Dogukan, A. T., and Basar, E. (2020a). Index Modulation-Based Flexible Non-orthogonal Multiple Access. IEEE Wireless Commun. Lett. 9 (11), 1942–1946. doi:10.1109/lwc.2020.3009100

CrossRef Full Text | Google Scholar

Arslan, E., Dogukan, A. T., and Basar, E. (2020b). Sparse-encoded Codebook index Modulation. IEEE Trans. Veh. Technol. 69, 9126–9130. doi:10.1109/tvt.2020.2996023

CrossRef Full Text | Google Scholar

Basar, E., Aygolu, U., Panayirci, E., and Poor, H. V. (2013). Orthogonal Frequency Division Multiplexing with index Modulation. IEEE Trans. Signal. Process. 61, 5536–5549. doi:10.1109/tsp.2013.2279771

CrossRef Full Text | Google Scholar

Basar, E. (2015). OFDM with index Modulation Using Coordinate Interleaving. IEEE Wireless Commun. Lett. 4, 381–384. doi:10.1109/lwc.2015.2423282

CrossRef Full Text | Google Scholar

Basar, E., Wen, M., Mesleh, R., Di Renzo, M., Xiao, Y., and Haas, H. (2017). Index Modulation Techniques for Next-Generation Wireless Networks. IEEE Access 5, 16693–16746. doi:10.1109/access.2017.2737528

CrossRef Full Text | Google Scholar

Caire, G., Taricco, G., and Biglieri, E. (1998). Bit-interleaved Coded Modulation. IEEE Trans. Inform. Theor. 44, 927–946. doi:10.1109/18.669123

CrossRef Full Text | Google Scholar

Dogukan, A. T., and Basar, E. (2020). Super-mode Ofdm with index Modulation. IEEE Trans. Wireless Commun., 19(11):7353–7362. doi:10.1109/twc.2020.3010839

CrossRef Full Text | Google Scholar

Feng, Z., Fang, Z., Wei, Z., Chen, X., Quan, Z., and Ji, D. (2020). Joint Radar and Communication: A Survey. China Commun. 17, 1–27. doi:10.23919/jcc.2020.01.001

CrossRef Full Text | Google Scholar

Hlawatsch, F., and Matz, G. (2011). Wireless Communications over Rapidly Time-Varying Channels. Elsevier/Academic Press.

Hoque, S. S. M., and Şahin, A. (2020). “Index-modulated Circularly-Shifted Chirps for Dual-Function Radar Communication Systems,” in 2020 IEEE Globecom Workshops, Taipei, Taiwan, December 7–11, 2020 (GC Wkshps, 1–6. doi:10.1109/GCWkshps50303.2020.9367423

CrossRef Full Text | Google Scholar

Huang, T., Shlezinger, N., Xu, X., Liu, Y., and Eldar, Y. C. (2020). MAJoRCom: A Dual-Function Radar Communication System Using index Modulation. IEEE Trans. Signal. Process. 68, 3423–3438. doi:10.1109/TSP.2020.2994394

CrossRef Full Text | Google Scholar

Kumari, P., Choi, J., González-Prelcic, N., and Heath, R. W. (2018). Ieee 802.11ad-Based Radar: An Approach to Joint Vehicular Communication-Radar System. IEEE Trans. Veh. Technol. 67, 3012–3027. doi:10.1109/tvt.2017.2774762

CrossRef Full Text | Google Scholar

Letzepis, N., Grant, A., Alexander, P., and Haley, D. (2011). Joint Estimation of Multipath Parameters from OFDM Signals in mobile Channels. 2011 Australian Communication Theory Workshop Melbourne, VIC, January 31–February 3, 2011, 106–111. doi:10.1109/AUSCTW.2011.5728746

CrossRef Full Text | Google Scholar

Liu, F., Masouros, C., Petropulu, A. P., Griffiths, H., and Hanzo, L. (2020). Joint Radar and Communication Design: Applications, State-Of-The-Art, and the Road Ahead. IEEE Trans. Commun. 68, 3834–3862. doi:10.1109/TCOMM.2020.2973976

CrossRef Full Text | Google Scholar

Luong, N. C., Lu, X., Hoang, D. T., Niyato, D., and Kim, D. I. (2021). Radio Resource Management in Joint Radar and Communication: A Comprehensive Survey. IEEE Commun. Surv. Tutorials 23, 780–814. doi:10.1109/comst.2021.3070399

CrossRef Full Text | Google Scholar

Mazahir, S., Ahmed, S., and Alouini, M.-S. (2021). A Survey on Joint Communication-Radar Systems. Front. Comms. Net. 1, 9. doi:10.3389/frcmn.2020.619483

CrossRef Full Text | Google Scholar

Mishra, K. V., Bhavani Shankar, M. R., Koivunen, V., Ottersten, B., and Vorobyov, S. A. (2019). Toward Millimeter-Wave Joint Radar Communications: A Signal Processing Perspective. IEEE Signal. Process. Mag. 36, 100–114. doi:10.1109/msp.2019.2913173

CrossRef Full Text | Google Scholar

Nguyen, D. H. N., and Heath, R. W. (2017). “Delay and Doppler Processing for Multi-Target Detection with Ieee 802.11 Ofdm Signaling,” in 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 3414–3418. doi:10.1109/ICASSP.2017.7952790

CrossRef Full Text | Google Scholar

Ozdemir, M., and Arslan, H. (2007). Channel Estimation for Wireless OFDM Systems. IEEE Commun. Surv. Tutorials 9, 18–48. doi:10.1109/COMST.2007.382406

CrossRef Full Text | Google Scholar

Ozkaptan, C. D., Ekici, E., Altintas, O., and Wang, C-H. (2018). “OFDM Pilot-Based Radar for Joint Vehicular Communication and Radar Systems,” in 2018 IEEE Vehicular Networking Conference (VNC), Taipei, Taiwan, December 5–7, 2018, 1–8. doi:10.1109/vnc.2018.8628347

CrossRef Full Text | Google Scholar

Sahin, M. M., and Arslan, H. (2021). Application-based Coexistence of Different Waveforms on Non-orthogonal Multiple Access. IEEE Open J. Commun. Soc. 2, 67–79. doi:10.1109/OJCOMS.2020.3044680

CrossRef Full Text | Google Scholar

Şahin, M. M., and Arslan, H. (2020). “Multi-functional Coexistence of Radar-Sensing and Communication Waveforms,” in 2020 IEEE 92nd Vehicular Technology Conference (VTC2020-Fall), Victoria, BC, November 18–December 16, 2020, 1–5. doi:10.1109/vtc2020-fall49728.2020.9348582

CrossRef Full Text | Google Scholar

Zheng, L., Lops, M., Eldar, Y. C., and Wang, X. (2019). Radar and Communication Coexistence: An Overview: A Review of Recent Methods. IEEE Signal. Process. Mag. 36, 85–99. doi:10.1109/msp.2019.2907329

CrossRef Full Text | Google Scholar