- 1Shandong Provincial Key Laboratory of Wireless Communication Technologies and School of Control Science and Engineering, Shandong University, Jinan, China
- 2Computer, Electrical and Mathematical Science and Engineering Division, King Abdullah University of Science and Technology, Thuwal, Saudi Arabia
- 3School of Computer Engineering, Weifang University, Weifang, China
Metasurface-based terahertz (THz) modulators, which carry information by changing the spatial pattern of the metasurface at every symbol time, are an important component to establish low-cost low-energy–consuming THz communication systems. This paper proposes a differential spatial THz modulation (DSTM) scheme for metasurface-assisted THz communications. In DSTM, the metasurface pattern activation orders are employed to carry information, instead of the metasurface patterns themselves. In this way, the DSTM receiver can perform differential detection without knowing the metasurface response to incident THz signals and the channel state information. The proposed DSTM scheme is applicable to all kinds of metasurfaces enabling THz communications, including transmissive metasurfaces and reflective metasurfaces. For high-rate DSTM systems, we propose an efficient bits-to-activation-order mapping method and a low-complexity detection method. Simulations are conducted to demonstrate the performance of the proposed scheme. It is shown that the proposed scheme pays acceptable penalty compared to the non-differential modulation scheme with coherent detection, which needs to know the metasurface response to the incident signals as well as all the channel state information.
1 Introduction
Recent growing needs in bandwidth have led to a proliferation of studies about terahertz (THz) communication (Dang et al., 2020). Specifically, THz frequency indicates the waves ranging from 0.1 to 10 THz leading to 3 mm to 30 μm wavelengths between the microwave and infrared regions (Sarieddeen et al., 2020). THz communication is expected to become the key technology for next-generation communication with high capacity and security, strong anti-interference ability, simple and compact hardware design brought by its high frequency, short wavelength, narrow beam, and good directivity. Much of the current literature on THz communication pays particular attention to modulation and demodulation technology, which is one of the promising ways to reduce complexity, cost, and geometry of THz systems greatly. Modulation and demodulation technology (Guo S. et al., 2019; Li et al., 2020a; Li et al., 2020b), acting as one of the promising ways to reduce complexity, cost, and geometry of wireless systems greatly, has gained momentum nowadays on THz communications. In recent years, many outstanding studies have been focused on improving the modulation speed, modulation depth, and bandwidth through various modulation approaches, such as optical electronic, photoelectric, thermal, and magnetic modulators.
1.1 Prior Works on THz Modulators
THz modulators can be roughly categorized into two types: internal modulators and external modulators. Internal modulators encode the information directly to the parameters of the THz waves (e.g., amplitude, phase), while external modulators are placed in front of the THz generator and carry the data by changing their status (e.g., the ON/OFF state, shape, pattern). Based on the employed materials, external modulators can be divided into two categories: non-programmable external modulators and programmable external modulators.
1.1.1 Internal Modulator
Internal modulators are widely adopted in macro-wave communication systems and millimeter-wave communication systems. Researchers have extended them to THz communication systems. Typical internal modulation schemes include conventional amplitude and phase modulation, pulse-based modulation, spatial modulation for multiple-antenna THz systems, or orthogonal frequency–division multiplexing (OFDM) for wideband communications. Yuan et al. (2019) proposed a hybrid THz multiple-input multiple-output (MIMO) OFDM scheme in adopting a normalized beam steering codebook search algorithm and a regularized channel inversion method to perform analog and digital beamforming, respectively. However, the efficiency of traditional OFDM is rendered by the resultant strict frequency synchronization and high peak-to-average power ratio, as well as the limitation of digital-to-analog conversions and analog-to-digital conversions (Hossain et al., 2019). The unique properties of the THz band including bandwidth abundance, non-overlapping, and equally spaced sub-windows motivate the utilization of single-carrier (SC) modulation, which is proved to be energy-efficient and much less complex than OFDM (Doré et al., 2018). Han and Akyildiz (2014) showed that the complexity of the modulation process and energy consumption can be relaxed by conducting transmission over sub-windows parallelly at the cost of simultaneously operating multiple modulators and a very fast signal generator. In practice, carrier-based transmission is still challenging because of the difficulty in generating more than short high-frequency pulses of few milliwatts with graphene at room temperature. Jornet and Akyildiz (2014) solved this problem through a pulse-based SC on–off keying modulation with an acceptable reduction in spectral efficiency, which is shown to achieve a Tbps data rate in nano-network scenarios. Furthermore, internal modulation schemes can turn the absorption effect into an advantage by dynamically optimizing transmission window allocations (Han and Akyildiz, 2014), frequency allocations (Zakrajsek et al., 2017), power allocation (Han et al., 2015), and single-user and multi-user distance-aware bandwidth-adaptive resource allocations (Han et al., 2014).
1.1.2 Non-Programmable External Modulator
An optically tuned THz modulator is a critical part of the non-programmable external modulator (Libon et al., 2000), which can be realized by metamaterials (Cong et al., 2018; Chen et al., 2018), two-dimensional (2D) materials (Fu et al., 2017), and flexible substrates (Khang et al., 2006). Cong et al. (2018) introduced an active hybrid metasurface integrated with patterned semiconductor inclusions, which aims to control THz waves actively. The experimental were investigated in Chen et al. results of actively controlled anisotropic near-field coupling based on a metamaterial with a closed-ring resonator functioning at THz frequencies in Chen et al. (2018). With the development of 2D material fabrication, Fu et al. (2017) showed that the modulation depth of the transmission could reach 74% for the proposed modulator under external photoexcitation. The flexible substrate–based modulator is regarded as a new potential THz modulator, which has many advantages such as transparency, lightweight, low cost, and consistent adhesion. By changing the surface shape of the flexible substrate, Khang et al. (2006) observed that the electrical parameters could be modified.
Another “hot” research field is an electrically tuned external THz modulator, which was proposed by Libon et al. in 2000 (Kersting et al., 2000) firstly. It can also be achieved by semiconductors, metamaterials, flexible substrates, and graphene. Shrekenhamer et al. established a new path toward achieving an electrically tunable THz modulator by incorporating metamaterials into mature semiconductor technologies (Shrekenhamer et al., 2011). The graphene-based modulator is a kind of electromodulator based on 2D materials, which is famous for adjustable thin layer conductivity and long mean free path. Zhang et al. (2005) reported an unusual half-integer quantum Hall effect for both electron and hole carriers in graphene, which may lead to new applications in carbon-based electronic and magneto-electronic devices. Moreover, a modulator based on a flexible substrate is shown to realize excellent flexibility and high modulation depth in Kaya et al. (2018).
There are other kinds of non-programmable THz modulators, such as photoelectric hybrid modulators (Li et al., 2015), mechanically tuned THz modulators (Han et al., 2017), thermally tuned THz modulators (Ben-Messaoud et al., 2008), magnetically tuned THz modulators (Zhou et al., 2017), and microelectromechanical system (MEMS)-tuned THz modulators (Bai et al., 2010). For example, Li et al. (2015) exhibited an optoelectronic hybrid modulator, which can achieve 83% transmission modulation. An ultrathin THz wave phase shifter was described by Han et al. (2017), which has high transmission with a coefficient of 91%. Since free carriers in most materials are affected by temperature changes, a metal oxide called the vanadium dioxide (VO2) film can be converted from the insulating state to the metallic state under heat (Chain, 1991), which is proved to have high transmittance in the insulating phase and opposite property in the metal phase (Ben-Messaoud et al., 2008). Zhou et al. (2017) presented a magnetically tuned THz modulator, whose resonant frequency can be tuned with the insertion loss of 0.3 dB with high modulation speed. The MEMS-tuned THz modulator utilizes MEMS-based slow-light–tunable effects, which is shown to have the ability to tune over a wide frequency range in the THz band (Bai et al., 2010).
1.1.3 Programmable External Modulator
Benefiting from the rapid evolution of electromagnetic metamaterials, more recent attention has focused on the provision of digital coding and programmable metasurfaces based on PIN diodes. The new concept of artificial “coding metamaterials” was firstly proposed by Cui et al. (2014), which can be controlled by binary code sequences compared with conventional metamaterials. Specifically, coding metasurfaces, also called reconfigurable intelligent surfaces or intelligent reflecting surfaces, can generate different code sequences in real time under the control of a field programmable by integrating with active elements. Its properties of digital description, analysis, and design simplify the design process and reduce the design difficulty. This promising technology is in fact gaining a lot of momentum because of its superiority in a variety of applications including but not limited to energy-efficient networks (Huang et al., 2019), massive access (Mursia et al., 2021), ultra-high capacity communications (Yan et al., 2020), and extremely low error rate systems (Ye et al., 2020). Although efficient metasurface-based modulation schemes such as reflecting modulation (Guo et al., 2020) and differential reflecting modulation (Guo et al., 2021) have been proposed in low frequency bands, there are only few works investigating the modulation functionality of metasurfaces at THz frequency. Liu et al. (2016a) made a valuable contribution to programmable THz modulator design. The work (Liu et al., 2016a; b, 2017) experimentally demonstrated a transmission-type coding metamaterial at THz frequency, which could bend the cross-polarized component of the normally incident wave in anomalous directions and generate non-diffractive Bessel beams in arbitrary directions. In the same year, a frequency-dependent dual-functional coding metasurface using two layers of metamaterial structures for THz frequencies is proposed in Liu et al. (2016b), which is able to independently control reflection phases at two distinct frequencies. The following work (Liu et al., 2017) proposed a tensor coding metasurface at THz frequency that could take full-state controls of an electromagnetic wave. By designing specific coding sequences, Gao et al. demonstrated that multi-bit coding metasurfaces have strong abilities to control THz waves (Gao et al., 2015). They proposed a new scattering strategy of THz waves––broadband and wide-angle diffusion to reducing the scattering of THz waves. More recently, another approach to form near-field THz imaging was proposed in Stantchev et al. (2017), which can selectively attenuate part of the incident light and achieve THz compression imaging through an encoded array. The applied angular spectrum method proposed by Yamagiwa et al. (2018) for wavefront reconstruction was shown to be more accurate at short reconstruction distances. Wang et al. realized multiple longitudinal operations of holograms by using the holographic metasurface regulating the phase and amplitude simultaneously (Wang et al., 2018). More recently, a novel approach for generating arbitrary wavefronts of a THz beam is presented in Guo J. et al. (2019), which was demonstrated by proof-of-concept experiments.
1.2 Contribution
In this paper, we are interested in a metasurface-based low-cost external THz modulator. Traditionally, such modulators carry information by changing the metasurface pattern per symbol time. Its detector at the receiver needs to know the exact metasurface response to the incident signal and know the wireless channels in between the THz wave generators. However, it is difficult to model the action of the metasurface and its reaction to the incident signals. Besides, channel estimation also leads to additional resource consumption.
• To avoid these problems, we propose a differential modulation scheme for metasurface-based THz communications. The proposed differential spatial THz modulation (DSTM) scheme is applicable to all kinds of metasurfaces enabling THz communications, including transmissive metasurfaces and reflective metasurfaces.
• We also analyze the encoding and computational complexity of the proposed DSTM, which are shown to greatly increase with the transmission rate. To address this problem, we further propose an effective encoding and low-complexity detection approach for high-rate DSTM systems.
• Simulations are conducted to show the performance of the proposed DSTM in comparison with non-differential modulation with coherent detection. The results show that even through the proposed DSTM is less comparable to non-differential modulation with coherent detection and perfect channel state information (CSI), it can achieve comparable performance to or even better performance than non-differential modulation with coherent detection and imperfect CSI.
1.3 Organization
The remainder of this paper is organized as follows. We introduce the system model and the used THz channel model in System Model. Differential Spatial THz Modulation Scheme describes the proposed DSTM scheme and the differential maximum-likelihood (DML) detection method. High-Rate Differential Spatial THz Modulation Scheme presents the proposed low-complexity encoding and detection method. Simulation and Discussion presents the simulation results and includes discussions.
1.4 Notation
In what follows, the following notations are adopted: x represents a scalar;
2 System Model
2.1 System Description
In this paper, we investigate the metasurface-enabled THz communication systems as illustrated in Figure 1. In this figure, we illustrate a THz generator radiates THz waves, which arrive at a transmissive metasurface or a reflective metasurface. Propagating through or being reflected by different metasurface patterns will generate different responses to THz waves. We assume that metasurface pattern sets are
where
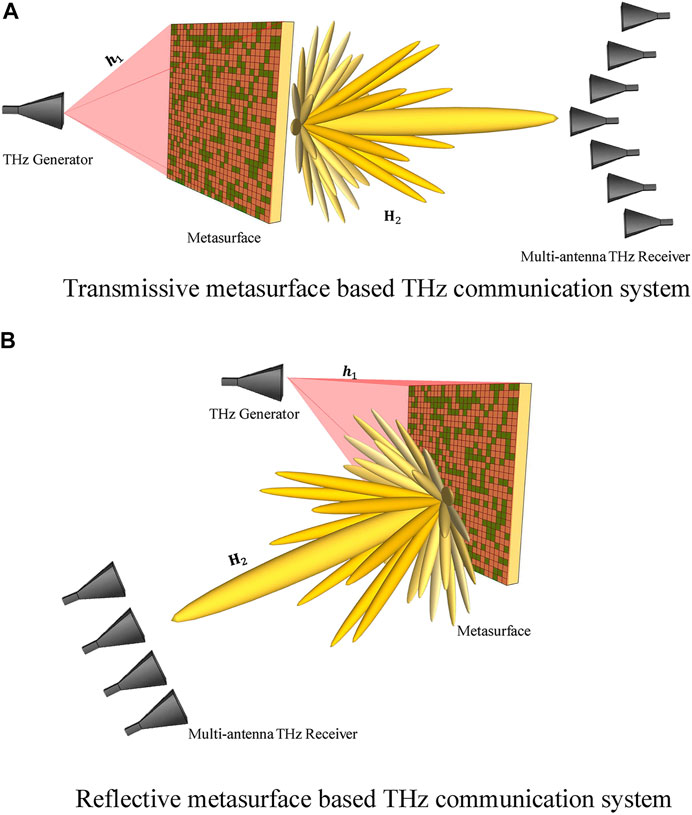
FIGURE 1. (A) Transmissive metasurface–based THz communication system. (B) Reflective metasurface–based THz communication system.
2.2 Channel Model
We assume the metasurface is placed close to the transmitter to capture the signal power and the signals from the THz generator to propagate in line-of-sight (LoS). The channel coefficient between the n-th metasurface unit and the THz generator can be written as
where
where
and
where
where
where
3 Differential Spatial THz Modulation Scheme
In this section, we will present a DSTM scheme, which is applicable to all kinds of metasurfaces enabling THz communications, including all the transmissive metasurfaces and the reflective metasurfaces. Here, we first introduce the encoding scheme, then present the detection scheme, and analyze its computational complexity.
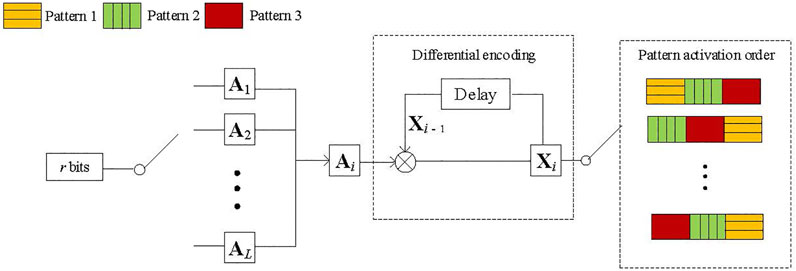
3.1 Encoding Mechanism
In DSTM, we use the
where
When
where
where
and
To clearly view the trend of the target transmission rate along with the increase in the number of metasurface patterns, i.e., K, we demonstrate it in Figure 3. As shown in the figure, the target transmission rate increases as the number of metasurface patterns increases.
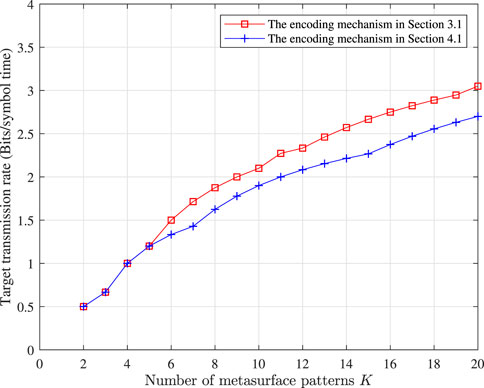
FIGURE 3. Trend of the target transmission rate along with the increase in the number of metasurface patterns.
3.2 Optimal Differential Maximum-Likelihood Detection
Substituting Eq. (8) into Eq. (10), we have
Recalling that
Thus, the optimal DML detector can be derived as
3.3 Computational Complexity Analysis
The detection computational complexity is dominated by the calculation of
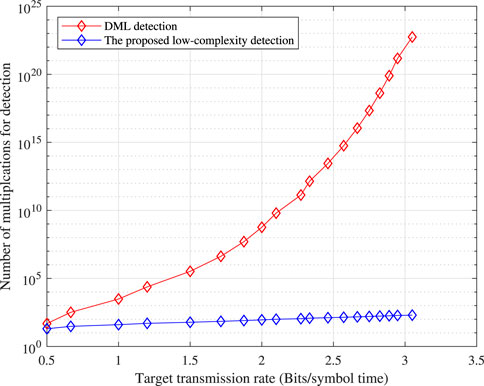
FIGURE 4. Trend of the computational complexity for detection along with the increase in the target transmission rate.
4 High-Rate Differential Spatial THz Modulation Scheme
As shown in Figure 3, the transmission rate grows with the number of metasurface patterns K. Thus, it is required to have more number of metasurface patterns to fulfill the target. However, increasing the number of metasurfaces will increase the computational complexity. In this section, we propose a low-complexity bit-to-activation-order mapping scheme. Inspired by the work in Xiao et al. (2015), we adopt a low-complexity detection scheme for DSTM.
4.1 Low-Complexity Bit-to-Activation-Order Mapping Scheme
The encoding method in Encoding Mechanism is not suitable for a high-rate DSTM scheme because there are a total of
4.2 Low-Complexity Detection and Demapping Scheme
For the purpose of reducing the computational complexity, we perform a column-by-column detection as
where
According to the procedures of mapping, we can perform demapping successively. That is, we firstly decode
5 Simulation and Discussion
In this section, simulations are included. This is further divided into two subsections. In the first subsection, we investigate the performance of the proposed DSTM by comparing it with STM using coherent detection. In the second subsection, we investigate the performance of high-rate DSTM with the proposed column-by-column detection and mapping scheme. In our simulations, the simple phase-shift metasurfaces are adopted. It is worth mentioning the proposed DSTM schemes are suitable for all kinds of metasurfaces.
5.1 Performance of the Proposed Differential Spatial THz Modulation
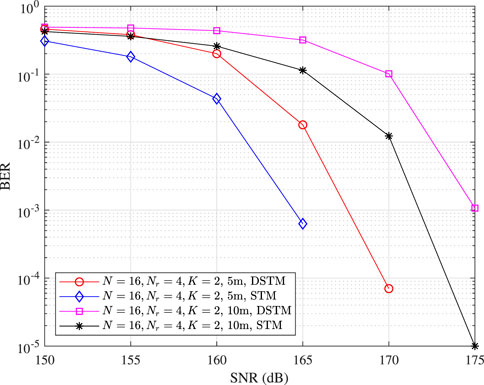
In this subsection, we investigate the performance of the proposed DSTM, by comparing it with STM using coherent detection. The distance from the THz source and metasurface is set to be 0.1 m, and the distance from the center of the metasurface to the receiver is 5 m or 10 m. The receiver is equipped with four antennas. The metasurface is equipped with 16 phase-shift units, and we use the activation orders of two random patterns
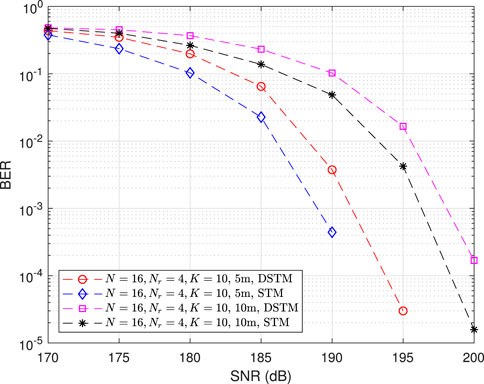
5.2 Performance of the Proposed High-Rate Differential Spatial THz Modulation
This subsection investigates the performance of the proposed high-rate DSTM with low-complexity mapping, detection, and demapping methods. The number of patterns used for transmission is set to be 10, and the transmission rate increases to be
6 Conclusion
This paper proposed an external differential spatial THz modulator for metasurface-aided THz communications. We adopt the metasurface activation pattern to carry information. The transmission rate and computational complexity of the proposed DSTM were analyzed. We proposed low-complexity mapping, detection, and demapping methods for high-rate DSTM. Simulations showed that DSTM provides an acceptable performance loss compared to STM, which has to know the response of the metasurface and CSI for information detection.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.
Author Contributions
SG conceived the work and suggested the outline of the article. SG, JY, and PZ carried out investigations and wrote the article.
Funding
The work was supported in part by the National Natural Science Foundation of China under Grant 61801266, in part by the Major Scientific and Technological Innovation Project of Shandong Province under Grant 2020CXGC010109.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Ben-Messaoud, T., Landry, G., Gariépy, J. P., Ramamoorthy, B., Ashrit, P. V., and Haché, A. (2008). High Contrast Optical Switching in Vanadium Dioxide Thin Films. Opt. Commun. 281, 6024–6027. doi:10.1016/j.optcom.2008.09.027
Chain, E. E. (1991). Optical Properties of Vanadium Dioxide and Vanadium Pentoxide Thin Films. Appl. Opt. 30, 2782–2787. doi:10.1364/AO.30.002782
Chen, J., Liu, C., Chen, J., Cheng, C., Kang, M., and Wang, H.-T. (2010). Tunable Slow Light in Semiconductor Metamaterial in a Broad Terahertz Regime. J. Appl. Phys. 107, 093104. doi:10.1063/1.3357291
Chen, X., Ghosh, S., Xu, Q., Ouyang, C., Li, Y., Zhang, X., et al. (2018). Active Control of Polarization-dependent Near-Field Coupling in Hybrid Metasurfaces. Appl. Phys. Lett. 113, 061111. doi:10.1063/1.5040162
Cong, L., Srivastava, Y. K., Zhang, H., Zhang, X., Han, J., and Singh, R. (2018). All-optical Active Thz Metasurfaces for Ultrafast Polarization Switching and Dynamic Beam Splitting. Light Sci. Appl. 7, 1–9. doi:10.1038/s41377-018-0024-y
Cui, T. J., Qi, M. Q., Wan, X., Zhao, J., and Cheng, Q. (2014). Coding Metamaterials, Digital Metamaterials and Programmable Metamaterials. Light Sci. Appl. 3, e218. doi:10.1038/lsa.2014.99
Dang, S., Amin, O., Shihada, B., and Alouini, M.-S. (2020). What Should 6G Be?. Nat. Electron. 3, 20–29. doi:10.1038/s41928-019-0355-6
Doré, J.-B., Corre, Y., Bicais, S., Palicot, J., Faussurier, E., Ktenas, D., et al. (2018). “Above-90Ghz Spectrum and Single-Carrier Waveform as Enablers for Efficient Tbit/s Wireless Communications,” in Proc. IEEE ICT (Saint-Malo, France: Saint Malo, France)), 274–278. doi:10.1109/ICT.2018.8464918
Fu, M., Wang, X., Wang, S., Xie, Z., Feng, S., Sun, W., et al. (2017). Efficient Terahertz Modulator Based on Photoexcited Graphene. Opt. Mater. 66, 381–385. doi:10.1016/j.optmat.2017.02.045
Gao, L.-H., Cheng, Q., Yang, J., Ma, S.-J., Zhao, J., Liu, S., et al. (2015). Broadband Diffusion of Terahertz Waves by Multi-Bit Coding Metasurfaces. Light Sci. Appl. 4, e324. doi:10.1038/lsa.2015.97
Guo, J., Wang, T., Zhao, H., Wang, X., Feng, S., Han, P., et al. (2019a). Reconfigurable Terahertz Metasurface Pure Phase Holograms. Adv. Opt. Mater. 7, 1801696. doi:10.1002/adom.201801696
Guo, S., Lv, S., Zhang, H., Ye, J., and Zhang, P. (2020). Reflecting Modulation. IEEE J. Select. Areas Commun. 38, 2548–2561. doi:10.1109/JSAC.2020.3007060
Guo, S., Ye, J., Zhang, P., Zhang, H., and Alouini, M.-S. (2021). Differential Reflecting Modulation for Reconfigurable Intelligent Surface-Based Communications. IEEE Commun. Lett. 25, 907–910. doi:10.1109/LCOMM.2020.3035751
Guo, S., Zhang, H., Zhang, P., Zhao, P., Wang, L., and Alouini, M.-S. (2019b). Generalized Beamspace Modulation Using Multiplexing: A Breakthrough in mmWave MIMO. IEEE J. Select. Areas Commun. 37, 2014–2028. doi:10.1109/JSAC.2019.2929399
Han, C., and Akyildiz, I. F. (2014). “Distance-aware Multi-Carrier (DAMC) Modulation in Terahertz Band Communication,” in Proc. IEEE ICC (Sydney, NSW), 5461–5467. doi:10.1109/ICC.2014.6884190
Han, C., Bicen, A., and Akyildiz, I. (2015). Multi-wideband Waveform Design for Distance-Adaptive Wireless Communications in the Terahertz Band. IEEE Trans. Signal. Process. 64, 1. doi:10.1109/TSP.2015.2498133
Han, C., Bicen, A. O., and Akyildiz, I. F. (2015). Multi-ray Channel Modeling and Wideband Characterization for Wireless Communications in the Terahertz Band. IEEE Trans. Wireless Commun. 14, 2402–2412. doi:10.1109/TWC.2014.2386335
Han, Z., Ohno, S., Tokizane, Y., Nawata, K., Notake, T., Takida, Y., et al. (2017). Thin Terahertz-Wave Phase Shifter by Flexible Film Metamaterial with High Transmission. Opt. Express 25, 31186–31196. doi:10.1364/OE.25.031186
Hossain, Z., and Jornet, J. M. (2019). “Hierarchical Bandwidth Modulation for Ultra-broadband Terahertz Communications,” in Proc. IEEE ICC (Shanghai, China, 1–7. doi:10.1109/ICC.2019.8761547
Huang, C., Zappone, A., Alexandropoulos, G. C., Debbah, M., and Yuen, C. (2019). Reconfigurable Intelligent Surfaces for Energy Efficiency in Wireless Communication. IEEE Trans. Wireless Commun. 18, 4157–4170. doi:10.1109/TWC.2019.2922609
Jornet, J. M., and Akyildiz, I. F. (2014). Femtosecond-long Pulse-Based Modulation for Terahertz Band Communication in Nanonetworks. IEEE Trans. Commun. 62, 1742–1754. doi:10.1109/TCOMM.2014.033014.130403
Kaya, E., Kakenov, N., Altan, H., Kocabas, C., and Esenturk, O. (2018). Multilayer Graphene Broadband Terahertz Modulators with Flexible Substrate. J. Infrared Milli Terahz Waves 39, 483–491. doi:10.1007/s10762-018-0480-8
Kersting, R., Strasser, G., and Unterrainer, K. (2000). Terahertz Phase Modulator. Electron. Lett. 36, 1156–1158. doi:10.1049/el:20000837
Khang, D.-Y., Jiang, H., Huang, Y., and Rogers, J. A. (2006). A Stretchable Form of Single-crystal Silicon for High-Performance Electronics on Rubber Substrates. Science 311, 208–212. doi:10.1126/science.1121401
Li, J., Dang, S., Yan, Y., Peng, Y., Al-Rubaye, S., and Tsourdos, A. (2020a). Generalized Quadrature Spatial Modulation and its Application to Vehicular Networks with NOMA. IEEE Trans. Intell. Transport. Syst. , 1, 1, 10. –10doi:10.1109/TITS.2020.3006482
Li, J., Li, Q., Dang, S., Wen, M., Jiang, X.-Q., and Peng, Y. (2020b). Low-complexity Detection for index Modulation Multiple Access. IEEE Wireless Commun. Lett. 9, 1. doi:10.1109/LWC.2020.2974730
Li, Q., Tian, Z., Zhang, X., Singh, R., Du, L., Gu, J., et al. (2015). Active Graphene-Silicon Hybrid Diode for Terahertz Waves. Nat. Commun. 6, 7082. doi:10.1038/ncomms8082
Libon, I. H., Baumgärtner, S., Hempel, M., Hecker, N. E., Feldmann, J., Koch, M., et al. (2000). An Optically Controllable Terahertz Filter. Appl. Phys. Lett. 76, 2821–2823. doi:10.1063/1.126484
Liu, S., Noor, A., Du, L. L., Zhang, L., Xu, Q., Luan, K., et al. (2016a). Anomalous Refraction and Nondiffractive Bessel-Beam Generation of Terahertz Waves through Transmission-type Coding Metasurfaces. ACS Photon. 3, 1968–1977. doi:10.1021/acsphotonics.6b00515
Liu, S., Zhang, H. C., Zhang, L., Yang, Q. L., Xu, Q., Gu, J., et al. (2017). Full-state Controls of Terahertz Waves Using Tensor Coding Metasurfaces. ACS Appl. Mater. Inter. 9, 21503–21514. doi:10.1021/acsami.7b02789
Liu, S., Zhang, L., Yang, Q. L., Xu, Q., Yang, Y., Noor, A., et al. (2016b). Frequency-dependent Dual-Functional Coding Metasurfaces at Terahertz Frequencies. Adv. Opt. Mater. 4, 1965–1973. doi:10.1002/adom.201600471
Mursia, P., Sciancalepore, V., Garcia-Saavedra, A., Cottatellucci, L., Pérez, X. C., and Gesbert, D. (2021). RISMA: Reconfigurable Intelligent Surfaces Enabling Beamforming for IoT Massive Access. IEEE J. Select. Areas Commun. 39, 1072–1085. doi:10.1109/JSAC.2020.3018829
Sarieddeen, H., Alouini, M.-S., and Al-Naffouri, Y. T. (2020). An Overview of Signal Processing Techniques for Terahertz Communications. Arxiv https://arxiv.org/abs/2005.13176.
Shrekenhamer, D., Rout, S., Strikwerda, A. C., Bingham, C., Averitt, R. D., Sonkusale, S., et al. (2011). High Speed Terahertz Modulation from Metamaterials with Embedded High Electron Mobility Transistors. Opt. Express 19, 9968–9975. doi:10.1364/OE.19.009968
Stantchev, R. I., Phillips, D. B., Hobson, P., Hornett, S. M., Padgett, M. J., and Hendry, E. (2017). Compressed Sensing with Near-Field Thz Radiation. Optica 4, 989–992. doi:10.1364/OPTICA.4.000989
Wang, Q., Xu, Q., Zhang, X., Tian, C., Xu, Y., Gu, J., et al. (2018). All-dielectric Meta-Holograms with Holographic Images Transforming Longitudinally. ACS Photon. 5, 599–606. doi:10.1021/acsphotonics.7b01173
Xiao, L., Yang, P., Lei, X., Xiao, Y., Fan, S., Li, S., et al. (2015). A Low-Complexity Detection Scheme for Differential Spatial Modulation. IEEE Commun. Lett. 19, 1516–1519. doi:10.1109/LCOMM.2015.2448616
Yamagiwa, M., Ogawa, T., Minamikawa, T., Abdelsalam, D. G., Okabe, K., Tsurumachi, N., et al. (2018). Real-time Amplitude and Phase Imaging of Optically Opaque Objects by Combining Full-Field off-axis Terahertz Digital Holography with Angular Spectrum Reconstruction. J. Infrared Milli Terahz Waves 39, 561–572. doi:10.1007/s10762-018-0482-6
Yan, W., Yuan, X., He, Z.-Q., and Kuai, X. (2020). Passive Beamforming and Information Transfer Design for Reconfigurable Intelligent Surfaces Aided Multiuser MIMO Systems. IEEE J. Select. Areas Commun. 38, 1793–1808. doi:10.1109/JSAC.2020.3000811
Ye, J., Guo, S., and Alouini, M.-S. (2020). Joint Reflecting and Precoding Designs for SER Minimization in Reconfigurable Intelligent Surfaces Assisted MIMO Systems. IEEE Trans. Wireless Commun. 19, 5561–5574. doi:10.1109/TWC.2020.2994455
Yuan, H., Yang, N., Yang, K., Han, C., and An, J. (2020). Hybrid Beamforming for Terahertz MIMO-OFDM Systems over Frequency Selective Fading. IEEE Trans. Commun. 68 (10), 6186–6199. doi:10.1109/TCOMM.2020.3008699
Zakrajsek, L. M., Pados, D. A., and Jornet, J. M. (2017). “Design and Performance Analysis of Ultra-massive Multi-Carrier Multiple Input Multiple Output Communications in the Terahertz Band,” in Image Sensing Technologies: Materials, Devices, Systems, and Applications IV, 10209, 26–36. doi:10.1117/12.2264424
Zhang, Y., Tan, Y.-W., Stormer, H. L., and Kim, P. (2005). Experimental Observation of the Quantum Hall Effect and Berry's Phase in Graphene. Nature 438, 201–204. doi:10.1038/nature04235
Keywords: terahertz communication, differential modulation, metasurface, maximum-likelihood detection, data rate
Citation: Guo S, Ye J and Zhang P (2021) A Differential Modulation Scheme for Metasurface-Based Terahertz Communications. Front. Comms. Net 2:687233. doi: 10.3389/frcmn.2021.687233
Received: 29 March 2021; Accepted: 26 May 2021;
Published: 22 June 2021.
Edited by:
Miaowen Wen, South China University of Technology, ChinaReviewed by:
Jun Li, Guangzhou University, ChinaPei Liu, Wuhan University of Technology, China
Ping Yang, University of Electronic Science and Technology of China, China
Copyright © 2021 Guo, Ye and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shuaishuai Guo, c2h1YWlzaHVhaV9ndW9Ac2R1LmVkdS5jbg==
 Shuaishuai Guo
Shuaishuai Guo Jia Ye
Jia Ye Peng Zhang
Peng Zhang