Polarity Reversal Effect of a Memristor From the Circuit Point of View and Insights Into the Memristor Fuse

As the memristor device is asymmetrical in nature, it is not a bilateral element like the resistor in terms of circuit functionality. Thus, it causes hindrance in some memristor-based applications such as in cellular nonlinear network neighborhood connections and in some application areas where its orientation is essentially expected to act as a bilateral circuit element reliable for bidirectional communication, for example, in signal and image processing or in electrical synapse devices. We introduce a memristor-based network for each purpose where we replace the conventional series resistances by memristors. The memristor asymmetry is described from the circuit point of view allowing us to observe its interaction within the network. Moreover, a memristor fuse is proposed in order to achieve the memristive effect with symmetry, which is formed basically by connecting two memristors antiserially. We, therefore, analyze the memristor fuse from its basic principle along with the theoretical analysis and then observe the response from the circuit point of view.

1 Introduction

The memristor was predicted in 1971 (Chua) by observing the symmetrical nature of the three known basic circuit elements, resistor R, capacitor C, and inductor L, with respect to the four circuit variables, namely, electric voltage v, electric current i, electric charge q, and magnetic flux ϕ, see Figure 1. As stated in the work of Chua (1971) for the sake of completeness, there should be a fourth passive circuit element describing the relationship between magnetic flux ϕ and electric charge q, hence named memristor. A broader class of this device known as the memristive system is given by Chua and Kang (1976). Memristor (M) is the short form of memory resistor, this name being due to the fact that the device remembers its previous history (resistance), hence the memory effect, and is analogous to a resistor with memory. Depending on the type of excitation, a memristor can be described as charge controlled $\varphi =\widehat{h}\left(q\right)$ or flux controlled $q=\widehat{h}\left(\varphi \right)$ (Chua (2015)) which are preferably described as memristance and memductance, having unit as Ohms ($\text{Ω}$) and Siemens (S), respectively.

FIGURE 1

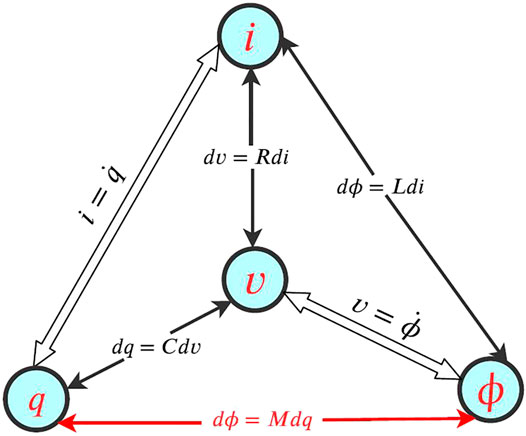
FIGURE 1. Symmetrical argument of the four basic passive circuit elements with respect to the four circuit variables.

For more than 3 decades, memristor remained a mystery until in 2008 (Strukov et al. (2008)) a group of researchers from the HP laboratory announced the successful realization of the first solid-state memristor in a device form (Stanley Williams (2013)). This recent discovery of the HP lab allured many scientists, engineers, and researchers to explore the feasible applications of memristor in discrete and crossbar array configurations Mazumder et al. (2012) and more possible device technologies.

Since the invention by Strukov et al. (2008), many memristor technologies emerged which are basically adhered to the principle of bipolar resistance switching between two extreme values, namely, $R_{on}$ and $R_{off}$ that, respectively, correspond to the lowest and highest resistance state of the device. Note that another commonly used memristor technology is the self-directed channel device (Campbell (2017)) whose conductivity is based on the formation and dissolution of ionic bridges that result in low and high resistance states, respectively, but we will mainly refer to the TiO₂ memristor in the remaining part of this article. Figure 2 shows the formation of the titanium-oxide memristor with the TiO₂ doped with some positive oxygen vacancies. Hence, the TiO₂ memristor is an example of MIM devices, i. e., metal–insulator–metal, in which a thin bilayer of TiO₂ film is sandwiched between platinum electrodes (labeled as $P{t}_1$ and $P{t}_2$). The small positive spots in the doped region refer to the positive charges due to the oxygen vacancies (Stanley Williams (2013); Paris and Taioli (2016)).

FIGURE 2

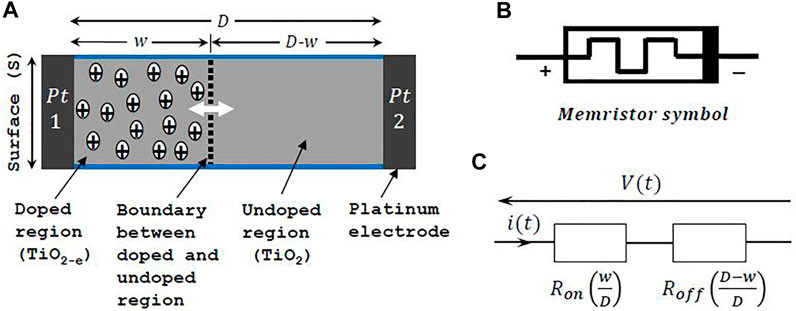
FIGURE 2. Structure of the TiO₂ memristor. The doped region TiO_2-e and the undoped region TiO₂ are, respectively, the higher and lower conducting regions with resistance $R_{on}\left(w/D\right)$ and $R_{off}\left(D-w/D\right)$. (A) Memristor schematic, (B) symbol, and (C) internal behavioral response.

The mathematical description of the titanium-oxide memristor when a positive voltage $V\left(t\right)$ is applied to the 2-port device shown in Figure 2A corresponds to a current $i\left(t\right)$ flowing into the memristor, while the voltage is shared in two parts: a voltage $V\left(t\right)R_{on}w/R_{on}w+R_{off}\left(D-w\right)$ across the doped region (the left part of Figure 2A) and the complementary part $V\left(t\right)R_{off}\left(D-w\right)/R_{on}w+R_{off}\left(D-w\right)$ present across the undoped region (the right part of Figure 2A). Let us consider the oxygen vacancies in the doped region. These charge carriers with mass m and charge q are accelerated by the electric field $E=V\left(t\right)R_{on}/R_{on}w+R_{off}\left(D-w\right)$ and are broken as they collide together. They finally reach a limit speed $V_l=q.E/m\text{Γ}$, where $\text{Γ}$ is the mean time between two consecutive collisions, leading to their averaged velocity $<v_{\text{oxygen}\text{vacancy}}>={\mu }_{v}E$, where ${\mu }_v$ is the mobility of the oxygen vacancies. They expand the doped region toward the right ($w\uparrow$), whose boundary increases with a positive current $i\left(t\right)$ such that $dw/dt={\mu }_{v}E={\mu }_v{R}_{on}/Di\left(t\right)$. Finally, with the normalized form $x=w/D$, the behavior of the memristor is given by

$V\left(t\right)=M\left(x\right)i\left(t\right),(\mathrm{1a})$

$M\left(x\right)=R_{off}-\delta Rx,(\mathrm{1b})$

$\frac{dx}{dt}={\mu }_v\frac{R_{on}}{D^2}i\left(t\right),(\mathrm{1c})$

where $M\left(x\right)$ is the memristance and $\delta R=R_{off}-R_{on}$ is the difference between $R_{off}$ and R_on. When integrating (1c) for x from 0 to 1,

$\begin{array}{c}{\displaystyle {\int }_0^{1}dx}=1={\mu }_v\frac{R_{on}}{D^2}{\displaystyle {\int }_{w=0}^{w=D}i\left(t\right)dt},\\ ={\mu }_v\frac{R_{on}}{D^2}{q}_d,\end{array}(2)$

where $\begin{array}{l}{q}_d={{\displaystyle \int }}_{w=0}^{w=D}i\left(t\right)dt=D^2/u_v{R}_{on}\\ \end{array}$ is the charge required to move completely the doped/undoped boundary from $w=0$ to $w=D$. Then, Eq. 1c can be rewritten as

$\frac{dx}{dt}=\frac{1}{q_d}i\left(t\right).(3)$

A window function $f\left(x\right)$ is often introduced as a factor in the right-hand side of Eq. 3 for nonlinear dopant drift modeling, i.e., to avoid x from taking values outside of the interval $\left[\mathrm{0,1}\right]$ (Joglekar and Wolf (2009)), to give

$\frac{dx}{dt}=\frac{f\left(x\right)i\left(t\right)}{q_d}.(4)$

Eq. 1 characterizes a bipolar memristor where the resistance switching depends on the voltage polarity (Strachan et al. (2011), Krzysteczko et al. (2009), Teixeira et al. (2009)). However, there are other reported memristors exhibiting symmetry in polarity, such as unipolar, nonpolar, and complementary resistive switching memristors (Yoshida et al. (2008), Huang et al. (2010), Wang et al. (2017), Linn et al. (2010)). Here, the resistance switching between $R_{off}$ and $R_{on}$ (and vice versa) can be completed in the same voltage polarity. As such, unipolar memristors are important elements in memory arrays and logic circuit implementation (Yin et al. (2020)).

Many memristor-based applications are reported (Prodromakis and Toumazou (2010), Marani et al. (2015), including implementation of chaotic circuits and field programmable gate array (Muthuswamy (2010), Xu et al. (2016)), high-density memory and data storage (Duan et al. (2012), Hamdioui et al. (2015)), cellular neural networks (Thomas (2013), Duan et al. (2014)), neuromorphicmemristance for one system (Chu et al. (2014), Yakopcic et al. (2018)), and logic circuits (Borghetti et al. (2010), Shin et al. (2010)). A memristor is reported to be a promising element as synapse owing to its flexibility in conductance modulation and very effective high-density connectivity Jo et al. (2010), Adhikari et al. (2012), Kim et al. (2011). There are many implemented electronic memristor-based synapses for various neumorphic computing architectures (Lecerf et al. (2014), Li et al. (2014), Saïghi et al. (2015), Prezioso et al. (2016), Wang et al. (2016), Boyn et al. (2017), Dongale et al. (2018)).

The interesting features of memristors, such as connection flexibility, nanoscaleability, memory capability, and conductance modulation, are essential properties affirming the reliability of the memristor in neuromorphic networks, especially as synaptic function. The memristor is studied in the coupling mode between two neuron cells where the synchronization phenomena is investigated numerically and theoretically (Ascoli et al. (2015), Zhang and Liao (2017), Xu et al. (2018), Bao et al. (2020)). Unidirectional coupling and bidirectional or mutual coupling are the commonly used coupling modes for nonlinear chaotic systems (Volos et al. (2015)). The synchronization and chaos between two neuron cells is also investigated by using unidirectional and bidirectional coupling (Zhang and Liao (2017)).

The main application of our work is to use the memristor as a synaptic link between neurons in electronic models, as for example, in hybrid technologies with neuronal electronic prosthesis between real neurons. The network is initially composed of a linear capacitor and a nonlinear resistance in each cell and a linear resistor in series (Comte et al. (2001)), see Figure 3A. The equivalent memristor-based network is shown in Figure 3B where the series resistance is replaced by a memristor. The memory circuit element being intrinsically asymmetric (Di Ventra et al. (2009)), the TiO₂ memristor crossbar is used to visualize the nature of current flowing through the device with respect to the polarities of the applied voltage. Using a memristor for the image processing technique was also reported by Prodromakis and Toumazou (2010), where a memristive grid is employed to perform edge detection. In a first step to implement 2D-memristor–based cellular nonlinear networks for signal and image processing purposes or for modeling a neural network with memristors as synapses, we rather focus here on the interaction of the memristor between pixel cells by considering a system of two cells in order to assess the behavior of the memristor quantitatively and qualitatively.

FIGURE 3

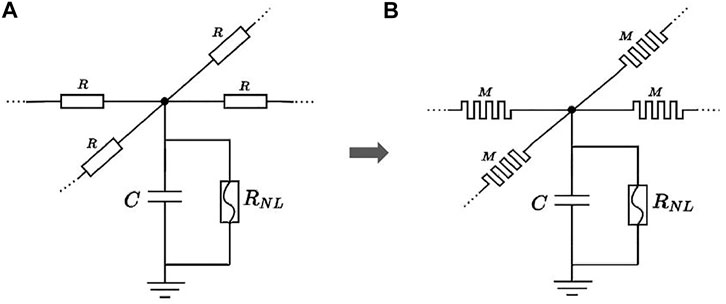
FIGURE 3. 2D cellular nonlinear networks (CNNs). C is a linear capacitor, and $R_{NL}$ is a nonlinear resistance. (A) Coupling using linear resistance R and (B) coupling using memristor M.

The underlining task is accompanied by observing the pinched hysteresis loop (PHL), memristance transition, voltage evolution of the cells, and the explanation of the memristor’s lack of bilaterality. We derive analytically a second-order nonlinear differential equation characterizing the interaction of the memristor between the two cells bidirectionally. The system is studied in the phase plane allowing visualizing the memristor asymmetry. The memristance variation of a bipolar memristor with respect to the direction of flowing current affects its reliability in some potential applications where sensitivity in direction is important, for example, the memristive grid for neuromorphic application and image processing, hence the need for the so-called memristor fuse (Jiang and Shi (2009)). The formation is achieved by connecting two identical memristors antiserially. We describe the memristor fuse and obtain some results in accordance to our application.

2 Description of the Polarity Reversal

Figures 4A,B show two identical memristors $M_1$ and $M_2$ connected in parallel across a voltage source V with terminals for a direct polarization for $M_1$ but reversed in the case of $M_2$, both memristors having the same initial condition. The schematic is shown in a way to illustrate the trending of the mobile charge carriers under the influence of external bias. The currents through $M_1$ and $M_2$ are measured as $I_1$ and $I_2$, respectively, and $V\left(t\right)=I_1\left(t\right)M_1=I_2\left(t\right)M_2$. Although the memristors are identical, we found that $\left|I_1\right|\ne \left|I_2\right|$; hence, the conductivity differs if the polarity is reversed, even though with the same initial condition and voltage excitation. Hence, the device offers low resistance path with the orientation of $M_1$ and high resistance path for that of $M_2$.

FIGURE 4

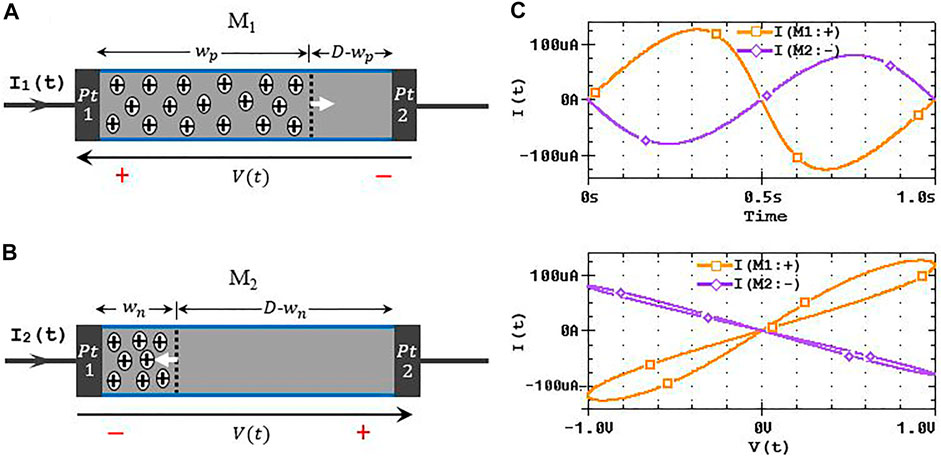
FIGURE 4. Concentration of the dopants in relation to charge carrier mobility with respect to the polarity of the input signal. (A) Application of positive bias causes the expansion of the doped region through the bulk of the device; (B) application of negative bias causes the contraction of the doped region (Joglekar and Wolf (2009)). Respectively, the overall process affects the device conducting channel widths $w_p$ and $w_n$, and it gives the trend on how w approaches 0 or D, (C) the currents $I_1$ and $I_2$ through $M_1$ and $M_2$, respectively, and the corresponding I-V curves for sine input voltage with $1V$ amplitude. Reversing the polarity of the memristor also affects the absolute value of the flowing current. The current $I_2\left(t\right)$ falls in the second and fourth quadrants due to the reversed polarity of the input voltage $V\left(t\right)$.

The schematic is shown in Figure 2A, where initially, the width of TiO₂ altogether is D and the width of the doped (TiO_2-e) region is w and the undoped one is $\left(D-w\right)$. Figure 4A shows that the positive charges in the doped region are repelled by the positive terminal of the power supply, thereby making the width of the doped region to expand such that $w\to D$, as illustrated by the width trending $w_p$. If the terminals of the applied voltage are reversed (Figure 4B), the negative terminal from the power supply attracts the positive charges in the doped region, thereby causing the contraction of the doped region such that $w\to 0$ with the width trending illustrated as $w_n$. Figure 4C shows the comparison of the current flowing through $M_1$ and $M_2$ with respect to the applied voltage source. The result is obtained using a sine input voltage source and a window function by Joglekar and Wolf (2009). The current $I_1\left(t\right)$ and $I_2\left(t\right)$ have different absolute values. The current–voltage graph of $I_2\left(t\right)$ falls in the second and fourth quadrants due to the reversed terminals of $V\left(t\right)$.

It follows that the conductivity of a memristor can be compared to that of a diode in terms of terminal polarity. However, unlike the diode, the memristor conducts electricity in both directions but the conductivity increases if its higher polarity terminal is connected to the positive terminal of the applied voltage source and decreases if its lower polarity terminal is connected to the positive terminal of the applied input voltage source.

In a nanoscale device, even small voltages can generate large electric field required to cause current to flow through the device. The smaller the device, the higher the electric field developed, and hence, more current flows through the device (Strukov et al. (2008)). The electroforming process forms the oxygen vacancies which cause a high-conducting channel (TiO_2-e) shunting the bulk of the insulation film TiO₂ (Yang et al. (2008), Pickett et al. (2009)). Depending on the nature of the bipolar input source, the conducting channel is affected by the variation of the tunneling barrier width ($D-w$). Therefore, the device conductivity can be described by the Simmons tunneling barrier model (Simmons (1963a), Simmons (1963b), Simmons (1971)), devoted to the conduction of a material in a given medium. Depending on the magnitude of the input source, the boundary moves back and forth proportionally to the concentration of the dopant, thus setting the resistance of the memristor. Note that, in Figure 2, in reality, the boundary can never be outside of the interval $[0,D]$ because there is always doped and undoped material present; in other words, the doped region can only expand or contract but never ceases to exist.

3 Memristor Asymmetry From the Circuit Point of View

To vividly visualize the effect of memristor asymmetry, we consider two identical RC cells shown in Figure 5, which is the simplified setup of the system in the work of Isah et al. (2020b). The cells are labeled as cell-1 and cell-2 having potentials $V_1$ and $V_2$, respectively, coupled together by a memristor M with its orientation as shown. Two tests are carried out which allow to observe the interaction of the memristor bidirectionally:

1. Cond-1: $V_1>V_2,$

2. Cond-2: $V_1<V_2.$

FIGURE 5

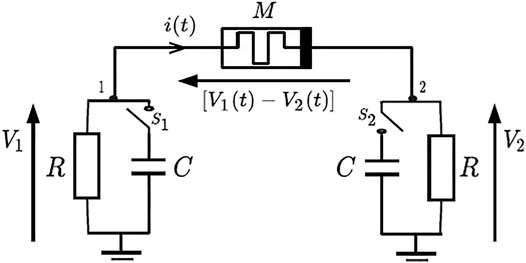
FIGURE 5. Memristor asymmetry from the circuit point of view: two charged RC cells coupled together by a memristor. The circuit is invoked by the switches $S_1$ and $S_2$. The cells are at different potentials so that the current $i\left(t\right)$ will flow through the memristor. The test is performed for $V_1>V_2$ and then $V_1<V_2$, namely, Cond-1 and Cond-2, respectively. For example $V_{1_0}=1V,V_{2_0}=0V$ and then $V_{1_0}=0V,V_{2_0}=1V$. For Cond-2, the voltage across the memristor becomes $\left[V_2\left(t\right)-V_1\left(t\right)\right]$.

In the former, the direction of $I\left(t\right)$ is as shown in Figure 5; meanwhile, in the latter, the direction is reversed. The voltage across the memristor is $\left[V_1\left(t\right)-V_2\left(t\right)\right]$ for Cond-1 and $\left[V_2\left(t\right)-V_1\left(t\right)\right]$ for Cond-2. By taking into account the history of the memristor, we have

$\begin{array}{l}q\left(t\right)={{\displaystyle \int }}_{-\infty }^{t}i\left(\tau \right)d\tau =q_0+{{\displaystyle \int }}_0^{t}i\left(\tau \right)d\tau ,\\ \end{array}(5)$

where $q_0$ is the amount of charge already flowed through the device from its last usage, and thus, it becomes the initial charge at time $t=0$. Therefore, we consider the same memristor M with the same previous history, characterized by the initial charge $q_0$. In Cond-1, it is placed in one way as shown in Figure 5 and in Cond-2, on the opposite way.

Figure 5 is simulated in SPICE using the memristor model by Biolek et al. (2009), which can easily be implemented experimentally. The setup is activated by closing the switches $S_1$ and $S_2$ simultaneously. For each Cond-1 and Cond-2, we considered the initial charge $q_0=38\mu C$; meanwhile, the low and high resistance limits of the memristor are $100\text{Ω}$ and $16K\text{Ω}$, respectively (Strukov et al. (2008)). Given the initial conditions of the cells, that is, for Cond-1, $V_{1_0}=1V$, $V_{2_0}=0V$ and for Cond-2, $V_{1_0}=0V$, $V_{2_0}=1V$, the result is shown in Figure 6. It is, however, important to note that the initial voltages can have any numerical values. Figure 6A shows the memristance transition for Cond-1 and Cond-2, illustrated, respectively, by the solid and dash curves. Figure 6B shows the corresponding time evolution of $V_1\left(t\right)$ and $V_2\left(t\right)$. The results show that Cond-1 and Cond-2 lead to quite different scenarios.

FIGURE 6

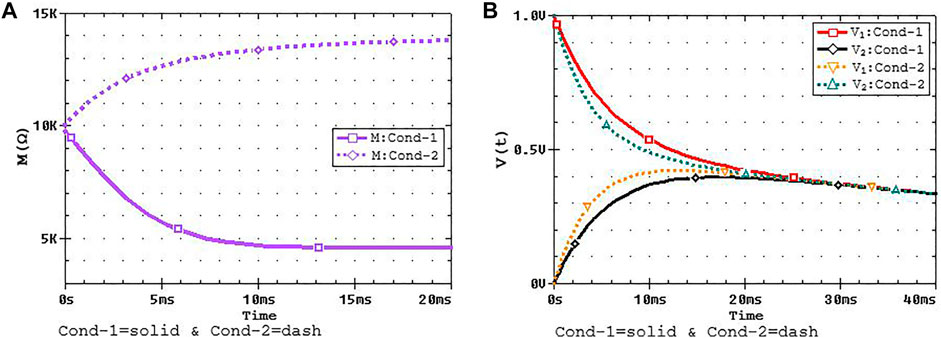
FIGURE 6. The interaction of the cells according to Cond-1 (solid curves) and Cond-2 (dash curves) for $q_0=38\mu C$, $R_{on}=100\text{Ω}$, and $R_{off}=16K\text{Ω}$ with $V_{1_0}=1V$, $V_{2_0}=0V$ for Cond-1 and $V_{1_0}=0V$, $V_{2_0}=1V$ for Cond-2. (A) Memristance transition; (B) time evolution of $V_1\left(t\right)$ and $V_2\left(t\right)$.

In Cond-1, the memristance decreases corresponding to the expansion of the doped region; meanwhile, for Cond-2, the memristance increases corresponding to the contraction of the doped region. In both Cond-1 and Cond-2, the memristance transition eventually flattens as the cells stabilize, that is, at a time when $V_1\left(t\right)=V_2\left(t\right)$. The memristance transition depends on the initial conditions of the cells. For example, Figure 7 shows the case where the initial conditions of the cells are changed with two different initial charges as $q_{0_1}=46\mu C$ and $q_{0_2}=31\mu C$. Figure 7A and 7B, respectively, show the memristance transition and the corresponding voltage evolution of the cells. Furthermore, Figure 6B and 7B show that the orientation of the memristor according to Cond-1 or Cond-2 affects the time taken for the system to stabilize. Let $V_m\left(t\right)$ represent the voltage across memristor; hence, $V_m\left(t\right)=V_1\left(t\right)-V_2\left(t\right)$ for Cond-1 and $V_m\left(t\right)=V_2\left(t\right)-V_1\left(t\right)$ Cond-2. No current flows through the memristor when $V_1\left(t\right)=V_2\left(t\right)$ because the voltage across the memrisor is also zero even though $V_1\left(t\right)=V_2\left(t\right)\ne 0$, see Figure 8. The combined evolution of $V_1\left(t\right)$ and $V_2\left(t\right)$ eventually stabilizes to zero due to the resistive nature of the cells.

FIGURE 7

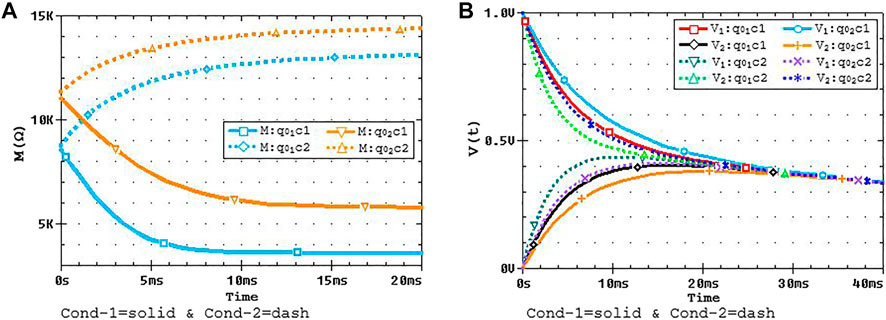
FIGURE 7. System evolution using two different initial charges $q_{0_1}=46\mu C$ and $q_{0_2}=31\mu C$ with $V_{1_0}=1V$, $V_{2_0}=0V$ for Cond-1 (solid curves) and $V_{1_0}=0V$, $V_{2_0}=1V$ for Cond-2 (dash curves). (A) Memristance transition showing the variation effect of the initial charge; (B) the corresponding evolution of $V_1\left(t\right)$ and $V_2\left(t\right)$.

FIGURE 8

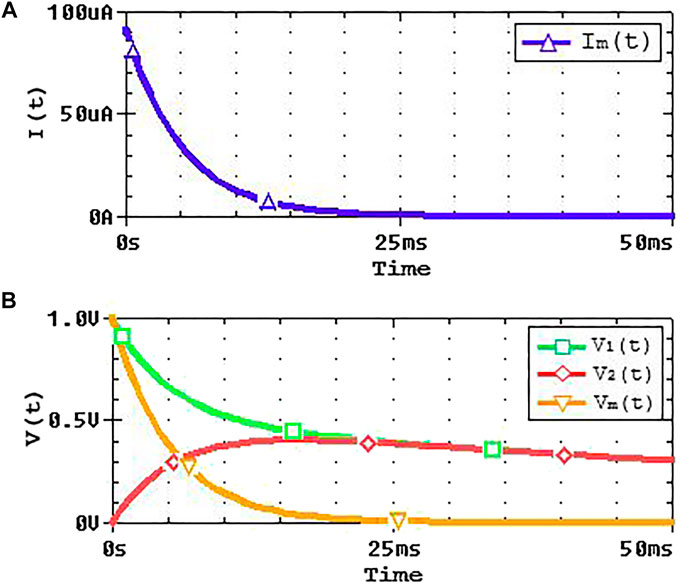
FIGURE 8. (A) Current through the memristor. (B) Evolution of $V_1\left(t\right)$ and $V_2\left(t\right)$ for cells one and two, respectively, and the voltage across the memristor $V_m\left(t\right)=V_1\left(t\right)-V_2\left(t\right)$. No current flows through the memristor when $V_1\left(t\right)=V_2\left(t\right)$, and the voltage across the memristor is also zero. $V_1\left(t\right)$ and $V_2\left(t\right)$ eventually decay to zero due to the resistive nature of the cells.

Furthermore, from Figure 5, one can deduce the following equations:

$i\left(t\right)=-C\frac{d{V}_1}{dt}-\frac{V_1}{R},(6)$

$i\left(t\right)=C\frac{d{V}_2}{dt}+\frac{V_2}{R},(7)$

$i\left(t\right)=\frac{dq}{dt},(8)$

$V_1-V_2=M\left(q\right)\frac{dq}{dt},(9)$

where $M\left(q\right)$ is defined in the work of Isah et al. (2020a) as follows:

$M\left(q\right)=R_{off}-3\delta R\frac{q^2}{q_d^2}+2\delta R\frac{q^3}{q_d^3},q\in \left[0,q_d\right],(10)$

with $M\left(q\right)=R_{off}$ if $q\left(t\right)\le 0$ and $M\left(q\right)=R_{on}$ if $q\left(t\right)\ge q_d$. The dynamics of the memristor between the two cells can be expressed analytically. Eqs. 6–8 are simplified to give

$\frac{d}{dt}\left(V_1-V_2\right)=-\frac{2R}{{\tau }_c}\frac{dq}{dt}-\frac{1}{{\tau }_c}\left(M\left(q\right)\frac{dq}{dt}\right),(11)$

where ${\tau }_c=RC$ is the time constant of the cell. Substituting Eq. 9 into 11 and taking the time derivative on the left-hand side give

$\begin{array}{l}\left[2R+M\left(q\right)\right]\frac{dq}{dt}+{\tau }_c \frac{d}{dt}\left[M\left(q\right)\right] \frac{dq}{dt}+{\tau }_c M\left(q\right) \frac{d^{2}q}{d{t}^2}=0\Rightarrow \\ \left[2R+M\left(q\right)\right]\frac{dq}{dt}+{\tau }_c\frac{dM\left(q\right)}{dq}{\left(\frac{dq}{dt}\right)}^2+{\tau }_{c}M\left(q\right)\frac{d^{2}q}{d{t}^2}=0.\end{array}(12)$

Eq. 12 can be expressed in a normalized form as

$\left(\frac{2R}{\delta R}+\mathcal{ℳ}\right)Y+\frac{d\mathcal{ℳ}}{dX}{Y}^2+\mathrm{ℳ}\dot{Y}=0,(13)$

where $\tau =t/{\tau }_c$ is the normalized time, $X=q/q_d$ is the normalized charge (Joglekar and Wolf (2009), Biolek et al. (2012)), $Y=dX/d\tau$ is the first derivative of X with respect to τ, $\dot{Y}=dY/d\tau =d{X}^2/d{\tau }^2$ is the second derivative of X with respect to τ, and $\mathcal{ℳ}=M/\delta R$ is the normalized form of (10), thus rewritten as follows:

$\mathcal{ℳ}\left(X\right)=\mathrm{ℛ}-3X^2+2X^3,X\in \left[\mathrm{0,1}\right],(14)$

with $\mathrm{ℛ}=\frac{R_{off}}{\delta R}$. Substituting (14) into (13) and posing ${\gamma }_1=\frac{\mathcal{R}}{\delta R}+\frac{R}{2}$ and ${\gamma }_2=\frac{\mathrm{ℛ}}{2}$, Eq. 13 is better studied when replaced by the set of equations

$\{\begin{array}{l}\frac{dX}{d\tau }=Y,\hfill \\ \frac{dY}{d\tau }=-\frac{\left(X^3-\frac{3}{2}{X}^2+{\gamma }_1\right)Y+3\left(X^2-X\right)Y^2}{X^3-\frac{3}{2}{X}^2+{\gamma }_2},\hfill \end{array}(15)$

allowing to study the system in the phase plane (X,Y) which facilitates the observation of cell interaction in relation to the memristive effect under different initial conditions. Furthermore, Eq. 13 requires a continuous first derivative of $\mathcal{ℳ}$ with respect to X at $X=0$ and $X=1$, and it is achieved perfectly by using Eq. 14. The history of a memristor marks its initial value in ohms, determined by the last amount of electric charge passed through it. However, it is reported in the work of Isah et al. (2020b) and Chua (2015)that the initial memristance is unknown. It is important to note that the state $X_0$ is not fixed (in other words, it is unknown) and it strongly depends on the history of the device. Moreover, from Eq. 15, we get

$\begin{array}{l}\frac{dY}{dX}=-\frac{\left(X^3-\frac{3}{2}{X}^2+{\gamma }_1\right)+3\left(X^2-X\right)Y}{X^3-\frac{3}{2}{X}^2+{\gamma }_2} \Rightarrow \\ H\left(X,Y\right)=\left(X^3-\frac{3}{2}{X}^2+{\gamma }_2\right)Y+\frac{1}{4}{X}^4-\frac{1}{2}{X}^3+{\gamma }_{1}X,\end{array}(16)$

where H is a conservative expression for the equation set Eq. 15, only depending on the initial conditions $X_0$, $V_{1_0}$, $V_{2_0}$, and $Y_0$. Hence, $X_0=\frac{q_0}{q_d}$, being simply the normalized form of $q_0$, and we obtained $Y_0$ from Eq. 9 as follows:

$Y_0=\frac{{\tau }_c}{q_d}\frac{\left(V_{1_0}-V_{2_0}\right)}{\delta R\mathcal{ℳ}\left(X_0\right)}.(17)$

Recall that $Y=\frac{dX}{d\tau }$; then, Eq. 16 can be expressed as

$\frac{X^3-\frac{3}{2}{X}^2+{\gamma }_2}{X^4-2X^3+4{\gamma }_{1}X-4H}dX=-\frac{1}{4}d\tau \Rightarrow$

$\left[\frac{{\tilde{\alpha }}_1}{X-X_1}+\frac{{\tilde{\alpha }}_2}{X-X_2}+\frac{{\tilde{\alpha }}_3+{\tilde{\alpha }}_{4}X}{X^2+{\tilde{\beta }}_{1}X+{\tilde{\beta }}_2}\right]dX=-\frac{1}{4}d\tau ,(18)$

and the analytical relation between the normalized time τ and the normalized charge X becomes

$\tau ={\tau }_1-4[\text{ln}\left[{\left(\frac{X-X_1}{X_0-X_1}\right)}^{{\tilde{\alpha }}_1}{\left(\frac{X-X_2}{X_0-X_2}\right)}^{{\tilde{\alpha }}_2}\right]+\text{ln}{\left[\frac{X^2+{\tilde{\beta }}_{1}X+{\tilde{\beta }}_2}{X_0^2+{\tilde{\beta }}_1{X}_0+{\tilde{\beta }}_2}\right]}^{\frac{{\tilde{\alpha }}_4}{2}}$

$+\frac{2{\tilde{\alpha }}_3-{\tilde{\alpha }}_4{\tilde{\beta }}_1}{\sqrt{4{\tilde{\beta }}_2-{\tilde{\beta }}_1^2}}\left(\text{arctan}\frac{2\left(X+\frac{{\tilde{\beta }}_1}{2}\right)}{\sqrt{4{\tilde{\beta }}_2-{\tilde{\beta }}_1^2}}-\text{arctan}\frac{2\left(X_0+\frac{{\tilde{\beta }}_1}{2}\right)}{\sqrt{4{\tilde{\beta }}_2-{\tilde{\beta }}_1^2}}\right)].(19)$

Here, $X_1$ and $X_2$ are the real roots in the denominators of Eq. 18; meanwhile, the coefficients ${\tilde{\alpha }}_1$, ${\tilde{\alpha }}_2$, ${\tilde{\alpha }}_3$, ${\tilde{\alpha }}_4$, ${\tilde{\beta }}_1$, ${\tilde{\beta }}_2$, and ${\tau }_1$ are

$\begin{array}{l}{\tilde{\alpha }}_1=\frac{X_1^3-\frac{3}{2}{X}_1^2+{\gamma }_2}{\left(X_1-X_2\right)\left(X_1^2+{\tilde{\beta }}_1{X}_1+{\tilde{\beta }}_2\right)},\\ {\tilde{\alpha }}_2=\frac{X_2^3-\frac{3}{2}{X}_2^2+{\gamma }_2}{\left(X_2-X_1\right)\left(X_2^2+{\tilde{\beta }}_1{X}_2+{\tilde{\beta }}_2\right)},\\ {\tilde{\alpha }}_3=\frac{{\gamma }_2+{\tilde{\alpha }}_1{\tilde{\beta }}_2{X}_2+{\tilde{\alpha }}_2{\tilde{\beta }}_2{X}_1}{X_1{X}_2},\\ {\tilde{\alpha }}_4=1-{\tilde{\alpha }}_1-{\tilde{\alpha }}_2,\\ {\tilde{\beta }}_1=X_1+X_2-2,{\tilde{\beta }}_2=\frac{-4H}{X_1{X}_2},\\ {\tau }_1=-\frac{{\gamma }_2}{{\gamma }_1}\left(\frac{H}{H-{\gamma }_1{X}_0}\right).\end{array}$

Furthermore, the equilibrium point of equation system Eq. 15 is met when $\frac{dY}{d\tau }=0$, that is, $Y=0$; in other words, $V_1\left(t\right)=V_2\left(t\right)$; then, from (15), $X^3-\frac{3}{2}{X}^2+{\gamma }_1=0$, having at least one real root corresponding to the value of $X\left(\tau \right)$ at the equilibrium point $Y=0$. The singularity point of the system is where the derivative $\frac{dY}{d\tau }$ does not exist, that is, $\frac{dY}{d\tau }=\infty$; hence, we get from (15)$X^3-\frac{3}{2}{X}^2+{\gamma }_2=0$, having at least one real root corresponding to the singular line, for any given ${\gamma }_2$. Depending on the initial conditions, Y evolves positively according to Cond-1 and negatively according to Cond-2. Recall that the value of $X_0$ is not known; however, we considered all the possible occurrences as shown in Figure 9. Each trajectory begins with the corresponding value of $Y_0$. Therefore, depending on $X_0$, we observed different evolution patterns in the phase portraits.

FIGURE 9

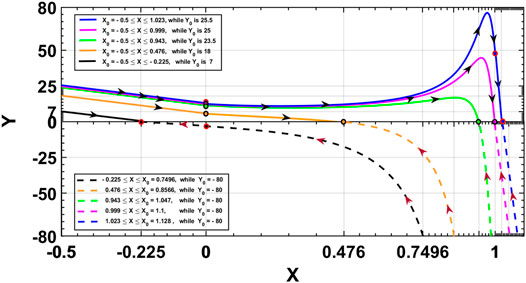
FIGURE 9. Phase portraits showing the charge evolution from left to right for $Y_0>0$ and from right to left for $Y_0<0$ under different initial conditions. The lack of symmetry is noticeable within the bulk of the device.

The phase portraits show the families of curves for different initial conditions. The results are obtained for $R_{on}=100\text{Ω}$ and $R_{off}=16K\text{Ω}$. Note that the memristance is unchanged for $X\le 0$ and $X\ge 1$ and is, respectively, given by $R_{off}$ and $R_{on}$ as depicted by the parallel evolution of the curves outside the interval $\left[\mathrm{0,1}\right]$. Therefore, different possibilities are considered that take into account the case where $X_0=0$ or one and beyond. The lack of symmetry is highly observable as the curves evolve from left to right for $Y>0$ and then from right to left for $Y<0$ according to Cond-1 and Cond-2, respectively. Furthermore, the time evolution of cells 1 and 2, respectively, can be obtained from Eqs. 6–9 as follows:

$V_1\left(t\right)=\frac{1}{2}\left(V_{1_0}+V_{2_0}\right)e^{-\frac{t}{{\tau }_c}}+\frac{1}{2}\left(V_{1_0}-V_{2_0}\right)-\frac{R}{{\tau }_c}\left(q-q_0\right)-\frac{ð}{2{\tau }_c},(20)$

$V_2\left(t\right)=\frac{1}{2}\left(V_{1_0}+V_{2_0}\right)e^{-\frac{t}{{\tau }_c}}-\frac{1}{2}\left(V_{1_0}-V_{2_0}\right)+\frac{R}{{\tau }_c}\left(q-q_0\right)+\frac{ð}{2{\tau }_c},(21)$

where

$\begin{array}{l}ð=\delta R{q}_d{{\displaystyle \int }}_{X0}^X\mathrm{ℳ}\left(X^{\text{*}}\right)\text{d}{X}^{\text{*}}.\\ \end{array}(22)$

4 Memristor Fuse

The lack of bilaterality manifested in a bipolar memristor device is challenging in terms of its usage for certain applications, such as communication link in bidirectional applications (Comte et al. (2001)). As shown in Figure 6 and Figure 7, using a memristor to link two possible sources of information communicating together bidirectionally is not advisable owing to its resistance dependency on the amount and direction of flowing current. To convert it, a memristor fuse is proposed and then demonstrated in the work of Jiang and Shi (2009), Gelencser et al. (2012), and Serb et al. (2016). It is basically formed by connecting two memristors antiserially in order to avoid the lack of bilaterality (Yildirim et al. (2018)). The memristor fuse is reported to be useful in a memristive grid network for CNN neighborhood connection and image processing (Pershin and Di Ventra (2011), Gelencser et al. (2012), Yang and Kim (2016), Yildirim et al. (2018), Sarmiento-Reyes and Rodríguez-Velásquez (2018), Lim et al. (2019)). In general (Fouda et al. (2013)), Figure 10 shows the four possible ways to form series connections of two memristors with respect to their polarities.

FIGURE 10

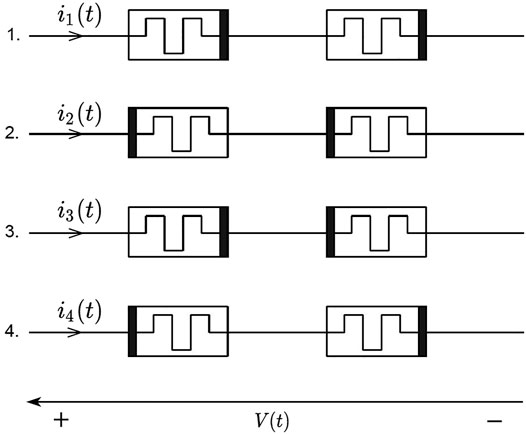
FIGURE 10. Four possible series connections of two memristors with respect to the input source. The memristive effect is retained for cases 1 and 2 whereas it is balanced for cases 3 and 4 (Joglekar and Wolf (2009)). Although cases 3 and 4 are identical and both form a memristor fuse, only case 3 is commonly considered as memristor fuse formation (Gelencser et al. (2012)).

As shown in Figure 10, cases 1 and 2 refer to a serial connection of two memristors and the memristive effect is retained for these branches. Meanwhile, cases 3 and 4 are identical in structure and refer to antiserial connection of two memristors, thus forming a memristor fuse. The memristive effect for branches in cases 3 and 4 could be suppressed (Joglekar and Wolf (2009)). However, case 3 is the commonly adopted formation of a memristor fuse (Gelencser et al. (2012)). Note that cases 1 and 2 resemble Figures 4A,B, respectively, with the exception that two memristors are involved.

It is important to note that the resistance of the memristor fuse is the sum of the resistance of each of the individual memristor because the equivalent memristance is additive in a serially connected memristor. In addition, this could be a disadvantage to the desired amount of current and it also affects the dynamic features of the memristor to the extent that the current–voltage graph is merely linear; hence, the formation resembles normal resistor. Therefore, the resistance limits of the memristor fuse must be the same as those of memristor if acting alone.

The pinched hysteresis loop is one of the most distinguished fingerprints of a memristor (Adhikari et al. (2013), Chua (2014)) and is a reflection of its memory effect. As pointed out in the work of Chua (1971) and Chua (2015), without the memory, a memristor is nothing different from a resistor. A verification test is performed to compare the memristor fuse with a standalone memristor, as demonstrated in Figure 11. $M_p$ and $M_n$ are set with their polarity reversed in parallel with a memristor fuse $M_f$, all connected across the same voltage source $V\left(t\right)$. Note that the orientation of $M_p$ and $M_n$ is, respectively, similar to $M_1$ and $M_2$ illustrated in Figures 4A,B. Therefore, for the same resistance limits, the memristance of a memristor fuse is higher than the memristance of a standalone memristor, as can be observed from the respective slopes of Figure 11.

FIGURE 11

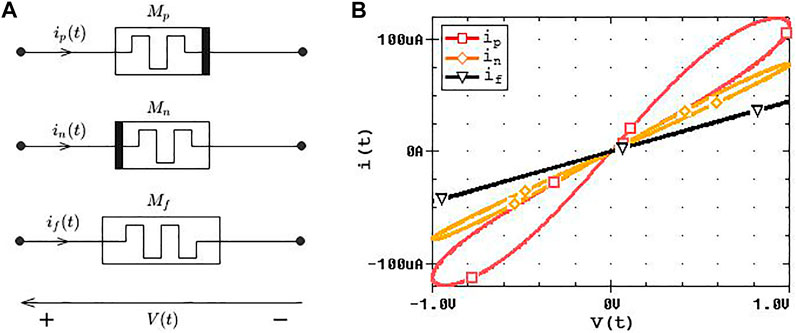
FIGURE 11. Circuit response comparison of a memristor fuse with standalone memristors. (A) Circuit schematic with a sine input voltage source. $M_p$ is the memristor with positive polarity preference, $M_n$ is with negative polarity preference, and $M_f$ is the memristor fuse; (B) current–voltage characteristics for $M_p$ (red), $M_n$ (orange), and $M_f$ (black).

Figure 12 shows the schematic of a memristor fuse formed by antiseries connection of two memristors $M_1$ and $M_2$ with the instantaneous dopant width denoted by $w_1$ and $w_2$, respectively. During positive bias, $w_1$ expands while $w_2$ contracts, and during negative bias, $w_1$ contracts while $w_2$ expands. As $w_1$ tends to D, $w_2$ tends to 0 and the converse gives the opposite. Moreover, $w_1$ and $w_2$ could be represented in normalized forms as $x_1$ and $x_2$, where $x_1=\frac{w_1}{D}$ and $x_2=\frac{w_2}{D}$. Then, the drift speeds of the respective dopant are expressed as

$\frac{d{x}_1\left(t\right)}{dt}=\frac{1}{q_{d_1}}i\left(t\right),(\mathrm{23a})$

$\frac{d{x}_2\left(t\right)}{dt}=-\frac{1}{q_{d_2}}i\left(t\right).(\mathrm{23b})$

FIGURE 12

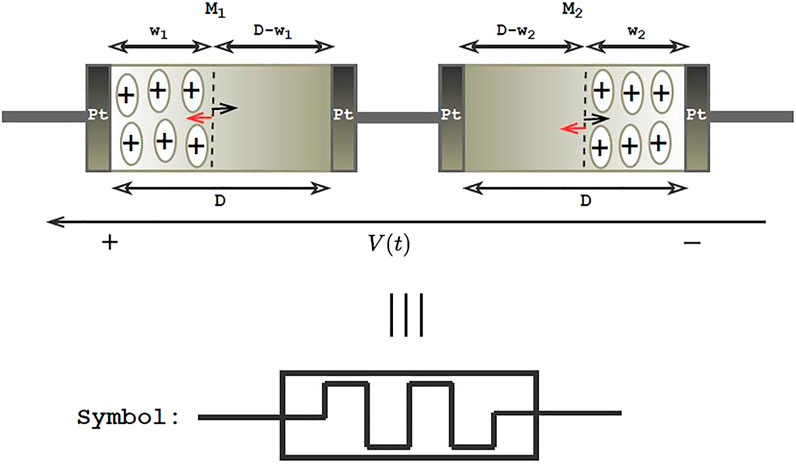
FIGURE 12. Schematic of a memristor fuse formed by two TiO₂ memristors $M_1$ and $M_2$. The positive spot signifies the positive oxygen vacancies, which serve as the higher conducting part of each memristors. $w_1$ and $w_2$ represent the instantaneous width of the doped region, meanwhile the black and red arrows describe the trending expansion and contraction of the doped region, respectively. Hence, for any input voltage, say $V\left(t\right)$, an increase in the width $w_1$ corresponds to a decrease in $w_2$ and vice versa.

The same current flows through a series connection of two memristors; hence, $i\left(t\right)$ is the same for both $M_1$ and $M_2$. Here, we consider the expression of the memristance given by Eq. 1b rather than the one given in Eq. 10 because it is simpler and already investigated in the work of Fouda et al. (2013). From Eqs. 1b, 23, the rates of change of the instantaneous memristance of $M_1$ and $M_2$ are, respectively, obtained to be

$\frac{d{M}_1\left(t\right)}{dt}={\mathit{\varrho }}_{1}i\left(t\right),(\mathrm{24a})$

$\frac{d{M}_2\left(t\right)}{dt}={\mathit{\varrho }}_{2}i\left(t\right),(\mathrm{24b})$

where ${\mathit{\varrho }}_1=-\frac{\delta R}{q_{d_1}}$ and ${\mathit{\varrho }}_2= \frac{\delta R}{q_{d_2}}$. Although the current $i\left(t\right)$ flowing through them is the same, however, the rate of change of memristance for one differs from the other. Therefore, from 24a and 24b, the rate of change of $M_1$ with respect to that of $M_2$ is given by

$\frac{d{M}_1\left(t\right)}{dt}=\frac{{\mathit{\varrho }}_1}{{\mathit{\varrho }}_2}\frac{d{M}_2\left(t\right)}{dt}=\mathit{\varrho }\frac{d{M}_2\left(t\right)}{dt},(25)$

where $\mathit{\varrho }=-\frac{q_{d_2}}{q_{d_1}}$ is called the mismatch factor (Fouda et al. (2013)) describing the increase of $M_1$ with respect to the decrease of $M_2$ and vice versa. Note that $q_{d_1}\ne q_{d_2}$, each possibly able to depend on the dimension (D), the mobility of charge carriers, and the value of the lowest resistance ($R_{on}$) for $M_1$ and $M_2$, respectively. Thus, the mismatch factor is determined by the mobilities and velocities of charge carriers in both memristors. Given the initial memristance of $M_1$ and $M_2$ as $M_{1_0}$ and $M_{2_0}$, respectively, integrating Eq. 25 gives

$M_1\left(t\right)=\mathit{\varrho }{M}_2\left(t\right)+\delta M_0,(26)$

where $\delta M_0=M_{1_0}-\mathit{\varrho }{M}_{2_0}$. The net memristance is additive in a series connection of memristors. The instantaneous memristance of the memristor fuse $M_f\left(t\right)$ is given by $M_f\left(t\right)=M_1\left(t\right)+M_2\left(t\right)$; thus,

$M_f\left(t\right)=\left(\mathit{\varrho }+1\right)M_2\left(t\right)+\delta M_0=\frac{\mathit{\varrho }+1}{\mathit{\varrho }}{M}_1\left(t\right)-\frac{\delta M_0}{\mathit{\varrho }}.(27)$

The instantaneous memristance of the memristor fuse depends then on the mismatch factor (ϱ).

Figure 13 shows the comparison of the circuit response for the memristor and memristor fuse using the setup shown in Figure 5. Then, for Cond-1, $V_{1_0}=1V$ and $V_{2_0}=0V$, while for Cond-2, $V_{1_0}=0V$ and $V_{2_0}=1V$ with $q_0=45.58\mu C$, $C=1\mu F$, and $R=100K\text{Ω}$ in each case. Furthermore, M_e1 and M_e2 represent memristor according to Cond-1 and Cond-2, respectively. Similarly, M_f1 and M_f2 represent the memristor fuse according to Cond-1 and Cond-2, respectively. For each case, the system evolves and eventually stabilizes when $V_1\left(t\right)=V_2\left(t\right)$.

FIGURE 13

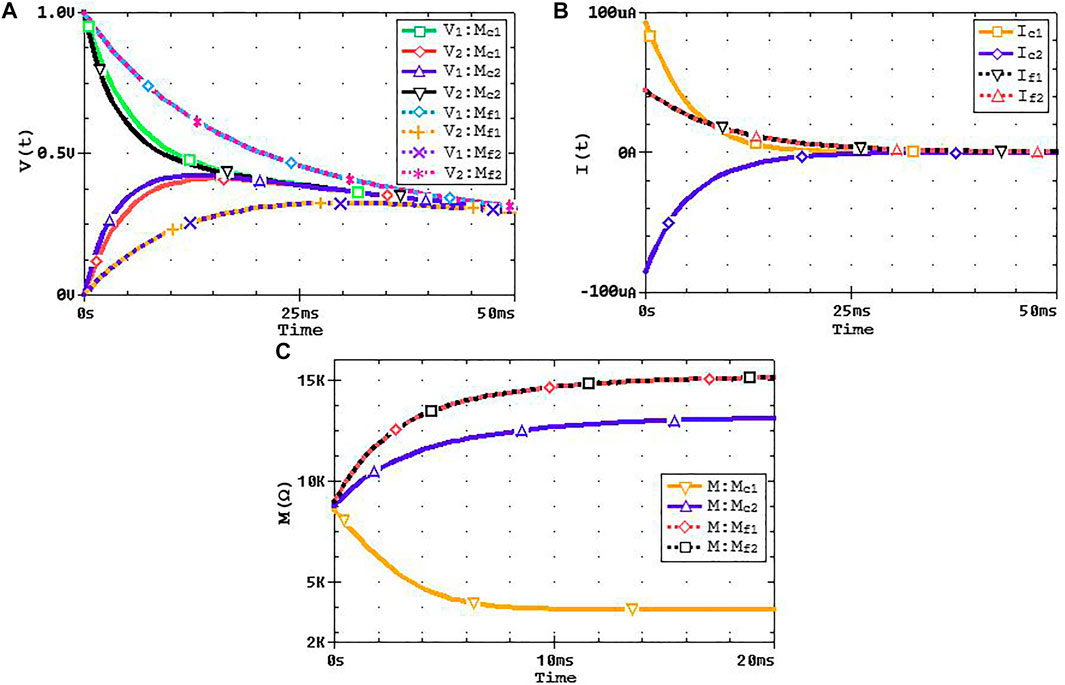
FIGURE 13. Comparing the system evolution using the circuit of Figure 5 by considering memristor (M) and then memristor fuse (M_f). Mc1 and Mc2 correspond, respectively, to a single memristor used according to Cond-1 and Cond-2, while Mf1 and Mf2 correspond, respectively, to a memristor fuse used according to Cond-1 and Cond-2. The results show the response for each case until the system stabilized: (A) the voltage evolution as $V_1\left(t\right)$ and $V_2\left(t\right)$, (B) the flowing currents through the memristor (I_e1 and I_e2 for Cond-1 and Cond-2, respectively) and memristor fuse (I_f1 and I_f2 for Cond-1 and Cond-2, respectively), and (C) memristance transition. Given the same initial condition, the results show that the memristor fuse conducts equally in both directions. For Mc1, Mc2, Mf1, and Mf2, c1, c2, f1, and f2 are subscripts denoting Cond-1 and Cond-2, accordingly.

Figure 13A shows the evolution of $V_1\left(t\right)$ and $V_2\left(t\right)$ for M_e1, M_e2, M_f1, and M_f2. The results of M_e1 and M_e2 show a shift difference during the transient state while there is no such shift between the curves of M_f1 and M_f2, showing that the memristor fuse behaves equally in both Cond-1 and Cond-2. Figure 13B shows the currents through the memristor as i_e1 and i_e2 according to Cond-1 and Cond-2, respectively, and then through the memristor fuse as i_f1 and i_f2 according to Cond-1 and Cond-2, respectively. Furthermore, the results show that no current is flowing through the memristor when $V_1\left(t\right)=V_2\left(t\right)$ as similarly observed in the analytical result of Figure 9, that is, $Y=0$ when $V_1\left(t\right)=V_2\left(t\right)$. Figure 13C shows the flowing current through the memristor and the memristor fuse. The results show the differences in the memristor responses according to Cond-1 and Cond-2, but the memristor fuse behaves indifferently in both conditions.

5 Conclusion

We introduced the application of memristor in a nonlinear network, focusing specifically on the behavior of the memristor with respect to the polarity reversal effect of the input signal. Our target is the implementation of memristor-based 2D nonlinear networks for versatile applications, such as signal processing and electronic prosthesis for a synaptic link between real neurons. Here, we investigate the interaction of a bipolar memristor between two RC cells communicating together bidirectionally. In this way, the interaction of the memristor within the network is studied qualitatively and quantitatively. We have shown from the circuit point of view and the analytical solution that the conductivity of the memristor depends on the polarity of the applied input signal, thus affecting the mobility of its charge carriers, this property being due to the intrinsic nature of the device. It is an inevitable nature of a bipolar memristor, irrespective of its device technology. Hence, the memristive effect changes according to the connection mode and the amount of current flowing through it, showing that the memristor is not a bilateral circuit element as verified by our study.

To achieve the memristive effect with symmetry, a memristor fuse is proposed. We present the detail analytical interpretation of the memristor fuse. We also authenticate the memristor fuse prior to apply it in a circuit, and the results show that the memristor fuse behaves like a standalone memristor under high input frequency. Although connecting two memristors antiserially to form a memristor fuse lets the dynamic of the two state variables system become more intricate, as well as the dynamics of the resistance switching (Serb et al. (2016)), terminals’ asymmetry is resolved as confirmed by the results shown in Figure 13. The symmetry displayed by the memristor fuse suggests it to be a promising element useful as a memristive grid in neighborhood connections and it could become an important concept for the ongoing study of our memristor-based network.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Adhikari, S. P., Changju Yang, C., Hyongsuk Kim, H., and Chua, L. O. (2012). Memristor Bridge Synapse-Based Neural Network and its Learning. IEEE Trans. Neural Netw. Learn. Syst. 23, 1426–1435. doi:10.1109/tnnls.2012.2204770

PubMed Abstract | CrossRef Full Text | Google Scholar

Adhikari, S. P., Sah, M. P., Kim, H., and Chua, L. O. (2013). Three Fingerprints of Memristor. IEEE Trans. Circuits Syst. 60, 3008–3021. doi:10.1109/tcsi.2013.2256171

CrossRef Full Text | Google Scholar

Ascoli, A., Lanza, V., Corinto, F., and Tetzlaff, R. (2015). Synchronization Conditions in Simple Memristor Neural Networks. J. Franklin Inst. 352, 3196–3220. doi:10.1016/j.jfranklin.2015.06.003

CrossRef Full Text | Google Scholar

Bao, B., Yang, Q., Zhu, D., Zhang, Y., Xu, Q., and Chen, M. (2020). Initial-induced Coexisting and Synchronous Firing Activities in Memristor Synapse-Coupled Morris-Lecar Bi-neuron Network. Nonlinear Dyn. 99, 2339–2354. doi:10.1007/s11071-019-05395-7

CrossRef Full Text | Google Scholar

Biolek, Z., Biolek, D., and Biolková, V. (2012). Computation of the Area of Memristor Pinched Hysteresis Loop. IEEE Trans. Circuits Syst. 59, 607–611. doi:10.1109/tcsii.2012.2208670

CrossRef Full Text | Google Scholar

Biolek, Z., Biolek, D., and Biolkova, V. (2009). Spice Model of Memristor with Nonlinear Dopant Drift. Radioengineering 18 (2), 210–214.

Google Scholar

Borghetti, J., Snider, G. S., Kuekes, P. J., Yang, J. J., Stewart, D. R., and Williams, R. S. (2010). 'Memristive' Switches Enable 'stateful' Logic Operations via Material Implication. Nature 464, 873–876. doi:10.1038/nature08940

PubMed Abstract | CrossRef Full Text | Google Scholar

Boyn, S., Grollier, J., Lecerf, G., Xu, B., Locatelli, N., Fusil, S., et al. (2017). Learning through Ferroelectric Domain Dynamics in Solid-State Synapses. Nat. Commun. 8, 14736–14737. doi:10.1038/ncomms14736

PubMed Abstract | CrossRef Full Text | Google Scholar

Campbell, K. A. (2017). Self-directed Channel Memristor for High Temperature Operation. Microelectronics J. 59, 10–14. doi:10.1016/j.mejo.2016.11.006

CrossRef Full Text | Google Scholar

Chu, M., Kim, B., Park, S., Hwang, H., Jeon, M., Lee, B. H., et al. (2014). Neuromorphic Hardware System for Visual Pattern Recognition with Memristor Array and Cmos Neuron. IEEE Trans. Ind. Electro. 62, 2410–2419. doi:10.1109/tie.2014.2356439

CrossRef Full Text | Google Scholar

Chua, L. (2015). Everything You Wish to Know about Memristors but Are Afraid to Ask. Radioengineering 24, 319–368. doi:10.13164/re.2015.0319

CrossRef Full Text | Google Scholar

Chua, L. (2014). If It's Pinched It's a Memristor. Semicond. Sci. Technol. 29, 104001. doi:10.1088/0268-1242/29/10/104001

CrossRef Full Text | Google Scholar

Chua, L. (1971). Memristor-the Missing Circuit Element. IEEE Trans. Circuit Theor. 18, 507–519. doi:10.1109/tct.1971.1083337

CrossRef Full Text | Google Scholar

Chua, L. O., and Sung Mo Kang, S. M. (1976). Memristive Devices and Systems. Proc. IEEE 64, 209–223. doi:10.1109/proc.1976.10092

CrossRef Full Text | Google Scholar

Comte, J. C., Marquié, P., and Bilbault, J. M. (2001). Contour Detection Based on Nonlinear Discrete Diffusion in a Cellular Nonlinear Network. Int. J. Bifurcation Chaos 11, 179–183. doi:10.1142/s0218127401002134

CrossRef Full Text | Google Scholar

Di Ventra, M., Pershin, Y. V., and Chua, L. O. (2009). Putting Memory into Circuit Elements: Memristors, Memcapacitors, and Meminductors [point of View]. Proc. IEEE 97, 1371–1372. doi:10.1109/jproc.2009.2022882

CrossRef Full Text | Google Scholar

Dongale, T. D., Desai, N. D., Khot, K. V., Volos, C. K., Bhosale, P. N., and Kamat, R. K. (2018). An Electronic Synapse Device Based on Tio2 Thin Film Memristor. J. Nanoelectronics Optoelectronics 13, 68–75. doi:10.1166/jno.2018.2297

CrossRef Full Text | Google Scholar

Duan, S., Hu, X., Dong, Z., Wang, L., and Mazumder, P. (2015). Memristor-based Cellular Nonlinear/neural Network: Design, Analysis, and Applications. IEEE Trans. Neural Netw. Learn. Syst. 26, 1202–1213. doi:10.1109/TNNLS.2014.2334701

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, S., Hu, X., Wang, L., Li, C., and Mazumder, P. (2012). Memristor-based Rram with Applications. Sci. China Inf. Sci. 55, 1446–1460. doi:10.1007/s11432-012-4572-0

CrossRef Full Text | Google Scholar

Fouda, M. E., Khatib, M. A., Mosad, A. G., and Radwan, A. G. (2013). Generalized Analysis of Symmetric and Asymmetric Memristive Two-Gate Relaxation Oscillators. IEEE Trans. Circuits Syst. 60, 2701–2708. doi:10.1109/tcsi.2013.2249172

CrossRef Full Text | Google Scholar

Gelencser, A., Prodromakis, T., Toumazou, C., and Roska, T. (2012). A Biomimetic Model of the Outer Plexiform Layer by Incorporating Memristive Devices. Phys. Rev. E 85, 041918. doi:10.1103/physreve.85.041918

CrossRef Full Text | Google Scholar

Hamdioui, S., Xie, L., Du Nguyen, H. A., Taouil, M., Bertels, K., Corporaal, H., et al. (2015). Memristor Based Computation-In-Memory Architecture for Data-Intensive Applications, 2015 Design, Automation & Test in Europe Conference & Exhibition (DATE); March 2015; Grenoble, France. IEEE, 1718–1725.

Google Scholar

Huang, H.-H., Shih, W.-C., and Lai, C.-H. (2010). Nonpolar Resistive Switching in the Pt/mgo/pt Nonvolatile Memory Device. Appl. Phys. Lett. 96, 193505. doi:10.1063/1.3429024

CrossRef Full Text | Google Scholar

Isah, A., Nguetcho, A. S. T., Binczak, S., and Bilbault, J. M. (2020a). Memristor Dynamics Involved in Cells Communication for a 2D Non‐linear Network. IET Signal. Process. 14, 427–434. doi:10.1049/iet-spr.2020.0136

CrossRef Full Text | Google Scholar

Isah, A., Nguetcho, A. T., Binczak, S., and Bilbault, J. (2020b). Dynamics of a Charge-Controlled Memristor in Master–Slave Coupling. Electro. Lett. 56, 168. doi:10.1049/el.2019.3322

CrossRef Full Text | Google Scholar

Jiang, F., and Shi, B. E. (2009). The Memristive Grid Outperforms the Resistive Grid for Edge Preserving Smoothing, 2009 European Conference on Circuit Theory and Design (IEEE); Aug. 2009; Antalya, Turkey. doi:10.1109/ECCTD.2009.5274947IEEE, 181–184.

CrossRef Full Text | Google Scholar

Jo, S. H., Chang, T., Ebong, I., Bhadviya, B. B., Mazumder, P., and Lu, W. (2010). Nanoscale Memristor Device as Synapse in Neuromorphic Systems. Nano Lett. 10, 1297–1301. doi:10.1021/nl904092h

PubMed Abstract | CrossRef Full Text | Google Scholar

Joglekar, Y. N., and Wolf, S. J. (2009). The Elusive Memristor: Properties of Basic Electrical Circuits. Eur. J. Phys. 30, 661–675. doi:10.1088/0143-0807/30/4/001

CrossRef Full Text | Google Scholar

Kim, H., Sah, M. P., Yang, C., Roska, T., and Chua, L. O. (2011). Memristor Bridge Synapses, Proceedings of the IEEE, 100. IEEE, 2061–2070. doi:10.1109/JPROC.2011.2166749

CrossRef Full Text | Google Scholar

Krzysteczko, P., Reiss, G., and Thomas, A. (2009). Memristive Switching of Mgo Based Magnetic Tunnel Junctions. Appl. Phys. Lett. 95, 112508. doi:10.1063/1.3224193

CrossRef Full Text | Google Scholar

Lecerf, G., Tomas, J., Boyn, S., Girod, S., Mangalore, A., Grollier, J., et al. (2014). Silicon Neuron Dedicated to Memristive Spiking Neural Networks, 2014 IEEE International Symposium on Circuits and Systems (ISCAS); June 2014; Melbourne, VIC, Australia. doi:10.1109/ISCAS.2014.6865448IEEE, 1568–1571.

CrossRef Full Text | Google Scholar

Li, Y., Zhong, Y., Zhang, J., Xu, L., Wang, Q., Sun, H., et al. (2014). Activity-dependent Synaptic Plasticity of a Chalcogenide Electronic Synapse for Neuromorphic Systems. Sci. Rep. 4, 4906. doi:10.1038/srep04906

PubMed Abstract | CrossRef Full Text | Google Scholar

Lim, C. K. K., Gelencser, A., and Prodromakis, T. (2019). Computing Image and Motion with 3-d Memristive Grids. Handbook of Memristor. Networks (Springer), 1177–1210.

CrossRef Full Text | Google Scholar

Linn, E., Rosezin, R., Kügeler, C., and Waser, R. (2010). Complementary Resistive Switches for Passive Nanocrossbar Memories. Nat. Mater 9, 403–406. doi:10.1038/nmat2748

PubMed Abstract | CrossRef Full Text | Google Scholar

Marani, R., Gelao, G., and Perri, A. G. (2015). A Review on Memristor Applications. arXiv preprint arXiv:1506.06899

Google Scholar

Mazumder, P., Kang, S. M., and Waser, R. (2012). Memristors: Devices, Models, and Applications [Scanning the Issue]. Proc. IEEE 100, 1911–1919. doi:10.1109/jproc.2012.2190812

CrossRef Full Text | Google Scholar

Muthuswamy, B. (2010). Implementing Memristor Based Chaotic Circuits. Int. J. Bifurcation Chaos 20, 1335–1350. doi:10.1142/s0218127410026514

CrossRef Full Text | Google Scholar

Paris, A., and Taioli, S. (2016). Multiscale Investigation of Oxygen Vacancies in TiO2 Anatase and Their Role in Memristor's Behavior. J. Phys. Chem. C 120, 22045–22053. doi:10.1021/acs.jpcc.6b07196

CrossRef Full Text | Google Scholar

Pershin, Y. V., and Di Ventra, M. (2011). Solving Mazes with Memristors: A Massively Parallel Approach. Phys. Rev. E 84, 046703. doi:10.1103/physreve.84.046703

CrossRef Full Text | Google Scholar

Pickett, M. D., Strukov, D. B., Borghetti, J. L., Yang, J. J., Snider, G. S., Stewart, D. R., et al. (2009). Switching Dynamics in Titanium Dioxide Memristive Devices. J. Appl. Phys. 106, 074508. doi:10.1063/1.3236506

CrossRef Full Text | Google Scholar

Prezioso, M., Bayat, F. M., Hoskins, B., Likharev, K., and Strukov, D. (2016). Self-adaptive Spike-time-dependent Plasticity of Metal-Oxide Memristors. Scientific Rep. 6, 1–6. doi:10.1038/srep21331

CrossRef Full Text | Google Scholar

Prodromakis, T., and Toumazou, C. (2010). A Review on Memristive Devices and Applications, 2010 17th IEEE International Conference on Electronics, Circuits and Systems; Dec. 2010; Athens, Greece. IEEE, 934–937. doi:10.1109/ICECS.2010.5724666

CrossRef Full Text | Google Scholar

Saïghi, S., Mayr, C. G., Serrano-Gotarredona, T., Schmidt, H., Lecerf, G., Tomas, J., et al. (2015). Plasticity in Memristive Devices for Spiking Neural Networks. Front. Neurosci. 9, 51. doi:10.3389/fnins.2015.00051

PubMed Abstract | CrossRef Full Text | Google Scholar

Sarmiento-Reyes, A., and Rodríguez-Velásquez, Y. (2018). Maze-solving with a Memristive Grid of Charge-Controlled Memristors (LASCAS), 2018 IEEE 9th Latin American Symposium on Circuits & Systems; Feb. 2018; Puerto Vallarta, Mexico. (IEEE), 1–4. doi:10.1109/LASCAS.2018.8399973

CrossRef Full Text | Google Scholar

Serb, A., Khiat, A., and Prodromakis, T. (2016). Practical Demonstration of a Memristive Fuse. arXiv preprint arXiv:1609.02410

Google Scholar

Shin, S., Kim, K., and Kang, S.-M. (2010). Memristor Applications for Programmable Analog IcsIEEE Transactions on Nanotechnology, 10. (IEEE), 266–274. doi:10.1109/TNANO.2009.2038610

CrossRef Full Text | Google Scholar

Simmons, J. G. (1971). Conduction in Thin Dielectric Films. J. Phys. D: Appl. Phys. 4, 613–657. doi:10.1088/0022-3727/4/5/202

CrossRef Full Text | Google Scholar

Simmons, J. G. (1963a). Electric Tunnel Effect between Dissimilar Electrodes Separated by a Thin Insulating Film. J. Appl. Phys. 34, 2581–2590. doi:10.1063/1.1729774

CrossRef Full Text | Google Scholar

Simmons, J. G. (1963b). Generalized Formula for the Electric Tunnel Effect between Similar Electrodes Separated by a Thin Insulating Film. J. Appl. Phys. 34, 1793–1803. doi:10.1063/1.1702682

CrossRef Full Text | Google Scholar

Stanley Williams, R. (2013). How We Found the Missing Memristor, Chaos, CNN, Memristors and Beyond: A Festschrift for Leon Chua With DVD-ROM, composed by Eleonora Bilotta (World Scientific). (IEEE), 483–489. doi:10.1109/MSPEC.2008.4687366

CrossRef Full Text | Google Scholar

Strachan, J. P., Strukov, D. B., Borghetti, J., Joshua Yang, J., Medeiros-Ribeiro, G., and Stanley Williams, R. (2011). The Switching Location of a Bipolar Memristor: Chemical, thermal and Structural Mapping. Nanotechnology 22, 254015. doi:10.1088/0957-4484/22/25/254015

PubMed Abstract | CrossRef Full Text | Google Scholar

Strukov, D. B., Snider, G. S., Stewart, D. R., and Williams, R. S. (2008). The Missing Memristor Found. nature 453, 80–83. doi:10.1038/nature06932

PubMed Abstract | CrossRef Full Text | Google Scholar

Teixeira, J. M., Ventura, J., Fermento, R., Araujo, J. P., Sousa, J. B., Wisniowski, P., et al. (2009). Electroforming, Magnetic and Resistive Switching in Mgo-Based Tunnel Junctions. J. Phys. D: Appl. Phys. 42, 105407. doi:10.1088/0022-3727/42/10/105407

CrossRef Full Text | Google Scholar

Thomas, A. (2013). Memristor-based Neural Networks. J. Phys. D: Appl. Phys. 46, 093001. doi:10.1088/0022-3727/46/9/093001

CrossRef Full Text | Google Scholar

Volos, C. K., Kyprianidis, I., Stouboulos, I., Tlelo-Cuautle, E., and Vaidyanathan, S. (2015). Memristor: A New Concept in Synchronization of Coupled Neuromorphic Circuits. J. Eng. Sci. Techn. Rev. 8. doi:10.25103/jestr.082.21

CrossRef Full Text | Google Scholar

Wang, C., He, W., Tong, Y., and Zhao, R. (2016). Investigation and Manipulation of Different Analog Behaviors of Memristor as Electronic Synapse for Neuromorphic Applications. Sci. Rep. 6, 22970. doi:10.1038/srep22970

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Joshi, S., Savel’ev, S. E., Jiang, H., Midya, R., Lin, P., et al. (2017). Memristors with Diffusive Dynamics as Synaptic Emulators for Neuromorphic Computing. Nat. Mater 16, 101–108. doi:10.1038/nmat4756

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, F., Zhang, J., Fang, T., Huang, S., and Wang, M. (2018). Synchronous Dynamics in Neural System Coupled with Memristive Synapse. Nonlinear Dyn. 92, 1395–1402. doi:10.1007/s11071-018-4134-0

CrossRef Full Text | Google Scholar

Xu Ya-Ming, Y.-M., Wang Li-Dan, L.-D., and Duan Shu-Kai, S.-K. (2016). A Memristor-Based Chaotic System and its Field Programmable Gate Array Implementation. wlxb 65, 120503. doi:10.7498/aps.65.120503

CrossRef Full Text | Google Scholar

Yakopcic, C., Hasan, R., and Taha, T. M. (2018). Flexible Memristor Based Neuromorphic System for Implementing Multi-Layer Neural Network Algorithms. Int. J. Parallel, Emergent Distributed Syst. 33, 408–429. doi:10.1080/17445760.2017.1321761

CrossRef Full Text | Google Scholar

Yang, C., and Kim, H. (2016). Linearized Programming of Memristors for Artificial Neuro-Sensor Signal Processing. Sensors 16, 1320. doi:10.3390/s16081320

CrossRef Full Text | Google Scholar

Yang, J. J., Pickett, M. D., Li, X., Ohlberg, D. A. A., Stewart, D. R., and Williams, R. S. (2008). Memristive Switching Mechanism for Metal/oxide/metal Nanodevices. Nat. Nanotech 3, 429–433. doi:10.1038/nnano.2008.160

PubMed Abstract | CrossRef Full Text | Google Scholar

Yildirim, M., Babacan, Y., and Kacar, F. (2018). Memristive Retinomorphic Grid Architecture Removing Noise and Preserving Edge. AEU - Int. J. Electro. Commun. 97, 38–44. doi:10.1016/j.aeue.2018.10.001

CrossRef Full Text | Google Scholar

Yin, L., Cheng, R., Wang, Z., Wang, F., Sendeku, M. G., Wen, Y., et al. (2020). Two-dimensional Unipolar Memristors with Logic and Memory Functions. Nano Lett. 20, 4144–4152. doi:10.1021/acs.nanolett.0c00002

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoshida, C., Kurasawa, M., Lee, Y. M., Aoki, M., and Sugiyama, Y. (2008). Unipolar Resistive Switching in CoFeB∕MgO∕CoFeB Magnetic Tunnel junction. Appl. Phys. Lett. 92, 113508. doi:10.1063/1.2898514

CrossRef Full Text | Google Scholar

Zhang, J., and Liao, X. (2017). Synchronization and Chaos in Coupled Memristor-Based Fitzhugh-Nagumo Circuits with Memristor Synapse. AEU - Int. J. Electro. Commun. 75, 82–90. doi:10.1016/j.aeue.2017.03.003

CrossRef Full Text | Google Scholar