Extreme (and non-extreme) punishments in sender-receiver games with judicial error: An experimental investigation

Fong, Meng-Jhang; Wang, Joseph Tao-yi

doi:10.3389/frbhe.2023.1096598

ORIGINAL RESEARCH article

Front. Behav. Econ., 03 March 2023

Sec. Behavioral Microfoundations

Volume 2 - 2023 | https://doi.org/10.3389/frbhe.2023.1096598

This article is part of the Research Topic What do we say? The content of communication in strategic interactions View all 5 articles

Extreme (and non-extreme) punishments in sender-receiver games with judicial error: An experimental investigation

$\nMeng-Jhang Fong$ Meng-Jhang Fong¹

Joseph Tao-yi Wang²^*

¹Division of the Humanities and Social Sciences, California Institute of Technology, Pasadena, CA, United States
²Department of Economics, National Taiwan University, Taipei, Taiwan

In many real world situations, decision-makers have the opportunity to punish informed senders for their biased recommendations, while lie-detection is far from perfect. Hence, we conduct an experiment which incorporates ex post punishment and monitoring uncertainty into the discrete sender-receiver game first introduced by Crawford and Sobel, where a knowledgeable sender sends a cheap-talk message to a receiver who determines a policy action. After taking this action, the receiver observes a noisy signal of the true state and can impose a costly punishment on the sender. We vary the strength of punishment from mild (nominal), strong (deterrent) to extreme (potential of losing everything), and vary receiver's signal uncertainty when punishment is extreme. We find that receivers punish less as the strength of punishment increases, which suggests people care more about wrongly punishing innocent senders harsher than not being able to hand liars harsher punishments they deserve. More importantly, the opportunity of punishment encourages receivers to follow senders more and thus improves overall information transmission and utilization, even though senders need not exaggerate less.

1. Introduction

In the decision-making process, people collect information and seek advice for better outcomes. Lawmakers gather policy suggestions from experts for diverse issues. Individuals also acquire information from advisers for decisions on choosing one's major, school, or job. Consumers in need of credence goods (Darby and Karni, 1973; Dulleck and Kerschbamer, 2006), such as medical treatments (Hughes and Yule, 1992; Gruber and Owings, 1996; Gruber et al., 1999) and repair services (Wolinsky, 1993, 1995; Hubbard, 1998; Kerschbamer et al., 2016), know how their own utility are shaped but do not know what meets their need, and rely on professional advice or services from suppliers. Nevertheless, conflicts of interest usually exist between experts and decision-makers, which could lead to lying and exaggeration. The strategic communication can thus cause inefficiency in overall information transmission and utilization, reducing the quality of decisions and even social welfare. For example, Balafoutas et al. (2013) report that passengers tend to be overcharged or taken on unnecessary detours when taking taxi rides in unfamiliar towns. Johnson and Rehavi (2016) show that non-physicians are more likely to receive C-sections than physicians when delivery, while Schneider (2012) records widespread under- and overtreatment in vehicle repair.

As shown by the above example, it might be natural to evaluate the impact of such information asymmetry by focusing on the behavior of informed agents. The amount of overall information transmission, however, depends on message-senders' interaction with receivers who make decisions for both players. A brilliant receiver who perfectly anticipates exaggeration could discount the message and still make the best choice accordingly. In contrast, when a suspicious receiver encounters a truth-telling sender, informative advice could be mis-perceived as a lie and ignored. Furthermore, a sender may trick a skeptic into taking the sender-preferred action by strategically telling the truth (Sutter, 2009). In short, decision-makers' behavior is (also) a vital factor in overall information transmission and worth investigating.

Moreover, in many real world cases, receivers are able to punish senders after observing the outcome. Punishment plays a prominent role in enforcing discipline and maintaining social order. In particular, ex post punishment deters self-interested humans from hurting others (Fehr and Gachter, 2000). The strength of punishment could vary from verbal reprimanding (Ellingsen and Johannesson, 2008; Xiao and Houser, 2009; Poulsen and Zevallos-Porles, 2019) to legal action. Occasionally, an expert's reputation and career could be completely destroyed, an extreme sanction for lying. For example, star Wall Street research analyst Henry Blodget was banned from the securities industry and fined $4 million in 2003 for exaggerating the values of Internet stocks in public reports while privately viewing them as “POS” (U.S. Securities and Exchange Commission, 2003). Just as punishment can facilitate cooperation among humans, punishment could also deter senders from lying and encourage receivers to follow sender messages, improving overall information transmission and utilization.

Nevertheless, perfect monitoring is rarely available, leading to potential punishment of innocent people. The unjust punishments can directly reduce people's compliance with social norms. In fact, Ambrus and Greiner (2012) find that subjects in a public good game are likely to lower their contributions after being wrongly punished in the previous round. Also, monitoring uncertainty can discourage people from imposing punishments, and sanctions could thus lose the power of deterrence. As a result, the effectiveness of punishment under judicial errors becomes an important issue, and if left unaddressed, can be extremely costly to the society.

Several questions arise from the above discussion: How do individuals, especially receivers, form their strategies under different strength of punishment? Are people still willing to punish under high error rates (holding other things equal)? Anticipating this, would potential liars change their behavior? Unfortunately, conducting empirical studies is extremely difficult, if not impossible, since distinguishing the innocent from guilty suspects is not easy in reality, making it difficult to estimate (let alone manipulate) the error rate of punishment. Additionally, decisions to perform undesirable behavior that leads to severe punishment are usually unobservable. Employing laboratory experiments can fill this gap. Thus, we construct an environment of potential liars and victims, and incorporate costly punishment into the experiment.

Theoretically, the seminal paper of Crawford and Sobel (1982) models a sender-receiver game in which one informed agent (sender) communicates with another uninformed decision-maker (receiver) via cheap talk, but has the incentive to overstate the true state. We design a fixed-role, random-matched experiment on discrete sender-receiver games. In the Baseline Game, a sender knows the true state s (= 1, 3, or 5) and sends a message m (= 1, 3, or 5). Observing the message, a receiver takes an action a (= 1, 2, 3, 4, or 5). Only the receiver's action (and state) determines both players' payoffs, so the sender's message is cheap talk. Bias b (= 0 or 2) captures the sender's preference bias. A sender maximizes her payoff if an action is equal to s+b, while a receiver prefers the action equivalent to the true state. Thus, when bias b = 2, senders have incentives to exaggerate.

The Punishment Game incorporates ex post punishment into the Baseline Game. After taking an action, the receiver observes a noisy signal ŝ, which is correlated with but not exactly equal to the true state s, and can punish the sender at a cost. We vary the scale of the uncertainty in receivers' signal and the strength of punishment across treatments. Most importantly, corresponding to extreme punishment in reality, we attempt to implement the most extreme penalty possible in the laboratory, namely, confiscation of the entire payoff, including both the current round and all other rounds. Note that this penalty is extreme not only in the absolute sense, but also in the relative sense due to the negative spill-over to all other rounds.

Our experimental results show that even though punishment is costly and ex post, it is still administered when available, but less frequently when more severe. What is more, when punishment is introduced, receivers follow messages more even though senders need not exaggerate less. Overall, more information is transmitted and utilized as shown in the increase in correlation between states and actions. This is due to receiver adoption, as shown in the increase in correlation between messages and actions. Thirdly, breaking down by treatment, extreme punishment deters lying when judicial error is low, but not when the error rate is large. The severity of punishment increases sender exaggeration and receiver adoption, but this effect diminishes as punishment becomes extreme. This result indicates that heavier punishments have a diminishing trust-encouraging effect on receivers, but create a backlash and induce an (also diminishing) effect on sender exaggeration.

We also employ a level-k model with “spike-logit” error structure (Costa-Gomes and Crawford, 2006) to classify players into different behavioral types. Based on behavior in either the Baseline Game or the Punishment Game, results from the level-k classification are consistent with those in the comparative static analysis. However, many players behave consistently across the two games, indicating a limited impact of punishment on their decisions. Last, we asked subjects their preferences over different institutions (incentivized by drawing six subjects to play it out in a follow-up experiment), and 70.6% of the subjects choose to play the Baseline Game, mainly because players prefer the game they received higher earnings.

Sender-receiver games are regularly embedded in credence goods transactions, so our results shed light on these markets when consumers are able to punish sellers ex post, say, by ruining a seller's reputation. In particular, suppliers are like senders, knowing the best decision for their opponents but have motivations for exaggerating, such as overcharging and offering overtreatment. In fact, Angelova and Regner (2013) and Danilov et al. (2013) employ sender-receiver game experiments for investigating the impact of team incentives and voluntary payments, respectively, on the quality of financial advice.

In addition, our results fill the gap of studies on extreme punishment, which negatively impacts payoffs in not only the round it occurred, but all other rounds as well.¹ One exception is the work of Eckel et al. (2022), which designed an extreme intergroup punishment to analyze revenge behavior under asymmetry of political power. Their “extreme punishment” is more related to extreme sacrifice, such as suicide bombing, instead of an extreme penalty imposed on a suspect. Notice that players in Eckel et al. (2022) will lose their earnings from all rounds, in contrast to punishment in the setting of ultimatum games, which (by construction) is “extreme” for that round (Bolton and Zwick, 1995; Anbarcı et al., 2015) or even the entire one-shot game experiment (Gehrig et al., 2007; Güth and Kirchkamp, 2012). In line with Eckel et al. (2022), our senders who received extreme punishment in one round will (likely) lose their earnings in all other rounds. In this sense, our extreme punishment has a spillover effect across multiple rounds and is relatively more extreme than earning zero in a single round alone.

The remainder of this paper proceeds as follows. Section 1.1 reviews related literature. Section 2.1 describes the theoretical model and prediction of the sender-receiver game. Section 2.2 presents the experimental design and procedure. Section 3 analyzes the data. Section 4 concludes.

1.1. Related literature

Since the experimental paper of Fehr and Gachter (2000), ex post punishment has been widely investigated in public goods games (PGG). For example, Grechenig et al. (2010) found that ex post punishment is still used when monitoring uncertainty is huge, but cooperation cannot be sustained. Ambrus and Greiner (2012) showed a “U-shaped” relationship of net payoffs between no, medium, and strong punishment when monitoring is imperfect. With third-party (cost-free) punishment, Dickson et al. (2009) showed the detrimental impact of “Type I errors” (wrongly accusatory signals). In contrast, we consider the impact of punishment severity under imperfect monitoring in sender-receiver games where lying is well-defined.

Since Crawford and Sobel (1982) developed the model, the sender-receiver game and its information transmission structure have been extensively studied under controlled experiments (Dickhaut et al., 1995; Cai and Wang, 2006; Wang et al., 2010). For example, Hsieh and Wang (2016) compared sender behavior under different complexity (3 vs. 5 states), while Jin et al. (2021) allowed senders to either tell the truth or remain silent.² Also, senders' social preferences, lying aversion, and preferences for truth-telling have been extensively explored in laboratories under a simpler binary-state sender-receiver game (Gneezy, 2005; Sánchez-Pagés and Vorsatz, 2007, 2009; Hurkens and Kartik, 2009; Peeters et al., 2013, 2015).³ Under perfect monitoring, Sánchez-Pagés and Vorsatz (2007, 2009), and Peeters et al. (2013) generated costly punishment in a 2 × 2 sender-receiver game by allowing receivers to reject the final allocation and found trust-encouraging effects of punishment.⁴ This paper introduces ex post punishment with monitoring uncertainty to the Crawford-Sobel framework with many states and different lie sizes.

In contrast to letting receivers always learn the true state ex post, Behnk et al. (2014), Greenberg et al. (2014), and Poulsen and Zevallos-Porles (2019) studied the impact of withholding such information on cheap talk messages but found mixed evidence—senders did not necessarily exaggerate more, neither did receivers follow the message less. Since ex post verification might be too weak to deter exaggeration, receivers in this paper always learn the truth, but have the option to implement more severe and publicly known punishments. When punishment is available, receivers follow sender messages more, though senders need not exaggerate less.

Experimentalists have also studied punishment with possible wrongful convictions in other one-on-one criminal-victim relationships. In “theft games” (inverse dictator games), Type I errors reduced deterrence of exogenous punishment (Rizzolli and Stanca, 2012) and third party's willingness to punish (Feess et al., 2018).⁵ This paper employs the sender-receiver game framework in which sender's inflated message could be discounted by the receiver instead of being taken at face value and punished later.

2. Materials and methods

2.1. The sender-receiver game

Our experiments consist of two parts: the Baseline Game, which is a discrete sender-receiver game similar to what is studied in the experimental cheap talk literature testing Crawford and Sobel (1982), and the Punishment Game, which incorporates a punishment stage into the sender-receiver game.

At the beginning of the Baseline Game, subjects are randomly assigned to be senders or receivers. Senders and receivers are randomly matched to play a cheap talk game which Crawford and Sobel (1982) call strategic information transmission. In the beginning of the game, nature randomly draws with equal probability the true state s∈S = {1, 3, 5}. The sender is informed of s, while the receiver only knows the prior distribution. Observing the true state, the sender then sends a message m∈M = {1, 3, 5} to the receiver. After receiving the message, the receiver takes an action a∈A = {1, 2, 3, 4, 5}. The true state and the receiver's action, but not the sender's message, determine the payoffs of players given by $u_{S} = 110 - 20 {(| s + b - a |)}^{1.4} and u_{R} = 110 - 20 {(| s - a |)}^{1.4}$ where b∈B = {0, 2} is the sender's bias, which captures the preference difference between the two players, and u_S and u_R denote the sender's and the receiver's payoffs, respectively. The realization of b is predetermined by a given probability distribution, which is unknown to players. Thus, the sender prefers an action equal to (s+b), while the receiver would like to choose an action matching the true state to maximize profit. Both the sender's bias and the payoff functions are public information.

The structure of the Punishment Game is the same as the Baseline Game except for one modification: After taking an action, the receiver observes a noisy signal ŝ of the true state and can impose a costly monetary punishment on the sender. The signal is noisy: when s is 3 or 5, the probability of ŝ being lower than s is q∈(0, 1). Specifically, when s is 3, the probability of ŝ being 1 is q, and when s is 5, both the probabilities of ŝ being 1 and being 3 are equal to $\frac{q}{2}$ .

There exist competing theoretical predictions of subject behavior in the Baseline Game. On the one hand, when the sender's bias is large (b = 2), the unique and most informative equilibrium is the babbling equilibrium where senders send uninformative messages and receivers take actions based on prior knowledge and always choose a = 3 (Crawford and Sobel, 1982). Note that ex post punishment will not affect the behavior predictions in the Punishment Game if all players are self-interested payoff-maximizers because receivers will then not use any costly punishment and senders anticipate this by backward induction. On the other hand, the level-k model for the sender-receiver game (Crawford, 2003; Cai and Wang, 2006; Kawagoe and Takizawa, 2009; Wang et al., 2010) predicts the existence of players with different levels of bounded rationality: L0 players, who are the least sophisticated, are composed of truth-tellers and message-followers (who are actually playing best response against truth-tellers). L1 senders best respond to message-followers (i.e., L0 receivers) by exaggerating the true state and send s+b, and L1 receivers best respond to L1 senders by discounting the message accordingly. Applying the same logic, L(n+1) senders and L(n+1) receivers best respond to L(n) receivers and L(n+1) senders, respectively (for all n∈ℕ). In addition, the sophisticated (SOPH) types best respond to the empirical distribution of their opponents' actions. Table 1 summarizes the behavioral predictions in detail.

TABLE 1

Table 1. Behavioral predictions of the level-k model.

2.2. The experiment

We ran 30 rounds of the Baseline Game, followed by 30 rounds of the Punishment Game. Before the real rounds, we also ran 3 (1) practice round(s) for the Baseline (Punishment) Game to let subjects be familiar with the experimental protocol. We adopted the random payment scheme, so the subjects earned 30 rounds of payoff from either the Baseline Game or Punishment Game. At the beginning of each session, the subject's role was randomly determined and fixed for the whole session. Then, three senders and three receivers were grouped to form a matching group. For each round, senders and receivers of the same matching group were randomly matched into pairs with no immediate rematch allowed, and each pair's sender bias b = 0, 2 was drawn with probabilities 0.2 and 0.8, respectively.

We implemented the Baseline Game described above with neutral labels replacing “true state” and “sender bias” with “secret number” and “difference,” respectively. At the end of each round, when subjects were informed of the results, receivers saw a noisy signal (instead of the “secret number”) and the corresponding payoff calculated assuming the signal was accurate. The error rate of the signal was q = 20% or 5%, which was publicly announced. In addition, we measured receivers' beliefs regarding senders' propensity to lie by eliciting receiver's estimate of the percentage of rounds in which the message was inconsistent with the true state, both before and after the 30 rounds of the Baseline Game. These belief elicitations are incentivized by awarded 50 Experimental Standard Currency (ESC) if the answers are within 2% of the correct percentage.

We implemented the Punishment Game as a Baseline Game plus an extra punishment stage. The punishment differed across treatments. Under error rate q = 20%, we varied the strength of punishment from minimum (20% Mild), substantial (20% Strong), to extreme (20% Extreme). Since the main focus is the extreme punishment, we also included a 5% Extreme treatment (q = 5%) as a benchmark with little uncertainty about the outcome. In the 20% Mild (and 20% Strong) treatments, each round a receiver could choose to pay 4 (and 12 ESC) in the punishment stage to deduct 18 (and 54 ESC) from the opponent, yielding a price of sanction fixed at 1:4.5. A penalty of 54 ESC is strong in the sense that it is greater than the maximum gain from exaggeration, 53 ESC, since if a = s+b, a sender could earn 110 ESC while a sender could earn 57 ESC when a = s. However, it is not actually deterrent (expected-wise) unless the punishment rate is close to 100%.

For the extreme punishment, we implemented the most extreme penalty possible in the laboratory, namely confiscation of the entire payoff and leaving the subject with only the show-up fee. However, to use neutral language and incentivize the subjects to complete the experiment, we employed a “number-guessing” procedure: A sender would have to “guess the number to collect the payment.” To do so, the receiver would have to sacrifice 10 ESC from each round (i.e., pay 300 ESC in total) and the opponent would earn nothing unless correctly guessing a die-roll at the end of the experiment. To prevent abuse of extreme punishment, we allowed a receiver to exercise it at most three times. In all sessions, no receivers used it more than twice, so this limit was non-binding. When required to guess the number more than once, say k times, a sender must correctly guess k die-rolls to collect payment, so the probability of a sender earning zero is $1 - {(\frac{1}{6})}^{k}$ . The tiny possibility for a criminal to “escape” the punishment resembles similar situation such as amnesty in the real world. The price of extreme punishment was set based on senders' average payoff in our pilots.⁶ As in the Baseline Game, both before and after the 30 rounds of the Punishment Game, we asked receivers to estimate the percentage of rounds in which the message was inconsistent with the true state. We also asked senders to estimate the percentage of rounds in which the receivers punished senders when seeing that the message was inconsistent with the signal of true state. These belief elicitations are incentivized by awarded 50 ESC if the answers are within 2% of the correct percentage.

At the end of the experiment, we added two additional tasks. First, the receivers were shown the result of one of the rounds in which they used the punishment, chosen randomly, and asked if they want to see the true state.⁷ Observing their decisions, we can examine if receivers intentionally ignored the (potential) errors they had made. Second, we asked the players to choose between the Baseline Game and Punishment Game if they were to play again, in order to evaluate how their experience in the experiment may affect their preferences for punishment when monitoring uncertainty is high. To incentivize their choices, six subjects of the same treatment were randomly invited to participate in a follow-up experiment, in which their roles would be randomly decided again at the beginning. The follow-up experiment replicated one of the two games, depending on the simple majority of the six participants' decisions. Ties were broken randomly.

We conducted 8 experimental sessions between February and April 2016 at the Taiwan Social Sciences Experiment Laboratory (TASSEL) at National Taiwan University (NTU). Each session lasted about 160 min, and all participants were NTU undergraduate and graduate students recruited via the online recruitment system of TASSEL. Except for one 18-participant session, each session had 12 subjects and thus 102 subjects in total. Each treatment had at least 4 matching groups, which shared the same parameters (state, bias, and pairing). Within each treatment, the same parameters of the Baseline Game were reused in the Punishment Game, but for a different matching group. The 20% Strong treatment had a fifth matching with new parameters freshly drawn. The subjects interacted anonymously through networked computers. The experiment was programmed (in Chinese) with the software zTree (Fischbacher, 2007). Paper experimental instructions were given to participants and read aloud. The exchange rate is 4 ESC for NT$1. At the time of the experiment, the foreign exchange rate was around NT$33 = US$1. Including a show-up fee of NT$100, the earnings in experiments ranged between NT$100 and NT$871, with an average of NT$624.

3. Results

3.1. Aggregate behavior

We first pool our Baseline Game results across all treatments and compare them with the most informative equilibrium. Focusing on b = 2, the zero-information transmission prediction of the babbling equilibrium does not hold (see Table 2); instead, we observe overcommunication (Dickhaut et al., 1995; Blume et al., 1998, 2001; Cai and Wang, 2006; Sánchez-Pagés and Vorsatz, 2007, 2009; Wang et al., 2010; Hsieh and Wang, 2016; Vespa and Wilson, 2016; Battaglini et al., 2019). The correlation between state and message, Corr(s, m), and the correlation between message and action, Corr(m, a), in the Baseline Game range between 0.51 and 0.64, and the correlation between state and action, Corr(s, a), is around 0.35, which are all statistically far above 0.⁸ In contrast, the babbling equilibrium seems to predict subject's average payoffs well, consistent with the above literature. In the Baseline Game, despite the diversity of average sender payoffs in different sessions (ranging between 33 and 58), the average for all senders (45.75) is very close to equilibrium prediction (46.00). Average receiver payoffs, on the other hand, are around the prediction (74.67) for all treatments.

TABLE 2

Table 2. Correlations between states, messages, and actions (b = 2).

Comparing the aggregate data for b = 2 in the Baseline and Punishment Game, we summarize our main findings in Result 1 and Result 2. Result 1. Punishment is used when available, but less frequent as it becomes more extreme.

Figure 1 displays the raw data of receiver signals (ŝ), messages, and punishments in the Punishment Game. The receiver signals {1, 3, 5} correspond to the three rows, and the sender messages {1, 3, 5} correspond to the three columns. The (stacked) bar chart within each signal-message cell reports the frequency of that receiver signal and message, with the light gray fraction showing the punishment frequency.

FIGURE 1

Figure 1. Outcome information and punishment.

Table 3 summarizes receivers' tendency to punish senders, which is measured by the frequency of punishing conditional on ŝ≠m, PunishRate= (the number of rounds punishing)/(the number of rounds seeing signal unequal to the message). The frequency of punishing is larger than 0 in all treatments. Further, receivers indeed view the reduction of payoffs as punishment since very few receivers punish senders when senders appear to tell the truth (4 of 553 rounds). In contrast, when senders are potentially lying (ŝ≠m), we observe considerable use if punishment is mild. The punishment rate, however, decreases monotonically as the strength of punishment increases, given the error rate q = 20%. In 20% Mild, receivers punish senders in one quarter of the rounds when observing ŝ≠m. The frequency of punishing declines to 12 percent in 20% Strong, and drops to 3 percent in 20% Extreme. Also, compared to 20% Extreme, the lower error rate in 5% Extreme leads to a positive but small rise from 3% to 5% in the PunishRate. Overall, the trend of PunishRate indicates that receivers, when the error rate is substantial, are less willing to punish as its intensity increases. In fact, the punishment rates conditional on various “severity” of lie show that receivers observing a larger discrepancy (|ŝ−m| = 4) punish their opponents significantly more often (46/191 vs. 32/487, p < 0.001, proportion test) compared to those who observe a smaller one (|ŝ−m| = 2). Breaking down by treatments, the effect comes from 20% Mild (19/44 vs. 20/112, p = 0.001) and 20% Strong (24/73 vs. 3/151, p < 0.001) since the extreme punishment was rarely used. This result is consistent with the finding that people care about not only outcomes but also lying behavior itself (Brandts and Charness, 2003). When the potential loss induced by a lie is larger (which implies a more substantial cost from false exoneration), receivers are more willing to enforce punishment (at the risk of punishing the innocent).

TABLE 3

Table 3. Receivers' tendency to punish: PunishRate (ŝ ≠ m).

Senders' pre-game and post-game estimations of overall PunishRate (including b = 0), PriorPredict(PR) and PostPredict(PR), are also provided in Table 3. The positive PriorPredict(PR) indicates that overall senders expect that punishment is used when available. Interestingly, senders, on average, initially overestimate the frequency of punishing at 30% to 33%, and do not realize how it depends on the strength of punishment. The average PostPredict(PR), on the other hand, is exactly the same as overall PunishRate (to two decimal places) except for that in 5% Extreme, suggesting that senders update their beliefs appropriately. In 5% Extreme, the average PostPredict(PR) is 0.11, which is twice the actual PunishRate (0.05). Result 2. Overall information transmission increases when punishment is available.

(i) This is mainly because receivers follow sender messages more when punishment is available.

(ii) Senders need not exaggerate less.

Figure 2 reports the raw data of states, messages, and actions for bias b = 2 in the Baseline and Punishment Game. As the main behavioral changes are observed in receivers, the figures are displayed from a receiver's viewpoint. Supplementary Figure 1 report the raw data in the Punishment Games of the four treatments separately, while Supplementary Figures 2–4 report from a sender's viewpoint. The messages {1, 3, 5} and the receiver actions {1, 2, 3, 4, 5} correspond to the three rows and the five columns, respectively. The size of the donut chart within each message-action cell is scaled by the occurrence of corresponding message and action. Hence, the rows indicate receivers' decisions with respect to different messages. The fractions in each donut chart show the distribution of states conditional on that message-action pair, and the number inside the donut shows the average state. White, gray, and black fractions correspond to the frequency of state 1, 3, and 5, respectively. Finally, the actions predicted by level-k types are connected by various lines. In fact, compared to the Baseline Game, receivers choose action a = 4 and 5 more often but take less a = 3 when received message m = 5 (receivers trust sender messages more when punishment is available). When punishment is available, the conditional mode of receiver actions when message m = 5 increases from 3 to 4, getting closer to the average states (overall information transmission increases).

FIGURE 2

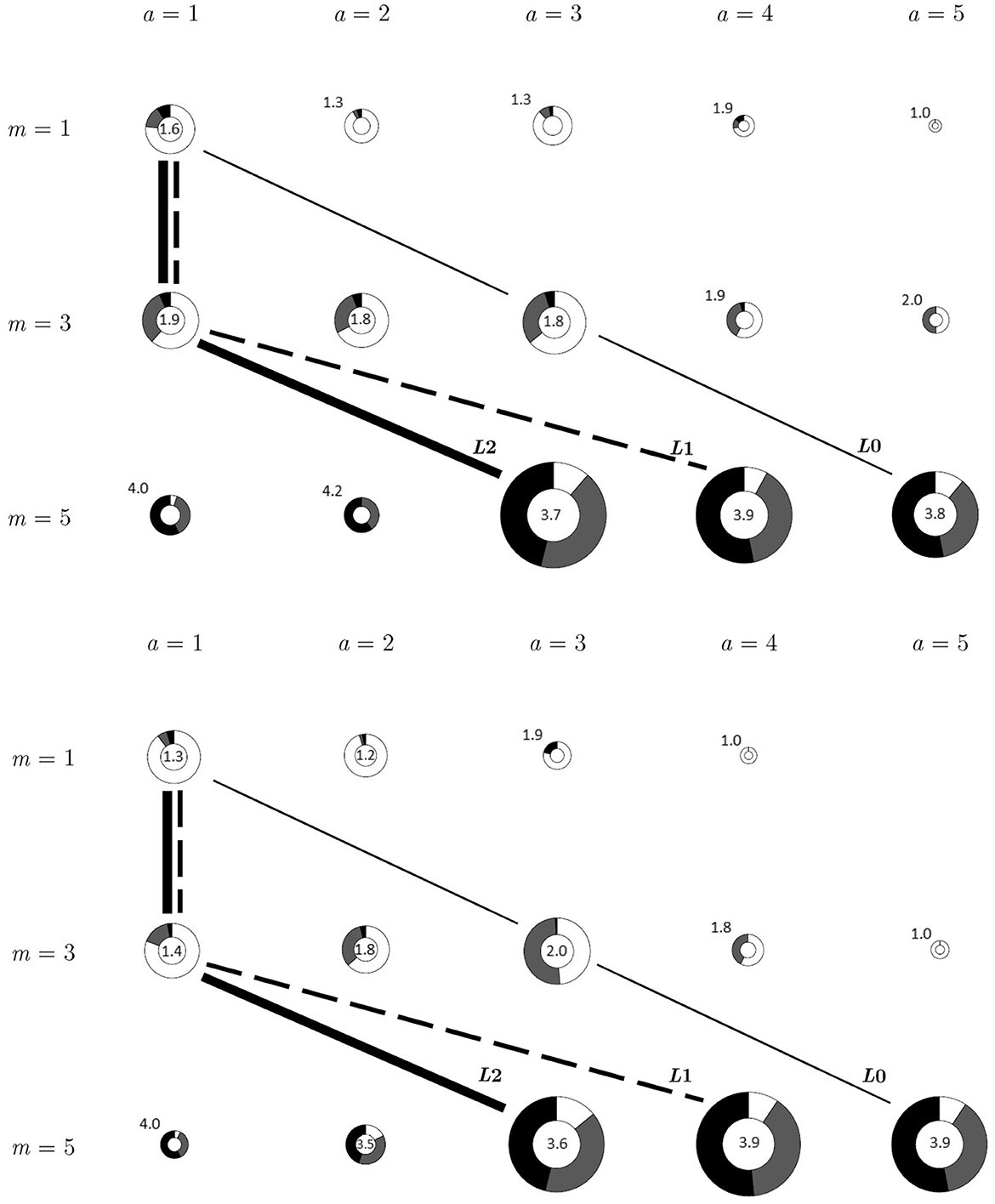
Figure 2. Receiver action and underlying states in baseline (top) and punishment (bottom) game (b = 2): donut size scaled by frequency of action taken. Fractions in each donut represent state occurrence for each message and action. The darker the color, the higher the state. The number inside or near each donut is the average realized state.

Table 2 provides the correlations among states s, messages m, and actions a, summarizing the information transmission in the Baseline and Punishment Games. Ex post punishment, despite possible judicial errors, generally improves information transmission, measured by the correlation between states and actions. Compared to the Baseline Game, Corr(s, a) increases significantly from 0.33 to 0.46 when punishment is added (p < 0.001, Jennrich correlation test), pooling all four treatments. Furthermore, it increases in each treatment, though the difference of correlations is only significant in 20% Extreme (p < 0.001) and 5% Extreme (p = 0.001). The p-value for 20% Mild and 20% Strong are 0.067 and 0.078, respectively, which are also marginally significant.

As indicated by the correlation between messages and actions, we find that receivers follow sender messages more and discount them less when punishment is available across all treatments (see Table 2), moving their behavior closer to the best response to Baseline sender subjects (SOPH receiver in Table 1). In the Punishment Games, Corr(m, a) increases in all treatments, three of which are statistically significant (all three p < 0.006), resulting in an overall increase from 0.53 to 0.66 (p < 0.001). We further examine receivers' tendency to follow, measured by the adoption rate, or (the number of rounds with m equal to a)/(total rounds), and the (average) size of discount (|m−a|). Consistent with the result of Corr(m, a), we find that receivers tend to discount their opponents' messages less in the Punishment Game. Overall, the adoption rate rises by 6 percent (from 29 to 35%, signed-rank test by matching groups p = 0.159) and the size of discount falls by 15 percent (from 1.20 to 1.02, signed-rank test by matching groups p = 0.035).

However, we observe unclear pattern of correlation between states and messages. Overall, Corr(s, m) only increases slightly from 0.58 to 0.60 in the Punishment Game, and even decreases in 20% Strong (p = 0.069). Surprisingly, we only find a significant rise in the 20% Mild Punishment Game among all treatments (p = 0.030). We examine senders' tendency to exaggerate, measured by the lie rate [(the number of rounds with s unequal to m)/(total rounds)] and the size of deception (|s−m|). We find that the lie rate remains unchanged at 50% (0.51 vs. 0.49, signed-rank test by matching groups p = 1.000), and the difference in the size of deception (|s−m|) is almost negligible (1.15 vs. 1.14, signed-rank test by matching groups p = 0.579). To sum up, the evidence from the correlations suggests that ex post punishment affects overall information transmission and utilization when b = 2, by encouraging receivers to adopt messages. Result 3. There is a positive correlation between punishment severity and overall information transmission/sender exaggeration/receiver adoption. However, the marginal effect of punishment strength on sender exaggeration/receiver adoption decreases in strength.

We run the following linear regressions to investigate the effect of punishment size: We first regress the dummy Optimal (being 1 if the action a equals to the true state s) and the distance between state and action (|s−a|) on PunishSize and its squared term (PunishSizeSq), controlling for the treatment dummy of the 5% Extreme Punishment Game (Extreme5), to evaluate how the amount of transmitted information is affected. Specifically, PunishmentSize equals to 0, 1, 3, and 75 in the Baseline, Mild, Strong, and Extreme Punishment Game, respectively, which represents the relative size of punishment in each treatment. For senders and receivers, we also regress the dummy of lying (Lie), the size of deception (LieSize), the dummy of trusting (Trust) and the size of discount (DiscountSize) on the sameindependent variables.

The results summarized in Table 4 indicate a significantly positive, though economically minor, correlation between punishment strength and information transmission [see column (1) and (3)]. Overall, increasing punishment size by the size of Mild raises the probability of receivers' choosing the optimal action by 0.12% (p = 0.003), and reduces the average distance between the true states and receivers' actions by 0.003 (p = 0.001). Still, implementing the extreme punishment could increase the optimal rate by 9%, a 31% (= $\frac{0.091}{0.291}$ ) increase compared to Baseline, and decrease the distance between state and action by 0.225, a 18% ( $= - \frac{0.225}{1.254}$ ) decrease.

TABLE 4

Table 4. Information regression results.

Table 5 lists the results for senders' lying behavior. We find that punishment size has insignificant effect on how often a sender lies, as reported in Column (1) and (2). The only exception is when the punishment is extreme and monitoring uncertainty is low: Compared to the Baseline, LieRate decreases by 7% in the 5% Extreme Punishment Game (F-test p = 0.035). The size of deception, on the other hand, is significantly affected by punishment size and its squared term [Column (5) of Table 5]. The positive coefficient of punishment size (0.056, p = 0.043) and negative coefficient of the quadratic term (−0.00075, p = 0.041) reflect an inverse U-shape of LieSize along the strength of punishment. Moderate monetary penalty backfires and cannot deter lying. In fact, the average size of deception increases by 0.055 (5 percentage points) and 0.161 (14 percentage points) in the Mild (F-test p = 0.043) and Strong Punishment Game (F-test p = 0.043), respectively. Extreme punishment, in contrast, insignificantly decreases senders' size of deception by 0.019 (F-test p = 0.876).⁹

TABLE 5

Table 5. Sender regression results.

Table 6 displays the results for receivers' message utilization. Overall, a positive correlation between the severity of punishment and receivers' tendency to follow is reported in column (1) and (3). Additionally, the negative coefficient of PunishSizeSq in column (2) and (4) indicates how the trust-encouraging effect diminishes as punishment becomes more severe. Compared to the Baseline Game, the adoption rate increases by 2.9, 8.3, and 10.9%, and the discount size decreases by 0.066 (5 percentage points), 0.194 (16 percentage points), and 0.309 (26 percentage points) in the Mild, Strong, and Extreme Punishment Game (F-test, all p < 0.001), respectively. The coefficient of Extreme5 on DiscountSize is positive, contrary to theory predicts. However, it is only marginally significant.¹⁰ We observe diminishing marginal effect of punishment size. When punishment is Mild, an additional Mild punishment increases the adoption rate by 2.8% and decreases the discount size by 0.066 (a 5% decrease). However, when the punishment is Extreme, an additional Mild punishment reduces the adoption rate by 2.6% and raises the discount size by 0.059.

TABLE 6

Table 6. Receiver regression results.

3.2. Judicial errors and lying

In our experiments, senders are punished fourteen times in total when telling the truth. Due to the rarity of judicial errors, we first directly examine their reactions in the next round to evaluate the influence of experiencing judicial errors.

We find that half of the 14 senders have incentives to lie (when b = 2 and s≠5) right after suffering judicial errors. Among them, all but one (6/7, 85.7%) exaggerate, indicating a higher lie rate compared to the average (73.8%) conditional on having incentives to lie. Furthermore, the only sender from 5% Extreme is exactly the one sender who does not exaggerate. These results suggest that experiencing judicial error could discourage players from obeying social norms.

To provide evidence of the discouraging effect of judicial error, we use all data from the rounds with b = 2 and s≠5 and predict lying or not (the dummy Lie) and the size of deception (LieSize) using judicial error in the previous round (L.TypeIError), controlling for senders' pre-game estimation of the percentage of rounds in which the receivers punished senders when seeing that the message is inconsistent with the signal of true state [PriorPredict(PR)], the dummy of lying (L.Lie) and being punished (L.Punishment) in the previous round, and trends over time (Round and RoundSq) [Column (1) and (3) of Table 7]. We observe a strongly positive correlation between senders' previous experiences of lying and their present lying behavior (p < 0.001), which indicates consistency of individual sender's behavior. We further control for individual fixed effects, which eliminates the foregoing correlation [and drop the individual-level variable PriorPredict(PR)]. As shown in Column (2) and (4) of Table 7, previous judicial error significantly increases lie rate by 24 percent (p = 0.009) and the size of deception by 0.58, or 34 percent ( $= \frac{0.58}{1.71}$ ) (p = 0.024), which is twice larger than the (marginally significant) deterrent effect from punishment (0.28, p = 0.068). However, this result should be interpreted carefully due to the rarity of judicial errors. In fact, we cannot find statistically significant effect of L.TypeIError on Lie when employing probit or logit regression analysis. The lack of observations for judicial errors stems from our design choice of having error rates to be 20 or 5%, which have to be raised to unrealistically high levels to obtain sufficient observations.

TABLE 7

Table 7. Regression of lying (b = 2 and s ≠ 5).

3.3. Level-k analysis and additional results

Considering players' bounded rationality and non-equilibrium beliefs, Wang et al. (2010) classify the senders into separate level-k types with a “spike-logit” error structure (Costa-Gomes and Crawford, 2006). Following their method, we classify both senders and receivers in the Baseline Game to analyze the strategies of all the players. For the purpose of comparing behavior across games, we classify the players in the Punishment Game as if they were playing the Baseline Game. Since the empirical distributions of players' actions are not the same in different games, we drop the SOPH type and classify all the players into L0 to L2 types only.

We conduct the following empirical estimation. We assume that a player of a certain type follows primarily its proposed strategy (see Table 1) yet makes a mistake with probability ε. Given an error occurring, the probability of a sender mistakenly choosing the specific message m other than the proposed message m^* follows the logit structure specified by $\frac{exp [λ Π (m | s)]}{\sum_{μ \neq m^{*}} exp [λ Π (μ | s)]}$ where Π(m|s) is the expected payoff of sending message m when the true state is s. Similarly, the probability of a receiver mistakenly choosing the specific action a other than the proposed action a^* follows the logit structure specified by $\frac{exp [λ Π (a | m)]}{\sum_{μ \neq a^{*}} exp [λ Π (μ | m)]}$ where Π(a|m) is the expected payoff of taking action a when the message is m. We estimate the spike-logit parameters (ε, λ) for each individual player using maximum likelihood for every level-k type. A player would then be classified into the type with the largest likelihood. The classification results are summarized in Supplementary Tables 3, 4. Result 4. In the Baseline Game, senders have lower levels of sophistication compared to receivers, which is persistent even after repetition and feedback.

Figure 3 and Supplementary Table 3 shows the classification results in the Baseline Game. We report subject compliance for the level-k model. Among 51 senders, 50 of them have compliance rate above 60%, exactly following the level-k prediction more than 60% of the time. The remaining sender has a compliance rate of 57%. Excluding that sender, 16% (8/50) and 62% (31/50) are classified as types L0 and L1, respectively. Twenty-two percent (11/50) of senders are classified as L2/SOPH types since they share the same strategies. Similar to Wang et al. (2010), we observe few L0 and mostly L1 type.

FIGURE 3

Figure 3. Level-k classification in the baseline game for subjects with compliance rate > 60%.

In contrast, the level-k model does not predict the behavior of receivers as precisely as of senders. As shown in Supplementary Table 4, 19 out of 51 receivers have compliance rate below 60%, in which nearly two-thirds (12/19) of whom exactly follow the level-k prediction less than half of the time. For the 32 receivers with good compliance, we observe a completely different pattern compared to the senders: Only one receiver is classified as L1 type; three-quarters of receivers are classified as L2 (14/32) and SOPH types (10/32) while most of senders are concentrated in L1 type. As a result, receivers (with good compliance) have an average thinking-step of 1.53 (coding L0 = 0, L1 = 1, L2 and SOPH = 2), significantly higher than 1.06 of senders (p = 0.001, rank-sum test). ¹¹

We find similar level-k classification results using receiver data from Hsieh and Wang (2016) (with logit error structure) and Wang et al. (2010), which focus on sender behavior and do not report receiver results (but do provide the data). First, receivers' types are weakly higher than senders' on average in Hsieh and Wang (2016) (1.66 vs. 1.56, p = 0.339), as well in Wang et al. (2010) (2.44 vs. 2.06, p = 0.263) (Note Wang et al. (2010)'s setting allows them to separate EQ, L3 and SOPH from L2, and code them as Type = 3.). Second, less than half the receivers behave with good compliance rate. In fact, only 33 of 77 receivers (28/59 in Hsieh and Wang, 2016 and 5/18 in Wang et al., 2010) behave with compliance rate above sixty percent.

We obtain similar results if we estimate level-k types using b = 2 data alone, or follow Hsieh and Wang (2016) to employ a logit structure, instead of spike-logit.¹² Under all specifications, we find more sophisticated receivers with higher level-k types, which indicates they have higher expectations of senders' level-k types (to whom they best respond). One possibility is they underestimate the amount of lying-averse senders who have a preference for truth-telling (Sánchez-Pagés and Vorsatz, 2007, 2009). Result 5. In the Punishment Game, level-k types are fairly persistent but exact rates rise. Otherwise, senders increase their levels in 20% Strong, and receivers lower their levels.

Figure 4 compares the type classification results in the Baseline and Punishment Game (with compliance rate greater than 60% in both games). All but 3 (out of 51) of senders behave with good compliance in both games. Among them, over 70% (34/48) are classified into the same type as in the Baseline. Around 20% (9/48) and 10% (5/48) are classified into higher and lower types, respectively. Those who exaggerate more are mainly concentrated in 20% Strong (4/9), accounting for over a quarter of senders in this treatment. Those who exaggerate less, on the other hand, are more equally distributed across all treatments. Furthermore, all but one sender in 20% Extreme maintain the same level-k types across games. These individual-level findings are consistent with the results shown in the comparative static analysis (Section 3.1): When punishment is added, the tendency to exaggerate is stronger in 20% Strong, and no effect on senders is observed in 20% Extreme. The remaining data, however, indicate that most senders do not change their strategies. A Wilcoxon signed-rank test on senders' level-k types yields an insignificant result (p = 0.341).

FIGURE 4

Figure 4. The comparison of level-k classification.

Only half of the receivers (25/51) can be consistently classified into level-k types in both games, but we can still observe a large proportion of type-unchanged players: Around 70% of well-compliant receivers (17/25) do not change their types. The signed-rank test also indicates insignificant changes in receivers' level-k types (p = 0.190). The stability of type classification indicates a limited impact of the punishment with judicial error on the whole group. Besides, most of the remaining subjects (6/25) are classified into lower types, which supports the finding of receivers' tendency to follow sender messages in the Punishment Game.¹³

Interestingly, the compliance rates of type classification increase when punishment is available. Overall, the average compliance rate of senders and receivers rises by 3 percent (from 88 to 91%, signed-rank test p = 0.026) and 9 percent (from 60 to 69%, signed-rank test p = 0.008), respectively. This mainly comes from an increase in 20% Extreme (p = 0.013), especially for senders (p = 0.044). This finding suggests that punishment stimulates subjects to behave more consistent with level-k types. However, this is likely due to initial learning effects, at least for senders. If we drop the first 10 rounds of both Games and conduct the same analysis, average sender compliance rate increases by only 1 percent (from 91 to 92%, signed-rank test p = 0.408), while average receiver compliance rate increases by 8 percent (from 63 to 71%, signed-rank test p = 0.044).

Finally, we summarize additional results reported in the supplementary online material (SOM), including the results of two post-game tasks. First, all but two receivers are willing to see the true state of a round in which punishment is employed, indicating little information avoidance (Eliaz and Schotter, 2010; Falk and Zimmermann, 2016; Masatlioglu et al., 2017; Nielsen, 2020). Second, when subjects can choose between the Baseline and Punishment Game, they tend to choose the one in which they earn the highest payoffs, leading to 70.6% voting for the Baseline Game.

In addition, we find that players' payoffs do not improve after punishment is introduced. For receivers, the cost of punishment offsets the increase in overall information transmission. For senders, the extreme punishment causes a significant drop in sender payoffs. Lastly, focusing on b = 2, we pool all the data of the Baseline Game and apply (two-sided) rank-sum tests to evaluate the effect of punishment in different treatments, treating individual data in each round as an observation. Consistent with Result 3, we find that senders exaggerate significantly more in the in 20% Strong Punishment Game, but tell the truth significantly more often in 5% Extreme. Receivers discount the message significant less (and follow it more often) for all treatments except 20% Mild.

4. Conclusion and discussion

We conduct an experiment that consists of the Baseline Game and the Punishment Game. The Baseline Game is a sender-receiver game with three discrete states (and corresponding message space), and receivers observe a noisy signal of the true state after the game. The Punishment Game incorporates costly ex post punishment with various strengths (Mild, Strong, and Extreme) and error rates of the signal (20 vs. 5%, under Extreme) into the Baseline Game. This model has a wide range of applications in economics and politics. For instance, how a salesperson sells its product to consumers and how professionals provide expert advice to policymakers are both sender-receiver games.

We find that punishment is used when available, but the punishing rate decreases as its strength increases. Moreover, there is a “trust-encouraging” effect of punishment—regardless of senders' tendency to exaggerate, any punishment unambiguously encourages receivers to follow their opponents' messages more and thus generally improves information transmission and utilization. This finding implies that even a weak penalty could be strong enough to improve overall information transmission. In the real world, people sometimes doubt professional advice due to conflicts of interest, impairing the efficiency of communication and potential for cooperation. For instance, a patient who is skeptical about his doctor's incentive may be risking his/her health by refusing to follow the prescription or deciding not to return to the clinic. However, the trust-encouraging effect from punishment indicates that cooperation increases when patients are allowed to “punish,” say through suing malpractices, even if it is non-deterrent. Other examples in online markets include feedback rating system and free return within 7 days. Interestingly, a strong punishment induces more lies. If we consider the cost of punishment and judicial errors, a draconian law may not be an effective and efficient way to improve social welfare.

Our work could further provide a glimmer into human behavior under criminal environments with ex post (flawed) punishment. The sender-receiver game consists of a criminal environment if we view a sender's exaggeration as fraud or perjury. On the other hand, every country establishes and enforces its own criminal law for deterrence. Governments regularly prescribe fines for speeding, incarcerations for stealing, and even capital punishments for murdering. Victims, like receivers in our Punishment Game, could punish criminals by taking legal action against them. Yet, as suggested by our results, victims may be unwilling to hand out the punishment due to imperfect monitoring, and potential criminals need not be deterred.

The issue of judicial error is especially evident when considering the death penalty, as the dead cannot resurrect. In the US, the rate of wrongful conviction for capital punishment is estimated conservatively at 4.1% (Gross et al., 2014). In fact, the governor of Illinois even suspended the executions of death penalty in 2000 since he concluded that “the capital justice system was fundamentally flawed” (Amnesty International, 2011). Paradoxically, some countries have a flawed legal system which is distrusted by the public, but exhibit public support for the capital punishment. Take Taiwan as an example. 83.2% of Taiwanese do not trust the courts, while at least 59.4% of Taiwanese support the death penalty according to the 2016 Public Satisfaction Survey on Criminal Justice and Crime Prevention (National Chung Cheng University Crime Research Center, 2016). Our experimental results indicate that extreme punishment has the most substantial receiver adoption-encouraging effect, and thus improvement in overall information transmission, despite its low enforcement rate and null deterrence. This finding may provide a reasonable explanation for the paradox: Since extreme punishment encourages overly skeptical receivers to lower their guards and become more willing to follow others' potentially truthful recommendations, people may support keeping the option of extreme punishment, despite merely being an apple of Sodom.

Note that our subjects experienced the Baseline Game prior to the Punishment Game, since receivers cannot fully understand the consequence of naively adopting sender messages without such experience.¹⁴ One could conduct an experiment in which subjects experienced the Baseline Game twice, and compare the “experienced” Baseline Game with Punishment Games. In addition, consistent with previous sender-receiver game experiments (Dickhaut et al., 1995; Cai and Wang, 2006; Sánchez-Pagés and Vorsatz, 2007, 2009; Wang et al., 2010; Hsieh and Wang, 2016; Battaglini et al., 2019), we find little supergame effects, despite subjects having public knowledge that matching group size is 6. Further investigation is required to see if a larger matching group size would eliminate any remaining supergame effects. Lastly, we do not separately measure lying aversion, guilt aversion, or cognitive ability, since the experiment is already more than 2.5 h long. However, we do classify subjects based on their behavior in the experiment. We find substantial portions of L0-senders (with lying aversion) and L1-senders (with limited cognitive ability).¹⁵ Linking subject behavior to separate measures (like cognitive reflection test) awaits future investigation.

A large proportion of senders and receivers can be consistently classified as the same level-k types (Costa-Gomes and Crawford, 2006) in the Baseline and Punishment Game. The evidence offers a caveat for our analysis: The persistence of level-k types across the two Games indicates a focused but limited impact of the punishment. The behavioral change in a small group of samples drives our findings, probably due to the low punishment rates. Reducing the price of punishment (and relaxing the limited use of extreme punishment) might be a way to encourage subjects to enforce sanctions. We also find some evidence that punishing the innocent can “backfire”: Truth-telling senders have higher propensity to lie after being wrongly punished. These mistakes are, however, too rare to be robustly analyzed with regression models, so raising the error rate to unrealistically high levels might be necessary to obtain more observations of judicial errors. Besides, mild/strong punishment with 5% error rate and punishment without monitoring uncertainty could be considered as comparison groups. Finally, the punishment system in our experiments is quite simple. It would thus be closer to reality to incorporate various punishments into one sender-receiver game, and then investigate the interaction between punishments.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation, at Open Science Framework (https://osf.io/qxfge/).

Ethics statement

The participants provided their written informed consent to participate in this study on the TASSEL website.

Author contributions

M-JF and JW contributed to conception and design of the study, analyzed the data, and wrote the paper. M-JF conducted the laboratory experiment. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

We thank financial support from the National Science and Technology Council of Taiwan (NSTC), formerly Ministry of Science and Technology (MOST) (Grants# MOST 106-2628-H-002-001-MY4, NSTC 111-2628-H-002-001, NSTC 111-2634-F-002-018) and Center for Research in Econometric Theory and Applications (CRETA) of National Taiwan University (111L900203).

Acknowledgments

This is an extensive revision of the master thesis of M-JF. We thank Po-Hsuan Lin, Wei-Ming Fu, and Ally Wu for excellent research assistance. We thank comments from Patrick Dejarnette, Daniel Martin, Kirby Nielsen, as well as the audience of various ESA Meetings, 18th Annual SAET Conference, and the Workshop on Behavioral Economics: Foundations and Applied Research at Sydney.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer CK declared a past co-authorship with the author JW to the handling editor.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frbhe.2023.1096598/full#supplementary-material

Footnotes

1. ^Abbink et al. (2002) constructed a “sudden death” treatment, where subjects engaging in corrupt activities suffered a tiny chance of being excluded from the experiment and got nothing. In their experiment, “death” is not a result from endogenous punishment but from exogenous probabilities.

2. ^Our paper is also related to pre-play communication with ex post verification and/or punishment. For example, Schwartz (1997) in a joint investment context allowed both players to send a cheap talk message regarding their outside options before playing prisoner's dilemma. They found increase in cooperation when cheap talk messages can be verified ex post. Brandts and Charness (2003) allowed Player 1 to express his intended play for a 2 × 2 game, in which Player 2 has a dominant strategy. Their results showed Player 2 subjects were more willing to punish if opponents lied.

3. ^In theory, Kartik et al. (2007) and Kartik (2009) built a model based on Crawford and Sobel (1982), considering the case of senders with lying costs.

4. ^Sánchez-Pagés and Vorsatz (2007) also ran an additional treatment with larger constant-sum payoff for comparison, but their price of sanctions varies when punishment increases, so one cannot isolate the effect of punishment severity alone. Note that lying in a constant-sum sender-receiver game is not clearly defined: A sender who expects a distrustful opponent would deceive the receiver into taking a sender-preferred action by strategically telling the truth.

5. ^Rizzolli and Tremewan (2018) also found that monetary sanctions could not deter stealing when Type I errors may happen, though the exogenous punishment was not certainly enforced and thus did not rule out the possible impact from Type II errors (wrongful acquittal). For further discussion on punishment with Type II errors in theft games, see Schildberg-Hörisch and Strassmair (2012) and Harbaugh et al. (2013).

6. ^In the actual experiment, senders on average earn 52.11 ESC per round in the Punishment Game, excluding punishment. Hence, the actual price of sanction is approximately 1:4.343 since $52.11 \times \frac{5}{6} = 43.43$ , which is close to 1:4.5.

7. ^Senders as well as receivers that did not use the punishment were randomly shown one of the 30 rounds.

8. ^Following Cai and Wang (2006), we run the panel regression (clustered at subject level): a = β·a+ϵ, testing the null hypothesis $β = \frac{σ_{m}}{σ_{a}} \cdot ρ_{m a} = 0$ where σ_m, σ_a, ρ_ma are the standard deviation of messages, the standard deviation of actions, and the correlation of messages and actions predicted by the most informative equilibrium, respectively.

9. ^When the cube of punishment size (PunishSizeCube) is included as another independent variable [Column (3) and (6) of Table 5], we find that this adjustment reverses the coefficients of punishment size and of its quadratic term. Two important insights into this result are noteworthy. First, a mild penalty might still provide deterrence, probably playing a role together with intrinsic lying aversion. Second, the statistical significance in the cubic term alerts us to a possible bias when we extrapolate the punishment effect to extreme cases. The lie-encouraging effect from a strong penalty is actually eliminated by an extremely stronger punishment.

10. ^Supplementary Tables 1, 2 show regression results clustered at the subject level. All qualitative results are unchanged, but with much larger standard errors.

11. ^Classifying all receivers rather than those with good compliance yields nearly identical results: Only three (out of 51) receivers are classified as L1 type, and about 60% of receivers are classified as L2/EQ (18/51) and SOPH types (13/51).

12. ^Using b = 2 data alone classifies 87.3% subjects as the same level-k type (49/50 of senders and 23/32 of receivers with good compliance), and another four receivers merely switch between L2 and SOPH. Under a logit error structure, 69.6% of our subjects are identified as the same level-k type (34/50 of senders and 24/32 of receivers with good compliance), and another six receivers switch between L2 and SOPH.

13. ^Like the results in the Baseline Game, classifying all receivers rather than those with good compliance also yields nearly identical results: 63% of well-compliant receivers (32/51) do not change their types, and more than half of the remaining subjects (13/51) are classified into lower types.

14. ^This is in contrast to, say, public goods games, in which consequences are much more transparent. Nevertheless, Fehr and Gachter (2000) find an even stronger effect when the punishment game was conducted before the baseline (public goods) game.

15. ^In contrast, guilt aversion was found to be at most marginally significant in Greenberg et al. (2014).

References

Abbink, K., Irlenbusch, B., Renner, E. (2002). An experimental bribery game. J. Law Econ. Organ. 18, 428–454. doi: 10.1093/jleo/18.2.428