A survey on detecting healthcare concept drift in AI/ML models from a finance perspective

Data is incredibly significant in today's digital age because data represents facts and numbers from our regular life transactions. Data is no longer arriving in a static form; it is now arriving in a streaming fashion. Data streams are the arrival of limitless, continuous, and rapid data. The healthcare industry is a major generator of data streams. Processing data streams is extremely complex due to factors such as volume, pace, and variety. Data stream classification is difficult owing to idea drift. Concept drift occurs in supervised learning when the statistical properties of the target variable that the model predicts change unexpectedly. We focused on solving various forms of concept drift problems in healthcare data streams in this research, and we outlined the existing statistical and machine learning methodologies for dealing with concept drift. It also emphasizes the use of deep learning algorithms for concept drift detection and describes the various healthcare datasets utilized for concept drift detection in data stream categorization.

Introduction

Machine Learning (ML) is a set of methods, techniques, and tools for diagnosing and prognosing medical issues (Kralj and Kuka, 1998). ML is used to forecast illness progression, extract medical knowledge for outcome study, plan and support therapy, and manage patients. ML is also used for data analysis, such as recognizing regularities in data by successfully dealing with defective data, interpreting continuous data used in the Intensive Care Unit, and intelligent alerts, which improves monitoring (Strausberg and Person, 1999). Successful machine learning approaches can help integrate computer-based systems into healthcare, making medical specialists' work easier and better, and enhancing efficiency and quality.

Society pays for healthcare services through healthcare finance. Healthcare finance includes accounting and financial management. Accounting measures a business's activities and finances in financial terms, while financial management (corporate finance) applies theory and concepts to help managers make better decisions.¹ Depending on disease severity, many AI/ML models anticipate financial costs. Concept drift occurs as illness severity grows and treatment costs change. The model's alteration owing to data changes is called concept drift. In this study, we will discuss concept drift, its types, and strategies for handling concept drift in healthcare and financial data.

In our paper, we outline the following:

Define concept drift in the healthcare domain and different drift types

Review the work done for handling concept drift in the healthcare sector

Classification techniques to handle concept drift

Concept drift and its types

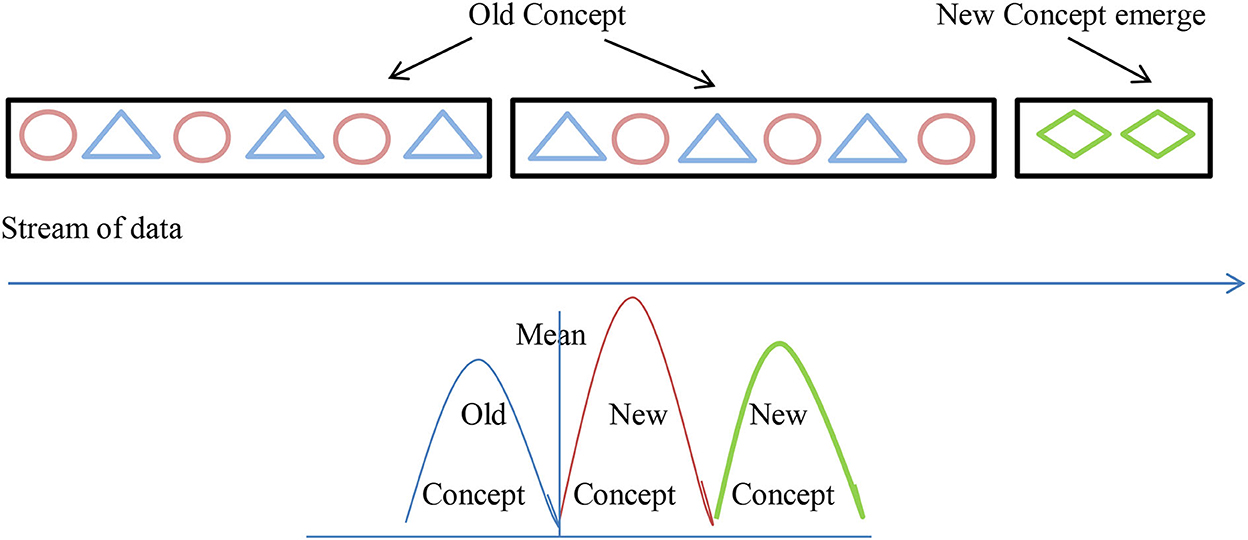
Concept drift is most commonly associated with an online supervised learning scenario in which the relationship between the input data and the target variable changes over time (Gama et al., 2014). As a result of this, the error rate of the model increases which leads to the degradation of models' prediction results causing drift. Concept drift is also referred to as model drift or model decay in AI terminologies. Due to concept drift, the model misclassifies the data during the classification technique (Liu et al., 2017b) as shown in Figure 1.

FIGURE 1

Figure 1. Concept drift.

Example: In the healthcare domain, the model created to predict the finance involved in treating a patient or insurance amount to be claimed from the company changes due to an increase in the complexity of the disease.

Types of concept drift

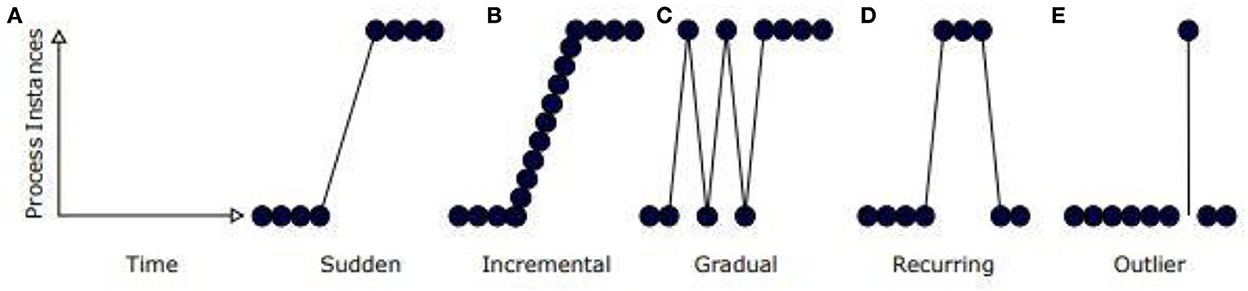
Figure 2 depicts different types of concept drift.

• Sudden—Sudden changes in health parameter values.

• Gradual—Concept is diminished slowly by another concept. For example, an increase in blood pressure leads to heart disease problems.

• Recurring—Changes reappear over the period. Example: Diabetic mellitus disease problems would reappear if there is a change in food habits.

• Incremental—Changes happen slowly over time.

FIGURE 2

Figure 2. (A–E) Types of concept drift.

Table 1 describes the different terminologies used to refer to different types of concept drift used in various works.

TABLE 1

Table 1. Concept drift by the probabilistic source of change (Bayram et al., 2022).

Figure 3 depicts the different ways of monitoring the occurrence of concept drift in data streams. The following are some of the ways:

• We can monitor the changes in data distribution

• We can monitor the feature changes in predicting the occurrence of concept drift.

• We can monitor the predictions of the classifier.

• We can monitor the labels of the data generated over time in finding the concept drift.

FIGURE 3

Figure 3. Different ways of occurrence of concept drift.

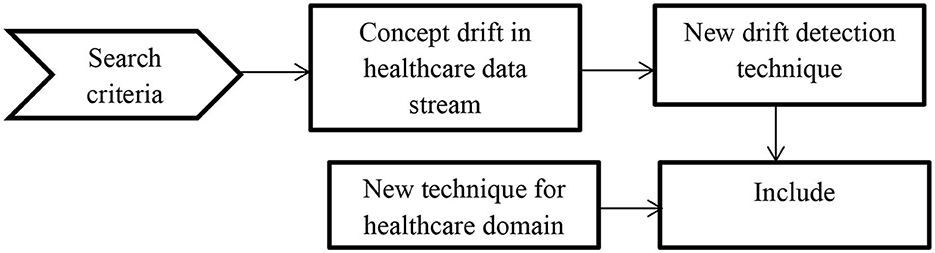
We picked potential papers based on the following inclusion criteria to determine applicable techniques.

• The method must be innovative for drift detection or integrate drift detectors into prediction systems.

• We listed all the papers related to different categories of drift detection from different authenticated journal databases.

• Papers related to concept drift in the healthcare sector are also listed.

In order to describe the review process involved in the manuscript to detect concept drift in healthcare application the following Figure 4 is used.

FIGURE 4

Figure 4. Systematic review process of concept drift.

Background review

General framework to detect concept drift

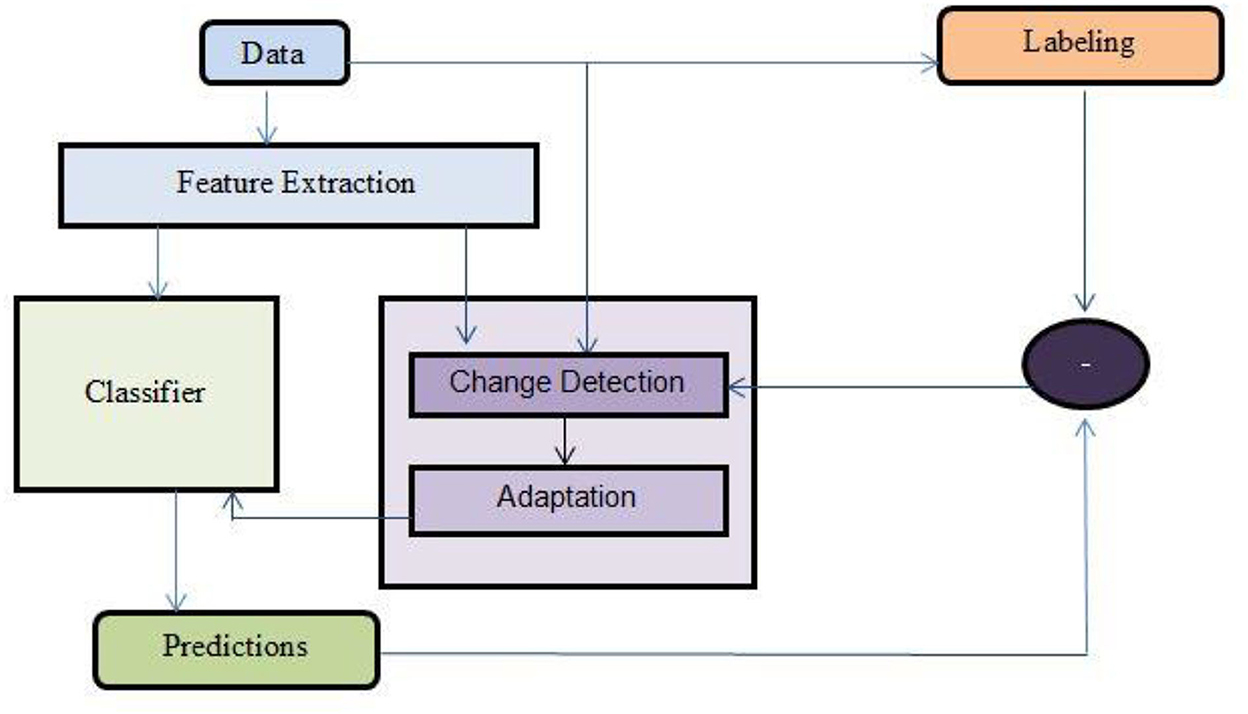
There are four stages in a generic framework for drift detection as shown in Figure 5.

Stage 1 (Data Retrieval): Data retrieval extracts data chunks from data streams. Because a single data instance cannot infer the general distribution, data stream analysis jobs require knowledge of how to arrange data pieces into meaningful patterns (Lu et al., 2016; Ramirez-Gallego et al., 2017).

Stage 2 (Data Modeling): Data modeling abstracts the returned data and extracts the sensitive features that most affect a system if they drift. Sample size reduction, or dimensionality reduction, to meet storage and online speed needs, is optional (Liu et al., 2017a).

Stage 3 (Test Statistics Calculation): In Stage 3, distance or dissimilarity is estimated (Test Statistics Calculation). The drift's severity is assessed, and hypothesis test statistics are prepared. This is the hardest aspect of concept drift detection. How to define an accurate dissimilarity assessment is unknown. Dissimilarity measurements can evaluate clustering (Silva et al., 2013) and compare sample sets (Dries and Ruckert, 2009).

Stage 4 (Hypothesis Test): Stage 4 (Hypothesis Test) uses the p-value to determine the statistical significance of Stage 3's change. Stage 3 test statistics are used to evaluate drift detection accuracy by showing their statistical bounds. Without Stage 4, Stage 3 test statistics cannot calculate the drift confidence interval, which reflects the likelihood that the change is due to concept drift rather than noise or random sample selection bias (Lu et al., 2014).

FIGURE 5

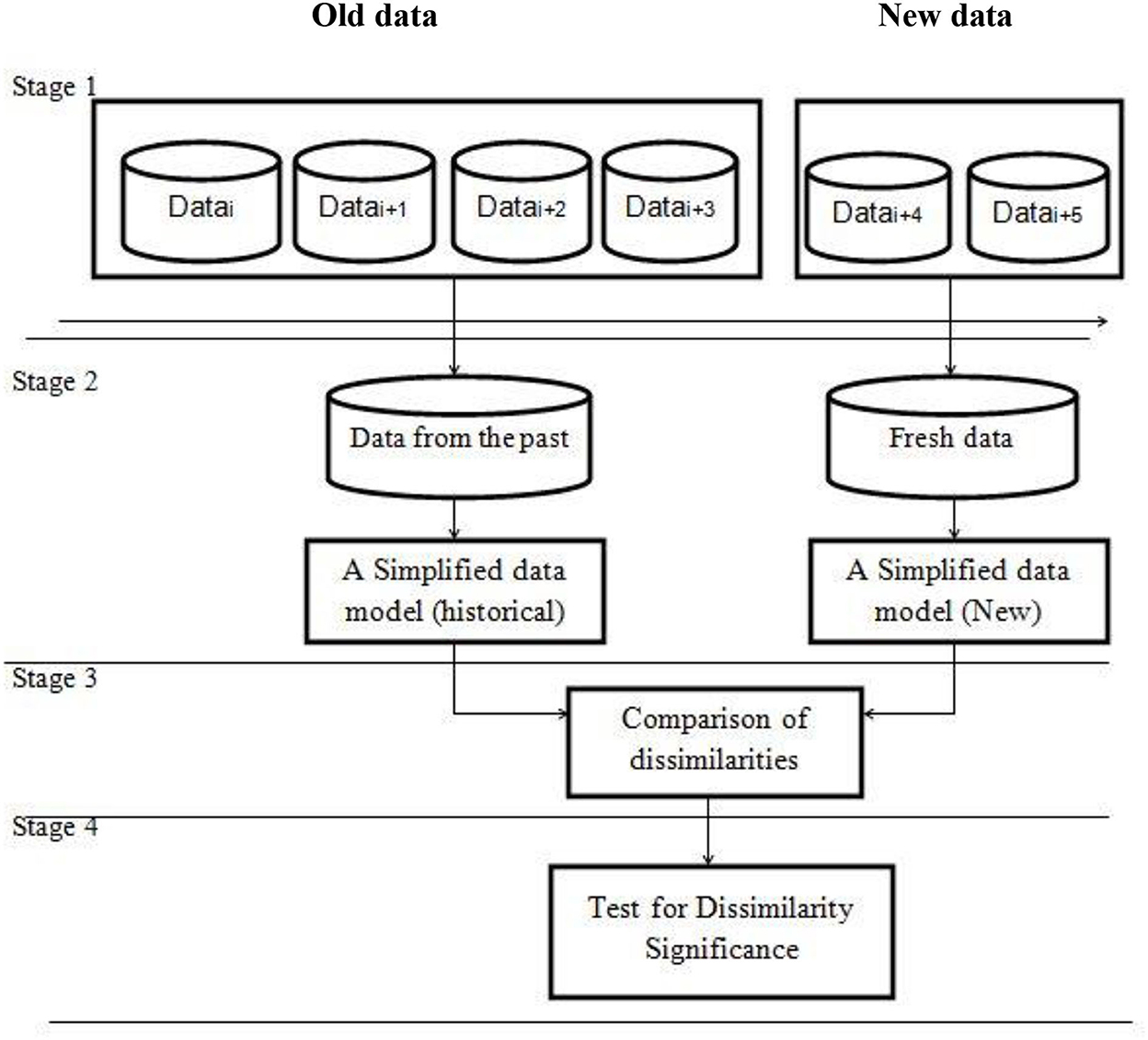
Figure 5. An overall framework for concept drift detection (Lu et al., 2019).

Concept drift in healthcare

On a multi-label hospital discharge dataset (Stiglic and Kokol, 2011) comprising diagnosis information, the suggested method employs relative risk and phi-correlation. The monthly discharge statistics and motion charts for visualization are used to detect concept drift. Static and dynamic ensemble classifiers are used to determine the accuracy and recommend the optimal classifier to use during concept drift.

Medical sensors that measure for general healthcare or rehabilitation (Toor et al., 2020) may be switched to ICU emergency procedures if necessary. When data have skewed class distributions, which is commonly the case with medical sensors' e-health data, detecting concept drifts becomes more difficult. The Reactive Drift Detection Method (RDDM) quickly finds long concepts. However, RDDM is error-prone and cannot handle class imbalance. The Enhanced Reactive Drift Detection Method (ERDDM) solves concept drift in class-imbalanced data streams.

We compared ERDDM to three recent techniques for prediction error, drift detection delay, latency, and data imbalance.

Clinicians triage patients referred to a medical facility using referral documents (Huggard et al., 2020), which contain free text and structured data. By training a model to predict triage decisions from referral documents, we may partially automate triage and make more efficient and methodical decisions. This task requires robustness against triage priority changes due to policy, budget, staffing, or other considerations. Concept drift occurs when document features and triage labels change. The model must be retrained to reflect these changes. This domain uses the unique calibrated drift detection method (CDDM). CDDM outperformed state-of-the-art detectors on benchmark and simulated medical triage datasets and had fewer feature drift-induced false positives.

Calibration drift detection alerts users to model performance degradation (Davis et al., 2020). Our detector maintains a rigorous calibration measure using dynamic calibration curves, a new method for tracking model performance as it grows. An adaptive windowing (Adwin) strategy monitors this calibration parameter for drift as data accumulate (Wang and Abraham, 2015).

In this study, a hip replacement dataset surgical prediction model was created (Davis et al., 2020). Concept drift is indicated by data distribution changes that increase mistake rate and classifier performance. The trigger-based ensemble method handles concept drift in surgical prediction by processing each sample and adapts the model quickly to data distribution changes.

Deep learning can detect early infection in CT, MRI, and X-Ray images of sick individuals from medical institutions or public databases. Analyzing infection rates and predicting outbreaks uses the same methodology. Many open-source pre-trained classification or segmentation models are available for the intended study. For example, transfer learning improves COVID-19 identification and prediction in medical picture datasets (Prashanth et al., 2022).

Table 2 describes the summary of concept drift detection methods in healthcare datasets. It briefs the drift detection method, the healthcare datasets used, the hypothesis test, features, and the given method's drawbacks.

TABLE 2

Table 2. Drift detection methods in healthcare datasets.

Categories of concept drift detection

There are two categories of detecting concept drift:

Supervised

Unsupervised

Supervised methods of concept drift detection categories

Performance-based Methods

This section examines performance-based concept drift detection techniques. Depending on the mechanism employed to identify performance dips, these techniques can be divided into one of several categories.

From the perspective of healthcare, performance-based techniques monitor the vital parameter values of patients' records. Any changes in the parameter values will alert the signal to take immediate actions. Following are some of the techniques used to monitor the performance of healthcare data:

Statistical process control/Error rate-based methods

Window based methods

Sequential analysis

Ensemble methods

Statistical process control/error rate based methods

Statistical process control checks our model's error. This is especially crucial while running production as the performance changes over time. Thus, we would like to have a system that will issue an alarm if the model passes the specified error rate.

Statistical process control methods are mentioned below:

DDM—Drift detection method: It models a number of errors as a binomial random variable. The key is to monitor the error rate. The parameters to monitor the error rate includes μ that is average error rate and σ, i.e., standard deviation (Gama et al., 2004).

p_t = error rate of algorithm/probability of misclassification

$\begin{array}{ll}\mu =n{p}_t\text{ and }\sigma =\sqrt{\frac{p_t(1-p_t)}{n}}& (1)\end{array}$

μ = mean, σ = Standarddeviation, n = numberofsamples

To alert if drift occurs, it uses the following equation

$\begin{array}{ll}{p}_t+{\sigma }_t\ge p_{min}+3{\sigma }_{min}& (2)\end{array}$

p_min = minimum value of the error rate

σ_min= minimum value of standard deviation

EDDM—Early drift detection method: It uses the distance between two consecutive errors rather than a number of errors. The distance should stay constant and any variations in the distance lead to drift. The method is good at detecting gradual concept drift (Baena-Garcia et al., 2006).

Warn and start caching:

$\begin{array}{ll}\frac{p_t+2{\sigma }_t}{p_{max}+2{\sigma }_{max}}<0.95& (3)\end{array}$

Alert and reset max

$\begin{array}{ll}\frac{p_t+2{\sigma }_t}{p_{max}+2{\sigma }_{max}}<0.90& (4)\end{array}$

CUSUM Test:

The CUSUM test (Manly and Mackenzie, 2000) calculates the difference of observed values from the mean and warns of concept drift if it exceeds a user-defined threshold. The cumulative total indicates concept drift when the error mean is significantly different from zero. The test alerts the user if the log-likelihood ratio of two probabilities before and after change exceeds this threshold.

$\begin{array}{ll}{T}_w^t=log\frac{P(x_{w.}\dots .,x_t|P2)}{P(x_{w,\dots .,x_t}|P1)}& (5)\end{array}$

The test declares a change when g_t is greater than the above equation threshold.

$\begin{array}{ll}{g}_t=S_t-m_t& (6)\end{array}$

$S_t=\sum _{i=1}^t{s}_i$ = ratio of log-likelihood between the two probabilities

$m_t=\underset{1\le i\le t}{min}{S}_i$

Page–Hinckley Test:

The test detects an abrupt change of the average of a Gaussian signal and the detection process (Qahtan et al., 2015) consists of running two tests in parallel, testing between the no-change hypothesis H0: r > n and the change hypothesis H1: r > n.

To detect an increase in average, we calculate:

$\begin{array}{ll}{U}_n={\sum }_{i=1}^n(x_i-m_0-\frac{{\delta }_m}{2})for\text{n}\ge 1\text{ and }{U}_0=0& (7)\end{array}$

$m_n=\underset{0\le k\le n}{min}(U_k)$ for n ≥ 1

To detect a decrease in average, we calculate:

$\begin{array}{ll}{U}_n={\sum }_{i=1}^n(x_i-m_0-\frac{{\delta }_m}{2})for\text{n}\ge 1\text{ and }{U}_0=0& (8)\end{array}$

$M_n={\max }_{0\le k\le n}(T_k)\text{for }n\ge 1$

To alarm, we use M_n−T_n ≥ τ

Hoeffding Drift Detection Method (HDDM):

The Hoeffding Drift Detection Method (HDDM) (Frías-Blanco et al., 2015) enhances DDM by utilizing Hoeffding inequality to identify significant alterations in the performance estimate's moving average.

The Hoeffding bound is defined as:

$\begin{array}{ll}ϵ=\frac{R^{2}ln(\frac{1}{\delta })}{2n}& (9)\end{array}$

ϵ = Hoeffding bound

R: Probability range. For probability, the range is 1, and for information gain, log c, where c is the number of classes.

δ: Confidence. 1 minus the required chance of choosing the right attribute at every given node.

n: Count of samples.

The variants in the HDDM family include:

✓ Hoeffding drift detection with an A_test (HDDM_A): Methods for learning in data stream situations exist that compute confidence intervals for various parameters (such as error rate) while taking into account well-known distributions. The Hoeffding drift detection method with an A_test (Frías-Blanco et al., 2015) considers the difference between moving averages. It estimates the error ϵ_α given a significant level of at most α.

✓ Hoeffding drift detection with weighted moving averages (HDDM_W): For weighted moving averages (Frías-Blanco et al., 2015), there is a broader statistical test that is quick and easy. Given that they are more likely to occur, the current real values are given greater weight than older ones in this situation.

✓ Fast Hoeffding Drift Detection Method (FHDDM): The FHDDM algorithm (Pesaranghader and Viktor, 2016) uses a sliding window and Hoeffding's inequality to compute and compare the highest probability of correct predictions with the most recent probability to detect drift.

✓ Stacking fast Hoeffding drift detection method (FHDDMS): The Stacking Hoeffding Drift Detection Approach (FHDDMS) (Pesaranghader et al., 2018), which maintains windows of various sizes, expands the FHDDM method. In other words, a short and a long sliding window are combined. This strategy's justification is to cut down on false negatives and detection delays. According to logic, a short window should be able to identify abrupt drifts more quickly than a lengthy window, which should do so with a lower rate of false negatives.

✓ Additive FHDDMS (FHDDMS_add): FHDDMS_add detects abrupt concept drifts with shorter delays and reduces false negatives for gradual drifts.

✓ Exponentially Weighted Moving Average (EWMA): EWMA for Concept Drift Detection adapts EWMA charts to detect classifier error rate changes (Ross et al., 2012). Time t computes the EWMA estimator's dynamic standard deviation Z_t and error rate $p_{0,t}^{ˆ}$. Concept drift is indicated if

$\begin{array}{ll}{Z}_{\text{t}}>p_{0,t}^{ˆ}+L{\sigma }_{\text{Zt}}& (10)\end{array}$

The control limit, or parameter L, specifies how much Z_t must deviate from μ0 before a change is noted.

Extreme Learning Machine (ELM): Extreme Learning Machine (ELM) (Huang et al., 2006) builds single-hidden layer feed-forward neural networks (SLFNs) by randomly selecting hidden nodes and calculating output weights. This technique provides good generalization performance at very fast learning speeds compared to gradient-based learning algorithms for feed-forward neural networks.

Dynamic Extreme Machine Learning (DELM): DELM (Xu and Wang, 2017) online learns a double hidden layer structure to improve ELM performance. ELM's notion drift alarm increases the classifier's generalization power by adding hidden layer nodes. If concept drift surpasses a threshold or ELM accuracy, the classifier will be withdrawn and retrained with new data to learn new concepts.

Online sequential learning algorithm for feed-forward networks (OS-ELM): Single-layer concealed a fast and accurate online sequential learning approach (OS-ELM) has built feed-forward neural networks with additive and radial basis functions (RBF) hidden nodes (Liang et al., 2006). Any limited non-constant piecewise continuous function can activate an additive node, and any integral piecewise continuous function can activate an RBF node. The algorithm can also process chunked data. Only the number of concealed nodes must be selected.

Sequential analysis-based methods

To determine how the context of the data stream has changed, the data instances are inspected one after the other. When the change in data distribution surpasses the predetermined threshold, it signals drift. The accuracy of the classifier is lowered as a result of concept drift. It can therefore be one of the methods used to identify concept drift in a particular data stream. Among the accuracy metrics of a classification model are recall, precision, F-measure, ROC, and AUC.

In Sequential analysis we monitor the contingency table. If the data are not stationary, we have different values in the table. If the data are not stationary, we have different values in the table. Rather than monitoring the contingency table values every time, we will monitor the four rates of the contingency table, i.e., precision, recall, sensitivity, and specificity to signal concept drift (Liu et al., 2016).

Liu et al. (2016) presented FP-ELM, which, like OS-ELM, can achieve incremental and on-line learning. Additionally, FP-ELM will apply a forgetting parameter to past training data based on current performance in order to adjust to possible changes after a new chunk is introduced.

Table 3 shows a categorical contingency table. A contingency table illustrates frequencies for specific combinations of two discrete random variables X and Y. The table cells contain mutually exclusive X–Y values.

TABLE 3

Table 3. Contingency table (Agrahari and Singh, 2021).

TP = True Positive FP = False Positive TN = True Negative FN = False Negative

Precision = $\frac{TP}{TP+FP}$, Recall = $\frac{TP}{TP+FN}$, sensitivity = $\frac{TN}{TN+FN}$, specificity = $\frac{TN}{TN+FP}$

This method sequentially evaluates prediction results as they become available and concept drift is flagged when a pre-defined threshold is met.

Window-based methods

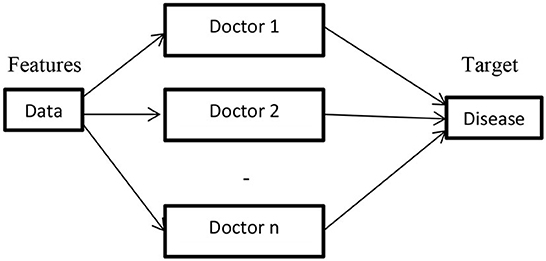
This method groups incoming data into a batch (or a window). Window-based methods have two windows. Figure 6 shows old data stream instances in the first window and new ones added afterward. These two window cases showed the drift and explained the data distribution change. This method can use either fixed or adjustable window sizes. A fixed window stays the same size during analysis. However, drift conditions change the adaptive window size. Drift shrinks the data window; no drift widens it (Agrahari and Singh, 2021).

FIGURE 6

Figure 6. Window-based concept drift detection.

From a healthcare perspective, the window can be considered as recording the patient's details every day or every hour and monitoring the changes over that period of time. Any improvements or fluctuations in that period will be carefully noticed and actions will be further taken.

The different window-based methods are as follows:

Adaptive windowing (ADWIN and ADWIN2): Adaptive windowing (Bifet and Gavalda, 2007) considers all partitions of the window and compares the distribution between two windows. Any changes in distribution between two windows signals concept drift. For each partition, the method calculates the mean error rate and compares its absolute difference to a threshold based on the Hoeffding bound and if the subpartition is violated then it drops the last element in the window.

$\begin{array}{ll}\text{Drop the last element}if|{\mu }_0-{\mu }_1|>{\theta }_{Hoeffding}& (11)\end{array}$

Due to its low false positive and false negative rate, ADWIN performs effectively. The one-dimensional data that ADWIN can handle is its only drawback. It keeps different windows open. ADWIN2 is a modified version that uses less time and memory than ADWIN. The average distribution difference between two successive windows must be greater than a predefined threshold in order for drift to be detected. By identifying the slow, gradual drift, ADWIN2 gets around ADWIN's drawback. It requires O(log WS) memory and time if the window size is WS (Agrahari and Singh, 2021).

μ₀ – Error rate of W0

μ₁ – Error rate of W1

Detection Method Using Statistical Testing (STEPD): Current and general accuracy is the rule. Two assumptions are made for this method: first, if the target concept is stationary, a classifier's accuracy for the most recent W examples will be equal to the overall accuracy from the start of learning; and second, a significantly lower recent accuracy signals that the concept is changing. Methods with an online classifier and monitoring its prediction errors during learning have been developed to detect concept drift in a limited number of samples. Nishida and Yamauchi (2007) created a detection approach that employs a statistical test of equal proportions.

The equation below calculates the statistic:

$\begin{array}{ll}T(r_0,r_r,n_0,n_r)=\frac{\left|\frac{r_0}{n_0}-\frac{r_r}{n_r}\right|-0.5(\frac{1}{n_0}+\frac{1}{n_r})}{\sqrt{\widehat{p}(1-\widehat{p}})\sqrt{(1/n_0+1/n_r)}}& (12)\end{array}$

Wilcoxon Rank Sum Test Drift Detector (WSTD): A novel two-window approach to STEPD-like concept drift detection in data streams. WSTD (de Barros et al., 2018) limits the older window size and employs the Wilcoxon rank sum statistical test instead of STEPD's test of equal proportions. The WSTD test equation is as follows:

$\begin{array}{ll}z=\frac{(R-{\mu }_R)}{{\sigma }_R}& (13)\end{array}$

μ_R = population mean = n1 × (n1+n2+1)

${\sigma }_R=standardeiation=\sqrt{\frac{n1*n2*(n1+n2+1)}{12}}$

n1 = n2 = Size of the smallest and largest samples.

Fishers Exact Test: The test proposed three approaches: Fisher Test Drift Detector (FTDD), Fisher Square Drift Detector (FSDD), and Fisher Proportions Drift Detector (FPDD) (de Lima Cabral and de Barros, 2018). Fisher's exact test was employed to get the p-value, which is the only distinction between these approaches and STEPD.

Cosine Similarity Drift Detection (CSDD): The Cosine Similarity Drift Detector (CSDD) produces the confusion matrix using a Positive Predictive Value (PPV) and the False Discovery (FDR) rates instead of TP and FP for each window. The Cosine Similarity (Hidalgo et al., 2019) between the vectors produced from the confusion matrices of the two windows indicates drift or warning.

McDiarmid Drift Detection Method (MDDM): MDDM identifies concept drift using McDiarmid's inequality (Pesaranghader et al., 2017). MDDM works by sliding a window over the predictions and weighting the window entries. Recent entries are weighted more to highlight their importance. As examples are processed, the detection method compares the maximum weighted mean to the sliding window's weighted mean. When the weighted means diverge beyond the McDiarmid inequality, concept drift is inferred.

Margin Density Drift Detection (MD3): To signal drift, MD3 uses the number of samples mapped to a classifier's uncertainty zone (Sethi and Kantardzic, 2015).

Kolmogorov–Smirnov test (KS test): A concept change detection technique called KSWIN (Kolmogorov–Smirnov Windowing) is based on the Kolmogorov–Smirnov (KS) statistical test. The KS test is a statistical test that makes no assumptions about the distribution of the underlying data. Data or performance distributions can be watched by KSWIN. The detector will accept an array of one-dimensional input. The KS test is run on identically sized windows, R and W. The distance of the empirical cumulative data distribution is compared using the KS test. KSWIN can identify concept drift if:

$\begin{array}{ll}dist(R,W)>\sqrt{-ln\frac{\alpha }{r}}& (14)\end{array}$

Because R and W are derived from the same distribution, if the difference in empirical data distributions between them is too great, concept drift can be identified

Raza et al. (2015) provide unique covariate shift-detection techniques based on a two-stage structure for both univariate and multivariate time-series. The first stage detects the covariate shift-point in non-stationary time-series using an exponentially weighted moving average (EWMA) model-based control chart in online mode. The second step confirms the first stage's shift detection using the Kolmogorov-Smirnov statistical hypothesis test (K-S test) for univariate time-series and the Hotelling T-Squared multivariate statistical hypothesis test for multivariate time-series.

CIDD-ADODNN Deep learning framework: The CIDD-ADODNN (Priya and Uthra, 2021) model classifies extremely imbalanced streaming data efficiently. The recommended adaptive synthetic (ADASYN) methodology weighs minority class examples based on learning difficulties to handle class imbalance data. Concept drift is detected using an adaptive sliding window (ADWIN).

Concept drift adaptation using Recurrent Neural Networks: Recurrent neural networks (RNNs) are utilized to detect time series anomalies (Saurav et al., 2018). Since new data are added gradually, the model can adapt to data distribution changes. RNN predictions of the time series are used to discover anomalies and change points. A significant prediction error indicates deviant behavior.

Ensemble methods

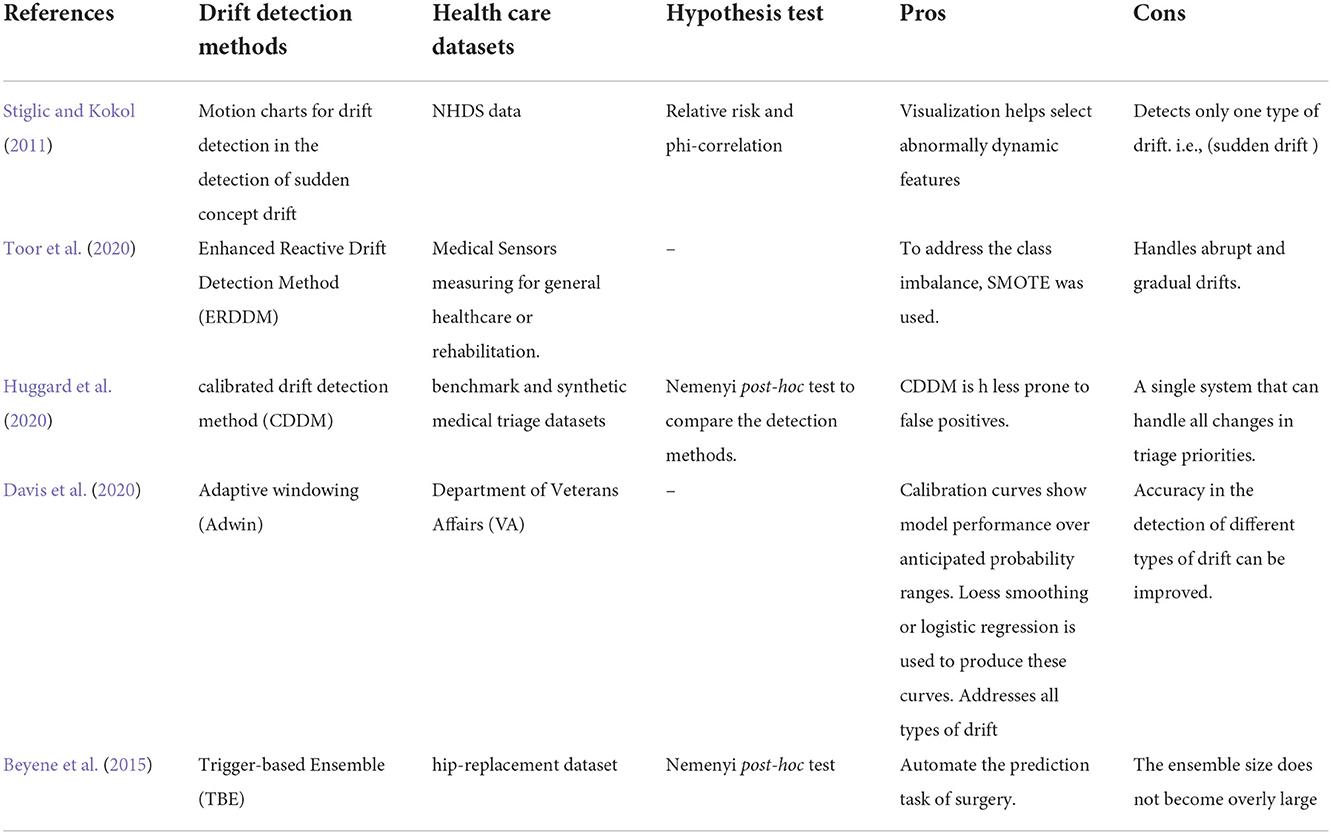
Figure 7 depicts the ensemble method architecture. The above architecture has n models and combines the predictions of all models to predict the output. From a healthcare perspective, the ensemble method resembles the consulting decisions of multiple doctors to ensure the disease type and level before diagnosing.

FIGURE 7

Figure 7. Ensemble methods.

The ensemble methods used for concept drift detection are as follows:

Streaming Ensemble Algorithm (SEA): By adding a new learner for each new chunk of data until the maximum number of learners is reached, SEA (Street and Kim, 2001) automatically manages drift. Based on their performance with predictions, the learners are improved.

Accuracy-Weighted Ensemble (AWE): An Accuracy-Weighted Ensemble (Wang et al., 2003) is a group of classification models where each model is carefully weighted according to how accurately they are projected to classify the test data in a time-evolving environment. The ensemble ensures that it is effective and resilient to concept-drifting streams.

Accuracy Updated Ensemble (AUE): By utilizing online component classifiers and updating them in accordance with the current distribution, Accuracy Updated Ensemble (AUE) (Brzeziński and Stefanowski, 2011), a development of AWE, increases accuracy. Additional weighting function adjustments address issues with unintended classifier discarding seen in AWE.

Dynamic Weighted Majority (DWM): Four strategies are employed by the dynamic weighted majority (DWM) (Kolter and Maloof, 2007) to counteract concept drift. It develops the ensemble's online learners, weights them depending on their performance, deposes them based on their performance, and adds fresh experts based on the ensemble's overall performance.

Learn++.NSE: A group of learners is trained in Learn++.NSE (Polikar et al., 2001) using examples of data chunks. The weighting of the training instances is based on the ensemble error for this particular case. Learn++.NSE increases the example's weight to 1 if the ensemble properly classifies it, otherwise, it is penalized to w_i = 1/e. Based on their mistakes in the previous and current chunks, the ensemble of learners is weighted using the sigmoid function.

Adaptive Random Forest (ARF): ARF (Gomes et al., 2017) uses efficient resampling and adaptive operators to tackle concept drifts without data set optimization.

DDD: DDD regulates learner diversity by including low and high-diversity ensembles. The low diversity ensemble and high diversity ensemble are used after drift detection.

DDE: Bruno Maciel et al., 2015 made a small ensemble to control how three drift detectors work and block their signals at both the warning level and the drift level. Depending on how sensitive the DDE is, it needs a certain number of detectors to confirm an alarm or drift level. Another parameter is the type of drift mechanism that is used. But each sensitivity setting has a default detector setup that goes with it.

Data distribution methods

To determine the contextual shift, this kind of drift detection approach compares examples of recent and previous data. These techniques often examine the statistical significance and are used in conjunction with the window-based approach. The location of the drift can be determined by computing the change in data distribution. As a result, computational costs might result and it depicted in Figure 8.

FIGURE 8

Figure 8. Feature distribution monitoring.

From a healthcare perspective, the distribution of current vital health parameters are studied with the previous day/week or previous hour, and even before diagnosis and after diagnosis. The patient's health parameters are carefully observed and studied and, depending on the health parameter value distributions, the doctor can further extend the medications to the patient or discharge the patient from the hospital.

SyncStream (Shao et al., 2014) is a prototype-based categorization model for evolving data streams that dynamically models time-changing ideas and offers local predictions. By constantly keeping a collection of prototypes in a new data structure known as the P-tree, SyncStream captures developing notions instead of learning a single model on a sliding window or ensemble learning. The prototypes are created using limited clustering and error-driven representativeness learning. Heuristics based on PCA and statistics are used to detect abrupt idea drift in data streams.

PCA-Based Change Detection Framework (Qahtan et al., 2015) methodology is built on estimating data for a subset of key constituents. Densities in reference and test windows are estimated and compared for each projection. Then, one of the divergence measures determines the change-score value. The largest change score among the several principal components is taken into account as the final change score by giving equal weight to all of the selected principal components.

A technique by Ditzler and Polikar (2011) uses an adjustable threshold to calculate the Hellinger distance as a measure to determine whether drift exists between two batches of training data.

A brand-new test, outlined in Bu et al. (2018), for detecting changes without using the probability density function that works online with multidimensional inputs has been created and is based on the least squares density-difference estimation method. By using a reservoir sampling mechanism, the test can start running right away after configuration and does not require any assumptions about the distribution of the underlying data. Once the application designer has established a false positive rate, the requested thresholds to detect a change are automatically derived.

A local drift degree (LDD) (Liu et al., 2017a) measurement can track alterations in local density over time. After a drift, we synchronize the regional density disparities in accordance with LDD rather than suspending all historical data.

Reactive Robust Soft Learning Vector Quantization (RRSLVQ) (Raab et al., 2020) is a method for detecting concept drift that combines the Kolmogorov–Smirnov (KS) test with the Robust Soft Learning Vector Quantization (RSLVQ).

Multiple hypothesis based methods

These algorithms are unusual in that they employ several hypothesis tests to track concept drift in various ways. The two types of multiple-hypothesis tests are parallel and hierarchical (Lu et al., 2019).

From a healthcare perspective, before diagnosing any disease, multiple tests should be done mandatorily. For a pandemic disease like SARS-CoV-2, the virus that causes COVID-19, testing specimens from your nose or mouth, NAATs, such as PCR-based tests, are most often performed in a laboratory. Furthermore, antigen tests and MRI scans of the chest have to be done to know the severity of the disease.

Two-stage covariate shift identification tests are available for both univariate and multivariate time series. The first stage uses an exponentially weighted moving average (EWMA) control chart to locate the covariate shift point in a non-stationary time series online. The second stage validates the shift found in the previous stage with the Kolmogorov–Smirnov statistical hypothesis test (K–S test) for univariate time series and Hotelling's T-squared multivariate test.

The study by Yu et al. (2019) proposes a concept drift detection framework (LFR) for detecting concept drift and finding data points linked with the new concept. LFR can handle batch, stream, unbalanced, and user-specified parameters.

As proposed by Yu et al. (2018), a rapid concept drift detection ensemble (DDE) that integrates three concept drift detection algorithms to improve drift detections. Accuracy improves without affecting execution time.

This article (Alippi and Roveri, 2008) proposes a pdf-free extension of the standard CUSUM using the CI-CUSUM test, which somehow inherits the extended CUSUM's detection skills and computational intelligence philosophy. Non-stationary data can be detected via the CI-CUSUM test.

A novel hierarchical hypothesis testing framework with a Request-and-Reverify technique detects idea drifts by asking for labels only when needed. The unique paradigm offers hierarchical hypothesis testing with classification uncertainty (HHT-CU) and attribute-wise “goodness-of-fit” (HHT-AG).

A hierarchical hypothesis testing (HHT) system that can detect and adjust to concept drift in unbalanced data labels (such as recurrent or irregular, gradual, or abrupt). HLFR, a new drift detector, is implemented using the HHT framework by switching to adaptive training.

Unsupervised methods of concept drift detection categories are as follows

Clustering/novelty detection

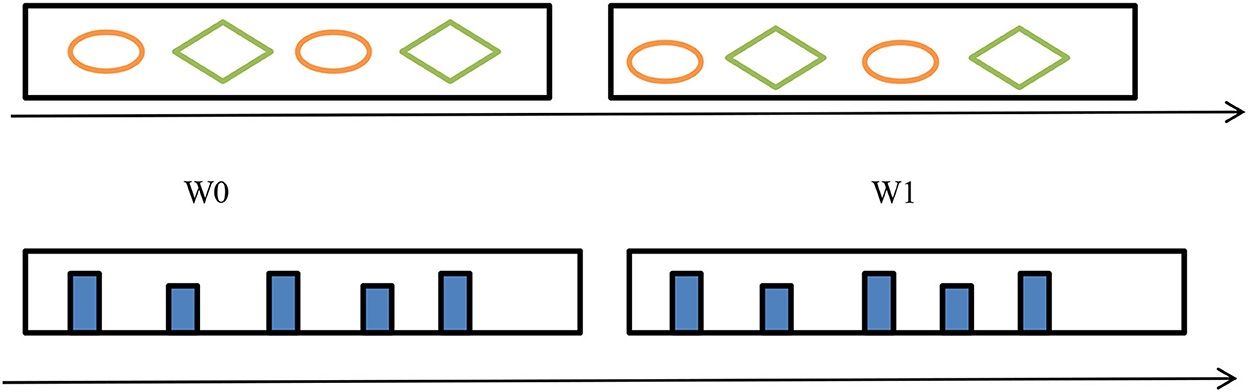
In clustering, each batch of data is assigned to a particular group and if it is not assigned to any particular group, concept drift is declared, as shown in Figure 9.

FIGURE 9

Figure 9. Clustering data streams.

From a healthcare perspective, we monitor all the health parameter values. After studying all health parameter values and reports the disease label is named.

The different clustering methods for stream data are as follows:

OLINDDA—This method uses k means clustering and periodically merges known and unknown batches of data. If the latter, concept drift is flagged (Spinosa et al., 2007).

MINAS—This method uses micro clustering and to gain efficiency it uses incremental clustering (Faria et al., 2013).

DETECTNOD—This method uses discrete cosine transform to estimate the distances efficiently (Hayat and Hashemi, 2010).

• Woo-Ensemble—This method treats outliers as potential emerging class centroids (Ryu et al., 2012).

• ECSMiner—Stores and uses cluster summary efficiently (Masud et al., 2011).

• GC3—This method uses grid-based clustering (Sethi et al., 2016).

Feature distribution monitoring

The idea is to monitor each feature individually. We monitor two sub-windows, W0 and W1, and compare their feature distribution either through Pearson correlation (Change of concept) or through Hellinger distance (HDDDM) (Lee and Magoules, 2012) as shown in Figure 9. If we have many features then the monitoring of features will be very difficult, so we can use principal component analysis (PCA) (Qahtan et al., 2015) to reduce features so that the monitoring of features will be easier.

Model-dependent monitoring

Unsupervised methods suffer from a high rate of false alarms because they constitute that any changes in observations are a reason for performance degradation. It is known that not all changes in observations lead to performance degradation. To reduce false alarm rates, we estimate the posterior probability (Dries and Ruckert, 2009).

The unsupervised methods under model-dependent monitoring are as follows:

A—Distance method: This method uses a generalized Kolmogorov–Smirnov distance to estimate the posterior probability.

Healthcare datasets

Some of the various healthcare datasets used in concept drift detection include:

• National Hospital Discharge Survey (NHDS) data² The dataset contains hospital discharge records for approximately 1% of US hospitals.

• MIMIC-III (Johnson et al., 2016)—a freely accessible critical care database: MIMIC-III (“Medical Information Mart for Intensive Care”) is a large, single-center database comprising information relating to patients admitted to critical care units at a large tertiary care hospital. Data include vital signs, medications, laboratory measurements, observations and notes charted by care providers, fluid balance, procedure codes, diagnostic codes, imaging reports, hospital length of stay, survival data, and more.

• The Veterans Health Administration (VHA) (Davis et al., 2020): It is one of three administrations within the Department of Veterans Affairs (VA), and is the largest integrated health system in the United States.

• Hip-replacement dataset (Clarke et al., 2015) from the orthopedics department of Blekinge hospital.

• Il Paese Ritrovato Dataset³ a healthcare facility located in Monza that was created for the residential care of people affected by Alzheimer's disease.

Future research prospects

The following are some directions we can explore in the future:

Drug Manufacturing Process: Changes in drugs can impact the economy of the company. Early information about the drugs could stop or increase further production.

Monitoring Health parameters during surgery: Early information about the health parameters during surgery could help during diagnosis.

Pandemic disease information: COVID-19 has disturbed regular processes in the health sector. Prior information could help to avoid further problems.

Deep Learning Techniques to address concept drift problems. New techniques to handle concept drift problems in the health industry could resolve many problems.

Conclusion

This article investigated the concept of drift-handling algorithms designed for healthcare applications. It addresses supervised learning tasks where the aim is to generate a map of the feature instances, the target variables, and unsupervised learning tasks where there is an absence of class labels in the given instances. This article addresses the machine learning algorithms used to handle concept drift for medical domain problems. It also addresses different types of concept drift and how to handle them using implicit and explicit approaches. Different techniques for handling concept drift in the medical sector can be incorporated as future scope.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author contributions

Conceptualization: AM, SB, and HL. Data curation, methodology, writing—original draft, and formal analysis: AM and NC. Funding acquisition: HL. Investigation: AM and SB. Supervision: NC and SB. Validation: HML, SB, and AM. Writing—review and editing: SB, HML, HL, and AM.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^Available online at: https://account.ache.org/iweb/upload/ReiterSong_Ch1-4e0b591e.pdf.

2. ^Available online at: https://www.cdc.gov/nchs/nhds/nhds_questionnaires.htm.

3. ^Available online at: https://www.cfsitalia.com/en/projects/il-paese-ritrovato/.

References

Agrahari, S., and Singh, A. K. (2021). Concept drift detection in data stream mining: a literature review. J. King Saud Univ. Comput. Inform. Sci. 34, 9523–9540. doi: 10.1016/j.jksuci.2021.11.006

CrossRef Full Text | Google Scholar

Alippi, C., and Roveri, M. (2008). Just-in-time adaptive classifiers-part I: detecting nonstationary changes. IEEE Trans. Neural Netw. 19, 1145–1153. doi: 10.1109/TNN.2008.2000082

PubMed Abstract | CrossRef Full Text | Google Scholar

Baena-Garcia, M., del Campo-Avila, J., Fidalgo, R., Bifet, A., Gavalda, R., and Morales-Bueno, R. (2006). “Early drift detection method,” in Proc. 4th Int. Workshop Knowledge Discovery from Data Streams.

Bayram, F., Ahmed, B. S., and Kassler, A. (2022). From concept drift to model degradation: an overview on performance-aware drift detectors. Knowledge Based Syst. 245, 108632. doi: 10.1016/j.knosys.2022.108632

CrossRef Full Text | Google Scholar

Beyene, A. A., Welemariam, T., Persson, M., and Lavesson, N. (2015). Improved concept drift handling in surgery prediction and other applications. Knowledge Inform. Syst. 44, 177–196. doi: 10.1007/s10115-014-0756-9

CrossRef Full Text | Google Scholar

Bifet, A., and Gavalda, R. (2007). “Learning from time-changing data with adaptive windowing,” in Proc. 2007 SIAM Int. Conf. Data Mining, SIAM 2007 (Minneapolis, MN). doi: 10.1137/1.9781611972771.42

CrossRef Full Text | Google Scholar

Bruno Maciel, I. F., Silas Santos, G. T. C., and Barros, R. S. M. (2015). “A lightweight concept drift detection ensemble,” in IEEE 27th International Conference on Tools with Artificial Intelligence (Vietri sul Mare). doi: 10.1109/ICTAI.2015.151

PubMed Abstract | CrossRef Full Text | Google Scholar

Brzeziński, D., and Stefanowski, J. (2011). “Accuracy updated ensemble for data streams with concept drift,” in Hybrid Artificial Intelligent Systems, HAIS, 2011, eds E. Corchado, M. Kurzyński, and M. Wozniak (Berlin; Heidelberg: Springer). doi: 10.1007/978-3-642-21222-2_19

PubMed Abstract | CrossRef Full Text | Google Scholar

Bu, L., Alippi, C., and Zhao, D. (2018). A pdf-free change detection test based on density difference estimation. IEEE Trans. Neural Netw. Learn. Syst. 29, 324–334. doi: 10.1109/TNNLS.2016.2619909

PubMed Abstract | CrossRef Full Text | Google Scholar

Clarke, A., Pulikottil-Jacob, R., Grove, A., Freeman, K., Mistry, H., Tsertsvadze, A., et al. (2015). Total hip replacement and surface replacement for the treatment of pain and disability resulting from end-stage arthritis of the hip (review of technology appraisal guidance 2 and 44): systematic review and economic evaluation. Health Technol. Assess. 19, 1–668. doi: 10.3310/hta19100

PubMed Abstract | CrossRef Full Text | Google Scholar

Davis, S. E., Greevy, R. A., Lasko, T. A., Walsh, C. G., and Matheny, M. E. (2020). Detection of calibration drift in clinical prediction models to inform model updating. J. Biomed. Inform. 112, 103611. doi: 10.1016/j.jbi.2020.103611

PubMed Abstract | CrossRef Full Text | Google Scholar

de Barros, R. S. M., Hidalgo, J. I. G., and de Lima Cabral, D. R. (2018). Wilcoxon rank sum test drift detector. Neurocomputing 275, 1954–1963. doi: 10.1016/j.neucom.2017.10.051

CrossRef Full Text | Google Scholar

de Lima Cabral, D. R., and de Barros, R. S. M. (2018). Concept drift detection based on Fisher's exact test. Inform. Sci. 442–443, 220–234. doi: 10.1016/j.ins.2018.02.054

CrossRef Full Text | Google Scholar

Ditzler, G., and Polikar, R. (2011). “Hellinger distance based drift detection for nonstationary environments,” in IEEE Symposium on Computational Intelligence in Dynamic and Uncertain Environments (CIDUE) (Paris), 41–48. doi: 10.1109/CIDUE.2011.5948491

CrossRef Full Text | Google Scholar

Dries, A., and Ruckert, U. (2009). Adaptive concept drift detection. Stat. Anal. Data Mining ASA Data Sci. J. 2, 311–327. doi: 10.1002/sam.10054

CrossRef Full Text | Google Scholar

Faria, E. R., Gama, J., and Carvalho, A. C. (2013). “Novelty detection algorithm for data streams multi-class problems,” in Proc of the 28th Annual ACM Symposium on Applied Computing (New York, NY: ACM), 795–800. doi: 10.1145/2480362.2480515

CrossRef Full Text | Google Scholar

Frías-Blanco, I., Campo-Ávila, J., Ramos-Jiménez, G., Morales-Bueno, R., Ortiz-Díaz, A., and Mota, Y. C. (2015). Online and non-parametric drift detection methods based on Hoeffding's bounds. IEEE Trans. Knowledge Data Eng. 27, 810–823. doi: 10.1109/TKDE.2014.2345382

CrossRef Full Text | Google Scholar

Gama, J., Medas, P., Castillo, G., and Rodrigues, P. (2004). “Learning with drift detection,” in Proc. 17th Brazilian Symp. Artificial Intelligence (New York, NY: Springer), 286–295. doi: 10.1007/978-3-540-28645-5_29

CrossRef Full Text | Google Scholar

Gama, J., Zliobaite, I., Bifet, A., Pechenizkiy, M., and Bouchachia, A. (2014). A survey on concept drift adaptation. ACM Comput. Surv. 46, 1–37. doi: 10.1145/2523813

CrossRef Full Text | Google Scholar

Gomes, H. M., Bifet, A., Read, J., et al. (2017). Adaptive random forests for evolving data stream classification. Mach. Learn. 106, 1469–1495. doi: 10.1007/s10994-017-5642-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Hayat, M. Z., and Hashemi, M. R. (2010). “A DCT based approach for detecting novelty and concept drift in data streams,” in International Conference of Soft Computing and Pattern Recognition (Cergy-Pontoise: IEEE), 373–378 doi: 10.1109/SOCPAR.2010.5686734

CrossRef Full Text | Google Scholar

Hidalgo, J. I. G., Mariño, L. M. P., and de Barros, R. S. M. (2019). “Cosine similarity drift detector,” in Artificial Neural Networks and Machine Learning - ICANN 2019: Text and Time Series, ICANN 2019, eds I. Tetko, V. Kurková, P. Karpov, and F. Theis (Cham: Springer). doi: 10.1007/978-3-030-30490-4_53

CrossRef Full Text | Google Scholar

Huang, G.-B., Zhu, Q.-Y., and Siew, C.-K. (2006). Extreme learning machine: theory and applications. Neurocomputing 70, 489–501. doi: 10.1016/j.neucom.2005.12.126

CrossRef Full Text | Google Scholar

Huggard, H., Koh, Y. S., Dobbie, G., and Zhang, E. (2020). “Detecting concept drift in medical triage,” in SIGIR '20: Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, 1733–1736 doi: 10.1145/3397271.3401228

CrossRef Full Text | Google Scholar

Johnson, A., Pollard, T., Shen, L., et al. (2016). MIMIC-III, a freely accessible critical care database. Sci. Data 3, 160035. doi: 10.1038/sdata.2016.35

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolter, J. Z., and Maloof, M. A. (2007). Dynamic weighted majority: an ensemble method for drifting concepts. J. Mach. Learn. Res. 8, 2755–2790.

Google Scholar

Kralj, K., and Kuka, M. (1998). “Using machine learning to analyze attributes in the diagnosis of coronary artery disease,” in Proceedings of Intelligent Data Analysis in Medicine and Pharmacology-IDAMAP98 (Brighton).

Lee, J., and Magoules, F. (2012). “Detection of concept drift for learning from stream data,” in 2012 IEEE 14th International Conference on High Performance Computing and Communication & 2012 IEEE 9th International Conference on Embedded Software and Systems (Liverpool: IEEE), 241–245. doi: 10.1109/HPCC.2012.40

CrossRef Full Text | Google Scholar

Liang, N. Y., Huang, G. B., Saratchandran, P., and Sundararajan, N. (2006). A fast and accurate online sequential learning algorithm for feedforward networks. IEEE Trans. Neural Netw. 17, 1411–1423. doi: 10.1109/TNN.2006.880583

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, A., Song, Y., Zhang, G., and Lu, J. (2017a). “Regional concept drift detection and density synchronized drift adaptation,” in Proc. 26th Int. Joint Conf. Artificial Intelligence. doi: 10.24963/ijcai.2017/317

CrossRef Full Text | Google Scholar

Liu, A., Zhang, G., and Lu, J. (2017b). “Fuzzy time windowing for gradual concept drift adaptation,” in Proc. 26th IEEE Int. Conf. Fuzzy Systems (IEEE). doi: 10.1109/FUZZ-IEEE.2017.8015596

CrossRef Full Text | Google Scholar

Liu, D., Wu, Y., and Jiang, H. (2016). FP-ELM: an online sequential learning algorithm for dealing with concept drift. Neurocomputing 207, 322–334. doi: 10.1016/j.neucom.2016.04.043

CrossRef Full Text | Google Scholar

Lu, J., Liu, A., Dong, F., Gu, F., Gama, J., and Zhang, G. (2019). Learning under concept drift: a review. IEEE Trans. Knowledge Data Eng. 31, 2346–2363. doi: 10.1109/TKDE.2018.2876857

CrossRef Full Text | Google Scholar

Lu, N., Lu, J., Zhang, G., and Lopez de Mantaras, R. (2016). A concept drift-tolerant case-base editing technique. Artif. Intell. 230, 108–133. doi: 10.1016/j.artint.2015.09.009

CrossRef Full Text | Google Scholar

Lu, N., Zhang, G., and Lu, J. (2014). Concept drift detection via competence models. Artif. Intell. 209, 11–28. doi: 10.1016/j.artint.2014.01.001

CrossRef Full Text | Google Scholar

Manly, B. F. J., and Mackenzie, D. (2000). A cumulative sum type of method for environmental monitoring. Environmetrics 11, 151–166. doi: 10.1002/(SICI)1099-095X(200003/04)11:2<151::AID-ENV394>3.0.CO;2-B

CrossRef Full Text | Google Scholar

Masud, M., Gao, J., Khan, L., Han, J., and Thuraisingham, B. M. (2011). Classifcation and novel class detection in concept-drifting data streams under time constraints. IEEE Trans. Knowledge Data Eng. 23, 859–874. doi: 10.1109/TKDE.2010.61

CrossRef Full Text | Google Scholar

Nishida, K., and Yamauchi, K. (2007). “Detecting concept drift using statistical testing,” in Discovery Science, DS 2007, eds V. Corruble, M. Takeda, and E. Suzuki (Berlin; Heidelberg: Springer).

Google Scholar

Pesaranghader, A., Viktor, H., and Paquet, E. (2017). McDiarmid drift detection methods for evolving data streams. arXiv preprint arXiv:1710.02030

Google Scholar

Pesaranghader, A., Viktor, H., and Paquet, E. (2018). Reservoir of diverse adaptive learners and stacking fast hoeffding drift detection methods for evolving data streams. Mach. Learn. 107, 1711–1743. doi: 10.1007/s10994-018-5719-z

CrossRef Full Text | Google Scholar

Pesaranghader, A., and Viktor, H. L. (2016). “Fast Hoeffding drift detection method for evolving data streams,” in Machine Learning and Knowledge Discovery in Databases. ECML PKDD 2016, eds P. Frasconi, N. Landwehr, G. Manco, and J. Vreeken (Cham: Springer). doi: 10.1007/978-3-319-46227-1_7

CrossRef Full Text | Google Scholar

Polikar, R., Udpa, L., Udpa, S. S., and Honavar, V. (2001). Learn++: an incremental learning algorithm for supervised neural networks. IEEE Trans. Syst. Man Cybernet. Appl. Rev. 31, 497–508. doi: 10.1109/5326.983933

CrossRef Full Text | Google Scholar

Prashanth, B. S., Manoj Kumar, M. V., Thomas, L., Ajay Kumar, M. A., Wu, D., Annappa, B., and Anirudh Hebbar, Y. V. (2022). Deep Learning for COVID-19. Stud. Comput. Intell. 963, 531–569. doi: 10.1007/978-3-030-74761-9_23

CrossRef Full Text | Google Scholar

Priya, S., and Uthra, R. A. (2021). Deep learning framework for handling concept drift and class imbalanced complex decision-making on streaming data. Complex Intell. Syst. 21, 1–17. doi: 10.1007/s40747-021-00456-0

CrossRef Full Text | Google Scholar

Qahtan, A. A., Alharbi, B., Wang, S., and Zhang, X. (2015). A PCA-based change detection framework for multidimensional data streams,” in Proc. 21th Int. Conf. on Knowledge Discovery and Data Mining, 935–944. doi: 10.1145/2783258.2783359

CrossRef Full Text | Google Scholar

Raab, C., Heusinger, M., and Schleif, F.-M. (2020). Reactive soft prototype computing for concept drift streams. Neurocomputing 416, 340–351. doi: 10.1016/j.neucom.2019.11.111

CrossRef Full Text | Google Scholar

Ramirez-Gallego, S., Krawczyk, B., Garc'ia, S., Wozniak, M., and Herrera, F. (2017). A survey on data preprocessing for data stream mining: current status and future directions. Neurocomputing 239, 39–57. doi: 10.1016/j.neucom.2017.01.078

CrossRef Full Text | Google Scholar

Raza, H., Prasad, G., and Li, Y. (2015). EWMA model based shift-detection methods for detecting covariate shifts in non-stationary environments. Pattern Recogn. 48, 659–669. doi: 10.1016/j.patcog.2014.07.028

CrossRef Full Text | Google Scholar

Ross, G. J., Adams, N. M., Tasoulis, D. K., and Hand, D. J. (2012). Exponentially weighted moving average charts for detecting concept drift. Pattern Recogn. Lett. 33, 191–198. doi: 10.1016/j.patrec.2011.08.019

CrossRef Full Text | Google Scholar

Ryu, J. W., Kantardzic, M. M., Kim, M. W., and Khil, A. R. (2012). “An efficient method of building an ensemble of classifers in streaming data,” in International Conference on Big Data Analytics (Berlin; Heidelberg: Springer), 122–133. doi: 10.1007/978-3-642-35542-4_11

CrossRef Full Text | Google Scholar

Saurav, S., Malhotra, P., and Vishnu, T. V. (2018). “Online anomaly detection with concept drift adaptation using recurrent neural networks,” in CoDS-COMAD '18: Proceedings of the ACM India Joint International Conference on Data Science and Management of Data (New York, NY), 78–87. doi: 10.1145/3152494.3152501

CrossRef Full Text | Google Scholar

Sethi, T. S., and Kantardzic, M. (2015). Don't pay for validation. Detecting drifts from unlabeled data using margin density. Proc. Comput. Sci. 53, 103–112. doi: 10.1016/j.procs.2015.07.284

CrossRef Full Text | Google Scholar

Sethi, T. S., Kantardzic, M., and Hu, H. (2016). A grid density based framework for classifying streaming data in the presence of concept drift. J. Intell. Inform. Syst. 46, 179–211. doi: 10.1007/s10844-015-0358-3

CrossRef Full Text | Google Scholar

Shao, J., Ahmadi, Z., and Kramer, S. (2014). “Prototype-based learning on concept-drifting data streams,” in KDD '14: Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (New York, NY), 412–421. doi: 10.1145/2623330.2623609

CrossRef Full Text | Google Scholar

Silva, J. A., Faria, E. R., Barros, R. C., Hruschka, E. R., Carvalho, P. L. F. A. C., and Gama, J. (2013). Data stream clustering: a survey. ACM Comput. Surv. 46, 1–31. doi: 10.1145/2522968.2522981

CrossRef Full Text | Google Scholar

Spinosa, E. J., de Carvalho, A. P. F., and Gama, J. (2007). “OLINDDA: a cluster-based approach for detecting novelty and concept drift in data streams,” in Proc of the ACM Symposium on Applied Computing (Seoul: ACM), 448–452. doi: 10.1145/1244002.1244107

CrossRef Full Text | Google Scholar

Stiglic, G., and Kokol, P. (2011). “Interpretability of sudden concept drift in medical informatics domain,” in IEEE 11th International Conference on Data Mining Workshops (Vancouver, BC) 609–613. doi: 10.1109/ICDMW.2011.104

CrossRef Full Text | Google Scholar

Strausberg, J., and Person, M. (1999). A process model of diagnostic reasoning in medicine. Int. J. Med. Inform. 54, 9–23. doi: 10.1016/S1386-5056(98)00166-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Street, W. N., and Kim, Y. S. (2001). “A streaming ensemble algorithm (SEA) for large-scale classification,” in KDD '01: Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (San Francisco, CA), 377–382. doi: 10.1145/502512.502568

CrossRef Full Text | Google Scholar

Toor, A. A., Usman, M., Younas, F., Fong, A. C. M., Ali Khan, S., and Fong, S. (2020). Mining massive e-health data streams for IoMT enabled healthcare systems. Sensors 20, 2131. doi: 10.3390/s20072131

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., and Abraham, Z. (2015). Concept drift detection for streaming data. arXiv preprint arXiv:1504.01044. doi: 10.48550/arXiv.1504.01044

CrossRef Full Text | Google Scholar

Wang, H., Fan, W., Yu, P. S., and Han, J. (2003). “Mining concept-drifting data streams using ensemble classifiers,” in Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD '03) (New York, NY: ACM), 226–235. doi: 10.1145/956750.956778

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, S., and Wang, J. (2017). Dynamic extreme learning machine for data stream classification. Neurocomputing 238, 433–449. doi: 10.1016/j.neucom.2016.12.078

CrossRef Full Text | Google Scholar

Yu, S., Abraham, Z., Wang, H., Shah, M., Wei, Y., and Príncipe, J. C. (2019). Concept drift detection and adaptation with hierarchical hypothesis testing. J. Franklin Inst. 356, 3187–3215. doi: 10.1016/j.jfranklin.2019.01.043

CrossRef Full Text | Google Scholar

Yu, S., Wang, X., and Príncipe, J. C. (2018). “Request-and-reverify: hierarchical hypothesis testing for concept drift detection with expensive labels,” in Proceedings of the 27th International Joint Conference on Artificial Intelligence (Stockholm), 3033–3039. doi: 10.24963/ijcai.2018/421

CrossRef Full Text | Google Scholar