- Department of Precision Instrument, Center for Brain Inspired Computing Research, Beijing Innovation Center for Future Chip, Tsinghua University, Beijing, China
Memristors show great promise in neuromorphic computing owing to their high-density integration, fast computing and low-energy consumption. However, the non-ideal update of synaptic weight in memristor devices, including nonlinearity, asymmetry and device variation, still poses challenges to the in-situ learning of memristors, thereby limiting their broad applications. Although the existing offline learning schemes can avoid this problem by transferring the weight optimization process into cloud, it is difficult to adapt to unseen tasks and uncertain environments. Here, we propose a bi-level meta-learning scheme that can alleviate the non-ideal update problem, and achieve fast adaptation and high accuracy, named Rapid One-step Adaption (ROA). By introducing a special regularization constraint and a dynamic learning rate strategy for in-situ learning, the ROA method effectively combines offline pre-training and online rapid one-step adaption. Furthermore, we implemented it on memristor-based neural networks to solve few-shot learning tasks, proving its superiority over the pure offline and online schemes under noisy conditions. This method can solve in-situ learning in non-ideal memristor networks, providing potential applications of on-chip neuromorphic learning and edge computing.
Introduction
Memristors are considered as leading device candidates for neural network accelerators (Yang et al., 2013; Chen et al., 2015; Tsai et al., 2018; Zidan et al., 2018) due to their ability to physically store synaptic weights in conductance state, which enable in-memory computing. Implementation of neural networks in memristor-based hardware exhibits high density integration, low power consumption and high efficiency (Cai et al., 2019; Yu 2018). It can also greatly promote the development of brain-inspired computing systems to achieve human-like intelligence (Zhang et al., 2016). However, memristors possess some non-ideal properties that challenge the hardware implementations. The weight updates on memristors are asymmetric, nonlinear and low precision, significantly degrading the learning accuracy (Kataeva et al., 2015; Agarwal et al., 2016; Wang et al., 2020a). Additionally, the outputs of networks, determined by input currents and conductance of memristors, are also perturbed by the variability of circuits, including input currents, reference voltage, output resistance (Yang et al., 2013; Agarwal et al., 2016).
Currently, there are mainly two types of co-optimization learning schemes to overcome these challenges (Hu et al., 2016; Zidan et al., 2018; Agarwal et al., 2016; Chen et al., 2015). One type is online learning, which allows training models to be implemented on neuromorphic hardware by using backpropagation (Yu et al., 2016) or biological local learning, such as spike-timing-dependent plasticity (STDP) (Guo et al., 2017). For fast online learning, conductance tuning with less operations on hardware is preferred, which the weights of networks are directly written without verification by reading. However, the nonlinearity and asymmetry of memristors cause the accuracy loss of the neural networks during learning (Yu et al., 2016; Kataeva et al., 2015). To mitigate the adverse effects of memristors, various approaches have been reported. Some work initialized the weights at each update step to achieve linear and symmetric weights (Li et al., 2019; Geminiani et al., 2018). Retraining of networks and developing highly robust algorithms, such as Neural State Machine, have also been proved to overcome the asymmetric properties of memristors to a certain degree (Liu et al., 2017; Tian et al., 2020; Tian et al., 2021). The other type is offline learning, which maps the pre-trained network to hardware, and only performs inference in neuromorphic chips (Hu et al., 2016; Shafiee et al., 2016; Chi et al., 2016). The non-ideality of weight updates can be concealed by iterative programming with a write-verify technique, reading the conductance and rewriting for accuracy. However, for a new task, the entire process must be restarted from scratch through offline learning. For most algorithms, all tunable parameters in the neural network must be re-trained for a new task, resulting in a large number of operations. Therefore, there is usually a trade-off between speed and performance for memristor networks from offline learning to online learning.
Different from the current on-chip learning schemes, humans can quickly adapt to the environment by drawing on prior experience or learning to learn. In machine learning, this learning approach is named meta-learning (Thrun and Pratt 1998), which has made significant progress in recent years (Wang et al., 2020b; Hospedales et al., 2020; Vanschoren, 2018). There are many meta-learning techniques, such as optimizee (Andrychowicz et al., 2016; Ravi and Larochelle 2017), metric based (Hu et al., 2020; Vinyals et al., 2016; Snell et al., 2017) and fine-tuning (Antoniou et al., 2018; Li et al., 2017; Finn et al., 2017; Nichol et al., 2018). Particularly, Model-Agnostic Meta-Learning (MAML) (Finn et al., 2017) is a general meta-learning framework that provides a good initial condition of network for fine-tuning on similar tasks, which can simplify the optimization to a few steps for new unseen tasks. MAML can also be applied to fields such as reinforcement learning (Gupta et al., 2018) and continual learning (Al-Shedivat et al., 2018). The studies on the silicon-based neuromorphic chips have proven that meta-learning schemes can significantly accelerate the learning of new tasks and improve their performance (Bohnstingl et al., 2019; Stewart et al., 2020). However, optimization methods for memristor-based networks with the meta-learning scheme have yet to be developed.
In this work, we propose a meta-learning scheme for memristor-based neural networks that can overcome the non-ideal synapse weights for training and provide improved performance. Our method consists of two phases, including pre-training and task adaptation, as shown in Figure 1. Firstly, a good initial network for a group of tasks is trained in software and then mapped to hardware by iterative programming with write-verify. Then, a rapid training in one-step adaption is performed for an unseen task with a few samples of the in-situ hardware network. This scheme can free the memristor networks from unnecessary operations, mitigating the problem of performance degradation in online learning. It also has the ability to accomplish new tasks through quick adaptations, which is more powerful than the offline trained networks. Since only one update step is needed, a new task requires significantly less training time, only a few samples and little computation consumption. These merits make our scheme very suitable for situations with limited computing power and limited data, such as edge computing. Our main contributions are as follows:
1. We propose a hybrid learning scheme of offline learning and online learning for meta-learning on memristor-based neural networks. It combines the advantages of offline learning and online learning for the hardware to achieve high accuracy and fast adaption for unseen tasks.
2. We report the Rapid One-step Adaption (ROA) algorithm, which enables memristor-based neural networks with meta-learning capability. It mitigates the effects of non-ideal characteristics of memristor-based neural networks, and achieves superior performance by introducing dynamic learning rate, regularization constraint and one-step adaption.
3. In order to evaluate our model on few-shot tasks, we built a simulator based on the experimental characteristics of memristor, which can better support the acceleration of large-scale network and the quantitative analysis of networks with noise. On this basis, we comprehensively evaluate the proposed model on two typical few-shot learning datasets. Our results reveal a good performance of memristor networks on few-shot learning task with significant improvement of accuracy than the baseline.
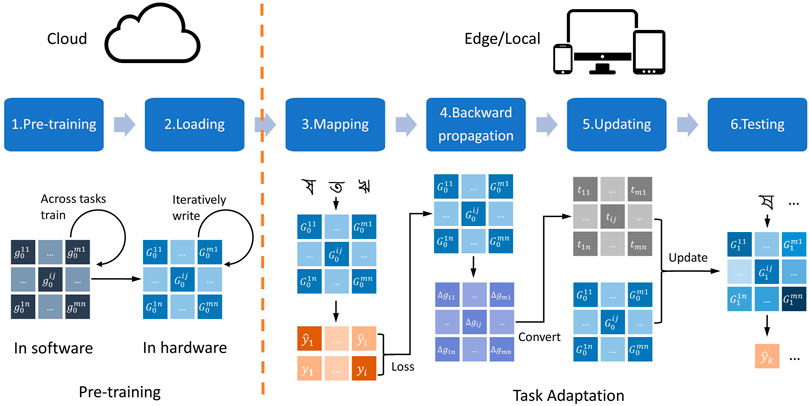
FIGURE 1. The framework of ROA (Rapid One-step Adaption). In the pre-training phase: (1) we train a good initial network across tasks with parameters
Experimental Setup
In this section, we discuss the setup of memristors for the simulation experiment. In Memristor Model, we introduce the model of memristors for simulation based on our experimental data and discuss the properties of memristors in this work. In Simulator for Memristor Networks, we introduce the simulator for this work, including weight update, noise setting and mapping.
Memristor Model
In this work, we implemented a two-terminal
where
where
In the measurement of the device, we applied negative pulses in increasing amplitudes from −0.8 to −3.8 V (in 0.1 V increments) and 100 µs width for the potentiation process, and positive pulses in decreasing amplitudes from 3.5 to 0.8 V (in 0.1 V decrements) and 100 µs width for the depression process. A model of the memristor behavior was built based on the experimental data. As shown in Figure 2B, the simulation results of the memristor are in good agreement with the experimental data, indicating that the model can properly reproduce the behavior of the device.
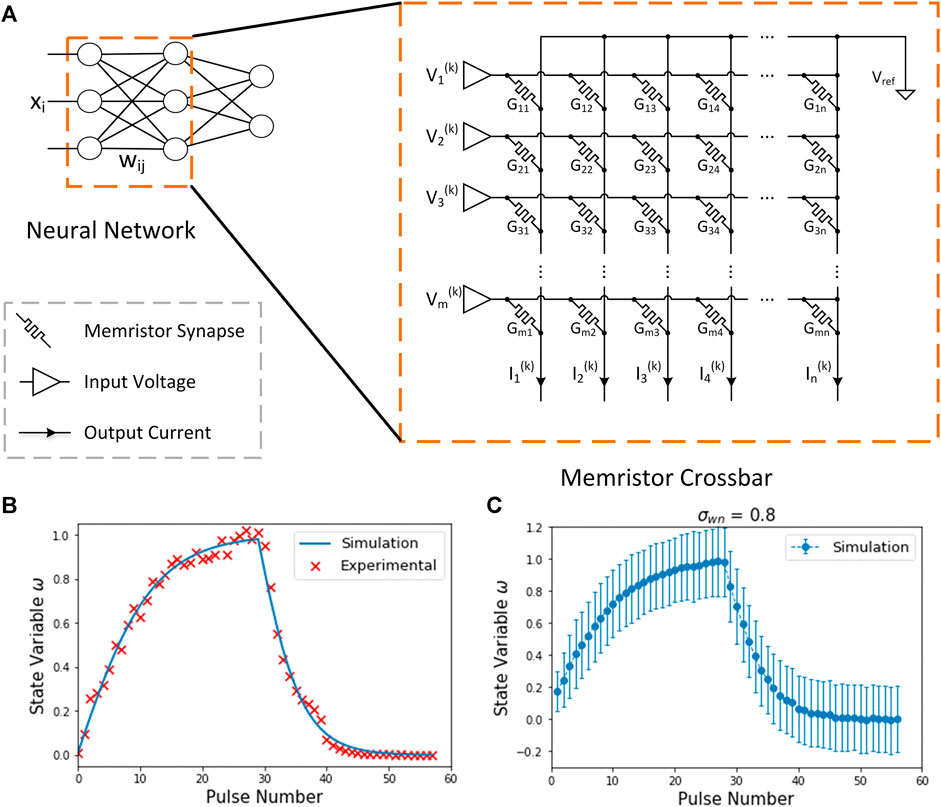
FIGURE 2. (A) Memristor Crossbar. The weights of neural network are mapped to memristor crossbar arrays as conductance
Memristors have a strong non-linear conductance. Particularly, the conductance change is more subtle when the conductance state is approaching its maximum or minimum value. Memristors also have an asymmetric conductance change behavior. The potentiation and depression pulses cause the conductance to change with different magnitudes depending on the direction of change. On the other hand, the variation in memristor devices is inherently a stochastic process due to the movement of atoms or oxygen vacancies. This process is interfered by various noises, and usually modeled using normal distribution (Agarwal et al., 2016). In addition, the updated states of memristor synapses are discrete because of the limited conductance levels and discrete programming pulse width. All these features will be considered in our simulation.
Simulator for Memristor Networks
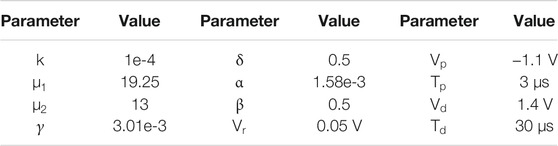
We built a simulator using Pytorch (Paszke et al., 2019) for the simulation of training and inference processes, and further quantitatively analyzed the effects of the non-ideal characteristics of the device. The simulator supports the GPU acceleration for large-scale network in Pytorch. The pulses of potentiation and depression were set with fixed amplitude and duration. The parameters of the memristor are shown in Table 1.
Normally, a crossbar structure is adopted in memristor networks, as shown in Figure 2A. The conductance state of a memristor represents the synaptic value in neural networks. The inputs are mapped to the input voltages and the outputs are represented by currents. In a crossbar structure, the transmitted signal is determined by the product of input signals and synaptic weights through Ohm’s law and Kirchhoff’s law. Thus, multiply-accumulations (MACs) can be physically performed at the weight locations, greatly reducing computing operations and energy consumption. For multilayer networks, the output currents of the previous layer can be converted to voltage for the input of the next layer. Each layer follows the configuration in the inference process until the final layer.
According to Eq. 2, the relation between voltage and current of a memristor is approximately linear when voltage is low (such as below 0.1 V). Then the conductance of a synapse in the crossbar can be read with read voltage
The state
During the updating process, the expected changing state
The (potentiation/depression) update pulses are defined as identical with fixed amplitudes (
To simulate the variation in real devices, we introduce write noise at each step of weight change following the work of Agarwal et al. (2016):
where
The input voltage
The synaptic weights,
where
The current collected at the output of each column
The output results
In the configuration of the simulation, the initial weights
Methods
In this section, we introduce ROA, the proposed meta-learning algorithm for memristor neural networks, and MAML, a typical meta-learning algorithm, together with its derivatives that are the basis of our algorithm.
Model-Agnostic Meta-Learning
Considering a supervised learning task
where
Generalization power of the model is the key to the realization of this hypothesis.
In conventional deep learning, the optimization of each task
MAML (Finn et al., 2017) is a typical meta-learning framework for few-shot learning tasks, which can be rapidly updated for a few-shot task by learning good initialization parameters
where
In the meta-training phase, it updates the initial parameters
where
Compared to other meta-learning frameworks (Vinyals et al., 2016; Ravi and Larochelle 2017; Snell et al., 2017), the fine-tuning based framework, such as MAML, can be more easily applied to other optimization methods. It has been proved that fine-tuning can improve the performance of other few-shot learning methods, such as transfer learning (Sun et al., 2019). Besides the supervised learning for classification, MAML also has the potential for rapid adaptation in reinforcement learning (Gupta et al., 2018) and imitation learning for robots (Yu et al., 2018). Hence, fine-tuning based meta-learning is expected to be applied to more fields than other meta-learning approaches. There are many studies to improve the performance of MAML (Li et al., 2017; Nichol et al., 2018; Antoniou et al., 2018). Here, our work is essentially developed from MAML++(Antoniou et al., 2018), including batch normalization, layer-wise learning rate, etc.
ROA: Rapid One-Step Adaption
Our proposed ROA method is a hybrid approach that implements offline learning in software and online learning in memristor hardware by introducing a special regularization constraint and a dynamic learning rate strategy for in-situ learning. Like most meta-learning methods, the learning scheme has two phases. In the pre-training phase, the network is trained from scratch in software. By learning from a group of tasks, it builds a good initial network, which can be rapidly updated for a new task. Then we map the initial network to the hardware through iterative programming with a write-verify technique to achieve high precision. This is inspired by the initial structure formed through evolution to provide a good foundation for the rapid learning ability of human beings (Jeong and Hwang 2018). The learned initial network is expected to provide the hardware with a rapid learning ability. In the task-adaptation phase, in-situ learning is performed in the memristor arrays. The hardware system would solve a new task with fewer data points in one update. We map the input samples to the input voltage of the memristor network and make predictions based on the output currents. Then we calculate the gradient descent by backpropagation and convert them into the number of update pulses for the specific task in the program. Finally, the hardware network is updated by one step for testing.
In our learning scheme, the initial network would be prepared in advance for the targeted tasks. Pre-training of the network can be completed before applications, such as in cloud. Therefore, for on-chip task-adaptation, only a few training samples are needed due to the previous experience gained from the pre-training. This way, the computation costs and time consumption are greatly reduced as compared to the previously reported methods. It can also be easily deployed on local or edge servers. It is worth noting that our ROA approach can also be transferred to other rapid learning strategies with fine-tuning, such as transfer learning (Pan and Yang 2010), which uses a previously trained back-bone network to quickly adapt to unseen domain.
The proposed ROA method thereby combines the advantages of offline and online training of the memristor networks. As compared to the inference-only memristor network, it achieves a similar performance due to the write-verified initial network with high precision that is implemented on hardware, and a more powerful generalization due to adaption for a new task. Meanwhile, the fast in-situ adaptation of ROA reduces the entanglement between the network and the hardware, thereby mitigating the accuracy loss caused by the nonlinearity and asymmetry of online learning of the memristor hardware. In the cases of limited resources, the performance of ROA is expected to exceed both online and offline methods.
To further mitigate the effects of discrete weight updates with asymmetric nonlinearity in hardware network, we develop the following two measurement methods for training:
Regularization Constraint
Because of the nonlinearity, the changes of memristor conductance are not proportional to the number of input pulses. As shown in Figure 2B, the conductance change close to the extreme value is more subtle than the change along the opposite direction. In other words, the precision of memristor weights depends on the state of the memristor and updating direction. In addition, compared with the simulation results, the range of weights in hardware is limited. A good initial state by limiting the weight update is expected to make the update of memristor synapses more stable. Hence, we propose a regularization constraint of the initial weights in the loss function of the meta-training as follows:
where
which restricts the initial weights in the range of
Learning Rate Adjustment
The duration and amplitudes of pulses are fixed in the simulation. So, there is a number rounding to convert weight updating to integer numbers. However, the weight updating in the fine-tuning is usually too small to be retained in the rounding pulse number. The good news is that we can increase the inner learning rate to neutralize the influence partially. On the other hand, when the variation of devices is too large, the excessive change of weights would cause larger noises, which will adversely affect the performance. Thus, we set the inner learning rate according to the device properties, which expands at low noise levels and shrinks at high noise levels. The learning rate of the inner loop follows the setup in Antoniou et al. (2018), which is learnable for each step and each layer. We multiply the inner learning rate by a factor, called the relative learning rate. The best relative learning rate is determined by the noise level and task complexity as shown in Figure 3, which was based on experience. The details are reported in the next section.

FIGURE 3. Comparison of the accuracy of 5-step update and 1-step update in different write noise and their best relative learning rate in different write noise. (A, E) 5way-1shot on Omniglot. (B, F) 10way-1shot on Omniglot. (C, G) 20way-1shot on Omniglot. (D, H) 5way-1shot on MiniImageNet.
Experiment
In this section, we describe the implementation details of the experiments and the results of our ROA model on few-shot learning tasks. A supervised few-shot learning task can be defined as an
Experiment Details
We conducted experiments on the Omniglot dataset (Lake et al., 2011) and miniImageNet (Ravi and Larochelle 2017). The Omniglot dataset is composed of 1,623 handwritten character classes from different alphabets. In each class, there are 20 instances in the dataset. We shuffled all classes and randomly split them into three parts: 1,150 for the training set, 50 for the validation set and 423 for testing. 15 samples are randomly picked in each class as the query set, and the rest are used as the support set according to the setting of the task. The MiniImageNet dataset is composed of 64 training classes, 12 validation classes, and 24 test classes, which is a subset of ImageNet. We evaluated our method on 5way-1shot, 10way-1shot and 20way-1shot learning tasks on the Omniglot and 5way-1shot learning task on the MiniImageNet.
The base model follows the same architecture in Antoniou et al. (2018), which has a 4-layer convolutional neural network with a
Result Analysis
In this section, we compare ROA with offline learning and online learning. The task of the traditional learning method for memristor networks is quite different from the few-shot learning, which is usually a supervised task with a large training dataset. For offline learning, we write a well-trained network on few-shot task by using MAML to the memristor array with limited write-verify steps. More inner update steps in meta-learning are believed to help to improve performance. Here, more update steps are added on memristors as an online learning scheme for comparison.
Comparison With Hardware Inference
In the comparison between offline learning and ROA, we used the same few-shot task but trained a network with ideal conditions in the simulator as the offline network. The parameters in the initial network for an offline learning follow a Gaussian distribution, while the initial network is the pre-trained network in ROA. Obviously, the offline inference can achieve results comparable to software, and there are enough of iterative writing steps to eliminate the variations in memristors. For comparison, they have the same number of update steps on hardware. Then, the trained network is mapped to the memristor array by one step writing. The ROA also updates its weights in the memristor array in one step. The tasks and training settings of the two networks are identical. The results are shown in Figure 4. We can see that due to the limitation of the iterative update steps, the offline schemes could not achieve similar performance when the write noise is zero. The accuracy rapidly drops when the noise increases. When the write noise is more than 0.3, its performance is close to random guessing. For a new unseen task, ROA only needs one update step, which is much more efficient than the offline scheme.
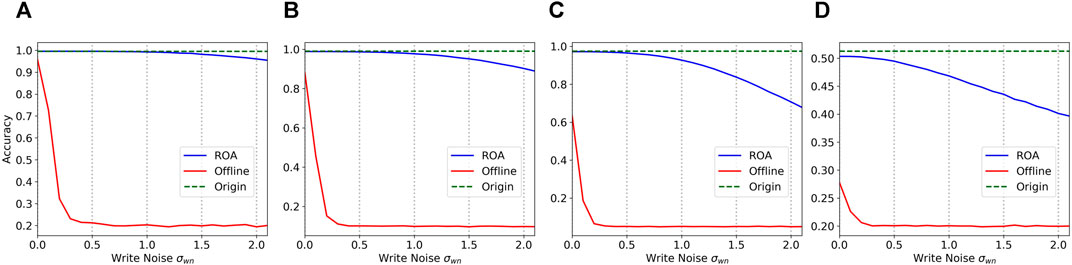
FIGURE 4. Comparison of the accuracy of 5-step update offline and ROA in different write noise. (A) 5way-1shot on Omniglot. (B) 10way-1shot on Omniglot. (C) 20way-1shot on Omniglot. (D) 5way-1shot on MiniImageNet.
Comparison With -More Update Steps
Here, we compare the results of 1-step update and 5-step update. The weights are updated in one step with ROA while the weights are updated in five steps with online learning schemes. The initial networks are pre-trained for their schemes separately. The results are shown in Table 2, Figure 3. There is no significant discrimination between the two different conditions when the noise level is at low. The greater the noise, the lower the accuracy. Depending on the task, the accuracy of 5-step update will drop significantly when the noise reaches a certain level. The accuracy of 1-step update decreases more slowly. The more classes in the task, the smaller the decrease in the threshold of 5-step update. Their best learning rate under different write noises also has a similar declining trajectory. The intuitive explanation is that the accumulation of errors in multiple steps causes the rapid decline. Multi-step updates are not suitable for noisy hardware networks, especially in the case of complex tasks. In other words, it is not a good choice to train a network entirely on the memristor with hundreds of updates in accordance with the online learning methods.
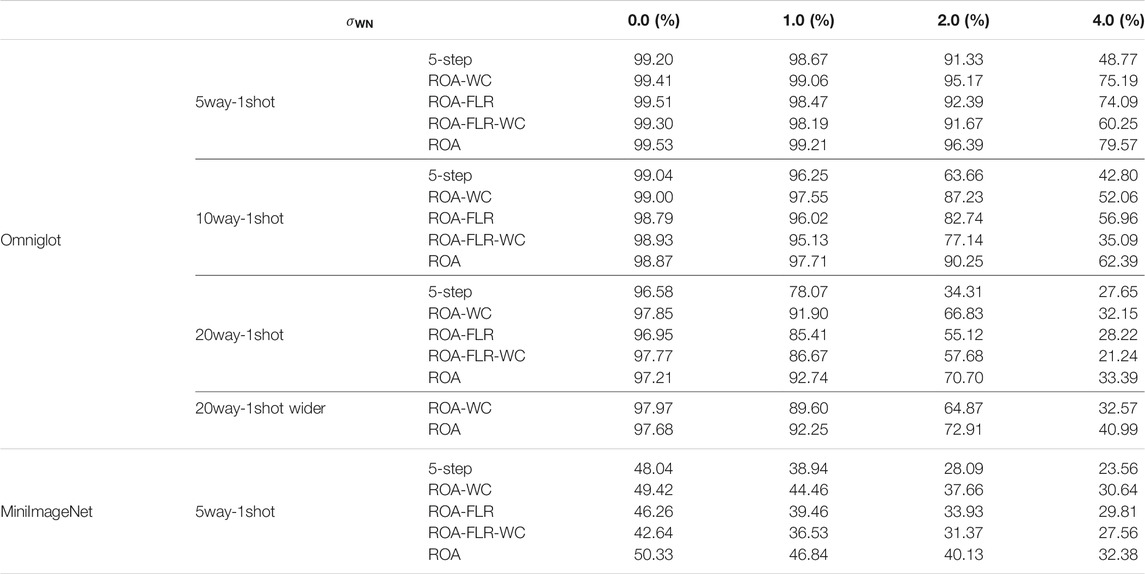
TABLE 2. Comparison of the accuracy of ROA, 5-step update, ROA without constraint (ROA-WC) and fixed learning rate (ROA-FLR) in different write noise.
Ablation Study
In this section, we further conduct several ablation experiments to demonstrate the functionality of our method. We compare ROA with ROA without constraint (ROA-WC), no adjustment on learning rate (ROA-FLR) and MAML baseline (ROA-WC-FLR) in different write noise, respectively. The results are shown in Figure 5.

FIGURE 5. Comparison of the accuracy of ROA, ROA without constraint (ROA-WC), no adjustment on learning rate (ROA-FLR) and baseline (ROA-WC-FLR) in different write noise. (A) 5way-1shot on Omniglot. (B) 10way-1shot on Omniglot. (C) 20way-1shot on Omniglot. (D) 20way-1shot with the wider network on Omniglot. (E) 5way-1shot on MiniImageNet.
Impact of Constraint
We investigated the impact of constraints on the accuracy of one-shot tasks in different ways. The comparisons of accuracy are shown in Figure 5, Table 2. The constraint used is Eq. 18 with
Impact of Learning Rate Adjustment
The best learning rate is determined by the validation set in the experiment. Figure 3 plots the learning rates against write noises. As the noise increases, the best learning rate increases slightly at the beginning,
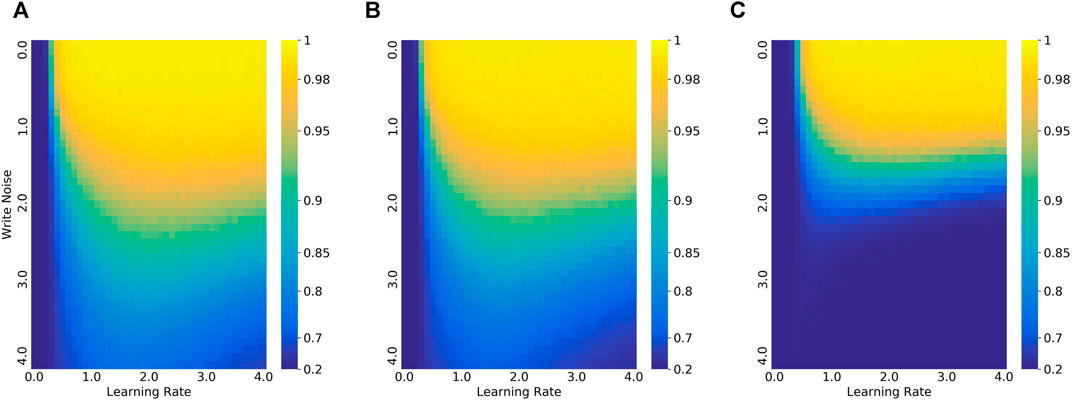
FIGURE 6. The impact of write noise and learning rate on 5way-1shot Omniglot task. (A) ROA. (B) ROA without constraint (ROA-WC). (C) 5-step update ROA.
Discussion and Conclusion
In this work, we developed a bi-level meta-learning scheme, ROA, for memristor neural networks. It is a hybrid approach that combines online learning and offline learning, which can effectively alleviate the impact of the non-ideal properties of memristors through one update step. A simulator was built based on the parameters extracted from our memristor devices and evaluated using the Omniglot dataset and MiniImageNet dataset. Our experimental results demonstrate that the ROA method can significantly improve data efficiency and training speed, thereby achieving better performance than multi-step adaption and offline learning under similar conditions. In addition, our method shows a strong robustness to noise, which facilitates the real-world applications of memristor networks. The results suggest that, with the proposed, the memristors are suitable as an accelerator for rapid learning hardware rather than just a hardware inference or in-situ learning with massive updates.
Moreover, memristor networks and the ROA method can benefit from each other. The rapid adaption of ROA requires that the weights in the neuromorphic hardware have on-chip plasticity, which can be easily achieved by memristor networks. On the other hand, the one-step adaption allows the hardware network to extricate the weight update from the non-ideal properties of memristors, thereby reducing the accuracy loss in the mapping process. Collectively, memristors are very suitable for accelerators to achieve learning-to-learn capability. Our ROA scheme can improve the performance of memristors, and facilitate broad applications in neuromorphic architecture. The rapid adaptation process could be implemented in a local mode without the support of cloud servers, indicating a low adaptation latency. Hence, the users’ personal data do not need to be uploaded to server, ensuring privacy and security. Furthermore, the flexible learning scheme can benefit hardware neural networks to handle uncertain environments and individual demands.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
WZ was in charge of the simulated experiment and performed the analysis. YaW was in charge of the simulator of devices. XJ contributed to experiment data of real memristor. WZ and YuW wrote the manuscript. RZ directed this work and revised it. All authors contributed to the article and approved the submitted version.
Funding
This work was partly supported by the National Nature Science Foundation of China (No. 61836004, No. 62088102), National Key R&D Program of China 2018YFE0200200, Brain-Science Special Program of Beijing under Grant Z181100001518006, Z191100007519009, and CETC Haikang Group-Brain Inspired Computing Joint Research Center.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Agarwal, S., Plimpton, S. J., Hughart, D. R., Hsia, A. H., Richter, I., Cox, J. A., et al. (2016). “Resistive Memory Device Requirements for a Neural Algorithm Accelerator,” in 2016 International Joint Conference on Neural Networks (IJCNN), IEEE, 2016, Vancouver, BC, Canada doi:10.1109/ijcnn.2016.7727298
Al-Shedivat, M., Bansal, T., Burda, Y., Sutskever, I., Mordatch, I., and Abbeel, P. (2018). “Continuous Adaptation via Meta-Learning in Nonstationary and Competitive Environments.” in 6th International Conference on Learning Representations, 2018., Vancouver, BC, Canada, April 30–May 3, 2018.
Andrychowicz, M., Denil, M., Gomez, S., Hoffman, M. W., Pfau, D., Tom, S., et al. (2016). “Learning to Learn by Gradient Descent by Gradient Descent”. Advances in Neural Information Processing Systems 29: Annual Conference on Neural Information Processing Systems 2016, Barcelona, Spain, December 5–10, 2016.
Antoniou, A., Edwards, H., and Amos, S. (2018). “How to Train Your MAML,” in 7th International Conference on Learning Representations, 2019, New Orleans, LA, May 6–9, 2019.
Bohnstingl, T., Scherr, F., Pehle, C., Meier, K., and Maass, W. (2019). Neuromorphic Hardware Learns to Learn. Front. Neurosci. 13 (483). Available at: https://www.frontiersin.org/article/10.3389/fnins.2019.00483. doi:10.3389/fnins.2019.00483
Cai, F., Correll, J. M., Lee, S. H., Lim, Y., Bothra, V., Zhang, Z., et al. (2019). A Fully Integrated Reprogrammable Memristor-CMOS System for Efficient Multiply-Accumulate Operations. Nat. Electron. 2 (7), 290–299. doi:10.1038/s41928-019-0270-x
Chen, P.-Y., Kadetotad, D., Xu, Z., Mohanty, A., Lin, B., Ye, J., et al. 2015, Technology-design Co-optimization of Resistive Cross-point Array for Accelerating Learning Algorithms on Chip, 2015 Design, Automation & Test in Europe Conference & Exhibition (DATE). IEEE,.Grenoble, France doi:10.7873/date.2015.0620
Chi, P., Li, S., Xu, C., Zhang, T., Zhao, J., Liu, Y., et al. (2016). Prime: A novel processing-in-memory architecture for neural network computation in reram-based main memory. 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA), Seoul, Korea (South), 18-22 June 2016 (IEEE), 27–39. doi:10.1145/3007787.3001140
Choi, S., Sheridan, P., and Lu, W. D. (2015). Data Clustering Using Memristor Networks. Sci. Rep. 5, 10492. doi:10.1038/srep10492
Finn, C., Abbeel, P., and Levine, S. (2017). Model-agnostic Meta-Learning for Fast Adaptation of Deep Networks. Proceedings of 34th International Conference on Machine Learning, 2017, Sydney, NSW, August 6–11, 2017.
Geminiani, A., Casellato, C., Antonietti, A., D’Angelo, E., and Pedrocchi, A. (2018). A Multiple-Plasticity Spiking Neural Network Embedded in a Closed-Loop Control System to Model Cerebellar Pathologies. Int. J. Neur. Syst. 28 (05), 1750017. doi:10.1142/s0129065717500174
Guo, X., Merrikh Bayat, F., Bavandpour, M., Klachko, M., Mahmoodi, M. R., Prezioso, M., et al. (2017), Fast, Energy-Efficient, Robust, and Reproducible Mixed-Signal Neuromorphic Classifier Based on Embedded NOR Flash Memory Technology, 2017 IEEE International Electron Devices Meeting (IEDM). IEEE, San Francisco, CA, USA doi:10.1109/iedm.2017.8268341
Gupta, A., Russell, M., Liu, Y. X., Abbeel, P., and Levine, S. (2018). Meta-Reinforcement Learning of Structured Exploration Strategies. Advances in Neural Information Processing Systems 31: Annual Conference on Neural Information Processing Systems 2018, NeurIPS 2018, Montreal, Canada, December 3–8, 2018.
Hospedales, T., Antoniou, A., Paul, M., and Amos, S. (2020). Meta-learning in Neural Networks: A Survey. arXiv preprint arXiv:2004.05439. Available at: https://arxiv.org/abs/2004.05439. (Accessed October 8, 2021).
Hu, Y., Gripon, V., and Pateux, S. (2021). Leveraging the Feature Distribution in Transfer-Based Few-Shot Learning. Artificial Neural Networks and Machine Learning - {ICANN} 2021 - 30th International Conference on Artificial Neural Networks, Bratislava, Slovakia, September 14–17, 2021. doi:10.1007/978-3-030-86340-139
Hu, E., Strachan, J. P., Li, Z., Grafals, E. M., Davila, N., Graves, C., Lam, S., et al. (2016). Dot-product Engine for Neuromorphic Computing: Programming 1T1M Crossbar to Accelerate Matrix-Vector Multiplication, 2016 53nd ACM/EDAC/IEEE Design Automation Conference (DAC), IEEE, Austin, TX, USA, 2016
Jeong, D. S., and Hwang, C. S. (2018) Nonvolatile Memory Materials for Neuromorphic Intelligent Machines, Adv. Mater., 30. e1704729. doi:10.1002/adma.201704729
Kataeva, I., Merrikh-Bayat, F, Zamanidoost, E., and Strukov, D. (2015). Efficient Training Algorithms for Neural Networks Based on Memristive Crossbar Circuits, International Joint Conference on Neural Networks (IJCNN), IEEE, Killarney, Ireland, July 12–17, 2015, doi:10.1109/ijcnn.2015.7280785
Kim, S., Abbas, Y., Jeon, Y.-R., Sokolov, A. S., Ku, B., and Choi, C. (2018). Engineering Synaptic Characteristics of TaOx/HfO2 Bi-layered Resistive Switching Device. Nanotechnology 29 (41), 415204. doi:10.1088/1361-6528/aad64c
Lake, B., Salakhutdinov, R., Gross, J., and Tenenbaum, J. (2011). One Shot Learning of Simple Visual Concepts. Proceedings of the Annual Meeting of the Cognitive Science Society, Boston, Massachusetts, July 20–23, 2011.
Li, C., Wang, Z., Rao, M., Belkin, D., Song, W., Jiang, H., et al. (2019). Long Short-Term Memory Networks in Memristor Crossbar Arrays. Nat. Mach Intell. 1 (1), 49–57. doi:10.1038/s42256-018-0001-4
Li, Z., Zhou, F., Chen, F., and Li, H. (2017). Meta-sgd: Learning to Learn Quickly for Few-Shot Learning. arXiv preprint arXiv:1707.09835.
Liu, C., Hu, M., Strachan, J. P., and Li, H. (2017). Rescuing Memristor-Based Neuromorphic Design with High Defects, 2017 54th ACM/EDAC/IEEE Design Automation Conference (DAC). doi:10.1145/3061639.3062310
Nichol, A., Achiam, J., and Schulman, J. (2018). "On First-Order Meta-Learning Algorithms." arXiv preprint arXiv:1803.02999.
Pan, S. J., and Yang, Q. (2010). A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 22 (10), 1345–1359. doi:10.1109/tkde.2009.191
Paszke, A., Gross, S., Massa, F., Adam, L., James, B., Gregory Chanan, , et al. (2019). Pytorch: An Imperative Style, High-Performance Deep Learning Library. Advances in Neural Information Processing.” in Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, Vancouver, BC, Canada, December 8–14, 2019.
Ravi, S., and Larochelle, H. (2017). “Optimization as a Model for Few-Shot Learning.” in 5th International Conference on Learning Representations, Toulon, France, April 24–26, 2017.
Shafiee, A., Nag, A., Muralimanohar, N., Balasubramonian, R., Strachan, J. P., Hu, M., et al. (2016). ISAAC: A Convolutional Neural Network Accelerator with In-Situ Analog Arithmetic in Crossbars. 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA) 14–26. doi:10.1145/3007787.3001139
Snell, J., Kevin, S., and Zemel, R. (2017). Prototypical Networks for Few-Shot Learning. Advances in Neural Information Processing Systems 30. Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, December 4–9, 2017.
Stewart, K., Orchard, G., Shrestha, S. B., and Neftci, E. (2020). "On-chip Few-Shot Learning with Surrogate Gradient Descent on a Neuromorphic Processor." 2020 2nd IEEE International Conference on Artificial Intelligence Circuits and Systems (AICAS). doi:10.1109/aicas48895.2020.9073948
Sun, Q., Liu, Y., Chua, T.-S., and Schiele, B. (2019). "Meta-transfer Learning for Few-Shot Learning." Proceedings of the IEEE conference on computer vision and pattern recognition. doi:10.1109/cvpr.2019.00049
Thrun, S., and Pratt, L. (1998). Learning to Learn. Boston, MA: Springer. doi:10.1007/978-1-4615-5529-2
Tian, L., Wang, Y., Shi, L., and Zhao, R. (2020). High Robustness Memristor Neural State Machines. ACS Appl. Electron. Mater. 2 (11), 3633–3642. doi:10.1021/acsaelm.0c00700
Tian, L., Wu, Z., Wu, S., and Shi, L. (2021). Hybrid Neural State Machine for Neural Network. Science China Information Sciences 64 (3), 1–13. doi:10.1007/s11432-019-2988-1
Tsai, H., Ambrogio, S., Narayanan, P., Shelby, R. M., and Burr, G. W. (2018). Recent Progress in Analog Memory-Based Accelerators for Deep Learning. J. Phys. D: Appl. Phys. 51 (28), 283001. doi:10.1088/1361-6463/aac8a5
Vinyals, O., Blundell, C., Lillicrap, T., and Wierstra, D. (2016). Matching Networks for One Shot Learning. Advances in Neural Information Processing Systems, 29: Annual Conference on Neural Information Processing Systems 2016, Barcelona, Spain, December 5-10, 2016.
Wang, Y., Wu, S., Tian, L., and Shi, L. (2020a). SSM: a High-Performance Scheme for In-Situ Training of Imprecise Memristor Neural Networks. Neurocomputing 407: 270–280. doi:10.1016/j.neucom.2020.04.130
Wang, Y., Yao, Q., Kwok, J. T., and Ni, L. M. (2020b). "Generalizing from a Few Examples: A survey on few-shot learning." ACM Comput. Surv. 53 (3): 1–34. doi:10.1145/3386252
Yang, J. J., Strukov, D. B., and Stewart, D. R. (2013). "Memristive Devices for Computing." Nat. Nanotech 8 (1): 13–24. doi:10.1038/nnano.2012.240
Yu, S., Li, Z., Chen, P.-Y., Wu, H., Gao, B., Wang, D., et al. (2016). Binary Neural Network with 16 Mb RRAM Macro Chip for Classification and Online Training, 2016 IEEE International Electron Devices Meeting (IEDM), IEEE, San Francisco, CA, USA, December 3 2016, doi:10.1109/iedm.2016.7838429
Yu, S. (2018). Neuro-inspired Computing with Emerging Nonvolatile Memorys. Proc. IEEE 106 (2), 260–285. doi:10.1109/jproc.2018.2790840
Yu, T., Finn, C., Xie, A., Dasari, S., Zhang, T., Abbeel, P., et al. (2018). "One-shot Imitation from Observing Humans via Domain-Adaptive Meta-Learning." arXiv preprint arXiv:1802.01557. doi:10.15607/rss.2018.xiv.002
Zhang, B., Shi, L., and Song, S. (2016). Creating More Intelligent Robots through Brain-Inspired Computing. in Science 354:1445. doi:10.1126/science.354.6318.1445-b
Keywords: memristor, meta-learning, fast adaptation, few-shot learning, neuromorphic
Citation: Zhang W, Wang Y, Ji X, Wu Y and Zhao R (2021) ROA: A Rapid Learning Scheme for In-Situ Memristor Networks. Front. Artif. Intell. 4:692065. doi: 10.3389/frai.2021.692065
Received: 04 May 2021; Accepted: 10 September 2021;
Published: 15 October 2021.
Edited by:
Sriraam Natarajan, The University of Texas at Dallas, United StatesReviewed by:
Kenneth Stewart, University of California, Irvine, United StatesSrijita Das, University of Alberta, Canada
Copyright © 2021 Zhang, Wang, Ji, Wu and Zhao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rong Zhao, cl96aGFvQG1haWwudHNpbmdodWEuZWR1LmNu
 Wenli Zhang
Wenli Zhang Yaoyuan Wang
Yaoyuan Wang Xinglong Ji
Xinglong Ji Yujie Wu
Yujie Wu Rong Zhao
Rong Zhao