
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Artif. Intell., 20 July 2021
Sec. Machine Learning and Artificial Intelligence
Volume 4 - 2021 | https://doi.org/10.3389/frai.2021.670538
This article is part of the Research TopicArtificial Intelligence - Editors' Pick 2021View all 8 articles
Cross-view or heterogeneous face matching involves comparing two different views of the face modality such as two different spectrums or resolutions. In this research, we present two heterogeneity-aware subspace techniques, heterogeneous discriminant analysis (HDA) and its kernel version (KHDA) that encode heterogeneity in the objective function and yield a suitable projection space for improved performance. They can be applied on any feature to make it heterogeneity invariant. We next propose a face recognition framework that uses existing facial features along with HDA/KHDA for matching. The effectiveness of HDA and KHDA is demonstrated using both handcrafted and learned representations on three challenging heterogeneous cross-view face recognition scenarios: (i) visible to near-infrared matching, (ii) cross-resolution matching, and (iii) digital photo to composite sketch matching. It is observed that, consistently in all the case studies, HDA and KHDA help to reduce the heterogeneity variance, clearly evidenced in the improved results. Comparison with recent heterogeneous matching algorithms shows that HDA- and KHDA-based matching yields state-of-the-art or comparable results on all three case studies. The proposed algorithms yield the best rank-1 accuracy of 99.4% on the CASIA NIR-VIS 2.0 database, up to 100% on the CMU Multi-PIE for different resolutions, and 95.2% rank-10 accuracies on the e-PRIP database for digital to composite sketch matching.
With increasing focus on security and surveillance, face biometrics has found several new applications and challenges in real-world scenarios. In terms of the current practices by law enforcement agencies, the legacy mugshot databases are captured with good quality face cameras operating in the visible spectrum (VIS) with inter-eye distance of at least 90 pixels (Wilson et al., 2007). However, for security and law enforcement applications, it is difficult to meet these standard requirements. For instance, in surveillance environment, when the illumination is not sufficient, majority of the surveillance cameras capture videos in the near-infrared spectrum (NIR). Even in daytime environment, an image captured at a distance may have only
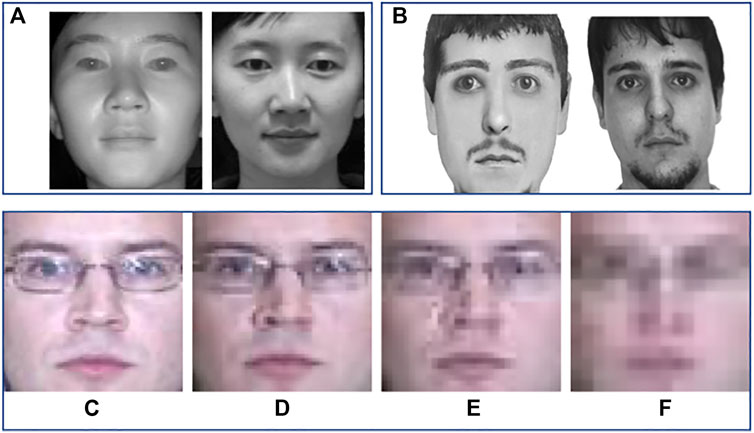
FIGURE 1. Examples of heterogeneous face recognition scenarios. Top row (A) shows heterogeneity due to difference in visible and near-infrared spectrum; (B) shows photo and composite sketches of a person. (C)–(F) illustrates heterogeneity due to resolution variation of 72x72, 48x48, 32x32, and 16x16, respectively. (The images of different resolution are stretched to common sizes.)
The challenge of heterogeneous face recognition is posed by the fact that the view1 of the query face image is not the same as that of the gallery image. In a broader sense, two face images are said to have different views if the facial information in the images is represented differently. For example, visible and near-infrared images are two views. The difference in views may arise due to several factors such as difference in sensors, their operating spectrum range, and difference in the process of sample generation. Most of the traditional face recognition research has focused on homogeneous matching (Bhatt et al., 2015), that is, when both gallery and probe images have the same views. In recent past, researchers have addressed the challenges of heterogeneous face recognition (Tang and Wang, 2003; Yi et al., 2007; Lei and Li, 2009; Lei et al., 2012a; Klare and Jain, 2013; Jin et al., 2015). Compared to homogeneous face recognition, matching face images with different views is a challenging problem as heterogeneity leads to increase in the intra-class variability.
The literature pertaining to heterogeneous face recognition can be grouped into two broad categories: 1) heterogeneity invariant features and 2) heterogeneity-aware classifiers. Heterogeneity invariant feature–based approaches focus on extracting features which are invariant across different views. The prominent research includes use of handcrafted features such as variants of histogram of oriented gradients (HOG), Gabor, Weber, local binary patterns (LBP) (Liao et al., 2009; Goswami et al., 2011; Kalka et al., 2011; Chen and Ross, 2013; Dhamecha et al., 2014), and various learning-based features (Yi et al., 2015; Liu et al., 2016; Reale et al., 2016; He et al., 2017; Hu et al., 2018; Cho et al., 2020). Heterogeneity-aware classifier–based approaches focus on learning a model using samples from both the views. In this research, we primarily focus on designing a heterogeneity-aware classifier.
One set of work focuses on addressing the heterogeneity in projection space or by statistically learning the features suitable for heterogeneous matching. On these lines, one of the earliest research related to visible to near-infrared matching, proposed by Yi et al. (2007), utilizes canonical correlation analysis (CCA) which finds the projections in an unsupervised manner. It computes two projection directions, one for each view such that the correlation between them is maximized in the projection space. Closely related to CCA, Sharma et al. (2012) proposed generalized multi-view analysis (GMA) by adding a constraint that the multi-view samples of each class are as much closer as possible. Similar multi-view extension to discriminant analysis is also explored (Kan et al., 2016). Further, dictionary learning is also utilized for heterogeneous matching (Juefei-Xu et al., 2015; Wu et al., 2016). Efforts to extract heterogeneity-specific features have resulted in common discriminant feature extractor (CDFE) (Lin and Tang, 2006), coupled spectral regression (CSR) (Lei and Li, 2009) and its extensions (Lei et al., 2012a, b), common feature discriminant analysis (CFDA) (Li et al., 2014), coupled discriminative feature learning (CDFL) (Jin et al., 2015), and coupled compact binary face descriptors (C-CBFD) (Lu et al., 2015). Similarly, mutual component analysis (MCA) Li et al. (2016) utilizes iterative EM approach along with a modeling of face generation process to capture view-invariant characteristics.
Although statistical in spirit, a body of work approaches the heterogeneity challenge as a manifold modeling problem. These works explore manifold learning–based approaches to learn heterogeneity-aware classifier. Li et al. (2010) proposed locality preserving projections (LPP)–based approach that preserves local neighborhood in the projection space. Biswas et al. (2013, 2012) proposed a multidimensional scaling (MDS)–based approach for matching low-resolution face images. The algorithm learns an MDS transformation which maps pairwise distances in kernel space of one view to corresponding pairwise distances of the other view. Klare and Jain (2013) proposed a prototyping-based approach. It explores the intuition that across different views, the relative coordinates of samples should remain similar. Therefore, the vector of similarities between the query sample and prototype samples in the corresponding view may be used as the feature.
Other research directions, such as maximum margin classifier (Siena et al., 2013) and transductive learning (Zhu et al., 2014), are also explored. Further, deep learning–based approaches are also proposed for heterogeneous matching to learn shared representation (Yi et al., 2015), to leverage large homogeneous data (Reale et al., 2016), to learn using limited data (Hu et al., 2018), to facilitate transfer learning (Liu et al., 2016), performing face hallucination via disentangling (Duan et al., 2020), and learning deep models using Wasserstein distance (He et al., 2019). Deng Z. et al. (2019) extend MCA to utilize convolutional neural networks for heterogeneous matching. Most recent representation learning methods have a large parameter space, hence require enormous amounts of data for training models for heterogeneous matching. Nevertheless, learned face representations from such approaches are found to be very effective (Taigman et al., 2014; Majumdar et al., 2016; Wu et al., 2018; Deng J. et al., 2019).
In the literature, we identify a scope for improving statistical techniques for heterogeneous matching scenarios. Specifically, we observe that for heterogeneous matching task, modeling of intra-view variability is not critical, as the task always involves matching an inter-view/heterogeneous face pair. The objective functions of the proposed approaches differ from the literature in focusing only on the inter-view variability. To this end, we present two subspace-based classifiers aiming at reducing the inter-view intra-class variability and increasing the inter-view inter-class variability for heterogeneous face recognition. Specifically, in this article, we
• propose heterogeneous discriminant analysis (HDA) and its nonlinear kernel extension (KHDA),
• demonstrate the effectiveness of these HDA and KHDA using multiple features on three challenging heterogeneous face recognition scenarios: matching visible to near-infrared images, matching cross-resolution face images, and matching digital photo to composite sketch, and
• utilize deep learning–based features and show that combined with the proposed HDA and KHDA, they yield impressive heterogeneous matching performance.
To address the issue of heterogeneity in face recognition, we propose a discriminant analysis–based approach. In this context, the heterogeneity can arise due to factors such as spectrum variations as shown in Figure 1. The same individual may appear somewhat different in two different spectrums. While a feature extractor may filter out some of the heterogeneity, most feature extractors are not designed to be heterogeneity invariant. Therefore, for practical purposes, the heterogeneity of the source image may be retained in the extracted features.
By definition, the end goal of heterogeneous matching is always a cross-view comparison, for example, VIS to NIR matching and never intra-view comparison, for example, VIS to VIS matching. Therefore, the cross-view information would contain stronger cues for the task than the intra-view information. In other words, optmizing the intra-view variation may have limited utility. It is our hypothesis that incorporating only the cross-view (e.g., cross-spectral) information along with intra- and inter-class variability can improve heterogeneous matching. The proposed heterogeneous discriminant analysis is inspired from the formulation of linear discriminant analysis. Therefore, we first briefly summarize the formulation and limitations of linear discriminant analysis (LDA) followed by presenting the details of HDA.
Traditionally, intra- and inter-class variabilities are represented using within-
The way the scatter matrices are defined ensures that all the samples are as close to the corresponding class mean as possible and that class means are as apart as possible. Any new sample resembling the samples of a certain class would get projected near the corresponding class mean. LDA attempts to optimize the projection directions assuming that the data conforms to a normal distribution. Obtaining such a projection space is useful when the samples to be compared are homogeneous, that is, there is no inherent difference in the sample representation. Even if we assume that each view of each class is normally distributed in itself, the restrictive constraint of LDA is not satisfied. As shown in Figure 2, when provided with a multi-view or heterogeneous data, the projection directions obtained from LDA may be suboptimal and can affect the classification performance. Therefore, for heterogeneous matching problems, we propose to incorporate the view information while computing the between- and within-class scatter matrices.
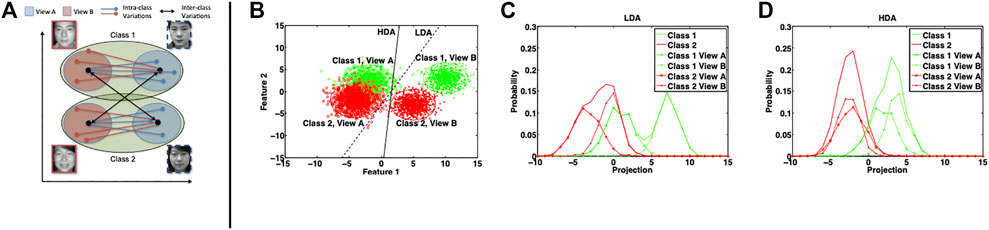
FIGURE 2. (A) Graphical interpretation of HDA and (B–D) illustration of the effectiveness of HDA with multiple views. Class 1 and 2 are generated using Gaussian mixture of two modes resulting in two views. (B) represents the scatter plot and the projection directions obtained using LDA and HDA (without regularization). The histograms of projections of data samples on the LDA and HDA directions are shown in (C) and (D), respectively.
The formulation of the proposed heterogeneous discriminant analysis is described in the following two stages: 1. adaptation of scatter matrices and 2. analytical solution.
Let
•
•
•
•
There can be four kinds of information: i) inter-class intra-view difference, ii) inter-class inter-view difference, iii) intra-class intra-view difference, and iv) intra-class inter-view difference. Optimizing the intra-view (homogeneous) distances would not contribute in achieving the goal of efficient heterogeneous matching. Therefore, the scatter matrices should be defined such that the objective function reduces the heterogeneity (inter-view variation) along with improving the classification accuracy. The distance between the inter-view samples of the non-matching class should be increased and the distance between inter-view samples of the matching class should be decreased. With this hypothesis, we propose the following two modifications in the scatter matrices for heterogeneous matching:
Inter-class inter-view difference encodes the difference between different views of two individuals (e.g.,
Intra-class inter-view difference encodes the difference between two different views of one person (e.g.,
Incorporating these yields a projection space in which same-class samples from different views are drawn closer, thereby fine tuning the objective function for heterogeneous matching. The heterogeneous between-class scatter matrix (
Here,
Since the proposed technique encodes data heterogeneity in the objective function and utilizes the definitions of between- and within-class scatter matrices, it is termed as heterogeneous discriminant analysis. Following the Fisher criterion, the objective function of HDA is proposed as
The optimization problem in Eq. 3 is modeled as a generalized eigenvalue decomposition problem which results into a closed-form solution such that w is the set of top eigenvectors of
In some applications including face recognition, the number of training samples is often limited. If the number of training samples is less than the feature dimensionality, it leads to problems such as singular within-class scatter matrix. In the literature, it is also known as the small sample size problem and shrinkage regularization is generally used to address the issue (Friedman, 1989). Utilizing the shrinkage regularization, Eq. 3 is updated as
Here, I represents the identity matrix and λ is the regularization parameter. Note that
To visualize the functioning of the proposed HDA as opposed to LDA, the distributions of the projections obtained using LDA and HDA are shown in Figure 2. Table 1 presents a quantitative analysis in terms of the overlap between projections of views of both classes. The overlap between two histograms is calculated as
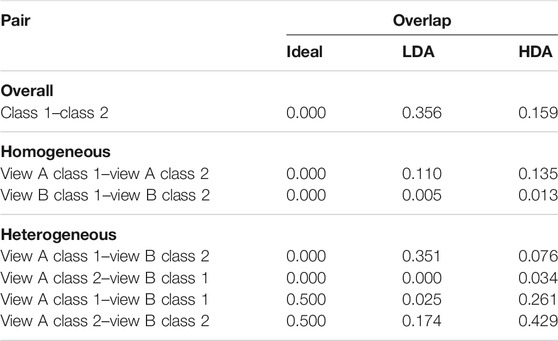
TABLE 1. Analyzing the overlap of projection distributions in Figures 2. LDA vs HDA comparison indicates that ignoring intra-view differences could be beneficial for heterogeneous matching.
The time complexity of computing
We further analyze the objective function in Eq. 3 to adapt it for nonlinear transformation
where
where
The main objective of this research is to utilize the proposed heterogeneity-aware classifiers in conjunction with robust and unique features for heterogeneous face recognition. Figure 3 showscases the steps involved in the face recognition pipeline. From the given input image, the face region is detected using a Haar face detector or manually annotated (for digital sketches) eye coordinates. It is our assertion that the proposed HDA and KHDA should yield good results with both handcrafted and learnt representations. Based on our formulation, to a large extent, HDA and KHDA should help obtain heterogeneity invariant representation of features. Therefore, the lesser heterogeneity invariant a feature is, the greater should be the extent of improvement by HDA and KHDA. Arguably, the learned features are more sophisticated and heterogeneity invariant compared to handcrafted features. Therefore, in this research, we have performed experiments with features of both types for detailed evaluation. In the literature, it has been observed that histogram of oriented gradients (HOG) and local binary patterns (LBP) are commonly used handcrafted features for heterogeneous face matching (Klare and Jain, 2013, 2010). Dhamecha et al. (2014) compared the performance of different variants of HOG and showed that DSIFT (Lowe, 2004) yields the best results. Therefore, among handcrafted features, we have demonstrated the results with DSIFT (extracted at keypoints on uniform grid and landmark points). For learnt representation, we use local class sparsity–based supervised encoder (LCSSE) (Majumdar et al., 2016), LightCNN (Wu et al., 2018), and ArcFace (Deng J. et al., 2019). For LightCNN (LightCNN29V2) and ArcFace, both the models pretrained on MS-Celeb 1M dataset are utilized as feature extractor. In this research, we have used the pretrained LCSSE model and fine-tuned with the training samples for each case study.
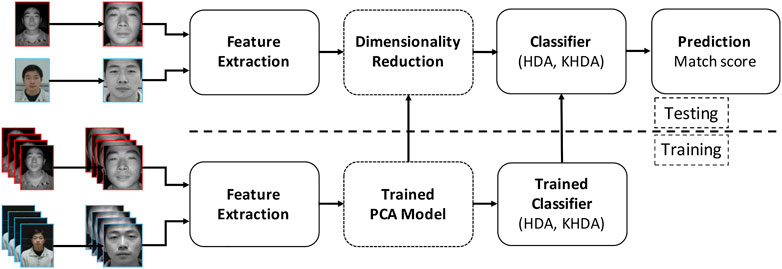
FIGURE 3. Illustrating the steps involved in the face recognition pipeline with the proposed HDA and KHDA.
As shown in Figure 3, once the features are obtained, they are projected on to a PCA space (preserving 99% eigenenergy), followed by projecting onto the
The effectiveness of the proposed heterogeneous discriminant algorithm is evaluated for three different case studies of heterogeneous face recognition: 1) visible to near-infrared matching, 2) cross-resolution face matching, and 3) composite sketch (CS) to digital photo (DP) matching. For all three case studies, we have used publicly available benchmark databases: CASIA NIR-VIS 2.0 (Li et al., 2013), CMU Multi-PIE (Gross et al., 2010), and e-PRIP composite sketch (Han et al., 2013; Mittal et al., 2014). Table 2 summarizes the characteristics of the three databases. The experiments are performed with existing and published protocols so that the results can be directly compared with reported results.

TABLE 2. Datasets utilized for evaluating the proposed HDA and KHDA on three heterogeneous face recognition challenges.
Researchers have proposed several algorithms for VIS to NIR matching and primarily used the CASIA NIR-VIS 2.0 face dataset (Li et al., 2013). The protocol defined for performance evaluation consists of 10 splits of train and test sets for random subsampling cross-validation. As required by the predefined protocol, results are reported for both identification (mean and standard deviation of rank-1 identification accuracy) and verification (GAR at 0.1% FAR).
The images are first detected and preprocessed. Seven landmarks (two eye corners, three points on nose, and two lip corners) are detected (Everingham et al., 2009) from the input face image and geometric normalization is applied to register the cropped face images. The output of preprocessing is grayscale face images of size
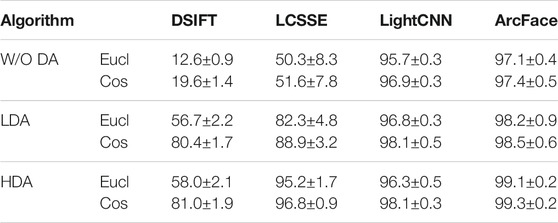
TABLE 3. Rank-1 identification accuracy for visible to near-infrared face matching on the CASIA NIR–VIS 2.0 database (Li et al., 2013).
As shown in Table 3, without discriminant analysis (LDA or HDA), the performance of individual features is lower. The deep learning–based LCSSE yields around 50% rank-1 accuracy. The LightCNN and ArcFace features yield impressive rank-1 accuracy of about 95% and 97%, respectively, which shows their superior feature representation. The next experiment illustrates the effect of applying LDA on individual features. Table 3 shows that LDA improves the accuracy up to 60%. Comparing the performance of HDA with LDA shows that HDA outperforms LDA. Utilizing HDA in place of LDA for discriminative learning improves the results up to 12.9%. The HDA and LDA performance is very high and almost same for LightCNN, which may point toward its spectrum-invariant representation capabilities. For ArcFace, although small, a consistently progressive improvement of about 1% is observed between raw features, LDA, and HDA, respectively. Understandably, if the feature is spectrum-invariant, the benefits of heterogeneity-aware classifier are expected to be limited. The improvement provided by HDA can be attributed to the fact that it learns a discriminative subspace specifically for heterogeneous matching. Similar to the toy example shown in Figure 2, it can be asserted that the multi-view information yields different clusters in the feature space. Under such scenarios, since the fundamental assumption of Gaussian data distribution is not satisfied, LDA can exhibit suboptimal results. However, by encoding the view label information, HDA is able to find better projection space, thereby yielding better results.
The results show that the proposed HDA improves the accuracy of DSIFT and LCSSE features by 40–60%. For instance, applying LCSSE with HDA improves the results by around 45%. As discussed earlier, even the raw LightCNN and ArcFace features yield very high performance, leaving very little room of improvement by LDA or HDA projections.
Cosine distance encodes only the difference in direction between samples, whereas the Euclidean distance encodes both direction and magnitude. For the given experiment, as shown in Table 3, cosine distance generally yields higher accuracy over Euclidean distance. This shows that for heterogeneous matching, the magnitude of projections may not provide useful information and only directional information can be used for matching.
From the above analysis, it can be seen that the proposed HDA in combination with DSIFT features and cosine distance measure yields an impressive 81% for a handcrafted feature. ArcFace features with HDA and cosine distance measure yield the best results. However, LightCNN and LCSSE are also within 3% of it. For the remaining experiments (and other case studies), we have demonstrated the results with DSIFT, LCSSE, LightCNN, and ArcFace features and cosine distance measure along with proposed heterogeneity-aware classifiers.
We next compare the results of the proposed approaches with the results reported in the literature. Comparative analysis is shown with a leading commercial off-the-shelf (COTS) face recognition system, FaceVACS5, and 20 recently published results. Table 4 shows that with pixel values as input, the proposed HDA approach outperforms other existing algorithms. For example, MvDA with pixel values yields 41.6% rank-1 identification accuracy and 19.2% GAR at 0.1% FAR, whereas the proposed approach yields similar rank-1 accuracy with lower standard deviation and much higher GAR of 31.4%. Further, Table 4 clearly6 demonstrates the performance improvement due to the proposed HDA and its nonlinear kernel variant KHDA. KHDA with learnt representation LCSSE and HDA with LightCNN yield almost equal identification accuracy. However, our best results are obtained with ArcFace with KHDA at 99.4% rank-1 and 99.1% GAR@FAR=0.1%. The reported results are comparable to the recently published state of the art.
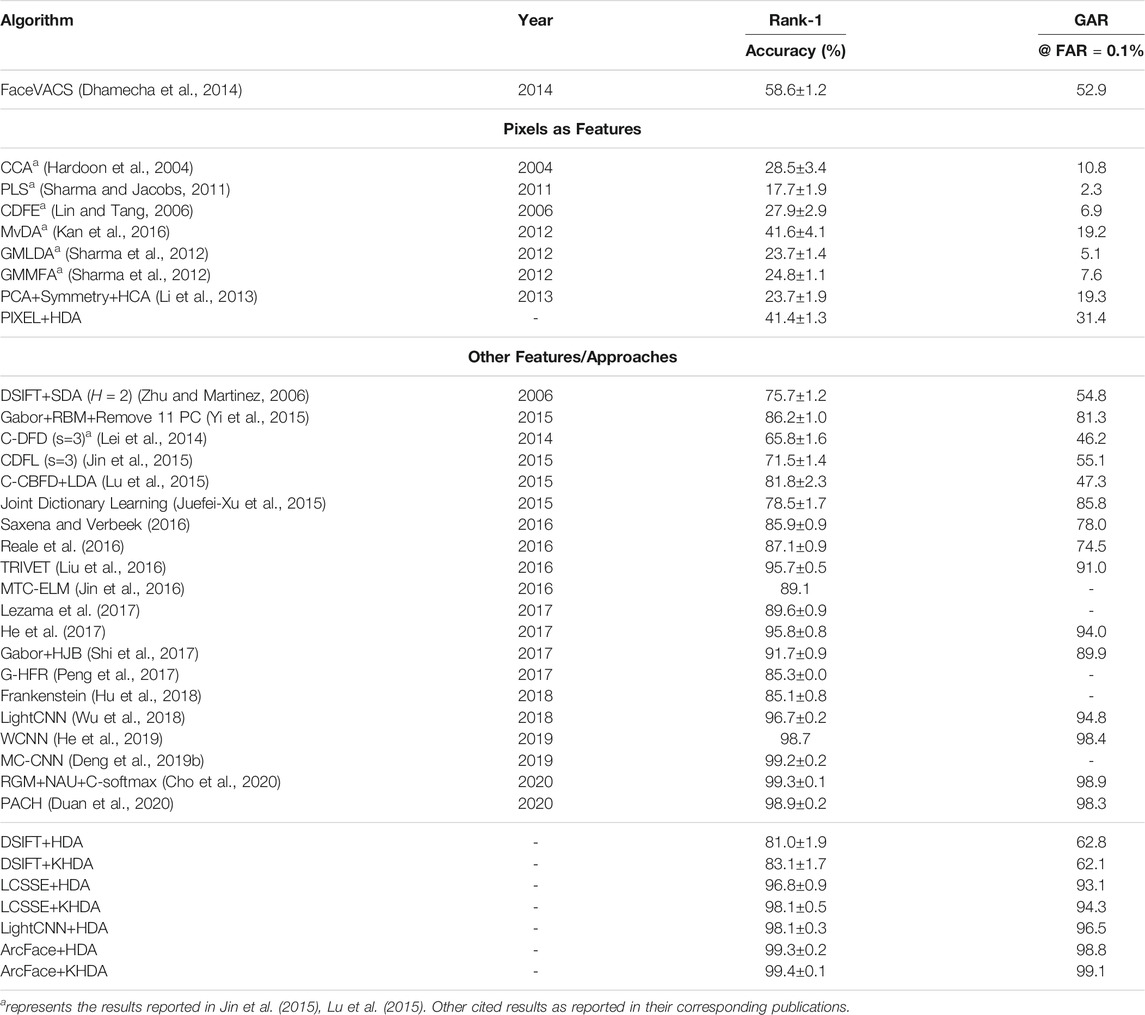
TABLE 4. Comparing the face recognition performance of the proposed and some existing algorithms for VIS to NIR face matching on CASIA NIR–VIS 2.0 dataset.
Also, LCSSE+KHDA and LightCNN+HDA achieve 94.3% and 96.5% GAR at 0.1% FAR, respectively. Also note that, in a fair comparison, DSIFT features with the proposed KHDA also yield results comparable to other non-deep learning–based approaches.
Cross-resolution face recognition entails matching high-resolution gallery images with low-resolution probe images. In this scenario, high resolution and low resolution are considered as two different views of a face image. We compare our approach with Bhatt et al. (2012, 2014) as they have reported one of the best results for the problem. We follow their protocol on CMU Multi-PIE database (Gross et al., 2010). Each image is resized to six different resolutions:
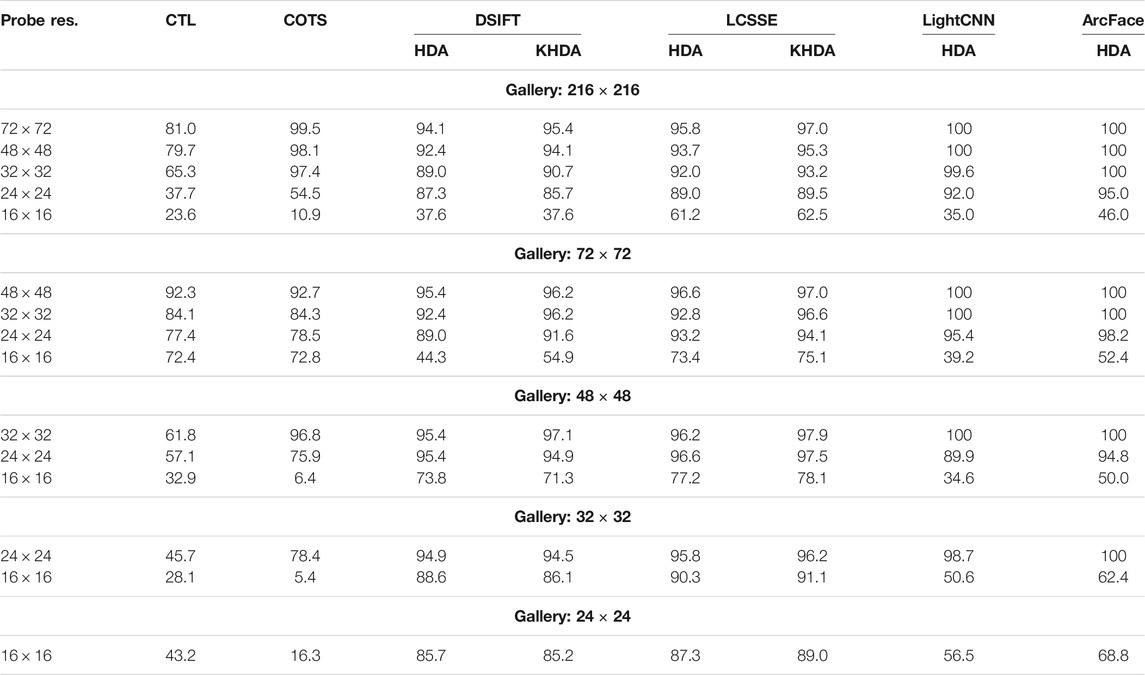
TABLE 5. Rank-1 identification accuracy of the proposed HDA, KHDA and existing algorithms, Cotransfer Learning (CTL) and a commercial off-the-shelf (COTS) (Bhatt et al., 2012, 2014), DSIFT (Lowe, 2004), LCSSE (Majumdar et al., 2016), LightCNN, and ArcFace on CMU Multi-PIE database (Gross et al., 2010) with different gallery and probe image sizes.
It can be seen that LCSSE+KHDA outperforms the cotransfer learning (Bhatt et al., 2012, 2014) in all the cross-resolution matching scenarios. For example, when
In many law enforcement and forensic applications, software tools are used to generate composite sketches based on eyewitness description and the composite sketch is matched against a gallery of digital photographs. Han et al. (2013) presented a component-based approach followed by score fusion for composite to photo matching. Later, Mittal et al. (2014, 2013, 2015, 2017) and Chugh et al. (2013) presented learning-based algorithms for the same. Klum et al. (2014) presented FaceSketchID for matching composite sketches to photos.
For this set of experiments, we utilize the e-PRIP composite sketch dataset (Han et al., 2013; Mittal et al., 2014). The dataset contains composite sketches of 123 face images from the AR face dataset (Martinez, 1998). It contains the composite sketches created using two tools, Faces and IdentiKit7. The PRIP dataset (Han et al., 2013) originally has composite sketches prepared by a Caucasian user (with IdentiKit and Faces softwares) and an Asian user (with Faces software). Later, the dataset is extended by Mittal et al. (2014) by adding composite sketches prepared by an Indian user (with Faces software) which is termed as the e-PRIP composite sketch dataset. In this work, we use composite sketches prepared using Faces software by the Caucasian and Indian users as they are shown to yield better results compared to other sets (Mittal et al., 2014, 2013). The experiments are performed with the same protocol as presented by Mittal et al. (2014). Mean identification accuracies, across five random cross-validations, at rank-10 are reported in Table 6, and Figure 4 shows the corresponding CMC curves.
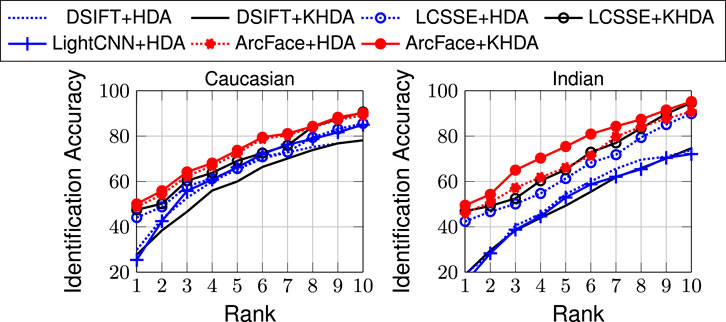
FIGURE 4. CMC curves for composite sketch to digital photo matching on the e-PRIP composite sketch dataset (Han et al., 2013; Mittal et al., 2014).
With the above mentioned experimental protocol, one of the best results in the literature has been reported by Mittal et al. (2017) with rank-10 identification accuracies of 59.3% (Caucasian) and 58.4% (Indian). Saxena and Verbeek (2016) have shown results with Indian users only and have achieved 65.5% rank-10 accuracy. As shown in the results, the proposed approaches, HDA and KHDA, with both DSIFT and LCSSE improve the performance significantly. Compared to existing algorithms, DSIFT demonstrates an improvement in the range of 11–23%, while LCSSE+HDA and LCSSE+KHDA improve the rank-10 accuracy by ∼30% with respect to state of the art (Saxena and Verbeek, 2016). Interestingly, LightCNN yields poorer performance compared to LCSSE in this case study. ArcFace yields the highest identification accuracy. Similar to previous results, this experiment also shows that application of HDA/KHDA improves the results of DSIFT, LCSSE, and ArcFace. However, the degree of improvement varies between handcrafted and learned features.
In this research, we have proposed a discriminant analysis approach for heterogeneous face recognition. We formulate heterogeneous discriminant analysis which encodes view labels and has the objective function optimized for heterogeneous matching. Based on the analytical solution, we propose its kernel extension, KHDA. The proposed techniques are heterogeneity aware. Potentially, they can be applied on top of any features to get heterogeneity invariant representation, to an extent. Experiments are performed on three heterogeneous face matching problems, namely, visible to NIR matching, cross-resolution matchings, and digital photo to sketch, with handcrafted DSIFT and deep learning–based LCSSE, LightCNN, and ArcFace features. The results show that incorporating the proposed discriminant analysis technique consistently improves the performance of both learnt and handcrafted features, without increasing much to the computational requirements. The improvement is more pronounced in handcrafted features and provides an efficient way to improve their performance.
Publicly available datasets were analyzed in this study. This data can be found here: http://www.cbsr.ia.ac.cn/english/HFB_Agreement/NIR-VIS-2.0_agreements.pdf, https://www.cs.cmu.edu/afs/cs/project/PIE/MultiPie/Multi-Pie/Home.html, https://www.iab-rubric.org/resources/eprip.html.
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements. Written informed consent was not obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.
TD, MV, and RS discussed the primary approach. TD, SG, and MV performed the experiments and all the authors prepared the manuscript.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
1The terms view and domain/modality are used synonymously in the heterogeneous face recognition literature.
2Detailed formulation is in the supplementary document.
3Results of LBP, HOG variants, and pixel are in supplementary document.
4There is slight difference between LightCNN + W/O DA of Table 3 and LightCNN in Table 4, as former is our implementation and later is as reported in (Wu et al., 2018).
5http://www.cognitec.com/technology.html
6ROC in the supplementary document.
7Faces: www.iqbiometrix.com, IdentiKit: www.identikit.net
Bhatt, H., Singh, R., and Vatsa, M. (2015). Covariates of Face Recognition. Tech. Report at IIIT Delhi.
Bhatt, H. S., Singh, R., Vatsa, M., and Ratha, N. K. (2014). Improving Cross-Resolution Face Matching Using Ensemble-Based Co-transfer Learning. IEEE Trans. Image Process. 23, 5654–5669. doi:10.1109/tip.2014.2362658
Bhatt, H. S., Singh, R., Vatsa, M., and Ratha, N. (2012). Matching Cross-Resolution Face Images Using Co-transfer Learning. IEEE ICIP, 1453–1456. doi:10.1109/ICIP.2012.6467144
Biswas, S., Aggarwal, G., Flynn, P. J., and Bowyer, K. W. (2013). Pose-robust Recognition of Low-Resolution Face Images. IEEE Trans. Pattern Anal. Mach. Intell. 35, 3037–3049. doi:10.1109/tpami.2013.68
Biswas, S., Bowyer, K. W., and Flynn, P. J. (2012). Multidimensional Scaling for Matching Low-Resolution Face Images. IEEE Trans. Pattern Anal. Mach. Intell. 34, 2019–2030. doi:10.1109/tpami.2011.278
Chen, C., and Ross, A. (2013). Local Gradient Gabor Pattern (LGGP) with Applications in Face Recognition, Cross-Spectral Matching, and Soft Biometrics. SPIE Defense, Security, and Sensing 8712, 87120R. doi:10.1117/12.2018230
Cho, M., Kim, T., Kim, I.-J., Lee, K., and Lee, S. (2020). Relational Deep Feature Learning for Heterogeneous Face Recognition. IEEE TIFS 16, 376–388. doi:10.1109/TIFS.2020.3013186
Chugh, T., Bhatt, H. S., Singh, R., and Vatsa, M. (2013). Matching Age Separated Composite Sketches and Digital Face Images. IEEE BTAS, 1–6. doi:10.1109/BTAS.2013.6712719
Deng, J., Guo, J., Xue, N., and Zafeiriou, S. (2019a). Arcface: Additive Angular Margin Loss for Deep Face Recognition. CVPR, 4690–4699. doi:10.1109/CVPR.2019.00482
Deng, Z., Peng, X., Li, Z., and Qiao, Y. (2019b). Mutual Component Convolutional Neural Networks for Heterogeneous Face Recognition. IEEE Trans. Image Process. 28, 3102–3114. doi:10.1109/tip.2019.2894272
Dhamecha, T. I., Sharma, P., Singh, R., and Vatsa, M. (2014). 1788–1793. On Effectiveness of Histogram of Oriented Gradient Features for Visible to Near Infrared Face Matching IAPR ICPR. doi:10.1109/ICPR.2014.314
Duan, B., Fu, C., Li, Y., Song, X., and He, R. (2020). Cross-spectral Face Hallucination via Disentangling Independent Factors. CVPR, 7930–7938. doi:10.1109/CVPR42600.2020.00795
Everingham, M., Sivic, J., and Zisserman, A. (2009). Taking the Bite Out of Automated Naming of Characters in Tv Video. Image Vis. Comput. 27, 545–559. doi:10.1016/j.imavis.2008.04.018
Friedman, J. H. (1989). Regularized Discriminant Analysis. J. Am. Stat. Assoc. 84, 165–175. doi:10.1080/01621459.1989.10478752
Goswami, D., Chan, C. H., Windridge, D., and Kittler, J. (2011). Evaluation of Face Recognition System in Heterogeneous Environments (Visible vs NIR). IEEE ICCV Workshops, 2160–2167. doi:10.1109/ICCVW.2011.6130515
Gross, R., Matthews, I., Cohn, J., Kanade, T., and Baker, S. (2010). Multi-PIE. Image Vis. Comput. 28, 807–813. doi:10.1016/j.imavis.2009.08.002
Han, H., Klare, B. F., Bonnen, K., and Jain, A. K. (2013). Matching Composite Sketches to Face Photos: A Component-Based Approach. IEEE TIFS 8, 191–204. doi:10.1109/TIFS.2012.2228856
Hardoon, D. R., Szedmak, S., and Shawe-Taylor, J. (2004). Canonical Correlation Analysis: An Overview with Application to Learning Methods. Neural Comput. 16, 2639–2664. doi:10.1162/0899766042321814
He, R., Wu, X., Sun, Z., and Tan, T. (2017). Learning Invariant Deep Representation for NIR-VIS Face Recognition. AAAI 4, 7.
He, R., Wu, X., Sun, Z., and Tan, T. (2019). Wasserstein CNN: Learning Invariant Features for NIR-VIS Face Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 41, 1761–1773. doi:10.1109/tpami.2018.2842770
Hu, G., Peng, X., Yang, Y., Hospedales, T. M., and Verbeek, J. (2018). Frankenstein: Learning Deep Face Representations Using Small Data. IEEE Trans. Image Process. 27, 293–303. doi:10.1109/tip.2017.2756450
Jin, Y., Li, J., Lang, C., and Ruan, Q. (2016). Multi-task Clustering ELM for VIS-NIR Cross-Modal Feature Learning. Multidimensional Syst. Signal Process. 1–16. doi:10.1007/s11045-016-0401-8
Jin, Y., Lu, J., and Ruan, Q. (2015). Coupled Discriminative Feature Learning for Heterogeneous Face Recognition. IEEE Trans.Inform.Forensic Secur. 10, 640–652. doi:10.1109/tifs.2015.2390414
Juefei-Xu, F., Pal, D. K., and Savvides, M. (2015). NIR-VIS Heterogeneous Face Recognition via Cross-Spectral Joint Dictionary Learning and Reconstruction. CVPR Workshops, 141–150. doi:10.1109/CVPRW.2015.7301308
Kalka, N. D., Bourlai, T., Cukic, B., and Hornak, L. (2011). Cross-spectral Face Recognition in Heterogeneous Environments: A Case Study on Matching Visible to Short-Wave Infrared Imagery. IEEE IJCB, 1–8. doi:10.1109/IJCB.2011.6117586
Kan, M., Shan, S., Zhang, H., Lao, S., and Chen, X. (2016). Multi-view Discriminant Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 38, 188–194. doi:10.1109/tpami.2015.2435740
Klare, B. F., and Jain, A. K. (2013). Heterogeneous Face Recognition Using Kernel Prototype Similarities. IEEE Trans. Pattern Anal. Mach. Intell. 35, 1410–1422. doi:10.1109/tpami.2012.229
Klare, B., and Jain, A. K. (2010). Heterogeneous Face Recognition: Matching NIR to Visible Light Images. IAPR ICPR, 1513–1516. doi:10.1109/ICPR.2010.374
Klum, S. J., Han, H., Klare, B. F., and Jain, A. K. (2014). The FaceSketchID System: Matching Facial Composites to Mugshots. IEEE Trans.Inform.Forensic Secur. 9, 2248–2263. doi:10.1109/tifs.2014.2360825
Lei, Z., Pietikäinen, M., and Li, S. Z. (2014). Learning Discriminant Face Descriptor. IEEE Trans. Pattern Anal. Mach Intell. 36, 289–302. doi:10.1109/TPAMI.2013.112
Lei, Z., and Li, S. Z. (2009). Coupled Spectral Regression for Matching Heterogeneous Faces. CVPR, 1123–1128. doi:10.1109/CVPR.2009.5206860
Lei, Z., Liao, S., Jain, A. K., and Li, S. Z. (2012a). Coupled Discriminant Analysis for Heterogeneous Face Recognition. IEEE Trans.Inform.Forensic Secur. 7, 1707–1716. doi:10.1109/tifs.2012.2210041
Lei, Z., Zhou, C., Yi, D., Jain, A. K., and Li, S. Z. (2012b). An Improved Coupled Spectral Regression for Heterogeneous Face Recognition. IEEE/IAPR Int. Conf. Biometrics, 7–12. doi:10.1109/icb.2012.6199751
Lezama, J., Qiu, Q., and Sapiro, G. (2017). Not afraid of the Dark: NIR-VIS Face Recognition via Cross-Spectral Hallucination and Low-Rank Embedding. CVPR, 6807–6816. doi:10.1109/cvpr.2017.720
Li, B., Chang, H., Shan, S., and Chen, X. (2010). Low-resolution Face Recognition via Coupled Locality Preserving Mappings. IEEE SPL 17, 20–23. doi:10.1109/LSP.2009.2031705
Li, S., Yi, D., Lei, Z., and Liao, S. (2013). The CASIA NIR-VIS 2.0 Face Database. CVPR Workshops, 348–353. doi:10.1109/CVPRW.2013.59
Li, Z., Gong, D., Qiao, Y., and Tao, D. (2014). Common Feature Discriminant Analysis for Matching Infrared Face Images to Optical Face Images. IEEE Trans. Image Process. 23, 2436–2445. doi:10.1109/TIP.2014.2315920
Li, Z., Gong, D., Li, Q., Tao, D., and Li, X. (2016). Mutual Component Analysis for Heterogeneous Face Recognition. ACM Trans. Intell. Syst. Technol. 7, 1–23. doi:10.1145/2807705
Liao, S., Yi, D., Lei, Z., Qin, R., and Li, S. Z. (2009). Heterogeneous Face Recognition from Local Structures of Normalized Appearance. Adv. Biometrics, 209–218. doi:10.1007/978-3-642-01793-3_22
Liu, X., Song, L., Wu, X., and Tan, T. (2016). Transferring Deep Representation for NIR-VIS Heterogeneous Face Recognition. IEEE ICB, 1–8. doi:10.1109/ICB.2016.7550064
Lowe, D. G. (2004). Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 60, 91–110. doi:10.1023/b:visi.0000029664.99615.94
Lu, J., Liong, V. E., Zhou, X., and Zhou, J. (2015). Learning Compact Binary Face Descriptor for Face Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 37, 2041–2056. doi:10.1109/tpami.2015.2408359
Majumdar, A., Singh, R., and Vatsa, M. (2016). Face Verification via Class Sparsity Based Supervised Encoding. IEEE Trans. Pattern Anal. Mach. Intell. 39, 1273–1280. doi:10.1109/TPAMI.2016.2569436
Mittal, P., Jain, A., Goswami, G., Singh, R., and Vatsa, M. (2014). Recognizing Composite Sketches with Digital Face Images via SSD Dictionary. IEEE IJCB, 1–6. doi:10.1109/BTAS.2014.6996265
Mittal, P., Jain, A., Goswami, G., Vatsa, M., and Singh, R. (2017). Composite Sketch Recognition Using Saliency and Attribute Feedback. Inf. Fusion 33, 86–99. doi:10.1016/j.inffus.2016.04.003
Mittal, P., Jain, A., Singh, R., and Vatsa, M. (2013). Boosting Local Descriptors for Matching Composite and Digital Face Images. IEEE ICIP, 2797–2801. doi:10.1109/ICIP.2013.6738576
Mittal, P., Vatsa, M., and Singh, R. (2015). Composite Sketch Recognition via Deep Network - a Transfer Learning Approach. IEEE/IAPR ICB, 251–256. doi:10.1109/ICB.2015.7139092
Peng, C., Gao, X., Wang, N., and Li, J. (2017). Graphical Representation for Heterogeneous Face Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 39, 301–312. doi:10.1109/tpami.2016.2542816
Reale, C., Nasrabadi, N. M., Kwon, H., and Chellappa, R. (2016). Seeing the forest from the Trees: A Holistic Approach to Near-Infrared Heterogeneous Face Recognition. CVPR Workshops, 320–328. doi:10.1109/cvprw.2016.47
Saxena, S., and Verbeek, J. (2016). Heterogeneous Face Recognition with CNNs. ECCV Workshops, 483–491.
Schölkopf, B., Herbrich, R., and Smola, A. J. (2001). A Generalized Representer Theorem. Comput. Learn. Theor., 416–426. doi:10.1007/3-540-44581-1_27
Sharma, A., and Jacobs, D. W. (2011). Bypassing Synthesis: PLS for Face Recognition with Pose, Low-Resolution and Sketch. CVPR Workshops, 593–600. doi:10.1109/CVPR.2011.5995350
Sharma, A., Kumar, A., Daume, H., and Jacobs, D. W. (2012). Generalized Multiview Analysis: A Discriminative Latent Space. CVPR, 2160–2167. doi:10.1109/cvpr.2012.6247923
Shi, H., Wang, X., Yi, D., Lei, Z., Zhu, X., and Li, S. Z. (2017). Cross-modality Face Recognition via Heterogeneous Joint Bayesian. IEEE SPL 24 (1), 81–85. doi:10.1109/LSP.2016.2637400
Siena, S., Boddeti, V., and Kumar, B. (2013). Maximum-margin Coupled Mappings for Cross-Domain Matching. IEEE BTAS. 1–8. doi:10.1109/BTAS.2013.6712686
Taigman, Y., Yang, M., Ranzato, M., and Wolf, L. (2014). Deepface: Closing the gap to Human-Level Performance in Face Verification. CVPR, 1701–1708. doi:10.1109/cvpr.2014.220
Tang, X., and Wang, X. (2003). Face Sketch Synthesis and Recognition. IEEE ICCV, 687–694. doi:10.1109/ICCV.2003.1238414
Wilson, C. L., Grother, P. J., and Chandramouli, R. (2007). Biometric Data Specification for Personal Identity Verification. Tech. Report NIST-SP-800-76-1. National Institute of Standards & Technology.
Wu, F., Jing, X.-Y., You, X., Yue, D., Hu, R., and Yang, J.-Y. (2016). Multi-view Low-Rank Dictionary Learning for Image Classification. Pattern Recognition 50, 143–154. doi:10.1016/j.patcog.2015.08.012
Wu, X., He, R., Sun, Z., and Tan, T. (2018). A Light Cnn for Deep Face Representation with Noisy Labels. IEEE Trans.Inform.Forensic Secur. 13, 2884–2896. doi:10.1109/tifs.2018.2833032
Yi, D., Lei, Z., and Li, S. Z. (2015). Shared Representation Learning for Heterogenous Face Recognition. IEEE FG, 1–7. doi:10.1109/FG.2015.7163093
Yi, D., Liu, R., Chu, R., Lei, Z., and Li, S. Z. (2007). Face Matching between Near Infrared and Visible Light Images. Adv. Biometrics, 523–530. doi:10.1007/978-3-540-74549-5_55
Zhu, J.-Y., Zheng, W.-S., Lai, J.-H., and Li, S. Z. (2014). Matching NIR Face to VIS Face Using Transduction. IEEE Trans.Inform.Forensic Secur. 9, 501–514. doi:10.1109/tifs.2014.2299977
Keywords: face recognition (FR), discriminant analysis (DA), heterogeneity, cross-spectral, cross-resolution
Citation: Dhamecha TI, Ghosh S, Vatsa M and Singh R (2021) Kernelized Heterogeneity-Aware Cross-View Face Recognition. Front. Artif. Intell. 4:670538. doi: 10.3389/frai.2021.670538
Received: 21 February 2021; Accepted: 06 May 2021;
Published: 20 July 2021.
Edited by:
Fabrizio Riguzzi, University of Ferrara, ItalyReviewed by:
Hiranmoy Roy, RCC Institute of Information Technology, IndiaCopyright © 2021 Dhamecha, Ghosh, Vatsa and Singh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mayank Vatsa, bXZhdHNhQGlpdGouYWMuaW4=
†Work carried when the author was affiliated to IIIT Delhi.
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.