Kernelized Heterogeneity-Aware Cross-View Face Recognition

Cross-view or heterogeneous face matching involves comparing two different views of the face modality such as two different spectrums or resolutions. In this research, we present two heterogeneity-aware subspace techniques, heterogeneous discriminant analysis (HDA) and its kernel version (KHDA) that encode heterogeneity in the objective function and yield a suitable projection space for improved performance. They can be applied on any feature to make it heterogeneity invariant. We next propose a face recognition framework that uses existing facial features along with HDA/KHDA for matching. The effectiveness of HDA and KHDA is demonstrated using both handcrafted and learned representations on three challenging heterogeneous cross-view face recognition scenarios: (i) visible to near-infrared matching, (ii) cross-resolution matching, and (iii) digital photo to composite sketch matching. It is observed that, consistently in all the case studies, HDA and KHDA help to reduce the heterogeneity variance, clearly evidenced in the improved results. Comparison with recent heterogeneous matching algorithms shows that HDA- and KHDA-based matching yields state-of-the-art or comparable results on all three case studies. The proposed algorithms yield the best rank-1 accuracy of 99.4% on the CASIA NIR-VIS 2.0 database, up to 100% on the CMU Multi-PIE for different resolutions, and 95.2% rank-10 accuracies on the e-PRIP database for digital to composite sketch matching.

Introduction

With increasing focus on security and surveillance, face biometrics has found several new applications and challenges in real-world scenarios. In terms of the current practices by law enforcement agencies, the legacy mugshot databases are captured with good quality face cameras operating in the visible spectrum (VIS) with inter-eye distance of at least 90 pixels (Wilson et al., 2007). However, for security and law enforcement applications, it is difficult to meet these standard requirements. For instance, in surveillance environment, when the illumination is not sufficient, majority of the surveillance cameras capture videos in the near-infrared spectrum (NIR). Even in daytime environment, an image captured at a distance may have only $16\times 16$ facial region for processing. For these applications, the corresponding gallery or database image is generally a good quality mugshot image captured in controlled environments. This leads to the challenge of heterogeneity in gallery and probe images. Figure 1 shows samples of these heterogeneous face matching cases. This figure also showcases another interesting application of matching composite sketch images with digital face images. In this problem, composite sketches are generated using a software tool based on eyewitness description, and this synthetic sketch image is then matched against a database of mugshot face images. Since the information content in sketches and photos is different, matching them can be viewed as heterogeneous matching problem.

FIGURE 1

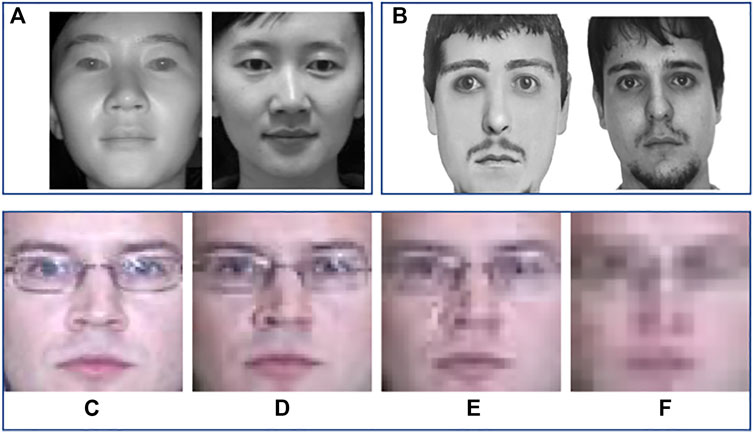
FIGURE 1. Examples of heterogeneous face recognition scenarios. Top row (A) shows heterogeneity due to difference in visible and near-infrared spectrum; (B) shows photo and composite sketches of a person. (C)–(F) illustrates heterogeneity due to resolution variation of 72x72, 48x48, 32x32, and 16x16, respectively. (The images of different resolution are stretched to common sizes.)

The challenge of heterogeneous face recognition is posed by the fact that the view¹ of the query face image is not the same as that of the gallery image. In a broader sense, two face images are said to have different views if the facial information in the images is represented differently. For example, visible and near-infrared images are two views. The difference in views may arise due to several factors such as difference in sensors, their operating spectrum range, and difference in the process of sample generation. Most of the traditional face recognition research has focused on homogeneous matching (Bhatt et al., 2015), that is, when both gallery and probe images have the same views. In recent past, researchers have addressed the challenges of heterogeneous face recognition (Tang and Wang, 2003; Yi et al., 2007; Lei and Li, 2009; Lei et al., 2012a; Klare and Jain, 2013; Jin et al., 2015). Compared to homogeneous face recognition, matching face images with different views is a challenging problem as heterogeneity leads to increase in the intra-class variability.

Literature Review

The literature pertaining to heterogeneous face recognition can be grouped into two broad categories: 1) heterogeneity invariant features and 2) heterogeneity-aware classifiers. Heterogeneity invariant feature–based approaches focus on extracting features which are invariant across different views. The prominent research includes use of handcrafted features such as variants of histogram of oriented gradients (HOG), Gabor, Weber, local binary patterns (LBP) (Liao et al., 2009; Goswami et al., 2011; Kalka et al., 2011; Chen and Ross, 2013; Dhamecha et al., 2014), and various learning-based features (Yi et al., 2015; Liu et al., 2016; Reale et al., 2016; He et al., 2017; Hu et al., 2018; Cho et al., 2020). Heterogeneity-aware classifier–based approaches focus on learning a model using samples from both the views. In this research, we primarily focus on designing a heterogeneity-aware classifier.

One set of work focuses on addressing the heterogeneity in projection space or by statistically learning the features suitable for heterogeneous matching. On these lines, one of the earliest research related to visible to near-infrared matching, proposed by Yi et al. (2007), utilizes canonical correlation analysis (CCA) which finds the projections in an unsupervised manner. It computes two projection directions, one for each view such that the correlation between them is maximized in the projection space. Closely related to CCA, Sharma et al. (2012) proposed generalized multi-view analysis (GMA) by adding a constraint that the multi-view samples of each class are as much closer as possible. Similar multi-view extension to discriminant analysis is also explored (Kan et al., 2016). Further, dictionary learning is also utilized for heterogeneous matching (Juefei-Xu et al., 2015; Wu et al., 2016). Efforts to extract heterogeneity-specific features have resulted in common discriminant feature extractor (CDFE) (Lin and Tang, 2006), coupled spectral regression (CSR) (Lei and Li, 2009) and its extensions (Lei et al., 2012a, b), common feature discriminant analysis (CFDA) (Li et al., 2014), coupled discriminative feature learning (CDFL) (Jin et al., 2015), and coupled compact binary face descriptors (C-CBFD) (Lu et al., 2015). Similarly, mutual component analysis (MCA) Li et al. (2016) utilizes iterative EM approach along with a modeling of face generation process to capture view-invariant characteristics.

Although statistical in spirit, a body of work approaches the heterogeneity challenge as a manifold modeling problem. These works explore manifold learning–based approaches to learn heterogeneity-aware classifier. Li et al. (2010) proposed locality preserving projections (LPP)–based approach that preserves local neighborhood in the projection space. Biswas et al. (2013, 2012) proposed a multidimensional scaling (MDS)–based approach for matching low-resolution face images. The algorithm learns an MDS transformation which maps pairwise distances in kernel space of one view to corresponding pairwise distances of the other view. Klare and Jain (2013) proposed a prototyping-based approach. It explores the intuition that across different views, the relative coordinates of samples should remain similar. Therefore, the vector of similarities between the query sample and prototype samples in the corresponding view may be used as the feature.

Other research directions, such as maximum margin classifier (Siena et al., 2013) and transductive learning (Zhu et al., 2014), are also explored. Further, deep learning–based approaches are also proposed for heterogeneous matching to learn shared representation (Yi et al., 2015), to leverage large homogeneous data (Reale et al., 2016), to learn using limited data (Hu et al., 2018), to facilitate transfer learning (Liu et al., 2016), performing face hallucination via disentangling (Duan et al., 2020), and learning deep models using Wasserstein distance (He et al., 2019). Deng Z. et al. (2019) extend MCA to utilize convolutional neural networks for heterogeneous matching. Most recent representation learning methods have a large parameter space, hence require enormous amounts of data for training models for heterogeneous matching. Nevertheless, learned face representations from such approaches are found to be very effective (Taigman et al., 2014; Majumdar et al., 2016; Wu et al., 2018; Deng J. et al., 2019).

In the literature, we identify a scope for improving statistical techniques for heterogeneous matching scenarios. Specifically, we observe that for heterogeneous matching task, modeling of intra-view variability is not critical, as the task always involves matching an inter-view/heterogeneous face pair. The objective functions of the proposed approaches differ from the literature in focusing only on the inter-view variability. To this end, we present two subspace-based classifiers aiming at reducing the inter-view intra-class variability and increasing the inter-view inter-class variability for heterogeneous face recognition. Specifically, in this article, we

• propose heterogeneous discriminant analysis (HDA) and its nonlinear kernel extension (KHDA),

• demonstrate the effectiveness of these HDA and KHDA using multiple features on three challenging heterogeneous face recognition scenarios: matching visible to near-infrared images, matching cross-resolution face images, and matching digital photo to composite sketch, and

• utilize deep learning–based features and show that combined with the proposed HDA and KHDA, they yield impressive heterogeneous matching performance.

Heterogeneous Discriminant Analysis

To address the issue of heterogeneity in face recognition, we propose a discriminant analysis–based approach. In this context, the heterogeneity can arise due to factors such as spectrum variations as shown in Figure 1. The same individual may appear somewhat different in two different spectrums. While a feature extractor may filter out some of the heterogeneity, most feature extractors are not designed to be heterogeneity invariant. Therefore, for practical purposes, the heterogeneity of the source image may be retained in the extracted features.

By definition, the end goal of heterogeneous matching is always a cross-view comparison, for example, VIS to NIR matching and never intra-view comparison, for example, VIS to VIS matching. Therefore, the cross-view information would contain stronger cues for the task than the intra-view information. In other words, optmizing the intra-view variation may have limited utility. It is our hypothesis that incorporating only the cross-view (e.g., cross-spectral) information along with intra- and inter-class variability can improve heterogeneous matching. The proposed heterogeneous discriminant analysis is inspired from the formulation of linear discriminant analysis. Therefore, we first briefly summarize the formulation and limitations of linear discriminant analysis (LDA) followed by presenting the details of HDA.

Traditionally, intra- and inter-class variabilities are represented using within- $S_W={\displaystyle {\sum }_{i=1}^c{\displaystyle {\sum }_{j=1}^{n_i}\left(x_{i,j}-{\mu }_i\right){\left(x_{i,j}-{\mu }_i\right)}^T}}$ and between-class scatter matrices $S_B={\displaystyle {\sum }_{i=1}^c{\displaystyle {\sum }_{l=i+1}^c\left({\mu }_i-{\mu }_l\right){\left({\mu }_i-{\mu }_l\right)}^T}}$; where c is the total number of classes, $n_i$ is the number of samples in $i^{th}$ class, $x_{i,j}$ is the $j^{th}$ sample of the $i^{th}$ class, and ${\mu }_i$ is the mean of the $i^{th}$ class. The Fisher criterion $J\left(w\right)=\left|w^T{S}_{B}w\right|/\left|w^T{S}_{W}w\right|$ attempts to find the projection directions that minimize the intra-class variability and maximize the inter-class variability in the projected space.

The way the scatter matrices are defined ensures that all the samples are as close to the corresponding class mean as possible and that class means are as apart as possible. Any new sample resembling the samples of a certain class would get projected near the corresponding class mean. LDA attempts to optimize the projection directions assuming that the data conforms to a normal distribution. Obtaining such a projection space is useful when the samples to be compared are homogeneous, that is, there is no inherent difference in the sample representation. Even if we assume that each view of each class is normally distributed in itself, the restrictive constraint of LDA is not satisfied. As shown in Figure 2, when provided with a multi-view or heterogeneous data, the projection directions obtained from LDA may be suboptimal and can affect the classification performance. Therefore, for heterogeneous matching problems, we propose to incorporate the view information while computing the between- and within-class scatter matrices.

FIGURE 2

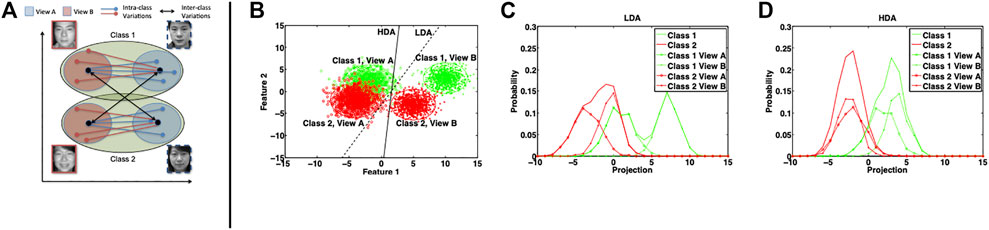
FIGURE 2. (A) Graphical interpretation of HDA and (B–D) illustration of the effectiveness of HDA with multiple views. Class 1 and 2 are generated using Gaussian mixture of two modes resulting in two views. (B) represents the scatter plot and the projection directions obtained using LDA and HDA (without regularization). The histograms of projections of data samples on the LDA and HDA directions are shown in (C) and (D), respectively.

The formulation of the proposed heterogeneous discriminant analysis is described in the following two stages: 1. adaptation of scatter matrices and 2. analytical solution.

Adaptation of Scatter Matrices

Let $x_{i,j}^a$ and $x_{i,j}^b$ denote the two views (A and B) of the $j^{\text{th}}$ sample of the $i^{\text{th}}$ class, respectively, and $n_i^a$ and $n_i^b$ represent the number of samples in view A and B of the $i^{\text{th}}$ class, respectively. ${\chi }_i^a=\left\{x_{i,j}^a|1\le j\le n_i^a\right\}$ represents the samples in view A of $i^{\text{th}}$ class. For example, ${\chi }_i^a$ represents the visible spectrum face images of $i^{\text{th}}$ subject, and ${\chi }_i^b$ represents the near-infrared spectrum face images of the subject.

_•${\chi }_1^a-{\chi }_1^a\text{and}{\chi }_1^a-{\chi }_1^b$ are examples of match pairs, that is, face images in a pair belong to the same subject.

_•${\chi }_1^a-{\chi }_2^b\text{and}{\chi }_1^a-{\chi }_2^b$ are examples of non-match pairs consisting of face images of different subjects.

_•${\chi }_1^a-{\chi }_1^a\text{and}{\chi }_1^b-{\chi }_2^b$ represent intra-view pairs where face images belong to the same view.

_•${\chi }_1^a-{\chi }_1^b\text{and}{\chi }_1^b-{\chi }_2^a$ are examples of inter-view pairs, that is, face images in a pair belong to different view.

There can be four kinds of information: i) inter-class intra-view difference, ii) inter-class inter-view difference, iii) intra-class intra-view difference, and iv) intra-class inter-view difference. Optimizing the intra-view (homogeneous) distances would not contribute in achieving the goal of efficient heterogeneous matching. Therefore, the scatter matrices should be defined such that the objective function reduces the heterogeneity (inter-view variation) along with improving the classification accuracy. The distance between the inter-view samples of the non-matching class should be increased and the distance between inter-view samples of the matching class should be decreased. With this hypothesis, we propose the following two modifications in the scatter matrices for heterogeneous matching:

Inter-class inter-view difference encodes the difference between different views of two individuals (e.g., ${\chi }_1^a-{\chi }_2^b\text{and}{\chi }_1^b-{\chi }_2^a$ pairs). This can be incorporated in the between-class scatter matrix.

Intra-class inter-view difference encodes the difference between two different views of one person (e.g., ${\chi }_1^a-{\chi }_1^b\text{and}-{\chi }_2^b-{\chi }_2^a$ pairs). This can be incorporated in the within-class scatter matrix. (see Figure 2)

Incorporating these yields a projection space in which same-class samples from different views are drawn closer, thereby fine tuning the objective function for heterogeneous matching. The heterogeneous between-class scatter matrix ($S_{HB}$) encodes the difference between different views of different classes

$\begin{array}{l}{S}_{HB}=\stackrel{c}{{\displaystyle \sum }_{i=1}}\stackrel{c}{{\displaystyle \sum }_{l=1,l\ne i}}{p}_i^a{p}_l^b\left({\mu }_i^a-{\mu }_l^b\right){\left({\mu }_i^a-{\mu }_l^b\right)}^T\\ {\mu }_i^k=\frac{1}{n_i^k}{\displaystyle \sum }_j{x}_{i,j}^k,p_i^k=\frac{n_i^k}{n^a+n^b},k\in \left\{a,b\right\}\end{array}(1)$

Here, ${\mu }_i^a$ and $p_i^a$ are the mean and prior of view A of class i, respectively; $n^a$ represents the number of samples in view A. Similarly, ${\mu }_i^b$ and $p_i^b$ represent the mean and prior of view B of class i, respectively; $n^b$ represents the number of samples in view B. $n_i^a$ and $n_i^b$ represent the number of samples in view A and B of the $i^{th}$ class, respectively, and c represents the total number of classes. Note that, unlike CCA, the number of samples does not have to be equal in both views. The within-class scatter matrix $S_{HW}$ is proposed as

$S_{HW}=\stackrel{c}{{\displaystyle \sum }_{i=1}}\left(\frac{1}{n_i^a}\stackrel{n_i^a}{{\displaystyle \sum }_{j=1}}\left(x_{i,j}^a-{\mu }_i^b\right){\left(x_{i,j}^a-{\mu }_i^b\right)}^T+\frac{1}{n_i^b}\stackrel{n_i^b}{{\displaystyle \sum }_{j=1}}\left(x_{i,j}^b-{\mu }_i^a\right){\left(x_{i,j}^b-{\mu }_i^a\right)}^T\right)(2)$

Since the proposed technique encodes data heterogeneity in the objective function and utilizes the definitions of between- and within-class scatter matrices, it is termed as heterogeneous discriminant analysis. Following the Fisher criterion, the objective function of HDA is proposed as

$w=\arg \underset{w}{\max }J\left(w\right)=\arg \underset{w}{\max }\frac{\left|w^T{S}_{HB}w\right|}{\left|w^T{S}_{HW}w\right|}(3)$

The optimization problem in Eq. 3 is modeled as a generalized eigenvalue decomposition problem which results into a closed-form solution such that w is the set of top eigenvectors of $S_{HW}^{-1}{S}_{HB}$. The geometric interpretation of HDA in Figure 2 shows that the objective function in Eq. 3 tries to achieve the following in the projected space: 1) Bring samples ${\chi }_1^a$ closer to mean ${\mu }_1^b$ of ${\chi }_1^b$ and vice versa; and similarly for class 2. This reduces the inter-view distance within each class, for example, the projections of visible and NIR images of the same person become similar. 2) Increase the distance between mean ${\mu }_1^a$ of ${\chi }_1^a$ and mean ${\mu }_2^b$ of ${\chi }_2^b$; and similarly increase the distance between mean of ${\chi }_1^b$ and mean of ${\chi }_2^a$, that is, the projections of mean visible face image of a subject become different from the mean NIR face image of another subject. The proposed way of encoding inter- (Eq. 1) and intra-class (Eq. 2) variations in the heterogeneous scenario requires that both the views are of the same dimensionality. In the application domain of face recognition, this is usually not an unrealistic constraint as, in practice, same kind of features, with same dimensionality, are extracted from both the views (Dhamecha et al., 2014).

In some applications including face recognition, the number of training samples is often limited. If the number of training samples is less than the feature dimensionality, it leads to problems such as singular within-class scatter matrix. In the literature, it is also known as the small sample size problem and shrinkage regularization is generally used to address the issue (Friedman, 1989). Utilizing the shrinkage regularization, Eq. 3 is updated as

$J\left(w\right)=\frac{\left|w^T{S}_{HB}w\right|}{\left|w^T\left(\left(1-\lambda \right)S_{HW}+\lambda I\right)w\right|}(4)$

Here, I represents the identity matrix and λ is the regularization parameter. Note that $\lambda =0$ results in no regularization, whereas $\lambda =1$ results into not utilizing the within-class scatter matrix $S_{HW}$.

To visualize the functioning of the proposed HDA as opposed to LDA, the distributions of the projections obtained using LDA and HDA are shown in Figure 2. Table 1 presents a quantitative analysis in terms of the overlap between projections of views of both classes. The overlap between two histograms is calculated as ${{\displaystyle \sum }}_m\text{min}\left(h_1\left(m\right),h_2\left(m\right)\right)$, where $h_1\left(m\right)$ and $h_2\left(m\right)$ are the values of the $m^{th}$ bin of the first and second histograms, respectively. In the ideal case, the projections of different views of the same class should completely overlap (i.e., area of overlap 0.5) and the projections of the views of different classes should be nonoverlapping (i.e., area of overlap 0). Since LDA does not take into account the view information, the overlap between projections of both classes is large. Further, it is interesting to note that LDA yields a significant overlap of 0.351 between view A of class 1 and view B of class 2. Such overlap can deteriorate the heterogeneous matching performance. In the heterogeneous analysis (last two rows of Table 1), the overlap between projections of two views of the same class is relatively low. Note that view A and view B of class 1 result in two individual peaks. This also increases the intra-class variation, that is, projection distributions of both classes are spread rather than peaked. HDA yields better projection directions with less than 50% of inter-class overlap compared to LDA. For the homogeneous matching scenarios (fourth and fifth rows), HDA has marginally poor overlap compared to LDA. However, for the heterogeneous scenarios, the overlap of HDA is significantly lower for non-match pair of view A class 1–view B class 2 (seventh row) and higher for match pairs (last two rows). For the view A class 2–view B class 1 (eighth row), the numbers are slightly poorer for HDA; however, the difference is small enough to be neglected in context of the overlap metrics of other three pairs.

TABLE 1

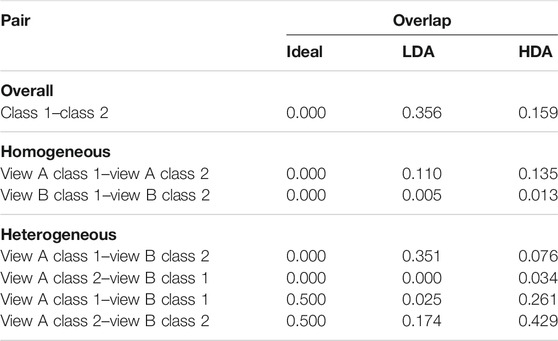
TABLE 1. Analyzing the overlap of projection distributions in Figures 2. LDA vs HDA comparison indicates that ignoring intra-view differences could be beneficial for heterogeneous matching.

The time complexity of computing $S_{HB}$ and $S_{HW}$ is $O\left(n{d}^2\right)$ and $O\left(c^2{d}^2\right)$, respectively. The generalized eigenvalue decomposition in Eq. 3 has time complexity of $O\left(d^3\right)$, where n, d, and c are the number of training samples, feature dimensionality, and number of classes, respectively.

Nonlinear Kernel Extension

We further analyze the objective function in Eq. 3 to adapt it for nonlinear transformation $x\to \varphi \left(x\right)$. Using the representer theorem (Schölkopf et al., 2001), the projection direction in w can be written as linear sum of the transformed samples, that is, $w={\displaystyle {\sum }_{p=1}^{n^a}{\alpha }_p\varphi \left(x_p^a\right)}+{\displaystyle {\sum }_{q=1}^{n^b}{\beta }_q\varphi \left(x_q^b\right)}$. Using this property, the Eq. 4 can be rewritten as²

$J\left(\alpha ,\beta \right)=\left(\frac{\left|\left[{\alpha }^T{\beta }^T\right]M_{\text{*}}\left[\begin{array}{c}\alpha \\ \beta \end{array}\right]\right|}{\left|\left[{\alpha }^T{\beta }^T\right][\left(1-\lambda \right)N_{\text{*}}+\lambda ]\left[\begin{array}{c}\alpha \\ \beta \end{array}\right]\right|}\right)(5)$

where $M_{\text{*}}$ and $N_{\text{*}}$ are analogous to $S_{HB}$ and $S_{HW}$, respectively, and are defined as

$M_{\ast }=\stackrel{c}{{\displaystyle \sum }_{i=1}}\stackrel{c}{{\displaystyle \sum }_{l=1,l\ne i}}{p}_i^a{p}_l^b\left[\begin{array}{c}\mathrm{ℳ}{\mathcal{A}}_i^a-\mathrm{ℳ}{\mathcal{A}}_l^b\\ \mathrm{ℳ}{\mathrm{ℬ}}_i^a-\mathrm{ℳ}{\mathrm{ℬ}}_l^b\end{array}\right]{\left[\begin{array}{c}\mathrm{ℳ}{\mathcal{A}}_i^a-\mathrm{ℳ}{\mathcal{A}}_l^b\\ \mathrm{ℳ}{\mathrm{ℬ}}_i^a-\mathrm{ℳ}{\mathrm{ℬ}}_l^b\end{array}\right]}^T$

$N_{\ast }=\stackrel{c}{{\displaystyle \sum }_{i=1}}\left(\frac{1}{n_i^a}\stackrel{n_i^a}{{\displaystyle \sum }_{j=1}}\left[\begin{array}{c}\mathcal{M}{\mathcal{A}}_{i,j}^a-\mathrm{ℳ}{\mathcal{A}}_i^b\\ \mathcal{M}{\mathrm{ℬ}}_{i,j}^a-\mathrm{ℳ}{\mathrm{ℬ}}_i^b\end{array}\right]{\left[\begin{array}{c}\mathcal{M}{\mathcal{A}}_{i,j}^a-\mathrm{ℳ}{\mathcal{A}}_i^b\\ \mathcal{M}{\mathrm{ℬ}}_{i,j}^a-\mathrm{ℳ}{\mathrm{ℬ}}_i^b\end{array}\right]}^T+\frac{1}{n_i^b}\stackrel{n_i^b}{{\displaystyle \sum }_{j=1}}\left[\begin{array}{c}\mathcal{M}{\mathcal{A}}_{i,j}^b-\mathrm{ℳ}{\mathcal{A}}_i^a\\ \mathcal{M}{\mathrm{ℬ}}_{i,j}^b-\mathrm{ℳ}{\mathrm{ℬ}}_i^a\end{array}\right]{\left[\begin{array}{c}\mathcal{M}{\mathcal{A}}_{i,j}^b-\mathrm{ℳ}{\mathcal{A}}_i^a\\ \mathcal{M}{\mathrm{ℬ}}_{i,j}^b-\mathrm{ℳ}{\mathrm{ℬ}}_i^a\end{array}\right]}^T\right)$

where ${\left(\mathrm{ℳ}{\mathrm{ℬ}}_i^a\right)}_q=\frac{1}{n_i^a}{\displaystyle \sum }_{s=1}^{n_i^a}K\left(x_q^b,x_{i,s}^a\right)$ and ${\left(\mathcal{M}{\mathrm{ℬ}}_{i,j}^a\right)}_q=K\left(x_q^b,x_{i,j}^a\right)$, where K is a kernel function. In this work, we use the Gaussian kernel function. Eq. 5 with linear kernel is equivalent to Eq. 4. However, if $d<n$, the criterion in Eq. 4 is computationally more efficient than Eq. 5 but if $d>n$, Eq. 5 is computationally more efficient than Eq. 4.

Proposed Cross-View Face Recognition Approach

The main objective of this research is to utilize the proposed heterogeneity-aware classifiers in conjunction with robust and unique features for heterogeneous face recognition. Figure 3 showscases the steps involved in the face recognition pipeline. From the given input image, the face region is detected using a Haar face detector or manually annotated (for digital sketches) eye coordinates. It is our assertion that the proposed HDA and KHDA should yield good results with both handcrafted and learnt representations. Based on our formulation, to a large extent, HDA and KHDA should help obtain heterogeneity invariant representation of features. Therefore, the lesser heterogeneity invariant a feature is, the greater should be the extent of improvement by HDA and KHDA. Arguably, the learned features are more sophisticated and heterogeneity invariant compared to handcrafted features. Therefore, in this research, we have performed experiments with features of both types for detailed evaluation. In the literature, it has been observed that histogram of oriented gradients (HOG) and local binary patterns (LBP) are commonly used handcrafted features for heterogeneous face matching (Klare and Jain, 2013, 2010). Dhamecha et al. (2014) compared the performance of different variants of HOG and showed that DSIFT (Lowe, 2004) yields the best results. Therefore, among handcrafted features, we have demonstrated the results with DSIFT (extracted at keypoints on uniform grid and landmark points). For learnt representation, we use local class sparsity–based supervised encoder (LCSSE) (Majumdar et al., 2016), LightCNN (Wu et al., 2018), and ArcFace (Deng J. et al., 2019). For LightCNN (LightCNN29V2) and ArcFace, both the models pretrained on MS-Celeb 1M dataset are utilized as feature extractor. In this research, we have used the pretrained LCSSE model and fine-tuned with the training samples for each case study.

FIGURE 3

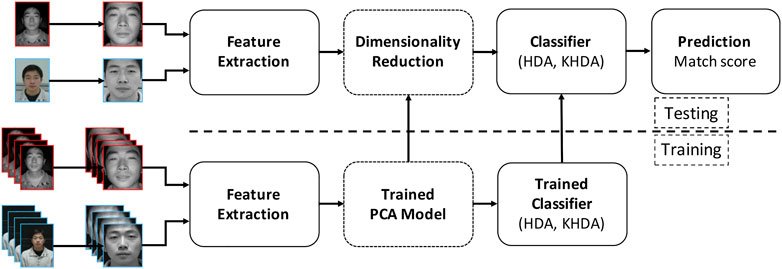
FIGURE 3. Illustrating the steps involved in the face recognition pipeline with the proposed HDA and KHDA.

As shown in Figure 3, once the features are obtained, they are projected on to a PCA space (preserving 99% eigenenergy), followed by projecting onto the $c-1$ dimensional HDA or KHDA space. It is to be noted that learning of PCA subspace does not use class labels, whereas HDA and KHDA training utilize identity labels and the view labels. Finally, distance score between gallery and probe feature vectors is computed using cosine distance measure.

Experimental Evaluation

The effectiveness of the proposed heterogeneous discriminant algorithm is evaluated for three different case studies of heterogeneous face recognition: 1) visible to near-infrared matching, 2) cross-resolution face matching, and 3) composite sketch (CS) to digital photo (DP) matching. For all three case studies, we have used publicly available benchmark databases: CASIA NIR-VIS 2.0 (Li et al., 2013), CMU Multi-PIE (Gross et al., 2010), and e-PRIP composite sketch (Han et al., 2013; Mittal et al., 2014). Table 2 summarizes the characteristics of the three databases. The experiments are performed with existing and published protocols so that the results can be directly compared with reported results.

TABLE 2

TABLE 2. Datasets utilized for evaluating the proposed HDA and KHDA on three heterogeneous face recognition challenges.

Cross-Spectral (Visible–NIR) Face Matching

Researchers have proposed several algorithms for VIS to NIR matching and primarily used the CASIA NIR-VIS 2.0 face dataset (Li et al., 2013). The protocol defined for performance evaluation consists of 10 splits of train and test sets for random subsampling cross-validation. As required by the predefined protocol, results are reported for both identification (mean and standard deviation of rank-1 identification accuracy) and verification (GAR at 0.1% FAR).

The images are first detected and preprocessed. Seven landmarks (two eye corners, three points on nose, and two lip corners) are detected (Everingham et al., 2009) from the input face image and geometric normalization is applied to register the cropped face images. The output of preprocessing is grayscale face images of size $130\times 150$ pixels. All the features³ are extracted from geometrically normalized face images. We evaluate the effectiveness of HDA over LDA. To compare the results with LDA, the pipeline shown in Figure 3 is followed with the exception of using LDA instead of HDA. The results are reported in Table 3 and the key observations are discussed below.⁴

TABLE 3

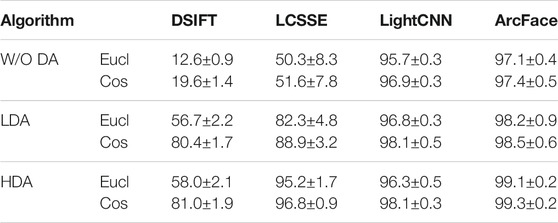
TABLE 3. Rank-1 identification accuracy for visible to near-infrared face matching on the CASIA NIR–VIS 2.0 database (Li et al., 2013).

Discriminative Learning using HDA

As shown in Table 3, without discriminant analysis (LDA or HDA), the performance of individual features is lower. The deep learning–based LCSSE yields around 50% rank-1 accuracy. The LightCNN and ArcFace features yield impressive rank-1 accuracy of about 95% and 97%, respectively, which shows their superior feature representation. The next experiment illustrates the effect of applying LDA on individual features. Table 3 shows that LDA improves the accuracy up to 60%. Comparing the performance of HDA with LDA shows that HDA outperforms LDA. Utilizing HDA in place of LDA for discriminative learning improves the results up to 12.9%. The HDA and LDA performance is very high and almost same for LightCNN, which may point toward its spectrum-invariant representation capabilities. For ArcFace, although small, a consistently progressive improvement of about 1% is observed between raw features, LDA, and HDA, respectively. Understandably, if the feature is spectrum-invariant, the benefits of heterogeneity-aware classifier are expected to be limited. The improvement provided by HDA can be attributed to the fact that it learns a discriminative subspace specifically for heterogeneous matching. Similar to the toy example shown in Figure 2, it can be asserted that the multi-view information yields different clusters in the feature space. Under such scenarios, since the fundamental assumption of Gaussian data distribution is not satisfied, LDA can exhibit suboptimal results. However, by encoding the view label information, HDA is able to find better projection space, thereby yielding better results.

Effect of HDA across Features

The results show that the proposed HDA improves the accuracy of DSIFT and LCSSE features by 40–60%. For instance, applying LCSSE with HDA improves the results by around 45%. As discussed earlier, even the raw LightCNN and ArcFace features yield very high performance, leaving very little room of improvement by LDA or HDA projections.

Direction vs Magnitude in Projection Space

Cosine distance encodes only the difference in direction between samples, whereas the Euclidean distance encodes both direction and magnitude. For the given experiment, as shown in Table 3, cosine distance generally yields higher accuracy over Euclidean distance. This shows that for heterogeneous matching, the magnitude of projections may not provide useful information and only directional information can be used for matching.

Optimum Combination

From the above analysis, it can be seen that the proposed HDA in combination with DSIFT features and cosine distance measure yields an impressive 81% for a handcrafted feature. ArcFace features with HDA and cosine distance measure yield the best results. However, LightCNN and LCSSE are also within 3% of it. For the remaining experiments (and other case studies), we have demonstrated the results with DSIFT, LCSSE, LightCNN, and ArcFace features and cosine distance measure along with proposed heterogeneity-aware classifiers.

Comparison with Existing Algorithms

We next compare the results of the proposed approaches with the results reported in the literature. Comparative analysis is shown with a leading commercial off-the-shelf (COTS) face recognition system, FaceVACS⁵, and 20 recently published results. Table 4 shows that with pixel values as input, the proposed HDA approach outperforms other existing algorithms. For example, MvDA with pixel values yields 41.6% rank-1 identification accuracy and 19.2% GAR at 0.1% FAR, whereas the proposed approach yields similar rank-1 accuracy with lower standard deviation and much higher GAR of 31.4%. Further, Table 4 clearly⁶ demonstrates the performance improvement due to the proposed HDA and its nonlinear kernel variant KHDA. KHDA with learnt representation LCSSE and HDA with LightCNN yield almost equal identification accuracy. However, our best results are obtained with ArcFace with KHDA at 99.4% rank-1 and 99.1% GAR@FAR=0.1%. The reported results are comparable to the recently published state of the art.

TABLE 4

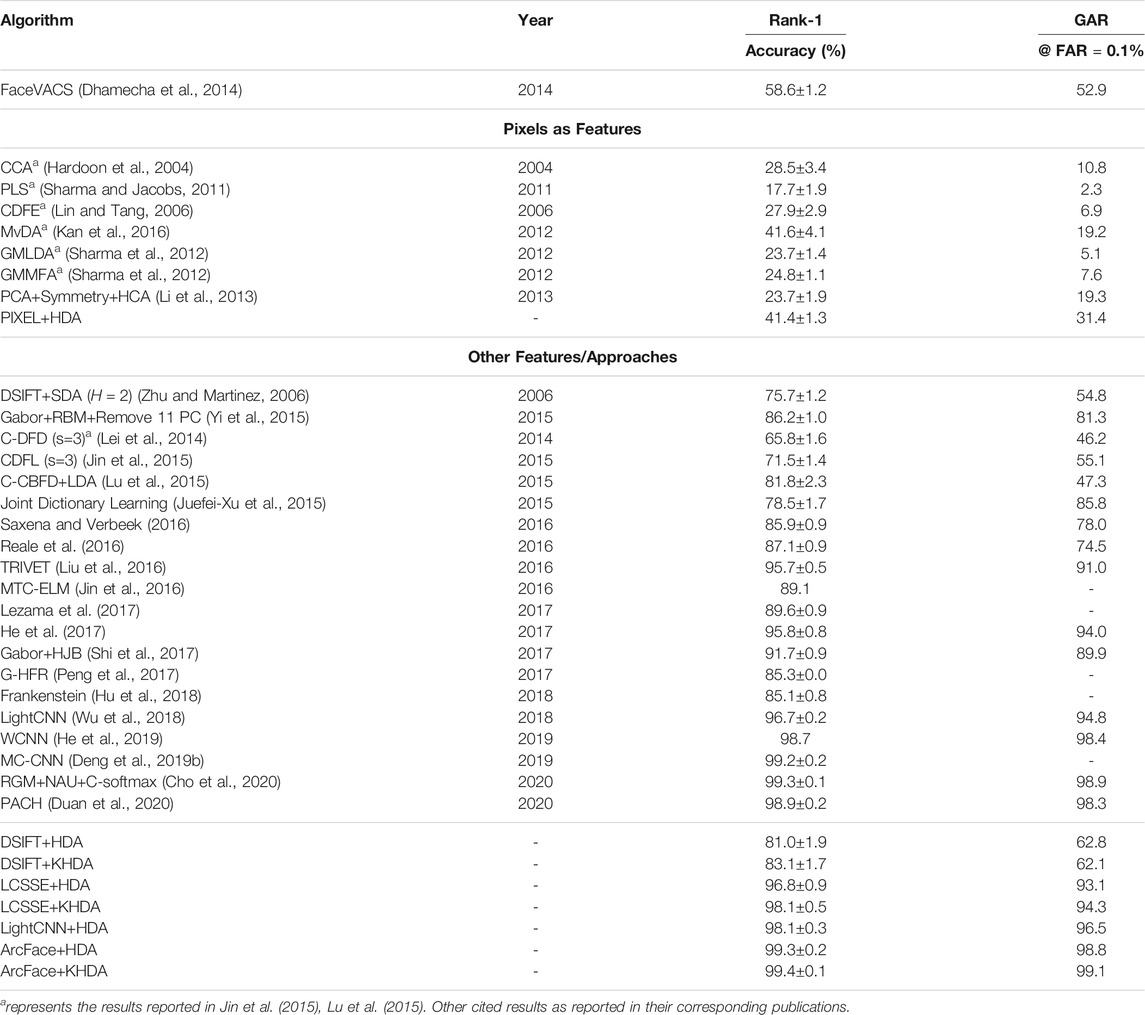
TABLE 4. Comparing the face recognition performance of the proposed and some existing algorithms for VIS to NIR face matching on CASIA NIR–VIS 2.0 dataset.

Also, LCSSE+KHDA and LightCNN+HDA achieve 94.3% and 96.5% GAR at 0.1% FAR, respectively. Also note that, in a fair comparison, DSIFT features with the proposed KHDA also yield results comparable to other non-deep learning–based approaches.

Cross-Resolution Face Matching

Cross-resolution face recognition entails matching high-resolution gallery images with low-resolution probe images. In this scenario, high resolution and low resolution are considered as two different views of a face image. We compare our approach with Bhatt et al. (2012, 2014) as they have reported one of the best results for the problem. We follow their protocol on CMU Multi-PIE database (Gross et al., 2010). Each image is resized to six different resolutions: $16\times 16$, $24\times 24$, $32\times 32$, $48\times 48$, $72\times 72$, and $216\times 216$. In total, $\left(\begin{array}{c}6\\ 2\end{array}\right)=15$ cross-resolution matching scenarios are considered. For every person, two images are selected and images pertaining to 100 subjects are utilized for training, whereas the remaining 237 subjects are utilized for testing. The results are reported in Table 5. Results for ArcFace+KHDA are similar to ArcFace+HDA, hence not reported here. Since the protocol (Bhatt et al., 2012, 2014) does not involve cross-validation, error intervals are not reported.

TABLE 5

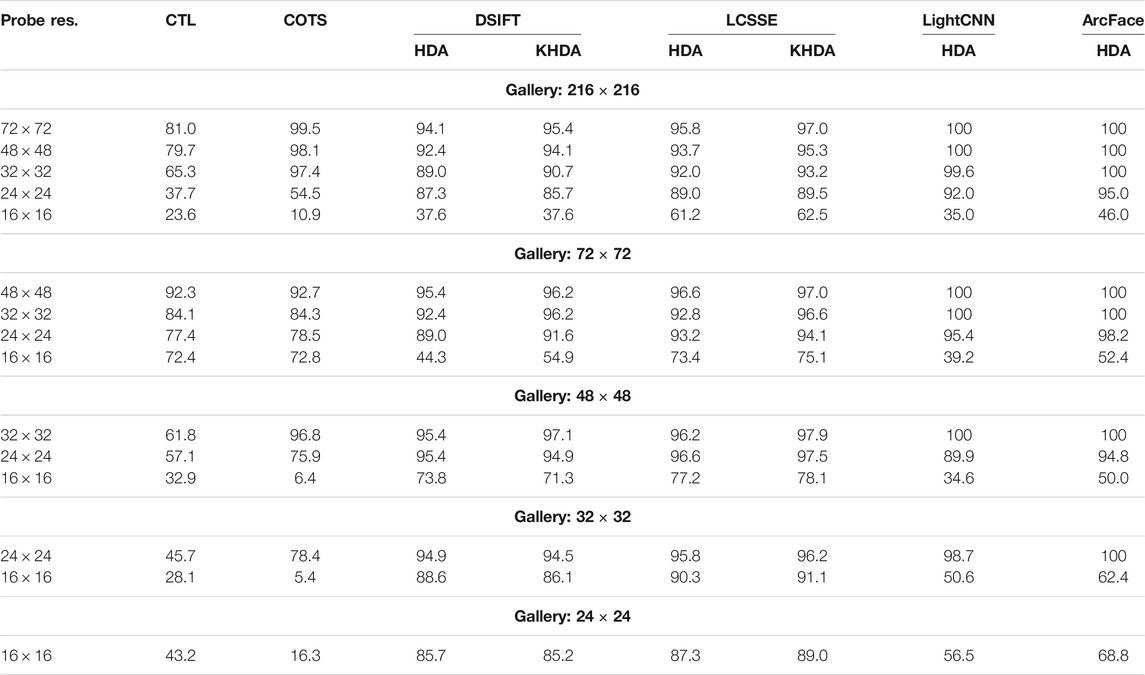
TABLE 5. Rank-1 identification accuracy of the proposed HDA, KHDA and existing algorithms, Cotransfer Learning (CTL) and a commercial off-the-shelf (COTS) (Bhatt et al., 2012, 2014), DSIFT (Lowe, 2004), LCSSE (Majumdar et al., 2016), LightCNN, and ArcFace on CMU Multi-PIE database (Gross et al., 2010) with different gallery and probe image sizes.

It can be seen that LCSSE+KHDA outperforms the cotransfer learning (Bhatt et al., 2012, 2014) in all the cross-resolution matching scenarios. For example, when $48\times 48$ pixel gallery images are matched with probe images of $32\times 32$, $24\times 24$, and $16\times 16$ pixels, performance improvement of about 30%–40% is observed. LightCNN and ArcFace yield even higher identification accuracy, except when the probe image is $16\times 16$. We believe that the feature extractor is unable to extract representative information at these resolutions. Analyzing the results across resolutions shows that the accuracy reduces with increase in resolution difference between the gallery and probe images. FaceVACS yields impressive performance when the size of both gallery and probe are higher than $32\times 32$. However, the performance deteriorates significantly with decrease in the gallery image size and with increase in the resolution difference. Generally, the performance of the proposed HDA and/or KHDA is less affected due to resolution difference in comparison to FaceVACS and CTL. We have also observed that for cross-resolution face recognition, learned features (LCSSE, LightCNN, and ArcFace) show higher accuracies compared to DSIFT with a difference of up to 25%.

Digital Photo to Composite Sketch Face matching

In many law enforcement and forensic applications, software tools are used to generate composite sketches based on eyewitness description and the composite sketch is matched against a gallery of digital photographs. Han et al. (2013) presented a component-based approach followed by score fusion for composite to photo matching. Later, Mittal et al. (2014, 2013, 2015, 2017) and Chugh et al. (2013) presented learning-based algorithms for the same. Klum et al. (2014) presented FaceSketchID for matching composite sketches to photos.

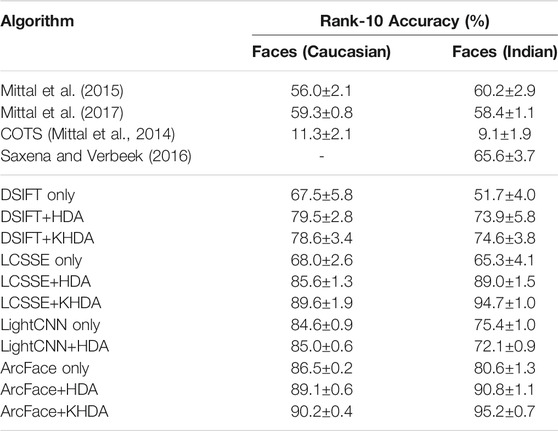
For this set of experiments, we utilize the e-PRIP composite sketch dataset (Han et al., 2013; Mittal et al., 2014). The dataset contains composite sketches of 123 face images from the AR face dataset (Martinez, 1998). It contains the composite sketches created using two tools, Faces and IdentiKit⁷. The PRIP dataset (Han et al., 2013) originally has composite sketches prepared by a Caucasian user (with IdentiKit and Faces softwares) and an Asian user (with Faces software). Later, the dataset is extended by Mittal et al. (2014) by adding composite sketches prepared by an Indian user (with Faces software) which is termed as the e-PRIP composite sketch dataset. In this work, we use composite sketches prepared using Faces software by the Caucasian and Indian users as they are shown to yield better results compared to other sets (Mittal et al., 2014, 2013). The experiments are performed with the same protocol as presented by Mittal et al. (2014). Mean identification accuracies, across five random cross-validations, at rank-10 are reported in Table 6, and Figure 4 shows the corresponding CMC curves.

TABLE 6

TABLE 6. Results for composite sketch to photo matching.

FIGURE 4

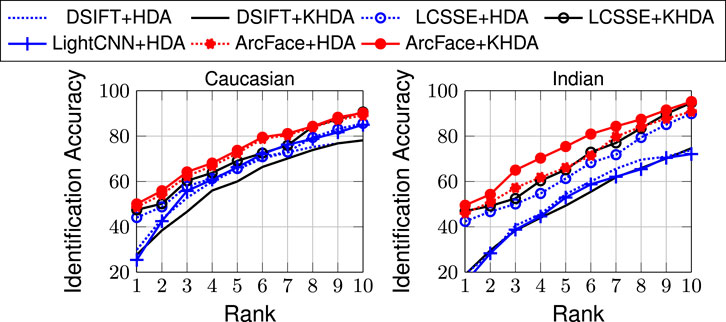
FIGURE 4. CMC curves for composite sketch to digital photo matching on the e-PRIP composite sketch dataset (Han et al., 2013; Mittal et al., 2014).

With the above mentioned experimental protocol, one of the best results in the literature has been reported by Mittal et al. (2017) with rank-10 identification accuracies of 59.3% (Caucasian) and 58.4% (Indian). Saxena and Verbeek (2016) have shown results with Indian users only and have achieved 65.5% rank-10 accuracy. As shown in the results, the proposed approaches, HDA and KHDA, with both DSIFT and LCSSE improve the performance significantly. Compared to existing algorithms, DSIFT demonstrates an improvement in the range of 11–23%, while LCSSE+HDA and LCSSE+KHDA improve the rank-10 accuracy by ∼30% with respect to state of the art (Saxena and Verbeek, 2016). Interestingly, LightCNN yields poorer performance compared to LCSSE in this case study. ArcFace yields the highest identification accuracy. Similar to previous results, this experiment also shows that application of HDA/KHDA improves the results of DSIFT, LCSSE, and ArcFace. However, the degree of improvement varies between handcrafted and learned features.

Conclusion

In this research, we have proposed a discriminant analysis approach for heterogeneous face recognition. We formulate heterogeneous discriminant analysis which encodes view labels and has the objective function optimized for heterogeneous matching. Based on the analytical solution, we propose its kernel extension, KHDA. The proposed techniques are heterogeneity aware. Potentially, they can be applied on top of any features to get heterogeneity invariant representation, to an extent. Experiments are performed on three heterogeneous face matching problems, namely, visible to NIR matching, cross-resolution matchings, and digital photo to sketch, with handcrafted DSIFT and deep learning–based LCSSE, LightCNN, and ArcFace features. The results show that incorporating the proposed discriminant analysis technique consistently improves the performance of both learnt and handcrafted features, without increasing much to the computational requirements. The improvement is more pronounced in handcrafted features and provides an efficient way to improve their performance.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: http://www.cbsr.ia.ac.cn/english/HFB_Agreement/NIR-VIS-2.0_agreements.pdf, https://www.cs.cmu.edu/afs/cs/project/PIE/MultiPie/Multi-Pie/Home.html, https://www.iab-rubric.org/resources/eprip.html.

Ethics Statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements. Written informed consent was not obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author Contributions

TD, MV, and RS discussed the primary approach. TD, SG, and MV performed the experiments and all the authors prepared the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

¹The terms view and domain/modality are used synonymously in the heterogeneous face recognition literature.

²Detailed formulation is in the supplementary document.

³Results of LBP, HOG variants, and pixel are in supplementary document.

⁴There is slight difference between LightCNN + W/O DA of Table 3 and LightCNN in Table 4, as former is our implementation and later is as reported in (Wu et al., 2018).

⁵http://www.cognitec.com/technology.html

⁶ROC in the supplementary document.

⁷Faces: www.iqbiometrix.com, IdentiKit: www.identikit.net

References

Bhatt, H., Singh, R., and Vatsa, M. (2015). Covariates of Face Recognition. Tech. Report at IIIT Delhi.

Bhatt, H. S., Singh, R., Vatsa, M., and Ratha, N. K. (2014). Improving Cross-Resolution Face Matching Using Ensemble-Based Co-transfer Learning. IEEE Trans. Image Process. 23, 5654–5669. doi:10.1109/tip.2014.2362658

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhatt, H. S., Singh, R., Vatsa, M., and Ratha, N. (2012). Matching Cross-Resolution Face Images Using Co-transfer Learning. IEEE ICIP, 1453–1456. doi:10.1109/ICIP.2012.6467144

Google Scholar

Biswas, S., Aggarwal, G., Flynn, P. J., and Bowyer, K. W. (2013). Pose-robust Recognition of Low-Resolution Face Images. IEEE Trans. Pattern Anal. Mach. Intell. 35, 3037–3049. doi:10.1109/tpami.2013.68

PubMed Abstract | CrossRef Full Text | Google Scholar

Biswas, S., Bowyer, K. W., and Flynn, P. J. (2012). Multidimensional Scaling for Matching Low-Resolution Face Images. IEEE Trans. Pattern Anal. Mach. Intell. 34, 2019–2030. doi:10.1109/tpami.2011.278

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, C., and Ross, A. (2013). Local Gradient Gabor Pattern (LGGP) with Applications in Face Recognition, Cross-Spectral Matching, and Soft Biometrics. SPIE Defense, Security, and Sensing 8712, 87120R. doi:10.1117/12.2018230

CrossRef Full Text | Google Scholar

Cho, M., Kim, T., Kim, I.-J., Lee, K., and Lee, S. (2020). Relational Deep Feature Learning for Heterogeneous Face Recognition. IEEE TIFS 16, 376–388. doi:10.1109/TIFS.2020.3013186

Google Scholar

Chugh, T., Bhatt, H. S., Singh, R., and Vatsa, M. (2013). Matching Age Separated Composite Sketches and Digital Face Images. IEEE BTAS, 1–6. doi:10.1109/BTAS.2013.6712719

Google Scholar

Deng, J., Guo, J., Xue, N., and Zafeiriou, S. (2019a). Arcface: Additive Angular Margin Loss for Deep Face Recognition. CVPR, 4690–4699. doi:10.1109/CVPR.2019.00482

Google Scholar

Deng, Z., Peng, X., Li, Z., and Qiao, Y. (2019b). Mutual Component Convolutional Neural Networks for Heterogeneous Face Recognition. IEEE Trans. Image Process. 28, 3102–3114. doi:10.1109/tip.2019.2894272

PubMed Abstract | CrossRef Full Text | Google Scholar

Dhamecha, T. I., Sharma, P., Singh, R., and Vatsa, M. (2014). 1788–1793. On Effectiveness of Histogram of Oriented Gradient Features for Visible to Near Infrared Face Matching IAPR ICPR. doi:10.1109/ICPR.2014.314

Google Scholar

Duan, B., Fu, C., Li, Y., Song, X., and He, R. (2020). Cross-spectral Face Hallucination via Disentangling Independent Factors. CVPR, 7930–7938. doi:10.1109/CVPR42600.2020.00795

Google Scholar

Everingham, M., Sivic, J., and Zisserman, A. (2009). Taking the Bite Out of Automated Naming of Characters in Tv Video. Image Vis. Comput. 27, 545–559. doi:10.1016/j.imavis.2008.04.018

CrossRef Full Text | Google Scholar

Friedman, J. H. (1989). Regularized Discriminant Analysis. J. Am. Stat. Assoc. 84, 165–175. doi:10.1080/01621459.1989.10478752

CrossRef Full Text | Google Scholar

Goswami, D., Chan, C. H., Windridge, D., and Kittler, J. (2011). Evaluation of Face Recognition System in Heterogeneous Environments (Visible vs NIR). IEEE ICCV Workshops, 2160–2167. doi:10.1109/ICCVW.2011.6130515

Google Scholar

Gross, R., Matthews, I., Cohn, J., Kanade, T., and Baker, S. (2010). Multi-PIE. Image Vis. Comput. 28, 807–813. doi:10.1016/j.imavis.2009.08.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, H., Klare, B. F., Bonnen, K., and Jain, A. K. (2013). Matching Composite Sketches to Face Photos: A Component-Based Approach. IEEE TIFS 8, 191–204. doi:10.1109/TIFS.2012.2228856

Google Scholar

Hardoon, D. R., Szedmak, S., and Shawe-Taylor, J. (2004). Canonical Correlation Analysis: An Overview with Application to Learning Methods. Neural Comput. 16, 2639–2664. doi:10.1162/0899766042321814

PubMed Abstract | CrossRef Full Text | Google Scholar

He, R., Wu, X., Sun, Z., and Tan, T. (2017). Learning Invariant Deep Representation for NIR-VIS Face Recognition. AAAI 4, 7.

Google Scholar

He, R., Wu, X., Sun, Z., and Tan, T. (2019). Wasserstein CNN: Learning Invariant Features for NIR-VIS Face Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 41, 1761–1773. doi:10.1109/tpami.2018.2842770

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, G., Peng, X., Yang, Y., Hospedales, T. M., and Verbeek, J. (2018). Frankenstein: Learning Deep Face Representations Using Small Data. IEEE Trans. Image Process. 27, 293–303. doi:10.1109/tip.2017.2756450

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, Y., Li, J., Lang, C., and Ruan, Q. (2016). Multi-task Clustering ELM for VIS-NIR Cross-Modal Feature Learning. Multidimensional Syst. Signal Process. 1–16. doi:10.1007/s11045-016-0401-8

Google Scholar

Jin, Y., Lu, J., and Ruan, Q. (2015). Coupled Discriminative Feature Learning for Heterogeneous Face Recognition. IEEE Trans.Inform.Forensic Secur. 10, 640–652. doi:10.1109/tifs.2015.2390414

CrossRef Full Text | Google Scholar

Juefei-Xu, F., Pal, D. K., and Savvides, M. (2015). NIR-VIS Heterogeneous Face Recognition via Cross-Spectral Joint Dictionary Learning and Reconstruction. CVPR Workshops, 141–150. doi:10.1109/CVPRW.2015.7301308

Google Scholar

Kalka, N. D., Bourlai, T., Cukic, B., and Hornak, L. (2011). Cross-spectral Face Recognition in Heterogeneous Environments: A Case Study on Matching Visible to Short-Wave Infrared Imagery. IEEE IJCB, 1–8. doi:10.1109/IJCB.2011.6117586

Google Scholar

Kan, M., Shan, S., Zhang, H., Lao, S., and Chen, X. (2016). Multi-view Discriminant Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 38, 188–194. doi:10.1109/tpami.2015.2435740

PubMed Abstract | CrossRef Full Text | Google Scholar

Klare, B. F., and Jain, A. K. (2013). Heterogeneous Face Recognition Using Kernel Prototype Similarities. IEEE Trans. Pattern Anal. Mach. Intell. 35, 1410–1422. doi:10.1109/tpami.2012.229

PubMed Abstract | CrossRef Full Text | Google Scholar

Klare, B., and Jain, A. K. (2010). Heterogeneous Face Recognition: Matching NIR to Visible Light Images. IAPR ICPR, 1513–1516. doi:10.1109/ICPR.2010.374

Google Scholar

Klum, S. J., Han, H., Klare, B. F., and Jain, A. K. (2014). The FaceSketchID System: Matching Facial Composites to Mugshots. IEEE Trans.Inform.Forensic Secur. 9, 2248–2263. doi:10.1109/tifs.2014.2360825

CrossRef Full Text | Google Scholar

Lei, Z., Pietikäinen, M., and Li, S. Z. (2014). Learning Discriminant Face Descriptor. IEEE Trans. Pattern Anal. Mach Intell. 36, 289–302. doi:10.1109/TPAMI.2013.112

PubMed Abstract | CrossRef Full Text | Google Scholar

Lei, Z., and Li, S. Z. (2009). Coupled Spectral Regression for Matching Heterogeneous Faces. CVPR, 1123–1128. doi:10.1109/CVPR.2009.5206860

Google Scholar

Lei, Z., Liao, S., Jain, A. K., and Li, S. Z. (2012a). Coupled Discriminant Analysis for Heterogeneous Face Recognition. IEEE Trans.Inform.Forensic Secur. 7, 1707–1716. doi:10.1109/tifs.2012.2210041

CrossRef Full Text | Google Scholar

Lei, Z., Zhou, C., Yi, D., Jain, A. K., and Li, S. Z. (2012b). An Improved Coupled Spectral Regression for Heterogeneous Face Recognition. IEEE/IAPR Int. Conf. Biometrics, 7–12. doi:10.1109/icb.2012.6199751

CrossRef Full Text | Google Scholar

Lezama, J., Qiu, Q., and Sapiro, G. (2017). Not afraid of the Dark: NIR-VIS Face Recognition via Cross-Spectral Hallucination and Low-Rank Embedding. CVPR, 6807–6816. doi:10.1109/cvpr.2017.720

CrossRef Full Text | Google Scholar

Li, B., Chang, H., Shan, S., and Chen, X. (2010). Low-resolution Face Recognition via Coupled Locality Preserving Mappings. IEEE SPL 17, 20–23. doi:10.1109/LSP.2009.2031705

Google Scholar

Li, S., Yi, D., Lei, Z., and Liao, S. (2013). The CASIA NIR-VIS 2.0 Face Database. CVPR Workshops, 348–353. doi:10.1109/CVPRW.2013.59

Google Scholar

Li, Z., Gong, D., Qiao, Y., and Tao, D. (2014). Common Feature Discriminant Analysis for Matching Infrared Face Images to Optical Face Images. IEEE Trans. Image Process. 23, 2436–2445. doi:10.1109/TIP.2014.2315920

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Z., Gong, D., Li, Q., Tao, D., and Li, X. (2016). Mutual Component Analysis for Heterogeneous Face Recognition. ACM Trans. Intell. Syst. Technol. 7, 1–23. doi:10.1145/2807705

CrossRef Full Text | Google Scholar

Liao, S., Yi, D., Lei, Z., Qin, R., and Li, S. Z. (2009). Heterogeneous Face Recognition from Local Structures of Normalized Appearance. Adv. Biometrics, 209–218. doi:10.1007/978-3-642-01793-3_22

CrossRef Full Text | Google Scholar

Lin, D., and Tang, X. (2006). Inter-modality Face Recognition. ECCV, 13–26. doi:10.1007/11744085_2

CrossRef Full Text | Google Scholar

Liu, X., Song, L., Wu, X., and Tan, T. (2016). Transferring Deep Representation for NIR-VIS Heterogeneous Face Recognition. IEEE ICB, 1–8. doi:10.1109/ICB.2016.7550064

Google Scholar

Lowe, D. G. (2004). Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 60, 91–110. doi:10.1023/b:visi.0000029664.99615.94

CrossRef Full Text | Google Scholar

Lu, J., Liong, V. E., Zhou, X., and Zhou, J. (2015). Learning Compact Binary Face Descriptor for Face Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 37, 2041–2056. doi:10.1109/tpami.2015.2408359

PubMed Abstract | CrossRef Full Text | Google Scholar

Majumdar, A., Singh, R., and Vatsa, M. (2016). Face Verification via Class Sparsity Based Supervised Encoding. IEEE Trans. Pattern Anal. Mach. Intell. 39, 1273–1280. doi:10.1109/TPAMI.2016.2569436

PubMed Abstract | CrossRef Full Text | Google Scholar

Martinez, A. M. (1998). The AR Face Database. CVC Tech. Rep. 24. doi:10.2118/46030-ms

CrossRef Full Text | Google Scholar

Mittal, P., Jain, A., Goswami, G., Singh, R., and Vatsa, M. (2014). Recognizing Composite Sketches with Digital Face Images via SSD Dictionary. IEEE IJCB, 1–6. doi:10.1109/BTAS.2014.6996265

Google Scholar

Mittal, P., Jain, A., Goswami, G., Vatsa, M., and Singh, R. (2017). Composite Sketch Recognition Using Saliency and Attribute Feedback. Inf. Fusion 33, 86–99. doi:10.1016/j.inffus.2016.04.003

CrossRef Full Text | Google Scholar

Mittal, P., Jain, A., Singh, R., and Vatsa, M. (2013). Boosting Local Descriptors for Matching Composite and Digital Face Images. IEEE ICIP, 2797–2801. doi:10.1109/ICIP.2013.6738576

Google Scholar

Mittal, P., Vatsa, M., and Singh, R. (2015). Composite Sketch Recognition via Deep Network - a Transfer Learning Approach. IEEE/IAPR ICB, 251–256. doi:10.1109/ICB.2015.7139092

Google Scholar

Peng, C., Gao, X., Wang, N., and Li, J. (2017). Graphical Representation for Heterogeneous Face Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 39, 301–312. doi:10.1109/tpami.2016.2542816

PubMed Abstract | CrossRef Full Text | Google Scholar

Reale, C., Nasrabadi, N. M., Kwon, H., and Chellappa, R. (2016). Seeing the forest from the Trees: A Holistic Approach to Near-Infrared Heterogeneous Face Recognition. CVPR Workshops, 320–328. doi:10.1109/cvprw.2016.47

CrossRef Full Text | Google Scholar

Saxena, S., and Verbeek, J. (2016). Heterogeneous Face Recognition with CNNs. ECCV Workshops, 483–491.

Google Scholar

Schölkopf, B., Herbrich, R., and Smola, A. J. (2001). A Generalized Representer Theorem. Comput. Learn. Theor., 416–426. doi:10.1007/3-540-44581-1_27

CrossRef Full Text | Google Scholar

Sharma, A., and Jacobs, D. W. (2011). Bypassing Synthesis: PLS for Face Recognition with Pose, Low-Resolution and Sketch. CVPR Workshops, 593–600. doi:10.1109/CVPR.2011.5995350

Google Scholar

Sharma, A., Kumar, A., Daume, H., and Jacobs, D. W. (2012). Generalized Multiview Analysis: A Discriminative Latent Space. CVPR, 2160–2167. doi:10.1109/cvpr.2012.6247923

CrossRef Full Text | Google Scholar

Shi, H., Wang, X., Yi, D., Lei, Z., Zhu, X., and Li, S. Z. (2017). Cross-modality Face Recognition via Heterogeneous Joint Bayesian. IEEE SPL 24 (1), 81–85. doi:10.1109/LSP.2016.2637400

CrossRef Full Text | Google Scholar

Siena, S., Boddeti, V., and Kumar, B. (2013). Maximum-margin Coupled Mappings for Cross-Domain Matching. IEEE BTAS. 1–8. doi:10.1109/BTAS.2013.6712686

Google Scholar

Taigman, Y., Yang, M., Ranzato, M., and Wolf, L. (2014). Deepface: Closing the gap to Human-Level Performance in Face Verification. CVPR, 1701–1708. doi:10.1109/cvpr.2014.220

CrossRef Full Text | Google Scholar

Tang, X., and Wang, X. (2003). Face Sketch Synthesis and Recognition. IEEE ICCV, 687–694. doi:10.1109/ICCV.2003.1238414

Google Scholar

Wilson, C. L., Grother, P. J., and Chandramouli, R. (2007). Biometric Data Specification for Personal Identity Verification. Tech. Report NIST-SP-800-76-1. National Institute of Standards & Technology.

CrossRef Full Text

Wu, F., Jing, X.-Y., You, X., Yue, D., Hu, R., and Yang, J.-Y. (2016). Multi-view Low-Rank Dictionary Learning for Image Classification. Pattern Recognition 50, 143–154. doi:10.1016/j.patcog.2015.08.012

CrossRef Full Text | Google Scholar

Wu, X., He, R., Sun, Z., and Tan, T. (2018). A Light Cnn for Deep Face Representation with Noisy Labels. IEEE Trans.Inform.Forensic Secur. 13, 2884–2896. doi:10.1109/tifs.2018.2833032

CrossRef Full Text | Google Scholar

Yi, D., Lei, Z., and Li, S. Z. (2015). Shared Representation Learning for Heterogenous Face Recognition. IEEE FG, 1–7. doi:10.1109/FG.2015.7163093

Google Scholar

Yi, D., Liu, R., Chu, R., Lei, Z., and Li, S. Z. (2007). Face Matching between Near Infrared and Visible Light Images. Adv. Biometrics, 523–530. doi:10.1007/978-3-540-74549-5_55

Google Scholar

Zhu, J.-Y., Zheng, W.-S., Lai, J.-H., and Li, S. Z. (2014). Matching NIR Face to VIS Face Using Transduction. IEEE Trans.Inform.Forensic Secur. 9, 501–514. doi:10.1109/tifs.2014.2299977

CrossRef Full Text | Google Scholar

Zhu, M., and Martinez, A. M. (2006). Subclass Discriminant Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 28, 1274–1286. doi:10.1109/TPAMI.2006.172

PubMed Abstract | CrossRef Full Text | Google Scholar