Utilization of three-layers heterogeneous mammographic phantom through MCNPX code for breast and chest radiation dose levels at different diagnostic X-ray energies: A Monte Carlo simulation study

Introduction: We report the breast and chest radiation dose assessment for mammographic examinations using a three-layer heterogeneous breast phantom through the MCNPX Monte Carlo code.

Methods: A three-layer heterogeneous phantom along with compression plates and X-ray source are modeled. The validation of the simulation code is obtained using the data of AAPM TG-195 report. Deposited energy amount as a function of increasing source energy is calculated over a wide energy range. The behavioral changes in X-ray absorption as well as transmission are examined using the F6 Tally Mesh extension of MCNPX code. Moreover, deposited energy amount is calculated for modeled body phantom in the same energy range.

Results and discussions: The diverse distribution of glands has a significant impact on the quantity of energy received by the various breast layers. In layers with a low glandular ratio, low-energy primary X-ray penetrability is highest. In response to an increase in energy, the absorption in layers with a low glandular ratio decreased. This results in the X-rays releasing their energy in the bottom layers. Additionally, the increase in energy increases the quantity of energy absorbed by the tissues around the breast.

1. Introduction

Mammography plays major role in diagnosing and assessing breast cancer. However, the advantages of mammography do not always outweigh the disadvantages. Some literature were concerned about the increase in the incidence of breast cancer after the start of the mammography screening programs (1). Due to the nature of the breast tissue, mammography X-ray tubes are manufactured with special anode/target materials and focal spot size. Mammography uses low tube voltage (25–30 kVp), low mA, longer exposure time and different filter combination to increase contrast difference as breast is composed of soft tissue. The use of the parameters leads to an increase in the radiation absorbed by the breast tissue due to photoelectric absorption and Compton scattering. With all advantages of screening mammography, it has been reported that the sensitivity of mammography decreases with the increase in breast density. Assessment of breast dose measurement is an essential aspect of radiation protection since screening mammography is performed periodically. The glandular tissue in the breast is the most tissue prone to radiation-induced mutations (2). Therefore, the Mean glandular dose (MGD) is the standard quantity used for radiation dosimetry in mammography as recommended by the ICRP in 1987. Radiation dose optimization is required to avoid increase in the MGD which might lead to increase of the breast cancer (3). Of course, direct measurement of the MGD is impossible, so conversion factors are used to relate measurable dose quantities to the MGD. Conversion factors are usually based on the characteristics of the breast (size and composition) and the x-ray spectrum used for mammography examination. Monte Carlo simulations were used to overcome the constraints of using phantoms to simulate breast composition and x-ray spectrum. Simple and complex geometrical models were developed to calculate conversion factors which relate the measurable quantity, the incident air kerma in mGy, to the MGD (4). In mammography, various Monte Carlo codes were used, including the MCNP or MCNPX (5, 6) and Geant4 (7). Notwithstanding, data on the density and composition of breast tissues are still minimal (4), and there is a need to estimate the energy imparted to the glandular tissues within the breast (8–10). The current study aims to perform a comprehensive study on establishing a detailed Monte Carlo simulation setup for different breast thicknesses and estimate MGD for these modeled breast phantoms. In contrast, the literature presents several models and concepts which would advance the simulation level of breast dosimetry techniques. Recently, Chang et al., (11) have proposed a three-layered homogeneous breast phantom for Monte Carlo simulation of normalized glandular dose coefficients in mammography. They described the dosimetry characteristics of this three-layer heterogeneous phantom with success. However, the absorbed energy ratios of these layers and the degree to which these ratios are dependent on layer properties remain unknown. With this momentum, we sought answers to a number of concerns that could provide motivation for further scientific community investigations, as well as to expand upon the findings of the first phase study by investigating the characteristics of this new three-layer heterogeneous model in deeper level. The results may be used for advanced assessment of MGD values during the patient risk assessment for mammography patients. The result can also be used for cancer risk assessment of those patients with existing cancer story or genetically tendency for some other cancer types.

2. Materials and methods

2.1. Monte Carlo simulations

In situations when experimental and clinical research is difficult or physically impossible to conduct, Monte Carlo simulation approaches may be used. This situation may range from organ dosimetry (12–15) in clinical research to shielding calculations (16–18) in radiation protection research, covering a broad spectrum. Some well-known Monte Carlo simulation-based radiation transportation codes such as MCNP (19), GEANT4 (20), EGSnrc (21), and FLUKA (22), have been utilized for such purposes. The geometric design and all simulation processes of the breast fandom used in the study were carried out with version 2.7.0 of MCNPX (19), which is a well-known and general-purpose Monte Carlo code. First, a three-layer breast phantom was constructed. For each layer, a unique Glandular Fraction value was assigned. The GF values of the layers were calculated in line with a previously researched geometric concept. In the MCNPX input file, each layer was specified as a separate CELL. The contents of these CELL volumes, as well as their elemental percentage fractions and densities, were specified in the INPUT file in accordance with the various GF values. In addition to their elemental percentages and densities, the skin layers surrounding the three-layer breast model's five surfaces were also defined. On the back of the designed breast model, a body phantom with the density of human tissue was added into the input file. In the last phase, a source with a source-image receptor distance of 65 cm was defined just on breast phantom. Figure 1 illustrates the breast phantom and source from a lateral view. As shown in Figure 1, the breast phantom is composed, from top to bottom, of cells 3, 4, and 5. The geometries of cells 8, 7, and 11 are carefully modeled from the lateral edge to the skin layer. Figure 1B depicts the cellular structure of cell 10 of the model body phantom. In addition, Figure 1B depicts lateral views of the compression plates placed on the top and lower sides of the breast phantom. After completing the input file, the modeled geometry was evaluated in 3D through using MCNPX image editor as well as any geometric mistakes were verified. Figure 2 displays the 3D geometries derived through the MCNPX visual editor (VE X22S) for the 2D geometries shown in Figure 1. As illustrated in Figure 2, the breast phantom is surrounded by compression plates in a way suited for clinical application. Meanwhile, the simulation studies were conducted through LENOVO ThinkStation P620 Tower Workstation with a processor of AMD Ryzen™ Threadripper.

FIGURE 1

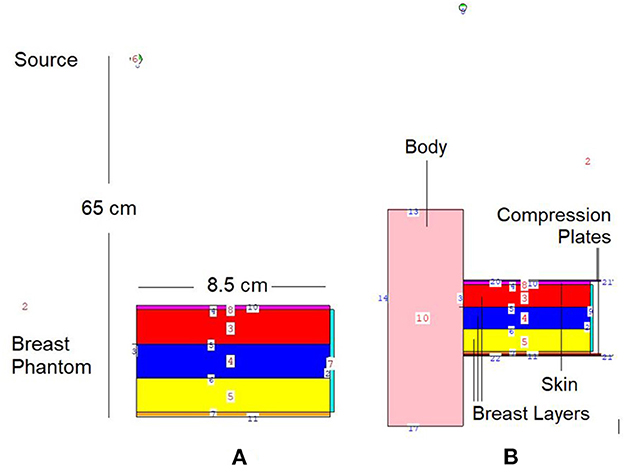
Figure 1. 2-D view of modeled MCNPX simulation setup from (A) breast phantom (B) breast phantom with body phantom and compression plates (via MCNPX Visual Editor X22S).

FIGURE 2

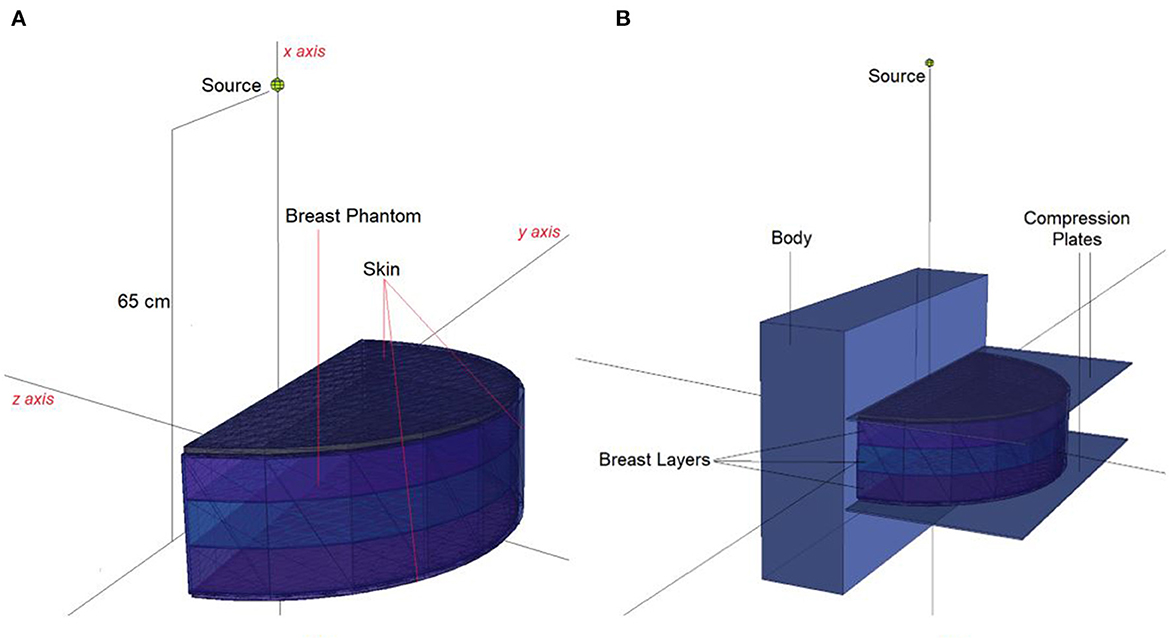
Figure 2. 3-D view of modeled MCNPX simulation setup from (A) breast phantom (B) breast phantom with body phantom and compression plates (via MCNPX Visual Editor X22S).

2.2. Validation of MCNPX code

For the validation process of the MCNPX code, the dosimeter guideline for the mammographic procedures specified in the previously published AAPM TG-195 (23) report was used. For this procedure, the manual's breast phantom was modeled using the same parameters (see Figure 3), and 80–20% adipose/glandular tissue was defined. Subsequently, the energy deposited in the modeled phantom was measured in accordance with the energy value specified in the guide (23). This amount (MeV/g) was calculated using the F6 (16, 19) tally mesh extension of the MCNPX code. Depending on the nature of the investigation and the anticipated result of photon-matter interaction, the MCNPX code employs a variety of tally meshes. Depending on the anticipated results of the investigation, each of them yields an unique outcome. The F6 Tally Mesh provides the amount of energy deposited per mass, often known as MeV/g. In light of our research objectives, we aimed to observe the quantity of energy deposited into the breast phantom's layers as a function of source energy. Therefore, it was appropriate to use F6 tally Mesh, which has been independently specified in there-layers, and at the end of the simulation, we acquired the deposited energy quantity for each layer. As the median value, the average of 4,754 eV/photon was determined after three iterations of counting. The observed deviation rate was below 0.3%. This minimal deviation rate was seen as an essential signal of the dependability of the data libraries and physics lists employed in this simulation investigation.

FIGURE 3

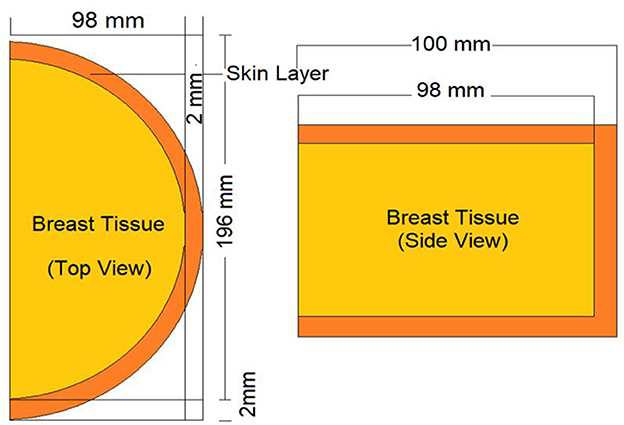
Figure 3. Appearance of modeled standard breast phantom in AAPM TG-195 report for validation phase of MCNPX.

3. Results and discussions

This study's objective was to investigate the amount of absorbed energy, which occurs in the 3-layers heterogeneous breast model given in the literature and the behavioral changes in different layers. In the INPUT file, each layer of the modeled breast phantom was therefore characterized with a different cellular structure and composition (see Table 1). In line with the purpose of the study, the source was operated three times for each energy value in the low energy range of 26–36 keV with a track number of 10⁸ NPS. Each run operation conducted in the 26–26 keV energy range was recorded individually, and the mean results were recorded. Figure 4A depicts the exposure of a heterogeneous three-layer breast phantom between compression plates to X-rays generated by the source. Figure 4B depicts, from a lateral perspective, the measurement axes that are considered in the study of the energy-dependent change of the amount of absorbed energy in the layers and the energy-dependent change of the amount of absorbed energy in the body phantom that serve as the two main focal points of the current investigation. Three different F6 Tally outcomes were obtained from the OUTPUT file for three different layers modeled as separate cellular zones (see Figure 1). This was achieved by defining the desired outputs from the code separately according to the cells, in the section where the tally mesh definition is made in the data card section of the INPUT file. The code lines below are the desired absorbed energy amount lines for cells 3, 4, and 5 of the F6 tally meshes defined in the INPUT file.

F6:p 3.

F16:p 4.

F26:p 5.

TABLE 1

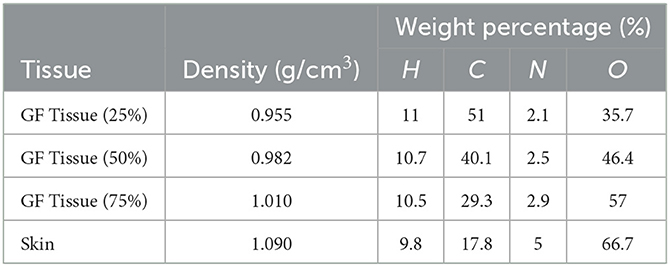
Table 1. Elemental properties and densities of the modeled breast layers (11).

FIGURE 4

Figure 4. (A) Appearance of X-ray source. (B) Lateral view for measurement points.

Consequently, the data acquired from the OUTPUT file were recorded individually for each energy value, and the quantity of energy absorbed in three distinct layers was analyzed as a function of increasing source energy. Figure 5 represents the amount of energy absorbed in the three different layers as a function of increasing source energy. As can be seen from Figure 1, the top layer closest to the source is the 3^rd cell and it is defined as Layer 1 in the INPUT file. The other layers are Cell 4 (Layer 2) and Cell 5 (Layer 3), respectively. As can be seen from Figure 5, the amount of energy absorbed in Layer 1 is at the maximum level at the lowest energy value of 26 keV. Along with this, the amount of energy absorbed in Layer 2 and Layer 3 decreased, respectively. Low-energy 26 keV photons penetrate the first layer after their first interaction with the skin layer, therefore releasing most of their energy into Layer 1. This is a natural consequence of the X-ray penetrating capabilities (24). However, the increase in energy from 26 keV to 27 keV caused a decrease in the quantity of energy absorbed by the first layer. Parallel to this, the quantity of energy absorbed by the second and third layers increased. This is due to the shift of X-rays, whose penetrating characteristics rise from 26 keV to 27 keV, to the second layer, where they are absorbed more than in the first layer. Reduced absorption in the first layer allows these unabsorbed X-rays to get through to the second layer (25, 26). Therefore, the unabsorbed X-rays have not released their energy in the first layer. This unreleased energy has been transmitted through first layer, absorbed by other layers, and has increased the quantity of energy absorbed by successive layers such as Layer 2 and Layer 3. Figure 5 depicts this occurrence as a decrease in Layer-1 and an increase in Layers 2 and 3 as a result of the rise from 26 keV to 36 keV. The layer with the lowest density among the three distinct layers specified for the heterogeneous breast model is Layer 1. This situation affected the energy increase process of primary X-rays in terms of transmission. Figure 5 demonstrates that the energy decrease trend in the first layer as a result of each subsequent energy increase is less significant than the increase trend in the second and third layers. This is because of the variation in density between the layers caused by the GF factors (11). After evaluating each layer separately, the total amount of energy absorbed by the three layers for each energy value is determined and shown in Figure 6 as a function of increasing energy. As shown in Figure 6, the rising trends in the total amount of energy absorbed by the three layers between 26 keV and 30 keV and between 30 keV and 36 keV differ. Low energy X-rays tend to release their energy to the first, second, and third layers, respectively, in the first energy range (26–30 keV). However, although this tendency may also be seen in the second energy range, it is less prominent compared to the first energy range (i.e., 26–30 keV). Although this demonstrates that X-rays with energy over 30 keV have absorption potentials in three layers, it also demonstrates that they have a higher tendency to pass through the third layer and reach the image receptor. As noted in the previous sections, the improvement in transmission properties permits X-rays to travel through a material while maintaining their energy. This is evident when observing the rising trend after 30 keV. Consequently, one can say that the energy-dependent variations in the quantity of energy absorbed in the three layers are maximal in the 26–30 keV energy range. In the meanwhile, the energy amounts absorbed in each of the three layers were computed over the energy range of 26 to 36 keV, and an average value was obtained. Figure 7 is obtained by averaging the results in each of the three layers for each energy value in the examined energy range. The first layer absorbed an average of 52.97 percent of the main X-rays, followed by the second layer with 31.32 percent and the third layer with 15.72 percent. The variation in the quantity of energy absorbed in the body phantom (see Figure 4), modeled behind the three-layered breast phantom was investigated as a function of increasing energy. Figure 8 illustrates the amount of energy absorbed by the body phantom as a function of the increasing energy values. The quantity of energy absorbed by the body phantom increases proportionally to the rise in energy. This tendency, on the other hand, did not change from layer to layer, but rather followed a very consistent rising trend. This condition may be explained by the possibility of scattering from the first, second, and third layers to affect the modeled body phantom. In other words, the inverse ratio of energy release resulting from an increase in transmission found in the layers is non-existent here. This is because the modeled body phantom is always in touch with the heterogeneous three-layered breast phantom. This finding indicates that high energy usage may result in a constant rise in the quantity of dose administered during mammographic examinations in areas other than the examination area. Considering the dose exposures and risks of the chest wall and, therefore, the thoracic region, which is in main contact with the breast tissue during mammography operations, the need of dose optimization may be highlighted once again.

FIGURE 5

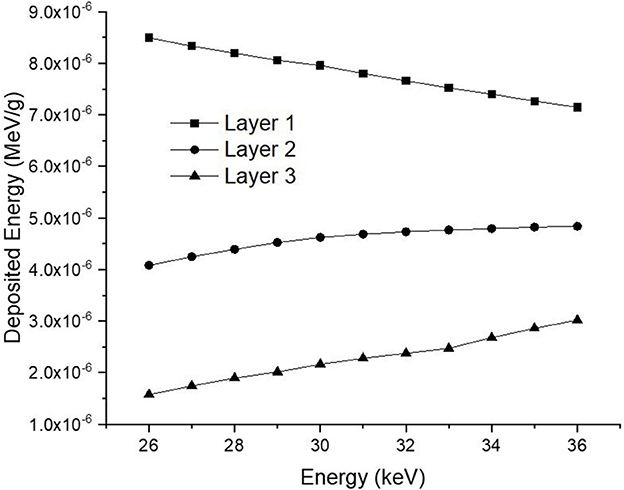
Figure 5. Variation of deposited energy (MeV/g) as a function of increasing energy (keV) for different breast layers.

FIGURE 6

Figure 6. Variation of total deposited energy (MeV/g) as a function of increasing energy (keV).

FIGURE 7

Figure 7. Average deposited energy amount (%) in different breast layers.

FIGURE 8

Figure 8. Variation of deposited energy amount (%) in modeled body phantom.

4. Conclusion

Dose distribution assessments for mammography operations are becoming increasingly essential. This is due to the fact that breast cancer has one of the highest fatality rates among women. The use of low-energy X-rays enables the very important early detection of this type of cancer. The usage of X-rays, which is a requirement and a necessity of this process, strongly drives the scientific community to perform various types of research on dosimetry procedures. Usually, mammography dosimetry techniques lack experimental feasibility. Thus, sophisticated Monte Carlo simulation approaches, such as EGSnrc, MCNPX, Geant4, Penelope, and codes that simulate radiation transport events are utilized. The purpose of this research was to extend the first phase investigations for the three-layer heterogeneous breast model given in the literature, to address thoroughly some unstudied situations, and to offer data as a continuation of the literature. The scientific community was given the following recommendations based on the findings of the investigation.

• The diverse distribution of glands has a significant impact on the quantity of energy received by the various breast layers.

• In layers with a low glandular ratio, low-energy primary X-ray penetrability is highest. In response to an increase in energy, the absorption in layers with a low glandular ratio decrease.

• This results in the X-rays releasing their energy in the bottom layers.

• Additionally, the increase in energy increases the quantity of energy absorbed by the tissues around the breast.

• The MCNPX code is an important tool that can be used in dosimetry for mammography procedures with the verification it presents together with the values given in standard reports.

In the future, the research group intends to examine the three-layer heterogeneous breast model from other perspectives, such as function of compression level and point distributions in each layer as well as body phantom. Finally, it should be highlighted that further dosimetry studies with such detailed phantoms may benefit the scientific community by giving more comprehensive information on dose reduction, advanced radiation protection strategies, and the assessment of protective materials.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

GA and ER: writing and calculations. WE: writing and literature review. GK and AE: calculations and visualization. HZ: writing and data analysis. HT: supervision, writing, calculations, and study concept. All authors contributed to the article and approved the submitted version.

Funding

Princess Nourah Bint Abdulrahman University Researchers Supporting Project Number (PNURSP2023R149), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.

Acknowledgments

The authors would like to express their deepest gratitude to Princess Nourah Bint Abdulrahman University Researchers Supporting Project Number (PNURSP2023R149), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia. The author AE acknowledges the support of Dunarea de Jos University of Galati.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Katalinic A, Eisemann N, Kraywinkel K, Noftz MR, Hübner J. Breast cancer incidence and mortality before and after implementation of the German mammography screening program. Int J Cancer. (2020) 147:709–18. doi: 10.1002/ijc.32767

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Massera RT, Tomal A. Breast glandularity and mean glandular dose assessment using a deep learning framework: virtual patients study. Physica Medica. (2021) 83:264–77. doi: 10.1016/j.ejmp.2021.03.007

PubMed Abstract | CrossRef Full Text | Google Scholar

3. International Commission on Radiological Protection (ICRP). Statement from the 1987 como meeting of the ICRP, ICRP Publication 52 Ann. ICRP. (1987) 17:i–v. doi: 10.1016/0146-6453(87)90046-7

CrossRef Full Text

4. Dance DR, Sechopoulos I. Dosimetry in x-ray-based breast imaging. Phy Med Biol. (2016) 61:R271. doi: 10.1088/0031-9155/61/19/R271

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Hernandez AM, Seibert JA, Boone JM. Breast dose in mammography is about 30% lower 30% lower when realistic heterogeneous glandular distributions are considered Med. Phys. (2015) 42:6337–48. doi: 10.1118/1.4931966

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Nosratieh A, Hernandez A, Shen SZ, Yaffe MJ, Seibert JA, Boone JM. Mean glandular dose coefficients (DgN) for x-ray spectra used in contemporary breast imaging systems. Phys Med Biol. (2015) 60:7179–90. doi: 10.1088/0031-9155/60/18/7179

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sechopoulos I, Bliznakova K, Qin X, Fei B, Feng SSJ. Characterization of the homogeneous tissue mixture approximation in breast imaging dosimetry. Med Phys. (2012) 39:5050–9. doi: 10.1118/1.4737025

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Dance DR, Young KC. Estimation of mean glandular dose for contrast enhanced digital mammography: factors for use with the UK, European and IAEA breast dosimetry protocols. Phys Med Biol. (2014) 59:2127–37. doi: 10.1088/0031-9155/59/9/2127

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Geeraert N, Klausz R, Muller S, Bloch I, Bosmans H. Evaluation of exposure in mammography: limitations of average glandular dose and proposal of a new quantity. Radiat Prot Dosim. (2015) 165:342–5. doi: 10.1093/rpd/ncv069

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Gennaro A, Toledano C, di Maggio E, Baldan E, Bezzon M, La Grassa L, et al. Toffoli, P.C. Muzzio Digital breast tomosynthesis vs. digital mammography: a clinical performance study. Eur Radiol. (2010) 20:1545–53. doi: 10.1007/s00330-009-1699-5

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Chang TY, Lai KJ, Tu CY, Wu J. Three-layer heterogeneous mammographic phantoms for Monte Carlo simulation of normalized glandular dose coefficients in mammography. Sci Rep. (2020) 10:2234. doi: 10.1038/s41598-020-59317-4

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Elshami W, Tekin HO, Issa SAS, Abuzaid MM, Zakaly HM, Issa B, et al. Impact of eye and breast shielding on organ doses during the cervical spine radiography: design and validation of MIRD computational phantom. Front Public Health. (2021) 9:751577. doi: 10.3389/fpubh.2021.751577

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Zhang X, Xie X, Cheng J, Ning J, Yuan Y, Pan J, et al. Organ dose conversion coefficients based on a voxel mouse model and MCNP code for external photon irradiation. Radiat Prot Dosimetry. (2012) 148:9–19. doi: 10.1093/rpd/ncr003

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Andersson M, Almén A, Ören Ü. IDACstar20: A MCNP application to perform realistic dose estimations from internal or external contamination with radiopharmaceuticals. Radiat Phy Chem. (2022) 193:109957. doi: 10.1016/j.radphyschem.2021.109957

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Krstic D, Nikezic D, Jeremic MZ, Dolicanin E, Miladinovic TB, Zivkovic M. Comparison between MCNP and planning system in brachytherapy of cervical cancer. Appl Radiat Isot. (2023) 192:110614. doi: 10.1016/j.apradiso.2022.110614

PubMed Abstract | CrossRef Full Text | Google Scholar

16. ALMisned G, Baykal DS, Kilic G, Ilik E, Zakaly HMH, Ene A, et al. A critical evaluation on nuclear safety properties of novel Cadmium oxide-rich glass containers for transportation and waste management: Benchmarking with a reinforced concrete container. Front Phy. (2022) 10:1080354. doi: 10.3389/fphy.2022.1080354

CrossRef Full Text | Google Scholar

17. ALMisned G, Baykal DS, Ali FT, Bilal G, Kilic G, Tekin HO. Gadolinium-tungsten-boron trioxide glasses: a multi-phase research on cross-sections, attenuation coefficients, build-up factors and individual transmission factors using MCNPX. Optik. (2022) 272:170216. doi: 10.1016/j.ijleo.2022.170216

CrossRef Full Text | Google Scholar

18. Tekin HO, Rainey C, ALMisned G, Issa SAM, Akkus B, Zakaly HMH. Heavy metal oxide added glassy portable containers for nuclear waste management applications: in comparison with reinforced concrete containers. Radiat Phy Chem. (2022) 201:110449. doi: 10.1016/j.radphyschem.2022.110449

CrossRef Full Text | Google Scholar

19. RSICC Computer Code Collection. MCNPX User's Manual Version 2.4.0. Monte Carlo N-Particle Transport Code System for Multiple and High Energy Applications. (2002).

Google Scholar

20. Agostinelli JA, Amako K, Apostolakis J, Araujo H, Arce P, Asai M, et al. Nuclear instruments and methods in physics research section a: accelerators, spectrometers, detectors and associated equipment. Geant4 Simulat Toolkit. (2003) 506:250–303. doi: 10.1016/S0168-9002(03)01368-8

CrossRef Full Text | Google Scholar

21. Kawrakow I, Mainegra-Hing E, Rogers DWO, Tessier F, Walters BRB. The EGSnrc code system: Monte Carlo simulation of electron and photon transport. Report PIRS-701, Techreport PIRS-701. Ottawa, ON: National Research Council Canada (2001–2015) (version 2021).

Google Scholar

22. Ballarini F, Battistoni G, Campanella M, Carboni M, Cerutti F, Empl A, et al. The FLUKA code: an overview. J Phy Conf Ser. (2006) 41:151. doi: 10.1088/1742-6596/41/1/014

CrossRef Full Text | Google Scholar

23. Sechopoulos J, Ali ESM, Badal A, Badano A, Boone JM, Kyprianou IS, et al. Monte Carlo reference data sets for imaging research: Executive summary of the report of AAPM Research Committee Task Group 195. Med Phy. (2015) 42:5679–91. doi: 10.1118/1.4928676

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Soomro NI, Bakhtiar SM. Chapter 8 - image-based modeling and precision medicine. Verma M, Barh D, editors. Progress and Challenges in Precision Medicine. Cambridge: Academic Press (2017). p. 141–70.

Google Scholar

25. Pfeiffer D, Pfeiffer F, Rummeny E. Advanced X-ray imaging technology. Recent Results Cancer Res. (2020) 216:3–30. doi: 10.1007/978-3-030-42618-7_1

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Aichinger H, Dierker J, Joite-Barfuß S, Säbel M. Penetration of X-rays. In: Radiation Exposure and Image Quality in X-Ray Diagnostic Radiology. Springer: Heidelberg (2012).

Google Scholar