Mathematical epidemiological modeling and analysis of monkeypox dynamism with non-pharmaceutical intervention using real data from United Kingdom

In this study, a mathematical model for studying the dynamics of monkeypox virus transmission with non-pharmaceutical intervention is created, examined, and simulated using real-time data. Positiveness, invariance, and boundedness of the solutions are thus examined as fundamental features of mathematical models. The equilibrium points and the prerequisites for their stability are achieved. The basic reproduction number and thus the virus transmission coefficient ℜ₀ were determined and quantitatively used to study the global stability of the model's steady state. Furthermore, this study considered the sensitivity analysis of the parameters according to ℜ₀. The most sensitive variables that are important for infection control are determined using the normalized forward sensitivity index. Data from the United Kingdom collected between May and August 2022, which also aid in demonstrating the usefulness and practical application of the model to the spread of the disease in the United Kingdom, were used. In addition, using the Caputo–Fabrizio operator, Krasnoselskii's fixed point theorem has been used to analyze the existence and uniqueness of the solutions to the suggested model. The numerical simulations are presented to assess the system dynamic behavior. More vulnerability was observed when monkeypox virus cases first appeared recently as a result of numerical calculations. We advise the policymakers to consider these elements to control monkeypox transmission. Based on these findings, we hypothesized that another control parameter could be the memory index or fractional order.

1. Introduction

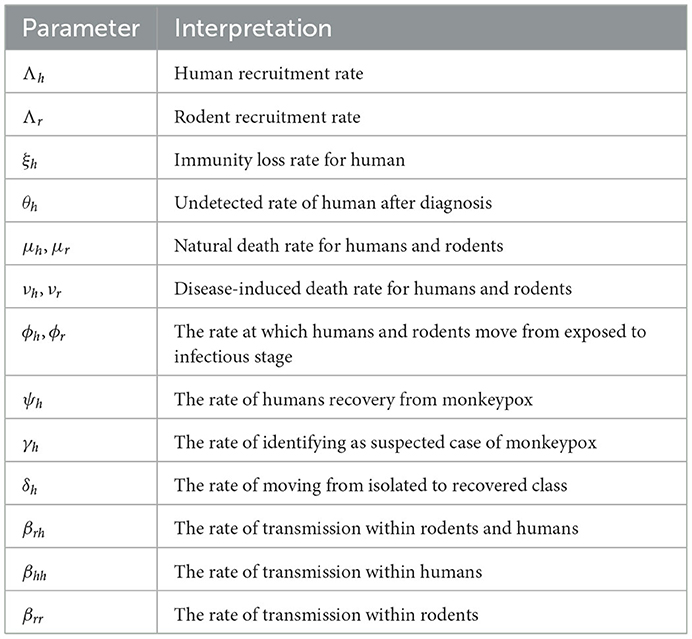
The unexpected breakout and global spread of monkeypox have drawn the attention of scientists due to the continuing COVID-19 pandemic. The prevalence of the largest and most pervasive monkeypox pandemic outside of Africa as of 22 June 2022, is 3,340 confirmed cases reported across the world. In addition to mother-to-child vertical transmission, the monkeypox virus can spread from person to person by direct contact with infectious skin or mucosal skin lesions, respiratory droplets, or indirect contact with contaminated objects or materials. The possibility of community transmission cannot be ruled out, and it may also be sexually transferred by semen or vaginal fluid. The virus that causes monkeypox is called the monkeypox virus, and it is an enveloped, linear, double-stranded DNA virus that belongs to the Chordopoxvirinae subfamily of the Poxviridae family. With symptoms of the disease lasting 2–4 weeks and a death rate that previously ranged from 0 to 11 deaths, monkeypox is often a self-limiting sickness. Intense headaches, fever, lesions, and lymphadenopathy are some of the symptoms of monkeypox. Antiviral medications and smallpox vaccines have been approved for use in various nations in response to the monkeypox outbreak, despite the fact that there is no specific treatment or vaccine for monkeypox virus infection. Before allowing the virus to successfully establish person-to-person transmission, quick action is required to stop the local development of the disease and, consequently, the global monkeypox outbreak (1–11). In Peter et al. (12), modeling and optimal control were used to study monkeypox and the cost-effective strategies were investigated. This study shows that, among all competing measures, combining preventative measures to reduce rodent-to-human disease transmission is the most practical and cost-effective option.

Numerous research articles have been published where both classical and fractional models were constructed, and there is a plethora of literature on modeling infectious diseases. Because fractional-order derivative has unique properties such as heredity and memory that enable it to fully comprehend the dynamics of real phenomena, an analysis based on fractional-order derivative is more advantageous and practical than an analysis based on classical derivative (13, 14). At two separate closed locations, the phenomenon is indistinguishable by the standard derivatives. A generalized derivative known as the fractional order was proposed to address the problems with ordinary derivatives (15). Many researchers used fractional- order derivatives in many fields, as shown in Kumar et al. (16), Higazy et al. (17), Djida and Atangana (18), Baba (19), Owolabi and Atangana (20), Mohammadi et al. (21), Baleanu et al. (22), and Wutiphol and Turab (23). In the realm of mathematical biology, the Mittag–Leffler-type kernel has been used continuously over other derivatives, and numerous epidemiological models, such as for dengue fever, smoking, tuberculosis, measles, Ebola, and other diseases, have been studied using this operator as shown in Asamoah et al. (24), Peter et al. (25, 26), Kumar et al. (27), Morales-Delgadoa et al. (28), Atangana and Baleanu (29), and Atangana et al. (30). Most notably, in Zhang et al. (31), the Mittag–Leffler-type kernel modeling for Ebola–malaria co-infection was investigated by the authors with the best possible control. They strongly recommended the Mittag–Leffler-type kernel. In Kumar et al. (32), investigated the COVID-19 model using singular and non-singular fractional operators and compared the results of these operators. In Aslam et al. (33), the authors examined a recent study on the mathematical modeling of HIV/AIDS using the Mittag–Leffler-type kernel and came to the conclusion that the infection rate decreases with decreasing operator. In Evirgen (34), the authors studied the transmission dynamics of the Nipah virus using the Caputo derivative. One of the interesting segments of their study was to focus on tracing the influence of fractional-order derivatives on the manner in which the model responds. In Ucar (35), the authors investigated a fractional SAIDR model within the framework of the Mittag–Leffler-type kernel. The effectiveness of the fractional operator is shown through a numerical simulation.

Considering the characteristics of exponential decay, the Caputo–Fabrizio fractional-order operator has been preferred over Atangana–Beleanu beta derivatives and a few other operators in the field of mathematical biology with more information (17–19, 24, 36–39). For instance, in Addai et al. (40), the authors studied a novel model of COVID-19 incorporating Alzheimer's disease using the Caputo–Fabrizio fractional-order operator. The results of the aforementioned study revealed that the two diseases have a link and the authors also concluded that the fractional operator is related to the rate of infection. In Shaikh and Nisar (41), the authors also considered the transmission dynamics of a fractional-order typhoid fever model using the Caputo–Fabrizio operator and the existence theory and achieved numerical solutions. In Shah et al. (42), Shah and his co-authors conducted a semi-analytical study of the Pine Wilt Disease (PWD) model with a convex rate via fractional order involving a non-singular kernel. To comprehend the trade-off between the lockdown and the transmission of the virus, Ahmed and his co-authors devised a five-term dynamical system (43). Another use of the Caputo–Fabrizio fractional-order operator was indicated, for instance, in Addai et al. (40), Shaikh and Nisar (41), Shah et al. (42), Ahmed et al. (43), Ullah et al. (44), Abboubakar et al. (45).

Furthermore, in Peter et al. (46), the authors used real data from Nigeria to study the dynamics of the transmission of the monkeypox virus using fractional calculus. The authors presented an argument on the modeling system by studying the infection control policies that will help the public to better understand the significance of control parameters in the eradication of the virus in the studied population. Furthermore, the transmission dynamics of the monkeypox virus was studied using a mathematical modeling approach in Peter et al. (47). In their findings, the authors indicated that the isolation of infected individuals in the human population helps reduce the transmission of the disease, which can serve as a form of intervention to control the spread of the virus.

We observed that none of the studies on the monkeypox virus and its modes of transmission took into account the interaction between the isolated and exposed compartments in the human subpopulation and the results of that contact rate with the rodent population and applied the modeling approach to real data from the United Kingdom. The major goals of this research are to calculate the exponential growth rate of the monkeypox virus, to forecast what might occur in future and how to stop it from spreading, and to understand the effects of non-pharmaceutical intervention on infected individuals, which will be able to guide us on how to deploy intervention resources to contain the spread of the disease. The remaining sections of the article are structured as follows: Section 2 presents some basic definitions and preliminary information, Section 3 presents the model formulation, Sections 4 deals with the dynamism of the model, Section 5 computes the basic reproduction number and some basic mathematical analysis, Section 6 present the endemic equilibrium of the model, Section 7 proves the existence and uniqueness of our model, Section 8 deals with the fitting of the model to real data from the United Kingdom, Section 9 presents numerical schemes and numerical simulations, Section 10 deals with sensitivity analysis, and Section 11 provides some perspectives, discussion, and conclusion.

2. Preliminaries

In this section, we review several key definitions, lemmas, and concepts that are necessary to understand the suggested model.

Definition 2.1 Let f ∈ Q¹(p, q), q > p, and α_∗ ∈ (0, 1) (17), (40). Then, the Caputo–Fabrizio fractional-order derivative can be defined as

${}_p^{CF}{D}_t^{\alpha }f(t)=\frac{G(\alpha )}{1-\alpha }{\displaystyle {\int }_p^t}{f}^{\prime }(x)exp\left[-\alpha \frac{t-s}{1-\alpha }\right]ds.$

Here, G(α) is a normalization function, where G(0) = G(1) = 1. The fractional integral of the Caputo–Fabrizio fractional order is defined by:

$I_t^{\alpha }f(t)=\frac{2(1-\alpha )}{2(1-\alpha )G(\alpha )}f(t)+\frac{2\alpha }{(2-\alpha )G(\alpha )}{\displaystyle {\int }_0^t}f(s)ds,t\ge 0.$

Lemma 2.2 Assuming there is a function u(t) ∈ W_l[0, η], then the solution of fractional differential equation

$\begin{array}{l}\{\begin{array}{l}{}^{CF}{D}_t^{\alpha }f(t)=u(t),t\in \left[0,\eta \right],\\ f(0)=f_0,\end{array}\end{array}$

is given by

$f(t)=f_0+\frac{2(1-\alpha )}{2(1-\alpha )G(t)}f(t)+\frac{2\alpha }{(2-\alpha )G(\alpha )}{\displaystyle {\int }_0^t}f(s)ds,t\ge 0$

(24),(17), (40).

Lemma 2.3 Suppose A ⊂ B be a closed convex non-empty subset of A and there exist two operators, T₁ and T₂, then it is Krasnoselskii's fixed point theorem (40) and it follows that:

(i) T₁u + T₁u ∈ A, ∀u ∈ A;

(ii) T₁ is contraction and T₂ continuous and compact. Then quantify at least one solution u ∈ A such that

$T_{1}u+T_{2}u=u.$

3. Model formulation

Using a system of differential equations, we studied both human and rodent populations in a closed homogeneous environment. There are five compartments in a human population of size N_h(t): Susceptible S_h(t); Exposed E_h(t); Infected I_h(t); Isolation/Quarantine Q_h(t); and Recovered R_h(t); where N_h(t) = S_h(t) + E_h(t) + I_h(t) + Q_h(t) + R_h(t). The rodent population N_r(t) is split into S_r(t) Susceptible; E_r(t) Exposed; and I_r(t) Infected. Let N_r(t) = S_r(t) + E_r(t) + I_r(t). From the aforementioned description, using the ideas in Yinka-Ogunleye et al. (5), we extend the studies of Peter et al. (46) and (47), then the ordinary differential equations in system (1) describe the dynamics of monkeypox transmission incorporating non-pharmaceutical intervention;

$\begin{array}{ll}\{\begin{array}{l}\frac{d{S}_h}{dt}={\Lambda }_h+{\xi }_h{R}_h+{\theta }_h{Q}_h-{\lambda }_h{S}_h-{\mu }_h{S}_h,\\ \frac{d{E}_h}{dt}={\lambda }_h{S}_h-{\gamma }_h{E}_h-{\varphi }_h{E}_h-{\mu }_h{E}_h,\\ \frac{d{I}_h}{dt}={\varphi }_h{E}_h-({\psi }_h+{\mu }_h+{\nu }_h)I_h,\\ \frac{d{Q}_h}{dt}={\gamma }_h{E}_h-({\theta }_h+{\delta }_h+{\mu }_h+{\nu }_h)Q_h,\\ \frac{d{R}_h}{dt}={\psi }_h{I}_h+{\delta }_h{Q}_h-{\xi }_h{R}_h-{\mu }_h{R}_h,\\ \frac{d{S}_r}{dt}={\Lambda }_r-{\lambda }_r{S}_r-{\mu }_r{S}_r\\ \frac{d{E}_r}{dt}={\lambda }_r{S}_r-{\varphi }_r{E}_r-{\mu }_r{E}_r,\\ \frac{d{I}_r}{dt}={\varphi }_r{E}_r-({\mu }_r+{\nu }_r)I_r,\\ \end{array}& (1)\end{array}$

where ${\lambda }_h=\frac{{\beta }_{rh}{I}_r+{\beta }_{hh}{I}_h}{N_h},{\lambda }_r=\frac{{\beta }_{rr}{I}_r}{N_r}$. To capture the memory in the predictions of the monkeypox virus transmission model and also to verify that both sides of the fractional equations have exact dimensions, the time-dependent kernel is defined by the power law correlation function, as in Tilahuna et al. (48); therefore, we propose the following fractional-order model for the monkeypox virus transmission model using the Caputo–Fabrizio fractional-order derivative;

$\begin{array}{ll}\{\begin{array}{l}{}^{CF}{D}_t^{\alpha }{S}_h(t)={\Lambda }_h+{\xi }_h{R}_h+{\theta }_h{Q}_h-{\lambda }_h{S}_h-{\mu }_h{S}_h,\\ {}^{CF}{D}_t^{\alpha }{E}_h(t)={\lambda }_h{S}_h-{\gamma }_h{E}_h-{\varphi }_h{E}_h-{\mu }_h{E}_h,\\ {}^{CF}{D}_t^{\alpha }{I}_h(t)={\varphi }_h{E}_h-({\psi }_h+{\mu }_h+{\nu }_h)I_h,\\ {}^{CF}{D}_t^{\alpha }{Q}_h(t)={\gamma }_h{E}_h-({\theta }_h+{\delta }_h+{\mu }_h+{\nu }_h)Q_h,\\ {}^{CF}{D}_t^{\alpha }{R}_h(t)={\psi }_h{I}_h+{\delta }_h{Q}_h-{\xi }_h{R}_h-{\mu }_h{R}_h,\\ {}^{CF}{D}_t^{\alpha }{S}_r(t)={\Lambda }_r-{\lambda }_r{S}_r-{\mu }_r{S}_r\\ {}^{CF}{D}_t^{\alpha }{E}_r(t)={\lambda }_r{S}_r-{\varphi }_r{E}_r-{\mu }_r{E}_r,\\ {}^{CF}{D}_t^{\alpha }{I}_r(t)={\varphi }_r{E}_r-({\mu }_r+{\nu }_r)I_r.\\ \end{array}& (2)\end{array}$

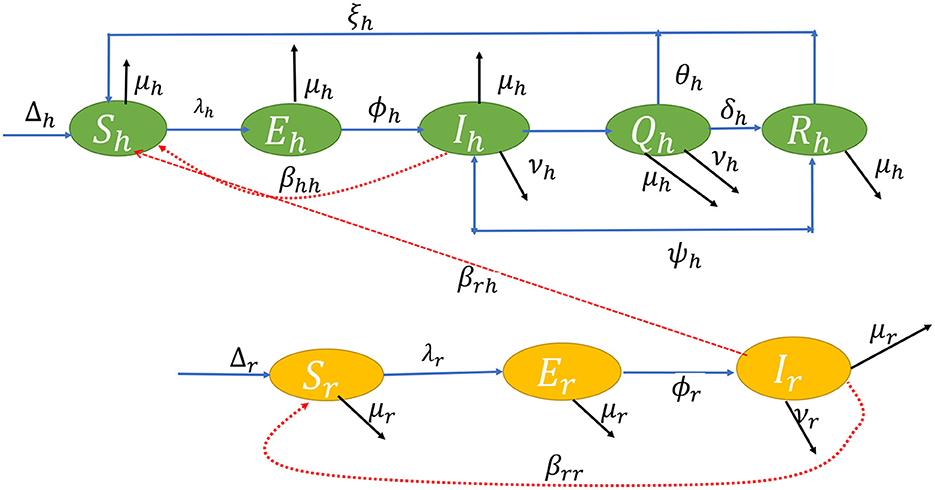
The flow diagram of the model equation is presented in Figure 1 while the parameters used in the model and their signification is presented in Table 1.

FIGURE 1

Figure 1. Transfer diagram of the dynamic transmission of the monkeypox virus.

TABLE 1

Table 1. Interpretation of parameters in the model.

4. Dynamics of the model

In this section, we focus on the dynamics of the solutions for the suggested models (1) and (2) that are positive, bounded, and invariant. In an epidemiological model, it is important to evaluate the population survival and the expansion that is naturally constrained by scarce resources. As a result, we demonstrate the following theorem.

Theorem 1. The solution of (1) along with initial conditions is positively invariant and bounded in ${\mathit{\text{R}}}_{+}^8$. Therefore,

$\begin{array}{ll}\{\begin{array}{l}{\displaystyle {lim}_{t\to \infty }}sup{S}_h(t)\le S_{h\infty }=\frac{{\Lambda }_h+{\theta }_h{Q}_{h\infty }+{\xi }_h{R}_{h\infty }}{{\lambda }_h+{\mu }_h},\\ {\displaystyle {lim}_{t\to \infty }}sup{E}_h(t)\le E_{h\infty }=\frac{{\lambda }_h{S}_{h\infty }}{({\xi }_h+{\varphi }_h+{\mu }_h)},\\ {\displaystyle {lim}_{t\to \infty }}sup{I}_h(t)\le I_{h\infty }=\frac{{\varphi }_h{E}_{h\infty }}{({\psi }_h+{\eta }_h+{\mu }_h)},\\ {\displaystyle {lim}_{t\to \infty }}sup{Q}_h(t)\le Q_{h\infty }=\frac{{\gamma }_h{E}_{h\infty }}{({\theta }_h+{\delta }_h+{\mu }_h+{\nu }_h)},\\ {\displaystyle {lim}_{t\to \infty }}sup{R}_h(t)\le R_{h\infty }=\frac{{\psi }_h{I}_{h\infty }+{\delta }_h{Q}_{h\infty }}{({\xi }_h+{\mu }_h)},\\ {\displaystyle {lim}_{t\to \infty }}sup{S}_r(t)\le S_{r\infty }=\frac{{\Lambda }_r}{{\lambda }_r+{\mu }_r},\\ {\displaystyle {lim}_{t\to \infty }}sup{E}_r(t)\le E_{r\infty }=\frac{{\lambda }_r{S}_{r\infty }}{({\varphi }_r+{\mu }_r)},\\ {\displaystyle {lim}_{t\to \infty }}sup{I}_r(t)\le I_{r\infty }=\frac{{\varphi }_r{E}_{r\infty }}{({\nu }_r+{\mu }_r)}.\\ \end{array}& (3)\end{array}$

Proof. Using the results in Lin (49) and taking into account the initial values given, from model (2), we obtain

$\begin{array}{ll}\{\begin{array}{l}{}^{CF}{D}_t^{\alpha }{S}_h(t){|}_{S_h(0)}={\Lambda }_h+{\xi }_h{R}_h+{\theta }_h{Q}_h\ge 0,\\ {}^{CF}{D}_t^{\alpha }{E}_h(t){|}_{E_h(0)}={\lambda }_h{S}_h\ge 0,\\ {}^{CF}{D}_t^{\alpha }{I}_h(t){|}_{I_h(0)}={\varphi }_h{E}_h\ge 0,\\ {}^{CF}{D}_t^{\alpha }{I}_h(t){|}_{Q_h(0)}={\gamma }_h{E}_h\ge 0,\\ {}^{CF}{D}_t^{\alpha }{R}_h(t){|}_{R_h(0)}={\psi }_h{I}_h+{\delta }_h{Q}_h\ge 0,\\ {}^{CF}{D}_t^{\alpha }{S}_v(t){|}_{S_r(0)}={\Lambda }_r\ge 0,\\ {}^{CF}{D}_t^{\alpha }{E}_v(t){|}_{E_r(0)}={\lambda }_r{S}_r\ge 0,\\ {}^{CF}{D}_t^{\alpha }{I}_v(t){|}_{I_r(0)}={\varphi }_r{E}_r\ge 0.\\ \end{array}& (4)\end{array}$

From Equation (4), we can see that S_h(0) > 0, E_h(0) > 0, I_h(0) > 0, R_h(0) > 0, S_v(0) > 0, E_v(0) > 0, I_v(0) > 0, for all t > 0. From Equation (2), the first equation gives

${}^{CF}{D}_t^{\alpha }{S}_h(t)\le {\Lambda }_h+{\xi }_h{R}_h+{\theta }_h{Q}_h-{\lambda }_h{S}_h-{\mu }_h{S}_h\ge 0.$

Then, by applying the fractional comparison technique, we obtain the first estimate of Equation (4). We continue for the second equation of the system of Equation (2), we obtain

${}^{CF}{D}_t^{\alpha }{E}_h(t)\le {\lambda }_h{S}_h-{\gamma }_h{E}_h-{\varphi }_h{E}_h-{\mu }_h{E}_h\ge 0.$

Therefore, we get the second estimate of Equation (1). We continue again for the third equation of the system of Equation (2), we obtain

${}^{CF}{D}_t^{\alpha }{I}_h(t)\le {\varphi }_h{E}_h-({\psi }_h+{\mu }_h+{\nu }_h)I_h\ge 0,$

and, consequently, we obtain the third estimate of Equation (4). Similarly, for the fourth to eighth equation, we obtain the estimate of Equation (4). Hence, Theorem 1 is complete.

4.1. Monkeypox equilibrium state

The monkeypox model is studied by obtaining the equilibrium states. To verify the existence of the equilibrium points, the derivatives of the model on the right-hand side are set to zero, which provides the monkeypox disease free equilibrium points.

We assume E_h, E_r, I_h, I_r, Q_h, R_h, S_h, S_r be the solution to the monkeypox model with the initial condition in a feasible region such that

$\begin{array}{ll}{\Gamma }_h=E_h,I_h,Q_h,R_h,S_h\in {ℝ}^5:N_h=\frac{{\Lambda }_h}{{\mu }_h},& (5)\end{array}$

$\begin{array}{ll}{\Gamma }_r=E_r,I_r,S_r\in {ℝ}^3:N_r=\frac{{\Lambda }_r}{{\mu }_r},& (6)\end{array}$

where the human population is represented as

$\begin{array}{ll}{N}_h=E_h(t)+I_h(t)+Q_h(t)+R_h(t)+S_h(t),& (7)\end{array}$

and the rodent population, respectively,

$\begin{array}{ll}{N}_r=E_r(t)+I_r(t)+S_r(t).& (8)\end{array}$

To achieve the disease-free equilibrium state, the derivatives are set to zero as seen in (10) to obtain

$\begin{array}{ll}{E}^{*}=(E_h^{*},E_r^{*},I_h^{*},I_r^{*},Q_h^{*},R_h^{*},S_h^{*},S_r^{*}).& (9)\end{array}$

By setting the derivatives to zero, we obtain

$\begin{array}{ll}\frac{d{E}_h}{dt}=\frac{d{E}_r}{dt}=\frac{d{I}_h}{dt}=\frac{d{I}_r}{dt}=\frac{d{Q}_h}{dt}=\frac{d{R}_h}{dt}=\frac{d{S}_h}{dt}=\frac{d{S}_r}{dt}=0;& (10)\end{array}$

hence, Equation (9) is represented as

$\begin{array}{ll}{E}^{*}=\left(0,0,0,0,0,0,\frac{{\Lambda }_h}{{\mu }_h},\frac{{\Lambda }_r}{{\mu }_r}\right).& (11)\end{array}$

This equation describes a population free of monkeypox infection and is denoted as E^*

5. The basic reproduction number

We derive the basic reproduction number ℜ₀ by using the next-generation matrix approach (25). Since E_h, I_h, Q_h, and I_r are the disease-infected classes, hence,

$\begin{array}{ll}f=\left(\begin{array}{c}0\\ {\lambda }_h{S}_h\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right),v=\left(\begin{array}{c}-{\Lambda }_h-{\xi }_h{R}_h-{\theta }_h{Q}_h+{\lambda }_h{S}_h+{\mu }_h{S}_h\\ {\gamma }_h{E}_h+{\varphi }_h{E}_h+{\mu }_h{E}_h\\ -{\varphi }_h{E}_h+({\psi }_h+{\mu }_h+{\nu }_h)I_h\\ -{\gamma }_h{E}_h+({\theta }_h+{\delta }_h+{\mu }_h+{\nu }_h)Q_h\\ -{\psi }_h{I}_h-{\delta }_h{Q}_h+{\xi }_h{R}_h+{\mu }_h{R}_h\\ -{\Lambda }_r+{\lambda }_r{S}_r+{\mu }_r{S}_r\\ -{\lambda }_r{S}_r+{\varphi }_r{E}_r+{\mu }_r{E}_r\\ -{\varphi }_r{E}_r+({\mu }_r+{\nu }_r)I_r\end{array}\right).& (12)\end{array}$

$\begin{array}{ll}F=& \left(\begin{array}{ccccc}0& 0& \frac{{\beta }_{hh}{\Lambda }_h}{{\mu }_h}& 0& \frac{{\beta }_{hh}{\Lambda }_h}{{\mu }_h}\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ \end{array}\right),\\ V=& \left(\begin{array}{cccc}{\gamma }_h+{\varphi }_h+{\mu }_h& 0& 0& 0\\ -{\varphi }_h& {\psi }_h+{\mu }_h+{\nu }_h& 0& 0\\ -{\gamma }_h& 0& {\theta }_h+{\delta }_h+{\mu }_h+{\nu }_h& 0\\ 0& 0& 0& {\mu }_r+{\nu }_r\\ \end{array}\right).& (13)\end{array}$

$\begin{array}{ll}{V}^{-1}=\left[\begin{array}{cccc}\frac{1}{{\gamma }_1+{\mu }_1+{\varphi }_1}& 0& 0& 0\\ \frac{{\varphi }_1}{{\gamma }_1{\mu }_1+{\gamma }_1{\nu }_1+{\gamma }_1{\psi }_1+{\mu }^2+{\nu }_1{\mu }_1+{\mu }_1{\varphi }_1+{\mu }_1{\psi }_1+{\nu }_1{\varphi }_1+{\psi }_1{\varphi }_1}& \frac{1}{{\nu }_1+{\mu }_1+{\psi }_1}& 0& 0\\ \frac{{\gamma }_1}{{\gamma }_1{\delta }_1+{\delta }_1{\mu }_1+{\delta }_1{\varphi }_1+{\gamma }_1{\mu }_1+{\nu }_1{\gamma }_1+{\gamma }_1{\theta }_1+{\mu }_1^2+{\mu }_1{\nu }_1+{\mu }_1{\varphi }_1+{\mu }_1{\theta }_1+{\nu }_1{\varphi }_1+{\theta }_1{\varphi }_1}& 0& \frac{1}{{\nu }_1+{\mu }_1+{\theta }_1+{\delta }_1}& 0\\ 0& 0& 0& \frac{1}{{\nu }_2+{\mu }_2}\\ \end{array}\right].& (14)\end{array}$

The next-generation matrix (G) is given by

$\begin{array}{ll}G=F.V^{-1}=\left[\begin{array}{cccc}\frac{{\beta }_1{\lambda }_1{\varphi }_1}{N_h{\mu }_1({\gamma }_1{\mu }_1+{\gamma }_1{\nu }_1+{\gamma }_1{\psi }_1+{\mu }^2+{\nu }_1{\mu }_1+{\mu }_1{\varphi }_1+{\mu }_1{\psi }_1+{\nu }_1{\varphi }_1+{\psi }_1{\varphi }_1)}& \frac{{\beta }_1{\lambda }_1}{N_h{\mu }_1({\nu }_1+{\mu }_1+{\psi }_1)}& 0& \frac{{\beta }_1{\lambda }_1}{N_h{\mu }_1({\nu }_1+{\mu }_1)}\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right].& (15)\end{array}$

The basic reproduction number ${\Re }_0$ is the dominant eigenvalue (spectral radius) of the next-generation matrix G, that is, ℜ₀ = ρ(G)

${\Re }_0=\frac{{\beta }_{hh}{\Lambda }_h{\varphi }_h}{{\mu }_h({\gamma }_h+{\varphi }_h+{\mu }_h)({\psi }_1+{\mu }_h+{\nu }_h)}$

5.1. Stability of monkeypox-free equilibrium (MFE)

Investigating the stability of the monkeypox disease-free equilibrium, we compute the Jacobian matrix of the system at the disease-free equilibrium by obtaining the eigenvalues, which will be used to determine the stability of the model.

$\begin{array}{l}{J}_{E^{*}}=\\ \left(\begin{array}{cccccccc}-\frac{{\beta }_{hh}{I}_h+{\beta }_{rh}{I}_r}{N_h}-{\mu }_h& 0& 0& {\theta }_h& {\xi }_h& 0& 0& -\frac{({\beta }_{hh}+{\beta }_{rh})S_h}{N_h}\\ \frac{{\beta }_{hh}{I}_h+{\beta }_{rh}{I}_r}{N_h}& {\zeta }_1& 0& 0& 0& 0& 0& \frac{({\beta }_{hh}+{\beta }_{rh})S_h}{N_h}\\ 0& {\phi }_h& 0& 0& 0& 0& 0& 0\\ 0& {\gamma }_h& 0& {\zeta }_2& 0& 0& 0& 0\\ 0& 0& 0& {\delta }_h& -{\mu }_h-{\xi }_h& 0& 0& 0\\ 0& 0& 0& 0& 0& -\frac{{\beta }_{rr}{I}_r}{N_r}-{\mu }_r& 0& -\frac{{\beta }_{rr}{S}_r}{N_r}\\ 0& 0& 0& 0& 0& \frac{{\beta }_{rr}{I}_r}{N_r}& -{\phi }_r-{\mu }_r& \frac{{\beta }_{rr}{S}_r}{N_r}\\ 0& 0& 0& 0& 0& 0& {\phi }_r& -{\mu }_r-{\nu }_r\end{array}\right),& (16)\end{array}$

where ζ₁ and ζ₂ are represented in Equations (17) and (18)

$\begin{array}{ll}{\zeta }_1=-{\gamma }_h-{\phi }_h-{\mu }_h,& (17)\end{array}$

$\begin{array}{ll}{\zeta }_2=-{\theta }_h-{\delta }_h-{\mu }_h-{\nu }_h.& (18)\end{array}$

Evaluating $J_{E^{*}}$ at the monkeypox-free equilibrium (MFE), we obtain

$\begin{array}{l}{J}_{MF{E}^{*}}\\ =\left(\begin{array}{cccccccc}-{\mu }_h& 0& 0& {\theta }_h& {\xi }_h& 0& 0& -\frac{({\beta }_{hh}+{\beta }_{rh}){\Lambda }_h}{N_h{\mu }_h}\\ 0& -{\gamma }_h-{\phi }_h-{\mu }_h& 0& 0& 0& 0& 0& \frac{({\beta }_{hh}+{\beta }_{rh}){\Lambda }_h}{N_h{\mu }_h}\\ 0& {\phi }_h& 0& 0& 0& 0& 0& 0\\ 0& {\gamma }_h& 0& -{\theta }_h-{\delta }_h-{\mu }_h-{\nu }_h& 0& 0& 0& 0\\ 0& 0& 0& {\delta }_h& -{\mu }_h-{\xi }_h& 0& 0& 0\\ 0& 0& 0& 0& 0& -{\mu }_r& 0& -\frac{{\beta }_{rr}{\Lambda }_r}{N_r{\mu }_r}\\ 0& 0& 0& 0& 0& 0& -{\phi }_r-{\mu }_r& \frac{{\beta }_{rr}{\Lambda }_r}{N_r{\mu }_r}\\ 0& 0& 0& 0& 0& 0& {\phi }_r& -{\mu }_r-{\nu }_r\end{array}\right).& (19)\end{array}$

We compute the eigenvalues from the $J_{MF{E}^{*}}$ using the characteristic polynomial of O⁸, which will not be represented as a result of its lengthiness. The eigenvalues and characteristic polynomial are calculated by $|J_{MF{E}^{*}}-I|$, where I is an 8 × 8 unit matrix, and the values of λ are obtained:

$\begin{array}{ll}\lambda =\left(\begin{array}{c}0\\ -{\mu }_h\\ -{\mu }_h-{\xi }_h\\ -{\mu }_r\\ -{\gamma }_h-{\phi }_h-{\mu }_h\\ -{\theta }_h-{\delta }_h-{\mu }_h-{\nu }_h\\ \frac{-2N_r{\mu }_r^2+(-{\nu }_r-{\phi }_r)N_r{\mu }_r+\sqrt{{\mu }_r(N_r{({\nu }_r-{\phi }_r)}^2{\mu }_r+4{\Lambda }_r{\beta }_{rr}{\phi }_r)N_r}}{2N_r{\mu }_r}\\ \frac{-2N_r{\mu }_r^2+(-{\nu }_r-{\phi }_r)N_r{\mu }_r-\sqrt{{\mu }_r(N_r{({\nu }_r-{\phi }_r)}^2{\mu }_r+4{\Lambda }_r{\beta }_{rr}{\phi }_r)N_r}}{2N_r{\mu }_r}\end{array}\right)& (20)\end{array}$

Let Δ₁ and Δ₂ be well represented from Equation (20) in Equations (21) and (22)

$\begin{array}{ll}{\Delta }_1={\mu }_r(N_r{({\nu }_r-{\phi }_r)}^2{\mu }_r+4{\Lambda }_r{\beta }_{rr}{\phi }_r)N_r,& (21)\end{array}$

$\begin{array}{ll}{\Delta }_2=2N_r{\mu }_r^2+(-{\nu }_r-{\phi }_r)N_r{\mu }_r.& (22)\end{array}$

Then,

$\begin{array}{ll}{\lambda }_1=0,& (23)\end{array}$

$\begin{array}{ll}{\lambda }_2=-{\mu }_h,& (24)\end{array}$

$\begin{array}{ll}{\lambda }_3=-({\mu }_h+{\xi }_h),& (25)\end{array}$

$\begin{array}{ll}{\lambda }_4=-{\mu }_r& (26)\end{array}$

$\begin{array}{ll}{\lambda }_5=-({\gamma }_h+{\phi }_h+{\mu }_h),& (27)\end{array}$

$\begin{array}{ll}{\lambda }_6=-({\theta }_h+{\delta }_h+{\mu }_h+{\nu }_h),& (28)\end{array}$

$\begin{array}{ll}{\lambda }_7=\frac{-{\Delta }_2+\sqrt{{\Delta }_1}}{2N_r{\mu }_r},& (29)\end{array}$

$\begin{array}{ll}{\lambda }_8=\frac{-{\Delta }_2-\sqrt{{\Delta }_1}}{2N_r{\mu }_r}.& (30)\end{array}$

From the calculated eigenvalues, we obtain negative real parts, that is, the monkeypox-free equilibrium is asymptotically stable if

$\begin{array}{ll}\frac{-{\Delta }_2-\sqrt{{\Delta }_1}}{2N_r{\mu }_r}<0.& (31)\end{array}$

Upon simplification, we obtain Equation (31):

$\begin{array}{ll}\frac{N_r{\mu }_r{(2{\mu }_r-{\nu }_r-{\phi }_r)}^2}{N_r{\mu }_r{({\nu }_r-{\phi }_r)}^2+4{\Lambda }_r{\beta }_{rr}{\phi }_r}<1.& (32)\end{array}$

Therefore, the monkeypox-free equilibrium state is asymptotically stable.

5.2. Global stability of the equilibrium state

If ℜ₀ < 1, then the monkeypox-free equilibrium is globally asymptotically stable; otherwise, it is unstable. This is proven by the Lyapunov function such that

$\begin{array}{ll}L(E_h)=E_h& (33)\end{array}$

Differentiating, we obtain

$\begin{array}{ll}{L}^{\prime }(E_h)=E_h^{{}^{\prime }}& (34)\end{array}$

$\begin{array}{ll}={\lambda }_h{S}_h-{\gamma }_h{E}_h-{\varphi }_h{E}_h-{\mu }_h{E}_h& (35)\end{array}$

$\begin{array}{ll}={\lambda }_h{S}_h-({\gamma }_h+{\varphi }_h+{\mu }_h)E_h.& (36)\end{array}$

At the disease-free equilibrium state as seen in Equation (11), $S_h=\frac{{\Lambda }_h}{{\mu }_h},$

$\begin{array}{ll}{L}^{\prime }(E_h)={\lambda }_h(\frac{{\Lambda }_h}{{\mu }_h})-({\gamma }_h-{\varphi }_h-{\mu }_h)E_h& (37)\end{array}$

$\begin{array}{ll}{E}_h^{{}^{\prime }}=({\gamma }_h+{\varphi }_h+{\mu }_h)\left[\frac{{\Lambda }_h{\lambda }_h}{{\mu }_h({\gamma }_h+{\varphi }_h+{\mu }_h)E_h}-1\right]E_h& (38)\end{array}$

$\begin{array}{ll}{E}_h^{{}^{\prime }}=({\gamma }_h+{\varphi }_h+{\mu }_h)({\Re }_0-1)E_h\le 0\text{ if }{\Re }_0\le 0.& (39)\end{array}$

From the result obtained in Equation (39), we can see that $E_h^{{}^{\prime }}\le 0$ provided ℜ₀ ≤ 0 as well as $E_h^{{}^{\prime }}=0$ provided that ℜ₀ = 0 or E_h = 0. Global stability of the disease-free equilibrium is asymptotically stable, if ℜ₀ ≤ 0; otherwise, it is unstable.

6. Endemic equilibrium state

The endemic equilibrium state occurs when the rate of infection persists in the population and it is represented in Equations (40 - 47) by $E_h^{**},E_r^{**},I_h^{**},I_r^{**},Q_h^{**},R_h^{**},S_h^{**},S_r^{**}.$

$\begin{array}{ll}{E}_h^{**}=\frac{\left[{\mu }_h^3+k_1{\mu }_h^2+(k_2+k_3){\mu }_h+k_4\right]{\Lambda }_h{\lambda }_h}{{\mu }_h^5+p_1{\mu }_h^4+p_2·{\mu }_h^3+p_3·{\mu }_h^2+{\mu }_h·p_4+{\lambda }_h{\nu }_h{\xi }_h·p_5}& (40)\end{array}$

$\begin{array}{ll}{E}_r^{**}=\frac{{\lambda }_r{\Lambda }_r}{({\mu }_r+{\phi }_r)({\mu }_r+{\lambda }_r)}& (41)\end{array}$

$\begin{array}{ll}{I}_h^{**}=\frac{({\mu }_h^2+({\delta }_h+{\nu }_h+{\theta }_h+{\xi }_h){\mu }_h+{\delta }_h{\xi }_h+{\nu }_h{\xi }_h+{\theta }_h{\xi }_h){\Lambda }_h{\lambda }_h{\phi }_h}{{\mu }_h^5+p_1{\mu }_h^4+p_2·{\mu }_h^3+p_3·{\mu }_h^2+{\mu }_h·p_4+{\lambda }_h{\nu }_h{\xi }_h·p_5+p_6}& (42)\end{array}$

$\begin{array}{ll}{I}_r^{**}=\frac{{\phi }_r{\lambda }_r{\Lambda }_r}{{\lambda }_r{\mu }_r^2+{\lambda }_r{\mu }_r{\nu }_r+{\lambda }_r{\mu }_r{\phi }_r+{\lambda }_r{\nu }_r{\phi }_r+{\mu }_r^3+{\mu }_r^2{\nu }_r+{\mu }_r^2{\phi }_r+{\mu }_r{\nu }_r{\phi }_r}& (43)\end{array}$

$\begin{array}{ll}{Q}_h^{**}=\frac{({\gamma }_h{\mu }_h^2+{\gamma }_h({\nu }_h+{\psi }_h+{\xi }_h){\mu }_h+{\gamma }_h({\nu }_h{\xi }_h+{\psi }_h{\xi }_h)){\Lambda }_h{\lambda }_h}{{\mu }_h^5+p_1{\mu }_h^4+p_2·{\mu }_h^3+p_3·{\mu }_h^2+{\mu }_h·p_4+{\lambda }_h{\nu }_h{\xi }_h·p_5+p_6}& (44)\end{array}$

$\begin{array}{l}{R}_h^{**}=\\ \frac{({\delta }_h{\psi }_h+{\mu }_h{\psi }_h+{\nu }_h{\psi }_h+{\psi }_h{\theta }_h){\lambda }_h{\Lambda }_h{\phi }_h+({\delta }_h{\gamma }_h{\mu }_h+{\delta }_h{\gamma }_h{\nu }_h+{\delta }_h{\gamma }_h{\psi }_h){\lambda }_h{\Lambda }_h}{{\mu }_h^5+p_1{\mu }_h^4+p_2·{\mu }_h^3+p_3·{\mu }_h^2+{\mu }_h·p_4+{\lambda }_h{\nu }_h{\xi }_h·p_5+p_6}& (45)\end{array}$

$\begin{array}{ll}{S}_h^{**}=\frac{{\Lambda }_h{\mu }_h^4+{\Lambda }_h·h_1·{\mu }_h^3+{\Lambda }_h·h_2·{\mu }_h^2+{\Lambda }_h·h_3·{\mu }_h+{\Lambda }_h·h_4}{{\mu }_h^5+p_1{\mu }_h^4+p_2·{\mu }_h^3+p_3·{\mu }_h^2+{\mu }_h·p_4+{\lambda }_h{\nu }_h{\xi }_h·p_5+p_6}& (46)\end{array}$

$\begin{array}{ll}{S}_r^{**}=\frac{{\Lambda }_r}{{\lambda }_r+{\mu }_r},& (47)\end{array}$

where

$\begin{array}{l}{d}_1=({\psi }_h+{\nu }_h),\\ d_2=({\delta }_h+{\nu }_h+{\theta }_h+{\xi }_h),\\ d_3=({\delta }_h+{\nu }_h+{\theta }_h),\\ k_1=({\psi }_h+2{\nu }_h+{\delta }_h+{\theta }_h+{\xi }_h)\\ k_2=d_1+d_2,\\ k_3={\xi }_h·d_3,\\ k_4=d_1·{\xi }_h·d_3,\\ p_1={\delta }_h+{\gamma }_h+{\lambda }_h+2{\nu }_h+{\psi }_h+{\theta }_h+{\phi }_h+{\xi }_h,\\ p_2={\delta }_h{\gamma }_h+{\delta }_h{\lambda }_h+{\delta }_h{\nu }_h+{\delta }_h{\psi }_h+{\delta }_h{\phi }_h+{\delta }_h{\xi }_h+{\gamma }_h{\lambda }_h\\ +2{\gamma }_h{\nu }_h+{\gamma }_h{\psi }_h+{\gamma }_h{\theta }_h+{\gamma }_h{\xi }_h+2{\lambda }_h{\nu }_h+{\lambda }_h{\psi }_h+{\lambda }_h{\theta }_h\\ +{\lambda }_h{\phi }_h+{\lambda }_h{\xi }_h+{\nu }_h^2+{\nu }_h{\psi }_h+{\nu }_h{\theta }_h+2{\nu }_h{\phi }_h+2{\nu }_h{\xi }_h\\ +{\psi }_h{\theta }_h+{\psi }_h{\phi }_h+{\psi }_h{\xi }_h\\ +{\theta }_h{\phi }_h+{\theta }_h{\xi }_h+{\phi }_h{\xi }_h,\\ p_3={\delta }_h{\gamma }_h{\lambda }_h+{\delta }_h{\gamma }_h{\nu }_h+{\delta }_h{\gamma }_h{\psi }_h+{\delta }_h{\gamma }_h{\xi }_h+{\delta }_h{\lambda }_h{\nu }_h+{\delta }_h{\lambda }_h{\psi }_h\\ +{\delta }_h{\lambda }_h{\phi }_h+{\delta }_h{\lambda }_h{\xi }_h+{\delta }_h{\nu }_h{\phi }_h+{\delta }_h{\nu }_h{\xi }_h+{\delta }_h{\psi }_h{\phi }_h+{\delta }_h{\psi }_h{\xi }_h\\ +{\delta }_h{\phi }_h{\xi }_h+2{\gamma }_h{\lambda }_h{\nu }_h+{\gamma }_h{\lambda }_h{\psi }_h+{\gamma }_h{\lambda }_h{\xi }_h+{\gamma }_h{\nu }_h^2+{\gamma }_h{\nu }_h{\psi }_h\\ +{\gamma }_h{\nu }_h{\theta }_h+2{\gamma }_h{\nu }_h{\xi }_h+{\gamma }_h{\psi }_h{\theta }_h+{\gamma }_h{\psi }_h{\xi }_h+{\gamma }_h{\theta }_h{\xi }_h+{\lambda }_h{\nu }_h^2\\ +{\lambda }_h{\nu }_h{\psi }_h+{\lambda }_h{\nu }_h{\theta }_h+2{\lambda }_h{\nu }_h{\phi }_h+2{\lambda }_h{\nu }_h{\xi }_h+{\lambda }_h{\psi }_h{\theta }_h+{\lambda }_h{\psi }_h{\phi }_h\\ +{\lambda }_h{\psi }_h{\xi }_h+{\lambda }_h{\theta }_h{\phi }_h+{\lambda }_h{\theta }_h{\xi }_h+{\lambda }_h{\phi }_h{\xi }_h+{\nu }_h^2{\phi }_h+{\nu }_h^2{\xi }_h+{\nu }_h{\psi }_h{\phi }_h\\ +{\nu }_h{\psi }_h{\xi }_h+{\nu }_h{\theta }_h{\phi }_h+{\nu }_h{\theta }_h{\xi }_h+2{\nu }_h{\phi }_h{\xi }_h+{\psi }_h{\theta }_h{\phi }_h+{\psi }_h{\theta }_h{\xi }_h\\ +{\psi }_h{\phi }_h{\xi }_h+{\theta }_h{\phi }_h{\xi }_h,\\ p_4={\delta }_h{\gamma }_h{\lambda }_h{\nu }_h+{\delta }_h{\gamma }_h{\lambda }_h{\psi }_h+{\delta }_h{\gamma }_h{\nu }_h{\xi }_h+{\delta }_h{\gamma }_h{\psi }_h{\xi }_h+{\delta }_h{\lambda }_h{\nu }_h{\phi }_h\\ +{\delta }_h{\lambda }_h{\nu }_h{\xi }_h+{\delta }_h{\lambda }_h{\psi }_h{\phi }_h+{\delta }_h{\lambda }_h{\psi }_h{\xi }_h+{\delta }_h{\lambda }_h{\phi }_h{\xi }_h+{\delta }_h{\nu }_h{\phi }_h{\xi }_h\\ +{\delta }_h{\psi }_h{\phi }_h{\xi }_h+{\gamma }_h{\lambda }_h{\nu }_h^2+{\gamma }_h{\lambda }_h{\nu }_h{\psi }_h+2{\gamma }_h{\lambda }_h{\nu }_h{\xi }_h+{\gamma }_h{\lambda }_h{\psi }_h{\xi }_h\\ +{\gamma }_h{\nu }_h^2{\xi }_h+{\gamma }_h{\nu }_h{\psi }_h{\xi }_h+{\gamma }_h{\nu }_h{\theta }_h{\xi }_h+{\gamma }_h{\psi }_h{\theta }_h{\xi }_h+{\lambda }_h{\nu }_h^2{\phi }_h+{\lambda }_h{\nu }_h^2{\xi }_h\\ +{\lambda }_h{\nu }_h{\psi }_h{\phi }_h+{\lambda }_h{\nu }_h{\psi }_h{\xi }_h+{\lambda }_h{\nu }_h{\theta }_h{\phi }_h+{\lambda }_h{\nu }_h{\theta }_h{\xi }_h+2{\lambda }_h{\nu }_h{\phi }_h{\xi }_h\\ +{\lambda }_h{\psi }_h{\theta }_h{\phi }_h+{\lambda }_h{\psi }_h{\theta }_h{\xi }_h+{\lambda }_h{\theta }_h{\phi }_h{\xi }_h+{\nu }_h^2{\phi }_h{\xi }_h\\ +{\nu }_h{\psi }_h{\phi }_h{\xi }_h+{\nu }_h{\theta }_h{\phi }_h{\xi }_h+{\psi }_h{\theta }_h{\phi }_h{\xi }_h,\\ p_5={\delta }_h{\phi }_h+{\gamma }_h{\nu }_h+{\gamma }_h{\psi }_h+{\nu }_h{\phi }_h+{\theta }_h{\phi }_h,\\ p_6={\delta }_h{\lambda }_h{\nu }_h{\phi }_h{\xi }_h+{\gamma }_h{\lambda }_h{\nu }_h^2{\xi }_h+{\gamma }_h{\lambda }_h{\nu }_h{\psi }_h{\xi }_h+{\lambda }_h{\nu }_h^2{\phi }_h{\xi }_h\\ +{\lambda }_h{\nu }_h{\theta }_h{\phi }_h{\xi }_h,\\ h_1={\delta }_h+{\gamma }_h+2{\nu }_h+{\psi }_h+{\theta }_h+{\phi }_h+{\xi }_h,\\ h_2={\delta }_h{\gamma }_h+{\delta }_h{\nu }_h+{\delta }_h{\psi }_h+{\delta }_h{\phi }_h+{\delta }_h{\xi }_h+2{\gamma }_h{\nu }_h+{\gamma }_h{\psi }_h+{\gamma }_h{\theta }_h\\ +{\gamma }_h{\xi }_h+{\nu }_h^2+{\nu }_h{\psi }_h+{\nu }_h{\theta }_h+2{\nu }_h{\phi }_h+2{\nu }_h{\xi }_h+{\psi }_h{\theta }_h+{\psi }_h{\phi }_h\\ +{\psi }_h{\xi }_h+{\theta }_h{\phi }_h+{\theta }_h{\xi }_h+{\phi }_h{\xi }_h,\\ h_3={\delta }_h{\gamma }_h{\nu }_h+{\delta }_h{\gamma }_h{\psi }_h+{\delta }_h{\gamma }_h{\xi }_h+{\delta }_h{\nu }_h{\phi }_h+{\delta }_h{\nu }_h{\xi }_h+{\delta }_h{\psi }_h{\phi }_h\\ +{\delta }_h{\psi }_h{\xi }_h+{\delta }_h{\phi }_h{\xi }_h+{\gamma }_h{\nu }_h^2+{\gamma }_h{\nu }_h{\psi }_h+{\gamma }_h{\nu }_h{\theta }_h\\ +2{\gamma }_h{\nu }_h{\xi }_h+{\gamma }_h{\psi }_h{\theta }_h+{\gamma }_h{\psi }_h{\xi }_h+{\gamma }_h{\theta }_h{\xi }_h+{\nu }_h^2{\phi }_h\\ +{\nu }_h^2{\xi }_h+{\nu }_h{\psi }_h{\phi }_h+{\nu }_h{\psi }_h{\xi }_h+{\nu }_h{\theta }_h{\phi }_h+{\nu }_h{\theta }_h{\xi }_h+2{\nu }_h{\phi }_h{\xi }_h\\ +{\psi }_h{\theta }_h{\phi }_h+{\psi }_h{\theta }_h{\xi }_h+{\psi }_h{\phi }_h{\xi }_h+{\theta }_h{\phi }_h{\xi }_h,\\ h_4={\delta }_h{\gamma }_h{\nu }_h{\xi }_h+{\delta }_h{\gamma }_h{\psi }_h{\xi }_h+{\delta }_h{\nu }_h{\phi }_h{\xi }_h+{\delta }_h{\psi }_h{\phi }_h{\xi }_h+{\gamma }_h{\nu }_h^2{\xi }_h\\ +{\gamma }_h{\nu }_h{\psi }_h{\xi }_h+{\gamma }_h{\nu }_h{\theta }_h{\xi }_h+{\gamma }_h{\psi }_h{\theta }_h{\xi }_h+{\nu }_h^2{\phi }_h{\xi }_h+{\nu }_h{\psi }_h{\phi }_h{\xi }_h\\ +{\nu }_h{\theta }_h{\phi }_h{\xi }_h+{\psi }_h{\theta }_h{\phi }_h{\xi }_h,& (48)\end{array}$

7. Existence and uniqueness results for the monkeypox transmission model with non-pharmaceutical intervention

We reformulate Equation (2) as follows:

$\begin{array}{l}\{\begin{array}{c}{\Phi }_1(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t))={\Lambda }_h+{\xi }_h{R}_h\\ +{\theta }_h{Q}_h-{\lambda }_h{S}_h-{\mu }_h{S}_h,\\ {\Phi }_2(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t))={\lambda }_h{S}_h\\ -{\gamma }_h{E}_h-{\varphi }_h{E}_h-{\mu }_h{E}_h,\\ {\Phi }_3(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t))={\varphi }_h{E}_h\\ -({\psi }_h+{\mu }_h+{\nu }_h)I_h,\\ {\Phi }_4(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t))={\gamma }_h{E}_h\\ -({\theta }_h+{\delta }_h+{\mu }_h+{\nu }_h)Q_h\\ {\Phi }_5(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t))={\psi }_h{I}_h\\ +{\delta }_h{Q}_h-{\xi }_h{R}_h-{\mu }_h{R}_h,\\ {\Phi }_6(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t))={\Lambda }_r-{\lambda }_r{S}_r\\ -{\mu }_r{S}_r\\ {\Phi }_7(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t))={\lambda }_r{S}_r-{\varphi }_r{E}_r\\ -{\mu }_r{E}_r,\\ {\Phi }_8(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t))={\varphi }_r{E}_r\\ -({\mu }_r+{\nu }_r)I_r.\\ \end{array}\end{array}$

From Equation (10), the developed model of Equation (1) can be written in the form

$\begin{array}{ll}\{\begin{array}{l}{}^{CF}{D}_t^{\alpha }\Phi (t)=\Upsilon (t,\Phi (t)),t\in \left[0,\eta \right],0<\alpha \le 1,\\ \Phi (0)={\Phi }_0,\end{array}& (49)\end{array}$

$\begin{array}{ll}\Phi (t)=\{\begin{array}{l}{S}_h(t),\\ E_h(t),\\ I_h(t),\\ Q_h(t),\\ R_h(t),\\ S_r(t),\\ E_r(t),\\ I_r(t),\\ \end{array}{\Phi }_0=\{\begin{array}{l}{S}_h(0),\\ E_h(0),\\ I_h(0),\\ Q_h(0),\\ R_h(0),\\ S_r(0),\\ E_r(0),\\ I_r(0),\\ \end{array}& (50)\end{array}$

therefore,

$\begin{array}{ll}\Upsilon (t,\Phi (t))=\{\begin{array}{l}{\Phi }_1(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t)),\\ {\Phi }_2(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t)),\\ {\Phi }_3(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t)),\\ {\Phi }_4(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t)),\\ {\Phi }_5(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t)),\\ {\Phi }_6(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t)),\\ {\Phi }_7(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t)),\\ {\Phi }_8(t,S_h(t),E_h(t),I_h(t),Q_h(t),R_h(t),S_r(t),E_r(t),I_r(t)).\\ \end{array}& (51)\end{array}$

With the help of Lemma 2.4, Equation (49) yields

$\begin{array}{ll}\{\begin{array}{l}\Phi (t)={\Phi }_0(t)+\frac{2(1-\alpha )}{2(1-\alpha )G(\alpha )}\Upsilon (t,\Phi (t))+\frac{2\alpha }{(2-\alpha )G(\alpha )}\\ \times {\int }_0^t\Upsilon (s,\Phi (s))ds.\end{array}& (52)\end{array}$

Furthermore, let ussay E = C([0, η]) is the Banach space, and supposing that the following assumptions hold;

(H₁), there exists a non-negative constant Q, W, and k ∈ [0, 1) such that

$\Upsilon (t,\Phi (t))\le Q|\Phi {|}^k+W.$

(H₂) There exists a nonnegative constant C_ρ > 0 for all $\Phi ,\tilde{\Phi }\in E$, then

$|\Upsilon (t,\Phi (t))-\Upsilon (t,\tilde{\Phi }(t))|\le {\text{C}}_{\rho }\left[|\Phi -\tilde{\Phi }|\right].$

Furthermore, let us define operator A_m : E → E such that

${\text{A}}_m\aleph (t)=M_1\Phi (t)+M_2\Phi (t),$

therefore, we can see that

$\begin{array}{ll}\{\begin{array}{l}{M}_1\Phi (t)={\Phi }_0(t)+\frac{2(1-\alpha )}{2(1-\alpha )G(\alpha )}\Upsilon (t,\Phi (t)),\\ M_2\Phi (t)=\frac{2\alpha }{(2-\alpha )G(\alpha )}{\int }_0^t\Upsilon (s,\Phi (s))ds.\end{array}& (53)\end{array}$

From this knowledge, Equation (52) can be written as

$\begin{array}{ll}\{\begin{array}{l}{\text{A}}_m\Phi (t)={\Phi }_0(t)+\frac{2(1-\alpha )}{2(1-\alpha )G(\alpha )}\Upsilon (t,\Phi (t))+\frac{2\alpha }{(2-\alpha )G(\alpha )}\\ \times {\int }_0^t\Upsilon (s,\Phi (s))ds.\end{array}& (54)\end{array}$

Theorem 2. Suppose that (H₁) and (H₂) hold, such that $\frac{2(1-\alpha )}{2(1-\alpha )G(\alpha )}{\mathbf{\text{C}}}_{\rho }<1$, then, the monkeypox transmission model with non-pharmaceutical intervention has at least one solution.

Proof. For simplicity, we divide the proof into two steps.

Step 1. We prove that operator M₁ is contraction. Then, let $\tilde{\Phi }\in \Omega$, where Ω = {Φ ∈ Z : ||Φ|| ≤ ϑ, ϑ > 0} is a close convex set, thus

$\begin{array}{ll}\begin{array}{l}|M_1\Phi (t)-M_2\Phi |=\frac{2(1-\alpha )}{2(1-\alpha )G(\alpha )}{\displaystyle {max}_{\alpha \in \left[0,\eta \right]}}\\ |\Upsilon (t,\Phi (t))-\Upsilon (t,\tilde{\Phi }(t))|,\\ \le \frac{2(1-\alpha )}{2(1-\alpha )G(\alpha )}{\text{C}}_{\rho }\left|\right|\Phi -\tilde{\Phi }\left|\right|.\\ \end{array}& (55)\end{array}$

Thus,

$||M_1\Phi -M_2\Phi (t)||\le \frac{2(1-\alpha )}{2(1-\alpha )G(\alpha )}{\text{C}}_{\rho }||\Phi -\tilde{\Phi }||.$

Hence, M₁ is contraction since $\frac{2(1-\alpha )}{2(1-\alpha )G(\alpha )}{\mathbf{\text{C}}}_{\rho }<1$.

Step 2. We also prove that M₂ is compact and also continuous; for all Φ ∈ Ω, then M₂ will be continuous as Φ is continuous, thus

$\begin{array}{ll}\begin{array}{l}\left|\right|M_2(\Phi )\left|\right|={\displaystyle {max}_{t\in \left[0,\eta \right]}}|\frac{2\alpha }{(2-\alpha )G(\alpha )}{\int }_0^t\Upsilon (s,\Phi (s))ds|,\\ \le \frac{2\alpha }{(2-\alpha )G(\alpha )}\eta {\int }_0^t|\Upsilon (s,\Phi (s))|ds.\\ \le \frac{2\alpha }{(2-\alpha )G(\alpha )}\eta \left[Q|\Phi {|}^k+W\right].\end{array}& (56)\end{array}$

Hence, M₂ is boundedness. For equicontinuous, let t₁, t₂ ∈ [0, η] such that

$\begin{array}{ll}\begin{array}{l}|(M_2\Phi )(t_1)-(M_2\Phi )(t_2)|=\frac{2\alpha }{(2-\alpha )G(\alpha )}{\displaystyle {max}_{t\in \left[0,\eta \right]}}|{\int }_0^{t_1}\Upsilon (s,\Phi (s))ds\\ -{\int }_0^{t_2}\Phi (s,\aleph (s))ds|\\ \le \frac{2\alpha }{(2-\alpha )G(\alpha )}\left[Q|\Phi {|}^k+W\right]|t_1-t_2|.\end{array}& (57)\end{array}$

As t₁ → t₂, then |(M₂Φ)(t₁) − (M₂Φ)(t₂)| → 0, which makes operator M₂ equicontinuous and compact by the Arzela–Ascoli theorem. Therefore, by Lemma 2.3, the existence for the monkeypox transmission model with non-pharmaceutical intervention has at least one solution.   □

Theorem 3. Suppose that ∃ is a nonnegative integer Λ_ρ is > 0 such that

$\begin{array}{ll}\begin{array}{c}{\Lambda }_{\rho }=\left[\frac{2(1-\alpha )}{2(1-\alpha )G(\alpha )}{\text{L}}_{\rho }+\frac{2\alpha }{(2-\alpha )G(\alpha )}\eta {\text{L}}_{\rho }\right]<1,\end{array}& (58)\end{array}$

then operator A_m has a unique fixed point.

Proof. Let $\Phi ,\tilde{\Phi }\in \Omega$, then we say

$\begin{array}{ll}\begin{array}{l}\left|\right|{\text{A}}_m\Phi -{\text{A}}_m\tilde{\Phi }\left|\right|\le \left|\right|M_1\Phi -M_1\tilde{\Phi }\left|\right|+\left|\right|M_2\Phi -M_2\tilde{\Phi }\left|\right|,\\ \le \frac{2(1-\alpha )}{2(1-\alpha )G(\alpha )}{\displaystyle {max}_{t\in \left[0,\eta \right]}}|\Upsilon (t,\Phi (t))-\Upsilon (t,\tilde{\Phi }(t))|\\ +\frac{2\alpha }{(2-\alpha )G(\alpha )}{\displaystyle {max}_{t\in \left[0,\eta \right]}}|{\int }_0^t\Upsilon (s,\Phi (s))ds\\ -{\int }_0^t\Upsilon (s,\tilde{\Phi }(s))ds|\\ \le \left[\frac{2(1-\alpha )}{2(1-\alpha )G(\alpha )}{\text{C}}_{\rho }+\frac{2\alpha }{(2-\alpha )G(\alpha )}\eta {\text{C}}_{\rho }\right]\left|\right|\Phi -\tilde{\Phi }\left|\right|,\\ ={\Lambda }_{\rho }\left|\right|\Phi -\tilde{\Phi }\left|\right|.\end{array}& (59)\end{array}$

Hence, by the Banach contraction principle, A_m has a unique fixed point. Consequently, the monkeypox transmission model with non-pharmaceutical intervention has a unique solution. □

8. Fitting of model to data

We used the available public database to collect our data while the formulated model of Equation (1) includes 16 parameters. To treat the waggliness of the reported daily new cases, we smoothed the data to remove noise from the data set so as to make it suitable for our analysis. The total population of the United Kingdom is 68,530,739 (1), which was used for calculating the initial number of susceptible humans, while the initial value for the number of infected humans was calculated from the reported daily new cases. Other initial values were assumed.

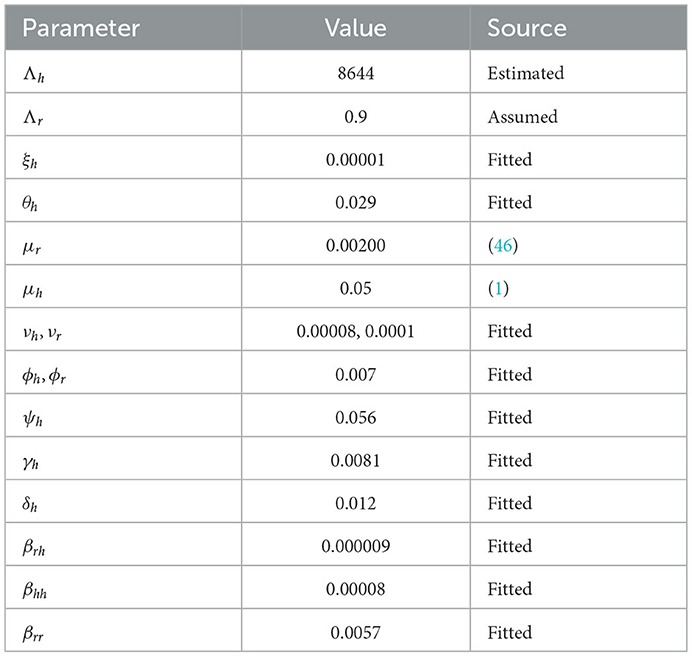
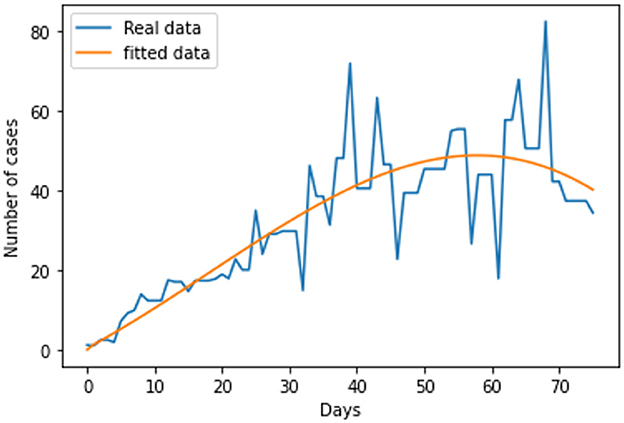
The link to the data used for this research and the initial values; S_h(t) = 68530739; E_h(t) = 0; I_h(t) = 31412; Q_h(t) = 0; S_r(t) = 1074103; E_r(t) = 1074103; and I_r(t) = 1074103; can be found in the Data Availability section. The parameters are fitted based on the smoothed reported daily new cases of infected humans from May to August 2022. This information was taken from the United Kingdom public health database (1). The nonlinear least square technique was used to fit the model using python programming. Table 2 shows all of the parameter values that were fitted, and Figure 2 shows the data fitting of the observed smoothed daily new cases.

TABLE 2

Table 2. Parameter values in the model.

FIGURE 2

Figure 2. Model fitting.

9. Numerical scheme

In this section, we present the numerical results for the monkeypox transmission model with non-pharmaceutical intervention based on the Lagrange interpolation. Details about the numerical scheme is presented in Atangana and Owolabi (50). The Cauchy problem of the CF fractional derivative can be given as:

$\begin{array}{ll}\begin{array}{c}{}^{CF}{D}_t^{\alpha }\Phi (t)=\Upsilon (t,\Phi (t)),\end{array}& (60)\end{array}$

On the other hand, we can express Equation (60) as

$\begin{array}{ll}\Phi (t)={\Phi }_0(t)+\frac{(1-\alpha )}{G(\alpha )}\Upsilon (t,\Phi (t))+\frac{\alpha }{G(\alpha )}\times {\int }_0^t\Upsilon (s,\Phi (s))ds.& (61)\end{array}$

Taking Equation (61) at the point t_n+1 = (n + 1)h and t_n = nh, n = 0, 1, 2, 3, …, with h being the time step, we have

$\begin{array}{ll}\begin{array}{l}\Phi (t_{n+1})=\Phi (0)+\frac{(1-\alpha )}{G(\alpha )}\Upsilon (t_n,\Phi (t_n))+\frac{\alpha }{G(\alpha )}\\ \times {\displaystyle {\int }_{t_n}^{t_{n+1}}}\Upsilon (s,\Phi (s))ds,\end{array}& (62)\end{array}$

$\begin{array}{ll}\begin{array}{l}\Phi (t_n)=\Phi (0)+\frac{(1-\alpha )}{G(\alpha )}\Phi (t_{n-1},\aleph (t_{n-1}))+\frac{\alpha }{G(\alpha )}\\ \times {\displaystyle {\int }_{t_n}^{t_{n+1}}}\Upsilon (s,\Phi (s))ds.\end{array}& (63)\end{array}$

Taking the results of Equations (62)-(63) in

$\begin{array}{ll}\begin{array}{l}\Phi (t_{n+1})-\aleph (t_n)=\frac{(1-\alpha )}{G(\alpha )}\left(\Upsilon (t_n,\Phi (t_n))-\Upsilon (t_{n-1},\Phi (t_{n-1}))\right)\\ +\frac{\alpha }{G(\alpha )}\times {\displaystyle {\int }_{t_n}^{t_{n+1}}}\Upsilon (s,\Phi (s))ds,\end{array}& (64)\end{array}$

Equation (64) in the two-step Lagrange polynomial gives

$\begin{array}{ll}\begin{array}{l}\Phi (t_{n+1})-\Phi (t_n)=\frac{(1-\alpha )}{G(\alpha )}\left(\Upsilon (t_n,\Phi (t_n))-\Upsilon (t_{n-1},\Phi (t_{n-1}))\right)\\ +\frac{\alpha }{G(\alpha )}\times {\displaystyle {\int }_{t_{\alpha }}^{t_{\alpha +1}}}[\frac{\Upsilon (t_n,\Phi (t_n))}{h}(s-t_{n-1})\\ -\frac{\Upsilon (t_{n-1},\Phi (t_{n-1}))}{h}(s-t_n)]ds.\end{array}& (65)\end{array}$

The aforementioned Equation (65) leads to

$\begin{array}{ll}\begin{array}{l}\Phi (t_{n+1})-\Phi (t_n)=\frac{(1-\alpha )}{G(\alpha )}\left(\Upsilon (t_n,\Phi (t_n))-\Upsilon (t_{n-1},\Phi (t_{n-1}))\right)\\ +\frac{\alpha }{G(\alpha )}\times [\frac{\Upsilon (t_n,\Phi (t_n))}{h}{\displaystyle {\int }_{t_n}^{t_{n+1}}}(s-t_{n-1})ds-\frac{\Upsilon (t_{n-1},\Phi (t_{n-1}))}{h}\\ {\displaystyle {\int }_{t_n}^{t_{n+1}}}(s-t_n)ds].\end{array}& (66)\end{array}$

Solving the integrals in Equation (66) yields

$\begin{array}{ll}\begin{array}{c}{\displaystyle {\int }_{t_n}^{t_{n+1}}}(s-t_{n-1})ds=\frac{3}{2}{h}^2,\\ {\displaystyle {\int }_{t_n}^{t_{n+1}}}(s-t_n)ds=\frac{1}{2}{h}^2.\end{array}& (67)\end{array}$

Substituting Equation (67) into Equation (66), then generalizing the numerical scheme of CF is as follows:

$\begin{array}{ll}\begin{array}{l}{\Phi }_{n+1}={\aleph }_n+\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{3h\alpha }{2G(\alpha )}\right]\Phi (t_n,{\Phi }_n)\\ -\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{h\alpha }{2G(\alpha )}\right]\Phi (t_{n-1},{\aleph }_{n-1}).\end{array}& (68)\end{array}$

Thus, in terms of our CF-fractional monkeypox transmission model with non-pharmaceutical intervention, we obtain;

$\begin{array}{ll}\begin{array}{l}{S}_{h_{n+1}}=S_{h_n}+\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{3h\alpha }{2G(\alpha )}\right]\Upsilon (t_n,S_{h_n})\\ -\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{h\alpha }{2G(\alpha )}\right]\Upsilon (t_{n-1},S_{h_{n-1}}).\end{array}& (69)\end{array}$

$\begin{array}{ll}\begin{array}{l}{E}_{h_{n+1}}=E_{h_n}+\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{3h\alpha }{2G(\alpha )}\right]\Upsilon (t_n,E_{h_n})\\ -\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{h\alpha }{2G(\alpha )}\right]\Upsilon (t_{n-1},E_{h_{n-1}}).\end{array}& (70)\end{array}$

$\begin{array}{ll}\begin{array}{l}{I}_{h_{n+1}}=I_{h_n}+\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{3h\alpha }{2G(\alpha )}\right]\Upsilon (t_n,I_{h_n})\\ -\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{h\alpha }{2G(\alpha )}\right]\Upsilon (t_{n-1},I_{h_{n-1}}).\end{array}& (71)\end{array}$

$\begin{array}{ll}\begin{array}{l}{Q}_{h_{n+1}}=Q_{h_n}+\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{3h\alpha }{2G(\alpha )}\right]\Upsilon (t_n,Q_{h_n})\\ -\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{h\alpha }{2G(\alpha )}\right]\Upsilon (t_{n-1},Q_{h_{n-1}}).\end{array}& (72)\end{array}$

$\begin{array}{ll}\begin{array}{l}{R}_{h_{n+1}}=S_{h_n}+\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{3h\alpha }{2G(\alpha )}\right]\Upsilon (t_n,R_{h_n})\\ -\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{h\alpha }{2G(\alpha )}\right]\Upsilon (t_{n-1},R_{h_{n-1}}).\end{array}& (73)\end{array}$

$\begin{array}{ll}\begin{array}{l}{S}_{r_{n+1}}=S_{h_n}+\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{3h\alpha }{2G(\alpha )}\right]\Upsilon (t_n,S_{r_n})\\ -\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{h\alpha }{2G(\alpha )}\right]\Upsilon (t_{n-1},S_{r_{n-1}}).\\ \end{array}& (74)\end{array}$

$\begin{array}{ll}\begin{array}{l}{E}_{r_{n+1}}=S_{h_n}+\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{3h\alpha }{2G(\alpha )}\right]\Upsilon (t_n,E_{r_n})\\ -\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{h\alpha }{2G(\alpha )}\right]\Upsilon (t_{n-1},E_{r_{n-1}}).\end{array}& (75)\end{array}$

$\begin{array}{ll}\begin{array}{l}{I}_{r_{n+1}}=S_{h_n}+\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{3h\alpha }{2G(\alpha )}\right]\Upsilon (t_n,I_{r_n})\\ -\left[\frac{(1-\alpha )}{G(\alpha )}+\frac{h\alpha }{2G(\alpha )}\right]\Upsilon (t_{n-1},I_{r_{n-1}}).\end{array}& (76)\end{array}$

10. Sensitivity analysis

Since an epidemiological system's parameters are either estimated or fitted, there is some degree of uncertainty in the numbers that are utilized to derive conclusions about the underlying epidemic. It is crucial to evaluate the individual effects of each parameter on the dynamics of the epidemic to identify those effects that have the greatest impact on the epidemic's spread or contraction. For biological factors included in the proposed monkeypox model, we perform the sensitivity analysis in this section. This analysis is investigated analytically by computing $\frac{\partial {\Re }_0}{\partial p}$, where, p = (β_hh, Λ_h, ϕ_h, μ_h, γ_h, ν_h, and ψ_h). The sensitivity of ℜ₀ to each parameter is as follows:

$\begin{array}{l}\begin{array}{l}\frac{\partial {\Re }_0}{\partial {\beta }_{hh}}=\frac{{\lambda }_h{\varphi }_h}{{\mu }_h({\gamma }_h+{\mu }_h+{\varphi }_h)({\nu }_h+{\mu }_h+{\psi }_h)}>0,\\ \frac{\partial {\Re }_0}{\partial {\Lambda }_h}=\frac{{\beta }_{hh}{\varphi }_h}{{\mu }_h({\gamma }_h+{\mu }_h+{\varphi }_h)({\nu }_h+{\mu }_h+{\psi }_h)}>0,\\ \frac{\partial {\Re }_0}{\partial {\varphi }_h}=\frac{{\beta }_{hh}{\Lambda }_h({\gamma }_h+{\mu }_h)}{{\mu }_h({\gamma }_h+{\mu }_h+{\varphi }_h)({\nu }_h+{\mu }_h+{\psi }_h)},\\ \frac{\partial {\Re }_0}{\partial {\mu }_h}=-\frac{\begin{array}{l}{\beta }_{hh}{\Lambda }_h({\mu }_h({\gamma }_h+{\mu }_h+{\varphi }_h)+{\mu }_h({\nu }_h+{\mu }_h+{\psi }_h)\\ +({\gamma }_h+{\mu }_h+{\varphi }_h)({\nu }_h+{\mu }_h+{\psi }_h))\end{array}}{{\mu }_h^2{({\gamma }_h+{\mu }_h+{\varphi }_h)}^2{({\nu }_h+{\mu }_h+{\psi }_h)}^2}<0,\\ \frac{\partial {\Re }_0}{\partial {\gamma }_h}=-\frac{{\beta }_{hh}{\lambda }_h{\varphi }_h}{{\mu }_h{({\gamma }_h+{\mu }_h+{\varphi }_h)}^2({\nu }_h+{\mu }_h+{\psi }_h)}<0,\\ \frac{\partial {\Re }_0}{\partial {\nu }_h}=-\frac{{\beta }_{hh}{\lambda }_h{\varphi }_h}{{\mu }_h{({\gamma }_h+{\mu }_h+{\varphi }_h)}^2{({\nu }_h+{\mu }_h+{\psi }_h)}^2}<0,\\ \frac{\partial {\Re }_0}{\partial {\psi }_h}=-\frac{{\beta }_{hh}{\lambda }_h{\varphi }_h}{{\mu }_h{({\gamma }_h+{\mu }_h+{\varphi }_h)}^2{({\nu }_h+{\mu }_h+{\psi }_h)}^2}<0,\\ \end{array}\end{array}$

thus,

$\begin{array}{ll}\begin{array}{l}\frac{\partial {\Re }_0}{\partial {\beta }_{hh}}=124645.995943846\\ \frac{\partial {\Re }_0}{\partial {\Lambda }_h}=16.9011519923859\\ \frac{\partial {\Re }_0}{\partial {\varphi }_h}=\frac{0.1746837421029776}{{(0.008139+{\psi }_h)}^2}\\ \frac{\partial {\Re }_0}{\partial {\mu }_h}=-\frac{\begin{array}{c}9.912\times 10^{-7}{\mu }_h^2+4.7035744\times 10^{-8}{\mu }_h^2\\ +2.797853632\times 10^{-10}\end{array}}{\begin{array}{c}{\mu }_h^2({\mu }_h^4+0.014236{\mu }_h^3+0.00012055158688{\mu }_1\\ +7.17083788864\times 10^{-7})\end{array}},\\ \frac{\partial {\Re }_0}{\partial {\gamma }_h}=-\frac{0.15096125860751}{{({\gamma }_h+0.007039)}^2},\\ \frac{\partial {\Re }_0}{\partial {\nu }_h}=-\frac{0.59600691709814}{{({\nu }_h+0.056039)}^2},\\ \frac{\partial {\Re }_0}{\partial {\psi }_h}=-\frac{0.59600691709814}{{({\nu }_h+0.056039)}^2}.\\ \end{array}& (77)\end{array}$

The sensitivity index technique will help measure the most sensitive parameters for the fundamental reproductive number ℜ₀ (Borgonovo et al. (51) for details about the method). The fundamental reproduction number's normalized sensitivity index is provided by $S_p^{{\Re }_0}=\frac{\partial {\Re }_0}{\partial p}.\frac{p}{{\Re }_0}$, where p is a parameter as defined earlier. We obtain

$\begin{array}{l}\begin{array}{l}{S}_{{\beta }_{hh}}^{{\Re }_0}=1,\\ S_{{\Lambda }_h}^{{\Re }_0}=1,\\ S_{{\varphi }_h}^{{\Re }_0}=\frac{{\gamma }_h+{\mu }_h}{{\gamma }_h+{\mu }_h+{\varphi }_h},\\ S_{{\mu }_h}^{{\Re }_0}=\frac{\begin{array}{c}{\mu }_h({\gamma }_h+{\mu }_h+{\varphi }_h)+{\mu }_h({\nu }_h+{\mu }_h+{\psi }_h)\\ +({\gamma }_h+{\mu }_h+{\varphi }_h)({\nu }_h+{\mu }_h+{\psi }_h)\end{array}}{({\gamma }_h+{\mu }_h+{\varphi }_h)({\nu }_h+{\mu }_h+{\psi }_h)},\\ \end{array}\end{array}$

$\begin{array}{l}\begin{array}{l}{S}_{{\gamma }_h}^{{\Re }_0}=\frac{{\gamma }_h}{{\gamma }_h+{\mu }_h+{\varphi }_h},\\ S_{{\nu }_h}^{{\Re }_0}=\frac{{\nu }_h}{{\nu }_h+{\mu }_h+{\psi }_h},\\ S_{{\psi }_h}^{{\Re }_0}=\frac{{\psi }_h}{{\nu }_h+{\mu }_h+{\psi }_h}.\\ \end{array}\end{array}$

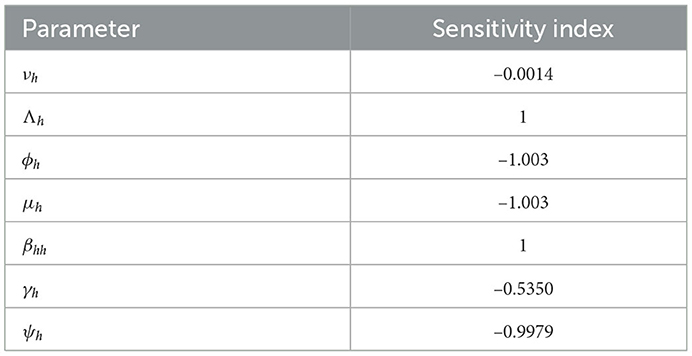
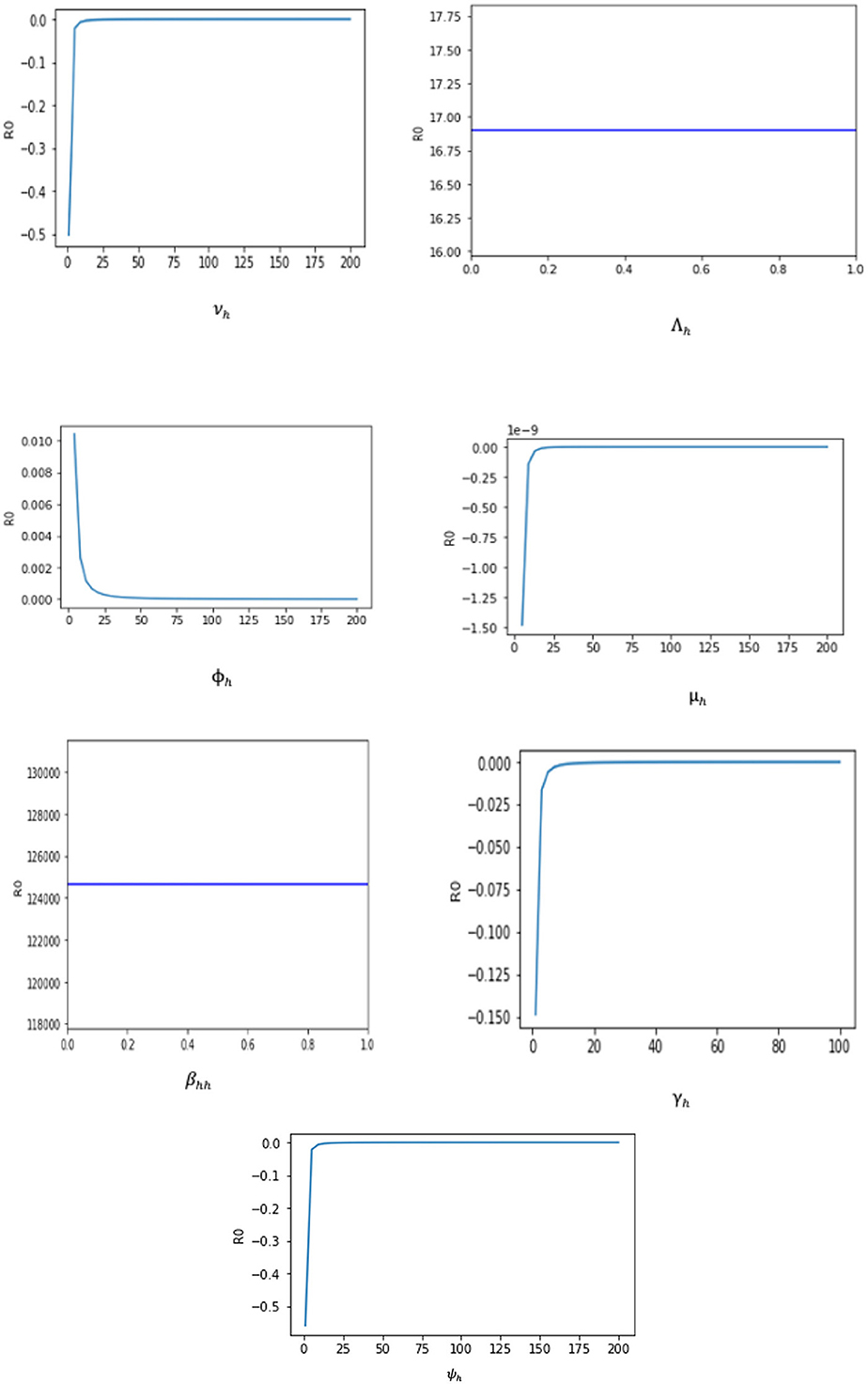
The sensitivity indices using the parameter values given in Table 2 are presented in Table 3. The sensitivity analysis of β_hh, Λ_h, ϕ_h, ψ_h, ν_h, γ_h, and μ_h with respect to ℜ₀ and their graphs are presented in Figure 3.

TABLE 3

Table 3. The sensitivity index of ℜ₀ with respect to parameter p of the system (1).

FIGURE 3

Figure 3. The sensitivity analysis of ℜ₀ with respect to the parameter p of the system (1).

Two of the sensitivity indices are positive while others are negative, as can be seen in Table 3. Additionally, the majority of these indices are functions of the Caputo–Fabrizio fractional monkeypox model parameters. This implies that changing one of the parameters slightly will alter the dynamics of the epidemic. The basic reproductive number ℜ₀ normalized sensitivity indices to the Caputo–Fabrizio fractional monkeypox model parameters are calculated. We conclude that increasing the rate of recovery and the rate of identifying suspected cases, that is, isolation and quarantining of the monkeypox virus carrier will aid in decreasing the ℜ₀, which is an affirmation of the effect of non-pharmaceutical intervention to combat the spread of the virus.

11. Discussion and conclusion

Following the estimation of parameter values and data fitting, we simulate the Caputo–Fabrizio fractional monkeypox virus model using the parameter values, as presented in Table 2. The fitted Caputo–Fabrizio curve and ℜ₀ are given in Figure 2. Figures 4, 5 show dynamic behavior for all the nine compartments involved in the proposed Caputo–Fabrizio fractional monkeypox virus model. We observed a significantly high susceptibility and infection in the solution pathways of individual species. The work of Hammouch et al. (52), Bonyah et al. (53), Peter (54), and Sene (55) have provided a strong basis for the discussion of our results. This indicates that, whenever the memory index increases, the rate at which people get infected with monkeypox virus reduces and vice versa, which then indicates that, using fractional order, we can obtain clear qualitative information on monkeypox virus transmission. In Figure 6, we varied the input parameter γ_h on quarantine and exposed, respectively, to observe variation in the system dynamics. We noticed the contribution of this parameter in the transmission pathways of infected individuals. In a similar way, we varied the input parameters δ_h and ψ_h on individual recovery and noticed the variation in the trajectory of monkeypox recovery. We discovered that the rate at which humans and rodents move from exposed to infectious stage is also important and potentially dangerous in terms of increasing the level of monkeypox infection.

FIGURE 4

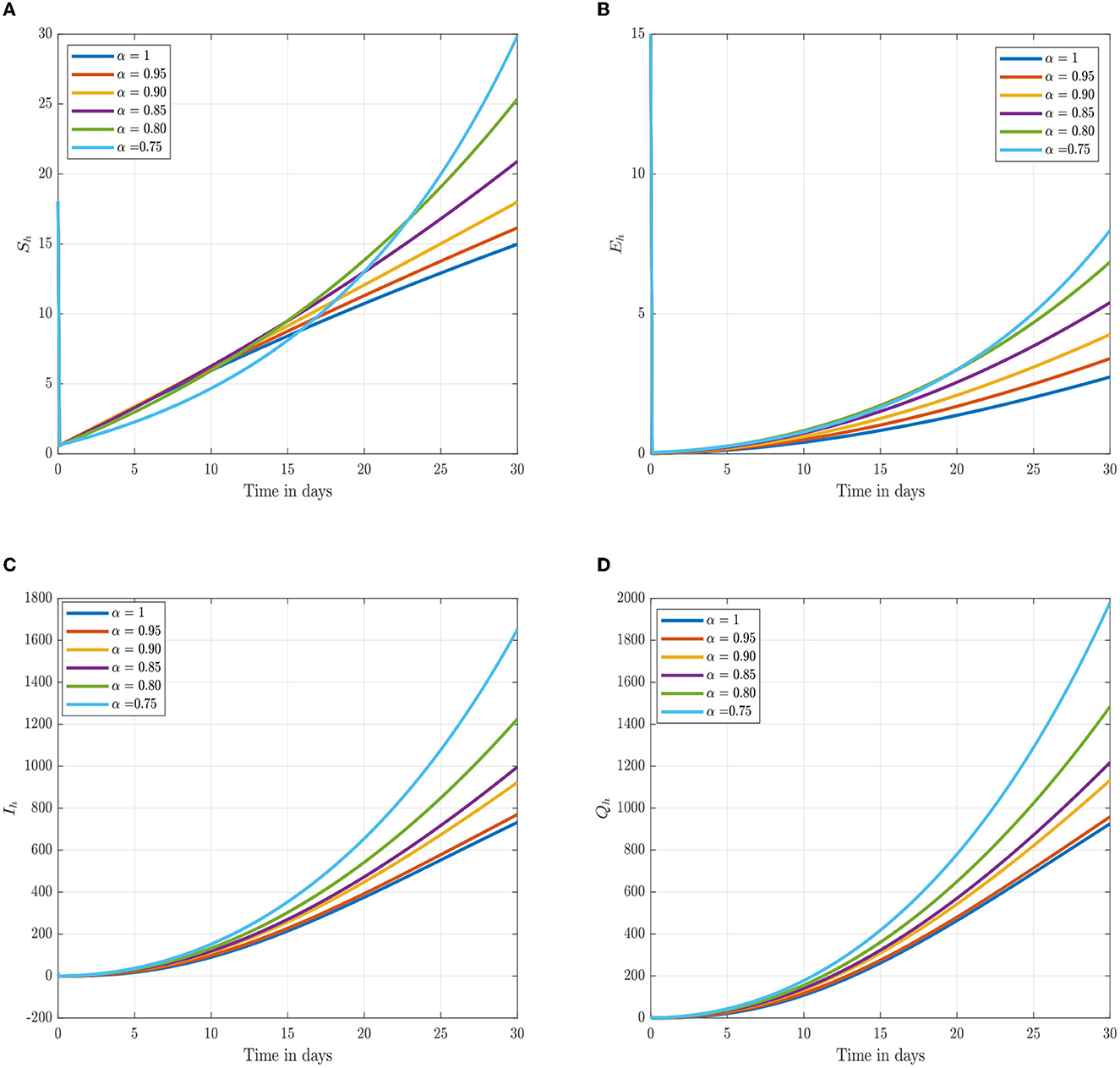
Figure 4. Numerical trajectory of the CF-fractional-order derivative, α, of Equation (2). (A) Dynamics of susceptible (S_h) humans class. (B) Dynamics of expose (E_h) humans class. (C) Dynamics of infected (I_h) humans class. (D) Dynamics of quarantine (Q_h) class.

FIGURE 5

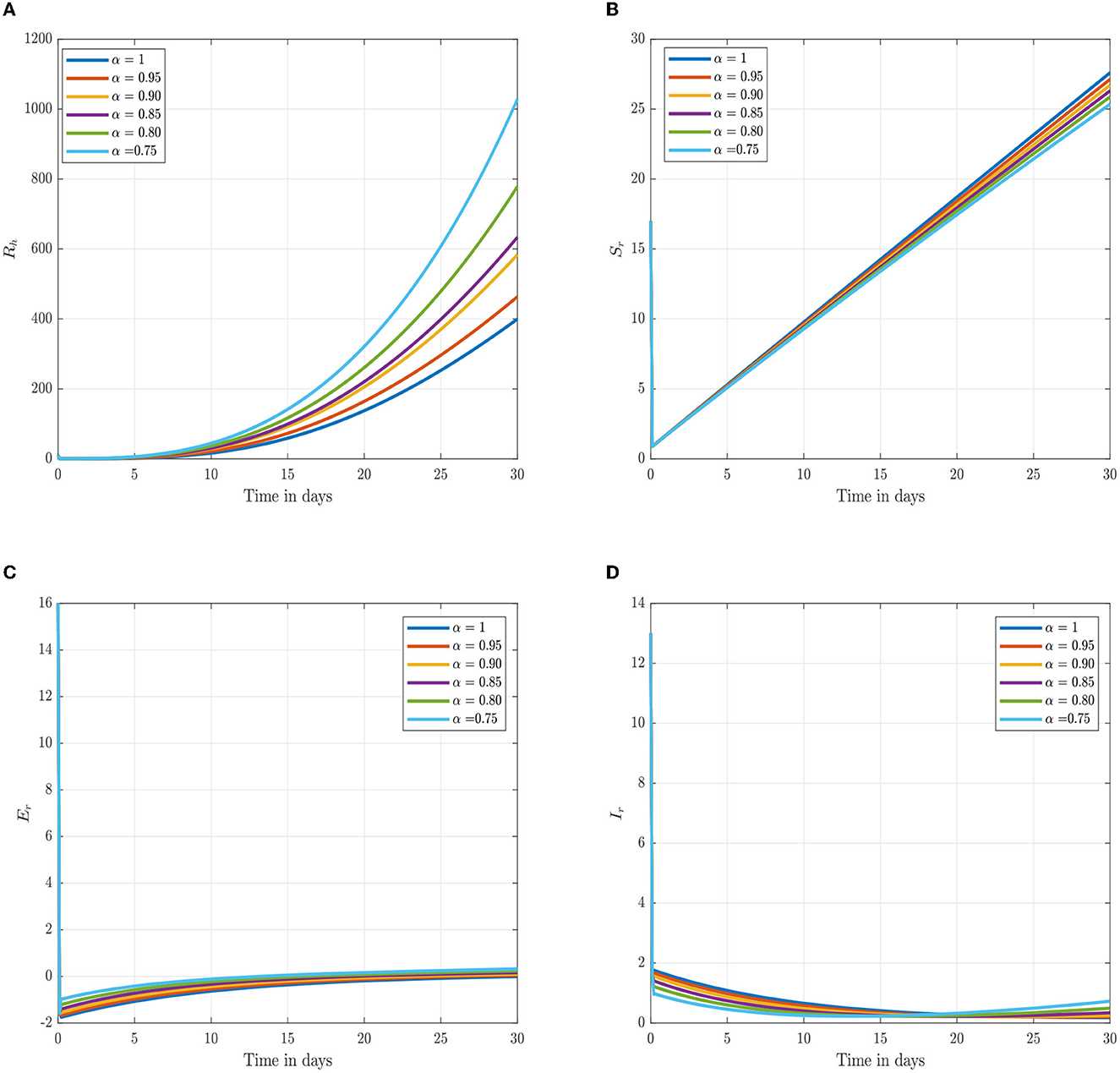
Figure 5. Numerical trajectory of the CF-fractional-order derivative, α, of Equation (2). (A) Dynamics of recovery (R_h) class. (B) Dynamics of susceptible (S_r) rodents class. (C) Dynamics of exposed (E_r) rodents class. (D) Dynamics of asymptomatic infected (I_r) rodents class.

FIGURE 6

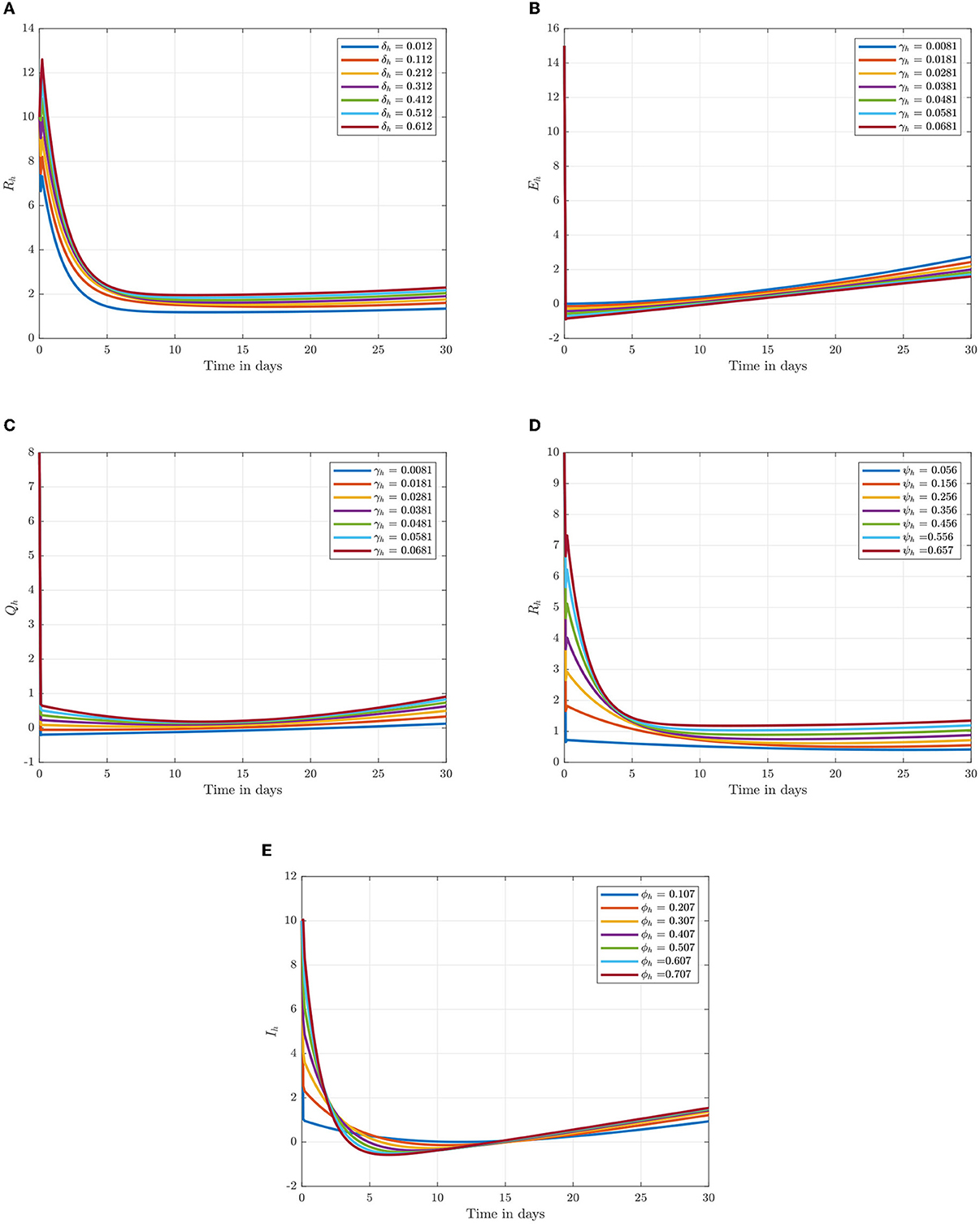
Figure 6. Numerical trajectory of varying δ_h, γ_h, ψ_h, and ϕ_h when α = 0.95. (A) Variation of δ_h on recovery class. (B) Variation of γ_h on expose class. (C) Variation of γ_h on quarantine class. (D) Variation of ψ_h on recovery class. (E) Variation of ϕ_h on infected class.

In conclusion, we provided a brief overview of the monkeypox virus and the dynamics of its transmission in this study. We investigated the spread of monkeypox virus and its effect on non-pharmaceutical intervention, thus quarantine. Positiveness, invariance, boundedness, and equilibrium points of the solutions are thus examined as fundamental features of mathematical models. We considered real data of the monkeypox virus from the United Kingdom, and the best fit curve has been obtained (see Figure 2). As a result, we created a novel, dimensionally consistent Caputo–Fabrizio fractional-order model. Krasnoselskii's fixed point theorem has been used to demonstrate that the system has a solution. The Adams–Bashforth method has been used to display numerical simulations of the suggested pandemic model for various fractional orders and parameter values. We looked into the impact of factors on the expansion and contraction of the quarantine compartment, recovery compartment, and infected compartment on the spread and regression of the pandemic with the use of numerical simulations. As can be inferred from the data, it is clear that the fractional-order equations can help explain this unique effect of the monkeypox. Real-world data can be used to test the accuracy of a mathematical model that has been created. The key challenge, however, is where to find these data and/or how to obtain the right curve for the collected data. The mathematical representation of the monkeypox has been the subject of numerous studies. To the best of our knowledge, there is still no research on fractional modeling that uses actual data on the monkeypox in the United Kingdom. Using actual data on the monkeypox from the United Kingdom, a fractional-order modeling has been shown in this study. The numerical results of this study show that the spread of monkeypox can be stopped if the number of contacts with infected people can be decreased through methods such as effective mass education, improved quarantine facilities, or increased testing of the general population, that is, performing routine tests not only on exposed individuals but also on those who have come into contact with infected patients. As a result, these studies offer other professionals and scientists who focus on infectious diseases insight that may help them in future to control the outbreak of monkeypox and contribute to the development of further treatment options. This study may provide insight into potential future research projects in this regard. Future study of the monkeypox can take into account other fractional operator types, both with and without single kernels. Furthermore, data imputation techniques can be used to fit rodent population parameters from the number of monkeypox disease since the number of rodents cannot be determined.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

KO, EA, and MN: conceptualization. EA, AA, UA, and KO: methodology, software, and formal analysis. EA, UA, and KO: validation, investigation, and visualization. MN and AA: resources. EA, MN, UA, and KO: data curation. EA and KO: writing and original draft preparation, writing, reviewing, and editing. KO and MN: supervision and project administration. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

Authors would like to appreciate the Black in Mathematics Association (BMA) and the Human Sciences Research Council (HSRC) for giving us the platform to collaborate as young researchers to carry out this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Monkeypox Cases Confirmed in England–Latest Updates. UK Health Security Agency (2022). Available online at: https://www.gov.uk/government/news/monkeypox-cases-confirmed-in-england-latest-updates (accessed August 29, 2022).

Google Scholar

2. Multi-country Monkeypox Outbreak: Situation Update. World Health Organization (2022). Available online at: https://www.who.int/emergencies/disease-outbreak-news/item/2022-DON392 (accessed August 10, 2022).

3. Mathieu E, Spooner F, Dattani S, Ritchie H, Roser M. Mpox (monkeypox). Our World Data. (2022). Available online at: https://ourworldindata.org/monkeypox (accessed August 28, 2022).

Google Scholar

4. Public Health Agencies Issue Monkeypox Guidance to Control Transmission. UK Health Security Agency (2022). Available online at: https://www.gov.uk/government/news/public-health-agencies-issue-monkeypox-guidance-to-control-transmission (accessed August 13, 2022).

5. Yinka-Ogunleye A, Aruna O, Dalhat M, Ogoina D, McCollum A, Disu Y, et al. Outbreak of human monkeypox in Nigeria in 2017-18: a clinical and epidemiological report. Lancet Infect Dis. (2019) 19:872–9. doi: 10.1016/S1473-3099(19)30294-4

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Hobson G, Adamson J, Adler H, Firth R, Gould S, Houlihan C, et al. Family cluster of three cases of monkeypox imported from Nigeria to the United Kingdom, May 2021. Euro Surveill. (2021) 26:2100745. doi: 10.2807/1560-7917.ES.2021.26.32.2100745

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Factsheet for Health Professionals on Monkeypox. UK Health Security Agency (2022). Available online at: https://www.ecdc.europa.eu/en/publications-data/data-mpox-monkeypox-cases-eueea (accessed August 27, 2022).

8. Harris E. What to know about monkeypox. JAMA. (2022) 327:2278–9. doi: 10.1001/jama.2022.9499

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Reynolds MG, Doty JB, McCollum AM, Olson VA, Nakazawa Y. Monkeypox re-emergence in Africa: a call to expand the concept and practice of one health. Expert Rev Anti Infect Ther. (2019) 17:129–39. doi: 10.1080/14787210.2019.1567330

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Durski KN, McCollum AM, Nakazawa Y, Petersen BW, Reynolds MG, Briand S, et al. Emergence of monkeypox - West and Central Africa, 1970-2017. MMWR Morb Mortal Wkly Rep. (2018) 67:306–10. doi: 10.15585/mmwr.mm6710a5

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Usman S, Adamu II. Modeling the transmission dynamics of the monkeypox virus infection with treatment and vaccination interventions. J Appl Math Phys. (2017) 5:2335. doi: 10.4236/jamp.2017.512191

CrossRef Full Text | Google Scholar

12. Peter OJ, Madubueze CE, Ojo MM, Oguntolu FA, Ayoola TA. Modeling and optimal control of monkeypox with cost-effective strategies. Model Earth Syst Environ. (2022) 1–19. doi: 10.1007/s40808-022-01607-z

CrossRef Full Text | Google Scholar

13. Samko SG, Kilbas AA, Marichev OI. Fractional Integrals and Derivatives, Theory and Applications. Yverdon: Gordon and Breach (1993).

Google Scholar

14. Katugampola UN. A new approach to generalized fractional derivatives. Bull Math Anal Appl. (2014) 6:1–15. doi: 10.48550/arXiv.1106.0965

CrossRef Full Text | Google Scholar

15. Caputo M, Fabrizio M. A new definition of fractional derivative without singular kernel. Progr Fract Differ Appl. (2015) 1:1–13. doi: 10.18576/pfda/020101

CrossRef Full Text

16. Kumar S, Ahmadian A, Kumar R, Kumar D, Singh J, Baleanu D, et al. An efficient numerical method for fractional SIR epidemic model of infectious disease by using Bernstein wavelets. Mathematics. (2020) 8:558. doi: 10.3390/math8040558

CrossRef Full Text | Google Scholar

17. Higazy M, Alyami MA. New Caputo-Fabrizio fractional order SEIASqEqHR model for COVID-19 epidemic transmission with genetic algorithm based control strategy. Alex Eng J. (2020) 59:4719–36. doi: 10.1016/j.aej.2020.08.034

CrossRef Full Text | Google Scholar

18. Djida JD, Atangana A. More generalized groundwater model with space-time Caputo Fabrizio fractional differentiation. Numer Methods Partial Differ Equ. (2017) 33:1616–27. doi: 10.1002/num.22156

CrossRef Full Text | Google Scholar

19. Baba IA. Existence and uniqueness of a fractional order tuberculosis model. Eur Phys J. (2019) 134:489. doi: 10.1140/epjp/i2019-13009-1

CrossRef Full Text | Google Scholar

20. Owolabi KM, Atangana A. Mathematical modelling and analysis of fractional epidemic models using derivative with exponential kernel. In: Fractional Calculus in Medical and Health Science. London: CRC Press (2020). p. 109–128.

Google Scholar

21. Mohammadi H, Kumar S, Rezapour S, Etemad, S. A theoretical study of the Caputo-Fabrizio fractional modeling for hearing loss due to Mumps virus with optimal control. Chaos Solit Fract. (2021) 144:110668. doi: 10.1016/j.chaos.2021.110668

CrossRef Full Text | Google Scholar

22. Baleanu D, Jajarmi A, Mohammad H, Rezapour S. A new study on the mathematical modelling of human liver with Caputo-Fabrizio fractional derivative. Chaos Solit Fract. (2020) 134:109705. doi: 10.1016/j.chaos.2020.109705

CrossRef Full Text | Google Scholar

23. Wutiphol S, Turab A. Mathematical analysis of an extended SEIR model of COVID-19 using the ABC-Fractional operator. Math Comput Simul. (2022) 198:65–84. doi: 10.1016/j.matcom.2022.02.009

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Asamoah JKK, Okyere E, Yankson E, Opoku AA, Adom-Konadu A, Acheampong E, et al. Non-fractional and fractional mathematical analysis and simulations for Q fever. Chaos Solit Fract. (2022) 156:111821. doi: 10.1016/j.chaos.2022.111821

CrossRef Full Text | Google Scholar

25. Peter OJ, Yusuf A, Ojo MM, Kumar S, Kumari N, Oguntolu FA. A mathematical model analysis of meningitis with treatment and vaccination in fractional derivatives. Int J Appl Comput Math. (2022) 8:117. doi: 10.1007/s40819-022-01317-1

CrossRef Full Text | Google Scholar

26. Peter OJ, Shaikh AS, Ibrahim MO, Nisar KS, Baleanu D, Khan I, et al. Analysis and dynamics of fractional order mathematical model of covid-19 in nigeria using atangana-baleanu operator. Comput Mater Continua. (2021) 66:1823–48. doi: 10.32604/cmc.2020.012314

CrossRef Full Text | Google Scholar

27. Kumar S, Ghosh S, Kumar R, Jleli M. A fractional model for population dynamics of two interacting species by using spectral and hermite wavelets methods. Numer Methods Part Diff Equ. (2020) 37:1652–72. doi: 10.1002/num.22602

CrossRef Full Text | Google Scholar

28. Morales-Delgadoa VF, Gómez-Aguilar JF, Taneco-Hernández MA, Escobar Jiménez RF, Olivares Peregrino VH. Mathematical modeling of the smoking dynamics using fractional differential equations with local and nonlocal kernel. J Nonlinear Sci Appl. (2018) 11:1004–14. doi: 10.22436/jnsa.011.08.06

CrossRef Full Text | Google Scholar

29. Atangana A, Baleanu D. New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. Therm Sci. (2016) 220:763–9. doi: 10.2298/TSCI160111018A

CrossRef Full Text | Google Scholar

30. Atangana A, Gomez-Aguilar JF. A new derivative with normal distribution kernel: theory, methods and applications. Physica A Stat Mech Appl. (2017) 476:1–14. doi: 10.1016/j.physa.2017.02.016

CrossRef Full Text | Google Scholar

31. Zhang L, Addai E, Ackora-Prah J, Arthur YD, Asamoah JKK. F. Fractional-order ebola-malaria coinfection model with a focus on detection and treatment rate Comput Math Methods Med. (2022) 2022:6502598. doi: 10.1155/2022/6502598

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Kumar S, Chauhan RP, Momani S, Hadid S. Numerical investigations on COVID-19 model through singular and non-singular fractional operators. Numer Methods Part Diff Equ. (2020) 2020:1–27. doi: 10.1002/num.22707

CrossRef Full Text | Google Scholar

33. Aslam M, Murtaza R, Abdeljawad T, Rahman, G, Khan A, et al. A fractional order HIV/AIDS epidemic model with Mittag-Leffler kernel. Adv Diff Equ. (2021) 2021:1–5. doi: 10.1186/s13662-021-03340-w

CrossRef Full Text | Google Scholar

34. Evirgen F. Transmission of Nipah virus dynamics under Caputo fractional derivative. J Comput Appl Math. (2023) 419:114654. doi: 10.1016/j.cam.2022.114654

CrossRef Full Text | Google Scholar

35. Ucar S. Analysis of hepatitis B disease with fractal fractional Caputo derivative using real data from Turkey. J Comput Appl Math. (2023) 419:114692. doi: 10.1016/j.cam.2022.114692

CrossRef Full Text | Google Scholar

36. Khan Y, Khan MA, Fatmawati, Faraz N. A fractional bank competition model in Caputo-Fabrizio derivative through newton polynomial approach. Alexandria Eng J. (2021) 60:711–8. doi: 10.1016/j.aej.2020.10.003

CrossRef Full Text | Google Scholar

37. Fatmawati, Khan MA, Alfiniyah C, Alzahrani E. Analysis of dengue model with fractal-fractional Caputo-Fabrizio operator. Adv Diff Equ. (2020) 2020:1–23. doi: 10.1186/s13662-020-02881-w

CrossRef Full Text | Google Scholar

38. Qureshi S, Yusuf A, Shaikh AA, Inc M, Baleanu D. Mathematical modeling for adsorption process of dye removal nonlinear equation using power law and exponentially decaying kernels. Chaos. (2020) 30:043106. doi: 10.1063/1.5121845

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Sher M, Shah K, Khan ZA, Khan H, Khan A. Computational and theoretical modeling of the transmission dynamics of novel COVID-19 under Mittag-Leffler Power Law. Alexandria Eng J. (2020) 59:3133–7. doi: 10.1016/j.aej.2020.07.014

CrossRef Full Text | Google Scholar

40. Addai E, Zhang LL, Preko AK, Asamoah JKK. Fractional order epidemiological model of SARS-CoV-2 dynamism involving Alzheimer's disease. Healthc Analyt. (2022) 2:100114. doi: 10.1016/j.health.2022.100114

CrossRef Full Text | Google Scholar

41. Shaikh AS, Nisar KS. Transmission dynamics of fractional order Typhoid fever model using Caputo-Fabrizio operator. Chaos Solit Fract. (2019) 128:355–65. doi: 10.1016/j.chaos.2019.08.012

CrossRef Full Text | Google Scholar

42. Shah K, Alqudah MA, Jarad F, Abdeljawad T. Semi-analytical study of Pine Wilt Disease model with convex rate under Caputo-Febrizio fractional order derivative. Chaos Solit Fract. (2020) 135:109754. doi: 10.1016/j.chaos.2020.109754

CrossRef Full Text | Google Scholar

43. Ahmed I, Baba IA, Yusuf A, Kumam P, Kumam W. Analysis of Caputo fractional-order model for COVID-19 with lockdown. Adv Differ Equ. (2020) 2020:110007. doi: 10.1186/s13662-020-02853-0

PubMed Abstract | CrossRef Full Text

44. Ullah S, Khan MA, Farooq M, Hammouch Z, Baleanu D. A fractional model for the dynamics of tuberculosis infection using Caputo-Fabrizio derivative. Discrete Cont Dyn Syst. (2020) 13:975–93. doi: 10.3934/dcdss.2020057

CrossRef Full Text | Google Scholar

45. Abboubakar H, Kumar P, Rangaig NA, Kumar S. A malaria model with Caputo-Fabrizio and Atangana-Baleanu derivatives. Int J Mod Simul Sci Comput. (2021) 12:2150013. doi: 10.1142/S1793962321500136

CrossRef Full Text | Google Scholar

46. Peter OJ, Oguntolu FA, Ojo MM, Oyeniyi AO, Jan R, Khan I. Fractional order mathematical model of monkeypox transmission dynamics. Phys Script. (2022) 97:084005. doi: 10.1088/1402-4896/ac7ebc

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Peter OJ, Kumar S, Kumari N, Oguntolu FA, Oshinubi K, Musa R. Transmission dynamics of Monkeypox virus: a mathematical modelling approach. Model Earth Syst Environ. (2022) 8:3423–34. doi: 10.1007/s40808-021-01313-2

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Tilahuna GT, Woldegerimab WA, Mohammed N. A fractional order model for transmission dynamics of hepatitis B virus with two-age structure in the presence of vaccination. Arab J Basic Appl Sci. (2022) 28:87–106. doi: 10.1080/25765299.2021.1896423

CrossRef Full Text | Google Scholar

49. Lin W. Global existence theory and chaos control of fractional differential equations. J Math Anal Appl. (2007) 332:709726. doi: 10.1016/j.jmaa.2006.10.040

CrossRef Full Text | Google Scholar

50. Atangana A, Owolabi KM. New numerical approach for fractional differential equations. Math Model Nat Phenom. (2018) 13:3. doi: 10.1051/mmnp/2018010

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Borgonovo E, Plischke E. Sensitivity analysis: a review of recent advances. Eur J Oper Res. (2016) 248:869–87. doi: 10.1016/j.ejor.2015.06.032

CrossRef Full Text | Google Scholar

52. Hammouch Z, Yavuz M, Özdemir N. Numerical solutions and synchronization of avariable-order fractional chaotic system. Math Model Numer Simul Appl. (2021) 1:11–23. doi: 10.53391/mmnsa.2021.01.002

CrossRef Full Text | Google Scholar

53. Bonyah E, Juga M, Fatmawati. Fractional dynamics of coronavirus with comorbidity via Caputo-Fabrizio derivative. Commun Math Biol Neurosci. (2022) 2022:12.

Google Scholar

54. Peter OJ. Transmission dynamics of fractional order brucellosis model using Caputo-Fabrizio operator. Int J Differ Equ. (2020) 2020:2791380. doi: 10.1155/2020/2791380

CrossRef Full Text | Google Scholar

55. Sene N. Theory and applications of new fractional-order chaotic systemunder Caputo operator. Int J Opt Cont Theor Appl. (2022)1:20–38. doi: 10.11121/ijocta.2022.1108

CrossRef Full Text | Google Scholar