Progress in biological age research

Biological age (BA) is a common model to evaluate the function of aging individuals as it may provide a more accurate measure of the extent of human aging than chronological age (CA). Biological age is influenced by the used biomarkers and standards in selected aging biomarkers and the statistical method to construct BA. Traditional used BA estimation approaches include multiple linear regression (MLR), principal component analysis (PCA), Klemera and Doubal’s method (KDM), and, in recent years, deep learning methods. This review summarizes the markers for each organ/system used to construct biological age and published literature using methods in BA research. Future research needs to explore the new aging markers and the standard in select markers and new methods in building BA models.

Introduction

Aging is accompanied by a progressive decline in physiological functions and an accumulation of damage to the body, leading to an increased risk of morbidity and mortality (1). Based on birth date, chronological age (CA) is the traditional criterion for assessing aging. However, the degree of aging may vary significantly between individuals with the same CA (2). Therefore, CA is not the best indicator for evaluating the degree of aging in human individuals.

To seek a better index to assess the degree of aging of individuals, biological age (BA) (3, 4) are used as alternatives to CA to estimate aging status. BA is the most popularly used model. Aging markers are the basis for constructing biological age, in this article we summarize the markers used in constructing biological age. There are many ways to classify markers of aging, e.g., the aging markers can classify into two categories: histology-based data (DNA methylation, metabolomics, proteomics, etc.), and clinical biomarkers obtained from blood chemistry, hematology, anthropometry, and organ function test measurements (5, 6). The “aging clock” developed from omics data is another form of biological age, multiple omics data can be combined to build the clock (7). Until now, omics data have rarely been used in the construction of BA because of the high cost of its application in large-scale populations. Previously built BA models commonly choose aging biomarkers in multiple organs/systems, such as blood biomarkers (8, 9), genetic indicators (10), and physical activity data (11, 12). Biomarkers from diverse organs are more reflective of the overall body state. To build the BA model, these biomarkers apply different model building methods like multiple linear regression (MLR) (13, 14), principal component analysis (PCA) (15, 16), Klemera and Doubal’s method (KDM) (3, 17), deep learning (8, 12), and other methods.

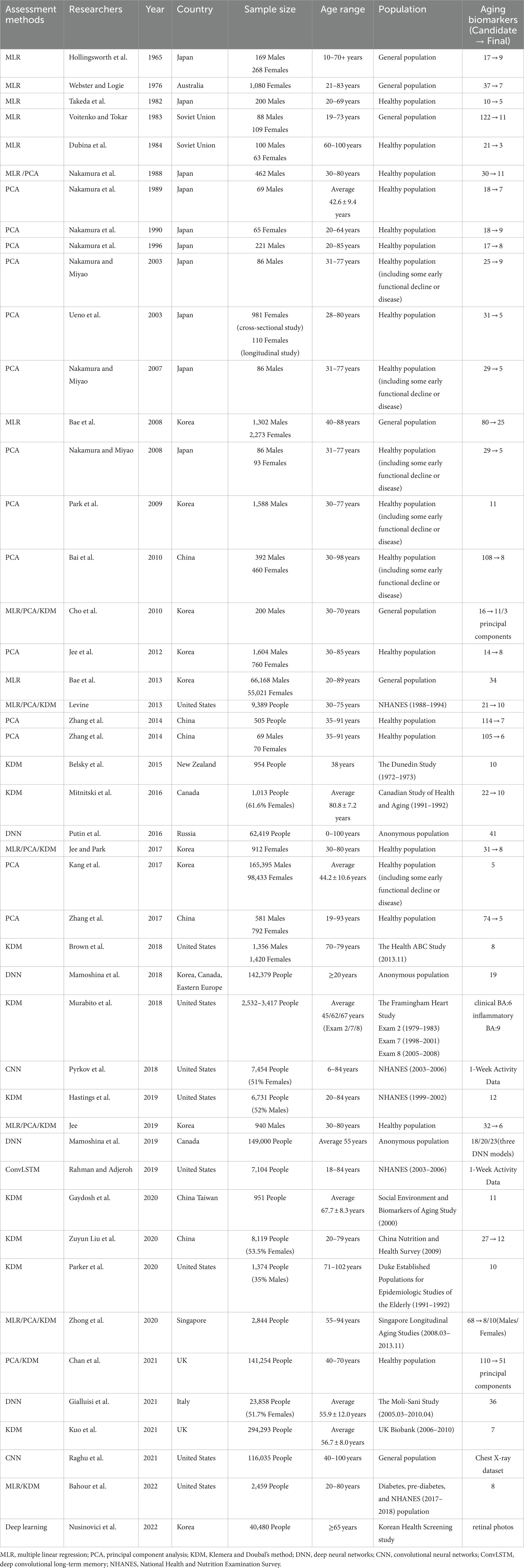
Previous studies have focused on the construction of BA models using different methods, but fewer studies have compared the BA models constructed by these methods, especially the advantages and disadvantages between deep learning and traditional methods. This review focuses on BA models constructed by four common approaches, namely composite or combined biomarkers that include a lot of aging markers. A more accurate biological age can only be constructed on the basis of knowing the advantages and disadvantages of existing methods. Table 1 provides a review of the more important, influential, and newly published literature with the four approaches above (3, 4, 8–16, 18–51), including cross-sectional and longitudinal studies.

TABLE 1

Table 1. The basic information of BA models in different populations.

Selection of aging biomarkers

Candidate biomarkers

The candidate biomarkers are a crucial factor to determine the final selected aging biomarkers. The most frequently used candidate biomarkers are routine clinical tests. These include age, sex, blood pressure, respiratory rate, pulse, heart rate, routine blood tests, blood biochemistry, routine urine tests, lung function, endocrine hormones (27, 34), and inflammatory factors (3, 38). Several metrics can be used to evaluate the same organ, and the best one is generally picked. For example, urea nitrogen (BUN), blood creatinine, and cystatin C (CYSC) are relevant to renal function. CYSC is a more sensitive marker of the endogenous glomerular filtration rate than blood creatinine (52). It has proven to be more suitable for BA models than blood creatinine and BUN (16, 30). Changes in body morphology (27, 29, 40) reflect the growth and nutritional statuses of the target population, such as waist circumference (WC), waist-to-hip ratio, waist-to-height ratio (WHtR), body mass index, and body fat. Abdominal obesity can occur in older adults with increased abdominal fat accumulation. Studies have shown that WHtR and WC are good indices to identify obesity in the elderly (53). Cognitive tests (4, 22, 45) are available to examine brain function, such as the trail making test, the digit symbol test, and the mini-mental state examination. Sensory tests (15, 29, 54), such as hearing, visual acuity, and vibration perception, are relatively less applied due to the cumbersome and specialist nature of the measurement process. Some parameters reflecting physical exercise capacities, such as grip strength (13) and vertical jump (31), are not only valuable for the BA model. They have also been used to structure physical (fitness) age (18, 19, 21) to assess aging. Imaging indices, such as cardiac and carotid ultrasound, are suitable biomarkers of aging for estimating BA (10, 16).

Aging is not a single process but is rather governed by a comprehensive range of factors, including disease, environment, lifestyle habits, and genetics. Health status, work experience, lifestyle, and dietary habits are often obtained through questionnaires (4, 22). Some genetic indicators are also taken as candidate aging biomarkers in the BA model, such as single nucleotide polymorphisms and terminal telomere restriction fragments (TRF). Nevertheless, probably because of its high detection cost in the population, genetic indicators are less applied in biological age. Zhang et al. (16) investigated polymorphic loci on P16, Sirt1, IL6, and Klotho genes associated with aging. Limited by the size of the sample population and the genes tested, the genes could not be used in BA models. TRF length is considered a genetic biomarker of aging at the cellular level (55), reflecting the dynamic aging process (56). TRF was found to be a promising aging biomarker in healthy aging populations (10).

Selection criteria for aging biomarkers

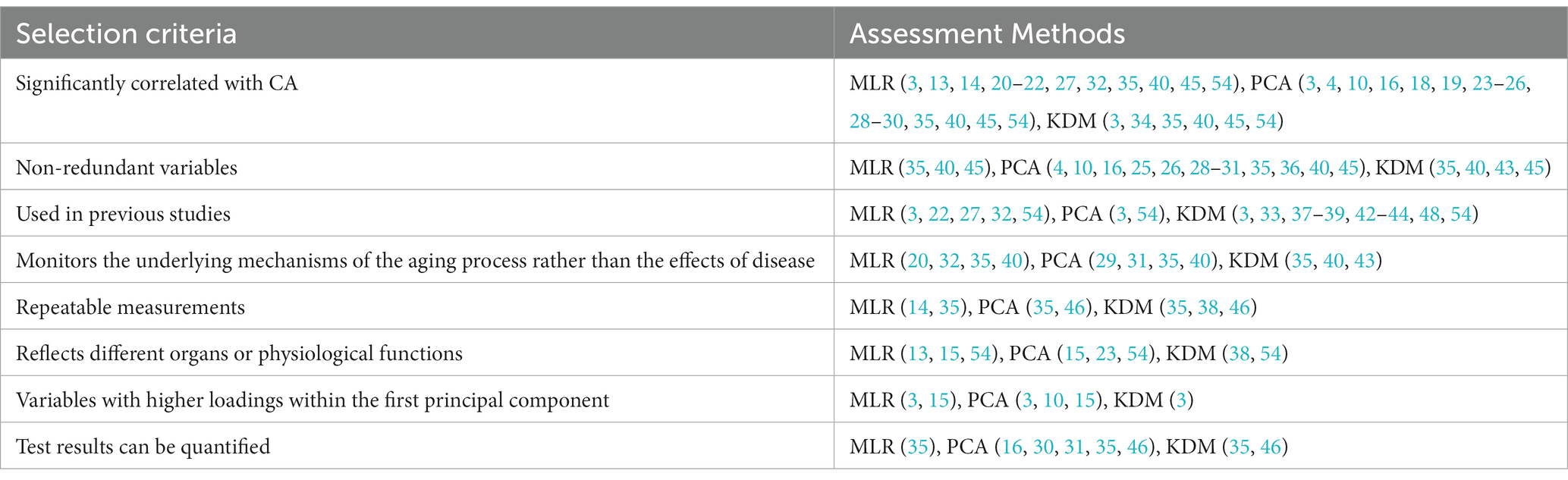
Researchers or organizations in the field of aging have proposed criteria for selecting aging biomarkers, such as Butler et al. (57) and the American Federation for Aging Research (58), but no consensus has been reached. There are also some commonalities between the criteria, including aging biomarkers that predict age-related body functions, low or noninvasive assays, and high reproducibility (55). Costa and McCrae concluded that generic biomarkers of aging explain most of the changes that occur with increasing age (59, 60). This is similar to the criterion, proposed by Butler et al. (57), that aging biomarkers change with CA. An interesting question is if aging biomarkers can be selected according to their correlation with CA. First, it is associated with the method of estimating BA. When using MLR, PCA, and KDM methods, the initial step is to calculate the correlation between biomarkers and CA. This process is replaced by automatic machine learning in deep learning methods, which have a series of complex algorithms. Second, consider experiments that discovered biomarkers of aging and empirically found various physiological, biochemical, and imaging indicators that significantly correlate with age or analyzed age correlations from extensive data obtained from multiomics (2). In contrast, the selection of aging biomarkers in studies oriented to aging mechanisms is based on a hypothesis about the causes of aging (2). Finally, some investigators (61, 62) have given the more reasonable view that this correlation is not a reasonable criterion for selecting, validating, or weighting aging biomarkers, and some biomarkers moderately associated with CA may be utterly unrelated to aging. It follows that the correlation of aging biomarkers with CA is not equivalent to a causal relationship between aging biomarkers and senescence simply because there is no better alternative to correlation for screening markers. We summarized the standard selection criteria for aging biomarkers in the BA model (Table 2), including those significantly correlated with CA; nonredundant variables; monitoring the underlying mechanisms of the aging process rather than the effects of disease; repeatable measurements; reflecting different organ or physiological functions; and biomarkers used in previous studies.

TABLE 2

Table 2. The selection criteria for aging biomarkers among MLR, PCA, and KDM.

Final selected aging biomarkers

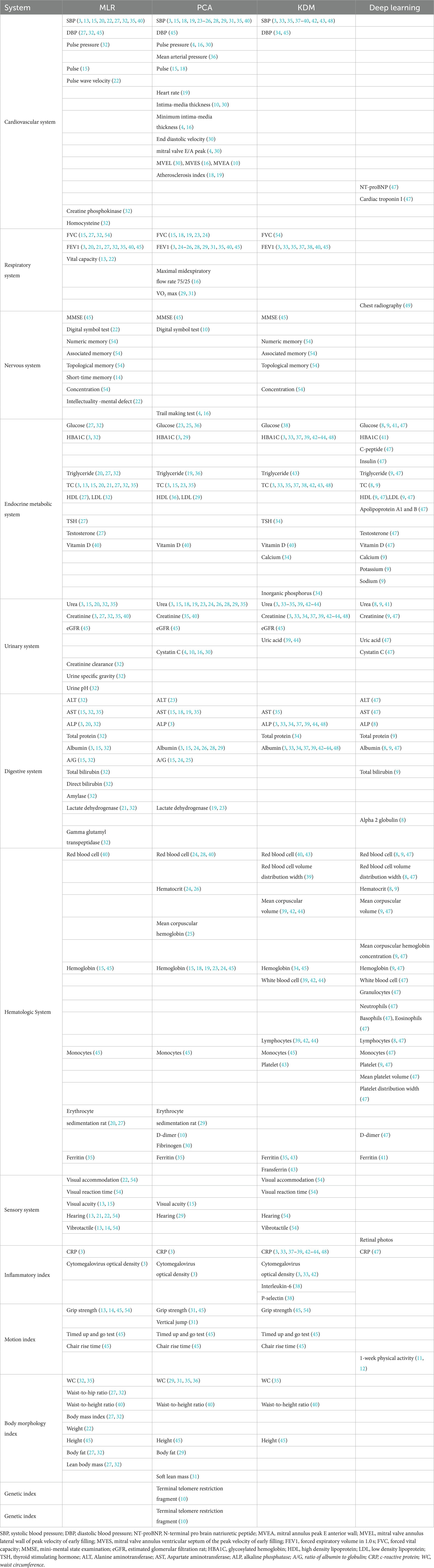
It is critical to select the correct number of representative aging biomarkers to evaluate BA. The aging biomarkers of BA models in different systems are summarized in Table 3. In analyzing the differences in the final selection of aging biomarkers by different investigators, the preference is related to the study population. Some researchers (16, 18) choose all subjects to be healthy or almost healthy to exclude the effects of disease. There were also studies (31, 36) in which people in the early stages of adisease were included. In addition, the sample size, gender composition, age, and ethnicity of the study population can also impact the results. Moreover, BA models for specific populations, such as the elderly (37, 44) and the young (33), offer the possibility to explore aging differences between individuals within the same age group and potential clinical applications. Second, the choice is associated with candidate aging biomarkers; candidate biomarkers and investigators’ research directions and perceptions have a significant impact. Then, the choice of biomarkers is related to the selection criteria. The thresholds for correlation selection varied across trials. In recent years, some investigators (42, 44) building BA models referred to previously published biomarkers of aging, which are generally screened in large populations, used by others and have good reliability. Examples include the 10 biomarkers of aging that Levine initially selected in the third National Health and Nutrition Examination Survey (NHANES) population and the nine biomarkers of aging that were subsequently acquired through machine learning (3, 63). Finally, the selection is affected by the BA assessment approach. The MLR and PCA select aging biomarkers that correlate linearly with CA, and the KDM can be used in the nonlinear case of aging biomarkers (17). On the other hand, deep learning also answers whether candidate aging biomarkers can be selected through powerful fitting capabilities. One example is that chest radiographs, which researchers once discarded because they could not be quantified, have recently been used to construct BA models (49). Briefly, the final selection of aging biomarkers by research staff affected the study population, the candidate aging biomarkers, the selection criteria, and the method of BA evaluation.

TABLE 3

Table 3. The common aging biomarkers of four methods in different systems.

Biological age assessment method

Multiple linear regression

Hollingsworth et al. (13) selected nine age-related indicators of physiological function and innovatively used MLR to predict BA in the Japanese Hiroshima population. This approach has since been widely used. The independent variable was selected according to the correlation between biomarkers and CA, and the individual’s BA was used as the dependent variable to establish the MLR equation:

$\begin{array}{ll}B{A}_i=b_0+{\displaystyle \sum }_{j=1}^m{b}_j{x}_{ji}& (1)\end{array}$

In Eq. (1), m is the number of aging biomarkers, and $x_{ji}$ (i = 1...n, j = 1...m) represents the jth aging biomarker of the ith individual (54). Moreover, b₀ and b_j are the intercept and regression coefficients, respectively, calculated by the least-squares method. The BA model constructed using the MLR requires an F test for the significance of the regression equation, a t test for the significance of variables, and a goodness-of-fit test for how well the model fits the variables.

MLR has collinearity problems (54, 62), which can be diagnosed by the variance expansion factor method and characteristic root determination method, eliminating some unimportant independent variables and increasing the sample size to eliminate collinearity. MLR fails to avoid the biomarker paradox, where biomarkers perfectly associated with CA are insensitive in individuals (54). In addition, the BA values calculated by MLR are distorted at both ends of the regression equation (54, 62). Dubine et al. (14) proposed using the Z score to solve this problem. The equation for the Z score corrected BA equation is as follows:

$\begin{array}{ll}CorrectedBA=B{A}_i+Z& (2)\end{array}$

Here, Z = (CA_i-MEAN_CA) × (1-b), where CA_i is the chronological age of the individual, MEAN_CA is the average chronological age of the population in which the individual is located, and b is the slope in the simple linear regression, representing the relationship between BA and CA.

Principal component analysis

PCA was first used by Nakamura et al. (15) to estimate BA in Japanese populations, subsequently becoming popular in Korea, China, and other countries (3, 16, 29, 30). Our team was the first to utilize PCA to evaluate BA in healthy populations in China (30). For nearly 20 years, we have structured BA models based on data from single-centered and multicentered populations, finding that aging biomarkers such as CYSC and carotid intima-media thickness were closely associated with aging in the Chinese population (4, 10, 16, 30).

The steps of building a BA model by PCA are summarized as follows: (1) select aging biomarkers by correlation analysis, stability analysis, and redundancy analysis (64); (2) convert potentially relevant aging biomarkers into linearly uncorrelated principal components by orthogonal transformation; and (3) select the first principal component or multiple principal components to create the formula for predicting BA. When the PCA selects only the first principal component, the critical aging biomarkers can be further screened by principal component loading (3). The colinearity problem can be avoided if multiple principal components are selected as new variables (54). Both approaches have their advantages. The biological age score (BAS) formula constructed by selecting the first principal component as an example is as follows:

$\begin{array}{ll}BAS=a_1{X}_1^{\prime }+a_2{X}_2^{\prime }+\dots +a_n{X}_n^{\prime }& (3)\end{array}$

Here, X’ is the standardized biomarker of aging, a_n is the score coefficient of aging biomarkers, where X’ is computed from the equation $\frac{X-MEAN\left(X\right)}{SD\left(X\right)}$ and MEAN(X) and SD(X) are the mean and standard deviation of the aging biomarkers, respectively. Because the BAS is not measured in years, Nakamura et al. (15) used the T-score to convert BAS to BA:

$\begin{array}{ll}BA=BAS\times S{D}_{CA}+MEA{N}_{CA}& (4)\end{array}$

In Equation (4), SD_CA and MEAN_CA are the variance and mean of the chronological age of subjects, respectively. Similar to the MLR method, to avoid regression of BA values toward the mean age of the sample, the Z score was used to correct BA (10, 16), as in Formula (2).

Klemera and Doubal’s method

KDM was first proposed by Klemera and Doubal (17) in 2006 and is now broadly available for aging and aging-related research. The KDM formula development process incorporates certain core hypotheses (17): (1) The hypothesis is that “the difference in BA is the difference among individuals aging in the same CA population.” A random variable $R_{BA}\left(0;S_{BA}^2\right)$ with mean 0 and variance $S_{BA}^2$ was used to replace the differences in individual BA, establishing the formula:

$\begin{array}{ll}BA=CA+R_{BA}\left(0;S_{BA}^2\right)& (5)\end{array}$

(2) Another hypothesis is that “the actual value of aging biomarker X is not only regulated by BA but also influenced by transient effects that are not BA dependent” (17). A random variable $R_X\left(0;S_X^2\right)$ with mean 0 and variance $S_X^2$ is used to represent the transient effect. An inverse regression equation similar to the Hochschild (65) view is obtained:

$\begin{array}{ll}X=F_X\left(BA\right)+R_X\left(0;S_X^2\right)& (6)\end{array}$

Here,$F_X\left(BA\right)$ is considered a simple linear equation with independent variable BA, intercept q, and slope k. Subsequently, Klemera and Doubal developed two formulations, shown in Eqs (7) and (8), for calculating BA through sophisticated mathematical derivations, the distinction being the inclusion of CA as an independent variable in Eq. (8) (17).

$\begin{array}{ll}B{A}_E=\frac{{{\displaystyle \sum }}_{j=1}^m\left(x_j-q_j\right)\left(\frac{k_j}{s_j^2}\right)}{{{\displaystyle \sum }}_{j=1}^m{\left(\frac{k_j}{s_j}\right)}^2}& (7)\end{array}$

$\begin{array}{ll}B{A}_{EC}=\frac{{{\displaystyle \sum }}_{j=1}^m\left(x_j-q_j\right)\left(\frac{k_j}{s_j^2}\right)+\frac{CA}{S_{BA}^2}}{{{\displaystyle \sum }}_{j=1}^m{\left(\frac{k_j}{s_j}\right)}^2+\frac{1}{S_{BA}^2}}& (8)\end{array}$

where $x_j$, $q_j$, $k_j$, and $s_j^2$ (j = 1...m) represent the jth aging biomarker and its intercept, slope, and transient effect, respectively. The detailed derivation process is available in their paper. Cho et al. (54) improved the algorithm of KDM to simplify the computing flow. In the KDM2 model they developed, PCA was introduced, and multiple sets of principal components were selected instead of the original aging biomarkers (54). Levine (3) used the modified method that combined PCA to construct the KDM2 model, with the difference being that they selected the key aging biomarkers within the first principal component. In addition, the Δage (Δage = BA-CA) was determined by the KDM method and is more practical than calculating the BA of an individual (34). Recently Kwon and Belsky developed an R package containing the KDM method: BioAge, for facilitating biological age measurement (66).

Deep learning

Deep learning is a subfield of machine learning, where good features can be learned automatically using a general-purpose learning procedure (67). Deep neural networks (DNNs) (8, 9, 41, 47), convolutional neural networks (CNNs) (11, 49), and recurrent neural networks (RNNs) (12) have been employed to build BA models in recent years.

A DNN consists of an input layer that receives external data, several hidden layers responsible for feature extraction, and an output layer that outputs the final result. Round-by-round iterations are performed with activation functions (68), gradient descent (69), and backpropagation algorithms to transform the input data into results for solving regression or classification problems. In 2016, Putin et al. constructed a model for predicting BA using a DNN, which is placed at www.aging.ai for public usage; the BA can be estimated by entering the complete 41 blood markers or just the most crucial 10 markers (8). The model performed poorly in non-Eastern European populations due to population differences (70). Mamoshina et al. trained a DNN with a dataset containing ethnically diverse populations to enhance accuracy in computing BA in Canadian, Korean, and Eastern European populations (9). More recently, Gialluisi et al. created a DNN based on 36 circulating biomarkers to estimate BA in Italians (47). It is worth considering that suitable approaches should be explored in deep learning to clarify the weight and importance ranking of individual aging biomarkers to assess their importance. Permutation feature importance (PFI) is an algorithm derived from the random forest that explains the importance of aging biomarkers in DNNs (8, 9). To explore the effect of smoking on BA, Mamoshina et al. used PFI to rank biomarkers and selected the top-ranked biomarkers to construct three DNNs and found that smoking accelerates aging (41).

Used chiefly for image analysis, CNNs are mainly composed of convolutional and pooling layers with features such as local connectivity and weight sharing, simplifying the number of parameters and the complexity of calculations (67). The convolutional layer converts the input information into an output feature map with multiple feature mappings employing a specific number of filters. The pooling layer is intended to reduce the information output from the convolution layer. It is executed immediately after the convolution, completed by the maximum, minimum, or average value of operations. Pyrkov et al. selected physical activity data recorded by wearable devices of NHANES participants for 1 week as a biomarker of aging and generated a BA model with a CNN (11). Raghu et al. built a BA model using chest radiograph data combined with a CNN (49).

RNNs are designed with a loop/repeat structure to preserve valuable historical information in sequences through “state vectors” to better process sequence data. RNNs suffer from long-term dependency problems (71) such as vanishing or exploding gradient when learning on long sequences. Hochreiter and Schmidhuber (72) proposed the long short-term memory network (LSTM) to solve this problem, adding the cell state unit and the gate unit based on the ordinary RNN. Thus, LSTM can handle short-term information sensitively and remember valuable information for a long time, which improves the network’s learning ability. Rahman and Adjeroh (12) also used physical activity data from 1 week. Considering the temporal information contained in the data, they adopted a deep convolutional long-term memory (ConvLSTM) method to develop a BA model that outperformed other deep learning approaches (12).

Other methods

In addition to the four popular methods mentioned above, some researchers have tried to find the best model to assess BA, starting from the aspect of the impact of aging markers on life expectancy. Hochschild (62, 65, 73) suggested a nonstandard, complex, but reasonable approach to estimating BA. Taking a questionnaire format, he collected mortality risk factors, such as smoking, diet, and exercise, and aggregated these indicators into a “composite validation variable (CVV).” The standardized biological age was then calculated by the correlation coefficient between CVV and aging markers and finally transformed into BA in years. Some studies used correlations with mortality to identify aging variables. Twelve clinical indicators associated with mortality were selected by Drewelies et al. and validated in two independent birth cohorts (74). Levin and coworkers (63, 75) determined the “phenotypic age” through a multifactorial analysis of mortality risk, an algorithm known to some researchers (39, 44) as “LM BA.” First, nine aging biomarkers associated with mortality were selected with machine learning. Then, two Gompertz proportional hazards models were developed to predict the mortality risk, called the “mortality score,” and converted to biological age values. In addition, Pyrkov et al. constructed BA models to predict both CA and life expectancy, further discussing the relative performance of the models in stratifying the effects of diseases and lifestyles (11). However, these approaches are not widely used for two main reasons: one, a mortality event is required to calculate the aging rate, which is a lengthy process for the follow-up of a normally aging population; second, even if death occurs, many cannot distinguish whether it is due to death from disease or natural death from aging.

Comparison of the four assessment methods

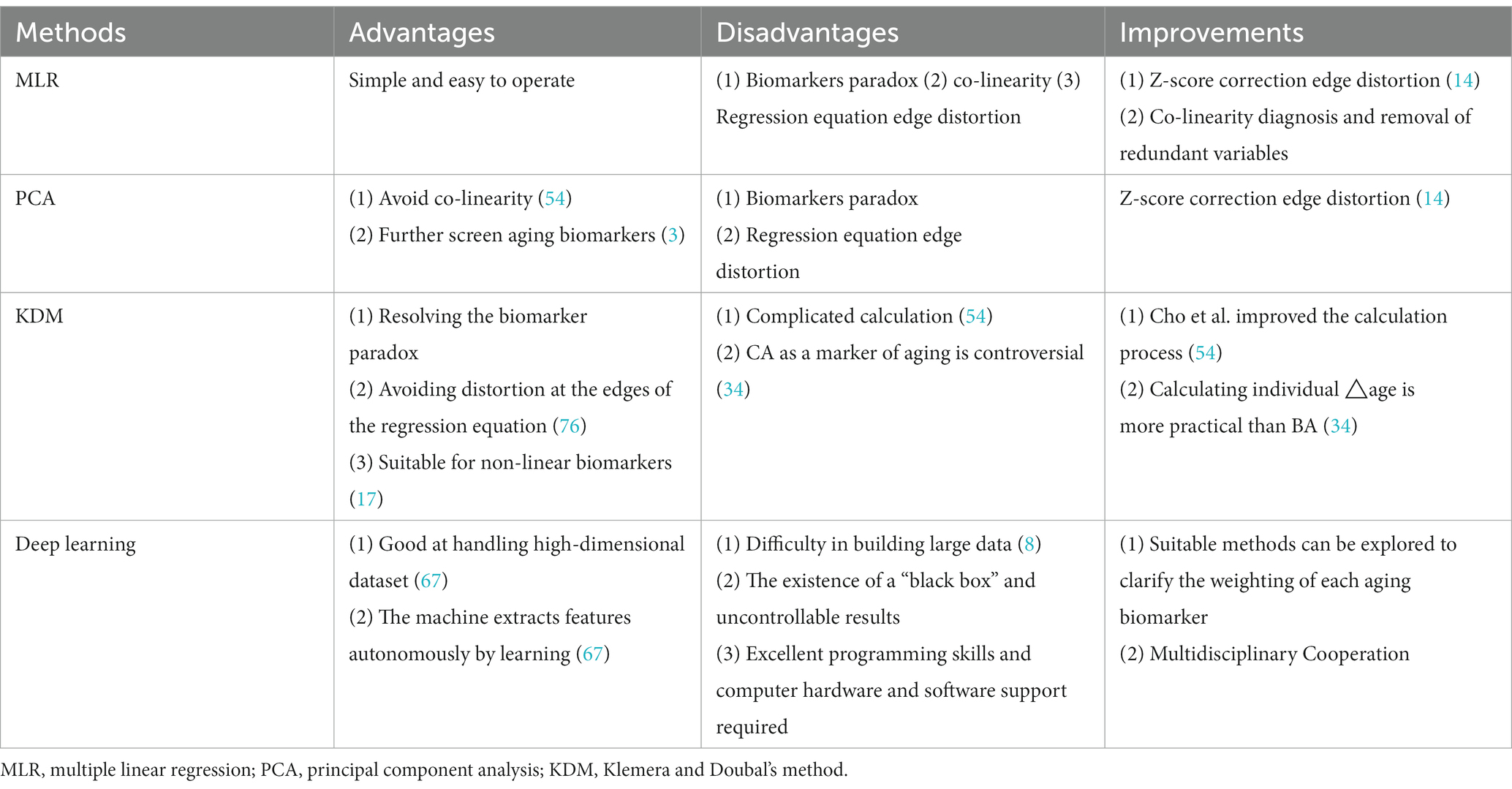
There is no perfect way to evaluate BA. Each researcher should select the proper approach according to the study’s purpose, sample population, laboratory conditions, funding, statistical knowledge, and programming ability. A summary of the strengths, limitations, and possible practical improvements of the four BA assessment methods is presented in Table 4. MLR is the simplest way to measure BA but suffers from the biomarker paradox, edge distortion, and colinearity (54). “collinearity” refers to linear regression in which the accuracy of the model may be affected by the presence of highly correlated relationships among the independent variables, and “edge distortion” refers to distortion at both ends of the linear regression, where the estimated BA values are too large or too small. PCA can further screen aging biomarkers or solve the covariance problem. However, PCA selects aging markers based on correlation with CA and cannot settle the paradox of biomarkers. KDM uses a reverse regression equation that solves the biological paradox (65) and avoids distortion at both ends of the regression equation (76). The KDM2 model combined with PCA allows for a better valuation of mortality (3). Although BA_EC is superior to BA_E in predicting BA, assigning CA a similar role to other biomarkers would be controversial, as proposed by Klemera and Doubal (17). Mitnitski et al. (34) argued that CA is made an independent variable to avoid extreme values (to prevent BA from being overcalculated, e.g., 120 years) at the expense of BA clarity. Deep learning allows machines to extract features and construct BA models autonomously by learning about biomarkers. Their strengths include the ability to handle high-dimensional datasets with complex interactions and correlations to resolve problems that people do not fully understand. However, it is challenging to structure large datasets (8), and there is a “black box” in deep learning, where the specific learning process is unknown, and the results are uncontrollable.

TABLE 4

Table 4. The advantages and disadvantages of the four methods and possible effective improvements.

Performance evaluation of biological age

Currently constructed BA models are mainly used to Predict the occurrence of disease or predict life expectancy. Their performance evaluation metrics, such as R (2), reflect the superiority of the training model by the degree of fit between the estimated BA and the actual CA, however, the nonlinear fitting strategy in machine learning can cause R² to suffer from overfitting problems. In contrast, Δage is superior, which response to the acceleration of biological age. The validity of the model was recently confirmed by Li and Zhang et al. who trained the BA model using a healthy Beijing population and later validated the acceleration of aging by disease in a diseased population (77). However, the value of ∆age may only serve a qualitative purpose, as relative acceleration or retardation of aging compared to a healthy population with the same CA. Some researchers have checked the efficacy of BA models through mortality (78). The introduction of a BA model with mortality training is similar to the inclusion of endpoint events in clinical trials. On the one hand, the incorporated life-length data may improve the accuracy of BA models more than the iteration of statistical methods alone; on the other hand, the exploration of endpoint mortality events may be more likely to generate public interest in BA. However, some emergencies or sudden events may affect the accuracy of biological age judgment.

Summary and prospects

BA is an integral part of the aging field. Only by accurately evaluating the individualized aging status, prompting an earlier window of aging prevention, and timely intervention for disease-prone and diseased individuals can we improve the quality of life of the elderly and prolong their lifespan (79). We investigated the selection and assessment methods of aging biomarkers in BA. Although researchers in aging have identified some aging biomarkers, due to the continuous application of new technologies, new ideas, and new groups of people, there are still many potentially better biomarkers waiting to be discovered. For example, with the increasing availability of longitudinal biological data, the organic state recovery time (resilience) has been found to be an important marker of aging, which cannot be obtained from cross-sectional data (80, 81). Moreover, the development of sequencing omics and image acquisition has provided a direction for exploring new aging biomarkers.

This review focuses on statistical methods for quantifying BA, discusses the advantages and disadvantages of different statistical methods, summarizes the different kinds of aging markers applied in biological age, also mentioned the selection criteria of aging markers. It compares traditional methods and new deep learning methods in BA research and helps clarify how to construct a more accurate new biological age. Of course, this paper has the following shortcomings: on the one hand, candidate markers and selected markers are different for each article, it cannot reflect the importance of each marker by the frequency of aging markers use; on the other hand, only a brief discussion on the performance aspects of statistical methods is made in this paper, and longitudinal or mortality verification is less; Third, there are few studies using the same population to compare the pros and cons of different methods, and more are theoretically compared. We suggest that, regarding the selection of aging markers, it is necessary to focus on both the discovery of new aging markers and the reassessment of the role of old aging markers. It is very important to develop standardized or equivalent screening criteria for aging markers. The new method is more accurate but requires a larger amount of data, and it is easy to overfit if the amount of data is small, so it is not the latest that is the best, but the right one is the best. Common BA evaluation methods have their own merits and demerits and are continuously optimized in practice. The combined use of multiple methods may yield superior results and facilitate the creation of new methods. Biological age is mostly constructed in healthy or community populations to avoid the influence of disease factors. We should pay more attention to the accuracy of applying biological age in different populations such as disease populations, progeria populations, and longevity populations. In the future, we should pay attention to the clinical translation of BA models and do further exploration for clinical utility, such as developing assessment models suitable for different disease individuals and further revealing the complex interaction between disease and aging.

Author contributions

ZL and WZ was written the first draft of the manuscript. YD, YN, YC, XL, ZD, YZ, XzC, ZF, YW, and DZ commented on previous versions of the manuscript. XS, GC, HJ, and XmC provided enough scientific suggestions and concrete actions during the revision. All authors read and approved the final version of the manuscript.

Funding

This study was supported by National Key Research and Development Program of China (2022YFC3602900, 2022YFC3602903, 2022YFC3602902), Innovation Platform for Academicians of Hainan Province (Academician Chen Xiangmei of Hainan Province Kidney Diseases Team Innovation Center), the Specialized Scientific Program of the Innovation Platform for Academicians of Hainan Province (YSPTZX202026), the Specialized Scientific Research Project of Military Health Care (21BJZ37), the Clinical Research Support Fund, Young Talent Project, Chinese PLA General Hospital (2019XXMBD-005, 2019XXJSYX01), the National Natural Science Foundation of China (82030025, 81601211).

Acknowledgments

This manuscript has been edited and proofread by a professional English translation service.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. López-Otín, C, Blasco, MA, Partridge, L, Serrano, M, and Kroemer, G. The hallmarks of aging. Cells. (2013) 153:1194–17. doi: 10.1016/j.cell.2013.05.039

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Moskalev, A. Introduction In: A Moskalev, editor. Biomarkers of human aging, vol. 10. New York: Healthy Ageing and Longevity. Springer International Publishing (2019)

Google Scholar

3. Levine, ME. Modeling the rate of senescence: can estimated biological age predict mortality more accurately than chronological age? J Gerontol A Biol Sci Med Sci. (2013) 68:667–4. doi: 10.1093/gerona/gls233

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Zhang, W, Jia, L, Cai, G, Shao, F, Lin, H, Liu, Z, et al. Model construction for biological age based on a cross-sectional study of a healthy Chinese han population. J Nutr Health Aging. (2017) 21:1233–9. doi: 10.1007/s12603-017-0874-7

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Hägg, S, Belsky, DW, and Cohen, AA. Developments in molecular epidemiology of aging. Pellegrini, M Emerg Top Life Sci (2019). 3:411–1. doi:doi: 10.1042/ETLS20180173

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Jylhävä, J, Pedersen, NL, and Hägg, S. Biological age predictors. EBioMedicine. (2017) 21:29–36. doi: 10.1016/j.ebiom.2017.03.046

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Xia, X, Wang, Y, Yu, Z, Chen, J, and Han, JDJ. Assessing the rate of aging to monitor aging itself. Ageing Res Rev. (2021) 69:101350. doi: 10.1016/j.arr.2021.101350

CrossRef Full Text | Google Scholar

8. Putin, E, Mamoshina, P, Aliper, A, Korzinkin, M, Moskalev, A, Kolosov, A, et al. Deep biomarkers of human aging: application of deep neural networks to biomarker development. Aging. (2016) 8:1021–33. doi: 10.18632/aging.100968

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Mamoshina, P, Kochetov, K, Putin, E, Cortese, F, Aliper, A, Lee, WS, et al. Population specific biomarkers of human aging: a big data study using south Korean, Canadian, and eastern European patient populations. J Gerontol Ser A. (2018) 73:1482–90. doi: 10.1093/gerona/gly005

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Zhang, WG, Zhu, SY, Bai, XJ, Zhao, DL, Jiang, SM, Li, J, et al. Select aging biomarkers based on telomere length and chronological age to build a biological age equation. Age. (2014) 36:9639. doi: 10.1007/s11357-014-9639-y

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Pyrkov, TV, Slipensky, K, Barg, M, Kondrashin, A, Zhurov, B, Zenin, A, et al. Extracting biological age from biomedical data via deep learning: too much of a good thing? Sci Rep. (2018) 8:5210. doi: 10.1038/s41598-018-23534-9

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Rahman, SA, and Adjeroh, DA. Deep learning using convolutional LSTM estimates biological age from physical activity. Sci Rep. (2019) 9:11425. doi: 10.1038/s41598-019-46850-0

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Hollingsworth, JW, Hashizume, A, and Jablon, S. Correlations between tests of aging in Hiroshima subjects--an attempt to define physiologic age. Yale J Biol Med. (1965) 38:11–26.

Google Scholar

14. Dubina, TL, Mints, AY, and Zhuk, EV. Biological age and its estimation. III. Introduction of a correction to the multiple regression model of biological age and assessment of biological age in cross-sectional and longitudinal studies. Exp Gerontol. (1984) 19:133–3. doi: 10.1016/0531-5565(84)90016-0

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Nakamura, E, Miyao, K, and Ozeki, T. Assessment of biological age by principal component analysis. Mech Ageing Dev. (1988) 46:1–18. doi: 10.1016/0047-6374(88)90109-1

CrossRef Full Text | Google Scholar

16. Zhang, WG, Bai, XJ, Sun, XF, et al. Construction of an integral formula of biological age for a healthy Chinese population using principle component analysis. J Nutr Health Aging. (2014) 18:137–2. doi: 10.1007/s12603-013-0345-8

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Klemera, P, and Doubal, S. A new approach to the concept and computation of biological age. Mech Ageing Dev. (2006) 127:240–8. doi: 10.1016/j.mad.2005.10.004

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Nakamura, E, Moritani, T, and Kanetaka, A. Biological age versus physical fitness age. Eur J Appl Physiol. (1989) 58:778–5. doi: 10.1007/BF00637391

CrossRef Full Text | Google Scholar

19. Nakamura, E, Moritani, T, and Kanetaka, A. Biological age versus physical fitness age in women. Eur J Appl Physiol. (1990) 61:202–8. doi: 10.1007/BF00357600

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Webster, IW, and Logie, AR. A relationship between functional age and health status in female subjects. J Gerontol. (1976) 31:546–14. doi: 10.1093/geronj/31.5.546

CrossRef Full Text | Google Scholar

21. Takeda, H, Inada, H, Inoue, M, Yoshikawa, H, and Abe, H. Evaluation of biological age and physical age by multiple regression analysis. Med Inform (Lond). (1982) 7:221–7. doi: 10.3109/14639238209010720

CrossRef Full Text | Google Scholar

22. Voitenko, VP, and Tokar, AV. The assessment of biological age and sex differences of human aging. Exp Aging Res. (1983) 9:239–4. doi: 10.1080/03610738308258458

CrossRef Full Text | Google Scholar

23. Nakamura, E, Moritani, T, and Kanetaka, A. Effects of habitual physical exercise on physiological age in men aged 20?85 years as estimated using principal component analysis. Eur J Appl Physiol. (1996) 73:410–8. doi: 10.1007/BF00334417

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Nakamura, E, and Miyao, K. Further evaluation of the basic nature of the human biological aging process based on a factor analysis of age-related physiological variables. J Gerontol A Biol Sci Med Sci. (2003) 58:B196–204. doi: 10.1093/gerona/58.3.B196

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Ueno, LM, Yamashita, Y, Moritani, T, and Nakamura, E. Biomarkers of aging in women and the rate of longitudinal changes. J Physiol Anthropol Appl Hum Sci. (2003) 22:37–46. doi: 10.2114/jpa.22.37

CrossRef Full Text | Google Scholar

26. Nakamura, E, and Miyao, K. A method for identifying biomarkers of aging and constructing an index of biological age in humans. J Gerontol A Biol Sci Med Sci. (2007) 62:1096–05. doi: 10.1093/gerona/62.10.1096

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Bae, CY, Kang, YG, Kim, S, Cho, C, Kang, HC, Yu, BY, et al. Development of models for predicting biological age (BA) with physical biochemical, and hormonal parameters. Arch Gerontol Geriatr. (2008) 47:253–5. doi: 10.1016/j.archger.2007.08.009

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Nakamura, E, and Miyao, K. Sex differences in human biological aging. J Gerontol A Biol Sci Med Sci. (2008) 63:936–4. doi: 10.1093/gerona/63.9.936

CrossRef Full Text | Google Scholar

29. Park, J, Cho, B, Kwon, H, and Lee, C. Developing a biological age assessment equation using principal component analysis and clinical biomarkers of aging in Korean men. Arch Gerontol Geriatr. (2009) 49:7–12. doi: 10.1016/j.archger.2008.04.003

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Bai, X, Han, L, Liu, Q, Shan, H, Lin, H, Sun, X, et al. Evaluation of biological aging process – a population-based study of healthy people in China. Gerontology. (2010) 56:129–14. doi: 10.1159/000262449

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Jee, H, Jeon, BH, Kim, YH, Kim, HK, Choe, J, Park, J, et al. Development and application of biological age prediction models with physical fitness and physiological components in Korean adults. Gerontology. (2012) 58:344–3. doi: 10.1159/000335738

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Bae, CY, Kang, YG, Piao, MH, Cho, BL, Cho, KH, Park, YK, et al. Models for estimating the biological age of five organs using clinical biomarkers that are commonly measured in clinical practice settings. Maturitas. (2013) 75:253–14. doi: 10.1016/j.maturitas.2013.04.008

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Belsky, DW, Caspi, A, Houts, R, Cohen, HJ, Corcoran, DL, Danese, A, et al. Quantification of biological aging in young adults. Proc Natl Acad Sci USA. (2015) 112:E4104–10. doi: 10.1073/pnas.1506264112

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Mitnitski, A, Howlett, SE, and Rockwood, K. Heterogeneity of human aging and its assessment. J Gerontol A Biol Sci Med Sci. (2016):glw089. doi: 10.1093/gerona/glw089

CrossRef Full Text | Google Scholar

35. Jee, H, and Park, J. Selection of an optimal set of biomarkers and comparative analyses of biological age estimation models in Korean females. Arch Gerontol Geriatr. (2017) 70:84–91. doi: 10.1016/j.archger.2017.01.005

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Kang, YG, Suh, E, Chun, H, Kim, SH, Kim, DK, and Bae, CY. Models for estimating the metabolic syndrome biological age as the new index for evaluation and management of metabolic syndrome. Clin Interv Aging. (2017) 12:253–1. doi: 10.2147/CIA.S123316

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Brown, PJ, Wall, MM, Chen, C, Levine, ME, Yaffe, K, Roose, SP, et al. Biological age, not chronological age, is associated with late-life depression. J Gerontol Ser A. (2018) 73:1370–6. doi: 10.1093/gerona/glx162

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Murabito, JM, Zhao, Q, Larson, MG, Rong, J, Lin, H, Benjamin, EJ, et al. Measures of biologic age in a community sample predict mortality and age-related disease: the Framingham offspring study. J Gerontol Ser A. (2018) 73:757–2. doi: 10.1093/gerona/glx144

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Hastings, WJ, Shalev, I, and Belsky, DW. Comparability of biological aging measures in the National Health and nutrition examination study, 1999–2002. Psychoneuroendocrinology. (2019) 106:171–8. doi: 10.1016/j.psyneuen.2019.03.012

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Jee, H. Selection of a set of biomarkers and comparisons of biological age estimation models for Korean men. J Exerc Rehabil. (2019) 15:31–6. doi: 10.12965/jer.1836644.322

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Mamoshina, P, Kochetov, K, Cortese, F, Kovalchuk, A, Aliper, A, Putin, E, et al. Blood biochemistry analysis to detect smoking status and quantify accelerated aging in smokers. Sci Rep. (2019) 9:142. doi: 10.1038/s41598-018-35704-w

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Gaydosh, L, Belsky, DW, Glei, DA, and Goldman, N. Testing proposed quantifications of biological aging in Taiwanese older adults. Le Couteur, D, J Gerontol Ser A. (2020). 75:1680–85. doi:doi: 10.1093/gerona/glz223

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Liu, Z. Development and validation of 2 composite aging measures using routine clinical biomarkers in the Chinese population: analyses from 2 prospective cohort studies. J Gerontol Ser A. (2020):glaa238. doi: 10.1093/gerona/glaa238

CrossRef Full Text | Google Scholar

44. Parker, DC, Bartlett, BN, Cohen, HJ, Fillenbaum, G, Huebner, JL, Kraus, VB, et al. Association of Blood Chemistry Quantifications of biological aging with disability and mortality in older adults. J Gerontol Ser A. (2020) 75:1671–9. doi: 10.1093/gerona/glz219

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Zhong, X, Lu, Y, Gao, Q, Nyunt, MSZ, Fulop, T, Monterola, CP, et al. Estimating biological age in the Singapore longitudinal aging study. Newman a, ed. J Gerontol Ser A. (2020) 75:1913–20. doi: 10.1093/gerona/glz146

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Chan, MS, Arnold, M, Offer, A, Hammami, I, Mafham, M, Armitage, J, et al. A biomarker-based biological age in UK biobank: composition and prediction of mortality and hospital admissions. Magaziner J, ed. J Gerontol Ser A. (2021) 76:1295–02. doi: 10.1093/gerona/glab069

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Gialluisi, A, Di Castelnuovo, A, Costanzo, S, Bonaccio, M, Persichillo, M, Magnacca, S, et al. Exploring domains, clinical implications and environmental associations of a deep learning marker of biological ageing. medRxiv (2021).

Google Scholar

48. Kuo, C, Pilling, LC, Liu, Z, Atkins, JL, and Levine, ME. Genetic associations for two biological age measures point to distinct aging phenotypes. Aging Cell. (2021) 20:e13376. doi: 10.1111/acel.13376

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Raghu, VK, Weiss, J, Hoffmann, U, Aerts, HJWL, and Lu, MT. Deep learning to estimate biological age from chest radiographs. JACC Cardiovasc Imaging. (2021) 14:2226–36. doi: 10.1016/j.jcmg.2021.01.008

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Bahour, N, Cortez, B, Pan, H, Shah, H, Doria, A, and Aguayo-Mazzucato, C. Diabetes mellitus correlates with increased biological age as indicated by clinical biomarkers. GeroScience. (2022) 44:415–7. doi: 10.1007/s11357-021-00469-0

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Nusinovici, S, Rim, TH, Yu, M, Lee, G, Tham, YC, Cheung, N, et al. Retinal photograph-based deep learning predicts biological age, and stratifies morbidity and mortality risk. Age Ageing. (2022) 51. doi: 10.1093/ageing/afac065

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Dharnidharka, VR, Kwon, C, and Stevens, G. Serum cystatin C is superior to serum creatinine as a marker of kidney function: a meta-analysis. Am J Kidney Dis. (2002) 40:221–6. doi: 10.1053/ajkd.2002.34487

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Corrêa, MM, Thumé, E, De Oliveira, ERA, and Tomasi, E. Performance of the waist-to-height ratio in identifying obesity and predicting non-communicable diseases in the elderly population: a systematic literature review. Arch Gerontol Geriatr. (2016) 65:174–2. doi: 10.1016/j.archger.2016.03.021

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Cho, IH, Park, KS, and Lim, CJ. An empirical comparative study on biological age estimation algorithms with an application of work ability index (WAI). Mech Ageing Dev. (2010) 131:69–78. doi: 10.1016/j.mad.2009.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Mather, KA, Jorm, AF, Parslow, RA, and Christensen, H. Is telomere length a biomarker of aging? A review. J Gerontol A Biol Sci Med Sci. (2011) 66A:202–3. doi: 10.1093/gerona/glq180

CrossRef Full Text | Google Scholar

56. Zglinicki, T, and Martin-Ruiz, C. Telomeres as biomarkers for ageing and age-related diseases. Curr Mol Med. (2005) 5:197–3. doi: 10.2174/1566524053586545

CrossRef Full Text | Google Scholar

57. Butler, RN, Sprott, R, Warner, H, Bland, J, Feuers, R, Forster, M, et al. Aging: the reality: biomarkers of aging: from primitive organisms to humans. J Gerontol A Biol Sci Med Sci. (2004) 59:B560–7. doi: 10.1093/gerona/59.6.B560

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Johnson, TE. Recent results: biomarkers of aging. Exp Gerontol. (2006) 41:1243–6. doi: 10.1016/j.exger.2006.09.006

CrossRef Full Text | Google Scholar

59. Costa, PT, and McCrae, RR. Functional age: a conceptual and empirical critique. Bethesda, MD: National Institute of Health (1980).

Google Scholar

60. Costa, PT, and McCrae, RR. Concepts of functional or biological age: a critical view. Princ Geriatr Med. (1985):30–7.

Google Scholar

61. Ingram, DK. Key questions in developing biomarkers of aging. Exp Gerontol. (1988) 23:429–4. doi: 10.1016/0531-5565(88)90048-4

CrossRef Full Text | Google Scholar

62. Hochschild, R. Improving the precision of biological age determinations. Part 1: a new approach to calculating biological age. Exp Gerontol. (1989) 24:289–14. doi: 10.1016/0531-5565(89)90002-8

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Levine, ME, Lu, AT, Quach, A, Chen, BH, Assimes, TL, Bandinelli, S, et al. An epigenetic biomarker of aging for lifespan and healthspan. Aging. (2018) 10:573–1. doi: 10.18632/aging.101414

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Jia, L, Zhang, W, Jia, R, Zhang, H, and Chen, X. Construction formula of biological age using the principal component analysis. Biomed Res Int. (2016) 2016:1–8. doi: 10.1155/2016/4697017

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Hochschild, R. Validating biomarkers of aging—Mathematical approaches and results of a 2462-person study. Boca Raton: CRC Press. (1994). 93–144.

Google Scholar

66. Kwon, D, and Belsky, DW. A toolkit for quantification of biological age from blood chemistry and organ function test data: BioAge. GeroScience. (2021) 43:2795–08. doi: 10.1007/s11357-021-00480-5

PubMed Abstract | CrossRef Full Text | Google Scholar

67. LeCun, Y, Bengio, Y, and Hinton, G. Deep learning. Nature. (2015) 521:436–4. doi: 10.1038/nature14539

CrossRef Full Text | Google Scholar

68. He, K, Zhang, X, Ren, S, and Sun, J. Delving deep into rectifiers: surpassing human-level performance on imagenet classification Proceedings of the IEEE International Conference on Computer Vision (2015). 1026–34.

Google Scholar

69. Duchi, J, Hazan, E, and Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J Mach Learn Res. (2011) 12:2121–2159.

Google Scholar

70. Cohen, AA, Morissette-Thomas, V, Ferrucci, L, and Fried, LP. Deep biomarkers of aging are population-dependent. Aging. (2016) 8:2253–5. doi: 10.18632/aging.101034

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Hochreiter, S. Untersuchungen zu dynamischen neuronalen Netzen. Diploma Tech Univ Münch. (1991) 91:1735–1780.

Google Scholar

72. Hochreiter, S, and Schmidhuber, J. Long short-term memory. Neural Comput. (1997) 9:1735–80. doi: 10.1162/neco.1997.9.8.1735

CrossRef Full Text | Google Scholar

73. Hochschild, R. Improving the precision of biological age determinations. Part 2: automatic human tests, age norms and variability. Exp Gerontol. (1989) 24:301–6. doi: 10.1016/0531-5565(89)90003-X

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Drewelies, J, Hueluer, G, Duezel, S, Vetter, VM, Pawelec, G, Steinhagen-Thiessen, E, et al. Using blood test parameters to define biological age among older adults: association with morbidity and mortality independent of chronological age validated in two separate birth cohorts. GeroScience. (2022) 44:2685–99. doi: 10.1007/s11357-022-00662-9

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Liu, Z, Kuo, PL, Horvath, S, Crimmins, E, Ferrucci, L, and Levine, M. A new aging measure captures morbidity and mortality risk across diverse subpopulations from NHANES IV: a cohort study. PLoS Med. (2018) 15:e1002718. doi: 10.1371/journal.pmed.1002718

CrossRef Full Text | Google Scholar

76. Krøll, J, and Saxtrup, O. On the use of regression analysis for the estimation of human biological age. Biogerontology. (2000) 6:363–8. doi: 10.1023/a:1026594602252

CrossRef Full Text | Google Scholar

77. Li, Z, Zhang, W, Duan, Y, Niu, Y, He, Y, Chen, Y, et al. Biological age models based on a healthy Han Chinese population. Arch Gerontol Geriatr. (2023) 107:104905. doi: 10.1016/j.archger.2022.104905

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Ashiqur Rahman, S, Giacobbi, P, Pyles, L, Mullett, C, Doretto, G, and Adjeroh, DA. Deep learning for biological age estimation. Brief Bioinform. (2021) 22:1767–81. doi: 10.1093/bib/bbaa021

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Ferrucci, L, Gonzalez-Freire, M, Fabbri, E, Simonsick, E, Tanaka, T, Moore, Z, et al. Measuring biological aging in humans: a quest. Aging Cell. (2020) 19:e13080. doi: 10.1111/acel.13080

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Pyrkov, TV, Sokolov, IS, and Fedichev, PO. Deep longitudinal phenotyping of wearable sensor data reveals independent markers of longevity, stress, and resilience. Aging. (2021) 13:7900–13. doi: 10.18632/aging.202816

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Pyrkov, TV, Avchaciov, K, Tarkhov, AE, Menshikov, LI, Gudkov, AV, and Fedichev, PO. Longitudinal analysis of blood markers reveals progressive loss of resilience and predicts human lifespan limit. Nat Commun. (2021) 12:2765. doi: 10.1038/s41467-021-23014-1

PubMed Abstract | CrossRef Full Text | Google Scholar