Survival model database of human digestive system cells exposed to electroporation pulses: An in vitro and in silico study

Background and objectives: This study aimed to establish a mathematical survival model database containing cell-specific coefficients from human digestive system cells exposed to electroporation pulses (EPs).

Materials and methods: A total of 20 types of human digestive system cell lines were selected to investigate the effect of EPs on cell viability. Cell viability was measured after exposure to various pulse settings, and a cell survival model was established using the Peleg–Fermi model. Next, the cell-specific coefficients of each cell line were determined.

Results: Cell viability tended to decrease when exposed to stronger electric field strength (EFS), longer pulse duration, and more pulse number, but the decreasing tendency varied among different cell lines. When exposed to a lower EFS (<1,000 V/cm), only a slight decrease in cell viability occurred. All cell lines showed a similar tendency: the extent of electrical injury (EI) increased with the increase in pulse number and duration. However, there existed differences in heat sensitivity among organs.

Conclusions: This database can be used for the application of electroporation-based treatment (EBT) in the digestive system to predict cell survival and tissue injury distribution during the treatment.

Introduction

Induced by electroporation pulses (EPs), pulsed electric fields (PEF) can alter the cell transmembrane potential and cause nanometer-sized defects or pores on the cell membrane, leading to reversible electroporation (RE) or irreversible electroporation (IRE) (1). In terms of RE, EPs can induce transitory exchange channels for exogenous molecules or substances into the cytoplasm and maintain cell viability (2); in terms of IRE, EPs can eliminate cancer or diseased tissue in situ through electrical injury (EI) without thermal injury (TI) (3, 4). As EPs can physically modulate cell membrane permeability and cause a series of alterations in cellular physiological activity, electroporation-based treatment (EBT) is considered a unique physical method for biotechnology, cancer treatment, and tissue ablation (3).

Although the mechanism of cell electroporation is still controversial, it is well-established that the electric field distribution plays a major role in the biological outcome of EPs, which is primarily determined by the pulse parameter, electrode configuration, environmental conditions, and tissue properties (5, 6). Therefore, the intensity and biological effects of EBT are theoretically controllable and predictable by applying the proper parameters to specific tissues. However, the parameter settings in EBT is often empirical and estimative, which may lead to undesired results, such as unexpected cell death when performing cell electrotransfection or unexpected tumor residue in tumor ablation (7, 8). Thus, it is necessary to provide mathematical evidence for the EBT to apply proper pulse settings. In 2014, Dermol and Miklavčič have demonstrated that mathematical models of cell permeabilization and survival can be used for clear treatment planning and better tissue damage prediction (9).

Electroporation is not a simple or instantaneous process but a cumulative effect based on pulse intensity and quantity. The pulse voltage, duration, number, and frequency should be considered to estimate EP outcomes. By combining in vitro experiment data and mathematical modeling, Dermol and Miklavčič compared the goodness of fit and applicable situation among different mathematical models of electroporation, confirming Peleg-Fermi model is suitable for treatment planning of electrochemotherapy and IRE (10). Therefore, the Peleg–Fermi model, which includes the parameters of electric field strength (EFS), pulse number, pulse duration, and several cell-specific coefficients, has been established to estimate the biological effect of the electroporation process with prominent efficacy in calculating the EI (9, 11). The cell-specific coefficient in the Peleg–Fermi model is a series of parameters reflecting the tendency and extent of cell viability changes exposed to EPs of a certain pulse duration and frequency, which may differ between different organs and even different cells. However, although the thermal effect is not indispensable for the electroporation process, there is still the possibility of thermal effect and even TI during the EPs when applying a high voltage to the cell or tissue due to the tissue resistance of electrical properties, which should be avoided during EBT (12, 13). The thermal effect is primarily determined by the temperature distribution, which can be calculated using Penne's bioheat transfer equation and the Arrhenius equation (14). The Joule heat generated by the EPs was incorporated into Pennes' bioheat transfer equation as an external heat source and increased the tissue temperature through time-dependent and electrical-thermal coupling effects that were determined by the pulse duration, number, and frequency (15, 16). Based on the mathematical model, it is possible to achieve a non-thermal EBT by adjusting the pulse parameter and electrode configuration for a specific tissue. Therefore, it is necessary to further optimize the mathematical model and investigate the specific parameters for various tissues, which is meaningful for the further application of EBT.

However, there is only one series of cell-specific coefficient data available for prostate cancer (17), rendering it inaccurate in model simulation and treatment planning for disease of other organs (18). As mentioned above, the pulse parameters are crucial for the outcomes of EBT; thus, it is reasonable to set the proper pulse parameter to achieve the expected results. Various types of EBT have been successfully used in cancer treatment and tissue ablation, such as electrochemotherapy (19), pulsed field ablation (20), and IRE. Moreover, the feasibility, safety, and efficacy of EBT for the focal treatment of cavity organs, which are usually the restricted areas of thermal-based ablation techniques, have been investigated. In our previous studies, the safety and efficacy of IRE in the stomach and bile duct have been investigated with favorable outcomes (21–24). These results demonstrate that EBT is an attractive candidate for the treatment of such endoluminal tumors. However, there is a lack of cell-specific coefficient data from the digestive system that renders it inaccurate for model simulation and treatment planning.

Herein, a mathematical model database containing the cell-specific coefficient from 20 types of human digestive system cell lines (including the esophagus, stomach, colon, liver, bile duct, and pancreas) exposed to EPs was established by in vitro and in silico studies. In addition, the efficacy of the survival model for IRE was evaluated via numerical analysis of the digestive system.

Materials and methods

Cell lines and cell culture

A total of 20 types of human digestive system cell lines, including 17 cancer cell lines and three normal cell lines, were selected to investigate the effect of EPs on cell viability in vitro. Detailed information on the cell lines is provided in Table 1. Major cells lines were chosen to be accord with primary pathological type of digestive tumor (e.g., squamous carcinoma in esophagus). All cells were cultured in Dulbecco's Modified Eagle Medium (DMEM; Biological Industries Co., Ltd., Kibbutz Beit-Haemek, Israel) supplemented with 10% fetal bovine serum (Biological Industries Co., Ltd., Kibbutz Beit-Haemek, Israel) and 1% penicillin–streptomycin solution (Beyotime Biotechnology, Nantong, Jiangsu, China). All cultures were maintained in a 5% CO₂ humidified incubator (Thermo Forma 371, Thermo Fisher Scientific, Waltham, MA, USA) at 37°C.

TABLE 1

Table 1. The information for the cell lines.

EPs protocols

Before exposure to EPs, the cells were washed with phosphate-buffered saline solution, harvested by trypsin, and resuspended in DMEM culture medium to a concentration of 8 × 10⁴ cells/ml. The cell suspension (500 μl) was added to a 2 mm gap cuvette (45-0135, Harvard Apparatus, Holliston, MA, USA). A square wave pulse generator (BTX ECM 830, Harvard Apparatus, Holliston, MA, USA) was used to generate a burst of EPs. The detailed protocol of the pulse setting for each procedure is summarized in Supplementary Table 1.

Cell counting kit-8 experiment for cell viability

After exposure to EPs, the cell suspension was re-collected immediately, dispensed into 96-well plates, and incubated for 24 h. Cell viability was assessed using the cell counting kit (CCK)-8 commercial kit (Dojindo Molecular Technologies Inc., Kumamoto, Japan) following the manufacturer's instructions. The optical density (OD) value at a wavelength of 450 nm was measured using an automatic microplate reader (Varioskan Flash Multiplate Reader, Thermo Fisher Scientific, Waltham, MA, USA). Cell viability was calculated using the following equation:

$\begin{array}{ll}S=\frac{Aexp-Ablan}{Acon-Ablan}\times 100\%& (1)\end{array}$

where Aexp, Ablan, and Acon are the mean OD values of the experimental, blank medium, and control groups, respectively. For each parameter setting of each cell line, the experiment was repeated 10 times. All data were analyzed using GraphPad (9.0, GraphPad Software Inc., San Diego, CA, USA).

Curve fitting for mathematical model

The equation for the Peleg–Fermi model was as following:

$\begin{array}{llll}S& =& \frac{1}{1+e^{\frac{E-E_c(N)}{A_c(N)}}}& (2)\end{array}$

$\begin{array}{llll}{E}_c(N)& =& E_{0}exp(-k_{1}N)& (3)\end{array}$

$\begin{array}{llll}{A}_c(N)& =& A_{0}exp(-k_{2}N)& (4)\end{array}$

where S is the cell viability after EP; E is the EFS; E_c(N) and A_c(N) are two functions that depend on the pulse number (N) and cell-specific coefficients, where E_c(N) represents the EFS required for the half lethality of cells, and A_c(N) is the constant of the cell survival curve slope under specific pulse parameters; and E₀, A₀, k₁, and k₂ are the coefficients related to the pulse duration, frequency, and cell type. R² was calculated as statistical measure for the goodness of fit, which indicates the correlation between the calculated and practically determined value. The value of E_c(N) and A_c(N) was calculated based on Equation (2) as first step. Then the value of the coefficients was calculated subsequently based on the results of the first step and Equations (3) and (4), respectively. Thus, two R² values was acquired in step 2 because E₀ and k₁ were fitted separately from A₀ and k₂ based on different equation.

Although the efficacy of the Peleg–Fermi model has been demonstrated by previous studies, it is still possible that the data of a certain cell line from the in vitro study were not suitable for curve fitting. To solve this problem, the modified Peleg–Fermi model and power function model was used instead (18, 25, 26).

The equation for the modified Peleg–Fermi model was as following:

$\begin{array}{llll}{E}_c(N)& =& E_{1}exp(-k_{1}N)+E_{2}exp(-k_{2}N)& (5)\end{array}$

$\begin{array}{llll}{A}_c(N)& =& A_{1}exp(-k_{3}N)+A_{2}exp(-k_{4}N)& (6)\end{array}$

where E₁, E₂, A₁, A₂, k₁, k₂, k₃, and k₄ are the coefficients related to the pulse duration, frequency, and cell type.

The equation for the power function model was as following:

$\begin{array}{cc}E=a{(\frac{t_p}{t_0})}^b& (7)\end{array}$

where t_p is the pulse duration given in (ms) and t₀ = 1 ms.

The survival model curve fitting and calculation of the coefficients were referenced from Goldberg et al. (27), and were performed using MATLAB software (R2020b, The Mathworks Inc., Natick, Massachusetts, USA). The MATLAB program code is shown in the Supplementary materials. The values of E_c(N) (N = 100) were estimated using Equation (3) for each cell line.

In Pelge-Fermi equation, with the increase of the pulse number, even very weak electric filed will induce electric injury, which is inconsistent with the reality. Therefore, a threshold is needed to limit the calculation for IRE. Here, we defined E_c(N), the field at which 50% of a population of cells, as the threshold for subsequent numerical analysis.

Numerical analysis for evaluation

To evaluate the efficacy of the mathematical model for IRE, a numerical analysis was performed using COMSOL Multiphysics (Version 5.6, COMSOL Co., Ltd., Burlington, MA, USA) using the finite element method in accordance with our previous study (16). To simplify the calculation, a two-dimensional tissue model with a couple of needle electrodes were established. The tissue domain was isotropic and homogeneous. The electrical and thermal properties of the tissue (including the esophagus, stomach, colon, liver, bile duct, and pancreas) are obtained from an open database and summarized in Table 2 (28). Detailed information on the simulation model is described in Supplementary materials.

TABLE 2

Table 2. The electrical and thermal properties of tissues.

A time-dependent study was performed to investigate the accumulative electrical and thermal effects of EP on the tissue. Specifically, the pulse parameter was set to 2,000 V in pulse voltage, 100 μs in pulse duration, and 1 Hz in frequency. A total of 100 pulses were used for EI analysis. To fully evaluate the thermal effect of IRE and heat sensitivity of each organ, 200 pulses (equal to 200 s) were set for the analysis of TI.

Because the results from the Peleg–Fermi model and Arrhenius model depicted survival rate, the threshold of irreversible injury for the probability of EI and TI was set as 0.5, implying that if the probability of EI or TI was >0.5, it could be treated as an irreversible injury. The effective electric field was defined as the threshold of EFS for electroporation that was set as the corresponding value of E_c(N) for each cell line.

To quantitatively evaluate the model from a certain cell line, the relative area ratio of the probability of EI and the probability of TI were calculated using Equations (7) and (8):

$\begin{array}{llll}\text{R}\text{e}\text{l}\text{a}\text{t}\text{i}\text{v}\text{e}\text{a}\text{r}\text{e}\text{a}\text{r}\text{a}\text{t}\text{i}\text{o}\text{o}\text{f}\text{E}\text{I}& =& S_{EI}/S_{total}& (8)\end{array}$

$\begin{array}{llll}\text{R}\text{e}\text{l}\text{a}\text{t}\text{i}\text{v}\text{e}\text{a}\text{r}\text{e}\text{a}\text{r}\text{a}\text{t}\text{i}\text{o}\text{o}\text{f}\text{T}\text{I}& =& S_{TI}/S_{total}& (9)\end{array}$

where S_EI is the area of EI, S_TI is the area of TI, and S_total is the total area of the tissue domain. All data were analyzed and compared using GraphPad (9.0, GraphPad Software Inc., San Diego, CA, USA). As the calculation of EI is based on the specific coefficients obtained from the Peleg–Fermi model at the cellular level, the corresponding S_EI can be acquired for each of the 20 cell lines. Since the calculation of TI is based on the Arrhenius equation at the organ level, S_TI can only be obtained for each organ.

Statistical analysis

Statistical analysis was performed using GraphPad. The results are expressed as mean ± SD.

Results

In vitro assessment of viability of cells exposed to EPs

The viability of each cell line exposed to EPs under various pulse durations, pulse numbers, and EFS was determined. Figure 1 shows the viability of each cell line exposed to EPs with a 100 μs pulse duration under various pulse numbers and EFS. The detailed data are summarized in the online database (29). Generally, cell viability tended to decrease with an increase in EFS, pulse duration, and pulse number, but the decreasing tendency was different among different cell lines. However, when exposed to a lower EFS (500 V/cm), only a slight decrease in cell viability occurred (Figure 1). In contrast, when exposed to a short pulse duration, cell viability even increased under a lower EFS.

FIGURE 1

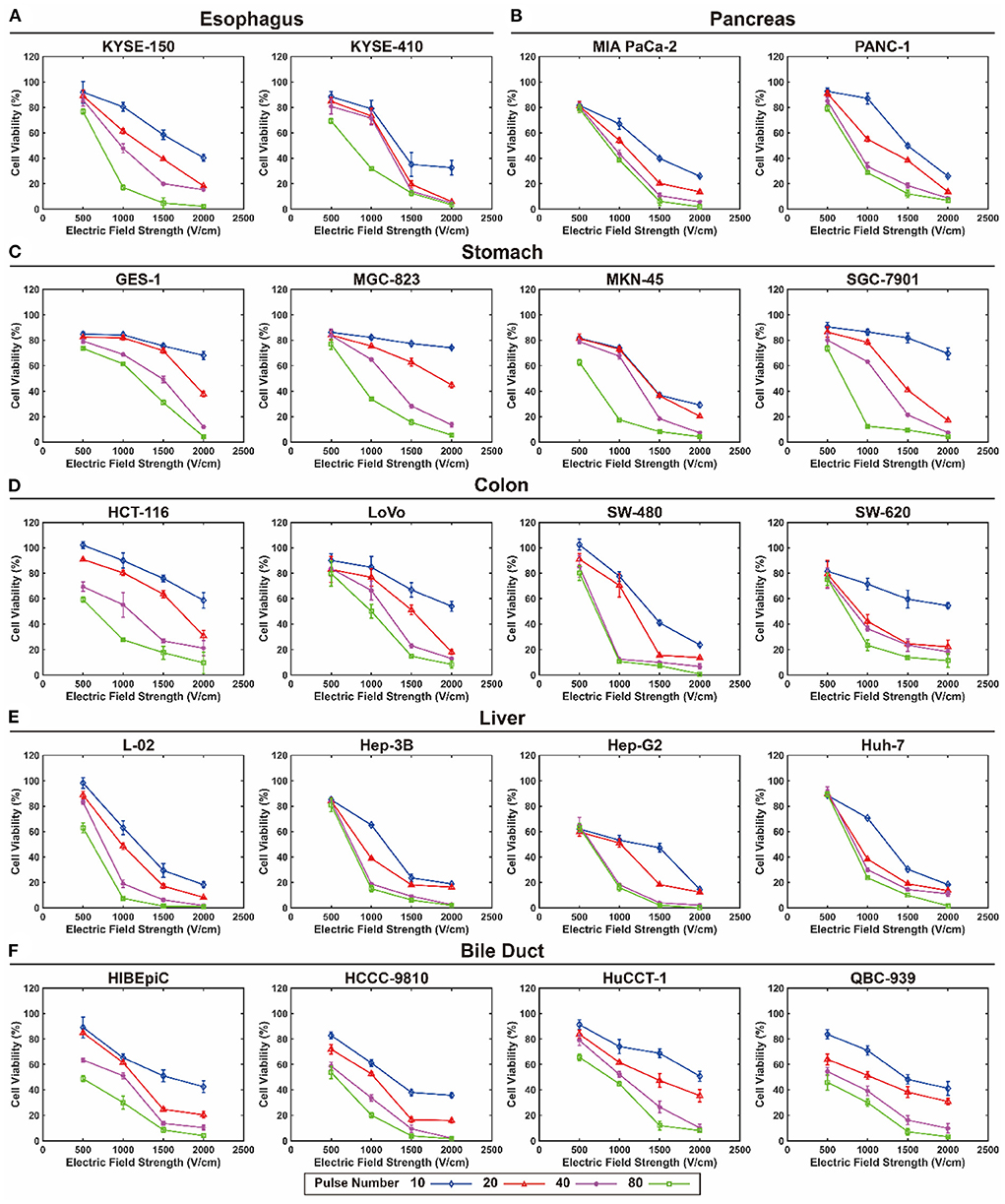
Figure 1. Viability of each cell line exposed to electroporation pulses with 100 μs pulse duration under various pulse numbers and electric field strengths. (A) Esophagus, (B) pancreas, (C) stomach, (D) colon, (E) liver, and (F) bile duct.

Survival curve based on the mathematical model

Table 3 summarizes the cell-specific coefficients, E_c, A_c, and E_c (100) of the 20 cell lines under different pulse durations. Figure 2 shows the fitting curve of E_c and A_c for each cell line with the increase in pulse number under a pulse duration of 100 μs. The data of E_c and A_c under pulse durations of 25, 50, and 75 μs are available in the online database. Moreover, the results of power function model of all cell lines are available in the online database as well (29). The lethality of the EPs increases with the accumulation of pulses, leading to a decline in the E_c and A_c values. Furthermore, the decline rate of the E_c and A_c values varied among the cells (Figure 2).

TABLE 3

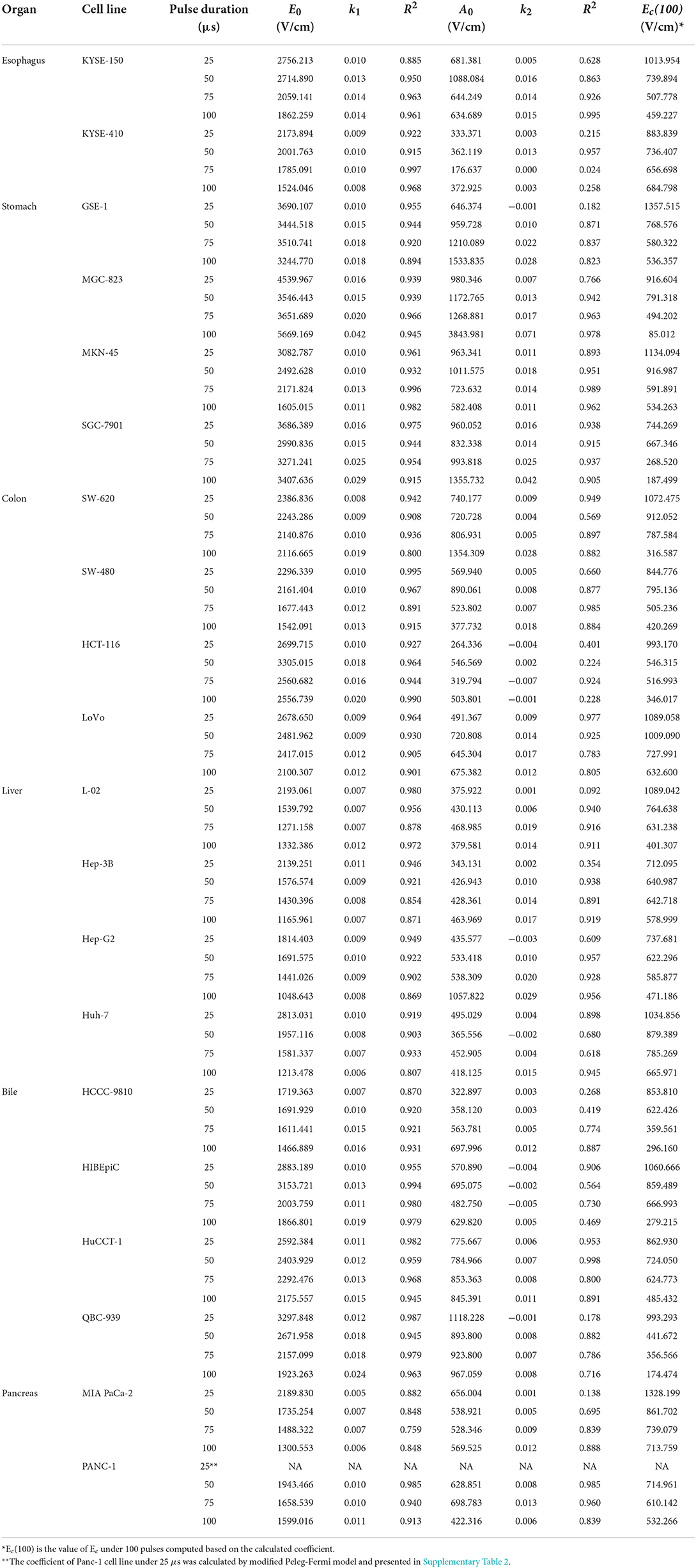
Table 3. The cell specific coefficients of the 20 digestive system cell lines under different pulse duration.

FIGURE 2

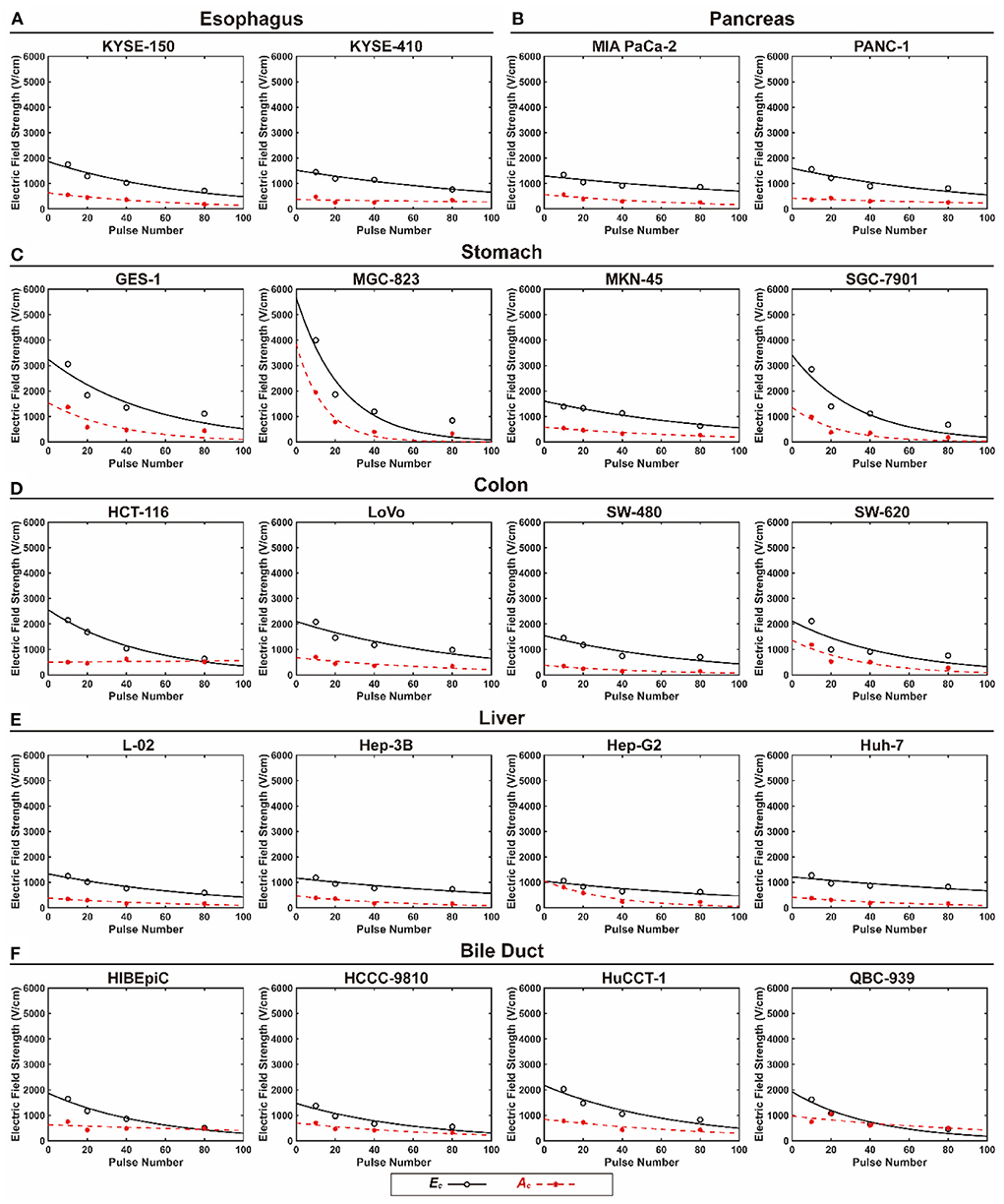
Figure 2. The fitting curve of E_c and A_c for each cell lines with the increase in pulse number under 100 μs pulse duration. (A) Esophagus, (B) pancreas, (C) stomach, (D) colon, (E) liver, and (F) bile duct.

For the 25 μs pulse duration, most of the E_c(100) values were in the range of 800–1,000 V/cm, and for a pulse duration of 100 μs, most of the E_c(100) values were between 400 and 600 V/cm. For most of the cell lines, the value of E_c(100) decreased with increasing pulse duration. When treated with EPs with a 100 μs pulse duration, the E_c(100) value varied from 459 to 684 V/cm for esophageal cells, 85 to 536 V/cm for gastric cells, 316 to 632 V/cm for colon cells, 401 to 665 V/cm for hepatic cells, 174 to 485 V/cm for biliary cells, and 532 to 713 V/cm for pancreatic cells.

Figure 3 shows the calculated survival curve of each cell line exposed to EPs with different pulse numbers and EFS under a 100 μs pulse duration. The survival curves for pulse durations of 25, 50, and 75 μs are available in the online database (29).

FIGURE 3

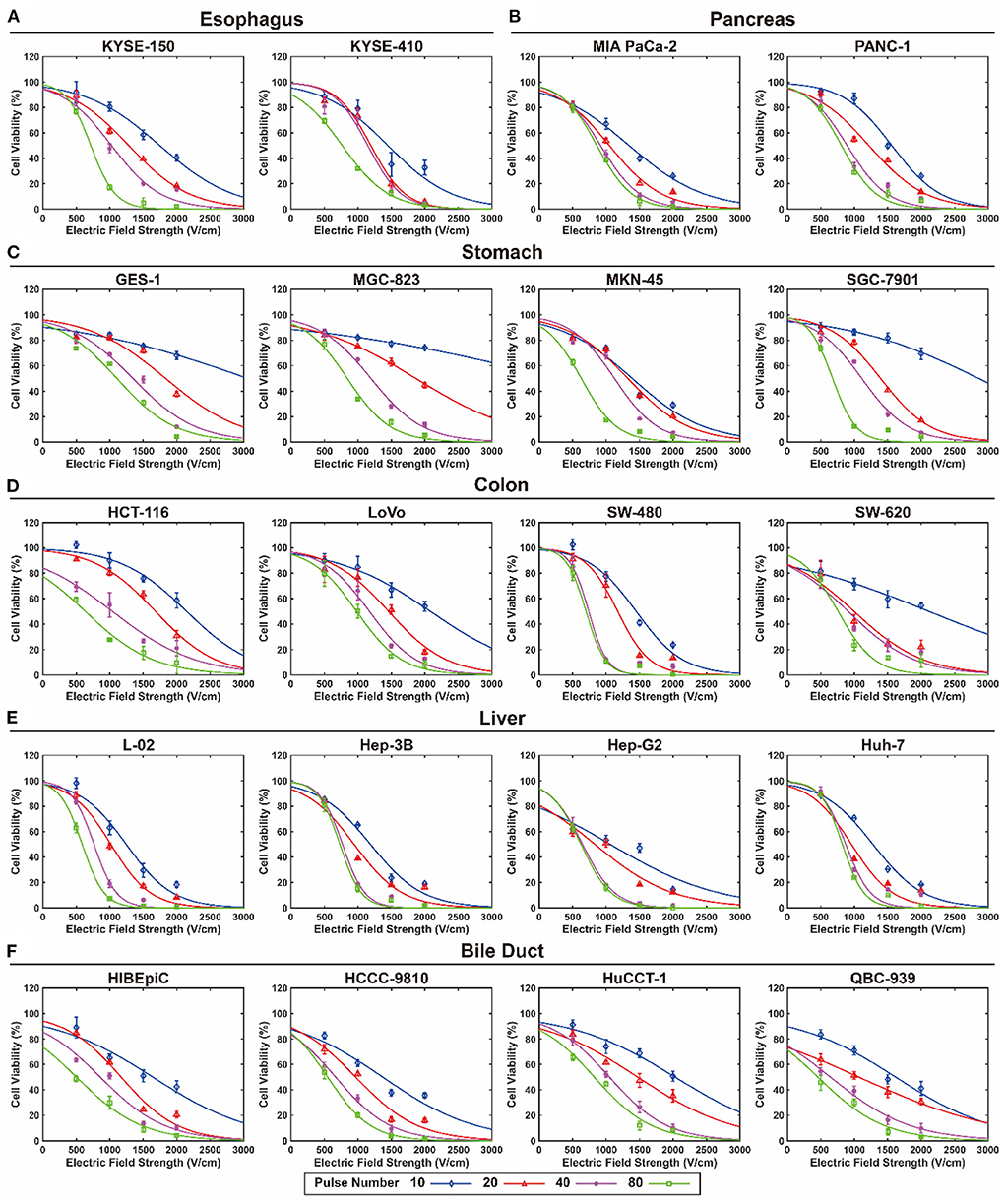
Figure 3. Survival curve of each cell line exposed to electroporation pulses with different pulse number and electric fields strength under 100 μs pulse duration. (A) Esophagus, (B) pancreas, (C) stomach, (D) colon, (E) liver, and (F) bile duct.

Evaluation of the model efficacy by numerical analysis

The calculated S_EI and S_TI of each cell line from the digestive system are shown in Figures 4, 5, respectively. The detailed values of S_EI and S_TI for specific pulse numbers can be found in the online database (29). All the cells showed a similar tendency: S_EI increased with the accumulation of pulse number and extension of pulse duration. The growth rate of the S_EI increased with increasing pulse duration; therefore, the S_EI with a pulse duration of 100 μs was the highest. The gastric cell lines (MGC-823 and SGC-7901) and cholangiocarcinoma cell lines (HCCC-9810 and QBC-939) showed higher slopes and maximum values of the S_EI curve than the other cell lines. In contrast, the viability of cell lines from the esophagus and pancreas showed a relatively lower inhibition rate when exposed to EPs (Figure 4).

FIGURE 4

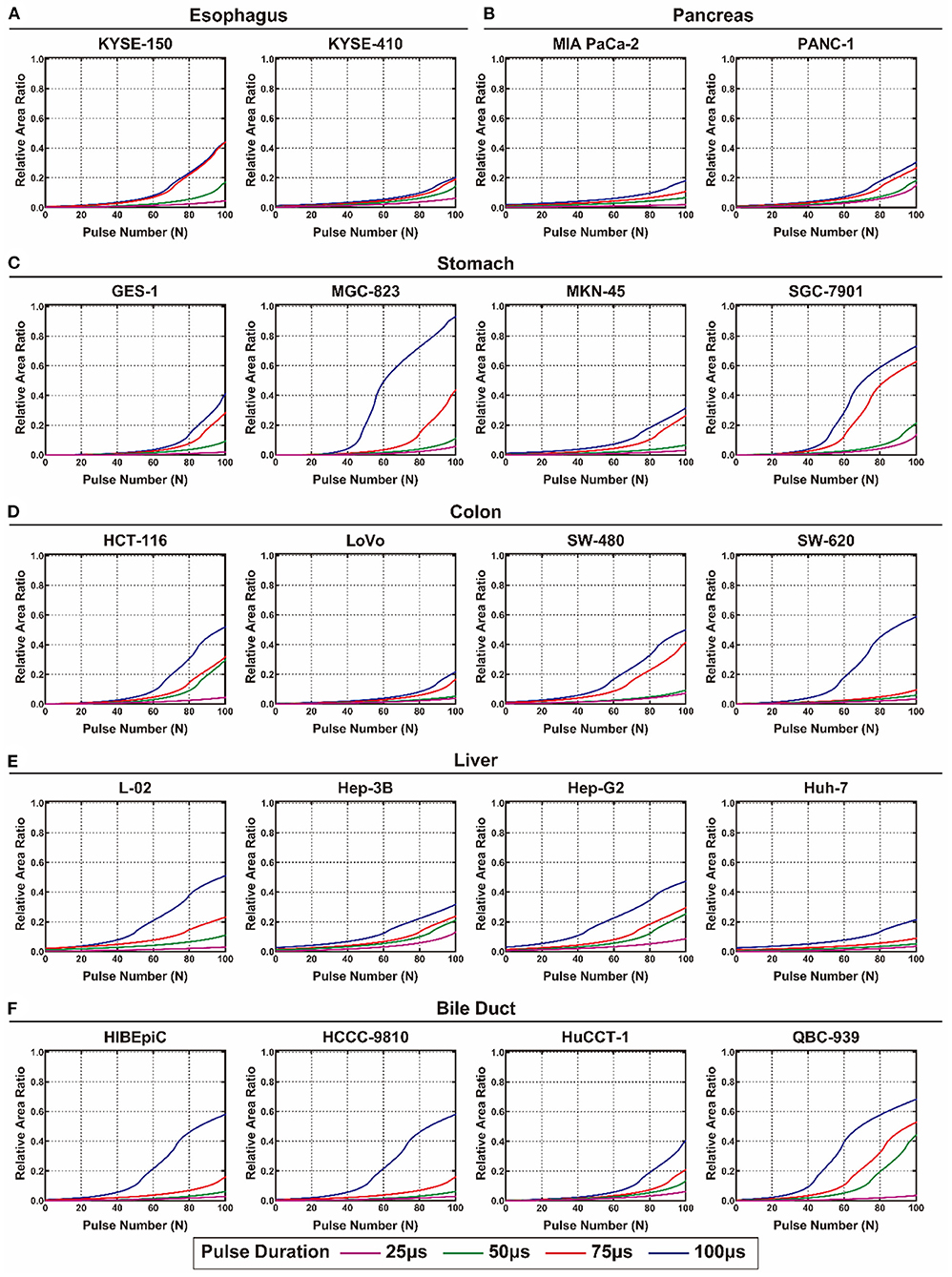
Figure 4. The calculated relative area ratio of the electrical injury to the digestive system. (A) Esophagus, (B) pancreas, (C) stomach, (D) colon, (E) liver, and (F) bile duct.

FIGURE 5

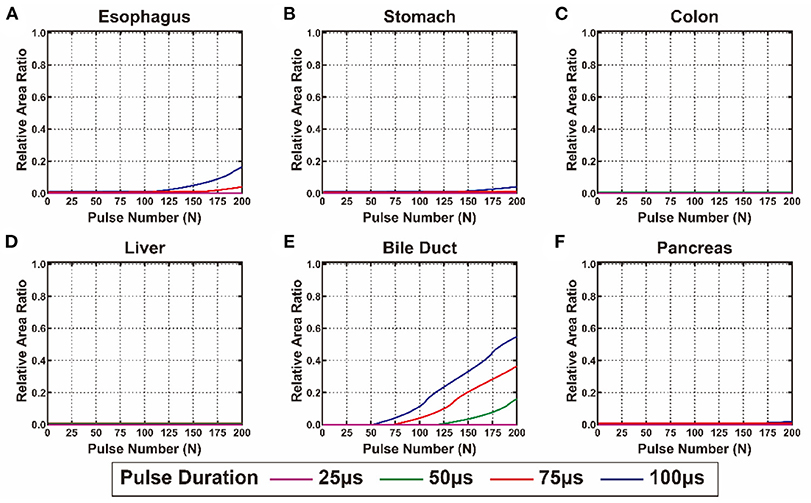
Figure 5. The calculated relative area ratio of the thermal injury to the digestive system. (A) Esophagus, (B) pancreas, (C) stomach, (D) colon, (E) liver, and (F) bile duct.

In terms of TI, there was no substantial TI in the liver and colon when exposed to <200 pulses. For the esophagus, stomach, and pancreas, only slight TI was caused by EPs under the condition of 100 and 75 μs pulse duration. The bile duct is the most heat-sensitive site in the digestive system that presented with high S_TI under the conditions of 50, 75, and 100 μs pulse duration (Figure 5). Supplementary Table 3 summarizes the pulse number required for the occurrence and maximum value of EI and TI of each cell line. For all cell lines, more than 100 pulses were required to reach the maximal S_EI that would cause no TI in the colon and liver and mild TI in the stomach and pancreas. However, under these conditions, TI will occur in the esophagus treated by EPs with 100 μs pulse duration and in the bile duct treated by EPs with 50, 75, and 100 μs pulse duration.

Discussion

In this study, a mathematical model database of cell survival after exposure to EPs from 20 types of human digestive system cell lines was established by in vitro and in silico studies. Moreover, the efficacy of the mathematical model for EBT was evaluated by numerical analysis for both EIs and TIs. This mathematical model database has potential value for theoretical analysis, computational simulation, numerical analysis, and treatment planning to help decision-making for basic research, medical device design, and clinical practice.

The cell survival model showed that cell viability decreased with an increase in pulse voltage, duration, and number, suggesting that the outcome of EPs is closely associated with the total electrical energy of EPs. This finding is consistent with that of Zheng et al., who showed IRE can cause substantial ablation volume in a 3D liver tumor model of Hep-G2 cells (30). In addition, Qi et al. have found that increased pulse number and higher electric field led to lower viability of both murine and human pancreatic cancer cells after IRE, and demonstrated that different cells have different susceptibility to IRE, suggesting the need for careful characterization of IRE response in the given cancer or tissue of interest (31). In this study, it is identical for most of the cell lines that the cell viability was not significantly affected by EPs under low EFS (<1,000 V/cm), and the EPs even exerted a positive effect on cell proliferation. When the EFS was >1,000 V/cm, cell viability was significantly decreased and was lower than 50%, implying that the EPs had a prominent negative effect on cell survival. This result was consistent with that of previous studies that the threshold for RE was lower than 500–800 V/cm in general, and the threshold for IRE was >1,000 V/cm (32). Therefore, selecting the appropriate pulse settings for a specific purpose is critical to the outcome of EBT. Notably, a low EFS promotes cell proliferation as the low intensity of electrical stimulation can promote adaptive proliferation of cancer cells (33).

For tissue ablation, there is general agreement that the EFS should be >1,000 V/cm to achieve IRE (34). However, the lethal effect of EPs is non-linear and cell-specific, implying that cell death due to EPs is an all-or-none phenomenon, and the threshold for electroporation differs between different cells. There is a complex relationship between pulse settings, cell types, and outcomes of cell viability. There are many factors affecting the outcomes of EPs, such as the cell shape, physical and chemical environment, composition of cell membrane, cholesterol content on cell membrane, cytoskeletal structural integrity, cell stiffness, cell volume, and transmembrane voltage (35). The lethal effect of EPs is more than a dose-response relationship because complete cell death relies on the cumulative effect of pulse voltage, duration, and number; thus, it is impossible to completely predict the outcome of EPs using simple pulse settings (32). Therefore, it is necessary to establish a mathematical model to comprehensively characterize the cell electroporation process.

The discrepancy between cancer and normal cells exposed to EPs is a problem worthy of attention (36). In a previous study, Danijela et al. found a disparate response to EPs between cancer and healthy cells (37). They demonstrated that cancer cells are more sensitive to EPs than normal cells, whereas in our study, the current data evidence cannot fully support this theory because there is a lack of an acceptable mathematical indicator to measure the EP sensitivity of a cell line. Nevertheless, the consensus is that cell sensitivity to EPs is determined by multiple factors, and it is possible to adjust the cell environment to promote the killing effect of EPs on cancer cells (35). Therefore, it is necessary to further investigate the mechanism of cell death by electroporation.

The Peleg–Fermi model was first introduced to microbial survival after exposure to PEFs by Peleg (11). This model contains two major factors of pulse settings: EFS and pulse number that can predict the cell survival rate under a specific pulse setting. Golberg et al. compared the performance of several mathematical models for EBT and demonstrated the value of the Peleg–Fermi model for prediction (27). There were two cell-specific coefficients, E_c and A_c that presented the change tendency of cell viability when exposed to EPs at the mathematical level. The E_c value showed a downward trend with the increase in EFS and pulse number, indicating that the EFS required for half lethality of the cells decreased when treated with EPs with enhanced energy. The A_c value showed a similar tendency with E_c, indicating that the decline rate of cell viability caused by EPs was elevated with an increase in EFS and pulse number. The decline in E_c and A_c suggests an elevation of cell death exposed to EPs, which can be deduced from the Peleg–Fermi equation and the results above. In clinical practice, multiple series of EP bursts were performed on tissues for IRE. A total of 100 pulses were commonly set in a single burst of EPs; therefore, the E_c(100) of all cell lines was calculated and compared in this study. For most cell lines, the value of E_c(100) was approximately 500–700 V/cm, which is generally considered as the threshold for electroporation (3).

However, the pulse duration and electric-thermal coupling effect have not been taken into consideration in the Peleg–Fermi model; therefore, the survival rate was only calculated for several given pulse durations, and TI was calculated independently using the Arrhenius equation. Thus, a more accurate and comprehensive model for electroporation needs to be established in future studies. Based on the Peleg–Fermi model, the probability of EI can be calculated for a series of EPs. However, the probability of TI should be considered during electroporation treatment because tissue resistance can induce Joule heating by electrical energy. Therefore, the heat sensitivity of the digestive system was calculated and compared. In this study, there were significant differences between the digestive organs with respect to TI. For example, no TI occurred in the colon and liver, mild TI occurred in the esophagus, stomach, and pancreas, whereas significant TI occurred in the bile duct under the same pulse settings. Thermal injury might be associated with tissue components, blood perfusion rate, and tissue metabolism.

Neven et al. performed IRE on the outer esophageal wall and showed evidence of cell death at 2 days (macroscopically visible lesion) and 60 days (microscopically visible scar). They also found that harmless, self-limiting adverse effect and lasting tissue regeneration occurred during the 60 days follow-up (38). Recently, Song et al. further validated the safety of pulsed field ablation on the esophagus in a rabbit model (39). Our previous studies have confirmed the safety and efficacy of gastric tissue IRE ablation (21, 22). However, the numerical analysis of IRE in the digestive tract was performed based on prostate cancer cells because of the lack of available data for digestive tumors (16). In addition, the bile duct has been treated as heat-sensitive; therefore, TI to the bile duct may result in complications such as bile leaks and bile duct strictures (40). In this study, relatively more TI occurred in the bile duct, suggesting that the electrical energy should be controlled when applied to the bile duct. In our previous study, biliary stricture was found after exposure of the bile duct to EPs in a rabbit model, which was consistent with the findings of a clinical report (24). Biliary stricture may be associated with fibrosis in the mucosal layer, which is easily induced by heating. Our results indicated the necessity of avoiding any risk of collateral injury and precisely determining the pulse settings. Therefore, a numerical analysis is needed for heat-sensitive organs when performing EBT. Thus, herein we provide a survival model database of cell-specific coefficients based on the Peleg–Fermi model for the whole digestive system, which can be used for further application of EBT.

This study has some limitations. First, the cell survival model was established based on in vitro cell experiments that cannot completely reflect the effect of EPs at the tissue level. However, there is still no qualified method for directly evaluating cell activity under EP in vivo. This study can assess the biological effect of EPs on the survival of the digestive system to a large extent, laying a theoretical foundation for future studies. Second, the Peleg–Fermi model contains the EFS, pulse number, and pulse duration without frequency; however, pulse frequency may have a considerable effect on both EIs and TIs. This model may not be suitable for high-frequency EPs. Third, the EI and TI were calculated via the Peleg–Fermi equation and Arrhenius equation; however, there may exist an electrical-thermal coupling effect during electroporation, which needs to be further investigated for a more accurate model. Additionally, normal tissue properties were used to establish the numerical analysis model due to the lack of data from the tumor; therefore, the efficacy of this model needs to be further verified by in vivo studies in the future.

Conclusions

In this study, a mathematical model database for cell survival containing cell-specific coefficients of 20 human digestive cell lines was established based on in vitro cell experiments and in silico analysis. The efficacy of the database was evaluated by numerical analysis of both EIs and TIs of the digestive system. This database can be used for basic research, computational simulation, medical device design, and treatment planning that can predict cell survival and tissue injury distribution after exposure to EPs during EBT.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary materials, further inquiries can be directed to the corresponding authors.

Author contributions

XH and NZ designed the study, performed the related experiment, and wrote and edited the manuscript. YZ, ZL, JZ, XC, and ZQ researched and analyzed the data, helped in writing, and reviewed the manuscript. QL, YW, LM, TH, and YLi helped to perform the related experiments. FR and YLv designed the study and revised the manuscript. All authors have approved the final manuscript.

Funding

This study was supported by National Natural Science Foundation of China (grant no. 81727802), the Fundamental Research Funds for Central Universities (grant no. XJH012020022), the Scientific Development Funding of the First Affiliated Hospital of Xi'an Jiaotong University (2020QN-08), and the Basic Natural Science Research Project of Shaanxi Province (2021JQ-401). The funders had no role in the design of the study and collection, analysis, and interpretation of data and in writing the manuscript.

Acknowledgments

We would like to thank the High-Performance Computing (HPC) Platform of Xi'an Jiaotong University for the support of model construction and numerical analysis.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpubh.2022.948562/full#supplementary-material

Abbreviations

EP, electroporation pulse; EFS, electric field strength; EBT, electroporation-based treatment; RE, reversible electroporation; IRE, irreversible electroporation; EI, electrical injury; TI, thermal injury.

References

1. Yarmush ML, Golberg A, Serša G, Kotnik T, Miklavčič D. Electroporation-based technologies for medicine: principles, applications, and challenges. Annu Rev Biomed Eng. (2014) 16:295–320. doi: 10.1146/annurev-bioeng-071813-104622

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Kotnik T, Frey W, Sack M, Haberl Meglič S, Peterka M, Miklavčič D. Electroporation-based applications in biotechnology. Trends Biotechnol. (2015) 33:480–8. doi: 10.1016/j.tibtech.2015.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Geboers B, Scheffer HJ, Graybill PM, Ruarus AH, Nieuwenhuizen S, Puijk RS, et al. High-voltage electrical pulses in oncology: irreversible electroporation, electrochemotherapy, gene electrotransfer, electrofusion, and electroimmunotherapy. Radiology. (2020) 295:254–72. doi: 10.1148/radiol.2020192190

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Dunki-Jacobs EM, Philips P, Martin RCG. Evaluation of thermal injury to liver, pancreas and kidney during irreversible electroporation in an in vivo experimental model. Br J Surg. (2014) 101:1113–21. doi: 10.1002/bjs.9536

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Kotnik T, Rems L, Tarek M, Miklavčič D. Membrane electroporation and electropermeabilization: mechanisms and models. Annu Rev Biophys. (2019) 48:63–91. doi: 10.1146/annurev-biophys-052118-115451

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Batista Napotnik T, PolajŽer T, Miklavčič D. Cell death due to electroporation – a review. Bioelectrochemistry. (2021) 141:107871. doi: 10.1016/j.bioelechem.2021.107871

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Muratori C, Casciola M, Pakhomova O. Electric pulse repetition rate: sensitization and desensitization. In: Miklavčič D, editor. Handbook of Electroporation. Cham: Springer International Publishing (2017) p. 353–67. doi: 10.1007/978-3-319-32886-7_23

CrossRef Full Text | Google Scholar

8. Weaver JC, Smith KC, Esser AT, Son RS, Gowrishankar TR. A brief overview of electroporation pulse strength-duration space: a region where additional intracellular effects are expected. Bioelectrochemistry. (2012) 87:236–43. doi: 10.1016/j.bioelechem.2012.02.007

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Dermol J, Miklavčič D. Predicting electroporation of cells in an inhomogeneous electric field based on mathematical modeling and experimental CHO-cell permeabilization to propidium iodide determination. Bioelectrochemistry. (2014) 100:52–61. doi: 10.1016/j.bioelechem.2014.03.011

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Dermol J, Miklavčič D. Mathematical models describing chinese hamster ovary cell death due to electroporation in vitro. J Membr Biol. (2015) 248:865–81. doi: 10.1007/s00232-015-9825-6

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Peleg M. A model of microbial survival after exposure to pulsed electric fields. J Sci Food Agric. (1995) 67:93–9. doi: 10.1002/jsfa.2740670115

CrossRef Full Text | Google Scholar

12. Fesmire CC, Petrella RA, Kaufman JD, Topasna N, Sano MB. Irreversible electroporation is a thermally mediated ablation modality for pulses on the order of one microsecond. Bioelectrochemistry. (2020) 135:107544. doi: 10.1016/j.bioelechem.2020.107544

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Van Den Bos W, Scheffer HJ, Vogel JA, Wagstaff PGK, De Bruin DM, De Jong MC, et al. Thermal energy during irreversible electroporation and the influence of different ablation parameters. J Vasc Interv Radiol. (2016) 27:433–43. doi: 10.1016/j.jvir.2015.10.020

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Hall SK, Ooi EH, Payne SJ. A mathematical framework for minimally invasive tumor ablation therapies. Crit Rev Biomed Eng. (2014) 42:383–417. doi: 10.1615/CritRevBiomedEng.2014011825

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Agnass P, van Veldhuisen E, van Gemert MJC, van der Geld CWM, van Lienden KP, van Gulik TM, et al. Mathematical modeling of the thermal effects of irreversible electroporation for in vitro, in vivo, and clinical use: a systematic review. Int J Hyperthermia. (2020) 37:486–505. doi: 10.1080/02656736.2020.1753828

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ren F, Li Q, Gao X, Zhu K, Zhang J, Chen X, et al. Electrical and thermal analyses of catheter-based irreversible electroporation of digestive tract. Int J Hyperthermia. (2019) 36:854–67. doi: 10.1080/02656736.2019.1646928

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Rubinsky J, Onik G, Mikus P, Rubinsky B. Optimal parameters for the destruction of prostate cancer using irreversible electroporation. J Urol. (2008) 180:2668–74. doi: 10.1016/j.juro.2008.08.003

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Yang Y, Moser MAJ, Zhang E, Zhang W, Zhang B. Development of a statistical model for cervical cancer cell death with irreversible electroporation in vitro. PLoS ONE. (2018) 13:e0195561. doi: 10.1371/journal.pone.0195561

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Bhutiani N, Li Y, Zheng Q, Pandit H, Shi X, Chen Y, et al. Electrochemotherapy with irreversible electroporation and FOLFIRINOX improves survival in murine models of pancreatic adenocarcinoma. Ann Surg Oncol. (2020) 27:4348–59. doi: 10.1245/s10434-020-08782-2

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Reddy VY, Neuzil P, Koruth JS, Petru J, Funosako M, Cochet H, et al. Pulsed field ablation for pulmonary vein isolation in atrial fibrillation. J Am Coll Cardiol. (2019) 74:315–26. doi: 10.1016/j.jacc.2019.04.021

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Ren F, Li Q, Hu L, Yan X, Gao Z, Zhang J, et al. Safety and efficacy of magnetic anchoring electrode-assisted irreversible electroporation for gastric tissue ablation. Surg Endosc. (2020) 34:580–9. doi: 10.1007/s00464-019-06800-3

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Zhang Y, Han X, Li Z, Zhang Y, Liang L, Ma X, et al. Physiological and histopathological effects of electroporation pulse on stomach of rats. BMC Gastroenterol. (2021) 21:351. doi: 10.1186/s12876-021-01924-0

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Li Q, Gao X, Zhang Y, Han X, Li Z, Zhang Y, et al. Magnetic anchoring and guidance-assisted endoscopic irreversible electroporation for gastric mucosal ablation: a preclinical study in canine model. Surg Endosc. (2021) 35:5665–74. doi: 10.1007/s00464-020-08245-5

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Li Q, Ren F, Zhang Y, Chang P, Wang Y, Ma T, et al. Acute and subacute effects of irreversible electroporation on normal common bile ducts in a rabbit model. J Hepatobiliary Pancreat Sci. (2020) 27:776–84. doi: 10.1002/jhbp.807

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Pucihar G, Krmelj J, Reberšek M, Napotnik TB, Miklavčič D. Equivalent pulse parameters for electroporation. IEEE Trans Biomed Eng. (2011) 58:3279–88. doi: 10.1109/TBME.2011.2167232

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Sharabi S, Kos B, Last D, Guez D, Daniels D, Harnof S, et al. A statistical model describing combined irreversible electroporation and electroporation-induced blood-brain barrier disruption. Radiol Oncol. (2016) 50:28–38. doi: 10.1515/raon-2016-0009

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Golberg A, Rubinsky B. A statistical model for multidimensional irreversible electroporation cell death in tissue. Biomed Eng Online. (2010) 9:1–9. doi: 10.1186/1475-925X-9-13

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Hasgall PA, Di Gennaro F, Baumgartner C, Neufeld E, Lloyd B, Gosselin MC, et al. Tissue Properties Database V4.0. IT'IS Foundation (2018).

Google Scholar

29. Han X, Zhang N, Zhang Y, Li Z, Wang Y, Mao L, et al. Survival Model Database of Human Digestive System Cells Exposed to Electroporation Pulses. Mendeley Data, V7 (2022).

Google Scholar

30. Fang Z, Mao H, Moser MAJ, Zhang W, Qian Z, Zhang B. Irreversible electroporation enhanced by radiofrequency ablation: an in vitro and computational study in a 3D liver tumor model. Ann Biomed Eng. (2021) 49:2126–38. doi: 10.1007/s10439-021-02734-x

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Shao Q, Liu F, Chung C, Elahi-Gedwillo K, Provenzano PP, Forsyth B, et al. Physical and chemical enhancement of and adaptive resistance to irreversible electroporation of pancreatic cancer. Ann Biomed Eng. (2018) 46:25–36. doi: 10.1007/s10439-017-1932-3

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Jiang C, Davalos RV, Bischof JC. A review of basic to clinical studies of irreversible electroporation therapy. IEEE Trans Biomed Eng. (2015) 62:4–20. doi: 10.1109/TBME.2014.2367543

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Love MR, Sripetchwandee J, Palee S, Chattipakorn SC, Mower MM, Chattipakorn N. Effects of biphasic and monophasic electrical stimulation on mitochondrial dynamics, cell apoptosis, and cell proliferation. J Cell Physiol. (2018) 234:816–24. doi: 10.1002/jcp.26897

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Shankara Narayanan JS, Ray P, Hayashi T, Whisenant TC, Vicente D, et al. Irreversible electroporation combined with checkpoint blockade and TLR7 stimulation induces antitumor immunity in a murine pancreatic cancer model. Cancer Immunol Res. (2019) 7:1714–26. doi: 10.1158/2326-6066.CIR-19-0101

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Kim HB, Lee S, Shen Y, Ryu PD, Lee Y, Chung JH, et al. Physicochemical factors that affect electroporation of lung cancer and normal cell lines. Biochem Biophys Res Commun. (2019) 517:703–8. doi: 10.1016/j.bbrc.2019.07.119

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Pakhomova O, Gianulis EC, Pakhomov AG. Different cell sensitivity to pulsed electric field. In: Miklavčič D, editor. Handbook of Electroporation. Cham: Springer International Publishing (2017). p. 337–52. doi: 10.1007/978-3-319-32886-7_22

CrossRef Full Text | Google Scholar

37. Cvetković DM, Živanović MN, Milutinović MG, Djukić TR, Radović MD, Cvetković AM, et al. Real-time monitoring of cytotoxic effects of electroporation on breast and colon cancer cell lines. Bioelectrochemistry. (2017) 113:85–94. doi: 10.1016/j.bioelechem.2016.10.005

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Neven K, Van Es R, Van Driel V, Van Wessel H, Fidder H, Vink A, et al. Acute and long-term effects of full-power electroporation ablation directly on the porcine esophagus. Circ Arrhythm Electrophysiol. (2017) 10:1–8. doi: 10.1161/CIRCEP.116.004672

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Song Y, Zheng J, Fan L. Nonthermal irreversible electroporation to the esophagus: evaluation of acute and long-term pathological effects in a rabbit model. J Am Heart Assoc. (2021) 10:1–13. doi: 10.1161/JAHA.120.020731

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Dupuy DE, Goldberg SN. Image-guided radiofrequency tumor ablation: challenges and opportunities-part II. J Vasc Interv Radiol. (2001) 12:1135–48. doi: 10.1016/s1051-0443(07)61670-4

PubMed Abstract | CrossRef Full Text | Google Scholar