Commentary: Statistical Modeling for the Prediction of Infectious Disease Dissemination With Special Reference to COVID-19 Spread

A Commentary on
Statistical Modeling for the Prediction of Infectious Disease Dissemination With Special Reference to COVID-19 Spread

by Yadav, S. K., and Akhter, Y. (2021). Front. Public Health. 9:645405. doi: 10.3389/fpubh.2021.645405

This commentary builds upon the recent study of Subhash Kumar Yadav and Yosuf Akhter entitled “Statistical Modeling for the Prediction of Infectious Disease Dissemination With Special Reference to COVID-19 Spread” published in Frontiers in Public health. The study describes the basics of the mathematical epidemiology of infectious diseases. The study attempted to introduce a history of epidemic modeling and pointed out some standard methods of modeling. After careful reading of the study, we identified erroneous definitions in multiple sections other than typos.

In sections “SI and SIS Models” and “SIR and SIRS Models,” the authors define β as an infectious rate and further write β as a chance, which is a misinterpretation of β. Additionally, in section “SI With Vital Dynamics,” the authors again wrongly define β as a rate of infection. Precisely, β is the per capita rate at which two different individuals come in effective contact per unit time (1). It neither refers to a chance or probability of infection nor is an infection rate. For a correct definition of infection rate in detail, please refer to the book (2), page number 127. To understand the basic difference between contact rate and transmission rate, we can use following simple SI model.

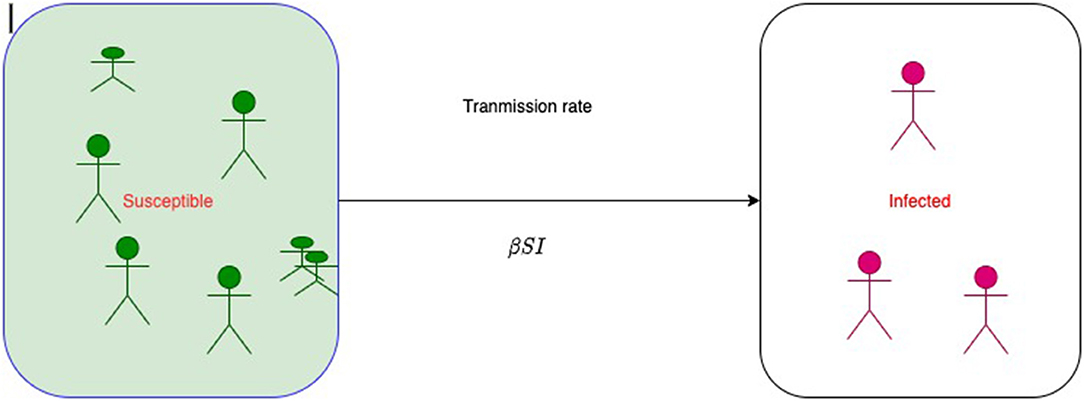
Figure 1 represents a simple SI model, where S is the size of susceptible class and I is the size of infected class at time t. At the beginning of infection, the size of susceptible class decreases; therefore, the size of infected class increases. Then, at time t + 1, the size of susceptible will be

$S_{t+1}=S_t-{\lambda }_t{S}_t$

where λ_t is called the force of infection or the risk of infection at time t and it varies with time. In 1906, W.H. Hamer postulated that the transmission of infection should depend on the number of susceptible individuals, the number of infective individuals, and the contact rate between them. So, the net rate of transmission of infection is proportional to the multiplication of the product of the density of susceptible and the density of infected. This statement has been recognized as a mass action principle in epidemiology and is a base of modern mathematical epidemiology and compartment models of infectious diseases. Therefore, λ_t = βI_t. Authors mistakenly write β as probability of infection or transmission probability as it does not follow the basic probability axioms. βSI is called transmission rate or an instantaneous rate from S to I, and it is not a chance or probability.

FIGURE 1

Figure 1. A simple SI model without demography. β is per capita contact rate.

In section, “The Distribution Fitting,” the authors mentioned that the infectious disease mainly depends on two factors, namely, the number of carriers and the time of infections. This line is very vague, especially for readers and definitely, and it needs improvements in terms of context writing. The possible context might be the infectious disease transmissibility, where the contagiousness of a pathogen depends on the chance of infection (infectivity), duration of infectiousness, and effective contact rates. Therefore, the authors should explain the context and the frame of the sentence with their biological interpretations.

In the section of “The Basic Reproduction Number,” the authors defined the basic reproduction number and the factors it depends on. Further, the authors wrote that R₀ is a unit-free quantity (without dimension of measurement), which is correct. However, in the following line, the authors used the word reproductive rate, which is inconsistent and confusing. Many prominent researchers in the epidemic modeling have suggested that the terms “reproductive rate” or “reproduction rate” are wrong because the estimation of R₀ does not involve time as a function of it. Moreover, in the compartmental model, the reproduction number R₀ can be calculated by using next-generation matrix method (NGMM) (3).

We define a matrix G that comprises two matrices F and V⁻¹ as follows,

$F=\left[\frac{\partial F_i(x_0)}{\partial x_j}\right]$

and

$V=\left[\frac{\partial V_i(x_0)}{\partial x_j}\right]$

where F_i is the new infections, while the V_i is the transfers of infections from one compartment to another. x₀ is the disease-free equilibrium state. The dominant eigenvalue of G = FV⁻¹ is R₀. In NGMM, the dominant eigenvalue does not represent any rate. However, it is very common to see such key-words as rates in routine publications and in even some books. If R₀ was a rate involving time, the measure would provide information about how fast an epidemic will spread through a population. More details, on how R₀ is not a rate but is a pure number, can be read in some highly influencing studies (4, 5). There are numerous inconsistencies in the name of reproduction number (4); therefore, we suggest authors at least follow a specific name (either rate or number) consistently throughout the study to avoid confusions for readers.

In section, “SIR and SIRS Models,” the authors mentioned “The SIRS model ξ represents the transmission rate from recovered to susceptible state because of decay in immunity” (page number 9), where ξ is an instantaneous rate from recovery class to susceptible class, and this line needs to be corrected, because ξ is a model parameter not the model.

In the section, “Further Suggestions and Future Prospectives,” the authors put a couple of suggestions, especially on sample size issues in modeling. It is vital in inferential statistics to incorporate the sample size effect on parameter estimation (sample size must be appropriately calculated). However, this compulsion can be avoided for the epidemic curve-based models using serial interval data and disease incidence. This means, to model short-term infections (SARS, MERS, and Influenza), some preamble methodologies do not have any assumptions about the sample size (6–8). To estimate the reproduction number of such short-term infection using epidemic curve-based models, we do not make any assumptions on sample size but it requires some assumptions on growth rate (6, 7, 9, 10). For example, if a school children get infected by COVID-19 and infects some other students of the class within few days and infection grows, we can estimate R0 and other parameters (β, γ) by doing model fitting even for small number of time series data without violating any model assumptions. Therefore, authors need to present specific models/methods that are significantly affected by sample size before generalizing the recommendations.

Author Contributions

HD drafted the manuscript and SG approved the final version the manuscript. Both authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank editor and reviewer of this commentary article.

References

1. Keeling MJ, Rohani P. Modeling Infectious Diseases in Humans and Animals. Princeton: NJ: Princeton University Press (2011).

2. Hartge P. A Dictionary of epidemiology, SIXTH EditionEdited by Miquel Porta. Am J Epidemiol. (2015) 181:633–4. doi: 10.1093/aje/kwv031

CrossRef Full Text | Google Scholar

3. Diekmann O, Heesterbeek JAP, Metz JAJ. On the definition and the computation of the basic reproduction ratio R 0 in models for infectious diseases in heterogeneous populations. J Math Biol. (1990) 28:365–82. doi: 10.1007/BF00178324

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Delamater PL, Street EJ, Leslie TF, Yang YT, Jacobsen KH. Complexity of the basic reproduction number (R0). Emerg Infect Dis. (2019) 25:1–4. doi: 10.3201/eid2501.171901

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Jones JH. Department of Anthropological Sciences, Stanford University. Technical report, California (2007).

6. Wallinga J. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Am J Epidemiol. (2004) 160:509–16. doi: 10.1093/aje/kwh255

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Cori A, Ferguson NM, Fraser C, Cauchemez S. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am J Epidemiol. (2013) 178:1505–12. doi: 10.1093/aje/kwt133

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Thompson RN, Stockwin JE, van Gaalen RD, Polonsky JA, Kamvar ZN, Demarsh PA, et al. Improved inference of time-varying reproduction numbers during infectious disease outbreaks. Epidemics. (2019) 29:100356. doi: 10.1016/j.epidem.2019.100356

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Dhungana HN. Comments on "Preliminary estimation of the basic reproduction number of novel Coronavirus (2019-nCoV) in China, from 2019 to 2020: a data-driven analysis in the early phase of the outbreak". Int J Infect Dis. (2020) 94:72–3. doi: 10.1016/j.ijid.2020.02.024

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Dhunagna HN, Ghimire S. Modelling of reproduction number for COVID-19 in India and high incidence states. Clin Epidemiol Glob Health. (2021) 9:85–6. doi: 10.1016/j.cegh.2020.07.004

PubMed Abstract | CrossRef Full Text | Google Scholar